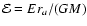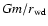In what follows it is convenient to represent different energy scales in dimensionless form. There are two natural units of energy per unit mass in our problem: the first associated the stellar cusp - GM/r_a and the second associated with the internal structure of star itself - $Gm/r_{\rm wd}$ . For the dimensionless quantities expressed in terms of the first unit we will use the calligraphic style while the quantities expressed in terms of the second unit will be denoted by tilde.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

Note that it is important to distinguish between the effect of emission of gravitational waves by perturbations of the white dwarf and the effect of emission of gravitational waves due to the orbital motion of the star. The former effect is important as a major process of mode energy loss while the latter significantly influences the orbital evolution and may provide a source of gravitational waves during the late stages of orbital evolution, see below.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... form

A more accurate expression has been derived in IP. See also this paper for the references on numerical and analytical studies of the stochastic instability.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...)

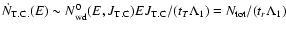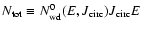Note an alternative form of Eq. (38) has already been provided in other studies, see e.g. Hopman $\&$ Alexander (2005), their Eq. (17) and references therein. To obtain this we write $\dot N_{\rm T.C.}(E)\sim N^{0}_{\rm wd}(E,J_{\rm T.C})EJ_{\rm T.C}/(t_{T}\Lambda_{1})= N_{\rm tot} /(t_{r} \Lambda_{1})$ , where $N_{\rm tot}\equiv N^{0}_{\rm wd}(E, J_{\rm circ})J_{\rm circ}E$ characterises the total number of stars having binding energies per unit mass of order of E, we introduce the global relaxation time scale 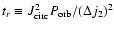$t_{r}\equiv J^{2}_{\rm circ}P_{\rm orb}/(\Delta j_{2})^{2}$ and use Eqs. (2), (4) and (35).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

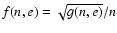
... $f(n,e)=\sqrt{g(n,e)}/n$

Note a misprint in Appendix of Peters $\&$ Mathews (1963) in their expression for g(n,e). The fifth term in the braces must contain the factor (4/e)² contrary to the factor (4/e²)² as in the text.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...H

Note that the average number of globular clusters is meaningful only when 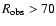$R_{\rm obs} > 70$ Mpc, where 70 Mpc is a typical distance between the elements of the Large Scale Structure in the Universe.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.