A&A 475, 991-1002 (2007)
DOI: 10.1051/0004-6361:20078267
S. Frandsen1 - H. Bruntt1,2 - F. Grundahl1,3 - G. Kopacki4 - H. Kjeldsen1,3 - T. Arentoft1,3 - D. Stello2 - T. R. Bedding2 - A. P. Jacob2 - R. L. Gilliland5 - P. D. Edmonds6 - E. Michel7 - J. Matthiesen1
1 - Department of Physics and Astronomy, University of Aarhus,
Ny Munkegade, Bygn. 520, 8000 Aarhus, Denmark
2 -
School of Physics A28, University of Sydney, 2006 NSW, Australia
3 -
Danish AsteroSeismology Center (DASC), University of Aarhus, 8000 Aarhus, Denmark
4 -
Institute of Astronomy, University of Wroc![]() aw, Poland
aw, Poland
5 -
Space Telescope Science Institute, Baltimore, USA
6 -
Center for Astrophysics, Cambridge, MA, USA
7 -
Observatoire de Paris, Meudon, France
Received 13 July 2007 / Accepted 10 August 2007
Abstract
Context. To expand the range in the colour-magnitude diagram where asteroseismology can be applied, we organized a photometry campaign to find evidence for solar-like oscillations in giant stars in the globular cluster M 4.
Aims. The aim was to detect the comb-like p-mode structure characteristic for solar-like oscillations in the amplitude spectra. The 24 main target stars are in the region of the bump stars and have luminosities in the range 50-140
![]() .
.
Methods. We collected 6160 CCD frames and light curves for about 14 000 stars were extracted. The frames consist of exposures in the Johnson B, V and R bands and were obtained at three different telescopes. Three different software packages were applied to obtain the lowest possible photometric noise level. The resulting light curves have been analysed for signatures of oscillations using a variety of methods.
Results. We obtain high quality light curves for the K giants, but no clear oscillation signal is detected. This is a surprise as the noise levels achieved in the amplitude spectra should permit oscillations to be seen at the levels predicted by extrapolating from stars at lower luminosities. In particular, when we search for the signature of oscillations in a large number of stars we might expect to see common features in the power spectra, but even here we fall short of having clear evidence of oscillations.
Conclusions. High precision differential photometry is possible even in very crowded regions like the core of M 4. Solar-like oscillations are probably present in K giants, but the amplitudes are lower than classical scaling laws predict. The reasons may be that the lifetime of the modes are short or the driving mechanism is relatively inefficient in giant stars.
Key words: stars: oscillations - stars: activity - techniques: photometric - methods: observational - stars: evolution
Asteroseismology has made great progress in
recent years due to improved observational techniques.
Extremely stable spectrographs have been designed
to detect exo-planets through Doppler shifts.
These instruments have allowed the unambiguous
detection of p-modes in about a dozen solar-type stars
(for a review see Bedding & Kjeldsen 2007).
Although most results have been
obtained for main-sequence and subgiant stars, some giant stars have also been
shown to oscillate: ![]() Hya (G7III; Frandsen et al. 2002),
Hya (G7III; Frandsen et al. 2002),
![]() Oph (G9.5III; De Ridder et al. 2006a; Barban et al. 2007),
and
Oph (G9.5III; De Ridder et al. 2006a; Barban et al. 2007),
and ![]() Ser (K0III; Barban et al. 2004).
Unambiguous detection of p-modes has so far been restricted to field
stars in our immediate neighbourhood.
Ser (K0III; Barban et al. 2004).
Unambiguous detection of p-modes has so far been restricted to field
stars in our immediate neighbourhood.
Döllinger et al. (2005) found that field stars show radial velocity and photometric variability, which seems to increase with increasing luminosity. This could either be due to a combination of activity and granulation, or to pulsations, either self-excited (Mira-like) or driven by convective motions (solar-like). Similar evidence for increased variability has been found for stars in the globular cluster 47 Tucanae (Edmonds & Gilliland 1996).
Stellar clusters present a highly interesting prospect, due to the large number of stars collected in a limited field of view and additional constraints from cluster properties, such as relative age, metallicity, and evolutionary stage. Gilliland et al. (1993) were the first to make a search for solar-like oscillations in the main sequence F-type stars in the open cluster M 67. However, based on their multi-site campaign using 4-m class telescopes they made no clear detection. Recently, another campaign was carried out on the same cluster (Stello et al. 2006b,2007), this time concentrating on stars on the lower part of the giant branch, where larger oscillation amplitudes are expected.
Knowing that p-modes are excited in giant stars, we decided to study K giants in the globular cluster M 4. The two main reasons are that M4 has a rich population of K giants (see Fig. 2) and the amplitudes are expected to be substantially higher than for subgiants. If we could measure the gross properties of the oscillations, such as amplitudes and the large splitting characteristic for solar-like oscillations, we could potentially study an ensemble of giant stars in different evolutionary stages.
According to the empirical calibration by Kjeldsen & Bedding (1995),
oscillation amplitudes scale as
![]() .
For the K giants
in M 4, taking the solar amplitude as 4.7 ppm (parts per million),
we expect amplitudes in the range 400-1000 ppm.
The noise level we expected to reach
in the amplitude spectra for the bright
giant stars was
.
For the K giants
in M 4, taking the solar amplitude as 4.7 ppm (parts per million),
we expect amplitudes in the range 400-1000 ppm.
The noise level we expected to reach
in the amplitude spectra for the bright
giant stars was ![]() 25 ppm at high frequencies.
This would allow us to detect any excess power, and possibly
the comb-like structure of the p-modes, in the amplitude spectra
for the brightest and least crowded targets.
However, the mode frequencies decrease with luminosity
and approach a range where noise caused by extinction and
transparency changes is difficult to eliminate in ground-based data.
25 ppm at high frequencies.
This would allow us to detect any excess power, and possibly
the comb-like structure of the p-modes, in the amplitude spectra
for the brightest and least crowded targets.
However, the mode frequencies decrease with luminosity
and approach a range where noise caused by extinction and
transparency changes is difficult to eliminate in ground-based data.
CCD frames were obtained with the Danish 1.54 m telescope at La Silla, the 1.5 m telescope at Cerro Tololo Inter-American Observatory (CTIO), both in Chile, and the 1 m telescope at the Siding Spring Observatory (SSO) in Australia. The observations took place over a period of almost three months, in order to get the necessary frequency resolution. We started at La Silla on April 13, 2001 and got the last data on June 27, 2001. We obtained useful data on 48 nights out of an allocation of 63 nights. Some nights had overlap between Australia and Chile, which we used to check the consistency of the photometric results. Table 1 gives a list of the collected dataset. In total we have 6160 CCD frames of M 4 (4014 from La Silla, 863 from CTIO, and 1283 from SSO). The time distribution is represented in Fig. 1, which includes 31 nights from La Silla, 6 nights from CTIO, and 11 nights from SSO.
To help identify the modes, we observed in three filters: B, V and R. Amplitude ratios between different colours can indicate which types of modes are present. To enhance the signal-to-noise ratio, the data can still be combined using an approximate scaling (Eq. (8)), since phase differences of p-modes between filters are small. About equal time was allocated to the three filters, giving more frames in R due to the shorter exposure times.
Table 1: Observing log for the M 4 campaign in 2001.
| |
Figure 1: Distribution of nights for the three observing sites. The time baseline is 78 days. |
| Open with DEXTER | |
The exposure times were adjusted to give the best results for stars in the range 12.5 < V < 13.5, which is the area of the RGB bump in M 4, as seen in Fig. 2. This meant typical exposure times at La Silla and CTIO of less than one minute in V and R and a few minutes in B, depending on seeing conditions. Exposure times at SSO were 2-4 min in V and 1-2 min in R. On average, this led to a mean duty cycle around 50%, since the readout time was 1-2 min.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{8267fg2.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg16.gif) |
Figure 2: The colour-magnitude diagram for M 4, showing the bump stars and part of the horizontal branch. The colours and magnitudes have been calibrated using the database provided by Stetson (2007). To show the range covered, some of the stars selected for a detailed analysis are indicated and labeled with the ID - see Table 2. |
| Open with DEXTER | |
The images were first calibrated by performing traditional bias subtraction and flat-fielding. In order to avoid nightly offsets, calibration frames were constructed for periods of several days, typically a week, and the same calibration frames were used for all images in that period. This point is quite important since the timescale of variability for the giant targets is in the range 9-31 h (see Sect. 5.1).
CCD non-linearity was considered, and in the case of the La Silla data it was corrected using the technique described by Stello et al. (2006b). The other cameras did not provide the same option for a correction and were assumed to be linear. We have not seen any evidence for non-linearity and, since we were able to find comparison stars with similar magnitudes in all cases, the influence of non-linearity should be negligible.
In Fig. 3 we present the calibrated CCD image that has been used as the reference image for the La Silla observations of M 4. The 24 K giant stars we selected for a detailed analysis are marked by boxes.
![\begin{figure}
\par\includegraphics[width=14.7cm,clip]{8267fg3.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg19.gif) |
Figure 3:
The field of M 4 observed with the Danish 1.54 m telescope at La Silla.
The 24 K giants we analysed in detail are marked by squares.
The center of the field is at
|
| Open with DEXTER | |
In order to achieve the highest possible photometric precision, we decided to use three different reduction programs, all of which have been successful in the past in producing high quality results: ISIS, DAOPHOT and MOMF. In the most crowded areas we expected ISIS (Alard & Lupton 1998; Alard 2000) to give the best results. In the less crowded areas we expected that DAOPHOT (Stetson 1987) would do best. Finally, we know that MOMF (Kjeldsen & Frandsen 1992) performs very well in fields with only mild crowding. All frames were reduced with ISIS and DAOPHOT and a subset of the V frames from La Silla were reduced with MOMF. Each of the three methods will be described in Sects. 3.1-3.3 and we compare the results in Sect. 3.4.
The main advantage of the difference-image technique is the ability to extract high precision photometry in the crowded regions near the core of M 4. In addition, any variations in airmass and transparency are removed to first order as a part of the image subtraction.
The image subtraction method ISIS (Alard & Lupton 1998; Alard 2000) was used by two members of the team independently ( ISIS1 and ISIS2). For each filter and each observing site we selected the images with the best seeing to make the reference images. While ISIS2 only used a single reference image for each site and filter, ISIS1 used subsets of data from about one week.
For each observed image, we computed a kernel which describes the variations of the PSF across the image relative to the reference image. We then convolved the reference image with the kernel and subtracted this from the observed image. The resulting difference image will contain the signal that is intrinsically different from the reference image, e.g., cosmic ray hits, hot pixels, and variable stars.
In the first approach ( ISIS1) only La Silla and CTIO data were included (Bruntt 2003). They were divided into five subsets and reduced separately. The reason for this was large differences in the positional angle of the CCD camera between different periods. We had problems using the photometry package that is part of ISIS. Instead, we modified the aperture photometry routine in DAOPHOT in order to be able to run it on the subtracted images, in particular allowing negative flux values. The necessary modifications were described in detail by Bruntt et al. (2003). ISIS needs a reference flux for each star, since only the change in the flux is calculated. This was taken from the DAOPHOT reduction of the reference images.
In the second reduction approach ( ISIS2), we constructed only one reference frame for each observing site and passband. The original ISIS software does not work correctly with frames that are significantly rotated with respect to the reference frame. The problem resides in the interpolation process and we used our own application, which performs this task correctly even for large rotation angles but requires much more computation time. For all stars detected in the reference frames (for all three observing sites), we derived differential fluxes from our CCD frames following standard procedures of ISIS reductions (for details see Kopacki 2000). We performed both the PSF fitting and aperture photometry on the difference frames. To transform differential fluxes into magnitudes we used total fluxes measured in the reference frames using aperture photometry tasks NEDA+ DAOGROW under DAOPHOT. Finally, all the data were merged into a uniform magnitude system by applying magnitude offsets determined from a carefully chosen set of bright unsaturated stars common to all three observing fields. In this way, the CTIO and SSO data were transformed into the magnitude scale of the La Silla data.
For this reduction we used the suite of photometry programs developed by Stetson (1987, 1990, 1994): DAOPHOT, ALLSTAR and ALLFRAME. The general use of these is well described in manuals and the literature. For our applications we adopted a slightly modified procedure, as follows. Firstly, a few of the deepest and best-seeing frames were used to produce a master list of stars, which was obtained by several iterations through DAOPHOT, ALLSTAR and ALLFRAME. Next, all frames were run through DAOPHOT/ ALLSTAR once. With the preliminary photometry in hand, positional transformations between each frame and our reference frame were derived using DAOMATCH and DAOMASTER (kindly provided by P. Stetson).
From the frames used to derive the master star list, we created two lists of stars
for generating the PSF for the individual images. The
first list contained ![]() 10 stars that were well isolated and these were used
to generate the first version of the PSF for each frame. Next the
second list, containing
10 stars that were well isolated and these were used
to generate the first version of the PSF for each frame. Next the
second list, containing ![]() 200 stars covering the observed field, was
used to generate the final PSF. We used this PSF when running ALLFRAME on all
the images to produce the final photometry.
We cross-identified all stars in the photometry files
and selected the brightest 7000 for further analysis.
200 stars covering the observed field, was
used to generate the final PSF. We used this PSF when running ALLFRAME on all
the images to produce the final photometry.
We cross-identified all stars in the photometry files
and selected the brightest 7000 for further analysis.
As an independent test we used the MOMF package (Kjeldsen & Frandsen 1992) on the La Silla images to derive time series in the V band. The reduction had to be done in a slightly different way than normal because the La Silla images were slightly rotated relative to each other. MOMF can only handle shifts and so introduced an additional coordinate transformation, changing the (x,y) coordinates for each image before doing photometry. For stars outside the very crowded regions, results were comparable to the other techniques. We conclude that we reach similar results for non-crowded regions by all of the techniques.
Our database contains photometry from the three different reduction methods and comprises light curves of 13 611 stars with up to 6160 data points. We also store information about each frame such as seeing, airmass, background level, the mid-time of each observation (Julian date), and position on the reference frame of each star. The data can be accessed at the web page http://astro.phys.au.dk/~srf/M4/.
The rms scatter in the light curves is plotted versus magnitude for relatively good and bad nights in Figs. 4 and 5, respectively. These results are based on the ISIS1 photometry in the V-band. For the bad night, the noise is considerably larger than the good night for all stars. The higher noise is due to high sky background as a result of the close proximity of the Moon to M 4. The lower envelope of stars for the good night is close to the expected precision based on the flux level (indicated by the solid line). We find a number of stars with rms scatter as low as 1.5 mmag. For the K giants the level is typically about 2 mmag per data point. The bump stars are found around V=13.5, where we obtain the lowest noise levels.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{8267fg4.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg21.gif) |
Figure 4:
The rms scatter around the mean for a good
night with the Danish 1.54 m telescope, for the ISIS1 reduction.
The red open squares give the noise
level for the final time series for the selected K giants in which
we have looked for solar-like oscillations.
The line indicates the noise expected from scintillation and
photon statistics.
The stars with high scatter near V=13.3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{8267fg5.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg22.gif) |
Figure 5: Same as Fig. 4, but for a bad night that was characterized by very a large sky background due to moon light. |
| Open with DEXTER | |
As shown in Fig. 5, some nights do not give good results, with noise levels considerably higher than the majority of the data. Naturally, the noise per data point depends on the level of exposure per frame. This will vary as we had to adjust the exposure time to avoid saturation. In good seeing we obtained fewer photons per frame due to smaller stellar images. Also, when cirrus clouds were present we did not increase exposures times too much, to avoid over-exposed images from occasional holes in the clouds.
We have investigated in which conditions the photometry was worse than expected from photon noise alone. To do this we considered the ISIS1 photometry of stars from La Silla. We selected an ensemble of 19 bright stars and calculated their average scatter per night. The average flux for the ensemble was also derived and converted to a magnitude. One good night was chosen as the reference and the magnitude for that night was subtracted from the magnitudes for all other nights.
The measured rms scatter is plotted against the magnitude for all the nights in Fig. 6.
If only photon noise were present the scatter
should follow the solid line in Fig. 6, i.e., following the
relation:
![]() .
.
Most of the nights follow this law, but there are exceptions. Nights with a high sky background clearly stand out as having poorer photometric precision (diamonds in Fig. 6). A second problem arises when the seeing is very good because the images are under-sampled (triangles in Fig. 6).
An important issue is whether any of the three reduction techniques are superior. In general, we find similar results for the different techniques. However, MOMF is clearly not suited for crowded fields and only performs as well as ISIS and DAOPHOT for a small fraction of stars. The quality of the DAOPHOT photometry is comparable to the ISIS results, although ISIS is superior in the most crowded areas. We also find the best results with ISIS for faint stars, especially on nights with bad seeing. This is shown in Fig. 7, where we compare the rms scatter in data from one bad night from La Silla using DAOPHOT (left panel) and ISIS (right panel). The rms noise of the K giant stars is 40% lower for the ISIS reduction.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{8267fg6.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg24.gif) |
Figure 6: The mean rms scatter per data point per night, plotted against the nightly mean flux level in the exposures represented by a corresponding magnitude difference between each night and a reference night. The filled symbols indicate two nights with very few observations. The over-plotted diamonds indicate nights with a high sky level and the triangles show nights with very good seeing. The rms uncertainty is marked for each point. |
| Open with DEXTER | |
It is possible that with a more careful choice of PSF stars and other parameters involved in the DAOPHOT reductions, it may be possible to improve these results. The optimum choice of parameters for good observing conditions might not be the best for frames obtained under non-photometric conditions.
A final illustration of the differences between the algorithms is presented in Fig. 8. Here, the rms scatter is presented for three different reductions: ISIS1, ISIS2 and DAOPHOT. Each point is for a particular star and the symbols define which reduction technique was being used. It is evident that none of the techniques produce the best results in all cases, although the image subtraction method ISIS1 has been the most successful.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{8267fg7.eps}\hspace*{5mm}
\includegraphics[width=6.7cm,clip]{8267fg8.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg25.gif) |
Figure 7: The mean scatter per data point per night for night 14 for the DAOPHOT ( left panel) and ISIS1 reduction ( right panel). The line gives the noise level for a good night (see Fig. 4). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{8267fg9.eps}\hspace*{4mm}
\includegraphics[width=6.9cm,clip]{8267fg10.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg26.gif) |
Figure 8: The rms noise level in K giant stars for La Silla data from two different nights. The noise level from the three reduction methods is similar for most stars, but in a few cases the DAOPHOT and ISIS2 noise levels are higher than for ISIS1. |
| Open with DEXTER | |
The time series from each observatory show different characteristics due to different observing conditions, telescopes and detector setups. At SSO the seeing was considerably worse, leading to more extended stellar images. This led to increased noise as a result of the higher influence of the background level, which is worse for fainter stars. This effect is shown in Fig. 9. The CTIO data are heavily influenced by the presence of the Moon close to the target field, particularly in the middle of the run, and this makes the data of rather poor quality. The results can be characterized by the rms noise per data point for a non-crowded K giants for the three sites on a good night: 1.6 mmag for La Silla, 3.0 mmag for CTIO and 2.1 mmag for SSO.
The outcome of the previous section is either absolute or differential
magnitudes. In both cases, it is necessary to make
differential photometry by comparing each target star
with a set of reference stars.
The effects of extinction, instrumental drifts and other sources
of non-stellar noise need to be
minimized for us to study any stellar signal at frequencies
below 30 ![]() Hz, corresponding to periods longer than 9 h.
The approach is described in the following sections.
Hz, corresponding to periods longer than 9 h.
The approach is described in the following sections.
An ensemble of reference stars was used to derive the relative magnitudes for all stars, in order to remove transparency and extinction variations. In M 4 there is a wide range of possibilities for choosing reference stars. However, the results depend strongly on the method used to calculate the ensemble average.
The algorithm we employed was the following:
for a given target star, a number of reference stars were selected,
which were required to have similar V magnitude and B-V colour to the target and
be within a certain distance (e.g., half the size of the CCD).
We calculated the magnitude difference between the target star and each reference star
for a whole observing block (![]() d)
and subtracted the median value, producing a time series
d)
and subtracted the median value, producing a time series
![]() ,
where the index i indicate the reference star.
,
where the index i indicate the reference star.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{8267fg11.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg29.gif) |
Figure 9: The rms noise levels in data from a good night at SSO. DAOPHOT is doing significantly worse than ISIS2. Notice the increased noise at faint magnitudes relative to the photon noise estimate (solid curve). |
| Open with DEXTER | |
We then did an analysis night by night.
For each night, the rms noise
![]() of each
of each
![]() time series
was calculated and a weight assigned using
time series
was calculated and a weight assigned using
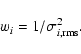 |
(1) |
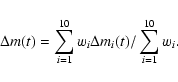 |
(2) |
Instrumental drifts and reduction noise may introduce correlations between the measured magnitudes and parameters such as the colour of the star, position on the CCD airmass and sky background. We found no clear correlations and so no decorrelation was performed.
The result from the procedures described in Sect. 4.1 is a set of light curves from the three sites in three filters: B, V and R. In our search for solar-like oscillations in the K giants, we assumed that phase shifts between observations in different filters are small (Jiménez et al. 1999). We also assumed that the oscillation amplitudes scale inversely with wavelength as Eq. (8) and we therefore scaled the B and R time series relative to the V filter: scaling factors were 1.222 and 0.846. The weights, described in the next subsection, were also scaled with the inverse factor following Eq. (4).
Table 2: The 24 K giants selected for detailed analysis. First block provides IDs and basic observational parameters. Second block gives stellar parameters. Third block presents the predicted asteroseismic parameters using Eqs. (5)-(8).
Due to the changes in observing conditions, there is a large variation in the data quality from night to night. It is therefore essential to apply weights when the Fourier spectra are calculated.
As a first step we removed obvious outliers. All points that
deviated by more than 5![]() from the mean were discarded.
Weights were then calculated for each star by combining
a weight for each night with a weight based on the point-to-point scatter.
Each night received a weight of
from the mean were discarded.
Weights were then calculated for each star by combining
a weight for each night with a weight based on the point-to-point scatter.
Each night received a weight of
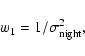 |
(3) |
The point-to-point weights were calculated by first fitting a spline
to an averaged time series with a smoothing width of ![]() 0.075 d and
subtracting this from the data. The noise level,
0.075 d and
subtracting this from the data. The noise level,
![]() ,
at any each point time was then
the average rms calculated using a Gaussian with a width of 0.05 d.
The weight was chosen as the inverse of the noise level:
,
at any each point time was then
the average rms calculated using a Gaussian with a width of 0.05 d.
The weight was chosen as the inverse of the noise level:
The final weight was the product of w1 and w2. A maximum weight (4 times the mean weight) was set to avoid nights with very few points being given very high weight.
We selected 24 K giants for a detailed analysis. The stars are found in the least crowded parts of M 4 and cover a range in luminosity on both sides of the bump stars. We selected stars with an rms scatter in the time series below 4 mmag. We list their ID numbers, standard V magnitude and B-V colour in Table 2. The positions of some of the stars in the colour-magnitude diagram are shown in Fig. 2 and their positions in the cluster are marked with squares in Fig. 3.
To calculate L/
![]() ,
,
![]() and R/
and R/
![]() for the targets, we used cluster parameters from
Ivans et al. (1999) for M 4: distance d = 2.1 kpc, reddening
E(B-V) = 0.37,
interstellar absorption
AV = 4.0E(B-V), metal content [Fe/H] = -1.2,
bolometric correction
BC = -0.48 and mass
for the targets, we used cluster parameters from
Ivans et al. (1999) for M 4: distance d = 2.1 kpc, reddening
E(B-V) = 0.37,
interstellar absorption
AV = 4.0E(B-V), metal content [Fe/H] = -1.2,
bolometric correction
BC = -0.48 and mass
![]() .
As pointed out by Ivans et al. (1999), the reddening varies across the cluster.
These parameters lead to a distance modulus of
(m-M)V=13.1.
This compares reasonably well with the mean magnitude of the RR Lyrae
stars (Kopacki & Frandsen 2007)
in the range 13.2-13.3, which have absolute magnitude
.
As pointed out by Ivans et al. (1999), the reddening varies across the cluster.
These parameters lead to a distance modulus of
(m-M)V=13.1.
This compares reasonably well with the mean magnitude of the RR Lyrae
stars (Kopacki & Frandsen 2007)
in the range 13.2-13.3, which have absolute magnitude
![]() .
The uncertainty of the cluster parameters introduces a
.
The uncertainty of the cluster parameters introduces a
![]() 10% uncertainty in the luminosities.
10% uncertainty in the luminosities.
![\begin{figure}
\par\includegraphics[width=13.1cm,clip]{8267fg12.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg52.gif) |
Figure 10:
Power spectra for the 12 K giants with the lowest noise at high frequencies.
The luminosities of the stars increase from left to right and bottom to top.
The predicted location of the maximum p-mode power and the acoustic cutoff frequency
(indicated by thick black lines) shift to lower frequencies with increasing luminosity.
Frequencies at multiples of 11.57 |
| Open with DEXTER | |
We have estimated the amplitude and frequency that is expected
for solar-like oscillations in each target.
We used the following scaling relations for the
frequency separation,
![]() ,
the expected
location of p-mode maximum frequency,
,
the expected
location of p-mode maximum frequency,
![]() ,
and the
acoustic cutoff frequency,
,
and the
acoustic cutoff frequency,
![]() :
:
The light curves were analysed using the Fourier analysis program
PERIOD98 (Sperl 1998). In Fig. 10 we show the
power spectra computed from the light curves using weights (see Sect. 4.4).
The spectra of these 12 K giants cover a range in luminosity
from 50 to 140
![]() ,
increasing from left to right and bottom to top.
,
increasing from left to right and bottom to top.
In general the white noise increases as the stars become fainter but
some stars have significantly higher noise than expected,
which may indicate the presence of a close neighbouring star
or an unidentified instrumental problem.
The noise levels in the amplitude spectra lie in the range 60-100 ppm
at 81-104 ![]() Hz (white noise), increasing to 100-140 ppm at 23-46
Hz (white noise), increasing to 100-140 ppm at 23-46 ![]() Hz.
With this low noise level we would expect to detect
oscillations if the amplitudes follow the extrapolations used in Sect. 5.1
(see Table 2), provided the mode lifetime is not as short as the few days found
by Stello et al. (2006a). Stochastic excitation often gives rise to higher than
average amplitudes for observing periods that do not exceed
the lifetimes by large factors.
Hz.
With this low noise level we would expect to detect
oscillations if the amplitudes follow the extrapolations used in Sect. 5.1
(see Table 2), provided the mode lifetime is not as short as the few days found
by Stello et al. (2006a). Stochastic excitation often gives rise to higher than
average amplitudes for observing periods that do not exceed
the lifetimes by large factors.
The highest peaks below the acoustic cutoff frequency
![]() range from
200 to 400 ppm in the spectra plotted in Fig. 10. We cannot claim
that they are real, since the signal-to-noise is low (S/N < 4) in all cases.
In a few stars we see suggestive evidence of power in the expected range (#181, #228 and #229)
that does not coincide with multiples of 1 c/d, but due to the low S/Nwe cannot claim to have detected p-modes.
range from
200 to 400 ppm in the spectra plotted in Fig. 10. We cannot claim
that they are real, since the signal-to-noise is low (S/N < 4) in all cases.
In a few stars we see suggestive evidence of power in the expected range (#181, #228 and #229)
that does not coincide with multiples of 1 c/d, but due to the low S/Nwe cannot claim to have detected p-modes.
The observing window will introduce frequency spacings that may be mistaken for those characteristic of solar-like oscillations. Note that the spectral window is slightly different for each star because the applied weights vary from star to star.
In Fig. 11 we show the autocorrelation function of
the spectral window for star #181. This is representative and
gives an idea of the effect of the complicated
spectral window, which is due to gaps in the time series.
The autocorrelation function has a very pronounced peak
at 11.57 ![]() Hz due to the daily side lobes. In addition, a
strong peak at
Hz due to the daily side lobes. In addition, a
strong peak at ![]() 0.81
0.81 ![]() Hz is seen.
The origin of the peak is found in the observing schedule,
where dark time was not allocated to the project (Fig. 1).
When searching for the presence of the large separation using
the autocorrelation technique, this will give rise to extra peaks.
For a few stars the window function shows a more complex
pattern giving rise to even more peaks in the autocorrelation.
This will considerably reduce our ability to see clear evidence of
stellar signal oscillations (see Sect. 7.1).
Hz is seen.
The origin of the peak is found in the observing schedule,
where dark time was not allocated to the project (Fig. 1).
When searching for the presence of the large separation using
the autocorrelation technique, this will give rise to extra peaks.
For a few stars the window function shows a more complex
pattern giving rise to even more peaks in the autocorrelation.
This will considerably reduce our ability to see clear evidence of
stellar signal oscillations (see Sect. 7.1).
![\begin{figure}
\par\includegraphics[width=6.25cm,clip]{8267fg13.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg58.gif) |
Figure 11:
The autocorrelation of the spectral window for star #181.
The vertical lines indicate peaks at 11.57, 5.84 and 0.81 |
| Open with DEXTER | |
We note that some of the observed excess peaks in the amplitude spectra
are close to multiples of 1 c/d (11.57 ![]() Hz),
as indicated by the vertical dashed lines in Fig. 10.
These peaks are probably due to residual effects of extinction.
In some light curves a peak in the range
Hz),
as indicated by the vertical dashed lines in Fig. 10.
These peaks are probably due to residual effects of extinction.
In some light curves a peak in the range ![]() = 0.8-0.9
= 0.8-0.9 ![]() Hz was
also detected, which is probably caused by the spectral window (see Sect. 6.2).
Therefore, following the approach of Stello et al. (2006b),
we subtracted low-frequency peaks down to S/N>4.
We specify below whether we used the raw or the cleaned
spectra (see Sect. 7).
Hz was
also detected, which is probably caused by the spectral window (see Sect. 6.2).
Therefore, following the approach of Stello et al. (2006b),
we subtracted low-frequency peaks down to S/N>4.
We specify below whether we used the raw or the cleaned
spectra (see Sect. 7).
In Fig. 12 we show an example of the process for star #66.
Daily alias variations are seen in the amplitude spectrum in
panel (a). Panel (b) is the amplitude spectrum after
subtracting two peaks indicated by the vertical tick marks in panel (a).
Panel (c) is the spectral window, which shows quite strong and complex sidelobes.
The white noise level is ![]() 60 ppm and
is calculated as the mean level in the frequency range 81-104
60 ppm and
is calculated as the mean level in the frequency range 81-104 ![]() Hz.
Hz.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{8267fg14.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg60.gif) |
Figure 12:
Amplitude spectra for star #66, which is the brightest, non-saturated star
in the subsample chosen for detailed analysis.
Panel a) is the raw spectrum with one low frequency
peak and a peak close to 2 c/d (23.14 |
| Open with DEXTER | |
To facilitate the interpretation of the observations in Sect. 7 we made simulations of the light curves. The time sampling and the noise properties are the same as for the observations and they include a known oscillation signal.
To mimic the noise we used the observed time series of two stars assuming that they resembled pure noise. The two stars (#66 and #292) are at either end of the luminosity range of the selected K giants. Both are among the K giant stars with the lowest noise in the amplitude spectra. The two stars show no clear evidence of power excess or a frequency separation that could arise from stellar oscillations.
We used different input amplitudes and mode lifetimes, using the simulation software described by De Ridder et al. (2006b) and Stello et al. (2004).
Inspection of the K giant amplitude spectra in Fig. 10
reveals that the noise increases towards low frequencies,
indicating that drift noise is present in the light curves.
This will seriously hamper the interpretation of the signal below ![]() 20
20 ![]() Hz.
We see no clear evidence of excess power or the comb-like pattern
expected for solar-like oscillations in any of the K giants.
We do find clear evidence for an increase in excess power
towards low frequencies, but it is not possible to disentangle drift
noise from variations intrinsic to the K giant stars
due to granulation or p-modes.
Hz.
We see no clear evidence of excess power or the comb-like pattern
expected for solar-like oscillations in any of the K giants.
We do find clear evidence for an increase in excess power
towards low frequencies, but it is not possible to disentangle drift
noise from variations intrinsic to the K giant stars
due to granulation or p-modes.
We have used two techniques to look for evidence of p-modes in the amplitude spectra:
Clear evidence for stellar oscillations would be a
systematic behaviour in the observed frequency separations.
The separation should increase with decreasing luminosity (Eq. (5)).
In a few cases the autocorrelation shows a peak that could
be indicative of the large separation. A prominent peak
is seen in star #181, as shown in Fig. 13, where there is
a peak at 2.75 ![]() Hz (predicted to be at 2.55
Hz (predicted to be at 2.55 ![]() Hz).
The highest peak at
Hz).
The highest peak at ![]() 0.9
0.9 ![]() Hz (vertical dashed line)
is due to the window function (see Fig. 11)
The autocorrelation was done on the raw spectrum.
We find a few other stars with peaks in the autocorrelation spectrum
that might come from the presence of a p-mode spectrum, but in
the majority of cases we are not able to find a single prominent peak.
Hz (vertical dashed line)
is due to the window function (see Fig. 11)
The autocorrelation was done on the raw spectrum.
We find a few other stars with peaks in the autocorrelation spectrum
that might come from the presence of a p-mode spectrum, but in
the majority of cases we are not able to find a single prominent peak.
![\begin{figure}
\par\includegraphics[width=6.25cm,clip]{8267fg15.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg62.gif) |
Figure 13:
The autocorrelation of the raw power spectrum for
the giant star #181. Vertical lines represent peaks in the window function.
The peak at 2.75 |
| Open with DEXTER | |
We made several simulations of stars #66 and #292 with various mode amplitudes and
lifetimes, as described in Sect. 6.4.
We used two methods to search for the known large separations of the inserted modes.
The first was a simple autocorrelation while
the second involved cutting the spectrum in small pieces and adding these
together (forming a collapsed echelle diagram). The latter method is
described by Christensen-Dalsgaard et al. (2007).
Both methods gave similar results.
For oscillations with a Q![]() value
above 200, the correct large frequency separation
value
above 200, the correct large frequency separation
![]() was recovered in both stars
for amplitudes down to 400 ppm.
was recovered in both stars
for amplitudes down to 400 ppm.
![\begin{figure}
\par\includegraphics[width=5.35cm,clip]{8267fg16.eps}\vspace*{5mm}
\includegraphics[width=5.35cm,clip]{8267fg17.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg63.gif) |
Figure 14:
Autocorrelation of a simulation of star #292 including oscillations.
In the top panel the spectrum of #292 was cleaned for multiples of 1 c/d before
adding the simulated signal and in the bottom panel, the same procedure was followed as for the observed time series data. The red dotted lines correspond to multiples of the large separation in the simulated signal. The blue vertical lines indicate parasitic peaks
from the window function at 0.85 and 11.57 |
| Open with DEXTER | |
In Fig. 14 we show the autocorrelation for star #292
after adding simulated oscillations with large separation 2.83 ![]() Hz,
amplitude A = 400 ppm and lifetime
Hz,
amplitude A = 400 ppm and lifetime ![]() = 32 d.
We note that this lifetime is at least a factor two longer than expected.
In the upper panel the spectrum of #292 was first cleaned for multiples of 1 c/d before adding the simulated signal. The autocorrelation clearly shows several peaks that correspond
to multiples of the large separation present in the simulated signal (red dotted lines).
The blue, dot-dash, vertical lines indicate aliases from peaks
in the spectral window at 0.85 and 11.57
= 32 d.
We note that this lifetime is at least a factor two longer than expected.
In the upper panel the spectrum of #292 was first cleaned for multiples of 1 c/d before adding the simulated signal. The autocorrelation clearly shows several peaks that correspond
to multiples of the large separation present in the simulated signal (red dotted lines).
The blue, dot-dash, vertical lines indicate aliases from peaks
in the spectral window at 0.85 and 11.57 ![]() Hz (see Fig. 11).
In the lower panel of Fig. 14, the procedure applied
to the observed time series data was followed (see #181 in Fig. 13).
In this case, the input large separation is much harder to recover.
Hz (see Fig. 11).
In the lower panel of Fig. 14, the procedure applied
to the observed time series data was followed (see #181 in Fig. 13).
In this case, the input large separation is much harder to recover.
For the bright star (#66) the large separation is recovered for large Q values (>30) for inserted amplitudes as low as A = 200 ppm. However, if the lifetime is shorter than ![]() 16 days (Q < 12), we find that it is not possible to recover the input separation in any of the
simulated series, even with amplitudes up to 800 ppm.
Thus, our upper limits of 200-400 ppm only hold if the lifetime
is greater than two weeks, as predicted by Houdek & Gough (2002)
and Houdek (2006), and not a few days as
found by Stello et al. (2006a).
16 days (Q < 12), we find that it is not possible to recover the input separation in any of the
simulated series, even with amplitudes up to 800 ppm.
Thus, our upper limits of 200-400 ppm only hold if the lifetime
is greater than two weeks, as predicted by Houdek & Gough (2002)
and Houdek (2006), and not a few days as
found by Stello et al. (2006a).
To search for excess power we followed the approach used by
Stello et al. (2007) in their analysis of K giants
in the open cluster M 67. The K giant stars in M 4 were divided into three groups
with luminosities around 60, 80, and 130
![]() (fainter, medium and brighter stars).
For each group we calculated a mean raw amplitude spectrum.
To demonstrate the effect of cleaning, we also
produced a mean cleaned spectrum for the faint group.
(fainter, medium and brighter stars).
For each group we calculated a mean raw amplitude spectrum.
To demonstrate the effect of cleaning, we also
produced a mean cleaned spectrum for the faint group.
In Fig. 15 we show the mean spectra. The raw spectra for the three groups of stars are quite similar, with prominent peaks near multiples of 1 c/d. This is unexpected and suggests that the power seen possibly is dominated by a noise component due to instrumental drift in the data.
Using the simulations described in Sect. 6.4, we probed our ability to identify an inserted oscillation signal. The black, solid spectrum in Fig. 15 is based on a mean of four time series of star #292 with the addition of simulated p-modes with lifetimes in the range 2-8 days and peak amplitudes of A=400 ppm per mode. These values cover the range of expected lifetimes, and averaging four simulations removes some of the stochastic features of the oscillations. This artificial spectrum clearly lies above any of the observed mean spectra. Our conclusion is that excess power from p-modes with amplitudes A > 300 ppm would show up clearly in our observed spectra.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{8267fg18.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg66.gif) |
Figure 15:
Average smoothed spectra for three groups of observed K giants
with luminosity
|
| Open with DEXTER | |
We have compared our results for the K giants in M 4 with 3D hydrodynamical simulations of granulation by Svensson & Ludwig (2005). They modelled the effect of granulation using simulations of the convective motions in a box, which was scaled to predict observations of a spherical star. The results of Svensson & Ludwig (2005) indicate that K giants should have a low-frequency component of granulation power, similar to the levels achieved for some of the K giants in M 4.
One of their simulations (Ludwig 2006; kindly provided by G. Ludwig)
is shown as the dotted black curve in Fig. 16.
The stellar parameters are
![]() ,
,
![]() ,
,
![]() = 4560 K, and metallicity [M/H] = 0.0. This corresponds to a luminosity
= 4560 K, and metallicity [M/H] = 0.0. This corresponds to a luminosity
![]() ,
which is
larger by roughly a factor two than the brightest K giants we have observed.
The larger luminosity means that the simulated granulation
has larger amplitudes and excess power at lower frequencies than for our brightest target.
,
which is
larger by roughly a factor two than the brightest K giants we have observed.
The larger luminosity means that the simulated granulation
has larger amplitudes and excess power at lower frequencies than for our brightest target.
A scaling of the solar power spectrum has been attempted by Kjeldsen & Bedding (in preparation) and by Stello et al. (2007). A white noise component with the same level as the star chosen for comparison (#66) is added to a scaled granulation signal and a scaled p-mode spectrum. The scaling is very crude, and a difference of a factor two from our K giants would not be surprising. The granulation spectrum is shown in a logarithmic plot of power density in Fig. 16.
The simulated spectrum (black dotted line) and the scaled spectrum (blue dashed line) both
show a larger power density at low frequencies than the observations (red solid line).
The peak of the observed spectrum coincides with the
peak around 10 ![]() Hz of the scaled spectrum, in which the power is due
to the presence of oscillations. In the observed spectrum it is likely
to be the 1 c/d alias.
Hz of the scaled spectrum, in which the power is due
to the presence of oscillations. In the observed spectrum it is likely
to be the 1 c/d alias.
Note that the 3D simulation (black dotted line) falls below the other curves at high frequencies
because no white noise was included. The excess power at low frequencies in the 3D simulations is because the luminosity of the simulation model is twice that of star #66.
The amplitude of the power density should scale with L2 and the frequency
with L-1, which will bring the 3D simulations closer to the other
curves, but still above the observations.
Svensson and Ludwig (2005) showed that lowering the metallicity in a
1
![]() model makes the power density drop considerably. The low metallicity of the cluster M 4 might explain the discrepancy between the observations and the 3D simulations.
model makes the power density drop considerably. The low metallicity of the cluster M 4 might explain the discrepancy between the observations and the 3D simulations.
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{8267fg19.eps} \end{figure}](/articles/aa/full/2007/45/aa8267-07/Timg71.gif) |
Figure 16: Power density for three cases: 1) the observed star #66 (red, solid line), 2) a scaled power spectrum including granulation, p-modes with A = 300 ppm and white noise as star #66 (blue, dashed line), 3) the simulation by Svensson and Ludwig (2005) (black, dotted line). |
| Open with DEXTER | |
We have presented results for a three-site multi-colour photometric campaign on the globular cluster M 4. We used data in the Johnson ![]() bands from 48 nights with a time baseline of 78 days.
bands from 48 nights with a time baseline of 78 days.
We compared the precision of the photometry obtained from three different photometric packages. In the most crowded parts of the field we found the best results using a difference image analysis (Alard 2000), while classical aperture photometry gave better results in the semi-crowded regions. The best photometry was found for stars not affected by crowding, in which case we achieved noise levels close to the theoretical limit.
The main goal of the campaign was to detect solar-like oscillations in the rich population of K giant stars in M 4. However, we are not able to claim an unambiguous detection and we summarize our conclusions here:
For the population II star ![]() Indi, which has a low luminosity (6
Indi, which has a low luminosity (6
![]() ),
p-modes have been detected (Bedding et al. 2006; Carrier et al. 2007).
While we cannot tell whether the stochastic driving still works in population II stars around
),
p-modes have been detected (Bedding et al. 2006; Carrier et al. 2007).
While we cannot tell whether the stochastic driving still works in population II stars around
![]() ,
we can say it cannot be very efficient and certainly does
not exceed amplitudes expected from the
(L/M)0.7 scaling relation
suggested by Samadi et al. (2007). This is contrary to the conclusion for the K giants in M 67 by Stello et al. (2007), who found indications of p-mode power
in stars at lower luminosities (10-20
,
we can say it cannot be very efficient and certainly does
not exceed amplitudes expected from the
(L/M)0.7 scaling relation
suggested by Samadi et al. (2007). This is contrary to the conclusion for the K giants in M 67 by Stello et al. (2007), who found indications of p-mode power
in stars at lower luminosities (10-20
![]() ). They found better agreement between observations and predictions if the amplitudes scale as L/M. Their noise level at low frequencies did
not permit any statement for stars at luminosities similar to the
stars investigated in M 4. It remains an open question whether the stochastic driving still
works in population II K giants.
). They found better agreement between observations and predictions if the amplitudes scale as L/M. Their noise level at low frequencies did
not permit any statement for stars at luminosities similar to the
stars investigated in M 4. It remains an open question whether the stochastic driving still
works in population II K giants.
Based on the results obtained from large multi-site campaigns on M 67 and M 4, it seems difficult to get conclusive positive results about the stochastic oscillations and the granulation from ground-based photometry. Improvements can be made, but extinction and other atmospheric effects will always be a limiting factor, especially at the timescales of the K giants. It is also difficult to get a clean window function due to changing weather patterns for campaigns lasting several weeks, which are needed to study solar-like oscillations in K giant stars.
If a new campaign is organized we recommend using a single filter, since colour information is not likely to be of a quality that can lead to mode identification. We found no use for the differences between the filters and we recommend that the V filter is used in the future; the B filter observations show strong colour-dependent extinction and the amplitudes will be very low in R.
From the ground, one would do better by organizing a long-term radial velocity campaign. One immediate advantage is that the noise from granulation is 10 times lower in velocity (Grundahl et al. 2007, their Fig. 1). One could observe several K giants during the night since the time scale of the oscillations is several hours. A dedicated network providing good time coverage would be needed in order to obtain a clean window function. The proposed SONG network (Grundahl et al. 2007) is an example of such a programme.
For rapidly rotating stars, where the broad spectral lines prevent precise velocity measurements, observations of solar-like oscillations can be made with photometry from space. Giants are among the targets for the new photometric satellite missions like CoRoT (Baglin et al. 2006) and the future Kepler mission (Christensen-Dalsgaard et al. 2007). The CoRoT mission observes each field for up to 150 days while the Kepler mission will cover many more targets in a single field for up to six years.
Acknowledgements
This work was supported by the Danish National Research Council and the Australian Research Council.