A&A 475, 791-799 (2007)
DOI: 10.1051/0004-6361:20065218

A 12 ${\mu }$m ISOCAM survey of the ESO-Sculptor field

Data reduction and analysis

N. Seymour^1,2 - B. Rocca-Volmerange^1,3 - V. de Lapparent¹

1 - Institut d'Astrophysique de Paris, UMR7095 CNRS / Univ. Pierre & Marie Curie, 98 bis boulevard Arago, 75014 Paris, France
2 - Spitzer Science Center, California Institute of Technology, Mail Code 220-6, 1200 East California Boulevard, Pasadena, CA 91125, USA
3 - Université Paris-Sud, Bât. 121, 91405 Orsay Cedex, France

Received 16 March 2006 / Accepted 24 May 2007

Abstract
We present a detailed reduction of a mid-infrared 12 ${\mu }$m (LW10 filter) ISOCAM open time observation performed on the ESO-Sculptor Survey field (Arnouts et al. 1997, A&AS, 124, 163). A complete catalogue of 142 sources (120 galaxies and 22 stars), detected with high significance (equivalent to 5$\sigma$), is presented above an integrated flux density of 0.24 ${\rm mJy}$. Star/galaxy separation is performed by a detailed study of colour-colour diagrams. The catalogue is complete to 1 ${\rm mJy}$ and, below this flux density, the incompleteness is corrected using two independent methods. The first method uses stars and the second uses optical counterparts of the ISOCAM galaxies; these methods yield consistent results. We also apply an empirical flux density calibration using stars in the field. For each star, the 12 ${\mu }$m flux density is derived by fitting optical colours from a multi-band $\chi^2$ to stellar templates (BaSel-2.0) and using empirical optical-IR colour-colour relations. This article is a companion analysis to our 2007 paper (Rocca-Volmerange et al. 2007, A&A, 475, 801) where the $12~\hbox{$\mu {\rm m}$ }$ faint galaxy counts are presented and analysed per galaxy type with the evolutionary code PÉGASE.3.

Key words: infrared: galaxies - Galaxy: evolution - methods: data analysis - catalogs - galaxies: photometry

1 Introduction

Deep infrared surveys performed with ISOCAM (Cesarsky et al. 1996) aboard ESA's ISO satellite (Kessler et al. 1996) have greatly increased our knowledge of the faint IR background (e.g. Aussel et al. 1999). From dust emission, the mid-infrared (MIR) is an ideal wavelength domain for studying the fundamental process of star formation at cosmological distances. There is also evidence of a strong evolution of sources in the MIR, including recent results from ISO and Spitzer satellites (Pozzi et al. 2004; Appleton et al. 2004). However, progress in this area has been complicated by technical difficulties in reducing the ISOCAM data. Despite the recent advances of Spitzer, there is still a great deal of information to be extracted from the ISOCAM data.

When examining faint sources with ISOCAM, to be confident in the reliability of a source, one must make certain to have removed all sources of flux variation above the background noise which are not due to astronomical objects. Principle amongst these are "glitches'' caused by cosmic ray impacts on the SiGa detector. There is additional transient behaviour comprising long-term transients that are effectively slow variations in the background and short-term transients that occur when a pixel moves on and off a source causing an upward or downward transient respectively. This memory effect is an unfortunate property of the type of detectors available when ISOCAM was developed. The temporal shape of this lagged response after a flux step has been corrected by a technique developed by Abergel et al. (1996), which successfully removes transients due to strong sources or changes in illumination. Then the software developed by Starck et al. (1999) known as PRETI (Pattern REcognition Technique for ISOCAM data) was designed to identify and remove the other artifacts due to cosmic rays effects and residual low-frequency variations.

The ultimate flux density calibration of ISOCAM has also been the subject of much research. Great care is not only needed to distinguish real astronomical sources from other transient effects in the detectors, but also to calculate the true flux density of these objects. A detailed analysis of the behaviour of the detector was applied to ISO observations of the Hubble Deep Field (HDF), which used the LW2 ( $6.75~\hbox{$\mu {\rm m}$ }$) and LW3 ( $15~\hbox{$\mu {\rm m}$ }$) filters (Aussel et al. 1999) and was found to be successful at removing most types of transients significantly above the noise. Although largely consistent at bright flux densities, the results of this analysis are considerably different at fainter flux densities from those previously derived by Serjeant et al. (1997) from the same observations. (There is, however, reasonable consistency with another analysis of Désert et al. 1999.) The method of Aussel et al. (1999) involved PRETI identifying and correcting the cosmic rays effects, as well as removing the low-frequency variation of the background left after applying the Abergel method; many simulations were performed to test the completeness and flux density calibration of these data. Another approach, which is empirical and does not depend on simulations, is that of Efstathiou et al. (2000), who used stars to calibrate their ISOPHOT $90~\hbox{$\mu {\rm m}$ }$ survey. Väisänen et al. (2002) and Oliver et al. (2002) also used stars to calibrate their ISOCAM LW2 and LW3 observations. Likewise, Clements et al. (1999) used observations of stars to verify their flux density calibration.

Over the past few years, the Lari method (Lari et al. 2001) has been successfully applied to other surveys (Gruppioni et al. 2002; Pozzi et al. 2003; Vaccari et al. 2005). This technique involves a full analysis of the history of each pixel and much simulation. We did not use this method in our desire to avoid simulations, but we note that several of these papers (Gruppioni et al. 2002; Vaccari et al. 2005), as well as the more recent work of Rodighiero et al. (2004), use the well-known IR properties of normal stars to verify their flux density calibration.

Here, we present ISOCAM observations that were designed to cover the portion of the ESO-Sculptor faint galaxy redshift survey (ESS; Arnouts et al. 1997) that is least affected by the cirrus confusion noise. The ISOCAM area was selected using the IPAC/IRSKY software that measured a mean sky flux density of 18.78 mJy/arcmin² at $12~\hbox{$\mu {\rm m}$ }$ and a rms of 5.42 mJy/arcmin²; these values were measured in 1.5 arcmin pixels in a large field of view of 90' $\times$ 90' centred on the ESS field. We also estimate the colour excess as 0.014<E_B-V<0.022 on the survey area (Schlegel et al. 1998). The ESO-Sculptor Survey is located close to the South Galactic Pole and covers a strip of approximately 0.24 $\times$ $1.53\deg=0.37$ deg² with CCD photometry complete to Johnson-Cousins B=24.5, V=24.0, and $R_{\rm c}=23.5$. The ESS also provides a nearly complete redshift sample to $R_{\rm c}=20.5$(de Lapparent et al. 2003,2004) over a sub-region of 0.24 $\times$ $1.02\deg = 0.25$ deg². The ISOCAM-ESS survey thus provides a unique complement to the other existing surveys in its combination of i) $\sim$700 square arcminute sky area, ii) $BVR_{\rm c}$ CCD photometry and NIR (DENIS and 2MASS) photometry, and iii) spectroscopic completeness to $R_{\rm c}=20.5$.

In the following, we present the data reduction and calibration of the ISOCAM-ESS survey. The observations were performed with the $\sim$ $12~\hbox{$\mu {\rm m}$ }$ LW10 ISOCAM filter, which was designed to have a similar passband to the IRAS $12~\hbox{$\mu {\rm m}$ }$ band. This similarity allows us to take advantage of the flux density calibration of the IRAS data. In Sect. 2, we first describe the adopted procedure for source extraction (Sect. 2.1) and astrometry (Sect. 2.2). This analysis is followed by the flux density re-calibration in Sect. 3. We provide the complete source catalogue in Sect. 4.

   
2 Observations and data reduction

The ISOCAM observations consist of 10 overlapping raster observations arranged in a 5 $\times$ 2 configuration centred on RA (J2000) 00$^{\rm h}$22$^{\rm m}$23.06$^{\rm s}$ and Dec (J2000) $-30^\circ$04'55.65''. Each of the 10 rasters is composed of $M\times N$ pointings (with M=N=8) of the long wavelength (LW) detector of ISOCAM, each offset by ${\rm d}M={\rm d}N=60''$ along the axis of the detector. Table 1 gives the target name, coordinates, observation number (ION), calculated on-target time (CoTT), number of stabilizing exposures ( $N_{\rm stab}$), and number of exposures ( $N_{\rm exp}$) for each raster pointing. Table 2 shows the parameters, which were constant for all observations. Each pointing of the 32 $\times$ 32 pixel detector used the 6'' pixel field of view (PFOV) mirror so that the detector's view at each pointing was a 192'' $\times$ 192'' area of the sky. The total field of view of the ISOCAM survey is therefore approximately 0.3 $\times$ 0.8 deg² intersecting over $\sim$$80\%$ of the ESS spectroscopic area. For ISO observations, it was not possible to request a particular orientation of the camera. In the event, our observations were performed at $\sim$$45\deg$ to the axes of the 5 $\times$ 2 arrangement of the observations (see Fig. 1).

This arrangement left four very small patches of $\sim$20'' diameter unobserved by ISOCAM, which are aligned at the middle declination of the ISO pointings Dec(J2000) $-30^\circ 04'50''$ and have the following values of RA(J2000): $0^{\rm h}23^{\rm m}15.4^{\rm s}$, $0^{\rm h}22^{\rm m}40.2^{\rm s}$, $0^{\rm h}22^{\rm m}5.2^{\rm s}$, $0^{\rm h}22^{\rm m}30.2^{\rm s}$ (these 4 patches are barely visible in Fig. 1).

Table 1: ISO observation log for 10 raster pointings.

Table 2: ISO observation parameters common to all rasters.

	Figure 1: Signal-to-noise map (shown as contours) of the 10 ISOCAM rasters overlaying a gray-scale image from the Digitized Sky Survey, with the $12~\mu$m detected sources marked by crosses. The declination $\delta$ (J2000) ticks range between $-29^\circ 54'$ and $-30^\circ 14'$. The right ascension $\alpha$ ticks range between $00^{\rm h}24^{\rm m}$ and $21^{\rm h}00^{\rm m}$.
Open with DEXTER

We used the latest version of the original raw data files obtained from the ISO Data Archive, corresponding to the 10 raster pointings with the most up-to-date FITS header information. The data reduction was largely done with the ISOCAM Interactive Users Analysis System, called CIA (Ott et al. 1997).

At this stage, PRETI (Starck et al. 1999) was run within the CIA/IDL environment to remove the cosmic rays effects and residual variation of the background, after subtracting the transients, to perform the flat correction and to suppress the time-varying baseline. We used the transient correction for the on-source detector response as described in Abergel et al. (1996). The flux density of each pixel may be converted from ADUs to ${\rm mJy}$ using the conversion given in CIA: 1 ADU = $0.242~{\rm mJy}$. (More details are given in Sect. 3 on the flux density calibration.) The 64 independent pointings of each raster were then projected onto the sky allowing for the known distortion of the sky due to the optics of ISOCAM.

Although the original pixel size of the individual exposures was 6'', each raster image was finely re-sampled to 2'' in order to increase the accuracy of the sky projection. Finally, the 10 raster pointing images were combined on the sky plane producing an image map and a map of the associated rms error at each pixel (henceforth referred to as the "noise'' map). The final pixel size of these maps, from the re-projection of the ten raster images, was chosen to be 3'' as a compromise between retaining the accurate high resolution of the sky projection and possibly lightly over-sampling the PSF whose FWHM is of order of the original 6'' pixels. We note that some additional correlated noise and potential small positional errors may be introduced by a second re-sampling of the image.

2.1 Source extraction

ISOCAM observations require specifically designed source extraction algorithms, as the noise in raster data is correlated and varies across the field. This effect is especially noticeable near the edge of a raster where there are fewer readouts per sky position. As a result, the border regions of the survey are noisier than the central part. One must therefore use the corresponding "noise'' map to determine the significance level of a source and to avoid false detections on the border of the survey.

In order to extract the ISOCAM faint sources of the ESS field, we used the multi-scale vision model (MVM, Rué & Bijaoui 1996) as applied to ISOCAM data of the Hubble Deep Field by Starck et al. (1999). This code is implemented in their Multi-Resolution (MR) software. This method searches for objects on different scales in wavelet space using the so-called "à trous'' algorithm. We refer the reader to Starck et al. (1999) for full details.

We apply the Multi-Resolution software with a detection threshold of $5\tau _{\rm w}$ where $\tau_{\rm w}$ is the noise level in wavelet space and is not directly equivalent to the dispersion of Gaussian data, but gives a qualitative idea of the significance of our detection. The ultimate limit to the detection of sources is the rate at which false detections occur due to residual glitches in the noise, which are too faint to be removed by PRETI. Starck et al. (1999) performed simulations to assess the reliability of their data and obtained a $2\%$ false detection rate at the completeness limit ( $5\tau _{\rm w}$). Here we choose to perform the simple test of applying the source extraction to the negative of our sky image for different thresholds. We detect no sources in the negative images above $4.5\tau_{\rm w}$. Hence we believe our detections to be quite robust, although we cannot quantify our false detection rate. We note, though, that we find optical counterparts to all our $12~\hbox{$\mu {\rm m}$ }$ sources covered by the ESS within 6'' and with R<25 (see Sect. 3). If randomly distributed we would have expected only $30\%$ to have had optical counterparts within 6''.

Using the MRDETECT task from MR with a PSF model sampled at 3'' and a detection threshold of $5\tau _{\rm w}$, we search for objects down to the 4th wavelet scale and obtain 142 sources to a detection limit of $\sim$ $0.24~{\rm mJy}$. This limit corresponds to the integrated flux density, reconstructed by the wavelet detection program, of the faintest object detected. The final source catalogue, after astrometry and flux density re-calibration, is presented in Sect. 4.

With the final goal of validating the adopted extraction method suited to raster data with ISO, we also investigate the application of SE XTRACTOR (Bertin & Arnouts 1996) to our field. For a high, approximately equivalent detection threshold of $\sim$$5\sigma$, SE XTRACTOR finds far fewer sources than MR. Of those sources found by SE XTRACTOR, only $90\%$ are also found by MR. This percentage then decreases rapidly with lower thresholds (i.e. $75\%$at $\sim$$3\sigma$). Additionally, the consistent sources in both catalogues are found to have a random rms offset of $\sim$1.5'' in their position. These offsets are most likely due to the different strategies of the two different codes, as MR searches for structure in wavelet space and SE XTRACTOR searches the standard sky plane. When compared to the list of ESS optical sources, we find that the SE XTRACTOR positions are marginally more accurate than those measured by MR (rms of 2.0'' instead of 2.75''). This comparison thus confirms that a standard source extraction algorithm such as SE XTRACTOR cannot compete with an extraction technique specifically designed for ISOCAM data, such as MR.

2.2 Astrometry

A first check of the astrometry is obtained by cross-correlation of our ISOCAM source list with the ESS bright objects ( $R_{\rm c}<21$) located within 6''. We obtain an rms offset of 2'' with no systematic offset, thus indicating that the absolute astrometry for both ISOCAM and ESS catalogues are reliable.

To obtain an independent astrometric calibration, we also searched for another infrared catalogue. The closest available data in wavelength is the 2 Micron All Sky Survey (2MASS), which includes J, H, and crucially K-band at $2~\hbox{$\mu {\rm m}$ }$. As the 2MASS and ISOCAM observations were taken within a few years of each other, the proper motion of stars (which make up most of the sources used for the astrometry) is unlikely to be a problem. We cross-correlate our ISOCAM list with the 2MASS Point Source Catalogue to search for objects within 3'' of each other. This correlation yields 34 ISOCAM objects with firm detections and provisional flux densities above $0.6~{\rm mJy}$, which were also detected in the $K_{\rm s}$-band. We then use these sources with the XTRAN task in AIPS to modify the header of the FITS file of the image and rms map. This modification leads to a maximum change of 0.3'' to the positions of the 142 final catalogue objects across the field and a 0.1'' improvement in the rms offset with respect to the ESS catalogue.

   
3 Flux density calibration

Although selected to be far from the galactic plane, the relatively large area of the ESS field provides a sample of stars of various types sufficient to estimate the empirical flux density calibration of the ISOCAM observations. This areal size has a significant advantage compared to most other medium/deep ISOCAM surveys (e.g. the ISO Hubble Deep Field North, which covers only $\sim$27 square arcminutes of the sky and thus contains only a few calibrating stars).

The following analysis uses a series of colour-colour diagrams and relationships involving optical, NIR and $12~\hbox{$\mu {\rm m}$ }$ colours. Due to the high galactic latitude of our survey, the low extinction $E(B-V)\sim0.02$ hardly affects these colour-colour relations. For example, the B to R-band flux density ratio varies by less than $5\%$, and this percentage is lower for flux density ratios of longer wavelength bands.

In the following sections, we describe the various stages of our calibration procedure. We first obtain optical and NIR magnitudes for the detected ISOCAM sources by cross-identification with the ESS and various other existing catalogues (Sect. 3.1). We then use colour-colour diagrams to identify stars among the ISOCAM sources (Sect. 3.2). The core of the calibration strategy uses a fitting procedure (D. Le Borgne, private communication) to search for the best-fit stellar template from the PÉGASE library (Sect. 3.3). We use the colours of the best-fit templates to predict $12~\hbox{$\mu {\rm m}$ }$ flux densities from known IRAS colour-colour relations (Waters et al. 1987, hereafter WCA) and then convert to an ISO flux density.

   
3.1 Optical and NIR cross-identification

The optical and NIR magnitudes are taken from a variety of sources:

1.

Deep B, V, and $R_{\rm c}$-band data from ESS, including the S EXTRACTOR (Bertin & Arnouts 1996) stellarity index - an indication of how similar a source is to the point-spread function, i.e. star-like or extended like a galaxy (see Arnouts et al. 1997 for more details).

2.

B, R, and I-band data from the USNO B catalogue, when B and R-band data are unavailable due to either saturation in the ESS, masking of ESS diffraction spikes, or because the object is outside the ESS field. It should be noted that USNO magnitudes are photographic, but for convenience we use them later with the labels B, R, and I-band.

3.

I-band data from the DENIS Survey Extended Source Catalogue (ESC). We use the ESC since DENIS is deep enough to detect more galaxies than stars.

4.

J, H, and $K_{\rm s}$-bands from the 2MASS Point Source Catalogue (PSC). We use the PSC as only the brighter ISOCAM sources will be detected and will mainly be stars.

We first correlate the $12~\hbox{$\mu {\rm m}$ }$ source list with the ESS catalogue using a 6'' search radius, which gives 111 objects out of 142 with one or more potential optical counterparts. For sources with one or more optical counterparts we took the nearer counterpart which in 11 out of 12 times was the brighter of two. The other source with two counterparts seemed to be an interacting pair of equal brightness in the optical images.

The remaining 31 objects are correlated with the USNO B catalogue in a similar fashion. This correlation leads to 23 further optical counterparts, which include objects either outside the ESS field or cut out of the ESS due to saturation or masking. This list of 134 optical sources is then correlated with the 2MASS data using the optical position and a 1'' search radius, yielding 41 cross-identifications. The I-band magnitudes from DENIS are also found for 79 sources with the same search radius. The more accurate DENIS I-band is used in preference to the USNO photographic I-band when available. Seven objects that remain are too faint to be detected in USNO, 2MASS or DENIS catalogues: sources 100 and 110 are masked by diffraction spikes in the ESS and sources 12, 51, 81, 114, and 137 are not coincident with the ESS area. One source (44) is only detected in 2MASS. Hence all ISOCAM sources covered by ESS have optical counterparts with R<25.

   
3.2 Star/galaxy separation and normal star selection

3.2.1 ${H} -K_{\rm s}$ versus ${J} -{K}_{\rm s}$

We use the following colour/colour diagrams to separate stars from galaxies. For all 41 objects with 2MASS counterpart, we select stars by examining their NIR colours using the criteria

$$% H-K_{\rm s} < 0.30$$ (1)

$$% J-K_{\rm s} < 1.0$$ (2)

for normal stars from Bessell & Brett (1988). This selection is illustrated in Fig. 2 and yields a separated sub-group of 22 objects. Note the ESS misidentified galaxy with $H-K_{\rm s}\sim0.1$ in this plot and others (object 13 in Table 4). In Fig. 4 this object has quite an extreme position and is likely a very cool star with a large MIR excess.

3.2.2 ${H} -K_{\rm s}$ versus ${K}_{\rm s-[12]}$

To check for MIR excess due to dust and circumstellar material, we examine ${H} -K_{\rm s}$ versus ${K}_{\rm s-[12]}$. The IRAS Explanatory Supplement provides a zero-magnitude flux density of $28.3~{\rm Jy}$ for the 12  $\hbox{$\mu {\rm m}$ }$magnitude. However, this value is not technically correct as it was obtained by assuming that Vega is a blackbody from 10.6  $\hbox{$\mu {\rm m}$ }$ to 12  $\hbox{$\mu {\rm m}$ }$, whereas Vega has quite a large IR excess that affects both the 10.6  $\hbox{$\mu {\rm m}$ }$ flux density and the spectrum. Here we adopt a value of $40.141~{\rm Jy}$ from Cohen et al. (1992). Therefore,

$$% [12]=-2.5\times\log\bigg(\frac{F_{{\rm Jy}}}{40.141}\bigg)\cdot$$ (3)

Among the 41 2MASS counterparts, 19 of the 22 stars selected previously are in a cloud defined by $0<H-K_{\rm s}<0.3$ and $-0.5<K_{\rm s}-[12]<0.5$ (see Fig. 3) and are unambiguously detected with a single optical/NIR counterpart within 3''. The five other objects with H-K<0.4, but K-[12]>1.5 are stars from the group of 22 with MIR excess.

3.2.3 $\log({f}{_{12}}/{f}{_R}$) versus $\log({f}{_B}/{f}{_R}$)

To extend the analysis to objects too faint to be detected by 2MASS (for which we have no NIR data) we examine the positions of all objects in a optical-MIR colour-colour diagram, shown in Fig. 4. On this diagram is marked the loci of blackbodies with a temperature ranging from 3000 K (upper right) to 10⁴ K (lower left). The 14 objects near the blackbody line are normal stars without IR excess; they define the subsample that we analyse with the fitting procedure. All the 14 objects belong to the subset of 19 objects with $K_{\rm s}-[12]\sim0$and $H-K_{\rm s}\sim0{-}0.25$ in Fig. 3. The remaining 5 objects are: i) 4 of the 5 S EXTRACTOR stars identified in the ESS, which lie immediately above the blackbody line, and ii) the misidentified galaxy to the right of the graph with $\log(f_B/f_R)\sim3$. The fifth star in the row above the blackbody line (with $\log(f_B/f_R)=0.1$) has $K_{\rm s}-[12]\sim1.5$ and hence does not satisfy the NIR/MIR colour selection criteria. Note that there are no objects previously not identified as stars in the lower part of Fig. 4. Therefore, among all the objects with optical counterparts, we identify only 22 stars from the colour-colour diagrams (i.e. all and only those selected in Fig. 2). With no further information available the 7 ISOCAM sources without either an optical or NIR counterpart are assumed to be galaxies.

At this stage we change the DENIS i-band magnitudes from the ESC to the PSC for all 22 sources found to be stars.

Figure 2: NIR colour-colour diagram of 40/41 objects with 2MASS counterparts (minus one object with extreme H-K colour, $\sim$2, which lies off the plot). The symbols refer to the stellarity index from the ESS (see text): circles are galaxies, open stars are stars and crosses are objects without counterpart in the ESS. The solid lines represent the selection criteria of stars from Eqs. (1) and (2).

Open with DEXTER

	Figure 3: NIR-MIR colour-colour diagram of 40 objects with 2MASS counterparts. The symbols are the same as in Fig. 2.
Open with DEXTER

Figure 4: Optical-MIR colour-colour diagram of all objects with optical (ESS/USNO) counterparts. The symbols are the same as in Figs. 2 and 3, but with the caveat that R and B-band magnitudes with no stellarity index are from the USNO catalogue (i.e. the crosses). The solid line represents the loci of blackbodies with a temperature ranging from 3000 K to 10 000 K for the Johnson-Cousins system. We note this line would vary by <0.1 dex for the USNO filter system. Furthermore, there are 7 ISOCAM sources (three misidentified, open stars, and four unknown, crosses) not in the ESS with $\log f_{12}/f_R\sim10$ which are assumed to be galaxies.

Open with DEXTER

   
3.3 Template fitting

For the template fitting we used the stellar library from the PÉGASE.2 (http://www2.iap.fr/pegase) code. This library has a significant coverage of the HR diagram. It is based on the Kurucz library rearranged by Lejeune et al. (1997): BaSel-2.0 (see Fioc & Rocca-Volmerange 1987, for details). The chi-squared fitting routine was applied to the 14 objects of the selected subsample, all have ${\it BRIJHK}_{\rm s}$ magnitudes with the B, R and I-band magnitudes from the USNO catalogue, not the ESS catalogue, as they were all saturated or off the ESS field. The 2MASS pass-bands come from the 2MASS web-page. The USNO pass-bands (from the Palomar Sky Survey and approximately equivalent to the Johnson B, R, and I-bands) were taken from Reid et al. (1991). We remind the reader that the extinction is low enough in this area of sky for its effect on the current analysis to be small, $\la$$5\%$ in the optical and less at longer wavelengths.

The chi-squared fitting of the sample of 14 normal stars is carried out in a 3-dimensional parameter space: effective temperature ( $T_{\rm eff}$), surface gravity (g), and metallicity (Z/Z₀). The fits are constrained by the errors of each magnitude: 0.05 mag for 2MASS, $\sim$0.05 mag for DENIS, and 0.25 mag for USNO. The $\chi^2$ exhibit a sharp minimum as a function of $T_{\rm eff}$ and with a reasonable dependence on the surface gravity. For 13 out of the 14 stars, best-fit templates have $\chi^2 < 1.7$, while the 14th star has $\chi^2=4.0$ so we exclude it from our sample. We show in Fig. 5 the stellar fit with the largest $\chi^2$ ( $\chi ^2 = 1.68$). The input magnitudes of the 13 stars are listed in Table 3 with the parameters values of the best-fit stellar SED. The first column lists the source number from Table 4. The next column contains the observed I-band magnitude from USNO (further photometry of these sources is presented in Table 4). The final 4 columns contain the results of the template fitting: the log surface gravity ( ${\rm m}~{\rm s}^{-2}$), the log metallicity (Z/Z₀), the effective temperature in Kelvin, and $\chi^2$ of the fit.

	Figure 5: Result of the stellar fitting to ISOCAM source 20 from Table 4. The open diamonds with error bars are the observation magnitudes ( ${\it BRIJHK}_{\rm s}$ bands) whilst the solid circles are the magnitudes of the best fit template (line) with $\chi ^2 = 1.68$. Details of this fit are given in the panel below the plot.
Open with DEXTER

Figure 5 illustrates that the NIR region of the SED is more constrained due to the higher accuracies of the NIR magnitudes ( ${\it IJHK}_{\rm s}$). This wavelength range corresponds to the region in which the effective temperature is essentially defined, as is the Wien-tail of the blackbody spectrum. From Fig. 5, one might expect that there would be many other stellar templates consistent with this fit, but with a different SED below $0.8~\hbox{$\mu {\rm m}$ }$. Although these different optical SEDs would probably not change the effective temperature by much, it could considerably affect the optical colours, B-V and R-I, which the WCA colour-colour relations use (see Sect. 3.4). To investigate this effect, we reran the fitting procedure to all 14 stars without using the B and R-band magnitudes (i.e. without constraining the fit below I-band wavelengths). In all cases but one, the effective temperatures changes by only one step in parameter space (200-250 K), and the SEDs below I-band are generally consistent with those derived using the B and R-band magnitudes; similar values of B-V and R-I colours are also obtained. The one case with a considerably different effective temperature and SED is found to be almost degenerate with 2 sharp troughs in $\chi^2$ parameter space, the slightly higher of the $\chi^2$corresponding to the original 6 band fit. The other fit can easily be discarded as it is inconsistent with the observed B and R-band magnitudes. Therefore, we conclude that the large errors of the B and R-band magnitudes do not significantly deteriorate the quality of the fits.

Table 3: Sub-sample of 13 stars selected for stellar fitting.

   
3.4 Predicted flux

Although the BaSeL-2.0 stellar libraries do extend to MIR wavelengths, they have not been widely tested, and then only at brighter flux densities (e.g. Cohen et al. 2003, using the Kurucz templates for certain A0-AV5 stars). We decided to use empirical stellar colours to verify the calibration of our flux densities and the long-wavelength part of the stellar template as a consistency check. We use the two colour-colour relationships of WCA to derive $12~\hbox{$\mu {\rm m}$ }$ flux densities. These WCA relations are for IRAS $12~\hbox{$\mu {\rm m}$ }$ flux densities of stars that specifically relate the V-[12] colour with B-V and R-I:

 

V-[12] = 0.05 + 3.13(B-V) - 1.26(B-V)² + 0.29(B-V)³ + 0.16(B-V)⁴ (4)

and

$$% V-[12]=4.33(R-I)+0.14 \;{\rm for} \; (R-I)<0.72$$ (5)

$$% V-[12]=2.69(R-I)+1.40 \;{\rm for} \; (R-I)>0.72.$$ (6)

These relationships were derived from IRAS observations of bright normal stars. We convert from magnitudes to flux density using the 40.141 Jy IRAS $12~\hbox{$\mu {\rm m}$ }$ zero point of Cohen et al. (1992). This zero point is very similar to the value used in Cohen et al. (1987), who obtained V-[12] colours in agreement with the WCA colours. The ISOCAM LW10 filter was designed to have a similar wavelength-dependent response as the IRAS $12~\hbox{$\mu {\rm m}$ }$band, but they are not identical. The ISO $12~\hbox{$\mu {\rm m}$ }$ filter has a redder blue cutoff than the IRAS $12~\hbox{$\mu {\rm m}$ }$ filter. Using these relationships we obtain predicted IRAS flux densities, which we can then convert to ISO flux densities by the ratios of the colour corrections for the stars. The ratio of colour corrections, $K_{12~\mu {\rm m}}^{\rm IRAS}/K_{12~\mu {\rm m}}^{\rm ISO}$, as defined in the respective handbooks is computed by the authors to be 1.11 for stars of temperatures 2000-10 000 K. Hence we convert the IRAS to ISO flux densities by dividing the predicted WCA flux densities by this factor.

Table 4: First ten lines of the complete $12~\hbox{$\mu {\rm m}$ }$ source catalogue. The full catalogue will be available in electronic form at the CDS.

	Figure 6: Ratio of predicted ISOCAM $12~\hbox{$\mu {\rm m}$ }$ flux density (from template fitting and the relationships of WCA) to "observed'' ISOCAM flux density plotted against observed $12~\hbox{$\mu {\rm m}$ }$ magnitude. The mean ratio is indicated by the horizontal solid line.
Open with DEXTER

The V magnitudes and B-V, R-I colours, which we used when applying Eqs. (4)-(6) to the 13 stars listed in Table 3, are those derived directly from best-fit template spectra. We apply both relationships for each star, thus yielding 2 estimates of the $12~\hbox{$\mu {\rm m}$ }$ magnitude. Equation (3) subsequently gives us 2 estimates of the flux density, from which we derive an average flux density. The ratio of this predicted ISOCAM flux density to the initially measured ISOCAM flux density, i.e. the observed flux density, is plotted in Fig. 6. We find a mean value of 1.01 $\pm$ 0.17, which we also mark in Fig. 6. This mean value of the flux density ratios includes the factor of 1.11 due to the colour corrections. The ratios presented in Fig. 6 indicate that, for our observational setup, at least, the flux densities are systematically overestimated for the normal stars, with no apparent systematic variation in the offset value with $12~\hbox{$\mu {\rm m}$ }$ flux density. Due to the large PSF of these ISOCAM observations, 6'', slightly extended sources (galaxies) have a similar response to the detector as unresolved (stars); hence, we apply this correction to our entire catalogue (see Table 4). Furthermore, the 1.01 correction factor is not too dissimilar to the combined flux density correction found by Rodighiero et al. (2004) of 0.84 (from the combination of their projection bias, mosaic bias and stellar flux density correction: 0.84 $\times$ 0.915 $\times$ 1.097=0.84).

We are confident we have successfully excluded all stars that exhibit unusual properties (e.g. Be-stars or those with dust around them). As a test, we also calculate the ratio of predicted to observed flux density using the $12~\hbox{$\mu {\rm m}$ }$ flux density derived from the Kurucz stellar template. The ratio for the Kurucz template flux density is 1.05 $\pm$ 0.18. We note that the Kurucz value agrees with the value from our template fitting procedure, given the error bars, suggesting that the Kurucz models are not too far off at MIR wavelengths.

   
4 The 12 ${\mu }$m source catalogue

Table 4 lists the full flux density-calibrated $12~\hbox{$\mu {\rm m}$ }$catalogue of 142 sources detected by ISOCAM above the minimum integrated flux density of $0.24~{\rm mJy}$. All available optical and NIR data are also given, as well as classification (star/galaxy) and the source of the optical data. This catalogue is used to compute the faint galaxy counts at 12$~\mu$m in the companion paper (Rocca-Volmerange et al. 2007). A complementary paper on the luminosity function at 12 ${\mu }$m is in preparation.

The uncertainties in the 12 ${\mu }$m flux density in Table 4 (Col. [16]) are obtained using

$$% \frac{\delta S_{12}}{S_{12}}\simeq\sqrt{\bigg(\frac{{\rm d}S}{{\rm S}}\bigg)^2 +\bigg(\frac{0.047}{1.01}\bigg)^2}\cdot$$ (7)

The first term in the quadratic sum is the original relative uncertainty in flux density provided by the source count extraction with the MR software. The second term results from the uncertainty in the 1.01 mean correction factor applied to the MR flux density (see Sect. 3.4): as the 1.01 factor is measured over 13 data points (see Fig. 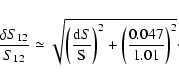6) with an rms dispersion of 0.17 around the mean, we approximate its uncertainty to $0.17/\sqrt{13}=0.047$.

Only the first 10 lines of the catalogue are presented in Table 4. The full catalogue is available in electronic form at the CDS. The first column contains the source number. The second column contains the IAU designated naming with the prefix IES (ISO ESO-Sculptor). The third and fourth columns contain the RA and Dec (J2000). The fifth column indicates the classification of each source (G = galaxy, S = star). The sixth column indicates the source of the $\it BVR$ magnitudes (ESS = ESS, USNO = USNO survey, OFFF = off ESS area and not detected by USNO, SPIK = hidden by a diffraction spike in ESS and not detected by USNO and SATD = saturated in ESS and not detected by USNO). The following 10 columns are, respectively the ${\it BVRIJHK}_{\rm s}$ and the $12~\hbox{$\mu {\rm m}$ }$ flux density and its uncertainty in mJy. The B_U and R_U magnitudes are from USNO, $\it BVR$ from ESS, I-band from DENIS and ${\it JHK}_{\rm s}$ from 2MASS.

5 Survey completeness

In order to use our ISOCAM source catalogue to derive galaxy numbers counts, one needs to evaluate the completeness of the catalogue as a function of flux density. We use two independent empirical methods. Firstly, we use the same method as used in the previous section to determine the flux density of stars (Sect. 3), which we extend to those stars not detected by ISOCAM. The second method is based on the optical counterparts to galaxies associated with ISOCAM sources, but detected with lower significance, in the interval  $3\tau _{\rm w}$ to $5\tau _{\rm w}$.

   
5.1 Completeness from stars

The method is based on the following stages: i) selecting stars from the 2MASS catalogue using their NIR colours, ii) confirming that they are stars by template fitting (as in Sect. 3.3), and iii) using the results of the fitting to predict the $12~\hbox{$\mu {\rm m}$ }$ flux density from the optical colours.

We select stars from the 2MASS catalogue as all objects with H-K<0.3, J-K<1 and K<14 within the area of the ISOCAM field. The two colour criteria are the same as were used earlier (Eqs. (1) and (2)) and are typical of normal stars (Allen 1976; Bessell & Brett 1988). The limiting magnitude criterion is intended to avoid selecting objects significantly fainter than the detection limit of the ISOCAM survey ( $F_{12~\mu {\rm m}} \sim0.2~{\rm mJy}$ is approximately equivalent to $K\sim13$ mag), but is faint enough to allow for stars with some MIR excess to be included. The resulting catalogue contains 51 stars. We discuss possible selection effects at the end of this section, especially the impact of stars with infrared excess.

Using all available magnitudes from ESS, 2MASS, DENIS, and USNO for each of the 51 stars, we find the best-fit template spectrum from the library of Lejeune et al. (1997), in the same fashion as in Sect. 3.3 for the 22 stars detected by ISOCAM. We then use the optical- $12~\hbox{$\mu {\rm m}$ }$ relations of WCA in Eqs. (5) and (6) to estimate the $12~\hbox{$\mu {\rm m}$ }$ flux density. Three of the 51 stars with predicted $F_{12~\mu {\rm m}}>0.2~{\rm mJy}$ have fits with $3<\chi^2<10$. For these 3 stars, we instead use the relation

$$% K-[12]=0.03\pm0.1$$ (8)

derived from the 13 well-fitted stars of Sect. 3.3. For all other stars, we find a well-fit spectrum with low $\chi^2$ (<3).

Of the 51 stars, 18 (including the 3 stars with $\chi^2>3$) have predicted $12~\hbox{$\mu {\rm m}$ }$ flux density above the detection limit, but were not found by the MR source extraction software. This sample, including the 22 flux-density calibrated, ISOCAM-detected stars is then used to determine the fraction of 2MASS stars detected by ISOCAM at $12~\hbox{$\mu {\rm m}$ }$ as a function of flux density. This result provides us with a first estimate of the completeness, presented in Fig. 7. The bins in Fig. 7 have equal sizes in log flux density space and the errors for each bin are assumed to be Poisson.

We now consider the possible selection effects. It is unlikely that we have missed stars due to the colour criteria (Eqs. (1) and (2)), which are robust for normal stars, even those with an MIR excess. It is also unlikely that we have included any galaxies, as they would be poorly fitted by the stellar templates. But it is possible that some of the selected stars have infrared excess, so their true $12~\hbox{$\mu {\rm m}$ }$ flux density is higher than that predicted. An excess of $K-[12] \sim 1{-}4$ would be equivalent to an increase of flux density equivalent to $\Delta\log(F_{\rm 12~\mu m})\sim0.4{-}1.6$. Hence, if our field contains stars with infrared excesses, then the completeness estimated here represents an upper limit. We note, however, that only 3 out of the 22 stars detected by ISOCAM have $12~\hbox{$\mu {\rm m}$ }$ excesses. Therefore, we estimate that the completeness may be overestimated by 15% at most, which is well inside the Poisson error bars.

Because the pixels are relatively large, 6'', most galaxies appear unresolved to ISOCAM. We can then assume that the sensitivity of the detector is the same for unresolved objects, i.e. stars, as for resolved objects like galaxies. Hence the completeness in galaxies is likely to be similar to that of stars and can be used as such. If the completeness for galaxies is however affected by the non-detection of low surface-brightness objects, then again the estimate plotted in Fig. 7 is an upper limit. We also suspect that this effect is smaller than the plotted Poisson errors.

   
5.2 Completeness from low significance sources

The second method provides an independent correction to the source counts. It is based on the association of ISOCAM sources detected at low significance with optically detected galaxies. A priori, some of the ISOCAM sources detected with a detection threshold located in the interval $3\tau _{\rm w}$ to $5\tau _{\rm w}$ may be real. By examining their association with the ESS optical sources, we can evaluate their reality in a statistical way. We use PRETI as in Sect. 2, but with a detection threshold in wavelet space of $3\tau _{\rm w}$. This threshold leads to detection of 328 sources, to be compared with the $5\tau _{\rm w}$ list of 142 objects presented in Table 4. After correcting the flux density of each object by the correction found in Sect. 3.4, and removing the sources with a flux density below the detection limit of $0.24~{\rm mJy}$, we end up with 292 potential sources (i.e. the 142 sources of the original catalogue and 150 new sources of lower significance).

Figure 7: Completeness of the ISOCAM catalogue as derived from both methods: stellar template fitting to the 2MASS stars in the ESS field and the inclusion of lower significance ISOCAM sources with a detection threshold between $3\tau _{\rm w}$ and $5\tau _{\rm w}$ and ESO-Sculptor optical counterparts detected within 6''. The dotted red line shows the fraction of detected stars as a function of predicted flux density, with Poisson errors. The solid line shows the fraction of galaxies detected with a high significance ( $5\tau _{\rm w}$) from all galaxies detected with a lower significance ( $3\tau _{\rm w}$) as a function of predicted flux density, with Poisson errors.

Open with DEXTER

We then cross-correlate the 150 new $3\tau _{\rm w}$ ISOCAM sources with the ESS catalogue. Using a 3'' (6'') search radius, we find 74 (110) optical counterparts. From f₁₂/f_R versus f_B/f_R diagrams, like Fig. 4, all these sources are found to be galaxies. As some of these matches are by chance, due to the size of our search radius and the space density of optical sources, we evaluate the excess matches by offsetting the positions of the 2 data sets by increasing multiples of half an arcsecond in RA and Dec. At large offsets ($\ga$6''), the number of matches becomes roughly constant with a value around 20 (55) for the 3'' (6'') search radius. These numbers are comparable with the theoretical numbers of 17 (70) sources expected within the 3'' (6'') search radius if one uses the sky density of objects and assumes a random distribution.

We now assume that adding the sources from either the 3'' or 6''list to the high-significance list of 142 sources, yields a nearly "complete'' source catalogue. This assumption is reasonable because there is a large excess of ISOCAM coincidences with the ESS above the theoretical and empirical random values. A "real'' object, detected with [12]<13 (corresponding to the $12~\hbox{$\mu {\rm m}$ }$ detection limit), must have V<22.5 if it is a star-forming galaxy at $z\la1$. This selection is derived from typical, maximum ${K}_{\rm s-[12]}$ colours ($\sim$5, see Fig. 3) and typical, maximum $V-K_{\rm s}$ colour ($\sim$4.5). The possibility that some sources are not real is taken into account in the errors on the source counts which are derived in Rocca-Volmerange et al. (2007).

The resulting completeness, defined as the ratio of the uncorrected number counts from the $5\tau _{\rm w}$ list to the counts from the "complete'' list, is plotted as a function of flux density in Fig. 7 (solid line). The bins again have equal sizes in log flux density space, albeit smaller than before, and the errors are simply Poisson. Note that the curve corresponding to a search radius of 3'' is indistinguishable from that with 6'' plotted in Fig. 7.

The sources counts extended to $3\tau _{\rm w}$ are subject to several biases: they probably include some sources that are false and might still miss some real sources, which would be above our $0.24~{\rm mJy}$ detection threshold. The former would lead to an over-estimation of the source counts (although we include it in our error), and the latter to an under-estimation. It is nevertheless significant that the source counts from both the low-significance lists (with 3''and 6'' search radii) yield a incompleteness consistent with what is derived from stars in the previous section (see Fig. 7). Although difficult to quantify, the agreement of these 2 independent methods for estimating the completeness indicates that these 2 selection effects affecting the low-significance sources cancel out to a certain extent.

Therefore both the full and dotted lines in Figs. 7 show that our ISOCAM catalogue is complete to $\sim$1 mJy, with a linearly decreasing completeness in log flux density down to the our flux density detection limit of 0.24 mJy. A complete analysis of the ISOCAM-ESS galaxy number-counts along with the fitting of theoretical models are presented in the companion paper (Rocca-Volmerange et al. 2007).

6 Conclusions

We present the data reduction of ISOCAM observations performed with the LW10 filter centred near $12~\hbox{$\mu {\rm m}$ }$, mostly in the field of the optical ESO-Sculptor survey (Arnouts et al. 1997; de Lapparent et al. 2003). The data reduction of the ISOCAM rasters was performed as in Aussel et al. (1999): we used the multi-scale vision model of Rué & Bijaoui (1996) implemented into the MR software (Starck et al. 1999), along with the PRETI algorithm aimed at removing all image artifacts above the noise level. Using a detection threshold of $5\tau _{\rm w}$ where $\tau_{\rm w}$ is the noise level in wavelet space, we reach a detection limit of $\sim$ $0.24~{\rm mJy}$.

The final catalogue contains 142 ISOCAM sources with optical counterparts in the ESO-Sculptor survey, which we complement by optical and NIR magnitudes from the USNO B catalogue and the 2MASS and DENIS surveys. Optical, near-infrared, and mid-infrared colour-colour diagrams subsequently allow us to identify 22 sources as stars and 120 as galaxies, which dominate at faint flux densities. By template fitting of 13 of these stars, we derived their predicted $12~\hbox{$\mu {\rm m}$ }$ flux density using the template optical colours combined with the optical-mid-infrared colour relations of Waters et al. (1987). By comparison with the observed ISOCAM flux densities normalized using the IRAS $12~\hbox{$\mu {\rm m}$ }$ zero-point, we found that the observed flux densities systematically overestimate the theoretical flux densities by a factor of 1.16 (1/0.86). We used this offset to correct all flux densities (i.e. stars and galaxies). We used a similar method (predicting the $12~\hbox{$\mu {\rm m}$ }$ flux density of stars) to determine the completeness of our survey as a function of flux density. This completeness function is found to be in good agreement with that from a statistical study of the coincidence of low-significance ISOCAM sources with the ESO-Sculptor optical sources.

The ISOCAM-ESO-Sculptor-Survey catalogue obtained here is used to analyse the mid-infrared galaxy number counts in Rocca-Volmerange et al. (2007). By using the available ESO-Sculptor redshifts (de Lapparent et al. 2003), we will also derive the $12~\hbox{$\mu {\rm m}$ }$ luminosity function, which is a valuable tool for interpreting the deep mid-infrared source counts and performing a detailed study of the evolution of galaxies at $12~\hbox{$\mu {\rm m}$ }$, a wavelength range unavailable to the MIPS and IRAC instruments aboard Spitzer (Gallagher et al. 2003).

Acknowledgements

We thank the referee for the many constructive comments improving the quality of this paper. We give thanks to René Gastaud, Jean-Luc Starck, David Elbaz (SAp/CEA), Carlos del Burgo (Heidelberg), and Emmanuel Bertin (IAP). We are also grateful to Damien Le Borgne (CEA) for aiding us in the use of his software. We thank Hervé Aussel for useful discussions. Part of this work (N.S.) was supported by the Probing the Origin of the Extragalactic background (POE), European Network number HPRN-CT-2000-00138. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. Additionally this research uses the USNOFS Image and Catalogue Archive operated by the United States Naval Observatory, Flagstaff Station (http://www.nofs.navy.mil/data/fchpix/). We also thank Gary Mamon for kind permission to use data from the DENIS survey. The DENIS project has been partly funded by the SCIENCE and the HCM plans of the European Commission under grants CT920791 and CT940627. It is supported by INSU, MEN, and CNRS in France, by the State of Baden-Württemberg in Germany, by DGICYT in Spain, by CNR in Italy, by FFwFBWF in Austria, by FAPESP in Brazil, by OTKA grants F-4239 and F-013990 in Hungary, and by the ESO C&EE grant A-04-046. The ISOCAM data presented in this paper were analysed using "CIA'', a joint development by the ESA Astrophysics Division and the ISOCAM Consortium. The ISOCAM Consortium was led by the ISOCAM PI, C. Cesarsky.

References

• Abergel, A., Bernard, J. P., Boulanger, F., et al. 1996, A&A, 315, L329 [NASA ADS] (In the text)
• Allen, C. W. 1976, Astrophysical Quantities, 3rd edition (London: Athlone)
• Appleton, P. N., Fadda, D. T., Marleau, F. R., et al. 2004, ApJS
• Arnouts, S., de Lapparent, V., Mathez, G., et al. 1997, A&AS, 124, 163 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Aussel, H., Cesarsky, C. J., Elbaz, D., & Starck, J. L. 1999, A&A, 342, 313 [NASA ADS] (In the text)
• Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] (In the text)
• Cesarsky, C. J., Abergel, A., Agnese, P., et al. 1996, A&A, 315, L32 [NASA ADS] (In the text)
• Clements, D. L., Desert, F.-X., Franceschini, A., et al. 1999, A&A, 346, 383 [NASA ADS] (In the text)
• Cohen, M., Walker, R. G., Barlow, M. J., & Deacon, J. R. 1992, AJ, 104, 1650 [NASA ADS] [CrossRef] (In the text)
• Désert, F.-X., Puget, J.-L., Clements, D. L., et al. 1999, A&A, 342, 363 [NASA ADS] (In the text)
• de Lapparent, V., Galaz, G., Bardelli, S., & Arnouts, S. 2003, A&A, 404, 831 [NASA ADS] [CrossRef] [EDP Sciences]
• de Lapparent, V., Arnouts, S., Galaz, G., & Bardelli, S. 2004, A&A, 422, 841 [NASA ADS] [CrossRef] [EDP Sciences]
• Efstathiou, A., Oliver, S., Rowan-Robinson, M., et al. 2000, MNRAS, 319, 1169 [NASA ADS] (In the text)
• Gallagher, D. B., Irace, W. R., & Werner, M. W. 2003, in IR Space Telescopes and Instruments, ed. J. C. Mather, Proc. SPIE, 4850, 17 (In the text)
• Gruppioni, C., Lari, C., Pozzi, F., et al. 2002, MNRAS, 335, 831 [NASA ADS]
• Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] (In the text)
• Lari, C., Pozzi, F., Gruppioni, C., et al. 2001, MNRAS, 325, 1173 [NASA ADS] (In the text)
• Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Oliver, S., Mann, R. G., Carballo, R., et al. 2002, MNRAS, 332, 536 [NASA ADS] (In the text)
• Ott, S., Abergel, A., Altieri, B., et al. 1997, in Astronomical Data Analysis Software and Systems VI, ed. G. Hunt, & H. Payne, ASP Conf. Ser., 125, 34 (In the text)
• Pozzi, F., Ciliegi, P., Gruppioni, C., et al. 2003, MNRAS, 343, 1348 [NASA ADS]
• Pozzi, F., Gruppioni, C., Oliver, S., et al. 2004, ApJ, 609, 122 [NASA ADS] [CrossRef]
• Reid, I. N., Brewer, C., Brucato, R. J., et al. 1991, PASP, 103, 661 [NASA ADS] [CrossRef] (In the text)
• Rocca-Volmerange, B., de Lapparent, V., Seymour, N., & Fioc, M. 2007, A&A, 475, 801 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Rodighiero, G., Lari, C., Fadda, D., et al. 2004, A&A, 427, 773 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Rué, F., & Bijaoui, A. 1996, Vistas in Astronomy, 40, 495 [NASA ADS] [CrossRef] (In the text)
• Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] (In the text)
• Serjeant, S. B. G., Eaton, N., Oliver, S. J., et al. 1997, MNRAS, 289, 457 [NASA ADS] (In the text)
• Starck, J. L., Aussel, H., Elbaz, D., Fadda, D., & Cesarsky, C. 1999, A&AS, 138, 365 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Väisänen, P., Morel, T., Rowan-Robinson, M., et al. 2002, MNRAS, 337, 1043 [NASA ADS] (In the text)
• Vaccari, M., Lari, C., & Angretti, L. 2005, MNRAS, 358, 397 [NASA ADS]
• Waters, L. B. F. M., Cote, J., & Aumann, H. H. 1987, A&A, 172, 225 [NASA ADS] (In the text)