A&A 475, 765-769 (2007)
DOI: 10.1051/0004-6361:20078640

Electron-impact excitation of Fe II[*]

Collision strengths and effective collision strengths for low-lying fine-structure forbidden transitions

C. A. Ramsbottom - C. E. Hudson - P. H. Norrington - M. P. Scott

Department of Applied Mathematics & Theoretical Physics, The Queen's University of Belfast, Belfast BT7 1NN, Northern Ireland

Received 10 September 2007 / Accepted 19 September 2007

Abstract
Context. Absorption or emission lines of Fe II are observed in many astrophysical spectra and accurate atomic data are required to interpret these lines. The calculation of electron-impact excitation rates for transitions among even the lowest lying levels of Fe II is a formidable task for theoreticians.
Aims. In this paper, we present collision strengths and effective collision strengths for electron-impact excitation of Fe II for low-lying forbidden transitions among the lowest 16 fine-structure levels arising from the four LS states 3d64s 6De, 3d7 4Fe, 3d64s 4De, and 3d7 4Pe. The effective collision strengths are calculated for a wide range of electron temperatures of astrophysical importance from 30-100 000 K.
Methods. The parallel suite of Breit-Pauli codes are utilised to compute the collision cross sections for electron-impact excitation of Fe II and relativistic terms are included explicitly in both the target and the scattering approximation. 100 LS or 262-jj levels formed from the basis configurations 3d64s, 3d7, and 3d64p were included in the wavefunction representation of the target, including all doublet, quartet, and sextet terms. Collision strengths for a total of 34 191 individual transitions were computed.
Results. A detailed comparison is made with previous theoretical works and significant differences were found to occur in the effective collision strengths, particularly at low temperatures.

Key words: atomic data - atomic processes - plasmas

1 Introduction

Fe II is one of the iron-peak elements whose spectra is of significant importance in astronomical observations. This is due to the fact that very few objects exist in any class of astronomy which do not show large numbers of emission or absorption lines of Fe II in their spectrum from the infrared to the ultraviolet wavelengths. For example Eriksson et al. (2006) presented a detailed study of the UV spectrum of the symbiotic star AG Pegasi where over 600 lines were observed in the spectra from IUE, HST and FUSE. Of the lines that were identified 346 were found to be emission lines of Fe II. More recently, Hubrig & Gonzalez (2007) have for the first time presented observational evidence for the appearance of variable high-excitation Fe II emission lines in the magnetic Bp star aCentauri. D'Elia et al. (2007) presented UVES/VLT high resolution spectroscopy of the optical afterglow of Gamma Ray Burst GRB 050730 and detected strong Fe II fine-structure absorption lines in the Inter Stellar Medium of the GRB host galaxy. In addition Smith & Hartigan (2006) found that the spectra of the radius nebula around P Cygni is dominated by bright emission lines of Fe II. In particular this work found that the observed [Fe II] line ratios disagreed with the theoretical predictions in the literature, indicating that the atomic data available for the low-lying forbidden transitions among the first few levels of Fe II may be in error. A valuable spectral diagnostic of P Cyg's nebula is its bright emission from infrared lines of Fe II and in particular the related forbidden transitions between the fine-structure terms of the ground 3d64s 6D and excited 3d7 4F and 3d64s 4D levels. These are collisionally excited lines and lie approximately 1 eV above the ground state and are particularly bright in the nebula of P Cyg and in the nebulae of several other LBVs. For the interpretation of these spectral lines therefore, it is imperative that accurate as well as extensive atomic data is available for collisional as well as radiative processes in Fe II.

The theoretical calculation of these atomic data is, however, a non-trivial task for many reasons. The important Fe II low-ionised species in the near-neutral iron-peak region is an extremely complex system with an open d shell which requires large configuration interaction expansions to properly represent the target wavefunctions and energies. Complications are further aggravated by the large number of coupled channels involved in the collision calculation and by the presence of Rydberg resonances in the low-energy collision cross sections which necessitates a very fine-mesh of energies to properly resolve. Despite these difficulties a number of theoretical works, ranging in sophistication, have been carried out over the last two decades. Nussbaumer & Storey (1980) evaluated electron-ion collision strengths for the lowest four Fe II terms using the close-coupling approximation with a 2 configuration basis. The work was limited, however, in that only three energy points were considered and hence no resonance effects were included. Subsequent work by Baluja et al. (1986) adopted a finer mesh of energies in the resonance region and predicted a factor of two difference in the excitation cross sections. A more sophisticated calculation was then performed by Berrington et al. (1988) where relativistic effects were incorporated by including the one-body terms of the Breit-Pauli Hamiltonian explicitly in the target and scattering description. Sixteen fine-structure levels arising from the lowest four states (3d64s 6D, 3d7 4F, 3d64s 4D and 3d7 4P) of Fe II were included but collision rates between the fine-structure levels of the first two only were presented. Little agreement was found between these three calculations for transitions among the lowest few levels of Fe II. The Berrington et al. (1988) rates were subsequently used by Keenan et al. (1988) to derive electron density sensitive relative populations for the ground-state fine-structure levels, for the range of temperatures $T_{\rm e} = 100$-30 000 ${\rm K}$ and densities $N_{\rm e} = 10^{2} {-} 10^{6}$ cm-3applicable to astrophysical plasmas. These results were again found to be a factor of two different from previous calculations.

Advances in computational power in the last decade has led to more sophisticated works being performed. Pradhan & Berrington (1993) carried out an extensive LS collision calculation incorporating all 38 quartet and sextet levels belonging to the 3d64s, 3d7 and 3d64p configurations. It was found that the additional terms corresponding to the the 3d64p configuration, omitted in all previous works, played a vital role due to the strong coupling with the 3d64s terms. Zhang & Pradhan (1995) have extended this work by including relativistic effects using a transformation from LS (38 levels) to jj (142 levels) based on the pair coupling scheme introduced by Racah (1942). Collision strengths were evaluated for 10 011 infrared, optical and ultraviolet transitions and Maxwellian averaged rate coefficients were presented for 618 of these lines at temperatures of 5000, 10 000, 20 000 and 50 000 K. The rate coefficents for the low-lying transitions among the lowest 16 fine-structure levels were, however, found to be substantially different to those predicted by either Keenan et al. (1988) or Nussbaumer & Storey (1980). Clearly convergence of the low-energy collision data, in LS coupling, had not yet been achieved.

To explore this convergence and investigate the importance of configuration interaction effects in low energy collisons with Fe II, a series of calculations were performed by Ramsbottom et al. (2002, 2004) using the program RMATRXII (Burke et al. 1994) and the parallel external R-matrix program PFARM (Sunderland et al. 2002) based on FARM (Burke & Noble 1995). In these works additional configuration interaction effects were systematically included both in the target and in the collision wavefunctions. It was found that in order to obtain converged low-energy partial wave collision strengths up to a further 21 configuration functions needed to be included in the CI expansion of the target, incorporating two-electron excitations from the 3s and 3p shells to the 3d shell. These studies defined an optimum model for the Fe II target and was adopted by Ramsbottom et al. (2005) to evaluate collision strengths and effective collision strengths for all sextet to quartet forbidden transitions among the lowest 113 LS states of Fe II formed from the 3d64s, 3d7, 3d64p, 3d54s2 and 3d54s4p basis configurations. This is the largest LS calculation performed to date for Fe II and rates are tabulated for the temperature range 30-100 000 ${\rm K}$ of particular importance for astrophysical applications.

All the theoretical models described above, whether performed in LS or jj coupling, are limited in their approximation in that they are only interested in total spin S = 2 and hence only the quartet and sextet terms of Fe II were considered in the target expansion. Important effects due to the omission of all the doublet levels were thus never investigated. In this work we initiate the largest systematic study of electron-impact excitation of Fe II incorporating relativistic effects via the Breit-Pauli Hamiltonian. The theoretical model includes the 100 LS (doublet, quartet and sextet) terms corresponding to configurations 3d64s, 3d7 and 3d64p. This corresponds to 262 fine-structure levels and a total of 34 191 individual forbidden and allowed transitions. Collision strengths are evaluated over a very fine mesh of incident electron energies (10-4) in the resonance region, and the corresponding Maxwellian averaged effective collision strengths for a wide range of electron temperatures 30-100 000 ${\rm K}$. We concentrate in this paper on the fine-structure forbidden lines among the lowest 16 levels of Fe II corresponding to the 3d64s 6D, 3d7 4F, 3d64s 4D and 3d7 4P multiplets. These particular data are required specifically for interstellar medium studies and due to the very low temperatures involved it is imperative that very accurate cross sections are determined near threshold. The calculation is described in detail in Sect. 2 and the overall results for the 120 forbidden lines of interest are discussed in Sect. 3. Here a comprehensive comparison is made with all previous theoretical works where possible and the differences analysed. A table of effective collision strengths for all the forbidden transitions is presented in this section for 27 individual temperatures, ranging from 30 to 100 000 ${\rm K}$. Finally in Sect. 4 conclusions are drawn as to the reliability of the present atomic data.

2 The target model

The ground state level of Fe II is of the form 3d64s, a configuration it shares with 23 other LS terms. The next excited level has configuration 3d7 of which there are a total of 8 LS terms, and finally the total number of 3d64p levels is 68. This gives a total of 100 LS levels if we include all doublet, quartet and sextet terms in the wavefunction expansion. These 100 target states are represented by configuration-interaction expansions in terms of nine orthogonal basis orbitals, eight spectroscopic (1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p) and one pseudo-type orbital $\overline{\rm {4d}}$ which is included to allow for additional correlation effects. The radial part of each orbital is expanded in terms of a linear combination of Slater-type orbitals

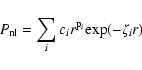\begin{displaymath}P_{{\rm nl}} = \sum_{{i}}c_{{i}}r^{{{\rm p}_{{i}}}}{\rm exp}(-\zeta_{{i}}r) \end{displaymath} (1)

and the orbital parameters ( $c_{i}, p_{i}, \zeta_{i}$) adopted in the present calculation can be found in Ramsbottom et al. (2005) and were generated using the configuration-interaction program CIV3 of Hibbert (1975).

Table 1 displays the target state energies in Rydbergs relative to the 3d64s 6De ground state of Fe II calculated in the present approximation. We present in this table only the lowest 16 fine-structure levels which we are particularly concerned with in this paper, although all 262 levels have been included in the scattering approximation. Comparisons are made in Table 1 with the observed values taken from the NIST database and the theoretical predictions of Berrington et al. (1988). For the 5 fine-structure levels of the 6De ground state the current energies are approximately 13$\%$ higher than the observations, whereas the values of Berrington et al. (1988) lie about 8$\%$ lower. For the 3d7 4Fe and 4Pefine-structure levels the present values lie approximately 30$\%$ and 10$\%$ respectively closer to observations than the work of Berrington et al. (1988). Finally the 4 levels of the 3d64s 4De configuration lie within 1$\%$ of the observed values. It should be noted that the present ab initio target state energies were adopted in the collision calculation and no shift was made to bring the thresholds in line with the experimental values as these were available only as an incomplete set. We also note that in Table 1 the levels are assigned an index value which will be referred to again later in the text when denoting a particular transition.

Table 1: Target state energies in rydbergs relative to the ground state of Fe II; NIST are the observed values from the NIST databank and B88 are the theoretical works of Berrington et al. (1988).

A parallel set of Breit-Pauli codes (Ballance & Griffin 2004) which were developed from modified serial versions of the RMATRX1 codes (Berrington et al. 1995) were used to compute the cross sections for this collision study. Twenty continuum orbitals were included for each channel angular momentum and the R-matrix boundary radius was set at 15 au. These parameters were sufficient to cover the range of electron-impact energies of interest 0-10 Ryds. The N-electron basis configurations included in the calculation were 3d64s, 3d7, 3d64p with additional correlation effects incorporated via the 3d $^{6}\overline{\rm 4d}$ configuration. The (N+1)-electron bound configurations included in the calculation were of the form 3d64s2, 3d64s4p, 3d64s4d, 3d74s, 3d8, 3d74p, 3d74d, 3d64p2, 3d64p4d and 3d64d2. The present 100 LS state (262jj) calculation was carried out for all singlet, triplet, quintet and septet spin states with even and odd parities, for all partial waves with total angular momentum $L\leq10$, giving a total of 88 (N + 1)-electron symmetry contributions. In Table 2 we present the J$\pi $ partial waves in ascending order alongside three quantities, the number of free scattering channels, the size of the (N + 1)-electron Hamiltonian matrix without those elements arising from the (N + 1)-electron bound levels, and the total size of the (N + 1)-electron Hamiltonian matrix. Clearly evident from this table is the sheer magnitude of this calculation with a maximum of 1800 coupled channels to be considered in the external region and a maximum Hamiltonian size of 36 000 to be diagonalised. In the external region we used a very fine mesh of incident electron energies (approximately 10-4) to properly delineate the rydberg resonance structures which dominate the resonance region from threshold to the highest-lying target threshold included at approxilately 1.5 ryds. Above this value we adopted a coarser mesh of 0.05 ryds in the energy region where no resonances are located. Such a mesh gave a total number of just over 16 200 distinct energy points, 16 000 in the resonance region and 200 above this.

Table 2: Channel coupling, correlation functions and Hamiltonian size for each 2J$\pi $ partial wave.

3 Results and discussion

The collision strength $\Omega_{{\rm if}}$ between an initial state "${\rm i}$'' and a final state "${\rm f}$'' has been computed in the present work using the parallel suite of Breit-Pauli codes over a very fine mesh of incident impact energies across the resonance region. The collision strength is defined in terms of the collision cross section by

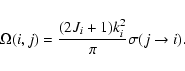\begin{displaymath}\Omega({i,j}) = \frac{(2{J_{i}} + 1){k_{i}^{2}}}{\pi} \sigma( {j} \rightarrow {i}) . \end{displaymath} (2)

The corresponding effective collision strength $\Upsilon_{{ij}}$, of importance in astrophysical and plasma applications, are obtained by averaging these finely resolved collision strengths over a Maxwellian distribution of electron velocities so that

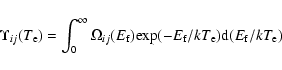\begin{displaymath}\Upsilon_{{ij}}(T_{{\rm e}}) = \int_{0}^{\infty} \Omega_{{ij}... ...p}(-E_{{\rm f}}/kT_{{\rm e}}){\rm d}(E_{{\rm f}}/kT_{{\rm e}}) \end{displaymath} (3)

where $E_{{\rm f}}$ is the final kinetic energy of the electron, T is the electron temperature in Kelvin and k is Boltzmann's constant.

We present in Fig. 1 the collision strength as a function of incident electron energy in Rydbergs, for the fine-structure transition among the ground state terms 3d64s 6D $^{e}_{9/2} - 3{\rm d}^{6}$4s 6D e7/2 (index 1-2). Although the collision strengths have been evaluated in the present work for energies up to 10 Ryds we concentrate in this figure on the low-energy resonance region up to 0.5 Ryds. Clearly evident are the mass of Rydberg resonances converging to the target state thresholds. Comparisons are made with the 142-level Breit-Pauli calculation of Zhang & Pradhan (1995) and the limited work of Nussbaumer & Storey (1980) who considered only three energy values and hence incorporated no resonance effects. Agreement with the work of Zhang & Pradhan (1995) is not unreasonable near threshold and the resonance features coincide quite nicely for many of the energies considered. Significant deviations occur, however, at energies between 0.15 and 0.3 Ryds. It is in this energy region that the first of the doublet target state levels appear, eight in all namely 2G e9/2,7/2, 2P e3/2,1/2, 2H e11/2,9/2 and 2D e5/2,3/2 all of configuration-type 3d7. These eight fine-structure levels lie between 0.17-0.24 Ryds in the present calculation but have been omitted in the work of Zhang & Pradhan (1995).

The effect these differing collision strengths have on the Maxwellian averaged effective collision strength for the 3d64s 6D $^{e}_{9/2} - 3{\rm d}^{6}$4s 6D e7/2 transition is presented in Fig. 2. Here we plot the effective collision strength as a function of log electron temperature in Kelvin. Twenty seven individual temperatures were considered in the present work ranging from 30 K up to 100 000 K to incorporate all the temperatures important to astrophysical and plasma applications. Comparisons are made in this figure with all effective collision strengths currently available in the literature for this transition. These include the rates of Zhang & Pradhan (1995) who published only two temperature values, 3000 and 4000 K, the early 16-level approximation of Berrington et al. (1988), the extrapolated work of Keenan et al. (1988) and the single temperature value (4000 K) of Bautista & Pradhan (1996). Little or no agreement exists between all sets of data with the exception of the single temperature value of Bautista & Pradhan (1996) which appears to agree well with the present data. The two temperature values published by Zhang & Pradhan (1995) predict rates approximately 20% and 10% higher than the present work, whereas the values of Keenan et al. (1988) and Berrington et al. (1988) produce effective collision strengths between 35% and 50% lower than the present data across the temperature range. Clearly the earlier calculations were not sophisticated enough to properly account for all the resonance features producing an underestimation of the effective collision strength which is well know to be enhanced by resonance effects in the cross section. Exactly the same trends were found to occur for the other fine-structure transitions among the ground-state terms.

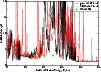  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{8640fig1.eps}} \end{figure} Figure 1: Collision strength for the 3d64s 6D e9/2 - 3d64s 6D e7/2 fine-structure transition (1-2): solid - present 262-level calculation, dashed - 142-level calculation of Zhang & Pradhan (1995), diamonds - Nussbaumer & Storey (1980).
Open with DEXTER


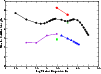  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{8640fig2.eps}} \end{figure} Figure 2: Effective collision strength as a function of log electron temperature in Kelvin for the 3d64s 6D e9/2 - 3d64s 6D e7/2 fine-structure transition (1-2): diamonds - present 262 level calculation, circles - 142 level calculation of Zhang & Pradhan (1995), triangles - Berrington et al. (1988), stars - Keenan et al. (1988), squares - Bautista & Pradhan (1996).
Open with DEXTER


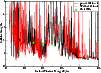  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{8640fig3.eps}} \end{figure} Figure 3: Collision strength for the 3d64s 6D e9/2 - 3d74F e9/2 fine-structure transition (1-6): solid - present 262 level calculation, dashed - 142 level calculation of Zhang & Pradhan (1995), diamonds - Nussbaumer & Storey (1980).
Open with DEXTER

In Fig. 3 we consider the collision strength for the forbidden transition from the ground-state 9/2 term to the 9/2 term of the first excited state, namely the 3d64s 6D e9/2 - 3d7 4F e9/2transition (index 1-6) . Again comparisons are made with the 142-level approximation of Zhang & Pradhan (1995) and the earlier Nussbaumer & Storey (1980) data which appears to lie much higher than the other two datasets at two of the three energies considered. Agreement is really quite good between the two Breit-Pauli calculations for many energies but the Zhang & Pradhan (1995) background cross section appears lower than the present at impact energies around 0.1 Ryds. The corresponding effective collision strength for this transition is plotted in Fig. 4 for the same temperature range considered in Fig. 2. Again the rates predicted by Zhang & Pradhan (1995) for the two temperatures lie between 10 and 15% higher than the current values. The single temperature value of Bautista & Pradhan (1996), however, lies a factor of three lower than the present value at the same temperature. For this transition the early predictions of Berrington et al. (1988) are in reasonably good agreement with the present work with only about 20-25% of a difference at any of the temperatures where a comparison is possible. The extrapolated values of Keenan et al. (1988), which we remember were obtained as an extension of the Berrington et al. (1988) approximation, are significantly different to the present values both as regards shape and magnitude. They present a very different rate profile at low temperatures which will significantly affect any diagnostic or application work which relies on these rates. The present 262-level approximation predicts effective collision strengths factors of three to four smaller at the lowest temperatures considered.


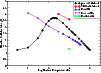  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{8640fig4.eps}} \end{figure} Figure 4: Effective collision strength as a function of log electron temperature in Kelvin for the 3d64s 6D e9/2 - 3d7 4F e9/2fine-structure transition (1-6): diamonds - present 262 level calculation, circles - 142 level calculation of Zhang & Pradhan (1995), triangles - Berrington et al. (1988), stars - Keenan et al. (1988), squares - Bautista & Pradhan (1996).
Open with DEXTER

In Table 3 we present the effective collision strengths calculated in the present 262-level approximation for all of the low-lying forbidden transitions among the lowest 16 fine-structure levels of Fe II. A total of 120 individual transitions are included in this tabulation for each of the 27 temperatures considered. Each transition is labelled according to the index values assigned to each level in Table 1. Due to the large number of incident electron energies considered in the collision cross sections ($\approx$16 200), these data are available from the authors only.

4 Conclusions

We report in this paper the computation of accurate collision strengths and effective collision strengths, using the parallel Breit-Pauli suite of programs, for electron-impact excitation of Fe II. Target states corresponding to the 3d64s, 3d7 and 3d64p configurations were included in the collision calculation, giving rise to 100 LS states. We have thus considered a 262 jj-level, 1800 coupled channel problem with a total number of 34 191 individual transitions, a formidable task. In this publication we concentrate on the low-lying forbidden transitions among the lowest 16 fine-structure levels corresponding to the 3d64s 6De, 3d7 4Fe, 3d64s 4De and 3d7 4Pe states, due to their particularimportance for many astrophysical and plasma applications. All previous works have failed to reach agreement for these important forbidden lines especially at low temperatures. To assess the accuracy of these effective collision strengths we consider a number of points. Firstly, this calculation represents the only one to date which systematically includes all doublet, quartet and sextet levels ,with basis configurations 3d64s, 3d7 and 3d64p, in the target representation at the same time. All previous works omitted large numbers of these to ensure that the approximations were maintained at a manageable level. In addition, the resonance structures in the low-energy region of the collision cross sections in the present work were properly delineated by including many thousands of incident electron energies, thereby ensuring that the Maxwellian averaging to compute the effective collision strengths was accurate. Finally this calculation incorporates all the temperature ranges which have an astrophysical imperative. Since forbidden lines of Fe II are observed in such a vast and diverse number of astrophysical objects across most of the electromagnetic spectrum, a wide range of electron temperature values is desirable. The present calculation, therefore provides the most extensive and accurate set of collisional data currently available for Fe II.

Acknowledgements
The authors wish to acknowledge the valuable help from, and useful discussions with Dr Connor Ballance of Rollins College Florida. The work presented in this paper has been supported by PPARC through a rolling grant PPA/G/O/2000/00024. The computations were carried out on the IBM HPCx facility at the CLRC Daresbury Laboratory.

References

 
Copyright ESO 2007