A&A 475, 729-746 (2007)
DOI: 10.1051/0004-6361:20077138
Interpreting and predicting the yield of transit surveys:
giant planets in the OGLE fields
F. Fressin1 - T. Guillot2 - V. Morello2 - F. Pont3
1 - Observatoire de la Côte d'Azur, Laboratoire Gemini, CNRS UMR 6203, BP 4229, 06304 Nice Cedex 4, France
2 -
Observatoire de la Côte d'Azur, Laboratoire Cassiopée, CNRS UMR 6202, BP 4229, 06304 Nice Cedex 4, France
3 -
Geneva University Observatory, Switzerland
Received 19 January 2007 / Accepted 8 April 2007
Abstract
Transiting extrasolar planets are now discovered jointly by
photometric surveys and by radial velocimetry, allowing measurements
of their radius and mass.
We want to determine whether the different data sets are compatible
between themselves and with models of the evolution of extrasolar
planets. We further want to determine whether to expect a population
of dense Jupiter-mass planets to be detected by future more sensitive
transit surveys.
We directly simulate a population of stars corresponding to the OGLE
transit survey and assign them planetary companions based on a list of 153
extrasolar planets discovered by radial velocimetry. We use a model
of the evolution and structure of giant planets that assumes that
they are made of hydrogen and helium and of a variable fraction of
heavy elements (between 0 and 100
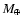 ).
The output list of detectable planets of the
simulations is compared to the real detections.
We confirm that the radial velocimetry and photometric survey data
sets are compatible within the statistical errors, assuming that
planets with periods between 1 and 2 days are approximately 5 times less
frequent than planets with periods between 2 and 5 days. We show
that evolution models fitting present observational constraints
predict a lack of small giant planets with large masses.
As a side result of the study, we identify two distinct populations of
planets: those with short periods (P<10 d),
which are found in orbit only around metal-rich stars with
).
The output list of detectable planets of the
simulations is compared to the real detections.
We confirm that the radial velocimetry and photometric survey data
sets are compatible within the statistical errors, assuming that
planets with periods between 1 and 2 days are approximately 5 times less
frequent than planets with periods between 2 and 5 days. We show
that evolution models fitting present observational constraints
predict a lack of small giant planets with large masses.
As a side result of the study, we identify two distinct populations of
planets: those with short periods (P<10 d),
which are found in orbit only around metal-rich stars with
![$\rm {[Fe/H]}>\sim-0.07$](/articles/aa/full/2007/44/aa7138-07/img31.gif) ,
and
those on longer orbits (P>10 d),
for which the metallicity bias is less marked. We further confirm the relative absence of
low-mass giant planets at small orbital distances.
Testing these results and the underlying
planetary evolution models requires the detection of a statistically significant
number of transiting planets, which should be provided over the next few years by
continued ground-based photometric
surveys, the space missions CoRoT and Kepler, and combined radial
velocity measurements.
,
and
those on longer orbits (P>10 d),
for which the metallicity bias is less marked. We further confirm the relative absence of
low-mass giant planets at small orbital distances.
Testing these results and the underlying
planetary evolution models requires the detection of a statistically significant
number of transiting planets, which should be provided over the next few years by
continued ground-based photometric
surveys, the space missions CoRoT and Kepler, and combined radial
velocity measurements.
Key words: stars: planetary systems: formation - surveys - techniques: photometric - methods: data analysis - stars: planetary systems
Extrasolar planets are now routinely discovered orbiting solar-type
stars by radial velocimetry, but the discovery of transiting
planets by photometric surveys is just beginning. Although still
marginal, the late success of transit surveys has given an additional
impulse to exoplanetology with the possibility of estimating the radius,
density, and hence composition of extrasolar planets.
Quantitatively, to date we know 206 extrasolar planets with masses
below 13
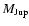 (e.g. Butler et al. 2006; Udry et al. 2007). Among those, a list of
14 currently known transiting planets is presented in
Table 1. These planets have been
discovered by radial velocimetry followed by photometry for 3 of them,
and by photometric surveys for the remaining 11.
(e.g. Butler et al. 2006; Udry et al. 2007). Among those, a list of
14 currently known transiting planets is presented in
Table 1. These planets have been
discovered by radial velocimetry followed by photometry for 3 of them,
and by photometric surveys for the remaining 11.
When considering the score of projects devoted to the detection of
planets by transit photometry, the present harvest appears meager. The
discrepancy between predictions (e.g. Horne 2001) and reality
has been attributed to various factors such as: imperfect duty cycle,
a reduced number of stars for which transiting planets are detectable
(Gould et al. 2006), and the presence of correlated noises that can
greatly limit the detectability of small planetary transits
(Pont et al. 2006b). Several generic studies have been conducted
to understand the yield of different transit surveys. Pepper & Gaudi (2005)
studied the optimization of transit searches as a function of the
observational setup, the site properties, and the planet properties.
Gillon et al. (2005) analyzed and compared deep field surveys, considering individual stellar ranges
and observation windows, but did not include the effects of stellar crowding nor time-correlated noises.
Gould et al. (2006) studied the yield of OGLE survey (Udalski et al. 2002), the most successful so far in terms of number of transiting planets discovered, with a model populating the line of sight with stars drawn from the Hipparcos Catalogue. With that model, they estimated the proportion of stars with sensitivity to close-in giant planets to derive from OGLE results the frequency of planets as a function of their period.
They find that the yield of the OGLE survey is globally consistent with the
detections by radial velocimetry and with planet radii distributed
between 1 and 1.25 jovian radii. The aim of the present work is to
further test these data sets and the underlying physical model by a
forward calculation of transit events with realistic stellar and
planetary populations. In particular, we include up-to-date models of
the evolution and structure of Pegasids (close-in extrasolar
planets) based on models reproducing the observational constraints
from known transiting planets
(Guillot et al. 2006; Guillot 2005). As a consequence, we should be
able to determine whether the presently known population of transiting
planets represents the "tip of the iceberg'', i.e. that many more
small, dense, extrasolar giant planets exist and await discovery by the
transit method, or whether it is relatively representative of the
global population.
We first describe the model that is used to simulate transit surveys
in general. In Sect. 3, we describe more particularly the OGLE
surveys and the hypothesis chosen for their modelling. We then discuss
the results of the simulation. A summary of the main conclusions and
predictions for future transit surveys are provided in Sect. 5.
Table 1:
Known transiting planets by 2006 .
.
The search for planets in transit in front of their star arose naturally
with the discovery that a non-negligeable fraction of planets orbit
very close to their stars. If orbital planes are randomly
oriented, the probability that a planet will transit in
front of its star at each orbital revolution is:
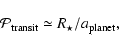 |
(1) |
where 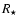 is the stellar radius, and
is the stellar radius, and
 the
planet's orbital semi-major axis. For systems such as 51 Peg b, this
probability is close to 10%. Because the probability for a solar-type
star to possess such a Pegasid (i.e. a 51 Peg b-like planet, planets
semi-major axis up to 0.1 AU)
is about 0.5% (e.g. Marcy et al. 2005), 1 in 2000 solar-type stars should possess a transiting Pegasid. Using current results from radial
velocity surveys and integrating over all periods, we estimate that
about 1 in 1100 solar-type stars possess a transiting giant
planet. Of course, depending on the magnitudes and field considered,
giant stars may severely outnumber the dwarfs, so that in a real field,
only one in, say, 3000 stars may harbor a transiting giant planet.
the
planet's orbital semi-major axis. For systems such as 51 Peg b, this
probability is close to 10%. Because the probability for a solar-type
star to possess such a Pegasid (i.e. a 51 Peg b-like planet, planets
semi-major axis up to 0.1 AU)
is about 0.5% (e.g. Marcy et al. 2005), 1 in 2000 solar-type stars should possess a transiting Pegasid. Using current results from radial
velocity surveys and integrating over all periods, we estimate that
about 1 in 1100 solar-type stars possess a transiting giant
planet. Of course, depending on the magnitudes and field considered,
giant stars may severely outnumber the dwarfs, so that in a real field,
only one in, say, 3000 stars may harbor a transiting giant planet.
Because of the dependence on a, and period distribution, most of
the transit events concerning giant planets occur for orbital periods
between 1 and 5 days. The transits typically last for a
couple of hours, as this quantity is weakly dependant on the orbital
period P:
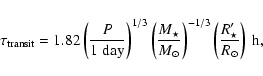 |
(2) |
where 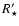 is the length of the cord traced on the stellar disk by the planet's trajectory.
(more precisely:
is the length of the cord traced on the stellar disk by the planet's trajectory.
(more precisely:
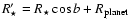 ,
where b is the impact parameter of the transit).
,
where b is the impact parameter of the transit).
The depth of the transits themselves is given directly by the
ratio of the planetary to the stellar disk surfaces:
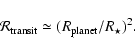 |
(3) |
This value is of order 1% for a Jupiter-size planet orbiting a
Sun-like star. For an F-type star with radius 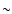
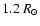 ,
the ratio decreases to 0.7%. Furthermore, transiting giant planets
discovered so far have radii between 0.72 and
,
the ratio decreases to 0.7%. Furthermore, transiting giant planets
discovered so far have radii between 0.72 and
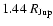 (see Table 1). Allowing for stellar radii
to vary between 0.8 and
(see Table 1). Allowing for stellar radii
to vary between 0.8 and
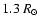 (a typical range, in magnitude
limited surveys), this implies that we should expect
(a typical range, in magnitude
limited surveys), this implies that we should expect
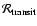 to vary between 0.3% and 3%, for giant planets only.
The lower limit is in reality even smaller because for
detection purposes we have to account for the fact that planets also
orbit stars that are in multiple systems (like HAT-P-1), and hence a
dilution factor may apply. Although grazing transits
are ignored in this simple analysis, they are included afterwards in our simulations.
to vary between 0.3% and 3%, for giant planets only.
The lower limit is in reality even smaller because for
detection purposes we have to account for the fact that planets also
orbit stars that are in multiple systems (like HAT-P-1), and hence a
dilution factor may apply. Although grazing transits
are ignored in this simple analysis, they are included afterwards in our simulations.
Altogether this implies that in order to detect transiting giant
planets, many thousands of dwarf stars have to be monitored over
periods of weeks for a photometric precision reaching below a fraction of a
percent on an equivalent integration time of about one hour. This is
typically done by following a relatively dense stellar field over a
long time with a stable telescope, and using a camera equiped with a
good CCD camera.
On paper, the simulation of the forward problem is simple: one has to
generate a complete stellar field, or obtain it from observations,
put it on a discrete grid (the CCD), include on probabilistic
arguments the planetary companions, calculate lightcurves including
the various sources of noise, and determine which events are
detectable. This is the principle of CoRoTlux, a code we first developed
to predict the transit yield of CoRoT space telescope (Baglin et al. 2002)
and quantify the need for follow-up observations, which is here applied to the case of OGLE.
The interesting point of such a forward simulation is the possibility
of including relatively easily fine details such as the fact that
planets are found more frequently around metal-rich stars, or,
on the basis of planetary evolution models, the fact that young planets
orbiting close to bright stars will be larger than old planets
orbiting smaller stars at larger orbital distances. This requires
however that a relatively large number of physically relevant
parameters (for example, the mass, size, metallicity, and age of the
stars) be properly defined.
We further detail the assumptions that we made for these simulations
by describing how we generate the stellar and planetary populations,
and how we attempt to include realistic sources of noise.
Stellar fields differ enormously in terms of densities and stellar
populations. It is therefore most important to properly account for
this in order to simulate any given transit survey.
It would be very appealing to use direct observations as much as
possible to closely match the observed target fields. But as we will
see hereafter, many different characteristics of the stars (stellar
metallicity, age, and subtype ...) are required, and these are
difficult to obtain with generic observations. We therefore adopt
the following procedure:
- the observed stellar densities are obtained from stellar counts
by magnitude, on the real stellar fields (see Sect. 3.1);
- the characteristics of the stars are obtained following a
Monte-Carlo method using the output of the Besançon model of the
galaxy (Robin et al. 2003) obtained for the proper location of the survey;
- where stellar counts are not available, or uncomplete (i.e. for
faint stars), we use both stellar counts and characteristics from
the Besançon model.
Specifically, we keep track of the following parameters obtained directtly from
the Besançon model:
- the mass of each star, used to compute orbital parameters of the
transiting object;
- the apparent magnitude of the star in the observed spectral
range (the I filter in the case of the OGLE survey);
- the V magnitude of the star, important to qualify the
confirmability of a transit event with radial velocimetry;
- the surface temperature of the star;
- the luminosity of the star, calculated from its absolute magnitude;
- the radius of the star, calculated from total luminosity and
effective temperature.
The mass and effective temperature of the stars are distributed linearly
around values given by the Besançon model (at 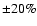 ). Figure 1
shows a simulated distribution of stars for the OGLE Carina field.
The ensemble of dwarf stars with
types F4 and later are highlighted as these represent targets for
which planetary transit events are detectable, and, within
observational limits, confirmable by radial velocimetry.
). Figure 1
shows a simulated distribution of stars for the OGLE Carina field.
The ensemble of dwarf stars with
types F4 and later are highlighted as these represent targets for
which planetary transit events are detectable, and, within
observational limits, confirmable by radial velocimetry.
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=0]{7138fig1.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg135.gif) |
Figure 1:
From top to bottom: distribution functions for the radii,
masses and effective temperatures for our fiducial stellar
population corresponding to the simulated OGLE Carina field. The
black line represents the ensemble of stars in the field. The filled
red region is a subset for dwarf stars with stellar type F4 and
later, as these are the only stars for which a transiting planet has
a reasonnable chance of being detected by present-day transit surveys. |
| Open with DEXTER |
The metallicity distribution is obtained from the model of Nordström et al. (2004), which is based on the Geneva-Copenhagen survey of the Solar neighbourhood. These authors find that the distribution of
the metallicities [Fe/H] is well approximated by a Gaussian function
with a mean of -0.14 and a dispersion of 0.19 dex. We use this
Gaussian distribution and choose to ignore possible dependencies
between stellar parameters (e.g. masses, ages...) and the
metallicities. (The link between stellar type and metallicity
appears to be negligible for F4 and later types anyway (F. Thévenin,
pers. communication 2007).)
Multiple stellar systems are important especially because of the
possibility that stellar eclispes mimic planetary transits (Brown 2003).
However, we choose to defer this problem to a later
article. Multiple systems are taken into account anyway because they
can yield a dilution of the planetary transit events that makes them
more difficult to detect. Planets may be present indifferently on the
primary, secondary or tertiary components of a stellar system. (However,
we find that only planets around the primary targets have a
non-negligible chance of being discovered by current ground based
photometric survey.)
Specifically, following Duquennoy & Mayor (1991), we consider
that 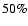 of the stars are binaries and
of the stars are binaries and 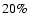 of those are
ternaries. Multiple systems are considered as individual stars at the same position on the CCD.
We choose to estimate their properties more simply
than for the other stars, on the basis of DM91:
of those are
ternaries. Multiple systems are considered as individual stars at the same position on the CCD.
We choose to estimate their properties more simply
than for the other stars, on the basis of DM91:
- We randomly add companions to the initial draw of primary stars,
without changing their properties. The total mass and luminosity of each multiple system
is thus slightly higher than initially.
- The mass ratio (primary/secondary) is defined as a Gaussian of
median value 0.23 and a full width at half maximum of 0.42. Outside
a range of 0.05 and 1, we redraw the mass ratio.
- The radius is defined as
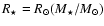 when
when
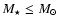 and
and
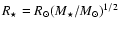 otherwise.
otherwise.
- The luminosity is assumed to be proportional to M2 so that:
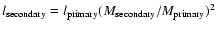 .
.
- Other stellar parameters are calculated on the basis of these
ones and of those of the primary component (same age, same distance,
same metallicity).
- Triple components are treated with the same method as binaries,
and are defined relatively to the primary star.
2.4 The planetary companions
With more than 200 planets known to orbit stars other than our Sun, we
are beginning to have a rather precise view of at least part of this
population. We can expect that biases on the detections are small in
the case of massive planets (the mass of Saturn and more) and planets
that are relatively close to their star (orbital
distances smaller than 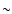 1 AU). These two conditions happen to
match quite exactly the requirement for
detectability by transit photometry, with one assumption: that only
massive giant planets can have large radii. Although not proven, this
assumption seems quite reasonnable.
1 AU). These two conditions happen to
match quite exactly the requirement for
detectability by transit photometry, with one assumption: that only
massive giant planets can have large radii. Although not proven, this
assumption seems quite reasonnable.
Hence we choose to focus this study on this well-characterized
population of objects. From the current list of 209 detected
exoplanets, we select the ones discovered by radial velocities with
mass higher than 0.3 Jupiter masses and known host star metallicity.
Our list of planets includes 153 objects, to which we may
add very-close in planets detected by transit photometry, as discussed
below. We are using this list as representative of an unbiased sample
of giant planets known from radial velocimetry, even though planetary
distribution models may have been made from slighlty different samples.
2.4.1 Planet incidence
A first important step is the determination of the probability for a
star to harbor a planet. As shown by numerous studies
(Fischer & Valenti 2005; Gonzalez 1998; Santos et al. 2004), this
probability depends mostly on the metallicity of the parent
star. Figure 2 shows one such probability
function, as well as the result in terms of planet counts on a
simulated stellar field.
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=0]{7138fig2.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg142.gif) |
Figure 2:
Upper panel: probability for a solar-type star to possess a
giant planet companion as a function of the stellar metallicity
(from Santos et al. 2004). Lower panel: relative normalised
distributions of stellar metallicities for stars in the field (black
line), and for stars with a giant planet companion (red line). |
| Open with DEXTER |
In this work, we will use the dependency from Santos et al. (2004)
shown in Fig. 2. Several points are to be
considered however:
- 1.
- This probability relation is valid only for solar-like stars,
i.e. F, G, K dwarf stars. Although there are strong indications that
it may change for other stars (e.g. M dwarfs), we will assume it to
hold independently of stellar properties. This assumption is sufficient
because F, G, and K dwarf stars form by far the majority of stars
with detectable planets in photometric surveys.
- 2.
- This relation has been calculated independently of the
properties of the planetary companion, in particular orbital
distance. Because in our case we are strongly biased towards
short-period planets, the distribution may be different. This point
will be considered in Sect. 4.4.
- 3.
- The possibility of multiple planetary systems is not
considered. This approach is justified because the probability that
several planets belonging to the same system are transiting planets
is small for giant planets.
2.4.2 Planetary masses and orbits
The masses and orbital characteristics of the planet population are
inferred almost entirely from the present radial-velocimetry
surveys. This technique yields an accurate determination of the
orbital period, and less accurately, of the eccentricity of the
orbit. It also yields the value of the mass of the planetary
companion times the sine of the orbital inclination from the knowledge
of the mass of the parent star. With these values, we can then derive
from a random inclination of the orbital planes the planets that are
transiting and those that are not as well as the characteristics of
their orbit.
We test several approaches for the derivations of these quantities:
Figure 3 shows a comparison between
observations, the carbon copy model and the analytical model. It is
interesting to notice at this point that the carbon copy and
analytical models are essentially indistinguishable in these
diagrams. The differences with the observations arise only because of
our choice to smear the masses and orbital periods when generating our
planet population.
Last but not least, we have to consider the existence of planets that
orbit extremely close to their star, with periods shorter than 2 days,
as discovered by transit surveys (see Table 1). Companions with such short orbital periods have been
discovered by radial velocimetry in two occasions: HD 41004 b and Gliese 876 d,
with respective masses 18.4 and 0.023Jupiter masses. These objects are outside the mass range considered
for this study, and therefore, there are no giant planets with periods
shorter than 2 days in the present radial velocimetry list. In order
to account for these very close-in planets anyway, we add the planets with
periods smaller than 2 days
discovered by transit photometry to the list, but with a small
tunable probability weight. The fiducial value of this parameter is
set so that, on average, the planet list contains one and a half such planets
(added to the list of 153 RV planets described in Sect. 2.4).
Tests on the effect of this parameter are presented in Sect. 4.3.4.
Our fiducial model is the mass-period-metallicity carbon copy
model, which includes the addition of very-close in planets and it is that model which is used
in all cases except where specified otherwise. Other approaches are also
tested depending on the model to highlight particular points.
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=0]{7138fig3.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg150.gif) |
Figure 3:
From top to bottom, distributions of orbital periods, masses
and radii, respectively, of the planets observed by radial
velocimetry (black lines), simulated as part of the mass-period
"carbon copy'' model (red lines), and simulated as part of the
analytical model (dotted blue lines) (see text). |
| Open with DEXTER |
2.4.3 Physical characteristics and the planetary evolution
model
Because we are focussing on planets more massive than Saturn, we
expect most of them to be made of a significant amount of hydrogen and
helium. These giant planets thus undergo a progressive contraction and
cooling that depends on four quantities: their age, mass, the amount
of flux the planet receives from the central star, and the global
amount of heavy elements in the planet (e.g. Guillot 2005).
Models attempting to reproduce the radii of known transiting giant
planets have however had problems in explaining the large radii of
some of them (Guillot & Showman 2002; Baraffe et al. 2005; Laughlin et al. 2005; Bodenheimer et al. 2001).
Several possibilities have been
proposed to explain the discrepancy. We can separate them into two
categories:
- Mecanisms invoking chance configurations of the planetary orbits
in the case of these anomalously large planets: this includes
the tidal circularization of an eccentric orbit (Bodenheimer et al. 2001),
and tidal dissipation for a planet locked in a Cassini
spin-orbit resonnance with the star (Winn & Holman 2005).
- Effects that would apply to all planets, including problems with
the equations of state or opacities, and the dissipation by stellar
tides of kinetic energy first generated in the atmosphere (Showman & Guillot 2002).
The first mecanisms appear to have a low probability of occurence
(Levrard et al. 2007; Laughlin et al. 2005; Deming et al. 2005). The second possibility therefore
seems more likely, but requires in some cases the presence of
relatively large masses of heavy elements to reproduce the observed
radii.
A model-dependant estimate of the masses of heavy elements present in
the currently known transiting Pegasids is shown in
Fig. 4. This model relies on the hypothesis that
0.5% of the absorbed stellar flux is used to generate kinetic energy
that is subsequently dissipated deep into the planetary interior (Guillot & Showman 2002).
As proposed by Guillot et al. (2006), there
appears to be a correlation between the amount of heavy elements
present in the planet and the metallicity of their parent star.
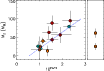 |
Figure 4:
Mass of heavy elements in transiting Pegasids known by 2006
as a function of the metal content of the parent star relative to
the Sun. The mass of heavy elements required to fit the measured
radii is calculated on the basis of evolution models including an
additional heat source slowing the cooling of the planet. This heat
source is assumed equal to 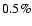 of the incoming stellar heat
flux (Showman & Guillot 2002). Horizontal error bars correspond
to the
of the incoming stellar heat
flux (Showman & Guillot 2002). Horizontal error bars correspond
to the 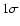 errors on the [Fe/H] determination. Vertical error
bars are a consequence of the uncertainties on the measured
planetary radii and ages. The metallicity of recently discovered planets
WASP-1 and WASP-2 ( right panel) is not precisely known.
The dotted line corresponds to a best fit model. (Adapted from Guillot et al. (2006).)
errors on the [Fe/H] determination. Vertical error
bars are a consequence of the uncertainties on the measured
planetary radii and ages. The metallicity of recently discovered planets
WASP-1 and WASP-2 ( right panel) is not precisely known.
The dotted line corresponds to a best fit model. (Adapted from Guillot et al. (2006).) |
| Open with DEXTER |
This correlation has to be ascertained, but we choose for our fiducial
model to adopt a unique relation between metallicity and mass of heavy
elements (treated as a central core in our calculations),
corresponding to the dotted line in Fig. 4:
![\begin{displaymath}M_Z=43.75\times 10^{\rm [Fe/H]}-23.7\ M_\oplus.
\end{displaymath}](/articles/aa/full/2007/44/aa7138-07/img152.gif) |
(4) |
We limit the range of possible values of MZ to
![$[0,100M_\oplus]$](/articles/aa/full/2007/44/aa7138-07/img153.gif) .
.
Similarly, we adopt a simple boundary condition for our evolution
calculations:
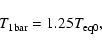 |
(5) |
where
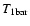 is the temperature at the 1 bar pressure level
and
is the temperature at the 1 bar pressure level
and
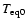 is the equilibrium temperature for a zero albedo
(see Guillot 2005 for a description), calculated as a function of
stellar effective temperature and radius and planet semi-major axis.
is the equilibrium temperature for a zero albedo
(see Guillot 2005 for a description), calculated as a function of
stellar effective temperature and radius and planet semi-major axis.
For simplicity, and because it yields only minor changes on the
results, we further choose to neglect the time-dependence in the
evolution calculations, and to adopt the equilibrium radius, or the
10 Gyr solution, whichever occurs first.
Practically, planetary radii are obtained from interpolations in a
table based on three parameters: the planetary mass ranging
from 100 to
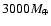 ,
the core mass from 0 to
,
the core mass from 0 to
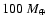 ,
and the
equilibrium temperature from 100 to 2000 K.
Models were not calculated beyond these values of
,
and the
equilibrium temperature from 100 to 2000 K.
Models were not calculated beyond these values of
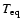 because of convergence
problems. However we allowed for a slight extrapolation of the tables to 2600 K to account for
rare extremely hot planets
because of convergence
problems. However we allowed for a slight extrapolation of the tables to 2600 K to account for
rare extremely hot planets![[*]](/icons/foot_motif.gif) .
.
Similarly, because of convergence problems for planets with small
total masses and large core masses, we limited the mass of the core to
75 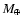 for planets with masses smaller than
180
for planets with masses smaller than
180 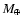 .
More detailed work is required to better simulate
this parameter space, including planets less massive than considered
in this study.
.
More detailed work is required to better simulate
this parameter space, including planets less massive than considered
in this study.
Figure 5 shows examples of radii obtained for
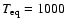 and 2000 K, and core masses of 0 and
and 2000 K, and core masses of 0 and
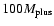 ,
respectively, compared to available measurements.
,
respectively, compared to available measurements.
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm]{7138fig5.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg162.gif) |
Figure 5:
Theoretical and observed mass-radius relations. The black
line is applicable to the evolution of solar composition planets,
brown dwarfs, and stars, when isolated or nearly isolated (as
Jupiter, Saturn, Uranus, and Neptune, defined by diamonds and their
respective symbols), after 5 Ga of evolution. The dotted line shows
the effect of a
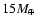 core on the mass-radius relation. Orange
and yellow curves represent the mass-radius relations for heavily
irradiated planets with equilibrium temperatures of 1000 and
2000 K, respectively, and assuming that 0.5% of the incoming
stellar luminosity is dissipated at the center (see
Sect. 2.4.3). For each irradiation level, two cases
are considered: a solar-composition planet with no core (top curve),
and one with a
core on the mass-radius relation. Orange
and yellow curves represent the mass-radius relations for heavily
irradiated planets with equilibrium temperatures of 1000 and
2000 K, respectively, and assuming that 0.5% of the incoming
stellar luminosity is dissipated at the center (see
Sect. 2.4.3). For each irradiation level, two cases
are considered: a solar-composition planet with no core (top curve),
and one with a
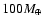 central core (bottom curve). The transiting
extrasolar giant planets for which a mass and a radius was measured
are shown with points that are color-coded in function of the
planet's equilibrium temperature. The masses and radii of very low
mass stars are also indicated as blue points with error bars.
central core (bottom curve). The transiting
extrasolar giant planets for which a mass and a radius was measured
are shown with points that are color-coded in function of the
planet's equilibrium temperature. The masses and radii of very low
mass stars are also indicated as blue points with error bars. |
| Open with DEXTER |
We now descibe how this population of stars, planets, and their
interactions during transits are modelled to reproduce real
observations.
Each image of a star is spread by the atmosphere and by the telescope
to grow to a specific size and shape when reaching the CCD in the
focal plane of the telescope, the so-called point spread function
(PSF). The CCD being composed of many discrete pixels, these PSFs are
then effectively discretized, so that the signal to be analyzed for
any given star is composed of many different lightcurves corresponding
to the many pixels over the size of its PSF. A further complication
arises from the fact that the stellar fields generally chosen by
transit surveys are dense, so that many PSFs overlap. Recovering
individual stellar light curves from real data is a complex
problem. Two popular methods are aperture photometry
(Stetson 1987) and image subtraction (Alard & Lupton 1998). (An adaptation
of the latter was used to extract the OGLE lightcurves.)
A refined simulation could include possible spatial and temporal
variations of the PSFs, and a realistic data reduction pipeline. In
our case, we choose to simplify the problem by relying on a posteriori
analyses of real light curves to provide us with a global noise
budget. We however include background stars because of the important
effect of signal dilution.
In order to do so, we assume that the PSFs are Gaussian with a uniform,
constant FWHM. (Non-Gaussian PSFs are not difficult to include but we
tested in the OGLE case that for a fixed equivalent FWHM, they have a
negligible effect on the resulting signal-to-noise ratio of simulated
transit events). We consider for each target of the survey the global
flux from the main star and the background stars in its neighborhood
up to magnitude 22 in the spectral band of observation. The neighborhood
zone for background stars is defined as a circle of
diameter equal to 4 times the PSF's FWHM around the photocenter of
each target star. Each background star whose photocenter is located in
that zone is taken into account for the calculation of the global
flux. The global flux is calculated as the sum of the pixels located at less
than twice the FWHM of the central star.
We thus simulate aperture photometry when image subtraction was used for OGLE
(Udalski et al. 2002). The choice of the reduction algorithm indeed affects the
sensitivity obtained from real observations. In our simulations, i.e. a
relatively idealized case, it would have marginal effects since realistic noises
are included a posteriori from the analysis of real lightcurves (see hereafter).
We choose to separate noise sources into two categories:
- "White noise'' sources, following Gaussian and Poisson laws.
The main source of white noise is the photon noise of target stars and their background.
The level of white noise for a given target star
is obtained from the simulation of the flux of that star and its background in the photometric
aperture.
- "Red noise'', or systematic effects on photometry, that undergo temporal correlation.
The structure of these systematics in the OGLE photometry have been explored in detail
by Pont et al. (2006b). These noise sources are both instrumental (jitter and
breathing of the CCD, frequency spectrum of stellar field moves on the camera,
change of the PSF shapes accross the CCD during the night), and
environmental (differential refraction and extinction, changes of
airmass and sky brightness, temperature changes). Rather than trying to simulate instrumental
and environmental noise sources accurately, which is difficult with the relatively poor
knowledge we have of the time spectrum of their combined effects, we use the
effective global `red noise' measurements of OGLE-III survey real light
curves mentionned in Pont et al. (2006b), which consider the combined effect of these noise sources.
Pont et al. (2006b) calculated that, in the presence of a
mixture of white and red noise (i.e. accounting for photometric
systematics), the detection threshold for a transit survey is well
described by a limit on the signal-to-noise ratio defined as:
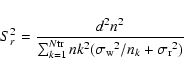 |
(6) |
where Ntr is the number of transits sampled and nk the number of
data points in the kth transit.
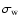 and
and
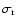 are the
standard deviation of measurement points of white and red noises,
respectively, d is the event depth and n the total number of
measurement points during the transit. Specifically, we obtain nk by counting for each
transit the number of observation points between the middle of ingress
and the middle of egress.
are the
standard deviation of measurement points of white and red noises,
respectively, d is the event depth and n the total number of
measurement points during the transit. Specifically, we obtain nk by counting for each
transit the number of observation points between the middle of ingress
and the middle of egress.
Equation (6) makes the disctinction between "white'' noise sources
that decrease with n1/2, where n is the number of successive
measurements, and "red'' noise sources that are limited by temporal
correlation. Pont et al. (2006b) indeed show that taking the red noise into
account makes a large difference on the detection threshold - in
general as well as in its dependence on the planet parameters - and
that models based on the assumption of white noise can be poor
approximations of the actual detection threshold.
3.1 Basic parameters and observational procedure
The Optical Gravitational Lensing Experiment (OGLE) has done 6 observation campaigns
looking for transiting planets towards different fields of view from 2001 (Udalski et al. 2002).
It took place at the Las Campanas Observatory, Chile, using the 1.3 m Warsaw
telescope and the 8k MOSAIC camera, with a total field of view of
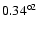 .
All observations were made through the I filter. We assume for our PSF simulation
an average seeing of 1 arcsec.
.
All observations were made through the I filter. We assume for our PSF simulation
an average seeing of 1 arcsec.
We analyze in this work the first three OGLE-III observation campaigns
dedicated to transit search, as their treatment, analysis, and follow-up (with current data
processing pipelines) has been completed:
- OGLE-III-1 (June 12 to July 28, 2001, described in Udalski 2002; Udalski et al. 2002). More than 800 images of
three fields in the direction of the galactic bulge were collected
within 32 nights. The exposure time was 120 s, and each field was
observed every 12 min.
- OGLE-III-2 (February 17 to May 22, described in Udalski (2003)). More than 1100images of three fields located in the Carina region of the galactic
disk were collected in 76 nights. The exposure time was 180 s,
and the temporal resolution was about 15 min.
- OGLE-III-3 (February 12 to March 26, described in Udalski et al. (2004)). The photometric data
were collected during 39 nights spanning the 43 days of the
survey. Three fields of the galactic disk were observed with a time
resolution of about 15 min. The exposure time was 180 s.
In this article, we will refer to these three observation campaigns
respectively as "Bulge'', "Carina'', and "Centaurus'' fields.
The simulations include the real observation windows of each survey,
as kindly provided by A. Udalski. For any transiting planet in the
simulation, the number of effectively observed transits is used in
Eq. (6).
In order to construct a realistic stellar population, we use the
stellar counts per magnitude range obtained by
Gould et al. (2006) based on OGLE-II data, which have calibrated photometry.
We then randomly select that number of stars per
magnitude from the Besançon model. In order to test the validity
of our approach, we calculated the fraction of "stars for which
transits are detectable'' and compared it to the one determined by
Gould. This fraction is defined for a given magnitude range as the
number of stars around which a planet orbiting edge-on with
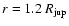 and
and
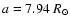 can be detected, divided by the total
number of stars of that magnitude. As shown by
Table 2, there is an excellent
agreement between our results and those of Gould et al. (2006). Note
however that for the global simulation, the complete star list
is used as the above definition for suitable stars is restricted to
planets of a given size and orbital distance.
can be detected, divided by the total
number of stars of that magnitude. As shown by
Table 2, there is an excellent
agreement between our results and those of Gould et al. (2006). Note
however that for the global simulation, the complete star list
is used as the above definition for suitable stars is restricted to
planets of a given size and orbital distance.
Table 2:
Fraction of stars suitable for transit detection.
We calculated the average flux for target stars, companions, and all the
background stars near enough to contribute to the target PSF.
We then checked that the average photon noise simulated for target stars at
a given magnitude was close to real values obtained in
OGLE light curves at given magnitude presented in Fig. 4 of Pont et al. (2006b).
3.2 Modelling the detection threshold
The candidates in the OGLE survey have been identified with the BLS
transit-search algorith of Kovács et al. (2002). A subset of the
candidates selected with cuts in the 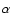 and SDE parameters of
the BLS were examined by eye, and only the best were included in the
final list. Therefore, the selection threshold is mainly defined by
subjective appreciation from an experienced specialist.
Recently, Pont et al. (2006b) have pointed out that the effective
detection threshold of ground-based transit surveys such as OGLE is
importantly affected by correlated noise (photometric systematics). The
subjective selection of candidates is in large part necessary because
of the presence of this correlated noise, which produce many spurious
detections near the threshold.
Gould et al. (2006) chose to model the OGLE selection threshold
with an
and SDE parameters of
the BLS were examined by eye, and only the best were included in the
final list. Therefore, the selection threshold is mainly defined by
subjective appreciation from an experienced specialist.
Recently, Pont et al. (2006b) have pointed out that the effective
detection threshold of ground-based transit surveys such as OGLE is
importantly affected by correlated noise (photometric systematics). The
subjective selection of candidates is in large part necessary because
of the presence of this correlated noise, which produce many spurious
detections near the threshold.
Gould et al. (2006) chose to model the OGLE selection threshold
with an 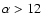 cut (alpha is equivalent to the signal-to-noise
ratio of the transit signal assuming uncorrelated noise and
homogeneous distribution of the data points in phase). Pont et al. (2006b)
have included the effect of correlated noise in the signal-to-noise
calculation and found that the OGLE selection could be
better described by a threshold of 8 on the signal-to-noise ratio of the
transit signal calculated including correlated noise ("
cut (alpha is equivalent to the signal-to-noise
ratio of the transit signal assuming uncorrelated noise and
homogeneous distribution of the data points in phase). Pont et al. (2006b)
have included the effect of correlated noise in the signal-to-noise
calculation and found that the OGLE selection could be
better described by a threshold of 8 on the signal-to-noise ratio of the
transit signal calculated including correlated noise ("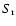 '' in
their notation, see Sect. 2.5.2), and without the assumption of
homogeneous coverage. While the two thresholds have similar effects
on the global number of planet detection, they have a very different
dependence on some parameters, such as planet period and host star
magnitude. Since the objective or our study is to examine the
detection statistics in a multi-dimensional parameter space, we use the Pont et al. (2006b)
description of the OGLE detection threshold.
'' in
their notation, see Sect. 2.5.2), and without the assumption of
homogeneous coverage. While the two thresholds have similar effects
on the global number of planet detection, they have a very different
dependence on some parameters, such as planet period and host star
magnitude. Since the objective or our study is to examine the
detection statistics in a multi-dimensional parameter space, we use the Pont et al. (2006b)
description of the OGLE detection threshold.
To calculate 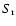 ,
one needs an assumption on the level of red noise
present in the photometry. Following Pont et al. (2006b), we use a single-parameter
description and assume
,
one needs an assumption on the level of red noise
present in the photometry. Following Pont et al. (2006b), we use a single-parameter
description and assume
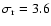 mmag in the Bulge fields,
mmag in the Bulge fields,
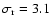 mmag in the Carina and Centaurus fields, and
mmag in the Carina and Centaurus fields, and
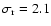 mmag
in all fields after application of decorrelation algorithms.
mmag
in all fields after application of decorrelation algorithms.
High-resolution spectra allow the confirmation of the planetary
events if spectral lines are deep enough. Several scenarios make the
follow up of candidates too difficult: early type stars have lines too
weak and too broadened by rotation (type F4 and earlier). Stars with
magnitudes V>17.5
are too faint for present instruments and telescopes.
This is the limit at which observers estimated not being able to
provide low-metallicity stars. Those stars having weaker lines, could also be
difficult to follow correctly, but as planets are unlikely to be found
near this kind of stars in our model, we did not take that parameter
into account.
To simulate the feasability of follow-up, we only considered in
CoRoTlux the stars matching the criteria V < 17.5and of type F4 and later.
4 Results of the simulations
We present hereafter runs for the three OGLE-III campaigns for the
fields in the Galactic bulge, in Carina, and in Centaurus. In order to
obtain a statistically significant population of detected planets, the
simulations were run multiple times.
We first examine the consistency between the models and observations
for relevant physical variables. In doing so, we choose to compare our
model population to the global population of transiting planets
discovered by OGLE and other surveys. There is a
slight inconsistency in assuming that the parameter comparison is almost
independant of the type of survey and observational strategy. In some
cases, this is not true, and a clear distinction between
the OGLE planets and the other detections has to be made.
We then discuss the problem of the detection statistics, whether
observations and models are consistent, and whether a constraint on
the (low) frequency of very close-in planets can be deduced.
4.1 Deviation of OGLE planets from maximum likelihood of the simulations
We use a Maximum-Likelihood (ML) technique in order to test whether model results and observations
agree with each other. We do the tests in two-dimension
spaces, in order to qualify possible correlation and exclusion zones.
The ML technique is our method of choice as it is a powerful tool for
fitting a model to a multi-dimentionnal independant-data distribution (Lyons 1986).
Instead of determining an approximate analytical law fitting our results, we use the results of a very large Monte-Carlo draw (1000 times the whole OGLE survey,
corresponding to 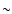 9000 planets) to get a map of the density of probability in each 2-dimension
grid. We bin our data on a
9000 planets) to get a map of the density of probability in each 2-dimension
grid. We bin our data on a
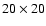 grid as a compromise between resolution of the models and characteristic
variations of the parameters
grid as a compromise between resolution of the models and characteristic
variations of the parameters![[*]](/icons/foot_motif.gif) .
The probability of an event in each bin is considered equal to the normalized number of draws in that bin.
.
The probability of an event in each bin is considered equal to the normalized number of draws in that bin.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fig6.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg178.gif) |
Figure 6:
Logarithm of the probability that a simulated
detection event occurs in each one of the
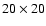 bins of the mass/radius diagram.
The likelihood of a multiple-events draw is the sum of the logarithms of the probabilities
of the events of this draw. Bins without any occuring event in the large Monte-Carlo draw do
not have any probability stated.
The likelihood of a n-events draw is the sum of the probabilities of its n events.
In this mass-radius diagram, OGLE planets are shown as red circles,
planets from other surveys are in orange, and planets from radial velocity surveys are in blue.
The likelihood of the 5 OGLE discoveries as
a result of a Monte-Carlo draw is -8.7, the maximum likelihood is -7 and the
standard deviation to maximum likelihood is 2.54. Hence, the result of the OGLE planets mass-radius
distribution is at
bins of the mass/radius diagram.
The likelihood of a multiple-events draw is the sum of the logarithms of the probabilities
of the events of this draw. Bins without any occuring event in the large Monte-Carlo draw do
not have any probability stated.
The likelihood of a n-events draw is the sum of the probabilities of its n events.
In this mass-radius diagram, OGLE planets are shown as red circles,
planets from other surveys are in orange, and planets from radial velocity surveys are in blue.
The likelihood of the 5 OGLE discoveries as
a result of a Monte-Carlo draw is -8.7, the maximum likelihood is -7 and the
standard deviation to maximum likelihood is 2.54. Hence, the result of the OGLE planets mass-radius
distribution is at
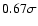 of the maximum likelihood of the model.
of the maximum likelihood of the model.
|
| Open with DEXTER |
Figure 6 shows the logarithm of the probability that an event occurs in each of the
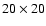 bins of the mass-radius diagram.
The likelihood of a draw of several independant events is defined as the sum of
the logarithms of the probabilities of these events. In order to compare our results to any n real discoveries, we first estimate the standard deviation of any n-planets-random-draw
compared to the maximum likelihood of the model. We randomly select n planets among the simulated detections and calculate the likelihood of this draw. We repeat this selection 1000 times in order to have the maximum likelihood and its standard deviation
bins of the mass-radius diagram.
The likelihood of a draw of several independant events is defined as the sum of
the logarithms of the probabilities of these events. In order to compare our results to any n real discoveries, we first estimate the standard deviation of any n-planets-random-draw
compared to the maximum likelihood of the model. We randomly select n planets among the simulated detections and calculate the likelihood of this draw. We repeat this selection 1000 times in order to have the maximum likelihood and its standard deviation 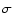 ,
then we compare the deviation of the likelihood of the n real detecions calculated the same way in terms of
,
then we compare the deviation of the likelihood of the n real detecions calculated the same way in terms of 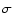 .
Henceforth, quantitative comparisons between the simulation results and the known planets are systematically given in the figure captions, whilst the text discusses qualitative comparisons and their implications.
For the different figures showing the results of our simulation, we compare the distribution of planets over the detection threshold to the 5 OGLE planets. We also compare our results to the 11 planets discovered by all transit surveys, as their detection biases are similar to OGLE, and to the 14 planets, the radii of which are known (11 from transits and 3 from radial velocity surveys) to show how our model can reproduce the whole known population.
.
Henceforth, quantitative comparisons between the simulation results and the known planets are systematically given in the figure captions, whilst the text discusses qualitative comparisons and their implications.
For the different figures showing the results of our simulation, we compare the distribution of planets over the detection threshold to the 5 OGLE planets. We also compare our results to the 11 planets discovered by all transit surveys, as their detection biases are similar to OGLE, and to the 14 planets, the radii of which are known (11 from transits and 3 from radial velocity surveys) to show how our model can reproduce the whole known population.
We first attempt to confirm whether the events detected by the model
are consistent with those found in the OGLE
fields. Figure 7 is a plot showing
transit depth as a function of the magnitude of the primary
star. Model results are considered detected when the signal-to-noise ratio
is sufficient for a detection (see Sect. 3.2).
We also show events that are considered photometrically
detectable but very hard or impossible to confirm by radial
velocimetry.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fig7.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg179.gif) |
Figure 7:
Depth of the planetary transit events versus magnitude of the
parent star in the V band. The five confirmed OGLE detections are shown
as circles. Model results are shown as black plusses for detectable
events and orange crosses for events that are considered
undetectable based on the photometric signal (see text). Blue diamonds
correspond to events that would be detectable by photometry
alone but that cannot be confirmed by radial velocimetry. Note that
the model results correspond to 3 times the full OGLE campaign
for more statistical significance. The OGLE planets depth-magnitude
distribution is at
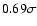 from the maximum likelihood of the model.
from the maximum likelihood of the model. |
| Open with DEXTER |
The figure evidently shows a good correlation between the black
crosses and the red circles that indicate real detections by OGLE,
with a range of transit depths and V magnitudes that is very similar
between the models and the observations. Our models slightly overpredict
the number of transit events around faint stars (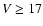 ),
but this may be due to the difficulty of the follow-up work for these
targets. Overall, the agreement between models and observations is
good.
),
but this may be due to the difficulty of the follow-up work for these
targets. Overall, the agreement between models and observations is
good.
4.3 Compatibility of transit surveys with radial-velocimetry
observations
Figure 8 compares the model and observated
mass-period relation. As it is independant of the planetary evolution
model, it is a direct test of the compatibility between the results of
transit surveys and those of radial-velocimetry observations that
drive our model results. Again, the comparison is very good, assuming
a high-enough frequency of very-close in planets (see discussion
in Sect. 4.3.4). One can note especially the absence of
planets of relatively large mass (several times that of Jupiter) at
short orbital distances (P<5 days), and of detectable transit
events for periods longer than 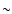 5 days. This is due especially to
the fact that only events with a relatively large number of observed transits are detectable, as
required by the
5 days. This is due especially to
the fact that only events with a relatively large number of observed transits are detectable, as
required by the 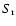 threshold, which, given the day/night
interruptions, imposes a constraint of a short orbital period. Note
that this feature is not well reproduced by models in which the threshold
is computed from white-noise only (Gillon et al. 2005; Gould et al. 2006).
threshold, which, given the day/night
interruptions, imposes a constraint of a short orbital period. Note
that this feature is not well reproduced by models in which the threshold
is computed from white-noise only (Gillon et al. 2005; Gould et al. 2006).
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fig8.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg181.gif) |
Figure 8:
Mass versus period of transiting giant planets.
(OGLE planets are red circles, other transit surveys in orange, planets from
radial velocity surveys in blue. Simulated planets detected: black plusses, under threshold: orange crosses).
The OGLE planets mass-period distribution is at
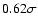 from the maximum likelihood of the model (
from the maximum likelihood of the model (
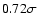 considering
the 11 planets discovered by transit surveys and
considering
the 11 planets discovered by transit surveys and
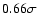 considering the 14 known planets).
considering the 14 known planets).
|
| Open with DEXTER |
Table 3:
OGLE yields with fixed red noise level.
We have tested the efficiency of the fiducial model at quantitatively estimating the yield of transit surveys. Gillon et al. (2005) have also simulated OGLE yield in their generic study of multiple transit surveys, but with restrictive assumptions on transit detectability (only complete events matter for detection purposes) and without considering background stars and red noise, or using OGLE-fields specific stellar population. We also included in our simulations the recent RV follow-up that was done on Centaurus and Carina.
We use unpublished information from
the OGLE/ESO follow-up team, who found one promising planetary
candidate among the Carina fields reprocessed with the systematics-
removal algorithm from Tamuz et al. (2005) and none in the Centarus
fields, with a magnitude limit near V=17 for the radial velocity
follow-up. Table 3 compares the average number of planets
detected for 1000 Monte-Carlo draws to real detections from the OGLE survey.
The total number of simulated discoveries obtained from this quantitative analysis is in good agreement with the real detections. The differences in the number of detections between the Carina and Centaurus surveys are mainly due to the lower duty cycle of the observations towards Centaurus. A red noise level fixed at 3.6 mmag in the direction of the galactic bulge bans most hot Jupiter detections.
The agreement between our quantitative result and the number of real detections is an indicator of the global efficiency of our approach (stellar and planetary distributions, evolution model and noise budget) for estimating transit survey yield.
So far, we have considered the level of red noise to depend only on the field considered. We attempt now to refine this by considering how the stellar density may affect it.
Whereas most ground-based transit surveys have a global red noise level from 2 to 3.5 mmag (Superwasp: Smith et al. (2006), Monitor: Irwin et al. (2007), Hatnet: Pont 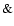 ISSI team (2007) and OGLE), the causes of these noise levels seem different, with instruments ranging from 10-cm wide field reflectors to deep-sky several-meter telescopes. As seen from Table 3, the OGLE fields have different mean red noise levels (
ISSI team (2007) and OGLE), the causes of these noise levels seem different, with instruments ranging from 10-cm wide field reflectors to deep-sky several-meter telescopes. As seen from Table 3, the OGLE fields have different mean red noise levels (
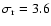 mmag for the bulge and
mmag for the bulge and
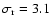 mmag for Centaurus and Carina before SYS-REM), although the instrument and observational strategy were unchanged.
Looking at what distinguishes these fields, it appears that the most significant difference is the stellar density and therefore the amount of crowding: the bulge field is about twice as dense as the Carina and Centaurus fields. Pont
mmag for Centaurus and Carina before SYS-REM), although the instrument and observational strategy were unchanged.
Looking at what distinguishes these fields, it appears that the most significant difference is the stellar density and therefore the amount of crowding: the bulge field is about twice as dense as the Carina and Centaurus fields. Pont  ISSI team (2007) raise the suspicion that the level of red noise depends strongly on the presence and characteristics of contaminating stars, because e.g. of their different colors and differential refraction in the atmosphere. It is hence natural to consider a red noise that depends on a crowding index.
ISSI team (2007) raise the suspicion that the level of red noise depends strongly on the presence and characteristics of contaminating stars, because e.g. of their different colors and differential refraction in the atmosphere. It is hence natural to consider a red noise that depends on a crowding index.
We define this crowding index as the fraction of the flux coming from background stars versus that from the target in the photometric aperture. Importantly, we do not consider stellar companions as contributing to the red noise because they are generally on the same CCD pixel as the target star and should affect the noise budget much less.
Figure 9 shows the differences of crowding index for the target
stars with planetary transits (detectable or not) in simulations of the Carina and Bulge fields of view.
The mean crowding index for target stars of I<17 is 0.11 in the Carina field and 0.233 in the Bulge field.
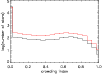 |
Figure 9:
Distribution of the crowding index (see text) of target stars in Carina (black) and in the bulge (red). |
| Open with DEXTER |
We can exclude the fact that all red noise is linked
with contamination as many stars in the Carina fields are unblended by background stars but
still show a high noise level.
In order to estimate of the influence of the crowding on the red noise level, we use the following simple relation between red noise level and crowding index:
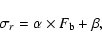 |
(7) |
where 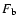 is the fraction of total flux from background stars, determined on a star-by-star basis in our simulations, and
is the fraction of total flux from background stars, determined on a star-by-star basis in our simulations, and 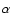 and
and 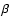 are parameters to be determined. This is
justified by the behaviour of the red noise seen for instance in
SuperWASP, showing a linear increase as a function of background flux (Smith et al. 2006).
In order to get the same mean red noise values as Pont et al. (2006b), we
obtain
are parameters to be determined. This is
justified by the behaviour of the red noise seen for instance in
SuperWASP, showing a linear increase as a function of background flux (Smith et al. 2006).
In order to get the same mean red noise values as Pont et al. (2006b), we
obtain
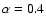 mmag and
mmag and
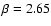 mmag. This value of
mmag. This value of 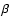 corresponds to the minimum red noise level obtained for non-contaminated stars in the OGLE fields.
corresponds to the minimum red noise level obtained for non-contaminated stars in the OGLE fields.
Table 4 shows the new number of detections when
considering this crowding-dependant red noise level. Compared to
Table 3, the number of detections is found to be
essentially unchanged for the Carina and Centaurus fields,
but it increases by a factor  3 for the bulge field.
This result is more satisfactory because in the previous case,
only
3 for the bulge field.
This result is more satisfactory because in the previous case,
only  5% of the simulations would yield the detection of
2 planets in the bulge, as observed.
5% of the simulations would yield the detection of
2 planets in the bulge, as observed.
Table 4:
OGLE yields with variable red noise level
4.3.4 Models, observations and the frequency of very close-in planets
As discussed in Sect. 2.4.1, three OGLE planets have
orbital periods shorter than 2 days and thus belong to a class of
objects yet to be detected by radial velocimetry. So far, we have
added one such planet (on average) to our carbon copy list of nearly
200 radial velocimetry planets. In Sect. 4.3, we
have shown that with this assumption, radial-velocity and photometric
transit surveys are compatible. We now test the range of
frequencies of very close-in planets for which this remains true.
In order to do so, we compute the deviation from maximum likelihood in
the mass-radius diagram like in Sect. 4.3, as a
function of the number of planets having a period of less than 2 days added to the RV list. The
result is presented in Fig. 10 and shows that a good match
is obtained by adding 1 to 3 short-period planets. Larger numbers are
also possible from the point of view of the transit surveys, but would
conflict with their non-detection by radial-velocimetry. Adding the
other transiting planets discovered thus far yields smaller
probabilities of occurence of these short-period planets, but not
by significant amounts.
All in all, and assuming that the radial velocity planets sample is
unbiased, we constrain the fraction of main-sequence late stars
orbited by very hot giant planets with orbital periods of less than 2
days to be
(1/1265)(1-0.33+0.33) at a 60% confidence level or
(1/1265)(1-0.5+0.83) at a 90% confidence level.
The distribution of planets in period between 2 and 5 days is directly
obtained from the metallicity-linked distribution (Santos et al. 2004)
and the RV planets sample. Adding the distribution we found for
planets between 1 and 2 days, we obtain a fraction of (1/215) late
main-sequence stars orbited by planets in the 1-to-5-day period
range, in good agreement with the results obtained in
Gould et al. (2006), who obtained
(1/220)(1+1.10-0.45).
Similarly, the distribution we obtain by cutting this sample into two
parts with the cut-off at 3 days is compatible, showing:
- a slightly higher fraction of really short-period planets (1-3 days) of (1/560)
instead of
(1/710)(1+1.10-0.54) at a 90% confidence level in
Gould et al. (2006);
- a similar fraction of short-period planets (3-5 days) of
(1/350)
instead of
(1/320)(1+1.39-0.59) at a 90% confidence level in
Gould et al. (2006).
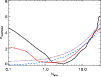 |
Figure 10:
Deviations from a maximum likelihood obtained as a function
of
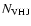 ,
the number of very hot jupiter of orbital periods
shorter than 2 days added to the radial velocities carbon-copy list.
Thick line: Deviation from the maximum likelihood obtained in
the mass-radius diagram for the OGLE planets. Thin line:
same deviation but when compared to the ensemble of planets.
Dashed line: standard deviation obtained from a comparison between
the number of simulated planets and the number of detected ones for
the OGLE survey (see Table 4).
Dotted line: standard deviation obtained from the non-detection of
these very close-in planets by radial-velocimetry. ,
the number of very hot jupiter of orbital periods
shorter than 2 days added to the radial velocities carbon-copy list.
Thick line: Deviation from the maximum likelihood obtained in
the mass-radius diagram for the OGLE planets. Thin line:
same deviation but when compared to the ensemble of planets.
Dashed line: standard deviation obtained from a comparison between
the number of simulated planets and the number of detected ones for
the OGLE survey (see Table 4).
Dotted line: standard deviation obtained from the non-detection of
these very close-in planets by radial-velocimetry. |
| Open with DEXTER |
The results presented hereafter use the variable red noise level
approach, and an RV planet list that is complemented with, on average,
1.5 very-close in planets with periods P<2 days taken from the OGLE
detections.
4.4 The metallicity of the stars harboring transiting planets
We now compare the metallicity of the parent stars for our observed
and modelled populations. A first test using the analytical scenario
for the radial-velocity population
(Fig. 11) yields a clearly different
metallicity distribution, with most of the transiting planets observed
around low-metallicity stars. We verified that this problem occurs
independantly of the assumed stellar metallicity distribution, for any
realistic stellar population. It arises fundamentally because the
global metallicity bias as obtained by Santos et al. (2004) or Fischer & Valenti (2005)
is not strong enough to compensate for the rarity of
very metal-rich stars in the Galaxy.
As seen in Fig. 12, the problem disappears
when one considers the carbon-copy model. Thus, we are led to an
important conclusion, that the metallicity distribution of pegasids
(periods shorter than 10 days) is fundamentally different from the
global exoplanet population. More specifically, there are no Pegasids
orbiting F, G, K stars with metallicities smaller than
![$\rm [Fe/H]=-0.07$](/articles/aa/full/2007/44/aa7138-07/img149.gif) .
This has
strong consequences for planet formation models (see also Guillot et al. 2006).
This work shows that this conclusion is robust, and is
needed to explain the results of the photometric surveys.
.
This has
strong consequences for planet formation models (see also Guillot et al. 2006).
This work shows that this conclusion is robust, and is
needed to explain the results of the photometric surveys.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi11.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg191.gif) |
Figure 11:
Period of transiting exoplanets versus metallicity of their
parent star. The model is based on analytic relations for the mass
and period distributions of planetary companions (see
Sect. 2.4.2). (OGLE planets are red circles, other transit surveys in orange, planets from radial velocity surveys in blue. Simulated planets detected: black plusses, under threshold: orange crosses).
The OGLE planets period-metallicity
distribution is at
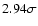 from the maximum likelihood of the model
(
from the maximum likelihood of the model
(
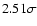 considering the 11 planets discovered by transit surveys and
considering the 11 planets discovered by transit surveys and
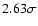 considering the 14 known planets).
considering the 14 known planets).
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi12.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg192.gif) |
Figure 12:
Period of transiting exoplanets versus metallicity of their
parent star. The figure differs from
Fig. 11 in that our fiducial model,
i.e. the mass-period-metallicity "carbon-copy'' model is used (see
Sect. 2.4.2).
(OGLE planets are red circles, other transit surveys in orange, planets from
radial velocitiy surveys in
blue. Simulated planets detected: black plusses, under threshold: orange crosses).
The OGLE planets period-metallicity
distribution is at
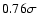 from the maximum likelihood of the model
(
from the maximum likelihood of the model
(
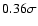 considering
the 11 planets discovered by transit surveys and
considering
the 11 planets discovered by transit surveys and
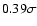 considering the 14 known planets)
.
considering the 14 known planets)
. |
| Open with DEXTER |
A finer examination of Fig. 12 shows that
while our model planets globally reproduce the metallicity of the
ensemble of transiting planets, OGLE stars with planets are on average
 0.1 dex more metal-rich.
0.1 dex more metal-rich.
This can tentatively be explained with a metallicity gradient in the
galaxy for OGLE TR-10 (
![$\rm [Fe/H]=0.28\pm{0.10}$](/articles/aa/full/2007/44/aa7138-07/img193.gif) )
and OGLE TR-56
(
)
and OGLE TR-56
(
![$\rm [Fe/H]=0.19\pm{0.07}$](/articles/aa/full/2007/44/aa7138-07/img194.gif) ), the two planets discovered in the direction
of the galactic bulge. The study of galactic cepheids by
Andrievsky et al. (2004) shows a metallicity gradient as a function of
distance to the galactic center. In the
[6.6,10.6] kpc-range
distance from galactic center, this study finds a linear relation
between [Fe/H] and galactocentric distance
), the two planets discovered in the direction
of the galactic bulge. The study of galactic cepheids by
Andrievsky et al. (2004) shows a metallicity gradient as a function of
distance to the galactic center. In the
[6.6,10.6] kpc-range
distance from galactic center, this study finds a linear relation
between [Fe/H] and galactocentric distance 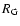 :
:
![\begin{displaymath}{\rm [Fe/H]}=-0.044(\pm {0.004}) R_{\rm G} + 0.363(\pm {0.032}) .
\end{displaymath}](/articles/aa/full/2007/44/aa7138-07/img196.gif) |
(8) |
Following that relation, the two stars with planets discovered in the
direction of the galactic bulge both at a distance around 1500 pc
would thus be in a 0.04 dex more metal rich region than the solar
neighborhood.
Concerning the high metallicity of stars with transiting planets
discovered by OGLE in the Carina region, we do not have any reason to
think that the metallicity distribution would be different from the
solar neighborhood. Our only hypothesis is a low-probability draw for
metallicity for the 3 OGLE-Carina planets.
Because evaporation may affect the planet population, it is
instructive to check whether the potential energy of the atmosphere
and the orbital period, two crucial quantities for this process
(e.g. Lecavelier des Etangs et al. 2004), also possess a relatively consistent
distribution. We first test the behavior of the analytical model for
the distribution of planets
(Fig. 13). This results in a prediction
of many planets with large radii (small values of the potential energy
for atmospheric escape) at small orbital distances, in patent
contradiction with the observations.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi13.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg197.gif) |
Figure 13:
Potential energy per unit mass (Ep=GM/R) versus orbital period of
transiting planets. (OGLE planets are red circles, other transit surveys in orange, planets from radial velocity surveys in
blue. Simulated planets detected: black plusses, under threshold: orange crosses).
Observations are compared to models based on the
analytical relations for the mass and period distribution of
planetary companions (see Sect. 2.4.2).
The OGLE planets' energy-period distribution is at
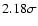 from the maximum likelihood of the model (
from the maximum likelihood of the model (
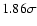 considering
the 11 planets discovered by transit surveys and
considering
the 11 planets discovered by transit surveys and
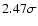 considering the 14 known planets).
considering the 14 known planets).
|
| Open with DEXTER |
The problem mostly disappears with the carbon-copy model:
Fig. 14) shows that in this case, although we do not
obtain a linear correlation between the two variables, we get
detections in the right area of the diagram. This is explained as
stemming from:
- The absence of low-mass planets at small orbital distances, with
a possible limiting relation between these two quantities (Mazeh et al. 2005);
- The difficulty in detecting planets with larger values of potential energy per unit mass
(smaller radii) at large orbital distances - although we predict
that some of these should be detected by future transit surveys.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi14.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg198.gif) |
Figure 14:
Potential energy per unit mass versus orbital period of
transiting planets. The figure is similar to
Fig. 13, except for the fact that our
fiducial model is used (see Sect. 2.4.2).
(OGLE planets are red circles, other transit surveys in orange, planets from radial velocity surveys in
blue. Simulated planets detected: black plusses, under threshold: orange crosses).
The OGLE planets energy-period distribution is at
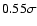 from the maximum likelihood of the model. (
from the maximum likelihood of the model. (
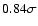 considering
the 11 planets discovered by transit surveys and
considering
the 11 planets discovered by transit surveys and
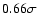 considering the 14 known planets).
considering the 14 known planets).
|
| Open with DEXTER |
Our results strengthen the case for the existence of a relation between
mass and orbital distance for short-period planets, as advocated by
Mazeh et al. (2005): Indeed, the analytic model which is characterized
by the presence of small mass planets at small distances yields a
distribution of detectable planets that is significantly different
from the observations (Fig. 13).
Our carbon-copy model that includes implicitely this correlation does
not (Fig. 14).
Radius and stellar irradiation (or equivalently equilibrium
temperature) should be positively correlated, as a planet with a
higher irradiation dose will tend to cool and contract more slowly
than one that endures less stellar insolation. As
Fig. 15 shows, the correlation exist, but is weak,
and with a signficant scatter. This is well reproduced by the
model.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi15.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg199.gif) |
Figure 15:
Radius as a function of equilibrium temperature of transiting
exoplanets.
(OGLE planets are red circles, other transit surveys in orange, planets from radial velocity surveys in
blue. Simulated planets detected: black plusses, under threshold: orange crosses).
The OGLE planets
equilibrium temperature-radius distribution is at
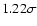 from the maximum
likelihood of the model (
from the maximum
likelihood of the model (
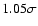 considering
the 11 planets discovered by transit surveys and
considering
the 11 planets discovered by transit surveys and
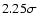 considering the 14 known planets).
considering the 14 known planets). |
| Open with DEXTER |
However, it can be noted that HD 149026 b lies away from the cloud of
points. In general, we find that our fiducial model generates few
points in this region. This can be easily accounted for by slightly
modifying the metallicity-core mass relation to allow for larger
masses. As planets of small masses and large core masses are more
difficult to model anyway, we chose not to attempt fine-tuning the
model to this level of detail. This should be postponed for further
studies, especially with the discovery of more Saturn-mass transiting
planets.
We have checked that our fiducial model predicts the detection of
transiting planets with properties that are globally consistent with
the observations. We can now examine in more detail the mass-radius
relation thus obtained, as it is directly tied to assumptions on the
compositions and evolutionary models of exoplanets. The predictions
also have implications for transit surveys as it is not clear
whether they have detected only the "tip of the iceberg'', ie the few
largest giant planets while many smaller ones would lie undetected or
not.
Results with our fiducial model are presented in
Fig. 16. We find that planets with low masses (say,
less than Jupiter's mass) can have either very large or very small
radii, depending on whether they contain a significant mass in heavy
elements or not. On the other hand, massive planets have radii which are
comparatively better defined. This is mostly due to the fact that we
assume a maximum mass of heavy elements of 100 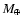 ,
a
hypothesis that will be tested directly by the discovery of a few
massive transiting planets.
,
a
hypothesis that will be tested directly by the discovery of a few
massive transiting planets.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi16.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg200.gif) |
Figure 16:
Mass-radius relation for transiting extrasolar giant
planets.
(OGLE planets are red circles, other transit surveys in orange, planets from radial velocity surveys
in blue. Simulated planets detected: black plusses, under threshold: orange crosses).
The OGLE planets mass-radius distribution is at 0.67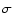 from themaximum likelihood of the model (
from themaximum likelihood of the model (
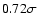 considering
the 11 planets discovered by transit surveys and 0.97
considering
the 11 planets discovered by transit surveys and 0.97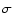 considering the 14 known planets).
considering the 14 known planets). |
| Open with DEXTER |
Our model results once again agree well with the detections made by
photometry. Importantly, the yellow crosses in
Fig. 16 do not lie significantly below the black
ones: we predict that future surveys will not discover a population of
small-sized giant planets, at least for masses above that of
Saturn.
The presence of planets with larger masses of heavy
elements should remain marginal because otherwise they would have
been detected by present-day surveys, Fig. 16
showing that planets below 1
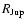 are already
detectable, although in favorable cases (small radius of the primary
and bright targets). Quantitatively, simulations in the OGLE fields
indicate that if planets had radii uniformly distributed between 0.5
and 1.5
are already
detectable, although in favorable cases (small radius of the primary
and bright targets). Quantitatively, simulations in the OGLE fields
indicate that if planets had radii uniformly distributed between 0.5
and 1.5
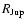 ,
18.5% of the planets discovered by the survey
would have radii below 1
,
18.5% of the planets discovered by the survey
would have radii below 1
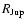 .
This fraction is not
negligible and is (although marginally) inconsistent with the sample
of 0/11 planets with
.
This fraction is not
negligible and is (although marginally) inconsistent with the sample
of 0/11 planets with
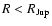 discovered by transit surveys
thus far.
discovered by transit surveys
thus far.
Therefore, although we cannot statistically rule out the presence of a
population of small planets, these would require the formation of
extremely metal-rich planets. Our prediction is a consequence
of evolution models and of our assumption that planets with masses of
heavy elements beyond 100 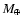 should be rare.
should be rare.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi17.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg202.gif) |
Figure 17:
Mass-radius relation for a very large number of Monte-Carlo
trials using the fiducial model. The curves show the ensemble of
planets with masses of heavy elements between 0 and 25, 25 and 50,
50 and 75, 75 and 100 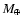 ,
respectively. Symbols are as in
Fig. 8. ,
respectively. Symbols are as in
Fig. 8. |
| Open with DEXTER |
Figure 17 shows the ensemble of planets obtained for an
extremely large number of draws, with our fiducial model. Voids in the
ensemble of crosses correspond to the absence of planets with these
masses in the radial-velocimetry list. They should not be considered
as significant. The contours in the figure indicate the ensemble of
masses and radii expected for planets with different masses of heavy
elements, from 0 to 100 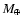 .
Importantly, the location of
these contours is linked to our assumption of an energy source in the
planetary interior equal to 0.5% times the irradiation received by
the planet. Independently of the details of this assumption, this shows that a statistically significant
ensemble of known transiting planets would allow a determination of
the presence or lack of heavy elements in these objects.
.
Importantly, the location of
these contours is linked to our assumption of an energy source in the
planetary interior equal to 0.5% times the irradiation received by
the planet. Independently of the details of this assumption, this shows that a statistically significant
ensemble of known transiting planets would allow a determination of
the presence or lack of heavy elements in these objects.
We have also tested another assumption regarding the planetary
evolution model: all planets possess 20 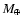 mass in heavy
elements, 70% of them have no extra heat source, whereas 30% have
mass in heavy
elements, 70% of them have no extra heat source, whereas 30% have
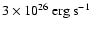 dissipated at the center. With this
assumption, one can qualitatively explain the observed transiting
planets (i.e. the "normal'' planets and the "anomalously large''
ones, respectively) with the exception of HD 149026 b, for which one
could argue that the planet comes from a different population. In this
case, Fig. 18 shows a distribution of radii that is
relatively similar to the previous one (Fig. 16),
with the exception that no planet has a radius smaller than
dissipated at the center. With this
assumption, one can qualitatively explain the observed transiting
planets (i.e. the "normal'' planets and the "anomalously large''
ones, respectively) with the exception of HD 149026 b, for which one
could argue that the planet comes from a different population. In this
case, Fig. 18 shows a distribution of radii that is
relatively similar to the previous one (Fig. 16),
with the exception that no planet has a radius smaller than
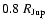 .
In this case, the 2 regions corresponding to the
"standard'' model, and to the "heat dissipation'' case are clearly
different, especially at the low-mass range of the diagram.
.
In this case, the 2 regions corresponding to the
"standard'' model, and to the "heat dissipation'' case are clearly
different, especially at the low-mass range of the diagram.
Present observations cannot distinguish between the two
models, showing the need for additional detections of transiting giant
planets. Particularly important are planets between the mass of Saturn
and that of Jupiter, as this is a mass regime where expected
compositional differences have the largest impact.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi18.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg207.gif) |
Figure 18:
Mass-radius relation obtained for an alternative model with
70% of "standard'' planets with no extra-energy source, and 30%
planets receiving an additional
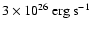 luminosity dissipated at the center. All planets are assumed to
possess
luminosity dissipated at the center. All planets are assumed to
possess
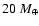 in heavy elements. Symbols are as in
Fig. 8.
in heavy elements. Symbols are as in
Fig. 8. |
| Open with DEXTER |
We have presented a simulation of photometric transiting surveys based
on basic knowledge of the stellar and planetary populations in the
galactic neighborhood and on a planetary evolution model tuned to the
information obtained from transiting giant planets with masses above
that of Saturn. This simulation was applied to the OGLE survey, and shown
to yield a generally excellent agreement with the transiting planets
detected by the survey.
We have thus shown that radial velocimetry and photometric surveys are
compatible within statistical uncertainties, in agreement with
Gould et al. (2006). We have derived a frequency of very close-in
planets with orbital periods shorter than 2 days around solar-type
stars, of
(1/1265)(1-0.33+0.33) at a 60 % confidence level or
(1/1265)(1-0.5+0.83) at a 90 % confidence level.
Using null results by photometric surveys for given ranges of
parameters, we are able to strengthen two results already present in
the radial velocimetry data:
- Stars with low metallicities (
![$\rm [Fe/H] < -0.07$](/articles/aa/full/2007/44/aa7138-07/img208.gif) )
do not, or
are very unlikely to harbour close-in giant planets with orbital periods
P < 10 days. This is unlike stars above that metallicity
threshold (see Fig. 12).
)
do not, or
are very unlikely to harbour close-in giant planets with orbital periods
P < 10 days. This is unlike stars above that metallicity
threshold (see Fig. 12).
- There is a lack of small-mass giant planets below the mass of
Jupiter and above that of Saturn for orbital periods
P < 3 days (see Fig. 8).
Further data is required to precisely quantify these empirical results that bear
important consequences for our understanding of planet formation and
migration.
On the basis of our model, and assumptions concerning the composition
of giant planets (i.e. masses of heavy elements between 0 and
100  ), we find that the present detections of transiting
planets have sampled a population that is quite representative of the
main population of giant planets, at least for the ones that are above
about half the mass of Jupiter. We hence predict that future
transit surveys with higher sensitivities will not discover a
significant population of yet undetected Jupiter-mass planets with small
sizes, i.e. radii smaller than that of Jupiter (see
Fig. 16).
), we find that the present detections of transiting
planets have sampled a population that is quite representative of the
main population of giant planets, at least for the ones that are above
about half the mass of Jupiter. We hence predict that future
transit surveys with higher sensitivities will not discover a
significant population of yet undetected Jupiter-mass planets with small
sizes, i.e. radii smaller than that of Jupiter (see
Fig. 16).
Many ground-based transit surveys are in progress, and with the space
missions CoRoT (Baglin et al. 2002) and Kepler (Borucki et al. 2003),
the number of known transiting planets is expected to rise rapidly over the next few years.
This will enable us to
better test the models and quantify some of the results presented in
this article. We also hope to be able to discriminate between various
models of the evolution and compositions of giant planets, a matter of
great importance for formation models.
We wish to stress however that a continuation of ground-based transit
surveys is desirable even in the presence of similar programs from
space. CoRoT will survey 60 000 dwarf stars over five 150-day
periods and Kepler about 100 000 over 4 years, implying a maximum
potential yield of 55 and 90 transiting giant planets, respectively,
plus many other smaller planets. Concerning giant planets,
quantifying the fraction of very close-in planets with a 10% accuracy
at the 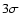 level would require the discovery of
level would require the discovery of  200
transiting planets. Understanding the evolution and compositions of
giant planets will require an even larger number of detections. The radius of a giant
planet itself depends mainly on four parameters: the planetary mass,
equilibrium temperature, age, and its composition (note that the
composition can be considered as a simple parameter only in the case
of planets mostly made of hydrogen and helium: smaller planets will be
more difficult to model!). Additional energy
sources may occur (such as in the presence of tidal heat dissipation),
and the initial conditions and formation history may have their say in
the matter as well. Furthermore, the
observational uncertainties are generally large. For example, the
planetary radius is generally only known to
200
transiting planets. Understanding the evolution and compositions of
giant planets will require an even larger number of detections. The radius of a giant
planet itself depends mainly on four parameters: the planetary mass,
equilibrium temperature, age, and its composition (note that the
composition can be considered as a simple parameter only in the case
of planets mostly made of hydrogen and helium: smaller planets will be
more difficult to model!). Additional energy
sources may occur (such as in the presence of tidal heat dissipation),
and the initial conditions and formation history may have their say in
the matter as well. Furthermore, the
observational uncertainties are generally large. For example, the
planetary radius is generally only known to 
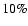 ,
for a global
variation that is relatively small (1 to 1.5
,
for a global
variation that is relatively small (1 to 1.5
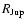 ). This
implies that to constrain a given correlation to, say 10%, and
with four independant variables, hundreds of data points are needed,
and thousands would be desirable.
). This
implies that to constrain a given correlation to, say 10%, and
with four independant variables, hundreds of data points are needed,
and thousands would be desirable.
This motivates us to
seek programs capable of detecting thousands of transiting planets in
the mid-term future, and ways to reduce the error bars on the
different parameters. One direction is to test the Dome C plateau in
Antarctica for such an ambitious program, which is the purpose of
A STEP (Fressin et al. 2005). Other directions exist, such as proposals
for similar surveys from space. In any case, it is most important that
a statistically significant population of exoplanets be characterized
for a better understanding of planet formation and our origins.
Acknowledgements
The code used for this work, CoRoTlux, was developped as part of
the CoRoT science program by the authors with major contributions by
Aurélien Garnier, Maxime Marmier, Martin Vannier, Suzanne Aigrain,
and help from Claire Moutou, Stéphane Lagarde, Antoine Llebaria,
Didier Queloz, and François Bouchy. We want to thank Andrzej
Udalski and Michael Gillon for their communications on OGLE data,
Frédéric Thévenin for his advice on stellar populations
simulation. F.F. was funded by grants from the French Ministère de la Recherche and by the Société des
Amis des Sciences. V.M. was funded by a grant from the C.N.R.S.. This work used Jean Schneider's exoplanet
database www.exoplanet.eu, and the Besançon model of the
Galaxy at physique.obs-besancon.fr/modele/ extensively. The
planetary evolution models used for this work can be downloaded at
www.obs-nice.fr/guillot/pegasids/.
- Alard, C.,
& Lupton, R. H. 1998, ApJ, 503, 325 [NASA ADS] [CrossRef] (In the text)
- Alonso, R.,
Brown, T. M., Torres, G., et al. 2004, ApJ, 613,
L153 [NASA ADS] [CrossRef]
-
Andrievsky, S. M., Luck, R. E., Martin, P., &
Lépine, J. R. D. 2004, A&A, 413, 159 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Baglin, A.,
Auvergne, M., Barge, P., et al. 2002, in ESA SP-485: Stellar
Structure and Habitable Planet Finding, ed. B. Battrick,
F. Favata, I. W. Roxburgh, & D. Galadi, 17
(In the text)
- Bakos,
G. A., Noyes, R. W., Kovacs, G., et al. 2006, ArXiv
Astrophysics e-prints
- Baraffe,
I., Chabrier, G., Barman, T. S., et al. 2005, A&A,
436, L47 [NASA ADS] [CrossRef] [EDP Sciences]
-
Bodenheimer, P., Lin, D. N. C., & Mardling,
R. A. 2001, ApJ, 548, 466 [NASA ADS] [CrossRef]
- Borucki,
W. J., Koch, D. G., Lissauer, J. J., et al.
2003, in Future EUV/UV and Visible Space Astrophysics Missions and
Instrumentation, ed. J. C. Blades, O. H. W.
Siegmund, Proc SPIE, 4854, 129
(In the text)
- Bouchy, F.,
Pont, F., Santos, N. C., et al. 2004, A&A, 421,
L13 [NASA ADS] [CrossRef] [EDP Sciences]
- Bouchy, F.,
Pont, F., Melo, C., et al. 2005, A&A, 431, 1105 [NASA ADS] [CrossRef] [EDP Sciences]
- Brown,
T. M. 2003, ApJ, 593, L125 [NASA ADS] [CrossRef] (In the text)
- Brown,
T. M., Charbonneau, D., Gilliland, R. L., Noyes,
R. W., & Burrows, A. 2001, ApJ, 552, 699 [NASA ADS] [CrossRef]
- Butler,
R. P., Wright, J. T., Marcy, G. W., et al.
2006, ApJ, 646, 505 [NASA ADS] [CrossRef]
-
Charbonneau, D., Winn, J. N., Latham, D. W., et al.
2006, ApJ, 636, 445 [NASA ADS] [CrossRef]
- Cody, A. M.,
& Sasselov, D. D. 2002, ApJ, 569, 451 [NASA ADS] [CrossRef]
- Collier Cameron, A., Bouchy, F.,
Hebrard, G., et al. 2006, ArXiv Astrophysics e-prints
- Deming, D.,
Seager, S., Richardson, L. J., & Harrington, J. 2005,
Nature, 434, 740 [NASA ADS] [CrossRef]
- Duquennoy, A., & Mayor, M.
1991, A&A, 248, 485 [NASA ADS] (In the text)
- Fischer, D. A., &
Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef]
- Fressin,
F., Guillot, T., Bouchy, F., et al. 2005, in EAS Pub. Ser.,
ed. M. Giard, F. Casoli, & F. Paletou, 309
(In the text)
- Gillon, M.,
Courbin, F., Magain, P., & Borguet, B. 2005, A&A, 442,
731 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gillon, M.,
Pont, F., Moutou, C., et al. 2006, A&A, 459, 249 [NASA ADS] [CrossRef] [EDP Sciences]
- Gonzalez,
G. 1998, A&A, 334, 221 [NASA ADS]
- Gould, A.,
Dorsher, S., Gaudi, B. S., & Udalski, A. 2006, Acta
Astron., 56, 1 [NASA ADS] (In the text)
- Guillot, T.
2005, Ann. Rev. Earth Planet. Sci., 33, 493 [NASA ADS]
- Guillot, T., & Showman,
A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences]
- Guillot,
T., Santos, N. C., Pont, F., et al. 2006, A&A, 453,
L21 [NASA ADS] [CrossRef] [EDP Sciences]
- Holman,
M. J., Winn, J. N., Latham, D. W., et al. 2006,
ApJ, 652, 1715 [NASA ADS] [CrossRef]
- Horne, K. 2001,
in Techniques for the detection of planets and life beyond the
solar system, 4th Annual ROE Workshop, held at Royal Observatory
Edinburgh, Scotland, Nov 7-8, 2001, ed. W. R. F. Dent
(Edinburgh, Scotland: Royal Observatory, Dent), 5
(In the text)
- Irwin, J.,
Irwin, M., Aigrain, S., et al. 2007, MNRAS, 375, 1449 [NASA ADS] (In the text)
- Knutson,
H. A., Charbonneau, D., Noyes, R. W., Brown, T. M.,
& Gilliland, R. L. 2007, ApJ, 655, 564 [NASA ADS] [CrossRef]
- Konacki,
M., Sasselov, D. D., Torres, G., Jha, S., & Kulkarni,
S. R. 2003, BAAS, 1416
- Konacki,
M., Torres, G., Sasselov, D. D., et al. 2004, ApJ, 609,
L37 [NASA ADS] [CrossRef]
- Konacki,
M., Torres, G., Sasselov, D. D., & Jha, S. 2005, ApJ, 624,
372 [NASA ADS] [CrossRef]
- Kovács,
G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Laughlin,
G., Wolf, A., Vanmunster, T., et al. 2005, ApJ, 621, 1072 [NASA ADS] [CrossRef]
- Lecavelier des
Etangs, A., Vidal-Madjar, A., McConnell, J. C., &
Hébrard, G. 2004, A&A, 418, L1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Levrard,
B., Correia, A. C. M., Chabrier, G., et al. 2007,
A&A, 462, L5 [NASA ADS] [CrossRef] [EDP Sciences]
- Lyons, L. 1986,
Statistics for Nuclear and Particle Physics (Cambridge Univ.
Press), 85
(In the text)
- Magain, P.,
Courbin, F., Gillon, M., et al. 2007, A&A, 461, 373 [NASA ADS] [CrossRef] [EDP Sciences]
- Marcy, G.,
Butler, R. P., Fischer, D., et al. 2005, Progr. Theor.
Phys. Suppl., 158, 24 [NASA ADS] (In the text)
- Mazeh, T.,
Zucker, S., & Pont, F. 2005, MNRAS, 356, 955 [NASA ADS] (In the text)
-
McCullough, P. R., Stys, J. E., Valenti, J. A.,
et al. 2006, ApJ, 648, 1228 [NASA ADS] [CrossRef]
- Moutou,
C., Pont, F., Bouchy, F., & Mayor, M. 2004, A&A, 424,
L31 [NASA ADS] [CrossRef] [EDP Sciences]
-
Nordström, B., Mayor, M., Andersen, J., et al. 2004,
A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
O'Donovan, F. T., Charbonneau, D., Mandushev, G., et al.
2006, ApJ, 651, L61 [NASA ADS] [CrossRef]
- Pepper, J.,
& Gaudi, B. S. 2005, ApJ, 631, 581 [NASA ADS] [CrossRef] (In the text)
- Pont, F., Bouchy,
F., Queloz, D., et al. 2004, A&A, 426, L15 [NASA ADS] [CrossRef] [EDP Sciences]
- Pont, F., Melo,
C. H. F., Bouchy, F., et al. 2005, A&A, 433,
L21 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pont, F.,
Moutou, C., Bouchy, F., et al. 2006a, A&A, 447, 1035 [NASA ADS] [CrossRef] [EDP Sciences]
- Pont, F., Zucker,
S., & Queloz, D. 2006b, MNRAS, 373, 231 [NASA ADS] (In the text)
- Robin,
A. C., Reylé, C., Derrière, S., & Picaud, S.
2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Santos,
N. C., Israelian, G., & Mayor, M. 2004, A&A, 415,
1153 [NASA ADS] [CrossRef] [EDP Sciences]
- Santos,
N. C., Pont, F., Melo, C., et al. 2006, A&A, 450,
825 [NASA ADS] [CrossRef] [EDP Sciences]
- Sato, B.,
Fischer, D. A., Henry, G. W., et al. 2005, ApJ, 633,
465 [NASA ADS] [CrossRef]
- Showman, A. P. &
Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Shporer,
A., Tamuz, O., Zucker, S., & Mazeh, T. 2007, MNRAS, 136
- Smith,
A. M. S., Collier Cameron, A., Christian, D. J.,
et al. 2006, MNRAS, 373, 1151 [NASA ADS] (In the text)
- Stetson,
P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] (In the text)
- Tamuz, O.,
Mazeh, T., & Zucker, S. 2005, MNRAS, 356, 1466 [NASA ADS] (In the text)
- Torres, G.,
Konacki, M., Sasselov, D. D., & Jha, S. 2003, in BAAS,
1235
- Udalski,
A. 2002, IAU Circ., 7925, 2
- Udalski, A.
2003, Acta Astron., 53, 291 [NASA ADS] (In the text)
- Udalski,
A., Paczynski, B., Zebrun, K., et al. 2002, Acta Astron., 52,
1 [NASA ADS] (In the text)
- Udalski,
A., Szymanski, M. K., Kubiak, M., et al. 2004, Acta
Astron., 54, 313 [NASA ADS] (In the text)
- Udry, S.,
Fischer, D., & Queloz, D. 2007, in Protostars and Planets V,
ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of
Arizona Press), 951, 685
- Wilson,
D. M., Enoch, B., Christian, D. J., et al. 2006,
PASP, 118, 1245 [NASA ADS] [CrossRef]
-
Winn, J. N. & Holman, M. J. 2005, ApJ, 628, L159 [NASA ADS] [CrossRef] (In the text)
- Winn, J. N.,
Noyes, R. W., Holman, M. J., et al. 2005, ApJ, 631,
1215 [NASA ADS] [CrossRef]
- Winn, J. N.,
Holman, M. J., & Fuentes, C. I. 2007, AJ, 133,
11 [NASA ADS] [CrossRef]
-
Wittenmyer, R. A., Welsh, W. F., Orosz, J. A.,
et al. 2005, ApJ, 632, 1157 [NASA ADS] [CrossRef]
- Zucker, S.
& Mazeh, T. 2001, ApJ, 562, 1038 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
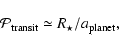
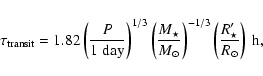
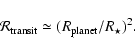
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=0]{7138fig1.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg135.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=0]{7138fig2.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg142.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=0]{7138fig3.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg150.gif)

![\begin{displaymath}M_Z=43.75\times 10^{\rm [Fe/H]}-23.7\ M_\oplus.
\end{displaymath}](/articles/aa/full/2007/44/aa7138-07/img152.gif)
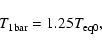
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm]{7138fig5.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg162.gif)
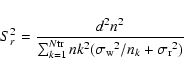
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fig6.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg178.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fig7.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg179.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fig8.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg181.gif)


![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi11.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg191.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi12.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg192.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi13.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg197.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi14.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg198.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi15.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg199.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi16.ps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg200.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi17.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg202.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7138fi18.eps}\end{figure}](/articles/aa/full/2007/44/aa7138-07/Timg207.gif)