A&A 475, 401-407 (2007)
DOI: 10.1051/0004-6361:20066808
Generation of potential/surface density pairs in flat disks
Power law distributions
J.-M. Huré1,2 - D. Pelat2 - A. Pierens3
1 - Université Bordeaux 1/CNRS/OASU/UMR 5804/LAB, 2 rue de l'Observatoire, BP 89, 33270 Floirac, France
2 - LUTh/Observatoire de Paris-Meudon-Nancay, Place Jules Janssen, 92195 Meudon Cedex, France
3 - Astronomy Unit, Queen Mary, University of London, Mile end Road, London E1 4NS, UK
Received 24 November 2006 / Accepted 5 June 2007
Abstract
Aims. We report a simple method to generate potential/surface density pairs in flat axially symmetric finite size disks.
Methods. Potential/surface density pairs consist of a ``homogeneous'' pair (a closed form expression) corresponding to a uniform disk, and a "residual'' pair. This residual component is converted into an infinite series of integrals over the radial extent of the disk. For a certain class of surface density distributions (like power laws of the radius), this series is fully analytical.
Results. The extraction of the homogeneous pair is equivalent to a convergence acceleration technique, in a matematical sense. In the case of power law distributions (i.e. surface densities of the form
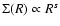 ), the convergence rate of the residual series is shown to be cubic inside the source. As a consequence, very accurate potential values are obtained by low order truncation of the series. At zero order, relative errors on potential values do not exceed a few percent typically, and scale with the order N of truncation as 1/N3. This method is superior to the classical multipole expansion whose very slow convergence is often critical for most practical applications.
), the convergence rate of the residual series is shown to be cubic inside the source. As a consequence, very accurate potential values are obtained by low order truncation of the series. At zero order, relative errors on potential values do not exceed a few percent typically, and scale with the order N of truncation as 1/N3. This method is superior to the classical multipole expansion whose very slow convergence is often critical for most practical applications.
Key words: gravitation - methods: analytical - accretion, accretion disks - methods: numerical
The construction of potential/density pairs is a common concern in the context of galactic dynamics (e.g. Binney & Tremaine 1987). More generally, the accurate determination of the gravitational potential corresponding to a given mass distribution is a critical step in astrophysical disk models and numerical simulations. Unfortunately, potential/density pairs are not closed-form expressions, except in a few cases only (de Zeeuw & Pfenniger 1988; Binney & Tremaine 1987; Mestel 1963), and most known pairs involve infinite matter distribution (e.g. Quan 1993; Binney & Tremaine 1987; Cuddeford 1993; Earn 1996), whereas astrophysical disks are finite (in size and mass).
For flat (i.e. zero thickness) and finite disks of interest here, the potential is mainly accessible through the double integration of the surface density weighted by the Green function
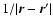 (see Binney & Tremaine 1987, for a review). This integral approach is very tricky due to the inevitable occurrence of singularities everywhere inside matter, i.e. when
(see Binney & Tremaine 1987, for a review). This integral approach is very tricky due to the inevitable occurrence of singularities everywhere inside matter, i.e. when
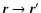 .
The difficulty is circumvented when the Green function is converted into series (Kellogg 1929). However, these are infinite and alternate series which do not converge inside sources, although their integration over the distribution does (Durand 1953). The efficiency of the series representation is therefore strongly misleading in practice because series truncations do not lead to a numerically stable description of the potential inside disks (Clement 1974). The errors in potential values can be as large as a few percent on average, even when the order of truncation attain several tens (Stone & Norman 1992). Singularities are no more present when the potential is expressed in terms of integrals of Bessel functions. But the oscillatory behavior of Bessel functions as well as their infinite definition domain pose technical difficulties, even for infinitely extended disks. Potential/density pairs can also be constructed by superposition of homeoids conveniently shrunk along one axis (Binney & Tremaine 1987), or by parametric expansion and ordering of the associated Poisson equation (Ciotti & Bertin 2005).
.
The difficulty is circumvented when the Green function is converted into series (Kellogg 1929). However, these are infinite and alternate series which do not converge inside sources, although their integration over the distribution does (Durand 1953). The efficiency of the series representation is therefore strongly misleading in practice because series truncations do not lead to a numerically stable description of the potential inside disks (Clement 1974). The errors in potential values can be as large as a few percent on average, even when the order of truncation attain several tens (Stone & Norman 1992). Singularities are no more present when the potential is expressed in terms of integrals of Bessel functions. But the oscillatory behavior of Bessel functions as well as their infinite definition domain pose technical difficulties, even for infinitely extended disks. Potential/density pairs can also be constructed by superposition of homeoids conveniently shrunk along one axis (Binney & Tremaine 1987), or by parametric expansion and ordering of the associated Poisson equation (Ciotti & Bertin 2005).
Huré & Pierens (2005) have reported a numerical method to compute the gravitational potential in flat axially symmetric disks with great accuracy by a correct treatment of the singularity. When the surface density profile is conveniently split into two components (namely, a homogeneous component plus a residual one), the contribution of the singularity to the potential can be accounted for exactly through a closed-form expression. In this paper, we explore this "splitting method'' from a purely theoretical point of view in search for fully analytical solutions (i.e. potential/surface density pairs). In particular, it is shown that the residual component is an infinite series of radial integrals which are known analytically for a certain class of surface density distributions. This is the case of power law profiles which are of great astrophysical interest (e.g. Pringle 1981). The convergence rate of the residual component is then cubic. This is a major issue, when compared with the classical multipole expansion whose converge speed is prohibitively low inside sources.
This paper is organized as follows. In Sect. 2, we briefly recall the density splitting method for one dimensional disks (Huré & Pierens 2005). We expand the residual component as an infinite series of the integrals over the modulus of the complete elliptic integral of the first kind. We then show that the construction of potential/surface density pairs is possible for a certain class of surface density distribution. The impact of the series truncation on potential values is discussed in Sect. 3. The case of surface densities scaling as a power of the radius is investigated in detail in Sect. 4 (a Fortran 90 code is available on request). For this kind of distribution, the convergence rate is cubic. This is established in Sect. 5. The paper ends with a summary and concluding remarks.
2 Exact potential/surface density pairs in flat axisymmetric disks
The gravitational potential 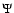 in the plane of a flat axially symmetric disk as pictured in Fig. 1 is given by the exact expression (e.g. Durand 1953):
in the plane of a flat axially symmetric disk as pictured in Fig. 1 is given by the exact expression (e.g. Durand 1953):
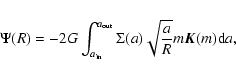 |
(1) |
where
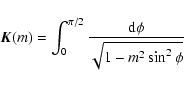 |
(2) |
is the complete elliptic integral of the first kind,
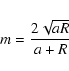 |
(3) |
is the modulus of 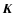 (with
(with
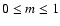 ), a and R are polar cylindrical radii (a refering to the matter distribution),
), a and R are polar cylindrical radii (a refering to the matter distribution),
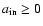 is the radius of the inner edge,
is the radius of the inner edge,
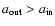 is the radius of the outer edge,
is the radius of the outer edge, 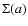 is the surface density, and G is the Gravitation constant. The function
is the surface density, and G is the Gravitation constant. The function 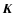 is plotted versus m in Fig. 2; it is characterized by a divergence for
is plotted versus m in Fig. 2; it is characterized by a divergence for
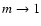 .
This is a logarithmic divergence (see e.g. Mestel 1963; Kellogg 1929), since we have (Gradshteyn & Ryzhik 1965):
.
This is a logarithmic divergence (see e.g. Mestel 1963; Kellogg 1929), since we have (Gradshteyn & Ryzhik 1965):
![\begin{displaymath}\lim_{m \rightarrow 1}{\vec K}(m) = \ln \frac{4}{\sqrt{1-m^2}}\left[ 1 + {\cal O}(1-m^2) \right].
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img37.gif) |
(4) |
Despite this singularity which occurs everywhere inside the disk (i.e. for
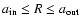 ), the potential is generally finite everywhere.
), the potential is generally finite everywhere.
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6808fig2.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg39.gif) |
Figure 2:
Complete elliptic integrals of the first and second kinds versus the modulus m. |
| Open with DEXTER |
In order to determine 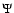 inside the disk, we set:
inside the disk, we set:
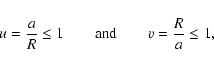 |
(5) |
and so, u locates matter of the inner disk
![$[a_{\rm in},R]$](/articles/aa/full/2007/44/aa6808-06/img41.gif) ,
whereas v is for the outer part
,
whereas v is for the outer part
![$[R,a_{\rm out}]$](/articles/aa/full/2007/44/aa6808-06/img42.gif) .
Using the transformation (e.g. Gradshteyn & Ryzhik 1965):
.
Using the transformation (e.g. Gradshteyn & Ryzhik 1965):
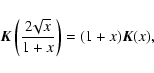 |
(6) |
where
 ,
Eq. (1) reads:
,
Eq. (1) reads:
![\begin{displaymath}\Psi(R) = -4GR \left[ \int_{u_{\rm in}}^1{\Sigma(u) {\vec K}(...
..._{\rm out}}{\Sigma(v) \frac{{\vec K}(v)}{v^2}{\rm d}v}\right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img45.gif) |
(7) |
where
 and
and
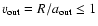 correspond to the position of the disk edges. As quoted,
correspond to the position of the disk edges. As quoted, 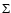 must now be regarded as a function of u in the first integral, and as a function of v=1/u in the second one. According to the "density splitting'' method (Huré & Pierens 2005), we divide
must now be regarded as a function of u in the first integral, and as a function of v=1/u in the second one. According to the "density splitting'' method (Huré & Pierens 2005), we divide 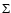 into two components, namely:
into two components, namely:
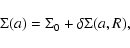 |
(8) |
where
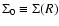 is the value of the surface density at the radius of the singularity (where the moduli m, u and v are unity), and
is the value of the surface density at the radius of the singularity (where the moduli m, u and v are unity), and
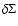 is the "residual'' surface density profile. The potential then takes the form:
is the "residual'' surface density profile. The potential then takes the form:
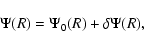 |
(9) |
where
![\begin{displaymath}\Psi_0(R) = -4GR \Sigma_0 \left[ \int_{u_{\rm in}}^1{{\vec K}...
... \int_1^{v_{\rm out}}{\frac{{\vec K}(v)}{v^2}{\rm d}v} \right]
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img53.gif) |
(10) |
is the potential due to a radially homogeneous disk with constant surface density 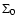 , and
, and
![$\displaystyle \delta \Psi(R) = - 4GR \Bigg[ \int_{u_{\rm in}}^1{\delta \Sigma(u...
...
- \int_1^{v_{\rm out}}{\delta \Sigma(v)\frac{{\vec K}(v)}{v^2}{\rm d}v} \Bigg]$](/articles/aa/full/2007/44/aa6808-06/img55.gif) |
|
|
(11) |
is the "residual'' potential associated with
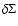 .
Note that
.
Note that 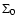 varies from place to place in the disk, as well as
varies from place to place in the disk, as well as
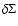 .
As demonstrated elsewhere (see also Huré 2005), this technique of density splitting can be numerically very accurate, for two reasons. First,
.
As demonstrated elsewhere (see also Huré 2005), this technique of density splitting can be numerically very accurate, for two reasons. First, 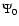 is known in a closed form:
is known in a closed form:
![\begin{displaymath}\Psi_0(R) = -4GR \Sigma_0 \left[ \frac{{\vec E}(v_{\rm out})}...
...E}(u_{\rm in}) + {u_{\rm in}'}^2 {\vec K}(u_{\rm in}) \right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img57.gif) |
(12) |
and is finite everywhere in the disk mid-plane. In Eq. (12),
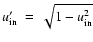 is the complementary modulus and
is the complementary modulus and 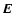 is the complete elliptic integral of the second kind (see Fig. 2):
is the complete elliptic integral of the second kind (see Fig. 2):
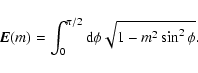 |
(13) |
Second, each integrand in Eq. (11) now vanishes at the singularity (this is the role of the splitting), making the two integrals easily computable with standard quadrature rules.
In order to determine analytical expressions for 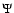 on the basis of the splitting method, we consider the expansion of the elliptic integral of the first kind over its modulus (e.g. Gradshteyn & Ryzhik 1965), namely:
on the basis of the splitting method, we consider the expansion of the elliptic integral of the first kind over its modulus (e.g. Gradshteyn & Ryzhik 1965), namely:
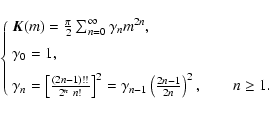 |
(14) |
When this infinite series is inserted into Eq. (11), the residual potential
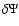 becomes an infinite series. Let
becomes an infinite series. Let
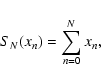 |
(15) |
be the sum of N+1 terms
 .
The residual potential is then given by:
.
The residual potential is then given by:
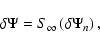 |
(16) |
with for any 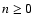
![$\displaystyle \delta \Psi_n = - 2 \pi G R \gamma_n \Bigg[ \int_{u_{\rm in}}^1{\...
...2n+1}{\rm d}u} - \int_1^{v_{\rm out}}{\delta \Sigma(v)v^{2n-2}{\rm d}v} \Bigg].$](/articles/aa/full/2007/44/aa6808-06/img66.gif) |
|
|
(17) |
Note that this expression for
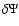 is still exact, provided all the terms
is still exact, provided all the terms
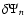 of the series are included. It follows that potential/surface density pairs
of the series are included. It follows that potential/surface density pairs
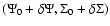 can easily be constructed for flat disks with finite size (or not, depending on
can easily be constructed for flat disks with finite size (or not, depending on
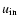 and
and
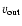 ). These pairs are analytical if the residual pair (
). These pairs are analytical if the residual pair (
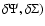 is analytical, that is, if the product of
is analytical, that is, if the product of 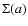 by a power law of a is analytically integrable. We immediately see that many simple functions
by a power law of a is analytically integrable. We immediately see that many simple functions 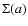 are concerned. In particular, if
are concerned. In particular, if  is a power law of the radius a - as often met in astrophysical disk models -, then
is a power law of the radius a - as often met in astrophysical disk models -, then
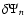 is a power law of the radius too (more precisely, a mixture of four power laws; see Sect. 4). Obviously, pairs determined through Eqs. (16) and (17) should generally remain in the form of an infinite series with no equivalent closed form expression. This is not a big problem, first because working with infinite expansions is common in potential theory, and second because the residual potential
is a power law of the radius too (more precisely, a mixture of four power laws; see Sect. 4). Obviously, pairs determined through Eqs. (16) and (17) should generally remain in the form of an infinite series with no equivalent closed form expression. This is not a big problem, first because working with infinite expansions is common in potential theory, and second because the residual potential
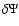 is a rapidly converging series (see Sect. 5).
is a rapidly converging series (see Sect. 5).
3 Approximate potential from truncated series
The estimate of 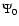 should generate no significant error since special functions
should generate no significant error since special functions 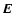 and
and 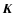 can be determined within the computer precision from a numerical library. In contrast, the computation of
can be determined within the computer precision from a numerical library. In contrast, the computation of
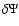 is not errorless because, in practice, any series is necessarily truncated at a certain order N. Does the truncation produce large errors in potential values? In order to answer this question, it is important to stress again that the occurrence of the condition
is not errorless because, in practice, any series is necessarily truncated at a certain order N. Does the truncation produce large errors in potential values? In order to answer this question, it is important to stress again that the occurrence of the condition
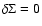 enables the neutralization of the logarithmic singularity, making the remaining integrands fully regular. As a consequence, the value of the residual potential
enables the neutralization of the logarithmic singularity, making the remaining integrands fully regular. As a consequence, the value of the residual potential
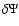 is mainly determined by the shape of the integrands far from the singularity, that is close to the edges. In other words, neither the precise behavior of the complete elliptic integral
is mainly determined by the shape of the integrands far from the singularity, that is close to the edges. In other words, neither the precise behavior of the complete elliptic integral 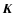 nor the shape of the residual surface density profile
nor the shape of the residual surface density profile
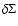 around the singularity are critical to estimate
around the singularity are critical to estimate
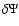 with a certain accuracy. We therefore expect that
with a certain accuracy. We therefore expect that
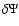 can be accurately determined if
can be accurately determined if 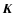 is replaced by any approximation which preserves at best the values of this function around the bounds
is replaced by any approximation which preserves at best the values of this function around the bounds
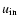 and
and
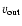 rather than at the radius of the singularity (where m=u=v=1). From this point of view, the series defined by Eq. (14) is fully appropriate as it converges very rapidly for moduli significantly less than unity. Figure 3 shows a typical example where
rather than at the radius of the singularity (where m=u=v=1). From this point of view, the series defined by Eq. (14) is fully appropriate as it converges very rapidly for moduli significantly less than unity. Figure 3 shows a typical example where 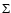 is a power law of the radius. We clearly see that the two integrands
is a power law of the radius. We clearly see that the two integrands
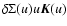 and
and
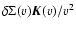 appearing in Eq. (11) are quite insensitive to the approximation adopted for
appearing in Eq. (11) are quite insensitive to the approximation adopted for 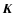 (one-term, two-term expansions or exact). This conclusion is independent of the
(one-term, two-term expansions or exact). This conclusion is independent of the 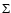 -profile and of R as well.
-profile and of R as well.
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6808fig3.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg75.gif) |
Figure 3:
Typical shape of the integrands appearing in Eq. (11) computed from different approximations for the function 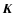 .
In this example, the disk has inner edge .
In this example, the disk has inner edge
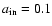 and outer edge
and outer edge
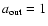 ,
the surface density obeys a power law of the radius with ,
the surface density obeys a power law of the radius with
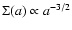 (that is s=-1.5), and the radius is
(that is s=-1.5), and the radius is
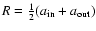 . . |
| Open with DEXTER |
For a truncation of the series at order N, the potential is given by the approximate value:
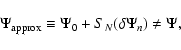 |
(18) |
and we have asymptotically:
![\begin{displaymath}\Psi_0 + \lim_{N \rightarrow \infty}{\left[ S_N ( \delta \Psi_n ) \right]} = \Psi.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img77.gif) |
(19) |
With only one term in Eq. (14), we have
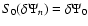 with:
with:
![\begin{displaymath}
\delta \Psi_0 = -2 \pi GR \left[ \int_{u_{\rm in}}^1{\delta ...
...1^{v_{\rm out}}{\delta \Sigma(v)\frac{{\rm d}v}{v^2}} \right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img79.gif) |
(20) |
and so the approximate potential is
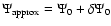 .
For a two-term expansion of the complete elliptic integral of the first kind, the residual potential is
.
For a two-term expansion of the complete elliptic integral of the first kind, the residual potential is
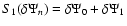 ,
where
,
where
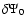 is given by Eq. (20), and:
is given by Eq. (20), and:
![\begin{displaymath}\delta \Psi_1 = -\frac{\pi}{2} G R \left[ \int_{u_{\rm in}}^1...
...d}u} - \int_1^{v_{\rm out}}{\delta \Sigma(v){\rm d}v} \right].
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img82.gif) |
(21) |
The approximate potential is then
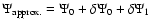 ,
and so on. Each new term added into the expansion brings a new component
,
and so on. Each new term added into the expansion brings a new component
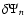 defined by Eq. (17). We then expect that the more terms in the expansion, the more accurate the potential. If the series converges rapidly (this is the case of power law distributions; see below), the absolute error made on
defined by Eq. (17). We then expect that the more terms in the expansion, the more accurate the potential. If the series converges rapidly (this is the case of power law distributions; see below), the absolute error made on 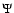 is roughly
is roughly
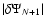 .
.
4 The case of power-law surface density profiles
Let us consider the case where 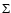 is a power-law of the radius, namely:
is a power-law of the radius, namely:
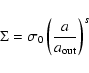 |
(22) |
where 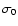 is the surface density at the outer edge of the disk. Power-law surface density solutions are found in many disk models (e.g. Pringle 1981) and match observations (e.g. Guilloteau & Dutrey 1998), with s<0 in general. We then have:
is the surface density at the outer edge of the disk. Power-law surface density solutions are found in many disk models (e.g. Pringle 1981) and match observations (e.g. Guilloteau & Dutrey 1998), with s<0 in general. We then have:
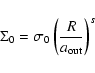 |
(23) |
and so:
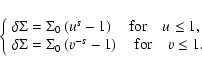 |
(24) |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6808fig4.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg89.gif) |
Figure 4:
Top: potential ( lines) inside the disk for three different surface density exponents s when computed with a one-term expanded elliptic integral (i.e.
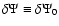 ). Reference values ). Reference values
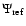 ( symbols) are obtained numerically within the computer precision. Bottom: decimal logarithm of the relative error (the average of
( symbols) are obtained numerically within the computer precision. Bottom: decimal logarithm of the relative error (the average of 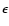 is also indicated).
is also indicated). |
| Open with DEXTER |
For a one-term expansion of the complete elliptic integral of the first kind, the residual potential is given by:
![\begin{displaymath}
\delta \Psi_0 = 2\pi G R \Sigma_0 \left[ \int_{u_{\rm in}}^1...
... out}}{\left(v^{-s}-1\right)\frac{{\rm d}v}{v^2}} \right]\cdot
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img90.gif) |
(25) |
If
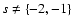 ,
this is (see Appendix A for these two cases):
,
this is (see Appendix A for these two cases):
![$\displaystyle \delta \Psi_0 = 2 \pi G R \Sigma_0 \Bigg[\frac{u_{\rm in}^{s+2}-1...
...m in}^2}{2} +\frac{1-v_{\rm out}^{-s-1}}{s+1} + \frac{1}{v_{\rm out}}-1 \Bigg].$](/articles/aa/full/2007/44/aa6808-06/img92.gif) |
|
|
(26) |
Figure 4 displays the approximate potential
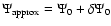 for disks with inner edge
for disks with inner edge
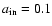 ,
outer edge
,
outer edge
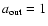 and power law exponents s=-1, -1.5 and -2.5. References potential values
and power law exponents s=-1, -1.5 and -2.5. References potential values
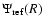 have been determined within the computer precision from the numerical splitting method (Huré & Pierens 2005) and compared to
have been determined within the computer precision from the numerical splitting method (Huré & Pierens 2005) and compared to
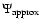 .
The decimal logarithm of the relative error
.
The decimal logarithm of the relative error
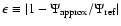 is also shown in Fig. 4. We see that the potential is reproduced with an accuracy better than
is also shown in Fig. 4. We see that the potential is reproduced with an accuracy better than 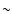 2% (on average) in the entire disk with only one term in the expansion of the
2% (on average) in the entire disk with only one term in the expansion of the 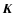 -function. This is already remarkable. The accuracy is relatively uniform, and it is slightly better at the outer edge. This point is particularly interesting to model young stellar objects or Active Galactic Nuclei. In these systems, the inner disk is dynamically under the control of a massive central object (a proto-star or a black hole), and so there is no need for very accurate potential values. On the other hand, in the outer regions where disks can be self-gravitating (e.g. Huré 2000), a reliable description of the potential is required.
-function. This is already remarkable. The accuracy is relatively uniform, and it is slightly better at the outer edge. This point is particularly interesting to model young stellar objects or Active Galactic Nuclei. In these systems, the inner disk is dynamically under the control of a massive central object (a proto-star or a black hole), and so there is no need for very accurate potential values. On the other hand, in the outer regions where disks can be self-gravitating (e.g. Huré 2000), a reliable description of the potential is required.
The accuracy of potential values can be improved by adding a second term. For N=1, we find:
![\begin{displaymath}\delta \Psi_1 = \frac{\pi}{2} G R \Sigma_0 \left[ \int_{u_{\r...
...+ \int_1^{v_{\rm out}}{\left(v^{-s}-1\right){\rm d}v} \right].
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img97.gif) |
(27) |
If
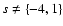 (see Appendix B for these two cases), the expression is:
(see Appendix B for these two cases), the expression is:
![$\displaystyle \delta \Psi_1 = 2 \pi G R \Sigma_0 \Bigg[ \frac{u_{\rm in}^{s+4}-...
... + \frac{1- v_{\rm out}^{-s+1}}{4(s-1)} + \frac{1 - v_{\rm out}}{4} \Bigg]\cdot$](/articles/aa/full/2007/44/aa6808-06/img99.gif) |
|
|
(28) |
Figure 5 displays the results obtained with a two-term expansion of 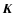 ,
i.e.
,
i.e.
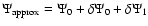 ,
under the same conditions as for Fig. 4. We see that the relative accuracy of mid-plane potential values (of the order of
,
under the same conditions as for Fig. 4. We see that the relative accuracy of mid-plane potential values (of the order of 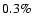 on average) is now better by a factor of
on average) is now better by a factor of 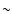 5.
5.
![\begin{figure}
\includegraphics[width=8.9cm,clip]{6808fig5.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg102.gif) |
Figure 5:
Same legend as for Fig. 4 but the residual potential
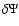 is determined from a two-term expanion of the complete elliptic integral of the first kind (i.e.
is determined from a two-term expanion of the complete elliptic integral of the first kind (i.e.
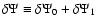 ). ). |
| Open with DEXTER |
Such a level of accuracy is probably sufficient for many disk models and applications. However, since the process of adding more and more terms represents no technical difficulty and converges rapidly (see Sect. 5), it can be repeated until a given accuracy is reached. In particular, for
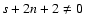 and
and
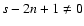 ,
we have (see the Appendix C for these two cases)
,
we have (see the Appendix C for these two cases)
![$\displaystyle \delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \Bigg[\frac{1-u_{\rm ...
...v_{\rm out}^{2n-s-1}-1}{2n-s-1} - \frac{v_{\rm out}^{2n-1}-1}{2n-1} \Bigg]\cdot$](/articles/aa/full/2007/44/aa6808-06/img105.gif) |
|
|
(29) |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6808fig6.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg106.gif) |
Figure 6:
Decimal logarithm of the relative error on potential values
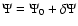 versus the order N of the truncation in Eq. (19) for five power law exponents s=-3.5, -3, -2.5, -1.5 and -0.5. The disk has inner edge
versus the order N of the truncation in Eq. (19) for five power law exponents s=-3.5, -3, -2.5, -1.5 and -0.5. The disk has inner edge
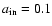 ,
outer edge ,
outer edge
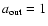 and the potential is computed at
and the potential is computed at
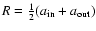 . . |
| Open with DEXTER |
5 Convergence rate of the series
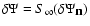 in the case of power law distributions
in the case of power law distributions
Figure 6 shows the rise of the accuracy of potential values 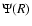 as the order N of the truncation increases for the same disk parameters as already considered and a few exponents s. We find that the relative error
as the order N of the truncation increases for the same disk parameters as already considered and a few exponents s. We find that the relative error
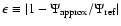 first decreases slowly as N increases. But above a certain rank
first decreases slowly as N increases. But above a certain rank
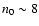 -10, this error approximately scales as 1/N3, before saturation near the computer precision, for
-10, this error approximately scales as 1/N3, before saturation near the computer precision, for
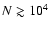 terms. We have checked that this conclusion holds for a wide variety of configurations and radii R. Convergence appears to be cubic. With this approach, we can easily select the lowest order corresponding to a given level of accuracy. From Fig. 6, we have roughly:
terms. We have checked that this conclusion holds for a wide variety of configurations and radii R. Convergence appears to be cubic. With this approach, we can easily select the lowest order corresponding to a given level of accuracy. From Fig. 6, we have roughly:
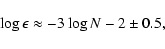 |
(30) |
for
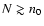 ,
or
,
or
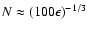 within about
within about 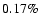 .
.
There are two remarkable cases. For s=0, the potential is fully analytical:
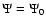 (i.e.
(i.e.
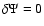 ). For s=-3, the relative accuracy rises with N much more drastically than for others exponents and reaches the maximum allowed by the computer for
). For s=-3, the relative accuracy rises with N much more drastically than for others exponents and reaches the maximum allowed by the computer for
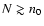 (see below).
(see below).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{6808fig8.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg117.gif) |
Figure 8:
Left: series
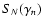 versus the truncation order N which diverges as
versus the truncation order N which diverges as
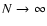 .
Right: series .
Right: series
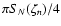 versus the truncation order N which converges towards Catalan's constant (see also Fig. 7).
versus the truncation order N which converges towards Catalan's constant (see also Fig. 7). |
| Open with DEXTER |
The expansion of
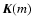 through Eq. (14) converges slowly as m approaches unity, and even diverges for m=1, although
through Eq. (14) converges slowly as m approaches unity, and even diverges for m=1, although 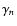 decreases rapidly as n increases (for large n,
decreases rapidly as n increases (for large n,
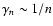 ). This is shown in Figs. 7 and 8. Note that the divergence of
). This is shown in Figs. 7 and 8. Note that the divergence of 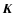 as
as
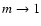 is the main reason why the determination of the potential inside sources by direct integration is generally not the appropriate way. What about the convergence of
is the main reason why the determination of the potential inside sources by direct integration is generally not the appropriate way. What about the convergence of
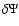 ? Since
? Since
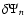 comes from the integration of
comes from the integration of 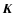 over its modulus,
over its modulus,
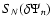 is made of terms of the form
is made of terms of the form
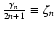 which decrease faster with n than terms
which decrease faster with n than terms 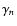 do. The series
do. The series
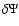 is then expected to converge (see the Appendix D). Figure 7 displays the terms
is then expected to converge (see the Appendix D). Figure 7 displays the terms 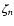 versus n, and the series
versus n, and the series
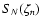 is plotted versus N in Fig. 8.
is plotted versus N in Fig. 8.
When the series
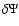 is truncated at order N, the relative error
is truncated at order N, the relative error
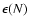 on the potential value is:
on the potential value is:
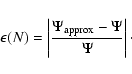 |
(31) |
From Eqs. (18) and (19), this expression can be re-written in the following form:
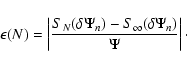 |
(32) |
The quantities
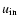 and
and
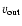 being always smaller than unity, their contribution in Eq. (29) - an exponential drop - is expected to vanish rapidly as n exceeds a certain rank. This transition occurs at
being always smaller than unity, their contribution in Eq. (29) - an exponential drop - is expected to vanish rapidly as n exceeds a certain rank. This transition occurs at
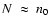 ;
it is clearly visible in Fig. 6 where
;
it is clearly visible in Fig. 6 where
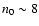 .
Thus, for
.
Thus, for
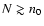 ,
the leading terms in
,
the leading terms in
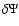 form a series
form a series
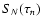 ,
with:
,
with:
![$\displaystyle \tau_n = \gamma_n \Bigg[ \frac{1}{2(n+1)} - \frac{1}{2(n+1)+s} +\frac{1}{2n-1}
- \frac{1}{2n-1-s}\Bigg],$](/articles/aa/full/2007/44/aa6808-06/img128.gif) |
|
|
(33) |
which can easily be rearranged:
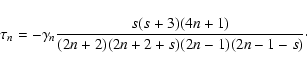 |
(34) |
For large values of n, we have:
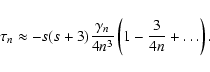 |
(35) |
and so, 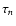 behaves like n-4, asymptotically. The coefficient
behaves like n-4, asymptotically. The coefficient 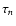 is displayed versus n for s=-1.5 in Fig. 7. Then, as soon as
is displayed versus n for s=-1.5 in Fig. 7. Then, as soon as 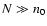 ,
the relative error is
,
the relative error is
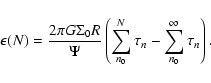 |
(36) |
Using Eq. (35), we have:
Since 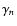 scales as 1/n for large n (see also Fig. (7)), we have:
scales as 1/n for large n (see also Fig. (7)), we have:
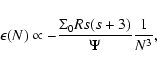 |
(38) |
as found "experimentally''. The convergence rate of this series is therefore cubic. This result holds irrespective of the radius R (except at the disk edges![[*]](/icons/foot_motif.gif) ) and whatever s, except in the case of the homogeneous disk (i.e. for s=0) and for s=-3 as well. In this latter case, the convergence rate is not limited by the terms
) and whatever s, except in the case of the homogeneous disk (i.e. for s=0) and for s=-3 as well. In this latter case, the convergence rate is not limited by the terms 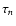 ,
but by the series asssociated with
,
but by the series asssociated with
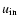 and
and
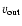 .
For s=-3, we have:
.
For s=-3, we have:
![\begin{displaymath}\delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \left[\frac{v_{\r...
...}-\frac{v_{\rm out}^{2n-1} - u_{\rm in}^{2n-1}}{2n-1} \right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img138.gif) |
(39) |
and so the convergence of
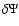 is exponential (see Fig. 6), except at the inner and outer edges (see Appendix E).
is exponential (see Fig. 6), except at the inner and outer edges (see Appendix E).
All numerical experiments have succesfully illustrated these results. This is a major issue, in particular because classical multipole expansions converge very slowly inside sources.
In this paper, we have reported a method to determine exact and approximate potential/surface density pairs in flat finite size axially symmetrical disks, in the continuity of the numerical splitting method described in Pierens & Huré (2005). At a given radius R, each pair is the sum of two components:
- a "homogeneous'' pair
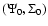 where
where
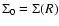 is the local value of the surface density and
is the local value of the surface density and 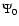 is given by Eq. (12),
is given by Eq. (12),
- a "residual'' pair
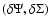 ,
where
,
where
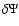 is an infinite series (see Eqs. (16) and (17)) and
is an infinite series (see Eqs. (16) and (17)) and
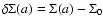 .
.
In general, the infinite series
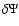 cannot be put into a closed form expression. However, in contrast to the multipole expansions commonly met in potential theory, this series has a cubic convergence rate inside the source. This major result is due to the splitting method which is equivalent to a convergence acceleration technique (in the mathematical sense). It means that very good approximations for the potential can be obtained by low order truncations of the series. Pairs can be constructed only for a certain class of the surface density profile
cannot be put into a closed form expression. However, in contrast to the multipole expansions commonly met in potential theory, this series has a cubic convergence rate inside the source. This major result is due to the splitting method which is equivalent to a convergence acceleration technique (in the mathematical sense). It means that very good approximations for the potential can be obtained by low order truncations of the series. Pairs can be constructed only for a certain class of the surface density profile 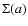 :
any function
:
any function 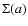 whose product by a power law of the radius a is analytically integrable does lead to a potential/surface density pair. This is the case of power laws. It would be interesting to list all functions satisfying this criterion.
whose product by a power law of the radius a is analytically integrable does lead to a potential/surface density pair. This is the case of power laws. It would be interesting to list all functions satisfying this criterion.
We have fully considered power law surface densities. Such profiles are particularly attractive for two main reasons: i) power laws underly many (if not most) astrophysical disk models, and ii) power laws may serve as a basis set to construct more complicated surface density profiles. This new approach along with associated computing tools![[*]](/icons/foot_motif.gif) should enable a much better representation of the gravitational potentials and forces in flat disks.
should enable a much better representation of the gravitational potentials and forces in flat disks.
Acknowledgements
We thank J. Braine for many fruitful comments. We are especially grateful to the referee L. Ciotti whose suggestions and criticisms allowed significant improvement of the paper.
Appendix A: Special cases for
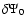
For s=-1 in Eq. (22), then Eq. (20) reads
![\begin{displaymath}\delta \Psi_0= 2 \pi G \Sigma_0 R\left\{ \left[\frac{u^2}{2}-...
...+ \left[ \ln v + \frac{1}{v} \right]_1^{v_{\rm out}} \right\}.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img144.gif) |
(A.1) |
For s=-2 in Eq. (22), then Eq. (20) reads
![\begin{displaymath}\delta \Psi_0= 2 \pi G \Sigma_0 R\left\{ \left[\frac{u^2}{2}-...
...}^1 + \left[ v + \frac{1}{v} \right]_1^{v_{\rm out}} \right\}.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img145.gif) |
(A.2) |
Appendix B: Special cases for
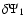
For s=-4 in Eq. (22), then Eq. (21) reads
![\begin{displaymath}\delta \Psi_1= \frac{\pi}{2} G \Sigma_0 R\left\{ \left[\frac{...
...1 + \left[ \frac{v^5}{5} - v \right]_1^{v_{\rm out}} \right\}.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img146.gif) |
(B.1) |
For s=+1 in Eq. (22), then Eq. (21) reads
![\begin{displaymath}\delta \Psi_1= \frac{\pi}{2} G \Sigma_0 R\left\{\left[\frac{u...
...rm in}}^1 + \left[ \ln v - v \right]_1^{v_{\rm out}} \right\}.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img147.gif) |
(B.2) |
Appendix C: Special cases for
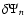
For s+2n+2=0 in Eq. (22), then
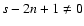 and Eq. (17) reads
and Eq. (17) reads
![$\displaystyle \delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \Bigg\{ \left[\frac{u...
...ac{v^{2n-s-1}}{2n-s-1} - \frac{v^{2n-1}}{2n-1} \right]_1^{v_{\rm out}} \Bigg\}.$](/articles/aa/full/2007/44/aa6808-06/img148.gif) |
|
|
(C.1) |
For
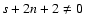 and s-2n+1=0 in Eq. (22), then Eq. (17) reads
and s-2n+1=0 in Eq. (22), then Eq. (17) reads
![$\displaystyle \delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \Bigg\{ \left[\frac{u...
... in}}^1
+ \left[ \ln v - \frac{v^{2n-1}}{2n-1} \right]_1^{v_{\rm out}} \Bigg\}.$](/articles/aa/full/2007/44/aa6808-06/img149.gif) |
|
|
(C.2) |
Appendix D: Convergence of S
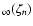
From (e.g. Gradshteyn & Ryzhik 1965), we see that
where C is Catalan's constant.
Appendix E: Convergence rate for s = -3 at the disk edges
At the disk outer edge where
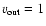 ,
we have:
,
we have:
![\begin{displaymath}\delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \left[\frac{1-\Delta^{2(n+1)}}{2(n+1)}-\frac{1 - \Delta^{2n-1}}{2n-1} \right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img158.gif) |
(E.1) |
where
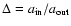 is the disk axis ratio. Since
is the disk axis ratio. Since
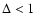 ,
the leading terms in
,
the leading terms in
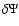 then form a series
then form a series
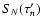 ,
with:
,
with:
For large n, we have
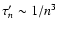 ,
and so
,
and so
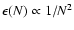 .
The convergence is therefore quadratic (as at the disk inner edge).
.
The convergence is therefore quadratic (as at the disk inner edge).
-
Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton,
NJ: Princeton University Press), 747
(In the text)
- Ciotti,
L., & Bertin, G. 2005, A&A, 437, 419 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Clement,
M. J. 1974, ApJ, 194, 709 [NASA ADS] [CrossRef] (In the text)
- Cuddeford, P.
1993, MNRAS, 262, 1076 [NASA ADS]
-
de Zeeuw, T., & Pfenniger, D. 1988, MNRAS, 235, 949 [NASA ADS]
- Durand, E. 1953,
Electrostatique, vol. I, Les distributions (Masson)
(In the text)
- Earn,
D. J. D. 1996, ApJ, 465, 91 [NASA ADS] [CrossRef]
- Gradshteyn,
I. S., & Ryzhik, I. M. 1965, Table of integrals,
series and products (New York: Academic Press), ed. Yu. V.
Geronimus, 4th Ed., M. Yu. Tseytlin
(In the text)
-
Guilloteau, S., & Dutrey, A. 1998, A&A, 339, 467 [NASA ADS] (In the text)
- Huré, J.-M. 2000,
A&A, 358, 378 [NASA ADS] (In the text)
- Huré, J.-M. 2005,
A&A, 434, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Huré, J.-M., & Pierens, A. 2005, ApJ, 624, 289 [NASA ADS] [CrossRef] (In the text)
- Kellogg,
O. D. 1929, Foundations of Potential Theory (New-York:
Frederick Ungar Publishing Company)
(In the text)
- Mestel, L. 1963,
MNRAS, 126, 553 [NASA ADS]
- Pringle,
J. E. 1981, ARA&A, 19, 137 [NASA ADS] (In the text)
- Quan, E. E. 1993,
MNRAS, 263, 394 [NASA ADS]
- Stone,
J. M., & Norman, M. L. 1992, ApJS, 80, 753 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
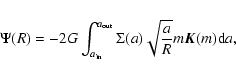
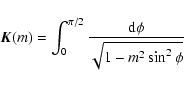
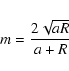
![\begin{displaymath}\lim_{m \rightarrow 1}{\vec K}(m) = \ln \frac{4}{\sqrt{1-m^2}}\left[ 1 + {\cal O}(1-m^2) \right].
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img37.gif)
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6808fig2.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg39.gif)
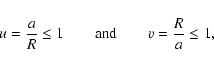
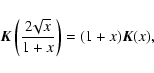
![\begin{displaymath}\Psi(R) = -4GR \left[ \int_{u_{\rm in}}^1{\Sigma(u) {\vec K}(...
..._{\rm out}}{\Sigma(v) \frac{{\vec K}(v)}{v^2}{\rm d}v}\right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img45.gif)
![\begin{displaymath}\Psi_0(R) = -4GR \Sigma_0 \left[ \int_{u_{\rm in}}^1{{\vec K}...
... \int_1^{v_{\rm out}}{\frac{{\vec K}(v)}{v^2}{\rm d}v} \right]
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img53.gif)
![$\displaystyle \delta \Psi(R) = - 4GR \Bigg[ \int_{u_{\rm in}}^1{\delta \Sigma(u...
...
- \int_1^{v_{\rm out}}{\delta \Sigma(v)\frac{{\vec K}(v)}{v^2}{\rm d}v} \Bigg]$](/articles/aa/full/2007/44/aa6808-06/img55.gif)
![\begin{displaymath}\Psi_0(R) = -4GR \Sigma_0 \left[ \frac{{\vec E}(v_{\rm out})}...
...E}(u_{\rm in}) + {u_{\rm in}'}^2 {\vec K}(u_{\rm in}) \right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img57.gif)
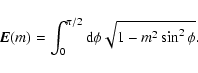
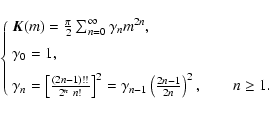
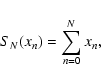
![$\displaystyle \delta \Psi_n = - 2 \pi G R \gamma_n \Bigg[ \int_{u_{\rm in}}^1{\...
...2n+1}{\rm d}u} - \int_1^{v_{\rm out}}{\delta \Sigma(v)v^{2n-2}{\rm d}v} \Bigg].$](/articles/aa/full/2007/44/aa6808-06/img66.gif)
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6808fig3.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg75.gif)
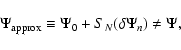
![\begin{displaymath}\Psi_0 + \lim_{N \rightarrow \infty}{\left[ S_N ( \delta \Psi_n ) \right]} = \Psi.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img77.gif)
![\begin{displaymath}
\delta \Psi_0 = -2 \pi GR \left[ \int_{u_{\rm in}}^1{\delta ...
...1^{v_{\rm out}}{\delta \Sigma(v)\frac{{\rm d}v}{v^2}} \right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img79.gif)
![\begin{displaymath}\delta \Psi_1 = -\frac{\pi}{2} G R \left[ \int_{u_{\rm in}}^1...
...d}u} - \int_1^{v_{\rm out}}{\delta \Sigma(v){\rm d}v} \right].
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img82.gif)
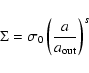
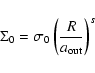
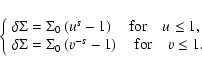
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6808fig4.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg89.gif)
![\begin{displaymath}
\delta \Psi_0 = 2\pi G R \Sigma_0 \left[ \int_{u_{\rm in}}^1...
... out}}{\left(v^{-s}-1\right)\frac{{\rm d}v}{v^2}} \right]\cdot
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img90.gif)
![$\displaystyle \delta \Psi_0 = 2 \pi G R \Sigma_0 \Bigg[\frac{u_{\rm in}^{s+2}-1...
...m in}^2}{2} +\frac{1-v_{\rm out}^{-s-1}}{s+1} + \frac{1}{v_{\rm out}}-1 \Bigg].$](/articles/aa/full/2007/44/aa6808-06/img92.gif)
![\begin{displaymath}\delta \Psi_1 = \frac{\pi}{2} G R \Sigma_0 \left[ \int_{u_{\r...
...+ \int_1^{v_{\rm out}}{\left(v^{-s}-1\right){\rm d}v} \right].
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img97.gif)
![$\displaystyle \delta \Psi_1 = 2 \pi G R \Sigma_0 \Bigg[ \frac{u_{\rm in}^{s+4}-...
... + \frac{1- v_{\rm out}^{-s+1}}{4(s-1)} + \frac{1 - v_{\rm out}}{4} \Bigg]\cdot$](/articles/aa/full/2007/44/aa6808-06/img99.gif)
![\begin{figure}
\includegraphics[width=8.9cm,clip]{6808fig5.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg102.gif)
![$\displaystyle \delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \Bigg[\frac{1-u_{\rm ...
...v_{\rm out}^{2n-s-1}-1}{2n-s-1} - \frac{v_{\rm out}^{2n-1}-1}{2n-1} \Bigg]\cdot$](/articles/aa/full/2007/44/aa6808-06/img105.gif)
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6808fig6.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6808fig7.eps}\end{figure}](/articles/aa/full/2007/44/aa6808-06/Timg116.gif)
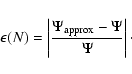
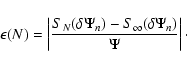
![$\displaystyle \tau_n = \gamma_n \Bigg[ \frac{1}{2(n+1)} - \frac{1}{2(n+1)+s} +\frac{1}{2n-1}
- \frac{1}{2n-1-s}\Bigg],$](/articles/aa/full/2007/44/aa6808-06/img128.gif)
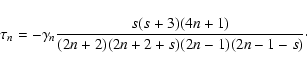
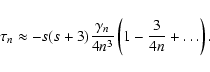
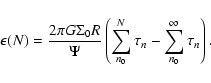
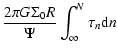
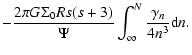
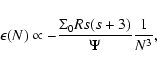
![\begin{displaymath}\delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \left[\frac{v_{\r...
...}-\frac{v_{\rm out}^{2n-1} - u_{\rm in}^{2n-1}}{2n-1} \right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img138.gif)
![\begin{displaymath}\delta \Psi_0= 2 \pi G \Sigma_0 R\left\{ \left[\frac{u^2}{2}-...
...+ \left[ \ln v + \frac{1}{v} \right]_1^{v_{\rm out}} \right\}.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img144.gif)
![\begin{displaymath}\delta \Psi_0= 2 \pi G \Sigma_0 R\left\{ \left[\frac{u^2}{2}-...
...}^1 + \left[ v + \frac{1}{v} \right]_1^{v_{\rm out}} \right\}.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img145.gif)
![\begin{displaymath}\delta \Psi_1= \frac{\pi}{2} G \Sigma_0 R\left\{ \left[\frac{...
...1 + \left[ \frac{v^5}{5} - v \right]_1^{v_{\rm out}} \right\}.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img146.gif)
![\begin{displaymath}\delta \Psi_1= \frac{\pi}{2} G \Sigma_0 R\left\{\left[\frac{u...
...rm in}}^1 + \left[ \ln v - v \right]_1^{v_{\rm out}} \right\}.
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img147.gif)
![$\displaystyle \delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \Bigg\{ \left[\frac{u...
...ac{v^{2n-s-1}}{2n-s-1} - \frac{v^{2n-1}}{2n-1} \right]_1^{v_{\rm out}} \Bigg\}.$](/articles/aa/full/2007/44/aa6808-06/img148.gif)
![$\displaystyle \delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \Bigg\{ \left[\frac{u...
... in}}^1
+ \left[ \ln v - \frac{v^{2n-1}}{2n-1} \right]_1^{v_{\rm out}} \Bigg\}.$](/articles/aa/full/2007/44/aa6808-06/img149.gif)
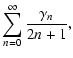
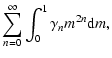
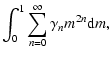
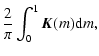
![\begin{displaymath}\delta \Psi_n = 2 \pi G \Sigma_0 R \gamma_n \left[\frac{1-\Delta^{2(n+1)}}{2(n+1)}-\frac{1 - \Delta^{2n-1}}{2n-1} \right],
\end{displaymath}](/articles/aa/full/2007/44/aa6808-06/img158.gif)
![$\displaystyle \gamma_n \left[ \frac{1}{2(n+1)} - \frac{1}{2n-1} \right],$](/articles/aa/full/2007/44/aa6808-06/img163.gif)