1 - Solar Physics and Space Plasma Research Centre (
2 - Physics Department, University of Warwick, Coventry CV4 7AL, UK
3 - Centrum voor Plasma Astrofysica, KU Leuven, Celestijnenlaan 200B, 3001 Heverlee, Belgium
A&A 475, 341-348 (2007)
DOI: 10.1051/0004-6361:20078086
G. Verth1 - T. Van Doorsselaere2 - R. Erdélyi1 - M. Goossens3
1 - Solar Physics and Space Plasma Research Centre (
![]() RC), University of Sheffield, Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK
RC), University of Sheffield, Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK
2 -
Physics Department, University of Warwick, Coventry CV4 7AL, UK
3 -
Centrum voor Plasma Astrofysica, KU Leuven, Celestijnenlaan 200B, 3001 Heverlee, Belgium
Received 14 June 2007 / Accepted 22 August 2007
Abstract
Context. The new generation of extreme-ultraviolet (EUV) imagers onboard missions such as the Solar Dynamics Observatory (SDO) and Solar Orbiter (SO) will provide the most accurate spatial measurements of post-flare coronal loop oscillations yet. The amplitude profiles of these loop oscillations contain important information about plasma fine structure in the corona.
Aims. We show that the position of the anti-nodes of the amplitude profile of the first harmonic of the standing fast kink wave of a coronal loop relate to the plasma density stratification of that loop.
Methods. The MHD kink transversal waves of coronal loops are modelled both numerically and analytically. The numerical model implements the implicit finite element code POLLUX. Dispersion relations are derived and solved analytically. The results of the two methods are compared and verified.
Results. Density stratification causes the anti-nodes of the first harmonic to shift towards the loop footpoints. The greater the density stratification, the larger the shift. The anti-node shift of the first harmonic of a semi-circular coronal loop with a density scale height H=50 Mm and loop half length L=100 Mm is approximately 5.6 Mm. Shifts in the Mm range are measureable quantities providing valuable information about the subresolution structure of coronal loops.
Conclusions. The measurement of the anti-node shift of the first harmonic of the standing fast kink wave of coronal loops is potentially a new tool in the field of solar magneto-seismology, providing a novel complementary method of probing plasma fine structure in the corona.
Key words: Sun: corona - Sun: magnetic fields - Sun: oscillations - Sun: fundamental parameters
Post-flare transversal coronal loop oscillations have been observed many times using the high-resolution EUV imager onboard the Transition Region And Coronal Explorer (TRACE) (see e.g., Aschwanden et al. 1999a, 2002; Nakariakov et al. 1999; Verwichte et al. 2004). These oscillations were identified as the fundamental mode of the standing fast-kink wave from MHD wave theory developed by e.g., Edwin & Roberts (1983). The theory used models a coronal loop as a straight magnetic cylinder with different external and internal plasma densities, both of which are taken to be constants.
However, it is now clear from EUV observations using, e.g, EIT (Extreme-ultraviolet Imaging Telescope) onboard SOHO (SOlar and Heliospheric Observatory) and TRACE, that even in "static'' active region coronal loops, the spatial and temporal behaviour of plasma is far more complex. Using emission measures, there is observational evidence that there is density stratification in coronal loops. In younger active regions there have been measurements of "super-hydrostatic'' density scale heights that are up to four times higher than expected (Aschwanden et al. 2000, 2001). On the other hand, loops have been observed in older active regions that are close to hydrostatic equilibrium (Aschwanden et al. 1999b) with density scale heights that can be explained by gravitational stratification. To complicate matters further, significant dynamical behaviour has also been observed in "static'' loops, e.g., flows (Brekke et al. 1997; Winebarger et al. 2001, 2002) and cooling events (Winebarger et al. 2003; Schrijver 2001).
In light of these observations, a more realistic theory of fast kink waves has been developed in the past five years to model oscillating coronal loops with inhomogeneous plasma density equilibria. Firstly, spatial variation of density in the radial direction has been included in the analysis leading to a change in period and damping of the MHD waves (Ruderman & Roberts 2002; Goossens et al. 2002; Aschwanden et al. 2003; Van Doorsselaere et al. 2004; Arregui et al. 2007). Secondly, spatial variation of density in the longitudinal direction has been included in the analysis leading to changes in the ratios of the periods of the overtone modes to that of the fundamental mode and to deviations of the eigenfunctions from a single sine term in the longitudinal direction (Díaz et al. 2002; Goossens et al. 2006; Andries et al. 2005b; Dymova & Ruderman 2005; Arregui et al. 2006; McEwan et al. 2006; Erdélyi & Verth 2007, EV07 hereafter; Verth & Erdélyi 2007; Verth 2007). It is expected that this theory can be used in solar magneto-seismology, particularly in applications to the corona, to determine more detailed information about plasma fine structures than was previously possible.
In their paper, EV07 proposed the novel diagnostic method of spatial magneto-seismology (SMS). In relation to standing fast kink waves in the corona, SMS requires measurement of the variance in maximum amplitude as a function of position along a loop. EV07 showed that for the fundamental mode, changes in amplitude caused by the density stratification in the corona are likely to be too small to observe at present. Correspondingly, in the frequency domain, it was shown by Andries et al. (2005a) that, for the expected range of plasma density scale heights in the corona, the frequency of fundamental mode is practically invariant.
However, theoretically it is predicted that the frequencies (e.g., Andries et al. 2005a) and amplitude profiles (e.g., Verth & Erdélyi 2007; Verth 2007) of higher harmonics have a much stronger dependence on density stratification. Since the first harmonic may already have been detected in TRACE data (see Verwichte et al. 2004), this is potentially the most useful higher harmonic to study for the purpose of obtaining more detailed plasma diagnostics of the corona. Therefore, as a continuation of the initial exploratory studies by EV07 regarding the fundamental mode, the dependence of the amplitude profile of the first harmonic on density stratification will be investigated. Importantly, the results will show that the spatial observational signatures of stratification can be used as a new seismological tool. SMS has great potential in light of the improved spatial resolution ground-based (e.g., the Advanced Technology Solar Telescope [ATST]) or space-borne observations (e.g., Hinode, the Solar Dynamics Observatory [SDO] and the Solar Orbiter [SO]).
In both the numerical investigation in this section and the analytical study in Sect. 3, coronal loops will be modelled as straight magnetic cylinders with length 2L and radius R. With cylindrical cooridinates
![]() ,
the plasma densities both outside (
,
the plasma densities both outside (
![]() )
and inside (
)
and inside (
![]() )
the tube are allowed to be arbitrary functions of z and the magnetic field,
)
the tube are allowed to be arbitrary functions of z and the magnetic field, ![]() is constant and parallel to the cylinder axis (see Fig. 1). The effects of varying the equilibrium density in the radial direction are neglected here to focus on the effects of the longitudinal variation on the eigenfunctions of the first harmonic. For standing fast kink modes, the amplitude profile, denoted by
is constant and parallel to the cylinder axis (see Fig. 1). The effects of varying the equilibrium density in the radial direction are neglected here to focus on the effects of the longitudinal variation on the eigenfunctions of the first harmonic. For standing fast kink modes, the amplitude profile, denoted by ![]() ,
is proportional to the eigenmode of the radial velocity component and is unique up to a constant scaling factor (subscript
,
is proportional to the eigenmode of the radial velocity component and is unique up to a constant scaling factor (subscript
![]() is mode number). To find the eigenfrequencies, denoted by
is mode number). To find the eigenfrequencies, denoted by ![]() and radial velocity eigenmodes of the employed coronal loop model, the numerical code POLLUX is used, originally developed by Van der Linden (1991). POLLUX was recently utilised to compute the frequencies of the fundamental kink oscillations (n=1) in coronal loops (Arregui et al. 2005).
and radial velocity eigenmodes of the employed coronal loop model, the numerical code POLLUX is used, originally developed by Van der Linden (1991). POLLUX was recently utilised to compute the frequencies of the fundamental kink oscillations (n=1) in coronal loops (Arregui et al. 2005).
The code discretizes the radial direction (r) with finite elements, and the longitudinal direction (z) with Fourier components. It calculates the eigenvalues and eigenmodes of the linearized, resistive MHD equations by using a shooting method.
To investigate the possible effects of density stratification on the amplitude profile of kink oscillations, a reasonable physical form of
![]() in the corona must be assumed. It is important to stress at this point that only the effect of a stratified plasma in static equilibrium will be addressed in the present paper. For completeness, a theory must also be developed that quantifies the effects of observed dynamical processes, such as flows on fast kink oscillations. In semi-circular coronal loops where the plasma is close to hydrostatic equilibrium, a reasonable assumption for the density profile is
in the corona must be assumed. It is important to stress at this point that only the effect of a stratified plasma in static equilibrium will be addressed in the present paper. For completeness, a theory must also be developed that quantifies the effects of observed dynamical processes, such as flows on fast kink oscillations. In semi-circular coronal loops where the plasma is close to hydrostatic equilibrium, a reasonable assumption for the density profile is
![\begin{figure}
\par\includegraphics[height=5cm,width=6.5cm,clip]{8086fig1.eps}\end{figure}](/articles/aa/full/2007/43/aa8086-07/Timg22.gif) |
Figure 1: The equilibrium configuration of a magnetic cylinder with longitudinally varying density. |
| Open with DEXTER | |
Equilibrium quantities, as explained before, are Fourier-analysed in the z-direction in POLLUX. Therefore, deviations occur between the imposed density profile and the actual profile used in the computations. These deviations become larger for a stronger stratification. However, Arregui et al. (2005) compared the numerically calculated eigenfrequences to the analytically established frequencies (Andries et al. 2005b). They found that the differences in the frequencies introduced by deviations in the longitudinal density profile are negligible.
In the case of constant longitudinal density, the amplitude profile of the first harmonic (n=2) is simply the first sine term in the Fourier series. However, longitudinal density stratification causes a different coupling between different longitudinal wave numbers. This means that the 1st sine term (with one node at the loop top) couples to the 3rd sine term (with three nodes along the loop). The superposition of these sine terms causes a distortion in the shape of the eigenfunction of the first harmonic. In fact, longitudinal density stratification causes the anti-nodes of the first harmonic to shift towards the footpoints of the loop, as also pointed out by Verth & Erdélyi (2007) and Verth (2007). This property is illustrated in Fig. 2 for the numerically calculated normalised eigenfunctions
![]() for different values of L/H. The size of the shift is greater for stronger stratification. Interestingly, it will be shown in Sect. 3 that the anti-node shift,
for different values of L/H. The size of the shift is greater for stronger stratification. Interestingly, it will be shown in Sect. 3 that the anti-node shift,
![]() (normalised to L) is only a function of L/H. This simple one-to-one relationship derived from the numerical simultations is shown in Fig. 3. For realistic coronal values of L/H, the relationship is linear to a very good approximation and can be calculated that
(normalised to L) is only a function of L/H. This simple one-to-one relationship derived from the numerical simultations is shown in Fig. 3. For realistic coronal values of L/H, the relationship is linear to a very good approximation and can be calculated that
![\begin{figure}
\par\includegraphics[height=6.2cm,width=7.9cm,clip]{8086fig2.eps}\end{figure}](/articles/aa/full/2007/43/aa8086-07/Timg25.gif) |
Figure 2:
Comparison of different levels of stratification. Normalised amplitude profiles
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=6.2cm,width=7.9cm,clip]{8086fig3.eps}\end{figure}](/articles/aa/full/2007/43/aa8086-07/Timg26.gif) |
Figure 3:
Normalised anti-node shift,
|
| Open with DEXTER | |
For analytical analysis of the anti-node shift, the equilibrium model of coronal loops is the same as for the numerical investigation in Sect. 2 (see Fig. 1). The coronal plasma is considered to be cold and ideal, and the loop is assumed to have footpoints fixed somewhere in the lower solar atmosphere. As mentioned previously in Sect. 2, coronal loops have ![]() ,
so the thin flux tube approximation will be applied. This approximation has been used before by Dymova & Ruderman (2005) and EV07 to model fast kink waves in loops with an arbitrary, longitudinal density profile. In addition to being physically relevant, it has the advantage of making the MHD equations more tractable for obtaining analytical solutions for a first insight.
,
so the thin flux tube approximation will be applied. This approximation has been used before by Dymova & Ruderman (2005) and EV07 to model fast kink waves in loops with an arbitrary, longitudinal density profile. In addition to being physically relevant, it has the advantage of making the MHD equations more tractable for obtaining analytical solutions for a first insight.
With these valid assumptions, Dymova & Ruderman (2005) show that the MHD equations can be linearised, and a simple second order ordinary differential equation can be derived, which describes the standing fast kink modes of the loop in terms of the maximum radial velocity at the tube boundary r=R. This equation can easily be re-written in terms of the maximum amplitude as a function of position z along a loop (see EV07),
We have no knowledge of an analytical solution for Eq. (4) when
![]() is described by profile (1). However, useful analytical insight into the behaviour of the solution can be gained by applying appropriate approximations to (1). In Sect. 3.1, density profile (1) will first be approximated by step functions, and then in Sect. 3.2 a much more refined approximation to density profile (1) will be made using a rational function.
is described by profile (1). However, useful analytical insight into the behaviour of the solution can be gained by applying appropriate approximations to (1). In Sect. 3.1, density profile (1) will first be approximated by step functions, and then in Sect. 3.2 a much more refined approximation to density profile (1) will be made using a rational function.
| |
Figure 4: Comparison of step density profile (7) to exponential profile (1). |
| Open with DEXTER | |
A simple approximation to density profile (1) can be made using step functions (see Fig. 4) as follows
Along with boundary conditions (5), the symmetry of density profile (7) about z=0, implies that the first harmonic must also have
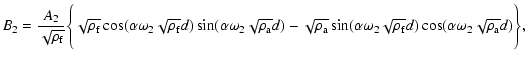 |
(12) |
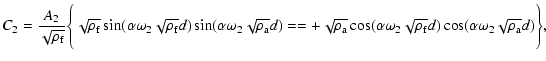 |
(13) |
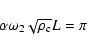 |
(15) |
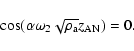 |
(19) |
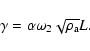 |
(21) |
There are various well-known elementary methods that can be used for solving cubic equations (see e.g., Abramowitz & Stegun 1965). It is found that there is one real root of Eq. (27) and a pair of complex conjugate roots. The physical solution corresponds to the real root of Eq. (27), which is
| (29) | |||
| (30) | |||
| (31) |
![\begin{displaymath}%
f_4=\left[ \epsilon\left( \pi^2 \epsilon+1\right)-3\right]\kappa^2 -\epsilon.
\end{displaymath}](/articles/aa/full/2007/43/aa8086-07/img83.gif) |
(32) |
![\begin{figure}
\par\includegraphics[height=4.6cm,width=6.7cm,clip]{8086fig5.eps}\end{figure}](/articles/aa/full/2007/43/aa8086-07/Timg88.gif) |
Figure 5:
Step density profile (7): anti-node shift
|
| Open with DEXTER | |
These two separate contributions to anti-node shift are illustrated in Figs. 5 and 6, where the asymptotic and numerical solutions of (17) are both plotted for comparison. In deriving the asymptotic solution (28), it was assumed that
![]() and
and
![]() were approximately equal, but as can be seen from Figs. 5 and 6, when
were approximately equal, but as can be seen from Figs. 5 and 6, when
![]() ,
the solution still works very well for much more pronounced stratification. Considering the case when
,
the solution still works very well for much more pronounced stratification. Considering the case when
![]() ,
for relatively weak stratification,
,
for relatively weak stratification,
![]() ,
the difference between the asymptotic and numerical solution is 3%, as would be expected. However, for a much lower density ratio, e.g.,
,
the difference between the asymptotic and numerical solution is 3%, as would be expected. However, for a much lower density ratio, e.g.,
![]() ,
the difference in solutions is still only 10%.
,
the difference in solutions is still only 10%.
The density ratio,
![]() ,
required to produce observable shifts, i.e.,
,
required to produce observable shifts, i.e., ![]() 1 Mm in a L= 100 Mm loop depends on the value of
1 Mm in a L= 100 Mm loop depends on the value of ![]() .
If a loop has a relatively large footpoint region with
.
If a loop has a relatively large footpoint region with
![]() (equivalent to 20 Mm), then one must have
(equivalent to 20 Mm), then one must have
![]() .
However, if the footpoint region is much smaller, e.g.,
.
However, if the footpoint region is much smaller, e.g.,
![]() (equivalent to 5 Mm), there must be a much greater density contrast with
(equivalent to 5 Mm), there must be a much greater density contrast with
![]() .
.
From Figs. 5 and 6, it is also important to note that different values of ![]() can result in the same anti-node shift depending on the value of
can result in the same anti-node shift depending on the value of
![]() .
That completely different density profiles can result in the same anti-node shift is important. Although the generic exponential profile (1) was chosen for the numerical study in Sect. 2, there may also physical conditions in active region post-flare coronal loops where this does not apply. To use the anti-node shift to determine accurate information about plasma density stratification in a loop, one must know the appropriate functional form of
.
That completely different density profiles can result in the same anti-node shift is important. Although the generic exponential profile (1) was chosen for the numerical study in Sect. 2, there may also physical conditions in active region post-flare coronal loops where this does not apply. To use the anti-node shift to determine accurate information about plasma density stratification in a loop, one must know the appropriate functional form of
![]() .
.
| |
Figure 6:
Step density profile (7): anti-node shift
|
| Open with DEXTER | |
| |
Figure 7: Comparison of smooth density profile (35) with exponentialprofile (1) shown by the dashed and solid lines, respectively. |
| Open with DEXTER | |
To make a more refined approximation to (1), the rational function
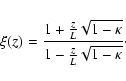 |
(38) |
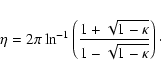 |
(39) |
| (41) |
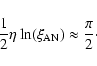 |
(42) |
| g1 | = | (49) | |
| g2 | = | ||
| (50) | |||
| g3 | = | (51) | |
| g4 | = | (52) | |
| g5 | = | (53) |
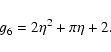 |
(54) |
| |
Figure 8:
Smooth density profile (35): anti-node shift
|
| Open with DEXTER | |
The power-series expansion of the asymptotic anti-node shift (47) is a convergent Laurent series with a singularity at ![]() .
Therefore, one cannot obtain a simple first-order expression for the anti-node shift (equivalent to Eq. (34) for the step density profile), since we need a very large number of terms for the series approximation to obtain a reasonable accuracy near the singularity at
.
Therefore, one cannot obtain a simple first-order expression for the anti-node shift (equivalent to Eq. (34) for the step density profile), since we need a very large number of terms for the series approximation to obtain a reasonable accuracy near the singularity at ![]() .
However, as can be seen from Fig. 8, the anti-node shift can be more easily approximated as a linear function of
.
However, as can be seen from Fig. 8, the anti-node shift can be more easily approximated as a linear function of
![]() .
For
.
For
![]() ,
,
Since the difference between the exponential profile (1) and the smooth profile (35) is not large (see Fig. 7), the difference in anti-node shifts should also be small. Assuming that
![]() is defined by exponential profile (1), i.e.,
is defined by exponential profile (1), i.e.,
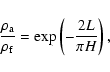 |
(56) |
To measure plasma density stratification directly in the solar atmosphere using e.g., spectroscopy, one must know precise elemental abundances and at what height and temperature the spectral lines are formed. However, these values may have large uncertainties. Furthermore, direct methods ideally need simultaneous measurements from different lines of sight. Unfortunately, for all the current and near future missions (apart from the Solar TErrestrial Relations Observatory [STEREO]), this will not be possible. Therefore, it is crucial that we have alternative methods for verifying the accuracy of direct measurements. Magneto-seismological methods such as the one proposed in this paper could prove to be invaluable in this regard.
The improved time cadence of the next generation of EUV imagers onboard SDO and SO will provide the best chance yet of observing higher harmonics in post-flare loop oscillations. Therefore, the SMS method proposed in this paper for measuring the anti-node shift of the first harmonic of transversal loop oscillations so as to determine density stratification, offers a promising complementary method of getting information regarding the plasma fine structure in the solar corona. Since anti-node shifts due to density stratification can be expected in the Mm range, resolution should not be a problem.
However, since the EUV imagers can only provide 2D spatial data, uncertainties in shift measurments may be introduced by projection effects. Therefore, one would ideally need an accurate 3D reconstruction of a loop's geometry to correct for this. Much progress has been made recently in developing techniques of reconstructing coronal 2D images in 3D. Some of the most successful approaches so far use stereoscopic methods, magnetic field extrapolation constraints, and loop curvature radius constraints (see Aschwanden 2005, for a detailed discussion). Although the two EUV imagers used in the STEREO mission do not have the time cadence or spatial resolution required for SMS, the quasi-3D images they are capable of producing can only help increase our understanding of the solar corona's complex and fascinating 3D structure.
Uncertainties may also be introduced from a number of different physical processes in active regions. Since plasma fine structure can be changed by dynamic phenomena such as flow or heating/cooling, this may cause a shift in the anti-node. Furthermore, a shift may occur due to a change in loop length caused by emerging magnetic flux or a flaring event. Hence, further theoretical investigation is required to quantify how these different physical processes affect the standing fast kink mode in coronal loops.
The effect of magnetic stratification on the standing fast kink mode must also be addressed. It is physically reasonable to assume that the magnetic field strength decreases with height in the solar corona. Since the kink speed is proportional to the magnetic field strength, this may play a significant role in the anti-node shift. To our current knowledge, there is no analytical model yet that describes the standing fast kink mode of a magnetic cylinder that has an inhomogeneous magnetic field along its axis, except a work in progress by ourselves. In the past five years, there have been 3D numerical studies of the interaction between fast magnetoacoustic waves and potential/linear force-free magnetic fields extrapolated from magnetogram data (Ofman & Thompson 2002; Terradas & Ofman 2004b; Ofman 2005). Further numerical investigations of this type should prove invaluable in understanding the properties of oscillations in more realistic magnetic field structures.
Since not all the observed oscillations can be considered to be in the linear regime, an even greater theoretical challenge is to understand the properties of nonlinear fast kink waves in magnetic cylinders. Some progess has been made in this area by Terradas & Ofman (2004a) using a 3D MHD numerical simulation. They find that nonlinear kink waves may actually cause a density enhancement at coronal loop tops. Their result could explain emission measure enhancements in oscillating loops observed after a flaring event on 1998 July 14 using TRACE data.
Acknowledgements
The authors thank M. Ruderman for a number of useful discussions. R.E. acknowledges M. Kéray for patient encouragement. The authors are also grateful to NSF, Hungary (OTKA, Ref. No. TO43741), and the Engineering and Physical Sciences Research Council (EPSRC), UK, for the financial support they received.