A&A 474, L37-L40 (2007)
DOI: 10.1051/0004-6361:20078541

LETTER TO THE EDITOR

Calibration of the galaxy cluster M₅₀₀-Y$_{\sf X}$ relation with XMM-Newton

M. Arnaud¹ - E. Pointecouteau² - G. W. Pratt³

1 - Laboratoire AIM, DAPNIA/Service d'Astrophysique - CEA/DSM - CNRS - Université Paris Diderot, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
2 - CESR, 9 Av. du colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
3 - Max-Planck-Institut für extraterrestriche Physik, Giessenbachstraße, 85748 Garching, Germany

Received 24 August 2007 / Accepted 9 September 2007

Abstract
The quantity $Y_{\rm X}$, the product of the X-ray temperature $T_{\rm X}$ and gas mass $M_{\rm g}$, has recently been proposed as a robust low-scatter mass indicator for galaxy clusters. Using precise measurements from XMM-Newton data of a sample of 10 relaxed nearby clusters, spanning a $Y_{\rm X}$ range of 10¹³- $10^{15}~M_\odot$ keV, we investigate the M₅₀₀-$Y_{\rm X}$ relation. The M₅₀₀-$Y_{\rm X}$ data exhibit a power law relation with slope $\alpha=0.548~\pm~~0.027$, close to the self-similar value (3/5) and independent of the mass range considered. However, the normalisation is $\sim$20% below the prediction from numerical simulations including cooling and galaxy feedback. We discuss two effects that could contribute to the normalisation offset: an underestimate of the true mass due to the hydrostatic equilibrium assumption used in X-ray mass estimates, and an underestimate of the hot gas mass fraction in the simulations. A comparison of the functional form and scatter of the relations between various observables and the mass suggest that $Y_{\rm X}$ may indeed be a better mass proxy than $T_{\rm X}$ or $M_{\rm g, 500}$.

Key words: cosmology: observations - cosmology: dark matter - galaxies: clusters: general - galaxies: intergalactic medium - X-rays: galaxies: clusters

1 Introduction

All theoretical approaches characterise galaxy clusters in terms of their mass. Models of structure formation predict the space density, distribution and physical properties of clusters as a function of mass and redshift (e.g. Bertschinger 1998). However, the mass is not easily measured. X-ray estimates from the hydrostatic equilibrium (HE) equation are valid only for reasonably relaxed clusters and require temperature profiles of high statistical quality; furthermore, the available precision rapidly degrades with redshift. Based on the regularity of the cluster population, other X-ray observables such as luminosity, temperature $T_{\rm X}$, or gas mass $M_{\rm g}$, have been used as proxies for the mass, e.g. to constrain cosmological parameters using cluster surveys (Voit 2005). Studies of cluster formation physics must also rely on mass proxies when considering unbiased (i.e., covering a variety of dynamical states) or distant cluster samples (e.g. Maughan 2007). The identification of the best mass proxy, and knowledge of its exact relation to the mass, are therefore important.

The most commonly used mass proxy, $T_{\rm X}$, is expected to be closely related to the mass via the virial theorem. Significant progress on the calibration of the local M-$T_{\rm X}$relation for relaxed clusters has recently been made, with excellent agreement now achieved between various observations (Arnaud et al. 2005; Vikhlinin et al. 2006), and comparison between observations and numerical models including cooling and galaxy feedback showing agreement to the $\sim$10% level (e.g. Arnaud et al. 2005; Nagai et al. 2007b). Kravtsov et al. (2006) recently proposed a new mass proxy, $Y_{\rm X}=T_{\rm X}M_{\rm g,500}$, where $M_{\rm g, 500}$ is the gas mass within R₅₀₀, the radius corresponding to a density contrast of $\delta=500$. $Y_{\rm X}$ is related to the thermal energy of the gas and is the X-ray analogue of the integrated SZ Comptonisation parameter, $Y_{\rm SZ}$. The numerical simulations of Kravtsov et al. showed that, as compared to $T_{\rm X}$ or $M_{\rm g, 500}$, $Y_{\rm X}$ is a better mass proxy, in the sense that the intrinsic scatter was lower than for any other mass indicator, regardless of cluster dynamical state (similar to previous results for the M- $Y_{\rm SZ}$ relation, e.g., da Silva et al. 2004; Motl et al. 2005; Nagai 2006). Furthermore, its evolution appears to be close to the standard self-similar expectation.

In this Letter, we present the M₅₀₀-$Y_{\rm X}$ relation derived from precise XMM-Newton data and compare it to the M₅₀₀- $M_{\rm g, 500}$ and M₅₀₀-$T_{\rm X}$ relations. The M₅₀₀-$Y_{\rm X}$ relation is discussed with respect to previous Chandra results and theoretical expectations (Nagai et al. 2007b). Other relations between observables, such as the variation of the gas mass fraction $f_{\rm g,500}$with mass, are also investigated to shed new light on the scatter and slope of the various mass-proxy relations.

Table 1: Physical cluster parameters. $M_{\rm 500}$, $M_{\rm g, 500}$ and $f_{\rm g,500}$ are the total mass, gas mass and gas mass fraction respectively, within the radius R₅₀₀, inside which the mean mass density is 500 times the critical density at the cluster redshift. $T_{\rm X}$ is the spectroscopic temperature within [0.15-0.75]R₅₀₀ and $Y_{\rm X}= M_{\rm g, 500} T_{\rm X}$. Values are given for a $\Lambda$CDM cosmology with $\Omega _{\rm m}=0.3$, $\Omega _{\Lambda }=0.7$, H₀=70 km s^-1 Mpc^-1. Errors are $1~\sigma$.

2 The data

  
2.1 The sample

The sample comprises ten nearby morphologically relaxed clusters in the temperature range [2-9] keV. We have previously used XMM-Newton data to study the structural and scaling properties of the total mass (Arnaud et al. 2005; Pointecouteau et al. 2005) and of the entropy (Pratt et al. 2006); the $T_{\rm X}$, $M_{\rm 500}$ and R₅₀₀ values derived in these papers are used in the present letter (Table 1). The observations and data reduction steps are fully described in Pointecouteau et al. (2005). $M_{\rm 500}$ values were derived from NFW model fits to mass profiles measured down to $\delta_{\rm obs}=600$-700, except for the two lowest mass clusters ( $\delta_{\rm obs}\sim1400$), thus the $M_{\rm 500}$ estimates involve some data extrapolation. However, as discussed in Arnaud et al. (2005), the $M_{\rm 500}$ estimates rely solely on the physically and observationally-motivated assumption that the best fitting NFW model remains valid between $\delta_{\rm obs}$ and $\delta=500$, and not on a less reliable extrapolation of density and temperature profiles. The temperature $T_{\rm X}$ was derived from a single-temperature fit to the integrated spectrum in the [0.1- 0.5] R₂₀₀ aperture, the inner radius defined to exclude the cooling core region and the outer radius chosen to ensure a sufficiently precise $T_{\rm X}$ estimate over the whole mass range. This aperture corresponds to [0.15- 0.75] R₅₀₀, while an aperture of [0.15- 1] R₅₀₀ is used for the definition of $T_{\rm X}$ in numerical simulations and in the Chandra analysis (Nagai et al. 2007b). For typical decreasing temperature profiles, these $T_{\rm X}$ values are expected to be slightly smaller by 3-$6\%$.

Table 2: Observed scaling relations. For each observable set (B,A), we fitted a power law relation of the form $B = C(A/A_0)^\alpha$, with $A_0 = 5~{\rm keV}; 4\times10^{13}~M_{\odot}; 2\times10^{14}~M_{\odot}~\rm keV$ for $T_{\rm X}$, $M_{\rm g, 500}$ and $Y_{\rm X}$ respectively. $\sigma _{\rm log,r}$ and $\sigma _{\rm log,i}$ are the raw and intrinsic scatter about the best fitting relation in the $\log$-$\log$ plane. The M₅₀₀-$T_{\rm X}$ relation is the same as that given in Arnaud et al. (2005).

Figure 1: The M500-$Y_{\rm X}$ relation as seen by XMM-Newton from a sample of 10 local relaxed clusters. The red solid line is the best fitting power law and the shaded orange area corresponds to the $1~\sigma$ uncertainty. The predicted relation from numerical simulations including cooling and galaxy feedback (Nagai et al. 2007b) is over-plotted as a green dot-dashed line (true mass) and as a green solid line (mass estimated from mock X-ray observations and the HE equation). The dotted and dashed blue lines are the observed relations derived from Chandra data by Nagai et al. (2007b) and Maughan (2007) respectively (see text).

Open with DEXTER

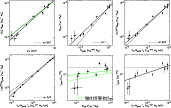Figure 2: Correlations between X-ray observables. Solid lines: best fitting power law relations. Dashed lines: standard self-similar relation (slope indicated in each figure) normalised to data from the three most massive clusters. Green dotted line in top-left panel: best fitting power law M500-$T_{\rm X}$ relation for the hot cluster sub-sample (Arnaud et al. 2005). Green lines in bottom-middle panel: gas mass fraction from the M500- $M_{\rm g, 500}$ relation in the numerical simulations of Nagai et al. (2007b), using the true mass (dash-dotted line) and the HE mass (full line).

Open with DEXTER

The integrated gas mass depends sensitively on the gas density at large radius. To compute $M_{\rm g, 500}$, we re-derived the gas density profile from the emissivity corrected surface brightness profiles using the deprojection and PSF-deconvolution technique recently developed by Croston et al. (2006). This derivation is free of any assumption on profile shape, such as power law behaviour at large radius, a feature common to all analytical fitting models used thus far (e.g. Pointecouteau et al. 2005; Vikhlinin et al. 2006; Pratt & Arnaud 2002). Furthermore, the statistical errors are readily estimated from a built-in Monte-Carlo procedure (see Croston et al. 2006, for details). For the present sample, there is excellent agreement between the deprojected density profiles and the analytical model profiles derived in our previous work (Pointecouteau et al. 2005; Pratt et al. 2006). The significant differences are in the very central regions of some clusters (e.g. Croston et al. 2006, Fig. 12) and for A2597 at large radii, where the deprojected profile is slightly steeper than the model profile. The gas mass estimated with the two methods differs by less than $3\%$, except for A2597 ($8\%$ difference). For all clusters, except for A1983 and MKW9, the surface brightness profiles extend at least up to R₅₀₀, or very close to it, so that extrapolation uncertainty is not an issue. For A1983 and MKW9, the $M_{\rm g, 500}$estimated from extrapolation in the $\log$-$\log$ plane are $31\%$(A1983) and $67\%$ (MKW9) larger than the gas mass measured at $\delta_{\rm obs}$; as shown below, these points do not however, have a significant effect on the results.

The resulting $M_{\rm g, 500}$, $f_{\rm g,500}$ and $Y_{\rm X}$ values are listed in Table 1. Errors on $M_{\rm g, 500}$ include both statistical errors and errors due to uncertainties in R₅₀₀, which are summed quadratically, with the latter dominating the error budget.

2.2 Scaling relations

For each observable set (B,A) we fitted a power law relation of the form $h(z)^nB = C(A/A_0)^\alpha$, where h(z) is the Hubble constant normalised to its present value and n is fixed to the expected scaling with z. The fit was performed using linear regression in the $\log$-$\log$ plane, taking into account the errors on both variables (FITEXY; Press et al. 1992). The pivot point A₀ is chosen so that the normalisation and slope are nearly independent parameters. For the M₅₀₀-Y_X relation for instance, the covariance in $\log(C)$ and $\alpha$ normalised to the product of their standard errors is 0.042. The resulting values are given in Table 2, and the various correlations are plotted in Fig. 1 and Fig. 2. Table 2 also shows the raw and intrinsic scatter about the best fitting relations in the $\log$-$\log$ plane. The raw scatter was estimated using the vertical distances to the regression line, weighted by the error. The intrinsic scatter was computed from the quadratic difference between the raw scatter and the scatter expected from the statistical errors.

The regression method is strictly only valid if the intrinsic scatter is negligible as compared to the statistical scatter; in fact they are of the same order (Table 2). We verified that the results are unchanged using the variation of the method discussed in Pratt et al. (2006). Finally, the M₅₀₀-$Y_{\rm X}$ relation is robust to exclusion of A1983 and MKW9, for which data extrapolations were required (see above): the differences are at the $+0.4~\sigma$ and $-0.2~\sigma$ levels for the slope and normalisation, respectively.

3 Discussion and conclusions

3.1 Comparison with theoretical predictions

The slope of the observed relation:

$$h(z)^{2/5}M_{\rm 500}= 10^{14.556 \pm 0.015} \left[\frac{Y_{\... ...}}~\rm keV}\right]^{0.548 \pm 0.027}{{ h}_{70}^{-1}~M_{\odot}}$$ (1)

is slightly smaller than the standard self-similar value ( $\alpha=3/5$), at the $1.9~\sigma$ significance level, consistent with the M₅₀₀- $M_{\rm g, 500}$ and M₅₀₀-$T_{\rm X}$ relations (Table 2 and Fig. 2 top panel). The M₅₀₀- $M_{\rm g, 500}$ relation is shallower than expected, reflecting the increase in gas mass fraction with mass (Fig. 2 bottom-middle panel), while the M₅₀₀-$T_{\rm X}$ is steeper. At a given mass the gas mass is smaller and the temperature is higher, leading to a partial cancellation in the product $Y_{\rm X}= M_{\rm g} T_{\rm X}$ (see also below).

The observed normalisation is $\sim 20\%$ smaller over the whole $Y_{\rm X}$ range than that derived from numerical simulations including cooling and galaxy feedback (Nagai et al. 2007b), while the observed slope is consistent with the predicted slope, $\alpha = 0.568\pm 0.006$, within the $1~\sigma$ error (Fig. 1). Better agreement is obtained with the simulated $M_{500}^{\rm HE}$-$Y_{\rm X}$ relation, where $M_{500}^{\rm HE}$ is the mass estimated from mock X-ray observations and the HE equation. Although the predicted slope, $\alpha = 0.596\pm 0.010$, is slightly higher, the difference in normalisation drops to $\sim$8% ( $2.4~\sigma$) at $Y_{\rm X}= 2\times10^{14}~{M_{\odot}}~\rm keV$. As discussed by Nagai et al. (2007b), the offset in normalisation, also observed with Chandra data, may arise from an underestimate of the true mass by the HE equation, perhaps due to residual non-thermal pressure support. These numerical simulations also predict a hot gas mass fraction systematically smaller than observed (Fig. 2 bottom-middle panel). The difference is smaller for simulated $f_{\rm g,500}$ using $M_{500}^{\rm HE}$ and again could be due, in part, to biases in X-ray mass estimates. Nevertheless, there may also be an underestimate of $f_{\rm g,500}$ in the simulations, possibly due in part to over-condensation of hot gas into the cold dense phase (Nagai et al. 2007b). This would contribute to the offset, by shifting the M₅₀₀-$Y_{\rm X}$ relation to the left in the $\log$-$\log$ plane. Finally, as the normalisation depends on $T_{\rm X}^{0.6}$, the difference in the exact definition of $T_{\rm X}$ (see Sect. 2.1) could contribute by $\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}$4% to the offset.

3.2 Comparison with Chandra results

Our M₅₀₀-$Y_{\rm X}$ relation is very similar to that derived by Nagai et al. (2007b) from the Chandra data presented in Vikhlinin et al. (2006, see our Fig. 1). The slope $\alpha =0.526 \pm0.038$ is consistent with our value, $\alpha = 0.548\pm0.027$, and the normalisation at $Y_{\rm X}= 2\times10^{14}~{M_{\odot}}~\rm keV$, $M_{\rm 500}= 3.82\times10^{14}~{\rm h_{70}^{-1}}~M_{\odot}$, is higher than our value, $(3.60\pm0.13)\times10^{14}M_{\odot}$, at only the $1.6~\sigma$ level. Even better agreement is obtained with the best fitting relation quoted by Maughan (2007, dashed line in Fig. 1), derived from the same data excluding the lowest mass cluster (A. Vikhlinin, priv. communication). Here the slope ( $\alpha =0.564$) is closer to the self-similar value, as we have found, and the difference in normalisation is less than $5\%$ over the whole mass range.

3.3 Comparison of mass proxies for relaxed clusters

For relaxed clusters, Kravtsov et al. (2006) found similar scatter in the M₅₀₀-$T_{\rm X}$ and M₅₀₀- $M_{\rm g, 500}$ relations ( $\sigma_{\rm log} = 0.055$ and 0.047 respectively), but two times less scatter in the M₅₀₀-$Y_{\rm X}$ relation (0.022). We can compare with the present data, the statistical quality allowing us to estimate the intrinsic scatter for the first time. The scatter (Table 2) is the same for the M₅₀₀-$Y_{\rm X}$ and M₅₀₀-$T_{\rm X}$ relations ( $\sigma_{\rm log,i} = 0.039$) and slightly larger for the M₅₀₀- $M_{\rm g, 500}$ relation ( $\sigma_{\rm log,i} = 0.044$). The latter may reflect that the M₅₀₀- $M_{\rm g, 500}$ relation is not actually a power law: the gas mass fraction appears constant at $M_{\rm 500} \mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$>$ }}}2-3\times10^{14} M_{\odot}$, with a progressive drop at lower mass (Fig. 2 bottom-middle panel).

In fact the behaviour of $f_{\rm g,500}$ appears to be the primary factor driving the scatter in the M₅₀₀-$Y_{\rm X}$ relation. The $M_{\rm g, 500}$-$Y_{\rm X}$ relation is extremely tight (Fig. 2 and Table 2), being well fitted by a power law with no measurable scatter, in spite of the precision of the data. Since $M_{\rm 500}=M_{\rm g,500}/f_{\rm g,500}$, the scatter in the M₅₀₀-$Y_{\rm X}$ relation simply reflects the scatter in the $f_{\rm g,500}$-$Y_{\rm X}$ relation (cf. top and bottom left panels of Fig. 2). This scatter could arise from true scatter in $f_{\rm g,500}$ and/or scatter in the X-ray mass to true mass ratio, e.g., due to variations in the magnitude of nonthermal pressure support. Note that a low-scatter correlation between $M_{\rm g, 500}$ and $Y_{\rm X}$ is expected: it is straightforward to show that the logarithmic scatter in the $M_{\rm g, 500}$-$Y_{\rm X}$ relation is 1/3 of the scatter in the $M_{\rm g, 500}$-$T_{\rm X}$ relation for $M_{\rm g,500}\propto T_{\rm X}^{\sim 2}$ (Table 2).

In terms of observed scatter in the relation with mass, $Y_{\rm X}$thus does not appear to be a better proxy than $T_{\rm X}$, and is only slightly better than $M_{\rm g, 500}$. However we caution against over-interpretation. Firstly, the present results are for relaxed clusters only: with the current data we cannot check if the scatter is insensitive to dynamical state (Kravtsov et al. 2006; Poole et al. 2007). Secondly, the scatter estimates should be confirmed using larger cluster samples with stricter selection criteria.

However, in terms of functional dependence with mass, $Y_{\rm X}$ is clearly a better proxy than $M_{\rm g, 500}$: it is better fitted by a simple power-law, and has a slope closer to the standard self-similar value (Table 2). Furthermore, although the quality of the power law fits to M₅₀₀-$T_{\rm X}$ and M₅₀₀-$Y_{\rm X}$ are formally similar ( $\chi^2/{\rm d.o.f}\sim13/8$), with similar ( $\sim2~\sigma$) deviations from the standard slope, there is some indication that $Y_{\rm X}$ is also a better proxy than $T_{\rm X}$ in this regard. The slope of the M₅₀₀-$T_{\rm X}$ relation may depend on mass range (Arnaud et al. 2005), reaching the standard value when cool clusters are excluded, but the slope of the M₅₀₀-$Y_{\rm X}$ relation remains stable in that case ( $0.7~\sigma$ difference).

3.4 Concluding remarks

Our results suggest that the various mass scaling relations might be better understood by considering the gas thermal energy ($Y_{\rm X}$) and mass ( $f_{\rm g,500}$) as its most fundamental properties. Let us suppose that the thermal energy content of the gas is the quantity most closely related to the mass (i.e. the best mass proxy is indeed $Y_{\rm X}$), and that its relation with mass has a quasi-standard slope. We further note that the gas mass fraction appears constant at high mass, with a progressive decrease below a "break'' mass (reflecting gas loss or incomplete accretion in low mass systems due to non gravitational effects). Since M/T^3/2 varies as $(M/Y_{\rm X}^{3/5})^{5/2} f_{\rm g}^{3/2}$, one then expects a steepening of the M₅₀₀-$T_{\rm X}$ relation at low mass, with a standard slope at high mass.

A deeper understanding of the mass scaling relations will come from the X-ray study of larger unbiased samples of local clusters, such as REXCESS (Böhringer et al. 2007), combined with lensing data. This is necessary to ascertain the dependence of the M₅₀₀-$Y_{\rm X}$ relation on the dynamical state, and to calibrate its normalisation and slope. This step is essential because the use of $Y_{\rm X}$ as a mass proxy, as in the case of $T_{\rm X}$, requires a detailed understanding of non-gravitational effects, in particular of the impact of cooling and feedback on the fraction of primordial gas that remains in the gravitationally bound hot phase. Precise measurements at z=0 are needed to constrain models, on which one must rely for high z studies. Significant progress is also expected from forthcoming SZ data (e.g from the Planck Surveyor all sky survey), especially if combined with XMM-Newton or Chandra data, which will allow a full study of the M- $Y_{\rm SZ}$ relation.

Acknowledgements

We thank A. Kravtsov and D. Nagai for useful comments on the manuscript, and the referee for a speedy and pertinent response.

References

• Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2005, A&A, 441, 893 [NASA ADS] [CrossRef] [EDP Sciences]
• Bertschinger, E. 1998, ARA&A, 36, 599 [NASA ADS] (In the text)
• Böhringer, H., Schuecker, P., Pratt, G. W. et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Croston, J. H., Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2006, A&A, 459, 1007 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• da Silva, A. C., Kay, S. T., Liddle, A. R., & Thomas, P. 2004, MNRAS, 348, 1401 [NASA ADS]
• Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [NASA ADS] [CrossRef] (In the text)
• Maughan, B. J. 2007, ApJ, in press, [arXiv:astro-ph/0703504] (In the text)
• Motl, P. M., Hallman, E. J., Burns, J. O., & Norman, M. L. 2005, ApJ, 623, L63 [NASA ADS] [CrossRef]
• Nagai, D. 2006, ApJ, 650, 538 [NASA ADS] [CrossRef]
• Nagai, D., Vikhlinin, A., & Kravtsov, A. 2007a, ApJ, 655, 98 [NASA ADS] [CrossRef]
• Nagai, D., Kravtsov, A., & Vikhlinin, A. 2007b, ApJ, submitted, [arXiv:astro-ph/0703661]
• Pointecouteau, E., Arnaud, M., & Pratt, G. W. 2005, A&A, 435, 1 [NASA ADS] [CrossRef] [EDP Sciences]
• Pratt, G. W., & Arnaud, M. 2002, A&A, 394, 375 [NASA ADS] [CrossRef] [EDP Sciences]
• Pratt, G. W., Arnaud, M., & Pointecouteau, E. 2006, A&A, 446, 429 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Poole, G. P., Babul, A., McCarthy, I. G., et al. 2007, MNRAS, submitted, [arXiv:astro-ph/0701586]
• Press, W. H., Teukolsky, S. A., Vetterling, S. A., & Flannery B.P. 1992, Numerical Recipes in Fortran 77, 2nd edn., 660 (In the text)
• Vikhlinin, A., Markevitch, M., Murray, S., et al. 2005, ApJ, 628, 655 [NASA ADS] [CrossRef]
• Vikhlinin A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef]
• Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] (In the text)