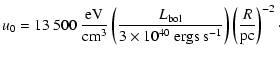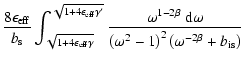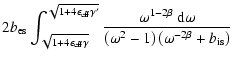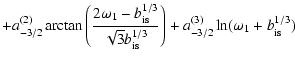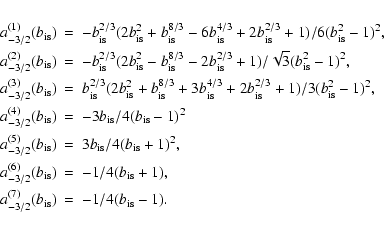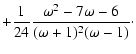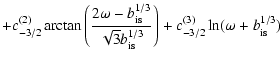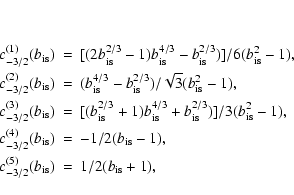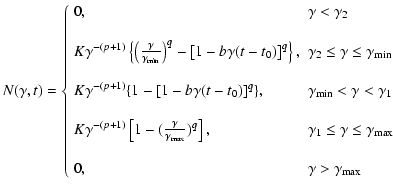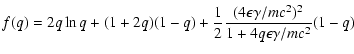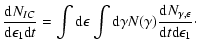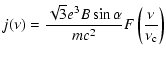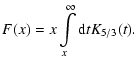A&A 474, 689-700 (2007)
DOI: 10.1051/0004-6361:20078298
Spectral evolution of non-thermal electron distributions
in intense radiation fields
K. Manolakou1 - D. Horns1 - J. G. Kirk2
1 - Institute for Astronomy and Astrophysics Tübingen (IAAT)
Sand 1, 72076 Tübingen, Germany
2 -
Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
Received 17 July 2007 / Accepted 4 August 2007
Abstract
Context. Models of many astrophysical gamma-ray sources assume they contain a homogeneous distribution of electrons that are injected as a power law in energy and evolve by interacting with radiation fields, magnetic fields, and particles in the source and by escaping. This problem is particularly complicated if the radiation fields have higher energy density than the magnetic field and are sufficiently energetic that inverse Compton scattering is not limited to the Thomson regime.
Aims. We present a simple, time-dependent, semi-analytical solution to the electron kinetic equation that treats both continuous and impulsive injection, cooling via synchrotron and inverse Compton radiation (taking Klein-Nishina effects into account), and energy-dependent particle escape. We used this solution to calculate the temporal evolution of the multi-wavelength spectrum of systems where energetic electrons cool in intense photon fields.
Methods. The kinetic equation for an arbitrary, time-dependent source function is solved by the method of Laplace transformations. Using an approximate expression for the energy-loss rate that takes synchrotron and inverse Compton losses into account, including Klein-Nishina effects for scattering off an isotropic photon field with either a power-law or black-body distribution, we find explicit expressions for the cooling time and escape probability of individual electrons. This enables the full, time-dependent solution to be reduced to a single quadrature. From the electron distribution, we then construct the time-dependent, multi-wavelength emission spectrum.
Results. We compare our solutions with several limiting cases and discuss the general appearance and temporal behaviour of spectral features (i.e., cooling breaks, bumps, etc.). As a specific example, we model the broad-band energy spectrum of the open stellar association Westerlund-2 at different times of its evolution, and compare it with observations. The model calculation matches the observations for a source with an age greater than 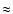 105 yrs. We predict that the GLAST gamma-ray observatory should easily detect this source.
105 yrs. We predict that the GLAST gamma-ray observatory should easily detect this source.
Conclusions. The technique we present enables simple, computationally efficient, time-dependent models of homogeneous sources to be constructed and compared with multi-wavelength observations.
Key words: gamma rays: theory - radiation mechanisms: non-thermal - stars: Wolf-Rayet - ISM: cosmic rays - open clusters and associations: individual: Westerlund 2
The discovery of very high-energy (VHE,
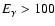 GeV)
gamma rays from many different astrophysical sources
(for a recent review see Völk 2006)
has motivated the construction of simple, physical
models of the emission regions. An important ingredient in such models is the interaction of
accelerated leptons with an intense ambient radiation field,
especially by inverse Compton scattering. For example,
the recent discovery of VHE emission from sources possibly associated with stellar clusters,
including Westerlund-2 (Wd-2) (Aharonian et al. 2007), Berk-87
(Abdo et al. 2007), and Cyg OB2 (Aharonian et al. 2005a,2002), provides evidence of particle acceleration in an environment dominated by hot massive
stars driving fast winds, as well as supernova remnants evolving in a
dilute, hot medium (Tang & Wang 2005). The detection of
VHE gamma-rays from high-mass X-ray binary systems like LS I+61 303
(Albert et al. 2006), LS 5039 (Aharonian et al. 2005b), and PSR B1259-63 (Aharonian et al. 2005c) adds another class of galactic sources where inverse Compton scattering is expected to be an important energy-loss mechanism.
GeV)
gamma rays from many different astrophysical sources
(for a recent review see Völk 2006)
has motivated the construction of simple, physical
models of the emission regions. An important ingredient in such models is the interaction of
accelerated leptons with an intense ambient radiation field,
especially by inverse Compton scattering. For example,
the recent discovery of VHE emission from sources possibly associated with stellar clusters,
including Westerlund-2 (Wd-2) (Aharonian et al. 2007), Berk-87
(Abdo et al. 2007), and Cyg OB2 (Aharonian et al. 2005a,2002), provides evidence of particle acceleration in an environment dominated by hot massive
stars driving fast winds, as well as supernova remnants evolving in a
dilute, hot medium (Tang & Wang 2005). The detection of
VHE gamma-rays from high-mass X-ray binary systems like LS I+61 303
(Albert et al. 2006), LS 5039 (Aharonian et al. 2005b), and PSR B1259-63 (Aharonian et al. 2005c) adds another class of galactic sources where inverse Compton scattering is expected to be an important energy-loss mechanism.
In addition to the VHE emission, these sources show evidence of non-thermal X-ray emission,
which is also spatially extended in the case of Wd-2 and Cyg OB2 (Horns et al. 2007; Townsley et al. 2005). Leptonic scenarios have been used both to predict and to model the multi-wavelength spectra (Murata et al. 2003; Hinton & Aharonian 2007; Kirk et al. 1999; Khangulyan et al. 2007), although hadronic models in which the gamma rays are produced in
nucleonic collisions also provide a natural explanation
(Bednarek 2007; Neronov & Chernyakova 2006; Horns et al. 2007).
Improved modelling of these sources is clearly necessary for a better understanding of the mechanisms at work.
However, even with drastic
simplifications, such as the assumption of spatial homogeneity,
and the ad hoc prescription of a distribution function of injected particles,
such models can be quite complicated to construct. Furthermore,
the need to investigate a large volume of parameter space makes
it important to find computationally efficient algorithms.
The temporal evolution of a non-thermal electron distribution
interacting with matter and photon fields has been studied in great
detail in the past
(see e.g. Ginzburg & Syrovatskii 1964; Blumenthal & Gould 1970; Felten & Morrison 1966; Sturner et al. 1997; Mastichiadis & Kirk 1997).
The problem can be described by an integro-differential equation
including all relevant energy-loss mechanisms for electrons
(e.g. Zdziarski 1989; Blumenthal & Gould 1970; Kusunose & Takahara 2005; Coppi 1992),
which is numerically quite difficult to treat. The problem can be simplified considerably by approximating the discrete jumps in energy suffered by an electron undergoing
Compton scatterings as a continuous energy-loss process. In this case, the kinetic equation reduces to a partial differential equation. This approximation, which is accurate in the
Thomson limit, also appears to be reasonably good
in the Klein-Nishina regime for a wide range of target photon
distributions (see, e.g., Zdziarski 1989).
Analytical solutions to the electron kinetic equation have been found for special cases
e.g., when continuous or impulsive injection is considered, with the
electrons cooling radiatively through synchrotron and inverse Compton
scattering in the Thomson limit, as well as escaping from the system (Kardashev 1962).
Although Klein-Nishina (KN) effects are well-known to have an impact on the steady-state spectra
(e.g., Moderski et al. 2005b; Kirk et al. 1999; Blumenthal 1971; Dermer & Atoyan 2002),
their inclusion in time-dependent models has so far necessitated a rather elaborate numerical treatment (Krawczynski et al. 2002; Mastichiadis & Kirk 1997).
However, recently, a useful approximation for the treatment of the inverse Compton energy
losses in an isotropic photon field, including the transition from the Thomson to the KN regime has been presented (Moderski et al. 2005a). In this paper, we use this approximation to develop a
semi-analytical solution to the electron kinetic equation. The numerical treatment of the time-dependent problem is thus reduced to a single quadrature.
We use this method to discuss the temporal evolution of characteristic features in the electron distribution as a consequence of energy losses in the KN regime. These effects are of
interest in the sources mentioned above, as well as in active galactic
nuclei. The paper is structured in the following way: in
Sect. 2, we derive our semi-analytical solution to the continuity
equation that describes the temporal evolution of an electron distribution
suffering synchrotron, inverse-Compton (including KN effects), and
escape losses for an arbitrary, time-dependent injection
spectrum. The necessary analytical calculations are summarised in
Appendices A and B. Numerical results found using this method
are presented in Sect. 3 and a specific
application to the case of the stellar
association Wd-2 is given in Sect. 4. We close the paper in
Sect. 5 with a discussion of the results and comment on
further refinements of the calculations.
2 Electron energy distribution
Assume a homogeneous source into which an unspecified acceleration
process injects electrons at the rate
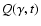 ,
which subsequently
cool and escape. The kinetic equation governing the evolution of
the number
,
which subsequently
cool and escape. The kinetic equation governing the evolution of
the number
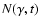 of electrons in the source with
Lorentz factors
of electrons in the source with
Lorentz factors 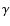 in the interval
in the interval
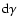 at time t is
at time t is
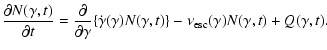 |
|
|
(1) |
In writing Eq. (1) we have assumed that each individual
electron in the source loses energy continuously, according to
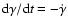 (note that
(note that
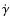 is defined as positive)
and has an energy-dependent probability
is defined as positive)
and has an energy-dependent probability
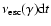 of escaping the source in a time interval
of escaping the source in a time interval
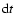 .
The continuous-loss approximation is appropriate for
synchrotron radiation and for Compton scattering in the Thomson limit,
as well as for collisional losses (ionisation losses) in
a fully ionised plasma. In the case of Compton scattering in the
Klein-Nishina regime, this approximation has been examined by several
authors (e.g., Zdziarski 1989; Blumenthal 1971). Provided one
is only interested in spectral features that appear in the transition
region between the Thomson limit and the extreme Klein-Nishina limit,
it appears to be justified.
In addition, we assume that Eq. (1) is linear in
.
The continuous-loss approximation is appropriate for
synchrotron radiation and for Compton scattering in the Thomson limit,
as well as for collisional losses (ionisation losses) in
a fully ionised plasma. In the case of Compton scattering in the
Klein-Nishina regime, this approximation has been examined by several
authors (e.g., Zdziarski 1989; Blumenthal 1971). Provided one
is only interested in spectral features that appear in the transition
region between the Thomson limit and the extreme Klein-Nishina limit,
it appears to be justified.
In addition, we assume that Eq. (1) is linear in
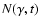 ,
i.e., that the the emitted radiation has no further effect on the
electron distribution or on the electron injection function. This
excludes situations encountered in compact sources in which feedback
effects can be important
(e.g., Katarzynski et al. 2006; Lightman & Zdziarski 1987; Stawarz & Kirk 2007),
but is not a significant restriction for objects such as stellar clusters.
,
i.e., that the the emitted radiation has no further effect on the
electron distribution or on the electron injection function. This
excludes situations encountered in compact sources in which feedback
effects can be important
(e.g., Katarzynski et al. 2006; Lightman & Zdziarski 1987; Stawarz & Kirk 2007),
but is not a significant restriction for objects such as stellar clusters.
In the case discussed here where the total energy-loss rate,
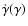 ,
and the escape rate,
,
and the escape rate,
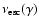 ,
are
independent of time, Eq. (1) can be solved by several
standard methods, e.g., by
means of the Green's function for the homogeneous equation
(Ginzburg & Syrovatskii 1964) or by using Laplace transforms
(Melrose 1980).
Following Melrose (1980), we define the
quantity
,
are
independent of time, Eq. (1) can be solved by several
standard methods, e.g., by
means of the Green's function for the homogeneous equation
(Ginzburg & Syrovatskii 1964) or by using Laplace transforms
(Melrose 1980).
Following Melrose (1980), we define the
quantity
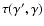 as the time required for an electron
to cool from a Lorentz factor of
as the time required for an electron
to cool from a Lorentz factor of 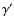 to one of
to one of 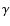 (
(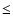
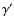 ),
),
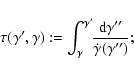 |
(2) |
and the quantity
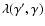 ,
such that
1 -
,
such that
1 -
![$\exp\left[-\lambda\left(\gamma',\gamma\right)\right]$](/articles/aa/full/2007/42/aa8298-07/img46.gif) is the probability that an electron escapes whilst cooling from
is the probability that an electron escapes whilst cooling from 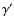 to
to 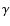 :
:
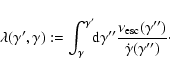 |
(3) |
This enables the solution to be written as
![$\displaystyle N(\gamma, t)~=~\frac{1}{\dot{\gamma}(\gamma)}\;\;\int_\gamma^\inf...
...ight]
\!+\! N(\gamma',0)\delta\left(t-\tau(\gamma',\gamma)\right)\right\rbrace,$](/articles/aa/full/2007/42/aa8298-07/img48.gif) |
|
|
(4) |
where H and 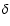 stand for the Heaviside and delta functions, respectively.
On multiplying Eq. (4) by
stand for the Heaviside and delta functions, respectively.
On multiplying Eq. (4) by
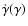 ,
it is
straightforward to assign a physical interpretation to each
term in this solution. Thus,
,
it is
straightforward to assign a physical interpretation to each
term in this solution. Thus,
-
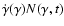 is the number of particles per
unit time that cool across the Lorentz factor
is the number of particles per
unit time that cool across the Lorentz factor 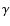 ,
,
-
![$\textrm{e}^{-\lambda(\gamma',\gamma)} Q\left[\gamma',t-\tau(\gamma',\gamma)\right]H
\left[t-\tau(\gamma',\gamma)\right]{\rm d}\gamma'$](/articles/aa/full/2007/42/aa8298-07/img51.gif) is the rate at which particles injected
with a Lorentz factor between
is the rate at which particles injected
with a Lorentz factor between 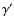 and
and
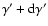 arrive at time t at a Lorentz factor
arrive at time t at a Lorentz factor 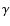 ,
and
,
and
-
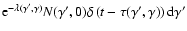 is the
rate at which particles whose initial Lorentz factor lies
between
is the
rate at which particles whose initial Lorentz factor lies
between 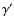 and
and
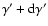 arrive at Lorentz factor
arrive at Lorentz factor 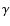 at time t.
at time t.
As we shall see below, the cooling rate is such that, in the limit of
large Lorentz factor, synchrotron losses always dominate:
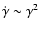 as
as
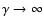 .
In this case, a finite
time suffices for an electron
to cool down to
.
In this case, a finite
time suffices for an electron
to cool down to 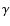 from an initially arbitrarily large Lorentz
factor. Defining the function
from an initially arbitrarily large Lorentz
factor. Defining the function
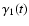 as
the Lorentz factor at time t of a particle
whose initial energy was infinite, i.e.,
as
the Lorentz factor at time t of a particle
whose initial energy was infinite, i.e.,
![$\displaystyle \tau[\infty,\gamma_1(t)]=t,$](/articles/aa/full/2007/42/aa8298-07/img57.gif) |
|
|
(5) |
one can rewrite Eq. (4) as
and
where
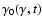 is defined (for
is defined (for
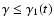 )
by the relation
)
by the relation
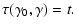 |
|
|
(8) |
The exact functional form of Eqs. (6) and (7)
is determined by the energy dependence of the
radiation processes involved and the escape
rate, as well as the injection function specified.
As an illustration, we present the
well-known case of constant injection of a power-law spectrum:
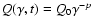 ,
starting at t=0 with
,
starting at t=0 with
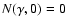 ,
where
radiative cooling is only due to synchrotron emission
,
where
radiative cooling is only due to synchrotron emission
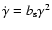 and no escape term is present (
and no escape term is present (
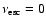 ). In this case
). In this case
 and
and
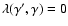 .
Equation (6) then gives
(see also Melrose 1980):
.
Equation (6) then gives
(see also Melrose 1980):
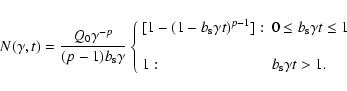 |
(9) |
As implied by Eq. (9) the electron spectrum steepens from
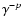 for
for
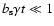 to
to
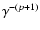 for
for
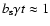 with a break at
with a break at
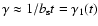 that moves to lower energies
as time progresses: the well-known spectral ageing effect.
that moves to lower energies
as time progresses: the well-known spectral ageing effect.
For an injection function that is non-zero only within a
range of the Lorentz factor
![$\gamma\in [\gamma_{\rm min},\gamma_{\rm max}]$](/articles/aa/full/2007/42/aa8298-07/img79.gif) ,
,
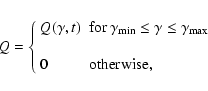 |
(10) |
it is computationally more efficient to account for this explicitly
by modifying the integration limits in Eqs. (6) and
(7). Specialising to
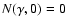 ,
one finds
,
one finds
with
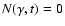 for
for
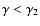 and
and
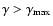 .
Here, the lower and upper integration limits are
.
Here, the lower and upper integration limits are
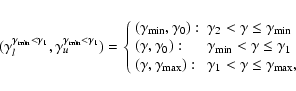 |
(12) |
when
 ,
while
,
while
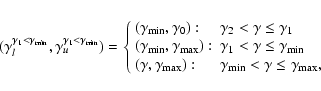 |
(13) |
for
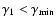 .
.
The value of 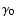 still fulfills Eq. (8), but
still fulfills Eq. (8), but 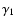 and
and 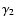 are now defined by
are now defined by
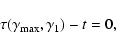 |
(14) |
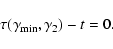 |
(15) |
Equations (14) and (15) describe the two breaks,
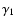 and
and 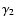 ,
introduced in the
evolved spectrum due to the existence in the injection spectrum of a
minimum and a maximum Lorentz factor,
,
introduced in the
evolved spectrum due to the existence in the injection spectrum of a
minimum and a maximum Lorentz factor,
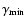 and
and
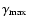 ,
respectively. Both breaks are moving to lower values as time evolves
with
,
respectively. Both breaks are moving to lower values as time evolves
with
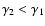 .
.
As a further illustration, Appendix B presents the solution of
Eq. (1) for a power-law
type injection function with finite energy spectrum, where synchrotron
and inverse Compton losses in the Thomson regime are present and
electrons escape at a rate
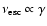 (see
Sect. 2.2).
(see
Sect. 2.2).
2.2 Energy-loss and escape rates
In the continuous energy-loss approximation,
the total energy-loss rate of a relativistic
electron (
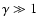 ), averaged over an isotropic distribution
and taking synchrotron cooling into account,
inverse Compton scattering of the electrons on ambient photons,
Coulomb losses, and Bremsstrahlung emission (in a fully ionised
hydrogen gas), is given by the formula:
), averaged over an isotropic distribution
and taking synchrotron cooling into account,
inverse Compton scattering of the electrons on ambient photons,
Coulomb losses, and Bremsstrahlung emission (in a fully ionised
hydrogen gas), is given by the formula:
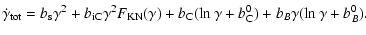 |
|
|
(16) |
The coefficients,
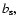
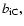 bC, and bB, and the
constants bC0 and bB0 are given by the following relations
(Ginzburg & Syrovatskii 1964):
bC, and bB, and the
constants bC0 and bB0 are given by the following relations
(Ginzburg & Syrovatskii 1964):
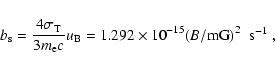 |
(17a) |
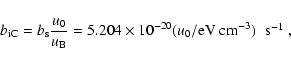 |
(17b) |
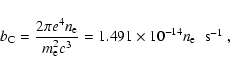 |
(17c) |
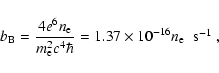 |
(17d) |
and
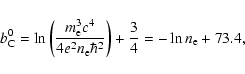 |
(18a) |
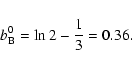 |
(18b) |
Here,
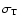 is the Thomson cross section, u0,
is the Thomson cross section, u0, 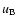 are
the total energy densities of the photon and magnetic fields,
respectively, while c,
are
the total energy densities of the photon and magnetic fields,
respectively, while c, 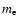 ,
and e are the velocity of light
in vacuum, the electron mass, and charge, respectively. Finally,
,
and e are the velocity of light
in vacuum, the electron mass, and charge, respectively. Finally, 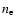 is the electron density in units of
cm-3.
In the case of ionisation or Bremsstrahlung losses (in neutral
hydrogen), the corresponding terms in Eq. (16)
should be replaced by
is the electron density in units of
cm-3.
In the case of ionisation or Bremsstrahlung losses (in neutral
hydrogen), the corresponding terms in Eq. (16)
should be replaced by
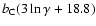 and
and
![$b_{\rm B}\left[\ln(191)+1/18\right]\simeq 5.3~b_{\rm B}$](/articles/aa/full/2007/42/aa8298-07/img111.gif) .
.
The escape of particles from the source may be modelled in
different ways. The simplest method is to assume that the
source is a region of relatively strong magnetic field and high target-photon density. When particles are carried out of this region by the motion
of the background plasma, they not only may leave the target fields behind,
but may also undergo a sudden drop in energy due to adiabatic expansion.
This scenario implies that the escape rate is independent of energy, being the reciprocal of the
average time taken by a fluid element to cross the region at a given speed.
An alternative method (which, however, does not account for a possible
energy loss) is to consider the particle transport as a diffusive
process with the spatial diffusion coefficient
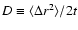 ,
being either constant or
a function of the energy of the particle or/and time,
,
being either constant or
a function of the energy of the particle or/and time,
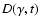 .
A common practice is to calculate the spatial diffusion coefficient in
the Bohm diffusion limit, which is defined by setting the step size of
the random walk of a particle equal to the Larmor radius,
.
A common practice is to calculate the spatial diffusion coefficient in
the Bohm diffusion limit, which is defined by setting the step size of
the random walk of a particle equal to the Larmor radius,
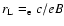 (for relativistic electrons). In this case,
(for relativistic electrons). In this case,
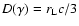 and the escape rate from
a spherical region with radial extension R,
and the escape rate from
a spherical region with radial extension R,
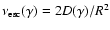 is, therefore, directly proportional to the particle's
energy:
is, therefore, directly proportional to the particle's
energy:
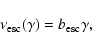 |
(19) |
where
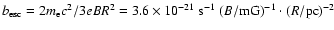 .
.
The function
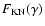 in Eq. (16) takes the full Klein-Nishina cross section for Compton
scattering into
account and is given by the relation
in Eq. (16) takes the full Klein-Nishina cross section for Compton
scattering into
account and is given by the relation
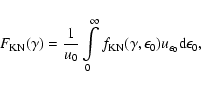 |
(20) |
where
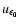 is the differential photon energy density:
is the differential photon energy density:
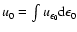 and
and
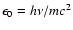 is the dimensionless
energy of a target photon of frequency
is the dimensionless
energy of a target photon of frequency 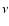 .
The
kernel,
.
The
kernel,
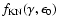 ,
was first given by Jones (1965).
It is important to note that this kernel, although originally derived for
an isotropic field of target photons, is also valid for an anisotropic
photon field, provided the average over an isotropic electron
distribution is taken (see Kirk et al. 1999, Appendix A).
A useful approximate expression in the limit
,
was first given by Jones (1965).
It is important to note that this kernel, although originally derived for
an isotropic field of target photons, is also valid for an anisotropic
photon field, provided the average over an isotropic electron
distribution is taken (see Kirk et al. 1999, Appendix A).
A useful approximate expression in the limit
 has recently been given by Moderski et al. (2005a)
has recently been given by Moderski et al. (2005a)
for
and these authors also estimate the implications of Eq. (2.3)
for the functional form of
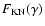 ,
for different photon energy distributions.
,
for different photon energy distributions.
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig1.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg131.gif) |
Figure 1:
The cooling time
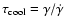 as a function of Lorentz factor
for the various energy-loss mechanisms for electrons
including Coulomb scattering (dash-dotted), Bremsstrahlung
(triple dotted), synchrotron (long dashed), inverse Compton
(Thomson limit: dotted,
approximation, see Eq. (2.3): short dashed,
no approximation: thin line), and total (heavy line). The parameters
are as a function of Lorentz factor
for the various energy-loss mechanisms for electrons
including Coulomb scattering (dash-dotted), Bremsstrahlung
(triple dotted), synchrotron (long dashed), inverse Compton
(Thomson limit: dotted,
approximation, see Eq. (2.3): short dashed,
no approximation: thin line), and total (heavy line). The parameters
are
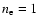 cm-3, u0=500 eV cm-3,
T=30 000 K, and cm-3, u0=500 eV cm-3,
T=30 000 K, and 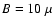 G, as expected
for a stellar environment with hot young stars. G, as expected
for a stellar environment with hot young stars. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig2.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg133.gif) |
Figure 2:
The solution
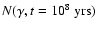 using
the approximate cooling term of Eq. (22)
in an environment identical to the one used in Fig. 1
(solid line) compared with
the steady-state solution using the full expression,
for
using
the approximate cooling term of Eq. (22)
in an environment identical to the one used in Fig. 1
(solid line) compared with
the steady-state solution using the full expression,
for
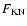 and including Coulomb losses (dashed line).
and including Coulomb losses (dashed line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm]{8298fig3a.eps}\includegraphics[width=8.6cm]{8298fig3b.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg134.gif) |
Figure 3:
The quantities
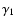 and and 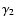 defined in Eqs. (14) and (15)
as functions of time for magnetic fields and
target photon fields of the same
energy density but for two different photon temperatures:
T=30 000 K ( left panel)
and T=30 K ( right panel). In both panels,
defined in Eqs. (14) and (15)
as functions of time for magnetic fields and
target photon fields of the same
energy density but for two different photon temperatures:
T=30 000 K ( left panel)
and T=30 K ( right panel). In both panels,
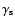 (transition from synchrotron to KN cooling)
and
(transition from synchrotron to KN cooling)
and
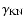 (transition from KN to Thomson) are indicated by
horizontal arrows.
For comparison, the thin lines indicate the evolution of
(transition from KN to Thomson) are indicated by
horizontal arrows.
For comparison, the thin lines indicate the evolution of 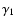 and
and 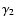 in the Thomson limit
(for
in the Thomson limit
(for 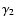 ,
the cooling proceeds at all times in the Thomson regime, since ,
the cooling proceeds at all times in the Thomson regime, since
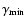 is chosen to be 100; therefore, the two curves are
superposed).
is chosen to be 100; therefore, the two curves are
superposed). |
| Open with DEXTER |
For a (possibly diluted) Planckian distribution of photon energies, the Compton energy
losses for electrons are dominated by scatterings on photons with
dimensionless energy
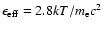 .
For
.
For
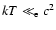 ,
the function
,
the function
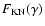 can
therefore be approximated by treating the Planckian as a
mono-energetic photon distribution (i.e.,
can
therefore be approximated by treating the Planckian as a
mono-energetic photon distribution (i.e.,
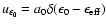 ).
Using this approximation and Eq. (2.3),
one finds
).
Using this approximation and Eq. (2.3),
one finds
with
and
For a power-law radiation field (
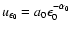 ),
),
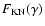 can be written in the same general form
as in Eq. (2.3), provided
the values of the parameters
can be written in the same general form
as in Eq. (2.3), provided
the values of the parameters
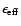 and
and 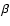 are suitably chosen.
For
are suitably chosen.
For
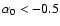 and
and
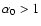 ,
inverse Compton losses in the KN limit are dominated by
scatterings on photons with the highest (
,
inverse Compton losses in the KN limit are dominated by
scatterings on photons with the highest (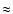
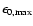 )
and the
lowest (
)
and the
lowest (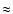
 )
photon energies available, respectively.
One may therefore write
)
photon energies available, respectively.
One may therefore write
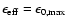 for
for
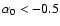 and
and
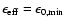 for
for
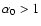 ,
with
,
with
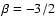 in each case.
in each case.
In the intermediate case of
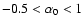 ,
the relevant photon
energy range for scattering is broader (
,
the relevant photon
energy range for scattering is broader (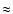
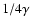 )
and one
may instead use the so-called Thomson edge or KN
cut-off approximation. In this range
)
and one
may instead use the so-called Thomson edge or KN
cut-off approximation. In this range
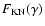 is
still given by Eq. (2.3) with
is
still given by Eq. (2.3) with
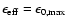 and
and
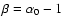 ,
provided
,
provided
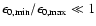 .
Table 1 summarises the values of the parameters
.
Table 1 summarises the values of the parameters
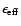 and
and 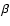 for the case of a black-body photon targets,
as well as for power-law target photon fields.
for the case of a black-body photon targets,
as well as for power-law target photon fields.
The cooling timescale for electrons
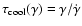 for the
various energy-loss mechanisms, assuming an environment where inverse
Compton cooling in the Klein-Nishina limit is important, is shown
in Fig. 1. The parameters used are
for the
various energy-loss mechanisms, assuming an environment where inverse
Compton cooling in the Klein-Nishina limit is important, is shown
in Fig. 1. The parameters used are
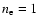 cm-3, u0=500 eV cm-3, T=30 000 K, and
cm-3, u0=500 eV cm-3, T=30 000 K, and
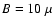 G, as expected in an
environment dominated by hot and young stars that provide a
relatively high-temperature target-photon field. The cooling time for Coulomb
scattering and Bremsstrahlung losses is calculated assuming a
fully ionised gas. This is a self-consistent assumption taking the high-temperature and energy density of the ambient photon field into account, which is sufficient
to ionise neutral hydrogen. The cooling time is dominated by different
mechanisms in different energy ranges. At the lowest energies,
Coulomb scattering (ionisation loss)
is the fastest energy loss mechanism, whereas inverse Compton scattering in the Thomson
regime takes over above approximately 100 MeV. For electron energies above a few GeV, the inverse
Compton scattering becomes less efficient because of the drop
in the cross section. At energies higher than 1 TeV, inverse Compton
scattering is less efficient than synchrotron radiation, which remains
the dominant mechanism at higher
energies. Although these transition energies
depend on the choice of the parameters
(u0,
G, as expected in an
environment dominated by hot and young stars that provide a
relatively high-temperature target-photon field. The cooling time for Coulomb
scattering and Bremsstrahlung losses is calculated assuming a
fully ionised gas. This is a self-consistent assumption taking the high-temperature and energy density of the ambient photon field into account, which is sufficient
to ionise neutral hydrogen. The cooling time is dominated by different
mechanisms in different energy ranges. At the lowest energies,
Coulomb scattering (ionisation loss)
is the fastest energy loss mechanism, whereas inverse Compton scattering in the Thomson
regime takes over above approximately 100 MeV. For electron energies above a few GeV, the inverse
Compton scattering becomes less efficient because of the drop
in the cross section. At energies higher than 1 TeV, inverse Compton
scattering is less efficient than synchrotron radiation, which remains
the dominant mechanism at higher
energies. Although these transition energies
depend on the choice of the parameters
(u0, 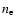 ,
T, and B), the qualitative picture remains the same.
It is interesting to compare the approximation for
,
T, and B), the qualitative picture remains the same.
It is interesting to compare the approximation for
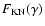 with
the exact calculation shown in Fig. 1
(using the expression for
with
the exact calculation shown in Fig. 1
(using the expression for
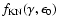 given by
Moderski et al. 2005a). The
approximation slightly overpredicts
given by
Moderski et al. 2005a). The
approximation slightly overpredicts
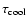 ,
but is fairly
accurate up to very high energies (
,
but is fairly
accurate up to very high energies (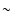 10% at
10% at
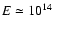 eV,
corresponding to
eV,
corresponding to
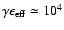 ).
However, as one can readily deduce from
Fig. 1, the approximation for
).
However, as one can readily deduce from
Fig. 1, the approximation for
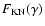 becomes inaccurate
only in the regime where synchrotron losses are likely to
dominate. Even in binary systems, where the radiation field
density can be substantially higher than the value assumed in
Fig. 1, the ratio of u0/uB is unlikely to be higher than
O(1000) and, therefore, electrons with
becomes inaccurate
only in the regime where synchrotron losses are likely to
dominate. Even in binary systems, where the radiation field
density can be substantially higher than the value assumed in
Fig. 1, the ratio of u0/uB is unlikely to be higher than
O(1000) and, therefore, electrons with
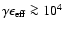 cool
predominantly through synchrotron radiation.
cool
predominantly through synchrotron radiation.
Table 1:
The values of the parameters 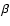 and
and
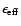 (see Eq. (2.3)) for
two different photon energy distributions.
(see Eq. (2.3)) for
two different photon energy distributions.
For astrophysical environments with dilute plasma and fields of high
energy density,
the most relevant energy-loss mechanisms for high-energy electrons are
synchrotron and inverse Compton radiation. Therefore, one may safely
discard in this case the last two terms in Eq. (16),
which then becomes
![\begin{displaymath}\dot{\gamma}=b_{\rm s}\gamma^2\left[1+b_{\rm is}F_{\rm KN}(\gamma)\right],
\end{displaymath}](/articles/aa/full/2007/42/aa8298-07/img161.gif) |
(21) |
where
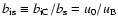 denotes
the ratio of the photon field total energy density to the magnetic
field energy density.
Using Eqs. (2.3) and (21), we may write
this in the general form:
denotes
the ratio of the photon field total energy density to the magnetic
field energy density.
Using Eqs. (2.3) and (21), we may write
this in the general form:
![\begin{displaymath}\dot{\gamma}=b_{\rm s}\gamma^2\left[1+b_{\rm is}
\left(1+4\gamma\epsilon_{\rm eff}\right)^\beta\right],
\end{displaymath}](/articles/aa/full/2007/42/aa8298-07/img163.gif) |
(22) |
where 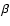 and
and
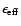 are chosen from
Table 1 for the appropriate target photon field.
Taking Eqs. (19) and (22) into account,
the functions describing cooling time and escape probability
given in Eq. (3)
can be expressed as
are chosen from
Table 1 for the appropriate target photon field.
Taking Eqs. (19) and (22) into account,
the functions describing cooling time and escape probability
given in Eq. (3)
can be expressed as
where the notation
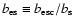 has been
used. Note that for
has been
used. Note that for
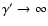 ,
,
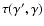 remains finite,
whereas
remains finite,
whereas
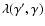 diverges. Physically, this is because
the synchrotron cooling rate, which goes as
diverges. Physically, this is because
the synchrotron cooling rate, which goes as 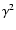 dominates at
high Lorentz factors, so that the time taken to cool to
dominates at
high Lorentz factors, so that the time taken to cool to 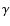 from an arbitrarily large
from an arbitrarily large 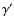 is finite. However, if the mean free path of the electrons increases in proportion to
is finite. However, if the mean free path of the electrons increases in proportion to
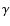 ,
as in the case of Bohm diffusion, the probability of escape during this finite cooling time
tends to unity as
,
as in the case of Bohm diffusion, the probability of escape during this finite cooling time
tends to unity as
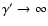 .
.
In Appendix A, we give the analytical form of the
functions
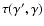 and
and
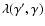 assuming that
assuming that
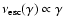 (see Eq. 19). For a power-law type photon
energy spectrum with spectral index
(see Eq. 19). For a power-law type photon
energy spectrum with spectral index
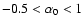 ,
these functions
are given only in closed form for the special
cases
,
these functions
are given only in closed form for the special
cases
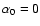 and
and
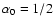 ,
although
a numerical evaluation is straightforward
using Eqs. (A.1) and (A.2).
The analytical expressions have the advantage that the solution of
Eq. (1) is reduced to the single quadrature given in
Eqs. (6) and (7)
or (11).
,
although
a numerical evaluation is straightforward
using Eqs. (A.1) and (A.2).
The analytical expressions have the advantage that the solution of
Eq. (1) is reduced to the single quadrature given in
Eqs. (6) and (7)
or (11).
In the Thomson limit for Compton scattering
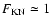 .
Therefore, assuming
.
Therefore, assuming
 ,
one has
,
one has
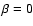 in Eqs. (23) and (24),
and the functions
in Eqs. (23) and (24),
and the functions
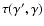 and
and
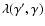 can be written down explicitly:
can be written down explicitly:
The solution of Eq. (1) follows from
Eqs. (6) and (7).
For
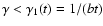 ,
,
where
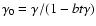 and, for
and, for
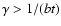 ,
,
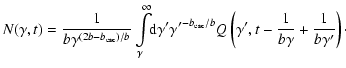 |
|
|
(29) |
The solution for a continuous power-law injection
with a finite energy spectrum is
given in Appendix B.
In the case where the escape rate does not depend on the particle
energy,
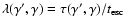 ,
where
,
where
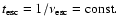 Then, in the Thomson limit of Compton scattering,
Then, in the Thomson limit of Compton scattering,
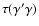 is
given, as before, by Eq. (26), and from
Eq. (6) one finds
is
given, as before, by Eq. (26), and from
Eq. (6) one finds
for
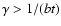 ,
and for
,
and for
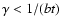 :
:
![$\displaystyle N(\gamma, t) =
\frac{1}{b \gamma^2} \textrm{e}^{-t_{\rm cool}/t_{...
...a't_{\rm esc}}
Q \bigl[\gamma',t-(b\gamma)^{-1}+(b\gamma')^{-1}\bigr]
\enspace,$](/articles/aa/full/2007/42/aa8298-07/img196.gif) |
|
|
(31) |
where the cooling time
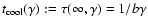 is
the time taken for an electron to cool from infinite
Lorentz factor to Lorentz factor
is
the time taken for an electron to cool from infinite
Lorentz factor to Lorentz factor 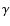 .
For
.
For
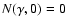 ,
with
a constant mono-energetic injection spectrum,
,
with
a constant mono-energetic injection spectrum,
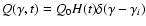 ,
and for
,
and for
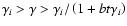 ,
Eq. (30) yields a steady-state solution:
,
Eq. (30) yields a steady-state solution:
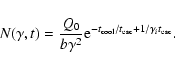 |
(32) |
This solution displays a cut-off towards lower Lorentz factors
at
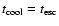 as has been pointed out by Kardashev (1962).
as has been pointed out by Kardashev (1962).
3 Numerical results
3.1 Comparison with the steady-state solution
Ignoring escape losses, Eq. (1)
in the steady-state limit,
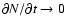 becomes
becomes
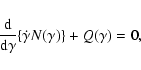 |
(33) |
which is easily integrated to give
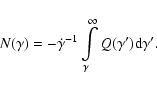 |
(34) |
In this case it is straightforward to incorporate the general
term for
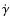 given by Eq. (16). In
Fig. 2, we compare this solution with the time-dependent
solution obtained by using Eqs. (6) and (7) with
the approximate cooling term given in Eq. (22). We
take t=108 years, which is sufficiently large to allow a steady
state to be achieved, and assume no particles are present initially,
given by Eq. (16). In
Fig. 2, we compare this solution with the time-dependent
solution obtained by using Eqs. (6) and (7) with
the approximate cooling term given in Eq. (22). We
take t=108 years, which is sufficiently large to allow a steady
state to be achieved, and assume no particles are present initially,
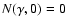 .
In this figure, escape is neglected,
.
In this figure, escape is neglected,
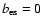 ,
and
the ratio of the energy density of the photon field to that of the
magnetic field is
,
and
the ratio of the energy density of the photon field to that of the
magnetic field is
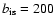 .
The remaining parameters are the same as
in Fig. 1 Note that here and in the following, we restrict
our calculations to the case of a thermal distribution of target
photons. The qualitative picture is similar to the case of a photon
field following a power law.
.
The remaining parameters are the same as
in Fig. 1 Note that here and in the following, we restrict
our calculations to the case of a thermal distribution of target
photons. The qualitative picture is similar to the case of a photon
field following a power law.
For
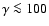 ,
Coulomb losses
harden the spectrum to p-1=1. Since the time-dependent solution is
based upon a simplified energy-loss term given in
Eq. (21) neglecting the Coulomb energy losses, the two
solutions deviate in this range.
Between
,
Coulomb losses
harden the spectrum to p-1=1. Since the time-dependent solution is
based upon a simplified energy-loss term given in
Eq. (21) neglecting the Coulomb energy losses, the two
solutions deviate in this range.
Between
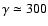 and
and
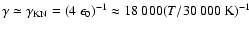 ,
electrons cool predominantly via inverse Compton scattering in the
Thomson limit. For values of
,
electrons cool predominantly via inverse Compton scattering in the
Thomson limit. For values of
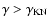 ,
the drop in the
inverse Compton scattering cross section in the Klein-Nishina regime
leads to a spectral hardening until synchrotron losses become dominant
for
,
the drop in the
inverse Compton scattering cross section in the Klein-Nishina regime
leads to a spectral hardening until synchrotron losses become dominant
for
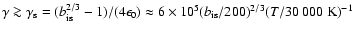 .
The positions
of
.
The positions
of
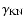 and
and
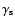 are indicated in Fig. 2.
The slight deviation observed for
are indicated in Fig. 2.
The slight deviation observed for
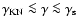 is the result of the approximation used for
is the result of the approximation used for
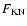 given in Eq. (2.3). From Fig. 2, it is obvious
that (a) the approximation used to take the energy dependence of the
inverse Compton scattering cross section into account follows the exact calculation quite
well and (b) neglecting Coulomb losses mainly
affects the low-energy part of the spectrum.
given in Eq. (2.3). From Fig. 2, it is obvious
that (a) the approximation used to take the energy dependence of the
inverse Compton scattering cross section into account follows the exact calculation quite
well and (b) neglecting Coulomb losses mainly
affects the low-energy part of the spectrum.
The temporal evolution of
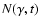 for an arbitrary injection
function
for an arbitrary injection
function
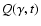 can now be calculated. In the following we
investigate the impact of the
relevant parameters (
can now be calculated. In the following we
investigate the impact of the
relevant parameters (
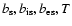 ).
To demonstrate the effect of KN cooling on the temporal
evolution, we plot the evolution of
).
To demonstrate the effect of KN cooling on the temporal
evolution, we plot the evolution of 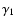 and
and 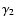 in Fig. 3 as a function of time for two different temperatures
(T=30 000 K and T=30 K), which are representative of an
environment dominated by either hot stars or by re-processed emission from
warm dust. For comparison, the evolution of
in Fig. 3 as a function of time for two different temperatures
(T=30 000 K and T=30 K), which are representative of an
environment dominated by either hot stars or by re-processed emission from
warm dust. For comparison, the evolution of 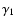 and
and 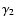 in the Thomson limit is depicted by thin lines. In both cases, the
parameters have been chosen similar to the ones used above
(
in the Thomson limit is depicted by thin lines. In both cases, the
parameters have been chosen similar to the ones used above
(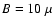 G, u0=500 eV cm-3 corresponding to
G, u0=500 eV cm-3 corresponding to
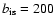 ,
,
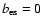 )
with
)
with
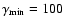 and
and
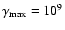 .
The evolution of
.
The evolution of
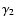 is dominated by slow cooling in the Thomson limit, and
therefore, the two lines are identical. For the high-temperature
environment (Fig. 3a),
is dominated by slow cooling in the Thomson limit, and
therefore, the two lines are identical. For the high-temperature
environment (Fig. 3a), 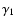 cools via synchrotron
radiation until roughly 1 Myr, when the
energy
losses in the KN limit take over. Within a few hundred thousand years,
the transition to Thomson-limit cooling takes place when
cools via synchrotron
radiation until roughly 1 Myr, when the
energy
losses in the KN limit take over. Within a few hundred thousand years,
the transition to Thomson-limit cooling takes place when
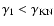 .
Qualitatively, the evolution of
.
Qualitatively, the evolution of 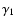 for a
cooler photon field proceeds in a similar way (Fig. 3b).
It is, however, important to note that the respective transitions occur
much earlier. Whereas for T=30 000 K, synchrotron cooling prevails
for about 1 Myr, for T=30 K, Compton
cooling in the KN regime is reached
within a few hundred years.
for a
cooler photon field proceeds in a similar way (Fig. 3b).
It is, however, important to note that the respective transitions occur
much earlier. Whereas for T=30 000 K, synchrotron cooling prevails
for about 1 Myr, for T=30 K, Compton
cooling in the KN regime is reached
within a few hundred years.
The effect on the temporal evolution of a particle distribution that
is partially cooling via inverse Compton radiation in the KN limit is
shown in Fig. 4.
Here, we have assumed a continuous power-law
electron injection with p=2 between
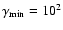 and
and
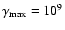 ,
neglected escape losses (
,
neglected escape losses (
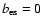 ), and included
the environmental parameters described above.
The solutions
), and included
the environmental parameters described above.
The solutions
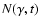 for
t=105,
for
t=105,
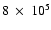 ,
and
,
and
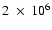 years,
weighted with
years,
weighted with 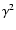 so
that the injected spectrum appears constant, are compared with
solutions found by
using expressions for the cooling valid in
the Thomson limit (see Appendix B), which are
depicted as thin lines.
so
that the injected spectrum appears constant, are compared with
solutions found by
using expressions for the cooling valid in
the Thomson limit (see Appendix B), which are
depicted as thin lines.
The solutions for t=105 yrs (see also Fig. 3a)
correspond to the case
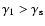 (the position of
(the position of
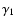 marked in Fig. 4). The
solution taking KN effects into account shows a break such that
marked in Fig. 4). The
solution taking KN effects into account shows a break such that
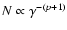 for
for
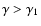 ,
while for smaller
,
while for smaller
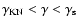 ,
a slight deviation from the p=2injection power law can be observed to mark the onset of rapid
energy loss in the KN regime. In the solution obtained in the Thomson
limit, the break occurs at a lower value of
,
a slight deviation from the p=2injection power law can be observed to mark the onset of rapid
energy loss in the KN regime. In the solution obtained in the Thomson
limit, the break occurs at a lower value of 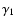 (see also
Fig. 3a), which marks the transition from the uncooled
part of the spectrum to the part that has already suffered from
cooling. At the solution at a later time (
(see also
Fig. 3a), which marks the transition from the uncooled
part of the spectrum to the part that has already suffered from
cooling. At the solution at a later time (
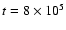 yrs) when
yrs) when
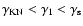 ,
the flattened spectral shape
presented earlier in the steady-state solution (see Fig. 2)
has already developed fully as a consequence of the large
,
the flattened spectral shape
presented earlier in the steady-state solution (see Fig. 2)
has already developed fully as a consequence of the large
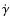 in the KN regime. The solution obtained in the Thomson limit
and the one obtained taking KN effects into account agree with each
other for
in the KN regime. The solution obtained in the Thomson limit
and the one obtained taking KN effects into account agree with each
other for
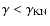 ,
which marks the transition to
cooling in the Thomson limit. Finally, for
,
which marks the transition to
cooling in the Thomson limit. Finally, for
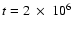 yrs,
yrs,
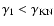 ,
and the further temporal evolution is
described in the Thomson limit well.
,
and the further temporal evolution is
described in the Thomson limit well.
In the next example, we consider a higher value of
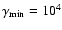 while keeping the same values for all other parameters as in the
examples above. Figure 5 shows
while keeping the same values for all other parameters as in the
examples above. Figure 5 shows
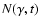 for three different times: t=10, 104, and 107 years. The shape of the spectrum mainly evolves, as expected, due to synchrotron cooling for
for three different times: t=10, 104, and 107 years. The shape of the spectrum mainly evolves, as expected, due to synchrotron cooling for 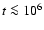 years. At later times (e.g., t=107 yrs), the spectrum shows a smooth transition between p=2 and p+1=3 at
years. At later times (e.g., t=107 yrs), the spectrum shows a smooth transition between p=2 and p+1=3 at
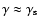 .
For lower values of
.
For lower values of
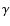 ,
the spectrum remains almost flat, showing a slight peak at
the position of
,
the spectrum remains almost flat, showing a slight peak at
the position of
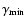 .
The overall shape of this evolved
spectrum could, in principle, mimic the case of an uncooled spectrum up
to TeV energies (depending on the value of
.
The overall shape of this evolved
spectrum could, in principle, mimic the case of an uncooled spectrum up
to TeV energies (depending on the value of
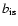 )
with a softening at
)
with a softening at
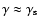 resembling a much younger source.
Remarkably, for p=2, the effect of cooling in KN is almost hidden when
resembling a much younger source.
Remarkably, for p=2, the effect of cooling in KN is almost hidden when
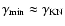 .
For higher values of
.
For higher values of
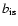 ,
a hard particle
spectrum can be retained up to even higher values of
,
a hard particle
spectrum can be retained up to even higher values of 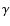 than those
shown here (see also next example).
than those
shown here (see also next example).
Changing the ratio of the photon and magnetic field energy densities
(
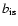 )
at a fixed photon temperature influences the location of the transition between inverse Compton and synchrotron cooling. In Fig. 6, the effect of varying
)
at a fixed photon temperature influences the location of the transition between inverse Compton and synchrotron cooling. In Fig. 6, the effect of varying
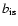 from values of 100 up to 104 is demonstrated. Increasing
from values of 100 up to 104 is demonstrated. Increasing
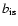 leads to more rapid
cooling and a more pronounced spectral hardening as a result of
inverse Compton cooling in the KN limit.
leads to more rapid
cooling and a more pronounced spectral hardening as a result of
inverse Compton cooling in the KN limit.
Finally, we consider the effect of particle escape via diffusive
particle transport leaving a sphere with radius R. In
Fig. 7, the solution
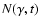 is shown for values of
is shown for values of
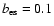 ,
100, and 1000 at t=106 yrs.
For comparison, the solution of Appendix B
in the Thomson limit is also shown.
All other parameters are the same
as in the previous example.
As expected, the effect of escape losses leads to
a reduction in the total particle number. Escape losses are negligible for
,
100, and 1000 at t=106 yrs.
For comparison, the solution of Appendix B
in the Thomson limit is also shown.
All other parameters are the same
as in the previous example.
As expected, the effect of escape losses leads to
a reduction in the total particle number. Escape losses are negligible for
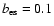 ,
whereas for
,
whereas for
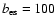 and
and
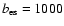 ,
escape losses modify the solution considerably in
comparison to the case of small
,
escape losses modify the solution considerably in
comparison to the case of small
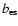 .
The solution taking KN effects
into account shows a stronger relative suppression of particle numbers
for
.
The solution taking KN effects
into account shows a stronger relative suppression of particle numbers
for
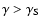 than in the Thomson limit. This is a
consequence of radiative cooling being
dominated by synchrotron losses for
than in the Thomson limit. This is a
consequence of radiative cooling being
dominated by synchrotron losses for
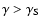 in the KN case which
implies that escape losses are relatively more important
(
in the KN case which
implies that escape losses are relatively more important
(
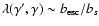 )
than in the Thomson limit, where
)
than in the Thomson limit, where
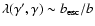 with
with
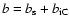 .
In general, when escape losses are important,
the spectral features characteristic of
cooling in the KN limit are suppressed, and the solution
resembles what is found in
the Thomson limit. Asymptotically, for very large
.
In general, when escape losses are important,
the spectral features characteristic of
cooling in the KN limit are suppressed, and the solution
resembles what is found in
the Thomson limit. Asymptotically, for very large
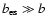 ,
radiative cooling is negligible and the two solutions
converge.
,
radiative cooling is negligible and the two solutions
converge.
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig4.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg234.gif) |
Figure 4:
The solution
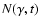 obtained
by including the effects of KN cooling (thick lines) and in the Thomson
limit (see Appendix C) for three different times chosen such that
obtained
by including the effects of KN cooling (thick lines) and in the Thomson
limit (see Appendix C) for three different times chosen such that
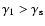 (t=105 yrs),
(t=105 yrs),
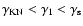 (
(
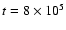 yrs), and yrs), and
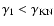 (
(
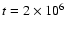 yrs). The parameters used are identical to the
ones used e.g. in Fig. 3a. The positions of yrs). The parameters used are identical to the
ones used e.g. in Fig. 3a. The positions of 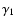 at different times, as well as of
at different times, as well as of
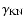 and
and
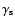 ,
are indicated by arrows and vertical lines, respectively. ,
are indicated by arrows and vertical lines, respectively. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig5.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg235.gif) |
Figure 5:
Temporal evolution of an electron
distribution injected with p=2 between
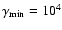 and
and
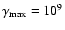 in a hot (T=30 000 K) photon field. The
evolution is shown for three distinct times:
t=10, 104, and 107 years. The energy density of the
photon field is
200 times that of the
magnetic field (
in a hot (T=30 000 K) photon field. The
evolution is shown for three distinct times:
t=10, 104, and 107 years. The energy density of the
photon field is
200 times that of the
magnetic field (
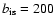 ), and escape losses are neglected
( ), and escape losses are neglected
(
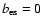 ). ). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig6.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg236.gif) |
Figure 6:
The effect
of varying
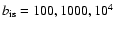 demonstrated for a similar set of parameters as described
in Fig. 5 and a fixed time (t=106 yrs).
demonstrated for a similar set of parameters as described
in Fig. 5 and a fixed time (t=106 yrs). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig7.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg237.gif) |
Figure 7:
The effect of escape losses is demonstrated
for three different values of
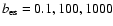 (thin, medium, and
heavy lines). The time has been fixed to 1 Myr. The injection
rate, as well as the other parameters, are identical to the cases
discussed in the previous figures. The solid lines are obtained
taking KN effects into account, while for comparison the analytical
solution for the Thomson limit is shown with dashed lines.
(thin, medium, and
heavy lines). The time has been fixed to 1 Myr. The injection
rate, as well as the other parameters, are identical to the cases
discussed in the previous figures. The solid lines are obtained
taking KN effects into account, while for comparison the analytical
solution for the Thomson limit is shown with dashed lines. |
| Open with DEXTER |
4 Application to a stellar association: Westerlund 2
The discovery of VHE gamma-ray emission from young stellar
associations like Westerlund 2 (Wd-2), Cyg OB2, and Berkeley 87
provides first clear evidence that particle acceleration can occur
in these systems. While the origin of the emission and the nature of
the accelerated particles is not clear, it has been suggested that
gamma rays from stellar associations could be the decay product of
neutral mesons in inelastic scattering of nuclei with the ambient
medium (Bednarek 2007; Torres et al. 2004) or could be
due to the excitation of giant resonances of nuclei by
Doppler boosted UV photons (Anchordoqui et al. 2007b).
Here, we calculate the broad-band spectral energy distribution of
Wd-2 at different stages of its evolution. The distance to this
system is not very well-constrained (Churchwell et al. 2004).
A recent estimate places
Wd-2 at 2.8 kpc, with an age of
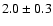 Myr and
a total mass of
Myr and
a total mass of
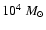 (Ascenso et al. 2007).
While
this distance estimate is based mainly on near infra-red
photometry and colours, the spectroscopic investigation of the cluster and the
light curve of the binary system WR 20a has provided a larger
distance estimate of
(Ascenso et al. 2007).
While
this distance estimate is based mainly on near infra-red
photometry and colours, the spectroscopic investigation of the cluster and the
light curve of the binary system WR 20a has provided a larger
distance estimate of 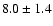 kpc (Rauw et al. 2007).
Another recent distance estimate is based upon the possible association of
RCW 49 with a giant molecular cloud with a mass
of
kpc (Rauw et al. 2007).
Another recent distance estimate is based upon the possible association of
RCW 49 with a giant molecular cloud with a mass
of
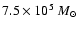 at a kinematic distance of
at a kinematic distance of 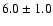 kpc
(Dame 2007). For our calculations, we adopt a distance of D=2.8 kpc and note that the larger distance would affect the total energetics, requiring a higher injection rate.
kpc
(Dame 2007). For our calculations, we adopt a distance of D=2.8 kpc and note that the larger distance would affect the total energetics, requiring a higher injection rate.
The angular extension, (
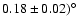 ,
of the VHE gamma-ray emission region
(Aharonian et al. 2007)
implies a radial extension of
,
of the VHE gamma-ray emission region
(Aharonian et al. 2007)
implies a radial extension of
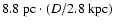 .
The total luminosity of the member stars of O-type has been
estimated to be
.
The total luminosity of the member stars of O-type has been
estimated to be
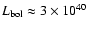 erg s-1 (Rauw et al. 2007). However, it is well known that the
number of UV photons emitted by the early cluster member stars is not
sufficient to power the HII region RCW 49 in which Wd-2 is embedded.
Based upon the estimates of Rauw et al. (2007), only
erg s-1 (Rauw et al. 2007). However, it is well known that the
number of UV photons emitted by the early cluster member stars is not
sufficient to power the HII region RCW 49 in which Wd-2 is embedded.
Based upon the estimates of Rauw et al. (2007), only
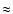 20% of the UV photons required to power RCW 49 can be
attributed to known O stars; therefore, the assumed luminosity of the
early type stars is certainly a lower limit and the total luminosity
could in fact reach values beyond 1041 erg s-1. It is
noteworthy that the population of later type stars shows a rather
flat projected spatial distribution even beyond a distance of
4 pc
(Ascenso et al. 2007), which would lead to a higher average
energy density of the photon field. In addition to the stellar
photons, re-processed emission from the dust present in Wd-2, and its
surrounding will provide a contribution to the seed photon field for
inverse Compton scattering, which is not included here and is
left for a more
detailed modelling.
20% of the UV photons required to power RCW 49 can be
attributed to known O stars; therefore, the assumed luminosity of the
early type stars is certainly a lower limit and the total luminosity
could in fact reach values beyond 1041 erg s-1. It is
noteworthy that the population of later type stars shows a rather
flat projected spatial distribution even beyond a distance of
4 pc
(Ascenso et al. 2007), which would lead to a higher average
energy density of the photon field. In addition to the stellar
photons, re-processed emission from the dust present in Wd-2, and its
surrounding will provide a contribution to the seed photon field for
inverse Compton scattering, which is not included here and is
left for a more
detailed modelling.
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig8.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg246.gif) |
Figure 8:
Broad-band spectral energy distribution of
Westerlund 2 (Wd 2) and multi-wavelength measurements (for
further details see the text).
For the inverse Compton
emission, the heavy line indicates the sum of the emissivity from
the stellar light (medium curve) allowing for KN effects as well
as from the cosmic microwave background (thin curve). |
| Open with DEXTER |
Taking into account just the total power emitted by the early type
stars in the cluster, the average energy density of the hot photon
field at a distance R corresponding to the extension of the VHE
gamma-ray source can be estimated as
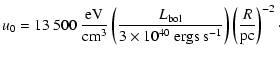 |
|
|
(35) |
Based upon the extension of the VHE source of 8.8 pc,
u0=174 eV cm-3. However, given the presence of additional
(diffuse) UV photons implied by the ionisation state of RCW 49, we
choose u0=500 eV cm-3 as the average energy density and a
temperature of T=30 000 K to characterise the
target photon field.
The magnetic field is set to
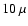 G, placing it in approximate equipartition
to the thermal energy density of the gas,
assuming a source
radius of 8.8 pc.
The injection rate
G, placing it in approximate equipartition
to the thermal energy density of the gas,
assuming a source
radius of 8.8 pc.
The injection rate 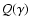 is assumed to be
constant in time with a total power of
is assumed to be
constant in time with a total power of
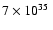 ergs s-1following a power law with p=2 between
ergs s-1following a power law with p=2 between
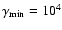 and
and
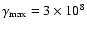 .
The required injection power can be compared, for example, with
the total power injected by the stellar winds driven
by the early type stars (mainly the Wolf-Rayet stars
WR 20a&b) present in Wd-2, which has
been estimated as
.
The required injection power can be compared, for example, with
the total power injected by the stellar winds driven
by the early type stars (mainly the Wolf-Rayet stars
WR 20a&b) present in Wd-2, which has
been estimated as
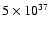 erg s-1
(Rauw et al. 2007).
If the emitting electrons are accelerated by these stellar winds,
they must take roughly 1% of the kinetic power of the bulk flow.
erg s-1
(Rauw et al. 2007).
If the emitting electrons are accelerated by these stellar winds,
they must take roughly 1% of the kinetic power of the bulk flow.
In hadronic scenarios, on the other hand, the required efficiency
is generally much greater,
because of the relatively long cooling times involved. For example,
inelastic proton-proton scattering
producing 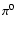 operates on a timescale of
operates on a timescale of
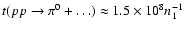 yrs
(
yrs
(
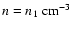 denotes the ambient medium density), which
is larger than the age of the accelerator, assuming this
is limited to the maximum time that massive stars
drive strong and fast stellar winds in their Wolf-Rayet phase
(this lasts approximately,
denotes the ambient medium density), which
is larger than the age of the accelerator, assuming this
is limited to the maximum time that massive stars
drive strong and fast stellar winds in their Wolf-Rayet phase
(this lasts approximately,
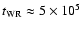 yrs, see also below).
This implies that, under most conditions, the efficiency required in
hadronic models is close or larger than unity.
A similar conclusion can be drawn for the case of gamma-ray production
through photo-excitation of heavy nuclei, where
the efficiency of acceleration of exclusively iron nuclei has to
reach values in excess of 8% (Anchordoqui et al. 2007a).
yrs, see also below).
This implies that, under most conditions, the efficiency required in
hadronic models is close or larger than unity.
A similar conclusion can be drawn for the case of gamma-ray production
through photo-excitation of heavy nuclei, where
the efficiency of acceleration of exclusively iron nuclei has to
reach values in excess of 8% (Anchordoqui et al. 2007a).
The electron distribution
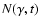 is computed for four different
times t=103, 104, 105, and 106 years. The synchrotron and inverse Compton
emissivities are calculated following the approach described in Appendix C,
and the resulting broad band spectral energy distribution (SED) is presented in Fig. 8. In addition to the UV photons from the early type stars, CMB photons are,
of course, also present with an energy density
is computed for four different
times t=103, 104, 105, and 106 years. The synchrotron and inverse Compton
emissivities are calculated following the approach described in Appendix C,
and the resulting broad band spectral energy distribution (SED) is presented in Fig. 8. In addition to the UV photons from the early type stars, CMB photons are,
of course, also present with an energy density
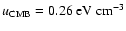 .
Although the energy loss due to inverse Compton scattering on these photons is negligible, they are nevertheless quite important for the total hard gamma-ray emission. This is because for sufficiently large
.
Although the energy loss due to inverse Compton scattering on these photons is negligible, they are nevertheless quite important for the total hard gamma-ray emission. This is because for sufficiently large 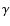 the inverse Compton scattering off UV photons is strongly suppressed,
leading to emissivities that are smaller than the contribution from scattering with CMB photons.
We therefore include the CMB photon field in the inverse Compton emissivity calculation and show in Fig. 8 the total inverse Compton emission as well as the contribution from UV
photons and from CMB photons. It is interesting to note how the inverse Compton emission from the CMB photons dominates for young sources. With increasing age, the UV-related component at about 1 TeV increases steadily until, after
the inverse Compton scattering off UV photons is strongly suppressed,
leading to emissivities that are smaller than the contribution from scattering with CMB photons.
We therefore include the CMB photon field in the inverse Compton emissivity calculation and show in Fig. 8 the total inverse Compton emission as well as the contribution from UV
photons and from CMB photons. It is interesting to note how the inverse Compton emission from the CMB photons dominates for young sources. With increasing age, the UV-related component at about 1 TeV increases steadily until, after  106 years - roughly the age of this stellar cluster - it exceeds the CMB-related contribution. This effect is due to the accumulation of electrons of Lorentz factor (
106 years - roughly the age of this stellar cluster - it exceeds the CMB-related contribution. This effect is due to the accumulation of electrons of Lorentz factor (
 )
within the source (see Fig. 5).
)
within the source (see Fig. 5).
The model SED is compared in Fig. 8 with VHE measurements (Aharonian et al. 2007) and with X-ray measurements by Townsley et al. (2005) taken with Chandra (indicated as a lower
limit) and earlier measurements taken with the Einstein X-ray telescope (Goldwurm et al. 1987; indicated as an upper limit). While the limited field of view of the Chandra observations
may underestimate the total extended X-ray emission, the Einstein observations may overestimate the diffuse flux, because of the limited spatial resolution that does not allow the
subtraction of the point sources present. In this figure we also show
the total integrated radio flux of 210 Jy at 843 MHz. This we consider as an upper limit that should not be exceeded by the non-thermal radio flux produced by the energetic electrons
(Whiteoak & Uchida 1997). Overall, the model SED is in good agreement with the observations. The
VHE energy spectrum is reproduced well for t>105 years, and the constraints from
X-ray and radio measurements are not violated. It is interesting to note
that, for stars with
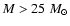 ,
the Wolf-Rayet phase is expected to
last up to roughly
,
the Wolf-Rayet phase is expected to
last up to roughly
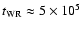 years (Maeder & Meynet 1987), which is consistent with the injection time required to match the data in this model. In contrast, an age of t>105 yrs would be too long for acceleration in a supernova remnant, a hypothesis that also has to contend with the fact that, so far, no indication for the presence of a supernova remnant associated with Wd-2 has been reported.
years (Maeder & Meynet 1987), which is consistent with the injection time required to match the data in this model. In contrast, an age of t>105 yrs would be too long for acceleration in a supernova remnant, a hypothesis that also has to contend with the fact that, so far, no indication for the presence of a supernova remnant associated with Wd-2 has been reported.
The predicted X-ray flux is quite close to the upper bound imposed by the Einstein
measurements. However, it should be noted that this prediction is sensitive to the energy density in the target photon field - a factor of 2 increase in the energy density in the seed-photon field (either from the late type stars and/or emission from dust) reduces the required injection
power and, consequently, the predicted X-ray flux is also reduced
by a factor of 2. We also indicate the one year
flux sensitivity of the upcoming GLAST gamma-ray
mission![[*]](/icons/foot_motif.gif) in Fig. 8.
Our calculations predict that GLAST
should detect the source easily. The combined energy spectrum of
GLAST and HESS would provide a broad band energy spectrum that in
turn might allow one to infer, for example, the age of the source in the model
scenario suggested here.
in Fig. 8.
Our calculations predict that GLAST
should detect the source easily. The combined energy spectrum of
GLAST and HESS would provide a broad band energy spectrum that in
turn might allow one to infer, for example, the age of the source in the model
scenario suggested here.
5 Conclusions
We have presented a method for computing the time-dependent electron
distribution in the continuous energy loss limit
for an arbitrary source
function, under the assumptions of
-
an isotropic electron distribution;
-
negligible ionisation and
Bremsstrahlung losses;
-
time-independent energy losses by
synchrotron radiation in a homogeneous
magnetic field and
-
by inverse Compton scattering off
a spatially
homogeneous mono-energetic or power-law energy
distribution of target photons;
-
an escape probability proportional to the particle energy,
as expected for diffusion in the Bohm limit.
The key innovation of the model is that it utilises
a simplified expression introduced by Moderski et al. (2005b)
for the inverse Compton scattering rate (including KN-effects) to
construct explicit analytic expressions (see Appendix A)
for the integrated cooling time
(
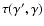 ,
Eq. (2))
and the integrated escape function
(
,
Eq. (2))
and the integrated escape function
(
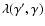 ,
Eq. (3)). This enables
the electron distribution to be computed in a single quadrature.
,
Eq. (3)). This enables
the electron distribution to be computed in a single quadrature.
The extension of this approach to different energy dependencies of
the escape probability would be relatively straightforward. However,
the treatment of multiple and/or time-dependent target photon fields
would probably require numerical evaluation of the functions
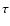 and
and 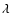 .
.
Based upon the method presented here, we have provided an
in-depth discussion of the
properties of cooling electron distributions and have identified
features characteristic of cooling by inverse Compton scattering:
- 1.
- The effect of spectral ageing observed in the Thomson limit
is strongly modified. While a well-defined
spectral break
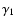 changes position with time in the Thomson limit (cooling
break), this spectral break is no longer evident for
changes position with time in the Thomson limit (cooling
break), this spectral break is no longer evident for
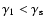 ,
when KN effects are taken into account
(see Fig. 4).
,
when KN effects are taken into account
(see Fig. 4).
- 2.
- For
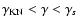 ,
a spectral hardening is
observed as a result of cooling in the KN regime (see
Figs. 2 and 4).
,
a spectral hardening is
observed as a result of cooling in the KN regime (see
Figs. 2 and 4).
- 3.
- When choosing
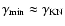 ,
the evolved
spectrum shows a smooth transition at
,
the evolved
spectrum shows a smooth transition at
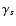 resembling a
cooling break. However, this transition is stationary in time and
may be mistakenly interpreted as a cooling break (see
e.g. Figs. 5, 6).
resembling a
cooling break. However, this transition is stationary in time and
may be mistakenly interpreted as a cooling break (see
e.g. Figs. 5, 6).
- 4.
- The effect of particle escape modifies the observed energy
spectra more strong for
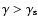 than for lower values of
than for lower values of
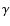 ,
which can lead to energy spectra resembling the ones
obtained in the Thomson limit more (see Fig. 7).
,
which can lead to energy spectra resembling the ones
obtained in the Thomson limit more (see Fig. 7).
We have illustrated our technique by applying it to high-energy
observations of the open stellar cluster Westerlund 2, and calculating
the broad band emission spectrum. Comparing our results with the
available observations, we identified a consistent set of parameters:
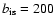 ,
,
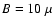 G, T=30 000 K, total injected power in
electrons
G, T=30 000 K, total injected power in
electrons
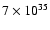 erg s-1, distance = 2.8 kpc,
R=8.8 pc,
erg s-1, distance = 2.8 kpc,
R=8.8 pc,
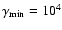 ,
,
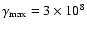 ,
p=2. Although the
uncertainty on the distance affects the values of some parameters
(e.g.
,
p=2. Although the
uncertainty on the distance affects the values of some parameters
(e.g.
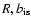 ,
and total power), it is interesting to note that the
suggested model of an electron accelerator embedded in the intense
stellar radiation field, which has been injecting a power-law type
spectrum for the past few 105 yrs, can naturally account for the
observed gamma-ray spectrum, without violating the constraints derived
from X-ray and radio observations.
Furthermore, the rather long injection time
favours acceleration in stellar winds of, for example, Wolf-Rayet stars
over acceleration in supernova remnants. A leptonic scenario of gamma-ray
production requires only a moderate fraction (
,
and total power), it is interesting to note that the
suggested model of an electron accelerator embedded in the intense
stellar radiation field, which has been injecting a power-law type
spectrum for the past few 105 yrs, can naturally account for the
observed gamma-ray spectrum, without violating the constraints derived
from X-ray and radio observations.
Furthermore, the rather long injection time
favours acceleration in stellar winds of, for example, Wolf-Rayet stars
over acceleration in supernova remnants. A leptonic scenario of gamma-ray
production requires only a moderate fraction ( 1%)
of the kinetic power of the stellar winds to be channelled into the
acceleration of a non-thermal particle population. Hadronic models, on the other hand, need a rather high ambient gas density in order to keep the required efficiency below unity.
The model presented here can be improved further by including a more realistic mixture of different temperature photon fields with different spatial extensions as observed in the
vicinity of Wd-2 (including a dust component and later-type stars
present in the system). However, it already allows order of magnitude predictions of the flux to be tested in a range accessible to the GLAST experiment.
1%)
of the kinetic power of the stellar winds to be channelled into the
acceleration of a non-thermal particle population. Hadronic models, on the other hand, need a rather high ambient gas density in order to keep the required efficiency below unity.
The model presented here can be improved further by including a more realistic mixture of different temperature photon fields with different spatial extensions as observed in the
vicinity of Wd-2 (including a dust component and later-type stars
present in the system). However, it already allows order of magnitude predictions of the flux to be tested in a range accessible to the GLAST experiment.
Acknowledgements
D.H. and K.M. acknowledge the support of the Eberhard Karls Universität
Tübingen. This research has made use of NASA's Astrophysics Data System.
Appendix A: Characteristic cooling and escape functions
The integrals in Eqs. (23) and (24)
can be rewritten as
and
where the indefinite integrals
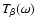 and
and
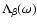 can be expressed in terms of elementary functions
for (negative) integer and half-integer values of
can be expressed in terms of elementary functions
for (negative) integer and half-integer values of 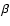 .
.
In the case of black-body target photons, as well as
for power-law photons with index
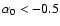 ,
and
,
and
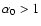 ,
one has
,
one has
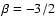 and finds
for
and finds
for
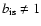 :
:
where
And for
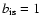 ,
,
For the indefinite integral
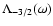 ,
one finds for
,
one finds for
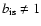
where
and, for
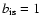 :
:
In the case of a power-law distribution of target photons with
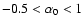 ,
closed-form expressions of the integrals can be
found for the special cases
,
closed-form expressions of the integrals can be
found for the special cases
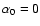 and
and
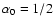 ,
corresponding to
,
corresponding to 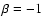 and
and
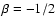 ,
respectively. For
,
respectively. For 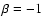 ,
,
whereas for
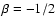 one has for
one has for
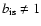
where
and, for
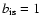 :
:
Similarly, for the function
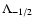 we find, for
we find, for
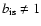 :
:
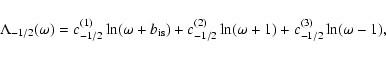 |
(A.11) |
where
And, finally, for
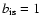 :
:
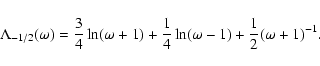 |
(A.12) |
Appendix B
For the case where accelerated particles start to inject from the central source at time t0 with a power-law
type finite energy spectrum:
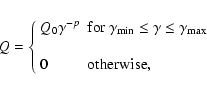 |
(B.1) |
undergoing synchrotron and inverse Compton losses in the Thomson regime,
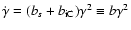 ,
and escaping from the system (with radius R) at a rate
,
and escaping from the system (with radius R) at a rate
 (see Sect. 2.2), the solution of Eq. (1) splits into two branches, depending on whether the maximum injected energy,
(see Sect. 2.2), the solution of Eq. (1) splits into two branches, depending on whether the maximum injected energy,
 ,
has had enough time to "cool down'' to a value
,
has had enough time to "cool down'' to a value  lower or higher than the minimum injected energy,
lower or higher than the minimum injected energy,
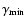 .
.
If
 ,
then the solution reads:
,
then the solution reads:
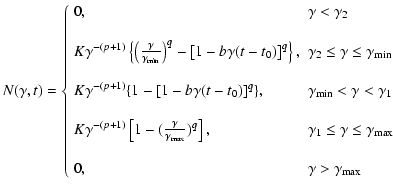 |
|
|
(B.2) |
If
 ,
one gets:
,
one gets:
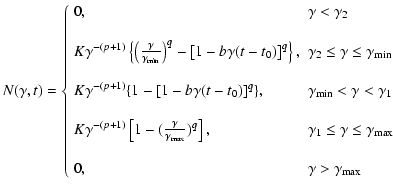 |
|
|
(B.3) |
where
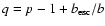 ,
K=Q0/ bq,
,
K=Q0/ bq,
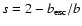 and the values of
and the values of 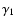 and
and 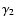 are given by Eqs. (14) and (15), respectively.
are given by Eqs. (14) and (15), respectively.
Appendix C: Inverse Compton and synchrotron emissivities
The spectrum of photons scattered by an energetic electron from an isotropic photon
gas that follows a differential photon number density
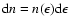 was
derived e.g. by Blumenthal & Gould (1970) in the head-on collision approximation and is given by their
Eq. (2.48):
was
derived e.g. by Blumenthal & Gould (1970) in the head-on collision approximation and is given by their
Eq. (2.48):
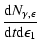 = = 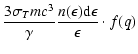 |
(C.1) |
with
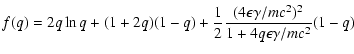 |
|
|
(C.2) |
and
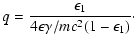 |
|
|
(C.3) |
The total inverse Compton spectrum from a distribution of electrons d
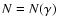 d
d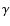 follows from the integration
over
follows from the integration
over 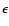 and
and 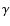 :
:
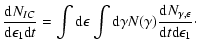 |
|
|
(C.4) |
The emitted synchrotron power per unit frequency interval emitted by a single electron
with pitch angle 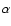 and magnetic field B is given e.g. by Ginzburg & Syrovatskii (1964)
and magnetic field B is given e.g. by Ginzburg & Syrovatskii (1964)
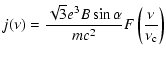 |
|
|
(C.5) |
with the critical frequency
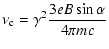 |
|
|
(C.6) |
and
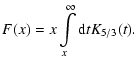 |
|
|
(C.7) |
A simple approximation of F(x) was used for the calculations presented in this paper
(see e.g. Melrose 1980):
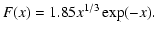 |
|
|
(C.8) |
This approximation provides a relative accuracy that is better than 1 per cent in the region
of the maximum at
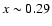 and still reasonable accuracy in the broad range of
and still reasonable accuracy in the broad range of
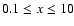 .
The luminosity-per-unit-frequency interval from an electron distribution
.
The luminosity-per-unit-frequency interval from an electron distribution
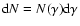 is
calculated by integration over
is
calculated by integration over 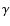 :
:
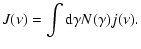 |
|
|
(C.9) |
We assume an isotropic magnetic field such that
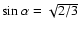 .
.
- Abdo, A. A.,
Allen, B., Berley, D., et al. 2007, ApJ, 658, L33 [NASA ADS] [CrossRef] (In the text)
- Aharonian, F.,
Akhperjanian, A., Beilicke, M., et al. 2002, A&A, 393,
L37 [NASA ADS] [CrossRef] [EDP Sciences]
- Aharonian, F.,
Akhperjanian, A., Beilicke, M., et al. 2005a, A&A, 431,
197 [NASA ADS] [CrossRef] [EDP Sciences]
- Aharonian, F.,
Akhperjanian, A. G., Aye, K.-M., et al. 2005b, Science,
309, 746 [NASA ADS] [CrossRef] (In the text)
- Aharonian, F.,
Akhperjanian, A. G., Aye, K.-M., et al. 2005c, A&A,
442, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Aharonian, F.,
Akhperjanian, A. G., Bazer-Bachi, A. R., et al.
2007, A&A, 467, 1075 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Albert, J., Aliu, E.,
Anderhub, H., et al. 2006, Science, 312, 1771 [NASA ADS] [CrossRef] (In the text)
- Anchordoqui,
L. A., Beacom, J. F., Butt, Y. M., et al.
2007a, ArXiv e-prints, 706
(In the text)
- Anchordoqui,
L. A., Beacom, J. F., Goldberg, H., Palomares-Ruiz, S.,
& Weiler, T. J. 2007b, Phys. Rev. Lett., 98, 121101 [NASA ADS] [CrossRef] (In the text)
- Ascenso, J., Alves,
J., Beletsky, Y., & Lago, M. T. V. T. 2007,
A&A, 466, 137 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bednarek, W. 2007,
ArXiv e-prints, 704
- Blumenthal, G. R.
1971, Phys. Rev. D, 3, 2308 [NASA ADS] [CrossRef]
- Blumenthal,
G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42,
237 [NASA ADS] [CrossRef]
- Churchwell, E.,
Whitney, B. A., Babler, B. L., et al. 2004, ApJS,
154, 322 [NASA ADS] [CrossRef] (In the text)
- Coppi, P. S.
1992, MNRAS, 258, 657 [NASA ADS]
- Dame, T. M. 2007,
ArXiv e-prints, 707
(In the text)
- Dermer, C. D.,
& Atoyan, A. M. 2002, ApJ, 568, L81 [NASA ADS] [CrossRef]
- Felten, J. E.,
& Morrison, P. 1966, ApJ, 146, 686 [NASA ADS] [CrossRef]
- Ginzburg, V. L.,
& Syrovatskii, S. I. 1964, The Origin of Cosmic Rays (New
York: Macmillan, 1964)
- Goldwurm, A., Caraveo,
P. A., & Bignami, G. F. 1987, ApJ, 322, 349 [NASA ADS] [CrossRef]
- Hinton, J. A.,
& Aharonian, F. A. 2007, ApJ, 657, 302 [NASA ADS] [CrossRef]
- Horns, D., Hoffmann,
A. I. D., Santangelo, A., Aharonian, F. A., &
Rowell, G. P. 2007, A&A, 469, L17 [NASA ADS] [CrossRef] [EDP Sciences]
- Jones, F. C.
1965, Phys. Rev., 137, 1306 [NASA ADS] [CrossRef] (In the text)
- Kardashev, N. S.
1962, AZh, 39, 393 [NASA ADS] (In the text)
- Katarzynski, K.,
Ghisellini, G., Svensson, R., & Gracia, J. 2006, A&A, 451,
739 [NASA ADS] [CrossRef] [EDP Sciences]
- Khangulyan, D.,
Hnatic, S., & Aharonian, F. 2007, Ap&SS, 212
- Kirk, J. G.,
Ball, L., & Skjaeraasen, O. 1999, Astropart. Phys., 10, 31 [NASA ADS] [CrossRef]
- Krawczynski, H.,
Coppi, P. S., & Aharonian, F. 2002, MNRAS, 336, 721 [NASA ADS]
- Kusunose, M., &
Takahara, F. 2005, ApJ, 621, 285 [NASA ADS] [CrossRef]
- Lightman, A. P.,
& Zdziarski, A. A. 1987, ApJ, 319, 643 [NASA ADS] [CrossRef]
- Maeder, A., &
Meynet, G. 1987, A&A, 182, 243 [NASA ADS] (In the text)
- Mastichiadis, A.
& Kirk, J. G. 1997, A&A, 320, 19 [NASA ADS]
- Melrose, D. B.
1980, Plasma astrophysics: Nonthermal processes in diffuse
magnetized plasmas, Astrophysical applications (New York, Gordon
and Breach Science Publishers), 2, 430
(In the text)
- Moderski, R., Sikora,
M., Coppi, P. S., & Aharonian, F. 2005a, MNRAS, 364,
1488 [NASA ADS] (In the text)
- Moderski, R., Sikora,
M., Coppi, P. S., & Aharonian, F. 2005b, MNRAS, 363,
954 [NASA ADS]
- Murata, K., Tamaki,
H., Maki, H., & Shibazaki, N. 2003, PASJ, 55, 473 [NASA ADS]
- Neronov, A., &
Chernyakova, M. 2006, ArXiv Astrophysics e-prints
- Rauw, G., Manfroid,
J., Gosset, E., et al. 2007, A&A, 463, 981 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stawarz, L. &
Kirk, J. G. 2007, ApJ, 661, L17 [NASA ADS] [CrossRef]
- Sturner, S. J.,
Skibo, J. G., Dermer, C. D., & Mattox, J. R.
1997, ApJ, 490, 619 [NASA ADS] [CrossRef]
- Tang, S., & Wang,
Q. D. 2005, ApJ, 628, 205 [NASA ADS] [CrossRef] (In the text)
- Torres, D. F.,
Domingo-Santamaría, E., & Romero, G. E. 2004, ApJ,
601, L75 [NASA ADS] [CrossRef]
- Townsley, L.,
Feigelson, E., Montmerle, T., et al. 2005, in X-Ray and Radio
Connections, ed. L. O. Sjouwerman & K. K Dyer, published
electronically by NRAO, http://www.aoc.nrao.edu/events/xraydio,
held 3-6 February 2004 in Santa Fe, New Mexico, USA
- Völk, H. J.
2006, in IAU Symp. 230, Populations of High Energy Sources in
Galaxies, ed. E. J. A. Meurs & G. Fabbiano,
95
(In the text)
- Whiteoak,
J. B. Z., & Uchida, K. I. 1997, A&A, 317,
563 [NASA ADS] (In the text)
- Zdziarski, A. A.
1989, ApJ, 342, 1108 [NASA ADS] [CrossRef]
Copyright ESO 2007
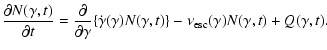
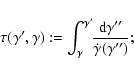
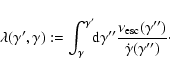
![$\displaystyle N(\gamma, t)~=~\frac{1}{\dot{\gamma}(\gamma)}\;\;\int_\gamma^\inf...
...ight]
\!+\! N(\gamma',0)\delta\left(t-\tau(\gamma',\gamma)\right)\right\rbrace,$](/articles/aa/full/2007/42/aa8298-07/img48.gif)
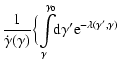
![$\displaystyle \frac{1}{\dot{\gamma}(\gamma)}
\int\limits_\gamma^{\infty}\!\!{\r...
...rm{e}^{-\lambda(\gamma',\gamma)}
Q \bigl[\gamma',t-\tau(\gamma',\gamma)\bigr]
,$](/articles/aa/full/2007/42/aa8298-07/img62.gif)
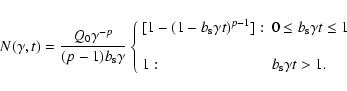
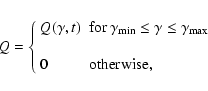
![$\displaystyle \frac{1}{\dot{\gamma}(\gamma)}\;\;\int\limits_{\gamma_l}^{\gamma_...
...\bigl[\gamma',t-\tau(\gamma',\gamma)\bigr]H \bigl[t-\tau(\gamma',\gamma)\bigr],$](/articles/aa/full/2007/42/aa8298-07/img81.gif)
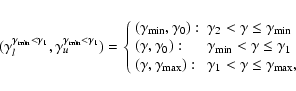
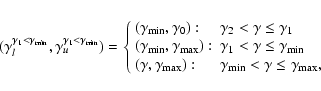
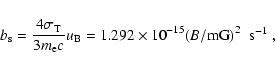
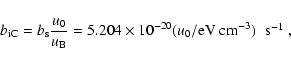
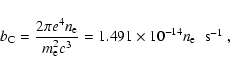
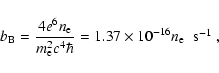
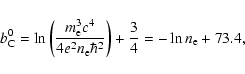
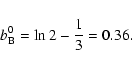
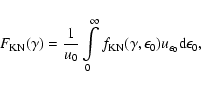
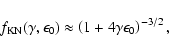
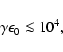
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig1.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg131.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig2.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg133.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm]{8298fig3a.eps}\includegraphics[width=8.6cm]{8298fig3b.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg134.gif)
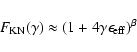
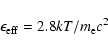
![\begin{displaymath}\dot{\gamma}=b_{\rm s}\gamma^2\left[1+b_{\rm is}F_{\rm KN}(\gamma)\right],
\end{displaymath}](/articles/aa/full/2007/42/aa8298-07/img161.gif)
![\begin{displaymath}\dot{\gamma}=b_{\rm s}\gamma^2\left[1+b_{\rm is}
\left(1+4\gamma\epsilon_{\rm eff}\right)^\beta\right],
\end{displaymath}](/articles/aa/full/2007/42/aa8298-07/img163.gif)
![$\displaystyle \int_\gamma^{\gamma'}\!\!\frac{{\rm d}\gamma''}{b_{\rm s} {\gamma''}^2
\left[1+b_{\rm is}\left(1+4\gamma''\epsilon_{\rm eff}\right)^{\beta}\right]}$](/articles/aa/full/2007/42/aa8298-07/img165.gif)
![$\displaystyle \int_\gamma^{\gamma'}\!\!\frac{b_{\rm es} {\rm d}\gamma''}
{\gamma''\left[1+b_{\rm is}\left(1+4\gamma''\epsilon_{\rm eff}\right)^{\beta}\right]}$](/articles/aa/full/2007/42/aa8298-07/img167.gif)
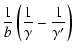
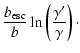
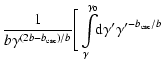
![$\displaystyle \times%
Q \left(\gamma',t-\frac{1}{b\gamma}+\frac{1}{b\gamma'}\right)
H \left(t-\frac{1}{b\gamma}+\frac{1}{b\gamma'}\right)\Bigg]$](/articles/aa/full/2007/42/aa8298-07/img184.gif)
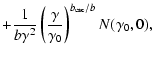
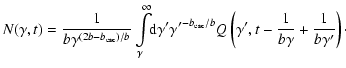
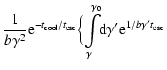
![$\displaystyle N(\gamma, t) =
\frac{1}{b \gamma^2} \textrm{e}^{-t_{\rm cool}/t_{...
...a't_{\rm esc}}
Q \bigl[\gamma',t-(b\gamma)^{-1}+(b\gamma')^{-1}\bigr]
\enspace,$](/articles/aa/full/2007/42/aa8298-07/img196.gif)
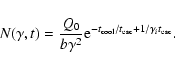
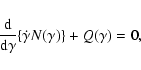
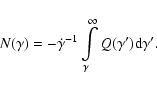
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig4.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg234.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig5.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg235.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig6.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg236.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig7.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg237.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{8298fig8.eps}
\end{figure}](/articles/aa/full/2007/42/aa8298-07/Timg246.gif)