![\begin{figure}
\par\includegraphics[width=8cm,clip]{7811fig1.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg3.gif) |
Figure 1: Jansky and his telescope (Sullivan 1978). |
| Open with DEXTER | |
A&A 474, 679-687 (2007)
DOI: 10.1051/0004-6361:20077811
J. G. Mangum1 - D. T. Emerson2 - E. W. Greisen3
1 - National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903, USA
2 - National Radio Astronomy Observatory, 949 North Cherry
Avenue, Tucson, AZ 85721, USA
3 -
National Radio Astronomy Observatory, PO Box O, 1003
Lopezville Road, Socorro, NM 87801, USA
Received 8 May 2007 / Accepted 31 August 2007
Abstract
Aims. The On-The-Fly (OTF) imaging technique enables single-dish radio telescopes to construct images of small areas of the sky with greater efficiency and accuracy.
Methods. This paper describes the practical application of the OTF imaging technique. By way of example the implementation of the OTF imaging technique at the NRAO 12 Meter Telescope is described.
Results. Specific requirements for data sampling, image formation, and Doppler correction are discussed.
Key words: telescopes - methods: observational - radio continuum: general - radio lines: general
In an effort to become scientifically more efficient, astronomical observatories have incorporated innovative observing techniques to increase the throughput of their telescopes. The On-The-Fly (OTF) imaging technique is an innovation which has been adopted at a number of radio observatories over the past forty years in a variety of forms. In the 1960's and 1970's, radio observatories which operate at centimeter wavelengths implemented the "drift scanning'' technique (sometimes referred to as "nodding'') to acquire continuum imaging measurements (cf. Haslam et al. 1970). Drift scanned measurements are obtained by slowly slewing the telescope in elevation with the Earth's rotation providing the second dimension. In the 1980's, a number of radio telescopes added beam-switched continuum imaging capabilities. Beam-switched continuum observations are acquired by slewing the telescope in a two-dimensional raster pattern over a given region of sky while rapidly wobbling the telescope's subreflector to obtain differential measurements of the total power. The Emerson et al. (1979) [EKH] algorithm allowed the deconvolution of these beam-switched measurements into total power images. This powerful imaging capability added considerably to our ability to understand the centimeter- and millimeter-wave continuum structure of the interstellar medium. In the 1990s a number of radio observatories implemented both spectral line and continuum OTF imaging capabilities (cf. Mangum 1999; Mangum et al. 2000).
As with many innovations, this "new'' OTF imaging technique was just an adaptation of an old observing technique. The observations which signaled the birth of radio astronomy, made by Karl Jansky in 1932, were actually OTF observations (see Janksy 1932; and Fig. 1). Jansky's 20.5 MHz synchrotron measurements of the galactic center represent the first astronomical OTF observations. In the following, we describe the adaptation of Jansky's imaging technique to total power images obtained using a single dish telescope.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7811fig1.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg3.gif) |
Figure 1: Jansky and his telescope (Sullivan 1978). |
| Open with DEXTER | |
OTF mapping is an observing technique in which the telescope is driven smoothly and rapidly across a region of sky, or "field'', while data and antenna position information are recorded continuously. This technique is in contrast to traditional mapping of discrete positions on the sky, which is sometimes called "step-and-integrate'' or "point-and-shoot'' mapping. The advantages to OTF mapping are:
where ![]() is the rms noise in a total power measurement,
is the rms noise in a total power measurement,
![]() is the system noise temperature,
is the system noise temperature, ![]() is the spectral
resolution of the measurement, and
is the spectral
resolution of the measurement, and
![]() is the spectrometer
efficiency. The optimum duration of an OFF measurement for any switched
measurement is given by (Ball 1976)
is the spectrometer
efficiency. The optimum duration of an OFF measurement for any switched
measurement is given by (Ball 1976)
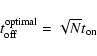 |
(2) |
![\begin{displaymath}\sigma = \frac{T_{\rm sys}}{\eta_{\rm spec}\sqrt{\Delta\nu t_{\rm scan}}}\left[1 + \frac{1}{\sqrt{N}}\right]
\end{displaymath}](/articles/aa/full/2007/41/aa7811-07/img11.gif) |
(3) |
When conducting single dish imaging observations, it is important to
keep in mind the following facts about sampling and aliasing in radio
astronomical mapping data. If you want to represent the full
resolution of the telescope, you have to sample the data often enough
to represent all the spatial frequencies detected by the antenna.
Figure 2 illustrates a typical continuum detection
scheme of a single dish telescope; this is the simplest case, but the
same principles apply to detection in a spectrometer, or even direct
digitization at the IF and subsequent processing by software or
firmware. In the example shown, the radio astronomical signal is
amplified and bandpass filtered, before passing into a square law
detector, possibly some simple filtering, and then into an
Analog-to-Digital (A/D) converter. The A/D converter, or later
processing, usually incorporates some signal integration before
delivering the sampled data.
| |
Figure 2: Typical continuum detection scheme for a single dish telescope. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7811fig3.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg15.gif) |
Figure 3: Illustration of the low-frequency spectral response of the signal and noise after square law detection. |
| Open with DEXTER | |
Figure 3 illustrates the low frequency
spectrum of the signal and noise immediately after the square law
detector and in the subsequent processing steps. With the antenna
scanning at a constant speed over a point source, its response
produces, after the detector, a time-varying signal whose spectrum
corresponds to the spatial frequency response of the antenna. The
horizontal axis of Fig. 3 could be spatial
frequency, measured in units proportional to
![]() (d is a baseline distance), or the frequency after the detector measured
in Hz. Any antenna has a spatial frequency cut-off; with an antenna
of diameter D and scanning speed of
(d is a baseline distance), or the frequency after the detector measured
in Hz. Any antenna has a spatial frequency cut-off; with an antenna
of diameter D and scanning speed of ![]() radians/second, after the
detector the signal voltage will have a cut-off frequency of
radians/second, after the
detector the signal voltage will have a cut-off frequency of
![]() ,
now measured in Hz. This is
illustrated by the bold curve in Fig. 3.
The signal cut-off frequency is shown by the vertical dashed line.
,
now measured in Hz. This is
illustrated by the bold curve in Fig. 3.
The signal cut-off frequency is shown by the vertical dashed line.
Figure 3 also shows the spectrum of noise (the dashed line) immediately after the detector; this is strictly the autocorrelation function of the IF passband, which means in practice that within the narrow range of post-detection frequencies of interest, it is white noise, with a flat spectrum. It is normal to include a simple low pass filter immediately after the detector, shown symbolically by the RC time constant in Fig. 2. This might have a gentle frequency cut-off such as illustrated by the dash-dot line of Fig. 3.
The digitizer usually includes some time integration as part of its
operation; the output samples might be sampled S times per second, but
each sample is an integration of
![]() seconds of data. This
integration is equivalent to convolving the time sequence of data with
a square-box function - equivalent also to convolving the sky image
along the scanning direction by the corresponding square-box function.
The integration of S seconds by this square-box translates into an
average of
seconds of data. This
integration is equivalent to convolving the time sequence of data with
a square-box function - equivalent also to convolving the sky image
along the scanning direction by the corresponding square-box function.
The integration of S seconds by this square-box translates into an
average of ![]() radians of angle along the sky scanning track.
The time-domain spectral response, or equivalently the spatial
frequency response, of this square-box integration is illustrated in
Fig. 3 for the case where the signal is
exactly Nyquist sampled (two independent samples per
radians of angle along the sky scanning track.
The time-domain spectral response, or equivalently the spatial
frequency response, of this square-box integration is illustrated in
Fig. 3 for the case where the signal is
exactly Nyquist sampled (two independent samples per
![]() interval on the sky).
interval on the sky).
The ideal signal processing and detection scheme might use a perfect square-edged anti-aliasing filter in place of the simple RC-filter illustrated in Fig. 2, followed by a sampler operating at least at twice the spatial frequency cut-off, with an infinitely narrow window in the sampler, thereby avoiding the loss of high frequencies caused by the normal square box integration. However, to avoid the complexities (and impossibility) of building a perfect anti-aliasing filter, very often in practice the square-box integration is retained, but with a substantial increase in the sample rate above the Nyquist value.
The spectrum of noise and of signal at the output of the detector of a total power system depends on the details of the electronic design, but a representative system is illustrated in Figs. 2 and 3.
With OTF observing, the astronomical sky is convolved with the
telescope beamshape. The telescope acts also as a low pass filter,
removing all astronomical components beyond the intrinsic angular
resolution of the antenna. The telescope beam and telescope scanning
speed together give a low pass filter, with the conversion from
spatial frequency to temporal frequencies being given by
The minimum sampling interval on the sky, for an antenna with maximum
dimension D, is at intervals of
![]() .
Assume that
one undersamples on the sky, rather than later in the data
processing. Suppose you have a 10 m dish, but you only sample at
.
Assume that
one undersamples on the sky, rather than later in the data
processing. Suppose you have a 10 m dish, but you only sample at
![]() m) rather than the
m) rather than the
![]() m)
that you should. This means that the spatial frequencies
present from the dish baselines of 8 m to 10 m get reflected back
into the spatial frequencies of 8 m down to 6 m. Not only have spatial
frequencies from the 8 m to 10 m baselines been lost, but valid spatial
frequencies from baselines of 6 m to 8 m have been corrupted. You can't
tell if structure in your map with a spatial wavelength of
m)
that you should. This means that the spatial frequencies
present from the dish baselines of 8 m to 10 m get reflected back
into the spatial frequencies of 8 m down to 6 m. Not only have spatial
frequencies from the 8 m to 10 m baselines been lost, but valid spatial
frequencies from baselines of 6 m to 8 m have been corrupted. You can't
tell if structure in your map with a spatial wavelength of
![]() m is genuine, or was really structure at
m is genuine, or was really structure at
![]() m which has been aliased on top of any genuine
m which has been aliased on top of any genuine
![]() m spatial wavelength signal. In this sense,
undersampling the sky is really twice as bad as you might have thought.
m spatial wavelength signal. In this sense,
undersampling the sky is really twice as bad as you might have thought.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{7811fig4.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg28.gif) |
Figure 4: Spatial frequency response for square box Nyquist sampling. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[angle=-90,width=8cm,clip]{7811fig5.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg29.gif) |
Figure 5: Aliased noise power for square box Nyquist sampling in the absence of a separate anti-aliasing filter. |
| Open with DEXTER | |
Figures 4 and 5 show the spatial
frequency response and aliased noise power for Nyquist sampling while
using a square box sampling function, of width equal to the sampling
interval. The power Ps in the random noise fluctuations in
frequencies up to the properly sampled spatial frequency, indicated by
the vertical dashed line at 0.5 on the abscissa of
Fig. 4, is proportional to:
The noise power degradation due to sampling is a function of the level of oversampling in the image plane. Figure 6 shows the amount of signal-to-noise degradation one can expect due to noise aliasing of an inadequately sampled signal using square box sampling.
![\begin{figure}
\par\includegraphics[angle=-90,width=6.6cm,clip]{7811fig6.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg33.gif) |
Figure 6: Signal-to-noise degradation due to noise aliasing of an inadequately sampled image using square box sampling. |
| Open with DEXTER | |
How important undersampling is depends on exactly what the
illumination taper is, how
important it is that you retain the maximum possible resolution of the
telescope, how good a dynamic range you want in the observations, and
at some level how much fine scale structure there is in the source itself.
If you only sample at 0.833 Nyquist (e.g. FWHM/2 rather than
FWHM/2.4 for a -13 dB illumination taper), what matters is the
energy in the data at spatial wavelengths shorter than
![]() .
So in
a sense you need to ask what the illumination taper is at a radius of
.
So in
a sense you need to ask what the illumination taper is at a radius of
![]() on the dish surface. The spatial frequency
response of a single dish is the autocorrelation function of the
voltage illumination pattern. So, you need to calculate how much
area there is under the 2-D autocorrelation function beyond spatial
frequencies of
on the dish surface. The spatial frequency
response of a single dish is the autocorrelation function of the
voltage illumination pattern. So, you need to calculate how much
area there is under the 2-D autocorrelation function beyond spatial
frequencies of
![]() ,
compared to the area within
,
compared to the area within
![]() .
This ratio is some measure of the dynamic range. A better
definition of dynamic range might take into account the spatial
frequency structure of the source. If the source has no structure on
scales smaller than
.
This ratio is some measure of the dynamic range. A better
definition of dynamic range might take into account the spatial
frequency structure of the source. If the source has no structure on
scales smaller than
![]() ,
then you
don't need to sample at the full
,
then you
don't need to sample at the full
![]() anyway.
anyway.
There are circumstances where it is perfectly rigorous to undersample the
data in the absence of a separate anti-aliasing filter. For example,
if you have a 10 m dish, and you are taking data
to compare with other observations that were made using a 1 m dish at
the same wavelength (or the
equivalent number of wavelengths at some other frequency) then you only
need to sample the data at
![]() m) or
m) or
![]() m. This is so because, when
sampling a 10 m dish as if it were a 5.5 m dish, the spatial frequency
components from baselines of 5.5 m out to 10 m will be reflected back
into the data as if corresponding to baselines of 5.5 m down to 1 m.
So, the spatial frequency terms of the 1 m baseline and below will not
have been
corrupted. The data analysis of this undersampled data would apply a
spatial frequency cutoff at 1 m, and there will have been no corruption
in this smoothed data caused by the undersampling. Putting it in more general
terms, if you are going to be smoothing observations from a dish of
diameter D to simulate observations made with a smaller dish of
diameter d, then the sampling interval only needs to be
m. This is so because, when
sampling a 10 m dish as if it were a 5.5 m dish, the spatial frequency
components from baselines of 5.5 m out to 10 m will be reflected back
into the data as if corresponding to baselines of 5.5 m down to 1 m.
So, the spatial frequency terms of the 1 m baseline and below will not
have been
corrupted. The data analysis of this undersampled data would apply a
spatial frequency cutoff at 1 m, and there will have been no corruption
in this smoothed data caused by the undersampling. Putting it in more general
terms, if you are going to be smoothing observations from a dish of
diameter D to simulate observations made with a smaller dish of
diameter d, then the sampling interval only needs to be
![]() rather than
rather than
![]() .
.
Since the telescope beam is effectively convolved with a square-box function equal to the distance the telescope moves in one sample period, there is a degradation of spatial resolution due to the data acquisition process. If you set an arbitrary criterion that the telescope beam shouldn't be broadened by more than 1%, then you need to sample at least 4.5 points per FWHM beam width. Note that since Nyquist sampling is about 2.4 points per FWHM, assuming an illumination taper of about -13 dB; for a uniformly illuminated circular aperture the factor would be about 2.06, while for a -20 dB taper it becomes 2.60. This means that one needs to sample at about twice Nyquist to avoid degradation of resolution worse than 1%.
The final image is constructed by smoothing the data at whatever coordinates they were observed and then re-sampling them on a regular image grid. The smoothing is, in fact, an interpolation, which can include weighting and averaging, rather than a strict convolution. However, when the data are sampled in a dense and nearly uniform fashion, the interpolation approximates a convolution. Figure 7 shows some representative convolving functions which may be used in the data gridding. The effect of the convolution is best seen by examining its impact, a multiplication, in the Fourier, spatial frequency, space. The Fourier transforms of the convolving functions are illustrated in Fig. 8.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{7811fig7.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg41.gif) |
Figure 7: Representative convolution functions. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{7811fig8.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg42.gif) |
Figure 8: Representative Fourier transforms of convolution functions. |
| Open with DEXTER | |
The spatial frequency response pattern of the single dish is
effectively multiplied by the Fourier transform of the convolving
function. If the function were to have no effect on the data, then
its Fourier transform should have value 1.0 out to the maximum spatial
frequency of the telescope and 0.0 outside that radius.
This function is, in one dimension, a sinc function,
![]() and, in two dimensions, a Bessel
function
and, in two dimensions, a Bessel
function
![]() .
Unfortunately, both of
these functions
die off very slowly, making the convolution operation excessively
expensive. A compromise function is obtained by tapering the
convolution function by a fairly narrow Gaussian, allowing the
function to be truncated outside a restricted region. In the Fourier
space, this has the effect of reducing the response to the largest
spatial frequencies available to the telescope. These spatial
frequencies are probably already tapered by the response pattern of
the feed horn, which is usually designed to avoid sensitivity to
ground spillover.
.
Unfortunately, both of
these functions
die off very slowly, making the convolution operation excessively
expensive. A compromise function is obtained by tapering the
convolution function by a fairly narrow Gaussian, allowing the
function to be truncated outside a restricted region. In the Fourier
space, this has the effect of reducing the response to the largest
spatial frequencies available to the telescope. These spatial
frequencies are probably already tapered by the response pattern of
the feed horn, which is usually designed to avoid sensitivity to
ground spillover.
Since we have a circular telescope and are gridding the image in two
dimensions simultaneously, we use the circularly symmetric version of
the convolving function,
![]() .
Optimizations of this function give the default values for a, b, and cof a = 1.55 (single-dish-beam-size / 3), b = 2.52(single-dish-beam-size / 3), c = 2 (see Table 1), and
a support radius equal to the single-dish-beam-size (FWHM) (Schwab 1980).
.
Optimizations of this function give the default values for a, b, and cof a = 1.55 (single-dish-beam-size / 3), b = 2.52(single-dish-beam-size / 3), c = 2 (see Table 1), and
a support radius equal to the single-dish-beam-size (FWHM) (Schwab 1980).
Table 1: Convolution function factor.
It is important to choose the sampling of the output image, and the width and support of the convolving function to avoid aliasing. This topic was discussed at length in Sect. 3.2.1. A suitable cell size would be less than or equal to one-third of the single-dish-beam-size.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{7811fig9.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg52.gif) |
Figure 9: An example of a raster scanning pattern. In this example, three scanning rows are acquired per reference ("off'') measurement. |
| Open with DEXTER | |
Other convolving functions have various undesirable effects. For
example, a sinc2 has a triangular Fourier transform. All non-zero
spatial frequencies are weighted down linearly with frequency,
degrading the telescope resolution. All other positive-only functions
have a similar effect. One can construct convolving functions such
as
![]() which will actually improve the spatial resolution of the image over
that of the single-dish beam. They do this at the cost of
down-weighting low spatial frequencies and thereby reducing the
signal-to-noise of the observation (Greisen 1998).
which will actually improve the spatial resolution of the image over
that of the single-dish beam. They do this at the cost of
down-weighting low spatial frequencies and thereby reducing the
signal-to-noise of the observation (Greisen 1998).
The scanning geometry used to acquire an OTF map is usually dependent upon the type of source you are imaging and the ability to command the antenna to execute complex patterns. Scanning geometries that have been implemented at existing radio telescopes include:
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{7811fig10.eps}\end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg54.gif) |
Figure 10: An example of the spiral scanning pattern. |
| Open with DEXTER | |
| |
Figure 11: An example of the hypocycloid scanning pattern. |
| Open with DEXTER | |
It is often important to estimate the amount of integration time and the rms noise level an OTF image will have based on the observing parameters. In the following, we derive these quantities for a raster scanned OTF map. We also discuss an often overlooked aspect of wide-field spectroscopy involving the doppler correction.
In the following we describe some of the OTF map parameters that one must generally calculate in order to setup an OTF observation.
It is very important that you set up your map to be properly sampled in all coordinates. If you under sample, you will miss information in the image field, you will be unable to combine your image accurately with that from interferometers or other single-dish telescopes, and you may introduce artifacts from the analysis algorithms (see Sect. 3.2.1). Keep in mind that you can always smooth the map after it is taken to degrade the resolution and improve signal-to-noise.
The scanning rows must be spaced at no more than the Nyquist spacing,
which is also known as "critical sampling'' and is given by
where the factor of 0.9 is an oversampling factor and the
factor of ![]() is a guard band to accommodate any
scanning errors. For the NRAO 12M Telescope
is a guard band to accommodate any
scanning errors. For the NRAO 12M Telescope
![]() was used.
Figure 12 is a plot of this relationship assuming a 12 m
aperture.
was used.
Figure 12 is a plot of this relationship assuming a 12 m
aperture.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm]{7811fig12.eps} \end{figure}](/articles/aa/full/2007/41/aa7811-07/Timg66.gif) |
Figure 12:
|
| Open with DEXTER | |
Map sampling along the scanning direction is dependent upon the
integration (or "dump'') time of the data acquisition system (i.e. spectrometer) being used. Since the spectrometers must integrate for
a finite interval before being dumped, the data are "square-box''
binned. To avoid noise aliasing and beam-smearing problems due to
this binning (see Sect. 3.2.1), one needs to oversample in the
scanning direction. The scan rate may be written as
When planning an OTF observing run you must calculate
how much integration time you need for each sampling cell to
reach the desired signal-to-noise level. First determine
the integration time required using the standard Radiometer
Equation (Eq. (1))
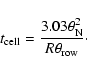 |
(19) |
Again assuming a raster scanning geometry, the total time required to
acquire a map must include not only the integration time scanning
across the field but also the time for calibration and OFF
integrations. This can be written as
Based on the following definitions:
| |
= | ||
| = | 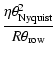 |
(23) |
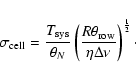 |
(24) |
Since the correction for the radial motions of the local standard of
rest relative to a given source vary as a function of position on the
sky, time, and telescope location, the conversion from spectral
frequency to velocity varies over a given image. This is a subtle
effect, traditionally ignored in spectral-line imaging. However, for a
coordinate ![]() from the reference (e.g. a
from the reference (e.g. a ![]() square
field with a center reference), the error can be as large as 1.16 km s-1 (LSR velocities) or 0.79 km s-1 (heliocentric) when
observed with the NRAO 12 Meter Telescope. The LSR velocity error
changes significantly with time of year. Narrow-band observations of
wide fields, such as observations of cold molecular regions, may be
seriously affected by this effect. Fortunately, so long as the
spectra are fully sampled in frequency, this effect can be fully
corrected by doing the LSR calculations separately for every point
of each map, for all dates, and then interpolating to a common
frame and date in frequency space.
square
field with a center reference), the error can be as large as 1.16 km s-1 (LSR velocities) or 0.79 km s-1 (heliocentric) when
observed with the NRAO 12 Meter Telescope. The LSR velocity error
changes significantly with time of year. Narrow-band observations of
wide fields, such as observations of cold molecular regions, may be
seriously affected by this effect. Fortunately, so long as the
spectra are fully sampled in frequency, this effect can be fully
corrected by doing the LSR calculations separately for every point
of each map, for all dates, and then interpolating to a common
frame and date in frequency space.
When you grid a critically-sampled (Nyquist-sampled) OTF map with a
sensible convolution function (such as
the Gaussian-tapered Bessel function described in Sect. 4),
the resulting spatial resolution is only minimally degraded. However,
the noise spectrum of your gridded map is flat (or,
equivalently, the noise in each gridded point is independent), while
the astronomy spectrum follows that of the spatial frequency
response of the antenna. If you now smooth the data significantly - say to
a resultant beamwidth several times greater than the original spatial
resolution - both the astronomical signal and the noise get smoothed.
The effective increase in integration time is given roughly by
![]() .
Obviously the signal-to-noise ratio increases by the square root of
this quantity. Note that it is the ratio of the new
convolution function to the
original sampling that counts. This is because the high
frequency terms of the original noise, which probably dominate the
total noise, are reduced in amplitude much more than the astronomical
signal, whose high-frequency components were already weighted down.
.
Obviously the signal-to-noise ratio increases by the square root of
this quantity. Note that it is the ratio of the new
convolution function to the
original sampling that counts. This is because the high
frequency terms of the original noise, which probably dominate the
total noise, are reduced in amplitude much more than the astronomical
signal, whose high-frequency components were already weighted down.
After you have smoothed the data once, the noise and astronomical signal now
have a very similar spectrum. If you smooth the data a second time, again
to a beamwidth several times larger than the current (smoothed) beamwidth,
the effective integration time now increases roughly by
![]() .
It is now
the ratio of the beams, independent of the sampling of
either measurement. This in a sense is because the noise
in adjacent samples of the smoothed data is no longer independent, so you
don't gain as much in the second smoothing as was gained in the first.
.
It is now
the ratio of the beams, independent of the sampling of
either measurement. This in a sense is because the noise
in adjacent samples of the smoothed data is no longer independent, so you
don't gain as much in the second smoothing as was gained in the first.
The conclusion is that to be rigorous you need to know the noise spectrum as well as the data beamwidth in order to calculate what the effective integration time becomes when you smooth critically-sampled data. It depends on whether you can consider noise in adjacent samples independent. After the initial gridding of a critically-sampled data set, the noise is independent in adjacent samples. After you have smoothed the data once, the noise is no longer independent.
Before starting a spectral line or continuum OTF map at the 12 Meter, the telescope control system was configured to raster map the target field. For spectral line OTF, the map was taken in a total power observing mode in the sense that you acquired a calibration spectrum (a vane calibration) and a total power off measurement, followed by one or more total power scanning rows, typically made up of hundreds of individual spectra (the on measurements). For continuum OTF, the map was acquired using the continuum beam-switched observing mode. In this mode, the subreflector is switched between two positions (the "+'' and "-'' beam) in azimuth while the telescope scans. Each of the individual spectra or continuum "+'' and "-'' beam total power measurements is tagged with the actual antenna encoder positions. As a result, antenna tracking errors caused by wind gusts, for example, are actually recorded and taken into account in the data analysis stage.
For spectral line OTF, the same calibration and off measurements were used to calibrate all of the on measurements in the scanning rows until another off measurement was taken. Each total power off measurement was given its own scan number. All of the spectra or continuum "+'' and "-'' beam total power measurements in each scanning row were concatenated along with arrays of time and position information and stored on disk under a single scan number with a single header. The header information for each scanning row contained the scan number of the previous off (for spectral line OTF) and calibration measurements.
Given the scanning parameters, the positioning system was configured for tracking rates, row offsets, and the duration of a scanning row. The spectral line data taking backend instructed the tracking system to move to position and begin scanning. Using some handshaking bits on the telescope's status and monitor (SAM) bus, the two systems were synchronized at the start of each row. In addition, both the tracking and backend computers had IRIG clock cards that were driven by the observatory GPS standard clock. The data backend read out the spectrometer system every 100 ms for spectral line OTF. The continuum data system was read out every 250 ms. For both spectral line and continuum OTF, the data backend tagged each data parcel with the UT time stamp. For the digital autocorrelation spectrometer at the 12 Meter Telescope (called the Millimeter Autocorrelator (MAC)), before the data could be read out Fourier transforms of the 100 ms data samples needed to be calculated. To make data analysis as fast as possible, the FFT's were performed in real-time by the MAC control computers. Every 10 ms, the tracking computer recorded its Az/El position with respect to the field center. Finally, at the end of the scanning row, the position information from the tracking system was merged with the data. An interpolation of the position information was then made to align slight differences between the time stamps of the two data sets.
AIPS (Greisen 2003) was the default analysis software used to process OTF data acquired with the NRAO 12 m Telescope (see Mangum 1999). The main processing task was SDGRD (developed by Eric Greisen), which read the raw 12 m ("sdd'') data and gridded it using a variety of user-selectable convolution functions. Figure 13 shows a sample of an OTF image obtained with the NRAO 12 Meter Telescope and processed with the AIPS OTF image analysis tasks.
| |
Figure 13:
CO
|
| Open with DEXTER | |
The On-The-Fly (OTF) imaging technique is an efficient single-dish radio telescope imaging mode that has been implemented at several radio telescope observatories. The relative gain in observing efficiency is most extreme for the "classic'' radio telescopes still in operation. This was certainly true for the NRAO 12 Meter Telescope. The NRAO 12 Meter Telescope began life as the 36 Foot Telescope, the telescope responsible for the birth of millimeter-wavelength molecular astronomy. Its history is one of success, innovation, and an unparalleled desire by the staff operating this facility over its 32-year lifetime to provide a high level of service to the astronomical community.
The 36 Foot Telescope made its first millimeter-wavelength astronomical measurements in October 1968. This was the start of a period of explosive growth in this new area of astronomical research, during which most of the dozens of molecular species known to exist in the interstellar medium were first detected with the 36 Foot.
In the early 1980s the telescope's reflecting surface and surface support structure were replaced and in 1984 it was re-christened as the 12 Meter Telescope. Its scientific program subsequently evolved from one dominated by astrochemistry to a broader mix of studies of molecular clouds and Galactic star formation, evolved stars, astrochemistry, and external galaxies.
The NRAO 12 Meter Telescope was the only millimeter-wavelength telescope in the US operated full-time as a national facility. More than 150 visitors used it each year. It offeredusers flexibility and the opportunity to respond quickly to new scientific developments. Its low-noise receiving systems covered a wide range of frequencies - all atmospheric windows from 68 GHz to 300 GHz - and much attention was given to making the instrument work reliably throughout this range. Flexible spectral line and continuum back-ends allowed the observer to match the instrument to the scientific goals. The development of multi-beam receivers and the on-the-fly observing technique inaugurated a new era of high-speed source mapping on angular scales complementary to those of the millimeter-wave interferometers. The telescope control system offered great flexibility and provided a proven remote observing capability.
On February 22, 2000, NRAO announced that it would close the 12 Meter
Telescope at the end of the current observing season. On 26 July 2000,
the NRAO 12 Meter Telescope made its final astronomical measurements
as a US national astronomical facility. The telescope however
continues to be operated as part of the University of Arizona's
Steward Observatory. The final NRAO data set was an
on-the-fly image of the CO
![]() emission from a star
formation region in the Cygnus-X region.
emission from a star
formation region in the Cygnus-X region.