![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6856fig1.eps} \end{figure}](/articles/aa/full/2007/41/aa6856-06/Timg13.gif) |
Figure 1: Dynamic radio spectrum recorded by the radio spectralpolarimeter (Mann et al. 1992) of the Astrophysical Institute Potsdam. It shows an example of a solar type II radio burst. Further explanations are given in Sect. 1. |
| Open with DEXTER | |
A&A 474, 617-625 (2007)
DOI: 10.1051/0004-6361:20066856
R. Miteva - G. Mann
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
Received 1 December 2006 / Accepted 26 July 2007
Abstract
Context. In the solar corona, shock waves are generated by flares and/or coronal mass ejections. They are able to accelerate electrons up to high energies and can thus be observed as type II bursts in the nonthermal solar radio radiation. In-situ measurements of shock waves in interplanetary space have shown that shock waves attached by whistler waves are preferably accompanied by the production of energetic electrons.
Aims. Motivated by these observations, we study the interaction of electrons with such whistlers, which are excited by the protons accelerated by the shock.
Methods. We start with a resonant whistler wave-proton interaction that accounts for the initial whistler wave generation. Then, we consider resonant whistler wave-electron interaction, treated with a relativistic approach that is responsible for the electron energization in the whistler wave field.
Results. As a result, we show that electrons can be accelerated by a resonant wave particle (i.e., whistler-electron) interaction. This mechanism acts in the case of quasi-perpendicular shock waves. After acceleration, the energetic electrons are reflected by the associated shock wave back into the upstream region. The theoretical results are compared with observations, e.g., solar type II radio bursts.
Key words: shock waves - acceleration of particles - Sun: flares - Sun: radio radiation
Shock waves play an important role in astrophysics, since they are responsible for particle acceleration in space plasmas (Schlickeiser 1984; Fermi 1949; Axford et al. 1978; Kirk 1994). The production of energetic electrons at shocks is of special interest, since these electrons can be the source of nonthermal radio and X-ray radiation, which can be observed by remote sensing techniques.
In the solar corona, shock waves can be generated either by blast waves due to the flare process (Uchida et al. 1973; Vrsnak et al. 1995) and/or by coronal mass ejections (CMEs) (Classen & Aurass 2002; Stewart et al. 1974a; Gopalswamy & Kundu 1992; Lara et al. 2003; Stewart et al. 1974b). It is still an ongoing debate whether the shock waves are generated by a flare-associated blast wave (Vrsnak et al. 1995) or if they are CME-driven (Gopalswamy 2006; Gopalswamy & Kundu 1992). But it should be emphasized that a shock wave is a discontinuity accompanied by an increase in the entropy. The jump in the density, temperature, and magnetic field across the shock is governed by the Rankine-Hugoniot relationships (Priest 1982); i.e., the shock itself and the processes immediately associated with it should be considered as independent of its exciter.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6856fig1.eps} \end{figure}](/articles/aa/full/2007/41/aa6856-06/Timg13.gif) |
Figure 1: Dynamic radio spectrum recorded by the radio spectralpolarimeter (Mann et al. 1992) of the Astrophysical Institute Potsdam. It shows an example of a solar type II radio burst. Further explanations are given in Sect. 1. |
| Open with DEXTER | |
In the corona, shock waves can be observed as type II bursts in the
solar radio radiation (Wild & McCready 1950; Uchida et al. 1973).
A type II radio burst can morphologically be divided into two types
of emission in its dynamic radio spectrum (see Fig. 1, for instance),
the "backbone'' and the "herringbone'' emission.
The so-called backbone emission (see Fig. 1), is slowly drifting from high
to low frequencies with a typical drift rate of about
-0.1375 MHz s-1 at 55 MHz
(whereas Mann & Klassen (2005) reported mean value on the order of -0.133 MHz s-1),
and shows often a fundamental-harmonic structure.
It is widely accepted to be the radio signature of a shock
wave traveling through the corona
(Mann 2006; Aurass 1997; Mann 1995; Nelson & Melrose 1985).
Sometimes, very fast, drifting patches of emission (see Fig. 1) can be seen to
emanate from the backbone, toward both lower or higher frequencies
with typical drift rates of about ![]() 7.2 MHz s-1 at 55 MHz
(whereas Mann & Klassen 2005, reported
7.2 MHz s-1 at 55 MHz
(whereas Mann & Klassen 2005, reported ![]() 9.1 MHz s-1). These features
are the so-called herringbone emission, regarded as the radio
signature of shock-accelerated electrons
(Cairns & Robinson 1987; Zlobec et al. 1993; Mann & Klassen 2005).
9.1 MHz s-1). These features
are the so-called herringbone emission, regarded as the radio
signature of shock-accelerated electrons
(Cairns & Robinson 1987; Zlobec et al. 1993; Mann & Klassen 2005).
In the solar corona, the radio emission mechanism is mainly
due to plasma emission at the local electron plasma frequency
![]() (e, elementary charge;
(e, elementary charge;
![]() ,
electron number density,
,
electron number density, ![]() ,
electron mass) and/or its harmonics
(Melrose 1985). Because
,
electron mass) and/or its harmonics
(Melrose 1985). Because
![]() depends only
on the electron number density, the observed
frequency corresponds to a certain, local electron number density level.
From observations (Newkirk 1961; Koutchmy 1994),
one could estimate how the electron number density varies
with the distance from the solar surface, so the correspondence of the
observed frequency to a certain height of the corona can be
established. Thus, a dynamic radio spectrum represents a height-time
diagram of the radio source in the solar corona, where high/low frequencies
are emitted in the low/high corona due to the gravitational stratification
of the solar atmosphere, respectively.
According to this, the drift rate Df (i.e., the ratio of the frequency bandwidth
depends only
on the electron number density, the observed
frequency corresponds to a certain, local electron number density level.
From observations (Newkirk 1961; Koutchmy 1994),
one could estimate how the electron number density varies
with the distance from the solar surface, so the correspondence of the
observed frequency to a certain height of the corona can be
established. Thus, a dynamic radio spectrum represents a height-time
diagram of the radio source in the solar corona, where high/low frequencies
are emitted in the low/high corona due to the gravitational stratification
of the solar atmosphere, respectively.
According to this, the drift rate Df (i.e., the ratio of the frequency bandwidth ![]() to the corresponding time duration
to the corresponding time duration ![]() )
at frequency f is related
to the radial source velocity
)
at frequency f is related
to the radial source velocity
![]() by
by
Holman & Pesses (1983) proposed that the electrons associated with
the herringbones are generated by shock-drift acceleration.
Other studies on this subject show that, this mechanism provides a beam-like
distribution function for the accelerated electrons (Mann & Klassen 2005),
which corresponds well to the observed characteristics of the herringbone
emission stripes. The beam has a velocity
Considering this mechanism for the herringbone emission, a nearly perpendicular shock configuration is therefore required to be present during the whole event. For the example shown in Fig. 1, the type II burst appears for about 1 min; i.e., it would cover a spatial scale in the corona of about 60 Mm. Even though the shock-drift acceleration is able to explain the electron acceleration rates, the physical conditions required for this mechanism to work are difficult to sustain, since the shock travels more than 60 Mm and needs to be nearly perpendicular all the time. That is an event with low probability. Thus, there is a need for another mechanism for electron acceleration at coronal shocks, and this new mechanism should avoid the restriction of a nearly perpendicular shock geometry. This is the purpose of the presented paper.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6856fig2.ps} \end{figure}](/articles/aa/full/2007/41/aa6856-06/Timg53.gif) |
Figure 2:
Behavior of the fluxes of energetic electrons (0.1-0.4 MeV)
and protons (0.8-1.0 MeV), the solar wind speed
|
| Open with DEXTER | |
Spacecraft observation of the Earth's bow shock, interplanetary shocks, and
shocks related to co-rotating interaction regions (CIRs) are the only
possibility for in-situ measurements of shocks in space plasmas.
Observations by the spacecraft Ulysses at the CIR-related shocks reveal that
electrons are really accelerated up to 0.1-0.4 MeV at such shocks
(see top panel of Fig. 2).
CIR related shocks are efficient at accelerating particles
when the conditions
![]() and
and
![]() are simultaneously fulfilled
by the shock waves (Classen et al. 1998). Such shocks can be
regarded as super-critical shocks (Kennel et al. 1985) and are usually
associated with whistler waves in the up- and downstream region,
immediately in the vicinity of the shock transition
(Gurnett et al. 1985; Classen et al. 1999; Mann et al. 2002).
In summary, quasi-perpendicular
and super-critical shocks with attached whistler waves tend to generate
energetic electrons.
are simultaneously fulfilled
by the shock waves (Classen et al. 1998). Such shocks can be
regarded as super-critical shocks (Kennel et al. 1985) and are usually
associated with whistler waves in the up- and downstream region,
immediately in the vicinity of the shock transition
(Gurnett et al. 1985; Classen et al. 1999; Mann et al. 2002).
In summary, quasi-perpendicular
and super-critical shocks with attached whistler waves tend to generate
energetic electrons.
The aim of the present study is to look for a new mechanism for electron acceleration at quasi-perpendicular shocks in the solar corona. Motivated by the observations at CIR related shocks, we consider an electron-whistler-shock interaction. Here, it is basically assumed that the same physical processes for the collisionless shocks in space (e.g., at CIRs) are also true for the coronal shock waves. The paper is organized as follows: the new mechanism is given in Sect. 2, where every stage is explained in the corresponding sections: Sect. 2.1 presents the acceleration of the protons at the shock; the whistler wave excitation due to the proton-wave resonant interaction is shown in Sect. 2.2; in the next section, 2.3, the resonant interaction of the incoming electrons with the excited whistlers is followed in detail; and the Sect. 2.4 includes the mirror reflection of the energized electrons at the shock that propagate in the upstream region later on. The results are discussed in Sect. 3. In addition, the description of the whistler wave fields and the general theory on the electron motion in homogeneous magnetic field as used in Sect. 2 are presented in Appendices A and B, correspondingly.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6856fig3.eps} \end{figure}](/articles/aa/full/2007/41/aa6856-06/Timg59.gif) |
Figure 3:
Sketch of the shock configuration. Both the in-flowing toward
the shock front and out-flowing protons (" |
| Open with DEXTER | |
The model presented in this paper considers the following scenario
(schematically shown in Fig. 3): a shock wave is moving through
the solar atmosphere with a velocity of about 1000 km s-1.
The inflowing protons
(i.e., toward the shock) can be successfully accelerated at the
shock. Due to their relatively slow thermal velocity
(on the order of 110 km s-1 for a typical coronal temperature
of 1.4 MK), the quasi-perpendicular configuration
(
![]() )
is sufficient for a substantial
velocity gain for the protons (of about 6000 km s-1).
The protons are accelerated
and reflected at the shock back to the upstream region, where they
are able to excite
whistler waves by resonant wave-particle interaction.
These excited whistlers can only interact with the inflowing electrons,
which fulfill the resonance condition.
These electrons are accelerated (i.e., gain energy) in the whistler electric field.
Consequently, the perpendicular electron velocity component with respect
to the ambient magnetic field is increasing during this resonant
interaction. That also leads to an increase in its magnetic moment.
Simultaneously with this process, the accelerating electrons are moving
toward the shock front. Since the shock is accompanied by a jump in the
magnetic field, it represents a traveling magnetic mirror. Finally, the
electrons are mirror reflected at the shock, and they propagate into the upstream
region. The outflowing electrons (i.e., away from the shock) do not fulfill
the resonance condition so are not in resonance with the whistler
wave. Then, they can travel undisturbed into the far upstream region and be
detected as herringbone emission, for example.
)
is sufficient for a substantial
velocity gain for the protons (of about 6000 km s-1).
The protons are accelerated
and reflected at the shock back to the upstream region, where they
are able to excite
whistler waves by resonant wave-particle interaction.
These excited whistlers can only interact with the inflowing electrons,
which fulfill the resonance condition.
These electrons are accelerated (i.e., gain energy) in the whistler electric field.
Consequently, the perpendicular electron velocity component with respect
to the ambient magnetic field is increasing during this resonant
interaction. That also leads to an increase in its magnetic moment.
Simultaneously with this process, the accelerating electrons are moving
toward the shock front. Since the shock is accompanied by a jump in the
magnetic field, it represents a traveling magnetic mirror. Finally, the
electrons are mirror reflected at the shock, and they propagate into the upstream
region. The outflowing electrons (i.e., away from the shock) do not fulfill
the resonance condition so are not in resonance with the whistler
wave. Then, they can travel undisturbed into the far upstream region and be
detected as herringbone emission, for example.
It is well-known from observations at Earth's bow shock
(Paschmann et al. 1981,1980)
that protons are reflected and accelerated by nearly conserving
their magnetic moment at quasi-perpendicular, super-critical shocks.
This process occurs in the range
![]() ,
with very few events
observed for
,
with very few events
observed for
![]() ,
as reported by
Paschmann et al. (1981, see also Fig. 3 there). The reflected protons establish a beam-like distribution with
a strong temperature anisotropy. The beam density is typically
in the range 0.3% to 13% of the number density of the incoming
protons (Paschmann et al. 1981).
Since, under coronal conditions, a quasi-perpendicular shock with an
Alfvén Mach number
,
as reported by
Paschmann et al. (1981, see also Fig. 3 there). The reflected protons establish a beam-like distribution with
a strong temperature anisotropy. The beam density is typically
in the range 0.3% to 13% of the number density of the incoming
protons (Paschmann et al. 1981).
Since, under coronal conditions, a quasi-perpendicular shock with an
Alfvén Mach number
![]() is super-critical
(Kennel et al. 1985; Mann et al. 1995), it is assumed that protons
are also reflected and accelerated at coronal shock waves.
The proton (denoted with a superscript "
is super-critical
(Kennel et al. 1985; Mann et al. 1995), it is assumed that protons
are also reflected and accelerated at coronal shock waves.
The proton (denoted with a superscript "![]() '') velocity gain parallel to
the upstream magnetic field can be expressed by
'') velocity gain parallel to
the upstream magnetic field can be expressed by
That demonstrates that the protons get a substantial gain in energy due to the encounter with the quasi-perpendicular coronal shock wave.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{6856fig4.eps} \end{figure}](/articles/aa/full/2007/41/aa6856-06/Timg87.gif) |
Figure 4: Dispersion relation for the LCP (dashed line) Alfvén and RCP (solid line) whistler wave for S = 20. Both propagate along the ambient magnetic field. |
| Open with DEXTER | |
To excite whistler waves by wave-particle interaction in the case of the
accelerated protons, they need to fulfill the resonance condition; see
Baumjohann & Treumann (1997),
From the resonance condition Eq. (9), one gets
![]()
![]() with the whistler-phase
velocity
with the whistler-phase
velocity
![]() .
Since the proton cyclotron frequency
.
Since the proton cyclotron frequency
![]() is positive, the proton velocity must be faster than the phase speed of the
whistlers, so that the righthand, circularly polarized whistlers appear to
be lefthanded in the rest frame of the energetic protons. Thus, the shock
accelerated protons do fulfill both the resonance condition and the condition
of providing the right whistler polarization, which is lefthand circularly
polarized in the proton rest frame, but righthand circularly polarized in the
laboratory frame.
is positive, the proton velocity must be faster than the phase speed of the
whistlers, so that the righthand, circularly polarized whistlers appear to
be lefthanded in the rest frame of the energetic protons. Thus, the shock
accelerated protons do fulfill both the resonance condition and the condition
of providing the right whistler polarization, which is lefthand circularly
polarized in the proton rest frame, but righthand circularly polarized in the
laboratory frame.
Simultaneously, the shock accelerated protons can also interact with
low-frequency lefthand circularly polarized Alfvén waves according to the
resonance condition (Baumjohann & Treumann 1997),
In summary, shock-accelerated protons are able to excite both whistler waves
with frequencies in the range (0.166-
![]() and low-frequency Alfvén waves.
These whistlers propagate away from the shock in the
upstream region, whereas the Alfvén waves travel towards the shock
(Winske & Leroy 1984).
and low-frequency Alfvén waves.
These whistlers propagate away from the shock in the
upstream region, whereas the Alfvén waves travel towards the shock
(Winske & Leroy 1984).
The excited whistler waves can resonantly interact with the electrons
in the upstream region. The electron resonance conditions is given by
To study relativistic electrons, one needs to correct the above
result using the extended, relativistic resonance condition; i.e.,
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{6856fig5.eps} \end{figure}](/articles/aa/full/2007/41/aa6856-06/Timg124.gif) |
Figure 5:
Solution of the resonance curve, Eq. (22),
for S=20 and
|
| Open with DEXTER | |
Taking relation (13) into account, an expression for the
parallel and the perpendicular component of the velocity is obtained
from Eq. (22) that is plotted in Fig. 5
in the (
![]() )-plane.
There, one could see two
curves, corresponding to the minimum (0.076) and maximum (0.093) values
of
)-plane.
There, one could see two
curves, corresponding to the minimum (0.076) and maximum (0.093) values
of
![]() at
at
![]() .
These two curves define the area in the
(
.
These two curves define the area in the
(
![]() )-plane
that is usually called "resonance band''. Only electrons that are initially
located in this "resonance band'' are able to resonantly interact with the
whistlers. The appearance of such an area is immediately related to the thermal
spread of the inflowing protons and, consequently, with the excitation of
a whistler spectrum in a finite frequency range.
The curvature (as enhanced on the plot) is due to the relativistic effects,
since in the nonrelativistic case it would be two straight lines parallel
to the
)-plane
that is usually called "resonance band''. Only electrons that are initially
located in this "resonance band'' are able to resonantly interact with the
whistlers. The appearance of such an area is immediately related to the thermal
spread of the inflowing protons and, consequently, with the excitation of
a whistler spectrum in a finite frequency range.
The curvature (as enhanced on the plot) is due to the relativistic effects,
since in the nonrelativistic case it would be two straight lines parallel
to the
![]() -axis. During the resonant interaction with the whistler
wave field, the electron is increasing its velocity component
perpendicular to the magnetic field. That represents a motion upward in
the
-axis. During the resonant interaction with the whistler
wave field, the electron is increasing its velocity component
perpendicular to the magnetic field. That represents a motion upward in
the
![]() -plane
(see Fig. 5) between these curves
or in the so-called "resonance band'', leading to an increase in its
kinetic energy (see Fig. 6). Normalized to the rest energy
(
-plane
(see Fig. 5) between these curves
or in the so-called "resonance band'', leading to an increase in its
kinetic energy (see Fig. 6). Normalized to the rest energy
(
![]() keV), the kinetic energy of the electron is usually defined by
keV), the kinetic energy of the electron is usually defined by
In general, the movement of an electron in given electric and
magnetic fields can be described by the momentum
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{6856fig6.eps} \end{figure}](/articles/aa/full/2007/41/aa6856-06/Timg141.gif) |
Figure 6:
Relation between
|
| Open with DEXTER | |
Note that Eq. (23) is already normalized. In order to find the
energy gain, the time derivative of Eq. (23) is calculated, i.e.,
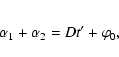
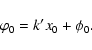 |
A fast magnetosonic shock wave is accompanied by a jump in the density and the
magnetic field. In this sense, it represents a moving magnetic mirror on which
charged particles can be reflected and subsequently accelerated. In a weakly
varying magnetic field, i.e.,
![]() ,
where
,
where ![]() is the Larmor radius, the particle motion is governed by
the conservation of the kinetic energy (or amount of momentum) and
the magnetic moment (Baumjohann & Treumann 1997), i.e.,
is the Larmor radius, the particle motion is governed by
the conservation of the kinetic energy (or amount of momentum) and
the magnetic moment (Baumjohann & Treumann 1997), i.e.,
Since the shock is moving, the consideration presented above must actually
be made in the so-called de Hoffmann-Teller frame; see
e.g., Mann & Klassen (2005).
The shock speed in the de Hoffmann-Teller frame is given by
![]() (Mann & Klassen 2005),
which has a typical value of 3000 km s-1 adopting
(Mann & Klassen 2005),
which has a typical value of 3000 km s-1 adopting
![]() km s-1and
km s-1and
![]() .
Since this value is essentially lower
than the thermal electron velocity
.
Since this value is essentially lower
than the thermal electron velocity
![]() ,
which has a typical value of 4600 km s-1for a coronal temperature of 1.4 MK, the influence of the motion
of the shock on the electron reflection process can be neglected for considering
electrons that has been done in this section.
Due to the motion of the shock, the electrons reflected back at it get an additional
energy gain due to shock drift acceleration, but it can be neglected in
the case of quasi-perpendicular shocks under coronal conditions.
,
which has a typical value of 4600 km s-1for a coronal temperature of 1.4 MK, the influence of the motion
of the shock on the electron reflection process can be neglected for considering
electrons that has been done in this section.
Due to the motion of the shock, the electrons reflected back at it get an additional
energy gain due to shock drift acceleration, but it can be neglected in
the case of quasi-perpendicular shocks under coronal conditions.
As already discussed, the electrons increase their momentum perpendicular to the ambient magnetic field due to the resonant electron-whistler interaction (see Fig. 5) and, consequently, their pitch angle (see Eq. (40)) as well. Thus, a major part of the energized electrons fulfill the reflection condition (43) and, finally, move away from the shock into the upstream region. After the reflection, the accelerated electrons are co-streaming with the whistlers and, thus, do not fulfill the resonance condition (22); i.e., they are out of resonance and can freely reach the far upstream region.
In the framework of the proposed mechanism, the electron acceleration
happens in the
![]() -plane due to
the resonant electron-whistler interaction as illustrated in Fig. 5.
It actually represents a motion toward higher values of
-plane due to
the resonant electron-whistler interaction as illustrated in Fig. 5.
It actually represents a motion toward higher values of
![]() within the so-called "resonance band''
within the so-called "resonance band''
![]() -plane. Figure 5 results from parameters, which are appropriate for a shock wave associated with solar type II radio bursts around 55 MHz.
In the initial state, the electron must be located in the "resonance band''
in order to become energized. In the "resonance band'',
the electrons with the lowest initial energy
have values of
-plane. Figure 5 results from parameters, which are appropriate for a shock wave associated with solar type II radio bursts around 55 MHz.
In the initial state, the electron must be located in the "resonance band''
in order to become energized. In the "resonance band'',
the electrons with the lowest initial energy
have values of
![]() and
and
![]() ;
i.e., they have an initial energy of 1.5 keV. In the case of the most
efficient energy gain, they move upward along a straight line
(see Fig. 5) parallel
to the
;
i.e., they have an initial energy of 1.5 keV. In the case of the most
efficient energy gain, they move upward along a straight line
(see Fig. 5) parallel
to the
![]() -axis. They leave the "resonance band'' at the point
(
-axis. They leave the "resonance band'' at the point
(
![]() ,
,
![]() )
in the
)
in the
![]() -plane. Then, they have a final kinetic
energy of 97 keV. During this process, the pitch angle changes
from
-plane. Then, they have a final kinetic
energy of 97 keV. During this process, the pitch angle changes
from ![]() to
to
![]() .
Particles with such a final pitch angle
are reflected at shock, since their pitch angle is greater than
the loss-cone angle
.
Particles with such a final pitch angle
are reflected at shock, since their pitch angle is greater than
the loss-cone angle
![]() (in Fig. 5) as required for
reflection, see Eq. (43). Such a value is obtained for the loss-cone
angle, if one assumes
a jump in the magnetic field
(in Fig. 5) as required for
reflection, see Eq. (43). Such a value is obtained for the loss-cone
angle, if one assumes
a jump in the magnetic field
![]() as a typical
value for coronal shock waves.
as a typical
value for coronal shock waves.
The inspection of Fig. 5 reveals that only electrons, which
are initially located within the "resonance band''
in the
![]() -plane,
are accelerated; i.e., their initial energy must be
-plane,
are accelerated; i.e., their initial energy must be ![]() 1.5 keV
corresponding to a velocity of
1.5 keV
corresponding to a velocity of
![]() (with
(with
![]() km s-1 as the thermal electron speed for a coronal temperature
of 1.4 MK). In the case of an initial Maxwellian distribution of the
electrons in the upstream region, the number density of the electrons
initially located within the "resonance band'' can be estimated to be
km s-1 as the thermal electron speed for a coronal temperature
of 1.4 MK). In the case of an initial Maxwellian distribution of the
electrons in the upstream region, the number density of the electrons
initially located within the "resonance band'' can be estimated to be
![]() 3.582
3.582 ![]()
![]() .
(In this case the integration of the Maxwellian distribution,
see Eqs. (7) and (8),
is performed from
.
(In this case the integration of the Maxwellian distribution,
see Eqs. (7) and (8),
is performed from
![]() to
to
![]() ,
which in this case are 4.96 and 6.06 of the electron thermal speed,
correspondingly.) Only these electrons can really be accelerated by the proposed mechanism;
i.e., only a minor part of the electrons in the upstream region gain energy.
,
which in this case are 4.96 and 6.06 of the electron thermal speed,
correspondingly.) Only these electrons can really be accelerated by the proposed mechanism;
i.e., only a minor part of the electrons in the upstream region gain energy.
Now, the energy budget of the different stages of the whole process is
discussed here. As already mentioned, those particles that
are initially located in the "resonance band'' of the
![]() -plane are finally
accelerated. These are
-plane are finally
accelerated. These are
![]()
![]()
![]() cm-3 electrons with
cm-3 electrons with
![]()
![]() 107 cm-3.
Assuming
107 cm-3.
Assuming
![]() and
and
![]() (see Fig. 5),
as mean values of the accelerated electrons,
the kinetic energy is calculated as
(see Fig. 5),
as mean values of the accelerated electrons,
the kinetic energy is calculated as
![]() keV.
Thus, the accelerated electrons have an energy density of
keV.
Thus, the accelerated electrons have an energy density of
![]()
![]() 10-7 erg cm-3.
The energy density of the protons inflowing towards the shock can be calculated as
10-7 erg cm-3.
The energy density of the protons inflowing towards the shock can be calculated as
![]() erg cm-3for
erg cm-3for
![]() km s-1. According to the observations at
Earth's bow shock (Paschmann et al. 1981), 2% of this incoming energy
is typically transferred into the accelerated protons; i.e., the energy density
km s-1. According to the observations at
Earth's bow shock (Paschmann et al. 1981), 2% of this incoming energy
is typically transferred into the accelerated protons; i.e., the energy density
![]() of the accelerated protons is about
of the accelerated protons is about
![]()
![]() 10-3 erg cm-3.
Thus,
10-3 erg cm-3.
Thus,
![]()
![]()
![]() ;
i.e.,
only a fraction of
;
i.e.,
only a fraction of ![]() 10-4 of the energy of the accelerated protons is really
needed for the electron acceleration. If one assumes that 10% of the
whistler energy is going into the accelerated electrons, the whistler
energy density is about
10-4 of the energy of the accelerated protons is really
needed for the electron acceleration. If one assumes that 10% of the
whistler energy is going into the accelerated electrons, the whistler
energy density is about
![]()
![]() 10-6 erg cm-3, corresponding to
a whistler amplitude of
10-6 erg cm-3, corresponding to
a whistler amplitude of
![]() G, i.e.,
0.011 B0 (because of B0 = 1 G).
In summary, only a very small fraction (
G, i.e.,
0.011 B0 (because of B0 = 1 G).
In summary, only a very small fraction (![]() 10-6) of the shock energy
is transferred into the accelerated electrons.
10-6) of the shock energy
is transferred into the accelerated electrons.
In order to give some estimation with respect to the acceleration time,
Eq. (36) is employed. Adopting
![]() (corresponding to an energy of
21.18 keV),
(corresponding to an energy of
21.18 keV),
![]() ,
,
![]() (corresponding to
(corresponding to
![]() and
k' = 0.4815),
and
k' = 0.4815),
![]() ,
and S = 20 as typical values for the
accelerated electrons (see above), one gets t' = 1130 and
,
and S = 20 as typical values for the
accelerated electrons (see above), one gets t' = 1130 and
![]()
![]() 10-6 s (because of
10-6 s (because of
![]()
![]() 107 s-1for B = 1 G). In summary, the electrons are accelerated within a few tens of
microseconds for this special choice of the parameters
and the electron velocity components in the resonance band.
107 s-1for B = 1 G). In summary, the electrons are accelerated within a few tens of
microseconds for this special choice of the parameters
and the electron velocity components in the resonance band.
The proposed mechanism is only able to explain the generation of energetic electrons in the upstream region. Usually, positively and negatively drifting herringbone structures are observed, as presented in Fig. 1. They are commonly interpreted as electron beams accelerated at the shock and traveling into the up- (negative drift) and downstream (positive drift) region (Nelson & Melrose 1985). But that may not necessarily be true. As seen in Fig. 1, the backbone is located within the range 50-55 MHz, corresponding to a height 478-441 Mm above the photosphere by using a twofold Newkirk (1961) model, see Eq. (2). In contrast to that, the herringbones appear in a wider frequency range 40-80 MHz corresponding to a height range of 574-316 Mm above the photosphere; i.e., the herringbone sources cover a wide range in the corona. Spatial radio-heliographic observations have revealed that solar type II radio burst sources mainly propagate nonradially away from active regions (Gopalswamy et al. 2000; Klein et al. 1999; Gopalswamy et al. 1997; Klassen et al. 1999; Aurass et al. 1998). Since the shock wave is a spatially extended feature in the corona, the electrons can be accelerated at different sites of the shock. If the shock shows a large-scale curved shape, the upstream region can be directed towards both lower and higher densities, so that the shock accelerated electron beam leads to a negatively and positively drifting signature (i.e., herringbone) in the dynamic radio spectrum. This scenario explains the appearance of negatively and positively drifting herringbones, although the associated beams are generated in the upstream region and traveling away from the shock; see also Fig. 2 in Holman & Pesses (1983).
The proposed mechanism of electron acceleration is applicable to
quasi-perpendicular shocks; i.e., the angle
![]() is
in the range of
is
in the range of ![]() -
-![]() .
It explains the production
of energetic electrons at shocks, as really observed
by spacecraft missions (see Fig. 2). A continuous regime for electron
acceleration is achieved, when the electron moves in the resonance band.
The proposed mechanism can also act at other shocks in space plasmas,
e.g., at supernova remnants.
.
It explains the production
of energetic electrons at shocks, as really observed
by spacecraft missions (see Fig. 2). A continuous regime for electron
acceleration is achieved, when the electron moves in the resonance band.
The proposed mechanism can also act at other shocks in space plasmas,
e.g., at supernova remnants.
Acknowledgements
R.M. was supported by Deutscher Akademischer Austauschdienst (DAAD) grant Ref. 324 A/03/10336.
In order to describe the electric and magnetic fields accompanied by the
whistler wave, the ambient magnetic field is assumed to be along
the ![]() -axis, i.e.,
B0(1,0,0). Since whistler waves propagating
along the magnetic field are considered, they are not accompanied by an
electric field along the magnetic field, i.e.,
-axis, i.e.,
B0(1,0,0). Since whistler waves propagating
along the magnetic field are considered, they are not accompanied by an
electric field along the magnetic field, i.e.,
![]() .
Likewise, all varying quantities are assumed to depend only on the spatial
and temporal coordinates x and t, respectively. Then, the Ansatz
.
Likewise, all varying quantities are assumed to depend only on the spatial
and temporal coordinates x and t, respectively. Then, the Ansatz
| (A.1) | |||
| (A.2) |
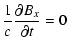 |
(A.3) | ||
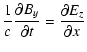 |
(A.4) | ||
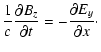 |
(A.5) |
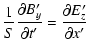 |
(A.6) | ||
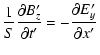 |
(A.7) |
![$\displaystyle E'_y = \frac{V'_{\rm ph}}{S} B'_{\rm wh} \cos{[k' x' -\omega't']}$](/articles/aa/full/2007/41/aa6856-06/img223.gif) |
(A.8) | ||
![$\displaystyle E'_z = - \frac{V'_{\rm ph}}{S} B'_{\rm wh} \sin{[k' x' -\omega't']}$](/articles/aa/full/2007/41/aa6856-06/img224.gif) |
(A.9) |
The motion of an electron in a homogeneous magnetic field along the
![]() -axis can be expressed in the normalized way (see Sect. 2) by:
-axis can be expressed in the normalized way (see Sect. 2) by:
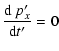 |
(B.1) | ||
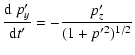 |
(B.2) | ||
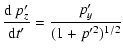 |
(B.3) |
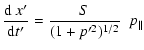 |
(B.4) | ||
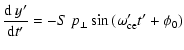 |
(B.5) | ||
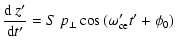 |
(B.6) |
| (B.7) | |||
| (B.8) | |||
| (B.9) |