A&A 474, 251-259 (2007)
DOI: 10.1051/0004-6361:20077739
On the properties of faculae at the poles of the Sun
J. Blanco Rodríguez1 - O. V. Okunev1,2
- K. G. Puschmann1 - F. Kneer1 - B. Sánchez-Andrade Nuño1,3
1 - Institut für Astrophysik, Friedrich-Hund-Platz 1,
37077 Göttingen, Germany
2 -
Central Astronomical Observatory at Pulkovo,
196140 St. Petersburg, Russia
3 -
Max-Plank-Institut für Sonnensystemforschung, Max-Planck-Str. 2,
37191 Katlenburg-Lindau, Germany
Received 27 April 2007 / Accepted 23 July 2007
Abstract
Context. Faculae at the poles of the Sun, or polar faculae (PFe), take part in the solar magnetic cycle. Their occurrence maximum is shifted by 5-6 years with respect to the sunspot cycle. PFe are stable phenomena, with lifetimes of several hours to days, and harbour magnetic fields of kilo-Gauss strength. Yet their role for the global magnetic field at the solar poles is unknown.
Aims. To contribute to the knowledge of the physical properties of PFe and to the understanding of their role in the global magnetism of the Sun.
Methods. PFe were observed on 21-24 August 2005 with the Vacuum Tower Telescope at the Observatorio del Teide. The "Göttingen'' Fabry-Perot spectrometer was used with a Stokes V polarimeter to scan the Fe I 6173 Å line (Landé factor g = 2.5) and the H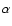 line in two-dimensional fields of view (FOVs). A large observational coverage of the polar caps was obtained. The data were analysed with speckle methods. Magnetic field strengths were determined with the weak field approximation, with the approximation of the strong field regime, and with the centre of gravity (COG) method. Velocities were measured with the COG method and from the zero-crossing of the Stokes V profiles.
line in two-dimensional fields of view (FOVs). A large observational coverage of the polar caps was obtained. The data were analysed with speckle methods. Magnetic field strengths were determined with the weak field approximation, with the approximation of the strong field regime, and with the centre of gravity (COG) method. Velocities were measured with the COG method and from the zero-crossing of the Stokes V profiles.
Results. PFe show a decrease of the continuum and broadband intensity contrast towards the disc centre and no decrease of contrast towards the limb, similar to as faculae in active regions near the equator. Extrapolating from the observed FOVs to the total areas of PF occurrence around the solar poles, we find 4 120 PFe in the northern polar cap and, asymmetrically to this number, 1 250 PFe near the south pole. The total area coverages by PFe are 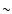
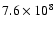 km2 and
km2 and 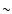
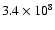 km2 near the solar north and south poles, respectively. Some of the PFe exhibit magnetic polarities opposite to the global polarity at the time of observation. The resulting total magnetic fluxes in PFe fall short by an order of magnitude from those found in the literature for the fluxes at the polar caps. This also holds if we include magnetic structures which are not related to brightenings. We conclude that with the present spatial resolution of
km2 near the solar north and south poles, respectively. Some of the PFe exhibit magnetic polarities opposite to the global polarity at the time of observation. The resulting total magnetic fluxes in PFe fall short by an order of magnitude from those found in the literature for the fluxes at the polar caps. This also holds if we include magnetic structures which are not related to brightenings. We conclude that with the present spatial resolution of
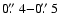 (FWHM), PFe represent the "large-scale'' end of a distribution of unipolar strands near the solar poles. The velocities in PFe show amplitudes of 2 km s-1, with systematic up-flows in the Stokes I profile, but no average velocity measured in the V zero-crossings.
(FWHM), PFe represent the "large-scale'' end of a distribution of unipolar strands near the solar poles. The velocities in PFe show amplitudes of 2 km s-1, with systematic up-flows in the Stokes I profile, but no average velocity measured in the V zero-crossings.
Key words: Sun: faculae, plages -
Sun: magnetic fields -
techniques: high angular resolution
1 Introduction
The polar areas of the Sun are of particular interest for understanding solar magnetism. They take part in the magnetic activity cycle with a shift by 5-6 years with respect to the sunspot activity. The polar coronal holes are largest during sunspot minimum. At the same time, the polar faculae (PFe), which are bright structures of approximately 1
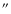 and are seen in white light and in chromospheric lines, show maximum occurrence and appear down to latitudes of
and are seen in white light and in chromospheric lines, show maximum occurrence and appear down to latitudes of
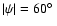 .
During maximum sunspot activity the regions of PFe appearance around the poles vanish (Sheeley 1964; Makarov et al. 2003b; Waldmeier 1955,1962; Sheeley 1991; Makarov et al. 2003a; Makarov & Sivaraman 1989). A study of the cycle variation of small-scale magnetic structures near the poles was performed by Lin et al. (1994).
.
During maximum sunspot activity the regions of PFe appearance around the poles vanish (Sheeley 1964; Makarov et al. 2003b; Waldmeier 1955,1962; Sheeley 1991; Makarov et al. 2003a; Makarov & Sivaraman 1989). A study of the cycle variation of small-scale magnetic structures near the poles was performed by Lin et al. (1994).
The modulation of the polar magnetic flux has been modelled by Wang et al. (2002) and Baumann et al. (2004) with simulations of surface flux transport including injection of bipolar fields during sunspot activity, diffusion, differential rotation, and meridional poleward flows. Wang & Sheeley (2003) show the consequences of such flux emergence and surface transport for the coronal magnetic field configurations, and Baumann et al. (2006) extend the surface transport to volume diffusion such that the "memory'' of the solar field structure becomes shortened. The surface transport of small magnetic flux elements instead of monolithic sunspot tubes appears reasonable in view of the dynamic disconnection of sunspots at near-surface layers discussed by Schüssler & Rempel (2005).
The polar caps with their magnetic field structure are also relevant for the polar coronal holes as the sources of the fast solar wind from the poles. DeForest et al. (1997) find from simultaneous observations with EIT (Delaboudinière et al. 1995) and MDI (Scherrer et al. 1995) on-board SOHO, that polar coronal plumes are rooted on X-ray bright points above unipolar magnetic fields at network boundaries. Yet Wilhelm et al. (2000,1998) favour a picture in which the plumes are footed on closed loops and they identify the outflow regions with dark coronal areas, not with bright plumes.
Tu et al. (2005) combine photospheric magnetic fields, measured with MDI near the poles, and intensities and velocities from SUMER measurements (Wilhelm et al. 1995). From extrapolation of the magnetic fields to the corona, they construct models of (open) magnetic funnels which they suggest are the origin of the fast solar wind. Wiegelmann et al. (2005) come to similar conclusions for equatorial coronal holes. Furthermore, Tu et al. (2005) invoke the furnace model by Axford & McKenzie (1997) to release energy by reconnection and to accelerate the wind by Alfvén waves.
PFe, as magnetic features at the poles of the Sun, are candidates for the magnetic footings of the coronal funnels. Homann et al. (1997), Okunev (2004) and Okunev & Kneer (2004) have established the kilo-Gauss field strength in PFe and fast small-scale evolution on short timescales (1 min), while as PF entities, they are long-lived (longer than 1 h). Three-dimensional atmospheric models of PFe were worked out by Okunev (2004) and Okunev & Kneer (2005). However, the role of PFe for the global magnetic field structure and its variation and dynamics of the transition zone and coronal dynamics is not yet understood. Okunev et al. (2005) point out that for a magnetic flux from PFe at the solar photospheric level, compatible with the average flux density of approximately 6 Gauss (Svalgaard et al. 1978) and with the radial magnetic flux density at 1 AU of 3.5 nT from Ulysses measurements (Smith & Balogh 1995), one would need of the order of
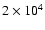 PFe simultaneously (during sunspot minimum), many more than are seen. A similar reasoning applies to the magnetic funnels in the Tu et al. (2005) model.
PFe simultaneously (during sunspot minimum), many more than are seen. A similar reasoning applies to the magnetic funnels in the Tu et al. (2005) model.
Thus, in this work, we study the role of PFe. While the observations presented by Okunev (2004) and Okunev & Kneer (2005) stem from a period of maximum sunspot activity, and thus of minimum appearance of PFe, the current years around the sunspot minimum are a better epoch to observe many PFe. Furthermore, since our earlier observations (before May 2002), important instrumental improvements have been achieved. The Kiepenheuer Adaptive Optics System (KAOS, von der Lühe et al. 2003) has been put into regular operation at the German Vacuum Tower Telescope (VTT), and during the first half of 2005 the "Göttingen'' Fabry-Perot interferometer (FPI) used for two-dimensional spectropolarimetry, was upgraded to have a substantially increased efficiency concerning FOV, frame rate, and noise (Puschmann et al. 2006). We may expect then, with improved techniques, better detection of small-scale magnetic features near the poles of the Sun.
We describe the two-dimensional observations with a large coverage of the northern and southern polar caps in Sect. 2 and the data analysis in Sect. 3. The results are discussed in Sect. 4. The variation of the contrast of PFe towards the limb from broadband measurements is presented. We study statistical properties of PFe, such as number density, magnetic polarity, and magnetic flux in comparison with the total magnetic flux from the poles. Gas velocities in PFe are also addressed. Section 5 concludes the paper.
2 Observations
The observations for the present contribution were taken from the area near the northern and southern poles of the Sun. They were obtained during 21-24 August 2005 with the VTT at the Observatorio del Teide/Tenerife. The observations were usually taken between 8 and 10 UT in the morning. The two-dimensional "Göttingen'' FPI spectrometer (Puschmann et al. 2006) was used with a Stokes V polarimeter. In addition to its high efficiency which has increased by a factor of 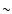 60, it now allows quasi-simultaneously scanning through several spectral lines. We observed the photospheric, magnetically-sensitive Fe I 6173 Å line (Landé factor g = 2.5) and in H
60, it now allows quasi-simultaneously scanning through several spectral lines. We observed the photospheric, magnetically-sensitive Fe I 6173 Å line (Landé factor g = 2.5) and in H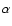 .
The latter line was observed to study the chromospheric dynamics above PFe. The results from this investigation will be published in a forthcoming paper.
.
The latter line was observed to study the chromospheric dynamics above PFe. The results from this investigation will be published in a forthcoming paper.
To obtain a large coverage of the northern polar cap, spectro-polarimetric scans were performed at 19 different heliographic latitudes, 14 at the north and 5 at the south pole. The coverage of the southern polar cap was smaller than at the north pole because the heliographic latitude of the disc centre was
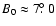 ,
so the northern polar area was more accessible for observation. No strong activity was present at high latitudes during the time of observation. The FOVs were 28
,
so the northern polar area was more accessible for observation. No strong activity was present at high latitudes during the time of observation. The FOVs were 28
 46
46
 for the narrow-band, spectroscopic FPI channel and 73
for the narrow-band, spectroscopic FPI channel and 73
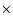 55
55
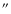 at the broadband speckle camera, with pixel sizes of both CCDs corresponding to
at the broadband speckle camera, with pixel sizes of both CCDs corresponding to
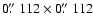 .
The seeing conditions were good and stable during the whole observation period, with a mean value of the Fried parameter
.
The seeing conditions were good and stable during the whole observation period, with a mean value of the Fried parameter
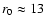 cm.
cm.
The scanning parameters were chosen slightly different for each day of the observing period. The scans covered sometimes 21 and sometimes 22 spectral positions around Fe I 6173 Å, with 15 exposures at each position, with an exposure time of 5 ms for Fe I 6173 Å, and a step width of 23.65 mÅ for Fe I 6173 Å.
Broadband images were taken at 6302 Å (FWHM 50 Å) and strictly simultaneously with these narrow-band data, which is necessary for post-facto image reconstruction. Additionally, scans with dark frames and flat fields were taken for the data analysis.
3 Data analysis
Dark corrections and flat fielding were applied to the data in the usual way. For the broadband images, we applied the Göttingen speckle reconstruction code (de Boer 1996) which uses the spectral ratio method by von der Lühe (1984) for the Fourier amplitudes and the speckle masking method by Weigelt (1977) for the Fourier phases. The code was recently improved by Puschmann & Sailer (2006) to take into account the field dependent correction of the adaptive optics (AO). This gives a constant spatial resolution over the whole FOV and improves the image quality beyond that achieved with KAOS.
The speckle reconstruction of the broadband images gives the instantaneous optical transfer function of the atmosphere together with the AO. The narrow-band images were thus reconstructed using the method by Keller & von der Lühe (1992), also described recently by Bello González et al. (2005). Before further analysis of the data, a careful, sub-pixel alignment of the images from both channels of the V polarimeter and of these images with the broadband images was performed. This included de-stretching with an extension of the code by Yi & Molowny Horas (1992), which corrected for small displacements due to different optical paths of the two polarised light channels and the broadband optical train. For comparison with the broadband images, the de-stretching parameters were calculated for averaged continuum images in the spectral channels and transferred to the (reconstructed) images taken within the spectral lines.
From the spectral data of each pixel in the FOV, the magnetic field strength was determined by three different methods: weak field approximation (WFA), strong field regime (SFR), and centre of gravity (COG). The two former methods extract the field strengths from the Stokes V profiles whereas the COG method uses the profiles corresponding to the two circular polarisation states
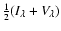 and
and
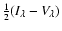 .
.
The Zeeman splitting,
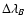 ,
is given as
,
is given as
where e, m, and c denote the electron charge, electron mass, and speed of light, respectively. In the last expression of Eq. (2)
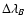 and
and 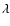 are measured in Å and the flux density B in G. In the following, we use magnetic field strength synonymously with magnetic flux density.
are measured in Å and the flux density B in G. In the following, we use magnetic field strength synonymously with magnetic flux density.
In the WFA, the Zeeman splitting is assumed to be much smaller than the Doppler width of the line. In this case, the amplitudes of the Stokes V profiles increase linearly with the line-of-sight (LOS) component of the magnetic field. From the expansion of Stokes V in a Taylor series to the first order (Landi Degl'Innocenti 1992) we have
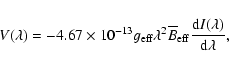 |
(3) |
where
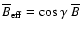 is the LOS component of the flux density averaged over the resolution element (and over the formation heights), with
is the LOS component of the flux density averaged over the resolution element (and over the formation heights), with 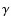 the angle between the LOS and
the angle between the LOS and 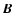 .
The rms noise level in the
.
The rms noise level in the 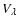 profiles is
profiles is 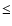
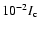 ,
where
,
where 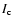 is the continuum intensity.
is the continuum intensity.
In the SFR, the Zeeman splitting is bigger than the Doppler width of the line and the Stokes V profiles are saturated. Its amplitudes no longer increase with the field strength, while the separation of the two lobes,
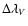 ,
increases and approaches twice the Zeeman splitting
,
increases and approaches twice the Zeeman splitting
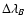 .
For sufficiently strong magnetic fields one thus obtains
.
For sufficiently strong magnetic fields one thus obtains
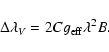 |
(4) |
The separations
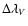 were determined by least square fits of two Gaussians to the V profiles (Okunev 2004; Okunev & Kneer 2004).
were determined by least square fits of two Gaussians to the V profiles (Okunev 2004; Okunev & Kneer 2004).
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{7739fig1.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg41.gif) |
Figure 1:
Examples of Stokes V profiles. Solid: measured profiles; dashed: double Gaussian fit to the data; dash-dotted:
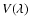 from Eq. (3) with appropriate
from Eq. (3) with appropriate
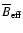 . . |
| Open with DEXTER |
Figure 1 presents two examples of Stokes V profiles obtained from our data in solid lines as well as the fit of two Gaussians to them, as dashed lines. For comparison, the curve corresponding to
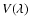 in Eq. (3) with the appropriate
in Eq. (3) with the appropriate
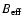 is overplotted as dash-dotted lines. The effective field strengths, obtained with the WFA, are -180 G and -80 G for the upper and lower panel, respectively.
is overplotted as dash-dotted lines. The effective field strengths, obtained with the WFA, are -180 G and -80 G for the upper and lower panel, respectively.
The WFA gives approximately correct magnetic field strengths for fields <1 kG, while the SFR applies only for fields >1.5 kG. Thus, the two methods of field measurement are mutually exclusive.
The COG method (cf. Semel 1967; Rees & Semel 1979) obtains the LOS component of the magnetic field from the separation of the COGs of the two circularly polarised line profiles
 and
and
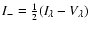 .
Using Eq. (2) we have
.
Using Eq. (2) we have
where the integration is performed over the line profile and 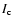 is the continuum intensity.
is the continuum intensity.
For the measurement of the velocities, two methods were applied: 1) the Doppler shift of the COG of the Stokes I profiles with respect to the average line position in the FOV gives the average LOS velocity of the magnetic and non-magnetic gas in the resolution element (and in the line forming layers along the LOS); 2) the position of the zero-crossing of the V profiles yields the LOS velocity in the magnetised plasma. The zero-crossings were determined from the above-mentioned fits of two Gaussians to the V profiles. Third order polynomials to the central parts of the V profiles gave essentially the same results. Yet for the latter method the V profiles should contain less (relative) noise than for the Gaussian fits, which use more parts of the line profiles.
The determinations of
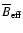 and of velocities, the latter from the positions of the V zero-crossings, are susceptible to instrumental crosstalk, especially
and of velocities, the latter from the positions of the V zero-crossings, are susceptible to instrumental crosstalk, especially
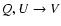 crosstalk. This has been estimated by Okunev (2004) and Bello González et al. (2005). While the
crosstalk. This has been estimated by Okunev (2004) and Bello González et al. (2005). While the
 crosstalk is corrected during data analysis, the Q and U profiles distort Stokes V. The crosstalk increases towards the limb with increasing Q and U. The separations of the V extrema are barely affected (i.e. in the SFR). According to our estimates for the WFA and for the COG method,
crosstalk is corrected during data analysis, the Q and U profiles distort Stokes V. The crosstalk increases towards the limb with increasing Q and U. The separations of the V extrema are barely affected (i.e. in the SFR). According to our estimates for the WFA and for the COG method,
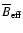 comes out too small by 20%. This will not change the counts of PFe and the estimates of the total magnetic flux from the polar caps below (Sects. 4.2 and 4.3.3). Yet the position of the zero-crossing has to be taken with caution. In future observations with the VTT, it will be possible to measure both the full Stokes vector and the instrumental crosstalk, which will allow correction of the latter.
comes out too small by 20%. This will not change the counts of PFe and the estimates of the total magnetic flux from the polar caps below (Sects. 4.2 and 4.3.3). Yet the position of the zero-crossing has to be taken with caution. In future observations with the VTT, it will be possible to measure both the full Stokes vector and the instrumental crosstalk, which will allow correction of the latter.
Figure 2 shows, as an example of the resulting reconstructed broadband images and magnetograms, a section from a FOV at
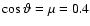 .
The spatial resolution here is estimated to be
.
The spatial resolution here is estimated to be
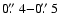 (FWHM). We note the facular substructure which does not differ substantially from the granular pattern. The right, large facula in Fig. 2 appears as abnormal granulation. The granules within the faculae appear brighter which is explained by the hot-wall effect (see the recent review by Steiner 2007, and references therein). Yet not all bright granules are related with substantial magnetic flux, e.g. in the lower left part of the panels of Fig. 2. And not all magnetic structures possess a conspicuous, very bright counterpart, e.g. in the upper right part of the panels of Fig. 2.
(FWHM). We note the facular substructure which does not differ substantially from the granular pattern. The right, large facula in Fig. 2 appears as abnormal granulation. The granules within the faculae appear brighter which is explained by the hot-wall effect (see the recent review by Steiner 2007, and references therein). Yet not all bright granules are related with substantial magnetic flux, e.g. in the lower left part of the panels of Fig. 2. And not all magnetic structures possess a conspicuous, very bright counterpart, e.g. in the upper right part of the panels of Fig. 2.
4 Results
4.1 Variation of contrast towards the limb
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7739fig2.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg52.gif) |
Figure 2:
Example of PFe at
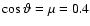 ,
sections of speckle reconstructed broadband image ( upper) and relevant magnetogram ( lower), obtained with the centre of gravity method. Dark and light shades in the magnetogram refer to negative and positive magnetic polarity, respectively. The minimum effective field strength is -230 G, the maximum is +120 G. Only fields with ,
sections of speckle reconstructed broadband image ( upper) and relevant magnetogram ( lower), obtained with the centre of gravity method. Dark and light shades in the magnetogram refer to negative and positive magnetic polarity, respectively. The minimum effective field strength is -230 G, the maximum is +120 G. Only fields with
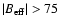 G have entered the magnetogram. Circles indicate areas with bright features but no significant magnetic flux ( lower left), and areas with significant flux, but without substantial brightness ( upper right). The arrow points towards the limb. G have entered the magnetogram. Circles indicate areas with bright features but no significant magnetic flux ( lower left), and areas with significant flux, but without substantial brightness ( upper right). The arrow points towards the limb. |
| Open with DEXTER |
A photometric measurement of PFe was performed to study their contrast and its variation towards the limb as observations were taken from
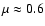 to
to
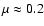 .
Since PFe are bright magnetic structures, the combination of thresholds in intensity and magnetic field strengths allows selection of the PFe in our FOVs. We required for the broadband intensity of PFe,
.
Since PFe are bright magnetic structures, the combination of thresholds in intensity and magnetic field strengths allows selection of the PFe in our FOVs. We required for the broadband intensity of PFe,
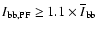 ,
with
,
with
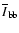 the average broadband intensity in the neighbourhood of the facula, and for the flux density measured with the COG method
the average broadband intensity in the neighbourhood of the facula, and for the flux density measured with the COG method
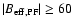 G (
G (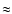
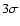 of the noise). Magnetic field signatures and facular brightenings do not necessarily coincide. Especially close to the limb, the magnetic fields appear to be displaced from the brightenings towards the disc centre (e.g., Okunev & Kneer 2005,2004, and references therein). The identification of magnetic PFe was therefore performed "manually'' by inspection of the intensity images and magnetograms. In addition, a size threshold for the minimum area of
of the noise). Magnetic field signatures and facular brightenings do not necessarily coincide. Especially close to the limb, the magnetic fields appear to be displaced from the brightenings towards the disc centre (e.g., Okunev & Kneer 2005,2004, and references therein). The identification of magnetic PFe was therefore performed "manually'' by inspection of the intensity images and magnetograms. In addition, a size threshold for the minimum area of
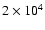 km2 (corresponding to three contiguous pixels on the detector) was used.
km2 (corresponding to three contiguous pixels on the detector) was used.
Before evaluating the contrasts, the intensities were normalised to a second order surface in each FOV to eliminate the centre-to-limb variation. The contrast C is defined as
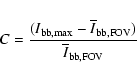 |
(7) |
where
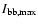 denotes the maximum broadband intensity in each faculae. It turned out to have a negligible effect irrespective of whether the
denotes the maximum broadband intensity in each faculae. It turned out to have a negligible effect irrespective of whether the
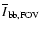 surfaces were calculated including or excluding the faculae or whether the contrast was measured relative to the average of the local surrounding intensity.
surfaces were calculated including or excluding the faculae or whether the contrast was measured relative to the average of the local surrounding intensity.
Figure 3 depicts the average contrast of PFe from each FOV as a function of heliocentric angle. The error bars correspond to the standard deviation of facular contrast within each FOV. The dashed straight lines are linear fits to the facular contrast. Obviously, towards the disc centre, the facular contrast decreases, similarly as for equatorial faculae. Towards the limb, the contrast stays constant at
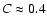 or is possibly slightly increasing. In any case, the PF contrast does not decrease, within our limited range of observations (
or is possibly slightly increasing. In any case, the PF contrast does not decrease, within our limited range of observations (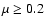 ), in contradiction with the result presented by Okunev & Kneer (2004) and in agreement with the centre-to-limb variation obtained with the same speckle imaging as here by Hirzberger & Wiehr (2005). Also the amplitude of the PF contrast is in good agreement with that given by the latter authors. This finding is relevant since it requires a revision of the facular models, i.e. of their physical structure (cf. Okunev & Kneer 2005; Spruit 1976, and references therein). We suggest that a temperature higher than those in these models at elevated photospheric layers, can explain the high PF contrasts near the limb. Such enhanced temperatures are a natural consequence of irradiation from the hot flux tube walls, as demonstrated e.g. in two-dimensional radiative equilibrium simulations by Fabiani Bendicho et al. (1992).
), in contradiction with the result presented by Okunev & Kneer (2004) and in agreement with the centre-to-limb variation obtained with the same speckle imaging as here by Hirzberger & Wiehr (2005). Also the amplitude of the PF contrast is in good agreement with that given by the latter authors. This finding is relevant since it requires a revision of the facular models, i.e. of their physical structure (cf. Okunev & Kneer 2005; Spruit 1976, and references therein). We suggest that a temperature higher than those in these models at elevated photospheric layers, can explain the high PF contrasts near the limb. Such enhanced temperatures are a natural consequence of irradiation from the hot flux tube walls, as demonstrated e.g. in two-dimensional radiative equilibrium simulations by Fabiani Bendicho et al. (1992).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{7739fig3.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg65.gif) |
Figure 3:
Contrast C of PFe and of granules vs. 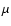 .
The asterisks give the mean contrast of PFe within one FOV and the error bars represent the standard deviation of facular contrast within the same FOV. The dashed straight lines are linear fits to the facular contrast. The crosses show twice the rms contrast of granules in the FOVs with no (or little) magnetic flux, .
The asterisks give the mean contrast of PFe within one FOV and the error bars represent the standard deviation of facular contrast within the same FOV. The dashed straight lines are linear fits to the facular contrast. The crosses show twice the rms contrast of granules in the FOVs with no (or little) magnetic flux,
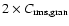 (see text). The dotted straight line is a least square fit to the granular contrast.
(see text). The dotted straight line is a least square fit to the granular contrast. |
| Open with DEXTER |
For comparison, the contrast variation towards the limb of the brightest, non-magnetic granules in the FOVs is also shown in Fig. 3. As an estimate for this contrast we use
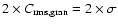 .
(For a pure two-dimensional sinusoidal intensity distribution one has
.
(For a pure two-dimensional sinusoidal intensity distribution one has
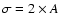 with amplitude A. For two-dimensional Gaussian noise, the threshold
with amplitude A. For two-dimensional Gaussian noise, the threshold
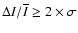 gives the brightest intensity values.) The crosses in Fig. 3 represent the measurements (not corrected for foreshortening or parasitic light), the straight dotted line, not based on a theoretical interpretation, is a fit to the data. The fluctuation of the granular contrast about the straight line is a result of the low numbers of granules with contrast
gives the brightest intensity values.) The crosses in Fig. 3 represent the measurements (not corrected for foreshortening or parasitic light), the straight dotted line, not based on a theoretical interpretation, is a fit to the data. The fluctuation of the granular contrast about the straight line is a result of the low numbers of granules with contrast 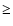
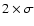 in each FOV. The decrease towards the limb and, apart from the factor of two, the amplitudes compare well with the values obtained by Sánchez Cuberes et al. (2000, see also references to earlier work therein). Towards the disc centre, the bright granules and faculae possess similar contrast, i.e. near the disc centre, faculae are difficult to detect among the bright granules in broadband (excluding G-band) or continuum observations alone (Fig. 2).
in each FOV. The decrease towards the limb and, apart from the factor of two, the amplitudes compare well with the values obtained by Sánchez Cuberes et al. (2000, see also references to earlier work therein). Towards the disc centre, the bright granules and faculae possess similar contrast, i.e. near the disc centre, faculae are difficult to detect among the bright granules in broadband (excluding G-band) or continuum observations alone (Fig. 2).
4.2 Number of PFe, magnetic polarity, and area distributions
The same criteria as described above for the definition of PFe can be used to estimate their total number present at one solar pole during the observation, at the epoch of minimum sunspot activity. Due to the similarity in contrast of granulation and PFe towards the disc centre, special care was taken when looking at those FOVs.
At the northern solar pole, most of the PFe have the same magnetic polarity as the global magnetic field. Yet in contrast to the conjecture raised by Okunev & Kneer (2004) which was based on a much smaller sample than analysed here, some PFe possess opposite polarity (Fig. 2). In fact, such opposite-polarity faculae are not uncommon, especially near the south pole.
Negative and positive polarity faculae appear as isolated magnetic patches, rather than in bipolar combinations, in agreement with the magnetograms shown by Lin et al. (1994).
Table 1 gives, in its first column, the numbers of PFe for the north and south pole separately as well as for positive and negative magnetic polarities. These numbers are extrapolated values from the observed FOVs to one total polar cap area,
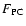 ,
with occurrence of PFe. The latter is given by
,
with occurrence of PFe. The latter is given by
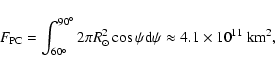 |
(8) |
where the integration is taken over the latitudes 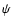 of a polar cap at which PFe occur during maximum appearance and
of a polar cap at which PFe occur during maximum appearance and 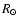 is the solar radius. The total numbers of PFe detected were 221 and 26 at the northern and southern polar caps, respectively. The coverage of the polar areas with our FOVs amounted to 5.5% at the northern cap and to 2.1% at the southern cap. The extrapolated numbers are clearly different for the north and south poles. A similar asymmetry between the two poles was also noticed by Benevolenskaya (2004), who analysed SOHO/MDI magnetograms between latitudes 78
is the solar radius. The total numbers of PFe detected were 221 and 26 at the northern and southern polar caps, respectively. The coverage of the polar areas with our FOVs amounted to 5.5% at the northern cap and to 2.1% at the southern cap. The extrapolated numbers are clearly different for the north and south poles. A similar asymmetry between the two poles was also noticed by Benevolenskaya (2004), who analysed SOHO/MDI magnetograms between latitudes 78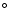 and 88
and 88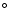 .
We point out that, with the achieved spatial resolution, the total numbers of PFe are one to two orders of magnitude larger than those estimated by Sheeley (1966).
.
We point out that, with the achieved spatial resolution, the total numbers of PFe are one to two orders of magnitude larger than those estimated by Sheeley (1966).
Table 1:
Extrapolated number counts and extrapolated areas of PFe.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7739fig4.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg76.gif) |
Figure 4:
Distributions of PF areas determined with the COG method, i.e. from the number of pixels covered by the magnetic field of the PFe, for the northern polar cap ( left two panels) and the southern cap ( right two panels). The areas are corrected for foreshortening (dividing by 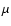 ). The dashed vertical line in the upper left panel indicates the area of a circular PFe with 1 ). The dashed vertical line in the upper left panel indicates the area of a circular PFe with 1
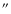 diameter.
diameter. |
| Open with DEXTER |
The area
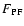 of a PF is measured from its magnetic field, i.e. from the number of pixels covered by the magnetic field of the PFe. The effective field strength, determined with the COG method, is again required to have
of a PF is measured from its magnetic field, i.e. from the number of pixels covered by the magnetic field of the PFe. The effective field strength, determined with the COG method, is again required to have
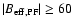 G. Surprisingly, the field strengths of PFe did not vary much towards the limb (see Sect. 4.3 below), indicating that the geometry of PF fields is more complex than just a vertical flux tube with constant diameter (e.g. numerical simulation results by Vögler et al. 2005; Keller et al. 2004).
Figure 4 shows the area distributions after correction for foreshortening, i.e. after dividing by
G. Surprisingly, the field strengths of PFe did not vary much towards the limb (see Sect. 4.3 below), indicating that the geometry of PF fields is more complex than just a vertical flux tube with constant diameter (e.g. numerical simulation results by Vögler et al. 2005; Keller et al. 2004).
Figure 4 shows the area distributions after correction for foreshortening, i.e. after dividing by 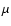 .
In the left panels, the observed distributions for the northern polar cap are depicted, with negative and positive magnetic polarities in the upper and lower panels, respectively. The right panels are for the southern polar cap. PFe with polarity opposite to the global magnetic field tend to be smaller than those with the same polarity as the global field.
.
In the left panels, the observed distributions for the northern polar cap are depicted, with negative and positive magnetic polarities in the upper and lower panels, respectively. The right panels are for the southern polar cap. PFe with polarity opposite to the global magnetic field tend to be smaller than those with the same polarity as the global field.
The total areas in PFe, extrapolated from the observed FOVs to the polar cap areas, are also given in Table 1. Here we see again a strong asymmetry between the northern and southern polar caps.
Table 2 gives the variation with 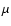 of the number of analysed PFe for intervals of
of the number of analysed PFe for intervals of
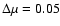 .
We note that the PFe counts are not related to the heliographic latitude
.
We note that the PFe counts are not related to the heliographic latitude 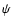 .
Apparently, the counts are lower for
.
Apparently, the counts are lower for  than for larger
than for larger 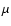 .
We interpret this as an observational selection effect: the AO system encounters increasing difficulties to lock onto a solar feature towards the limb. Although the PFe have high contrast, their apparent size and absolute brightness become smaller and their surrounding area becomes structureless with decreasing
.
We interpret this as an observational selection effect: the AO system encounters increasing difficulties to lock onto a solar feature towards the limb. Although the PFe have high contrast, their apparent size and absolute brightness become smaller and their surrounding area becomes structureless with decreasing 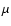 .
.
Table 2:
Number of observed PFe in intervals of
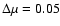 .
.
4.3 Magnetic fields and total flux
4.3.1 Weak field approximation and centre of gravity
The WFA and COG methods gave very similar results for
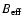 .
Figure 5 presents the centre-to-limb variation of the field strength determined with the COG method, irrespective of the magnetic polarity or whether the PF occurred at the solar north or south pole. The straight dashed line in Fig. 5 gives
.
Figure 5 presents the centre-to-limb variation of the field strength determined with the COG method, irrespective of the magnetic polarity or whether the PF occurred at the solar north or south pole. The straight dashed line in Fig. 5 gives
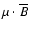 representing a hypothetical limb variation of the COG measurement for a purely vertical and constant flux density of
representing a hypothetical limb variation of the COG measurement for a purely vertical and constant flux density of
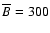 G. The measured
G. The measured
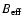 does not exhibit an obvious centre-to-limb variation. It is unlikely that the puzzling result, against naive expectation, is caused by instrumental
does not exhibit an obvious centre-to-limb variation. It is unlikely that the puzzling result, against naive expectation, is caused by instrumental
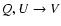 crosstalk. Our experience with simulations of crosstalk gives generally a "measured'' field strength weaker than the input field. This means that crosstalk would result in even more reduced measured fields towards the limb with increased Q and U signals.
crosstalk. Our experience with simulations of crosstalk gives generally a "measured'' field strength weaker than the input field. This means that crosstalk would result in even more reduced measured fields towards the limb with increased Q and U signals.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7739fig5.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg80.gif) |
Figure 5:
Variation towards the limb of PF magnetic field strengths
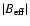 measured with the COG method. The asterisks represent averages from each PF. The straight dashed line gives
measured with the COG method. The asterisks represent averages from each PF. The straight dashed line gives
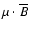 representing a hypothetical limb variation of the COG measurement for a purely vertical and constant flux density of
representing a hypothetical limb variation of the COG measurement for a purely vertical and constant flux density of
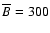 G. G. |
| Open with DEXTER |
The requirement
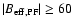 G to identify a PF does definitely not introduce a bias, i.e. missing counts towards the limb. Whenever a bright facula was seen near the limb its effective field strength was sufficiently large to be counted.
G to identify a PF does definitely not introduce a bias, i.e. missing counts towards the limb. Whenever a bright facula was seen near the limb its effective field strength was sufficiently large to be counted.
4.3.2 Strong field regime
We present in Fig. 6 histograms for the magnetic field strengths in PFe derived from the separation of the Stokes V extrema, i.e. assuming the SFR. The values for the north and south poles of the Sun are given by the solid and dashed histograms, respectively. The percentages (ordinate of Fig. 6) refer to the observed facular pixels, separately for the northern and southern polar caps. The criterion for an entry into the histograms was again
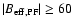 G in the COG measurements.
G in the COG measurements.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7739fig6.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg81.gif) |
Figure 6:
Histogram of magnetic field strengths from the separation of Stokes V extrema. The solid lines correspond to the northern PFe and the dashed lines to the southern PFe. |
| Open with DEXTER |
The V profiles could not be fitted at all pixels in the FOV with two Gaussians to determine the separation of their extrema. For this reason, the histograms in Fig. 6 show different statistical properties than those for the area distributions, Fig. 4, especially in the ratio of positive to negative magnetic polarity.
The histograms exhibit maxima at field strengths of 1400-1600 G. It was shown earlier that PFe harbour kilo-Gauss fields (Okunev & Kneer 2005; Okunev 2004; Homann et al. 1997). The latter two works also demonstrated by means of model calculations that the strong field tails in the distributions, towards 2000 G and beyond, arise from overestimating the strengths with the SFR method. For further use below we adopt a field strength of 1500 G at the base of PFe, i.e. where, on average,
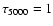 in the quiet Sun.
in the quiet Sun.
4.3.3 Total magnetic flux
From magnetic flux densities in PFe and from the areas of PFe extrapolated from the observed FOVs to the polar cap areas, we can conclude on the total magnetic fluxes from PFe.
Okunev et al. (2005) estimated the total magnetic flux from PFe to be much too low for the global magnetic flux at the polar caps, because approximately
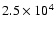 PFe would be needed, many more than observed.
PFe would be needed, many more than observed.
Sheeley (1966), via a calibration of the PF flux with equatorial faculae of similar size, obtained a flux of
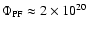 Mx per facula and arrived, with approximately 60 PFe present during maximum PF occurrence, at a total flux from a polar cap of
Mx per facula and arrived, with approximately 60 PFe present during maximum PF occurrence, at a total flux from a polar cap of
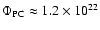 Mx.
For comparison, our estimate of the upper limit of the magnetic flux in one PF, assuming a circular shape with a diameter of 725 km (
Mx.
For comparison, our estimate of the upper limit of the magnetic flux in one PF, assuming a circular shape with a diameter of 725 km (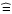 1
1
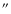 )
and a field strength of 1500 G, gives
)
and a field strength of 1500 G, gives
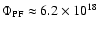 Mx. This is a factor of 30 less flux than Sheeley's (1966) estimate. Note that the area of a PFe with 1
Mx. This is a factor of 30 less flux than Sheeley's (1966) estimate. Note that the area of a PFe with 1
 diameter is significantly larger than the usual areas of observed PFe (Fig. 4).
diameter is significantly larger than the usual areas of observed PFe (Fig. 4).
According to Svalgaard et al. (1978) the average polar magnetic field is of the order of 6 G. With the polar cap area (Eq. (8)), one obtains a signed magnetic flux of
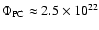 Mx. From the variation of the average magnetic flux density towards the poles, these authors obtained a total flux
Mx. From the variation of the average magnetic flux density towards the poles, these authors obtained a total flux
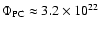 Mx.
Mx.
The (signed) magnetic flux in the fast wind,
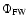 ,
calculated at 1 AU with
,
calculated at 1 AU with
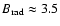 nT (=35
nT (=35 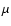 G) (Smith & Balogh 1995) is
G) (Smith & Balogh 1995) is
Here the integration from 25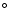 to 90
to 90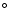 takes into account the angular expansion of the solar wind (McComas et al. 2000). The flux in the fast solar wind is consistent with the value given by Svalgaard et al. (1978). For the magnetic flux at 1 AU approximately 4500 PFe, with flux per PF from our optimum estimate, are needed.
takes into account the angular expansion of the solar wind (McComas et al. 2000). The flux in the fast solar wind is consistent with the value given by Svalgaard et al. (1978). For the magnetic flux at 1 AU approximately 4500 PFe, with flux per PF from our optimum estimate, are needed.
Benevolenskaya (2004), from an analysis of SOHO/MDI magnetograms between
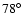 and
and
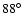 ,
obtained total unsigned magnetic fluxes for the north polar cap
,
obtained total unsigned magnetic fluxes for the north polar cap
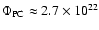 Mx and for the south polar cap
Mx and for the south polar cap
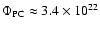 Mx. She pointed out the asymmetry in both poles, however it was not as strong as that identified in the present study.
Mx. She pointed out the asymmetry in both poles, however it was not as strong as that identified in the present study.
The above numbers for the total magnetic fluxes are compiled in Table 3. We compare them with the values obtained in the present study from PFe. For this, we took the areas (in cm2) of PFe,
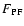 ,
from Table 1 and multiplied them with a magnetic filling factor
,
from Table 1 and multiplied them with a magnetic filling factor 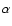 and a field strength of 1500 G, i.e.
and a field strength of 1500 G, i.e.
![\begin{displaymath}\Phi_{\rm PC}=\alpha\times1500\times\left(\sum F_{\rm PF}\right)~[{\rm Mx}] .
\end{displaymath}](/articles/aa/full/2007/40/aa7739-07/img100.gif) |
(11) |
This was done separately for the northern and southern polar caps, for both magnetic polarities. Magnetic filling factors of
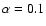 ,
,
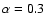 ,
and
,
and
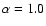 were used. In view of the COG measurements of PF magnetic fields (Fig. 5) which gave strengths of
were used. In view of the COG measurements of PF magnetic fields (Fig. 5) which gave strengths of 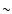 100 G without variation towards the limb, a magnetic filling factor of
100 G without variation towards the limb, a magnetic filling factor of
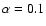 appears reasonable.
appears reasonable.
Table 3 shows that, with this latter filling factor, the summed magnetic fluxes in PFe are lower by factors 30-100 than needed, to account for the fluxes emanating from the polar caps of the Sun. This is in agreement with the estimate by Okunev et al. (2005). Around the south pole, more flux is "missing'' in the PFe than near the north pole. Yet, since the southern polar area with
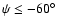 was not well observable during the end of August 2005, the extrapolation from the observations to the polar cap is uncertain for the south pole.
was not well observable during the end of August 2005, the extrapolation from the observations to the polar cap is uncertain for the south pole.
The filling factor 1.0 appears unlikely as we would have seen much stronger magnetic signals. But even with
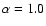 ,
the measured total signed fluxes are too low by factors of 3 and 10 for the northern and southern polar caps, respectively.
,
the measured total signed fluxes are too low by factors of 3 and 10 for the northern and southern polar caps, respectively.
We include in Table 3 the magnetic fluxes in non-facular structures (see the example shown in Fig. 2), but only for the north pole. For their selection, a flux density of
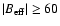 G within at least three contiguous pixels was also required. Usually, the field strengths (from COG) of the non-magnetic structures were smaller than 100 G and, on average, their areas a little smaller than those of PFe. We see from Table 3 that these non-facular structures can account for the same amount of magnetic flux as the PFe. Yet here also a filling factor of 1.0 is unrealistic. We expect that in this case they would appear as bright structures. Thus the non-PFe magnetic structures seen in this study also do not harbour the missing flux.
G within at least three contiguous pixels was also required. Usually, the field strengths (from COG) of the non-magnetic structures were smaller than 100 G and, on average, their areas a little smaller than those of PFe. We see from Table 3 that these non-facular structures can account for the same amount of magnetic flux as the PFe. Yet here also a filling factor of 1.0 is unrealistic. We expect that in this case they would appear as bright structures. Thus the non-PFe magnetic structures seen in this study also do not harbour the missing flux.
Table 3:
Total magnetic fluxes
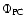 at the polar areas of the Sun around the minimum of the sunspot cycle. The three numbers for the entries from this work refer to the fluxes with magnetic filling factor
at the polar areas of the Sun around the minimum of the sunspot cycle. The three numbers for the entries from this work refer to the fluxes with magnetic filling factor 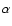 = 0.1,
= 0.1, 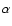 = 0.3, and
= 0.3, and 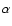 = 1.0, from left to right. The signs indicate the polarity.
= 1.0, from left to right. The signs indicate the polarity.
We made two further estimates as follows:
- 1.
- A measurement of 60 G in three contiguous pixels (as a minimum requirement for a PF identification) at
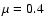 (as an example) gives after correction for foreshortening of the area, a flux of
(as an example) gives after correction for foreshortening of the area, a flux of
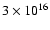 Mx. Then assume a magnetic feature which is spread due to limited resolution to a Gaussian field distribution of
Mx. Then assume a magnetic feature which is spread due to limited resolution to a Gaussian field distribution of
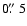 FWHM from which we measure a maximum field strength of 60 G. This structure contains a flux of
FWHM from which we measure a maximum field strength of 60 G. This structure contains a flux of 
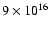 Mx, i.e. a factor of three more than the three pixels above. We conclude that the filling factor
Mx, i.e. a factor of three more than the three pixels above. We conclude that the filling factor 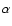 is possibly larger than 0.1.
is possibly larger than 0.1.
- 2.
- We adopt a total (extrapolated) number of detected PFe per polar cap of 3500 (Table 1). The polar areas with
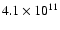 km2 of PFe occurrence contain approximately 500 supergranulation (or chromospheric) network cells (NCs) of
km2 of PFe occurrence contain approximately 500 supergranulation (or chromospheric) network cells (NCs) of
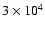 km average diameter. This yields 7 detected PFe per NC. We further assume an unsigned flux per polar area of
km average diameter. This yields 7 detected PFe per NC. We further assume an unsigned flux per polar area of
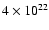 Mx, with 25% of it in flux of magnetic polarity opposite to the global general field at the solar poles (Table 3). Thus each NC harbours a flux of
Mx, with 25% of it in flux of magnetic polarity opposite to the global general field at the solar poles (Table 3). Thus each NC harbours a flux of
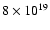 Mx. This flux would be contained in 13 PFe with the above upper flux estimate per PF of
Mx. This flux would be contained in 13 PFe with the above upper flux estimate per PF of
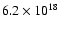 Mx. These numerous strong flux features were not identified and are definitely not present.
Mx. These numerous strong flux features were not identified and are definitely not present.
Magnetic fields are prone to become intermittent and concentrated flux tubes by convective collapse and to be advected to the borders of granular and supergranular convection cells (Hasan 1985; Vögler et al. 2005; Galloway & Weiss 1981). We therefore retain the picture of small-scale, strong-field flux tubes as the building blocks for the general, unipolar magnetic field at the solar poles. Mixed-polarity structures are not excluded, yet require sufficient surplus of one polarity over the other. Assuming a magnetic filling factor
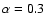 (Table 3), we measure in PFe 3-10% of the net flux in polar areas. The magnetic non-PFe structures in the polar areas detected in this investigation also carry much too little flux to account for the global magnetic field at the poles of the Sun.
(Table 3), we measure in PFe 3-10% of the net flux in polar areas. The magnetic non-PFe structures in the polar areas detected in this investigation also carry much too little flux to account for the global magnetic field at the poles of the Sun.
We conclude that the overwhelming part of the total flux is still hidden in smaller flux tubes or bundles with fewer flux tubes than those seen in PFe with the present resolution. We suggest that PFe represent the "large-scale'' end of a distribution of flux tubes with kilo-Gauss field strength, with increasing number but decreasing magnetic flux towards smaller scales.
4.4 Velocities
A statistical study of LOS velocities in PFe was performed. First, an analysis of the variation of velocities towards the limb was carried out. Studying separately upflows and downflows, we found an increase in both of them towards the disc centre. In Fig. 7 the mean velocities, determined from the COG shifts of the I profiles, of PFe within each FOV are depicted. The error bars correspond to the standard deviation of facular velocities within the same FOV, negative velocities are towards the observer, and zero reference velocity refers to the average of all line positions in the FOVs. The dotted straight line is the least square fit to the data. A clear dependence of velocities on 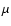 is seen, in the sense of increasing blueshift towards the disc centre. On average, there is a surplus of negative velocities, i.e. flows towards the observer. We interpret this as predominant up-flows in the bright convective elements as the main constituents of faculae (Fig. 2). Regarding the observed downflows, one explanation is that near the limb, at
is seen, in the sense of increasing blueshift towards the disc centre. On average, there is a surplus of negative velocities, i.e. flows towards the observer. We interpret this as predominant up-flows in the bright convective elements as the main constituents of faculae (Fig. 2). Regarding the observed downflows, one explanation is that near the limb, at 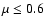 ,
and depending on the inclination of the convective up- and down-flows, the velocities may also appear in the direction away from the observer.
,
and depending on the inclination of the convective up- and down-flows, the velocities may also appear in the direction away from the observer.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{7739fig7.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg116.gif) |
Figure 7:
Variation towards the limb of velocities in PFe measured with the COG method from Stokes I profiles. Asterisks represent the mean velocity of PFe for each FOV and the error bars are the standard deviation of facular velocities within the same FOV. Reference zero velocity (horizontal dashed line) is the average of all line positions (from COG) in the corresponding FOVs. The dotted line is a linear regression. Positive velocities are away from the observer. |
| Open with DEXTER |
Second, Fig. 8 shows separately for PFe near the north and south poles, the velocities measured from all PFe pixels with the COG method applied to the I profiles and with the zero-crossing of the V profiles. As is also seen in Fig. 7, the PF I profiles tend to be blue-shifted, with velocities
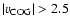 km s-1. The average COG velocities are -0.30 km s-1 and -0.61 km s-1 at the north and south pole, respectively. The velocities from the V zero-crossings are as well spread between
km s-1. The average COG velocities are -0.30 km s-1 and -0.61 km s-1 at the north and south pole, respectively. The velocities from the V zero-crossings are as well spread between 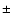 2 km s-1, with averages
2 km s-1, with averages
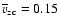 km s-1 and
km s-1 and
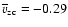 km s-1 at the north and south pole, respectively.
km s-1 at the north and south pole, respectively.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{7739fig8.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg121.gif) |
Figure 8:
Velocities measured from Doppler shift of Stokes I COG and from V zero-crossing. Reference zero velocity is the average of the line positions in the FOVs. Vertical dotted lines indicate the average velocities. Positive velocities are away from the observer. |
| Open with DEXTER |
These findings, i.e. a tendency to negative velocities measured in I profiles and, within the measurement accuracy, zero average velocity from V zero-crossings, is consistent with the results by Okunev & Kneer (2004, see their Fig. 11). After adding a velocity due to the gravitational limb effect (Schröter 1957), a net up-flow was found by the latter authors. Okunev et al. (2005) argued that very few PFe with an up-flow of
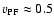 km s-1 would suffice to feed the fast solar wind from the polar coronal holes. In view of the large width of the velocity distributions and in view of the limited accuracy, we refrain from further estimates into this direction, especially since the reference zero velocity in the present observations refers to the average of the line positions in the FOVs, not to the position of the average I profile. This means that the limb effect must not be taken into account in the determination of the zero veloctiy. We conclude that a method of infering the properties of PF flows is to compare the observed velocities with numerical magneto-hydrodynamic simulations of facular magnetic flux tubes and bundles of flux tubes.
km s-1 would suffice to feed the fast solar wind from the polar coronal holes. In view of the large width of the velocity distributions and in view of the limited accuracy, we refrain from further estimates into this direction, especially since the reference zero velocity in the present observations refers to the average of the line positions in the FOVs, not to the position of the average I profile. This means that the limb effect must not be taken into account in the determination of the zero veloctiy. We conclude that a method of infering the properties of PF flows is to compare the observed velocities with numerical magneto-hydrodynamic simulations of facular magnetic flux tubes and bundles of flux tubes.
5 Conclusions
This study intended to shed light on the physical structure of PFe of the Sun and their role for the global magnetic field. To this end, observations during maximum appearance of PFe (and minimum sunspot activity) were performed with large coverage of the polar areas. During the observations, the northern pole was most visible, thus most of the observations were taken from the northern polar cap. To detect as many PFe as possible, high spatial resolution measurements in Stokes I and V were performed with speckle methods, yielding a spatial resolution of
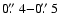 .
.
At the time of the observations, only I and V could be measured with the "Göttingen'' FPI spectro-polarimeter. Thus, the instrumental
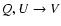 crosstalk had to be estimated, and corrections were not applied to V. Our estimates showed that the magnetic fields
crosstalk had to be estimated, and corrections were not applied to V. Our estimates showed that the magnetic fields
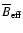 ,
determined with the centre-of-gravity method (Rees & Semel 1979), are measured too low by
,
determined with the centre-of-gravity method (Rees & Semel 1979), are measured too low by  20%, possibly still lower near the solar limb with decreasing V and increasing Q,U signals. Yet the results on PF counts and on total flux estimates from the polar caps are not affected by the instrumental crosstalk.
20%, possibly still lower near the solar limb with decreasing V and increasing Q,U signals. Yet the results on PF counts and on total flux estimates from the polar caps are not affected by the instrumental crosstalk.
The following are the main conclusions of this work:
- 1.
- The earlier finding by Okunev & Kneer (2004) on the decrease of the facular contrast towards the limb has been revised. In the present study, we find that the contrast stays rather constant towards the limb, in agreement with the results by Hirzberger & Wiehr (2005) from equatorial faculae.
- 2.
- Several thousand PFe were found after extrapolation of the area covered by the observations to the polar caps in which PFe occur, many more than assumed hitherto. The north and south poles behaved asymmetrically. At the time of observation, the southern polar cap contained about three times fewer PFe than the northern polar cap. Yet during the observational period for this study, many fewer, and thus not sufficiently conclusive, data could be taken from the southern polar cap than from the region around the north pole.
- 3.
- There exist faculae with magnetic fields of polarity opposite to the global magnetic fields at the solar poles. These contain of the order of 25% of the unsigned flux in PFe.
- 4.
- Many faculae of subarcsec size were found. The smaller the covered area, the larger the number count.
- 5.
- The center-of-gravity method (Rees & Semel 1979) gave no variation of the measured field strength towards the limb, presumably because the magnetic structures of PFe are not simply vertically oriented but more complex.
- 6.
- The magnetic flux contained in the PFe studied here is too small by an order of magnitude to account for the global flux from the solar poles. The north and south poles also behaved asymmetrically in relation to the amount of magnetic flux. From the south pole, a factor of three more magnetic flux is "missing'' compared to the north pole.
- 7.
- The non-PFe flux seen in this study is of the same order as the PFe flux. Thus, it also can clearly not account for the global magnetic flux.
- 8.
- The Stokes I profiles from PFe exhibit Doppler shifts corresponding to velocities of up to 2.5 km s-1 with average velocities of
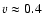 km s-1 towards the observer. The average velocities from V zero-crossings are close to zero. Comparison with numerical magneto-hydrodynamic simulations are needed to understand the dynamics revealed by the velocity observations within PFe and in their vicinity.
km s-1 towards the observer. The average velocities from V zero-crossings are close to zero. Comparison with numerical magneto-hydrodynamic simulations are needed to understand the dynamics revealed by the velocity observations within PFe and in their vicinity.
Magnetic fields in the solar photosphere are destined to be advected by convective flows and to collapse to intense flux tubes (Hasan 1985; Vögler et al. 2005; Galloway & Weiss 1981). It is thus unlikely that the global polar field of the Sun is rooted in diffuse fields of 5-6 G measured as average flux density by Svalgaard et al. (1978). Instead, we keep the picture of small-scale kilo-Gauss fields as the building blocks of the magnetic fields at the solar poles. The PFe found in this study harbour apparently too little flux to cover the total flux from the poles. There must exist many more flux regions, smaller still than those detected here and eventually not related with brightenings, i.e. with faculae proper. The PFe seen so far may be considered as the "large-scale'' end of a wealth of tiny magnetic strands in the polar caps. The numerical modelling by Baumann et al. (2004,2006) of surface flux transport via meridional flows suggests that the magnetic flux in PFe and thousands more small-scale flux tubes are disconnected remnants from the activity belts closer to the solar equator. Higher polarimetric sensitivity and higher spatial resolution than are available at present are needed to study the very small-scale flux tubes or bundles of flux tubes at the solar poles. They are certainly relevant for the corona above the solar poles and the fast solar wind from the polar coronal holes.
Acknowledgements
J.B.R. thanks the Deutsche Forschungsgemeinschaft (DFG) for a Ph.D. grant, 418 SPA-112/15/04. The work of OVO was partly supported by a DFG visiting scholarship, 436 RUS 17/61/05. K.G.P. acknowledges the financial support by the Deutsche Forschungsgemeinschaft through grants Kn 152/29-1,2. BS-AN thanks the Max-Planck-Gesellschaft for a Ph.D. grant of the International Max Planck Research School On Physical Processes in the Solar System and Beyond. The Vacuum Tower Telescope is operated by the Kiepenheuer-Institut für Sonnenphysik, Freiburg, at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias.
- Axford, W. I.,
& McKenzie, J. F. 1997, in Cosmic Winds and the Heliosphere,
ed. J. R. Jokipii, C.- P. Sonett, & M. S. Giampapa (Tucson:
Arizona University Press), 31
(In the text)
- Baumann, I.,
Schmitt, D., Schüssler, M., & Solanki, S. K. 2004,
A&A, 426, 1075 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Baumann, I.,
Schmitt, D., & Schüssler, M. 2006, A&A, 446, 307 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bello González,
N., Okunev, O. V., Domínguez Cerdeña, I., Kneer, F.,
& Puschmann, K. G. 2005, A&A, 434, 317 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Benevolenskaya, E. E. 2004, A&A, 428, 5 [NASA ADS] [CrossRef] (In the text)
- de Boer, C. R.
1996, A&AS, 120, 195 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- DeForest, C.
E., Hoeksema, J. T., Gurman, J. B., et al. 1997,
Sol. Phys., 175, 393 [NASA ADS] [CrossRef] (In the text)
-
Delaboudinière, J.-P., Artzner, G. E., Brunaud, J.,
et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] (In the text)
- Fabiani Bendicho,
P., Kneer, F., & Trujillo Bueno, J. 1992, A&A, 264,
229 [NASA ADS] (In the text)
- Galloway, D.
J., & Weiss, N. O. 1981, ApJ, 243, 945 [NASA ADS] [CrossRef]
- Hasan, S. S. 1985,
A&A, 151, 69 [NASA ADS]
- Homann, T., Kneer,
F., & Makarov, V. I. 1997, Sol. Phys., 175, 81 [NASA ADS] [CrossRef] (In the text)
- Hirzberger,
J., & Wiehr, E. 2005, A&A, 438, 1059 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Keller, C. U.,
& von der Lühe, O. 1992, A&A, 261, 321 [NASA ADS] (In the text)
- Keller, C. U.,
Schüssler, M., Vögler, A., & Zakharov, V. 2004, ApJ,
607, L59 [NASA ADS] [CrossRef]
- Landi Degl'Innocenti,
E. 1992, in Solar Observations: Techniques and Interpretation,
First Canary Islands Winter School, ed. F. Sánchez, M.
Collados, & M. Vázquez (Cambridge, UK: Cambridge Univ.
Press), 77
(In the text)
- Lin, H., Varsik, J.,
& Zirin, H. 1994, Sol. Phys., 155, 243 [NASA ADS] [CrossRef] (In the text)
- Makarov, V. I., &
Sivaraman, K. R. 1989, Sol. Phys., 123, 367 [NASA ADS] [CrossRef]
- Makarov, V. I.,
Tlatov, A. G., & Sivaraman, K. R. 2003a, Astron. Nachr., 324,
382 [NASA ADS]
- Makarov, V. I.,
Tlatov, A. G., & Sivaraman, K. R. 2003b, Sol. Phys., 214,
41 [NASA ADS] [CrossRef]
-
McComas, D. J., Barraclough, B. L.,
Funsten, H. O., et al. 2000,
J. Geophys. Res., 105(A5), 10419
(In the text)
- Okunev, O. V.
2004, PhD thesis, Göttingen university
(In the text)
- Okunev, O. V.,
& Kneer, F. 2004, A&A, 425, 321 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Okunev, O. V.,
& Kneer, F. 2005, A&A, 439, 323 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Okunev, O. V.,
Domínguez Cerdeña, I., Puschmann, K. G., Kneer, F., &
Sánchez Almeida, J. 2005, Astron. Nachr., 326, 205 [NASA ADS] (In the text)
- Puschmann, K.
G., Kneer, F., Seelemann, T., & Wittmann, A. D. 2006, A&A,
445, 337 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Puschmann,
K. G., & Sailer, M. 2006, A&A, 454, 1011 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rees, D. E., &
Semel, M. D. 1979, A&A, 74, 1 [NASA ADS]
- Sánchez
Cuberes, M., Bonet, J. A., Vázquez, M., & Wittmann, A. D.
2000, A&A, 538, 940 [NASA ADS] (In the text)
- Scherrer, P.
H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys.,
162, 129 [NASA ADS] [CrossRef] (In the text)
-
Schröter, E. H. 1957, ZAp, 41, 141 [NASA ADS] (In the text)
-
Schüssler, M., & Rempel, M. 2005, A&A, 441, 337 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Semel, M. D. 1967,
Ann. Astrophys., 30, 513 [NASA ADS]
- Sheeley, N. R.,
Jr. 1964, ApJ, 140, 731 [NASA ADS] [CrossRef]
- Sheeley, N. R.,
Jr. 1966, ApJ, 144, 723 [NASA ADS] [CrossRef] (In the text)
- Sheeley, N. R.,
Jr. 1991, ApJ, 374, 386 [NASA ADS] [CrossRef]
- Smith, E. J., &
Balogh, A. 1995, Geophys. Res. Lett., 22, 3317 [NASA ADS] [CrossRef] (In the text)
- Spruit, H. C. 1976,
Sol. Phys., 50, 269 [NASA ADS] [CrossRef]
- Steiner, O. 2007,
in Modern Solar Facilities - Advanced Solar Science, ed.
F. Kneer, K. G. Puschmann, &
A. D. Wittmann, Universitätsverlag Göttingen,
321
(In the text)
- Svalgaard,
L., Duvall, T. L., Jr., & Scherrer, P. H. 1978,
Sol. Phys., 58, 225 [NASA ADS] [CrossRef] (In the text)
- Tu, C.-Y., Zhou, C.,
Marsch, E., et al. 2005, Science, 308, 519 [NASA ADS] [CrossRef] (In the text)
- von der Lühe, O.
1984, J. Opt. Soc. Am. A1, 510
(In the text)
- von der Lühe,
O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003, SPIE, 4853,
187 [NASA ADS] (In the text)
- Vögler, A.,
Shelyag, S., Schüssler, M., et al. 2005, A&A, 429,
335 [NASA ADS] [CrossRef] [EDP Sciences]
- Waldmeier, M. 1955,
ZAp, 38, 37 [NASA ADS]
- Waldmeier, M. 1962,
ZAp, 54, 260 [NASA ADS]
- Wang, Y.-M., &
Sheeley, N. R., Jr. 2003, ApJ, 599, 1404 [NASA ADS] [CrossRef] (In the text)
- Wang, Y.-M., Sheeley,
N. R., Jr., & Lean, J. 2002, ApJ, 580, 1188 [NASA ADS] [CrossRef] (In the text)
- Weigelt, G. P.
1977, Optics Comm., 21, 55 [NASA ADS] [CrossRef] (In the text)
- Wiegelmann,
T., Xia, L. D., & Marsch, E. 2005, A&A, 432, L1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wilhelm, K.,
Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162,
189 [NASA ADS] [CrossRef] (In the text)
- Wilhelm, K.,
Marsch, E., Dwivedi, B. N., et al. 1998, ApJ, 500, 1023 [NASA ADS] [CrossRef]
- Wilhelm, K.,
Dammasch, I. E., Marsch, E., & Hassler, D. M. 2000, A&A,
353, 749 [NASA ADS]
- Yi, Z., & Molowny
Horas, R. L. 1992, LEST Technical Report 56, ed. O. Engvold, &
Ø. Hauge, Institute of Theoretical Astrophysics, Oslo
University, 69
(In the text)
Copyright ESO 2007
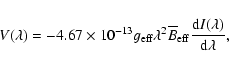
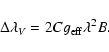
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{7739fig1.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg41.gif)
![$\displaystyle \frac{\int[I_{\rm c}-I_+(\lambda)]~\lambda~{\rm d}\lambda}{\int[I...
...lambda)]~\lambda~{\rm d}\lambda}{\int[I_{\rm c}-I_-(\lambda)]~{\rm d}\lambda} ,$](/articles/aa/full/2007/40/aa7739-07/img47.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7739fig2.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg52.gif)
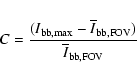
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{7739fig3.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg65.gif)
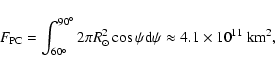
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7739fig4.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7739fig5.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg80.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7739fig6.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg81.gif)
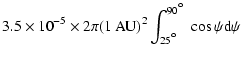
![\begin{displaymath}\Phi_{\rm PC}=\alpha\times1500\times\left(\sum F_{\rm PF}\right)~[{\rm Mx}] .
\end{displaymath}](/articles/aa/full/2007/40/aa7739-07/img100.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{7739fig7.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg116.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{7739fig8.ps}\end{figure}](/articles/aa/full/2007/40/aa7739-07/Timg121.gif)