A&A 474, 43-53 (2007)
DOI: 10.1051/0004-6361:20077650
S. Verley1,2,3 - F. Combes1 - L. Verdes-Montenegro2 - G. Bergond2,4 - S. Leon5,2
1 - LERMA, Observatoire de Paris, 61 avenue de l'Observatoire, 75014 Paris, France
2 -
Instituto de Astrofísica de Andalucía - CSIC, C/ Camino Bajo de Huétor, 50, 18008 Granada, Spain
3 -
INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi, 5, 50125 Firenze, Italy
4 -
GEPI, Observatoire de Paris-Meudon, 61, avenue de l'Observatoire, 75014 Paris, France
5 -
Instituto de RadioAstronomía Milimétrica,
Avenida Divina Pastora, 7, Núcleo Central, 18012 Granada, Spain
Received 16 April 2007 / Accepted 20 July 2007
Abstract
Context. Star formation depends strongly on both the local environment of galaxies and the internal dynamics of the interstellar medium. To disentangle the two effects, we obtained, in the framework of the AMIGA project, H![]() and Gunn r photometric data for more than 200 spiral galaxies lying in very low-density regions of the local Universe.
and Gunn r photometric data for more than 200 spiral galaxies lying in very low-density regions of the local Universe.
Aims. We characterise the H![]() emission, tracing current star formation, of the 45 largest and least inclined galaxies observed for which we estimate the torques between the gas and the bulk of the optical matter. We subsequently study the H
emission, tracing current star formation, of the 45 largest and least inclined galaxies observed for which we estimate the torques between the gas and the bulk of the optical matter. We subsequently study the H![]() morphological aspect of these isolated spiral galaxies.
morphological aspect of these isolated spiral galaxies.
Methods. Using Fourier analysis, we focus on the modes of the spiral arms and also on the strength of the bars, computing the torques between the gas and newly formed stars (H![]() ), and the bulk of the optical matter (Gunn r).
), and the bulk of the optical matter (Gunn r).
Results. We interpret the various bar/spiral morphologies observed in terms of the secular evolution experienced by galaxies in isolation. We also classify the different spatial distributions of star forming regions in barred galaxies. The observed frequency of particular patterns brings constraints on the lifetime of the various evolution phases. We propose an evolutive sequence accounting for the transitions between the different phases we observed.
Conclusions. Isolated galaxies do not appear to be preferentially barred or unbarred. Fitting the H![]() distributions using numerical simulations yields constraints on the star formation law, which is likely to differ from a genuine Schmidt law. In particular, it is probable that the relative velocity of the gas in the bar also needs to be taken into account.
distributions using numerical simulations yields constraints on the star formation law, which is likely to differ from a genuine Schmidt law. In particular, it is probable that the relative velocity of the gas in the bar also needs to be taken into account.
Key words: galaxies: general - galaxies: evolution - galaxies: kinematics and dynamics - galaxies: spiral - galaxies: statistics
The presence of a bar in a spiral galaxy is a striking feature and, as such, is one of the fundamental elements of the first morphological classification performed by Hubble. The bar (including ovals) frequency determined in galaxies depends on the wavelength of the images but is always higher than 65%. Some estimations based on NIR images, not affected by extinction and tracing mainly the old population, reveal that as many as 90% of the galaxies have bars (Seigar & James 1998).
Numerical simulations have established that bars in gas-rich spiral galaxies are short-lived structures (Bournaud & Combes 2002). At least two mechanisms have been proposed to weaken the bars. The first one is the build-up of a large central mass concentration, due to the gas inflow to the centre through the negative torques exerted on the gas by the bar (Athanassoula et al. 2005; Bournaud et al. 2005). These torques are proportional to the phase shift between the gas and the stellar bar. It is well known that the gas is concentrated on the leading side of the stellar bar (e.g. de Vaucouleurs & de Vaucouleurs 1963). The gravitational torque of the bar makes the gas lose angular momentum, driving it towards the centre and creating a central mass concentration. The latter is able to perturb the elongated orbits supporting the stellar bar, deflecting the stars passing close to the centre, so weakening the bar (Pfenniger & Norman 1990). However, Bournaud et al. (2005) have shown, using fully self-consistent simulations, that with gas parameters typical for normal spirals, the mass concentration is not sufficient to fully dissolve the bar, as was also claimed by Shen & Sellwood (2004).
The second proposed mechanism to weaken a bar is the bar torques themselves. The bar is a negative angular momentum wave, while the gas exerts a positive torque on the bar, due to the balance between action and reaction forces. The angular momentum lost by the gas is gained by the bar, which dissolves progressively. For typical Sb-Sc galaxies, the bar is destroyed in about 2 Gyr (Bournaud & Combes 2002). The observation of a high bar frequency from ![]() to
to
![]() (Jogee et al. 2004; Eskridge et al. 2002; Sheth et al. 2005) cannot therefore be interpreted to support the existence of robust, long-lived bars. Instead, this supports the frequent renewal of bars. Berentzen et al. (2004) have shown that interactions can only form bars in gas-poor galaxies, which is not the case for most spiral galaxies.
(Jogee et al. 2004; Eskridge et al. 2002; Sheth et al. 2005) cannot therefore be interpreted to support the existence of robust, long-lived bars. Instead, this supports the frequent renewal of bars. Berentzen et al. (2004) have shown that interactions can only form bars in gas-poor galaxies, which is not the case for most spiral galaxies.
Bar renewal can occur when the disks of spiral galaxies are replenished in cold gas through external accretion, able to increase significantly the disk to bulge ratio. Block et al. (2002) suggest that external accretion of gas in the disk of spirals plays a fundamental role in explaining the high fraction of barred spirals and the observed torque distribution. For instance, a recent study of M 33 by Block et al. (2004) illustrates that gas is feeding the galaxy through external accretion. Isolated, non-accreting spiral galaxies are very unlikely. To better understand the frequency of bars and their origin, measurements of the gravitational torques and bar forces in field galaxies have been made (Block et al. 2002; Buta et al. 2004; Laurikainen et al. 2004b,a), but not for a sample of isolated galaxies. Such a sample is provided by the AMIGA project (Analysis of the interstellar Medium of Isolated GAlaxies), which constitutes a statistically significant template in the study of star formation and galaxy evolution in denser environments. We used as a starting point the Catalogue of Isolated Galaxies (CIG) compiled by Karachentseva (1973, see Sect. 2) for which a careful reevaluation of degree of isolation is presented in Verley et al. (2007a,b). Previous AMIGA papers evaluate, refine and improve the sample in different ways including revised positions (Leon & Verdes-Montenegro 2003), optical characterisation (Verdes-Montenegro et al. 2005), morphological revision (Sulentic et al. 2006), analysis of mid- and far-infrared properties using data from the IRAS survey (Lisenfeld et al. 2007), and a study of the neutral (CO and H I) gas (Espada 2006; Espada et al. 2005). We also plan to study radio-continuum emission to determine current star formation rate and possible nuclear activity. The data are being released and periodically updated at http://www.amiga.iaa.es.
In this paper we present a study of a carefully selected subsample of AMIGA, which is described in detail in Sect. 2. The observations and main reduction steps are summarised in Sect. 3. Then, we analyse, through Fourier analysis of gravitational potential and density, the intensity of the perturbations in each of the 45 galaxies (Sect. 4). Numerical simulations (Sect. 5) of stars and gas in isolated galaxies give us the theoretically expected star formation. Our results are discussed in Sect. 6 and the conclusions are summarised in Sect. 7.
As explained above, the AMIGA catalogue is based on the CIG (Karachentseva 1973). This catalogue is a compilation of 1051 objects with apparent B magnitude brighter than 15.7 and declination >
![]() .
Karachentseva (1973) visually inspected the Palomar Sky Survey prints, trying to identify those galaxies in the Catalogue of Galaxies and Clusters of Galaxies (CGCG, Zwicky et al. 1968) that have no near neighbours. An extensive study of the isolation of these galaxies is presented in Verley et al. (2007a,b), as a part of the AMIGA project, and discussed in Sect. 6.
.
Karachentseva (1973) visually inspected the Palomar Sky Survey prints, trying to identify those galaxies in the Catalogue of Galaxies and Clusters of Galaxies (CGCG, Zwicky et al. 1968) that have no near neighbours. An extensive study of the isolation of these galaxies is presented in Verley et al. (2007a,b), as a part of the AMIGA project, and discussed in Sect. 6.
One objective of our project was to study the different aspects of H![]() emission from isolated spiral galaxies. With this aim, and in order to avoid well known biases due to flux- or magnitude-limited samples and to end with a complete and homogeneous sample, we kept all the galaxies in a volume-limited sample, i.e. with observed recession heliocentric velocities
emission from isolated spiral galaxies. With this aim, and in order to avoid well known biases due to flux- or magnitude-limited samples and to end with a complete and homogeneous sample, we kept all the galaxies in a volume-limited sample, i.e. with observed recession heliocentric velocities ![]() :
:
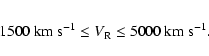
For the study presented here two further requirements were imposed:
The 224 galaxies comprising our sample for star formation studies, including the 45 studied in this paper, have been imaged in H![]() and Gunn r filters in order to trace the regions ionised by newly born stars (H II regions) and the older stellar component, respectively. The observations and data reduction will be described in more detail in a separate paper (Bergond et al., in prep.), and are just summarised here. For each galaxy, we selected the more appropriate red-shifted H
and Gunn r filters in order to trace the regions ionised by newly born stars (H II regions) and the older stellar component, respectively. The observations and data reduction will be described in more detail in a separate paper (Bergond et al., in prep.), and are just summarised here. For each galaxy, we selected the more appropriate red-shifted H![]() filter (narrow-band filter, typically 50 Å), based on its observed recession velocity and we used the Gunn r filter (broad-band filter, typically 870 Å) to subtract the continuum contribution affecting the narrow-band filter. The Gunn r broad-band images trace the stellar component of the galaxy, and the H
filter (narrow-band filter, typically 50 Å), based on its observed recession velocity and we used the Gunn r filter (broad-band filter, typically 870 Å) to subtract the continuum contribution affecting the narrow-band filter. The Gunn r broad-band images trace the stellar component of the galaxy, and the H![]() images show the young stars born from the gas (H II regions). The individual exposure times were 300 s for the Gunn r filter and 1200 s in H
images show the young stars born from the gas (H II regions). The individual exposure times were 300 s for the Gunn r filter and 1200 s in H![]() .
We applied small shifts between two successive exposures to enable treatment of bad pixels on the chip. We applied the usual corrections (bias subtraction and division by twilight flat fields) to remove the instrumental signature.
.
We applied small shifts between two successive exposures to enable treatment of bad pixels on the chip. We applied the usual corrections (bias subtraction and division by twilight flat fields) to remove the instrumental signature.
The removal of the continuum contribution to the flux in the images taken through the narrow-band H![]() filter is the most delicate task of the reduction process. James et al. (2004) tested various methods: numerical integration to find the ratio of the filter profile integrals, photometry of standard spectrophotometric stars through the pair of filters to find the scaling factor, use of foreground stars in the narrow-band and continuum images of each galaxy. The two last methods gave the most consistent and accurate results. The latter method has two advantages: it takes into account any changes in the sky transparency between the two images, and the possibility of using several stars improves the statistics and leads to the most accurate removal. Hence, we applied this last method to find the scaling factor to be applied to the images used for continuum subtraction. As the H
filter is the most delicate task of the reduction process. James et al. (2004) tested various methods: numerical integration to find the ratio of the filter profile integrals, photometry of standard spectrophotometric stars through the pair of filters to find the scaling factor, use of foreground stars in the narrow-band and continuum images of each galaxy. The two last methods gave the most consistent and accurate results. The latter method has two advantages: it takes into account any changes in the sky transparency between the two images, and the possibility of using several stars improves the statistics and leads to the most accurate removal. Hence, we applied this last method to find the scaling factor to be applied to the images used for continuum subtraction. As the H![]() wavelength is comprised in the Gunn r filter, a significant H
wavelength is comprised in the Gunn r filter, a significant H![]() emission would perturb the continuum removal. The uncertainties involved can be estimated in various ways. In a first approximation, with the hypothesis of negligible line emission (assuming a flat spectrum), the ratio of the width of the filters shows that the uncertainties amount to about 6% (using typical width of 50 and 870 Å). Photometry of the total emission on the Gunn r and H
emission would perturb the continuum removal. The uncertainties involved can be estimated in various ways. In a first approximation, with the hypothesis of negligible line emission (assuming a flat spectrum), the ratio of the width of the filters shows that the uncertainties amount to about 6% (using typical width of 50 and 870 Å). Photometry of the total emission on the Gunn r and H![]() -continuum images confirms that the H
-continuum images confirms that the H![]() emission generally represents a small fraction (typically 3%) of the Gunn r emission. This latter value agrees with the estimations reported by James et al. (2004) and Knapen et al. (2004).
emission generally represents a small fraction (typically 3%) of the Gunn r emission. This latter value agrees with the estimations reported by James et al. (2004) and Knapen et al. (2004).
In order to calculate the gravitational potential, density and torques in the plane of the disks of the galaxies, we processed the H![]() and Gunn r corrected images as follows: the r band image (not scaled to H
and Gunn r corrected images as follows: the r band image (not scaled to H![]() )
and the H
)
and the H![]() continuum subtracted image were used. The Gunn r images were used in order to estimate the gravitational potential of the galaxies. This step is generally done with near-infrared images, which trace more closely the gravitational potential (absence of extinction); unfortunately we do not possess these images for all the galaxies in our sample. Nevertheless, CIG 1004 (NGC 7479) is in the OSUBGS sample (Eskridge et al. 2002) and its near-infrared potential has been estimated by Block et al. (2002). The potentials obtained from the Gunn r and near-infrared images are very similar (only the potential due to the optical spiral arm shows a slight enhancement in the Gunn r with respect to the near-infrared estimation) and hence the Gunn r image is a rather good approximation for deriving the gravitational potential of a galaxy, in the absence of near-infrared information. We defined the centre as the maximum in luminosity near the geometrical centre. The centre is the same in the r and H
continuum subtracted image were used. The Gunn r images were used in order to estimate the gravitational potential of the galaxies. This step is generally done with near-infrared images, which trace more closely the gravitational potential (absence of extinction); unfortunately we do not possess these images for all the galaxies in our sample. Nevertheless, CIG 1004 (NGC 7479) is in the OSUBGS sample (Eskridge et al. 2002) and its near-infrared potential has been estimated by Block et al. (2002). The potentials obtained from the Gunn r and near-infrared images are very similar (only the potential due to the optical spiral arm shows a slight enhancement in the Gunn r with respect to the near-infrared estimation) and hence the Gunn r image is a rather good approximation for deriving the gravitational potential of a galaxy, in the absence of near-infrared information. We defined the centre as the maximum in luminosity near the geometrical centre. The centre is the same in the r and H![]() images to avoid artificial torques between the two components. We then cut 512
images to avoid artificial torques between the two components. We then cut 512 ![]() 512 pixels2 subsections, as fast Fourier transform (FFT) will be applied on these images. Foreground galactic stars were removed in order to avoid a contamination in the density and potential derived from the luminosity of the pixels. The galaxy was deprojected to obtain the gravitational potential in the disk plane. The deprojection assumes that the outer disk of galaxies are circular and that the bulges are as flat as the disks. For galaxies inclined by less than 70
512 pixels2 subsections, as fast Fourier transform (FFT) will be applied on these images. Foreground galactic stars were removed in order to avoid a contamination in the density and potential derived from the luminosity of the pixels. The galaxy was deprojected to obtain the gravitational potential in the disk plane. The deprojection assumes that the outer disk of galaxies are circular and that the bulges are as flat as the disks. For galaxies inclined by less than 70![]() ,
Block et al. (2002) found that the observational uncertainties on the inclination angles of the galaxies barely affect the estimation of the torques. Our conservative limit includes galaxies inclined less than 50
,
Block et al. (2002) found that the observational uncertainties on the inclination angles of the galaxies barely affect the estimation of the torques. Our conservative limit includes galaxies inclined less than 50![]() ,
which assures us that the uncertainties in the deprojection do not affect our results.
,
which assures us that the uncertainties in the deprojection do not affect our results.
To determine the bar/arm force at each radius, we made use of the method developed by García-Burillo et al. (2005,1993) to compute the gravitational potential, applying it to our red images, assuming a constant stellar mass-to-light (M/L) ratio. A Fourier-component analysis of the potential was performed using the m = 2 component to obtain the tangential forces (Block et al. 2002) and the m = 0 component to obtain the axisymmetric forces. Their quotient gives us a measurement of the bar/arm force.
We estimated the average torque depending on the radius: using the gravitational forces and the young stars born from the gas (H![]() ), we obtained the phase shift between the gaseous arms and the potential well that creates the torques. Generally, due to the bar gravity torques, the gas flows into the centre (negative torque) from the corotation radius to the inner Linblad resonance (ILR), and flows outwards (positive torque) when outside the corotation radius, until the outer Lindblad resonance (OLR). This can be effectively observed for the galaxies in our sample. Finally, we estimated the angular momentum transfer and therefore the evolution time for bars in isolated galaxies (see Sect. 6.4.2).
), we obtained the phase shift between the gaseous arms and the potential well that creates the torques. Generally, due to the bar gravity torques, the gas flows into the centre (negative torque) from the corotation radius to the inner Linblad resonance (ILR), and flows outwards (positive torque) when outside the corotation radius, until the outer Lindblad resonance (OLR). This can be effectively observed for the galaxies in our sample. Finally, we estimated the angular momentum transfer and therefore the evolution time for bars in isolated galaxies (see Sect. 6.4.2).
The gravitational potential was decomposed as:
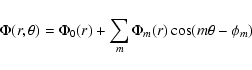
The (disk) surface density was decomposed as:
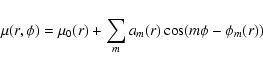
The maximal torque at a given radius was defined by:
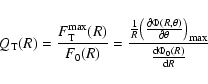
As an example, Figs. 1 and 2 display the images and graphics of the potential, density and torques corresponding to CIG 30 and CIG 1004, respectively. The first row shows the Gunn r broadband filter (left) and H![]() narrow-band filter (right) deprojected images, from which the potential, density and torques have been estimated. The second row corresponds to the amplitude (left) and the phase (right) of the Fourier components of the potential. The third row corresponds to the amplitude (left) and phase (right) of the Fourier components of the density. For the graphics of the potential and the density, the legend is the following: dashed line represents m = 1; full line represents the m = 2 component (and also the sum for the amplitude of the potential, distinguishable from the others since it is consistently above); dot-dash-dot-dash represents m = 3; dotted line represents m = 4. The torques as a function of the radius of the galaxy are presented in the bottom left panel. The corotation occurs at the radius defined by the change of sign for dL/L. dL/L shows that in one rotation, the gas loses a non-negligible fraction of its angular momentum, which can bring constraints on the life time of the morphological patterns of the galaxy. The legend in the bottom right corner gives the CIG number, the observed recession velocity (in km s-1), the optical diameter D25 (in '), the blue luminosity (logarithm, in
narrow-band filter (right) deprojected images, from which the potential, density and torques have been estimated. The second row corresponds to the amplitude (left) and the phase (right) of the Fourier components of the potential. The third row corresponds to the amplitude (left) and phase (right) of the Fourier components of the density. For the graphics of the potential and the density, the legend is the following: dashed line represents m = 1; full line represents the m = 2 component (and also the sum for the amplitude of the potential, distinguishable from the others since it is consistently above); dot-dash-dot-dash represents m = 3; dotted line represents m = 4. The torques as a function of the radius of the galaxy are presented in the bottom left panel. The corotation occurs at the radius defined by the change of sign for dL/L. dL/L shows that in one rotation, the gas loses a non-negligible fraction of its angular momentum, which can bring constraints on the life time of the morphological patterns of the galaxy. The legend in the bottom right corner gives the CIG number, the observed recession velocity (in km s-1), the optical diameter D25 (in '), the blue luminosity (logarithm, in ![]() ;
see Table 3 in Lisenfeld et al. 2007), the morphological type (from NED), and the group in which the galaxy belongs (see Sect. 6). The Gunn r and H
;
see Table 3 in Lisenfeld et al. 2007), the morphological type (from NED), and the group in which the galaxy belongs (see Sect. 6). The Gunn r and H![]() images, along with the graphics of the potential, density and torques of the full sample of the 45 galaxies, are presented as Online Material (Figs. 10 to 54) and are also available at http://www.amiga.iaa.es/publications.
images, along with the graphics of the potential, density and torques of the full sample of the 45 galaxies, are presented as Online Material (Figs. 10 to 54) and are also available at http://www.amiga.iaa.es/publications.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{aa7650f1.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg24.gif) |
Figure 1:
IC 35 (CIG 0030). V = 4586 km s-1. Optical diameter: 1.0 arcmin. Blue luminosity: 9.82. Morphology: Scd: Group: E. For the potential, |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f2.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg25.gif) |
Figure 2:
NGC 7479 (CIG 1004). V = 237 km s-1. Optical diameter: 4.1 arcmin. Blue luminosity: 10.40. Morphology: SB(s)c; LINER Sy2 Group: G. For the potential, |
| Open with DEXTER | |
In order to understand the observed H![]() distributions, and the different phases identified, we performed N-body simulations with stars and gas, including star formation. Since we want to explore many physical parameters, we chose to carry out 2D simulations, which should capture the essential components of the bar evolution, and location of star formation in these isolated galaxies. The 3D components, bulge and dark matter halo, are therefore considered as rigid and spherical potentials, in which the disk component evolves. The rigid or live character of the spheroidal components would only have a significant effect, by exchanging angular momentum, if their masses were relatively significant. But in the inner parts of galaxies, the dark matter halo is not dominant, and therefore this phenomenon would only induce small changes. The same is true for the spheroidal bulges, which are relatively small in mass, in these mostly late-type galaxies. Self-gravity is only included for the disk (gas + stars). 2D N-body simulations were carried out using the FFT algorithm to solve the Poisson equation, with a Cartesian grid varying from 256
distributions, and the different phases identified, we performed N-body simulations with stars and gas, including star formation. Since we want to explore many physical parameters, we chose to carry out 2D simulations, which should capture the essential components of the bar evolution, and location of star formation in these isolated galaxies. The 3D components, bulge and dark matter halo, are therefore considered as rigid and spherical potentials, in which the disk component evolves. The rigid or live character of the spheroidal components would only have a significant effect, by exchanging angular momentum, if their masses were relatively significant. But in the inner parts of galaxies, the dark matter halo is not dominant, and therefore this phenomenon would only induce small changes. The same is true for the spheroidal bulges, which are relatively small in mass, in these mostly late-type galaxies. Self-gravity is only included for the disk (gas + stars). 2D N-body simulations were carried out using the FFT algorithm to solve the Poisson equation, with a Cartesian grid varying from 256 ![]() 256 to 512
256 to 512 ![]() 512 (useful grid, free of periodic images). Two spatial resolutions were selected to appreciate its influence on the star formation physics. The cell size is from 62.5 to 125 pc, and the total size of the grid is 32 kpc. The softening length of the gravity has the characteristic scale of the cell (62.5 to 125 pc). More details on the numerical techniques can be found in Combes et al. (1990).
512 (useful grid, free of periodic images). Two spatial resolutions were selected to appreciate its influence on the star formation physics. The cell size is from 62.5 to 125 pc, and the total size of the grid is 32 kpc. The softening length of the gravity has the characteristic scale of the cell (62.5 to 125 pc). More details on the numerical techniques can be found in Combes et al. (1990).
The stellar component is represented by 100 000 or 400 000 particles, and the gas component by 40 000 and 160 000 for the low and high resolutions adopted, respectively.
The bulge is modelled as a rigid spherical potential with Plummer shape:
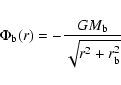
The stellar disk is initially a Kuzmin-Toomre disk of surface density:
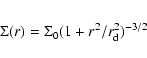
Table 1:
Initial conditions for the numerical simulations. ![]() is the number of particles considered,
is the number of particles considered,
![]() and
and
![]() the galaxy bulge/disk/halo radii and masses,
and
the galaxy bulge/disk/halo radii and masses,
and
![]() the collision elasticity factor.
the collision elasticity factor.
The gas is treated as a self-gravitating component in the N-body simulation, and its dissipation is treated by a sticky particle code, as in Combes & Gerin (1985). The initial gas-to-total mass ratio (
![]() )
in the disk ranges between 6 and 14%, since the star formation in the simulation is capable of reducing
)
in the disk ranges between 6 and 14%, since the star formation in the simulation is capable of reducing
![]() to a final lower value. The mass of one gas particle therefore varies between 8
to a final lower value. The mass of one gas particle therefore varies between 8 ![]() 104 and 3
104 and 3 ![]()
![]() .
.
The initial distribution of gas in the model is an exponential disk, truncated at 15 kpc, and with a characteristic radial scale of 6 kpc. Initially, its velocity dispersion corresponds to a Toomre ![]() parameter of 1. The gas clouds are subject to inelastic collisions, with a collision cell size between 60 and 120 pc (region where particles are selected to possibly collide). This corresponds to a lower limit for the average mean free path of clouds between two collisions. The collisions are considered every 5 to 10 Myr. In a collision, the sign of the relative cloud velocities is reversed and the absolute values are reduced: relative velocities after the collision are only
parameter of 1. The gas clouds are subject to inelastic collisions, with a collision cell size between 60 and 120 pc (region where particles are selected to possibly collide). This corresponds to a lower limit for the average mean free path of clouds between two collisions. The collisions are considered every 5 to 10 Myr. In a collision, the sign of the relative cloud velocities is reversed and the absolute values are reduced: relative velocities after the collision are only
![]() times their original value, the elasticity factor
times their original value, the elasticity factor
![]() being between 0.65 and 0.85, as indicated in Table 1. The dissipation rate is controlled by this factor. All gas particles have the same mass.
being between 0.65 and 0.85, as indicated in Table 1. The dissipation rate is controlled by this factor. All gas particles have the same mass.
Star formation is taken into account following a generalised Schmidt law: the star formation rate is proportional to the volume density to the power n=1.2, provided that the gas volumic density is larger than
![]() H-atom cm-3, i.e. the rate of gas mass transformed into stars is d
H-atom cm-3, i.e. the rate of gas mass transformed into stars is d
![]() .
To compute this rate, at regular intervals of dt= 5-10 Myr, the gas density is averaged in each cell, and the probability of the gas particles being transformed into stars is computed by:
.
To compute this rate, at regular intervals of dt= 5-10 Myr, the gas density is averaged in each cell, and the probability of the gas particles being transformed into stars is computed by:
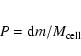
To reproduce a model equivalent of the H![]() maps, we plot only the recently born stars, still able to ionise their surroundings. In order to have more statistics, we choose to plot all new stars of age less than 200 Myr (Figs. 4 and 6).
maps, we plot only the recently born stars, still able to ionise their surroundings. In order to have more statistics, we choose to plot all new stars of age less than 200 Myr (Figs. 4 and 6).
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7650f3.ps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg44.gif) |
Figure 3: Particle plots of the stars ( top) and gas ( bottom) at the epoch T=1.1 Gyr ( left) and T=1.5 Gyr ( right), in the simulation of Run 1. The scale of the square is 64 kpc. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7650f4.ps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg45.gif) |
Figure 4:
Plots of recently formed stars (less than 200 Myr ago), at the epoch T=1.1 Gyr ( left) and T=1.5 Gyr ( right), in the simulation of Run 1. The scale of the square is 32 kpc. These plots should give an idea of the H |
| Open with DEXTER | |
We tried several runs corresponding to the various morphological types of the Hubble sequence, varying the bulge to disk mass ratio, the halo to disk mass ratio, and the gas content. A consequence of this was variations in the dynamical stability of the disk: the bar appears within different time-scales, and with mainly two different morphologies for early- and late-types, respectively. In the case of late-types, the bar develops without any resonant ring, and quickly the gas infalls to the centre, and destroys the bar. The H![]() morphology then has a bar shape during a short period, and quickly peaks at the centre. For early-types, the high central mass concentration allows the formation of ILRs, and gaseous resonant rings are developped inside the bar. Also the life-time of the bar is long enough to develop a resonant ring at the 4:1 resonance near corotation surrounding the bar (Fig. 3). However, the gas density there is not enough to produce substantial star formation (Fig. 4).
morphology then has a bar shape during a short period, and quickly peaks at the centre. For early-types, the high central mass concentration allows the formation of ILRs, and gaseous resonant rings are developped inside the bar. Also the life-time of the bar is long enough to develop a resonant ring at the 4:1 resonance near corotation surrounding the bar (Fig. 3). However, the gas density there is not enough to produce substantial star formation (Fig. 4).
Whatever the morphological type of the galaxy, the models always show a first stage where the main star formation is aligned with the bar, and a second stage, where the star forming regions concentrate towards the nucleus. Variations of the degree of dissipation of the gas component, through the variation of collision elasticity
![]() ,
do not change the picture, as shown by the comparison between Run 1 and Run 4 in Figs. 4 and 6. The corresponding H
,
do not change the picture, as shown by the comparison between Run 1 and Run 4 in Figs. 4 and 6. The corresponding H![]() maps that can then be predicted are either of group G, as defined in the next section, or group H. But it is not possible to obtain the most frequently observed morphology of group E. In other words, the equivalent H
maps that can then be predicted are either of group G, as defined in the next section, or group H. But it is not possible to obtain the most frequently observed morphology of group E. In other words, the equivalent H![]() maps are predicted to correlate tightly to the gaseous maps. This is expected from the type of recipe adopted for the star formation rate, i.e. a Schmidt law, with a density threshold. We defer the discussion of these results to Sect. 6.4.2.
maps are predicted to correlate tightly to the gaseous maps. This is expected from the type of recipe adopted for the star formation rate, i.e. a Schmidt law, with a density threshold. We defer the discussion of these results to Sect. 6.4.2.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7650f5.ps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg46.gif) |
Figure 5: Particle plots of the stars ( top) and gas ( bottom) at the epoch T=0.6 Gyr ( left) and T=1.0 Gyr ( right), in the simulation of Run 4. The scale of the square is 64 kpc. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7650f6.ps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg47.gif) |
Figure 6: Plots of recently formed stars (less than 200 Myr ago), at the epoch T=0.6 Gyr ( left) and T=1.0 Gyr ( right), in the simulation of Run 4. The scale of the square is 32 kpc. Note the orientation of the young star component, which keeps the phase shift of the gas component during some time, and is leading with respect to the old stellar bar of Fig. 5 by about 3 degrees. |
| Open with DEXTER | |
With our sample being 94% complete (we are only missing data for 3 galaxies from the 48 we had selected, which could not have been observed), we can describe statistically significant characteristics for a sample of isolated galaxies.
Verley et al. (2007a,b) lead an extensive study to revise the degree of isolation of 950 CIG galaxies. Within a projected radius of 0.5 Mpc, all the neighbours that could exert an influence on the evolution of the CIG galaxies were catalogued. Parameters quantifying the degree of isolation of each CIG galaxy were defined. A particularly relevant parameter, Q, measures the strength of the tidal forces affecting the central galaxy, normalised to the inner binding forces of the galaxy itself. In the subsample of 45 galaxies defined in the present study, three of the galaxies present tidal forces amounting to more than 10% (![]() )
of their inner binding forces. This means that their evolution could have been seriously affected by nearby companions. These three galaxies are CIGs 80, 85 and 1001.
)
of their inner binding forces. This means that their evolution could have been seriously affected by nearby companions. These three galaxies are CIGs 80, 85 and 1001.
An additional eleven galaxies present values of the external forces amounting to more than 1% of their internal binding forces (![]() ), which is the limit from which the environment can partially influence the evolution of the central galaxy (Athanassoula 1984). These galaxies are CIGs 59, 84, 96, 176, 376, 382, 512, 645, 808, 812 and 1004. Nevertheless, these galaxies are isolated from similar size neighbours (within a factor 4 in size, as originally defined by Karachentseva 1973). A statistical rejection of the projected distant neighbours (with a difference in recession velocity of almost 20 000 km s-1) reveals that all but one (CIG 176) can, indeed, be galaxies whose evolution is dominated by their internal properties. More data on the recession velocities of the neighbours are needed in order to access a definitive picture of the environment of each CIG galaxy.
), which is the limit from which the environment can partially influence the evolution of the central galaxy (Athanassoula 1984). These galaxies are CIGs 59, 84, 96, 176, 376, 382, 512, 645, 808, 812 and 1004. Nevertheless, these galaxies are isolated from similar size neighbours (within a factor 4 in size, as originally defined by Karachentseva 1973). A statistical rejection of the projected distant neighbours (with a difference in recession velocity of almost 20 000 km s-1) reveals that all but one (CIG 176) can, indeed, be galaxies whose evolution is dominated by their internal properties. More data on the recession velocities of the neighbours are needed in order to access a definitive picture of the environment of each CIG galaxy.
To know the percentage of barred galaxies in a sample of isolated galaxies, we visually classified the 45 galaxies into three subsamples, as a function of the presence or absence of a bar:
We now focus on the existence of shift angle between the location of the gas and the location of the older stellar component, which has already been noted by Martin & Friedli (1997) in a sample of eleven galaxies (for other examples, see also de Vaucouleurs & de Vaucouleurs 1963; Phillips 1996). It was sometimes difficult to define exactly where the arms began because the H![]() could be very clumpy, but we frequently saw bright H
could be very clumpy, but we frequently saw bright H![]() knots at the end of the bars, even when there was no emission in the bar. Consequently, we could use the star formation spots at the end of the bars to define the starting point of the spiral arms. The H
knots at the end of the bars, even when there was no emission in the bar. Consequently, we could use the star formation spots at the end of the bars to define the starting point of the spiral arms. The H![]() emission was always leading with respect to the bar in the Gunn r image. The most evident cases of bar shifts between the Gunn r and the H
emission was always leading with respect to the bar in the Gunn r image. The most evident cases of bar shifts between the Gunn r and the H![]() images are (with an estimation of the shift angle in degrees shown in parentheses): CIG 30 (30
images are (with an estimation of the shift angle in degrees shown in parentheses): CIG 30 (30![]() ), CIG 53 (10
), CIG 53 (10![]() ), CIG 66 (5
), CIG 66 (5![]() ), CIG 96 (10
), CIG 96 (10![]() ), CIG 176 (10
), CIG 176 (10![]() ), CIG 376 (30
), CIG 376 (30![]() ), CIG 512 (10
), CIG 512 (10![]() ), CIG 840 (15
), CIG 840 (15![]() ), and CIG 1004 (5
), and CIG 1004 (5![]() ). Three cases are illustrated in Fig. 7, where the orientations of the H
). Three cases are illustrated in Fig. 7, where the orientations of the H![]() and stellar bars have been marked by dashed black lines.
and stellar bars have been marked by dashed black lines.
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{7650f7a.eps}\includegraphi...
...cm,clip]{7650f7e.eps}\includegraphics[width=5.8cm,clip]{7650f7f.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg50.gif) |
Figure 7:
Examples of shift angles between the H |
| Open with DEXTER | |
As some characteristics were frequently found among the galaxies of our sample, we chose to group the galaxies presenting similar features. In decreasing frequency order, we defined the three main groups:
Many N-body simulations of galaxies with gas have revealed that bars are not long-lived in late-type galaxies (e.g. Friedli & Benz 1993; Bournaud & Combes 2002; Berentzen et al. 1998). Bournaud et al. (2005) have shown that the bar dissolution is due to the gas inflow towards the centre, and that bars can be renewed by external gas accretion. Our goal here is to obtain insight into the various dynamical processes that could be involved in the interpretation of the different observed morphologies as different stages of an evolutive sequence. In our sample, we can identify various main steps occurring during the formation and evolution of the bars.
By gravitational instability, a galaxy accretes gas from the inter-galactic medium, which makes it unstable for bar formation. The bar creates a torque that drives the gas inflow towards the centre. This phase corresponds to our identified G phase (see, for instance, Fig. 2 for a typical galaxy belonging to this group).
The second step is a transition between the G and E phases: the gas inflows towards the centre while a ring is slowly forming at the resonance (pseudo-ring due to the winding of the spiral arms, at the ILR).
In a third step, the gas is progressively depopulated from the bar, and accumulates first in the very centre of the galaxy (or a very small nuclear ring, at ILR), and also at the ultra harmonic resonance (UHR), near the corotation. The gas there is quite stable, with very small relative velocity with respect to the bar pattern, and the star formation could be quite efficient in these regions. This corresponds to our most frequently identified phase, the E phase, where galaxies could spend more than 40% of their life-span (see, for instance, Fig. 1 for a typical galaxy belonging to this group).
Since the gas infall destroys the bar, the latter becomes progressively weaker and weaker: the F phase is then reached. The stars in the centre become an old population, contributing to increase the bulge mass. Without more gas fuelling, the H![]() spot in the centre fades away over 108 years (OB stars). The frequency of the F phase means that a galaxy spends typically 20% of its life in this stage, where the bar is weakened or destroyed.
spot in the centre fades away over 108 years (OB stars). The frequency of the F phase means that a galaxy spends typically 20% of its life in this stage, where the bar is weakened or destroyed.
The various classes proposed in the previous section were based on the H![]() map morphologies. By plotting images of the recent stars formed in the simulations, we have tried to predict those H
map morphologies. By plotting images of the recent stars formed in the simulations, we have tried to predict those H![]() morphologies in Sect. 5. However, the two most frequently predicted morphologies correspond to either group G (H
morphologies in Sect. 5. However, the two most frequently predicted morphologies correspond to either group G (H![]() emission aligned along the bar) or H (when the emission is concentrated in the nucleus). The configuration E, where the star formation avoids the bar, is not reproduced in the simulation, in contradiction to our observations where the E phase is about two times more frequent than the G phase.
emission aligned along the bar) or H (when the emission is concentrated in the nucleus). The configuration E, where the star formation avoids the bar, is not reproduced in the simulation, in contradiction to our observations where the E phase is about two times more frequent than the G phase.
We think that this feature mainly arises from the star formation recipe adopted in the simulation. The efficiency of the star formation as a function of the gas density is still a challenging issue. The predicted gas density appears to reproduce the observations. Our simulations reveal the formation of rings at the UHR, but this is always accompanied by a large gas density along the bar.
In most of the barred galaxies, the gas is observed in the bar through the dust lane or through molecular line emission, like CO (e.g. Helfer et al. 2003), but little or no star formation and H![]() are observed. With the Schmidt law used in the present simulations (SFR
are observed. With the Schmidt law used in the present simulations (SFR ![]()
![]() ), one would expect to find recent star formation in the bar, while in the actual galaxies this is avoided, maybe through too large relative velocities (e.g. Reynaud & Downes 1998). Therefore, to remove the discrepancy between H
), one would expect to find recent star formation in the bar, while in the actual galaxies this is avoided, maybe through too large relative velocities (e.g. Reynaud & Downes 1998). Therefore, to remove the discrepancy between H![]() morphologies and predictions, it would be necessary to change the expression of the star formation rate: it should not only depend on
morphologies and predictions, it would be necessary to change the expression of the star formation rate: it should not only depend on
![]() but should also take into account the relative velocity of the gas with respect to the bar. This will be presented in a future work.
but should also take into account the relative velocity of the gas with respect to the bar. This will be presented in a future work.
The absence of star formation and H![]() emission in the bar, while the gas density is abundant, is a frequently observed phenomenon. We do not have galaxies in common with the BIMA Survey Of Nearby Galaxies (BIMA SONG, Helfer et al. 2002). However, the BIMA SONG gives us some clues about the gas density. The E phase, although also present there, is less frequent relative to the G phase, as we could expect. There is more CO emission in the bars of their galaxy sample (NGC 2903, 3627, 4535, 5457) compared to our H
emission in the bar, while the gas density is abundant, is a frequently observed phenomenon. We do not have galaxies in common with the BIMA Survey Of Nearby Galaxies (BIMA SONG, Helfer et al. 2002). However, the BIMA SONG gives us some clues about the gas density. The E phase, although also present there, is less frequent relative to the G phase, as we could expect. There is more CO emission in the bars of their galaxy sample (NGC 2903, 3627, 4535, 5457) compared to our H![]() sample. The H
sample. The H![]() emission is obviously a more efficient tracer of star formation than of the total amount of gas available.
emission is obviously a more efficient tracer of star formation than of the total amount of gas available.
Other groups have also imaged and classified spiral galaxies as a function of their H![]() morphology. Hameed & Devereux (1999), for instance, concentrated their work on 27 early-type spiral galaxies (Sa-Sab) in the nearby Universe. As our sample involves mainly Sb-Sc galaxies, the two samples are somehow complementary, although it has to be noted that their galaxies are selected without any regard to isolation criterion. We can group their galaxies according to our classification. The E group would consist of 11 galaxies: NGC 1350, NGC 1371, NGC 1398, NGC 1433, NGC 1515, NGC 1617, NGC 2273, NGC 3169, NGC 5156, NGC 7213 and 1108-48. Four galaxies would be classified in the G group: NGC 986, NGC 5188, NGC 7552 and NGC 7582. The central emission characteristic of the H group is seen in 5 galaxies: NGC 1022, NGC 1482, NGC 3471, NGC 3885 and NGC 5728. The galaxies NGC 972 and NGC 5915 would be classified in the transitional EG group, while it would not be possible to classify five galaxies (NGC 660, NGC 2146, NGC 3717, NGC 6810 and NGC 7172) generally due to their high inclination angle, which makes it difficult to disentangle the emission of the disk from the emission specifically from the bar itself.
morphology. Hameed & Devereux (1999), for instance, concentrated their work on 27 early-type spiral galaxies (Sa-Sab) in the nearby Universe. As our sample involves mainly Sb-Sc galaxies, the two samples are somehow complementary, although it has to be noted that their galaxies are selected without any regard to isolation criterion. We can group their galaxies according to our classification. The E group would consist of 11 galaxies: NGC 1350, NGC 1371, NGC 1398, NGC 1433, NGC 1515, NGC 1617, NGC 2273, NGC 3169, NGC 5156, NGC 7213 and 1108-48. Four galaxies would be classified in the G group: NGC 986, NGC 5188, NGC 7552 and NGC 7582. The central emission characteristic of the H group is seen in 5 galaxies: NGC 1022, NGC 1482, NGC 3471, NGC 3885 and NGC 5728. The galaxies NGC 972 and NGC 5915 would be classified in the transitional EG group, while it would not be possible to classify five galaxies (NGC 660, NGC 2146, NGC 3717, NGC 6810 and NGC 7172) generally due to their high inclination angle, which makes it difficult to disentangle the emission of the disk from the emission specifically from the bar itself.
The comparison between the two samples shows that three groups present the same percentages of galaxies: the percentage of group E galaxies is almost the same in the two samples (41 and 42% in their sample and our sample, respectively). The same percentage of galaxies is also found for the G group (15 and 18%, respectively) and for the EG group (about 7% in both samples). Additionally, all of their extended nuclear emission-line region (ENER) galaxies fall into our E group. Nevertheless, some differences are also observed. Our F group is not represented in their sample, which totally lacks the galaxies without central emission. The other notable difference is that their sample presents a proportion of H group galaxies 3 times higher. This can easily be explained since all of their galaxies are Sa-Sab, hence more early-type (with less gas and very few H![]() emission) than the bulk of our sample.
emission) than the bulk of our sample.
Other works have targeted the inner H![]() emission of galaxies: Knapen et al. (2006) focussed their work on the central regions (within 2 pc) of 73 spiral galaxies, which can have relatively close companions, as is the case for 26 galaxies (36%) in their sample. We classified the 73 galaxies following our nomenclature: 45 galaxies (62%) are in the E group, 2 galaxies (3%) in the F group, 4 galaxies (5%) in the G group, 9 galaxies (12%) in the H group, 10 galaxies (14%) in the EG group, 1 galaxy (1%) in the EF group and 2 galaxies could not be classified (Irr group), partly due to their to high inclination. The restriction of their sample to only the 26 galaxies that possess a physically linked companion does not change significantly the percentages of the galaxies in the groups (61% in E, 4% in F, 0% in G, 19% in H, 12% in EG, 0% in EF and 1% in Irr). This is not surprising as Knapen et al. (2006) already noticed that the presence of a close companion does not produce particularly strong trend in the H
emission of galaxies: Knapen et al. (2006) focussed their work on the central regions (within 2 pc) of 73 spiral galaxies, which can have relatively close companions, as is the case for 26 galaxies (36%) in their sample. We classified the 73 galaxies following our nomenclature: 45 galaxies (62%) are in the E group, 2 galaxies (3%) in the F group, 4 galaxies (5%) in the G group, 9 galaxies (12%) in the H group, 10 galaxies (14%) in the EG group, 1 galaxy (1%) in the EF group and 2 galaxies could not be classified (Irr group), partly due to their to high inclination. The restriction of their sample to only the 26 galaxies that possess a physically linked companion does not change significantly the percentages of the galaxies in the groups (61% in E, 4% in F, 0% in G, 19% in H, 12% in EG, 0% in EF and 1% in Irr). This is not surprising as Knapen et al. (2006) already noticed that the presence of a close companion does not produce particularly strong trend in the H![]() morphology.
morphology.
The very low percentage of F galaxies with respect to our work is due to a selection criterion in the sample by Knapen et al. (2006) as they selected galaxies with some prior evidence for H![]() structure in their central regions. The same reason enhanced the proportion of group E galaxies because they selected galaxies with already known nuclear or inner rings. Their sample is not complete and the comparison and interpretation with our work should therefore be performed with care. With respect to the isolation, the criterion they used can not ensure that the galaxies without a "very close companion'' would be isolated following Karachentseva's criterion (even if it seems that the presence of a companion does not have drastic repercussions on the H
structure in their central regions. The same reason enhanced the proportion of group E galaxies because they selected galaxies with already known nuclear or inner rings. Their sample is not complete and the comparison and interpretation with our work should therefore be performed with care. With respect to the isolation, the criterion they used can not ensure that the galaxies without a "very close companion'' would be isolated following Karachentseva's criterion (even if it seems that the presence of a companion does not have drastic repercussions on the H![]() features). As a result we cannot directly compare our isolated galaxies with their sample. Nevertheless, the Hameed & Devereux (1999) and Knapen et al. (2006) studies show that the groups we defined are also seen in samples that might not be isolated, so that the evolutive sequence could also be applied to galaxies marginally in interaction. For more detailed comparisons, samples better defined in terms of isolation (or interaction) and better statistics would be needed.
features). As a result we cannot directly compare our isolated galaxies with their sample. Nevertheless, the Hameed & Devereux (1999) and Knapen et al. (2006) studies show that the groups we defined are also seen in samples that might not be isolated, so that the evolutive sequence could also be applied to galaxies marginally in interaction. For more detailed comparisons, samples better defined in terms of isolation (or interaction) and better statistics would be needed.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{7650f8.ps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg55.gif) |
Figure 8: Distribution of total non-axisymmetric strengths in the CIGsample. |
| Open with DEXTER | |
We have computed the total strength of bar and spiral waves in our galaxy sample by the method outlined in Sect. 4. We have adopted an exponential scaleheight equal to 1/12 of the radial scale length, independent of Hubble type, consistent with previous studies (e.g. Quillen et al. 1994), although de Grijs (1998) found a type-dependent relationship and thicker disks. Varying this parameter will slightly change the absolute bar strengths in Figs. 8 and 9, but will have little impact on the relative values. The maximum of the parameter ![]() ,
dominated by the bar strength and its harmonics, is used to build the histogram of the bar frequency for isolated galaxies (Fig. 8). It is then possible to compare with the same histogram (see Fig. 9), built for a general sample, the OSU sample (Eskridge et al. 2002). This sample of galaxies, selected without regard to any isolation criterion, appears to give quite similar results. Our histogram here is more uncertain and noisy, because of the much smaller sample size. However, it is possible to see that isolated galaxies sustain comparable bar strengths.
,
dominated by the bar strength and its harmonics, is used to build the histogram of the bar frequency for isolated galaxies (Fig. 8). It is then possible to compare with the same histogram (see Fig. 9), built for a general sample, the OSU sample (Eskridge et al. 2002). This sample of galaxies, selected without regard to any isolation criterion, appears to give quite similar results. Our histogram here is more uncertain and noisy, because of the much smaller sample size. However, it is possible to see that isolated galaxies sustain comparable bar strengths.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{7650f9.ps} \end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg56.gif) |
Figure 9: Distribution of total non-axisymmetric strengths in the OSU sample. |
| Open with DEXTER | |
From the detailed morphological study of a sample of 45 isolated spiral galaxies, in H![]() emission and optical red continuum, and comparison with numerical simulations, we come to the following conclusions:
emission and optical red continuum, and comparison with numerical simulations, we come to the following conclusions:
Acknowledgements
We are very grateful to Gary A. Mamon, Chantal Balkowski, Alessandro Boselli, Santiago García-Burillo and José M. Vílchez for their comments. We thank P. A. James for providing us data from the HGalaxy Survey and the anonymous referee for her/his helpful comments. The numerical simulations have been carried out on the Fujitsu NEC-SX5 of the CNRS computing center, at IDRIS (Palaiseau, France). We have made use of the LEDA database (http://leda.univ-lyon1.fr), and of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This work has been partially supported by DGI Grant AYA 2005-07516-C02-01 and the Junta de Andalucía (Spain). G.B. is supported at the IAA/CSIC by an I3P contract (I3P-PC2005-F) funded by the European Social Fund.
Table 2: Properties of the 45 CIG galaxies selected.
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f10.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg63.gif) |
Figure 10:
IC 35 (CIG 0030). V = 4586 km s-1. Optical diameter: 1.0 arcmin. Blue luminosity: 9.82. Morphology: Scd:. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f11.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg64.gif) |
Figure 11:
UGC 1014 (CIG 0050). V = 2132 km s-1. Optical diameter: 1.2 arcmin. Blue luminosity: 8.73. Morphology: Sm. Group: F. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f12.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg65.gif) |
Figure 12:
NGC 575 (CIG 0053). V = 3128 km s-1. Optical diameter: 1.7 arcmin. Blue luminosity: 9.71. Morphology: SB(rs)c. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f13.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg66.gif) |
Figure 13:
UGC 1167 (CIG 0059). V = 4303 km s-1. Optical diameter: 2.7 arcmin. Blue luminosity: 9.63. Morphology: SA(rs)cd. Group: F. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f14.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg67.gif) |
Figure 14:
UGC 1285 (CIG 0066). V = 4655 km s-1. Optical diameter: 1.3 arcmin. Blue luminosity: 10.16. Morphology: Sbc. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f15.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg68.gif) |
Figure 15:
NGC 718 (CIG 0068). V = 1733 km s-1. Optical diameter: 2.3 arcmin. Blue luminosity: 9.61. Morphology: SAB(s)a. Group: H. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f16.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg69.gif) |
Figure 16:
NGC 772 (CIG 0080). V = 2458 km s-1. Optical diameter: 7.2 arcmin. Blue luminosity: 10.48. Morphology: SA(s)b. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f17.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg70.gif) |
Figure 17:
IC 193 (CIG 0084). V = 4649 km s-1. Optical diameter: 1.7 arcmin. Blue luminosity: 9.82. Morphology: SA(rs)c. Group: F. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f18.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg71.gif) |
Figure 18:
UGC 1547 (CIG 0085). V = 2640 km s-1. Optical diameter: 2.2 arcmin. Blue luminosity: 9.14. Morphology: IBm. Group: Irr.. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f19.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg72.gif) |
Figure 19:
NGC 864 (CIG 0096). V = 1559 km s-1. Optical diameter: 4.7 arcmin. Blue luminosity: 9.81. Morphology: SAB(rs)c. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f20.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg73.gif) |
Figure 20:
NGC 1050 (CIG 0116). V = 3901 km s-1. Optical diameter: 1.4 arcmin. Blue luminosity: 10.12. Morphology: (R')SB(s)a H II. Group: G. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f21.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg74.gif) |
Figure 21:
UGC 3581 (CIG 0176). V = 4955 km s-1. Optical diameter: 1.3 arcmin. Blue luminosity: 10.00. Morphology: SAB(rs)c:. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f22.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg75.gif) |
Figure 22:
UGC 3826 (CIG 0188). V = 1733 km s-1. Optical diameter: 3.5 arcmin. Blue luminosity: 8.86. Morphology: SAB(s)d. Group: F. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f23.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg76.gif) |
Figure 23:
UGC 4107 (CIG 0217). V = 3504 km s-1. Optical diameter: 1.4 arcmin. Blue luminosity: 9.86. Morphology: SA(rs)c. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f24.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg77.gif) |
Figure 24:
UGC 4393 (CIG 0250). V = 2125 km s-1. Optical diameter: 2.2 arcmin. Blue luminosity: 9.65. Morphology: SBc? H II. Group: G. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f25.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg78.gif) |
Figure 25:
UGC 4500 (CIG 0267). V = 4256 km s-1. Optical diameter: 1.5 arcmin. Blue luminosity: 9.45. Morphology: SAB(s)cd. Group: F. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f26.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg79.gif) |
Figure 26:
NGC 2649 (CIG 0281). V = 4244 km s-1. Optical diameter: 1.6 arcmin. Blue luminosity: 10.34. Morphology: SAB(rs)bc:. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f27.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg80.gif) |
Figure 27:
UGC 4684 (CIG 0291). V = 2521 km s-1. Optical diameter: 1.4 arcmin. Blue luminosity: 9.42. Morphology: SA(rs)dm:. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f28.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg81.gif) |
Figure 28:
NGC 2960 (CIG 0359). V = 4932 km s-1. Optical diameter: 1.8 arcmin. Blue luminosity: 10.56. Morphology: Sa? Sy3. Group: H. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f29.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg82.gif) |
Figure 29:
UGC 5277 (CIG 0376). V = 3365 km s-1. Optical diameter: 1.5 arcmin. Blue luminosity: 9.48. Morphology: SB(rs)bc. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f30.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg83.gif) |
Figure 30:
NGC 3061 (CIG 0382). V = 2457 km s-1. Optical diameter: 1.7 arcmin. Blue luminosity: 9.56. Morphology: (R')SB(rs)c. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f31.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg84.gif) |
Figure 31:
UGC 6903 (CIG 0512). V = 1892 km s-1. Optical diameter: 2.6 arcmin. Blue luminosity: 9.41. Morphology: SB(s)cd. Group: EG. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f32.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg85.gif) |
Figure 32:
NGC 5016 (CIG 0575). V = 2612 km s-1. Optical diameter: 1.7 arcmin. Blue luminosity: 9.51. Morphology: SAB(rs)c SBNG. Group: Irr.. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f33.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg86.gif) |
Figure 33:
IC 1057 (CIG 0645). V = 4027 km s-1. Optical diameter: 1.8 arcmin. Blue luminosity: 9.81. Morphology: Sb. Group: G. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f34.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg87.gif) |
Figure 34:
NGC 5768 (CIG 0652). V = 1962 km s-1. Optical diameter: 1.9 arcmin. Blue luminosity: 9.49. Morphology: SA(rs)c:. Group: EG. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f35.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg88.gif) |
Figure 35:
UGC 9730 (CIG 0660). V = 2137 km s-1. Optical diameter: 1.3 arcmin. Blue luminosity: 8.71. Morphology: SB(s)d. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f36.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg89.gif) |
Figure 36:
UGC 9734 (CIG 0661). V = 3341 km s-1. Optical diameter: 1.3 arcmin. Blue luminosity: 9.18. Morphology: Sm. Group: F. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f37.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg90.gif) |
Figure 37:
UGC 10005 (CIG 0700). V = 3838 km s-1. Optical diameter: 1.3 arcmin. Blue luminosity: 9.33. Morphology: SA(s)d?. Group: G. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f38.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg91.gif) |
Figure 38:
NGC 6012 (CIG 0712). V = 1854 km s-1. Optical diameter: 2.1 arcmin. Blue luminosity: 9.91. Morphology: (R)SB(r)ab: LINER:. Group: G. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f39.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg92.gif) |
Figure 39:
UGC 10437 (CIG 0744). V = 2596 km s-1. Optical diameter: 2.1 arcmin. Blue luminosity: 8.93. Morphology: Sc. Group: EG. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f40.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg93.gif) |
Figure 40:
UGC 10449 (CIG 0750). V = 4020 km s-1. Optical diameter: 1.1 arcmin. Blue luminosity: 9.26. Morphology: Sdm. Group: EF. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f41.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg94.gif) |
Figure 41:
UGC 10490 (CIG 0754). V = 4594 km s-1. Optical diameter: 1.0 arcmin. Blue luminosity: 9.60. Morphology: Sd. Group: G. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f42.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg95.gif) |
Figure 42:
UGC 10862 (CIG 0808). V = 1691 km s-1. Optical diameter: 2.8 arcmin. Blue luminosity: 8.90. Morphology: SB(rs)c. Group: F. |
| Open with DEXTER | |
![\begin{figure}\par
\includegraphics[width=18cm,clip]{aa7650f53.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg97.gif) |
Figure 43:
NGC 6389 (CIG 0812). V = 3119 km s-1. Optical diameter: 2.8 arcmin. Blue luminosity: 10.00. Morphology: Sbc. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par
\includegraphics[width=18cm,clip]{aa7650f54.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg99.gif) |
Figure 44:
UGC 11058 (CIG 0840). V = 4757 km s-1. Optical diameter: 1.5 arcmin. Blue luminosity: 9.95. Morphology: SB(s)b. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f45.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg100.gif) |
Figure 45:
UGC 11287 (CIG 0854). V = 4856 km s-1. Optical diameter: 1.5 arcmin. Blue luminosity: 9.55. Morphology: Sc. Group: G. |
| Open with DEXTER | |
![\begin{figure}\par
\includegraphics[width=18cm,clip]{aa7650f52.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg102.gif) |
Figure 46:
NGC 6711 (CIG 0862). V = 4671 km s-1. Optical diameter: 1.3 arcmin. Blue luminosity: 10.05. Morphology: SBbc:. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f47.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg103.gif) |
Figure 47:
UGC 11536 (CIG 0875). V = 4880 km s-1. Optical diameter: 1.0 arcmin. Blue luminosity: 9.70. Morphology: (R')SB(s)a. Group: H. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f48.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg104.gif) |
Figure 48:
UGC 11790 (CIG 0924). V = 4540 km s-1. Optical diameter: 1.5 arcmin. Blue luminosity: 9.54. Morphology: SA(rs)d:. Group: F. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f49.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg105.gif) |
Figure 49:
UGC 11816 (CIG 0931). V = 4750 km s-1. Optical diameter: 1.5 arcmin. Blue luminosity: 9.82. Morphology: SB(rs)c:. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f50.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg106.gif) |
Figure 50:
NGC 7156 (CIG 0935). V = 3985 km s-1. Optical diameter: 1.6 arcmin. Blue luminosity: 10.08. Morphology: SAB(rs)cd:. Group: F. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=18cm,clip]{aa7650f51.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg107.gif) |
Figure 51:
UGC 12224 (CIG 0992). V = 3506 km s-1. Optical diameter: 2.1 arcmin. Blue luminosity: 9.26. Morphology: Scd:. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par
\includegraphics[width=18cm,clip]{aa7650f52.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg102.gif) |
Figure 52:
NGC 7428 (CIG 1001). V = 3078 km s-1. Optical diameter: 2.4 arcmin. Blue luminosity: 9.75. Morphology: (R)SAB(r)a pec:. Group: E. |
| Open with DEXTER | |
![\begin{figure}\par
\includegraphics[width=18cm,clip]{aa7650f53.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg97.gif) |
Figure 53:
NGC 7479 (CIG 1004). V = 2376 km s-1. Optical diameter: 4.1 arcmin. Blue luminosity: 10.40. Morphology: SB(s)c; LINER Sy2. Group: G. |
| Open with DEXTER | |
![\begin{figure}\par
\includegraphics[width=18cm,clip]{aa7650f54.eps}\end{figure}](/articles/aa/full/2007/40/aa7650-07/Timg99.gif) |
Figure 54:
IC 5355 (CIG 1039). V = 4859 km s-1. Optical diameter: 1.0 arcmin. Blue luminosity: 9.95. Morphology: SBcd: H II. Group: E. |
| Open with DEXTER | |