A&A 474, 221-228 (2007)
DOI: 10.1051/0004-6361:20066735

Ruthenium and hafnium abundances in giant and dwarf barium stars^,

D. M. Allen - G. F. Porto de Mello

Observatório do Valongo/UFRJ, Ladeira do Pedro Antonio 43, 20080-090 Rio de Janeiro, RJ, Brazil

Received 10 November 2006 / Accepted 6 July 2007

Abstract
Aims. We present abundances for Ru and Hf, compare them to abundances of other heavy elements, and discuss the problems found in determining Ru and Hf abundances with laboratory gf-values in the spectra of barium stars.
Methods. We determined Ru and Hf abundances in a sample of giant and dwarf barium stars, by the spectral synthesis of two Ru I ($\lambda$4080.574 and $\lambda$4757.856) and two Hf II ($\lambda$4080.437 and $\lambda$4093.155) transitions. The stellar spectra were observed with FEROS/ESO, and the stellar atmospheric parameters lie in the range 4300 <  $T_{\rm eff}$/K < 6500, -1.2 < [Fe/H] $\leq$ 0 and $1.4\leq \log g < 4.6$.
Results. The Hf II $\lambda$4080 and the Ru I $\lambda$4758 observed transitions result in a unreasonably high solar abundance, given certain known uncertainties, when fitted with laboratory gf-values. For these two transitions we determined empirical gf-values by fitting the observed line profiles of the spectra of the Sun and Arcturus. For the sample stars, this procedure resulted in a good agreement of Ru and Hf abundances given by the two available lines. The resulting Ru and Hf abundances were compared to those of Y, Nd, Sm and Eu. In the solar system Ru, Sm and Eu are dominated by the r-process and Hf, Nd and Y by the s-process, and all of these elements are enhanced in barium stars since they lie inside the s-process path. Ru abundances show large scatter when compared to other heavy elements, whereas Hf abundances show less scatter and closely follow the abundances of Sm and Nd, in good agreement with theoretical expectations. We also suggest a possible, unexpected, correlation of Ru and Sm abundances. The observed behaviour in abundances is probably due to variations in the ¹³C pocket efficiency in AGB stars, and, though masked by high uncertainties, hint at a more complex scenario than proposed by theory.

Key words: stars: abundances - stars: chemically peculiar - stars: late-type

  
1 Introduction

Barium stars are chemically peculiar objects which present large excesses of the elements due to the neutron capture s-process. These stars are not evolved enough to self-enrich during the thermal pulses in the AGB phase. The standard explanation for their peculiarities is a binary status. The former primary, more massive, evolves faster and goes into the AGB phase, whereby it convectively enriches its atmosphere with s-process products. After a phase of strong mass loss through stellar wind, it becomes a white dwarf and is detected in the ultraviolet only with difficulty (Böhm-Vitense et al. 2000), if at all. The former secondary is enriched by mass accretion from the stellar wind of its companion, and presents in its atmosphere vestiges of the nucleosynthesis of the former AGB star, being presently observed as the barium star.

Such stars usually have been studied by their strong excesses of the heavy elements chiefly synthesized by the s-process, Sr, Y, Zr, Ba, La, Ce and Nd being the most spectroscopically accessible. Ruthenium and hafnium, in their turn, have been very little studied even for this chemically peculiar class of stars. In fact, the literature on abundances of Ru and Hf, for any class of star, is very scarce.

These elements were previously detected in the very metal-poor stars CS 22892-052 (Sneden et al. 2003, and references therein) and CS 31082-001 (Hill et al. 2002), thanks to their large enhancement of neutron-capture elements. The lines of Hf and Ru are weak and most of them lie blended in the crowded near-UV region of the spectrum, generally hampering their detection in normal stars. Sneden et al. found [Ru/Fe] = +1.34 and [Hf/Fe] = +1.24 for CS 22892-052, at [Fe/H] = -3.1 and Hill et al. found [Ru/Fe] = +1.42 and [Hf/Fe] = +1.43 for CS 31082-001, at [Fe/H] = -2.9. Both these works only employed spectral lines with $\lambda< 4000$ $\rm\AA$. For another very metal poor star, HD 122563 with [Fe/H] = -2.7, Honda et al. (2006) found [Ru/Fe] = 0.07 from two lines with $\lambda< 4000$ $\rm\AA$. For the very metal poor ([Fe/H] = -3.5) TP-AGB star, CS 30322-023, Masseron et al. (2006) found [Ru/Fe] = 1.05 and [Hf/Fe] = 0.53. Ruthenium and hafnium were also observed in some chemically peculiar stars. Tomkin & Lambert (1983) found [Fe/H] = -0.32, [Ru/Fe] = +0.78 and [Hf/Fe] = +1.09 for the barium star HR 774, from the $\lambda$4584 and $\lambda$5309 Ru I lines, and the $\lambda$7132 Hf II line. For the symbiotic star AG Draconis, Smith et al. (1996) found [Hf/Fe] = +0.86 and [M/Fe] = -1.5 by using the $\lambda$7132 line. Yushchenko et al. (2002) found for the barium star $\zeta$ Cyg [Ru/Fe] $\approx$ -0.04 and [Hf/Fe] $\approx$ 0.47, for which they also found [Fe I/H] = +0.02 $\pm$ 0.10 and [Fe II/H] = +0.06 $\pm$ 0.08, employing the $\lambda$4584, $\lambda$4869 and $\lambda$5026 Ru I lines, and the $\lambda$4093 Hf II line. We note that the lines of Ru I used by Yushchenko et al. are not visible in our spectra.

Ruthenium lies close to Nb and Mo in the periodic table. This element could be called an r-process element, since, according to Arlandini et al. (1999), the contributions from the s-, r-, and p-processes for its abundance are respectively, 32.3%, 59.7%, and 8%. Hafnium is a heavy s-process element, lying close to La and Ba, and the abundance contributions from the s-, r-, and p-processes are, respectively, 55.5%, 44.16% and 0.34%, according to Arlandini et al. (1999). Abundance determinations of Ru and Hf for a statistically significant sample of barium stars might help increase the number of elements studied in these objects, thereby shedding further light on the detailed abundance distribution of heavy elements in these stars. The abundance ratio of the heavy group of the s-process elements, Ba to Nd, to the lighter group, Sr to Zr, has been traditionally used as a neutron exposure parameter (Allen & Barbuy 2006b; Smiljanic et al. 2007; North et al. 1994; Luck & Bond 1991). These data are necessary to clarify the mechanism that accounts for the large spread in abundance excesses of neutron capture elements between the mild barium and barium stars. The notion that these differences could be accounted for by differing metallicities, which in its turn results in different neutron exposure levels due to a higher ratio of neutron to seed nuclei density for lower metallicity stars, is not corroborated by the data (Smiljanic et al. 2007; Boyarchuk et al. 2002). A possible correlation with orbital parameters, in the sense that the mild barium stars have smaller s-process excesses due to longer orbital periods, has been claimed (Böhm-Vitense et al. 1984) but does not seem to explain the observations either (Jorissen et al. 1998). This has led Smiljanic et al. (2007) to suggest that a possible explanation might lie in a different mass range of the progenitors of mild barium and barium stars, or in different mixing properties in the two classes of stars. In order to test these and other possible scenarios, detailed abundance data are mandatory.

In this work, we present Ru and Hf abundances for a large sample of dwarf barium stars, mild barium stars and classical barium stars, based on high resolution and high signal-to-noise spectra. We also discuss discrepancies in the Ru and Hf oscillator strengths available in the literature, and their effect on the derived abundances. This paper is organized as follows. Section 2 briefly presents the data and the determination of the stellar atmospheric parameters; Sect. 3 describes the choice of spectral lines and the evaluation of published laboratory oscillator strengths; in Sect. 4 the uncertainty calculations are detailed; in Sect. 5 the derivation of abundances is described, and in Sect. 6 our conclusions are drawn.

  
2 Data source and atmospheric parameters

All spectra for the sample stars were obtained with the 1.52 m telescope at ESO, La Silla, using the Fiber Fed Extended Range Optical Spectrograph (FEROS, Kaufer et al. 2000). FEROS spectra have a constant resolving power of R = 48 000 from 3600 $\rm\AA$to 9200 $\rm\AA$. The target sample for the present study includes 25 dwarf, subgiant and giant barium stars from Allen & Barbuy (2006a): the S/N of the spectra of this sample ranges from 100 to 250. To this we added the sample described in detail by Smiljanic et al. (2007), involving 8 mild and classical barium stars, plus 6 normal giants, with spectral S/N ratio ranging from 500 to 600. The journal of observations and derivation of atmospheric parameters have been described in detail by these authors.

Allen & Barbuy (2006a) determined effective temperatures  $T_{\rm eff}$ from photometry, surface gravities $\log g$ from the stellar positions in theoretical HR diagrams, and iron abundances from equivalent widths of approximately 150 Fe I lines and 30 Fe II lines. Smiljanic et al. (2007) determined $T_{\rm eff}$, $\log g$ and metallicities from the simultaneous excitation and ionization equilibria of the equivalent widths of an average number of 120 Fe I and 12 Fe II lines. Surface gravities were also computed from the stellar luminosities and theoretical HR diagrams, and a very good agreement was found for the two sets of gravities.

The LTE abundance analysis and the spectrum synthesis calculations for Ru and Hf were performed by employing the codes by Spite (1967, and subsequent improvements in the past thirty years), described in Cayrel et al. (1991) and Barbuy et al. (2003). The adopted model atmospheres (NMARCS) were computed with a version of the MARCS code, initially developed by Gustafsson et al. (1975) and subsequently updated by Plez et al. (1992), used here for stars with gravities $\log g < 3.3$, and Edvardsson et al. (1993), here used for less evolved stars with $\log g \geq 3.3$. Abundances for Y, Nd, Sm, and Eu were taken from Allen & Barbuy (2006a) and for stars of Smiljanic et al. (2007), abundances based on spectrum synthesis calculations were performed and will be detailed in a forthcoming paper.

  
3 The oscillator strengths of ruthenium and hafnium

Ruthenium and hafnium present spectral lines ranging from the UV to the IR: for the lines that appear for $\lambda< 4000$ $\rm\AA$, the FEROS spectra do not allow good fits to synthetic ones, this region being too crowded for cool stars. So, in this work we looked for lines with larger wavelengths. The following lines, detected in the spectra of the Sun (Kurucz et al. 1984) and Arcturus (Hinkle et al. 2000), were considered for abundance determinations in the barium star spectra: $\lambda$4080.574, $\lambda$4144.1968, $\lambda$4381.272, and $\lambda$4757.856 for Ru I and $\lambda$4080.437 and $\lambda$4093.155 for Hf II. The lines $\lambda$4144.1968 and $\lambda$4381.272 are not visible in our barium star spectra, and so were discarded. Table 1 shows the oscillator strengths ($\log gf$) and excitation potential ( $\chi_{\rm ex}$) for the Ru I and Hf II lines used in this work, as well as the references for the $\log gf$values. The main $\log gf$ source was the Vienna Atomic Line Database (VALD, Piskunov et al. 1995). The $\log gf$ for Hf II $\lambda$4080.437 line is given by Lundqvist et al. (2006) and Lawler et al. (2007). If the value of -1.596 is used, the solar abundance of Hf is 0.7 dex higher than the value given by Grevesse & Sauval (1998), as shown in Fig. 1. For Arcturus (Fig. 2), the resulting abundance is $\log\epsilon$(Hf) = 0.98 and [Hf/Fe] = +0.64, much higher than expected for a normal, slightly metal-poor giant like Arcturus. Similarly, if the VALD $\log gf$value (-0.890) for the Ru I $\lambda$4757.856 line is used, the solar abundance of Ru is 0.35 dex higher than in Grevesse & Sauval, as shown in Fig. 3. These results are deemed as unreasonable in the face of the known uncertainties. For these two transitions we determined gf-values by fitting the observed line profiles of the spectra of the Sun and Arcturus, shown in Table 1 and Figs. 1, 2, and 3. We used for the Sun $T_{\rm eff} = 5780$ K, $\log g = 4.44$ (cgs) and a microturbulent velocity of $\xi = 0.93$ km s^-1, and an atmospheric model from Edvardsson et al. (1993). For Arcturus, we used atmospheric parameters from Meléndez et al. (2003), $T_{\rm eff} = 4275$ K, $\log g = 1.55$ (cgs), [Fe/H] = -0.54, excepting $\xi = 1.5$ km s^-1 which was fitted in this work. The Plez et al. (1992) grid was used to derive the atmospheric model.

It is conceivable that an unidentified transition, blended with the Ru and Hf lines, explains these large discrepancies. The region around $\lambda$4080 contains molecular lines of CN, so one must be careful in fitting synthetic spectra there. One possibility is that a CN feature, missing in our molecular lines database, might be blended with the Hf II $\lambda$4080.574 transition. Using the gf-values given by Lundqvist et al. (2006) or Lawler et al. (2007) could make the synthetic line weaker than the observed one, consequently increasing the resulting abundance from this line.

	Figure 1: Fits for two oscillator strengths of the Hf II $\lambda$4080.437 line in the solar spectrum. Solid line: observed spectrum; dotted line: $\log gf = -0.896$; dashed line: $\log gf = -$1.596. All synthetic spectra were created with $\log\epsilon$(Hf) = 0.88.
Open with DEXTER

	Figure 2: Fits for two oscillator strengths of the Hf II $\lambda$4080.437 line in the Arcturus spectrum. Solid line: observed spectrum; dotted line: $\log\epsilon$(Hf) = 0.28 ([Hf/Fe] = -0.06) and $\log gf$ = -0.896 or $\log\epsilon$(Hf) = 0.98 ([Hf/Fe] = +0.64) and $\log gf$ = -1.596; dashed line: $\log\epsilon$(Hf) = 0.28 and $\log gf = -$1.596.
Open with DEXTER

	Figure 3: Fits for two oscillator strengths in the solar spectrum for the Ru I $\lambda$4757.856 line. Solid line: observed spectrum; dotted line: $\log\epsilon$(Ru) = 1.84 and $\log gf$ = -0.540 or $\log\epsilon$(Ru) = 2.19 and $\log gf$ = -0.890; dashed line: $\log\epsilon$(Ru) = 1.84 and $\log gf = -0.890$.
Open with DEXTER

  
4 Uncertainties

Two stars were used to compute the abundance uncertainties: HD 181053 from Smiljanic et al. (2007) with $T\rm _{eff} = 4810 \pm 50$ K, $\log g = 2.48 \pm 0.35$, [Fe/H] = - $0.19 \pm 0.12$, and $\xi =1.70 \pm 0.06$, and HD 87080 from Allen & Barbuy (2006a) with $T_{\rm eff} = 5460 \pm 100$ K, $\log g = 3.7~\pm~0.2$, $\rm [Fe/H] = -0.44~\pm~0.04$, and $\xi = 1.0~\pm~0.1$. The abundance uncertainties were calculated by verifying how much the variation of 1$\sigma$on the atmospheric parameters affects the output value of the synthesis program, here $\log{A_p}$. Table 2 shows the values taken into account in this calculation and the resulting uncertainties.

Under the simplifying hypothesis of independent errors, the uncertainty of the output value is given by

$$\sigma_{Ap}=\sqrt{(\Delta A_T)^2+(\Delta A_{mt})^2+(\Delta A_l)^2+(\Delta A_\xi)^2},$$ (1)

where $\Delta A_T$, $\Delta A_{mt}$, $\Delta A_l$, and $\Delta A_\xi$, are the average differences in A_p from two lines of each element shown in Table 2 due to variations of 1$\sigma$ in the temperature, metallicity, $\log g$, and microturbulent velocity, respectively.

The average value of A_p (A_pm) is obtained by averaging the individual abundances of two lines and not from several measurements of the same line. In the latter case, the standard deviation could be used to calculate the uncertainty on A_pm. Considering this, we found it more suitable to apply a propagation of errors taking into account the uncertainty calculated with Eq. (1). Thus, the uncertainty on A_pm is

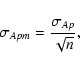$$\sigma_{Apm}={\sigma_{Ap}\over \sqrt{n}},$$ (2)

where n is the number of lines. The uncertainty on the logarithm of A_pm is

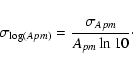$$\sigma_{\log(Apm)}={\sigma_{Apm}\over A_{pm}\ln{10}}\cdot$$ (3)

The abundance $\log\epsilon$(X) is related to the output of the synthesis program by $\log\epsilon$(X) = $\log{A_{pm}}$ + [Fe/H]. Therefore, the uncertainty is

$$\sigma_{\log\epsilon({\rm X})}=\sqrt{\sigma_{\log{(Apm)}}^2+\sigma_{\rm [Fe/H]}^2}.$$ (4)

The relation between the abundance excess relative to iron [X/Fe] and the output value of the synthesis program is [X/Fe] =  $\log{A_{pm}}$ - $\log\epsilon_\odot({\rm X})$, where $\log\epsilon_\odot({\rm X})$is the solar abundance of the element "X''. The uncertainty is calculated by

$$\sigma_{\rm [X/Fe]}=\sqrt{\sigma_{\log(Apm)}^2+\sigma_{\log\epsilon_\odot(X)}^2}.$$ (5)

The uncertainties shown in Table 2 for HD 181053 and HD 87080 are typical for stars with $\log g < 3.3$ and $\log g \geq 3.3$, respectively. Figures 4 and 5 show the synthetic spectra considering 1$\sigma$of the abundance and Figs. 6 and 7 show the maximum value of uncertainties on each axis.

For [Hf/Ru] the uncertainties are determined by

$$\sigma_{\rm [Hf/Ru]}=\sqrt{\sigma_{\rm [Hf/Fe]}^2+\sigma_{\rm [Ru/Fe]}^2},$$ (6)

and they are 0.48 and 0.14 for stars with $\log g < 3.3$ and $\log g \geq 3.3$, respectively.

Uncertainties on elements other than Ru and Hf were described in Allen & Barbuy (2006a).

Table 1: Atomic constants for the Ru I and Hf II lines used in this work, and references for $\log gf$. "Sun'' denotes the gf-values fitted on the solar and Arcturus spectra. Other gf-values were taken from VALD, Lundqvist et al. (2006) (L06), and Lawler et al. (2007) (L07).

Table 2: Uncertainties on abundances. $\log{A_{pf}}$: output with the atmospheric parameters adopted; $\log{A_{pT}}$: output by altering 1$\sigma$ on adopted $T\rm _{eff}$; $\log{A_{pmt}}$: output by altering 1$\sigma$ on adopted metallicity; $\log{A_{pl}}$: output by altering 1$\sigma$ on adopted $\log g$; $\log{A_{p\xi}}$: output by altering 1$\sigma$ on adopted microturbulent velocity $\xi$; $\sigma _l$: $\sigma_{\log\epsilon}$, the uncertainty on $\log\epsilon$(X) from Table 4; $\sigma _f$: $\sigma _{\rm [X/Fe]}$, the uncertainty on [Ru/Fe] or [Hf/Fe] from Table 4.

  
5 The abundance results

The Ru and Hf transitions in the spectra of the barium stars of our sample are generally weak, and this makes the abundance determinations from them difficult. Figure 4 shows the synthetic spectrum fit in the star HD 181053 for the $\lambda$4080.437 (Hf II), and $\lambda$4080.574 (Ru I) lines. Figure 5 shows the fit for the $\lambda$4757.856 Ru I line in the star HD 87080.

The results for each line of our sample barium stars used for the abundance calculations are shown in Table 3, and the average values are given in Table 4. The latter shows that the average values are mainly in the ranges +0.18 $\leq$ [Ru/Fe] $\leq$ +2.00 and +0.20 $\leq$ [Hf/Fe] $\leq$ +1.71. Only for the star HD 210910 were the values lower than these ranges. Some stars indicated in Tables 3 and 4 were considered normal rather than barium stars by Smiljanic et al. (2007) and their abundances were found to be in the ranges -0.05 $\leq$ [Ru/Fe] $\leq$ +0.43 and -0.20 $\leq$ [Hf/Fe] $\leq$ +0.37. The upper values of these ranges in the normal stars, when compared with those of the barium stars, while showing the extent of the uncertainties, also highlight the large overabundance of Ru and Hf in most barium stars of the sample. In Fig. 6 we plot the run of [Ru/Fe] and [Hf/Fe] with [Fe/H] for all stars we analyzed. They show a distinctive decreasing trend of both [Ru/Fe] and [Hf/Fe] towards increasing [Fe/H] for the sample barium stars. It is noteworthy, however, that the normal stars present no trend in their [Ru/Fe] and [Hf/Fe] abundances, having [Ru, Hf/Fe] $\sim$ 0 over almost an order of magnitude variation in metallicity.

In some cases only an upper limit for the abundance could be derived, as indicated in Tables 3 and 4. If only one of the two lines has an upper limit for the Ru abundance while the other has a good fit, the adopted abundance was that resulting from the best line and only this line was taken into account to compute the average of the abundance, as seen comparing Tables 3 and 4. For some stars the fit at $\lambda$4080 is very uncertain and we chose not to derive any abundance from it. The fit for BD+18 5215 at $\lambda$4757 could not be carried out, and there is a spike of noise at $\lambda$4093 for HD 147609, so there are no results for these transitions in these stars. For HD 20894, considered a normal star by Smiljanic et al. (2007), and the barium stars HD 48565 and HD 76225, we found a large difference (>0.3 dex) between the abundance results of the two Ru (barium stars) or Hf (HD 20894) lines. For all the other stars, the two lines used led to similar abundance values for Ru as well as Hf. In Table 5 the stars are ordered by increasing temperature, where the problems of the abundance derivation seem to be related to higher temperatures. Although the temperatures of HD 210910 and HD 204075 are not very high, their broad lines cause some difficulties in deriving the abundances. HD 106191 has an upper limit for Hf, and no fit for the $\lambda$4080 line, yet its temperature is not very high either. However, its S/N is lower (S/N $\sim$ 100) than for other stars (see Smiljanic et al. 2007; Allen & Barbuy 2006a). As a counter-example, the S/N $\sim$ 250 spectrum of HD 89948 allowed good fits for all lines, despite the high temperature of this object. Regarding the lines of Ru I, the fit of the $\lambda$4757.856 line for the sample barium stars had higher quality than for the $\lambda$4080.574 line due to its freedom from neighboring perturbing lines.

	Figure 4: Fitting of the Hf II $\lambda$4080.437 and Ru I $\lambda$4080.574 lines for the barium star HD 181053. Solid line: observed spectrum; dotted lines: synthetic spectra with [Hf/Fe] = 0.25, 0.40 and [Ru/Fe] = 0.15, 0.61.
Open with DEXTER

	Figure 5: Fitting of the Ru I line $\lambda$4757.856 for the barium star HD 87080. Solid line: observed spectrum; dotted lines: synthetic spectra with [Ru/Fe] = 1.60, 1.71.
Open with DEXTER

	Figure 6: [X/Fe] vs. [Fe/H] and [Hf/Ru] vs. [[Fe/H] for the sample stars. Symbols: squares: barium stars; triangles: stars considered normal rather than barium stars by Smiljanic et al. (2007). The arrows in the hafnium panel indicate an upper limit for HR 107, HD 106191, HD 147609, and HD 210910. The error bars indicate the maximum value of uncertainties on each axis.
Open with DEXTER

Figure 7: Comparison of the [Hf/Fe] and [Ru/Fe] behavior with [Y/Fe], [Nd/Fe], [Sm/Fe], and [Eu/Fe]. Filled squares are the barium stars and open triangles are those considered normal rather than barium stars by Smiljanic et al. (2007). The least-square fits for [Hf/Fe] vs. [Nd/Fe] and [Hf/Fe] vs. [Sm/Fe] are explained in the text. The full line indicates the fit for all sample stars and the dashed line, that excluding the normal stars.

Open with DEXTER

From Fig. 6, the run of [Hf/Ru] with Fe shows very large scatter, up to $\sim$2 dex, with an apparent advantage for Ru abundances over those of Hf, since most of the values of [Hf/Ru] lie below zero. According to the Table 4, among 33 barium stars, 17 have [Hf/Ru] < 0, 2 have [Hf/Ru] = 0, and 14 have [Hf/Ru] > 0. Yet for normal stars of this table, 5 among 6 stars have [Hf/Ru] < 0. However, the highest values for [Ru/Fe] correspond mainly to stars that have only one line available and also when for one of the lines only an upper limit is available, which is much lower than the other estimate. As shown in Sect. 4, uncertainties for [Ru/Fe] are much larger than ones for [Hf/Fe]. Furthermore, in cases where only one line was available, the error must be larger than for other stars when the two lines gave a result. The highest value of Ru abundance was found for HD 107574. The spectral lines of this star are broader than those of most other stars, and, although the broadening is not as strong as for HD 210910 and HD 204075, this line may be blended with another line that does not exist in our linelists, and it may be enough to give such high result. In fact, the line $\lambda$4757.856 usually gives higher results than $\lambda$4080.574. Note that if the gf-value from VALD was used, the result would be higher. Hence, this spectral region merits further spectroscopic analysis. A similar dificulty in determining abundances was found for the star HD 2454, with quite similar atmospheric parameters, in particular, microturbulent velocity. According to the values of [X/Fe] for other neutron capture elements found for this star, these very low values of [Hf/Ru] may not be real.

Table 6: Contributions of s- and r-processes for the abundances of Hf, Ru, Y, Eu, Sm, and Nd in solar system, following Arlandini et al. (1999). The last column is the sum of s- and r-processes.

Table 7: Least-square fits, [X₁/Fe] = A[X₂/Fe] + B, where X₁ is Ru or Hf and X₂ can be Y, Nd, Eu or Sm; "cov'' is the covariance between A and B; "d.o.f.'' is the number of degrees of freedom. Numbers in parenthesis are errors in last decimals.

Figure 7 shows the Ru and Hf abundances compared to those of Y, Nd, Sm, and Eu for all stars of the sample. Yttrium can properly represent the s-process, given that, according to Arlandini et al. (1999), 92% and 8% of its abundance is due to s- and r-processes in the solar system, respectively, as shown in Table 6. In this table, the missing abundance fractions are due to processes other than s(main component) and r, and are seen to be of little significance. Europium, compared to yttrium, has almost opposite behavior, with 5.78% and 94.25% of its contribution from the s- and r-processes, respectively. In their turn, neodymium and hafnium may be considered as mild s-elements since the s-process forms the bulk of their abundances but does not entirely dominate their production, as it does for yttrium. Ruthenium and samarium, on the other hand, are mainly contributed, but not entirely dominated, by the r-process. These elements were chosen for a comparison since they span a wide range of contributions from the s- and r-processes, from a strong dominance of the s-process for yttrium, through a more or less balanced contribution to a high dominance of the r-process for europium.

To study the correlations between abundances shown in Fig. 7, least-square fits are shown in Table 7. A remarkable feature of Fig. 7 is the large scatter of Ru abundances, not found in the Hf abundances. Also, Ru abundances seem to present little correlation with those of other elements, as shown by the values of $\chi^2_{\rm red}$ in Table 7.

The results for Hf have much lower scatter and are no less remarkable: high scatter is found only in the [Hf/Fe] run with [Y/Fe]. Rather tight positive correlations are found between the Hf abundances and those of Nd and Sm, as can be judged by the value of the $\chi^2_{\rm red}$ of Table 7. For Nd and Sm, two fits for each are represented in Fig. 7: if all sample stars are included in the fit, the results are:

$$[{\rm Hf/Fe}]= (1.053 \pm 0.048)[{\rm Nd/Fe}] + (0.089 \pm 0.042)$$ (7)

$$[{\rm Hf/Fe}]= (1.305 \pm 0.076)[{\rm Sm/Fe}] + (0.119 \pm 0.050).$$ (8)

If those objects considered normal rather than barium stars by Smiljanic et al. (2007) are withdrawn from the sample, the results are:

$$[{\rm Hf/Fe}]= (1.022 \pm 0.055)[{\rm Nd/Fe}] + (0.121 \pm 0.050)$$ (9)

$$[{\rm Hf/Fe}]= (1.211 \pm 0.083)[{\rm Sm/Fe}] + (0.201 \pm 0.058).$$ (10)

Nd and Sm however differ markedly in that Sm is fairly well dominated by the r-process, whereas Nd shows a more balanced fractional contribution in the solar system, similarly to Hf. One should, on these grounds, expect a good correlation between the [Hf/Fe] and [Nd/Fe] ratios, which we verify, and also a reasonably clear correlation between the [Hf/Fe] and [Sm/Fe] ratios, with higher slope, also verified by our data. The correlation of the Hf abundances with Eu is distinctly less clear. Since only $\sim$6% of the solar abundance of Eu is from the s-process, a very weak correlation between the [Hf/Fe] and [Eu/Fe] ratios is to be expected, as we found, and only for higher values of [Hf/Fe], above 1.5 dex or so, should a correlation be detectable, but this lies outside the range of our data.

The main component of the s-process is believed to occur as a chain from $\sp {56}$Fe seed nuclei up to Bi. The neutron fluency may be enough to feed the first s-process peak (near magic neutron number N = 50, in our discussion represented by Y and Ru), then the second peak (near magic neutron number N = 82, here Nd and Sm) and then on to the third peak (near magic neutron number N = 126), as a function of the so-called ¹³C pocket efficiency (still a free parameter in current modelling), providing the bulk of the neutron flux (at least for low fluxes) through the $^{\rm 13}$C($\alpha$, n)$^{\rm 16}$O reaction (Busso et al. 1999). It is thus possible that, in a round of s-processing, not all peaks are equally fed by the neutron fluency, generating scatter on the abundance ratios involving elements from different peaks. Figure 16 of Busso et al. (1999) illustrates this scatter on a diagram of [hs/ls] vs. [Fe/H], as a function of the efficiency of the ¹³C pocket. For the [Ru/Fe] vs. [Y/Fe] ratios we could in principle expect a good correlation, since they both belong to the first peak, but Y is a magic neutron element, for which an abundance enhancement is expected, partially masking this correlation. In fact, according to the $\chi^2_{\rm red}$ in Table 7, the abundance correlation between Ru and Y is only just as good as for Ru and Sm, and not very clear. The [Ru/Fe] and [Eu/Fe] run demonstrates a very poor correlation, not unexpected, these being elements from different peaks, and with dissimilar fractional contributions from the s- and r-processes. The correlation between Ru (a first peak element) and Nd or Sm is also expected to be worse under this reasoning, since the latter are both near the second peak. Indeed, the run of [Ru/Fe] and [Nd/Fe] does not show a good correlation, but that of [Ru/Fe] and [Sm/Fe], somewhat unexpectedly, shows the hint of one, as judged by the $\chi^2_{\rm red}$ value. On the other hand, Hf, Nd, and Sm are all near the second s-process peak, so one would expect lower scatter in the abundance ratios shown in Fig. 7, also confirmed by our data. Some of the theoretical expectations of AGB s-process nucleosynthesis are therefore borne out by our results, but these, taken together, suggest a more complex behavior of the abundance ratios of Ru and Hf with Y, Nd, Eu and Sm than established by the current state of theory. Clearly, more data on the abundances of these two little-studied, spectroscopically not very accessible, elements, are desirable to better constrain theoretical scenarios of s-process nucleosynthesis.

  
6 Conclusions

We present abundances of Ru and Hf determined through the spectrum synthesis of two lines for each element available in the spectra of dwarf and giant barium stars. Good agreement was obtained for each pair of Ru and Hf lines for most sample stars. For a few stars, the abundance difference derived from the two lines was higher than 0.3 dex. We found that for the $\lambda$4080.437 of Hf II, and $\lambda$4757.856 of Ru I lines, published gf-values do not fit well to the observed solar spectrum. We offer tentative explanations for these discrepancies, which merit further study. New experiments determining the $\log gf$ for these lines are needed. Further, reliable abundance determinations of these elements can contribute considerably to our knowledge of heavy element abundances in this class of chemically peculiar stars, besides helping better constrain theoretical scenarios of AGB s-process nucleosynthesis, still prone to important uncertainties.

We compared the run of [Hf/Fe] and [Ru/Fe] abundance ratios with other heavy elements, chosen to represent different fractional contributions from the s- and r-process, as judged by the solar system isotopic composition. The abundance of Hf is closely correlated with that of Sm and Nd, in reasonable agreement with theoretical expectations. It is noteworthy that, although Sm is an r-process dominated element, and Nd presents abundance fractions from s- and r-process nucleosynthesis similar to Hf in the solar system abundance pattern, in our barium star data both elements are well correlated with Hf, probably because all three elements lie near the second s-process peak. Ru is not clearly correlated with the other heavy elements, excepting possibly Y and Sm. A correlation of Ru and Y abundances may be masked partially by the magic neutron number nature of the latter. The possibility of a correlation in the Ru and Sm abundances, in the light of a similar fractional contribution from the s- and r-processes even though these elements belong to different s-processing peaks, deserves further investigation. The stars should span a larger metallicity interval than the one studied here. These results suggest a more complex relationship between the excesses of the various heavy elements in barium stars than implied by theoretical considerations.

Acknowledgements

D.M.A. acknowledges a FAPERJ post-doctoral fellowship N$^{\circ}$152.680/2004, as well as CAPES, for the post-doctoral fellowship N$^{\circ}$ BEX 3448/06-1. We are also grateful to Licio da Silva, Luciana Pompéia, Paula Coelho, and Jorge Meléndez for carrying out some observations of our sample spectra. We are grateful to Beatriz Barbuy for make available part of the spectra and the spectrum synthesis code. GFPM acknowledges financial support by CNPq/Conteúdos Digitais (grant 552331/01-5), CNPq/MEGALIT/Institutos do Milênio program, and a FAPERJ (grant APQ1/26/170.687/2004). We thank the referee, Dr. Roberto Gallino, for his criticism and comments, which very considerably improved this paper.

References

• Allen, D. M., & Barbuy, B. 2006a, A&A, 454, 895 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Allen, D. M., & Barbuy, B. 2006b, A&A, 454, 917 [NASA ADS] [CrossRef] [EDP Sciences]
• Arlandini, C., Käppeler, F., & Wisshak, K. 1999, ApJ, 525, 886 [NASA ADS] [CrossRef] (In the text)
• Barbuy, B., Perrin, M.-N., Katz, D., et al. 2003, A&A, 404, 661 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Böhm-Vitense, E., Nemec, J., & Proffit, C. 1984, ApJ, 278, 726 [NASA ADS] [CrossRef] (In the text)
• Böhm-Vitense, E., Carpenter, K., Robinson, R., Ake, T., & Brown, J. 2000, ApJ, 533, 969 [NASA ADS] [CrossRef] (In the text)
• Boyarchuk, A. A., Pakhomov, Yu. V., Antipova, L. I., & Boyarchuk, M. E. 2002, ARep, 46, 819 [NASA ADS]
• Busso M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] (In the text)
• Cayrel, R., Perrin, M. N., Barbuy, B., & Buser, R. 1991, A&A, 247, 108 [NASA ADS] (In the text)
• Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] (In the text)
• Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
• Gustafsson, B., Bell, K. A., Eriksson, K., & Nordlund, Å. 1975, A&A, 42, 407 [NASA ADS] (In the text)
• Hill, V., Plez, B., Cayrel, R., et al. 2002, A&A, 387, 560 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727-9300 Å (In the text)
• Honda, S., Aoki, W., Ishimaru, Y., Wanajo, S., & Ryan, S. G. 2006, ApJ, 643, 1180 [NASA ADS] [CrossRef] (In the text)
• Kaufer, A., Stahl, O., Tubbesing, S., et al. 2000, Proc. SPIE, 1008, 459 (In the text)
• Kurucz, R. L., Furenlid, I., & Brault, J. 1984, Solar flux atlas from 296 to 1300 nm, National Solar Observatory Atlas, Sunspot (New Mexico: National Solar Observatory) (In the text)
• Jorissen, A., Van Eck, S., Mayor, M., & Udry, S. 1998, A&A, 332, 877 [NASA ADS] (In the text)
• Lawler, J. E., Den Hartog, E. A., Labby, Z. E., Sneden, C., Cowan, J. J., & Ivans, I. I. 2007, ApJS, 169, 120 [NASA ADS] [CrossRef] (In the text)
• Luck, R. E., & Bond, H. E. 1991, ApJS, 77, 515 [NASA ADS] [CrossRef]
• Lundqvist, M., Nilsson, H., Wahlgren, G. M., et al. 2006, A&A, 450, 407 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Masseron, T., Van Eck, S., Famaey, B., et al. 2006, A&A, 455, 1059 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Meléndez, J., Barbuy, B., Bica, E., et al. 2003, A&A, 411, 417 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• North, P., Berthet, S., & Lanz, T. 1994, A&A, 281, 775 [NASA ADS]
• Piskunov, N., Kupka, F., Ryabchikova, T., Weiss, W., & Jeffery, C. 1995, A&AS, 112, 525 [NASA ADS] (In the text)
• Plez, B., Brett, J. M., & Nordlund, A. 1992, A&A, 256, 551 [NASA ADS] (In the text)
• Smiljanic, R., Porto de Mello, G. F., & da Silva, L. 2007, A&A, 468, 679 [NASA ADS] [CrossRef] [EDP Sciences]
• Smith, V. V., Cunha, K., Jorissen, A., & Boffin, H. M. J. 1996, A&A, 315, 179 [NASA ADS] (In the text)
• Sneden, C., Cowan, J. J., Lawler, J. E., et al. 2003, ApJ, 591, 936 [NASA ADS] [CrossRef] (In the text)
• Spite, M. 1967, Ann. Astrophys. 30, 211
• Tomkin, J., & Lambert, D. L. 1983, ApJ, 273, 722 [NASA ADS] [CrossRef] (In the text)
• Yushchenko, A., Gopka, V., Kim, C., Khokhlova, V., et al. 2002, JKAS, 35, 209 [NASA ADS] (In the text)

 

  
Online Material

Table 3: Equivalent width and abundance results for the sample stars, line by line. The symbol "<'' indicates an upper limit. The stars signaled with "*'' were considered normal rather than barium stars by Smiljanic et al. (2007).

Table 4: [Fe/H] and the mean values for $\log\epsilon$(X) and [X/Fe] for all stars of the sample. The symbol "<'' indicates an upper limit. The stars signaled with "*'' were considered normal rather than barium stars by Smiljanic et al. (2007). The number of lines used to compute the medium is shown in brackets.

Table 5: This table was organized in increasing order of $T\rm _{eff}$, with the comments about the results shown in the last column of each series of 4 columns.