A&A 474, 301-306 (2007)
DOI: 10.1051/0004-6361:20065891
M. Barthélémy1 - J. Lilensten1 - C. D. Parkinson2
1 - Laboratoire de Planétologie de Grenoble, CNRS-UJF, BP 53, 38041 Saint Martin d'Hères Cedex 9, France
2 -
Dept. of Atmospheric, Oceanic, and Space Sciences, University of Michigan, Ann Arbor, MI 48109, USA
Received 23 June 2006 / Accepted 9 July 2007
Abstract
Aims. We present a method to detect the molecular hydrogen in extrasolar planetary atmospheres.
Methods. We model the coupling between H-Lyman lines and H2 lines due to wavelength overlapping between these lines. We also explore the overlapping between other stellar EUV lines especially the C III line at 977.02 Å and planetary H2 lines.
Results. If the spectrum of the planet is resolved, we show that H2 modifies the intensity and shape of the H-Lyman lines emitted by the planet. However, if observed in absorption spectroscopy during a transit, the modification of the stellar lines in the Lyman series by the atmospheric H2 is too low to be detectable with the current observing facilities. On the contrary, for HD 209458b with a 25 000 km thick H2 layer, the intensity of the stellar C III line at 977.02 Å decreases by 2.64% during the transit. In the case of the newly discovered planet HD 189733b, the decrease of the intensity of the C III line reaches 3.78%.
Conclusions. Such decreases could be detectable with a FUSE observation of several transits thereby constituting a way to detect H2 in exoplanetary atmospheres.
Key words: radiative transfer - stars: planetary systems - molecular processes - ultraviolet: general
The first exoplanet orbiting a solar type star was discovered using the radial velocity method (Mayor & Queloz 1995). Since that time, more than 20 transit planets have been detected, such as HD 209458b (Charbonneau et al. 2000). The investigation of the atmosphere of an extrasolar planet, through transit effects, is possible with techniques already available. HD 209458b is very interesting because of its extended hydrogen atmosphere (Vidal Majar et al. 2003). In the atmosphere of this planet, atoms or atomic ions have been detected, such as Na I at low altitudes (Charbonneau et al. 2001) or O I and CII at upper altitudes (Vidal Majar et al. 2004), but no molecular species have been detected so far. In our solar system, the most abundant species in giant planet atmospheres is H2 (Yelle 2004). The aim of this paper is to explore different UV spectroscopic ways to detect H2, to estimate the thickness of the H2 layer in the atmosphere, and to obtain information about the thermodynamic state of this molecule using radiative transfer calculations.
We propose a method to detect H2 using the effect of the coupling of several lines on the line shape and intensity. The line shapes and intensities are calculated through a simulation of the radiative transfer in the atmosphere of the planet. Similar calculations have been performed for the Jovian case to study the intensity and line shape of the planetary H-Lyman lines taking into account the radiative transfer coupling between H-Lyman lines and the H2 Lyman and Werner systems (Barthelemy et al. 2004, 2005). The basic principle underlying our method is to use the wavelength coincidences between H2 Werner and Lyman systems and stellar lines in the far or extreme UV. For example, the Lyman ![]() line (1025.67 Å) is very close to the H2 6-0 P(1) line of the Lyman system at 1025.93 Å. Considering that the width of the stellar line is larger than the wavelength difference, it is possible to determine the H2 excitation due to the Lyman
line (1025.67 Å) is very close to the H2 6-0 P(1) line of the Lyman system at 1025.93 Å. Considering that the width of the stellar line is larger than the wavelength difference, it is possible to determine the H2 excitation due to the Lyman ![]() line. The effect in the Jovian case has been calculated (Liu & Dalgarno 1996; Barthelemy et al. 2004). In the case of extrasolar planets, the intensity and line shape of the stellar line will be modified during a transit and we will study whether this could be detectable with the current observing facilities.
line. The effect in the Jovian case has been calculated (Liu & Dalgarno 1996; Barthelemy et al. 2004). In the case of extrasolar planets, the intensity and line shape of the stellar line will be modified during a transit and we will study whether this could be detectable with the current observing facilities.
The radiative transfer calculations follow the Feautrier approach used by Gladstone (1983, 1988), Griffioen (2000) and Parkinson et al. (2002, 2006). We extended this model to include the case of coupled H2 and H Lyman lines (Barthelemy et al. 2004). The coupled case uses a rapidly convergent lambda operator method for to solve the resonance line scattering problems (Griffioen et al. 1994). The Feautrier technique allows us to keep information about the emission for each altitude level and allows the sphericity of the planet to be taken into consideration for precise limb computations. We will apply our method to the case of the planet HD 209458b which is the most studied extrasolar planet.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5891f1a.eps}\par\vspace*{2mm}
\includegraphics[width=6.5cm,clip]{5891f1b.eps}\end{figure}](/articles/aa/full/2007/40/aa5891-06/Timg7.gif) |
Figure 1: HD 209458b atmospheric model. Upper panel: temperature profile in the atmosphere of the planet HD 209458b; from Yelle (2004). Lower panel: density profiles of H (solid line) and H2 (dashed line) in the atmosphere of HD 209458b; from Yelle (2004). |
| Open with DEXTER | |
In this model (Fig. 1, lower panel) H2 is the major species below 8000 km. At upper altitudes H becomes the major constituent, and at very high altitudes up to around 60 000 km, protons become the main species (not shown in the figure). The model stops at 150 000 km. This is smaller than the Vidal-Madjar et al. (2003) upper altitude observation. We do not take protons into account in our simulation. The H2 layer has a cut-off at an altitude of about 25 000 km and we will study the sensitivity of our result with the variation of this reference altitude.
This two assumptions could seem artificial because we do not compute a new complete atmospheric model each time we change the altitude of the H2 cut-off. This also violates the hydrodynamic equilibrium condition but our aim is to test the sensitivity of possible measurement to the thickness of the H2 layer. It is important to keep this limitation in mind in the interpretation of the results.
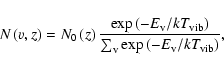 |
(1) |
We consider two geometries between the planet, the star and the line of sight. In the first case the star, the planet and the observer are aligned and the planet is in transit in front of the star. In the second case, there is a right angle between the (star-planet) axis and the line of sight. In this latter case, it is impossible to separate the star from the planet in the case of HD 209458b with a telescope like HST, because the distance between them is 0.045 AU and the star is at 47 pc from the earth.
Since HD 209458 is similar to the sun, the line widths will be taken similar to the solar line. The Lyman ![]() and
and ![]() lines are modelled by a double Gaussian. The width and offset are respectively 0.125 Å and 0.145 Å in the Lyman
lines are modelled by a double Gaussian. The width and offset are respectively 0.125 Å and 0.145 Å in the Lyman ![]() case and 0.22 Å and 0.216 Å in the Lyman
case and 0.22 Å and 0.216 Å in the Lyman ![]() case (Barthelemy et al. 2004, 2005). The other ones are modelled by a simple Gaussian with a full width mid height of 0.28 Å. We checked that this is consistent with the observations. We calculate the line characteristics between -0.8 and +0.8 Å for the Lyman
case (Barthelemy et al. 2004, 2005). The other ones are modelled by a simple Gaussian with a full width mid height of 0.28 Å. We checked that this is consistent with the observations. We calculate the line characteristics between -0.8 and +0.8 Å for the Lyman ![]() case, -0.7 and 0.7 Å for the Lyman
case, -0.7 and 0.7 Å for the Lyman ![]() case,
case, ![]() 0.3 Å for the remaining cases.
0.3 Å for the remaining cases.
The Lyman lines are amongst the most intense of the stellar spectrum. There are very close coincidences between the v=2 H2 lines and the H-Lyman ![]() lines. In the case of Lyman
lines. In the case of Lyman ![]() ,
the coincidences are with one line of the ground vibrational level and one other with the v=1 level (Table 1).
,
the coincidences are with one line of the ground vibrational level and one other with the v=1 level (Table 1).
Table 1:
H2 lines in coincidence with H-Lyman ![]() and
and ![]() .
.
We first compute the modifications of the Lyman ![]() line in a transit geometry. At this stage, the vibrational temperatures are equal to the kinetic ones. We consider an atmospheric H layer 150 000 km thick and an H2 layer 25 000 km thick (Fig. 1). We sample the atmosphere with 49 lines of sight positioned from the planetary limb to the limit of the atmosphere and we average the results to take into account the fact that the planet-star system represents less than one pixel on a telescope like HST. We do not take into account the interstellar absorption which may significantly change the line profile close to the centre of the line. For this calculation, the diminution of the intensity is equal to 10.45%. If the line was totally absorbed by the atmosphere, we should find an 11.99% diminution. The difference is due to the atmospheric emissions of the planet itself. Our calculated values are lower than the values measured by Vidal-Madjar et al. (2003), if we extrapolate to the entire line, the absorption they obtain in the useful part of their spectra i.e. between 1215.2 Å and 1215.5 Å and between 1215.8 Å and 1216.1 Å. This is because the Yelle model considers an atmosphere with only 150 000 km of H instead of 200 000 km deduced from Vidal-Madjar et al. (2003). Considering this last case, the maximal absorption reaches 17.44% which is consistent with Vidal-Madjar et al. (2003) values considering their 1
line in a transit geometry. At this stage, the vibrational temperatures are equal to the kinetic ones. We consider an atmospheric H layer 150 000 km thick and an H2 layer 25 000 km thick (Fig. 1). We sample the atmosphere with 49 lines of sight positioned from the planetary limb to the limit of the atmosphere and we average the results to take into account the fact that the planet-star system represents less than one pixel on a telescope like HST. We do not take into account the interstellar absorption which may significantly change the line profile close to the centre of the line. For this calculation, the diminution of the intensity is equal to 10.45%. If the line was totally absorbed by the atmosphere, we should find an 11.99% diminution. The difference is due to the atmospheric emissions of the planet itself. Our calculated values are lower than the values measured by Vidal-Madjar et al. (2003), if we extrapolate to the entire line, the absorption they obtain in the useful part of their spectra i.e. between 1215.2 Å and 1215.5 Å and between 1215.8 Å and 1216.1 Å. This is because the Yelle model considers an atmosphere with only 150 000 km of H instead of 200 000 km deduced from Vidal-Madjar et al. (2003). Considering this last case, the maximal absorption reaches 17.44% which is consistent with Vidal-Madjar et al. (2003) values considering their 1![]() error bars. This validates our approach in treating the atmosphere as we have and shows that the choice made regarding the H atmospheric thickness is not critical.
error bars. This validates our approach in treating the atmosphere as we have and shows that the choice made regarding the H atmospheric thickness is not critical.
In the case of the Lyman ![]() line, the decrease of the intensity during a transit is 10.53%. This is slightly larger than the decrease for the Lyman
line, the decrease of the intensity during a transit is 10.53%. This is slightly larger than the decrease for the Lyman ![]() case (10.45%). This discrepancy may be easily explained: the Lyman
case (10.45%). This discrepancy may be easily explained: the Lyman ![]() single scattering albedo is 0.86 while the Lyman
single scattering albedo is 0.86 while the Lyman ![]() single scattering albedo is 1. This means in the
single scattering albedo is 1. This means in the ![]() case, some photons are lost to other transitions which does not occur in the Lyman
case, some photons are lost to other transitions which does not occur in the Lyman ![]() case.
case.
For Jupiter, the presence of H2 results in a slight perturbation of the wings of the H line profiles. In the case of HD 209458b, this effect is undetectable (cf. Fig. 2). It is 3 orders of magnitude smaller than the H layer effects (Fig. 3). If we increase the H2 vibrational temperature, we cannot detect any differences in the line profile. Therefore, it is not possible to detect planetary atmospheric H2 by considering its effects on the stellar H-Lyman spectrum. Whatever the temperature, this effect is smaller than the errors bars of any existing facility.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5891f2a.eps}\par {\hspace*{5mm}\includegraphics[width=5.8cm,clip]{5891f2b.eps}\hspace*{5mm}}
\end{figure}](/articles/aa/full/2007/40/aa5891-06/Timg17.gif) |
Figure 2:
Lyman |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5891f3.eps}\end{figure}](/articles/aa/full/2007/40/aa5891-06/Timg18.gif) |
Figure 3:
Ratio of the Lyman |
| Open with DEXTER | |
If we could separate angularly the planet from the star, it would be interesting to calculate the self emission of the planet when the planet is at its maximum angular separation i.e. in the second position listed above. In this position, we are only able to observe half of the portion of the planet illuminated by its parent star. We have considered this scenario and our results shown in Fig. 4 illustrate that the effect of H2 is clearly visible on the line profile for the Lyman ![]() case. We can see the lack of symmetry due to the H2 line on the red side of the line and a dip around 0.22 Å (corresponding to the 6-0 P(1) transition) in the low vibrational temperature case. When the H2 vibrational temperatures increase, the level v=0 of the electronic ground state is depopulated and the rate of the transition 6-0 P(1) is less important. On the contrary, the v=1 line remains important and explains the lack of symmetry.
In the Lyman
case. We can see the lack of symmetry due to the H2 line on the red side of the line and a dip around 0.22 Å (corresponding to the 6-0 P(1) transition) in the low vibrational temperature case. When the H2 vibrational temperatures increase, the level v=0 of the electronic ground state is depopulated and the rate of the transition 6-0 P(1) is less important. On the contrary, the v=1 line remains important and explains the lack of symmetry.
In the Lyman ![]() case, it is difficult to detect the lack of symmetry due to the H2 lines. This is due to the fact that the hydrogen molecules are at relatively cold temperature so that the H2 (v=2) levels are not populated very much and also that the Lyman
case, it is difficult to detect the lack of symmetry due to the H2 lines. This is due to the fact that the hydrogen molecules are at relatively cold temperature so that the H2 (v=2) levels are not populated very much and also that the Lyman ![]() line is optically thick. The low layers where H2 is abundant have a very faint effect compared to the top of the atmosphere. This shows that the Lyman
line is optically thick. The low layers where H2 is abundant have a very faint effect compared to the top of the atmosphere. This shows that the Lyman ![]() line is insensitive to the vibrational temperature.
line is insensitive to the vibrational temperature.
![\begin{figure}
\par {\hspace*{5mm}\includegraphics[width=5.8cm,clip]{5891f4a.eps}\hspace*{5mm}}
\par\includegraphics[width=6.8cm,clip]{5891f4b.eps}\end{figure}](/articles/aa/full/2007/40/aa5891-06/Timg19.gif) |
Figure 4:
Planetary emission in the Lyman |
| Open with DEXTER | |
To justify our hypothesis regarding the atomic hydrogen density when changing the H2 density, we tested the sensitivity of our model to a significant change in the H column density. If we double it, the effect in a transiting situation will be very small: around a few thousandths of the total intensity. However, if we consider the self emission of the planet, the difference when doubling the H column density is between 4 and 5% when averaging over the frequencies. This is not negligible and should be kept in mind when it will become possible to detect the self emission of the planet itself. This shows that the approximation of a constant H column density is valid in the frame of our calculations and so can be kept constant when changing the H2 density.
Using the current observing facilities, it is not possible to detect H2 by using the overlapping of its emission lines with the H-Lyman lines. Looking to the future, when it will become possible to angularly separate the star and the planet in the UV wavelength domain, H2 should be detectable by deformation of the Lyman ![]() line profile emitted by the planet itself. Via the measurement of the H-Lyman lines, we should be able to then obtain the H column density and temperature as has already been done for Jupiter or Saturn (Emerich et al. 1993).
line profile emitted by the planet itself. Via the measurement of the H-Lyman lines, we should be able to then obtain the H column density and temperature as has already been done for Jupiter or Saturn (Emerich et al. 1993).
From the preceding discussion, we see that the detection of H2 during a transit cannot be performed in the same wavelength range as the H-Lyman lines. Therefore we extend our simulations to coincidences between H2 and other stellar lines. To observed larger H2 effects, it is important to find a stellar line corresponding to an element that has very little probability of existence in the atmosphere. In such a case, we would be sure that during the transit the observed modifications of the stellar line are due to H2.
To compute the effect of the H2 layer, we can easily calculate the extremum differences of the line intensity during the transit, by considering the two extreme cases, viz., no H2 absorption at all and that the complete stellar line is absorbed by the H2 layer. If there is no H2 atmosphere, the line should be 1.7% less intense during the transit due to the absorption by the planet itself in the case of HD 209458b. With a molecular hydrogen layer that totally absorbs the line, the maximal variation of the intensity is 2.86% with a 25 000 km thick H2 layer, 4.13% with 50 000 km and 7.55% with 100 000 km. The absorption is not complete because the H2 line profiles are thinner than the stellar line.
To find the relevant line to work with, two wavelength regions have been studied: the region above 1200 Å dominated by the Lyman ![]() line corresponding to the HST-STIS wavelength domain and the region below 1050 Å corresponding to the FUSE wavelength domain.
The first region has been studied by Vidal-Madjar et al. (2004) to find the atomic oxygen and the ionized carbon. The most intense lines in this region are Si III (1206 Å) N V (1239 Å, 1243 Å), O I (1302 Å), C II (1335 Å), Si IV (1394 Å and 1403 Å), S I (1474 Å), Si II (1527 Å), C IV (1548 Å and 1551 Å), and C I (1560 Å and 1657 Å). Following Abgrall et al. (1993a), there is no close coincidence of H2 lines in this region for the three first vibrational levels. In the other wavelength region, there exist intense stellar lines that could be interesting in this regime. For example, the C III line at 977.02 Å (2s2 1S0-2s2p 1P1) coincides with few H2 lines (see Table 2).
line corresponding to the HST-STIS wavelength domain and the region below 1050 Å corresponding to the FUSE wavelength domain.
The first region has been studied by Vidal-Madjar et al. (2004) to find the atomic oxygen and the ionized carbon. The most intense lines in this region are Si III (1206 Å) N V (1239 Å, 1243 Å), O I (1302 Å), C II (1335 Å), Si IV (1394 Å and 1403 Å), S I (1474 Å), Si II (1527 Å), C IV (1548 Å and 1551 Å), and C I (1560 Å and 1657 Å). Following Abgrall et al. (1993a), there is no close coincidence of H2 lines in this region for the three first vibrational levels. In the other wavelength region, there exist intense stellar lines that could be interesting in this regime. For example, the C III line at 977.02 Å (2s2 1S0-2s2p 1P1) coincides with few H2 lines (see Table 2).
Table 2: H2 lines in coincidence with the C III line.
In the spectrum of a solar type star, the C III line is as intense as the Lyman ![]() line (Feldman & Doschek 1991; Kretzschmar et al. 2004). Its width is 0.28 Å as seen in the FUSE data, comparable to the SUMER observations (Kretzschmar et al. 2004). In the stellar spectrum of sun-like stars, this line is very intense and its width is large enough to be able to excite some H2 transitions.
line (Feldman & Doschek 1991; Kretzschmar et al. 2004). Its width is 0.28 Å as seen in the FUSE data, comparable to the SUMER observations (Kretzschmar et al. 2004). In the stellar spectrum of sun-like stars, this line is very intense and its width is large enough to be able to excite some H2 transitions.
In a first step, we consider that the vibrational temperatures are equal to the kinetic ones and that the H2 atmospheric cut-off is at 25 000 km. The stellar line is modelled by a simple Gaussian profile with an arbitrary intensity and a FWHM of 0.143 Å which is the line width of each peak of the Lyman ![]() double Gaussian profile used by Gladstone (1988) for Jovian calculations. The line shape parameter is very important because it controls the possibility of exciting the H2 lines.
Considering these assumptions the intensity is 2.64% smaller during the transit. When the H2 layer is 50 000 km (100 000 km), the intensity decreases by 3.68% (6.45%).
double Gaussian profile used by Gladstone (1988) for Jovian calculations. The line shape parameter is very important because it controls the possibility of exciting the H2 lines.
Considering these assumptions the intensity is 2.64% smaller during the transit. When the H2 layer is 50 000 km (100 000 km), the intensity decreases by 3.68% (6.45%).
We can see that there is an absorption due to the planetary atmosphere but it is quite faint, as expected. There are no significant differences in the line profile because the effects of H2 are too faint, but if we plot the difference between the profiles with or without transit, we can see some important deformations due to the H2 absorption (Fig. 5). The effects of the Werner 7-2 P(7) and the Lyman 18-0 R(12) lines are the most important in the case of a simple Gaussian stellar line because they are very close to the centre of the C III line. The other H2-lines coincide with the wing of the C III line.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{5891f5.eps}\end{figure}](/articles/aa/full/2007/40/aa5891-06/Timg20.gif) |
Figure 5: Stellar C III line in a situation just before an transit (solid line) and during the transit with an H2 layer 25 000 km thick (dashed line) and with an H2 layer 100 000 km thick (dotted line). The wavelength centre of the C III line is at 977.02 Å. The bottom lines represent the difference between the two curves (25 000 km for the crosses, 100 000 km for the triangles). |
| Open with DEXTER | |
The calculated absorption changed by less than 0.05% when we change the stellar line shape, particularly if we consider a double Gaussian line or if we enlarge the stellar line to 0.40 Å. The result is quite insensitive to the H2 vibrational temperature: if we increase this temperature to 4 times the kinetic one, the absorption rate becomes respectively 2.66%, 3.71% and 6.51% for the different H2 thicknesses.
Comparing with the previous case, we calculate the emission of the planet itself in this wavelength domain in a geometry corresponding to a maximum angular separation. Those emissions are H2 emissions due to C III line excitation. The effects of the H2-lines are clearly visible, but the total integrated emission is very small, representing 0.22% of the emission of the C III (977.02 Å) star. It is extremely difficult to separate such an emission from the stellar one despite the planetary lines being shifted from the star ones by about 0.46 Å because of the orbital motion with a radial velocity of ![]() 140 km s-1 at the quadrature position. The line shape of the planetary emission is a mix of the effects of all the coupled lines. Paradoxically, the peaks are in a position where there is no H2-line. For each line it is important to consider the fact that the single scattering albedo is very low and that the wings are less scattered.
140 km s-1 at the quadrature position. The line shape of the planetary emission is a mix of the effects of all the coupled lines. Paradoxically, the peaks are in a position where there is no H2-line. For each line it is important to consider the fact that the single scattering albedo is very low and that the wings are less scattered.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5891f6.eps}
\end{figure}](/articles/aa/full/2007/40/aa5891-06/Timg22.gif) |
Figure 6: Emission of the planet in the region of the C III line in a geometry similar to the Fig. 4, i.e. with a maximum angular separation. |
| Open with DEXTER | |
It is possible to perform those simulations with other UV stellar lines. In choosing the lines to study, it is important to avoid stellar lines with possible resonances in the planetary atmosphere. This may be achieved by choosing stellar lines from multiply charged ion species that do not exist in the planetary atmosphere. The lines with wavelengths close to 900 Å have greater chance to come from low H2 levels in the Lyman system which is the H2 system with the most lines. The S VI line at 933.38 Å is very promising with more than 10 H2 lines coinciding, with energies of the ground level at less than 10 000 cm-1. The problem is its low intensity, 0.4 times the C III line intensity (Feldman & Doschek 1991) which will make it difficult to get enough photons during the transit to detect the expected variation. Another interesting line is the C III multiplet around 1175 Å. This multiplet is composed of six very intensives lines (Table 3). The sum of the intensities of those lines is 4.6 times greater than the C III 977 Å line.
Table 3: C III multiplet around 1175 Å (from Feldman & Doschek 1991).
We calculated the effects of the H2 layer with the same conditions as the C III 977 Å line. We made the hypothesis that each line of the multiplet has the same width. This width is equal to 0.28 Å as in the previous case. Due to this width which can generate an overlap between the multiplet lines, we choose to calculate the multiplet as a unique line with a complex structure. In that case, the decrease of the intensity during the transit due to the 25 000 km thick H2 layer is equal to 2.51%. This is slightly less than in the C III 977 Å case but still observable.
The last interesting line to study in this frame is the O VI 1032 Å and 1038 Å doublet. The second of these lines is not intensive enough to be interesting representing less than 0.1 times the intensity of the C III line, but the 1032 Å component is as intense as the C III line (Feldman & Dosheck 1991). This line has already been used to measure the H2 column density in circumstellar disks (Roberge et al. 2000; Lecavelier et al. 2001). We have calculated in the same conditions the decrease of the intensity with a 25 000 km thick H2 layer. It is 2.49%, less than for the C III 977 Å line but quite the same as for the C III 1175 multiplet. Thus, these two last cases are also favourable to detect the H2 layer in the atmosphere of an exoplanet but the O VI case does not present the advantage of a very large total intensity compare to the C III 1175 Å multiplet.
The detection of H2 in HD 209458b is difficult to achieve since it requires the use of existing instrumentation at the current performance limit. Since it is very unlikely that the H2 layer is thicker than 25 000 km, we will have to detect variations between 2% and 3% in the intensity of the line. In the case of a star with the same spectral type (GOV), HD 129333, as observed by Guinan et al. (2003) with FUSE, the flux of the C III line is
![]() erg s-1 cm-2. This star is at a distance of 33.9 pc from the Earth. If we scale this measurement to the distance of HD 209458, 47 pc, we obtain a flux of
erg s-1 cm-2. This star is at a distance of 33.9 pc from the Earth. If we scale this measurement to the distance of HD 209458, 47 pc, we obtain a flux of
![]() erg s-1 cm-2. The exposure time was 24.2 ks i.e. around 2.25 transit time, the one
erg s-1 cm-2. The exposure time was 24.2 ks i.e. around 2.25 transit time, the one ![]() uncertainty was
uncertainty was
![]() erg s-1 cm-2. For the same time of exposure we obtain an uncertainty of 8.5% in our case. To overcome this problem, it will be necessary to monitor a large number of transits (around 30 for 1
erg s-1 cm-2. For the same time of exposure we obtain an uncertainty of 8.5% in our case. To overcome this problem, it will be necessary to monitor a large number of transits (around 30 for 1![]() equal to 2.5%) and treat the problem statistically. It is also important to consider that a detection needs 2 or 3
equal to 2.5%) and treat the problem statistically. It is also important to consider that a detection needs 2 or 3![]() to be quite sure. This will require many more transits, 9 times if we consider 3
to be quite sure. This will require many more transits, 9 times if we consider 3![]() .
A way to diminish the number of transits necessary to detect H2 could be to work with the C III multiplet at 1175 Å. Unless the diminution of the intensity is lower, we could hope for lower error bars because of the larger intensity of this multiplet. It will quite likely be impossible to obtain precise information on the thermodynamical state of H2. The sensitivity of the method is too small. Another way to detect H2 could be to apply the same method to H2 infrared lines. However, the emission of the star is more continuous in this wavelength region because the thermal emission becomes predominant, making the radiative problem much more complicated. Alternatively, it could be possible to make measurements from the earth with larger instruments and to diminish the uncertainty of the transit effect on the line intensity. For these reasons HD 209458b is probably not the best candidate for the detection of H2.
.
A way to diminish the number of transits necessary to detect H2 could be to work with the C III multiplet at 1175 Å. Unless the diminution of the intensity is lower, we could hope for lower error bars because of the larger intensity of this multiplet. It will quite likely be impossible to obtain precise information on the thermodynamical state of H2. The sensitivity of the method is too small. Another way to detect H2 could be to apply the same method to H2 infrared lines. However, the emission of the star is more continuous in this wavelength region because the thermal emission becomes predominant, making the radiative problem much more complicated. Alternatively, it could be possible to make measurements from the earth with larger instruments and to diminish the uncertainty of the transit effect on the line intensity. For these reasons HD 209458b is probably not the best candidate for the detection of H2.
The case of other transiting planets depends on the spectral type of the star, on the distance between the star and the earth and on the size of the planet and its atmosphere. At the beginning of 2007, 14 of the extrasolar planets detected were in a transiting geometry. At this time, HD 209458b is the only extrasolar planet with a detected atmosphere. The question is to determine whether atmospheric H2 detection is possible in the other transiting planets.
The five planets OGLE-TR 10, 56, 111, 113, and 132 are very far away (at 1500 pc). It will be difficult to obtain high resolution FUV-EUV data with those extrasolar systems. Six transit planets are at distances greater than 100 pc (Wasp 1 and 2, Tres 1 and 2, XO-1 and HAT-P-1).
There are two other planets that could be very interesting in terms of H2 detection: HD 149026b has good conditions for detection but may prove less interesting than HD 209458b because it is further and the radius is smaller (Sato et al. 2005).
The planet HD 189733b (Bouchy et al. 2005) is a good candidate since it is the closest one at 19.3 pc, and the parent star is bright. Considering an H2 layer of 25 000 km, we could obtain a maximal diminution of the intensity of 3.78% in the C III 977 Å line compared to 2.35%, if there is no H2 in the atmosphere. Dupree et al. (2005) observed similar stars with FUSE. ![]() Cet (HD 4128) has a spectral type K0 III and is at 29.4 pc. Its C III line flux has been measured at
Cet (HD 4128) has a spectral type K0 III and is at 29.4 pc. Its C III line flux has been measured at
![]() erg s-1 cm-2 with an exposure time of 3182 s. The uncertainty has been estimated as around 10%. With a survey of two or three transits, it becomes possible to obtain error bars less than the expected intensity variation. If we scale to the distance of HD 189733, the flux reaches
erg s-1 cm-2 with an exposure time of 3182 s. The uncertainty has been estimated as around 10%. With a survey of two or three transits, it becomes possible to obtain error bars less than the expected intensity variation. If we scale to the distance of HD 189733, the flux reaches
![]() erg s-1 cm-2, but we have to consider that this star has a spectral type K1-K2. We could expect the flux to be slightly smaller in this case. However this last planet is a good candidate for H2 detection considering that we will obtain more photons and that the H2 effects are larger.
erg s-1 cm-2, but we have to consider that this star has a spectral type K1-K2. We could expect the flux to be slightly smaller in this case. However this last planet is a good candidate for H2 detection considering that we will obtain more photons and that the H2 effects are larger.
We have calculated the effect of H2 in the atmosphere of HD 209458b for the case of the H-Lyman lines. We have shown that it is impossible to detect H2 with this technique using instruments currently available. The cases of the 977.02 Å C III line, the 1175 Å C III multiplet and the 1032 Å O VI line have been also investigated. For the first line, we have shown that it becomes possible to expect a diminution of the intensity of the line, due to the H2 Lyman and Werner Systems, of 2.64% with a H2 layer 25 000 km thick. For the second one, the expected diminution is 2.51%. In the case of the planet HD 189733b, the diminution reaches 3.78% for the C III 977 Å line. Those diminutions should be detectable with FUSE. In order to extract the signal out of the noise, it could be necessary to perform a statistical analysis on several measurements. Due to the proximity of the planet HD 189733b, the number of transits necessary to perform the detection is small (![]() 3) considering 1
3) considering 1![]() error bars. For this reason this planet is the best candidate for H2 detection.
error bars. For this reason this planet is the best candidate for H2 detection.