| (1) |
A&A 473, 701-705 (2007)
DOI: 10.1051/0004-6361:20077726
A. Bonanno1,2 - V. Urpin1,3
1 - INAF, Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
2 -
INFN, Sezione di Catania, via S. Sofia 72, 95123 Catania, Italy
3 -
A.F.Ioffe Institute of Physics and Technology and Isaac Newton Institute of Chile, Branch in St. Petersburg, 194021 St. Petersburg, Russia
Received 26 April 2007 / Accepted 18 July 2007
Abstract
Aims. We evaluate the generation of magnetosonic waves in differentially rotating magnetized plasma.
Methods. Differential rotation leads to an increase of the azimuthal field by winding up the poloidal field lines into the toroidal field lines. An amplification of weak seed perturbations is considered in this time-dependent background state.
Results. It is shown that seed perturbations can be amplified by several orders of magnitude in a differentially rotating flow. The only necessary condition for this amplification is the presence of a non-vanishing component of the magnetic field in the direction of the angular velocity gradient.
Key words: magnetohydrodynamics (MHD) - instabilities - accretion, accretion disks - galaxies: magnetic fields - stars: magnetic fields
In recent years, many simulations of differentially rotating magnetized bodies have been performed, and much of the dynamics was interpreted as being a direct consequence of the MRI (Brandenburg et al. 1995; Hawley at al. 1995; Matsumoto & Tajima 1995; Hawley 2000). Obviously, the MRI cannot be the only instability that operates in a rotating magnetized gas. For example, stratification can lead to a number of strong non-axisymmetric instabilities (Agol et al. 2001; Narayan et al. 2002; Keppens et al. 2002). Blokland et al. (2005) consider the influence of a toroidal field on the growth rate of the MRI and find that it leads to overstability (complex eigenvalue). Van der Swaluw et al. (2005) study the interplay between different instabilities and argue that the growth rate of convection can be essentially increased due to magnetorotational effects. Note, however, that these studies treat the stability of the magnetic field with a vanishing radial component, a condition which is often not met in astrophysical bodies. In fact, the presence of a radial magnetic field can change substantially the stability properties (Bonanno & Urpin 2006, 2007).
In this paper, we consider stability of a differentially rotating gas in the presence of a non-vanishing radial magnetic field. Differential rotation causes the azimuthal field to increase with time by winding up the poloidal field lines into the toroidal ones. Therefore, a development of small perturbations occurs in the time-dependent background state. We show that stretching of the azimuthal field leads to the generation of magnetosonic waves in a flow. Magnetohydrodynamic waves and turbulence generated by this instability can play an important role in enhancing transport processes in various astrophysical bodies, such as accretion and protoplanetary disks, galaxies, stellar radiative zones, etc.
The equations of compressible MHD read
| (1) |
| (2) |
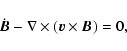 |
(3) |
| (4) |
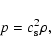 |
(5) |
We work in cylindrical coordinates (s, ![]() ,
z) with the unit
vectors (
,
z) with the unit
vectors (
![]() ,
,
![]() ,
,
![]() ). The basic state
on which the stability analysis is performed is assumed to be axisymmetric
with the angular velocity
). The basic state
on which the stability analysis is performed is assumed to be axisymmetric
with the angular velocity
![]() and
and
![]() .
In the
presence of the non-vanishing radial field Bs and differential rotation, the
azimuthal field increases with time by winding up the radial field lines. If
the magnetic Reynolds number is large, then one obtains from Eq. (4) that the
azimuthal field grows linearly with time in the basic state,
.
In the
presence of the non-vanishing radial field Bs and differential rotation, the
azimuthal field increases with time by winding up the radial field lines. If
the magnetic Reynolds number is large, then one obtains from Eq. (4) that the
azimuthal field grows linearly with time in the basic state,
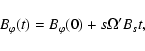 |
(6) |
For the sake of
simplicity, we assume that gravity is radial,
![]() ,
and the basic state is in hydrostatic equilibrium, then
,
and the basic state is in hydrostatic equilibrium, then
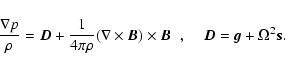 |
(7) |
Consider stability of axisymmetric short wavelength perturbations with the
spatial dependence ![]()
![]() where
where
![]() is the wavevector. Small perturbations will be indicated by
subscript 1, while unperturbed quantities will have no subscript. For the
purpose of illustration, we treat in this paper the simplest case when
is the wavevector. Small perturbations will be indicated by
subscript 1, while unperturbed quantities will have no subscript. For the
purpose of illustration, we treat in this paper the simplest case when
![]() has only the vertical component,
has only the vertical component,
![]() .
Then, the
condition
.
Then, the
condition
![]() yields B1z=0. The other
non-trivial linearized MHD-equations to lowest order in
yields B1z=0. The other
non-trivial linearized MHD-equations to lowest order in
![]() read
read
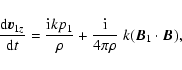 |
(8) |
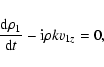 |
(9) |
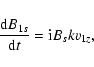 |
(10) |
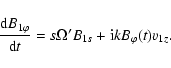 |
(11) |
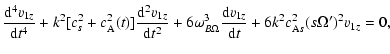 |
(12) |
To follow the behaviour of perturbations, it is convenient to
introduce the dimensionless quantities
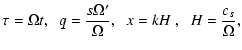 |
|||
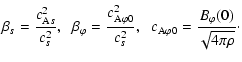 |
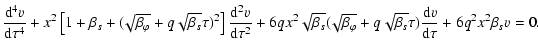 |
(13) |
Equations (10), (11) can also be written in a dimensionless form. We have
| (14) | |||
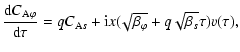 |
(15) |
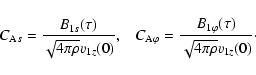 |
(16) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7726fig1.eps}\end{figure}](/articles/aa/full/2007/39/aa7726-07/Timg60.gif) |
Figure 1:
The time dependence of v (solid line),
|
| Open with DEXTER | |
In Fig. 1, we plot the time dependence of v,
![]() ,
and
,
and
![]() in the regions where the angular velocity increases slowly with s (q=
0.1). The other parameters are x=3,
in the regions where the angular velocity increases slowly with s (q=
0.1). The other parameters are x=3,
![]() ,
and
,
and
![]() .
Integrating Eq. (13), we choose the following initial conditions:
.
Integrating Eq. (13), we choose the following initial conditions:
![]() and
and
![]() .
The
behaviour of the velocity and magnetic field turns out to be substantially
different. During the initial stage, the velocity reaches a flat maximum at
.
The
behaviour of the velocity and magnetic field turns out to be substantially
different. During the initial stage, the velocity reaches a flat maximum at
![]() -70 which corresponds approximately to 10 P where P is the
rotation period. At that time, the perturbation of velocity is
-70 which corresponds approximately to 10 P where P is the
rotation period. At that time, the perturbation of velocity is ![]() 25
times greater than its initial value. Perturbations of the magnetic field
are much larger. After
25
times greater than its initial value. Perturbations of the magnetic field
are much larger. After
![]() (
(
![]() ),
),
![]() approaches the saturation level that is approximately a factor 103
greater than the initial perturbation of v1z. The amplification of the
azimuthal field is even larger. After
approaches the saturation level that is approximately a factor 103
greater than the initial perturbation of v1z. The amplification of the
azimuthal field is even larger. After
![]() ,
,
![]() is a
factor 104 stronger than the initial perturbation v1z(0), and it
continues to grow approximately linearly with time. Note that the long-term
behaviour (
is a
factor 104 stronger than the initial perturbation v1z(0), and it
continues to grow approximately linearly with time. Note that the long-term
behaviour (
![]() )
of these quantities is also different. The velocity
v changes the sign and exhibits some sort of oscillatory behaviour with the
amplitude growing
)
of these quantities is also different. The velocity
v changes the sign and exhibits some sort of oscillatory behaviour with the
amplitude growing ![]() t1/2 whereas
t1/2 whereas
![]() reaches the saturation
level. A perturbation of the azimuthal field
reaches the saturation
level. A perturbation of the azimuthal field
![]() is still
is still
![]() t at very large t.
t at very large t.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7726fig2.eps}\end{figure}](/articles/aa/full/2007/39/aa7726-07/Timg69.gif) |
Figure 2: Same as in Fig. 1 but for q= -0.1 and x=10. |
| Open with DEXTER | |
In contrast with the magnetorotational instability, the behaviour of
perturbations is not crucially sensitive to the sign of ![]() .
To
illustrate this point, we show in Fig. 2 the time dependence in the case q=
- 0.1 (
.
To
illustrate this point, we show in Fig. 2 the time dependence in the case q=
- 0.1 (![]() decreases slowly with s). Qualitatively, the
dependences are the same. The only essential difference is that the azimuthal
field generated by differential rotation has a negative sign because the
radial gradient of the angular velocity is negative. Initially (
decreases slowly with s). Qualitatively, the
dependences are the same. The only essential difference is that the azimuthal
field generated by differential rotation has a negative sign because the
radial gradient of the angular velocity is negative. Initially (
![]() ), the main contribution to
), the main contribution to
![]() is provided by compressibility
(the second term on the r.h.s. of Eq. (11)). Later on, however the azimuthal
magnetic perturbations are determined by winding up the radial field
perturbations
and becomes negative. In Fig. 2, the modulus of
is provided by compressibility
(the second term on the r.h.s. of Eq. (11)). Later on, however the azimuthal
magnetic perturbations are determined by winding up the radial field
perturbations
and becomes negative. In Fig. 2, the modulus of
![]() is shown.
Since x is larger in this figure, perturbations of all quantities can reach
higher values compared to Fig. 1. For instance, the velocity becomes
is shown.
Since x is larger in this figure, perturbations of all quantities can reach
higher values compared to Fig. 1. For instance, the velocity becomes ![]() 200 times greater than the initial value after 15 rotation periods. The radial
perturbation of the Alfvén velocity reaches the saturation level which is
200 times greater than the initial value after 15 rotation periods. The radial
perturbation of the Alfvén velocity reaches the saturation level which is
![]()
![]() times greater than v1z(0), and the azimuthal
perturbation is even about 10 times larger. For very long t (
times greater than v1z(0), and the azimuthal
perturbation is even about 10 times larger. For very long t (
![]() ), the velocity exhibits the oscillatory behaviour with the
amplitude
), the velocity exhibits the oscillatory behaviour with the
amplitude ![]() t1/2.
In Fig. 3, we plot the behaviour of perturbations in the case of a very
weak differential rotation, q = 0.01. For a weak rotation shear, the
amplification of initial perturbations is slower. The velocity reaches the
maximum after
t1/2.
In Fig. 3, we plot the behaviour of perturbations in the case of a very
weak differential rotation, q = 0.01. For a weak rotation shear, the
amplification of initial perturbations is slower. The velocity reaches the
maximum after ![]() 40 P, and this maximum is rather high: v1z exceeds
its initial value by a factor
40 P, and this maximum is rather high: v1z exceeds
its initial value by a factor ![]() 100. Despite a slower growth rate,
saturation of
100. Despite a slower growth rate,
saturation of
![]() still occurs at a rather high level (
still occurs at a rather high level (
![]() ). As expected, the azimuthal field grows linearly with time and
can reach a very high value.
). As expected, the azimuthal field grows linearly with time and
can reach a very high value.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7726fig3.eps}\end{figure}](/articles/aa/full/2007/39/aa7726-07/Timg74.gif) |
Figure 3:
Same as in Fig. 2 but for q=-0.01,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{7726fig4.eps}\end{figure}](/articles/aa/full/2007/39/aa7726-07/Timg75.gif) |
Figure 4:
Same as in Fig. 1 but for q=1 and
|
| Open with DEXTER | |
The same dependences, for a relatively large value of q, are shown in
Fig. 4. In this case, perturbations exhibit a clear oscillatory behaviour.
This concerns particularly perturbations of the vertical velocity. After a
short initial relaxation (lasting ![]() 2-3 rotation period), v reaches
a self-similar regime when the amplitude of oscillations grows with time
2-3 rotation period), v reaches
a self-similar regime when the amplitude of oscillations grows with time
![]()
![]() and the frequency
and the frequency ![]()
![]() .
Perturbations of the
magnetic field also exhibit a weak oscillatory behaviour but the amplitude of
oscillations is much smaller. This is because the field components are given
by the integrals of a rapidly oscillating function v (see Eqs. (10) and
(11)), and oscillations in B1s and
.
Perturbations of the
magnetic field also exhibit a weak oscillatory behaviour but the amplitude of
oscillations is much smaller. This is because the field components are given
by the integrals of a rapidly oscillating function v (see Eqs. (10) and
(11)), and oscillations in B1s and
![]() are smoothed.
Perturbations of the radial field reaches a saturation level after
are smoothed.
Perturbations of the radial field reaches a saturation level after ![]() 2-3 P. In saturation, the radial Alfvén velocity
2-3 P. In saturation, the radial Alfvén velocity
![]() is approximately 10 times greater than the initial perturbation of the vertical velocity.
Perturbations of the azimuthal field grow rather rapidly at the initial stage
however, later on (at
is approximately 10 times greater than the initial perturbation of the vertical velocity.
Perturbations of the azimuthal field grow rather rapidly at the initial stage
however, later on (at ![]() ), they continue to grow linearly with time.
), they continue to grow linearly with time.
In Fig. 5, we show the long-term behaviour of the amplitude of the vertical
velocity. Except for the initial stage, the numerical results are well fitted by
the same dependence ![]()
![]() as that in Fig. 4. We can compare these
numerical results with the analytical solution of Eq. (13) for large
as that in Fig. 4. We can compare these
numerical results with the analytical solution of Eq. (13) for large ![]() .
It can be easily checked that the asymptotic solution of Eq. (13) at large
.
It can be easily checked that the asymptotic solution of Eq. (13) at large
![]() is given by
is given by
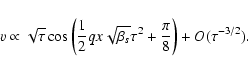 |
(17) |
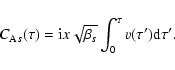 |
(18) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7726fig5.eps}\end{figure}](/articles/aa/full/2007/39/aa7726-07/Timg82.gif) |
Figure 5:
The long-term behaviour of the amplitude of v for
|
| Open with DEXTER | |
We have shown that the winding up of toroidal field lines from the poloidal field lines is accompanied by an amplification of seed perturbations of the velocity and magnetic field. A very simplified model has been considered in this paper, but we believe that qualitatively the same results can be obtained for more general background states and perturbations. Differential rotation and compressibility of the gas lead to the generation of magnetosonic waves with the amplitude that grows with time. The physical processes responsible for this amplification are exactly the same that result in the instability considered by Bonanno & Urpin (2006, 2007). The only difference is that, in this paper, we consider the development of perturbations on a time-dependent background state and, as a result, the growth of perturbations is not exponential.
The behaviour of seed perturbations depends essentially on various parameters
and can generally be rather complex. If the parameter
![]() is relatively small (
is relatively small (![]() 0.1), then the perturbations of velocity and
magnetic field initially grow monotonously and can reach quite high values.
For example, the perturbation of the vertical velocity becomes approximately
150-200 times greater than its initial value after only 15-30 rotation
periods (see Figs. 2 and 3). Perturbations of the magnetic field reach even
higher values during the initial stage. For instance, the Alfvén velocity
corresponding to the perturbation of the radial field component,
0.1), then the perturbations of velocity and
magnetic field initially grow monotonously and can reach quite high values.
For example, the perturbation of the vertical velocity becomes approximately
150-200 times greater than its initial value after only 15-30 rotation
periods (see Figs. 2 and 3). Perturbations of the magnetic field reach even
higher values during the initial stage. For instance, the Alfvén velocity
corresponding to the perturbation of the radial field component,
![]() ,
can exceed the initial velocity perturbation by a factor
,
can exceed the initial velocity perturbation by a factor ![]() (1-3)
(1-3) ![]() 105 after the same time, but the perturbations of the toroidal field are
even stronger. As a result of such a strong initial amplification, seed
perturbations can already reach a non-linear regime after 15-30 rotation
periods if their initial values are sufficiently large. Further
evolution of perturbations will then be entirely determined by non-linear effects.
However, if the non-linear regime is not reachedduring this initial stage, the
behaviour of perturbations becomes oscillatory with slowly growing amplitude
(
105 after the same time, but the perturbations of the toroidal field are
even stronger. As a result of such a strong initial amplification, seed
perturbations can already reach a non-linear regime after 15-30 rotation
periods if their initial values are sufficiently large. Further
evolution of perturbations will then be entirely determined by non-linear effects.
However, if the non-linear regime is not reachedduring this initial stage, the
behaviour of perturbations becomes oscillatory with slowly growing amplitude
(![]() t1/2). At sufficiently large t, the frequency of oscillations
grows linearly with time and is given approximately by
t1/2). At sufficiently large t, the frequency of oscillations
grows linearly with time and is given approximately by
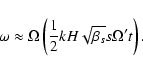 |
(19) |
The generation of magnetosonic waves occurs even if the magnetic field is very strong and suppresses different MHD-instabilities which can arise in a differentially rotating flow (for example, the MRI). The presence of differential rotation and radial magnetic field is, however, crucially important for the considered process. Since both differential rotation and radial field are quite common in astrophysics, we believe that the considered mechanism can occur in various astrophysical bodies and plays an important role in enhancing transport processes in plasma.
Acknowledgements
This research project has been supported by a Marie Curie Transfer of Knowledge Fellowship of the European Community's Sixth Framework Programme under contract number MTKD-CT-002995. V.U. thanks INAF-Ossevatorio Astrofisico di Catania for hospitality.