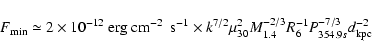A&A 473, 551-559 (2007)
DOI: 10.1051/0004-6361:20077398
Long-term pulse profile study of the Be/X-ray pulsar SAX J2103.5+4545
A. Camero Arranz1 - C. A. Wilson2 - M. H. Finger2,3 - V. Reglero1
1 - GACE, Instituto de Ciencias de los Materiales, Universidad de
Valencia, PO Box 20085, 46071 Valencia, Spain
2 - VP62, National Space Science and Technology Center, 320 Sparkman Drive, Huntsville, AL 35805, USA
3 - Universities Space Research Association, Huntsville, AL 35805, USA
Received 3 March 2007 / Accepted 17 July 2007
Abstract
Aims. We present the first long-term pulse profile study of the X-ray pulsar SAX J2103.5+4545. Our main goal is to study the pulse shape correlation either with luminosity, time or energy.
Methods. This Be/X-ray binary system was observed from 1999 to 2004 by RXTE PCA, and by INTEGRAL from 2002 to 2005, during the Performance and Verification (PV) phase and the Galactic Plane Scan survey (GPS). X-ray pulse profiles were obtained in different energy ranges. The long-term spectral variability of this source is studied. The long-term flux, frequency and spin-up rate histories are computed. A new set of orbital parameters are also determined.
Results. The pulse shape is complex and highly variable. Despite this fact, the strength of almost all the peaks increases with luminosity. In addition, an energy dependence pattern was found. Single, double, triple or even quadruple peaks pulse profile structure was obtained. It was confirmed that SAX J2103.5+4545 becomes harder when the flux is higher. The new orbital solution obtained is:
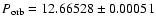 days,
days,
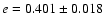 ,
,
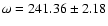 deg and
deg and
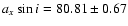 lt-s.
lt-s.
Key words: X-rays: binaries - stars: pulsars: general - stars: individual: SAX J2103.5+4545 - stars: binaries: close - stars: emissions-line, Be
SAX J2103.5+4545 is a Be High Mass X-ray Binary
pulsar with an orbital period of 12.68 d (the shortest known in Be/X-ray
binary systems) and X-ray pulsations of 358 s. These systems
consist of a neutron star orbiting a Be companion, hence forming a
Be/X-ray binary. Be stars are rapidly rotating objects with a
quasi-Keplerian disk around their equator. The optical and infrared emission
is dominated by the donor star and its equatorial disk, and it is
characterized by spectral lines in emission (particularly
those of the Balmer series) and IR excess. The standard model of a
Be/X-ray binary ascribes the high-energy radiation to an accreting
mechanism that takes place when the compact object interacts with the Be
star's circumstellar disk, giving rise to an X-ray outburst.
This source was discovered by the BeppoSAX satellite (Hulleman et al. 1998). The X-ray
spectrum (2-25 keV) was fitted by a power-law with
a photon index of
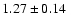 plus a photoelectric absorption at lower energies
(
plus a photoelectric absorption at lower energies
(
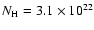 cm-2). The likely optical
counterpart is a B0Ve star (V = 14.2) at a
distance of 6.5 kpc (Reig et al. 2004). Using XMM-Newton data a quasi-periodic
oscillation at 22.7 s was discovered by Inam et al. (2004). Baykal et al. (2002)
found a correlation between spin-up rate and X-ray flux
during the 1999 outburst. This suggests the formation of an accretion disk during
periastron passage of the neutron star. However,
SAX J2103.5+4545 is not a regular Be/X-ray system. For instance, it does not follow
the Corbet
cm-2). The likely optical
counterpart is a B0Ve star (V = 14.2) at a
distance of 6.5 kpc (Reig et al. 2004). Using XMM-Newton data a quasi-periodic
oscillation at 22.7 s was discovered by Inam et al. (2004). Baykal et al. (2002)
found a correlation between spin-up rate and X-ray flux
during the 1999 outburst. This suggests the formation of an accretion disk during
periastron passage of the neutron star. However,
SAX J2103.5+4545 is not a regular Be/X-ray system. For instance, it does not follow
the Corbet
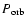 /
/
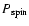 correlation found in other accreting pulsar systems. Previous works of SAX J2103.5+4545 during quiescence by Reig et al. (2005) showed that this is a very interesting case. They found that the source was emitting X-rays even after the complete loss of the circumstellar disk. On the other hand, Baykal et al. (2002) and Inam et al. (2004) found single and double peak pulse profiles respectively in the soft X-ray range. In the hard X-ray range, Filippova et al. (2004)
found only a single peak profile. However, a double peak profile was then found by Falanga et al. (2005) and Sidoli et al. (2005). We find the overall picture of SAX J2103.5+4545 still puzzling.
correlation found in other accreting pulsar systems. Previous works of SAX J2103.5+4545 during quiescence by Reig et al. (2005) showed that this is a very interesting case. They found that the source was emitting X-rays even after the complete loss of the circumstellar disk. On the other hand, Baykal et al. (2002) and Inam et al. (2004) found single and double peak pulse profiles respectively in the soft X-ray range. In the hard X-ray range, Filippova et al. (2004)
found only a single peak profile. However, a double peak profile was then found by Falanga et al. (2005) and Sidoli et al. (2005). We find the overall picture of SAX J2103.5+4545 still puzzling.
As a review, this source has been analyzed previously by Hulleman et al. (BeppoSAX, 1998), Baykal et al. (2000, 2007) and Inam et al. (2004) (RXTE, XMM-Newton)
(optical & IR wavelengths, 2004, 2005), Filippova et al. (optical wavelength; RXTE, XMM-Newton, INTEGRAL, 2004), Blay et al. (2004), Falanga et al. (2005) and Sidoli et al. (2005) only with INTEGRAL data,
Blay (optical/X-ray correlation; INTEGRAL 2006) and Camero-Arranz et al. (2006) with RXTE  INTEGRAL .
INTEGRAL .
We present a long-term pulse profile study, as well as a spectral and pulse-timing
analysis of SAX J2103.5+4545 using data from both INTEGRAL and RXTE missions.
The INTErnational Gamma-Ray Astrophysics
Laboratory (INTEGRAL, Winkler et al. 2003) consists of three
coded mask telescopes, the spectrometer SPI (20 keV-8 MeV), the imager IBIS
(15 keV-10 MeV), and the X-ray monitor JEM-X (4-3 keV), as well as the
optical monitoring camera OMC (V, 500-600 nm).
SAX J2103.5+4545 has been detected by IBIS/ISGRI during the INTEGRAL PV phase and the GPS survey from 2002 to 2005 (MJD 52 618-MJD 53 356), with a total observing time of  860 ks. INTEGRAL data reduction was carried out with the
Offline Scientific Analysis software, release 5.0, distributed
by the ISDC (Courvoisier et al. 2003). A software description can be found in Goldwurm et al. (2003), Diehl et al. (2003), Wetergaard et al. (2003).
860 ks. INTEGRAL data reduction was carried out with the
Offline Scientific Analysis software, release 5.0, distributed
by the ISDC (Courvoisier et al. 2003). A software description can be found in Goldwurm et al. (2003), Diehl et al. (2003), Wetergaard et al. (2003).
RXTE Bradt et al. (1993) carries 3 instruments on board. The
Proportional Counter Array (PCA; Jahoda et al. 1996)
is sensitive from 2-60 keV. The High Energy X-ray Timing
Experiment (HEXTE; Gruber et al. 1996) extends the X-ray sensitivity
up to 200 keV. Monitoring the long-term behavior of some of the brightest X-ray sources, the All Sky Monitor (ASM; Levine et al. 1996) scans most of the sky every 1.5 h at 2-10 keV.
SAX J2103.5+4545 was also observed with RXTE PCA and HEXTE from 1999 to 2004
(MJD 51 512.8-MJD 53 047.9), with a total observing time of  1900 ks. However, it is important to note that during that period there were two gaps with no observations taken by those instruments (MJD 51 900-MJD 52 000 and MJD 52 025-MJD 52 430). For each available observation, we have analyzed PCA Standard1 data (0.125 s time resolution, no energy resolution) for the light curves and Standard2 data (16 s time resolution, 129 channel energy resolution) for spectral analysis using FTOOLs 6.2. In addition, GoodXenon PCA data were selected for the pulse profile study, and HEXTE binned mode data from clusters A and B for the spectral analysis.
1900 ks. However, it is important to note that during that period there were two gaps with no observations taken by those instruments (MJD 51 900-MJD 52 000 and MJD 52 025-MJD 52 430). For each available observation, we have analyzed PCA Standard1 data (0.125 s time resolution, no energy resolution) for the light curves and Standard2 data (16 s time resolution, 129 channel energy resolution) for spectral analysis using FTOOLs 6.2. In addition, GoodXenon PCA data were selected for the pulse profile study, and HEXTE binned mode data from clusters A and B for the spectral analysis.
In order to study the long-term pulse profile dependence on luminosity, time or orbital
phase we extracted 548 RXTE PCA Standard1 light curves
in the 2-60 keV energy range. The background was not subtracted in this first
step. Then, we corrected the times to the barycenter of the solar
system, as well as for the orbital motion using the binary orbital parameters by
Baykal et al. (2002). We constructed pulse profiles by fitting the data with a
harmonic expansion in pulse phase (6 harmonics were used). Typically we
use data spanning a 4000 s interval ( 11 pulse periods). Initially we used a
simple phase model (
11 pulse periods). Initially we used a
simple phase model (
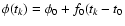 );
where f0 is the pulse frequency at time t0 and
);
where f0 is the pulse frequency at time t0 and 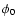 is the phase
at time t0). The errors on the Fourier coefficients were corrected for
the non-Poisson noise found in the power spectra (Wilson et al. 2002). In a later
stage, a more precise quadratic-spline phase model was created, which was
used to remake the profiles.
is the phase
at time t0). The errors on the Fourier coefficients were corrected for
the non-Poisson noise found in the power spectra (Wilson et al. 2002). In a later
stage, a more precise quadratic-spline phase model was created, which was
used to remake the profiles.
We have obtained 2-60 keV RXTE PCA pulse shapes varying from only single
sinusoidal-like peak (phases 0.9-1), to profiles with two peaks (phases 0.7-0.9),
and even occasionally with three (phases 0.5-0.7) and four peaks (0.2-0.5)
(see Figs. 1, 2, or 3).
![\begin{figure}
\par\includegraphics[width=9cm,height=14cm]{7398fig1.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg17.gif) |
Figure 1:
RXTE PCA (2-60 keV) pulse profiles consecutive in time during outburst. Two cycles are plotted for clarity. The evolution of intensity of the first part of the outburst is plotted on the left column increasing from bottom to top. The fall is plotted on the right, with intensity decreasing from top to bottom. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=9cm,height=4.5cm]{7398fig2.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg18.gif) |
Figure 2:
PCA (2-60 keV) pulse profiles at the same orbital phase (
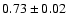 cycles) and at the same luminosity state ( cycles) and at the same luminosity state (
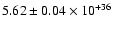 erg s-1). erg s-1). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=18.8cm,height=3cm]{7398fig3.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg19.gif) |
Figure 3:
RXTE PCA 2-60 keV pulse profiles at the same luminosity state (
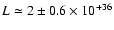 erg s-1; see Fig. 4 bottom). erg s-1; see Fig. 4 bottom). |
| Open with DEXTER |
Taking consecutive pulse profiles in time during outbursts, and after visual inspection, we found a non correlated shape pattern from one outburst to another, and even different patterns either going up or down for a given outburst (see Fig. 1, where Relative Flux is the number of counts per second and per PCU relative to the mean rate). As we stated before, generally the shapes vary from a strong single sinusoidal-like peak to double. However, three or even four weaker peaks are often found in addition to the main one. This source showed the same arbitrary conduct when profiles are sorted by orbital phase (see Fig. 2). Moreover, we expected to obtain a base profile for a given X-ray luminosity. Nevertheless, we discovered a diversified range of shapes with no clear resemblance (see Fig. 3).
![\begin{figure}
\par\includegraphics[width=8.6cm,height=7.5cm]{7398fig4.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg20.gif) |
Figure 4:
Top. Sample of PCA observations selected for the pulse profile intensity analysis. An extra circle indicates the existence in addition of an INTEGRAL IBIS/ISGRI observation. Bottom. RXTE PCA flux in the 2-30 keV energy range. The horizontal dotted line denotes the luminosity level of
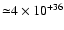 erg s-1. erg s-1. |
| Open with DEXTER |
In addition we have quantified the strength of all the peaks. We have defined the strength
of one peak of the pulse profile as the ratio (
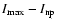 )/
)/
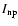 ,
where
,
where
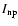 was defined as the "non-pulsed "flux at the middle point between the two adjacent
minima of the peak. We have plotted this magnitude in time as well as versus the orbital
phase and luminosity (2-60 keV rms flux) for 548 RXTE observations (see Fig. 5). The root-mean-square flux of each observation was estimated as
was defined as the "non-pulsed "flux at the middle point between the two adjacent
minima of the peak. We have plotted this magnitude in time as well as versus the orbital
phase and luminosity (2-60 keV rms flux) for 548 RXTE observations (see Fig. 5). The root-mean-square flux of each observation was estimated as
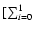 (aih2-a
(aih2-a
![$_{ih{\rm err}}^2))/2]^{1/2}$](/articles/aa/full/2007/38/aa7398-07/img24.gif) ,
where aih are the cosine and sine coefficients of the Fourier series for profile i and harmonic h, and
,
where aih are the cosine and sine coefficients of the Fourier series for profile i and harmonic h, and
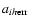 are the errors of those coefficients.
are the errors of those coefficients.
From Fig. 5 it appears that the strength of the four peaks increases with the luminosity.However, the correlation coefficients of the main, second, third and fourth peaks were 0.95, 0.83, 0.30 and 0.56, respectively (with significance values of their deviations from zero being 0,
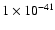 ,
0.0002,
,
0.0002,
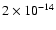 ). This suggests that all but the third are correlated with luminosity. In addition, computing the ratio of the main to the second peak of the pulse profile (P1/P2), and to the third (P1/P3) and to the fourth one (P1/P4), we found a wide range of the ratio values for a given luminosity state (see Fig. 6). This confirms our initial visual inspection, i.e., the pulse shapes vary with no clear pattern. On the other hand, we believed it was worthwile to compute also the correlation coefficients of P1/P2, P1/P3, P1/P4. They were all found to be
). This suggests that all but the third are correlated with luminosity. In addition, computing the ratio of the main to the second peak of the pulse profile (P1/P2), and to the third (P1/P3) and to the fourth one (P1/P4), we found a wide range of the ratio values for a given luminosity state (see Fig. 6). This confirms our initial visual inspection, i.e., the pulse shapes vary with no clear pattern. On the other hand, we believed it was worthwile to compute also the correlation coefficients of P1/P2, P1/P3, P1/P4. They were all found to be 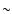 0.44, after rejecting some values with very large uncertainties. When we focused on the lower part of the flux range (rms flux from 0 to
0.44, after rejecting some values with very large uncertainties. When we focused on the lower part of the flux range (rms flux from 0 to 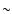 10), there was only a slight improvement on the P1/4 correlation coefficient, with a value of
10), there was only a slight improvement on the P1/4 correlation coefficient, with a value of 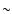 0.50.
0.50.
Once we confirmed that no evident temporal, orbital or luminosity pulse shape correlations were found in the original PCA data sample in the 2-60 keV range, we decided to select only 24 goodXenon RXTE PCA observations for the energy dependence study. The chosen data set follows the long-term light curve behavior and covers MJD 51512.8 to 53 047.9 (see Fig. 4). The PCA background subtracted light curves were obtained in four energy ranges: 2.06-5.31 keV, 5.31-7.76 keV, 7.76-13.93 keV, 13.93-20.62 keV. Then, the same procedure was followed to construct the phases and then the profiles, as we described before. Typically, the duration of a RXTE PCA observation is about 3000 s and the profiles contain about
8 pulse cycles. To complete this study, we obtained a list of good events times per science window (ScW) with IBIS/ISGRI in the 20-60 keV energy band. Table 1 shows a summary of the detections and non detections with this instrument, as well as the number of ScWs used for making profiles. In Fig. 4 we marked in red (and an extra circle)
those 6 points in which we also have an IBIS/ISGRI positive detection.
Table 1:
Pulse period detections of SAX J2103.5+4545 with IBIS/ISGRI. The second column shows
0000the number of ScWs used for the computation in each epoch.
![\begin{figure}
\par\includegraphics[width=7.75cm,height=5.3cm]{7398fig5top.eps} ...
....eps}\includegraphics[width=7.75cm,height=5.3cm]{7398fig5bottom.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg34.gif) |
Figure 5:
We have obtained 2-60 keV RXTE PCA pulse shapes varying from only single sinusoidal-like peak (phases 0.9-1), to profiles with two peaks (phases 0.7-0.9), and even occasionally with three (phases 0.5-0.7) and four peaks (0.2-0.5). From top to bottom, the four peaks strength is plotted vs. time, luminosity (2-60 keV rms flux) and orbital phase. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,height=7cm]{7398fig6.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg35.gif) |
Figure 6:
From top to bottom, the ratio of the main to the second, the third
and the fourth peak plotted vs. luminosity (2-60 keV rms flux). We have rejected few observations with large uncertainties for clarity. |
| Open with DEXTER |
Figures 7 and 8 show the evolution of some of the PCA profiles in four energy bands (with energy increasing from top to bottom). As we already mentioned, the profiles present a prominent sinusoidal-like peak among other features. These can vary from one to three peaks in addition to the main one. The general behavior is:
- 1.
- the right side of the main peak (phases 0.0-0.2) remains quite similar as energy increases;
- 2.
- the region at phases 0.2-0.5 is not always a peak. But when a peak is present then it tends to strengthen as energy increases;
- 3.
- when a peak is present at phases 0.5-0.7, the larger is the energy the weaker is the feature;
- 4.
- at phases 0.7 to 0.9 a secondary peak or shoulder is present. It gets smaller with increasing energy;
- 5.
- the dip in the main peak (phase 0.9) becomes deeper as the energy range increases. The maximum depth is found in the 7.76-13.93 keV band, and then decreases again with energy. In particular, observations 70082-03-16-00 and 70082-04-57-00 show this notch especially deep and wide, the last one evolving to a strong double peak (see Figs. 7 and 8).
This trend is also seen in the 20-60 keV IBIS/ISGRI profiles (see Fig. 9),
where the second and the third peaks are almost missing and the fourth one
is stronger, but still weaker than the main peak. It should be noted that in Fig. 9,
the profile in the upper left is substantially offset from phase 1.0. The reason is that all of these profiles are arbitrary pulse phased and are not phase aligned with one another, hence there is no reason for them to be close in phase. The two profiles on the right are rather close in time to each other, so the phases of the main peak are similar while the ones on the left are more widely spaced in time.
The averaged strength of the main and the rest of the peaks have been plotted vs. energy band in Fig. 10. We can see the peaks evolution with energy suggested in points 1 to 5.
![\begin{figure}
\par\includegraphics[width=18.5cm,height=8.2cm,clip]{7398fig7.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg37.gif) |
Figure 7:
Evolution of SAX J2103.5+4545 PCA pulse profile with intensity in 4 energy bands ( from top to bottom). They are sorted consecutive in time during the brightest period (MJD 52 650-52 800) of the source. |
| Open with DEXTER |
We have obtained 548 spectra from 6 years of RXTE PCA and HEXTE data
(MJD 51 512.8 - MJD 53 047.9). For each observation, we have selected PCA
Standard2 data and HEXTE binned mode data from clusters A and B.
Then, fluxes in all the different energy ranges were obtained by fitting a
cut-off power law model plus a photoelectric absorption (phabs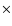 (Gauss + cutoffpl)) to each 2.7-70 keV spectrum, fixing the iron line value and its width to 6.43 keV and 0.165, respectively (Baykal et al. 2002). We have included 1
(Gauss + cutoffpl)) to each 2.7-70 keV spectrum, fixing the iron line value and its width to 6.43 keV and 0.165, respectively (Baykal et al. 2002). We have included 1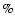 of systematics. They were also background subtracted.
of systematics. They were also background subtracted.
In Fig. 12 (bottom) we show the long-term flux history of
SAX J2103.5+4545 using RXTE and INTEGRAL data, which follows very nicely the general trend of the long-term frequency derivatives history obtained after the timing analysis (see next section).
To study the spectral variability of SAX J2103.5+4545 we have computed the
long-term hardness ratios (HR) using two energy bands: 2-10 keV, 10-30 keV (defined as HR= H/S). Figure 11 (top) shows an average of the calculated HR
vs. time and intensity, using those energy bands. In the HR vs. intensity plot we took out
few detections corresponding to the faintest state, due to their enormous error bars, which hid the general trend. The correlation between the HR either with time or intensity is clear. We can see that the source becomes harder when the flux is higher. In the same figure we have included some plots showing the evolution of the absorption, the Photon Index, the cutoff and the reduced 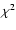 with intensity.
We have also rejected the faintest flux values since the uncertainties obtained in the
parameters were very large, adding only confusion to the study. We found variable behavior
only in the Photon Index vs. intensity plot. The larger the flux the lower the
the photon index. This anti-correlation was the expected and shows again that
in the bright state the spectrum of SAX J2103.5+4545 is harder than in the faint state. It is clear that the fitting model applied is not the perfect one for
the bright state, as we can see in the reduced
with intensity.
We have also rejected the faintest flux values since the uncertainties obtained in the
parameters were very large, adding only confusion to the study. We found variable behavior
only in the Photon Index vs. intensity plot. The larger the flux the lower the
the photon index. This anti-correlation was the expected and shows again that
in the bright state the spectrum of SAX J2103.5+4545 is harder than in the faint state. It is clear that the fitting model applied is not the perfect one for
the bright state, as we can see in the reduced 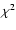 vs. intensity figure. Nevertheless, it was found to be the best simple model for all the
vs. intensity figure. Nevertheless, it was found to be the best simple model for all the  500 spectra analyzed. Baykal et al. (2007) suggested that this type of spectral softening with decreasing flux was found to be mainly a consequence of mass accretion rate change and was not necessary to be related to a significant accretion geometry change.
500 spectra analyzed. Baykal et al. (2007) suggested that this type of spectral softening with decreasing flux was found to be mainly a consequence of mass accretion rate change and was not necessary to be related to a significant accretion geometry change.
![\begin{figure}
\par\includegraphics[width=8.9cm,height=8cm,clip]{7398fig8.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg41.gif) |
Figure 8:
Some examples of SAX J2103.5+4545 PCA pulse profiles showing a more complex structure, in the same 4 energy bands. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,height=5.5cm,clip]{7398fig9.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg42.gif) |
Figure 9:
ISGRI (20-60 keV) mean pulse profiles of SAX J2103.5+4545
generated by combining profiles from individual INTEGRAL ScWs. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,height=7.6cm,clip]{7398fig10.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg43.gif) |
Figure 10:
Averaged peaks strength evolution with energy. The behaviour displayed here follows the one proposed from points 1 to 5 in the text. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.7cm,height=11cm,clip]{7398fig11.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg44.gif) |
Figure 11:
Top. Long-term hardness ratios history. From middle to bottom: HR-intensity diagram and spectral parameters evolution vs. intensity. |
| Open with DEXTER |
We selected again the 548 RXTE PCA observations for the long-term
timing analysis. Then we obtained either a list of good
events times per science window (INTEGRAL IBIS/ISGRI, 20-60 keV)
or binned light curves (RXTE PCA, 2-60 keV). The times were
corrected to the barycenter of the solar system
and for the orbital motion. We constructed pulse profiles in those energy
bands by fitting the data with a harmonic expansion in pulse phase, as we described
in the pulse profile section. Initially we used the same simple phase model and the errors on the Fourier coefficients were corrected for the non-Poisson noise.
The profiles were grouped into 12.69 d intervals with
frequencies and frequencies derivatives being estimated for each interval
using a grid search of the Yn statistics (Finger et al. 1999). The measured
frequencies were then fitted with a piecewise-linear model. Then the profiles
were remade using the integral of the fitted frequency model as a phase model.
For the INTEGRAL IBIS/ISGRI data the approach was different,
due to the non continuous observational pattern and the sensitivity of the ISGRI
detector (see Table 1). A template profile was then created from the average profile from the set of ISGRI ScWs and from the collected pulse profiles from the RXTE PCA data. To generate phase offsets from the model, we then cross-correlated the individual profiles with the template profiles. The new phases (model + offset) were then fitted with a quadratic-spine phase model, which was used to remake the profiles. New phase offsets were then estimated.
Figure 12 shows the long-term spin-frequency and spin-up rate history obtained after repeating the grid search with the new profiles and phases. For IBIS/ISGRI the spin rates were computed by differencing adjacent frequency measurements and dividing by
the corresponding time difference. The PCA spin rates were computed by fitting a quadratic function to the phases, which were divided in 29 time intervals.
We see that the first outburst of SAX J2103.5+4545
started with a spin-up trend (bright state),
made a transition to a steady spin rate (faint state), and
then appeared to begin a spin-down trend. The following available
data started with a quick spin-up trend (bright state), and then a transition
to a slower spin-up rate (faint state).
Comparing the fluxes obtained in the non averaged long-term
light curve (the one composed of around 500 individual flux measurements
from the spectra; see bottom of Fig. 4), we realized that while SAX J2103.5+4545 was in the faint state (MJD 53 100), suddenly it increased
dramatically its luminosity for a short time period. This was not
the first episode of such a behavior but the strongest one. Therefore,
the ISGRI frequency derivative outlier cannot be ruled out since it seems it is related to a significant event.
Table 2:
Orbital solution for SAX J2103.5+4545.
![\begin{figure}
\par\includegraphics[width=8cm,height=6cm,clip]{7398fig12.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg64.gif) |
Figure 12:
Top: long-term frequency history. Middle: averaged spin-up rates history. Bottom: 40-60 keV RXTE HEXTE averaged fluxes. A spin-up rate and X-ray flux correlation was found, confirming that an accretion disk during periastron passage is present. |
| Open with DEXTER |
Errors in the orbital parameters caused by coupling between the
intrinsic spin variations of the pulsar with orbital effects, can
scatter the detected pulse frequencies. In order to achieve a better
characterization of the geometry of this binary system, we have used
RXTE PCA Standard1 data to obtain a new set of orbital parameters.
To take into account the phase noise caused by pulse
profile variations we split the RXTE results into
29 intervals (3 orbits) and fitted an orbit to the phases in each interval
(the orbital Period was fixed). The fitting model for each interval consisted of a quadratic phase model combined with an orbital model parametrized by the elements
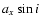 ,
,
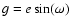 ,
,
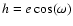 ,
and
,
and 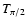 ,
with the orbital period
,
with the orbital period
 fixed, and the epoch
fixed, and the epoch  placed near the middle of the interval. Where
placed near the middle of the interval. Where 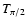 is the epoch when the mean orbital longitude is equal to 90 deg,
is the epoch when the mean orbital longitude is equal to 90 deg,
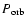 is the orbital period,
is the orbital period,
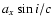 is
the light-travel time for the projected semi-major axis (i is the inclination angle), e is the eccentricity and
is
the light-travel time for the projected semi-major axis (i is the inclination angle), e is the eccentricity and 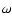 is the longitude of periastron.
is the longitude of periastron.
The final orbital parameters were obtained from a unweighted average of the best
fit parameters from just 28 intervals. As we mentioned above, taking a look at the long-term light curve we noticed that around MJD 53 100 a huge and narrow spike occurred while the source was in the faint state. This surprising behavior was also
noticed in orbital fit number 26, resulting in a highly dispersed fit that was finally
rejected. The final orbital epoch and period were obtained by making a linear fit to the 28 best fit orbital epochs. The errors in these parameters were estimated from the scatter of the best fit parameters. Finally the eccentricity e and argument of periastron 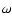 where obtained from the average values of g and h. Table 2 lists the final orbital parameters obtained.
where obtained from the average values of g and h. Table 2 lists the final orbital parameters obtained.
Our orbital parameters agree within errors with those obtained by
Baykal et al. (2007) with the exception of 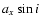 ,
where our value is
,
where our value is
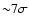 larger than theirs. Since both
results were obtained from essentially the same data set,
the difference must be due to the different approaches taken in the
analysis. Baykal et al. analyzed data from 11 intervals of
varying size which where fit with a global orbital model, with
independent 5th order phase models for each interval. We made local
orbital fits for 28 intervals of three orbit duration including a
second order phase model with each, and then averaged the local
orbital parameters to obtain a mean orbit model. This method of
averaging local orbits was introduced by Boynton et al. (1986) so
that the errors in the orbital elements introduced by random torque
variations could be empirically accounted for. Here however the
torque variations are not random, but are correlated with the flux,
which at higher flux levels is correlated with orbital phase. One
possibility is that some of the orbital signature is being absorbed
into the phase model used for each interval in the Baykal et al.
analysis, which contains 4 parameters to describe the intrinsic
torque during the each interval. The Baykal et al. analysis used on
average 0.55 torque parameters per binary orbit, while our torque
models were stiffer, using 0.33 torque parameters per orbits. In
addition, the shortest intervals in the Baykal analysis, which used
up to 1.9 torque parameters per orbit, tended to occur at the highest
flux levels, where the data has more weight in the global fit. Out of
28 estimations of
larger than theirs. Since both
results were obtained from essentially the same data set,
the difference must be due to the different approaches taken in the
analysis. Baykal et al. analyzed data from 11 intervals of
varying size which where fit with a global orbital model, with
independent 5th order phase models for each interval. We made local
orbital fits for 28 intervals of three orbit duration including a
second order phase model with each, and then averaged the local
orbital parameters to obtain a mean orbit model. This method of
averaging local orbits was introduced by Boynton et al. (1986) so
that the errors in the orbital elements introduced by random torque
variations could be empirically accounted for. Here however the
torque variations are not random, but are correlated with the flux,
which at higher flux levels is correlated with orbital phase. One
possibility is that some of the orbital signature is being absorbed
into the phase model used for each interval in the Baykal et al.
analysis, which contains 4 parameters to describe the intrinsic
torque during the each interval. The Baykal et al. analysis used on
average 0.55 torque parameters per binary orbit, while our torque
models were stiffer, using 0.33 torque parameters per orbits. In
addition, the shortest intervals in the Baykal analysis, which used
up to 1.9 torque parameters per orbit, tended to occur at the highest
flux levels, where the data has more weight in the global fit. Out of
28 estimations of
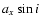 we find only two that have values below the Baykal et al. value.
we find only two that have values below the Baykal et al. value.
![\begin{figure}
\par\includegraphics[width=6.3cm,height=6.3cm,clip]{7398fig13.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg70.gif) |
Figure 13:
Spin-up rates vs. RXTE 2-100 keV non absorbed averaged flux every 1.5 and 2.5 orbits. A linear fit was found the best one. |
| Open with DEXTER |
We averaged the non absorbed flux every 1.5 and 2.5 pulsar orbits. The 1.5 orbits average is the smallest time interval that allowed us to fit a quadratic function to the phases when the spin rates were computed. The second time interval of 2.5 orbits was chosen as a good representative of the general trend. Figure 13 shows more clearly the spin-up rate vs. flux correlation. We have fitted both data sets with a single power law (solid line). In the same figure, a dashed line denotes our best-fit power law with an index fixed at 6/7, which represents the relationship between spin-up and flux predicted by simple accretion theory.
In principle, Fig. 13 seems to be nearly identical to Fig. 5
from Baykal et al. (2007), and our results confirm those found by them. However, we believe that an interesting feature should be emphasized. Data averaging over 1.5 orbits scatters more than averaging over 2.5 orbits. It appears that the smaller is the average the bigger is the scattering. This might suggest that, in addition to the disk accretion mechanism, there seems to exist another mechanism producing erratic variations.
Some X-ray pulsars, like EXO 2030+375 (Parmar et al. 1989),
show a clear pulse shape dependence on source luminosity, most likely controlled by accretion rate. Differences in X-ray pulse profiles are considered to be due to the differences in the geometrical configuration with respect to the rotational axis of the neutron star, the axis of
magnetic dipole moment, and the observer's line of sight (Nagase 1989). The structure
of the accretion column determines the basic profile of the pulse pattern. However,
simple geometric models with two pencil beams coming from the magnetic poles
or two bright spots on the neutron star surface, cannot explain the variability
observed in some other systems, like Vela X-1. Previous
studies by Kreykenbohm et al. (2002) confirmed for Vela X-1 a very complex
pulse profile at low energies (below 6 keV), showing a five peak structure. Above
10 keV the pulse profiles evolved into a simple double peak. They pointed out that
a good description of the processes responsible for the complex shape at low energies
is still missing.
In the present work, the 2-60 keV SAX J2103.5+4545 pulse shapes obtained with RXTE PCA were found to be peculiarly complex and variable either with luminosity, time or orbital phase.
For the first time the pulse shapes seem to vary randomly
from not only single sinusoidal-like peak but profiles with two, three and even occasionally four peaks, with no evident interrelationship. For a given energy range, temporal variability of the pulse profile of SAX J2103.5+4545 was explained by Sidoli et al. (2005) as likely due
to a time-dependent emission pattern, or to changes in the opacity of the
magnetized plasma through which the radiation propagates.
Previous works by Baykal et al. (2002), Falanga et al. (2005) and Sidoli et al. (2005) obtained a single peak pulse profile in soft X-ray bands, using RXTE and INTEGRAL data. However, Inam et al. (2004) found a double peak profile using XMM-Newton, but this exception could be compatible with the variability seen in our study for SAX J2103.5+4545.
In the hard X-ray range, we have obtained much simpler double peak profiles 20-40 keV INTEGRAL ISGRI profiles, in agreement with previous results by Falanga et al. (2005) and Sidoli et al. (2005). Filippova et al. (2004) published a 20-100 keV single peak pulse profile using PV phase INTEGRAL data. Taking into account the uncertainties in their results, this could be compatible with our PV phase results (see Fig. 9, MJD 52 630 pulse profile).
In addition, our study allowed us to confirm an energy dependence pattern for SAX J2103.5+4545.
Unfortunately, as in Vela X-1, we did not find out a straightforward explanation for
the low energy pulse profiles. Inam et al. (2004) found practically no
variation in the energy dependence of the 0.9-11 keV
pulse profiles, which is not in agreement with our results. Falanga et al. (2005)
obtained an energy dependent secondary peak around phase 0.2, which became
more evident at energies above 20 keV. This peak might be compatible with the evolution of our peak at phase 0.7. They also claimed that at phase 0.6 some very short variation features (hicc-ups) were present, in agreement with those observed by Inam et al. (2004) using
XMM-Newton data. These "hicc-ups'' were only visible at high energies (40-80 keV). Again, these features might be compatible with our dip at phase 0.9.
It is generally accepted that in order to explain the energy-dependent changes seen in the pulse profile, the anisotropic radiation transfer must be taken into account (Nagase 1989). Previous studies by Krauss et al. (2003) found that energy-dependent peaks in medium luminosity binary X-ray pulsars, are mainly due to the energy-dependent relative importance of the halo (which forms around the accretion funnel where the neutron star surface is irradiated) and the column contributions to
the observed flux (Sidoli et al. 2005). For SAX J2103.5+4545, Falanga et al. (2005) found that
changes in the morphology of the pulse profile as a function of energy were consistent with variations in the spectral components visible in their pulse phase resolved spectra analysis. Their study also showed that differences in the double-peak can be modeled by a different scattering fraction between the radiation from the two magnetic poles.
First studies of SAX J2103.5+4545 by Baykal et al. (2002) showed a transition from spin-up to spin-down in the RXTE observations from an outburst in November 1999, suggesting the presence of an accretion disk. The detection of a quasi-periodic oscillation at 22.7 s discovered by Inam et al. in 2004, provided further evidence
for its existence. The spin-up rate and X-ray flux correlation
is also observed in the present work, confirming that an accretion disk is present during periastron passage. Previous works by Inam et al. (2004) and Baykal et al. (2002, 2007) are in good agreement with our results. In general, either the pulse period estimations from Sidoli et al. (2005) or those ones from Blay et al. (2006) are not in very good agreement with our results.
An accretion disk will form if the specific angular momentum of the accreted material 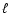 is comparable to the Keplerian specific angular momentum at the magnetospheric radius
is comparable to the Keplerian specific angular momentum at the magnetospheric radius
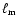 .
To estimate
.
To estimate 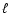 for SAX J2103.5+4545, we assumed typical pulsar parameters, and typical values of
for SAX J2103.5+4545, we assumed typical pulsar parameters, and typical values of
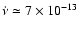 Hz s-1, F
Hz s-1, F
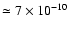 erg cm-2 s-1 (see Fig. 13) (Wilson et al. 2003, 2005 and references therein). The distance of the source from optical observations is
erg cm-2 s-1 (see Fig. 13) (Wilson et al. 2003, 2005 and references therein). The distance of the source from optical observations is
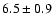 kpc (Reig et al. 2004, 2005). Several authors have discussed a possible value for the magnetic field. Recently, Baykal et al. (2007) obtained a value of
kpc (Reig et al. 2004, 2005). Several authors have discussed a possible value for the magnetic field. Recently, Baykal et al. (2007) obtained a value of
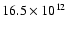 Gauss. But this implied a distance of 4.5 kpc. In order to explain the spin-up rate observed, and assuming that the distance of 6.5 kpc is correct, Sidoli et al. (2005) obtained a magnetic field of
Gauss. But this implied a distance of 4.5 kpc. In order to explain the spin-up rate observed, and assuming that the distance of 6.5 kpc is correct, Sidoli et al. (2005) obtained a magnetic field of
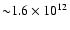 Gauss. No cyclotron lines have been observed from this source. One explanation could be a high magnetic field as proposed by Baykal et al. (2007) which would imply a fundamental line at
Gauss. No cyclotron lines have been observed from this source. One explanation could be a high magnetic field as proposed by Baykal et al. (2007) which would imply a fundamental line at 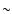 200 keV.
200 keV.
We have summarized in Table 3 the different values obtained for 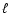 ,
using the two magnetic field measurements discussed above, assuming two distance values of 6.5 kpc and 4.5 kpc, and for k = 0.91 (simple spherical accretion model) and 0.47 (Ghosh
,
using the two magnetic field measurements discussed above, assuming two distance values of 6.5 kpc and 4.5 kpc, and for k = 0.91 (simple spherical accretion model) and 0.47 (Ghosh 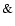 Lamb 1979, model). As expected, all cases confirm that a disk is likely to be present. Only those cases with lower
Lamb 1979, model). As expected, all cases confirm that a disk is likely to be present. Only those cases with lower 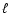 /
/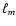 ratio might indicate that alternating periods of wind accretion and disk accretion could also take place in this system.
ratio might indicate that alternating periods of wind accretion and disk accretion could also take place in this system.
It is generally accepted that the propeller effect is likely connected to quiescence states. Reig et al. (2005, and references therein) stated as possible values for the threshold X-ray luminosity 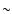 1032-1033 erg s-1. Unusually, from photometric and spectroscopic observations performed in 2004 (Reig et al. 2005) and during the faint state of this source, SAX J2103.5+4545 continued emitting X-rays even after having completely lost the disk.
1032-1033 erg s-1. Unusually, from photometric and spectroscopic observations performed in 2004 (Reig et al. 2005) and during the faint state of this source, SAX J2103.5+4545 continued emitting X-rays even after having completely lost the disk.
To determine whether or not centrifugal inhibition of accretion is operating, we estimated the flux at the onset of this effect by equating the magnetospheric radius to the corotation radius. For SAX J2103.5+4545 the threshold flux for the onset of centrifugal inhibition of accretion, i.e.,
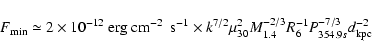 |
(1) |
where 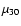 ,
M1.4, R6, and P354.9 are the pulsar's magnetic moment in units of 1030 G cm3, mass in units of 1.4
,
M1.4, R6, and P354.9 are the pulsar's magnetic moment in units of 1030 G cm3, mass in units of 1.4 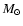 ,
radius in units of 106 cm, and spin period in units of 354.9 s, respectively. Table 3 shows our measured
,
radius in units of 106 cm, and spin period in units of 354.9 s, respectively. Table 3 shows our measured 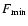 using Eq. (1). Our observed upper limit fluxes are in the range
using Eq. (1). Our observed upper limit fluxes are in the range 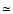 (5-0.9)
(5-0.9)
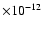 erg cm-2 s-1, consistent with
SAX J2103.5+4545 entering the centrifugal inhibition of accretion regime only for
erg cm-2 s-1, consistent with
SAX J2103.5+4545 entering the centrifugal inhibition of accretion regime only for
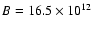 G (see Table 3).
G (see Table 3).
Table 3:
Comparison of the specific angular momentum of the accreted material to the
Keplerian specific angular momentum at the magnetospheric radius. An estimation of the flux for the onset of centrifugal inhibition of accretion is also shown.
In principle, as Reig et al. (2005, and references therein) pointed out, it is still possible to produce X-rays when the propeller effect is working (e.g. through accretion onto the magnetosphere as opposed to onto the neutron star surface or through leakage through the magnetosphere). However, due to the fact that SAX J2103.5+4545 is located in the region of wind-fed supergiant binaries in the
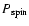 -
-
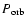 diagram, accretion from the stellar wind of the B0 companion might be the origin of the observed luminosity. Reig et al. (2005) closed their work saying that the relatively narrow orbit of SAX J2103.5+4545 implies that the wind, at the position of the neutron star, does not reach its terminal velocity, but varies in the range
diagram, accretion from the stellar wind of the B0 companion might be the origin of the observed luminosity. Reig et al. (2005) closed their work saying that the relatively narrow orbit of SAX J2103.5+4545 implies that the wind, at the position of the neutron star, does not reach its terminal velocity, but varies in the range 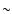 [0.7-0.9].
[0.7-0.9].
Up to now, SAX J2103.5+4545 has been classified as a transient Be/X-ray
binary system. However, as we stated above, this source is a very interesting case.
Maybe, its location in the wind-fed supergiant region might also be the origin of its complex pulse profile behavior. It should be noted that a large population of
persistent, likely wind-accreting supergiants are being discovered by the INTEGRAL mission.
![\begin{figure}
\par\includegraphics[width=8.4cm,height=3cm]{7398fig14.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg96.gif) |
Figure 14:
RXTE ASM orbital light curve of SAX J2103.5+4545 from MJD 52 200-52 500. |
| Open with DEXTER |
In the present work SAX J2103.5+4545 was detected clearly in all our observations, hence there is no well-defined limit dividing outbursting vs. quiescence. Defining a threshold for the observed flux at
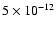 erg cm-2 s-1, we can identify 5 outbursts from Fig. 4 (bottom). Ignoring the fact that the
luminosity never exceeds 1037 erg cm-2 s-1, the first three might qualify as type II outbursts because: a) they last for multiple orbits, b) there is only moderate orbital modulation (see Fig. 14), c) there is a flux-spin up correlation. The last two outbursts are short andcould be considered as type I. In the "quiescence'' state where
the luminosity is
erg cm-2 s-1, we can identify 5 outbursts from Fig. 4 (bottom). Ignoring the fact that the
luminosity never exceeds 1037 erg cm-2 s-1, the first three might qualify as type II outbursts because: a) they last for multiple orbits, b) there is only moderate orbital modulation (see Fig. 14), c) there is a flux-spin up correlation. The last two outbursts are short andcould be considered as type I. In the "quiescence'' state where
the luminosity is 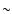 1035 erg cm-2 s-1, we see a gradual flux decline after the third "type II'' outburst, yet the frequency continues to increase. This is again not typical, but it has been seen
in other wind-fed systems (Bildsten et al. 1997). Overall, the behavior
of the source does not fit well with the standard picture of Be/X-ray transients.
We also believe that this peculiar Be/X-ray system with the narrowest of orbits, may be classified as a Persistent (but highly variable) source.
1035 erg cm-2 s-1, we see a gradual flux decline after the third "type II'' outburst, yet the frequency continues to increase. This is again not typical, but it has been seen
in other wind-fed systems (Bildsten et al. 1997). Overall, the behavior
of the source does not fit well with the standard picture of Be/X-ray transients.
We also believe that this peculiar Be/X-ray system with the narrowest of orbits, may be classified as a Persistent (but highly variable) source.
Acknowledgements
We thank Peter Kretschmar for very useful comments and his support. We appreciate
the very useful comments from the referee, which have helped us to improve the paper. We also would like to thank to NASA Marshall Space Flight Center, the National Space Science Technology Center and the Universities Space Research Association for the opportunity to develop the present work. This research is supported by the Spanish Ministerio de Educación y Ciencia through grant-no ESP2002-04124-C03-02. Thank also to Paul Connell for his support.
- Baykal, A.,
Stark, M. J., & Swank, J. H. 2000, ApJ, 544, L129 [NASA ADS] [CrossRef] (In the text)
- Baykal, A.,
Stark, M. J., & Swank, J. H. 2002, ApJ, 569, 903 [NASA ADS] [CrossRef] (In the text)
- Baykal, A.,
Inam, S. ÃG, Stark, M. J., et al. 2007, MNRAS, 374,
1108 [NASA ADS] (In the text)
- Blay, P. 2006, Ph.D.
Thesis work, Multiwavelength Analysis of two peculiar High Mass
X-ray binary systems: 4U 2206+45 and SAX J2103.5+4545. New insights
from INTEGRAL
- Blay, P., Reig, P.,
Martínez Núñez, S., & Camero, A. 2004, A&A,
427,293
- Boynton, P. E.,
Deeter, J. E., Lamb, F. K., & Zylstra, G. 1986, ApJ, 307,
545 [NASA ADS] [CrossRef]
- Bradt, H. V.,
Rothschild, R. E., & Swank, J. H. 1993, A&AS, 97, 355 [NASA ADS] (In the text)
- Camero Arranz,
A., Wilson, C. A., Finger, M. H., & Reglero, V. 2006, Proc. 6th
INTEGRAL Workshop, in press
(In the text)
-
Courvoisier, T. J.-L., Walter, R., Beckmann, V., et al. 2003,
A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Diehl, R., Baby,
N., Beckmann, V., et al. 2003, A&A, 411, L117 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Falanga, M.,
di Salvo, T., Burderi, L., & Bonnet-Bidaud, J. M. 2005,
A&A, 436, 313 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Filippova, E. V., Lutovinov, A. A., Shtykovsky, P. E., et al. 2004,
Astron. Lett., 30, 12 [CrossRef], 824
(In the text)
- Finger, M. H.,
Wilson, R. B., Chakrabarty, D., et al. 1996, A&AS, 120,
209 [NASA ADS]
- Finger, M. H.,
Bildsten, L., Chakrabarty, D., et al. 1999, ApJ, 517, 449 [NASA ADS] [CrossRef] (In the text)
- Ghosh, P., &
Lamb, F. K. 1979, ApJ, 234, 296 [NASA ADS] [CrossRef]
- Goldwurm,
A., David, P., Foschini, L., et al. 2003, A&A, 411, L223 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gruber, D. E.,
Blanco, P. R., Heindl, W. A., et al. 1996, A&AS, 120, 641 [NASA ADS] (In the text)
- Hulleman,
F., in 't Zand, J. J. M., & Heise, J. 1998, A&A, 337,
L25 [NASA ADS] (In the text)
-
Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS]
- Inam, S. Ã.,
Baykal, A., Swank, J., & Stark, M. J. 2004, ApJ, 616, 463 [NASA ADS] [CrossRef] (In the text)
- Jahoda, K.,
Swank, J., Giles, A. B., et al. 1996, Proc. SPIE, 2808, 59 [NASA ADS] (In the text)
- Kraus, U., Zahn,
C., Weth, C., & Ruder, H. 2003, ApJ, 590, 424 [NASA ADS] [CrossRef] (In the text)
-
Kreykenbohm, I., Coburn, W., Wilms, J., et al. 2002, A&A, 395,
129 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lamb, F. K.,
Pethick, C. J., & Pines, D. 1973, ApJ, 184, 271 [NASA ADS] [CrossRef]
- Levine, A. M.,
Bradt, H., Cui, W., et al. 1996, ApJ, 469, L33 [NASA ADS] [CrossRef] (In the text)
- Nagase, F.
1989, Publ. Astron. Soc. Japan, 41, 1 [NASA ADS]
- Parmar, A. N.,
White, N. E., Stella, L., et al. 1989, ApJ, 338, 373 [NASA ADS] [CrossRef]
- Pringle, J.
E., & Rees, M. J. 1972, A&A, 312, 872
- Reig, P.,
Negueruela, I., Fabregat, J., et al. 2004, A&A, 421, 673 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Reig, P.,
Negueruela, I., Papamastorakis, G., et al. 2005, A&A, 440,
637 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sidoli, L.,
Mereghetti, S., Larsson, S., & Chernyakova, M. 2004, Proc. 5th
INTEGRAL Workshop, ESA SP-552, 475
- Sidoli, L.,
Mereghetti, S., Larsson, S., & Chernyakova, M. 2005, A&A,
440, 1033S [NASA ADS] [CrossRef] (In the text)
-
Stollberg, M. T., Finger, M. H., Wilson, R. B., et al. 1999, ApJ,
512, 313 [NASA ADS] [CrossRef]
-
Westergaard, N. J., Kretschmar, P., Oxborrow, C. A., et al. 2003,
A&A, 411, L257 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wilson, C. A.,
Finger, M. H., Harmon, B. A., et al. 1997, ApJ, 479, 388 [NASA ADS] [CrossRef]
- Wilson, C. A.,
Finger, M. H., Coe, M. J., Laycock, S., & Fabregat, J. 2002,
ApJ, 570, 287 [NASA ADS] [CrossRef] (In the text)
- Wilson, C. A.,
Finger, M. H., Coe, M. J., & Negueruela, I. 2003, ApJ, 584,
996 [NASA ADS] [CrossRef] (In the text)
- Wilson, C. A.,
Fabregat, J., & Coburn, W. 2005, ApJ, 620, L99 [NASA ADS] [CrossRef]
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=9cm,height=14cm]{7398fig1.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=9cm,height=4.5cm]{7398fig2.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg18.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,height=7.5cm]{7398fig4.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg20.gif)
![\begin{figure}
\par\includegraphics[width=7.75cm,height=5.3cm]{7398fig5top.eps} ...
....eps}\includegraphics[width=7.75cm,height=5.3cm]{7398fig5bottom.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg34.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,height=7cm]{7398fig6.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=18.5cm,height=8.2cm,clip]{7398fig7.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg37.gif)
![\begin{figure}
\par\includegraphics[width=8.9cm,height=8cm,clip]{7398fig8.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg41.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,height=5.5cm,clip]{7398fig9.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=7.6cm,clip]{7398fig10.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg43.gif)
![\begin{figure}
\par\includegraphics[width=8.7cm,height=11cm,clip]{7398fig11.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg44.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=6cm,clip]{7398fig12.eps}\end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=6.3cm,height=6.3cm,clip]{7398fig13.eps} \end{figure}](/articles/aa/full/2007/38/aa7398-07/Timg70.gif)