A&A 472, L51-L54 (2007)
DOI: 10.1051/0004-6361:20077936
LETTER TO THE EDITOR
Spicule emission profiles observed in He I 10 830 Å
B. Sánchez-Andrade Nuño1,2 -
R. Centeno3,5 -
K. G. Puschmann2 -
J. Trujillo Bueno2,3,4 -
J. Blanco Rodríguez2 -
F. Kneer2
1 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
2 -
Institut für Astrophysik, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
3 -
Instituto de Astrofísica de Canarias, C/ Vía Láctea, s/n, 38205 La Laguna, Tenerife, Spain
4 -
Consejo Superior de Investigaciones Científicas, Spain
5 -
High Altitude Observatory (NCAR), 3080 Center Green Dr. (CG-1), Boulder 80301 CO, USA
Received 24 May 2007 / Accepted 25 July 2007
Abstract
Aims. Off-the-limb observations with high spatial and spectral resolution will help us understand the physical properties of spicules in the solar chromosphere.
Methods. Spectropolarimetric observations of spicules in the He I 10 830 Å multiplet were obtained with the Tenerife Infrared Polarimeter on the German Vacuum Tower Telescope at the Observatorio del Teide (Tenerife, Spain). The analysis shows the variation of the off-limb emission profiles as a function of the distance to the visible solar limb. The ratio between the intensities of the blue and the red components of this triplet
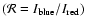 is an observational signature of the optical thickness along the light path, which is related to the intensity of the coronal irradiation.
is an observational signature of the optical thickness along the light path, which is related to the intensity of the coronal irradiation.
Results. We present observations of the intensity profiles of spicules above a quiet Sun region. The observable  as a function of the distance to the visible limb is also given. We have compared our observational results to the intensity ratio obtained from detailed radiative transfer calculations in semi-empirical models of the solar atmosphere assuming spherical geometry. The agreement is purely qualitative. We argue that future models of the solar chromosphere and transition region should account for the observational constraints presented here.
as a function of the distance to the visible limb is also given. We have compared our observational results to the intensity ratio obtained from detailed radiative transfer calculations in semi-empirical models of the solar atmosphere assuming spherical geometry. The agreement is purely qualitative. We argue that future models of the solar chromosphere and transition region should account for the observational constraints presented here.
Key words: Sun: chromosphere - line: profiles - techniques: spectroscopic - instrumentation: spectrographs
The solar chromosphere is in a highly dynamic state. Its small-scale structures
evolve in timescales of minutes or even less.
Due to its low density, the chromosphere is transparent in most of the optical
spectrum. Nevertheless, in lines such as H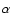 and He I 10 830 Å, the
significant absorption provides a mean for direct studies of the chromosphere's
peculiar characteristics, such as bright plages in active regions, dark and
bright fibrils on the disc in both the quiet Sun's network and around
sunspots, as well as spicules above the limb. Recent studies
(e.g. Tziotziou et al. 2003) claimed that it is possible that many of these chromospheric
features have the same physical nature within different scenarios.
and He I 10 830 Å, the
significant absorption provides a mean for direct studies of the chromosphere's
peculiar characteristics, such as bright plages in active regions, dark and
bright fibrils on the disc in both the quiet Sun's network and around
sunspots, as well as spicules above the limb. Recent studies
(e.g. Tziotziou et al. 2003) claimed that it is possible that many of these chromospheric
features have the same physical nature within different scenarios.
In the chromosphere, between the photosphere and the much hotter
corona, the average temperature starts to rise outwards, along with a
decrease of the density. The dynamics of a magnetised gas depends on the ratio of the gas pressure and magnetic pressure, the plasma 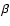 parameter,
parameter,
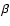 =
=
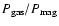 ,
with
,
with
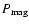 =
=
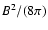 .
From the low chromosphere into the
extended corona, this plasma parameter decreases from values
.
From the low chromosphere into the
extended corona, this plasma parameter decreases from values 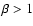 to a
low-beta regime,
to a
low-beta regime,
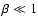 ,
where the plasma motions are magnetically driven.
,
where the plasma motions are magnetically driven.
Spicules, known for more than 130 years (see hand drawings in Secchi 1877), represent a prominent example of the dynamic
chromosphere. We refer the reader to reviews by Beckers (1972,1968) and to the paper by
Wilhelm (2000) on UV properties. Spicules are seen at and outside the limb
of the Sun as thin,
elongated features that develop speeds of 10-30 km s-1 and reach
heights of 5-9 Mm on average, during their lifetimes of 3-15 min. As pointed out by Sterling (2000), a key impediment to develop a satisfactory understanding has been the
lack of reliable observational data.
Many theoretical models have been developed to understand the
nature of spicules, using a wide variety
of motion triggers and driving mechanisms.
In this study we focus on the He I 10 830 Å triplet emission line using recent
technical improvements in observational facilities. We are able to provide
observational evidence of the link between the corona and the infrared
emission of this line, in the frame of the current theoretical models of the
solar atmosphere.
The He I 10 830 Å multiplet consists of the three transitions from the upper term 3P2,1,0, which has three levels, to the lower metastable term 3S1, which has one single level. The two transitions from the J=2 and J=1 upper levels appear blended at typical chromospheric temperatures, and form the so-called red component, at
10 830.3 Å. (Note that the two red transitions are only 0.09 Å apart.) The blue component, at 10 829.1 Å, corresponds to the transition from the upper level with J=0 to the lower level with J=1. The energy levels that take part in these transitions are basically populated via
an ionization-recombination process (Avrett et al. 1994). The EUV coronal irradiation (CI) at
wavelengths lambda
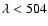 Å ionizes the neutral helium, and subsequent recombinations
of singly ionized helium with free electrons lead to an overpopulation of these levels.
Å ionizes the neutral helium, and subsequent recombinations
of singly ionized helium with free electrons lead to an overpopulation of these levels.
Alternative theories suggest other mechanisms that might also contribute to the formation of the helium lines relying on the collisional excitation of the electrons in regions with higher temperature (e.g., Andretta & Jones 1997).
Centeno (2006) modelled the ionisation and recombination processes using various
amounts of CI, non-LTE radiative transfer, and different atmospheric
models (see also Centeno et al. 2007, in preparation).
They have simulated limb observations for different heights, obtaining
synthetic emission profiles in spherically symmetric models of the solar atmosphere. One
conclusion of their
study is that the ratio of intensities
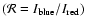 of the "blue'' to the "red'' components of the He I 10 830 Å emission
is a very good candidate for diagnosing the CI.
The population of the metaestable level depends on optical thickness,
whose variation with height governs the change in the ratio
of the "blue'' to the "red'' components of the He I 10 830 Å emission
is a very good candidate for diagnosing the CI.
The population of the metaestable level depends on optical thickness,
whose variation with height governs the change in the ratio  as
a function of the distance to the limb.
as
a function of the distance to the limb.
Trujillo Bueno et al. (2005) measured the four Stokes parameters of quiet-Sun chromospheric spicules and could show evidence of the Hanle effect by the action of inclined magnetic fields with an average strength of the order of 10 G. They modelled the He I 10 830 Å profiles assuming the medium along the integrated line of sight as
a slab of constant properties and with its optical thickness as a free
parameter. Trujillo Bueno et al. (2005) showed that the observed intensity profiles and their ensuing  values can be reproduced by choosing an optical thickness significantly larger than unity. Centeno (2006) demonstrated that this optical thickness is related to the coronal irradiance (through the ratio
values can be reproduced by choosing an optical thickness significantly larger than unity. Centeno (2006) demonstrated that this optical thickness is related to the coronal irradiance (through the ratio  ), thus providing a physical meaning to the free parameter in the slab model (see also Centeno et al. 2007).
), thus providing a physical meaning to the free parameter in the slab model (see also Centeno et al. 2007).
We present novel observations showing the spectral emission of He I 10 830 Å and its dependence on the height of the
spicules above a quiet region. We compare the deduced observational  with that obtained from detailed non-LTE numerical calculations using available atmospheric profiles.
with that obtained from detailed non-LTE numerical calculations using available atmospheric profiles.
The observations were carried out on December 4th, 2005, at the Vacuum
Tower Telescope (VTT) at Observatorio del Teide. They were supported by the
Kiepenheuer Adaptive Optics System (KAOS, von der Lühe et al. 2003). We used the Echelle spectrograph of the VTT and the new version (TIP-2) of the Tenerife Infrared Polarimeter (Martínez Pillet et al. 1999), which has a larger CCD camera (Collados et al. 2007). The seeing conditions were good (average seeing after KAOS correction around 7 cm, maximum 12 cm).
The strong darkening close to the solar limb and the actual presence of the
limb make it difficult to use KAOS for off-limb observations, since the
correlation algorithm was not developed for this kind of observation. Fortunately, we could use a nearby facula inside the limb for the tracking lock point of the adaptive optics system.
Although we carried out full Stokes vector observations, in
this study we have used only the intensity profiles. The spectral
region covered by TIP-2 spans from 10 826 to 10 837 Å and contains
the He I 10 830 Å multiplet. The spectral
sampling was 11 mÅ/px, and the slit was 40
 long and 0
long and 0
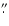 5 wide. It was oriented parallel to the NE limb, in a region far from major activity at that time, at 59
5 wide. It was oriented parallel to the NE limb, in a region far from major activity at that time, at 59
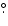 8 from North. We scanned the full height of the spicules, up to
7
8 from North. We scanned the full height of the spicules, up to
7
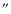 off the visible solar limb, with a step size of 0
off the visible solar limb, with a step size of 0
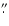 35.
35.
At each position, 5 consecutive spectra were measured with 10 accumulations of
250 ms each, with a total integration time of 2.5 s per off-limb slit
position. A nearby disc profile was also taken to help remove the scattered light from the off-limb spectra via the data analysis.
3 Data reduction and processing
We applied usual flatfielding and dark current corrections to the data. A high frequency, quasi-periodic, spurious electronic pattern in the profiles
was removed using a low-pass Fourier filter, which left the frequencies containing the spectral line information untouched.
We define the position of the solar limb as the height of the first scanning position where the helium line appears in emission. For increasing distances to the solar limb a decreasing amount of sunlight is added by scattering in the Earth's atmosphere and by the telescope optical surfaces to the signal. Since the true off-limb continuum must be close to zero, i.e. below our detection limit, the observed continuum signal measures the spurious
light. Therefore, we removed the spurious continuum intensity level by using the information given by a nearby average disc spectrogram. This first subtraction estimates the continuum level on a region 6 Å away from the He I 10 830 Å emission lines.
After this correction with a coarse estimate of the spurious light, a
second correction was applied to remove the residual continuum level
seen around the emission lines. This was needed since the transmission
curve of the used prefilter is not flat but variable with wavelength.
Figure 1 shows the emission profiles of the He I 10 830 Å (after the reduction process) for different heights above the limb.
Figure 2 illustrates this in three dimensions, as a function of
wavelength and the distance to the solar limb, clearly showing
a change in the intensity ratio of the blue and red components of the
multiplet
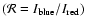 with height.
This will be discussed in Sect. 4.
with height.
This will be discussed in Sect. 4.
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{7936fig1.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg16.gif) |
Figure 1:
Measured He I 10 830 Å emission profiles for increasing
distances to the solar limb, scanning a broad range of the height extension of the
spicules. Each profile is the average of the 312 pixels along the slit (which was always kept parallel to the limb). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7936fig2.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg17.gif) |
Figure 2:
3D representation of the measured He I 10 830 Å emission
profiles for increasing distances to the solar visible limb. Note that the x-axis is
wavelength, the y-axis the height above solar limb and the z-axis the intensity
normalised to the maximum emission in the line centre of the red component. |
| Open with DEXTER |
For the calculation of  we need to determine the amplitudes of the
blue and red components of the emission profile (as shown in Fig. 3).
we need to determine the amplitudes of the
blue and red components of the emission profile (as shown in Fig. 3).
To determine the core wavelength of the red
component of the triplet we fitted a Gaussian profile to its core, in a 1.3 Å
range around the maximum. After symmetrising the observed profile around this
maximum, using the values on the red side of the red component, we fitted another Gaussian
function to the resulting symmetric profile. Subtraction of the fitted
symmetric profile from the data leaves the emission profile of the blue
component, which was also approximated by a Gaussian to determine its central wavelength. Our tests trying to fit directly both profiles using two Gaussians failed in a number of cases, probably due to the following reasons: (a) the red component is in fact the result of two blended lines, (b) the much weaker blue component was almost hidden in the broadened red component, and (c) the presence of noise. Our technique determines first the red component and then, after subtraction of the fitted profile, the blue one.
We have thus separated the helium emissions into their red and blue
components assuming only 2 that both are present and that they are both symmetric. We can now measure their widths and intensities and also check that the line core positions coincide with the theoretical ones. After the fitting process the residuals
between measured and observed profiles were small, the largest errors occurring
in the determination of the core intensities of the red line. This happens because the red component consists of two blended lines (with a separation of 0.09 Å), a fact that flattens the emission profile near the core as opposed to a more peaked Gaussian function. Nevertheless, the differences between fitted profiles
and data are only significant in the red core and are always lower than
+0.08 of the maximum normalised intensity, with a mean difference of 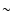 0.02. To avoid systematic errors, we used the observational values for the centre of
the red component when calculating
0.02. To avoid systematic errors, we used the observational values for the centre of
the red component when calculating  .
.
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{7936fig3.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg19.gif) |
Figure 3:
Determination of the blue and red components of the He I 10 830 Å triplet from the observed emission profiles. In this example the
slit was placed at 1
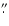 4 off the solar visible limb. See text for details.
The solid line represents the average emision profile. The dotted line is the Gaussian fit to the symmetrised red component. Subtraction of this from the observed profile leaves the blue
component, which is also fitted by a Gaussian profile (thin solid line).
The sum of both Gaussians (dashed line) gives the fit to the observed profile. 4 off the solar visible limb. See text for details.
The solid line represents the average emision profile. The dotted line is the Gaussian fit to the symmetrised red component. Subtraction of this from the observed profile leaves the blue
component, which is also fitted by a Gaussian profile (thin solid line).
The sum of both Gaussians (dashed line) gives the fit to the observed profile. |
| Open with DEXTER |
4 Results
The chromospheric temperature and density are too low to populate the
ortho-helium levels via collisions (Avrett et al. 1994). The EUV irradiation from
the corona (CI) ionises the para-helium, and
the subsequent recombinations lead to an overpopulation of all the
ortho-helium levels, in particular those involved in the 10 830 Å transitions. Centeno (2006) and Centeno et al. (2007) have modelled the off-the-limb emission profiles and concluded that the ratio  =
=
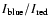 is a function of the height and a direct tracer of the amount of CI. Here we compare the results from the theoretical modelling with observations.
is a function of the height and a direct tracer of the amount of CI. Here we compare the results from the theoretical modelling with observations.
Trujillo Bueno et al. (2005) modelled their spectropolarimetric observations assuming a slab with constant physical properties with a given optical thickness. In the optically thin regime 
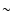 0.12, which is the ratio of the relative oscillator strengths of the triplet. As the optical
thickness (at the line-centre of the red blended component) grows, this ratio also increases
until it reaches a saturation value slightly larger than 1 for
0.12, which is the ratio of the relative oscillator strengths of the triplet. As the optical
thickness (at the line-centre of the red blended component) grows, this ratio also increases
until it reaches a saturation value slightly larger than 1 for
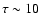 .
(This type of calculation can be done and improved as explained in Trujillo Bueno & Asensio Ramos 2007.) To reproduce the observed emission profile Trujillo Bueno et al. (2005) had to choose
.
(This type of calculation can be done and improved as explained in Trujillo Bueno & Asensio Ramos 2007.) To reproduce the observed emission profile Trujillo Bueno et al. (2005) had to choose
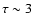 .
Interestingly, the values of
.
Interestingly, the values of 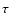 yielded by this modelling strategy are consistent with the more realistic
approach of Centeno (2006), where non-LTE radiative transfer calculations in
semi-empirical models of the solar atmosphere are presented, using spherical
geometry and taking into account the ionising coronal irradiation.
With our data we are able to test such theoretical calculations by comparing
the measured values of
yielded by this modelling strategy are consistent with the more realistic
approach of Centeno (2006), where non-LTE radiative transfer calculations in
semi-empirical models of the solar atmosphere are presented, using spherical
geometry and taking into account the ionising coronal irradiation.
With our data we are able to test such theoretical calculations by comparing
the measured values of  with those resulting from various chromospheric
models. This way we may eventually trace the amount of CI inciding on the
spicules. The analysis described in Sect. 3 yielded the
values of
with those resulting from various chromospheric
models. This way we may eventually trace the amount of CI inciding on the
spicules. The analysis described in Sect. 3 yielded the
values of  for the observed profiles. The resulting dependence on
the distance to the solar limb, for each pixel along the slit and each position of the slit above the limb, are presented in Fig. 4. The solid black line gives the average value of
for the observed profiles. The resulting dependence on
the distance to the solar limb, for each pixel along the slit and each position of the slit above the limb, are presented in Fig. 4. The solid black line gives the average value of  .
.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7936fig4.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg23.gif) |
Figure 4:
Measured ratio  = =
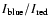 as a function of
distance to the solar limb. Thin lines come from each pixel along the slit. The thick solid line represents the average and the dashed line the value of the optically thin regime.
as a function of
distance to the solar limb. Thin lines come from each pixel along the slit. The thick solid line represents the average and the dashed line the value of the optically thin regime. |
| Open with DEXTER |
The dependence of  with height can be understood in a qualitative way as
follows: in the outer layers of the chromosphere the density is so low
that the transitions occur in the optically thin regime.
With decreasing altitude the ratio
with height can be understood in a qualitative way as
follows: in the outer layers of the chromosphere the density is so low
that the transitions occur in the optically thin regime.
With decreasing altitude the ratio  increases (proportionally with
density) until a maximum optical thickness is reached. At even lower
layers, although the density still continues to rise, the extinction of the coronal
irradiance leads to a reduction in the number of ionizations, which results
in a decrease of the optical thickness in the core wavelength of the red
component, and thus in a decrease of
increases (proportionally with
density) until a maximum optical thickness is reached. At even lower
layers, although the density still continues to rise, the extinction of the coronal
irradiance leads to a reduction in the number of ionizations, which results
in a decrease of the optical thickness in the core wavelength of the red
component, and thus in a decrease of  .
.
For a quantitative comparison with theoretical modelling we have
used the results from Centeno (2006) and Centeno et al. (2007) where they calculated the ratios  for different
standard model atmospheres: FAL-C and FAL-P (Fontenla et al. 1991) and
FAL-X (Avrett 1995). The FAL-C and FAL-X models may be considered as illustrative of the thermal conditions in the quiet Sun, while the FAL-P model of a plage region. The FAL-X model has a relatively cool atmosphere in order to explain the molecular CO absorption at 4.6
for different
standard model atmospheres: FAL-C and FAL-P (Fontenla et al. 1991) and
FAL-X (Avrett 1995). The FAL-C and FAL-X models may be considered as illustrative of the thermal conditions in the quiet Sun, while the FAL-P model of a plage region. The FAL-X model has a relatively cool atmosphere in order to explain the molecular CO absorption at 4.6 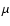 .
.
The comparison is shown in Fig. 5. We notice that the modelled
height variations of  agree only in a qualitative manner with what is
found in our observations. However, the calculations from different models of
the solar atmosphere are unable to reproduce the measured ratio. Higher values of the coronal irradiance lead to an increase of the optical thickness (at the line centres of the He I multiplet) and an upward shift in the run of
agree only in a qualitative manner with what is
found in our observations. However, the calculations from different models of
the solar atmosphere are unable to reproduce the measured ratio. Higher values of the coronal irradiance lead to an increase of the optical thickness (at the line centres of the He I multiplet) and an upward shift in the run of  vs. height. Yet the shape of the height dependence is mainly given by the atmospheric density profile and the attenuation of the ionising radiation as it reaches the lower layers of the chromosphere.
It is also clear from Fig. 5 that the models do not extend high enough.
vs. height. Yet the shape of the height dependence is mainly given by the atmospheric density profile and the attenuation of the ionising radiation as it reaches the lower layers of the chromosphere.
It is also clear from Fig. 5 that the models do not extend high enough.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7936fig5.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg25.gif) |
Figure 5:
Observed (average) vs. theoretical variation of the ratio  = =
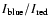 with height.
with height. |
| Open with DEXTER |
5 Conclusions
The theoretical behaviour of the ratio  agrees
qualitatively with observations. Yet, a quantitative comparison showspoor
agreement. Also, the simulated ratios are highly model dependent.
As already explained, the failure to reproduce the observed profiles is very likely due to the density stratification not being adequate for spicule modelling and to the limited vertical extension of the atmospheric models.
Modelling of the intensity ratio
agrees
qualitatively with observations. Yet, a quantitative comparison showspoor
agreement. Also, the simulated ratios are highly model dependent.
As already explained, the failure to reproduce the observed profiles is very likely due to the density stratification not being adequate for spicule modelling and to the limited vertical extension of the atmospheric models.
Modelling of the intensity ratio  in the
He I infrared triplet should account for the fact that the solar
chromosphere is inhomogeneous on small scales and that the spicules are
small-scale intrusions of chromospheric matter into the hot corona.
in the
He I infrared triplet should account for the fact that the solar
chromosphere is inhomogeneous on small scales and that the spicules are
small-scale intrusions of chromospheric matter into the hot corona.
New data of spicule regions near the poles and the equator, below coronal
holes or coronal active regions should help us to understand the detailed
behaviour of the He I 10 830 Å lines. In further work, we will extend this study to the full Stokes vector, in order to see the variation of the linear polarization - or even the variation of the Hanle effect - with height. It would also be interesting to use the most recent models of active region fibrils and spicules (e.g., Heggland et al. 2007) in order to see whether or not they agree with our observations. Future models of the solar chromosphere should be constrained by the observational evidences presented here.
Acknowledgements
We thank M. Collados for the extensive help and discussions, as
well as for the reduction software. The help from A. Lagg was very
valuable during the reduction phase. B.S.A.N. acknowledges a Ph.D. fellowship at the International Max Planck Research School On Physical Processes in the Solar System and Beyond. K.G.P. thanks the Deutsche Forchungsgemeinschaft for support through grant KN 152/29. R.C. and J.T.B.
acknowledge the support of the Spanish Ministerio de Educación y Ciencia through project AYA2004-05792. J.T.B. thanks the Akademie der Wissenschaften zu Göttingen for the Gauss-Professur during a sabatical stay at the Institut für Astrophysik of the University
of Göttingen. The Vacuum Tower Telescope is operated by the Kiepenheuer-Institut für Sonnenphysik, Freiburg, at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias. The National Center for Atmospheric Research is sponsored by the National Science Foundation
- Andretta, V., & Jones,
H. P. 1997, ApJ, 375, 489 (In the text)
- Avrett, E. H.,
Fontenla, J. M., & Loeser, R. 1994, in Infrared Solar
Physics, ed. D. M. Rabin, J. T. Jefferies, & C.
Lindsey (Dordrecht: Kluwer), IAU Symp., 154, 35
(In the text)
- Avrett, E. H.
1995, in Infrared tools for solar astrophysics: What's next?,
ed. J. R. Kuhn, & M. J. Penn (Singapore: World
Scientific), 303
(In the text)
- Beckers,
J. M. 1968, Sol. Phys., 3, 367 [NASA ADS]
- Beckers,
J. M. 1972, ARA&A, 10, 73 [NASA ADS]
- Centeno, R. 2006,
Ph.D. Thesis. University of La Laguna (Tenerife; Spain)
(In the text)
- Centeno, R., Trujillo
Bueno, J., Uitenbroek, H., & Collados, M. 2007, in
preparation
(In the text)
- Collados, M.,
Lagg, A., Díaz García, J., et al. 2007, in The
Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovi,
& R. J. Rutten, ASP Conf. Ser., 368, 611
(In the text)
- Fontenla,
J. M., Avrett, E. H., & Loeser, R. 1991, ApJ, 377,
712 [NASA ADS] [CrossRef] (In the text)
- Heggland, L., De
Pontieu, B., & Hansteen, V. H. 2007,
[arXiv:astro-ph/0703498]
(In the text)
- Martínez
Pillet, V., Collados, M., Sánchez Almeida, J., et al.
1999, in High Resolution Solar Physics: Theory, Observations, and
Techniques, ed. T. R. Rimmele, K. S.
Balasubramaniam, & R. R. Radick, ASP Conf. Ser., 183,
264
(In the text)
- Secchi, P. A.
1877, Le Soleil, Vol. 2, 2nd edn. (Paris: Gauthier-Villars)
(In the text)
- Sterling,
A. C. 2000, Sol. Phys., 196, 79 [NASA ADS] [CrossRef] (In the text)
- Trujillo Bueno,
J., Merenda, L., Centeno, R., Collados, M., &
Landi Degl'Innocenti, E. 2005, ApJ, 619, L191 [NASA ADS] [CrossRef] (In the text)
- Trujillo Bueno,
J., & Asensio Ramos, A. 2007, ApJ, 655, 642 [NASA ADS] [CrossRef]
- Tziotziou,
K., Tsiropoula, G., & Mein, P. 2003, A&A, 402, 361 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- von der Lühe,
O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003, SPIE, 4853,
187 [NASA ADS] (In the text)
- Wilhelm, K. 2000,
A&A, 360, 351 [NASA ADS] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{7936fig1.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg16.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7936fig2.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{7936fig3.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7936fig4.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7936fig5.ps}\end{figure}](/articles/aa/full/2007/36/aa7936-07/Timg25.gif)