A&A 472, 29-49 (2007)
DOI: 10.1051/0004-6361:20077150
V. de Lapparent1 - E. Slezak2
1 - Institut d'Astrophysique de Paris, UMR 7095 CNRS, Univ. Pierre et Marie Curie,
98bis boulevard Arago, 75014 Paris, France
2 -
Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex 4, France
Received 23 January 2007 / Accepted 4 June 2007
Abstract
Context. Galaxy clustering shows segregation effects with galaxy type, color and luminosity, which bring clues on the relationship with the underlying density field.
Aims. We explore these effects among the populations of giant and dwarf galaxies detected in the ESO-Sculptor survey.
Methods. We calculate the spatial two-point auto and cross-correlation functions for the 765 galaxies with
![]() and
and
![]() and for subsets by spectral type and luminosity.
and for subsets by spectral type and luminosity.
Results. At separation of 0.3 h-1 Mpc, pairs of early-type galaxies dominate the clustering over all the other types of pairs. At intermediate scales, 0.3-5 h-1 Mpc, mixed pairs of dwarf and giant galaxies contribute equally as pairs of giant galaxies, whereas the latter dominate at ![]() 10 h-1 Mpc. Moreover, the correlation functions per galaxy type display the expected transition between the 1-halo and 2-halo regimes in the scenario of hierarchical merging of dark matter halos. The 1-halo component of the early-type galaxies largely outdoes that for the late spiral galaxies, and that for the dwarf galaxies is intermediate between both. In contrast, the 2-halo component of the early-type galaxies and late spiral galaxies are comparable, whereas that for the dwarf galaxies is consistent with null clustering.
10 h-1 Mpc. Moreover, the correlation functions per galaxy type display the expected transition between the 1-halo and 2-halo regimes in the scenario of hierarchical merging of dark matter halos. The 1-halo component of the early-type galaxies largely outdoes that for the late spiral galaxies, and that for the dwarf galaxies is intermediate between both. In contrast, the 2-halo component of the early-type galaxies and late spiral galaxies are comparable, whereas that for the dwarf galaxies is consistent with null clustering.
Conclusions. We link the clustering segregation of the early-type and late spiral galaxies to their spatial distribution within the underlying dark matter halos. The early-type galaxies are preferentially located near the centers of the most massive halos, whereas late spiral galaxies tend to occupy their outskirts or the centers of less massive halos. This appears to be independent of luminosity for the early-type galaxies, whereas faint late spiral galaxies might reside in less dense regions than their bright analogs. The present analysis also unveils unprecedented results on the contribution from dwarf galaxies: at the scale at which they significantly cluster inside the halos (![]() 0.3 h-1 Mpc), they are poorly mixed with the late spiral galaxies, and appear preferentially as satellites of early-type galaxies.
0.3 h-1 Mpc), they are poorly mixed with the late spiral galaxies, and appear preferentially as satellites of early-type galaxies.
Key words: surveys - galaxies: distances and redshifts - cosmology: large-scale structure of Universe - galaxies: elliptical and lenticular, cD - galaxies: spiral - galaxies: dwarf
The two-point correlation function is a fundamental statistic for characterizing the galaxy distribution. It partly quantifies the visual impression of clustering provided by the redshift maps, and subsequently allows one to perform direct comparison with the theoretical predictions. One of the issues is to determine how galaxies trace the underlying mass distribution, and whether and how this is related to their internal properties. This in turn can provide crucial information on how galaxies have formed and evolved until now.
Here we use the ESO-Sculptor Survey (hereafter ESS;
de Lapparent et al. 2003) to statistically characterize the large-scale
clustering of galaxies at ![]() ,
and to examine its dependence on
galaxy type. The ESS provides a nearly complete
redshift survey of galaxies at
,
and to examine its dependence on
galaxy type. The ESS provides a nearly complete
redshift survey of galaxies at ![]() over a contiguous area of the
sky (Bellanger et al. 1995), supplemented by CCD-based photometry
(Arnouts et al. 1997) and a template-free spectral classification
(Galaz & de Lapparent 1998). In agreement with the other existing redshift surveys
to smaller or similar distances
(Zehavi et al. 2002; Shectman et al. 1996; Small et al. 1997; de Lapparent et al. 1986; Colless et al. 2001), the ESS
redshift map reveals a highly structured cell-like distribution out to
over a contiguous area of the
sky (Bellanger et al. 1995), supplemented by CCD-based photometry
(Arnouts et al. 1997) and a template-free spectral classification
(Galaz & de Lapparent 1998). In agreement with the other existing redshift surveys
to smaller or similar distances
(Zehavi et al. 2002; Shectman et al. 1996; Small et al. 1997; de Lapparent et al. 1986; Colless et al. 2001), the ESS
redshift map reveals a highly structured cell-like distribution out to
![]() in which numerous sharp walls or filaments alternate with
regions devoid of galaxies on a typical scale of
in which numerous sharp walls or filaments alternate with
regions devoid of galaxies on a typical scale of ![]() 25 h-1 Mpc (Bellanger & de Lapparent 1995). The deep pencil-beam geometry of the survey is
characterized by a long line-of-sight of 1300 h-1 Mpc, and a transverse
extent of
25 h-1 Mpc (Bellanger & de Lapparent 1995). The deep pencil-beam geometry of the survey is
characterized by a long line-of-sight of 1300 h-1 Mpc, and a transverse
extent of ![]() 11 h-1 Mpc at z=0.3, corresponding to
11 h-1 Mpc at z=0.3, corresponding to ![]() 3 correlation lengths (quoted scales are in comoving coordinates). The ESS therefore provides a sufficiently large sample for performing a useful two-point correlation analysis.
3 correlation lengths (quoted scales are in comoving coordinates). The ESS therefore provides a sufficiently large sample for performing a useful two-point correlation analysis.
Using the ESS spectral classification and the corresponding luminosity
functions per galaxy class (de Lapparent et al. 2003), we examine the
variations in the ESS clustering as a function of galaxy type. Various
surveys have detected the stronger clustering of early-type/red
galaxies over late-type/blue galaxies at redshifts ![]() (Norberg et al. 2002; Magliocchetti & Porciani 2003; Zehavi et al. 2005; Loveday et al. 1999; Giuricin et al. 2001), and
at higher redshifts
(Norberg et al. 2002; Magliocchetti & Porciani 2003; Zehavi et al. 2005; Loveday et al. 1999; Giuricin et al. 2001), and
at higher redshifts ![]() (Shepherd et al. 2001; Coil et al. 2004; Meneux et al. 2006; Phleps & Meisenheimer 2003). Further details were
obtained by Li et al. (2006) from low redshift galaxies, whose analysis
shows that the observed clustering differences between red and blue
galaxies, namely a higher amplitude and steeper slope than for blue
galaxies, are largest at small scales and for low mass galaxies; the
authors also measure the same clustering segregation effects when
considering galaxy age as traced by the 4000 Å break strength,
instead of galaxy color. To examine in further details the
relationship between galaxy type and clustering, we propose here a new
approach based on the separation of the giant and dwarf galaxies. We
also measure the cross-correlation of the various samples, which
provides complementary clues on the relative distribution of the
different galaxy types.
(Shepherd et al. 2001; Coil et al. 2004; Meneux et al. 2006; Phleps & Meisenheimer 2003). Further details were
obtained by Li et al. (2006) from low redshift galaxies, whose analysis
shows that the observed clustering differences between red and blue
galaxies, namely a higher amplitude and steeper slope than for blue
galaxies, are largest at small scales and for low mass galaxies; the
authors also measure the same clustering segregation effects when
considering galaxy age as traced by the 4000 Å break strength,
instead of galaxy color. To examine in further details the
relationship between galaxy type and clustering, we propose here a new
approach based on the separation of the giant and dwarf galaxies. We
also measure the cross-correlation of the various samples, which
provides complementary clues on the relative distribution of the
different galaxy types.
The paper is organized as follows. Section 2 reviews the
characteristics of the ESS galaxy redshift survey, defines the
sub-samples used in the present analysis, and describes the luminosity
functions used for calculating the selection functions. In
Sect. 3, we evaluate the various sources of random and
systematic errors. Results on the redshift space auto-correlation
function ![]() for the full ESS sample and the sub-samples by
galaxy types are given in Sect. 4. The correlation as a
function of projected separation
for the full ESS sample and the sub-samples by
galaxy types are given in Sect. 4. The correlation as a
function of projected separation
![]() for the various ESS samples are described in Sect. 5, along with the cross-correlation functions between the different galaxy types. The
auto and cross-correlation functions are then interpreted in
Sect. 6 in terms of the occupation of the dark matter halos by
the different galaxy types. In Sect. 7, we compare our results
on
for the various ESS samples are described in Sect. 5, along with the cross-correlation functions between the different galaxy types. The
auto and cross-correlation functions are then interpreted in
Sect. 6 in terms of the occupation of the dark matter halos by
the different galaxy types. In Sect. 7, we compare our results
on
![]() to those from the other existing redshift
surveys. Finally, Sect. 8 summarizes our conclusions and
Sect. 9 discusses them in view of other existing results
on galaxy clustering. In the Appendix, we describe the estimators
which we use for calculating the two-point correlation functions, and
we address the issues of the weighting scheme, the normalization of
the correlation function, and the estimation of the mean density.
to those from the other existing redshift
surveys. Finally, Sect. 8 summarizes our conclusions and
Sect. 9 discusses them in view of other existing results
on galaxy clustering. In the Appendix, we describe the estimators
which we use for calculating the two-point correlation functions, and
we address the issues of the weighting scheme, the normalization of
the correlation function, and the estimation of the mean density.
Throughout the present analysis, we assume a flat Universe with, at
the present epoch, a scale parameter
H0 = 100 h km s-1 Mpc-1, a
matter density
![]() and a cosmological energy
density
and a cosmological energy
density
![]() (Riess et al. 1998; Phillips et al. 2001; Tonry et al. 2003; Perlmutter et al. 1999). All absolute
absolute magnitude are defined modulo
(Riess et al. 1998; Phillips et al. 2001; Tonry et al. 2003; Perlmutter et al. 1999). All absolute
absolute magnitude are defined modulo ![]() .
.
The ESS covers a rectangular area of 0.37 deg2 defined as a thin
strip of
![]()
![]()
![]() near the south Galactic pole
(
near the south Galactic pole
(
![]() )
and centered at
)
and centered at
![]() (2000) in the Sculptor
constellation. The observations were performed using the New
Technology Telescope (NTT) and the 3.6 m telescope at the European
Southern Observatory (ESO). The photometric catalogue is based on CCD multicolor imaging in the Johnson-Cousins
(2000) in the Sculptor
constellation. The observations were performed using the New
Technology Telescope (NTT) and the 3.6 m telescope at the European
Southern Observatory (ESO). The photometric catalogue is based on CCD multicolor imaging in the Johnson-Cousins
![]() system, and
contains nearly 13 000 galaxies to
system, and
contains nearly 13 000 galaxies to ![]() (Arnouts et al. 1997). The
spectroscopic survey provides flux-calibrated spectra and redshifts
(with an rms "external'' uncertainty
(Arnouts et al. 1997). The
spectroscopic survey provides flux-calibrated spectra and redshifts
(with an rms "external'' uncertainty
![]() )
for
)
for
![]() 600 galaxies with
600 galaxies with
![]() ,
within a slightly
smaller field of
,
within a slightly
smaller field of ![]() 0.25 deg2 =
0.25 deg2 =
![]()
![]()
![]() (Bellanger et al. 1995). The
(Bellanger et al. 1995). The
![]() sample has a 92%
redshift completeness and its median redshift and effective depth are
sample has a 92%
redshift completeness and its median redshift and effective depth are
![]() 0.3 and
0.3 and ![]() 0.5, respectively. Additional redshifts for
0.5, respectively. Additional redshifts for
![]() 250 galaxies with
250 galaxies with
![]() were also
measured in the same area, leading to a 52% redshift completeness to
this fainter limit (see de Lapparent et al. 2003 for details).
were also
measured in the same area, leading to a 52% redshift completeness to
this fainter limit (see de Lapparent et al. 2003 for details).
The ESS spectroscopic catalogue was also used to perform a
template-free spectral classification based on a principal component
analysis of the flux-calibrated spectra, which yields a well-defined
sequence parameterized continuously using 2 indices denoted ![]() and
and ![]() (Galaz & de Lapparent 1998; de Lapparent et al. 2003):
(Galaz & de Lapparent 1998; de Lapparent et al. 2003): ![]() measures the shape
of the continuum, hence the relative contribution from red and blue
stellar populations, whereas the departures of
measures the shape
of the continuum, hence the relative contribution from red and blue
stellar populations, whereas the departures of ![]() from the
sequence measure the strength of the nebular emission lines, hence the
current star formation rate. Comparison with the Kennicutt templates
(Kennicutt 1992) shows that the
from the
sequence measure the strength of the nebular emission lines, hence the
current star formation rate. Comparison with the Kennicutt templates
(Kennicutt 1992) shows that the
![]() sequence is
strongly related to the Hubble morphological type (see
also Bromley et al. 1998; Folkes et al. 1996; Baldi et al. 2001), and provides a better estimate of
the galaxy Hubble type than any color information (as used for
example in Lin et al. 1999; Lilly et al. 1995).
sequence is
strongly related to the Hubble morphological type (see
also Bromley et al. 1998; Folkes et al. 1996; Baldi et al. 2001), and provides a better estimate of
the galaxy Hubble type than any color information (as used for
example in Lin et al. 1999; Lilly et al. 1995).
The ESS catalogue is also complemented by precise type-dependent
K-corrections derived from the joint use of the spectral
classification and the PEGASE spectrophotometric models
(Fioc & Rocca-Volmerange 1997). These in turn yield absolute magnitudes in the
rest-frame filter bands (Johnson-Cousins
![]() ), from which
de Lapparent et al. (2003) have derived detailed luminosity functions as a
function of spectral type. Here, we make use of these various
parameters and characteristics of the ESS survey, to measure the
two-point correlation functions.
), from which
de Lapparent et al. (2003) have derived detailed luminosity functions as a
function of spectral type. Here, we make use of these various
parameters and characteristics of the ESS survey, to measure the
two-point correlation functions.
The ESS spectroscopic sample was selected in ![]() magnitude,
and is thus most complete in this band, whereas the V and B samples suffer color-related selection effects at faint magnitudes
(see de Lapparent et al. 2003). The present analysis is therefore based on
the
magnitude,
and is thus most complete in this band, whereas the V and B samples suffer color-related selection effects at faint magnitudes
(see de Lapparent et al. 2003). The present analysis is therefore based on
the
![]() redshift sample, and all the quoted absolute
magnitudes are in this band. In order to use only galaxies with a
redshift value unaffected by peculiar motions within the local group,
we omit in all samples the few ESS galaxies with
redshift sample, and all the quoted absolute
magnitudes are in this band. In order to use only galaxies with a
redshift value unaffected by peculiar motions within the local group,
we omit in all samples the few ESS galaxies with ![]() .
We also
reject distant galaxies with
.
We also
reject distant galaxies with ![]() :
at these redshifts, the
selection function becomes of the order of 10% and decreases
steeply, which causes a very sparse sampling of the large-scale
structures. The bounding redshifts 0.1 and 0.51 correspond to
comoving distances
:
at these redshifts, the
selection function becomes of the order of 10% and decreases
steeply, which causes a very sparse sampling of the large-scale
structures. The bounding redshifts 0.1 and 0.51 correspond to
comoving distances
To examine the varying clustering properties of the ESS with galaxy
type, we define various sub-samples by galaxy type and absolute
luminosity. We first consider the 3 spectral classes defined by
de Lapparent et al. (2003): early-type with
![]() ,
intermediate-type
with
,
intermediate-type
with
![]() ,
and late-type with
,
and late-type with ![]() .
As shown in
de Lapparent et al. (2003), projection of the Kennicutt (1992) templates
onto the ESS classification space indicates that these 3 classes
approximately correspond to the following mixes of giant morphological
types: E + S0 + Sa in the early class; Sb + Sc in the
intermediate class; and Sc + Sd/Sm in the late class.
.
As shown in
de Lapparent et al. (2003), projection of the Kennicutt (1992) templates
onto the ESS classification space indicates that these 3 classes
approximately correspond to the following mixes of giant morphological
types: E + S0 + Sa in the early class; Sb + Sc in the
intermediate class; and Sc + Sd/Sm in the late class.
|
Furthermore, the analysis of the ESS luminosity functions suggests that the ESS intermediate-type and late-type classes also contain dwarf morphological populations (de Lapparent et al. 2003): (1) gas-poor dwarf galaxies which are classified as intermediate spectral type due to their intermediate color, and most likely include dwarf elliptical (dE) and dwarf lenticular (dS0) galaxies, together with their nucleated analogs (Grant et al. 2005); here, these objects are altogether denoted dE; (2) dwarf irregular (dI) galaxies, which are detected in the late spectral class due to their richer gas content, hence blue colors.
In the hierarchical scenario of galaxy formation, variations in the
clustering properties of high mass and low mass galaxies are predicted
(Pearce et al. 2001; Yang et al. 2004), which lead to the expectation of variations
in the clustering properties of giant and dwarf galaxies. To separate
the giant and dwarf galaxy populations which are mixed within the
intermediate-type and late-type ESS spectral classes, we take
advantage of their respective relative contribution at the bright and
faint ends of the corresponding luminosity functions (see Fig. 11 in
de Lapparent et al. 2003; or Fig. 1 of de Lapparent et al. 2004): we apply an
![]() absolute luminosity cut at
absolute luminosity cut at
![]() for
the intermediate-type galaxies, and at
for
the intermediate-type galaxies, and at
![]() for
the late-type galaxies. We then merge the bright, resp. faint,
populations of both spectral classes, to built 2 samples which are
expected to include essentially:
for
the late-type galaxies. We then merge the bright, resp. faint,
populations of both spectral classes, to built 2 samples which are
expected to include essentially:
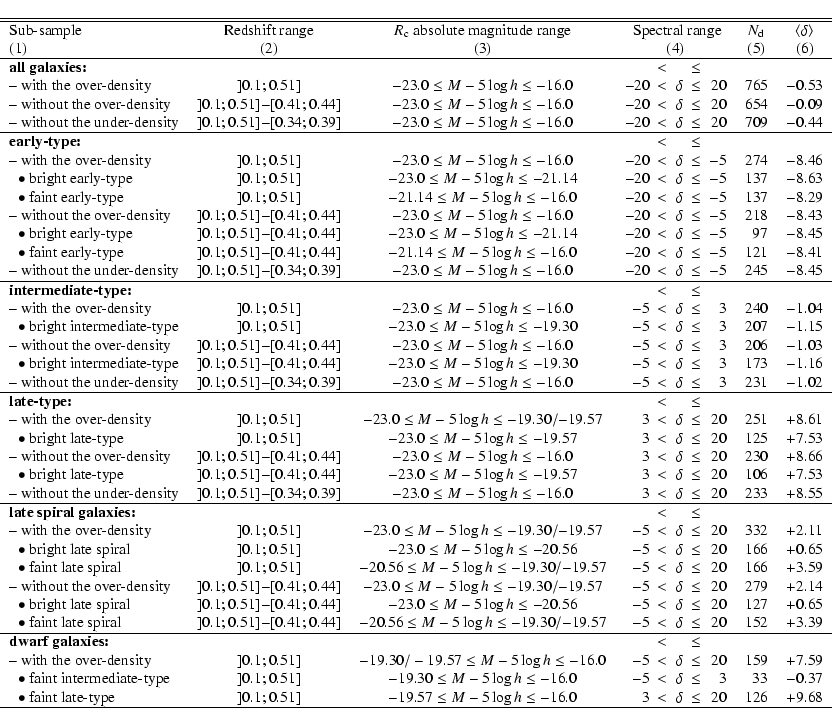
| Luminosity function parameters | Early-type | Intermediate-type | Late -type | |
| Gaussian component: | ||||
| Morphol. content | E + S0 + Sa | Sb + Sc | Sc + Sd/Sm | |
|
|
|
|
|
|
|
|
|
|
||
| 0.00333 | 0.00326 |
|
||
| Schechter component: | ||||
| Morphol. content | dE | dI | ||
|
|
|
|
||
|
|
-0.30 | |||
| 0.00426 |
|
|||

For the luminosity function ![]() ,
we use the composite luminosity
functions proposed by de Lapparent et al. (2003): a two-wing Gaussian
function for the early-type galaxies, and the sum of a Gaussian
function and a Schechter (1976) function for the intermediate-type
and late-type galaxies. These composite fits are motivated by their
better adjustment to the ESS luminosity functions than pure Schechter
functions, and by their good agreement with the luminosity functions
per galaxy type measured locally (Jerjen & Tammann 1997; see
de Lapparent et al. 2003 for details). The composite fits of the ESS luminosity functions also confirm the morphological content of the ESS spectral classes in terms of giant galaxies and dwarf galaxies.
,
we use the composite luminosity
functions proposed by de Lapparent et al. (2003): a two-wing Gaussian
function for the early-type galaxies, and the sum of a Gaussian
function and a Schechter (1976) function for the intermediate-type
and late-type galaxies. These composite fits are motivated by their
better adjustment to the ESS luminosity functions than pure Schechter
functions, and by their good agreement with the luminosity functions
per galaxy type measured locally (Jerjen & Tammann 1997; see
de Lapparent et al. 2003 for details). The composite fits of the ESS luminosity functions also confirm the morphological content of the ESS spectral classes in terms of giant galaxies and dwarf galaxies.
Table 2 lists the various giant and dwarf components of the
luminosity functions for the 3 spectral classes and the corresponding
parameters. The two-wing Gaussian luminosity function for the
early-type galaxies is parameterized as
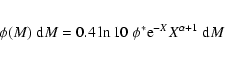
The parameters listed in Table 2 are those derived by
de Lapparent et al. (2004) from the
![]() sample. For the
early-type and intermediate-type classes, the listed values of
sample. For the
early-type and intermediate-type classes, the listed values of
![]() are those listed as
are those listed as
![]() in Table 2 of
de Lapparent et al. (2004), derived using an "equal pair'' weighting for the
mean density estimator (see Eqs. (F.1) and (D.1));
they thus yield a total expected number of galaxies over the redshift
interval
0.1-0.51 for a homogeneous distribution which is equal to
the observed number of galaxies in each spectral class. For the
late-type class, we use (and list here in Table 2) the
parameterization
in Table 2 of
de Lapparent et al. (2004), derived using an "equal pair'' weighting for the
mean density estimator (see Eqs. (F.1) and (D.1));
they thus yield a total expected number of galaxies over the redshift
interval
0.1-0.51 for a homogeneous distribution which is equal to
the observed number of galaxies in each spectral class. For the
late-type class, we use (and list here in Table 2) the
parameterization ![]() provided in Table 2 of
de Lapparent et al. (2004), which reflects the marked evolution of the
amplitudes
provided in Table 2 of
de Lapparent et al. (2004), which reflects the marked evolution of the
amplitudes ![]() and
and ![]() for the ESS late-type galaxies. This
evolution could also be due to pure luminosity evolution, but the
available data do not allow us to discriminate between the 2 effects
(de Lapparent et al. 2004). Whatever the nature of this evolution, the
parameterized amplitude evolution listed in Table 2 does allow
us to estimate the selection function (Appendix C) required for
calculating correlation functions.
for the ESS late-type galaxies. This
evolution could also be due to pure luminosity evolution, but the
available data do not allow us to discriminate between the 2 effects
(de Lapparent et al. 2004). Whatever the nature of this evolution, the
parameterized amplitude evolution listed in Table 2 does allow
us to estimate the selection function (Appendix C) required for
calculating correlation functions.
For the intermediate-type and late-type class, the values of ![]() are derived from the values of
are derived from the values of ![]() using the ratios
using the ratios
| (5) | |||
| (6) |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7150fg01.eps}\end{figure}](/articles/aa/full/2007/34/aa7150-07/Timg95.gif) |
Figure 1: Redshift histograms for the early-type ( top panel), intermediate-type ( middle panel), and late-type ( bottom panel) spectral classes of the ESO-Sculptor survey, using a redshift bin of 0.02. The solid curves show the expected distributions for a homogeneous sample given the luminosity functions defined in Table 2, the magnitude limits and the angular coverage of the survey. |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7150fg02.eps}\end{figure}](/articles/aa/full/2007/34/aa7150-07/Timg96.gif) |
Figure 2: Redshift histograms for the late spiral ( top panel) and dwarf ( bottom panel) sub-samples of the ESO-Sculptor survey (see Fig. 1 for details). |
These various luminosity functions allow us to derive the
corresponding selection functions affecting the ESS sub-samples (see
Sect. C). These yield the expected redshift distribution for
homogeneous samples, which are shown in Figs. 1 and 2 and are compared with the ESS observed distributions
for each spectral class and galaxy type. To calculate the expected
redshift distribution, we also use for each sub-sample the
K-correction function
![]() provided by de Lapparent et al. (2004)
at the mean value of the spectral-type
provided by de Lapparent et al. (2004)
at the mean value of the spectral-type ![]() listed in the
Table 1. Note that comparison of the observed and expected
distributions for the 3 spectral classes shown in Fig. 1
confirms the validity of the luminosity functions and amplitudes
listed in Table 2, and in particular validates the
parameterization of the amplitude evolution for the late-type
galaxies.
listed in the
Table 1. Note that comparison of the observed and expected
distributions for the 3 spectral classes shown in Fig. 1
confirms the validity of the luminosity functions and amplitudes
listed in Table 2, and in particular validates the
parameterization of the amplitude evolution for the late-type
galaxies.
The formalism for derivation of the comoving distances r from the
redshifts, for calculating the three different estimators of the
redshift-space and projected correlation function (Davis-Peebles DP,
Landy-Szalay LS, and Hamilton H), the various selection functions and
the corresponding three weighting schemes (J3, "equal volume'' EV,
and "equal pair'' EP), the normalization, and the mean density are
defined in the Appendix. Because the variance in the estimates of
![]() depends on the chosen statistical weights, it is useful to
apply the three weighting schemes to each of the 3 estimators of the
correlation function, and to cross-check the results; this is done in
the Sect. 4. Here, as a preliminary, we describe and estimate
the various uncertainties at play in the correlation function
measurements.
depends on the chosen statistical weights, it is useful to
apply the three weighting schemes to each of the 3 estimators of the
correlation function, and to cross-check the results; this is done in
the Sect. 4. Here, as a preliminary, we describe and estimate
the various uncertainties at play in the correlation function
measurements.
From the experimental point of view, statistical error bars in
![]() would be best determined from the ensemble error by splitting
the survey into independent regions containing approximately equal
numbers of galaxies and taking the standard deviation of the
correlation function estimates calculated in these
sub-areas. Unfortunately, the size of the ESS redshift sample is too
small to allow for such an approach. Here we consider both the Poisson
error
would be best determined from the ensemble error by splitting
the survey into independent regions containing approximately equal
numbers of galaxies and taking the standard deviation of the
correlation function estimates calculated in these
sub-areas. Unfortunately, the size of the ESS redshift sample is too
small to allow for such an approach. Here we consider both the Poisson
error
A priori, derivation of distances for the ESS galaxies requires to
correct the ESS velocities for the motion within the Local Group
(Courteau & van den Bergh 1999; Yahil et al. 1977), the infall onto Virgo
(Ekholm et al. 2001; Ramella et al. 1997), and the cosmic microwave background dipole
(Smoot et al. 1991). We estimate the impact of these velocity corrections
by calculating the difference in correction value for 4 imaginary
points located at the extreme 4 "corners'' or the ESS survey
region. Each "corner'' point is defined by the constant value of
either one of the 2 coordinates RA (J2000), Dec (J2000) among
The uncertainties in the ESS redshifts (
![]() )
is
also a source of random error in the measurement of the correlation
function. To estimate its impact, we add to all galaxies in the ESS
early-type sub-sample an additional dispersion in the redshift
)
is
also a source of random error in the measurement of the correlation
function. To estimate its impact, we add to all galaxies in the ESS
early-type sub-sample an additional dispersion in the redshift ![]() defined by a Gaussian probability distribution centered at zero and
with an rms deviation
defined by a Gaussian probability distribution centered at zero and
with an rms deviation
![]() .
We repeat this
procedure 30 times, and measure an rms dispersion in
.
We repeat this
procedure 30 times, and measure an rms dispersion in
![]() at scales 1<s<15 h-1 Mpc which is 2 to 3 times
smaller than the bootstrap uncertainty. Similar results are obtained
using the intermediate-type and late-type sub-samples. We thus neglect
this additional source of random error.
at scales 1<s<15 h-1 Mpc which is 2 to 3 times
smaller than the bootstrap uncertainty. Similar results are obtained
using the intermediate-type and late-type sub-samples. We thus neglect
this additional source of random error.
As far as systematic errors are concerned, a dominant contribution to
the correlation function may be the uncertainty in the selection
function (Appendix C), which results from the uncertainties in
the luminosity function. As shown by Peebles (1980), the quadratic
H estimator (Eq. (B.6)) is more affected than the DP and LS estimators (Eqs. (B.5) and (B.7); see Sect. B). For power-law correlation functions (Eq. (D.4)), such biases have more impact on the
correlation length s0 than on the power-law index ![]() .
As
described in Sect. 2.2 and Table 2, five luminosity functions
are involved in the computation according to the considered spectral
class. In principle, any derivation of s0 and
.
As
described in Sect. 2.2 and Table 2, five luminosity functions
are involved in the computation according to the considered spectral
class. In principle, any derivation of s0 and ![]() should be
repeated by varying the selection function parameters along the six
principal axes of its error ellipsoid, and the scatter among the
results added in quadrature to their statistical uncertainties. In
practise, we change the value of M0 for the early-type and
intermediate-type luminosity functions, and the value of the Schechter
slope
should be
repeated by varying the selection function parameters along the six
principal axes of its error ellipsoid, and the scatter among the
results added in quadrature to their statistical uncertainties. In
practise, we change the value of M0 for the early-type and
intermediate-type luminosity functions, and the value of the Schechter
slope ![]() for the intermediate-type and late-type luminosity
functions by plus or minus their rms uncertainty (listed in
Table 2). The resulting systematic shifts in
for the intermediate-type and late-type luminosity
functions by plus or minus their rms uncertainty (listed in
Table 2). The resulting systematic shifts in
![]() for
for
![]() h-1 Mpc are
h-1 Mpc are ![]() 4.2% and
4.2% and
![]() 8.6% when changing M0 for the early-type and
intermediate-type samples resp.; and
8.6% when changing M0 for the early-type and
intermediate-type samples resp.; and
![]() and
and
![]() when changing
when changing ![]() for the intermediate-type
and late-type samples respectively; these various shifts are
for the intermediate-type
and late-type samples respectively; these various shifts are ![]() 4to 10 times smaller than the bootstrap errors for each sample.
4to 10 times smaller than the bootstrap errors for each sample.
Another source of uncertainty is the choice of the parameterization
for J3(s) in the case of a J3 weighting scheme (see
Eq. (D.3)). We estimate this uncertainty by comparing
![]() for the ESS early-type sub-sample with that using
the following J3 weighting parameterization
for the ESS early-type sub-sample with that using
the following J3 weighting parameterization
The correlation function is also affected by a systematic bias called
"cosmic bias'', which is caused by using the observed density of
galaxies in the sample for normalization of the number of pairs (see
Appendix E). This results in an implicit normalization to zero of
the integral of the correlation function over the survey
volume. However, in finite samples, the two-point correlation function
is positive out to scales of ![]() 20 h-1 Mpc, and the mean density of
galaxies estimated from a sample of comparable scale is an
over-estimate of the mean density of the Universe. The corresponding
bias in the correlation function is then expected to be negative. In
that case, the cosmic bias can be corrected for by an additive
correction, called "integral constraint''
(Brainerd et al. 1995; Ratcliffe et al. 1996). In contrast, for sample sizes of
20 h-1 Mpc, and the mean density of
galaxies estimated from a sample of comparable scale is an
over-estimate of the mean density of the Universe. The corresponding
bias in the correlation function is then expected to be negative. In
that case, the cosmic bias can be corrected for by an additive
correction, called "integral constraint''
(Brainerd et al. 1995; Ratcliffe et al. 1996). In contrast, for sample sizes of
![]() 100 h-1 Mpc or larger, the presence of an under-density occupying
a large volume may instead lead to an under-estimation of the mean
density and a corresponding over-estimation of the correlation
function.
100 h-1 Mpc or larger, the presence of an under-density occupying
a large volume may instead lead to an under-estimation of the mean
density and a corresponding over-estimation of the correlation
function.
To estimate the cosmic bias for the ESS, we vary by ![]() 4% (which
corresponds to
4% (which
corresponds to
![]() ,
where N=765 is the number of
galaxies in the full ESS sample, see Table 1) the amplitude
,
where N=765 is the number of
galaxies in the full ESS sample, see Table 1) the amplitude ![]() of the Gaussian component of the early-type,
intermediate-type and late-type luminosity functions, and the
amplitude
of the Gaussian component of the early-type,
intermediate-type and late-type luminosity functions, and the
amplitude ![]() of the Schechter components of the
intermediate-type and late-type luminosity functions (see
Table 2), and calculate the resulting
of the Schechter components of the
intermediate-type and late-type luminosity functions (see
Table 2), and calculate the resulting ![]() for the full ESS
sample. The shift in
for the full ESS
sample. The shift in ![]() for the full ESS sample is
for the full ESS sample is ![]() 4%
for
4%
for
![]() h-1 Mpc, which is 10 times smaller than the bootstrap
error; the shift then increases at larger scales, taking its largest
value at
h-1 Mpc, which is 10 times smaller than the bootstrap
error; the shift then increases at larger scales, taking its largest
value at
![]() h-1 Mpc, as it is comparable to the transverse
extent of the survey.
h-1 Mpc, as it is comparable to the transverse
extent of the survey.
Nevertheless, we show in Sect. 4.2 that a marked over-dense region of the ESS causes a larger systematic shift in the correlation function than the above estimated cosmic bias, and furthermore, this shift is in the opposite direction (an excess correlation). We thus choose to neglect the standard "cosmic bias'', and instead, we evaluate the impact of this over-density onto the various measured correlation functions in Sects. 4.1, 4.2, 4.3, 5.1 and 5.3. In Sect. 5.2, we further discuss the role of this structure in terms of cosmic variance.
Top panel of Fig. 3 shows the 9 combinations of the 3 estimators H, LS and DP (see Sect. B) and the 3 weighting
schemes J3, EV and EP (see Sect. D) applied to the full ESS
sample limited to
![]() ,
,
![]() and
0.10<z<0.51 (765 objects, see Table 1).
Comparison of the various estimators confirms that the J3 weighting
behaves as the EP weighting at small separation s, and as the EV weighting at large s. For a given weighting scheme and at scales
and
0.10<z<0.51 (765 objects, see Table 1).
Comparison of the various estimators confirms that the J3 weighting
behaves as the EP weighting at small separation s, and as the EV weighting at large s. For a given weighting scheme and at scales
![]() h-1 Mpc, the differences between the 3 estimators are
significantly smaller than the error bars in each estimate. The
bootstrap errors for the LS estimate of
h-1 Mpc, the differences between the 3 estimators are
significantly smaller than the error bars in each estimate. The
bootstrap errors for the LS estimate of ![]() are shown in
Fig. 4; the bootstrap errors in the DP and H estimates are
comparable to those in the LS estimate, but have a less stable
behavior with varying separation. For this reason, and because the
J3 weighting is the minimum variance weighting and does not favor
nearby nor distant pairs, we only show and examine in the following
the LS estimate of
are shown in
Fig. 4; the bootstrap errors in the DP and H estimates are
comparable to those in the LS estimate, but have a less stable
behavior with varying separation. For this reason, and because the
J3 weighting is the minimum variance weighting and does not favor
nearby nor distant pairs, we only show and examine in the following
the LS estimate of ![]() with J3 weighting; note, however, that
the results and conclusions of the article are unchanged using the
other estimators and weighting schemes.
with J3 weighting; note, however, that
the results and conclusions of the article are unchanged using the
other estimators and weighting schemes.
The various pairs of objects in top panel of Fig. 3 are
counted in logarithmic bins of equal size with
![]() .
In the following, we adopt this bin size, as it allows one to probe
the small scale regime
.
In the following, we adopt this bin size, as it allows one to probe
the small scale regime ![]() h-1 Mpc. Note that even if
h-1 Mpc. Note that even if ![]() for
the ESS is biased on these scales,
for
the ESS is biased on these scales,
![]() can successfully
be measured down to
can successfully
be measured down to
![]() h-1 Mpc (see Sect. 5). We show in
bottom panel of Fig. 3 that the overall behavior of
h-1 Mpc (see Sect. 5). We show in
bottom panel of Fig. 3 that the overall behavior of ![]() for the ESS is kept unchanged when shifting the bin set by half the
bin size, or when using larger bin sizes with
for the ESS is kept unchanged when shifting the bin set by half the
bin size, or when using larger bin sizes with
![]() and
and
![]() ;
similar conclusions are drawn for the correlation
functions
;
similar conclusions are drawn for the correlation
functions
![]() and
and
![]() considered in
the following sections.
considered in
the following sections.
In Fig. 4, we show the LS estimate of ![]() with J3weighting from the full ESS sample (labeled as "
0.10<z<0.51''),
along with its bootstrap errors; in top panel,
with J3weighting from the full ESS sample (labeled as "
0.10<z<0.51''),
along with its bootstrap errors; in top panel, ![]() is in
logarithmic scale, and in bottom panel, in linear scale. The
redshift-space correlation function has the usual power-law behavior
at small scales, and a smooth roll-off at
is in
logarithmic scale, and in bottom panel, in linear scale. The
redshift-space correlation function has the usual power-law behavior
at small scales, and a smooth roll-off at ![]() h-1 Mpc. The
adjustment of a power-law (see Eq. (D.4)) in the interval
0.5<s< 5.0 h-1 Mpc yields a correlation length and correlation slope
of
h-1 Mpc. The
adjustment of a power-law (see Eq. (D.4)) in the interval
0.5<s< 5.0 h-1 Mpc yields a correlation length and correlation slope
of
Top panel of Fig. 4 shows that at larger scales, ![]() h-1 Mpc,
h-1 Mpc, ![]() breaks down from the power-law fit. Then at
breaks down from the power-law fit. Then at
![]() h-1 Mpc, the amplitude of the correlation function crosses
zero, as seen in bottom panel of Fig. 4.
h-1 Mpc, the amplitude of the correlation function crosses
zero, as seen in bottom panel of Fig. 4. ![]() rises up
again at scales
rises up
again at scales
![]() h-1 Mpc, and another peak occurs at
50<s<60 h-1 Mpc. This large-scale behavior is discussed in the next
sub-sections.
h-1 Mpc, and another peak occurs at
50<s<60 h-1 Mpc. This large-scale behavior is discussed in the next
sub-sections.
Part of the deviations of ![]() from null clustering at
from null clustering at ![]() h-1 Mpc (seen in bottom panel of Fig. 4) appear to be due
to the presence of a marked over-density in the redshift interval
0.41< z<0.44. This structure is clearly seen in the redshift-cones
of the survey shown in Fig. 5. It also appears in the
redshift histograms shown in Fig. 1 as an integrated
excess by nearly a factor 2 over the expected number for a homogeneous
distribution (indicated by the solid lines) for the early-type and
late-type galaxies.
h-1 Mpc (seen in bottom panel of Fig. 4) appear to be due
to the presence of a marked over-density in the redshift interval
0.41< z<0.44. This structure is clearly seen in the redshift-cones
of the survey shown in Fig. 5. It also appears in the
redshift histograms shown in Fig. 1 as an integrated
excess by nearly a factor 2 over the expected number for a homogeneous
distribution (indicated by the solid lines) for the early-type and
late-type galaxies.
The ESS over-dense region at
0.41< z<0.44 has an impact on the
redshift-space correlation function at both intermediate and large
scales. Top panel of Fig. 4 shows that when removing the
over-density, ![]() shifts to lower amplitudes in the interval
shifts to lower amplitudes in the interval
![]() h-1 Mpc, which results in a lower amplitude and steeper
slope for the power-law fit:
h-1 Mpc, which results in a lower amplitude and steeper
slope for the power-law fit:
When the galaxies in the redshift interval
0.41< z<0.44 are removed
from the ESS full sample, the deviations of ![]() from zero at
scales
from zero at
scales
![]() h-1 Mpc (see bottom panel of Fig. 4)
are reduced to less than the bootstrap uncertainty for most points.
In particular, the second peak at 50<s<60 h-1 Mpc becomes
insignificant. The peak at
h-1 Mpc (see bottom panel of Fig. 4)
are reduced to less than the bootstrap uncertainty for most points.
In particular, the second peak at 50<s<60 h-1 Mpc becomes
insignificant. The peak at
![]() h-1 Mpc is also significantly
reduced to a "marginal'' detection, as
h-1 Mpc is also significantly
reduced to a "marginal'' detection, as ![]() deviates by less than
twice the bootstrap error for
deviates by less than
twice the bootstrap error for ![]() h-1 Mpc. One possible
interpretation of the shift towards negative values of
h-1 Mpc. One possible
interpretation of the shift towards negative values of ![]() at
at
![]() h-1 Mpc, when removing the over-density within
0.41< z<0.44,
could be the artificial anti-correlation thus created between this
empty region and the foreground/background walls of galaxies: the
difference in comoving distance between z=0.41 and z=0.44 is
h-1 Mpc, when removing the over-density within
0.41< z<0.44,
could be the artificial anti-correlation thus created between this
empty region and the foreground/background walls of galaxies: the
difference in comoving distance between z=0.41 and z=0.44 is
![]() 72 h-1 Mpc.
72 h-1 Mpc.
When removing a given redshift interval from an ESS sample, the
selection function of each of the 3 spectral-type samples is assigned
to zero in that interval, and no points are generated in that redshift
interval of the random distributions. To check that the procedure does
not introduces any bias, we also calculate ![]() for the full ESS
sample with all galaxies in the redshift interval
0.34< z<0.39removed: this region of the ESS has a similar volume as the region
defined by
0.41< z<0.44, and corresponds to an under-dense region in
the ESS early-type and intermediate-type redshift histograms
(Fig. 1). The resulting
for the full ESS
sample with all galaxies in the redshift interval
0.34< z<0.39removed: this region of the ESS has a similar volume as the region
defined by
0.41< z<0.44, and corresponds to an under-dense region in
the ESS early-type and intermediate-type redshift histograms
(Fig. 1). The resulting ![]() with the
0.34< z<0.39interval removed is over-plotted in both panels of Fig. 4,
and compared to that for the full ESS sample: it shows negligeable
changes at all scales. Although the
0.34< z<0.39 region is
under-dense compared to the rest of the ESS, it has little impact on
the two-point correlation function at all scales.
with the
0.34< z<0.39interval removed is over-plotted in both panels of Fig. 4,
and compared to that for the full ESS sample: it shows negligeable
changes at all scales. Although the
0.34< z<0.39 region is
under-dense compared to the rest of the ESS, it has little impact on
the two-point correlation function at all scales.
The excess in ![]() at
at
![]() h-1 Mpc, seen in bottom panel
of Fig. 4, might also be due in part to the pencil-beam
geometry of the ESS. The large-scale clustering of galaxies is
characterized by walls and filaments which delineate large voids
(Zehavi et al. 2002; Shectman et al. 1996; Small et al. 1997; de Lapparent et al. 1986; Colless et al. 2001). This
results in an alternation of voids and narrow portions of walls or
filaments intercepted at a wide range of angles with the line-of-sight
of the survey, as one then expects few walls, and even fewer
filaments, to be intercepted parallel to the line-of-sight, and thus
to appear as an extended over-density along the line-of-sight (the
over-density at
0.41< z<0.44 may however be one of these rare
occurrences). Then, the particular line-of-sight and limited volume
sampled by the ESS may define a typical scale for the
wall/filament separation, which would appear as excess signal in the
two-point correlation.
h-1 Mpc, seen in bottom panel
of Fig. 4, might also be due in part to the pencil-beam
geometry of the ESS. The large-scale clustering of galaxies is
characterized by walls and filaments which delineate large voids
(Zehavi et al. 2002; Shectman et al. 1996; Small et al. 1997; de Lapparent et al. 1986; Colless et al. 2001). This
results in an alternation of voids and narrow portions of walls or
filaments intercepted at a wide range of angles with the line-of-sight
of the survey, as one then expects few walls, and even fewer
filaments, to be intercepted parallel to the line-of-sight, and thus
to appear as an extended over-density along the line-of-sight (the
over-density at
0.41< z<0.44 may however be one of these rare
occurrences). Then, the particular line-of-sight and limited volume
sampled by the ESS may define a typical scale for the
wall/filament separation, which would appear as excess signal in the
two-point correlation.
A pair separation analysis provides quantitative evidence for the
impact of the ESS pencil-beam geometry onto the detected large-scale
clustering. Top panel of Fig. 6 shows the histogram of the
galaxy pair separations in comoving distance for the ESS full
sample. This distribution exhibits numerous peaks which seem to define
a preferred scale. The bottom panel of Fig. 6 shows the
"periodogram'' obtained by a spectral density analysis of the pair
separation distribution from which the continuum has been subtracted.
A marked peak occurs at 34 h-1 Mpc (
![]() ), which indicates an
increased probability of having pairs of ESS galaxies separated by
this scale. This in turn explains the excess signal in
), which indicates an
increased probability of having pairs of ESS galaxies separated by
this scale. This in turn explains the excess signal in ![]() at
at
![]() h-1 Mpc (bottom panel of Fig. 4). Note that
this scale corresponds to the mean interval picked up by the eye
between adjacent walls/filaments in the cone diagram of the ESS
(Fig. 5): 34 h-1 Mpc corresponds to
h-1 Mpc (bottom panel of Fig. 4). Note that
this scale corresponds to the mean interval picked up by the eye
between adjacent walls/filaments in the cone diagram of the ESS
(Fig. 5): 34 h-1 Mpc corresponds to
![]() at
z=0.3, that is 30% larger than the tick mark separation. When the
over-dense region with
0.41< z<0.44 is removed from the ESS, the
results of the pair separation analysis remain; the peak at 34 h-1 Mpc in the periodogram becomes however weaker, which confirms that the
over-dense region also contributes excess pairs in
at
z=0.3, that is 30% larger than the tick mark separation. When the
over-dense region with
0.41< z<0.44 is removed from the ESS, the
results of the pair separation analysis remain; the peak at 34 h-1 Mpc in the periodogram becomes however weaker, which confirms that the
over-dense region also contributes excess pairs in ![]() at
at
![]() h-1 Mpc.
h-1 Mpc.
We emphasize that the result shown in Fig. 6 is not interpreted as evidence for periodicity in the galaxy distribution (see Yoshida et al. 2001). It is symptomatic of the fact that the ESS does not represent a fair sample of the galaxy distribution, due to its limited volume: as a result, the alternation of voids and walls/filaments along the line-of-sight, and the presence of one over-density parallel to the line-of-sight, both leave an imprint in the correlation function.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7150fg07.eps}\end{figure}](/articles/aa/full/2007/34/aa7150-07/Timg153.gif) |
Figure 7:
The redshift-space correlation function |
Top panel of Fig. 7 shows ![]() for the early-type, late
spiral and dwarf galaxies (see Table 1 for details on each
sub-sample). For comparison, the power-law fit to
for the early-type, late
spiral and dwarf galaxies (see Table 1 for details on each
sub-sample). For comparison, the power-law fit to ![]() for the
full sample is also plotted. This comparison shows that the
correlation functions for the early-type, fitted by
for the
full sample is also plotted. This comparison shows that the
correlation functions for the early-type, fitted by
We emphasize that the different clustering for the late spiral and
dwarf galaxies in Fig. 7 strongly supports the fact that
both galaxy types are physically relevant classes for distinguishing
the different components of the galaxy density field. Note also that
in Fig. 7 and in most of the following graphs, the
mentioned clustering differences among the various sub-samples are
often significant at the ![]() level at most, due to the limited
size of the ESS. We however take them at face value and derive an
interpretation in terms of type segregation in the two-point
clustering.
level at most, due to the limited
size of the ESS. We however take them at face value and derive an
interpretation in terms of type segregation in the two-point
clustering.
The clustering differences among the ESS galaxy types confirm the
visual impression from the ESS redshift cone (Fig. 5): the
early-type galaxies are concentrated within the densest regions,
corresponding to groups of galaxies, whereas the late spiral and dwarf
galaxies also populate the sparser regions of the density field. The
observed behavior of the ![]() for the 3 ESS galaxy types is
related to the type-density relation, originally named
"morphology-density'' relation (Dressler 1980; Postman & Geller 1984). The
elliptical galaxies tend to populate the densest regions of the
Universe, namely clusters and groups of galaxies, and thus tend to
have a stronger two-point correlation function on scales of a few
h-1 Mpc, corresponding to the extent of these concentrations. The
late-type spiral galaxies are much more weakly clustered and populate
the lowest density regions, whereas the early spiral galaxies have an
intermediate behavior.
for the 3 ESS galaxy types is
related to the type-density relation, originally named
"morphology-density'' relation (Dressler 1980; Postman & Geller 1984). The
elliptical galaxies tend to populate the densest regions of the
Universe, namely clusters and groups of galaxies, and thus tend to
have a stronger two-point correlation function on scales of a few
h-1 Mpc, corresponding to the extent of these concentrations. The
late-type spiral galaxies are much more weakly clustered and populate
the lowest density regions, whereas the early spiral galaxies have an
intermediate behavior.
Recently, using the Sloan Digital Sky Survey, Blanton et al. (2005) showed
that it is the present star formation rate which is directly related
to the local density, and the correlation with the morphology is a
consequence of the relationship between the present star formation
rate of a galaxy and its morphology. The ESS spectral classification
has the advantage to be tightly related to the present star formation
rate (Galaz & de Lapparent 1998), and the observed trends of ![]() seen in
Fig. 7 are in agreement with the earlier-type galaxies
residing in higher density environments than the late spiral galaxies.
seen in
Fig. 7 are in agreement with the earlier-type galaxies
residing in higher density environments than the late spiral galaxies.
The correlation function for the dwarf galaxies points to a more
subtle effect, which is detected here for the first time. At the
smallest scales, the amplitude is as high as that for the early-type
galaxies, and it steadily decreases at larger and larger scales: at
![]() h-1 Mpc,
h-1 Mpc, ![]() for the dwarf galaxies is comparable
to that for the late spiral galaxies, and it becomes a factor of
for the dwarf galaxies is comparable
to that for the late spiral galaxies, and it becomes a factor of
![]() 2-10 times lower at
2-10 times lower at
![]() h-1 Mpc. This is consistent
with the dwarf galaxies populating the dense groups (small scale
behavior of
h-1 Mpc. This is consistent
with the dwarf galaxies populating the dense groups (small scale
behavior of ![]() ), whereas on scales of 2-4 h-1 Mpc, they appear
much more weakly clustered than both types of giant galaxies
(early-type and late spiral).
), whereas on scales of 2-4 h-1 Mpc, they appear
much more weakly clustered than both types of giant galaxies
(early-type and late spiral).
Bottom panel of Fig. 7 shows ![]() for the ESS
early-type and late spiral galaxies when excluding all galaxies with
0.41<z<0.44. For the dwarf galaxies, we plot the same curve as in
Fig. 10 as this sample contains only 2 galaxies with z>0.41(see Fig. 2). The power-law fit to
for the ESS
early-type and late spiral galaxies when excluding all galaxies with
0.41<z<0.44. For the dwarf galaxies, we plot the same curve as in
Fig. 10 as this sample contains only 2 galaxies with z>0.41(see Fig. 2). The power-law fit to ![]() for the full
sample without the over-density is also plotted
(Eq. (11)). A power-law model is still a good fit to
both functions. For the early-type class, we measure
for the full
sample without the over-density is also plotted
(Eq. (11)). A power-law model is still a good fit to
both functions. For the early-type class, we measure
The differences in the spatial correlation function between different
galaxy types may actually be larger than those seen in ![]() ,
because of the redshift distortions caused by the galaxy peculiar
velocities (see Appendix G), which tend to erase the type
effects. At small scales (
,
because of the redshift distortions caused by the galaxy peculiar
velocities (see Appendix G), which tend to erase the type
effects. At small scales (![]() h-1 Mpc), the redshift distortions
caused by the random motions in dense regions tend to weaken the
amplitude increase of
h-1 Mpc), the redshift distortions
caused by the random motions in dense regions tend to weaken the
amplitude increase of ![]() for the early-type galaxies with
respect to the other types; although there are no rich clusters of
galaxies in the ESS, the survey contains contains numerous groups of
galaxies (seen as small "fingers-of-god'' in Fig. 5) which
contribute to this effect at small scales. At larger scales
(
for the early-type galaxies with
respect to the other types; although there are no rich clusters of
galaxies in the ESS, the survey contains contains numerous groups of
galaxies (seen as small "fingers-of-god'' in Fig. 5) which
contribute to this effect at small scales. At larger scales
(![]() h-1 Mpc), the coherent bulk flows tend to increase
h-1 Mpc), the coherent bulk flows tend to increase ![]() for
the late spiral galaxies, which dominate in the medium and low density
environments. In order to free the type measurements from the
redshift distortion effect, we calculate in the following sections the
projected spatial correlation function
for
the late spiral galaxies, which dominate in the medium and low density
environments. In order to free the type measurements from the
redshift distortion effect, we calculate in the following sections the
projected spatial correlation function
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7150fg09.eps}\end{figure}](/articles/aa/full/2007/34/aa7150-07/Timg167.gif) |
Figure 9:
Projected correlation function
|
To measure
![]() ,
one must first calculate the correlation
function
,
one must first calculate the correlation
function
![]() as a function of separation parallel
and perpendicular to the line-of-sight (see Appendix G). Figure 8 shows
as a function of separation parallel
and perpendicular to the line-of-sight (see Appendix G). Figure 8 shows
![]() for all ESS galaxies
using the LS estimator (Eq. (B.7)) with the minimum-variance
weights (Eq. (D.3)) and bin widths of 2 h-1 Mpc. The contours of
constant clustering amplitude are drawn as solid
lines. Figure 8 exhibits a stretching along the line-of-sight
(
for all ESS galaxies
using the LS estimator (Eq. (B.7)) with the minimum-variance
weights (Eq. (D.3)) and bin widths of 2 h-1 Mpc. The contours of
constant clustering amplitude are drawn as solid
lines. Figure 8 exhibits a stretching along the line-of-sight
(![]() direction) for separations smaller than 4 h-1 Mpc, caused by the
peculiar velocities within the numerous groups of galaxies present in
the ESS (see Fig. 5). The flattening of the contours of
direction) for separations smaller than 4 h-1 Mpc, caused by the
peculiar velocities within the numerous groups of galaxies present in
the ESS (see Fig. 5). The flattening of the contours of
![]() along the line-of-sight due to the coherent
infall of galaxies onto the over-dense regions, which was first
detected in the 2dFGRS by Hawkins et al. (2003), is hardly seen here, due
to the limited angular extent of the ESS in right ascension, which
subtends
along the line-of-sight due to the coherent
infall of galaxies onto the over-dense regions, which was first
detected in the 2dFGRS by Hawkins et al. (2003), is hardly seen here, due
to the limited angular extent of the ESS in right ascension, which
subtends ![]() 8 h-1 Mpc at
8 h-1 Mpc at ![]() .
.
Because
![]() is a decreasing function of both
is a decreasing function of both
![]() and
and ![]() ,
one can estimate the projected real-space
correlation function
,
one can estimate the projected real-space
correlation function
![]() by an integral over
by an integral over ![]() (see
Eq. (G.2)). In practise, the integral can only be performed to a
finite bound, which needs to be determined. To this end, we have
calculated the various functions
(see
Eq. (G.2)). In practise, the integral can only be performed to a
finite bound, which needs to be determined. To this end, we have
calculated the various functions
![]() with integration
bounds of 6.31 h-1 Mpc, 12.59 h-1 Mpc, 25.12 h-1 Mpc, and 50.12 h-1 Mpc. The
12.59 h-1 Mpc integration bound appears as the smallest bound with
evidence for stabilization, and we thus adopt this value. The chosen
integration bound of 12.59 h-1 Mpc also insures that the random noise
fluctuations visible at larger values of
with integration
bounds of 6.31 h-1 Mpc, 12.59 h-1 Mpc, 25.12 h-1 Mpc, and 50.12 h-1 Mpc. The
12.59 h-1 Mpc integration bound appears as the smallest bound with
evidence for stabilization, and we thus adopt this value. The chosen
integration bound of 12.59 h-1 Mpc also insures that the random noise
fluctuations visible at larger values of ![]() in Fig. 8
are excluded, as we interpret these as symptomatic of the limited
sampling volume of the ESS (see Sect. 4).
in Fig. 8
are excluded, as we interpret these as symptomatic of the limited
sampling volume of the ESS (see Sect. 4).
The resulting projected real-space correlation function
![]() for the full ESS sample is shown in Fig. 9. In the interval
for the full ESS sample is shown in Fig. 9. In the interval
![]() h-1 Mpc,
h-1 Mpc,
![]() is well fitted by a power-law with parameters
is well fitted by a power-law with parameters
We also plot in Fig. 9
![]() for the ESS sample
without the over-density. The resulting correlation function can be
fitted by a power-law over a larger interval of
for the ESS sample
without the over-density. The resulting correlation function can be
fitted by a power-law over a larger interval of ![]() than
for the full ESS sample: for
than
for the full ESS sample: for
![]() h-1 Mpc, we obtain the
following best fit parameters
h-1 Mpc, we obtain the
following best fit parameters
Close examination of Fig. 9 indicates that the over-density
in the
0.41<z<0.44 redshift interval also has a differential effect
on
![]() at both small and large scales, with an excess
clustering at
at both small and large scales, with an excess
clustering at
![]() h-1 Mpc and
h-1 Mpc and
![]() h-1 Mpc compared to the power-law fits. The small
scale 0.2 h-1 Mpc corresponds to the typical virial radius of galaxy
groups (Yang et al. 2005d), suggesting that the over-density may be due to
richer groups than in the rest of the survey. Besides, the
3 h-1 Mpc intermediate scale is close to the minimum separation between
the galaxy groups (Yang et al. 2005c), which suggest that the groups
located within the over-density are more densely clustered than in the
rest of the ESS.
h-1 Mpc compared to the power-law fits. The small
scale 0.2 h-1 Mpc corresponds to the typical virial radius of galaxy
groups (Yang et al. 2005d), suggesting that the over-density may be due to
richer groups than in the rest of the survey. Besides, the
3 h-1 Mpc intermediate scale is close to the minimum separation between
the galaxy groups (Yang et al. 2005c), which suggest that the groups
located within the over-density are more densely clustered than in the
rest of the ESS.
Calculation of
![]() therefore clarifies the nature of the
over-density, and quantifies the visual impression that this redshift
interval contains richer groups and with a higher spatial contrast
than in the rest of the survey (see Fig. 5). This region is
thus clearly peculiar. Because of its large size and strong excess in
clustering, it has a visible impact on the ESS clustering
measurements, which can be interpreted in terms of cosmic variance.
When this structure is excluded, the ESS clustering measurements are
in good agreement with the other measurements from larger redshift
surveys at
therefore clarifies the nature of the
over-density, and quantifies the visual impression that this redshift
interval contains richer groups and with a higher spatial contrast
than in the rest of the survey (see Fig. 5). This region is
thus clearly peculiar. Because of its large size and strong excess in
clustering, it has a visible impact on the ESS clustering
measurements, which can be interpreted in terms of cosmic variance.
When this structure is excluded, the ESS clustering measurements are
in good agreement with the other measurements from larger redshift
surveys at ![]() and
and ![]() (see Sect. 7). Moreover,
there is enough clustering signal in the ESS survey outside the
over-density for allowing us to measure the galaxy correlation
functions. Thanks to a detailed account of the various selection
effects related to the galaxy types and the luminosity functions, the
signal-to-noise in the ESS correlation measurements when excluding the
over-density is only slightly reduced. The gain in revealing the
1-halo and 2-halo components of dark matter halos (see Sect. 6)
largely compensates for this slight loss in signal-to-noise.
(see Sect. 7). Moreover,
there is enough clustering signal in the ESS survey outside the
over-density for allowing us to measure the galaxy correlation
functions. Thanks to a detailed account of the various selection
effects related to the galaxy types and the luminosity functions, the
signal-to-noise in the ESS correlation measurements when excluding the
over-density is only slightly reduced. The gain in revealing the
1-halo and 2-halo components of dark matter halos (see Sect. 6)
largely compensates for this slight loss in signal-to-noise.
In the following, we thus only consider the correlation functions obtained when the over-density at 0.41<z<0.44 is excluded, as these best reflect the typical galaxy clustering.
Figure 10 shows the projected real-space correlation
function
![]() for each of the 3 ESS galaxy types:
early-type, late spiral and dwarf galaxies. The relative behavior of
for each of the 3 ESS galaxy types:
early-type, late spiral and dwarf galaxies. The relative behavior of
![]() for the late spiral galaxies and early-type galaxies
is somewhat similar to that seen in
for the late spiral galaxies and early-type galaxies
is somewhat similar to that seen in ![]() .
The late spiral have a
significantly weaker correlation function than for the early-type
galaxies at small scales (
.
The late spiral have a
significantly weaker correlation function than for the early-type
galaxies at small scales (
![]() h-1 Mpc). Then at larger
scale,
h-1 Mpc). Then at larger
scale,
![]() for the late spiral galaxies has a very
similar behavior to that for the early-type galaxies, with a
comparable slope, and a factor
for the late spiral galaxies has a very
similar behavior to that for the early-type galaxies, with a
comparable slope, and a factor ![]() 1.5-2.0 lower amplitude.
1.5-2.0 lower amplitude.
A remarkable result in Fig. 10 is that for
![]() h-1 Mpc, the correlation function for the dwarf
galaxies is consistent with null clustering within the error
bars. This is best seen in Fig. 11, which shows
h-1 Mpc, the correlation function for the dwarf
galaxies is consistent with null clustering within the error
bars. This is best seen in Fig. 11, which shows
![]() in linear scale for the dwarf galaxies (with the
same color coding as in Fig. 10). Significant clustering
of the dwarf galaxies is only detected for
in linear scale for the dwarf galaxies (with the
same color coding as in Fig. 10). Significant clustering
of the dwarf galaxies is only detected for
![]() h-1 Mpc (with a
h-1 Mpc (with a ![]() significance level).
significance level).
We emphasize the noteworthy differences in the correlation functions
for the three galaxy types in Fig. 10. First, pairs of
early-type galaxies tend to dominate over pairs of both other galaxy
types at all scales (except maybe at
![]() h-1 Mpc), and
the effect is even stronger at small scales,
h-1 Mpc), and
the effect is even stronger at small scales,
![]() h-1 Mpc. Once the early-type galaxies are set aside,
the complementary clustering of the late spiral and dwarf galaxies is
worth attention: dwarf galaxies have a dominating clustering at
h-1 Mpc. Once the early-type galaxies are set aside,
the complementary clustering of the late spiral and dwarf galaxies is
worth attention: dwarf galaxies have a dominating clustering at
![]() h-1 Mpc, and fall-off to null clustering at larger
scales; in contrast, Fig. 11 shows that
h-1 Mpc, and fall-off to null clustering at larger
scales; in contrast, Fig. 11 shows that
![]() for the late spiral galaxies have moderate clustering at
for the late spiral galaxies have moderate clustering at
![]() h-1 Mpc, a factor 2 below the dwarf galaxies;
then
h-1 Mpc, a factor 2 below the dwarf galaxies;
then
![]() is consistent with null clustering at
is consistent with null clustering at
![]() h-1 Mpc, whereas significant signal is detected
at larger scales, from
h-1 Mpc, whereas significant signal is detected
at larger scales, from
![]() h-1 Mpc to
h-1 Mpc to
![]() h-1 Mpc.
h-1 Mpc.
These differences with galaxy types are quantified by the power-law
fits of
![]() .
For the early-type galaxies, we obtain
.
For the early-type galaxies, we obtain
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7150fg10.eps}\end{figure}](/articles/aa/full/2007/34/aa7150-07/Timg190.gif) |
Figure 10:
Projected correlation function
|
Binggeli et al. (1990) showed from a local wide-angle survey of low
surface brightness galaxies that although dwarf galaxies delineate the
same large-scale structures as the giant galaxies, there is a strong
segregation among dwarf galaxies: (1) dE lie preferentially in
concentrations of galaxies, whereas dI are more dispersed; (2) outside
clusters, dE also tend to be satellites of giant galaxies. Indeed,
studies of dense galaxy clusters show extensive populations of red
dwarf or dE galaxies (Andreon & Cuillandre 2002; Trentham 1997). In less dense
environments, one well-studied example being the Local Group, dE galaxies and the even fainter dwarf spheroidal (dSph) galaxies are
preferentially found as satellites of the giant spiral galaxies, with
typical distances ![]() 0.1 h-1 Mpc; in contrast, the dI galaxies are more
sparsely distributed, and in the Local Group, most of them populate
the outskirts at distances of
0.1 h-1 Mpc; in contrast, the dI galaxies are more
sparsely distributed, and in the Local Group, most of them populate
the outskirts at distances of ![]() 0.5 h-1 Mpc (http://www.astro.washington.edu/mayer/LG/LG.html). It is remarkable
that the 2 quoted scales are consistent with the interval over which
the ESS dwarf galaxies show significant clustering. In the picture of
the local Universe, the dE would be responsible for the dwarf
clustering at
0.5 h-1 Mpc (http://www.astro.washington.edu/mayer/LG/LG.html). It is remarkable
that the 2 quoted scales are consistent with the interval over which
the ESS dwarf galaxies show significant clustering. In the picture of
the local Universe, the dE would be responsible for the dwarf
clustering at
![]() h-1 Mpc whereas the dI would
contribute to the signal at
h-1 Mpc whereas the dI would
contribute to the signal at
![]() h-1 Mpc.
h-1 Mpc.
To directly measure how dwarf galaxies cluster around giant galaxies,
we plot in Fig. 12 the cross-correlation
![]() between the dwarf galaxies and either the early-type
galaxies or the late spiral galaxies. As for the auto-correlation
function, we adopt the LS estimator with J3 weighting (see
Appendix B). Strikingly, the cross-correlation functions of
the dwarf galaxies versus both types of giant galaxies show
significant signal, with an amplitude comparable to or intermediate
between the auto-correlation functions of the early-type and late
spiral galaxies at
between the dwarf galaxies and either the early-type
galaxies or the late spiral galaxies. As for the auto-correlation
function, we adopt the LS estimator with J3 weighting (see
Appendix B). Strikingly, the cross-correlation functions of
the dwarf galaxies versus both types of giant galaxies show
significant signal, with an amplitude comparable to or intermediate
between the auto-correlation functions of the early-type and late
spiral galaxies at
![]() h-1 Mpc (also shown in the graph).
h-1 Mpc (also shown in the graph).
First, we have also calculated the dwarf versus giant galaxy cross-correlation functions after excluding the dE galaxies: the resulting curves are identical to those shown in Fig. 12, indicating that both the dE galaxies and the dI galaxies contribute similarly to the cross-correlation signal. The smaller number of dE galaxies in the dwarf sub-sample may nevertheless indicate a weaker correlation for these objects, compared to the dI galaxies.
In Fig. 12, the cross-correlation of the dwarf
versus early-type galaxies has a ![]() 1.5-2 higher amplitude
(
1.5-2 higher amplitude
(![]() effect) than that for the dwarf versus late spiral
galaxies, over the full scale range
effect) than that for the dwarf versus late spiral
galaxies, over the full scale range
![]() h-1 Mpc. Moreover,
both functions have a comparable amplitude as the auto correlation of
the dwarf galaxies at small scales (
h-1 Mpc. Moreover,
both functions have a comparable amplitude as the auto correlation of
the dwarf galaxies at small scales (
![]() h-1 Mpc). At
these scales, the auto-correlation of the early-type galaxies is
stronger by a factor
h-1 Mpc). At
these scales, the auto-correlation of the early-type galaxies is
stronger by a factor ![]() 2 (
2 (![]() effect) than the
dwarf/early-type cross-correlation, and by a factor
effect) than the
dwarf/early-type cross-correlation, and by a factor ![]() 3-4(
3-4(![]() effect) than the dwarf/late spiral cross-correlation. This
indicates that at
effect) than the dwarf/late spiral cross-correlation. This
indicates that at
![]() h-1 Mpc, pairs of early-type
galaxies may dominate over all the other types of pairs, namely
late-spiral/late-spiral, dwarf/dwarf, dwarf/early-type, and
dwarf/late-spiral pairs. It also suggests that the small-scale
clustering of the dwarf galaxies may be due to the combined effects of
them being satellites of early-type galaxies, and of the early-type
galaxy clustering.
h-1 Mpc, pairs of early-type
galaxies may dominate over all the other types of pairs, namely
late-spiral/late-spiral, dwarf/dwarf, dwarf/early-type, and
dwarf/late-spiral pairs. It also suggests that the small-scale
clustering of the dwarf galaxies may be due to the combined effects of
them being satellites of early-type galaxies, and of the early-type
galaxy clustering.
In the intermediate scale range
![]() h-1 Mpc, mixed
pairs of dwarf and giant galaxies appear to contribute equally to the
clustering as pairs of giant galaxies, whereas pairs of dwarf galaxies
are significantly less frequent. At larger scale
(
h-1 Mpc, mixed
pairs of dwarf and giant galaxies appear to contribute equally to the
clustering as pairs of giant galaxies, whereas pairs of dwarf galaxies
are significantly less frequent. At larger scale
(
![]() h-1 Mpc), the cross-correlation signal of dwarf
versus giant galaxies vanishes, indicating that the remaining
clustering signal is fully dominated by pairs of giant galaxies.
h-1 Mpc), the cross-correlation signal of dwarf
versus giant galaxies vanishes, indicating that the remaining
clustering signal is fully dominated by pairs of giant galaxies.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7150fg13.eps}\end{figure}](/articles/aa/full/2007/34/aa7150-07/Timg197.gif) |
Figure 13: The same cross-correlation functions as in Fig. 12, namely the ESO-Sculptor dwarf versus early-type galaxies (filled black circles) and the dwarf versus late spiral galaxies (blue open squares), overlaid with the cross-correlation function of the late spiral versus early-type galaxies (magenta asterisks). The over-density in the interval 0.41<z<0.44 has been removed from the early-type and late spiral samples. |
The significant cross-correlation signal between the dwarf galaxies
and the late spiral galaxies in the full scale range
![]() h-1 Mpc, seen in Fig. 12,
provides direct indication that the dE and dI galaxies are also
clustered in the vicinity of the late spiral galaxies. However, the
different behavior of the auto-correlation functions for the two
galaxy populations, with the dominating clustering of the dwarf
galaxies at
h-1 Mpc, seen in Fig. 12,
provides direct indication that the dE and dI galaxies are also
clustered in the vicinity of the late spiral galaxies. However, the
different behavior of the auto-correlation functions for the two
galaxy populations, with the dominating clustering of the dwarf
galaxies at
![]() h-1 Mpc and that of the late spiral
galaxies at larger scales, may indicates that the two populations have
distinct distributions at these scales.
h-1 Mpc and that of the late spiral
galaxies at larger scales, may indicates that the two populations have
distinct distributions at these scales.
In Fig. 13, we compare the
cross-correlation function of the dwarf versus late spiral galaxies
with the cross-correlation of the late spiral versus early-type
galaxies. We observe that at all scales with
![]() h-1 Mpc,
both functions are indistinguishable
h-1 Mpc,
both functions are indistinguishable![]() , whereas the amplitude of the dwarf versus
early-type cross-correlation function (also plotted in
Fig. 13) is a factor of 1.5-2 higher
(
, whereas the amplitude of the dwarf versus
early-type cross-correlation function (also plotted in
Fig. 13) is a factor of 1.5-2 higher
(![]() effect). This suggests the interesting property that the
clustering of the dwarf galaxies around late spiral galaxies might be
a consequence of how both galaxy types cluster in the environment of
early-type galaxies. This is further developed in the next
sub-section, where we interpret these observed clustering properties
in terms of the occupation of the dark matter halos by the different
galaxy types.
effect). This suggests the interesting property that the
clustering of the dwarf galaxies around late spiral galaxies might be
a consequence of how both galaxy types cluster in the environment of
early-type galaxies. This is further developed in the next
sub-section, where we interpret these observed clustering properties
in terms of the occupation of the dark matter halos by the different
galaxy types.
Based on respectively the 2dF Galaxy Redshift Survey (2dFGRS
hereafter) and the Sloan Digital Sky Survey (SDSS hereafter),
Magliocchetti & Porciani (2003) and Zehavi et al. (2004) showed evidence for a
deviation of the projected correlation function
![]() from
a power-law, with a change of slope at
from
a power-law, with a change of slope at
![]() h-1 Mpc. Both groups of authors interpret this
inflexion point as the transition from the small-scale regime where
pairs of galaxies located within the same dark matter halos dominate
(denoted hereafter "1-halo component''), to the large-scale regime
where pairs of galaxies residing in separate halos overtake the
clustering signal (denoted hereafter "2-halo component''), this
transition occurring near the virial diameter of the halos. This
interpretation is further confirmed by the excellent fit of the
observed deviations of
h-1 Mpc. Both groups of authors interpret this
inflexion point as the transition from the small-scale regime where
pairs of galaxies located within the same dark matter halos dominate
(denoted hereafter "1-halo component''), to the large-scale regime
where pairs of galaxies residing in separate halos overtake the
clustering signal (denoted hereafter "2-halo component''), this
transition occurring near the virial diameter of the halos. This
interpretation is further confirmed by the excellent fit of the
observed deviations of
![]() from a power-law using the
general formalism of the "halo occupation distribution'' (HOD
hereafter; Zehavi et al. 2004; Magliocchetti & Porciani 2003; Zehavi et al. 2005). This
approach has the advantage of providing an analytical description of
the clustering of biased galaxy populations
(Berlind & Weinberg 2002; Benson et al. 2000), and comparison with observations provides
constraints on the HOD parameters.
from a power-law using the
general formalism of the "halo occupation distribution'' (HOD
hereafter; Zehavi et al. 2004; Magliocchetti & Porciani 2003; Zehavi et al. 2005). This
approach has the advantage of providing an analytical description of
the clustering of biased galaxy populations
(Berlind & Weinberg 2002; Benson et al. 2000), and comparison with observations provides
constraints on the HOD parameters.
The projected correlation function
![]() for the full ESS sample without the over-density at
0.41<z<0.44, shown in Fig. 9, displays a similar deviation from a power-law, with
an inflexion point at
for the full ESS sample without the over-density at
0.41<z<0.44, shown in Fig. 9, displays a similar deviation from a power-law, with
an inflexion point at ![]() 1 h-1 Mpc. At scales smaller than the
inflexion point, the correlation function
1 h-1 Mpc. At scales smaller than the
inflexion point, the correlation function
![]() is poorly
fitted by a power-law. This matches the theoretical expectation that
the 1-halo component follows the halo mass function, which flattens
off at small scales (Zehavi et al. 2004; Jenkins et al. 2001). At
is poorly
fitted by a power-law. This matches the theoretical expectation that
the 1-halo component follows the halo mass function, which flattens
off at small scales (Zehavi et al. 2004; Jenkins et al. 2001). At
![]() h-1 Mpc, the 2-halo regime takes over and is
determined by the matter correlation function and the halo bias
(Zehavi et al. 2004). At larger scales, the correlation function is also
expected to deviate from a power-law, but this is not visible in
Fig. 9, due to limited statistics.
h-1 Mpc, the 2-halo regime takes over and is
determined by the matter correlation function and the halo bias
(Zehavi et al. 2004). At larger scales, the correlation function is also
expected to deviate from a power-law, but this is not visible in
Fig. 9, due to limited statistics.
We now turn to the analysis of the ESS correlation functions by galaxy
type, as they provide a new insight into the contribution of the
different galaxy populations to the halo components. Figure 10 shows that for the three ESS galaxy types,
![]() does deviate from a simple power-law fit. For the
early-type galaxies, the 1-halo to 2-halo transition is clearly
detected, and is located at
does deviate from a simple power-law fit. For the
early-type galaxies, the 1-halo to 2-halo transition is clearly
detected, and is located at
![]() h-1 Mpc. Moreover, both
the 1-halo and 2-halo components have the similar non power-law
behavior as that measured from the 2dFGRS early-type galaxies by
Magliocchetti & Porciani (2003); the two components are modelled by a standard
mass profile (Navarro et al. 1997), and a prescription for the two-point
correlation function of dark matter halos respectively. Similar
results and modelling are derived from the SDSS by Zehavi et al. (2005).
h-1 Mpc. Moreover, both
the 1-halo and 2-halo components have the similar non power-law
behavior as that measured from the 2dFGRS early-type galaxies by
Magliocchetti & Porciani (2003); the two components are modelled by a standard
mass profile (Navarro et al. 1997), and a prescription for the two-point
correlation function of dark matter halos respectively. Similar
results and modelling are derived from the SDSS by Zehavi et al. (2005).
Nevertheless, there are indications of differences between the ESS
early-type clustering and those measured locally from the 2dFGRS and
SDSS: an apparently smaller transition scale of
![]() h-1 Mpc, instead of
h-1 Mpc, instead of
![]() h-1 Mpc; and
the fall-off of the ESS large-scale clustering power at
h-1 Mpc; and
the fall-off of the ESS large-scale clustering power at
![]() h-1 Mpc, whereas both the 2dFGRS and SDSS have
significant clustering out to at least
h-1 Mpc, whereas both the 2dFGRS and SDSS have
significant clustering out to at least
![]() h-1 Mpc.
The cut-off at
h-1 Mpc.
The cut-off at
![]() h-1 Mpc for all the ESS auto and
cross-correlation functions is likely due to the limited angular
extent of the survey: its angular size is
h-1 Mpc for all the ESS auto and
cross-correlation functions is likely due to the limited angular
extent of the survey: its angular size is ![]()
![]() ,
which
subtends
,
which
subtends
![]() h-1 Mpc at the median redshift of the
survey (z=0.3); as a result, any existing correlation signal beyond
h-1 Mpc at the median redshift of the
survey (z=0.3); as a result, any existing correlation signal beyond
![]() 10 h-1 Mpc cannot be detected in
10 h-1 Mpc cannot be detected in
![]() .
In contrast,
the smaller transition scale in the ESS may be real and could be due
to evolution effects related to the higher redshift range of the ESS
(
.
In contrast,
the smaller transition scale in the ESS may be real and could be due
to evolution effects related to the higher redshift range of the ESS
(
![]() )
compared to
)
compared to ![]() for the 2dFGRS and SDSS.
for the 2dFGRS and SDSS.
Figure 10 shows that the higher amplitude and slope of the
ESS early-type auto-correlation compared to that for the late spiral
galaxies can be decomposed into a 50% higher amplitude but similar
slope for the 2-halo component, and a factor ![]() 2-4 higher
amplitude and significantly flatter slope for the 1-halo component.
This is in good agreement with the results obtained by
Magliocchetti & Porciani (2003) and Zehavi et al. (2005) from the 2dFGRS and SDSS
respectively. These authors successfully model the clustering of both
galaxy types (early/red, late/blue) using the HOD prescription, which
confirms that both galaxy types follow the dark matter distribution
within the halos.
2-4 higher
amplitude and significantly flatter slope for the 1-halo component.
This is in good agreement with the results obtained by
Magliocchetti & Porciani (2003) and Zehavi et al. (2005) from the 2dFGRS and SDSS
respectively. These authors successfully model the clustering of both
galaxy types (early/red, late/blue) using the HOD prescription, which
confirms that both galaxy types follow the dark matter distribution
within the halos.
One of the major predictions of hierarchical clustering is that the most massive halos have the strongest two-point clustering (Zheng et al. 2002). In this context, the 50% excess amplitude of the early-type auto-correlation function over that for the late spiral galaxies in the 2-halo regime indicates that early-type galaxies tend to reside in more massive halos than the late spiral galaxies. Moreover, the relative behavior in the 1-halo regime shows that the excess of early-type clustering is even stronger within the halos, and increases at higher clustering levels. Given that the clustering is stronger in higher density regions, at all scales from 0.1 to 30 h-1 Mpc (Abbas & Sheth 2006), and that the density increases towards the center of the halos (Navarro et al. 1997), the excess small scale clustering of the ESS early-type galaxies is consistent with them being preferentially located at smaller radii from the halos centers than the late spiral galaxies.
The auto-correlation function of the ESS dwarf galaxies can also be
conveniently interpreted in terms of halo membership. Figure 10 shows a clear 1-halo component which falls off at
![]() h-1 Mpc, thus indicating that the dwarf galaxies are
confined to the densest parts of the halos. This is in agreement with
the fact that these regions are dominated by early-type galaxies, and
that dwarf galaxies are preferentially satellites of early-type
galaxies (see Sect. 5.4). A possible weak 2-halo component
of the dwarf galaxies at
h-1 Mpc, thus indicating that the dwarf galaxies are
confined to the densest parts of the halos. This is in agreement with
the fact that these regions are dominated by early-type galaxies, and
that dwarf galaxies are preferentially satellites of early-type
galaxies (see Sect. 5.4). A possible weak 2-halo component
of the dwarf galaxies at
![]() h-1 Mpc (Fig. 10) could be the replica of the early-type 2-halo
component with the appropriately scaled amplitude.
h-1 Mpc (Fig. 10) could be the replica of the early-type 2-halo
component with the appropriately scaled amplitude.
Information on the degree of mixing of the early-type and late spiral
galaxies within halos can be obtained from their cross-correlation
function. It is displayed in Fig. 14, where it
is compared with the auto-correlation functions
![]() for
both galaxy types. The cross-correlation is close to the mean of the
two auto-correlation functions at all scales but
for
both galaxy types. The cross-correlation is close to the mean of the
two auto-correlation functions at all scales but
![]() h-1 Mpc. In the 2-halo regime, this is naturally expected and
provides no additional information over the auto-correlation functions
(Zehavi et al. 2005). In contrast, in the 1-halo regime, it suggests that
both galaxy types are well mixed within halos at
h-1 Mpc. In the 2-halo regime, this is naturally expected and
provides no additional information over the auto-correlation functions
(Zehavi et al. 2005). In contrast, in the 1-halo regime, it suggests that
both galaxy types are well mixed within halos at
![]() h-1 Mpc, that is that they do not avoid
residing in the same halos. Using the cross-correlation function,
Zehavi et al. (2005) also found a good level of mixing of the red and blue
SDSS galaxies, at all scales of the 1-halo regime.
h-1 Mpc, that is that they do not avoid
residing in the same halos. Using the cross-correlation function,
Zehavi et al. (2005) also found a good level of mixing of the red and blue
SDSS galaxies, at all scales of the 1-halo regime.
Nevertheless, in the ESS analysis presented here, the identical
amplitude of the early-type versus late spiral cross-correlation
function and the late spiral auto-correlation function at
![]() h-1 Mpc, together with a factor
h-1 Mpc, together with a factor ![]() 5 higher amplitude
for the early-type auto-correlation function at this scale indicate a
lack of mixing of the two galaxy types: pairs of early-type galaxies
dominate over pairs of late spiral galaxies and cross-pairs of
early-type and late spiral galaxies. We notice that
5 higher amplitude
for the early-type auto-correlation function at this scale indicate a
lack of mixing of the two galaxy types: pairs of early-type galaxies
dominate over pairs of late spiral galaxies and cross-pairs of
early-type and late spiral galaxies. We notice that
![]() h-1 Mpc is also the smallest detected scale of
correlation signal in the 2dFGRS (Magliocchetti & Porciani 2003) and SDSS
(Zehavi et al. 2005), which have higher statistics than the ESS. This
scale is likely to correspond to the highest density regions, hence to the
very centers of the most massive halos (Navarro et al. 1997). The
cross-correlation functions therefore bring the additional information
that the centers of the most massive halos are dominated by pairs of
early-type galaxies. Conversely, these observations suggest that the
late spiral galaxies tend to lie either in the outer regions of the
densest halos or in the centers of less dense halos.
h-1 Mpc is also the smallest detected scale of
correlation signal in the 2dFGRS (Magliocchetti & Porciani 2003) and SDSS
(Zehavi et al. 2005), which have higher statistics than the ESS. This
scale is likely to correspond to the highest density regions, hence to the
very centers of the most massive halos (Navarro et al. 1997). The
cross-correlation functions therefore bring the additional information
that the centers of the most massive halos are dominated by pairs of
early-type galaxies. Conversely, these observations suggest that the
late spiral galaxies tend to lie either in the outer regions of the
densest halos or in the centers of less dense halos.
These results are consistent with the HOD-based model proposed by
Zehavi et al. (2005), in which blue galaxies are the central galaxies of
the least massive halos, whereas red-type galaxies are the central
galaxies in all other halos, including the most massive. Such a
segregation effect is also detected by Magliocchetti & Porciani (2003), whose
HOD modelling using a common dark matter profile can successfully
predict
![]() for both the early-type and late-type
galaxies, provided that the former populate the halos out to one
virial radius, and the latter are allowed to extend out to twice that
distance. The marked deficit of pairs of ESS late spiral galaxies at
for both the early-type and late-type
galaxies, provided that the former populate the halos out to one
virial radius, and the latter are allowed to extend out to twice that
distance. The marked deficit of pairs of ESS late spiral galaxies at
![]() h-1 Mpc (see Fig. 10) could be
interpreted as further evidence that a significant part of these
objects tend to populate the outer regions of the halos.
h-1 Mpc (see Fig. 10) could be
interpreted as further evidence that a significant part of these
objects tend to populate the outer regions of the halos.
It has been widely observed that intrinsically luminous galaxies
cluster more strongly than faint ones (e.g. Benoist et al. 1996; Zehavi et al. 2002; Guzzo et al. 2000). To examine whether such systematic variations are
present in the ESS, we separate the early-type and late spiral
galaxies into bright and faint sub-samples using the median absolute
magnitude of each sample: -21.14 for the early-type galaxies,
-20.56 for the late spiral galaxies; the corresponding numbers of
galaxies for the sub-samples are listed in Table 1. The
resulting projected auto-correlation functions
![]() for
both the early-type and late spiral sub-samples are displayed in
Fig. 15, using filled, open symbols for the bright
and faint sub-samples respectively.
for
both the early-type and late spiral sub-samples are displayed in
Fig. 15, using filled, open symbols for the bright
and faint sub-samples respectively.
For the early-type galaxies (left panel of Fig. 15),
the correlation function is unchanged when restricting to the bright
sub-sample, except at
![]() h-1 Mpc where the signal
decreases by a factor
h-1 Mpc where the signal
decreases by a factor ![]() 2, and at
2, and at
![]() h-1 Mpc where the signal vanishes. The faint sub-sample has nearly the same
clustering strength as the full early-type sample at
h-1 Mpc where the signal vanishes. The faint sub-sample has nearly the same
clustering strength as the full early-type sample at
![]() h-1 Mpc; then the correlation function decreases to
nearly half that for the bright galaxies at
h-1 Mpc; then the correlation function decreases to
nearly half that for the bright galaxies at
![]() h-1 Mpc, and the power vanishes beyond. Altogether, the
relative behavior of the early-type luminosity sub-samples indicates
that in the 1-halo regime, both sub-samples contribute equally, with
maybe a dominant contribution from the fainter galaxies at the very
small scale
h-1 Mpc, and the power vanishes beyond. Altogether, the
relative behavior of the early-type luminosity sub-samples indicates
that in the 1-halo regime, both sub-samples contribute equally, with
maybe a dominant contribution from the fainter galaxies at the very
small scale
![]() h-1 Mpc. Whereas in the 2-halo
regime, the bright early-type galaxies tend to dominate at
h-1 Mpc. Whereas in the 2-halo
regime, the bright early-type galaxies tend to dominate at
![]() h-1 Mpc. This is in agreement with the results of
Zehavi et al. (2005) that bright red galaxies exhibit the strongest
clustering at large scale, whereas faint red galaxies exhibit the
strongest clustering at small scales. The authors reproduce this
behavior using an HOD model in which nearly all faint red galaxies are
satellite in high mass halos.
h-1 Mpc. This is in agreement with the results of
Zehavi et al. (2005) that bright red galaxies exhibit the strongest
clustering at large scale, whereas faint red galaxies exhibit the
strongest clustering at small scales. The authors reproduce this
behavior using an HOD model in which nearly all faint red galaxies are
satellite in high mass halos.
When compared to the early-type galaxies, the relative clustering of
the faint and bright late spiral galaxies (right panel of
Fig. 15) shows a somewhat similar behavior at large
scales, and a difference at small scales. Indeed, the 2-halo component
of the bright late spiral sub-sample is consistent with a factor
![]() 2-5 (
2-5 (![]() deviation) stronger clustering than for the faint
sub-sample. In contrast to the early-type galaxies, the 1-halo
component of the bright late spiral sub-sample tends to have stronger
clustering than for the faint sub-sample. This is again in agreement
with the steadily decreasing amplitude of
deviation) stronger clustering than for the faint
sub-sample. In contrast to the early-type galaxies, the 1-halo
component of the bright late spiral sub-sample tends to have stronger
clustering than for the faint sub-sample. This is again in agreement
with the steadily decreasing amplitude of
![]() for the
faint blue SDSS galaxies. At variance with the early-type galaxies,
there is no indication of excess clustering of the faint late spiral
galaxies at
for the
faint blue SDSS galaxies. At variance with the early-type galaxies,
there is no indication of excess clustering of the faint late spiral
galaxies at
![]() h-1 Mpc; on the contrary, they might
be less clustered than their bright analogs.
h-1 Mpc; on the contrary, they might
be less clustered than their bright analogs.
Yet another prediction of hierarchical clustering is that luminous
galaxies are expected to be preferentially located within massive
halos, which in turn are more strongly clustered. Here again,
although the clustering deviations in the luminosity sub-samples of
the early-type and late spiral galaxies are only significant at the
2![]() level at most, we take them at face value and derive an
interpretation in terms of dark matter halo membership. The excess
clustering in the 2-halo regime of the ESS bright sub-samples over the
faint sub-samples, which is detected for both the early-type and late
spiral galaxies in Fig. 15, is consistent with this
expected property of hierarchical clustering.
level at most, we take them at face value and derive an
interpretation in terms of dark matter halo membership. The excess
clustering in the 2-halo regime of the ESS bright sub-samples over the
faint sub-samples, which is detected for both the early-type and late
spiral galaxies in Fig. 15, is consistent with this
expected property of hierarchical clustering.
In contrast, the difference in the relative behavior of the 1-halo components for the early-type and late spiral galaxies suggests that the two galaxy types trace the dark matter profiles of the halo in a different way. In the previous section, we suggested that early-type galaxies tend to occupy the centers of the most massive halos, and that late spiral galaxies tend to lie either in the centers of less dense halos and/or in the outer regions of the densest halos. The additional information brought here is that this is nearly independent of luminosity for the early-type galaxies, whereas faint late spiral galaxies might tend to reside in even less dense regions than their bright analogs. This implies a specific spatial segregation of the early-type and late spiral galaxies inside the dark matter halos.
| Survey | Redshift range | Absolute magnitude range | Numb. | r0 ( h-1 Mpc) | Reference | |
| Galaxy type | ||||||
| ESS |
|
|
654 |
|
|
present analysis |
| VVDS |
|
|
1089 |
|
|
Pollo et al. (2006) |
| SDSS |
|
8730 |
|
|
Zehavi et al. (2005) | |
| SDSS |
|
23 560 |
|
|
id. | |
| 2dFGRS |
|
165 659 |
|
|
id. | |
| ESS: | ||||||
| - early-type galaxies |
|
|
218 |
|
|
present analysis |
| - late spiral galaxies |
|
|
279 |
|
|
id. |
| - dwarf galaxies |
|
|
159 |
|
|
id. |
| VVDS: | ||||||
| - elliptical/S0 galaxies |
|
|
164 |
|
Meneux et al. (2006) | |
| - Sb-Sc galaxies |
|
|
736 |
|
id. | |
| - Magellanic irregulars |
|
|
507 |
|
id. | |
| 2dFGRS: | ||||||
| - passive galaxies |
|
36 318 |
|
|
Madgwick et al. (2003) | |
| - active galaxies |
|
60 473 |
|
|
id. | |
| SDSS: | ||||||
| - red galaxies |
|
|
5804 |
|
|
Zehavi et al. (2005) |
| - blue galaxies |
|
|
8419 |
|
|
id. |
| SDSS: | ||||||
| - red |
|
343 |
|
|
Budavári et al. (2003) | |
| - blue |
|
316 |
|
|
id. |
|
Notes:
|
Before the establishment of the currently standard cosmology
![]() and
and
![]() (Riess et al. 1998; Phillips et al. 2001; Tonry et al. 2003; Perlmutter et al. 1999), various surveys have
obtained measures of the galaxy two-point correlation function in
redshift space and/or projected separation assuming either a low or
high matter density Universe and a null cosmological constant (at
(Riess et al. 1998; Phillips et al. 2001; Tonry et al. 2003; Perlmutter et al. 1999), various surveys have
obtained measures of the galaxy two-point correlation function in
redshift space and/or projected separation assuming either a low or
high matter density Universe and a null cosmological constant (at
![]() :
Shepherd et al. 2001; Hogg et al. 2000; Carlberg et al. 2000; Small et al. 1999; Cole et al. 1994; Le Fevre et al. 1996; Guzzo et al. 2000;
at
:
Shepherd et al. 2001; Hogg et al. 2000; Carlberg et al. 2000; Small et al. 1999; Cole et al. 1994; Le Fevre et al. 1996; Guzzo et al. 2000;
at ![]() :
Baugh 1996; Ratcliffe et al. 1998b; Tucker et al. 1997; Park et al. 1994; Loveday et al. 1992; Giuricin et al. 2001).
To compare our results with those from the other surveys, we
thus consider only the more recent measurements, which use the new
standard cosmological parameters.
:
Baugh 1996; Ratcliffe et al. 1998b; Tucker et al. 1997; Park et al. 1994; Loveday et al. 1992; Giuricin et al. 2001).
To compare our results with those from the other surveys, we
thus consider only the more recent measurements, which use the new
standard cosmological parameters.
We specifically focus on the projected-separation correlation function
![]() and list in Table 3 its amplitude and slope
obtained for the full ESS sample without the over-density in the
redshift interval
and list in Table 3 its amplitude and slope
obtained for the full ESS sample without the over-density in the
redshift interval
![]() .
For comparison, we list the
measurements from the SDSS, the 2dFGRS, and the VIMOS-VLT Deep Survey
(VVDS). The ESS values are in good agreement with those obtained from
the VVDS (Pollo et al. 2006) in a similar redshift interval. The
comparatively higher ESS amplitude r0= 5.25
.
For comparison, we list the
measurements from the SDSS, the 2dFGRS, and the VIMOS-VLT Deep Survey
(VVDS). The ESS values are in good agreement with those obtained from
the VVDS (Pollo et al. 2006) in a similar redshift interval. The
comparatively higher ESS amplitude r0= 5.25 ![]() 1.82 h-1 Mpc, derived
when the over-density at
1.82 h-1 Mpc, derived
when the over-density at
![]() is included, strengthens
our conclusion that this structure is a peculiar region of the survey.
is included, strengthens
our conclusion that this structure is a peculiar region of the survey.
The parameters of
![]() derived from the ESS are also
consistent with those obtained from the 8 730 SDSS galaxies with
derived from the ESS are also
consistent with those obtained from the 8 730 SDSS galaxies with
![]() (Zehavi et al. 2005). Our value of r0 is nevertheless
below that obtained from 23 560 SDSS galaxies with
(Zehavi et al. 2005). Our value of r0 is nevertheless
below that obtained from 23 560 SDSS galaxies with
![]() (Zehavi et al. 2005), and that from 165 659 2dFGRS galaxies (for
supposedly
(Zehavi et al. 2005), and that from 165 659 2dFGRS galaxies (for
supposedly
![]() ,
Hawkins et al. 2003). In a
,
Hawkins et al. 2003). In a ![]() CDM
universe undergoing hierarchical clustering, an evolution in r0 is
expected between redshifts 0 and 0.5, specifically a decrease by
CDM
universe undergoing hierarchical clustering, an evolution in r0 is
expected between redshifts 0 and 0.5, specifically a decrease by
![]() 0.5 h-1 Mpc (Kauffmann et al. 1999b; Benson et al. 2001). Although such a
variation is compatible with the comparison of the ESS and the local
SDSS and 2dFGRS correlation measurements, the wide error bars of the
ESS correlation function do not allow us to draw any firm conclusion
on the evolution in r0.
0.5 h-1 Mpc (Kauffmann et al. 1999b; Benson et al. 2001). Although such a
variation is compatible with the comparison of the ESS and the local
SDSS and 2dFGRS correlation measurements, the wide error bars of the
ESS correlation function do not allow us to draw any firm conclusion
on the evolution in r0.
The second part of Table 3 lists the parameters of the
power-law fits to
![]() for the same surveys as quoted in
the top of the Table, split by galaxy type. For the VVDS, we list the
measurements for the elliptical/S0 (type 1), Sb-Sc spiral (type 2) and
Magellanic irregular galaxies (type 4) (Meneux et al. 2006); note that we
do not consider the correlation function for galaxy types Sc-Sd (type 3) measured by Meneux et al. (2006), because the results are nearly
identical to those for types Sb-Sc; moreover, among the ESS late
spiral galaxies, intermediate-type galaxies which correspond to Sb-Sc type dominate in number over later type galaxies (see
Table 1). Both the ESS early-type and VVDS elliptical/S0 on the one
hand, and the ESS late spiral and the VVDS Sb-Sc galaxies on the other
hand, have values of the amplitude r0 and the slope
for the same surveys as quoted in
the top of the Table, split by galaxy type. For the VVDS, we list the
measurements for the elliptical/S0 (type 1), Sb-Sc spiral (type 2) and
Magellanic irregular galaxies (type 4) (Meneux et al. 2006); note that we
do not consider the correlation function for galaxy types Sc-Sd (type 3) measured by Meneux et al. (2006), because the results are nearly
identical to those for types Sb-Sc; moreover, among the ESS late
spiral galaxies, intermediate-type galaxies which correspond to Sb-Sc type dominate in number over later type galaxies (see
Table 1). Both the ESS early-type and VVDS elliptical/S0 on the one
hand, and the ESS late spiral and the VVDS Sb-Sc galaxies on the other
hand, have values of the amplitude r0 and the slope ![]() which
are in 1
which
are in 1![]() agreement. The amplitude for the ESS dwarf galaxies
and the VVDS Magellanic irregulars are also in good agreement, whereas
the slope is significantly steeper in the ESS. The slope of
agreement. The amplitude for the ESS dwarf galaxies
and the VVDS Magellanic irregulars are also in good agreement, whereas
the slope is significantly steeper in the ESS. The slope of
![]() for the ESS dwarf galaxies could be even steeper as
the signal at
for the ESS dwarf galaxies could be even steeper as
the signal at
![]() h-1 Mpc may not be real in this
population (see Fig. 10).
h-1 Mpc may not be real in this
population (see Fig. 10).
At the smaller redshifts covered by the SDSS and 2dFGRS, the correlation function for the red galaxies has a higher amplitude and steeper slope than for the blue galaxies (Zehavi et al. 2005; Madgwick et al. 2003), indicating similar segregation effects as in the ESS. This type effect was also detected from the SDSS angular correlation function (Budavári et al. 2003), with good agreement in the power-law parameters. Note however that the correlation functions by galaxy type for the SDSS and 2dFGRS have higher amplitudes than for the ESS and VVDS, which may also be the trace of clustering evolution.
We calculate the two-point correlation function for the ESO-Sculptor
redshift survey. The sample is limited to the 765 galaxies with
![]() in the redshift interval
in the redshift interval
![]() .
We
use on the one hand the template free spectral classification of the
sample into early, intermediate, and late-type galaxies, which
correspond to the following mixes of morphological type: E + S0 + Sa,
Sb + Sc, and Sc + Sd/Sm, respectively (Galaz & de Lapparent 1998); and on the
other hand the results of the ESS luminosity function analysis, which
indicates that the three ESS spectral classes contain two additional
components, dwarf elliptical and dwarf irregular galaxies, mixed into
the intermediate and late-type classes respectively
(de Lapparent et al. 2003). This leads us to separate the intermediate-type
and late-type spectral classes into their giant and dwarf galaxy
components, which we merge into two classes dominated by late spiral
(Sb + Sc + Sd/Sm), and dwarf (dE + dI) galaxies respectively. The
resulting three galaxy classes (early-type, late spiral, dwarf
galaxies) are therefore defined by spectral/morphological and
luminosity criteria, which are both relevant for studying segregation
effect in galaxy clustering. We use the corresponding Schechter and
Gaussian luminosity functions for defining the selection function for
each of the three galaxy types.
.
We
use on the one hand the template free spectral classification of the
sample into early, intermediate, and late-type galaxies, which
correspond to the following mixes of morphological type: E + S0 + Sa,
Sb + Sc, and Sc + Sd/Sm, respectively (Galaz & de Lapparent 1998); and on the
other hand the results of the ESS luminosity function analysis, which
indicates that the three ESS spectral classes contain two additional
components, dwarf elliptical and dwarf irregular galaxies, mixed into
the intermediate and late-type classes respectively
(de Lapparent et al. 2003). This leads us to separate the intermediate-type
and late-type spectral classes into their giant and dwarf galaxy
components, which we merge into two classes dominated by late spiral
(Sb + Sc + Sd/Sm), and dwarf (dE + dI) galaxies respectively. The
resulting three galaxy classes (early-type, late spiral, dwarf
galaxies) are therefore defined by spectral/morphological and
luminosity criteria, which are both relevant for studying segregation
effect in galaxy clustering. We use the corresponding Schechter and
Gaussian luminosity functions for defining the selection function for
each of the three galaxy types.
We test the various estimators of the correlation function, and adopt
the Landy & Szalay (1993) estimator with J3 weighting, which combines
stability and minimum variance. The redshift-space correlation
function ![]() can be fitted by a power-law with amplitude
s0=7.49
can be fitted by a power-law with amplitude
s0=7.49 ![]() 3.18 h-1 Mpc and slope
3.18 h-1 Mpc and slope
![]()
![]() 0.13 in the
interval 0.5<s< 5 h-1 Mpc. At larger scales,
0.13 in the
interval 0.5<s< 5 h-1 Mpc. At larger scales, ![]() oscillates
between negative and positive low amplitude values, with a peak at
oscillates
between negative and positive low amplitude values, with a peak at
![]() 35 h-1 Mpc and its multiples. This is due to the combination of
the pencil-beam geometry of the ESS survey with the alternation of
walls and voids, as demonstrated by a pair separation analysis. The
ESS also contains an over-dense region located in the redshift
interval
0.41< z<0.44, which affects the correlation function by
adding excess large-scale power in
35 h-1 Mpc and its multiples. This is due to the combination of
the pencil-beam geometry of the ESS survey with the alternation of
walls and voids, as demonstrated by a pair separation analysis. The
ESS also contains an over-dense region located in the redshift
interval
0.41< z<0.44, which affects the correlation function by
adding excess large-scale power in ![]() .
When removing this
region, the power-law fit to
.
When removing this
region, the power-law fit to ![]() yields s0=4.22
yields s0=4.22 ![]() 1.15 h-1 Mpc and
1.15 h-1 Mpc and
![]()
![]() 0.15 (in
0.15 (in
![]() h-1 Mpc), in better
agreement with the other existing surveys.
h-1 Mpc), in better
agreement with the other existing surveys.
We then calculate the redshift-space correlation function ![]() for
the three galaxy types. These show marked differences, with a dominant
signal originating from the early-type galaxies at nearly all scales.
The late spiral galaxies show a weaker correlation amplitude at small
and large scales, in agreement with the type-density relationship
(Blanton et al. 2005). The new result is that the dwarf galaxies show a
very steep correlation function over a narrow range of scales:
for
the three galaxy types. These show marked differences, with a dominant
signal originating from the early-type galaxies at nearly all scales.
The late spiral galaxies show a weaker correlation amplitude at small
and large scales, in agreement with the type-density relationship
(Blanton et al. 2005). The new result is that the dwarf galaxies show a
very steep correlation function over a narrow range of scales: ![]() decreases from the clustering amplitude of the early-type galaxies at
very small scale, to more than one order of magnitude weaker at
decreases from the clustering amplitude of the early-type galaxies at
very small scale, to more than one order of magnitude weaker at
![]() h-1 Mpc. These segregation effects in the two-point
clustering quantify the visual impression drawn from the redshift cone
of the ESS.
h-1 Mpc. These segregation effects in the two-point
clustering quantify the visual impression drawn from the redshift cone
of the ESS.
To free the correlation function measurements from the effect of
peculiar velocities, as they decrease the clustering amplitude at
small scales due to random motions and increase its amplitude at large
scales due to coherent bulk flows, we then calculate the real-space
correlation function as a function of projected separation
![]() .
This is done by integrating the 2-dimensional
correlation function
.
This is done by integrating the 2-dimensional
correlation function
![]() along the line-of-sight
separation
along the line-of-sight
separation ![]() .
The resulting projected-separation correlation
function
.
The resulting projected-separation correlation
function
![]() can be adjusted by a power-law over a larger
range of scales than
can be adjusted by a power-law over a larger
range of scales than ![]() ,
from 0.15 h-1 Mpc to 10 h-1 Mpc. In
this scale range, and after removing the over-density at
0.41<
z<0.44, we obtain a best fit amplitude r0=3.50
,
from 0.15 h-1 Mpc to 10 h-1 Mpc. In
this scale range, and after removing the over-density at
0.41<
z<0.44, we obtain a best fit amplitude r0=3.50 ![]() 1.21 h-1 Mpc and a
slope
1.21 h-1 Mpc and a
slope
![]()
![]() 0.09 which, as expected, is significantly
steeper than that measured from
0.09 which, as expected, is significantly
steeper than that measured from ![]() .
.
When splitting the ESS by galaxy type, the projected-separation
correlation function
![]() shows similarities with
shows similarities with
![]() ,
with again the early-type galaxies dominating over the other
types at all scales. At variance with
,
with again the early-type galaxies dominating over the other
types at all scales. At variance with ![]() ,
the dwarf galaxies
clustering dominates over the late spiral galaxies at
,
the dwarf galaxies
clustering dominates over the late spiral galaxies at
![]() h-1 Mpc. At larger scales, the dwarf galaxies
have a spatial correlation function consistent with null clustering,
whereas the late spiral galaxies take over at
h-1 Mpc. At larger scales, the dwarf galaxies
have a spatial correlation function consistent with null clustering,
whereas the late spiral galaxies take over at
![]() h-1 Mpc, with a similar shape of the correlation
function as for the early-type galaxies and a 50% lower amplitude.
h-1 Mpc, with a similar shape of the correlation
function as for the early-type galaxies and a 50% lower amplitude.
Comparison of ![]() and
and
![]() with and without
inclusion of the over-dense region at
0.41<z<0.44 provides useful
clues on the nature of this region: the excess clustering appears
entirely due to the fact that it contains richer and more densely
clustered groups of galaxies than in the rest of the survey; and both
the early-type and late spiral galaxies contribute to the excess
clustering in the region. We then consider that the correlation
functions for the ESS survey without the over-density are more
representative of the overall galaxy distribution.
with and without
inclusion of the over-dense region at
0.41<z<0.44 provides useful
clues on the nature of this region: the excess clustering appears
entirely due to the fact that it contains richer and more densely
clustered groups of galaxies than in the rest of the survey; and both
the early-type and late spiral galaxies contribute to the excess
clustering in the region. We then consider that the correlation
functions for the ESS survey without the over-density are more
representative of the overall galaxy distribution.
A subsequent analysis of the cross-correlation of the dwarf galaxies
with the early-type and late spiral galaxies provides direct evidence
that the dwarf galaxies are satellites of the giant galaxies. At
![]() h-1 Mpc, pairs of early-type galaxies dominate over
all the other types of pairs. Pairs of dwarf/early-type galaxies,
dwarf galaxies, dwarf/late spiral galaxies, and late spiral galaxies
are the next contributors to the small-scale two-point clustering, in
decreasing order of contribution to the correlation function. In the
intermediate scale range
h-1 Mpc, pairs of early-type galaxies dominate over
all the other types of pairs. Pairs of dwarf/early-type galaxies,
dwarf galaxies, dwarf/late spiral galaxies, and late spiral galaxies
are the next contributors to the small-scale two-point clustering, in
decreasing order of contribution to the correlation function. In the
intermediate scale range
![]() h-1 Mpc, mixed pairs of
dwarf and giant galaxies contribute equally to the clustering as pairs
of giant galaxies. Then at
h-1 Mpc, mixed pairs of
dwarf and giant galaxies contribute equally to the clustering as pairs
of giant galaxies. Then at
![]() h-1 Mpc, the clustering
signal is dominated by pairs of giant galaxies. Moreover, the
cross-correlation analysis indicates that at
h-1 Mpc, the clustering
signal is dominated by pairs of giant galaxies. Moreover, the
cross-correlation analysis indicates that at
![]() h-1 Mpc, that dwarf and late spiral galaxies are
not well mixed at
h-1 Mpc, that dwarf and late spiral galaxies are
not well mixed at
![]() h-1 Mpc. Altogether, this
suggests that the clustering of the dwarf galaxies around late spiral
galaxies at
h-1 Mpc. Altogether, this
suggests that the clustering of the dwarf galaxies around late spiral
galaxies at
![]() h-1 Mpc may be an indirect consequence
of how both galaxy types cluster in the environment of early-type
galaxies.
h-1 Mpc may be an indirect consequence
of how both galaxy types cluster in the environment of early-type
galaxies.
We then interpret the variations in the correlation function with
galaxy type in terms of membership to the underlying dark matter
halos. This approach is eased by the separation into the giant and
dwarf galaxies, as they exhibit a clear dichotomy in their halo
components: the correlation function for the early-type galaxies shows
a dip at
![]() h-1 Mpc, which is interpreted as the
transition between the regimes in which the 1-halo and 2-halo pairs
dominate resp., and both components show a significant contribution;
in contrast, the dwarf and late spiral galaxy correlation functions
are dominated by their 1-halo and 2-halo components, at small and
large scales respectively. Altogether, this indicates that early-type
galaxies tend to lie predominantly at the centers of the massive
halos, whereas late spiral galaxies tend to lie either in the centers
of less dense halos and/or in the outer regions of the densest halos.
The small scale clustering is then not only determined by the dominant
galaxies in the massive halos, but also by their dwarf satellites.
h-1 Mpc, which is interpreted as the
transition between the regimes in which the 1-halo and 2-halo pairs
dominate resp., and both components show a significant contribution;
in contrast, the dwarf and late spiral galaxy correlation functions
are dominated by their 1-halo and 2-halo components, at small and
large scales respectively. Altogether, this indicates that early-type
galaxies tend to lie predominantly at the centers of the massive
halos, whereas late spiral galaxies tend to lie either in the centers
of less dense halos and/or in the outer regions of the densest halos.
The small scale clustering is then not only determined by the dominant
galaxies in the massive halos, but also by their dwarf satellites.
We also examine the two-point clustering for the bright and faint
sub-samples of the early-type and late spiral galaxies. For both the
early-type and late spiral galaxies, we detect a 1![]() excess
clustering in the 2-halo regime of the bright sub-samples over the
faint sub-samples, which is consistent with the expected properties of
hierarchical clustering: the most massive halos have the strongest
2-halo clustering, and luminous galaxies are preferentially located
within massive halos. Comparison of the 1-halo component brings the
additional information that the relationship between halo mass and
giant galaxy type is nearly independent of luminosity for the
early-type galaxies, whereas faint late spiral galaxies might tend to
reside in even less dense regions than their bright analogs.
excess
clustering in the 2-halo regime of the bright sub-samples over the
faint sub-samples, which is consistent with the expected properties of
hierarchical clustering: the most massive halos have the strongest
2-halo clustering, and luminous galaxies are preferentially located
within massive halos. Comparison of the 1-halo component brings the
additional information that the relationship between halo mass and
giant galaxy type is nearly independent of luminosity for the
early-type galaxies, whereas faint late spiral galaxies might tend to
reside in even less dense regions than their bright analogs.
At last, we compare our results with those from the other published
analyses. Our power-law fits to
![]() for the full ESS
sample, and for the sub-samples by galaxy type are consistent with
those measured at comparable and lower redshifts from the other
surveys.
for the full ESS
sample, and for the sub-samples by galaxy type are consistent with
those measured at comparable and lower redshifts from the other
surveys.
One of the major results obtained here from the ESO-Sculptor redshift
survey is that the projected-separation correlation function
![]() for each of the three galaxy types (early-type, late spiral and dwarf galaxies)
presents marked deviations from a power-law, which can be interpreted
as the transition between galaxies belonging to a same dark matter
halo, and galaxies belonging to two different halos. This provides
confirmation that the results obtained at low redshift (
for each of the three galaxy types (early-type, late spiral and dwarf galaxies)
presents marked deviations from a power-law, which can be interpreted
as the transition between galaxies belonging to a same dark matter
halo, and galaxies belonging to two different halos. This provides
confirmation that the results obtained at low redshift (![]() )
by
Zehavi et al. (2005) and Magliocchetti & Porciani (2003) extend to higher redshift
(
)
by
Zehavi et al. (2005) and Magliocchetti & Porciani (2003) extend to higher redshift
(![]() ). A similar result was recently obtained at even higher
redshifts (
). A similar result was recently obtained at even higher
redshifts (![]() )
based on the COMBO17 survey with broad and
medium band photometric redshifts (
)
based on the COMBO17 survey with broad and
medium band photometric redshifts (
![]() ;
Phleps et al. 2006). The ESS brings a useful confirmation based on
spectroscopic redshifts, with
;
Phleps et al. 2006). The ESS brings a useful confirmation based on
spectroscopic redshifts, with
![]() at
at
![]() .
.
In this context, the ESS results provide evidence in favor of the
gravitational instability scenario for the formation of structure, in
which the evolution of galaxy clustering is driven by the hierarchical
merging of halos. Most recently, Conroy et al. (2006) have directly
demonstrated that high-resolution dissipationless ![]() CDM simulations can reproduce the observed bimodal behavior of the
correlation function for absolute magnitude-limited samples at various
redshift limits: these results are entirely based on combining the
spatial clustering of the halos with a prescription that relates the
galaxy luminosities to the maximum circular velocity of the sub-halos
at the time of accretion. The hierarchical merging scenario is
further validated by the detailed shape of the correlation functions
for ESS early-type and late spiral galaxies, which allow a
straightforward identification of the 1-halo and 2-halo components.
CDM simulations can reproduce the observed bimodal behavior of the
correlation function for absolute magnitude-limited samples at various
redshift limits: these results are entirely based on combining the
spatial clustering of the halos with a prescription that relates the
galaxy luminosities to the maximum circular velocity of the sub-halos
at the time of accretion. The hierarchical merging scenario is
further validated by the detailed shape of the correlation functions
for ESS early-type and late spiral galaxies, which allow a
straightforward identification of the 1-halo and 2-halo components.
Direct modelling of the projected-separation correlation function
using the "Halo Occupation Distribution'' (HOD)
(Berlind & Weinberg 2002; Benson et al. 2000), or the more refined "Conditional
Luminosity Function'' approach (which takes into account the
luminosity and colour distribution of galaxies within dark matter
halos of varying mass; Yang et al. 2003), provides constraints on the
halo parameters describing the central and satellite galaxies
parameters
(Abazajian et al. 2005; Magliocchetti & Porciani 2003; Phleps & Meisenheimer 2003; Zehavi et al. 2005; Cooray 2006).
Nevertheless, several measurements of the correlation function at
small scale also challenge the current version of the halo model for
galaxy clustering: the very small scale clustering of luminous red
galaxies from the SDSS is too steep and would require either a steeper
dark halo profile or a galaxy distribution which is steeper than the
dark matter at scales
![]() h-1 Mpc (Masjedi et al. 2006). In contrast, Díaz et al. (2005) obtained projected
density profiles of galaxy groups which are too flat compared to the
standard Navarro et al. (1997) profile.
h-1 Mpc (Masjedi et al. 2006). In contrast, Díaz et al. (2005) obtained projected
density profiles of galaxy groups which are too flat compared to the
standard Navarro et al. (1997) profile.
The second major result obtained from the ESS is the markedly
different clustering properties of the two giant galaxy types,
early-type and late spiral. Both types have comparable 2-halo
components with a 50% higher amplitude for the early-type galaxies,
whereas the 1-halo component of the early-type galaxies largely
dominates over that for the late spiral galaxies. These results are
remarkably similar to the predicted correlation functions calculated
by Kauffmann et al. (1999a) in a ![]() CDM semi-analytical simulation,
which exhibit a higher amplitude and steeper slope for the
early-type/red galaxies, and a lower amplitude and a marked
small-scale flattening at
CDM semi-analytical simulation,
which exhibit a higher amplitude and steeper slope for the
early-type/red galaxies, and a lower amplitude and a marked
small-scale flattening at
![]() h-1 Mpc for the
starforming galaxies.
h-1 Mpc for the
starforming galaxies.
In the framework of hierarchical clustering of the dark matter halos, our results imply a specific spatial segregation of the early-type and late spiral galaxies inside the dark matter halos, with the early-type galaxies residing in the center of the most massive halos, whereas the late spiral reside in their outskirts or in less dense halos. These segregation effects are consistent with the 50% higher pairwise velocity dispersion measured by Madgwick et al. (2003) for the 2dFGRS passive galaxies compared to the starforming galaxies, as it indicates that the passive galaxies inhabit preferentially the cores of high-mass virialized regions.
The link between the ESS type-segregation effects and the dark matter
halos also finds direct confirmation from other recent analyses based
on group catalogs. Zandivarez et al. (2003) and Yang et al. (2005c) show that
the clustering properties of galaxy groups in the 2dFGRS match those
of the dark matter halos in ![]() CDM N-body simulations.
Yang et al. (2005b) thus derive a "halo-based'' group finder algorithm
which is optimized to associate a group to those galaxies which belong
to the same dark matter halo. This allows one to directly examine the
link between galaxies and their dark matter halos. Most interestingly,
Yang et al. (2005c) separate the galaxy correlation function into the
1-group and 2-group components, and thus directly measure the
individual 1-halo and 2-halo components.
CDM N-body simulations.
Yang et al. (2005b) thus derive a "halo-based'' group finder algorithm
which is optimized to associate a group to those galaxies which belong
to the same dark matter halo. This allows one to directly examine the
link between galaxies and their dark matter halos. Most interestingly,
Yang et al. (2005c) separate the galaxy correlation function into the
1-group and 2-group components, and thus directly measure the
individual 1-halo and 2-halo components.
The detected different distribution of ESS early-type and late spiral galaxies inside the dark matter halos raises the issue of whether the effect is due to each population belonging to different types of halos, or whether both galaxy types coexist within the same halos, but with a different spatial distribution. In the former case, the segregation effect would be related to the global halo properties like mass, whereas in the latter case, it would be related to the local properties such as dark matter density. The existence of both a 1-halo and 2-halo components in the cross-correlation function of the two ESS giant galaxy types (see Fig. 14) indicates that both effects may be at play. This is confirmed from the analyses performed with the 2dFGRS group catalogue of Yang et al. (2005b): on the one hand, Yang et al. (2005a) measure that central galaxies in high-mass, low-mass halos are mostly early-type, respectively late-type galaxies; on the other hand, Yang et al. (2005d) obtain direct evidence that early-type galaxies are closer to the luminosity-weighted group center than the late-type galaxies.
Another analysis of the three-dimensional density profiles of the
2dFGRS and SDSS groups found by a "friend-of-friend'' algorithm
indicates a type segregation, namely a decrease of the early-type
galaxy fraction at larger group-centric distance and a corresponding
increase of the late-type fraction (Díaz et al. 2005). At higher
redshifts (
![]() ), Coil et al. (2006) show that red galaxies
are more centrally concentrated than blue galaxies in the galaxy
groups extracted from the DEEP2 survey; this work uses yet another
algorithm for group selection, based on the search for galaxy
over-densities in redshift space which accounts for redshift-space
distortions.
), Coil et al. (2006) show that red galaxies
are more centrally concentrated than blue galaxies in the galaxy
groups extracted from the DEEP2 survey; this work uses yet another
algorithm for group selection, based on the search for galaxy
over-densities in redshift space which accounts for redshift-space
distortions.
These various results find confirmation in the thorough analysis of Weinmann et al. (2006), based on the SDSS "halo-based'' catalogue: the authors show that the fractions of early and late galaxy types not only vary with distance from the halo center, but also with halo mass over the full mass range probed, with more massive halos having higher/lower fractions of early-type/late-type galaxies (Weinmann et al. 2006). Interestingly, Weinmann et al. (2006) find a flat distribution of intermediate-type galaxies as a function of mass and distance to the halo center, with types based on both color and specific star formation rate.
We also note that the detected segregation effects in the distribution of early-type and late-type galaxies within the dark matter halos are consistent with the type/density relationship, namely the trend for early-type galaxies to preferentially inhabit high-density regions. Although dense regions of a survey contain more galaxies that in the other regions, it is not obvious that they undergo stronger clustering. However, Abbas & Sheth (2006) have shown that in high density regions of the SDSS, galaxies are more clustered than in low density regions, and this is valid at all scales from 0.1 to 30 h-1 Mpc. This remarkable property is interpreted by Abbas & Sheth (2006) as providing strong support to the hierarchical models, as it is well reproduced by numerical and analytical models in which the entire effect is due to the correlation of galaxy properties with the mass of the parent halo, and to the fact that more massive halos populate dense regions.
The type-density relationship was clarified by the detailed study of Blanton et al. (2005), who found that color (present star formation rate) and luminosity (hence stellar mass, resulting from the history of past star formation) are the two properties most predictive of local density. Therefore, the detected segregation effects in the clustering of ESS galaxies for different spectral type (early-type versus late spiral) and luminosity (giant versus dwarf) are naturally expected. The uniqueness of the results presented here is that we identify for the first time the joint type/luminosity clustering segregation effect in terms of the very galaxy types which correspond to the locally well known morphological types.
The third major result obtained by the present ESS analysis is the
correlation function for the dwarf galaxies. This function is measured
for the first time, thanks to the separation of the dwarf galaxy
component which the ESS allows, based on the type specific luminosity
functions (de Lapparent et al. 2003). The projected-separation correlation
function of the ESS dwarf galaxies can also be interpreted in terms of
halo membership, as it displays a clear 1-halo component which falls
off at
![]() h-1 Mpc. By their stronger clustering at all
scales, the early-type galaxies appear as a key component of galaxy
clustering. The auto-correlation function of the dwarf galaxies and
their cross-correlation function with the early-type galaxies indicate
that they are the next contributor to galaxy clustering at small
scales. The additional evidence, based on the cross-correlation
analysis, that dwarf and late spiral galaxies are not well
mixed at scales
h-1 Mpc. By their stronger clustering at all
scales, the early-type galaxies appear as a key component of galaxy
clustering. The auto-correlation function of the dwarf galaxies and
their cross-correlation function with the early-type galaxies indicate
that they are the next contributor to galaxy clustering at small
scales. The additional evidence, based on the cross-correlation
analysis, that dwarf and late spiral galaxies are not well
mixed at scales ![]() 0.3 h-1 Mpc leads to a picture in which dwarf
galaxies are confined to the densest, hence central parts of the
halos, and are preferentially satellites of early-type galaxies. This
is in agreement with the observation that in local groups and clusters
of galaxies, the dwarf-to-giant galaxy ratio is an increasing function
of the richness of the galaxy concentration
(Ferguson & Sandage 1991; Trentham & Tully 2002; Trentham & Hodgkin 2002).
0.3 h-1 Mpc leads to a picture in which dwarf
galaxies are confined to the densest, hence central parts of the
halos, and are preferentially satellites of early-type galaxies. This
is in agreement with the observation that in local groups and clusters
of galaxies, the dwarf-to-giant galaxy ratio is an increasing function
of the richness of the galaxy concentration
(Ferguson & Sandage 1991; Trentham & Tully 2002; Trentham & Hodgkin 2002).
Most halo models parameterize the halo content in terms of a dominant galaxy and it satellites (Cooray 2006; Berlind et al. 2003). In their analysis of SDSS data, Zehavi et al. (2005) perform a two-component HOD modelling based on either red and blue central galaxies surrounded by red and blue satellite respectively. However, in the ESS, the dwarf galaxy sample is largely dominated by dwarf irregular hence blue galaxies, and these appear as satellites of the early-type hence red galaxies. Moreover, the late spiral galaxies may play the role of central galaxies in the less massive halos, whereas in the more massive halos, they may be considered as satellite galaxies. Another subtle effect is that detected by Weinmann et al. (2006) in the relative distribution of central and satellite galaxies in halos, which they name "galaxy conformity'': for a halo of a given mass, the early-type fraction of satellites is significantly higher when the central galaxy is early-type rather than late-type. Altogether, these various results indicate that reality may be more complex than the simple two-component HOD models.
To illustrate the variety in galaxy types among a given halo, and their specific spatial distributions, let us consider our local group, which is typical of an intermediate-mass halo. It is dominated by the Milky Way, an Sb galaxy, and Andromeda, an Sab galaxy. In the ESS classification, the Milky Way would be classified as a late spiral, and Andromeda would be at the limit between early-type and late spiral. The third giant, although smaller galaxy, M33, is an Sdm galaxy, and would be classified as a late spiral. The blue Sm/Irr satellites of the Milky Way, the Magellanic Clouds, and the red dE satellites of Andromeda, M32 and M110, would all be classified as dwarf galaxies. There are in addition many dSph and dI galaxies in the local group, distributed at typically 0.05-0.1 h-1 Mpc and 0.5 h-1 Mpc from the giant galaxies (http://www.astro.washington.edu/mayer/LG/LG.html).
The present analysis emphasizes the need for further studies of galaxy clustering as a function of galaxy type. This requires statistical analyses of large galaxy samples effectively containing halos within a large mass range, and a detailed knowledge of their galaxy content as a function of galaxy mass, luminosity and type. The specific clustering of the dwarf galaxies evidenced in the present ESS analysis suggests that probing the dark halo content in terms of the full sequence of giant and dwarf galaxy types would significantly enrich our understanding of galaxy clustering. Higher signal-to-noise measurement of the galaxy correlation functions for the various giant and dwarf galaxy types, and interpretation using the "Halo Occupation Distribution'' or "Conditional Luminosity Function'' would bring new insight into their distribution within the dark matter halos, and the relative role of the central and satellite galaxies in the halos.
The ultimate goal when identifying the different segregation effects which galaxies undergo in a given halo, is to make a link with the past history of star formation and mass accumulation of each system. In such studies, the definition of the galaxy types will be important, and the choice of the classification method will have an decisive impact. The innovative approach of programme EFIGI at IAP (see http://terapix.iap.fr/), aimed at obtaining a quantitative morphological classification (Baillard et al., in preparation), should allow one to reliably classify large samples of galaxies, hence to better understand how each morphological type contributes to galaxy clustering.
Acknowledgements
We thank C. Benoist (OCA), A. Cappi (INAF, Osservatorio Astronomico di Bologna) and S. Maurogordato (OCA/CNRS) for useful discussions about subtleties of the two-point correlation function estimators. We also wish to express our thanks to F. Mignard (OCA/CNRS) who generously supplied the frequency mapping FAMOUS software (ftp://ftp.obs-nice.fr/pub/mignard/Famous) which has been used to produce the periodogram displayed in Fig. 6.
Redshifts z are converted into comoving distances rfrom the observer by using ![]() the dimensionless radial comoving
coordinate of the Robertson-Walker line element (Weinberg 1972):
the dimensionless radial comoving
coordinate of the Robertson-Walker line element (Weinberg 1972):
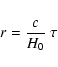
The galaxy-galaxy correlation function in redshift space ![]() is
defined as the probability in excess of a homogeneous Poisson
distribution of finding in any direction two galaxies at distance sfrom each other:
is
defined as the probability in excess of a homogeneous Poisson
distribution of finding in any direction two galaxies at distance sfrom each other:
| (B.1) |
In the following, we also denote ![]() the number of observed
galaxies in the data sample and
the number of observed
galaxies in the data sample and ![]() the number of points in
the corresponding random set (see Appendix E).
the number of points in
the corresponding random set (see Appendix E).
For investigating the correlation properties of the ESO-Sculptor
redshift survey, we consider three of the demonstrated best estimators
of ![]() .
The first estimator is that by Davis & Peebles (1983, denoted DP estimator hereafter). If we denote
.
The first estimator is that by Davis & Peebles (1983, denoted DP estimator hereafter). If we denote
![]() and
and
![]() the weighted object counts in the galaxy and random
samples resp. (see Appendix E for the definition of these
quantities), this estimator may be defined for large enough samples
(
the weighted object counts in the galaxy and random
samples resp. (see Appendix E for the definition of these
quantities), this estimator may be defined for large enough samples
(
![]() 1) as:
1) as:
To minimize the effects of the finite solid angle on the sky,
Landy & Szalay (1993) introduced yet another quadratic estimator, denoted LS
estimator hereafter:
Finally, we define the cross-correlation function between two
different sub-samples. It measures the excess probability over random
of finding a galaxy belonging to sample #2 at a separation s from a
galaxy belonging to sample #1. The same estimators as for the
auto-correlation function, but with slightly modified expressions and
normalization factors can be used. The DP, H and LS estimators for
the two-point cross-correlation can be written respectively as:
In magnitude-limited surveys, the observed galaxy density varies
strongly with distance r from the origin, because such surveys do
not include all the galaxies within a limiting redshift distance, but
only those bright enough to be detected. To calculate the correlation
functions, one must account for this selection effect. The
corresponding selection function is derived from the galaxy luminosity
function, denoted ![]() .
The probability that a galaxy at comoving
distance r (see Appendix A) with absolute magnitude M is
detected in a sample can be written as:
.
The probability that a galaxy at comoving
distance r (see Appendix A) with absolute magnitude M is
detected in a sample can be written as:
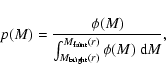 |
(C.1) |
Here, we use for M1 and M2 the effective boundaries (rounded to the first decimal place) of each considered sub-sample, in order to have the same distribution in absolute magnitude for the observed sample and the comparison random set (see Appendix E). The values of M1 and M2 adopted for each considered ESS sub-sample are listed in the third column of Table 1. In the case of a sub-sample with a cut in absolute magnitude, M1 or M2 in Eq. (C.2) are replaced with the appropriate bound.
Because only 92% of the ESS galaxies with
![]() ,
and
52% with
,
and
52% with
![]() have a measured redshift, we also
include the redshift incompleteness in the calculation of the
selection function. As the redshift incompleteness is uncorrelated
with the position on the sky and only depends on the apparent
magnitude (see de Lapparent et al. 2003), we proceed as follows. We bin
the redshift incompleteness in fixed intervals of 0.5 mag in
apparent magnitude. At each comoving distance r, we calculate the
corresponding intervals in absolute magnitude and split the numerator
integral in Eq. (C.2) into sub-integrals using these
intervals; then in each sub-integral, the incompleteness is accounted
for as a constant factor
have a measured redshift, we also
include the redshift incompleteness in the calculation of the
selection function. As the redshift incompleteness is uncorrelated
with the position on the sky and only depends on the apparent
magnitude (see de Lapparent et al. 2003), we proceed as follows. We bin
the redshift incompleteness in fixed intervals of 0.5 mag in
apparent magnitude. At each comoving distance r, we calculate the
corresponding intervals in absolute magnitude and split the numerator
integral in Eq. (C.2) into sub-integrals using these
intervals; then in each sub-integral, the incompleteness is accounted
for as a constant factor ![]() 1.
1.
Combined sub-samples including more than one class have their
selection function defined as follows. The expected distance
distribution for a homogeneous distribution with a single spectral
class is
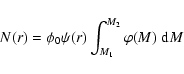 |
(C.3) |
By equating the total expected number of galaxies to the sum of the
expected numbers for each sub-sample, we obtain
The selection functions described in Appendix C can be
accounted for in the calculation of correlation functions by weighting
each pair of galaxies in the various estimators of
Appendix B according to three different schemes. When the
weighting function is constant
It was also shown that the J3 weighting scheme gives the minimum
uncertainty in the clustering amplitude on scales where
![]() 1
(Efstathiou 1988; Saunders et al. 1992). Equation (D.3) results from a
separable approximation of the true minimum-variance pair weighting
which is valid in the linear regime applicable at large separations,
when higher-order statistics can be neglected (Hamilton 1993). The
integral J3(s) can be calculated without involving any iterative
technique by modeling the required correlation function with a
power-law model and still yield accurate estimates of
1
(Efstathiou 1988; Saunders et al. 1992). Equation (D.3) results from a
separable approximation of the true minimum-variance pair weighting
which is valid in the linear regime applicable at large separations,
when higher-order statistics can be neglected (Hamilton 1993). The
integral J3(s) can be calculated without involving any iterative
technique by modeling the required correlation function with a
power-law model and still yield accurate estimates of ![]() ,
especially if one uses unbiased estimators for
,
especially if one uses unbiased estimators for ![]() (see
Appendix B; see also Ratcliffe et al. 1998b; Guzzo et al. 2000).
(see
Appendix B; see also Ratcliffe et al. 1998b; Guzzo et al. 2000).
Here, we estimate J3(s) using the power-law model which provides a
good fit to most observed samples
Because the two-point correlation measures the excess number of pairs
over a homogeneous distribution, it requires a normalization which is
obtained by comparison of the number of pairs in a given ESS sample,
with that derived from a mock homogeneous distribution occupying the
same volume as the ESS sample, and having the selection function
![]() derived from the luminosity function of that sample. Because
the redshift incompleteness is accounted for in the selection function
derived from the luminosity function of that sample. Because
the redshift incompleteness is accounted for in the selection function ![]() (see Appendix C), it is automatically accounted
for in the random distributions, and does not need to be included into
the weighting functions of Eqs. (D.1)-(D.3).
(see Appendix C), it is automatically accounted
for in the random distributions, and does not need to be included into
the weighting functions of Eqs. (D.1)-(D.3).
The Monte-Carlo set containing ![]() points, and
corresponding to each data sub-sample defined in Table 2
includes at least fifty times as many objects as the observational
catalogue:
points, and
corresponding to each data sub-sample defined in Table 2
includes at least fifty times as many objects as the observational
catalogue:
Each random distribution is then generated by randomly drawing points
with a redshift probability distribution defined by the selection
function ![]() corresponding to the data sub-sample
(Eq. (C.2)). The RA and Dec coordinates of each random point
are also drawn randomly between the ESS extreme values while
accounting for the small excluded RA and Dec regions due to saturated
stars. For a sub-sample in Table 1 which is based on one
spectral type and has cuts in either redshift or absolute
magnitude, the number of observed objects
corresponding to the data sub-sample
(Eq. (C.2)). The RA and Dec coordinates of each random point
are also drawn randomly between the ESS extreme values while
accounting for the small excluded RA and Dec regions due to saturated
stars. For a sub-sample in Table 1 which is based on one
spectral type and has cuts in either redshift or absolute
magnitude, the number of observed objects ![]() after
applying the redshift or magnitude cut is listed in Table 1 and
used in Eq. (E.1), and the random distributions is
generated using the cut-updated selection function for that spectral
type (see Appendix C). For the combined samples (for example
the sample containing "all galaxies''), we use the reunion of the
random sets corresponding to each spectral-type sub-sample and each
satisfying Eq. (E.1), which ensures that the selection
functions and relative proportions for each spectral-type are taken
into account.
after
applying the redshift or magnitude cut is listed in Table 1 and
used in Eq. (E.1), and the random distributions is
generated using the cut-updated selection function for that spectral
type (see Appendix C). For the combined samples (for example
the sample containing "all galaxies''), we use the reunion of the
random sets corresponding to each spectral-type sub-sample and each
satisfying Eq. (E.1), which ensures that the selection
functions and relative proportions for each spectral-type are taken
into account.
Then, from each observed sample and its corresponding random set,
we calculate the data pairs counts DD(s) (Eq. (B.2))
and the comparison random pair counts DR(s) and RR(s)(Eqs. (B.4) and (B.3)). In the case of "equal pair'' or
"equal volume'' weighting, the normalizing ratio of weighted counts
of objects which appear in the DP and LS estimators (see Eqs. (B.5) and (B.7)) is defined as
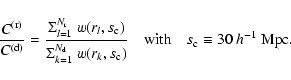 |
(E.3) |
In the case of the J3 pair-weighting function (Eq. (D.3)),
one must define an estimator of the mean number density ![]() .
Given
a magnitude-limited sample of N galaxies, we denote
.
Given
a magnitude-limited sample of N galaxies, we denote
![]() the mean density of galaxies with absolute magnitude M in the interval M1<M<M2 (corresponding to the bounds used in
the selection function, in Eq. (C.2)). An estimator of
the mean density of galaxies with absolute magnitude M in the interval M1<M<M2 (corresponding to the bounds used in
the selection function, in Eq. (C.2)). An estimator of
![]() which is unbiased by the selection function
which is unbiased by the selection function ![]() can be obtained using
can be obtained using
Davis & Huchra (1982) showed that in the case of "equal pair'' weighting (Eq. (D.1)), this estimator is the most stable, but heavily weights galaxies near the peak of the redshift distribution. In the case of "equal volume'' weighting (Eq. (D.2)), Davis & Huchra (1982) also showed that Eq. (F.1) is close to the minimum variance estimator, but that it heavily weights distant structures. The J3weighting defined in Eq. (D.3) provides an intermediate estimate of the mean density.
To estimate the mean density required for a J3 pair-weighting
(Eq. (D.2)), we iterate over Eqs. (F.1) and (D.3). The "equal volume'' weighting (Eq. (D.1)) is
used for calculating a first value of ![]() .
Then, in each
calculation of w(r), we use Eq. (D.3) with
.
Then, in each
calculation of w(r), we use Eq. (D.3) with
![]() h-3 Mpc3 (see
Eq. (D.6)), because the estimate of
h-3 Mpc3 (see
Eq. (D.6)), because the estimate of ![]() in
Eq. (F.1) requires a weighting function with the comoving
distance r as the only variable, whereas the J3 weighting
function w(r,s) varies with both r and separation s; we thus
ensure that the weights, and therefore the mean density estimate, are
not affected by galaxy clustering. This yields for the 3 spectral-type sub-samples:
in
Eq. (F.1) requires a weighting function with the comoving
distance r as the only variable, whereas the J3 weighting
function w(r,s) varies with both r and separation s; we thus
ensure that the weights, and therefore the mean density estimate, are
not affected by galaxy clustering. This yields for the 3 spectral-type sub-samples:
| (F.2) |
Peculiar velocities distort the redshift-space correlation function ![]() ,
which then differs from the real-space correlation function
,
which then differs from the real-space correlation function ![]() .
In redshift-space, internal random motions within bound structures create the so-called "finger-of-god'' structures
(elongated along the line-of-sight), while coherent motions on large
scales tend to flatten the over-densities along the observer's line of
sight (Hawkins et al. 2003). Moreover, the rms uncertainty of
.
In redshift-space, internal random motions within bound structures create the so-called "finger-of-god'' structures
(elongated along the line-of-sight), while coherent motions on large
scales tend to flatten the over-densities along the observer's line of
sight (Hawkins et al. 2003). Moreover, the rms uncertainty of
![]() 1.6 h-1 Mpc on the line-of-sight separation caused by the
redshift measurement uncertainties in the ESS, also contributes to
smooth out any clustering in redshift space on scales comparable
1.6 h-1 Mpc on the line-of-sight separation caused by the
redshift measurement uncertainties in the ESS, also contributes to
smooth out any clustering in redshift space on scales comparable
![]() h-1 Mpc (see Sect. 3.1 and Fig. 4 in Cole et al. 1994).
h-1 Mpc (see Sect. 3.1 and Fig. 4 in Cole et al. 1994).
Because the redshift-space distortions are
only radial, one can compute the correlation function as a function of
separation parallel (![]() )
and perpendicular (
)
and perpendicular (![]() )
to the
line-of-sight, which allows one to disentangle the effects of peculiar
velocities from the genuine spatial correlations. Following the
formalism of Fisher et al. (1994), for any two galaxies with redshift
positions
)
to the
line-of-sight, which allows one to disentangle the effects of peculiar
velocities from the genuine spatial correlations. Following the
formalism of Fisher et al. (1994), for any two galaxies with redshift
positions ![]() and
and ![]() ,
the redshift separation
and line-of-sight vectors are defined as
,
the redshift separation
and line-of-sight vectors are defined as
![]() and
and
![]() ,
respectively. Therefore, the
parallel and perpendicular separations are:
,
respectively. Therefore, the
parallel and perpendicular separations are:
In a second stage,
![]() allows one to derive the
correlation function
allows one to derive the
correlation function
![]() as a function of projected
separation
as a function of projected
separation ![]() ,
which is unaffected by redshift distortions
(Davis & Peebles 1983), and is obtained by integrating
,
which is unaffected by redshift distortions
(Davis & Peebles 1983), and is obtained by integrating
![]() over
over ![]() :
:
The model parameters r0 and ![]() in Eq. (G.4) are
derived by minimizing the value of
in Eq. (G.4) are
derived by minimizing the value of ![]() defined as:
defined as: