A&A 472, 187-198 (2007)
DOI: 10.1051/0004-6361:20066467
J. Hatchell1 - G. A. Fuller2 - J. S. Richer3
1 - School of Physics, University of Exeter, Stocker Road, Exeter EX4 4QL, UK
2 - School of Physics and Astronomy, University of Manchester, PO Box 88, Manchester M60 1QD, UK
3 - Cavendish Laboratory, Cambridge CB3 0HE, UK
Received 28 September 2006 / Accepted 11 June 2007
Abstract
Context. We present a search for outflows towards 51 submillimetre cores in the Perseus molecular cloud.
Aims. Our first objective is to identify the protostellar population through the detection of molecular outflows. Our second aim is to consistently derive outflow properties from a large homogeneous dataset within one molecular cloud in order to investigate further the mass dependence and time evolution of protostellar mass loss.
Methods. We used the James Clerk Maxwell Telescope to map 2' ![]() 2' regions around each core in 12CO 3-2. Where molecular outflows were detected we derived momentum fluxes.
2' regions around each core in 12CO 3-2. Where molecular outflows were detected we derived momentum fluxes.
Results. Of the 51 cores, 37 show broad linewings indicative of molecular outflows. In 13 cases, the linewings could be due to confusion with neighbouring flows but 9 of those sources also have near-infrared detections confirming their protostellar nature. The total fraction of protostars in our sample is 65%. All but four outflow detections are confirmed as protostellar by Spitzer IR detections and only one Spitzer source has no outflow, showing that outflow maps at this sensitivity are equally good at identifying protostars as Spitzer. Outflow momentum flux correlates both with source luminosity and with core mass but there is considerable scatter even within this one cloud despite the homogeneous dataset. We fail to confirm the result of Bontemps et al. (1996) that Class I sources show lower momentum fluxes on average than Class 0 sources, with a KS test showing a significant probability that the momentum fluxes for both Class 0s and Class Is are drawn from the same distribution.
Conclusions. We find that outflow power may not show a simple decline between the Class 0 to Class I stages. Our sample includes low momentum flux, low-luminosity Class 0 sources, possibly at a very early evolutionary stage. If the only mass loss from the core were due to outflows, cores would last for 105-108 years, longer than current estimates of 1.5-4 ![]() 105 years for the mean lifetime for the embedded phase. Additional mechanisms for removing mass from protostellar cores may be necessary.
105 years for the mean lifetime for the embedded phase. Additional mechanisms for removing mass from protostellar cores may be necessary.
Key words: submillimeter - stars: formation - stars: evolution - ISM: jets and outflows
Submillimetre (submm) continuum surveys of the Perseus molecular
cloud, such as our SCUBA survey, (Hatchell et al. 2005, hereafter Paper I,
see also Kirk et al. 2006), and the similar 1300
![]() survey with
Bolocam (Enoch et al. 2006), have identified over 100 submm cores. These
cores could be either protostellar or starless in nature: protostellar
cores can be identified by radio or infrared detection of a central
source, or evidence for a protostellar outflow. In a sister paper
(Hatchell et al. 2007, hereafter Paper II) we classify the protostellar cores
on the basis of their spectral energy distributions, including the new
data from Spitzer (Jørgensen et al. 2007; Evans et al. 2003). Here we take a
complementary approach and look for the presence of molecular outflows
in order to separate the protostellar cores from the starless
population. As outflow activity is thought to begin almost as soon as
the formation of a hydrostatic core, outflows are a good indicator of
the presence of embedded protostars.
survey with
Bolocam (Enoch et al. 2006), have identified over 100 submm cores. These
cores could be either protostellar or starless in nature: protostellar
cores can be identified by radio or infrared detection of a central
source, or evidence for a protostellar outflow. In a sister paper
(Hatchell et al. 2007, hereafter Paper II) we classify the protostellar cores
on the basis of their spectral energy distributions, including the new
data from Spitzer (Jørgensen et al. 2007; Evans et al. 2003). Here we take a
complementary approach and look for the presence of molecular outflows
in order to separate the protostellar cores from the starless
population. As outflow activity is thought to begin almost as soon as
the formation of a hydrostatic core, outflows are a good indicator of
the presence of embedded protostars.
In addition, studying molecular outflows is an important way to get
information on the accretion/mass ejection process which drives
protostellar evolution. Several important studies have shown that the
outflow force or momentum flux
![]() is correlated with both mass and
luminosity of the protostellar core (Cabrit & Bertout 1992; Bontemps et al. 1996), a
correlation which recently has been shown to hold over several orders
of magnitude (Zhang et al. 2005; Churchwell 1997; Beuther et al. 2002) and held to be strong evidence
for a common protostellar formation mechanism for high- and low-mass
sources alike. The details of mass accretion and ejection, however,
remain uncertain with competing mechanisms for the interaction between
mass flow and magnetic fields in the inner parts of accretion disks
(Wardle & Koenigl 1993; Pelletier & Pudritz 1992; Shu et al. 1994) and considerable uncertainty
on how the accretion rate
varies with time. One certainty, however, seems to be that the
accretion rate and the momentum output in the jet/wind are strongly linked
(Bontemps et al. 1996; Ferreira & Pelletier 1995; Shu et al. 1994), and therefore, assuming a roughly
constant mass entrainment fraction, one can use the outflow
momentum as a
surrogate measure of the momentum in the jet/wind, and therefore the mass
accretion rate onto the protostar.
is correlated with both mass and
luminosity of the protostellar core (Cabrit & Bertout 1992; Bontemps et al. 1996), a
correlation which recently has been shown to hold over several orders
of magnitude (Zhang et al. 2005; Churchwell 1997; Beuther et al. 2002) and held to be strong evidence
for a common protostellar formation mechanism for high- and low-mass
sources alike. The details of mass accretion and ejection, however,
remain uncertain with competing mechanisms for the interaction between
mass flow and magnetic fields in the inner parts of accretion disks
(Wardle & Koenigl 1993; Pelletier & Pudritz 1992; Shu et al. 1994) and considerable uncertainty
on how the accretion rate
varies with time. One certainty, however, seems to be that the
accretion rate and the momentum output in the jet/wind are strongly linked
(Bontemps et al. 1996; Ferreira & Pelletier 1995; Shu et al. 1994), and therefore, assuming a roughly
constant mass entrainment fraction, one can use the outflow
momentum as a
surrogate measure of the momentum in the jet/wind, and therefore the mass
accretion rate onto the protostar.
We therefore set out to make small outflow maps around the submm cores in Perseus to determine their outflow properties. With a consistent dataset for a moderately large sample drawn from one molecular cloud, we can look statistically at the outflow detection rate and the variation of the momentum flux with other parameters.
We assume a distance of 320 pc for the Perseus molecular cloud based on the Hipparcos distance of IC 348 (de Zeeuw et al. 1999), consistent with our earlier paper (Paper I), though readers should be aware that other recent studies (Enoch et al. 2006; Kirk et al. 2006) have assumed a closer distance of 250 pc based on extinction studies (Cernis & Straizys 2003, and references therein).
In Sect. 2 we describe the observations. Section 3 contains the results and an examination of the detection statistics. Momentum fluxes and outflow evolution are considered in Sect. 4. In Sect. 5 we discuss the derived outflow mass loss rates and the implications for core destruction timescales given the core masses implied by the submm emission (Paper I; Paper II). Finally, our conclusions are given in Sect. 6.
Outflow maps were made in
![]() in the years
2000-2003 using RxB3 on the James Clerk Maxwell Telescope (JCMT).
12CO 3-2 is a better tracer of molecular outflows than lower-J
transitions as it is more sensitive to warm outflow than cold ambient
emission. The sample consisted of contiguous areas around the known
clusters B1, IC 348, L1448, L1455, NGC 1333 (Knee & Sandell 2000), and
a number of isolated submm cores. The map areas were extended
2'
in the years
2000-2003 using RxB3 on the James Clerk Maxwell Telescope (JCMT).
12CO 3-2 is a better tracer of molecular outflows than lower-J
transitions as it is more sensitive to warm outflow than cold ambient
emission. The sample consisted of contiguous areas around the known
clusters B1, IC 348, L1448, L1455, NGC 1333 (Knee & Sandell 2000), and
a number of isolated submm cores. The map areas were extended
2' ![]() 2' around each isolated source or tiled to cover the
cluster regions. The submm cores which lie within the outflow maps
are listed in Table 1. Positions and further
information on these cores can be found in Paper I and
Paper II. The beamsize at 345 GHz is 14'' and the maps were
fully sampled at 5'' spacing in RA and Dec. A correction for main
beam efficiency of
2' around each isolated source or tiled to cover the
cluster regions. The submm cores which lie within the outflow maps
are listed in Table 1. Positions and further
information on these cores can be found in Paper I and
Paper II. The beamsize at 345 GHz is 14'' and the maps were
fully sampled at 5'' spacing in RA and Dec. A correction for main
beam efficiency of
![]() was applied. The noise
level was 0.5 K or less on 625 kHz (
was applied. The noise
level was 0.5 K or less on 625 kHz (
![]() )
channels. The weather conditions were various and resulting system
temperatures were 350-500 K.
)
channels. The weather conditions were various and resulting system
temperatures were 350-500 K.
The 12CO 3-2 data for NGC 1333 were published in
Knee & Sandell (2000), and kindly made available by the authors. The
spatial sampling of the NGC 1333 observations was 10'' rather than
the 5'' of the more recent observations. In order to
match the other datasets as closely as possible for analysis, the maps
were resampled onto a 5'' grid. This was done by interpolating with
a 14'' Gaussian truncated at 40''. This results in a map with the
same intensity (
![]() )
scale but with 20'' resolution.
)
scale but with 20'' resolution.
The sample (Table 1) was selected before the analysis of the corresponding SCUBA
data was complete, and therefore is biased towards the obvious bright
clusters and previously known protostars. In Fig. 2 we
show the outflow sample (marked by stars) on a plot of luminosity vs.
core mass for the entire population of submm cores in Perseus
(Paper II). The sample is indeed biased towards high
luminosities with no outflow maps of sources below 0.25 ![]() .
The
proportion of the total number of cores decreases with decreasing
mass. However, the fraction of
.
The
proportion of the total number of cores decreases with decreasing
mass. However, the fraction of
![]() cores studied
remains fairly constant except for the very lowest mass sources below
our completeness limit at 10 K of
cores studied
remains fairly constant except for the very lowest mass sources below
our completeness limit at 10 K of
![]() (
(![]() ).
For the very highest mass sources,
).
For the very highest mass sources,
![]() ,
all sources were
observed as there were no low-luminosity sources in the SCUBA sample.
Thus the most significant bias of the sample is its lack of low
luminosity sources.
,
all sources were
observed as there were no low-luminosity sources in the SCUBA sample.
Thus the most significant bias of the sample is its lack of low
luminosity sources.
Small outflow maps provide a good estimate of the momentum flux (Fuller & Ladd 2002; Mangum et al. 1998) but, except for very small flows, do not provide estimates of the full extent, mass, kinetic energy, or dynamical timescale of outflows. Our map radius of 1' corresponds to 0.1 pc assuming a distance of 320 pc for the Perseus molecular clouds, or a dynamical time of 2000 years for an outflow advancing at 50 km s-1.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{6467f1.ps} \end{figure}](/articles/aa/full/2007/34/aa6467-06/Timg28.gif) |
Figure 1:
12CO 3-2 outflow maps. Colourscale: 850
|
![\begin{figure}
\par\includegraphics[width=9.4cm,clip]{6467f2.eps}
\end{figure}](/articles/aa/full/2007/34/aa6467-06/Timg29.gif) |
Figure 1:
continued. NGC 1333 from data first published in Knee & Sandell (2000). The renzogram intensity level is 3 K km s-1 and included channels from -5-3 km s-1 (blue) and 12-18 km s-1 (red). 850
|
| Nr. | Name1 | Outflow | Class2 |
|
|
|
| (y/n?) | km s-1 | '' |
|
|||
| 1 | b1-c | y | 0 | 6.4 | 12.0 | 1.7 (0.8) |
| 2 | b1-bS | y | 0 | 6.8 | 30.0 | 12.3 (1.0) |
| 4 | b1-d | y | 0 | 6.7 | 15.0 | 1.8 (0.3) |
| 7 | IRAS 03301+3057 | y | I | 6.6 | 30.0 | 12.6 (0.8) |
| 10 | B1 SMM11 | y | I | 6.6 | 30.0 | 4.4 (0.4) |
| 12 | HH211 | y | 0 | 8.8 | 30.0 | 6.2 (0.8) |
| 13 | IC 348 MMS | y | 0 | 8.6 | 30.0 | 5.1 (0.5) |
| 14 | y? | I | 9.1 | 10.0 | 1.2 (0.3) | |
| 15 | IC 348 SMM3 | y | 0 | 8.8 | 30.0 | 0.6 (0.2) |
| 16 | n | S | 8.8 | - | - - | |
| 17 | y?c133 | S | 8.4 | 10.0 | 0.8 (0.6) | |
| 18 | n | S | 8.6 | - | - - | |
| 19 | n | S | 9.5 | - | - - | |
| 20 | n | S | 8.5 | - | - - | |
| 21 | n | S | 8.6 | - | - - | |
| 23 | n | S | 9.0 | - | - - | |
| 24 | n | S | 8.7 | - | - - | |
| 25 | n | S | 9.2 | - | - - | |
| 26 | n | S | 8.8 | - | - - | |
| 27 | L1448 NW | y | 0 | 4.4 | 30.0 | 27.5 (3.0) |
| 28 | L1448 N A/B | y | 0 | 4.4 | 30.0 | 36.4 (2.9) |
| 29 | L1448 C | y | 0 | 4.8 | 30.0 | 20.9 (1.5) |
| 30 | L1448 IRS2 | y | 0 | 4.1 | 30.0 | 10.1 (0.8) |
| 31 | y?c303 | 0 | 4.1 | 15.0 | 3.6 (0.5) | |
| 35 | L1455 FIR4 | y | I | 5.3 | 30.0 | 9.4 (0.6) |
| 36 | y | 0 | 5.8 | 20.0 | 6.6 (0.5) | |
| 37 | L1455 PP9 | y? | I | 5.3 | 30.0 | 3.2 (0.4) |
| 39 | L1455 FIR1/2 | y? | I | 5.3 | 20.0 | 1.8 (0.2) |
| 40 | y?c35,363 | S | 5.4 | 30.0 | 2.6 (0.3) | |
| 41 | NGC 1333 IRAS 4A | y | 0 | 7.6 | 30.0 | 45.5 (2.9) |
| 42 | NGC 1333 IRAS 4B | y | 0 | 7.5 | 10.0 | 10.4 (1.6) |
| 43 | NGC 1333 SVS13 | y | I | 7.9 | 30.0 | 195.9 (14.2) |
| 44 | NGC 1333 IRAS 2A | y | 0 | 7.7 | 30.0 | 72.7 (4.4) |
| 45 | NGC 1333 SK24 | y | I | 7.6 | 30.0 | 50.3 (3.4) |
| 46 | NGC 1333 SK20/21 | y | 0 | 7.9 | 30.0 | 59.5 (3.3) |
| 47 | NGC 1333 SK31 | y | 0 | 7.6 | 30.0 | 19.2 (1.9) |
| 48 | NGC 1333 IRAS 4C | y?c41,423 | 0 | 7.6 | 20.0 | 2.7 (1.6) |
| 50 | NGC 1333 SK15 | y?c43,513 | I | 7.9 | 20.0 | 166.2 (10.9) |
| 51 | NGC 1333 SK16 | y?c43,503 | S | 7.6 | 20.0 | 54.5 (8.2) |
| 52 | NGC 1333 SK14 | y?c43,503 | 0 | 7.6 | 30.0 | 32.5 (2.6) |
| 53 | NGC 1333 SK26 | y?c453,4 | S | 7.6 | 20.0 | 4.4 (0.6) |
| 61 | n | 0 | 7.6 | - | - - | |
| 62 | NGC 1333 SK18 | y?c463 | 0 | 7.9 | 20.0 | 25.6 (4.1) |
| 64 | NGC 1333 Per 4A3/4D | n | S | 7.4 | - | - - |
| 68 | NGC 1333 MBO146 | y?c453 | 0 | 7.7 | 30.0 | 27.5 (2.3) |
| 76 | IRAS 03292+3039 | y | 0 | 6.9 | 10.0 | 1.2 (0.5) |
| 77 | IRAS 03282+3035 | y | 0 | 7.2 | 30.0 | 4.8 (0.5) |
| 78 | B5 IRS1 | y | I | 10.0 | 10.0 | 1.5 (0.2) |
| 79 | n | S | 10.0 | - | - - | |
| 80 | IRAS 03235+3004 | n | I | 5.0 | - | - - |
| 81 | B1 SMM1 | n | I | 5.9 | - | - - |
|
1 Common name. For positions, further names, references and further data see Paper II. 2 From SED-based evolutionary indicators (Paper II). 3 Sources of potential confusion. 4 At edge of mapped area. Possible S blue lobe. |
Maps of the outflows superimposed on the submm continuum map are shown
in Fig. 1. We identified sources with outflows based
on the objective criterion of 12CO linewings more than 1.5 K
(![]() )
at 3 km s-1 from the line centre (as measured in
C18O). Of the 51 sources in Table 1 observed in
12CO 3-2, 37 sources (73%) were classified as outflows on this
basis. Spectra for these sources at the source position and the
outflow lobes are shown in Fig. 1 (online version
only). In some cases the outflow lobe spectra are missing due to
confusion or because the driving source lies at the edge of the mapped
area. From the maps (Fig. 1), we identify 13 cases
where the broad linewings may be wholly or partly due to nearby flows
driven by other sources in crowded regions. These uncertain flows are
marked with "y?'' in Table 1. The remaining 14 sources
show no evidence for outflow activity in the form of either line wings
or red/blueshifted lobes, as shown in Fig. 2
(online version only).
)
at 3 km s-1 from the line centre (as measured in
C18O). Of the 51 sources in Table 1 observed in
12CO 3-2, 37 sources (73%) were classified as outflows on this
basis. Spectra for these sources at the source position and the
outflow lobes are shown in Fig. 1 (online version
only). In some cases the outflow lobe spectra are missing due to
confusion or because the driving source lies at the edge of the mapped
area. From the maps (Fig. 1), we identify 13 cases
where the broad linewings may be wholly or partly due to nearby flows
driven by other sources in crowded regions. These uncertain flows are
marked with "y?'' in Table 1. The remaining 14 sources
show no evidence for outflow activity in the form of either line wings
or red/blueshifted lobes, as shown in Fig. 2
(online version only).
All but four of the sources with outflows on the basis of linewings
also have a near-infrared detection from Spitzer IRAC
(Paper II), (Jørgensen et al. 2007). The exceptions are 17, 40,
51 (SK16) and 53 (SK26), all of which are classified as starless
(Table 1). In all of these cases the linewings are
likely due to confusion. In the following analysis of the outflow
properties, we leave out these four sources, assuming that they are
indeed starless. For most of the protostars it is the driving source which
is being detected by Spitzer but in some cases the infrared emission
may be due to HH objects (examples are HH211 (12), and (15)). In 9 of
the 13 uncertain outflow sources, their protostellar nature is
confirmed by IR detections. All but one of the sources with Spitzer
IRAC detections and observed in CO have molecular outflows. The
exception is in NGC 1333: the Class 0 source 61 lies to the north of
the luminous Herbig Ae-Be star NGC 1333 IRAS 8/SSV3 and B star
IRAS 9/BD
![]() and the interaction with radiation and winds
from these sources may well explain the outflow non-detection. The
detection of outflows from all but one Spitzer-confirmed protostar
shows that both types of observation are similarly effective in
identifying protostars among submm cores. Outflow-based
identification avoids the Spitzer confusion with extragalactic objects
but can be difficult in crowded regions where the outflows overlap.
and the interaction with radiation and winds
from these sources may well explain the outflow non-detection. The
detection of outflows from all but one Spitzer-confirmed protostar
shows that both types of observation are similarly effective in
identifying protostars among submm cores. Outflow-based
identification avoids the Spitzer confusion with extragalactic objects
but can be difficult in crowded regions where the outflows overlap.
If we consider the outflows as a function of core mass
(Fig. 3, top), we find that the fraction of
sources with outflows decreases with decreasing core mass. In
order to estimate our ability to detect outflows in the lower mass
bins, we performed the following simulation. We considered the 14 outflow sources in the three highest mass bins (
![]()
![]() ).
We then simulated outflows from lower mass cores by scaling the
outflow spectra (Fig. 1, online version only) for
these 15 sources according to the modelled core mass as
).
We then simulated outflows from lower mass cores by scaling the
outflow spectra (Fig. 1, online version only) for
these 15 sources according to the modelled core mass as
![]() .
The motivation for this power law scaling comes from
Fig. 4 which shows a rough correlation between momentum
flux and core mass with a gradient of
.
The motivation for this power law scaling comes from
Fig. 4 which shows a rough correlation between momentum
flux and core mass with a gradient of ![]() (see Sect. 4). We also formed
the simulated outflow maps by multiplying the original (x,y,v) datacube by these scaling factors and adding back on the unscaled
noise levels (from sampling the noise in the outer velocity channels
of the unscaled maps).
Several scaling factors were used,
corresponding to moving the core masses an integer number of mass bins
to the left. By this means we generated an artificial population of
spectra and maps of outflows for cores in the range 0.6-50
(see Sect. 4). We also formed
the simulated outflow maps by multiplying the original (x,y,v) datacube by these scaling factors and adding back on the unscaled
noise levels (from sampling the noise in the outer velocity channels
of the unscaled maps).
Several scaling factors were used,
corresponding to moving the core masses an integer number of mass bins
to the left. By this means we generated an artificial population of
spectra and maps of outflows for cores in the range 0.6-50 ![]() .
We
tested the spectra according to our criterion for linewings (>1.5 K
at 3 km s-1 from line centre). We also additionally displayed
these maps using our usual visualisation software kvis (Gooch 1996) and
considered whether we could visually detect the resulting outflows
above the noise. In all cases where the linewings satisfied the
objective criteria, we could see the outflows in the maps. The
detection statistics for our simulated population are given in
Table 2.
.
We
tested the spectra according to our criterion for linewings (>1.5 K
at 3 km s-1 from line centre). We also additionally displayed
these maps using our usual visualisation software kvis (Gooch 1996) and
considered whether we could visually detect the resulting outflows
above the noise. In all cases where the linewings satisfied the
objective criteria, we could see the outflows in the maps. The
detection statistics for our simulated population are given in
Table 2.
There is a decline in our detection ability at lower mass, and in the
lowest mass bins we detect few of the model outflows. In the lowest
two mass ranges in Fig. 3, 0.4-2.5 ![]() ,
0 and
1 respectively out of 14 of the simulated low-mass outflows were
detected. In the next highest mass bin (2.5-6
,
0 and
1 respectively out of 14 of the simulated low-mass outflows were
detected. In the next highest mass bin (2.5-6 ![]() ), the detection
rate improved and 29% of simulated outflows were detected. The mean
detection rate below 6
), the detection
rate improved and 29% of simulated outflows were detected. The mean
detection rate below 6 ![]() is predicted to be 12%, or roughly 1 in
8 outflows detected.
is predicted to be 12%, or roughly 1 in
8 outflows detected.
The outflow detection rate predicted by the simulation is lower than
the actual detection rate for all sources below 6 ![]() .
This can be
seen in the lowest three mass bins of Table 2.
This is true even if we include all the submm cores from the SCUBA
survey, and not just those with existing outflow observations. We
have already detected 14 outflows among 75 submm cores with masses
below 6
.
This can be
seen in the lowest three mass bins of Table 2.
This is true even if we include all the submm cores from the SCUBA
survey, and not just those with existing outflow observations. We
have already detected 14 outflows among 75 submm cores with masses
below 6 ![]() (Fig. 2), or 19% compared to an average
of 12% for the simulated flows. This suggests that our assumptions
about how outflow linewings scale with core mass are pessimistic,
and we are more likely to detect flows than the simulation predicts -
due to higher optical depth in more massive flows, for example.
(Fig. 2), or 19% compared to an average
of 12% for the simulated flows. This suggests that our assumptions
about how outflow linewings scale with core mass are pessimistic,
and we are more likely to detect flows than the simulation predicts -
due to higher optical depth in more massive flows, for example.
The bottom panel of Fig. 3 shows our best
estimate of the true fraction of outflow sources in each mass bin,
corrected for the detection statistics using (true outflow fraction) =
(fraction of outflows detected)/(detection probability in this mass
bin). The calculation of the uncertainties (greyscales) shown in the
figure is given in Appendix A. In mass bins where
the observed detection rate equals or exceeds the simulated rate, this
model would predict that all the apparently starless cores contain
undetected protostars. Only in the 6-16 ![]() mass range is the
predicted number of outflow sources smaller than the number of
apparently starless cores. If this model is correct, then we fail to
detect outflows from the majority of protostars at masses <
mass range is the
predicted number of outflow sources smaller than the number of
apparently starless cores. If this model is correct, then we fail to
detect outflows from the majority of protostars at masses <
![]() .
.
Thus, the modelling suggests that the low number of outflow detections from low mass cores is a selection effect.
If this is the case then this outflow survey and Spitzer c2d
Evans et al. (2003) must have very similar sensitivities to embedded
protostars as only one mid-IR detected sources in the sample had no
corresponding outflow and conversely only four outflow sources
had no mid-IR detection. Therefore any selection effect must operate
both in the infrared and molecular lines. Orientation could help
produce such close agreement as infrared sources are hard to detect
where disks are edge-on and outflows are hard to detect when they lie
close to the plane of the sky. Assuming random outflow orientation,
though, the number of infrared non-detections due to edge-on disks
(within ![]() of the line-of-sight) can only be
of the line-of-sight) can only be ![]()
![]() of
the total protostellar fraction.
of
the total protostellar fraction.
This modelling suggests that the low-mass cores without outflow or Spitzer detections may also be protostellar, but of course does not prove that they are. For one thing, the assumptions in our model about how outflow masses vary with core mass may not be correct. Only further searching for outflows, infrared or radio sources towards the apparently starless cores can determine the true nature of the apparently starless cores. Note that such observations would need to be with higher sensitivity than this outflow survey, the Spitzer Cores to Disks programme (Evans et al. 2003), or its successor, the Spitzer Gould's Belt survey, in order to identify less luminous protostars.
|
|
-0.2 | 0.2 | 0.6 | 1.0 | 1.4 | 1.8 |
| Simulated maps | 14 | 14 | 14 | 14 | 11 | 1 |
| Sim. detections | 0 | 1 | 4 | 13 | 11 | 1 |
| Sim. rate | 0% | 7% | 29% | 93% | 100% | 100% |
| Obs. rate | 50% | 18% | 50% | 64% | 100% | 100% |
Outflow momentum fluxes (or outflow luminosities) are given in
Table 1 for all the possible outflow sources. The
method is developed from the momentum flux per beam calculation of
Fuller & Ladd (2002), rather than calculating the momentum flux within
an annulus (Bontemps et al. 1996), though the two methods should yield
comparable results. The momentum flux crossing a cylinder radius ![]() perpendicular to the plane of the sky and centred on the
source, contributed by the mass within one beam, is calculated
individually for each beam as:
perpendicular to the plane of the sky and centred on the
source, contributed by the mass within one beam, is calculated
individually for each beam as:
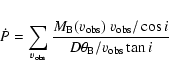
The mass within one beam ![]() is calculated from the CO
integrated intensity over the velocity channel
is calculated from the CO
integrated intensity over the velocity channel
![]() assuming a CO abundance of
assuming a CO abundance of
![]() (Frerking et al. 1982; Wilson & Rood 1994) and a LTE excitation at an outflow
temperature of 50 K resulting in
(Frerking et al. 1982; Wilson & Rood 1994) and a LTE excitation at an outflow
temperature of 50 K resulting in
![]()
![]()
![]() .
A
temperature of 50 K is chosen as there is increasing evidence that
outflows contain warm gas
(Hatchell et al. 1999a; Nisini et al. 2000; Giannini et al. 2001; Hatchell et al. 1999b) but the conversion
is relatively insensitive to the temperature, increasing by only
40% over the temperature range 20-100 K. The mass within one beam
is calculated as
.
A
temperature of 50 K is chosen as there is increasing evidence that
outflows contain warm gas
(Hatchell et al. 1999a; Nisini et al. 2000; Giannini et al. 2001; Hatchell et al. 1999b) but the conversion
is relatively insensitive to the temperature, increasing by only
40% over the temperature range 20-100 K. The mass within one beam
is calculated as
![]()
The momentum flux contributions from individual beams are then
summed in annuli, according to:
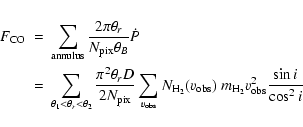
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{6467f5.ps}\end{figure}](/articles/aa/full/2007/34/aa6467-06/Timg58.gif) |
Figure 4:
Relationships between momentum flux and ( top to bottom) bolometric luminosity
|
The driving source positions were taken to be the SCUBA emission peaks from Paper I. To reduce the contribution due to emission outside the outflow region, the outflow areas to be included in the momentum flux calculation were selected by masking with 12CO integrated intensity at a cutoff of 3 times the noise level in the integrated intensity map. We default to calculating the momentum flux within a circle of outer radius 30'' unless it was clear from the map that the outflow was shorter than this or there was potential confusion within this radius, in which case the radius of the circle was reduced. In practice we find the choice of circle or annulus and the radius of the circle (except for the case of confusing flows) makes little difference to the resulting momentum fluxes, as expected at radii where there is no large variation in the injection of momentum.
The inner velocity channels, contaminated by ambient emission, were
cut out to ![]() 2 km s-1 and the highest velocity considered was
2 km s-1 and the highest velocity considered was
![]() 15 km s-1. Ideally, for a fair comparison of the momentum flux
between strong (massive) and weak flows, one wants good
signal-to-noise (S/N) in the linewings out to similar velocities.
With roughly constant sensitivity and line strengths varying by an
order of magnitude the strong linewings can be measured with good S/N
to higher velocities in the stronger flows. Adjusting the velocity
range on a flow-by-flow basis according to where the S/N is good
therefore introduces a strong bias in momentum flux towards massive
flows. Not only are these more massive but also more of the high
velocity channels are included in the calculation. Therefore we
consider it fairer to use the same velocity cut for each source, even
though this excludes the contribution from the highest velocity
channels in all flows.
15 km s-1. Ideally, for a fair comparison of the momentum flux
between strong (massive) and weak flows, one wants good
signal-to-noise (S/N) in the linewings out to similar velocities.
With roughly constant sensitivity and line strengths varying by an
order of magnitude the strong linewings can be measured with good S/N
to higher velocities in the stronger flows. Adjusting the velocity
range on a flow-by-flow basis according to where the S/N is good
therefore introduces a strong bias in momentum flux towards massive
flows. Not only are these more massive but also more of the high
velocity channels are included in the calculation. Therefore we
consider it fairer to use the same velocity cut for each source, even
though this excludes the contribution from the highest velocity
channels in all flows.
The uncertainties on the momentum flux, listed in
Table 1, are the root sum-of-squares of the
uncertainties of each contributing pixel. The pixel uncertainty is
taken to be the difference from the mean momentum flux in the
contributing (integrated intensity >![]() )
region.
)
region.
We have not applied a correction factor for either inclination or
optical depth, unlike Bontemps et al. (1996). Therefore our momentum fluxes
are strictly lower limits. Bontemps et al. (1996) point out that inclination i reduces the momentum flux by a factor
![]() for a mean angle of 57.3 degrees. For an optical depth
for a mean angle of 57.3 degrees. For an optical depth ![]() ,
uncorrected CO column densities are underestimated by a factor
,
uncorrected CO column densities are underestimated by a factor
![]() or a typical factor of 3.5 so that true momentum
fluxes are typically a factor of 10 greater than measured. Outflow
optical depths are high even in the J=3-2 line with with
or a typical factor of 3.5 so that true momentum
fluxes are typically a factor of 10 greater than measured. Outflow
optical depths are high even in the J=3-2 line with with
![]() in the line wings (Margulis & Lada 1985; Hogerheijde et al. 1998).
in the line wings (Margulis & Lada 1985; Hogerheijde et al. 1998).
The (uncorrected) momentum flux results for all the possible outflow
sources are given in Table 1. Comparing the sources in
common, our momentum fluxes are typically lower by a factor of a few
than previous analyses by Bontemps et al. (1996) (taking the optical depth/inclination correction into account) and Knee & Sandell (2000). The main
reason for this is that we assume the outflows are warm (50 K), which
reduces mass estimates by a factor of ![]() 4 over the 10 K assumed by
Bontemps et al. (1996). This is a systematic difference, reducing the
momentum fluxes for all sources by the same fraction. For flows with
high velocity gas, we can also underestimate momentum fluxes because
we do not include the highest velocity channels (as discussed above).
For two sources, IRAS 03282+3035 (77) and B5 IRS1 (78), we measure
momentum fluxes more than a factor of 10 lower than previous
estimates. We have no reason to suspect the calibration for these two
maps, and they do not have particularly broad linewings (as can be
seen in Fig. 1, online). It is possible that in
these flows, the momentum flux measured at greater radii in the flow
is larger than in the region covered by our 2' maps.
4 over the 10 K assumed by
Bontemps et al. (1996). This is a systematic difference, reducing the
momentum fluxes for all sources by the same fraction. For flows with
high velocity gas, we can also underestimate momentum fluxes because
we do not include the highest velocity channels (as discussed above).
For two sources, IRAS 03282+3035 (77) and B5 IRS1 (78), we measure
momentum fluxes more than a factor of 10 lower than previous
estimates. We have no reason to suspect the calibration for these two
maps, and they do not have particularly broad linewings (as can be
seen in Fig. 1, online). It is possible that in
these flows, the momentum flux measured at greater radii in the flow
is larger than in the region covered by our 2' maps.
The outflow momentum flux
![]() is plotted versus core mass
is plotted versus core mass
![]() ,
bolometric luminosity
,
bolometric luminosity
![]() and bolometric temperature
and bolometric temperature
![]() in
Fig. 4 (see Paper II, for the calculation of those
quantities from the SEDs). The well known relationship between
momentum flux and bolometric luminosity (Cabrit & Bertout 1992; Bontemps et al. 1996)
is evident despite the intrinsic scatter in the momentum flux due to
uncorrected outflow inclination. This correlation is often taken as
evidence that the outflow and the accretion luminosity are both being
powered by the same mechanism, infall, and despite the details of the
magnetic ejection/accretion process in the inner few tens of AU of the
disk, the energy input into each remains strongly linked. The
correlation is tighter towards higher
in
Fig. 4 (see Paper II, for the calculation of those
quantities from the SEDs). The well known relationship between
momentum flux and bolometric luminosity (Cabrit & Bertout 1992; Bontemps et al. 1996)
is evident despite the intrinsic scatter in the momentum flux due to
uncorrected outflow inclination. This correlation is often taken as
evidence that the outflow and the accretion luminosity are both being
powered by the same mechanism, infall, and despite the details of the
magnetic ejection/accretion process in the inner few tens of AU of the
disk, the energy input into each remains strongly linked. The
correlation is tighter towards higher
![]() and holds for both
Class 0 and Class I sources (marked by red asterisks and blue open
stars, respectively; see Paper II for details of classification).
and holds for both
Class 0 and Class I sources (marked by red asterisks and blue open
stars, respectively; see Paper II for details of classification).
Bontemps et al. (1996) found a decline of momentum flux between the Class 0
and Class I phases which has been taken as evidence that outflow power
declines with age. In our sample, this is less clear cut. The mean
![]() of the
Class 0 population is -6.0 with a sample standard deviation of
0.6, close to the Class I mean of -6.1 (standard deviation 0.8). A histogram of the momentum flux distribution for Class 0 and
Class I sources (Fig. 5) shows that both of the
distributions are very flat. Applying the Kolmogorov-Smirnov (K-S) test indicates a 27% probability that the two samples come
from the same parent distribution and therefore there is no evidence
for evolution in momentum flux between Class 0 and Class I. There is
considerable scatter with objects of both classes with both low and
high-
of the
Class 0 population is -6.0 with a sample standard deviation of
0.6, close to the Class I mean of -6.1 (standard deviation 0.8). A histogram of the momentum flux distribution for Class 0 and
Class I sources (Fig. 5) shows that both of the
distributions are very flat. Applying the Kolmogorov-Smirnov (K-S) test indicates a 27% probability that the two samples come
from the same parent distribution and therefore there is no evidence
for evolution in momentum flux between Class 0 and Class I. There is
considerable scatter with objects of both classes with both low and
high-
![]() .
.
In particular, three Class I objects- NGC 1333 SVS13 (43), NGC 1333
ASR114 (45) and NGC 1333 HH7-11 MMS4 (50)- have particularly high
momentum flux and four Class 0 sources - b1-c (1), b1-d (4), B1 SMM5
(76) and IC 348 SMM3 (15) - have low momentum flux. The third panel of
Fig. 4, in which momentum flux is plotted against
![]() ,
shows clearly that the Class Is (on the right hand side of the plot)
have more scatter in momentum flux than the Class 0s. The two high
,
shows clearly that the Class Is (on the right hand side of the plot)
have more scatter in momentum flux than the Class 0s. The two high
![]() sources are the well-known Class I sources L1455 PP9 (37),
which may contain multiple protostars, and L1455 FIR1/2 (39).
sources are the well-known Class I sources L1455 PP9 (37),
which may contain multiple protostars, and L1455 FIR1/2 (39).
All three of the high momentum flux Class I cores, NGC 1333 SSV13 (43), NGC 1333 ASR114 (45) and HH7-11 MMS4 (50) are in the confused NGC 1333 region. HH7-11 MMS4 (50) is a confused source where a major contribution to the momentum flux comes from the HH7-11 driving source SSV13. Both SSV13 and ASR114 contain multiple protostars as evidenced by radio emission (Rodriguez et al. 1997; Knee & Sandell 2000). Can this explain their high momentum fluxes despite Class I classification? NGC 1333 SSV13 (43) is a multiple source (SSV13 and 13B) potentially consisting of a Class I source (providing the infrared-based classification) and a Class 0 source (powering the outflow). The flows from SSV13/13B are confused and the momentum flux includes contributions from both, though Knee & Sandell (2000) attributed more momentum flux to the Class I SSV13 than the potential Class 0 counterpart SSV13B. Likewise ASR114 (45) contains multiple embedded radio sources (Rodriguez et al. 1997), and the outflows are confused by the flow from the 4' distant SSV13B which is believed to drive the nearby HH 12 (Knee & Sandell 2000), and the momentum fluxes could be overestimated by the contribution from the flow from the south. It is possible that in both these cases the high momentum flux is due to a Class 0 source, either in the same submm core or nearby - an open question which could be resolved by interferometric observations of the flows.
However, the Class 0 sources with low momentum flux - b1-c (1), b1-d
(4), IC 348-SMM3 (15) and B1-SMM5 (76) - are less easy to explain
away. Three of these sources (1, 4, 76) also have low bolometric
luminosity for their mass. Our sample, because of its submm-based
sample selection, may well contain a population of low-luminosity,
low-
![]() Class 0 sources which were not included in earlier studies.
Class 0 sources which were not included in earlier studies.
There are physical reasons why outflow force may vary between sources
at the same evolutionary stage. The momentum in the driving wind
depends on the mass accretion rate and in turn on the history of the
mass reservoir available for accretion. For example, this may differ
between clustered and more isolated protostars (Henriksen et al. 1997),
though this does not appear to explain the results in Perseus. Early
Class 0 sources may not have reached their full accretion rates
(Smith 2000). The low momentum flux Class 0 sources b1-c (1), b1-d
(4) and B1-SMM5 (76) which also have low bolometric luminosity are
likely to be early Class 0 sources which have not yet reached their
full accretion power. The fraction of the wind momentum which is
transferred to the molecular outflow depends on entrainment of the
ambient material, which may vary in efficiency. In the competitive
accretion model, mass may continue to flow onto already-accreting
envelopes and boost accretion at late stages, which would lead to a
natural scatter in accretion rates. Jet ejection is known to be
episodic (Raga et al. 1990,2004) but the swept-up molecular outflow
smooths out any variability on timescales of ![]() 100 years, such as
those which produce jet knots.
100 years, such as
those which produce jet knots.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{6467f7.ps}\end{figure}](/articles/aa/full/2007/34/aa6467-06/Timg70.gif) |
Figure 6:
|
Bontemps et al. (1996) show in their Fig. 4 a plot in which momentum flux and mass are compensated for source luminosity. In Fig. 6 we show the analogous figure for our dataset. For our sources the relationship between mass and luminosity is
![]() (Paper II) so the abscissa becomes
(Paper II) so the abscissa becomes
![]() and the ordinate
and the ordinate
![]() .
The luminosity correction separates the Class I sources from the Class 0s, which tend to be more massive for the same luminosity. This separation in mass is seen in Fig. 6, with the Class 0 sources lying to the right of the diagram. It also takes out the effect of distance, though this is irrelevant for our Perseus-only sample.
.
The luminosity correction separates the Class I sources from the Class 0s, which tend to be more massive for the same luminosity. This separation in mass is seen in Fig. 6, with the Class 0 sources lying to the right of the diagram. It also takes out the effect of distance, though this is irrelevant for our Perseus-only sample.
The luminosity correction has to be treated with caution because it does not differentiate between luminosity and momentum flux evolution. Evidence for luminosity evolution comes from Paper II, which shows that Class 0 sources have, on average, lower luminosities at a given mass than Class I sources. Some evolutionary schemes (Smith 2000) interpret this as an increase in luminosity between the Class 0 to Class I phases. On the luminosity-corrected diagram, decreasing luminosity can be mistaken for increasing momentum flux.
Nonetheless, in the luminosity-corrected diagram, the
![]() values for the Class 0 sources are similar to their Class I counterparts, with no obvious evolution between the two stages.
values for the Class 0 sources are similar to their Class I counterparts, with no obvious evolution between the two stages.
There is a general trend of increasing momentum flux with
![]() (middle panel of Fig. 4) although there is more than an
order of magnitude of scatter, as found for
(middle panel of Fig. 4) although there is more than an
order of magnitude of scatter, as found for
![]() -
-
![]() .
A physical
explanation for such scatter is that the energy in the mass infall,
which powers both the mass outflow and the bolometric luminosity, is
dependent on the infall rate which is not set by the current mass of
the core but by its past history. Hogerheijde et al. (1998) found a
better correlation of
.
A physical
explanation for such scatter is that the energy in the mass infall,
which powers both the mass outflow and the bolometric luminosity, is
dependent on the infall rate which is not set by the current mass of
the core but by its past history. Hogerheijde et al. (1998) found a
better correlation of
![]() with
with
![]() than
than
![]() ,
but we see no
evidence for this.
,
but we see no
evidence for this.
In summary, there is broad agreement between our results on the
momentum flux and previous studies, with similar scatter on the
correlations with
![]() or
or
![]() despite the consistent derivation
of these quantities and the single distance of our sample. A
difference is the significant population of low-
despite the consistent derivation
of these quantities and the single distance of our sample. A
difference is the significant population of low-
![]() Class 0 sources
and the small number of high-
Class 0 sources
and the small number of high-
![]() Class Is which suggest that
evolution of
Class Is which suggest that
evolution of
![]() from Class 0 to Class I is not a simple decline but
that there may be variation within each class, e.g. as luminosity and
outflow power increase at the beginning of the Class 0 phase.
from Class 0 to Class I is not a simple decline but
that there may be variation within each class, e.g. as luminosity and
outflow power increase at the beginning of the Class 0 phase.
![\begin{figure}
\par\includegraphics[angle=-90,width=12cm,clip,origin=rb]{6467f8.ps}\end{figure}](/articles/aa/full/2007/34/aa6467-06/Timg73.gif) |
Figure 7: Core destruction timescales at current outflow mass loss rate, vs. left bolometric temperature; right current core mass. Class I sources (Hatchell et al. 2007, based on the SED), are marked by (blue) open stars and Class 0 sources by (red) asterisks. |
A significant proportion of the momentum from the driving jet/wind is deposited in the protostellar core and removes matter from the core in the molecular outflow (Fuller & Ladd 2002; Arce & Sargent 2006; Parker et al. 1991; Lada 1985). The time it would take to clear a protostellar core of mass via the outflow is a constraint on the lifetime of the embedded protostellar phase, especially when taken together with an indication of whether the source is at the start (early Class 0) or end (Class I) of its embedded lifetime.
In addition to the outflow, mass is lost from the protostellar core by
accretion onto the disk/star. The ratio of mass ejected in the
wind/jet to mass accretion, f, varies significantly with different
models for jet/wind launching. Observations suggest that
![]() is a good estimate (Richer et al. 2000). Although the mass loss in
the jet is then less than half of the total accretion, momentum
transfer to the slower molecular outflow can lead to mass loss rates
in the outflow that are a factor of 10 higher than the total mass
accretion rate:
is a good estimate (Richer et al. 2000). Although the mass loss in
the jet is then less than half of the total accretion, momentum
transfer to the slower molecular outflow can lead to mass loss rates
in the outflow that are a factor of 10 higher than the total mass
accretion rate:
![]() ,
taking
the jet ejection fraction fa = 0.3 and typical values for the jet
and CO velocities of 150 and 5 km s-1 respectively,
and assuming all the wind/jet momentum is deposited in the cloud.
At early times when this is true, before the outflow has broken out
of the cloud, then mass loss in the outflow dominates by an
order of magnitude over the mass accreted onto the central object, and
can be taken as a good estimate of the total mass loss rate. For more evolved flows less of the wind/jet momentum may be transferred to the CO and in the most evolved sources the accretion rate may begin to dominate over the mass loss in the outflow.
,
taking
the jet ejection fraction fa = 0.3 and typical values for the jet
and CO velocities of 150 and 5 km s-1 respectively,
and assuming all the wind/jet momentum is deposited in the cloud.
At early times when this is true, before the outflow has broken out
of the cloud, then mass loss in the outflow dominates by an
order of magnitude over the mass accreted onto the central object, and
can be taken as a good estimate of the total mass loss rate. For more evolved flows less of the wind/jet momentum may be transferred to the CO and in the most evolved sources the accretion rate may begin to dominate over the mass loss in the outflow.
The outflow mass loss rate ![]() can be calculated from the momentum
flux
can be calculated from the momentum
flux ![]() by dividing by the mean outflow velocity
by dividing by the mean outflow velocity ![]() .
.
![]() is
a difficult quantity to estimate accurately. At low velocities it is
difficult to separate outflow material from protostellar core. Any
mass at high velocities can also make a large difference to
is
a difficult quantity to estimate accurately. At low velocities it is
difficult to separate outflow material from protostellar core. Any
mass at high velocities can also make a large difference to ![]() with
correspondingly high uncertainties. Making an estimate using
with
correspondingly high uncertainties. Making an estimate using
![]() where
where
![]() is the
integrated spectrum over the observed inner section of the outflow, we
calculate values for individual flows which range from
1-10 km s-1 depending on where the integration limits - inner
and outer velocity channel cutoffs - are set. We take a value of
is the
integrated spectrum over the observed inner section of the outflow, we
calculate values for individual flows which range from
1-10 km s-1 depending on where the integration limits - inner
and outer velocity channel cutoffs - are set. We take a value of
![]() as typical, in agreement with previous estimates
of P and M (Zhang et al. 2005; Knee & Sandell 2000), with an uncertainty
of a factor of 2.
as typical, in agreement with previous estimates
of P and M (Zhang et al. 2005; Knee & Sandell 2000), with an uncertainty
of a factor of 2.
The resulting mass loss rates in the outflow range from 1 ![]() 10-7-6
10-7-6 ![]()
![]() ,
from the
momentum fluxes in Table 1, and assuming a factor of 10
to take into account inclination and optical depth into account (see
Sect. 4 and Bontemps et al. 1996). These core mass loss
rates are similar to those calculated by Fuller & Ladd (2002) from the
rarer CO isotopologues in molecular cores. Mass loss rates of above
,
from the
momentum fluxes in Table 1, and assuming a factor of 10
to take into account inclination and optical depth into account (see
Sect. 4 and Bontemps et al. 1996). These core mass loss
rates are similar to those calculated by Fuller & Ladd (2002) from the
rarer CO isotopologues in molecular cores. Mass loss rates of above
![]() have also been found for massive flows
(Zhang et al. 2005; Churchwell 1997; Beuther et al. 2002) and it is not a surprise to
find rates approaching this in Perseus, which is forming stars up
to spectral type B.
have also been found for massive flows
(Zhang et al. 2005; Churchwell 1997; Beuther et al. 2002) and it is not a surprise to
find rates approaching this in Perseus, which is forming stars up
to spectral type B.
The destruction timescale ![]() of the core at the current
mass loss rate can be calculated by dividing the current core mass
by the total mass loss rate, including the optical depth/inclination
correction factor of 10. These timescales are plotted in
Fig. 7 and range from 0.2-60 Myr, with a
mean
of the core at the current
mass loss rate can be calculated by dividing the current core mass
by the total mass loss rate, including the optical depth/inclination
correction factor of 10. These timescales are plotted in
Fig. 7 and range from 0.2-60 Myr, with a
mean
![]() Myr. These destruction timescales are
then lower limits to the lifetime remaining to each core, if outflows
are the only source of mass loss and outflows only become weaker over
time. This is believed to be true for all but the youngest Class 0
sources.
Myr. These destruction timescales are
then lower limits to the lifetime remaining to each core, if outflows
are the only source of mass loss and outflows only become weaker over
time. This is believed to be true for all but the youngest Class 0
sources.
The sources with the longest lifetimes are the sources with the
highest mass to momentum flux ratios. As luminosity and momentum flux
are correlated (Fig. 4), these are also the sources with
high mass-to-luminosity ratios and cold temperatures, a signpost of an
early Class 0 source. Indeed, we find that the Class 0 sources b1-c
(1), b1-d (4), IRAS 03292+3039 (76) and the newly identified protostar
IC 348-SMM3 (15, Paper I, Walawender et al. 2006) have long lifetimes
(>10 Myr). In all cases this is due to low momentum flux for the
given core mass. Sources with particularly short destruction
timescales ![]() 104 years are IRAS 03301+3057 (7), B1 SMM11 (10)
and HH7-11 MMS (43). These sources have little mass in their
cores and are believed to be Class I sources near the end of the
embedded phase. Thus the objects with the most extreme lifetimes are
Class 0 for the longest lifetimes and Class I for the shortest
lifetimes. The absence of short lifetimes for low
104 years are IRAS 03301+3057 (7), B1 SMM11 (10)
and HH7-11 MMS (43). These sources have little mass in their
cores and are believed to be Class I sources near the end of the
embedded phase. Thus the objects with the most extreme lifetimes are
Class 0 for the longest lifetimes and Class I for the shortest
lifetimes. The absence of short lifetimes for low
![]() sources is
because only high
sources is
because only high
![]() sources can produce a low
sources can produce a low
![]() ,
and these
tend to have a long lifetime. Low-mass sources have lower optical
depth in their cores and higher
,
and these
tend to have a long lifetime. Low-mass sources have lower optical
depth in their cores and higher
![]() for the same evolutionary
state, as discussed in Paper II.
for the same evolutionary
state, as discussed in Paper II.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{6467f9.ps}\end{figure}](/articles/aa/full/2007/34/aa6467-06/Timg86.gif) |
Figure 8: Histograms of core destruction timescales for Class 0 (solid) and Class I (dotted) protostars. Sources with upper limits on the lifetime are excluded. |
The mean destruction timescale for Class Is (6 Myr) is shorter than for Class 0s (14 Myr), suggesting that there might be some evolution between Class 0 and Class I, with mass
declining faster than outflow force. Yet the evidence for evolution
is weak: the scatter in ![]() is large with both classes
showing a range of destruction timescales from a few times 105 to
is large with both classes
showing a range of destruction timescales from a few times 105 to
![]() 108 years at the current outflow rate, as shown in the
histogram of lifetimes (Fig. 8), and a K-S test
confirms a 43% probability that these populations could be drawn
from the same underlying distribution.
108 years at the current outflow rate, as shown in the
histogram of lifetimes (Fig. 8), and a K-S test
confirms a 43% probability that these populations could be drawn
from the same underlying distribution.
The mean lifetime of the protostellar stage is estimated to be
1.5-4 ![]() 105 years
(Wilking et al. 1989; Kenyon & Hartmann 1995; Kenyon et al. 1990; Greene et al. 1994; Hatchell et al. 2007). This is
significantly shorter than our mean
105 years
(Wilking et al. 1989; Kenyon & Hartmann 1995; Kenyon et al. 1990; Greene et al. 1994; Hatchell et al. 2007). This is
significantly shorter than our mean ![]() of 107 years
for the removal of the core mass by outflows. It was also
recently suggested by Arce & Sargent (2006) that outflows may play an
important role in mass loss and core evolution during the Class I
phase. However, for the majority of sources, Class 0 and Class I,
either we have overestimated the timescales due to systematic errors
or the bulk of the mass is removed by a means other than molecular
outflows. This is compounded by the fact that not all of the mass
accelerated in the low velocity flow will have velocities sufficient
to remove it from the gravitational field of the central object, so
the outflows then give an upper limit on the mass loss rate to the
protostellar core.
of 107 years
for the removal of the core mass by outflows. It was also
recently suggested by Arce & Sargent (2006) that outflows may play an
important role in mass loss and core evolution during the Class I
phase. However, for the majority of sources, Class 0 and Class I,
either we have overestimated the timescales due to systematic errors
or the bulk of the mass is removed by a means other than molecular
outflows. This is compounded by the fact that not all of the mass
accelerated in the low velocity flow will have velocities sufficient
to remove it from the gravitational field of the central object, so
the outflows then give an upper limit on the mass loss rate to the
protostellar core.
There are several factors which could introduce systematic errors in the calculation, which might result in an overestimate of the core destruction timescales. We may have overestimated the core masses: as discussed in Paper II, our core masses lie at the high end of the range consistent with the data, and could be overestimated by a factor of 4 or more - though half of this is due to the uncertain distance, which affects dust and CO masses equally, so again it is hard to see how this can explain more than a factor of 2 difference between protostellar lifetimes and core destruction rates by outflows. The outflow mass loss rates are calculated using several uncertain factors in the conversion of CO 3-2 intensity to mass. Firstly, there is the optical depth and inclination correction, for which we assumed a factor of 10, and the outflow temperature, for which we assumed 50 K, though this cannot affect the masses by more than a factor of 1.5. The mean velocity is also uncertain to a factor 2 but the destruction timescales would only reduce if it were lower than the assumed 5 km s-1.
If protostellar cores are not destroyed by outflows and accretion, where does the mass go? A possibility is that we are detecting material that will ultimately form not single stars but small clusters, and stars will continue to form until the mass is used up, as is seen in hydrodynamical models (e.g. Bate et al. 2003). Many of the most massive cores are already known to contain multiple protostars (Sect. 4, Paper II). A further possibility is that some cores will ultimately form massive stars and the molecular cores will be destroyed by ionisation. Finally, as mass is lost from the system and the core heats up some material may become gravitationally unbound and dissipate.
We have searched for molecular outflows towards 51 of the 103 known submm cores in Perseus listed in Paper II and based on the SCUBA (Paper I) and Bolocam (Enoch et al. 2006) surveys. The outflow sample is biased towards the higher luminosity submm cores but the fraction of cores sampled is fairly independent of mass except at the lowest masses. The main results of this study are the following:
Acknowledgements
Our thanks go to Jane Buckle, Ned Ladd and others who carried out the 12CO observations, and to an anonymous referee for prompting several improvements to the paper. The James Clerk Maxwell Telescope is operated by the Joint Astronomy Centre on behalf of the Particle Physics and Astronomy Research Council of the United Kingdom, the Netherlands Organisation for Scientific Research, and the National Research Council of Canada. J.H. acknowledges support from DFG SFB 494 and the PPARC Advanced Fellowship programme. This research made use of the SIMBAD query facility of the Centre de Données Astronomiques de Strasbourg and extensive use of the Karma visualisation package developed by Richard Gooch at CSIRO (Gooch 1996), which includes an implementation of the Renzogram developed by Renzo Sancisi of the Kapteyn Institute in Groningen.
Two measured quantities are involved in calculating the fraction of
protostars (outflow sources) in each mass bin. The first is the
observed fraction of outflow sources in each mass bin m, B = b/n (nis the total observed sources in the bin). The second is the
detection probability in that mass bin calculated from the simulation:
A = a/N (N is the total simulated sources in the bin). Both a and
b are expected to follow a binomial distribution so we can easily
calculate the corresponding uncertainties on B and C: they are
just
![]() and
and
![]() respectively, where
respectively, where
![]() is the binomial distribution for k successes from n trials with
probability p. With our estimates for the detected outflow fraction A and detection probability B we can then estimate the true protostellar fraction in the bin C = B/A.
is the binomial distribution for k successes from n trials with
probability p. With our estimates for the detected outflow fraction A and detection probability B we can then estimate the true protostellar fraction in the bin C = B/A.
Given that a and b are binomially distributed, we can also calculate the
probability distribution for C=A/B by integrating the probability space P(A,B) where B = A/C is satisfied.
| P(C) | = | ||
| = | |||
| = |