A&A 472, 141-153 (2007)
DOI: 10.1051/0004-6361:20042120

The evolution of interstellar clouds in a streaming hot plasma including heat conduction[*]

W. Vieser1,2 - G. Hensler1


1 - Institute of Astronomy, University of Vienna, Türkenschanzstr. 17, 1180 Vienna, Austria
2 - Christoph-Probst-Gymnasium, Talhofstr. 7, 82205 Gilching, Germany

Received 5 October 2004 / Accepted 13 October 2006

Abstract
Context. The interstellar medium contains warm clouds that are embedded in a hot dilute gas produced by supernovae. Because both gas phases are in contact, an interface forms where mass and energy are exchanged. Whether heat conduction leads to evaporation of these clouds or whether condensation dominates has been analytically derived. Both phases behave differently dynamically so that their relative motion has to be taken into account.
Aims. Real clouds in static conditions that experience saturated heat conduction are stabilized against evaporation if self-gravity and cooling play a role. Here, we investigte to what extent heat conduction can hamper the dynamical disruption of clouds embedded in a streaming hot plasma.
Methods. To examine the evolution of giant molecular clouds in the stream of a hot plasma we performed two-dimensional hydrodynamical simulations that take full account of self-gravity, heating and cooling effects and heat conduction by electrons. We use the thermal conductivity of a fully ionized hydrogen plasma proposed by Spitzer and a saturated heat flux according to Cowie & McKee in regions where the mean free path of the electrons is large compared to the temperature scaleheight.
Results. Significant structural and evolutionary differences occur between simulations with and without heat conduction. Dense clouds in pure dynamical models experience dynamical destruction by Kelvin-Helmholtz (KH) instability. In static models heat conduction leads to evaporation of such clouds. Heat conduction acting on clouds in a gas stream smooths out steep temperature and density gradients at the edge of the cloud because the conduction timescale is shorter than the cooling timescale. This diminishes the velocity gradient between the streaming plasma and the cloud, so that the timescale for the onset of KH instabilities increases, and the surface of the cloud becomes less susceptible to KH instabilities. The stabilisation effect of heat conduction against KH instability is more pronounced for smaller and less massive clouds. As in the static case more realistic cloud conditions allow heat conduction to transfer hot material onto the cloud's surface and to mix the accreted gas deeper into the cloud.
Conclusions. In contrast to pure dynamical models of clouds in a plasma and to analytical considerations of heat conduction that can evaporate such clouds embedded in a hot plasma, our realistic numerical simulations demonstrate that this destructive effect of KH instability is significantly slowed by heat conduction so that clouds can survive their passage through hot gas.

Key words: ISM: clouds - conduction - hydrodynamics - instabilities

1 Introduction

1.1 The multi-phase interstellar medium

The Interstellar Medium (ISM) is frequently described as an inhomogeneous ensemble of three phases (Mc Kee & Ostriker 1977: MO77). The cold neutral phase with temperature $T \sim 80~ \mbox{ K}$ and density $n \sim 40 ~\mbox{ cm}^{-3}$ is represented by the cores of molecular clouds which are confined by a warm neutral to slightly ionized medium ( $T \sim 8000~ \mbox{ K}$, $n \sim 0.3 ~\mbox{ cm}^{-3}$). These two components are in pressure equilibrium if the gas is externally heated and can cool radiatively (Field et al. 1969). According to MO77 they are embedded in a third phase of the ISM: the hot dilute intercloud medium (HIM) with $T \sim 10^6~ \mbox{ K}$ and $n \sim 10^{-3} {-} 10^{-4} ~\mbox{ cm}^{-3}$. Since this component is produced locally by supernova explosions at even higher temperatures and densities, originally it cannot be in pressure equilibrium with the cooler phases and therefore has to expand. During this expansion shocks arise and the HIM penetrates the ambient clumpy ISM. Denser clouds cannot be swept-up by the shock front but are overrun and become engulfed by the HIM. Because of hot gas expansion the relative velocity between both gas phases leads to strong distortion of the clouds, resulting in a stripped-off gas tail. Clouds of this type can be found as remnants of larger clouds in galactic chimneys such as the one associated with the H II region W4 (Heyer et al. 1996; Taylor et al. 1999) or behind shock fronts of supernovae. Due to the strong discrepancy in the physical states between the phases an interface has to form where the hot phase and the molecular cloud are in contact. Temperatures and densities are connected through steep gradients that lead to energy and mass transfer.

This situation occurs in many astrophysical phenomena such as High-Velocity Clouds (HVCs), H I structures characterized by radial velocities that are incompatible with simple models of the differential rotation of the galactic disk (see Wakker & van Woerden 1997, for a recent review). Interferometer measurements of the 21 cm H I line at 1$^\prime$ resolution show several small clumps embedded in larger emission regions (Wakker & Schwarz 1991). This, along with their line width, led Wakker & Schwarz to conclude that the HVCs have a multi-phase structure consisting of a cold, dense core and a warmer, more tenuous halo. Distance measurements of the cloud complexes remain difficult. For at least two of them upper limits for their distances are deduced by Danly et al. (1993), Keenan et al. (1995) and van Woerden et al. (1997) which place them in the galactic halo. From absorption line and X-ray observations it is well established that the galactic halo is filled with hot gas with a scaleheight of 4 kpc (Pietz et al. 1998) so that the HVCs have to interact with the hot gas. ROSAT observations show an increase of X-ray emission at the edges of the clouds that can be assumed as evidence for the existence of a hot interface (Kerp et al. 1994, 1995). The detection of velocity bridges (Pietz et al. 1996), connections of H I gas in velocity-space-diagrams, could also stem from the interaction of HVCs with low or intermediate-velocity gas. Although the origin of most of the complexes is still speculative, HVCs are a classical example of cold multi-phase structures moving through a hot plasma.

Another possibility for the scenario described above is much more massive and larger proto-globular cluster clouds (PCCs) with temperatures near 104 K and densities several hundred times that of the surrounding gas. They therefore are gravitationally unstable at Jeans masses larger than 106 $M_{\odot}$. An upper limit for their mass can be approximated by the critical mass for an isothermal sphere that is embedded in a surrounding medium with pressure $P_{\mbox{\tiny {ISM}}}$ (Ebert 1955; Bonner 1965):

 \begin{displaymath}{ } M_{\mbox{\tiny max}} = 1.2 \left ( \frac{k_{\rm B}T}{\mu} \right )^2 G^{-3/2} P^{-1/2}_{\mbox{\tiny {ISM}}} \end{displaymath} (1)

where G is the gravitational constant, $k_{\rm B}$ Boltzmann's constant, T a PCC temperature and $\mu$ its mean molecular weight. These clouds are assumed to originate from condensations of thermally unstable gas with temperatures of some million Kelvin in the early epoch of galaxy formation and can be envisaged as progenitors of globular clusters (Fall & Rees 1985). The PCCs had to resist their gravitational collapse until star formation ignites with a very high efficiency. This condition is not easily fulfilled because the PCC is accelerated by the gravitational potential of the forming protogalaxy. While moving through the hot halo it will become subject to the growth of Kelvin-Helmholtz (KH) and Rayleigh-Taylor (RT) instabilities (Drazin & Reid 1981).

1.2 Numerical models of clouds in a hot plasma stream

To investigate an influence of KH and RT instabilities on the evolution of molecular clouds several authors have used numerical simulations. Murray et al. (1993) compared the evolution of clouds embedded in the subsonic stream of a dilute medium with and without self-gravity. Radiative losses are neglected and the gravitational potential of the clouds remain fixed to the initial value of the calculation. Models without self-gravity and cloud masses $M_{\mbox{\tiny cl}} \ll M_{\mbox{\tiny max}}$ break up after only a few dynamical times $\tau_{\mbox{\tiny dyn}} = R_{\mbox{\tiny cl}}/c_{\mbox{\tiny cl}}$, where $R_{\mbox{\tiny cl}}$ is the cloud radius and  $c_{\mbox{\tiny cl}}$ is the sound speed inside the cloud. The mass loss after 2.5  $\tau_{\mbox{\tiny dyn}}$ is 20% and increases to 75% after 3.8  $\tau_{\mbox{\tiny dyn}}$. On the other hand, gravitationally bound clouds with a gravitational acceleration $g = g_{\mbox{\tiny crit}}$, the value where perturbations with wavelengths of the order of $R_{\mbox{\tiny cl}}$ are totally damped, show a different evolution. The value for $g_{\mbox{\tiny crit}}$ results from the relative velocity U, the cloud density $\rho_{\mbox{\tiny cl}}$ and the density of the background material $\rho_{\mbox{\tiny bg}}$ to $g_{\mbox{\tiny crit}} = 2 \pi U^2 \rho_{\mbox{\tiny bg}} / ( \rho_{\mbox{\tiny cl}} R_{\mbox{\tiny cl}} ) $.

The gravity is sufficient to stabilize the cloud although the cloud edge is distorted. After 3.2  $\tau_{\mbox{\tiny dyn}}$only 2% of the initial cloud mass is lost and after 10 $\tau_{\mbox{\tiny dyn}}$, 11%. Severing (1995) improved the simulations done by Murray et al. (1993) by solving the Poisson equation for self-gravity self-consistently at each timestep and by including heating and cooling effects. The cooling takes a collisionally dominated plasma in thermal and ionization equilibrium into account (Böhringer & Hensler 1989) and is balanced by heating for a cloud at rest. He demonstrated that clouds in a stream with Mach number 0.1 and with $g > g_{\mbox{\tiny crit}}$ gain mass while at higher but still subsonic Mach numbers and with $g < g_{\mbox{\tiny crit}}$ similar results to those by Murray et al. are achieved. Dinge (1997) applied cooling only to the gas ablated from the cloud and showed that cooling tends to accelerate the destruction of the cloud by RT instability. However, this arises due to the fact that the stripped cloudlets hit the cloud from the rear and thus trigger soundwaves which move through the cloud and stretch it along the symmetry axis. Globally, his results agree qualitatively with those of the former authors.

Vietri et al. (1997) examined the influence of radiative losses on the evolution of KH instabilities. By analytic approximations they proved that plane parallel identical fluids are destabilized if they stream relative to each other at high Mach numbers while low Mach number flows tend to be more stable. For fluids having different densities, cooling processes exacerbate the KH instabilities and all Mach numbers become unstable although with moderate growth rates. For clouds without self-gravity this means that KH instabilities cannot be suppressed. The instability is constrained to a small volume around the surface because cooling and heating timescales are shorter than the dynamical ones so that the instability cannot extend much beyond the interface.

In addition, observationally derived structure parameters allow the conclusion that HVCs are bound by a significant Dark Matter halo mass. Quilis & Moore (2001) studied with hydrodynamical simulations the behavior of HVCs passing the dilute hot halo gas of a typical disk galaxy at large distances. The main purpose of their numerical models was to compare the head-tail structure with observations to study the necessity for a Dark Matter content and a possible lower density limit of the surrounding intergalactic medium (IGM). Although they do not trace the evolution with respect to mass loss and structure survival (e.g. the pure gas clouds are shown after 3 Myr only), the main conclusions are two-fold, namely, at first that the observed head-tail structures with sufficient densities are produced if the wind density of the IGM exceeds $n_{\rm IGM} \geq 10^{-4}$ cm-3 due to ram-pressure stripping (RPS) but independent of the existence of a DM halo. This supports the galactic fountain scenario for their origin because the outermost IGM is expected to fall short of this density threshold. Secondly, the velocity was varied between 200 and 400 km s-1 without any substantial change in the structure.

1.3 Heat conduction

Stable models for Giant Molecular Clouds (GMCs) like HVCs and PCCs assuming hydrostatic and thermal equilibrium consist of large temperature and density gradients at the surfaces of the clouds where the energy densities of the surrounding ISM and the cloud become equal.

There are indications that the observed H I masses of some HVCs are orders of magnitude too low to provide gravitational stabilization, so they must be confined by external pressure (Konz et al. 2002). On the other hand, the core-halo structure seen in some HVCs (e.g. Wolfire et al. 1995) may result from minihalos composed of gas and dark matter that would likely move together as the clouds fall onto the Milky Way (Blitz et al. 1999). In this picture, the largest HVCs are gravitationally bound by the dark matter rather than pressure confined (Braun & Burton 1999, 2000).

Because of the large temperature gradients and the high temperature of the surrounding medium of the order of some million Kelvin, heat conduction must play a substantial rôle in the evolution of such clouds.

Analytical studies of the influence of heat conduction on the evolution of clouds at rest were undertaken by several authors: Cowie & McKee (1977, hereafter: CM77) investigated the evaporation of spherical clouds in general. For the classical regime described by a collision-dominated plasma they used the conductivity of Spitzer (1962). In this case, the heat flux due to heat conduction can be written as

\begin{displaymath}\vec{q}_{\mbox{\tiny class}} = - \kappa \cdot \vec{\nabla} T \end{displaymath} (2)

with

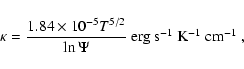\begin{displaymath}\kappa = \frac{1.84 \times 10^{-5} T^{5/2}}{\ln \Psi}~ \mbox{erg s$^{-1}$\space K$^{-1}$\space cm$^{-1}$ } , \end{displaymath} (3)

where the Coulomb logarithm is

\begin{displaymath}\ln \Psi = 29.7 + \ln \left [ \frac{T_{6,\rm e}} {\sqrt{n_{\rm e}} } \right ] , \end{displaymath} (4)

with the electron density $n_{\rm e}$ (in cm-3) and the electron temperature $T_{6,\rm e}$ in units of 106 K.

In a collisionless plasma the diffusion approximation for the heat flux breaks down because the mean free path of electrons becomes comparable to or even larger than the temperature scaleheight. In this so-called saturated regime described by a collisionless plasma, CM77 used a flux-limited heat flux. This takes charge conservation into account and yields results in good agreement with more sophisticated treatments (e.g. Max et al. 1980) and with numerical simulations of laser heated plasmas (Morse & Nielsen 1973; Mannheimer & Klein 1975). The saturated heat flux as an upper limit takes the form (CM77)

 \begin{displaymath}{ } \vert\vec{q}_{\mbox{\tiny sat}}\vert = 5 \Phi_{\rm s} \rho c^3 \end{displaymath} (5)

with the sound speed c. $\Phi_{\rm s}$ is an efficiency factor less than or of the order of unity, which embodies some uncertainties connected with the flux-limited treatment and flux suppression by magnetic fields ( $\Phi_{\rm s} =1$ in our calculations).

For an abrupt change of the conductivity from the classical to the saturated regime this leads to an envelope around the cloud consisting of three layers: a saturated zone embedded in an inner and outer classical zone. CM77 obtain a classical mass-loss rate of

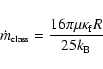\begin{displaymath}\dot{m}_{\mbox{\tiny class}} = \frac{16 \pi \mu \kappa_{\rm f} R}{25 k_{\rm B}} \end{displaymath} (6)

where $\kappa_{\rm f}$ is the conductivity evaluated for the unperturbed hot medium far away from the cloud. R is the cloud radius and $\mu$ the mean molecular weight. The mass-loss rate is lower for the saturated case. In McKee & Cowie (1977) they included radiative losses in their studies. As a criterion to separate the classical and the saturated case for a cloud of radius R embedded in a hot gas with temperature $T_{\rm f}$ and electron density  $n_{\rm ef}$, CM77 introduced a global saturation parameter $\sigma_0$ which is the ratio of the electron mean free path to the cloud radius

 \begin{displaymath}{ } \sigma_0=\frac{0.08 \kappa_{\rm f} T_{\rm f}}{\Phi_{\rm ... ...R} = \frac{1.23 \times 10^4 T^2_{\rm f}}{n_{\rm ef} R} \cdot \end{displaymath} (7)

For $\sigma_0 < 0.027/\Phi_{\rm s}$ material condenses onto the cloud because radiative losses exceed the conductive heat input. For $0.027/\Phi_{\rm s} < \sigma_0 \le 1$ the cloud suffers classical evaporation, while for $\sigma_0 > 1$ the evaporation is saturated. McKee & Begelman (1990) found similar results introducing the so-called Field length

 \begin{displaymath}{ } \lambda_{\mbox{\tiny F}} = \left[ \frac{ \kappa T}{n^2 ... ...th} \quad {\cal{L}}_{\rm M} \equiv \max~(\Lambda,\Gamma/n) , \end{displaymath} (8)

in which the cooling or heating is comparable to the conductive energy exchange. For $R > \lambda_{\mbox{\tiny F}}$ condensation occurs, otherwise the cloud will be evaporated. n is the particle density, $\Lambda$ the cooling rate, $\Gamma$ the heating rate.

These studies concluded that cold clouds in a dilute medium at a temperature of some million Kelvin always experience evaporation, but none of them examined more realistic multi-phase clouds or included self-gravity.

In a seperate paper (Vieser & Hensler 2005, hereafter: Paper I) we studied the differences caused by heat conduction on the evaporation/condensation competition between the fixed analytical description and the more realistic approach of flux saturation that adopts flexibly to the temporal physical state.

The main results of these investigations are as follows: the analytical mass loss rates of a cloud at rest in a hot and rarefied medium can be reproduced in numerical simulations for the pure classical case, because the evaporated material is pushed away with supersonic speed. The initial large density and temperature jump at the edge of the cloud remains unaltered during the calculation. Taking the more realistic saturated heat flux into account, a transition zone forms at the cloud edge in which the steep temperature and density gradients are reduced. This results in a lower evaporation rate than predicted. Simulations that include additional heating and cooling show an even more dramatic effect. The clouds can even gain material if radiative cooling exeeds the energy input by heat conduction.

Here we examine the evolution of molecular clouds in the stream of a hot, dilute medium. The treatment of heat conduction in the context of hydrodynamical simulations is described in Sect. 2. Analytical estimates of the influence of heat conduction are compared with the results of dynamical models with and without heat conduction in Sect. 3. Conclusions are drawn in Sect. 4.

2 Hydrodynamical treatment

The evolution of clouds in the subsonic stream of a hot plasma is studied by two-dimensional hydrodynamic simulations.

The hydro-part of this Eulerian, explicit code is based on the prescription of Rozyczka (1985) and has been extensively tested and used by different authors (e.g. Yorke & Welz 1996). The hydrodynamic equations have been formulated in cylindrical coordinates (r, z), assuming axial symmetry around the z-axis that is also the flow direction. The cloud's center is located on the z-axis. The differencing scheme used to discreticize the equations is second-order accurate in space because a "staggered grid'' is used . We applied operator splitting for time integration, because numerical experiments have shown that a multi-step solution procedure is more accurate than a single integration step based on preceding values (Stone & Norman 1992). The advection scheme of van Leer (1977) is employed. Since the basic code is explicit, the Courant-Friedrichs-Lewy (CFL) condition determines the maximum time step for the hydro-part. Because the conduction time step is smaller than the CFL one, the temperature distribution has to be calculated several times in one hydro time step. Von Neumann-Richtmyer artificial viscosity is used for the treatment of shocks. In order to prevent the cloud from moving out of the computational domain due to drag forces, the cloud center of mass is re-adjusted at each time step.

The grid parameters, the resulting physical domain and the resolution are listed in Table 1 for three representative models. The grid resolution is 28-33 zones per initial cloud radius.

Table 1: Numerical parameters for the simulations.

The boundary conditions on the upper and right-hand sides are semi-permeable to allow for an outflow of gas from the computational domain. The physical parameters at the lower boundary, the symmetry axis, are mirrored. The parameters, density and temperature at the left-hand boundary are fixed and the inflow of the plasma is initialized at a constant value. In order to trace the condensation of the streaming material onto the cloud a new quantity, "colour'', is introduced that is set in each cell to the density fraction of hot ISM. At the beginning only the cells around the cloud possess a non-zero "colour'' of value unity. During the calculation this quantity is advected like the others, such as mass density or energy density. The Poisson equation for self-gravity was solved at each tenth timestep because significant density changes of the cloud structure happen on a much longer timescale than the dynamical one. The energy equation includes heating, cooling and heat conduction:

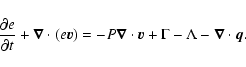\begin{displaymath}\frac{\partial e}{\partial t} + \vec{\nabla} \cdot (e \vec{v... ...ot \vec{v} + \Gamma - \Lambda - \vec{\nabla} \cdot \vec{q} . \end{displaymath} (9)

Here e denotes the energy density, $\vec{v}$ the velocity, P the pressure, $\Gamma$ the heating rate, $\Lambda$ the cooling rate and $\vec{q}$ the heat flux. The equation of state for an ideal gas is assumed to be valid:

\begin{displaymath}P=(\gamma - 1)e \qquad \mbox{with} \qquad \gamma = 5/3. \end{displaymath} (10)

The cooling function used assumes collisional ionisation equilibrium and is a combination of the function introduced by Böhringer & Hensler (1989) for T>104 K and solar metallicity and by Dalgarno & McCray (1972) for the lower temperature regime. The heating function considers cosmic rays (Black 1987), X-rays and the photoelectric effect on dust grains (de Jong 1977; de Jong et al. 1980).

The heat flux is calculated by taking both the classical and the saturated flux into account. In order to apply a smooth transition between the classical and saturated regimes we use the analytical form by Slavin & Cox (1992)

\begin{displaymath}\vec{q}=\vert\vec{q}_{\mbox{\tiny sat}}\vert \left( 1- \exp ... ...\vert\vec{q}_{\mbox{\tiny sat}}\vert} \right] \right) \cdot \end{displaymath} (11)

This guarantees that the lower flux is taken if both differ significantly. The heat flux due to electron diffusion is calculated separately using an implicit method which follows a scheme introduced by Crank & Nicolson (1947) and Juncosa & Young (1971). To couple the two directions in space the method of fractional steps by Yanenko (1971) is used.

A detailed description of the implementation of heat conduction in the existing hydro-code is given in Paper I, as well as a comparison of analytical solutions and numerical test cases to prove the reliability of the code.

The initial temperature and density profiles of the clouds are generated for hydrostatic and thermal equilibrium under the constraint of spherical symmetry:

 \begin{displaymath}{ } \vec{\nabla}\Phi = - \frac{1}{\rho} ~\vec{\nabla} P \end{displaymath} (12)


 \begin{displaymath}{ } \Gamma(\vec{r}) = \Lambda(\vec{r}) ; \end{displaymath} (13)

$\Phi(r)$ is the gravitational potential. Setting the temperature $T_{\mbox{\tiny ISM}}$ and particle density $n_{\mbox{\tiny ISM}}$ of the hot and tenuous outer medium, the energy density $e_{\mbox{\tiny ISM}}$ of the plasma is given. The density and temperature profile of the cloud is then calculated by integrating Eqs. (12) and (13) from inside-out using the core temperature of the cloud as a boundary condition and truncating the cloud's outer border where the energy density reaches $e_{\mbox{\tiny ISM}}$.

3 Models

Here we present the evolution of three different models. Their parameters are given in Table 2. For all models the temperature of the HIM is fixed to $5.6 \times 10^{6}$ K. In two models their density is set to $6.6 \times 10^{-4}$ cm-3to allow for comparison with static models of Paper I and for one model (E) is increased by one order of magnitude.

Table 2: Model parameters used in simulations as described in the text. Valid for all simulations: $T_{\mbox{\tiny ISM}} = 5.6 \times 10^{6}$ K i.e. sound velocity $c_{\mbox{\tiny ISM}} = 357$ km s-1, $v_{\mbox{\tiny ISM}} = v_{\mbox{\tiny rel}} = 0.3 c_{\mbox{\tiny ISM}} = 107$ km s-1.

In model U we consider a massive cloud of $6.4 \times 10^{4}$ $M_{\odot}$ representing a GMC or PCC. This cloud serves as a reference model for Paper I in which the fate of this cloud was investigated in an identical but static environment. Model E with a cloud mass of 486.7 $M_{\odot}$ and a cloud radius one order of magnitude smaller than model U represents a small molecular cloud. Clouds of this type can be found as remnants of larger clouds in galactic chimneys such as the one associated with the H II region W4 (Heyer et al. 1996; Taylor et al. 1999) or behind shock fronts of supernovae. The size of model K is similar to model E but the mass is decreased to 15.9 $M_{\odot}$ to reach an almost homogeneous density distribution that can be compared in its evaporation rate with Eq. (6) which is valid for uniform clouds. This represents an extreme case of a small cloud that is only slightly gravitationally bound.

All models show a typical multi-phase structure. While Model U and E possess a dense core and a density decrease outwards, Model K is homogeneous. Their radial density profiles are plotted in Fig. 1. With respect to dealing with more realistic interstellar clouds with self-gravity and non-equilibrium boundary conditions, these models differ clearly from the situation implied by CM77.


  \begin{figure} \par\includegraphics[width=8cm,clip]{density.ps} \end{figure} Figure 1: Density distribution for the various initial models. Model U and E show a typical multi-phase structure whereas model K has a uniform density distribution.
Open with DEXTER

For comparison all models were studied with and without heat conduction. The parameters $\sigma_0$, $\lambda_{\mbox{\tiny F}}$ and $\tau_{\mbox{\tiny eva}}$ (evaporation time) are therefore only defined for calculations with heat conduction. In all models the hot gas streams subsonically with $v_{\mbox{\tiny ISM}} = 0.3$ Mach and all clouds are kept at rest so that the relative velocity $v_{\mbox{\tiny rel}}$ important for the KH instability (see Appendix B) is identical to $v_{\mbox{\tiny ISM}}$. Such a large velocity difference between clouds and the HIM is only observed for HVCs, PCCs, and interstellar clouds overtaken by supernova shocks. Here we wish to study dynamical effects on clouds in addition to heat conduction. For smaller relative velocities, as GMCs move through the ISM, the models will approach those of numerical heat conduction for clouds at rest in a static HIM (presented by us in Paper I).

The cloud masses were chosen to cover a range between 101-105 $M_{\odot}$. Because the initial model has to fulfill Eqs. (12) and (13), mass and radius are fixed by the initial central cloud density and external pressure and temperature.

The saturation parameter $\sigma_0$ (Table 2) indicates a moderately saturated heat conduction for model U and E while model K lies nearly in the suprathermal regime (Balbus & McKee 1982). The importance of heat conduction in these simulations is also indicated by the fact that the Field length $\lambda_{\mbox{\tiny F}}$ is much larger than the cloud radius $R_{\mbox{\tiny cl}}$which means that evaporation of the clouds is expected and that the temperature structure of the gas is dominated by conduction (Begelman & McKee 1990).

The different dynamical timescales $\tau_{\mbox{\tiny dyn}}$ defined as the sound travel time over one cloud radius, the timescales $\tau_{\mbox{\tiny KH}}$for the growth of KH instability (see Appendix B) and for evaporation are listed in Table 3. Because of the huge density contrast and the large gravitational acceleration of the models U and E, KH instability should be suppressed, at least at the beginning. Because of the stability reasons mentioned in Appendix B and because the cloud mass of model E is close to the lower stability limit, this cloud is expected to be disrupted during the calculation. Model U is further inside the mass limit than Model E and will therefore survive longer than the less massive cloud. Model K on the other hand should develop KH instability after $\tau_{\mbox{\tiny KH}} = 0.45~$Myr.

Although the evaporation time of Model U and E is too large to be reached during the simulation, we should be able to follow the disintegration process due to evaporation of Model K.

In all calculations of $\tau_{\mbox{\tiny eva}}$ the effect of saturation is considered.

Table 3: Timescales for the three models at their initial configuration.

3.1 Large, massive cloud (model U)


  \begin{figure} \includegraphics[width=11cm,clip]{u301_new.eps} \end{figure} Figure 2: Evolution of the density distribution for model U without heat conduction. The evolution is shown at the times 25 Myr ( upper panel), 50 Myr ( middle) and 75 Myr ( lower). Arrows indicate gas velocities scaling linearly with respect to the maximum velocity shown in the upper left. The greyscale represents the density distribution (logarithmic scale). The contour lines represent 5, 10, 50, 100, ... $\times \rho_{\mbox{\tiny ISM}}$. The thick contour encloses the gravitationally bound part of the cloud.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=11cm,clip]{u311.eps} \end{figure} Figure 3: Same as Fig. 2: model U with heat conduction.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=16cm,clip]{u_comb.eps} \end{figure} Figure 4: Comparison of the evolution of important quantities of model U in the case without (solid curve) and with heat conduction (dashed). a) Evolution of the bound cloud mass. The analytical cloud mass (dotted line) is calculated taking mass-loss due to evaporation into account. b) Thickness of the transition layer perpendicular to the stream. The thick solid and dashed lines represent the mean value for both cases. c) Evolution of the amount of accreted material. d) Evolution of the mean density.
Open with DEXTER

The inclusion of heat conduction tends to stabilize massive and large clouds as illustrated by comparing the density contours at the same times (25 Myr, 50 Myr and 75 Myr after the beginning of the calculations) for the model U without (Fig. 2) and with heat conduction (Fig. 3). Without heat conduction the edge of the cloud is torn by KH instability shortly after the beginning as mentioned in Appendix B. A very complex velocity structure with many vortices behind the cloud forms. The increase in the maximum velocity during the calculation is due to acceleration of the gas by Bernoulli's effect when it streams around the formed cloudlets. It is therefore only a local effect which does not affect the large cloud as a whole. In the presence of cooling stripped-off cloud material becomes thermally unstable and forms cloudlets that hit the cloud from the rear. As mentioned by Dinge (1997) these cloudlets produce soundwaves which propagate through the cloud. On the front side these waves produce distortions that can act as seeds for RT instability that lead to an elongation of the cloud perpendicular to the stream direction. This effect is artifically intensified by the applied numerical symmetry.

Material once collected on the z-axis sticks there and cannot be removed because the velocity in the radial direction is set to zero at the axis. A detailed analysis of this artefact and the influence of this axis effect is given in Appendix A.

The cloud develops a compound envelope, with a radially decreasing density in the core region and a diluted outer part of material that is only slightly gravitationally bound. The loss of gas by stripping and the recapture from the rear leads to a complex mass-loss function with unsteady losses and gains. The mass of individual cloudlets that escape into the ISM lies in the range of some ten solar masses.

Figure 4a shows the evolution of the gravitationally bound cloud mass of the simulations without and with heat conduction. For comparison the analytical result of the cloud mass is shown taking mass-loss by evaporation into account (Eq. (6)). From this figure we see: 1) the pure evaporation effect on a static homogeneous cloud from CM77 is the most destructive because of its shortest timescale, but it overestimates the strength of heat conduction and its heating effect; 2) the pure dynamical destruction by KH instability happens on a much longer timescale. As in a static self-gravitating and cooling cloud model (Paper I), saturated heat conduction yields stabilization against evaporation; this more realistic approach also reduces the dynamical mass loss. While in the static models this is solely caused by an increase of heat capacity due to energy transfer to denser regions, the dynamical destruction is reduced by weakening the KH effect. This also means that a cloud that is stabilized in the static case by heat conduction is ablated solely but less effectively by KH instability.

Obviously the dynamical interaction between the gas phases is the dominating effect for cloud destruction in all models.

After 81 Myr the cloud mass with heat conduction reaches a value approximately 7% larger than without, indicating that heat conduction reduces the ablation of material from the cloud. A comparison of Fig. 2 with Fig. 3 shows significant differences in both the cloud structure and its evolution. Heat conduction suppresses large-scale KH instabilities as indicated by the almost laminar flow pattern around the cloud. During the whole simulation only a single large circulation in the slipstream of the cloud is visible. This smoothing process can be understood by conducting electrons moving along the steepest temperature gradient, i.e. radially toward the cloud, so that the stream close to the contact interface is decelerated, the velocity gradient decreases and the transition layer (described in Appendix B) grows. Numerically, the transition layer is by definition the region in which the velocities transit from the HIM to the clouds' thermal value.

Figure 4b shows that over the entire simulation time the thickness of the transition layer perpendicular to the stream is, in the heat conduction case, nearly twice as thick as in the non-conductive case. Comparison with Fig. B.2 reveals that the transition layer without heat conduction lies in the instability zone while it approaches or even exceeds the critical layer thickness d for stability. This effect is also responsible for the more efficient accretion and incorporation of streaming material into the cloud visible in Fig. 4c. The lower velocities in the contact interface enable the streaming hot ISM to condense onto the cloud surface. Thereafter it is very efficiently mixed with cloud material and transported into deeper layers of the cloud by turbulent motion. This turbulence is also driven by heat conduction that acts as an additional energy source in low-density regions where it exceeds the cooling. Without heat conduction the accreted material is peeled off from the surface by the grazing high-velocity gas before it could be incorporated into the cloud.

The multi-phase cloud in our simulation can be divided into two parts (see Fig. 5): 1) regions smaller than $\lambda_{\mbox{\tiny F}}$where the heat conduction exceeds the cooling so that the density distribution becomes homogenized; 2) very dense regions, such as near the core where the density structure is unaffected by heat conduction. A further surprising result from the numerical models is that the heat conduction becomes less effective after the low-density outermost shells of the cloud are dissolved. The resistance of the major part of the cloud against the disruptive KH instability and evaporation processes can be revealed from the temporal behaviour of the mean density of the bound mass (see Fig. 4d). Until $2.5 \tau_{\mbox{\tiny dyn}}$ the decline of the mean density is due to the dissolution of the outer parts of the cloud. Thereafter the mean density increases again and remains nearly constant at a value of around 80% of the initial mean density. In contrast the decrease of the mean density in the model without heat conduction shows the continuous dispersion of the whole cloud by lowering the density also in the core regions. This leads to a flat gravitational potential which further destabilizes the cloud.

  \begin{figure} \par\includegraphics[width=12cm,clip]{e_cloud.eps} \end{figure} Figure 5: Snapshot of the density distribution for the simulation E without heat conduction ( upper part) and with heat conduction ( lower part). The evolution is shown at 22.5 Myr. Arrows indicate gas velocities scaling linearly with respect to the maximum velocity shown in the upper left. The greyscale represents the density distribution (logarithmic scale). The contour lines represent 5, 10, 50, 100, ... $\times \rho_{\mbox{\tiny ISM}}$. The thick contour encloses the gravitationally bound part of the cloud.
Open with DEXTER

3.2 Dense cloud (model E)

To investigate the effect of heat conduction on denser, less massive, i.e. more compact clouds we increase the external density $\rho_{\mbox{\tiny ISM}}$ by one order of magnitude. Because the evolution of this model is not as violent as the previous one, a snapshot of the evolution 22.5 Myr after the begining of the calculations is shown in Fig. 5 without (upper part) and with heat conduction (lower part) for comparison.


  \begin{figure} \par\includegraphics[width=16cm,clip]{e_comb_2.eps} \end{figure} Figure 6: Comparison of the evolution of important quantities of model E in the case without (solid curve) and with heat conduction (dashed). a) Evolution of the bound cloud mass. The analytical cloud mass (dotted line) is calculated taking mass-loss due to evaporation into account. b) Evolution of the mean density. c) Evolution of the specific internal energy. d) Evolution of the amount of accreted material.
Open with DEXTER

In the non-conductive case even after 22.5 Myr no KH instability is visible because of the stabilizing effect by the high gravitational acceleration at the cloud surface.

While the shape of the cloud remains unaltered, variations of the mean cloud density and the specific internal energy are present in Fig. 6c. These pulsations stem from quasiadiabatic oscillations with a timescale given by $\tau_{\mbox{\tiny ad}}=\sqrt{ 3 \pi/[ (3 \gamma - 4)\rm {G} \bar{\rho}] }$. $\bar{\rho}$ is the mean cloud density.

For model E and the adiabatic index $\gamma = 5/3$ , $\tau_{\mbox{\tiny ad}}$ is 7 Myr which agrees well with the obtained one. These oscillations originate from the interaction of the plasma stream with the cloud at the beginning of the simulation. This process triggers accoustic waves that run through the cloud and lead locally to density enhancements.

In addition, the static models (Paper I) demonstrate that heat conduction produces inward travelling sound waves which are able to transport energy from the conductive interface to the denser cloud interior. By this additional effect the cloud releases the transferred energy.

In the case with heat conduction, small-scale mixing at the cloud surface with the outer HIM leads to an increase of the cloud volume visible as a decrease in the mean density (Fig. 6b). The oscillations occurring in the non-conductive case are efficiently damped by turbulent motions of the cloud material driven by heat conduction. The incorporation of hot material into the cloud acts as an additional heating agent that raises the temperature and therefore the pressure of the cloud and results in an expansion. This temperature increase is reflected by the increase of the specific internal energy (Fig. 6c). Regions of the cloud near the vortex in the slipstream are especially heated and diluted because of the more efficient mixing there. This material is only slightly gravitationally bound and therefore preferentially stripped off the cloud which can be revealed by the distorted cloud shape in those regions. Also the small mass-loss of 2% at about 25 Myr (12.8  $\tau_{\mbox{\tiny dyn}}$) is caused by this effect. The distortion of the cloud to a more streamlined shape as visible in the lower part of Fig. 5 leads the flow around the cloud in a more laminar manner.

As in model U the amount of accreted material is again higher with heat conduction than without (Fig. 6d). This is caused by the suppression of the velocity differences in the transition layer. However, in the conductive model the absolute accretion rate normalized to the total mass is much higher here on absolute timescales (after 20 Myr e.g. 0.3% are accreted in model E at constant rate but almost 0.1% in model U) but lower on $\tau_{\mbox{\tiny dyn}}$(0.26% within 10 $\tau_{\mbox{\tiny dyn,E}}$ in model E, while 0.25% within 3  $\tau_{\mbox{\tiny dyn,U}}$ in model U).

In order to understand this effect quantitatively for the different parameters of the two models one can make a zeroth-order approach neglecting density and mass changes. An accretion rate $\Omega$ can be defined as $M_{\mbox{\tiny acc}}$ per dynamical time $\tau_{\mbox{\tiny dyn}}$ and reformulated by normalization to the total mass $M_{\mbox{\tiny tot}}$ as shown for model U in Fig. 4c and for model E in Fig. 6d, respectively, by

 \begin{displaymath}{ } \Omega = {\frac{M_{\mbox{\tiny acc}}}{M_{\mbox{\tiny tot}}}} \; M_{\mbox{\tiny tot}} \; \tau_{\mbox{\tiny dyn}}^{-1} \end{displaymath} (14)

where $\tau_{\mbox{\tiny dyn}}$ must not be further determined. Applying this relation, the ratio $\Omega_{\mbox{\tiny U}}/\Omega_{\mbox{\tiny E}}$ follows as

 \begin{displaymath}{ } {\frac{\Omega_{\mbox{\tiny U}}}{\Omega_{\mbox{\tiny E}}}... ...\tiny cl,E}}}{10 \; \tau_{\mbox{\tiny dyn,E}}} }\right) \cdot \end{displaymath} (15)

With Eq. (14), $M_{\mbox{\tiny acc}} = \Omega \; \tau_{\mbox{\tiny dyn}}$follows so that one can write the ratio $M_{\mbox{\tiny acc,U}}/M_{\mbox{\tiny acc,E}}$where the different $\tau_{\mbox{\tiny dyn}}$ cancel out with Eq. (15) and one obtains the value 421. This value agrees as an order-of-magnitude effect within the uncertainties and being aware of the simple estimates of the structure, if one assumes that the condensation $M_{\mbox{\tiny acc}}$ depends on the cloud's surface, the surrounding density and the Field length by:

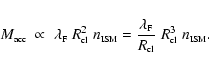\begin{displaymath}M_{\mbox{\tiny acc}} \; \propto \; \lambda_{\mbox{\tiny F}}... ...iny cl}}} \; R_{\mbox{\tiny cl}}^3 \; n_{\mbox{\tiny ISM}} . \end{displaymath} (16)

This ratio for models U and E is 361.

Compared to model U where heat conduction prevents the disruption of the cloud, in this model the cloud is already stabilized without heat conduction and condensation dominates the evolution. The dip in the mass loss curve (Fig. 6a) after 18 Myr is caused by the separation of a small cloudlet with successive rebounce so that it remains invisible in Fig. 6d. Evaporation, however, is then not directly caused by heat conduction. Instead, conduction expands the cloud and KH instabilities dissolve the back parts of the cloud. Figure 6a reveals that the total bound mass remains constant for the case without heat conduction but decreases with heat conduction only by 2% within 12.8 $\tau_{\mbox{\tiny dyn}}$. Interestingly both conductive models U and E experience an expansion that reduces the mean density by nearly 20%. Although heat conduction leads to a slight expansion of the cloud and, by this, to this minor fraction of mass loss, the analytical result in contrast requires evaporation of 30% of the cloud after 12.8  $\tau_{\mbox{\tiny dyn}}$. The analytical prescription overestimates the real effect by far, when both gas phases are dynamically different.

3.3 Small, homogeneous cloud (model K)

A third model describes an extreme case: model K represents a small cloud with no distinct core and a density contrast of almost one order of magnitude lower than the stable model E. The analytical consideration of the classical heat conduction (CM77), therefore, requires fast and efficient evaporation (see Table 3 and Fig. 9b). This cloud is only marginally gravitationally bound, so that its gravitational acceleration cannot sufficiently stabilize it against KH instability (see Appendix B). The timescale for the onset of KH instability is approximately $\tau_{\mbox{\tiny KH}} = 0.45$ Myr, i.e. almost half of $\tau_{\mbox{\tiny dyn}}$. The cloud should therefore be destroyed within a few dynamical timescales. The violent action of KH instability is easily visible in Fig. 7 where the density contours for Model K without heat conduction are shown in steps of 3.4 Myr after the beginning of the calculations. The density contours in the case with heat conduction are revealed in Fig. 8 for the same timesteps.


  \begin{figure} \includegraphics[width=9.7cm,clip]{k301new.eps} \end{figure} Figure 7: Same as Fig. 6: model K with heat conduction.
Open with DEXTER
  \begin{figure} \includegraphics[width=9.7cm,clip]{k311new.eps} \end{figure} Figure 8: Evolution of the density distribution for the simulation K without heat conduction. The evolution is shown at the times 3.4 Myr ( upper panel), 6.8 Myr ( middle) and 10.2 Myr ( lower). Arrows indicate gas velocities scaling linearly with respect to the maximum velocity shown in the upper left. The greyscale represents the density distribution (logarithmic scale). The contour lines represent 5, 10, 50, 100, ... $\times \rho_{\mbox{\tiny ISM}}$. The thick contour encloses the the domain where $\rho_{\mbox{\tiny cl}} > 100 \times \rho_{\mbox{\tiny ISM}}$.
Open with DEXTER

Figure 7 shows that the cloud model K is already very fragile at the beginning of the simulation. The cloud is soon perpendicularly stretched because of the low pressure at both sides due to Bernoulli's theorem. The density in these regions is lowered and its cooling ability diminished. This, together with the mixing of hot ISM into the cloud due to small scale perturbations triggered by means of KH instability leads to an increase of the temperature which can be discerned as an increase of the specific internal energy (Fig. 9b). This energy input is sufficient to unbind the cloud material. From Fig. 9b one also sees that the stripped-off gas contains a larger specific internal energy than the rest, i.e. energy that is acquired from dynamically excited turbulence is lost. Due to the initiated turbulent velocity field inside the cloud the mass distribution changes throughout the calculation. Consequently, no distinct core can be formed. The low binding energy allows the cloud material to be caught by the gas flow and to be carried away at about 5 Myr (5.9  $\tau_{\mbox{\tiny dyn}}$). Because the stripped cloud material is disrupted into small packages, the mass-loss rate (Fig. 9a) shows a step-wise function. After about 10.8 Myr (12.8  $\tau_{\mbox{\tiny dyn}}$) the cloud is nearly destroyed and only 30% of the initial cloud mass has survived.

  \begin{figure} \par\includegraphics[width=16cm,clip]{k_comb.eps} \end{figure} Figure 9: Comparison of the evolution of important quantities of model K in the case without (solid curve) and with heat conduction (dashed). a) Evolution of the bound cloud mass. The analytical cloud mass (dotted line) is calculated taking mass loss due to evaporation into account. b) Evolution of the specific internal energy.
Open with DEXTER

The evolution in the case with heat conduction is very similar during the first 5 Myr to that without heat conduction. Both the elongation of the cloud and the mass-loss rate show nearly the same behaviour. In contrast to the non-conductive case, KH instability is suppressed and thus the additional heat input through mixing with the hot ISM is reduced. The temperature and therefore the specific internal energy rises only moderately (Fig. 9b). Consequently, the velocity field within the cloud is less turbulent so that a core can form. The cloud interior develops a relatively stable mass distribution with a dense core which stabilizes this model against mass loss at least twice as long (Fig. 9a). Due to heat conduction a transition layer with a radial decrease of the density and velocity gradient has formed and with this a radial temperature gradient along which the cloud material flows. Some material is lost after 7.5 Myr when a large cloudlet with a mass of about 30% of the whole cloud decouples from the elongated cloud at its top.

As in large massive clouds (model U) where the development of a transition zone near the cloud surface leads to a reduction of KH instability, the same is valid for small homogeneous clouds. No large-scale KH instability is seen although the initial state of the cloud is very unstable against it. At the end of the calculation the total mass of the cloud is about 30% higher in the case with heat conduction than without.

The heat conduction process leads to dynamical processes at the clouds' surface that decelerates the disintegration of the whole cloud by suppressing the large scale KH instability. In addition, considering cooling in the heat conduction description stabilizes this cloud against mass loss, while the analytical solution would again destroy the cloud by evaporation much more rapidly, within 6  $\tau_{\mbox{\tiny dyn}}$.

4 Discussion

In agreement with analytical results for the static case (CM77) we have proven that heat conduction must not be neglected in investigations of the evolution of interstellar clouds in a hot dilute plasma and, in general, of the coexistence of the multi-phase ISM. While CM77 indicate that all the clouds in this paper would undergo evaporation due to heat conduction, we demonstrated in Paper I and in Sect. 1.3 that a realistic approach that accounts for the electron conductivity properly leads to the opposite results, namely, that condensation dominates. The cloud conditions applied to our models differ from the consideration of CM77. In this paper we have shown with models that the fate of a cloud and its evolution is drastically changed by a gas stream and depend strongly on the mass and its internal structure of the cloud, i.e. mainly on its binding energy. In general, the relative motion of a subsonically hot plasma stream stabilizes the clouds.

Without heat conduction, clouds with their initial states close to or inside the KH-unstable regime suffer from huge mass loss in the form of stripped-off cloudlets. While a small homogeneous cloud (model K) is stable for about 5  $\tau_{\mbox{\tiny dyn}}$ and then strongly exposed to disruption into small gas packets, small dense clouds (model E) can avoid the transition into the KH-unstable state and resist the violent hot plasma so that mass loss or even any strong deformation of the cloud does not occur. Large massive clouds (model U) lose about 17% of their mass within 5  $\tau_{\mbox{\tiny dyn}}$ and may dissolve on larger timescales.

For the static case of the coexistence of two gas phases, namely, clouds embedded in a HIM, the mass transfer according to heat conduction can be calculated analytically (CM77). We have chosen plasma conditions that would require evaporation of cloud material and therefore mass loss from the cloud from analytical considerations. Under the dynamical action of a relative motion between the gas phases the conditions change with respect to the static case in two ways: dynamical instabilities can change the shape of the cloud and can increase its surface. In contrast to the analytical results, the state of the hot ISM remains constant because of its replenishment by the fixed streaming conditions and therefore cannot react to the evaporation and condensation process and by this e.g. self-regulate the mass transfer to find an equilibrium (see e.g. Köppen et al. 1998).

Large and massive clouds survive longer in the hot plasma flow with heat conduction than without. Because of electron invasion through the surface, a transition zone forms at the edge of the cloud where density and velocity gradients are lowered. A state can be reached where the KH instability is suppressed and the formerly unstable cloud becomes stabilized. This can be shown analytically and numerically reproduced (model U). Since the evaporation rate is much less than the one predicted by CM77 these facts lead to a cloud mass at the end of the calculation that is even slightly higher (7%) than in the case without heat conduction.

Although the maximum cloud mass implied here is much lower than those of HVC complexes moving through the galactic halo with masses of a few 106 $M_{\odot}$ such as Complex C (Wakker et al. 1988) or compact HVCs located in the intergalactic medium (Braun & Burton 1999), only clumpy substructures seem to decouple from complexes and approach the galactic disk and experience on their path through the halo interaction with the hot gas that leads to the observed head-tail structures (Brüns et al. 2000). Their masses, on the other hand, range from a few umpteen solar masses to a few 104 $M_{\odot}$, like recently found compact HVCs in the inner galaxy (Stil et al. 2006). Nevertheless, calculations with even higher masses are in preparation but it can be expected that the tendency to stabilize the cloud and to reduce the ablation of material from the cloud will continue. Heat conduction is therefore a physical process that enhances the dynamical stabilization and has to be taken into account in the consideration of the survival of HVCs.

For the PCCs, heat conduction offers a mechanism to incorporate metal-rich hot gas that becomes homogeneously mixed. Even with a low accretion fraction of only 0.3% a hot gas metal content of solar and above, which is reasonable e.g. from X-ray determinations of the halo gas around giant ellipticals (Matsushita et al. 2003), would lead to almost 1/100 $Z_{\odot}$. Globular clusters formed from PCCs and enriched by this accretion mechanism caused by heat conduction must be expected to show a large range of metallicities.

When star formation sets in, all protostars are formed from molecular clouds with nearly equal metallicity. The absence of a significant spread in [Fe/H] in most globular clusters (Freeman & Norris 1981; Fahlmann et al. 1985; Norris 1988) is an indication that the stars have formed out of well mixed metal-enriched substrates that could have been polluted by an external source (Murray & Lin 1990). This mechanism provides an alternative explanation to the self-enrichment scenario of globular clusters (Brown et al. 1991, 1995).

When looking at smaller clouds one has to distinguish between a homogeneous (model K) and a clearly centrally peaked density distribution (model E). In the latter case the gravitational potential is strong enough to stabilize the cloud against large-scale perturbations triggered by the dynamical action of the streaming ISM. The influence of the HIM is limited to an additional heat input due to heat conduction and small-scale mixing especially in regions near the vortex in the slipstream of the cloud. Because of the high density in the core regions, the additional heat input is nearly compensated by cooling. Only the rim of the cloud becomes diluted and so susceptible to evaporation. Thus, the mass loss (2%) is reduced by more than a factor of 15 with respect to the analytical approach ($\sim $30%). In this case the fate of the cloud depends only on small-scale, not on large-scale dynamics.

These results cannot be extrapolated to homogeneous clouds (model K), where already a small additional heat input is sufficient to unbind the whole cloud. Although KH instability is also suppressed in this case, the cloud becomes elongated by the Bernoulli effect, which is very efficient because of the flat gravitational potential. It is this large-scale phenomenon that peels off a large fragment of the cloud. Evaporation due to heat conduction is negligible in comparison to the mass loss due to the large-scale effects. Heat conduction acts instead as an agent to extend the survival time of the cloud by the suppression of KH instability and therefore the reduction of the mass-loss in comparison to the non-conductive case. While the analytical approach of model K leads to cloud destruction by evaporation within almost 6  $\tau_{\mbox{\tiny dyn}}$ (Fig. 9a), in the numerical simulation the dynamics stabilize the cloud and heat conduction extends the destruction time to more than 11  $\tau_{\mbox{\tiny dyn}}$. After the loss of a large fragment with 30% of the cloud mass, the total disruption of the cloud is most likely a consequence of the dynamics of the streaming ISM. It is therefore not surprising that the analytical evaporation rates of CM77 are incompatible with our calculations.

Comparing the CM77 evaporation rates with computed models for the static case (Paper I) reveal that condensation may occur for large clouds in temperature regimes where CM77 also predict evaporation.

The three presented models can only give a first insight into the fundamental importance of dynamics and additional heat conduction in the evolution of the ISM phases. Further investigations are necessary to determine the dependence of evaporation and condensation on the physical state of the phases. This is necessary for the simulation of galaxy evolution (see e.g. Samland et al. 1997; Hensler 1999).

The effect of magnetic fields on heat conduction must be discussed, especially when it is neglected, as in our models. When electrons of the HIM enter an interstellar cloud they transfer their energy to the cloud by collisions with mainly neutral HI atoms of density  $n_{\rm HI}$ and collisional cross section  $q_{\rm HI}$. Their collisional mean free path $\lambda_{\rm c,{\rm HI}}$/cm = ( $n_{\rm HI} \cdot q_{\rm HI})^{-1}$ is about 1016 cm. On the other hand, magnetic fields force charged particles with mass $m_{\rm e}$ moving with velocity $u_{\rm e,ISM}$ perpendicular to the B field vectors due to the Lorentz force to gyrate with the (Larmor) radius $a_{\rm L,e}$. For electrons this reads as

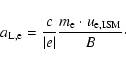\begin{displaymath}{a}_{\rm L,e} = \frac{c}{\vert e\vert} \frac{m_{\rm e} \cdot u_{\rm e,ISM}}{B} \cdot \end{displaymath} (17)

Since we assume in our modelling that at the clouds' surface, both gas phases achieve pressure equilibrium we can also set the magnetic pressure $P_{\rm mag} = B^2/8\pi$ in equilibrium. Replacing $m_{\rm e}\cdot u_{\rm e,ISM}^2$ by the ISM temperature $T_{\rm ISM}$, it cancels with that of the pressure and one gets $a_{\rm L,e} = 4.46\times 10^5~ {n}^{-1/2}_{{\rm H},\rm ISM}$.

The ratio of mean free path to electron Larmor radius then is

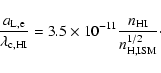\begin{displaymath}\frac{{a}_{\rm L,e}}{\lambda_{\rm c,{\rm HI}}} = 3.5\times 10^{-11} \frac{n_{\rm HI}}{n^{1/2}_{{\rm H},\rm ISM}} \cdot \end{displaymath} (18)

For weaker B fields than in gas pressure equilibrium the ratio can become much larger, i.e. the free electron motion is less hampered. But this only holds for the fraction of electrons moving perpendicular to the B vector, while electrons moving parallel to the B field are unaffected. Malyshkin & Kulsrud (2001), however, showed that random magnetic fields also reduce the diffusivity of electrons traveling along the B field lines. This reduction of free electron motion and thus heat conduction by magnetic fields can also be parametrized by $\Phi_{\rm s}$ as in Eq. (5).

Acknowledgements
The authors thank Tim Freyer, Miguel Avillez, and Dieter Breitschwerdt for stimulating discussions, and Tomek Plewa for providing us with his numerical code solving the heat conduction equation. The authors are grateful for very constructive comments of an anonymous referee. This work was partly supported by the Deutsche Forschungsgemeinschaft (DFG) under grant numbers HE 1487/5-3 and HE 1487/25-1. The computations were performed at the Rechenzentrum der Universität Kiel, the Konrad-Zuse-Zentrum für Informationstechnik in Berlin, and the John von Neumann-Institut für Computing in Jülich.

References

 

  
Online Material

Appendix A: Axis effects (model U$^\star $)

The numerical models in this paper are calculated assuming cylindrical symmetry. This method has numerical artefacts near the symmetry axis. Material, once fallen onto this axis, cannot be removed from it because of mirrored conditions, i.e. zero gradients. As a result a nozzle is formed at the front of the cloud, which Dinge (1997) interprets as RT instability. On the other hand, ablated material that is pushed towards the axis by vortices behind the cloud builds up elongated spurs. In contrast, in 3D simulations these clumps of a typical thickness of a few cells oscillate in the slipstream of the cloud because of asymmetrical instabilities. In order to test the influence of these artefacts the evolution of the clouds we switched to a 2D Cartesian grid and so removed the symmetry axis. Fully 3D simulations with sufficient spatial resolution including heat conduction are still too time consuming to be produced. The initial model of the simulated clouds are therefore no longer spheres but infinite cylinders. As a consequence, the velocity field, the gravitational potential and the density distribution of the initial model differ from the axisymmetric case but are close to model U.


  \begin{figure} \par\includegraphics[width=9cm,clip]{cau2.eps} \end{figure} Figure A.1: Evolution of the density distribution for the 2d simulation using a cartesian grid with heat conduction. The evolution is shown at the times 25 Myr ( upper panel), 50 Myr ( middle) and 75 Myr ( lower). Arrows indicate gas velocities scaling linearly with respect to the maximum velocity shown in the upper left. The contour lines represent 5, 10, 50, 100, ... $\times \rho_{\mbox{\tiny ISM}}$. The thick contour encloses the gravitationally bound part of the cloud.

The evolution of this model U$^\star $ is shown 25 Myr, 50 Myr and 75 Myr after the beginning of the calculations with consideration of heat conduction (Fig. A.1). Because of the infinite cylinder instead a sphere, the velocity of the stream near the top and the bottom of the cloud is much higher than in the simulations shown before. As a result, the onset of KH instability is facilitated. The tail of ablated cloud material at the rear of the cloud can wave in the stream. Regions of the tail that become too dilute are cut. Nevertheless a massive tail similar to model U forms. No spur forms at the front of the cloud and must therefore be identified as an artefact of the axisymmetric conditions.

Although there are some differences in the appearance of the clouds in cylindrical and Cartesian geometry, the global formation of a head-tail structure of the cloud remains the same in both geometries. The thin elongated structures stripped off the cloud in the Cartesian grid are comparable to the material that get stuck on the symmetry axis in cylindrical symmetry. In both cases the filaments leave the computational domain and do not influence the evolution of the gravitationally bound cloud. Therefore the use of a cylindrical symmetry is justified.

Appendix B: Stability analysis

B.1 Rayleigh-Taylor instability

If a cool, dense cloud moves through a hot, tenuous gas, its surface will become subject to KH and RT instabilities. If the cloud is massive enough so that the effective gravity is directed toward the cloud center, RT instabilities can be suppressed. The growth rate for the RT instability in the absence of a gravitational field is expressed as (Chandrasekhar 1961)

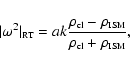\begin{displaymath}\vert\omega^2\vert _{\mbox{\tiny RT}} = a k \frac{\rho_{\mbo... ...ny ISM}}} {\rho_{\mbox{\tiny cl}}+\rho_{\mbox{\tiny ISM}}} , \end{displaymath} (B.1)

where k is the wavenumber of the perturbation, a the acceleration of the cloud due to the wind, $\rho_{\mbox{\tiny cl}}$ and $\rho_{\mbox{\tiny ISM}}$are the densities of the cloud and of the streaming medium, respectively. This means that perturbations with shorter wavelengths grow faster than larger ones. As long as the wavelength is small compared to the cloud radius, the net effect of RT instability is a small-scale mixing of the ISM with the cloud but does not lead to its disruption. The cloud is stabilized against RT by a gravitational field and RT is totally suppressed if the gravitational acceleration g is larger than the acceleration due to the wind (Murray et al. 1993).

B.2 Kelvin-Helmholtz instability

In order to study the influence of KH instability we perturb the incompressible fluid equations

\begin{displaymath}\rho \frac{\partial v_i}{\partial t} + \rho \sum_{j=1}^{3} v... ... g_i - \frac{\partial p}{\partial x_i} \qquad \quad [i=1,2,3] \end{displaymath} (B.2)


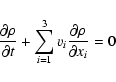\begin{displaymath}\frac{\partial \rho}{\partial t} + \sum_{i=1}^{3} v_i \frac{\partial \rho}{\partial x_i} = 0 \end{displaymath} (B.3)

and

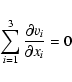\begin{displaymath}\sum_{i=1}^{3} \frac{\partial v_i}{\partial x_i} = 0 \end{displaymath} (B.4)

for a solenoidal velocity field according to Chandrasekhar (1961). The quantities density $\rho$, pressure p and velocity $\vec{v}$, are replaced by the perturbed ones $\rho + \delta\rho$, $p + \delta p$ and $\vec{v} = \vec{v_0}+\delta\vec{v}$. The acceleration due to the gravitational force $\vec{g}$ remains unperturbed. The initial velocity field $\vec{v_0}$for the KH stability analysis is zero except for vx(z) which is the flow velocity and therefore an arbitrary function of the height z. After linearization we have five partial differential equations (PDEs) for the five perturbed quantities. We now consider perturbations of the form

\begin{displaymath}\delta X \propto \exp~[ {\rm i} ( k_xx + k_yy + \omega t) ] . \end{displaymath} (B.5)

Inserting this into the five PDEs and combining them we have a differential equation for the z-dependence of the perturbation $\delta v_z$ which is perpendicular to the streaming vx
 
$\displaystyle {} \frac{\mbox{d}}{\mbox{dz}} \left[ \rho ( \omega + k_x v_x ) \l... ...c{\mbox{d} \rho}{\mbox{dz}} \right) \frac{\delta v_z}{ \omega + k_x v_x } \cdot$     (B.6)

This equation can be solved analytically for two homogeneous fluids of densities $\rho_{\mbox{\tiny ISM}}$ and $\rho_{\mbox{\tiny cl}}$ separated by a horizontal boundary and moving with horizontal velocities $v_{\mbox{\tiny ISM}}$and $v_{\mbox{\tiny cl}}$. Starting with a stable configuration, i.e. the density of the upper fluid $\rho_{\mbox{\tiny ISM}}$ is less than the lower one, we obtain the dispersion relation for $\omega(k)$

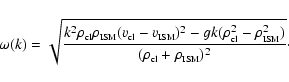\begin{displaymath}\omega(k) = \sqrt{\frac{ k^2 \rho_{\mbox{\tiny cl}} \rho_{\m... ...(\rho_{\mbox{\tiny cl}} + \rho_{\mbox{\tiny ISM}})^2} } \cdot \end{displaymath} (B.7)

Instability occurs for real values of $\omega(k)$, so there is a minimal wavenumber $k_{\mbox{\tiny min}}$ above which no stable mode exists. With $v_{\mbox{\tiny rel}} = v_{\mbox{\tiny cl}}- v_{\mbox{\tiny ISM}}$ and $\rho_{\mbox{\tiny cl}} \gg \rho_{\mbox{\tiny ISM}}$ this upper limit for stability reads:

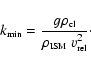\begin{displaymath}k_{\mbox{\tiny min}} = \frac{g \rho_{\mbox{\tiny cl}} } {\rho_{\mbox{\tiny ISM}} \: v_{\mbox{\tiny rel}}^2} \cdot \end{displaymath} (B.8)

For unstable wavenumbers the timescale for the exponential increase of the perturbation reads

 \begin{displaymath}{ } \tau_{\mbox{\tiny KH}} = \frac{1}{\omega(k)} \cdot \end{displaymath} (B.9)

Because most destructive perturbations are those with wavelengths of the order of the cloud radius ( $\lambda = R_{\mbox{\tiny cl}} = 2 \pi / k$) there is a critical gravitational acceleration $g_{\mbox{\tiny crit}}$ above which the cloud is stabilized:

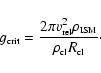\begin{displaymath}g_{\mbox{\tiny crit}}=\frac{2 \pi v^2_{\mbox{\tiny rel}} \rh... ...ny ISM}}} {\rho_{\mbox{\tiny cl}} R_{\mbox{\tiny cl}}} \cdot \end{displaymath} (B.10)

If a spherical cloud with uniform density is assumed, its gravitational acceleration is

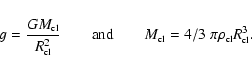\begin{displaymath}g=\frac{G M_{\mbox{\tiny cl}}} {R^2_{\mbox{\tiny cl}}} \qqu... ...}} = 4/3 ~\pi \rho_{\mbox{\tiny cl}} R^3_{\mbox{\tiny cl}} . \end{displaymath} (B.11)

This leads to a critical mass of the cloud

 \begin{displaymath}{ } M_{\mbox{\tiny lower}} = \sqrt{6} \pi \frac {v^3_{\mbo... ...mbox{\tiny ISM}}} {G \rho_{\mbox{\tiny cl}}} \right )^{3/2} \end{displaymath} (B.12)

above which KH instabilities are suppressed. Clouds with $M_{\mbox{\tiny lower}} < M_{\mbox{\tiny cl}}$ $< M_{\mbox{\tiny max}}$should survive long enough so that star formation can occur. These estimates are valid for the case of density and velocity jumps at the cloud boundary.

If we take dissipative forces like heat conduction or viscosity into account, which are able to diminish the density and velocity gradient, the picture changes drastically. For further investigations we introduce an artificial transition layer of thickness 2d and density $\rho_0$ in which the velocity decreases linearly from the value U0 outside the cloud (z>d) to -U0 inside the cloud (z<-d) (see Fig. B.1). The ISM at velocity U0 has a density $\rho_0 \cdot (1 - \epsilon)$, the cloud material with -U0 has $\rho_0 \cdot (1 + \epsilon)$.


  \begin{figure} \par\includegraphics[angle=-90,width=8.4cm,clip]{diagram1.eps} \end{figure} Figure B.1: Density and velocity structure for the stability study: a cloud moving with 2U0 relatively to a hot gas with density contrast $(1+\epsilon )/(1-\epsilon )$.


  \begin{figure} \par\includegraphics[width=8cm,clip]{stable2.eps} \end{figure} Figure B.2: Kelvin-Helmholtz instability strip for Model U with a density contrast $\epsilon $ of $1.2 \times 10^4$ at various wave numbers k and extents of the transition layer d.

For a stability analysis we solve Eq. (B.6) together with the boundary conditions at the transition zone. The relation between $\omega$ and k as a function of d and $\epsilon $ is given by

 
$\displaystyle {} \exp~[-2 ~ \kappa] = \left[ 1 - \frac{\kappa (\nu +1)^2} {J + ... ...{\kappa (\nu -1)^2} {J - (\nu - 1) - 0.5 ~ \epsilon ~ \kappa (\nu-1)^2} \right]$     (B.13)

with the Richardson number J for this problem

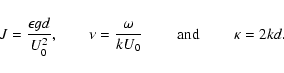\begin{displaymath}J = \frac{\epsilon g d}{U_0^2} , \qquad \nu = \frac{\omega}{k U_0} \qquad \mbox{ and } \qquad \kappa = 2kd . \end{displaymath} (B.14)

Modes with wavenumbers k are stable if there are no complex solutions for $\omega$. The case $\epsilon \rightarrow 0$ is discussed in Chandrasekhar (1961). For arbitrary $\epsilon $we solved Eq. (B.13) numerically, yielding an instability strip in the k-space. For some combinations of d and $\epsilon $, most destructive perturbations with wavelengths of the order of the cloud radius can be stabilized.

As an example, we investigate a model with a density contrast of $1.2 \times 10^4$, comparable to the model U in subsequent calculations, which corresponds to $\epsilon = 0.99983$. For different values of the transition zone thickness d, the consequence of perturbations by certain wave vectors k is calculated and shown in Fig. B.2. From this, two facts become obvious: clouds that are unstable for certain k are stabilized if the transition zone thickens. In this particular case, e.g., perturbations with wavelengths on the order of the cloud radius ( $k = 2 \pi / R_{\rm cl}$) that are usually most destructive, are damped for transition layer thicknesses d of more than 4 pc (upper right zone in Fig. B.2). Secondly, self-gravity leads to smaller ds and, by this, to stability for low ks (lower left region in Fig. B.2). For $k = 2 \pi / R_{\rm cl}$ this model is stable for d smaller than 0.002 pc.

Spatially poorly resolved numerical simulations produce artificially thick boundary layers due to numerical noise. Since such extensions would put the model into the instability strip, KH instability sets in. Heat conduction broadens the boundary layer to values d > 4 pc so that the cloud becomes stabilized.


Copyright ESO 2007