A&A 471, 1069-1075 (2007)
DOI: 10.1051/0004-6361:20077568
S. M. Kudryavtsev
Sternberg Astronomical Institute of Moscow State University, Universitetsky Pr. 13, Moscow, 119992, Russia
Received 29 March 2007 / Accepted 28 May 2007
Abstract
Aims. The aim of this study is to develop new analytical series representing lunar coordinates to accuracy compatible with the accuracy of the modern numerical ephemeris of the Moon.
Methods. An improved method of spectral analysis of tabulated function is used to make harmonic development of the latest long-term numerical ephemeris of the Moon LE-406 which covers a six thousand-year interval. A feature of the method is that the development is made directly to Poisson series where both amplitudes and arguments of the series' terms are high-degree polynomials of time.
Results. The new analytical development includes 42 270 Poisson series' terms of minimal amplitude equivalent to 1 cm and is valid over 1500-2500. A simplified version of the development includes 7952 series' terms of minimal amplitude equivalent to 1 m and is valid over 3000BC-3000AD. Over 1500-2500 the maximum difference between lunar coordinates calculated by means of the new analytical series and numerical ephemeris LE-406 is 3.2 m in geocentric distance, 0
![]() 0056 in ecliptic longitude, and 0
0056 in ecliptic longitude, and 0
![]() 0018 in ecliptic latitude. This is 9-70 times better than the accuracy of the latest analytical theory of lunar motion ELP/MPP02, and the number of terms in the new development is less than that in ELP/MPP02.
0018 in ecliptic latitude. This is 9-70 times better than the accuracy of the latest analytical theory of lunar motion ELP/MPP02, and the number of terms in the new development is less than that in ELP/MPP02.
Key words: celestial mechanics - methods: analytical - Moon
Lunar motion theory is a classical task of celestial mechanics. It was a research topic dealt with by Newton, Clairaut, d'Alembert, Euler, Lagrange, Laplace, Hansen, Adams, Delaunay, Andoyer, Newcomb and others. Also important is the famous analytical theory by Hill & Brown (Hill 1878a,b,c; Brown 1897, 1899, 1905, 1908); for a long time the relevant tables (Brown 1919) were the basis for calculation of lunar coordinates. Recent progress in computer technology and new requirements for accuracy of lunar ephemeris stimulated further studies to improve the Hill-Brown method and series (Eckert et al. 1954; Schmidt 1980) as well as on the development of new analytical theories of lunar motion (Deprit et al. 1971a,b; Henrard 1979, 1980, 1981; Chapront-Touzé & Chapront 1983, 1988; Chapront & Chapront-Touzé 1997; Bidart 2001; Chapront et al. 2002; Chapront & Francou 2003).
At the same time, numerical ephemerides of the Moon have been successfully developed; among them the most recent and
accurate are the ephemerides of DE/LE-series done at the Jet Propulsion Laboratory (JPL), USA
(Standish & Williams 1981; Standish et al. 1995; Standish 1998, 2003a,b, 2006), the ephemerides of the EPM-series done at Russian Institute of Applied Astronomy
(Krasinsky 2002; Pitjeva 2001, 2003, 2005) and the ephemerides of
INPOP-series done at IMCCE-Observatoire de Paris, France (Fienga et al. 2006).
Currently, the accuracy of the above-mentioned numerical ephemerides of the Moon
is better than that of available analytical theories of lunar motion, but an important advantage of the
latter is their compactness and computer platform independence which is important in many practical applications.
In particular, JPL-based numerical ephemerides of the Moon and planets have been recently replaced with analytical
motion theories of these bodies within all key elements of ground software systems used for Hubble Space Telescope (HST)
mission support (McCuttcheon 2003). For this purpose the HST personnel chose the
analytical theory of lunar motion ELP2000-82B (Chapront-Touzé & Chapront 1983) and the "planetary series 1996'' (Chapront & Francou 1996) representing planetary ephemerides by Poisson series. According to HST tests,
the selected analytical motion theories reproduce the modern numerical planetary/lunar ephemerides DE/LE-405/406
(Standish 1998) to an
accuracy of at least 0
![]() 008 for all major planets (which meets all requirements for
the mission support), and to an accuracy of 0
008 for all major planets (which meets all requirements for
the mission support), and to an accuracy of 0
![]() 5 for the Moon. The main reason of the relatively low accuracy
obtained for the Moon is that ELP2000-82B theory is adjusted to an old version of numerical lunar ephemeris,
LE-200 (Standish & Williams 1981).
(Recently Chapront & Francou (2003) developed a new
analytical theory of lunar motion, ELP/MPP02, which is adjusted to LE-405/406, but coefficients of the theory
are not published yet).
5 for the Moon. The main reason of the relatively low accuracy
obtained for the Moon is that ELP2000-82B theory is adjusted to an old version of numerical lunar ephemeris,
LE-200 (Standish & Williams 1981).
(Recently Chapront & Francou (2003) developed a new
analytical theory of lunar motion, ELP/MPP02, which is adjusted to LE-405/406, but coefficients of the theory
are not published yet).
Along with construction of purely analytical (or semi-analytical) theories of lunar motion and development of purely numerical lunar ephemeris a combined approach can be used. This is a spectral analysis of values for lunar coordinates pre-calculated with a small sampling step on the basis of the latest long-term numerical ephemeris of the Moon. The form of the resulting series is very similar to that given by the modern analytical theories of lunar motion and keeps all the advantages of the latter, and the series accuracy proves to be compatible with the accuracy of the source numerical ephemeris. Note that a similar approach was used by Chapront (1995, 2000) in his improvement of analytical planetary theories. However, a typical disadvantage of any spectral method is the well-known problem of "close frequencies'' which can only be resolved by increasing the time interval over which the analysis is done. We thus evolved a new modification of the spectral analysis method which allowed us to perform harmonic development of the latest long-term numerical ephemeris of the Moon LE-406 over six thousand years (the complete time interval covered by LE-406). The feature of the method is that the development is directly made to Poisson series where both amplitudes and arguments of the series' terms are high-degree polynomials of time as opposed to the classical Fourier analysis where the terms' amplitudes and frequencies are constants. This approach leads to an essential improvement in accuracy of harmonic development of a function tabulated over a long-term interval and to reduction of the series' length. The details of the method are given in the next section (see also Kudryavtsev 2004).
Let f(t) be an arbitrary function tabulated by its numerical values over an interval of time [-T,T] with a small sampling step.
Over the same interval we will build an analytical
representation of the function by a finite h-order Poisson
series of the following form
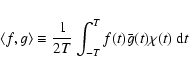 |
(6) |
However, the basis functions
![]() are not usually
orthogonal. We thus have to perform an orthogonalization process
over the expansion coefficients to improve the quality
of representation (1) and avoid superfluous terms. For
this procedure we used the algorithm developed by Sidlichovský
& Nesvorný (1997). Expressions (7)-(14) present a minimal algorithm
which we have generalized as indicated below.
are not usually
orthogonal. We thus have to perform an orthogonalization process
over the expansion coefficients to improve the quality
of representation (1) and avoid superfluous terms. For
this procedure we used the algorithm developed by Sidlichovský
& Nesvorný (1997). Expressions (7)-(14) present a minimal algorithm
which we have generalized as indicated below.
Let f(t) be a tabulated complex function and let
![]() be a set of M basis functions [in our study
equal to the complete set of
be a set of M basis functions [in our study
equal to the complete set of
![]() so that
so that
![]() ]. The function f(t) is developed
in the basis
]. The function f(t) is developed
in the basis
![]() as
as
Thus coefficients Ai(M) are iteratively calculated as follows. At the
first step
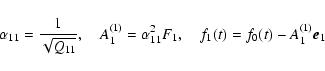 |
(8) |
At the ![]() step, for every
step, for every
![]() we compute the
following complex coefficients:
we compute the
following complex coefficients:
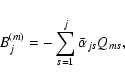 |
(9) |
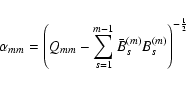 |
(10) |
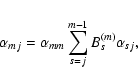 |
(11) |
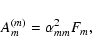 |
(12) |
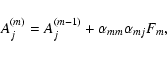 |
(13) |
For the selected basis (3) the projections
![]() are numerically calculated according
to expressions (4)-(5). The values for scalar products of the basis functions
are numerically calculated according
to expressions (4)-(5). The values for scalar products of the basis functions
![]() can be found analytically through
the following steps.
can be found analytically through
the following steps.
Step 1. As far as trigonometric functions can be represented in
exponential form, we shall further deal with definite integrals
of the form
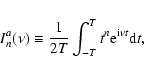 |
(16) |
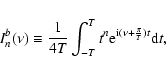 |
(17) |
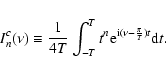 |
(18) |
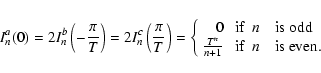 |
(19) |
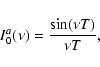 |
(20) |
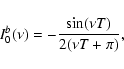 |
(21) |
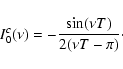 |
(22) |
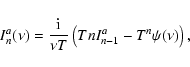 |
(23) |
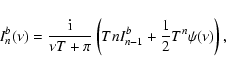 |
(24) |
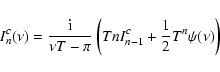 |
(25) |
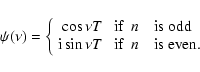 |
(26) |
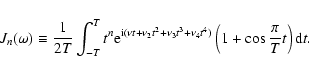 |
(28) |
| (29) |
| |
= | 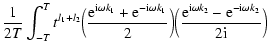 |
|
| = | |||
| (30) |
| (31) |
| (32) |
The formalism described in the previous section has been applied to accurate harmonic development of the numerical lunar ephemeris LE-405/406. As a set of variables describing the position of the Moon in space we chose spherical coordinates of its centre: r (geocentric distance), V (ecliptic longitude reckoned along the moving ecliptic from the mean equinox of epoch) and U (ecliptic latitude reckoned from the moving ecliptic). The same variables are used in all modern ELP-theories of lunar motion (although the ELP-theories use a different origin of the ecliptic longitude V).
On the base of LE-406 numerical lunar ephemeris, we calculated daily values for spherical coordinates of the Moon r, V, U over 3000BC-3000AD (the complete time interval covered by LE-406). We then performed a spectral analysis of
the tabulated values using the method presented in the previous section. As a result, the geocentric spherical coordinates
of the Moon r, V, U are represented by Poisson series of the following form
The arguments
![]() in expansions (34)-(36) are defined as follows. First, from Simon et al.
(1994) we took fourth-degree time polynomial expressions for the mean longitude of the ascending
node of the Moon
in expansions (34)-(36) are defined as follows. First, from Simon et al.
(1994) we took fourth-degree time polynomial expressions for the mean longitude of the ascending
node of the Moon ![]() (referred to the mean ecliptic and equinox of J2000.0), for Delaunay variables
D, l', l, F (mean elongation of the Moon from the Sun, mean anomaly of the Sun, mean anomaly of the Moon,
and mean longitude of the Moon subtracted by
(referred to the mean ecliptic and equinox of J2000.0), for Delaunay variables
D, l', l, F (mean elongation of the Moon from the Sun, mean anomaly of the Sun, mean anomaly of the Moon,
and mean longitude of the Moon subtracted by ![]() ,
respectively), for mean longitudes of the eight major planets
(referred to the mean ecliptic and equinox of J2000.0), and for the general precession in
longitude pA
(based on Williams et al. 1991)
,
respectively), for mean longitudes of the eight major planets
(referred to the mean ecliptic and equinox of J2000.0), and for the general precession in
longitude pA
(based on Williams et al. 1991)
| D | = | ||
| (39) |
| l' | = | ||
| (40) |
| l | = | ||
| (41) |
| F | = | ||
| (42) |
| |
= | ||
| (43) |
| |
= | ||
| (44) |
| |
= | ||
| (45) |
| |
= | ||
| (46) |
| |
= | ||
| (47) |
| |
= | ||
| (48) |
| |
= | ||
| (49) |
| |
= | ||
| (50) |
Transformation of lunar rectangular coordinates from the reference frame of LE-405/406 (defined by the mean geoequator
and equinox of J2000.0) to the reference frame defined by the moving ecliptic and mean equinox of epoch has been
done with use of the following precession quantities (Simon et al. 1994)
| |
= | ||
| (53) |
| zA | = | ||
| (54) |
The characteristics of the new harmonic development of lunar coordinates r, V, U are given in the following section.
There are two versions of the new Poisson series representing the geocentric ecliptic spherical coordinates of the Moon r, V, U. The complete solution, LEA-406a, includes 42270 terms of minimal amplitude equivalent to 1 cm and is valid over 1500-2500. The simplified solution, LEA-406b, includes 7952 terms of minimal amplitude equivalent to 1 m and is valid over 3000BC-3000AD.
Tables 1, 2 present characteristics of both solutions. For every coordinate we give the total number of non-zero trigonometric and Poisson terms in the relevant expression ((34), (35) or (36)). The value of minimum amplitude for Poisson terms corresponds to the maximum range of the terms' amplitude at the ends of the interval of time where the solution is valid. The value of maximum error stands for the maximum deviation between the lunar coordinates calculated by means of the new analytical development LEA-406 and lunar coordinates provided by the numerical ephemeris LE-405/406 at every 0.1 days within the considered interval of time. We made a comparison with the ephemeris LE-405 over the time intervals 1900-2100 and 1600-2200 and a comparison with the ephemeris LE-406 over the time intervals 1500-2500 and 3000BC-3000AD. (The ephemeris LE-405 is formally more accurate than LE-406, but covers a shorter time interval, 1600-2200; the ephemeris LE-406 is an extension of LE-405 over the interval of time 3000BC-3000AD.)
Table 1: Harmonic development of lunar ephemeris LE-405/406 over 1500-2500 (complete solution LEA-406a).
Table 2: Harmonic development of lunar ephemeris LE-405/406 over 3000BC-3000AD (simplified solution LEA-406b).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7568fig1.eps} %\end{figure}](/articles/aa/full/2007/33/aa7568-07/Timg131.gif) |
Figure 1: Differences between lunar coordinates given by numerical ephemeris LE-406 and by analytical series LEA-406a over 1500-2500. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7568fig2.eps} %\end{figure}](/articles/aa/full/2007/33/aa7568-07/Timg132.gif) |
Figure 2: Dependence of LEA-406a accuracy on the number of series' terms. |
| Open with DEXTER | |
Figure 1 shows the differences between the lunar coordinates r, V, U calculated by means of the latest long-term numerical ephemeris LE-406 and by the complete harmonic development LEA-406a over 1500-2500.
Figure 2 demonstrates how the accuracy of calculation of lunar coordinates r, V, U over 1500-2500 depends on the number of terms taken from LEA-406a series.
The main terms of LEA-406a series are presented in Tables 3-5. The complete LEA-406 harmonic development of the lunar ephemeris LE-405/406 is given in Tables 6-11 only available in electronic form at the CDS.
LEA-406, the new harmonic development of lunar ephemeris, and ELP/MPP02 (Chapront & Francou 2003), the modern analytical theory of lunar motion, are both adjusted to the latest long-term numerical ephemeris of the Moon LE-405/406 (Standish 1998) which is recommended for use by the current IERS Conventions (McCarthy & Petit 2003). Both solutions are expansions of the geocentric ecliptic spherical coordinates of the Moon r, V, U to Poisson series where amplitudes of the series' terms are second-order polynomials of time, and their arguments are polynomials of the fourth degree of time.
For quantitative comparison of LEA-406 harmonic development with ELP/MPP02 lunar motion theory we give characteristics of the latter in Table 12 (following Chapront & Francou 2003).
When comparing the characteristics of the two analytical representation of lunar ephemeris given in Tables 1, 2 and in Table 12 one sees that the accuracy of the new harmonic development LEA-406 is better than that of ELP/MPP02 analytical theory over both short-term and long-term intervals. Over a one thousand-year interval centered at J2000.0 (1500-2500) the gain in accuracy is from a factor of 9 to a factor of 70 (depending on the coordinate). The total number of terms included to the new harmonic development of lunar ephemeris is 42 270 in its complete version (LEA-406a) and 7952 in its simplified version (LEA-406b) vs. 45 053 terms composing the analytical lunar motion theory ELP/MPP02.
Table 3: The main terms of LEA-406a harmonic development of lunar geocentric distance r.
Table 4: The main terms of LEA-406a harmonic development of lunar ecliptic longitude V.
Table 5: The main terms of LEA-406a harmonic development of lunar ecliptic latitude U.
Table 12: Expansion of lunar coordinates in ELP/MPP02 theory.
Acknowledgements
The author is grateful to Dr. Jean Chapront for his valuable comments on the manuscript. Research supported in part by the Russian Foundation for Basic Research under grant no. 05-02-16436.