A&A 471, 1011-1022 (2007)
DOI: 10.1051/0004-6361:20077418
Angular momentum conservation and torsional oscillations in the Sun and solar-like stars
A. F. Lanza
INAF - Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
Received 6 March 2007 / Accepted 7 June 2007
Abstract
Context. The solar torsional oscillations, i.e., the perturbations of the angular velocity of rotation associated with the eleven-year activity cycle, are a manifestation of the interaction among the interior magnetic fields, amplified and modulated by the solar dynamo, and rotation, meridional flow and turbulent thermal transport. Therefore, they can be used, at least in principle, to put constraints on this interaction. Similar phenomena are expected to be observed in solar-like stars and can be modelled to shed light on analogous interactions in different environments.
Aims. The source of torsional oscillations is investigated by means of a model for the angular momentum transport within the convection zone.
Methods. A description of the torsional oscillations is introduced, based on an analytical solution of the angular momentum equation in the mean-field approach. It provides information on the intensity and location of the torques producing the redistribution of the angular momentum within the convection zone of the Sun along the activity cycle. The method can be extended to solar-like stars for which some information on the time-dependence of the differential rotation is becoming available.
Results. Illustrative applications to the Sun and solar-like stars are presented. Under the hypothesis that the solar torsional oscillations are due to the mean-field Lorentz force, an amplitude of the Maxwell stresses
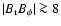
 103 G2 at a depth of
103 G2 at a depth of  0.85
0.85  at low latitude is estimated. Moreover, the phase relationship between
at low latitude is estimated. Moreover, the phase relationship between  and
and  can be estimated, suggesting that
can be estimated, suggesting that
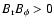 below
below  0.85
0.85  and
and
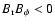 above.
above.
Conclusions. Such preliminary results show the capability of the proposed approach to constrain the amplitude, phase and location of the perturbations leading to the observed torsional oscillations.
Key words: Sun: rotation - Sun: activity - Sun: magnetic fields - Sun: interior - stars: rotation - stars: activity
Doppler measurements of the surface rotation of the Sun show
bands of faster and slower zonal flows that appear at midlatitudes and migrate toward the
equator with the period of the eleven-year cycle, accompanying the bands of sunspot activity.
The amplitude of such velocity perturbations, called torsional oscillations, is  5 m s-1 and faster rotation is observed on the side equatorward of
the sunspot belt (Howard & LaBonte 1980). Helioseismology has revealed that the torsional
oscillations are not at all a superficial phenomenon but involve much of the
convection zone, as shown, for example, by Howe et al. (2000), Vorontsov et al. (2002), Basu & Antia (2003) and more recently by Howe et al. (2006,2005). The amplitude of the
angular velocity variation is
5 m s-1 and faster rotation is observed on the side equatorward of
the sunspot belt (Howard & LaBonte 1980). Helioseismology has revealed that the torsional
oscillations are not at all a superficial phenomenon but involve much of the
convection zone, as shown, for example, by Howe et al. (2000), Vorontsov et al. (2002), Basu & Antia (2003) and more recently by Howe et al. (2006,2005). The amplitude of the
angular velocity variation is
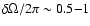 nHz at least down to 10%-15% of the solar radius, although the precise depth of penetration
of the oscillations is difficult to establish given the present uncertainties of
the inversion methods in the lower half of the solar convection zone (e.g., Howe et al. 2006).
In addition to such a low-latitude branch of the torsional oscillations, helioseismic studies have
detected the presence of a high-latitude branch (above
nHz at least down to 10%-15% of the solar radius, although the precise depth of penetration
of the oscillations is difficult to establish given the present uncertainties of
the inversion methods in the lower half of the solar convection zone (e.g., Howe et al. 2006).
In addition to such a low-latitude branch of the torsional oscillations, helioseismic studies have
detected the presence of a high-latitude branch (above 
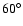 latitude) that propagates poleward and the amplitude of which is about
latitude) that propagates poleward and the amplitude of which is about
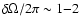 nHz (e.g., Toomre et al. 2000; Basu & Antia 2001).
Such a branch seems to propagate almost all the way down to the base of the convection zone.
nHz (e.g., Toomre et al. 2000; Basu & Antia 2001).
Such a branch seems to propagate almost all the way down to the base of the convection zone.
A general description of the perturbation of the angular velocity of the torsional oscillations, given the present accuracy of the observations, is provided by the simple formula (e.g., Howe et al. 2005; Vorontsov et al. 2002):
where r is the distance from the centre of the Sun, 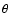 the colatitude measured from the North pole,
the colatitude measured from the North pole, 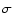 the frequency of the eleven-year cycle, t the time, and the amplitude functions
the frequency of the eleven-year cycle, t the time, and the amplitude functions
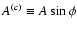 ,
,
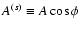 depend on the amplitude A and the initial phase
depend on the amplitude A and the initial phase 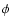 .
Moreover, the velocity perturbation is symmetric with respect to the equator:
.
Moreover, the velocity perturbation is symmetric with respect to the equator:
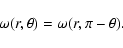 |
(2) |
Several models have been proposed to interpret the torsional oscillations beginning with the
pioneering work by Schüssler (1981) and Yoshimura (1981) who considered the Lorentz
force associated with the magnetic fields in the activity belts as the cause of the velocity perturbations observed in the solar photosphere. Later models, based on the effects of the Lorentz force on the turbulent Reynolds stresses, were proposed, by e.g., Küker et al. (1996) and Kichatinov et al. (1999), following an original suggestion by Rüdiger & Kichatinov (1990).
Spruit (2003) proposed that the low-latitude branch of the torsional oscillations is a
geostrophic flow driven by temperature variations due to the enhanced radiative losses in
the active region belts.
More recent studies by Covas et al. (2004,2005) present models based on the simultaneous solution of
non-linear mean-field dynamo equations and the azimuthal component of the Navier-Stokes
equation with a uniform turbulent viscosity. They reproduce the gross features of the
torsional oscillations and of the solar activity cycle with an appropriate tuning of the free
parameters. Rempel (2006,2007) considers the role of the meridional component of the
Navier-Stokes equation in mean-field models and finds that the perturbation of the meridional flow
cannot be neglected in the interpretation of the torsional oscillations. His models suggest that
the low-latitude branch of the torsional oscillations cannot be explained solely by the effect of
the mean-field Lorentz force, but that thermal perturbations in the active region belt and
in the bulk of the convection zone do play an active role, as proposed by Spruit (2003).
In the present study, the angular momentum conservation is
considered and the relevant equation in the mean-field approximation is solved analytically
for the case of a turbulent viscosity that depends on the radial co-ordinate. A general solution is derived independently of
any specific dynamo model, allowing us to put constraints on the localization of the torques
producing the torsional oscillations. An illustrative application of
the proposed methods is presented using the available data.
The observations of young solar-like stars by means of tomographic techniques based on high-resolution spectroscopy have provided recent evidence for time variation of their surface
differential rotation (e.g., Donati et al. 2003; Jeffers et al. 2007). Lanza (2006a)
has recently shown how such variations can be related to the
intensity of the magnetic torque produced by a non-linear dynamo in their convective
envelopes, in the case of rapidly rotating stars for which the Taylor-Proudman theorem applies.
In the near future, the possibility of
measuring the time variation of the rotational splittings of p-mode oscillations in solar-like stars
may provide us with information on the changes of their internal rotation, although
with limited spatial resolution. In the present study,
we extend the considerations of Lanza (2006a) to the case of a generic internal rotation profile,
not necessarily verifying the Taylor-Proudman theorem, to obtain hints on the amplitude of
the torque leading to the rotation change.
We consider an inertial reference frame with the origin in the
barycentre of the Sun and the z-axis in the direction of
the rotation axis. A spherical polar co-ordinate system
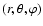 is adopted,
where r is the distance from the origin,
is adopted,
where r is the distance from the origin, 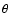 the co-latitude measured from the
North pole and
the co-latitude measured from the
North pole and 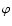 the azimuthal angle. We assume that all variables
are independent of
the azimuthal angle. We assume that all variables
are independent of 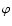 and that the solar density stratification is spherically symmetric.
and that the solar density stratification is spherically symmetric.
The equation for the angular momentum conservation in the mean-field approach reads
(e.g., Rüdiger & Hollerbach 2004; Rüdiger 1989):
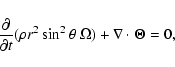 |
(3) |
where 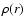 is the density,
is the density,
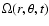 the angular velocity and
the angular velocity and
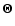 the angular momentum flux vector given by:
the angular momentum flux vector given by:
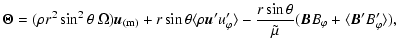 |
|
|
(4) |
where
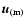 is the meridional circulation,
is the meridional circulation,
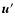 the fluctuating velocity field,
the fluctuating velocity field,
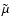 the magnetic permeability,
the magnetic permeability, 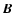 the mean magnetic field and
the mean magnetic field and
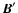 the fluctuating magnetic
field; angular brackets indicate the Reynolds average defining the mean-field quantities. The Reynolds stresses can be written as:
the fluctuating magnetic
field; angular brackets indicate the Reynolds average defining the mean-field quantities. The Reynolds stresses can be written as:
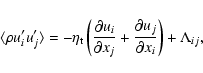 |
(5) |
where 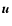 is the mean flow field,
is the mean flow field,
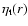 is the turbulent viscosity, assumed to be a scalar function of r only, and
is the turbulent viscosity, assumed to be a scalar function of r only, and
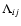 indicates the non-diffusive part of the Reynolds stresses due to the velocity
correlations in a rotating star (see Rüdiger & Hollerbach 2004; Rüdiger 1989, for details). The conservation of the total angular momentum of the convection zone implies:
indicates the non-diffusive part of the Reynolds stresses due to the velocity
correlations in a rotating star (see Rüdiger & Hollerbach 2004; Rüdiger 1989, for details). The conservation of the total angular momentum of the convection zone implies:
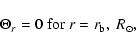 |
(6) |
where 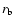 is the radius at the lower boundary of the convection zone and
is the radius at the lower boundary of the convection zone and  is the radius of the Sun.
is the radius of the Sun.
The equation for the conservation of the angular momentum can be recast in the form:
![$\displaystyle %
\frac{\partial \Omega}{\partial t}\! -\! \frac{1}{\rho r^{4}} \...
...} \left[ (1 - \mu^{2})^{2} \frac{\partial \Omega}{\partial \mu}\right] \!=\! S,$](/articles/aa/full/2007/33/aa7418-07/img60.gif) |
|
|
(7) |
where
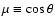 and the source term S is given by:
and the source term S is given by:
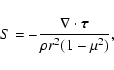 |
(8) |
and
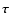 is a vector whose components are:
is a vector whose components are:
![\begin{displaymath}%
\tau_{i} = r \sin \theta \left[ \Lambda_{i \varphi} - \frac...
...ht) \right] + \rho r^{2} \sin^{2} \theta \Omega u_{\rm (m) i}.
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img64.gif) |
(9) |
The boundary conditions given by Eq. (6) can be written as:
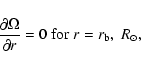 |
(10) |
when we assume
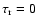 at the surface.
Note that helioseismic measurements indicate the presence of a subsurface shear layer
with
at the surface.
Note that helioseismic measurements indicate the presence of a subsurface shear layer
with
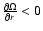 at low latitudes (Corbard & Thompson 2005), but we prefer to adopt the stress-free
boundary condition (10) at the surface to ensure the conservation of the
total angular momentum of the convection zone in our model.
at low latitudes (Corbard & Thompson 2005), but we prefer to adopt the stress-free
boundary condition (10) at the surface to ensure the conservation of the
total angular momentum of the convection zone in our model.
The solar angular velocity can be split into a time-independent component
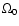 and a time-dependent component
and a time-dependent component 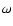 ,
i.e., the torsional oscillations:
,
i.e., the torsional oscillations:
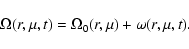 |
(11) |
The equation for the torsional oscillations thus becomes:
![$\displaystyle %
\frac{\partial \omega}{\partial t} \!-\! \frac{1}{\rho r^{4}} \...
... (1 \!-\! \mu^{2})^{2} \frac{\partial \omega}{\partial \mu}\right] \!=\! S_{1},$](/articles/aa/full/2007/33/aa7418-07/img71.gif) |
|
|
(12) |
where the perturbation of the source term is:
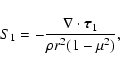 |
(13) |
with
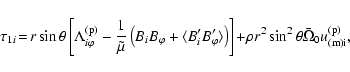 |
(14) |
where
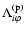 and
and
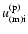 are the time-dependent perturbations of the non-diffusive Reynolds stresses and of the meridional circulation, respectively, and
are the time-dependent perturbations of the non-diffusive Reynolds stresses and of the meridional circulation, respectively, and
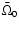 is the
average of the solar angular velocity over the convection zone. Note that the Maxwell stresses
appear in Eq. (14), but not in the corresponding equation for
is the
average of the solar angular velocity over the convection zone. Note that the Maxwell stresses
appear in Eq. (14), but not in the corresponding equation for
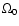 because the solar magnetic field has no time-independent component.
Moreover, in deriving Eq. (14), the variation of the angular velocity
over the convection zone has been neglected in the term containing the perturbation of the meridional circulation since
because the solar magnetic field has no time-independent component.
Moreover, in deriving Eq. (14), the variation of the angular velocity
over the convection zone has been neglected in the term containing the perturbation of the meridional circulation since
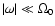 (e.g., Rempel 2007; Rüdiger 1989). Equation (12) must be solved together with the boundary conditions:
(e.g., Rempel 2007; Rüdiger 1989). Equation (12) must be solved together with the boundary conditions:
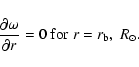 |
(15) |
2.2 Solution of the angular momentum equation
The general solution of Eq. (12) with the boundary conditions (15) can be obtained by the method of separation of the variables and expressed as a series of the form (e.g., Lanza 2006b, and references therein):
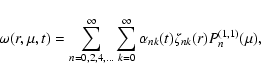 |
(16) |
where
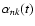 and
and
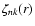 are functions that will be specified below
and
are functions that will be specified below
and
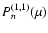 are Jacobian polynomials, i.e., the finite solutions of the equation:
are Jacobian polynomials, i.e., the finite solutions of the equation:
![\begin{displaymath}%
\frac{{\rm d}}{{\rm d} \mu} \left[ (1- \mu^{2})^{2} \frac{{...
...\rm d} \mu }\right] + n(n+3) (1 - \mu^{2}) P_{n}^{(1, 1)} = 0,
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img83.gif) |
(17) |
in the interval
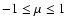 including its ends (e.g., Smirnov 1964a).
The Jacobian polynomials form a complete and orthogonal set in the interval [-1, 1] with
respect to the weight function
including its ends (e.g., Smirnov 1964a).
The Jacobian polynomials form a complete and orthogonal set in the interval [-1, 1] with
respect to the weight function
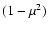 .
Only the polynomials of even degree appear in Eq. (16) because the angular velocity perturbation is symmetric with respect to the equator (see Eq. (2)).
For
.
Only the polynomials of even degree appear in Eq. (16) because the angular velocity perturbation is symmetric with respect to the equator (see Eq. (2)).
For 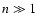 the asymptotic expression of the Jacobian polynomials is (e.g., Gradshteyn & Ryzhik 1994):
the asymptotic expression of the Jacobian polynomials is (e.g., Gradshteyn & Ryzhik 1994):
![\begin{displaymath}%
P_{n}^{(1,1)} (\cos \theta) =
\frac{\cos \left[ (n + \frac...
...\frac{\theta}{2}\right)\right]^{3/2}}
+ O( n^{-\frac{3}{2}}).
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img87.gif) |
(18) |
The functions
 are the solutions of the Sturm-Liouville
problem defined in the interval
are the solutions of the Sturm-Liouville
problem defined in the interval
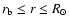 by the equation:
by the equation:
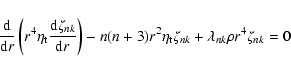 |
(19) |
with the boundary conditions (following from Eq. (15)):
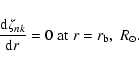 |
(20) |
We shall consider normalized eigenfunctions, i.e.:
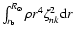 = 1. The eigenfunctions
= 1. The eigenfunctions
 for a fixed n, form a complete and orthonormal set in the interval
for a fixed n, form a complete and orthonormal set in the interval
![$[r_{\rm b}, R_{\odot}]$](/articles/aa/full/2007/33/aa7418-07/img93.gif) with respect to the weight function
with respect to the weight function
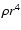 that does not depend on n. We recall
from the theory of the Sturm-Liouville problem that the eigenvalues verify the inequality:
that does not depend on n. We recall
from the theory of the Sturm-Liouville problem that the eigenvalues verify the inequality:
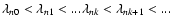 and that the
eigenfunction
and that the
eigenfunction
 has k nodes in the interval
has k nodes in the interval
![$[r_{\rm b}, R_{\odot}]$](/articles/aa/full/2007/33/aa7418-07/img93.gif) for each n. For n=0, the first eigenvalue corresponding to the eigenfunction
for each n. For n=0, the first eigenvalue corresponding to the eigenfunction
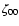 is zero and the eigenfunction vanishes at all points in
is zero and the eigenfunction vanishes at all points in
![$[r_{\rm b}, R_{\odot}]$](/articles/aa/full/2007/33/aa7418-07/img93.gif) ,
as it is evident by integrating both sides of Eq. (19) in the same interval, applying the
boundary conditions (20) and considering that
,
as it is evident by integrating both sides of Eq. (19) in the same interval, applying the
boundary conditions (20) and considering that
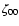 has no nodes. For n >0, all the eigenvalues
has no nodes. For n >0, all the eigenvalues
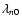 are positive, as can be derived by integrating both sides of Eq. (19) in the interval
are positive, as can be derived by integrating both sides of Eq. (19) in the interval
![$[r_{\rm b}, R_{\odot}]$](/articles/aa/full/2007/33/aa7418-07/img93.gif) ,
applying the boundary conditions (20) and considering that
,
applying the boundary conditions (20) and considering that
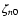 has no nodes. In view of the inequality given above, all the eigenvalues
has no nodes. In view of the inequality given above, all the eigenvalues
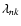 are then positive for
are then positive for 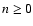 .
Moreover, it is possible to prove
that
.
Moreover, it is possible to prove
that
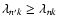 if
if
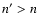 and that (see Smirnov 1964b):
and that (see Smirnov 1964b):
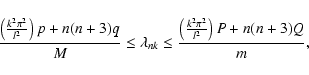 |
(21) |
where P, Q and M are the maximum values of the functions
 ,
,
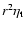 and
and
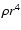 in the interval
in the interval
![$[r_{\rm b}, R_{\odot}]$](/articles/aa/full/2007/33/aa7418-07/img93.gif) ,
respectively, and p, q and m their minimum values in the same interval, respectively; and
,
respectively, and p, q and m their minimum values in the same interval, respectively; and
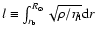 .
For
.
For 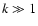 the asymptotic expression for the eigenfunction
the asymptotic expression for the eigenfunction
 is (e.g., Morse & Feshbach 1953):
is (e.g., Morse & Feshbach 1953):
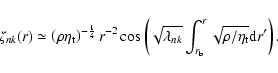 |
(22) |
The time dependence of the solution in Eq. (16) is specified by the functions
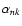 that are given by:
that are given by:
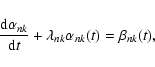 |
(23) |
where the functions
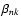 appear in the development of the perturbation term S1:
appear in the development of the perturbation term S1:
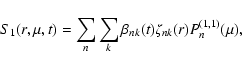 |
(24) |
and are given by (Lanza 2006b):
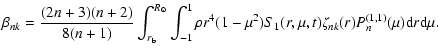 |
|
|
(25) |
The solution of Eq. (23) is:
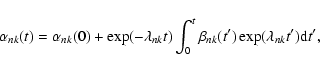 |
(26) |
which allows us to specify the general solution of Eq. (12) with the boundary conditions (15) when the perturbation term
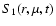 and the
initial conditions are given.
and the
initial conditions are given.
2.3 Solution for the solar torsional oscillations
To find the solution appropriate to the solar torsional oscillations as specified by Eqs. (1) and (2), it is useful to derive an alternative expression for the functions
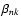 as follows. Substituting Eq. (13)
into Eq. (25) and taking into account that the element of volume is
as follows. Substituting Eq. (13)
into Eq. (25) and taking into account that the element of volume is
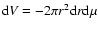 ,
the right hand side of Eq. (25) can be recast in the form of a volume integral extended to the solar convection zone:
,
the right hand side of Eq. (25) can be recast in the form of a volume integral extended to the solar convection zone:
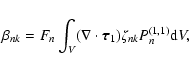 |
(27) |
where:
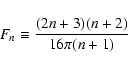 |
(28) |
is a factor coming from the normalization of the Jacobian polynomials.
It is possible to further simplify Eq. (27) by considering the identity:
![\begin{displaymath}%
\nabla \cdot [\zeta_{nk} P_{n}^{(1,1)} {\vec \tau}_{1}] = \...
...{1}) + {\vec \tau}_{1} \cdot \nabla[\zeta_{nk} P_{n}^{(1,1)}].
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img119.gif) |
(29) |
Integrating both sides of Eq. (29) over the volume of the convection zone
and considering that the integral of the left hand side vanishes
thanks to the Gauss's theorem and the condition that the radial component of the stresses
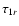 is zero on the boundaries, we find:
is zero on the boundaries, we find:
![\begin{displaymath}%
\beta_{nk} = - F_{n} \int_{V} {\vec \tau}_{1} \cdot \nabla[\zeta_{nk} P_{n}^{(1,1)}] {\rm d}V.
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img121.gif) |
(30) |
The time dependence of the solar torsional oscillations specified in Eq. (1) suggests that a similar dependence for the perturbation term should be considered:
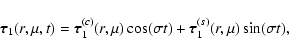 |
(31) |
from which a similar expression for the
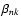 follows by substitution into Eq. (27). If we put such an expression for
follows by substitution into Eq. (27). If we put such an expression for
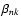 into
Eq. (26) and perform the integrations with respect to the time, we find the stationary solution:
into
Eq. (26) and perform the integrations with respect to the time, we find the stationary solution:
This expression can be substituted into Eq. (16) to give the angular velocity
perturbation. It can be written in the form of Eq. (1) with:
| |
|
![$\displaystyle A^{(c)} (r, \mu) \!=\! \! \int_{V} \left[ G_{1}(r, \mu , r^{\prim...
...mu^{\prime}) \nabla \!\cdot\! {\vec \tau}_{1}^{(s)} \right] {\rm d} V^{\prime},$](/articles/aa/full/2007/33/aa7418-07/img127.gif) |
|
| |
|
![$\displaystyle A^{(s)} (r, \mu) \!=\!\! \int_{V} \!\left[ G_{1}(\!r, \mu , r^{\p...
...mu^{\prime}) \nabla \!\cdot\! {\vec \tau}_{1}^{(c)} \right] {\rm d} V^{\prime},$](/articles/aa/full/2007/33/aa7418-07/img128.gif) |
(33) |
where the symbol
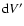 means that the volume integration is to be performed with respect to the variables
means that the volume integration is to be performed with respect to the variables
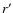 and
and
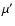 ,
and the functions G1 and G2 are Green functions defined as:
,
and the functions G1 and G2 are Green functions defined as:
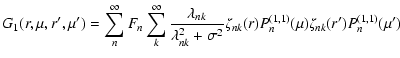 |
|
|
|
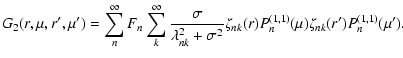 |
|
|
(34) |
The Green functions are continuous with respect to the arguments r,  ,
,
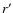 ,
,
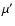 ,
but their partial derivatives with respect to
,
but their partial derivatives with respect to
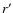 ,
,
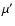 have discontinuities of the first kind in the
points where
have discontinuities of the first kind in the
points where
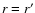 or
or
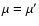 .
The convergence of the series in Eqs. (34), here used to represent the Green functions, is assured by the general theory of the Green function (e.g., Smirnov 1964b) and is also proven in Appendix A.
.
The convergence of the series in Eqs. (34), here used to represent the Green functions, is assured by the general theory of the Green function (e.g., Smirnov 1964b) and is also proven in Appendix A.
Equations (33) can be used to compute the angular velocity perturbation when
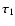 is known.
Note that in the case in which the Lorentz force due to the mean field and
the meridional flow are the only sources of angular momentum redistribution, Eq. (14) gives:
is known.
Note that in the case in which the Lorentz force due to the mean field and
the meridional flow are the only sources of angular momentum redistribution, Eq. (14) gives:
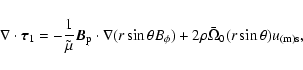 |
(35) |
where
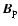 is the mean poloidal magnetic field and
is the mean poloidal magnetic field and
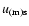 the component of the meridional flow in the direction orthogonal to the rotation axis. To obtain Eq. (35) we made use of the solenoidal nature of the mean poloidal field and of the continuity equation for the meridional flow.
the component of the meridional flow in the direction orthogonal to the rotation axis. To obtain Eq. (35) we made use of the solenoidal nature of the mean poloidal field and of the continuity equation for the meridional flow.
2.4 Localization of the source of the torsional oscillations in the solar convection zone
The results derived above allow us to introduce methods to localize the torques producing the torsional oscillations in the convection zone. Suppose that the observations provide us with the functions
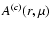 and
and
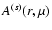 appearing in Eq. (1). The functions
appearing in Eq. (1). The functions
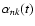 can be written as:
can be written as:
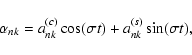 |
(36) |
where the constants
ank(c,s) are given by:
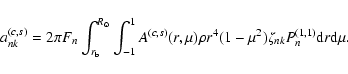 |
(37) |
Similarly, we can write:
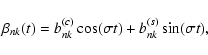 |
(38) |
with the relationships:
| |
|
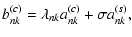 |
|
| |
|
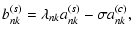 |
(39) |
that follow from Eq. (23).
The divergence of
 can be obtained from
Eqs. (13) and (24) as:
can be obtained from
Eqs. (13) and (24) as:
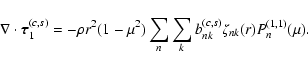 |
(40) |
Moreover, it is possible to construct a localized estimate of the perturbation term
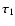 by considering a function
by considering a function 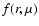 the gradient of which is different from zero only within a given volume Vf. It can be developed in series of the eigenfunctions in the form:
the gradient of which is different from zero only within a given volume Vf. It can be developed in series of the eigenfunctions in the form:
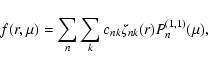 |
(41) |
where the coefficient cnk are given by:
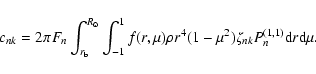 |
(42) |
Let us consider the equation:
![$\displaystyle \int_{V_{\rm f}} \left( {\vec \tau}_{1}^{(c,s)} \cdot \nabla f \r...
...}
\sum_{k} \nabla [c_{nk} \zeta_{nk} (r) P_{n}^{(1,1)} (\mu)] \right) {\rm d}V,$](/articles/aa/full/2007/33/aa7418-07/img152.gif) |
|
|
(43) |
obtained by means of Eq. (41). Considering Eqs. (30) and (38), Eq. (43) can be recast as:
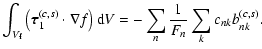 |
|
|
(44) |
Moreover, if we introduce the volume average of the modulus of the perturbation
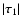 with respect to the weight function
with respect to the weight function
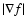 ,
i.e.:
,
i.e.:
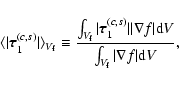 |
(45) |
then Eq. (44) gives a lower limit for it in the form:
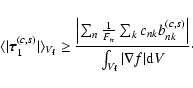 |
(46) |
The minimum dimensions of the volume  are set by the spatial resolution of the measurements of the angular velocity variations. They depend on the accuracy of the rotational splitting coefficients, the inversion technique and the position within the convection zone (e.g., Schou et al. 1998; Howe et al. 2005). The minimum order of the Jacobian polynomials
are set by the spatial resolution of the measurements of the angular velocity variations. They depend on the accuracy of the rotational splitting coefficients, the inversion technique and the position within the convection zone (e.g., Schou et al. 1998; Howe et al. 2005). The minimum order of the Jacobian polynomials  needed to reproduce an angular velocity variation with a latitudinal resolution
needed to reproduce an angular velocity variation with a latitudinal resolution
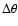 is
is
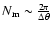 .
Similarly, the minimum order of the radial eigenfunctions
.
Similarly, the minimum order of the radial eigenfunctions 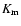 is set by the radial resolution
is set by the radial resolution 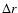 as
as
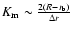 .
Therefore, it is possible to truncate the
series in Eqs. (44) and (46) to those upper limits
for n and k because the coefficients cnk will decrease
rapidly for
.
Therefore, it is possible to truncate the
series in Eqs. (44) and (46) to those upper limits
for n and k because the coefficients cnk will decrease
rapidly for
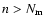 and
and
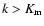 giving a negligible contribution to the sum.
giving a negligible contribution to the sum.
The statistical errors in the measurements of the angular velocity variations can be easily propagated through the linear Eqs. (37), (39), (40) and (44) to find the errors on the estimates of
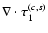 or the average of
or the average of
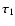 .
For instance, if we consider the standard deviations
.
For instance, if we consider the standard deviations
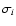 of the data di, i.e., the rotational
splittings or the splitting coefficients from which the internal rotation is derived, the standard deviation
of the data di, i.e., the rotational
splittings or the splitting coefficients from which the internal rotation is derived, the standard deviation
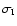 of the integral in Eq. (44) is:
of the integral in Eq. (44) is:
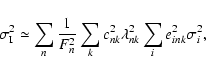 |
(47) |
where
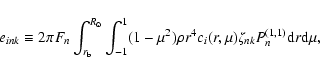 |
(48) |
and the functions
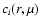 are the rotational inversion coefficients defined in Eq. (8) of Schou et al. (1998).
are the rotational inversion coefficients defined in Eq. (8) of Schou et al. (1998).
Note that a constant relative error
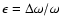 in the measurements of
A(c,s) leads to the same relative error in Eq. (40) and in Eqs. (44) and (46), given the linear equations that relate the corresponding quantities. Indeed, there is also a systematic error in our inversion method
related to the poor knowledge of the turbulent viscosity
in the measurements of
A(c,s) leads to the same relative error in Eq. (40) and in Eqs. (44) and (46), given the linear equations that relate the corresponding quantities. Indeed, there is also a systematic error in our inversion method
related to the poor knowledge of the turbulent viscosity
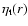 that determines the form of the radial eigenfunctions
that determines the form of the radial eigenfunctions
 .
.
The variation of the kinetic energy of rotation associated with the torsional oscillations, averaged over the eleven-year cycle, can be computed according to Lanza (2006b) and is:
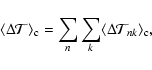 |
(49) |
where
![\begin{displaymath}%
\langle \Delta {\cal T}_{nk} \rangle_{\rm c} = \frac{1}{4F_{n}} \left\{ [a_{nk}^{(c)}]^{2} + [a_{nk}^{(s)}]^{2} \right\}.
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img175.gif) |
(50) |
The average dissipation rate of the kinetic energy of the torsional oscillations due to the turbulent viscosity is:
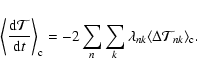 |
(51) |
2.6 Torsional oscillations due to mean-field Lorentz force
Most models of the torsional oscillations assume that they are due to the Lorentz force
produced by the mean field as derived from dynamo models. Therefore, let us consider the case in which only the mean-field Maxwell stresses contribute to the perturbation, i.e.:
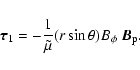 |
(52) |
If the mean radial  and toroidal fields
and toroidal fields  are given by:
are given by:
| |
|
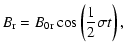 |
|
| |
|
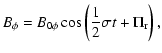 |
(53) |
where
 is the phase lag between the two field components,
the components of
is the phase lag between the two field components,
the components of 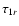 in Eq. (31) are:
in Eq. (31) are:
| |
|
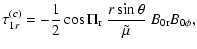 |
|
| |
|
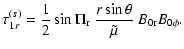 |
(54) |
An estimate of
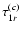 and
and
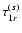 can be obtained from the method outlined
in Sect. 2.4, considering a localization function f(r) that depends only on the radial co-ordinate. Specifically, Eq. (44) can be used to compute a volume average of
can be obtained from the method outlined
in Sect. 2.4, considering a localization function f(r) that depends only on the radial co-ordinate. Specifically, Eq. (44) can be used to compute a volume average of
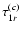 and
and
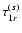 from which the average stress amplitude
from which the average stress amplitude
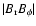 and phase lag
and phase lag
 can be determined. Analogous considerations are valid for the meridional component of the mean field
can be determined. Analogous considerations are valid for the meridional component of the mean field
 and
and  .
Adopting a localization function
.
Adopting a localization function 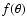 depending only on
depending only on 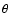 ,
it is possible to estimate
,
it is possible to estimate
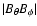 and the phase lag
and the phase lag
 between
between
 and
and  .
Such results are important to constrain mean-field dynamo models of the solar cycle, as discussed by, e.g., Schlichenmaier & Stix (1995) (see also Sect. 3.3).
.
Such results are important to constrain mean-field dynamo models of the solar cycle, as discussed by, e.g., Schlichenmaier & Stix (1995) (see also Sect. 3.3).
2.7 Application to solar-like stars
Sequences of Doppler images can be used to measure the surface differential rotation of solar-like stars and its time variability, as done by, e.g.,
Donati et al. (2003) and Jeffers et al. (2007) in the cases of AB Dor and LQ Hya. Lanza (2006a) discussed the
implications of the observed changes of the surface differential rotation on the internal
dynamics of their convection zones, assuming that the angular velocity is
constant over cylindrical surfaces co-axial with the rotation axis. The present model
allows us to relax the Taylor-Proudman constraint on the internal angular velocity, but
some different assumptions must be introduced to obtain the internal
torques in the active stars. Here we assume that the variation of the surface
differential rotation is entirely due to the Maxwell stresses of the internal magnetic
fields, localized in the overshoot layer below the convection zone, as in the interface dynamo model by, e.g., Parker (1993). The interior model of the Sun can also be applied to AB Dor and LQ Hya because they have a similar relative depth of the convection zone. Therefore, the basic quantities can be scaled according to the stellar parameters, as explained in Lanza (2006a).
Following Donati et al. (2003), we consider a surface differential rotation of the form:
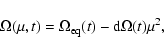 |
(55) |
where
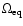 is the equatorial angular velocity and
is the equatorial angular velocity and
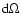 the latitudinal shear, both regarded as time-dependent. Since
P0(1,1) = 1 and
the latitudinal shear, both regarded as time-dependent. Since
P0(1,1) = 1 and
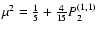 ,
it can be recast in the form of Eq. (16) leading to:
,
it can be recast in the form of Eq. (16) leading to:
| |
|
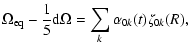 |
|
| |
|
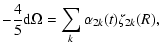 |
(56) |
where R is the radius of the star. The functions
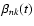 can be computed by assuming that the timescale of variation of the differential rotation
can be computed by assuming that the timescale of variation of the differential rotation
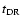 is significantly shorter than the timescales for angular momentum
transport, as given by
is significantly shorter than the timescales for angular momentum
transport, as given by
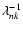 .
This assumption is
justified in the case of rapidly rotating stars by the observed variation timescales of the order of a few years together with the expected rotational quenching of
the viscosity (e.g., Kichatinov et al. 1994). Therefore, Eq. (23) leads to
.
This assumption is
justified in the case of rapidly rotating stars by the observed variation timescales of the order of a few years together with the expected rotational quenching of
the viscosity (e.g., Kichatinov et al. 1994). Therefore, Eq. (23) leads to
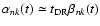 .
The angular velocity can be written in a form similar to Eq. (33) by introducing
an appropriate Green function. For instance,
considering the first of Eqs. (56), we find:
.
The angular velocity can be written in a form similar to Eq. (33) by introducing
an appropriate Green function. For instance,
considering the first of Eqs. (56), we find:
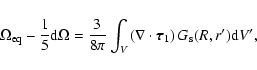 |
(57) |
where:
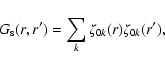 |
(58) |
and the integration is extended over the stellar convection zone.
Assuming that
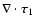 is different from zero only in an overshoot layer of volume
is different from zero only in an overshoot layer of volume 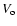 and applying considerations similar to those of Sects. 2.3 and 2.4, we find a lower limit for the variation of the averaged perturbation term:
and applying considerations similar to those of Sects. 2.3 and 2.4, we find a lower limit for the variation of the averaged perturbation term:
![\begin{displaymath}%
\langle \Delta (\nabla \cdot {\vec \tau}_{1}) \rangle_{V_{\...
...} - \frac{1}{5} \Delta ({\rm d}\Omega) }{V_{\rm o} M} \right],
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img201.gif) |
(59) |
where
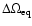 and
and
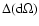 are the amplitudes of variation of the differential rotation parameters, and M is the maximum of
are the amplitudes of variation of the differential rotation parameters, and M is the maximum of
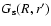 in the overshoot layer.
in the overshoot layer.
This result made use of the limited information we can get from
surface differential rotation. However, in the near future,
the observations of the rotational splittings of stellar oscillations promise to
give information on the internal rotation
and its possible time variations. Since only the
modes of low degrees (
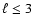 )
are detectable in disk-integrated measurements, the
spatial resolution of the derived internal angular velocity profile is very low.
Lochard et al. (2005) considered the case in which only the mean radial profile of
)
are detectable in disk-integrated measurements, the
spatial resolution of the derived internal angular velocity profile is very low.
Lochard et al. (2005) considered the case in which only the mean radial profile of
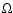 is measurable.
is measurable.
In view of such an information accessible through asteroseismology,
let us consider a more general case
in which some average of the internal angular velocity of the star, say
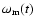 ,
can be
measured as a function of the time:
,
can be
measured as a function of the time:
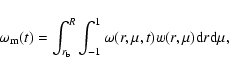 |
(60) |
where w is an appropriate weight function that takes into account the averaging effects of
the limited spatial resolution, and 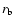 is the radius at the base of the stellar convective envelope. We introduce an auxiliary weight function:
is the radius at the base of the stellar convective envelope. We introduce an auxiliary weight function:
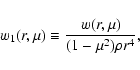 |
(61) |
which will not diverge toward the poles (
 )
and the
surface (
)
and the
surface ( )
because the weight function w is localized in the stellar interior and
goes to zero rapidly enough toward the rotation axis and the
stellar surface. We can develop the function w1 as:
)
because the weight function w is localized in the stellar interior and
goes to zero rapidly enough toward the rotation axis and the
stellar surface. We can develop the function w1 as:
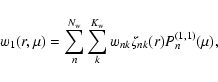 |
(62) |
where the summation can be truncated at some low
orders, say, 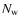 and
and 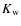 ,
because the function w1 is not sharply localized in the stellar interior.
Considering Eq. (60), we find:
,
because the function w1 is not sharply localized in the stellar interior.
Considering Eq. (60), we find:
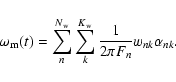 |
(63) |
For the sake of simplicity, we assume now that the time scale of variation of the functions
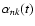 is
long with respect to
is
long with respect to
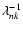 so that Eq. (23) gives:
so that Eq. (23) gives:
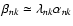 .
Considering Eq. (30), we find:
.
Considering Eq. (30), we find:
![\begin{displaymath}%
\omega_{\rm m}(t) = - \int_{V} {\vec \tau}_{1} \cdot \left\...
..._{nk}} \nabla \left[ \zeta_{nk} P_{n}^{(1,1)} \right]\right\}.
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img216.gif) |
(64) |
Equation (64) can be used to find a lower limit to the average of
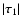 over the convection zone volume. If we indicate by
over the convection zone volume. If we indicate by 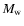 the maximum of the function:
the maximum of the function:
![\begin{displaymath}%
\left\vert \sum_{n}^{N_{\rm w}} \sum_{k}^{K_{\rm w}} \frac{...
...k}} \nabla \left[ \zeta_{nk} P_{n}^{(1,1)} \right] \right\vert
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img218.gif) |
(65) |
over the volume of the convection zone, we find:
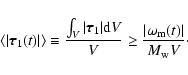 |
(66) |
3.1 Interior model, eigenvalues and eigenfunctions
A model of the solar interior can be used to specify the functions 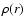 and
and
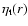 that appear in our equations. While the density stratification can be determined with an accuracy better than 0.5%, the turbulent dynamical viscosity is uncertain by at least one order of magnitude and it is estimated
from the mixing-length theory according to the formula:
that appear in our equations. While the density stratification can be determined with an accuracy better than 0.5%, the turbulent dynamical viscosity is uncertain by at least one order of magnitude and it is estimated
from the mixing-length theory according to the formula:
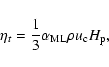 |
(67) |
where
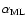 is the ratio of the mixing-length to the pressure scale height
is the ratio of the mixing-length to the pressure scale height 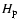 and
and 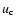 is the convective velocity given by:
is the convective velocity given by:
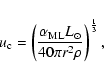 |
(68) |
where 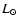 is the luminosity of the Sun. In our computations we adopt
is the luminosity of the Sun. In our computations we adopt
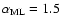 and assume the solar model S for the interior quantities
and assume the solar model S for the interior quantities![[*]](/icons/foot_motif.gif) (Christensen-Dalsgaard et al. 1996). In that model, the base of the convection zone is at
(Christensen-Dalsgaard et al. 1996). In that model, the base of the convection zone is at
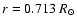 .
We consider also the effect of an overshoot layer extending between
.
We consider also the effect of an overshoot layer extending between
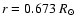 and the base of the convection zone within which the turbulent dynamical viscosity is assumed to increase linearly from zero up to the value
at the base of the convection zone. The density and the turbulent viscosity are
plotted in Fig. 1 where their values have been normalized to the values at the base of the convection zone (i.e.,
and the base of the convection zone within which the turbulent dynamical viscosity is assumed to increase linearly from zero up to the value
at the base of the convection zone. The density and the turbulent viscosity are
plotted in Fig. 1 where their values have been normalized to the values at the base of the convection zone (i.e.,
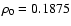 g cm-3 and
g cm-3 and

 1012 g cm-1 s-1, respectively).
1012 g cm-1 s-1, respectively).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7418f1.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg230.gif) |
Figure 1:
The ratio of the density to the density at the base of the convection zone (
 - solid line) and the ratio of the turbulent dynamical viscosity to the turbulent viscosity at the base of the convection zone ( - solid line) and the ratio of the turbulent dynamical viscosity to the turbulent viscosity at the base of the convection zone (
 - dotted) versus the
fractionary radius - dotted) versus the
fractionary radius
 in our solar interior model.
in our solar interior model. |
| Open with DEXTER |
The basic equations of our model (i.e., 12, 13 and 14) can be made nondimensional by adopting as the unit of length the solar radius  ,
as the unit of density
,
as the unit of density 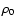 ,
i.e., the density at
the base of the solar convection zone, and as a unit of time
,
i.e., the density at
the base of the solar convection zone, and as a unit of time
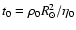 ,
where
,
where 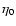 is the turbulent viscosity at the base of the convection zone. Indeed, the value of the diffusion coefficients estimated from the mixing-length theory leads
to a too short period for the solar cycle in mean-field dynamo models. Covas et al. (2004) adopted a turbulent magnetic diffusivity
is the turbulent viscosity at the base of the convection zone. Indeed, the value of the diffusion coefficients estimated from the mixing-length theory leads
to a too short period for the solar cycle in mean-field dynamo models. Covas et al. (2004) adopted a turbulent magnetic diffusivity
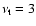
 1011 cm2 s-1
to get a sunspot cycle of
1011 cm2 s-1
to get a sunspot cycle of  11 yr. This implies
11 yr. This implies
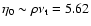
 1010 g cm-1 s-1 in our model.
1010 g cm-1 s-1 in our model.
The radial eigenfunctions
 and the Jacobian polynomials
Pn(1,1) have been computed from the respective Sturm-Liouville problem equations
by means of the Fortran 77 subroutine sleign2.f
and the Jacobian polynomials
Pn(1,1) have been computed from the respective Sturm-Liouville problem equations
by means of the Fortran 77 subroutine sleign2.f![[*]](/icons/foot_motif.gif) (Bailey et al. 2001). For the radial eigenfunctions
(Bailey et al. 2001). For the radial eigenfunctions
 ,
the Sturm-Lioville problem
has been solved with Neumann boundary conditions at both ends, set at
,
the Sturm-Lioville problem
has been solved with Neumann boundary conditions at both ends, set at
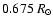 and
and
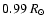 to avoid divergence at the surface. For the Jacobian polynomials,
limit point boundary conditions have been adopted at
to avoid divergence at the surface. For the Jacobian polynomials,
limit point boundary conditions have been adopted at
 .
.
Note that, to be rigorous, it would be better to use the helioseismic estimate of
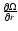 at r=0.99 where we fixed our outer boundary for
the computation of the radial eigenfunctions instead of the stress-free boundary condition that is valid only at the surface. However, the differences are confined to the outermost layer of the solar convection zone, the moment of inertia of which is so small that there are no pratical consequences.
at r=0.99 where we fixed our outer boundary for
the computation of the radial eigenfunctions instead of the stress-free boundary condition that is valid only at the surface. However, the differences are confined to the outermost layer of the solar convection zone, the moment of inertia of which is so small that there are no pratical consequences.
The eigenvalues
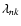 and the eigenfunctions
and the eigenfunctions
 computed by sleign2.f
have been compared with those computed by means of the code introduced by Lanza (2006b).
The relative differences in the eigenvalues and in the eigenfunctions are lower than 1.5% for
computed by sleign2.f
have been compared with those computed by means of the code introduced by Lanza (2006b).
The relative differences in the eigenvalues and in the eigenfunctions are lower than 1.5% for 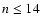 ,
,
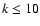 .
However, some problems of convergence of the numerical algorithm used by sleign2.f have been found for
.
However, some problems of convergence of the numerical algorithm used by sleign2.f have been found for 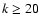 ,
particularly
for
,
particularly
for 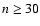 ,
so we decided to limit its application up to k = 19.
,
so we decided to limit its application up to k = 19.
The Jacobian polynomials and the eigenvalues computed by sleign2.f are very good up to n =30, as it has been found by comparison with their analytic expressions up to n=10 and their asymptotic expressions for 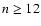 .
We conclude that for
.
We conclude that for 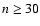 and
and 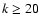 it is better to use the asymptotic formulae (22) and (18) instead of the numerically computed
it is better to use the asymptotic formulae (22) and (18) instead of the numerically computed
 and
Pn(1,1).
and
Pn(1,1).
The eigenvalue
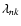 gives the inverse of the characteristic timescale of
angular momentum transfer of the mode corresponding to
gives the inverse of the characteristic timescale of
angular momentum transfer of the mode corresponding to
 under the action of the turbulent viscosity. The longest timescale corresponds to
the lowest eigenvalue, i.e.,
under the action of the turbulent viscosity. The longest timescale corresponds to
the lowest eigenvalue, i.e.,
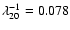 in nondimensional units.
It corresponds to a timescale of
0.86 yr with the turbulent viscosity given by the mixing-length theory
and to 39.5 yr with
in nondimensional units.
It corresponds to a timescale of
0.86 yr with the turbulent viscosity given by the mixing-length theory
and to 39.5 yr with

 1010 g cm-1 s-1.
1010 g cm-1 s-1.
3.2 Localization functions for the source of the torsional oscillations
The available data on the torsional oscillations are displayed with a typical
radial resolution of 0.05  and a latitudinal resolution of
and a latitudinal resolution of
 in
Howe et al. (2006,2005). The rotational inversion kernels of
Schou et al. (1998) show a higher radial resolution close to the surface, but, given the
small amplitude of the torsional oscillations, the choice of a uniform resolution of 0.05
in
Howe et al. (2006,2005). The rotational inversion kernels of
Schou et al. (1998) show a higher radial resolution close to the surface, but, given the
small amplitude of the torsional oscillations, the choice of a uniform resolution of 0.05  seems to be better.
seems to be better.
We have found that the best results of the localization of the source term with the method
outlined in Sect. 2.4 are obtained with localization functions that depend on
r or  only and that have a smooth derivative. As a typical function to probe the
radial localization, we adopt:
only and that have a smooth derivative. As a typical function to probe the
radial localization, we adopt:
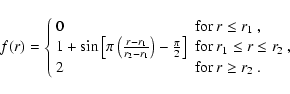 |
(69) |
This function has zero derivative, except in the interval
]r1, r2[ where its derivative
varies smoothly reaching a maximum in the mid of the interval. In Fig. 2 we plot the
modulus of the derivative
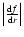 ,
as given by the sum of the series of the radial eigenfunctions truncated at k =19, for three different intervals centered at 0.725, 0.85 and 0.965
,
as given by the sum of the series of the radial eigenfunctions truncated at k =19, for three different intervals centered at 0.725, 0.85 and 0.965  ,
all with an amplitude of
r2 - r1 = 0.05
,
all with an amplitude of
r2 - r1 = 0.05  .
The derivative is well approximated by the truncated series, with small sidelobes
the amplitude of which increases toward the surface of the Sun because the eigenfunctions
scale as
.
The derivative is well approximated by the truncated series, with small sidelobes
the amplitude of which increases toward the surface of the Sun because the eigenfunctions
scale as
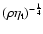 ,
according to the asymptotic expression (22).
,
according to the asymptotic expression (22).
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f2.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg249.gif) |
Figure 2:
The modulus of the radial localization kernel versus the relative radius
for the function (69), as obtained by truncating the series of
the radial eigenfunctions at
 ,
for three different intervals centered at r=0.725 ( upper panel), 0.85
( middle panel) and 0.965 ,
for three different intervals centered at r=0.725 ( upper panel), 0.85
( middle panel) and 0.965  ( lower panel), all with an
amplitude of
r2 - r1 = 0.05
( lower panel), all with an
amplitude of
r2 - r1 = 0.05  .
The modulus of the derivative has been normalized to its maximum value. .
The modulus of the derivative has been normalized to its maximum value. |
| Open with DEXTER |
The performance of the localization method introduced in Sect. 2.4 has been tested with
simulated data in the absence of noise. The results of two such tests are plotted in Fig. 3 where we consider the case of a purely radial perturbation
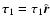 localized within an interval of amplitude 0.05
localized within an interval of amplitude 0.05  .
Its time dependence is assumed to be purely cosinusoidal and the corresponding coefficients
.
Its time dependence is assumed to be purely cosinusoidal and the corresponding coefficients
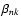 are computed by means of Eq. (30) up to the orders n=38 and k=19. From the
are computed by means of Eq. (30) up to the orders n=38 and k=19. From the
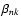 ,
the coefficients
,
the coefficients
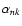 are computed by means of Eq. (26) and the simulated angular velocity
perturbation follows from Eq. (16).
are computed by means of Eq. (26) and the simulated angular velocity
perturbation follows from Eq. (16).
When the interval in which
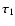 is localized coincides with one of the inversion
intervals
[r1, r2], the lower limit for
is localized coincides with one of the inversion
intervals
[r1, r2], the lower limit for
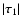 turns out to be
turns out to be  80%-90% of the value
assumed in the simulation (Fig. 3, upper panel). The agreement increases up to 90%-95% if we consider
a case in which
80%-90% of the value
assumed in the simulation (Fig. 3, upper panel). The agreement increases up to 90%-95% if we consider
a case in which 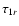 has a constant sign and put the value of the derivative
has a constant sign and put the value of the derivative
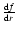 in the denominator of Eq. (46) instead of its modulus.
This happens because the modulus of the derivative
increases the effects of the sidelobes by increasing the value of the denominator in Eq. (46).
When the interval in which the assumed
in the denominator of Eq. (46) instead of its modulus.
This happens because the modulus of the derivative
increases the effects of the sidelobes by increasing the value of the denominator in Eq. (46).
When the interval in which the assumed
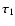 is localized does not coincide with an interval of the inversion grid, the inversion method still performs well distributing the contributions among neighbour intervals
nearly in the correct proportion (Fig. 3, lower panel).
The case of simulations including a noise component is straightforward to treat thanks to the linear character of our inversion method. The inverted value turns out to be the sum of the inverted noiseless value and of the contribution coming from the inversion of the noise. Their amplitude ratio is equal to the ratio of the amplitudes of the input
noise to the input signal (for constant relative signal errors), as discussed in Sect. 2.4.
is localized does not coincide with an interval of the inversion grid, the inversion method still performs well distributing the contributions among neighbour intervals
nearly in the correct proportion (Fig. 3, lower panel).
The case of simulations including a noise component is straightforward to treat thanks to the linear character of our inversion method. The inverted value turns out to be the sum of the inverted noiseless value and of the contribution coming from the inversion of the noise. Their amplitude ratio is equal to the ratio of the amplitudes of the input
noise to the input signal (for constant relative signal errors), as discussed in Sect. 2.4.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{7418f3.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg253.gif) |
Figure 3:
Upper panel: test case of the application of the inversion method from Sect. 2.4. An input profile
with
 in nondimensional units between 0.80 and 0.85
in nondimensional units between 0.80 and 0.85  (solid line) is used to simulate a noiseless profile of angular velocity perturbation. The reconstructed lower-limit profile according to Eq. (46)
is plotted as a dotted line. Lower panel: same as in the upper panel, but with an
input profile localized between 0.775 and 0.825
(solid line) is used to simulate a noiseless profile of angular velocity perturbation. The reconstructed lower-limit profile according to Eq. (46)
is plotted as a dotted line. Lower panel: same as in the upper panel, but with an
input profile localized between 0.775 and 0.825  . . |
| Open with DEXTER |
The localization in latitude can be sampled by means of a localization function of the kind:
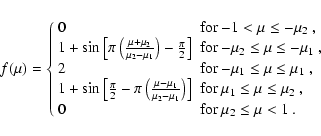 |
(70) |
Such a function is symmetric with respect to the equator so that its derivative
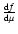 is antisymmetric, as it is the source term
is antisymmetric, as it is the source term
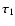 leading to a symmetric perturbation of the angular velocity.
The localization function has a derivative always equal to zero except in two intervals
leading to a symmetric perturbation of the angular velocity.
The localization function has a derivative always equal to zero except in two intervals
![$]\!-\!\mu_{2}, -\mu_{1}[$](/articles/aa/full/2007/33/aa7418-07/img256.gif) and
and
![$]\mu_{1}, \mu_{2}[$](/articles/aa/full/2007/33/aa7418-07/img257.gif) ,
symmetric with respect to the solar equator. Its representation by means of the Jacobian polynomials with degree up to
,
symmetric with respect to the solar equator. Its representation by means of the Jacobian polynomials with degree up to
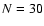 is given in Fig. 4. Note that the maximum of
is given in Fig. 4. Note that the maximum of
 is reached in two sharp peaks at
is reached in two sharp peaks at
 .
However, they are so narrow that their contribution to the integral in Eq. (46) is modest in comparison to those of the broader peaks in the intervals
.
However, they are so narrow that their contribution to the integral in Eq. (46) is modest in comparison to those of the broader peaks in the intervals
![$[-\mu_{2}, -\mu_{1}]$](/articles/aa/full/2007/33/aa7418-07/img260.gif) and
and
![$[\mu_{1}, \mu_{2}]$](/articles/aa/full/2007/33/aa7418-07/img261.gif) .
Several tests have been performed, as in the case of the radial localization, to assess the performance of the proposed method. The results are similar to those obtained for the radial case and are not discussed here.
.
Several tests have been performed, as in the case of the radial localization, to assess the performance of the proposed method. The results are similar to those obtained for the radial case and are not discussed here.
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{7418f4.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg262.gif) |
Figure 4:
The modulus of the latitudinal localization kernel versus  for the function (70), obtained by truncating the series of the Jacobian polynomials at
for the function (70), obtained by truncating the series of the Jacobian polynomials at
 ,
for three different intervals of ,
for three different intervals of  in the Northern hemisphere, i.e., [0, 0.26] ( upper panel),
[0.5, 0.7] ( middle panel) and
[0.87, 0.99] ( lower panel). Note the symmetry of the modulus of the kernel with respect to the equator. The value of
in the Northern hemisphere, i.e., [0, 0.26] ( upper panel),
[0.5, 0.7] ( middle panel) and
[0.87, 0.99] ( lower panel). Note the symmetry of the modulus of the kernel with respect to the equator. The value of
 is normalized at its maximum at is normalized at its maximum at
 . . |
| Open with DEXTER |
We conclude that our choice of
 and
and
 is perfectly adequate to invert the available data on the solar torsional oscillations to derive information on
the location of the perturbation term within the convection zone.
is perfectly adequate to invert the available data on the solar torsional oscillations to derive information on
the location of the perturbation term within the convection zone.
3.3 Results on the sources of the torsional oscillations
The data plotted in Fig. 4 of Howe et al. (2006) can be used for an illustrative application of the inversion methods introduced in Sect. 2.4. They are given with a sampling of
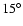 between the equator and
between the equator and
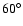 of
latitude, i.e., in the range in which the rotational inversion techniques perform better (Schou et al. 1998).
The features distinguishable on the plots indicate an actual radial resolution of
of
latitude, i.e., in the range in which the rotational inversion techniques perform better (Schou et al. 1998).
The features distinguishable on the plots indicate an actual radial resolution of  0.05
0.05  ,
in agreement with the sampling adopted in Fig. 3 of Howe et al. (2005).
An average statistical error of about 30% can be assumed for the amplitude, whereas the phase errors become very large below 0.80
,
in agreement with the sampling adopted in Fig. 3 of Howe et al. (2005).
An average statistical error of about 30% can be assumed for the amplitude, whereas the phase errors become very large below 0.80  ,
especially at low latitudes, because of the uncertainty in the reconstruction of the signal
in the deep layers. Note that the error intervals reported in Fig. 4 of Howe et al. (2006) indicate only how the particular method solution (here an OLA inversion of SoHO/MDI data) would vary with a different realization of the input data affected by a randon Gaussian noise. Unfortunately, they do not give the statistical ranges in which the true values of the amplitude and phase are likely to lie. This is not a major limitation in the
context of the present study because we aim at illustrating the capabilities of the proposed approach rather than derive definitive conclusions.
,
especially at low latitudes, because of the uncertainty in the reconstruction of the signal
in the deep layers. Note that the error intervals reported in Fig. 4 of Howe et al. (2006) indicate only how the particular method solution (here an OLA inversion of SoHO/MDI data) would vary with a different realization of the input data affected by a randon Gaussian noise. Unfortunately, they do not give the statistical ranges in which the true values of the amplitude and phase are likely to lie. This is not a major limitation in the
context of the present study because we aim at illustrating the capabilities of the proposed approach rather than derive definitive conclusions.
To perform our inversion, we interpolate linearly the values of the amplitude and phase over the grid used to compute the radial eigenfunctions and the Jacobian polynomials. We assume that the amplitude is zero at the poles and increases linearly toward
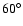 of latitude whereas the phase is constant poleward of
of latitude whereas the phase is constant poleward of
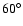 of latitude.
of latitude.
The divergence of the angular momentum flux perturbation
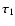 can be obtained from Eq. (40). We define its amplitude and phase as:
can be obtained from Eq. (40). We define its amplitude and phase as:
![\begin{displaymath}%
A_{\tau} \equiv \sqrt{[\nabla \cdot {\vec \tau}_{1}^{(c)}]^{2} + [\nabla \cdot {\vec \tau}_{1}^{(s)}]^{2}},
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img263.gif) |
(71) |
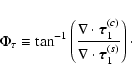 |
(72) |
They are plotted in Figs. 5 and 6, respectively, in the case of

 1012 g cm-1 s-1. A suitable smoothing has been applied
to have a resolution of
1012 g cm-1 s-1. A suitable smoothing has been applied
to have a resolution of  0.05
0.05  in the radial coordinate and
in the radial coordinate and 
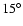 in latitude. In order to show the effect of a smaller value of the turbulent viscosity, we plot in Figs. 7 and 8 the isocontours of
in latitude. In order to show the effect of a smaller value of the turbulent viscosity, we plot in Figs. 7 and 8 the isocontours of  and
and
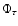 for
for
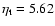
 1010 g cm-1 s-1.
The amplitude of the perturbation term is higher close to the equator because the data in Fig. 4 of
Howe et al. (2006) mainly sample the low-latitude branch of the torsional oscillations. The relative maxima of
1010 g cm-1 s-1.
The amplitude of the perturbation term is higher close to the equator because the data in Fig. 4 of
Howe et al. (2006) mainly sample the low-latitude branch of the torsional oscillations. The relative maxima of  are reached close to the base of the convection zone and at a radius of
are reached close to the base of the convection zone and at a radius of  0.85
0.85  and their locations show only a minor dependence on the value of
and their locations show only a minor dependence on the value of 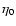 .
Conversely, the value of
.
Conversely, the value of 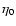 significantly
affects
significantly
affects
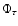 ,
as it follows from Eqs. (39). When
,
as it follows from Eqs. (39). When 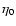 is large, the timescales for angular momentum exchange, as given by the inverse of the lowest eigenvalues, are significantly shorter than the eleven-year cycle and
the perturbations are almost in phase with the angular velocity variations. When
is large, the timescales for angular momentum exchange, as given by the inverse of the lowest eigenvalues, are significantly shorter than the eleven-year cycle and
the perturbations are almost in phase with the angular velocity variations. When
 is sufficiently low, the timescales for angular momentum exchange
become comparable or longer than the eleven-year cycle so the torsional oscillations lag behind the perturbations. Considering Fig. 6, we see that the phase is in agreement with that in
Fig. 4 of Howe et al. (2006), except for
is sufficiently low, the timescales for angular momentum exchange
become comparable or longer than the eleven-year cycle so the torsional oscillations lag behind the perturbations. Considering Fig. 6, we see that the phase is in agreement with that in
Fig. 4 of Howe et al. (2006), except for
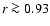
 .
The disagreement in those layers
is due to the small values of
.
The disagreement in those layers
is due to the small values of
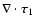 close to the surface that makes the
corresponding phases uncertain (cf. Fig. 5). The phase lag is apparent by comparing Fig. 8 with Fig. 6, especially close to the equator for
close to the surface that makes the
corresponding phases uncertain (cf. Fig. 5). The phase lag is apparent by comparing Fig. 8 with Fig. 6, especially close to the equator for
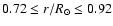 .
It is less evident
near the base of the convection zone and in the upper layers due to the smaller values of
.
It is less evident
near the base of the convection zone and in the upper layers due to the smaller values of
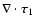 in those regions.
in those regions.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f5.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg270.gif) |
Figure 5:
The isocontours of the function
 as defined by Eq. (71) in the case of
as defined by Eq. (71) in the case of
  1012 g cm-1 s-1. The scale on the left indicates the ranges corresponding to the different colors and is in units of 105 g cm-1 s-2. The relative statistical uncertainty of
1012 g cm-1 s-1. The scale on the left indicates the ranges corresponding to the different colors and is in units of 105 g cm-1 s-2. The relative statistical uncertainty of  is
is  30%, as it follows
from the relative uncertainty of the data. 30%, as it follows
from the relative uncertainty of the data. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f6.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg273.gif) |
Figure 6:
The isocontours of
 as defined by Eq. (72) in the case of
as defined by Eq. (72) in the case of
  1012 g cm-1 s-1. The phase ranges from
1012 g cm-1 s-1. The phase ranges from
 to
to
 .
The scale on the left indicates the
phase ranges corresponding to the different colors and is in radians. .
The scale on the left indicates the
phase ranges corresponding to the different colors and is in radians. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f7.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg274.gif) |
Figure 7:
As for Fig. 5 in the case of
  1010 g cm-1 s-1. The scale on the left is in units of 103 g cm-1 s-2. The relative statistical uncertainty of
1010 g cm-1 s-1. The scale on the left is in units of 103 g cm-1 s-2. The relative statistical uncertainty of  is about 30%.
is about 30%. |
| Open with DEXTER |
It is interesting to note that the dependence of the amplitude and phase of the torsional oscillations on the turbulent
viscosity can lead to its estimate in the framework of mean-field models
(e.g., Rüdiger et al. 1986; Rüdiger 1989). Specifically, Rempel (2007) finds that
a mean turbulent kinematic viscosity about one order of magnitude smaller than the mixing-length estimate is needed
to reproduce the polar branch of the torsional oscillations.
Lower limits for the modulus of the angular momentum flux vector
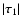 can be derived
from Eq. (46). From the lower limits on
can be derived
from Eq. (46). From the lower limits on
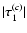 and
and
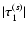 ,
a lower limit on
,
a lower limit on
![$\vert{\vec \tau}_{1}\vert= \sqrt{[{\vec \tau}_{1}^{(c)}]^{2} + [{\vec \tau}_{1}^{(s)}]^{2}}$](/articles/aa/full/2007/33/aa7418-07/img278.gif) can be derived
and it is plotted in Figs. 9 and 10 for the radial and latitudinal
localizations described in Sect. 3.2, respectively.
Given the uncertainty in the penetration depth of the torsional
oscillations, in addition to the results for a penetration down to the base of the convection zone,
we also plot those for penetration depths of 0.80 and 0.90
can be derived
and it is plotted in Figs. 9 and 10 for the radial and latitudinal
localizations described in Sect. 3.2, respectively.
Given the uncertainty in the penetration depth of the torsional
oscillations, in addition to the results for a penetration down to the base of the convection zone,
we also plot those for penetration depths of 0.80 and 0.90  ,
respectively. They are obtained simply by assuming that the oscillation amplitude has the value in Fig. 4 of
Howe et al. (2006) above the penetration depth and drops to zero immediately below it.
,
respectively. They are obtained simply by assuming that the oscillation amplitude has the value in Fig. 4 of
Howe et al. (2006) above the penetration depth and drops to zero immediately below it.
When the oscillations penetrate down to the base of the convection zone, the maximum of the perturbation term is reached between 0.80 and 0.85  .
It is mainly
localized into two latitude zones, i.e., within
.
It is mainly
localized into two latitude zones, i.e., within 
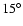 from the
equator and between
from the
equator and between
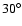 and
and
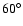 .
Note that our data refer mainly to the low-latitude branch of the oscillations,
so the possible source at latitude >
.
Note that our data refer mainly to the low-latitude branch of the oscillations,
so the possible source at latitude >
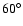 cannot be detected. When the turbulent dynamical viscosity is reduced with respect to the mixing-length value, the amplitude of the perturbation term drops, but its radial and latitudinal localizations
are not greatly affected, except for a shift of the nearly equatorial band towards higher latitudes.
cannot be detected. When the turbulent dynamical viscosity is reduced with respect to the mixing-length value, the amplitude of the perturbation term drops, but its radial and latitudinal localizations
are not greatly affected, except for a shift of the nearly equatorial band towards higher latitudes.
According to the hypothesis that the Lorentz force is the only source of the torsional oscillations, the amplitude of the Maxwell stress
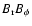 can be estimated from the lower limit of
can be estimated from the lower limit of
 and is
and is  2.7
2.7  105 G2 in the case of
105 G2 in the case of

 1012 g cm-1 s-1. Considering that the poloidal field
1012 g cm-1 s-1. Considering that the poloidal field  is of the order of 1-10 G, this leads to very high toroidal fields in the bulk of the convection zone, which would be highly unstable because of magnetic buoyancy. On the other hand, with
is of the order of 1-10 G, this leads to very high toroidal fields in the bulk of the convection zone, which would be highly unstable because of magnetic buoyancy. On the other hand, with

 1010 g cm-1 s-1, the Maxwell stress is
1010 g cm-1 s-1, the Maxwell stress is
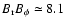
 103 G2 which leads to a toroidal field intensity of the order of 103 G. It may be stably stored for timescales comparable to the solar cycle thanks to the effects of the downward turbulent pumping in the convection zone (Brandenburg 2005, and references therein).
103 G2 which leads to a toroidal field intensity of the order of 103 G. It may be stably stored for timescales comparable to the solar cycle thanks to the effects of the downward turbulent pumping in the convection zone (Brandenburg 2005, and references therein).
Note that the maximum radial stress
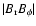 is reduced by a factor of
is reduced by a factor of  30 when
30 when
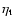 is decreased from 2.56
is decreased from 2.56  1012 to 5.62
1012 to 5.62  1010 g cm-1 s-1, whereas the maximum of
1010 g cm-1 s-1, whereas the maximum of
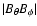 is
reduced only by a factor of
is
reduced only by a factor of  4 (Figs. 9 and 10). This mainly reflects the predominance of the radial gradient over the latitudinal gradient of the angular velocity perturbation in the deeper layers of the solar convection zone.
4 (Figs. 9 and 10). This mainly reflects the predominance of the radial gradient over the latitudinal gradient of the angular velocity perturbation in the deeper layers of the solar convection zone.
The average phase lags
 and
and
 between
between  and
and
 and the azimuthal field
and the azimuthal field  ,
as derived by the method in Sect. 2.6, are plotted in Figs. 11 and 12, respectively. It is interesting to note that
,
as derived by the method in Sect. 2.6, are plotted in Figs. 11 and 12, respectively. It is interesting to note that
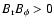 below
below  0.85
0.85  when
when
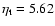
 1010 g cm-1 s-1, in agreement with the finding of most dynamo models in which the
azimuthal field is produced by the stretching of the radial field in the low-latitude region,
where
1010 g cm-1 s-1, in agreement with the finding of most dynamo models in which the
azimuthal field is produced by the stretching of the radial field in the low-latitude region,
where
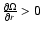 for r < 0.95
for r < 0.95  (e.g., Schlichenmaier & Stix 1995; Rüdiger & Hollerbach 2004).
Above
(e.g., Schlichenmaier & Stix 1995; Rüdiger & Hollerbach 2004).
Above  0.85
0.85  ,
the phase relationship between the radial and the azimuthal fields leads to
,
the phase relationship between the radial and the azimuthal fields leads to
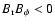 with a phase lag of
with a phase lag of 
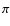 ,
in agreement with the early finding that the photospheric zone equatorward of the activity belt is rotating faster than that at higher latitudes (Rüdiger 1989). Note that
,
in agreement with the early finding that the photospheric zone equatorward of the activity belt is rotating faster than that at higher latitudes (Rüdiger 1989). Note that
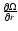 becomes negative
for r > 0.95
becomes negative
for r > 0.95  at low latitudes, leading to a reversal of the phase relationship between the two field components in the outer layers of the solar convection zone. Our limited spatial resolution and the uncertainty of the measurements of the torsional oscillations inside the Sun might explain why we find the transition from a mostly positive
to a negative
at low latitudes, leading to a reversal of the phase relationship between the two field components in the outer layers of the solar convection zone. Our limited spatial resolution and the uncertainty of the measurements of the torsional oscillations inside the Sun might explain why we find the transition from a mostly positive
to a negative
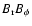 at
at  0.85
0.85  .
.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f9.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg287.gif) |
Figure 9:
Upper panel: the lower limit of the amplitude of the perturbation term
 averaged over spherical shells of
thickness 0.05
averaged over spherical shells of
thickness 0.05  versus the relative radius; different linestyles and colors refer to the depth at which the torsional oscillations are assumed to vanish: black solid line - oscillations extending down to the base of the convection zone;
green dotted line - oscillations extending down to 0.80
versus the relative radius; different linestyles and colors refer to the depth at which the torsional oscillations are assumed to vanish: black solid line - oscillations extending down to the base of the convection zone;
green dotted line - oscillations extending down to 0.80  ;
red dashed line - oscillations extending down to 0.90 ;
red dashed line - oscillations extending down to 0.90  .
Results are obtained assuming a turbulent dynamical viscosity at the base of the convection zone .
Results are obtained assuming a turbulent dynamical viscosity at the base of the convection zone
  1012 g cm-1 s-1. Lower panel: as in the upper panel, but for
1012 g cm-1 s-1. Lower panel: as in the upper panel, but for
  1010 g cm-1 s-1. The relative statistical uncertainties are in all cases about 30%, as follows from the uncertainties of the data.
1010 g cm-1 s-1. The relative statistical uncertainties are in all cases about 30%, as follows from the uncertainties of the data. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{7418f10.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg289.gif) |
Figure 10:
Upper panel: the lower limit of the amplitude of the perturbation term
 averaged over different latitude zones
versus their average value of
averaged over different latitude zones
versus their average value of  .
Different linestyles and colors are used to indicate the results for different penetration depths
of the torsional oscillations, as in Fig. 9. Results are obtained assuming
a turbulent dynamical viscosity at the base of the convection zone .
Different linestyles and colors are used to indicate the results for different penetration depths
of the torsional oscillations, as in Fig. 9. Results are obtained assuming
a turbulent dynamical viscosity at the base of the convection zone
  1012 g cm-1 s-1. Lower panel: as in the upper panel, but for
1012 g cm-1 s-1. Lower panel: as in the upper panel, but for
  1010 g cm-1 s-1. The relative statistical uncertainties are in all cases about 30%, as follows from the uncertainties of the data.
1010 g cm-1 s-1. The relative statistical uncertainties are in all cases about 30%, as follows from the uncertainties of the data. |
| Open with DEXTER |
The phase lag between
 and
and  depends remarkably
on the colatitude for
depends remarkably
on the colatitude for
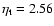
 1012 g cm-1 s-1, whereas it is almost constant for
1012 g cm-1 s-1, whereas it is almost constant for
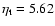
 1010 g cm-1 s-1, leading in the latter case mostly to
1010 g cm-1 s-1, leading in the latter case mostly to
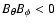 .
This, together with
.
This, together with
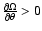 ,
suggests
that the toroidal field is mainly produced by the stretching of the radial field.
,
suggests
that the toroidal field is mainly produced by the stretching of the radial field.
On the other hand, if the angular momentum transport leading to the torsional oscillations is
produced only by a perturbation of the meridional flow, as in the thermal wind model, then a very small perturbation follows from the lower limit of
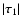 .
For
.
For

 1012 g cm-1 s-1,
we find a minimum amplitude of the meridional flow component oscillating with the eleven-year cycle of
1012 g cm-1 s-1,
we find a minimum amplitude of the meridional flow component oscillating with the eleven-year cycle of 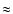 3 cm s-1 at a depth of 0.85
3 cm s-1 at a depth of 0.85  and a latitude of
and a latitude of
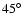 .
Note, however, that if we estimate
.
Note, however, that if we estimate
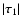 from its divergence and the typical lengthscale of its variations in Fig. 5,
we find a value about one order of magnitude larger, that is in agreement with the estimate by Rempel (2007). A similar argument
applies also to the estimate of the Maxwell stresses made above.
from its divergence and the typical lengthscale of its variations in Fig. 5,
we find a value about one order of magnitude larger, that is in agreement with the estimate by Rempel (2007). A similar argument
applies also to the estimate of the Maxwell stresses made above.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f11.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg294.gif) |
Figure 11:
Upper panel: the phase lag
 between
between  and
and  as derived by Eqs. (54) averaged over spherical shells of
thickness 0.05
as derived by Eqs. (54) averaged over spherical shells of
thickness 0.05  versus the relative radius.
Different linestyles are used to indicate the results for different penetration depths
of the torsional oscillations, as in Fig. 9.
Results are obtained assuming a turbulent dynamical viscosity at the base of the convection zone
versus the relative radius.
Different linestyles are used to indicate the results for different penetration depths
of the torsional oscillations, as in Fig. 9.
Results are obtained assuming a turbulent dynamical viscosity at the base of the convection zone
  1012 g cm-1 s-1. Lower panel: as in the upper panel, but for
1012 g cm-1 s-1. Lower panel: as in the upper panel, but for
  1010 g cm-1 s-1.
1010 g cm-1 s-1. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{7418f12.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg295.gif) |
Figure 12:
Upper panel: the phase lag
 between
between
 and
and  ,
as derived by equations analogous to (54), averaged over different latitude zones
versus their average value of ,
as derived by equations analogous to (54), averaged over different latitude zones
versus their average value of  .
Different linestyles are used to indicate the results for different penetration depths
of the torsional oscillations, as in Fig. 9.
Results are obtained assuming a turbulent dynamical viscosity at the base of the convection zone .
Different linestyles are used to indicate the results for different penetration depths
of the torsional oscillations, as in Fig. 9.
Results are obtained assuming a turbulent dynamical viscosity at the base of the convection zone
  1012 g cm-1 s-1. Lower panel: as in the upper panel, but for
1012 g cm-1 s-1. Lower panel: as in the upper panel, but for
  1010 g cm-1 s-1.
1010 g cm-1 s-1. |
| Open with DEXTER |
The average kinetic energy variation associated with the
torsional oscillations, as computed from Eq. (49), is
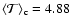
 1028 erg, whereas the average dissipated power is 6.7
1028 erg, whereas the average dissipated power is 6.7  1026 erg s-1, when
1026 erg s-1, when

 1012 g cm-1 s-1, and only
1.5
1012 g cm-1 s-1, and only
1.5  1025 erg s-1, when
1025 erg s-1, when
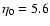
 1010 g cm-1 s-1.
1010 g cm-1 s-1.
When the torsional oscillations are assumed to be confined to shallower and shallower layers,
the location of the perturbation term is shifted closer and closer to the surface and it
becomes more and more uniformly distributed in latitude. Its amplitude shows a remarkable decrease because of the smaller moment of inertia of the surface layers.
The results of Sect. 2.7 can be applied to the variation of the surface differential rotation observed in, e.g., LQ Hya between 1996.99 and 2000.96 (see Table 2 of Donati et al. 2003). Assuming an internal
structure analogous to the solar one and that the differential rotation variations observed at the surface are representative of those at a depth of 0.99 R, we can estimate a lower limit for
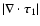 in the overshoot layer from Eq. (59).
This is used to estimate the Maxwell stresses by assuming that:
in the overshoot layer from Eq. (59).
This is used to estimate the Maxwell stresses by assuming that:
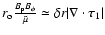 ,
where
,
where
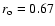 R is the radius of the overshoot layer and
R is the radius of the overshoot layer and
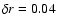 R its thickness. As such, the minimum magnetic field strength is:
R its thickness. As such, the minimum magnetic field strength is:
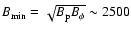 G. However, if we assume a poloidal field strength of
G. However, if we assume a poloidal field strength of
 100 G, as indicated by the Zeeman Doppler imaging, we find an azimuthal field of
100 G, as indicated by the Zeeman Doppler imaging, we find an azimuthal field of
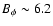
 104 G,
which is in the range of the values estimated by Lanza (2006a) in the framework of the Taylor-Proudman hypothesis. Note that the
result is independent of
104 G,
which is in the range of the values estimated by Lanza (2006a) in the framework of the Taylor-Proudman hypothesis. Note that the
result is independent of 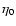 in the limit
in the limit
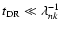 .
Although this application is purely illustrative, it suggests that our method can be applied to derive estimates of the
internal magnetic torques (as well as other sources of angular momentum transport) when
asteroseismic results are available, in combination with surface rotation measurements,
to further constrain rotation variations in solar-like stars.
.
Although this application is purely illustrative, it suggests that our method can be applied to derive estimates of the
internal magnetic torques (as well as other sources of angular momentum transport) when
asteroseismic results are available, in combination with surface rotation measurements,
to further constrain rotation variations in solar-like stars.
We introduced a general solution of the angular momentum
transport equation that takes into account the density stratification and the radial dependence of the turbulent viscosity
 .
Its main limitation is due to the uncertainty of the
turbulent viscosity in stellar convection zones. It is interesting to note that the method of the separation of variables to solve Eq. (3) can be applied also when
.
Its main limitation is due to the uncertainty of the
turbulent viscosity in stellar convection zones. It is interesting to note that the method of the separation of variables to solve Eq. (3) can be applied also when
 is the product of a function of the radius
by one of the latitude. However, when
is the product of a function of the radius
by one of the latitude. However, when
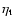 depends on the latitude,
the angular eigenfunctions are no longer Jacobian polynomials.
depends on the latitude,
the angular eigenfunctions are no longer Jacobian polynomials.
Our formalism can be applied to compute the response of a turbulent convection zone to prescribed time-dependent Lorentz force and meridional circulation. From the
mathematical point of view, it is a generalization of that of Rüdiger et al. (1986) and can be easily compared with it by considering that:
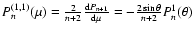 ,
where Pn is the Legendre polynomial of degree n and
,
where Pn is the Legendre polynomial of degree n and
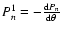 .
Moreover, our method can be used to estimate the torques leading to the angular momentum redistribution
within the solar (or stellar) convection zone, thus generalizing the approach suggested by Komm et al. (2003). The main limitation, in addition to the uncertainty of the turbulent viscosity, comes from the low resolution and the limited accuracy of the present data on solar torsional oscillations, particularly in the deeper layers
of the convection zone. In fact, these layers are the most important because
torsional oscillations with an amplitude of
.
Moreover, our method can be used to estimate the torques leading to the angular momentum redistribution
within the solar (or stellar) convection zone, thus generalizing the approach suggested by Komm et al. (2003). The main limitation, in addition to the uncertainty of the turbulent viscosity, comes from the low resolution and the limited accuracy of the present data on solar torsional oscillations, particularly in the deeper layers
of the convection zone. In fact, these layers are the most important because
torsional oscillations with an amplitude of  0.5%-1% of the solar angular velocity
extending down to the base of the convection zone lead to Maxwell stresses with an intensity of at least
0.5%-1% of the solar angular velocity
extending down to the base of the convection zone lead to Maxwell stresses with an intensity of at least  8
8  103 G2 around 0.85
103 G2 around 0.85  or a perturbation of the order of several percents of the meridional flow speed at the same depth (e.g., Rempel 2007).
If the torsional oscillations are due solely to the Maxwell stresses associated with the mean field of the solar dynamo, we can also estimate the phase relationships between
or a perturbation of the order of several percents of the meridional flow speed at the same depth (e.g., Rempel 2007).
If the torsional oscillations are due solely to the Maxwell stresses associated with the mean field of the solar dynamo, we can also estimate the phase relationships between  ,
,
 and
and  .
Our preliminary results
indicate that
.
Our preliminary results
indicate that
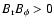 in the layers below
in the layers below 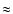 0.85
0.85  and
and
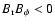 in the outer layers which, together with helioseismic measurements of the internal angular velocity, suggest that the toroidal field is
mainly produced by the stretching of the poloidal field by the radial shear.
in the outer layers which, together with helioseismic measurements of the internal angular velocity, suggest that the toroidal field is
mainly produced by the stretching of the poloidal field by the radial shear.
Future helioseismic measurements may improve our knowledge of the
torsional oscillations, essentially by extending the time series of the data or by means of space-borne instruments, such as those foreseen for the Solar Dynamic Observatory (e.g., Howe et al. 2006). On the other hand, asteroseismic measurements may open the possibility of investigating similar phenomena in solar-like stars,
particularly in those young, rapidly rotating objects showing
variations of the angular velocity one or two orders of magnitude larger than the Sun.
Acknowledgements
The author wishes to thank an anonymous Referee for valuable comments and Professor G. Rüdiger for interesting discussion. Solar physics and active star research at INAF-Catania Astrophysical Observatory and the Department of Physics
and Astronomy of Catania University is funded by MIUR (Ministero dell'Università e della Ricerca), and by Regione Siciliana, whose financial support is gratefully
acknowledged.
This research has made use of the ADS-CDS databases, operated at the CDS, Strasbourg, France.
The convergence of the Green function series in Eqs. (34) can be studied by considering
the asymptotic formulae for
 and the
Jacobian polynomials, i.e., for
and the
Jacobian polynomials, i.e., for 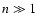 and
and 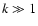 .
In the asymptotic limit, those series can be written as:
.
In the asymptotic limit, those series can be written as:
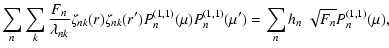 |
|
|
(A.1) |
where:
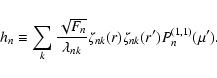 |
(A.2) |
From the asymptotic formulae it follows that for a point in the
domain
![$[r_{\rm b}, R_{\odot}]$](/articles/aa/full/2007/33/aa7418-07/img93.gif)

![$[r_{\rm b}, R_{\odot}]$](/articles/aa/full/2007/33/aa7418-07/img93.gif)
 ]-1, 1[, the
quantity
]-1, 1[, the
quantity
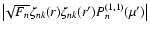 is limited with an upper bound independent of n and k. Therefore, the series (A.2) that defines the coefficient hn is uniformly convergent in that
domain if the series
is limited with an upper bound independent of n and k. Therefore, the series (A.2) that defines the coefficient hn is uniformly convergent in that
domain if the series
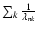 converges.
converges.
This can be proven by considering the inequalities in (21) and the formula:
![\begin{displaymath}%
\sum_{k=1}^{\infty} \frac{z}{a k^{2} + y} = \frac{1}{2} \le...
...ft[ g\left( \frac{y}{a}\right) \sqrt{\frac{y}{a}} - 1 \right],
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img311.gif) |
(A.3) |
where z, 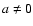 and y are real numbers and the function g(x) is defined as:
and y are real numbers and the function g(x) is defined as:
![\begin{displaymath}%
g(x) \equiv \pi \left[ \frac{\exp(\pi x) + \exp(-\pi x)}{\exp(\pi x) - \exp(-\pi x)} \right]\cdot
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img313.gif) |
(A.4) |
Equation (A.3) follows from the equality (1.217.1) of Gradshteyn & Ryzhik (1994). In this way, we find:
![$\displaystyle \frac{m}{2n(n+3)Q}\left\{ g\left[ \frac{n(n+3) Q l^{2}}{\pi^{2} P...
... q l^{2}}{\pi^{2} p}\right]
\sqrt{\frac{n(n+3) q l^{2}}{\pi^{2}p}} -1 \right\}.$](/articles/aa/full/2007/33/aa7418-07/img314.gif) |
|
|
(A.5) |
This result indicates that
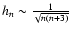 for
for 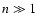 .
Since the eigenfunctions
.
Since the eigenfunctions
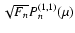 form an orthonormal set,
the convergence of the
series in (A.1) follows by the Riesz-Fisher Theorem given that the
series
form an orthonormal set,
the convergence of the
series in (A.1) follows by the Riesz-Fisher Theorem given that the
series
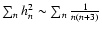 converges.
As such, the uniform convergence of the series in Eqs. (34) in the domain
converges.
As such, the uniform convergence of the series in Eqs. (34) in the domain
![$[r_{\rm b}, R_{\odot}] \times [r_{\rm b}, R_{\odot}] \times ]-1, 1[ \times ]-1, 1[ $](/articles/aa/full/2007/33/aa7418-07/img318.gif) is proven.
is proven.
- Bailey, P.
B., Everitt, W. N., & Zettl, A. 2001, ACM Trans. Math.
Software, 21, 143 (In the text)
- Basu, S.,
& Antia, H. M. 2001, ApJ, 559, L67 [NASA ADS] [CrossRef]
- Basu, S.,
& Antia, H. M. 2003, ApJ, 585, 553 [NASA ADS] [CrossRef] (In the text)
-
Brandenburg, A. 2005, ApJ, 625, 539 [NASA ADS] [CrossRef] (In the text)
-
Christensen-Dalsgaard, J., Däppen, W., Ajukov, S. V.,
et al. 1996, Science, 272, 1286 [NASA ADS] [CrossRef] (In the text)
-
Corbard, T., & Thompson, M. J. 2005, Sol. Phys., 205, 211 [NASA ADS] [CrossRef] (In the text)
- Covas, E.,
Moss, D., & Tavakol, R. 2004, A&A, 416, 775 [NASA ADS] [CrossRef] [EDP Sciences]
- Covas, E.,
Moss, D., & Tavakol, R. 2005, A&A, 429, 657 [NASA ADS] [CrossRef] [EDP Sciences]
- Donati,
J.-F., Collier Cameron, A., & Petit, P. 2003, MNRAS, 345,
1187 [NASA ADS]
-
Gradshteyn, I. S., & Ryzhik, I. M. 1994, Table of
Integrals, Series, Products, 5th edn., ed. A. Jeffrey
(San Diego: Academic Press)
(In the text)
-
Howard, R., & LaBonte, B. 1980, ApJ, 239, L33 [NASA ADS] [CrossRef] (In the text)
- Howe, R.,
Christensen-Dalsgaard, J., Hill, F., et al. 2000, Science,
287, 2456 [NASA ADS] [CrossRef] (In the text)
- Howe, R.,
Christensen-Dalsgaard, J., Hill, F., et al. 2005, ApJ, 634,
1405 [NASA ADS] [CrossRef]
- Howe, R.,
Rempel, M., Christensen-Dalsgaard, J., et al. 2006, ApJ, 649,
1155 [NASA ADS] [CrossRef]
- Jeffers,
S. V., Donati, J.-F., & Collier Cameron, A. 2007, MNRAS, 375,
567 [NASA ADS]
-
Kitchatinov, L. L., Pipin, V. V., Makarov, V. I., & Tlatov,
A. G. 1999, Sol. Phys., 189, 227 [NASA ADS] [CrossRef] (In the text)
-
Kichatinov, L. L., Pipin, V. V., & Rüdiger, G. 1994,
Astron. Nachr., 315, 157 [NASA ADS] (In the text)
- Komm, R., Howe,
R. Durney, B. R., & Hill, F. 2003, ApJ, 586, 650 [NASA ADS] [CrossRef] (In the text)
- Küker,
M., Rüdiger, G., & Pipin, V. V. 1996, A&A, 312,
615 [NASA ADS] (In the text)
- Lanza, A. F. 2006a,
MNRAS, 373, 819 [NASA ADS] (In the text)
- Lanza, A. F. 2006b,
MNRAS, 369, 1773 [NASA ADS] (In the text)
- Lochard,
J., Samadi, R., & Goupil, M. J. 2005, A&A, 438,
939 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Morse, P. M., & Feshbach, H. 1953, Methods of Theoretical
Physics (New York: McGraw-Hill)
(In the text)
- Parker, E. N. 1993,
ApJ, 408, 707 [NASA ADS] [CrossRef] (In the text)
- Rempel, M. 2006,
ApJ, 647, 662 [NASA ADS] [CrossRef]
- Rempel, M. 2007,
ApJ, 655, 651 [NASA ADS] [CrossRef]
- Rüdiger, G.
1989, Differential rotation and stellar convection: Sun and
solar-type stars (Gordon & Breach Sci. Publ.)
- Rüdiger, G., &
Hollerbach, R. 2004, The magnetic Universe (Weinheim:
Wiley-VCH)
- Rüdiger, G., &
Kichatinov, L. L. 1990, A&A, 236, 503 [NASA ADS] (In the text)
-
Rüdiger, G., Tuominen, I., Krause, F., & Virtanen, H.
1986, A&A, 166, 306 [NASA ADS]
-
Schlichenmaier, R., & Stix, M. 1995, A&A, 302, 264 [NASA ADS] (In the text)
- Schou, J.,
Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef]
-
Schüssler, M. 1981, A&A, 94, L17 [NASA ADS] (In the text)
- Smirnov, V. I.
1964a, A Course of Higher Mathematics, Vol. III, Part II
(Oxford: Pergamon Press)
(In the text)
- Smirnov V. I.,
1964b, A Course of Higher Mathematics, Vol. IV (Oxford:
Pergamon Press)
(In the text)
- Spruit, H. C. 2003,
Sol. Phys., 213, 1 [NASA ADS] [CrossRef] (In the text)
- Toomre, J.,
Christensen-Dalsgaard, J., Howe, R., et al. 2000, Sol. Phys.,
192, 437 [NASA ADS] [CrossRef]
-
Vorontsov, S. V., Christensen-Dalsgaard, J., Schou, J., Strakhov,
V. N., & Thompson, M. J. 2002, Science, 296, 101 [NASA ADS] [CrossRef] (In the text)
- Yoshimura, H.
1981, ApJ, 247, 1102 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
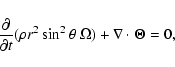
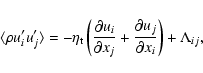
![$\displaystyle %
\frac{\partial \Omega}{\partial t}\! -\! \frac{1}{\rho r^{4}} \...
...} \left[ (1 - \mu^{2})^{2} \frac{\partial \Omega}{\partial \mu}\right] \!=\! S,$](/articles/aa/full/2007/33/aa7418-07/img60.gif)
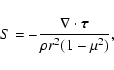
![\begin{displaymath}%
\tau_{i} = r \sin \theta \left[ \Lambda_{i \varphi} - \frac...
...ht) \right] + \rho r^{2} \sin^{2} \theta \Omega u_{\rm (m) i}.
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img64.gif)
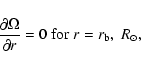
![$\displaystyle %
\frac{\partial \omega}{\partial t} \!-\! \frac{1}{\rho r^{4}} \...
... (1 \!-\! \mu^{2})^{2} \frac{\partial \omega}{\partial \mu}\right] \!=\! S_{1},$](/articles/aa/full/2007/33/aa7418-07/img71.gif)
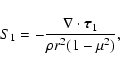
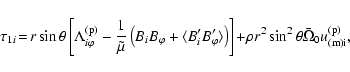
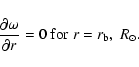
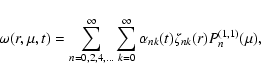
![\begin{displaymath}%
\frac{{\rm d}}{{\rm d} \mu} \left[ (1- \mu^{2})^{2} \frac{{...
...\rm d} \mu }\right] + n(n+3) (1 - \mu^{2}) P_{n}^{(1, 1)} = 0,
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img83.gif)
![\begin{displaymath}%
P_{n}^{(1,1)} (\cos \theta) =
\frac{\cos \left[ (n + \frac...
...\frac{\theta}{2}\right)\right]^{3/2}}
+ O( n^{-\frac{3}{2}}).
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img87.gif)
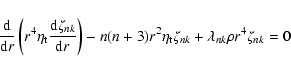
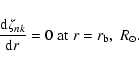
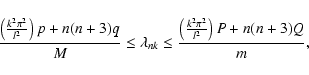
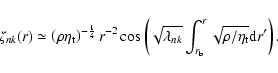
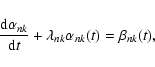
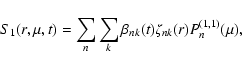
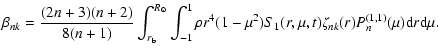
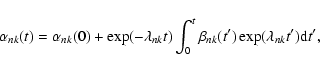
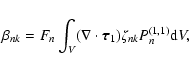
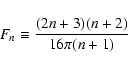
![\begin{displaymath}%
\nabla \cdot [\zeta_{nk} P_{n}^{(1,1)} {\vec \tau}_{1}] = \...
...{1}) + {\vec \tau}_{1} \cdot \nabla[\zeta_{nk} P_{n}^{(1,1)}].
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img119.gif)
![\begin{displaymath}%
\beta_{nk} = - F_{n} \int_{V} {\vec \tau}_{1} \cdot \nabla[\zeta_{nk} P_{n}^{(1,1)}] {\rm d}V.
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img121.gif)
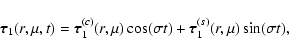
![$\displaystyle \times \left\{ \left[ \int_{V} \zeta_{nk} P_{n}^{(1,1)}
\left( \l...
...la \cdot {\vec \tau}_{1}^{(s)} \right) {\rm d}V \right] \cos (\sigma t) \right.$](/articles/aa/full/2007/33/aa7418-07/img125.gif)
![$\displaystyle \left. +\! \left[ \int_{V} \zeta_{nk} P_{n}^{(1,1)}
\left( \lambd...
...cdot\! {\vec \tau}_{1}^{(c)} \right) {\rm d}V \right] \sin (\sigma t) \right\}.$](/articles/aa/full/2007/33/aa7418-07/img126.gif)
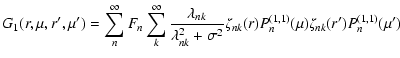
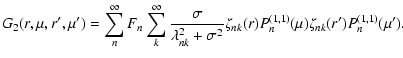
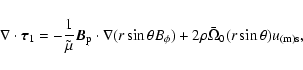
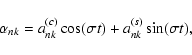
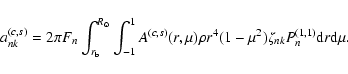
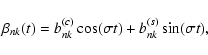
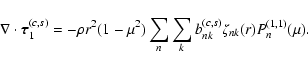
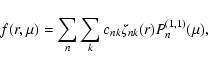
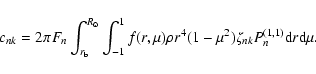
![$\displaystyle \int_{V_{\rm f}} \left( {\vec \tau}_{1}^{(c,s)} \cdot \nabla f \r...
...}
\sum_{k} \nabla [c_{nk} \zeta_{nk} (r) P_{n}^{(1,1)} (\mu)] \right) {\rm d}V,$](/articles/aa/full/2007/33/aa7418-07/img152.gif)
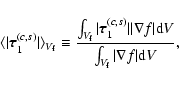
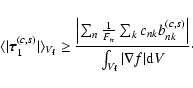
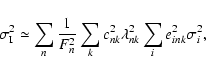
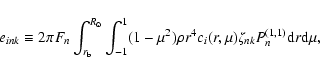
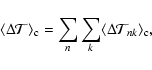
![\begin{displaymath}%
\langle \Delta {\cal T}_{nk} \rangle_{\rm c} = \frac{1}{4F_{n}} \left\{ [a_{nk}^{(c)}]^{2} + [a_{nk}^{(s)}]^{2} \right\}.
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img175.gif)
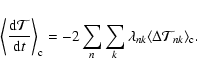
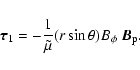
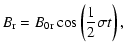
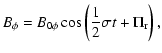
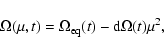
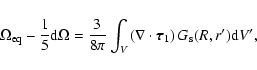
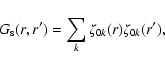
![\begin{displaymath}%
\langle \Delta (\nabla \cdot {\vec \tau}_{1}) \rangle_{V_{\...
...} - \frac{1}{5} \Delta ({\rm d}\Omega) }{V_{\rm o} M} \right],
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img201.gif)
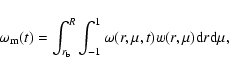
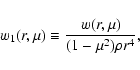
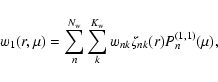
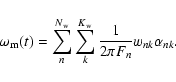
![\begin{displaymath}%
\omega_{\rm m}(t) = - \int_{V} {\vec \tau}_{1} \cdot \left\...
..._{nk}} \nabla \left[ \zeta_{nk} P_{n}^{(1,1)} \right]\right\}.
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img216.gif)
![\begin{displaymath}%
\left\vert \sum_{n}^{N_{\rm w}} \sum_{k}^{K_{\rm w}} \frac{...
...k}} \nabla \left[ \zeta_{nk} P_{n}^{(1,1)} \right] \right\vert
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img218.gif)
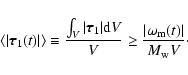
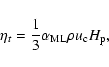
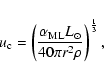
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7418f1.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg230.gif)
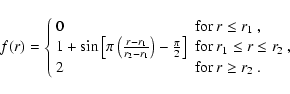
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f2.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg249.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{7418f3.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg253.gif)
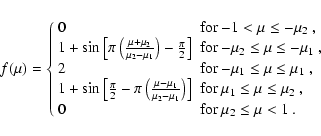
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{7418f4.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg262.gif)
![\begin{displaymath}%
A_{\tau} \equiv \sqrt{[\nabla \cdot {\vec \tau}_{1}^{(c)}]^{2} + [\nabla \cdot {\vec \tau}_{1}^{(s)}]^{2}},
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img263.gif)
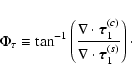
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f5.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg270.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f6.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg273.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f7.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg274.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f8.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg275.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f9.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg287.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{7418f10.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg289.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7418f11.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg294.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{7418f12.ps}\end{figure}](/articles/aa/full/2007/33/aa7418-07/Timg295.gif)
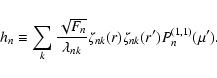
![\begin{displaymath}%
\sum_{k=1}^{\infty} \frac{z}{a k^{2} + y} = \frac{1}{2} \le...
...ft[ g\left( \frac{y}{a}\right) \sqrt{\frac{y}{a}} - 1 \right],
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img311.gif)
![\begin{displaymath}%
g(x) \equiv \pi \left[ \frac{\exp(\pi x) + \exp(-\pi x)}{\exp(\pi x) - \exp(-\pi x)} \right]\cdot
\end{displaymath}](/articles/aa/full/2007/33/aa7418-07/img313.gif)
![$\displaystyle \frac{m}{2n(n+3)Q}\left\{ g\left[ \frac{n(n+3) Q l^{2}}{\pi^{2} P...
... q l^{2}}{\pi^{2} p}\right]
\sqrt{\frac{n(n+3) q l^{2}}{\pi^{2}p}} -1 \right\}.$](/articles/aa/full/2007/33/aa7418-07/img314.gif)