A&A 471, 1043-1055 (2007)
DOI: 10.1051/0004-6361:20077169
Vortex generation in protoplanetary disks with an embedded giant planet
M. de Val-Borro1,2 -
P. Artymowicz3,2 -
G. D'Angelo4 -
A. Peplinski2
1 - Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA 02138, USA
2 -
Stockholm University, AlbaNova University Center, 106 91 Stockholm, Sweden
3 -
University of Toronto at Scarborough, 1265 Military Trail, Toronto, Ontario M1C 1A4, Canada
4 -
NASA-ARC, Space Science and Astrobiology Division, MS 245-3, Moffett Field, CA 94035, USA
Received 25 January 2007 / Accepted 18 June 2007
Abstract
Context. Vortices in protoplanetary disks can capture solid particles and form planetary cores within shorter timescales than those involved in the standard core-accretion model.
Aims. We investigate vortex generation in thin unmagnetized protoplanetary disks with an embedded giant planet with planet to star mass ratio 10-4 and 10-3.
Methods. Two-dimensional hydrodynamical simulations of a protoplanetary disk with a planet are performed using two different numerical methods. The results of the non-linear simulations are compared with a time-resolved modal analysis of the azimuthally averaged surface density profiles using linear perturbation theory.
Results. Finite-difference methods implemented in polar coordinates generate vortices moving along the gap created by Neptune-mass to Jupiter-mass planets. The modal analysis shows that unstable modes are generated with growth rate of order
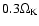 for azimuthal numbers m=4,5,6, where
for azimuthal numbers m=4,5,6, where
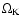 is the local Keplerian frequency. Shock-capturing Cartesian-grid codes do not generate very much vorticity around a giant planet in a standard protoplanetary disk. Modal calculations confirm that the obtained radial profiles of density are less susceptible to the growth of linear modes on timescales of several hundreds of orbital periods. Navier-Stokes viscosity of the order
is the local Keplerian frequency. Shock-capturing Cartesian-grid codes do not generate very much vorticity around a giant planet in a standard protoplanetary disk. Modal calculations confirm that the obtained radial profiles of density are less susceptible to the growth of linear modes on timescales of several hundreds of orbital periods. Navier-Stokes viscosity of the order
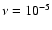 (in units of
(in units of
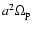 )
is found to have a stabilizing effect and prevents the formation of vortices. This result holds at high resolution runs and using different types of boundary conditions.
)
is found to have a stabilizing effect and prevents the formation of vortices. This result holds at high resolution runs and using different types of boundary conditions.
Conclusions. Giant protoplanets of Neptune-mass to Jupiter-mass can excite the Rossby wave instability and generate vortices in thin disks. The presence of vortices in protoplanetary disks has implications for planet formation, orbital migration, and angular momentum transport in disks.
Key words: planet and satellites: general -
accretion, accretion disks -
hydrodynamics -
instabilities -
methods: numerical
Stability of rotationally supported gas disks is an area of active research,
motivated among other reasons, by a need to understand the origin and stability
of hydrodynamics turbulence underlying the so-called anomalous viscosity in
accretion disks.
The concept of 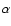 -turbulence in accretion disks was introduced
more than three decades ago by Shakura & Sunyaev (1973) to
account for the angular momentum transfer and explain accretion
onto the central object. The magnetorotational instability (MRI)
has been proposed to explain
the enhanced viscosity in hot and sufficiently ionized accretion disks
with a Keplerian angular velocity profile
threaded by a weak magnetic field
(Balbus & Hawley 1998,1991; Balbus et al. 1996).
However, in the context of cold protoplanetary disks, the ionization
by cosmic rays and stellar radiation is limited to the surface layers
of the disk while the so called "dead zone'' in the vicinity of the
central plane is expected to have low ionization
(Gammie 1996). In some astrophysical systems such as
cataclysmic variables and outer regions of active
galactic nuclei the coupling between the magnetic field and
the gas is also weak and MHD effects may be negligible.
-turbulence in accretion disks was introduced
more than three decades ago by Shakura & Sunyaev (1973) to
account for the angular momentum transfer and explain accretion
onto the central object. The magnetorotational instability (MRI)
has been proposed to explain
the enhanced viscosity in hot and sufficiently ionized accretion disks
with a Keplerian angular velocity profile
threaded by a weak magnetic field
(Balbus & Hawley 1998,1991; Balbus et al. 1996).
However, in the context of cold protoplanetary disks, the ionization
by cosmic rays and stellar radiation is limited to the surface layers
of the disk while the so called "dead zone'' in the vicinity of the
central plane is expected to have low ionization
(Gammie 1996). In some astrophysical systems such as
cataclysmic variables and outer regions of active
galactic nuclei the coupling between the magnetic field and
the gas is also weak and MHD effects may be negligible.
The stability of differentially rotating disks has been considered analytically
and numerically in the purely hydrodynamical case
(Papaloizou & Pringle 1985,1987,1984; Goldreich et al. 1986)
with applications to circumstellar disks and
galactic disks. A rotating isentropic torus with a gradient of
specific angular momentum is found
to be unstable to low-order non-axisymmetric perturbations
due to the Papaloizou-Pringle instability.
Several mechanisms have been proposed that are able to sustain
purely hydrodynamical turbulence and generate an anomalous 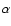 -viscosity
in accretion disks (Mukhopadhyay et al. 2005; Klahr & Bodenheimer 2003; Li et al. 2000).
Dubrulle et al. (2005) studied non-axisymmetric instabilities in stratified Keplerian disks using numerical and analytical methods. A linear instability
appears for Reynolds numbers of order 103 and perturbations with characteristic
scales smaller than the vertical scale of the disk,
assuming the angular velocity decreases with radius.
These results suggest that despite the stabilizing
effect of the Coriolis force, a Keplerian flow
may undergo a transition to turbulence.
Nevertheless, some of those mechanisms may depend on boundary
or edge effects.
-viscosity
in accretion disks (Mukhopadhyay et al. 2005; Klahr & Bodenheimer 2003; Li et al. 2000).
Dubrulle et al. (2005) studied non-axisymmetric instabilities in stratified Keplerian disks using numerical and analytical methods. A linear instability
appears for Reynolds numbers of order 103 and perturbations with characteristic
scales smaller than the vertical scale of the disk,
assuming the angular velocity decreases with radius.
These results suggest that despite the stabilizing
effect of the Coriolis force, a Keplerian flow
may undergo a transition to turbulence.
Nevertheless, some of those mechanisms may depend on boundary
or edge effects.
Rossby waves in thin Keplerian disks have been studied in the linear approximation
(Lovelace et al. 1999; Li et al. 2000) and with fully non-linear numerical simulations
(Tagger 2001). The existence of unstable modes has been found to be associated
with radial gradients of an entropy-modified version of vortensity. Rossby waves in disks
break up forming vortices in the nonlinear limit (Li et al. 2001) in agreement
with the predictions from linear theory. The dispersion relation of this
Rossby Wave Instability (RWI) is analogous to the one for Rossby waves in planetary atmospheres.
Reynolds stresses produced by the RWI can yield outward transport of angular momentum
and accretion onto the central star. Varnière & Tagger (2006) have discussed the generation of Rossby waves in the "dead zones'' of protoplanetary disks where they may
enhance the accretion rate of solids and favor planet formation.
The angular momentum transport in disks around supermassive black holes at the center of galaxies can also be explained by the formation of Rossby vortices when there is
a steep enough density gradient (Colgate et al. 2003). The angular momentum transfer
due to vortices in galactic disks is found to be greater than in an 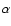 -viscosity disk.
Recently, Tagger & Melia (2006) have described a magnetohydrodynamics version of the RWI
and applied it to the study of the quasiperiodic oscillations in Sgr A*.
Rossby waves can also appear in thin planetary atmospheres with solid rotation
leading to the formation of vortices like
Jupiter's "Great red spot'' (Marcus 1988).
-viscosity disk.
Recently, Tagger & Melia (2006) have described a magnetohydrodynamics version of the RWI
and applied it to the study of the quasiperiodic oscillations in Sgr A*.
Rossby waves can also appear in thin planetary atmospheres with solid rotation
leading to the formation of vortices like
Jupiter's "Great red spot'' (Marcus 1988).
Long-lived vortices are able to capture solid materials
to form massive bodies and speed up the formation of planetary cores
(Bracco et al. 1999; Klahr & Bodenheimer 2006; Barge & Sommeria 1995).
The stability of three-dimensional vortices in a three dimensional stratified disk has been studied by Barranco & Marcus (2005,2006) using spectral anelastic hydrodynamics
simulations. They find that vortices are hydrodynamically stable
for several orbits away from the mid-plane of the disk. The formation of vortices
in the corotation region excited by a protoplanet has been studied
numerically by Balmforth & Korycansky (2001) including the saturation of the corotation torque
and the effects of dissipation in the non-linear dynamics of the flow.
Several numerical schemes studied by de Val-Borro et al. (2006)
show vortex formation but the aim of the study did not include
a detailed investigation of vortex generation.
In this paper, we intend to look at this formation process in more
detail. We also wish to check that codes that do not predict vortex
generation do not artificially damp unstable modes due to the numerical viscosity.
Some simulations produce waves and vortices at the edge of the gap, which could in principle
interact with the wake to cause semi-periodic disturbances
propagating away along the shock. In simulations using the Piecewise Parabolic Method (hereafter PPM), low-m perturbations are observed at the edges of the gap
(Ciecielag et al. 2000). Wave-like disturbances with mode number 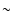 5are observed at the edge of the gap created by a Jupiter-size planet
in the numerical results presented by Nelson & Benz (2003).
Instabilities close to the planet or along the edges of the gap created
by a giant planet, as well as the time variability of the flow near the Roche lobe
may affect the speed and direction of planetary migration.
5are observed at the edge of the gap created by a Jupiter-size planet
in the numerical results presented by Nelson & Benz (2003).
Instabilities close to the planet or along the edges of the gap created
by a giant planet, as well as the time variability of the flow near the Roche lobe
may affect the speed and direction of planetary migration.
In this paper, we study the effect of an annular gap cleared by a
planet on the stability of a protoplanetary disk.
We consider non-axisymmetric linear perturbations to the
inviscid and compressible Euler equations.
In Sect. 2, we present the semi-analytical methods used to
study the stability of disks. We describe the numerical codes in Sect. 3.
In Sect. 4 we present the results of the numerical simulations and the
perturbative linear analysis. We discuss the results in the context
of protoplanetary disks in Sect. 5. Finally, the numerical diffusivity in our
numerical codes is calibrated in Appendix A.
We perform a modal analysis of analytical and numerically obtained density profiles,
in order to see if there is agreement between the vortex generation in the simulations
and growing unstable modes in the linear stability analysis.
Linear perturbative analysis provides a valuable
tool to study the stability of disks. The solution of the linearized Euler equations is
treated along the lines of the work of Lovelace et al. (1999) and Li et al. (2000),
where the stability can be evaluated solving a numerical
eigenvalue problem for a given profile.
Alternatively, the growth of the initial perturbations
can be determined by solving the equations
as an initial value problem.
We consider non-axisymmetric small perturbations
sinusoidally varying in azimuth to the inviscid Euler equations
| |
|
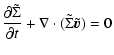 |
(1) |
| |
|
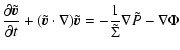 |
(2) |
where
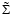 is the surface mass density,
is the surface mass density, 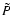 the vertically integrated pressure,
the vertically integrated pressure,
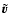 the velocity of the flow and
the velocity of the flow and 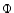 is the gravitational potential.
The perturbed quantities have the form
is the gravitational potential.
The perturbed quantities have the form
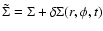 ,
,
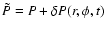 and
and
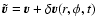 with perturbations in the disk plane depending on the azimuthal angle as
with perturbations in the disk plane depending on the azimuthal angle as
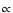
![$\exp \left[{\rm i}(m\phi - \omega t)\right]$](/articles/aa/full/2007/33/aa7169-07/img28.gif) ,
where m is the azimuthal mode number
and
,
where m is the azimuthal mode number
and
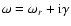 is the complex mode frequency.
The initial velocity component in the radial direction
is neglected and the angular velocity
is the complex mode frequency.
The initial velocity component in the radial direction
is neglected and the angular velocity 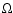 is obtained from the force balance between gravity,
pressure gradients and centrifugal force
is obtained from the force balance between gravity,
pressure gradients and centrifugal force
![\begin{displaymath}%
\Omega^2 = \frac{1}{r} \left[
\frac{1}{\Sigma} \frac{{{\rm d}}P}{{{\rm d}}r} +
\frac{{{\rm d}}\Phi}{{{\rm d}}r} \right]
\end{displaymath}](/articles/aa/full/2007/33/aa7169-07/img31.gif) |
(3) |
we use a barotropic equation of state,
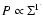 with adiabatic index
with adiabatic index
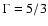 ,
to perform the modal analysis on the analytical disk profiles studied by
Lovelace et al. (1999).
,
to perform the modal analysis on the analytical disk profiles studied by
Lovelace et al. (1999).
A locally isothermal equations of state is used to calculate unstable modes from
the numerical simulations described in Sect. 3. The vertically integrated pressure is given by
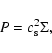 |
(4) |
where
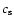 is the sound speed. The temperature can be calculated from
the ideal gas equation of state
is the sound speed. The temperature can be calculated from
the ideal gas equation of state
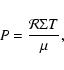 |
(5) |
where
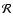 is the gas constant and
is the gas constant and 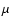 is the mean atomic weight.
The initial unperturbed density is uniform in our simulations
and the temperature has a fixed profile
is the mean atomic weight.
The initial unperturbed density is uniform in our simulations
and the temperature has a fixed profile 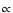 r-1 for the isothermal
calculations, where r is the distance from the rotation axis.
The sound speed profile of the disk is that of a standard
slightly flaring solar nebula with constant aspect ratio
r-1 for the isothermal
calculations, where r is the distance from the rotation axis.
The sound speed profile of the disk is that of a standard
slightly flaring solar nebula with constant aspect ratio
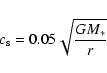 |
(6) |
where G is the gravitational constant and M* the mass of the central star.
The linearized equations can be reduced to a second order differential equation
for the enthalpy of the fluid,
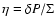 ,
in the general case when the pressure is a function
of both density and temperature (Lovelace et al. 1999; de Val Borro & Artymowicz 2004; Li et al. 2000).
,
in the general case when the pressure is a function
of both density and temperature (Lovelace et al. 1999; de Val Borro & Artymowicz 2004; Li et al. 2000).
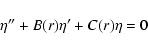 |
(7) |
where the coefficients B(r) and C(r) depend on the radial distance,
and
where 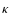 is the epicyclic frequency,
is the epicyclic frequency,
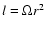 is the
angular momentum per unit mass,
is the
angular momentum per unit mass,
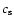 the adiabatic sound speed
and
the adiabatic sound speed
and 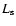 ,
,
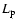 are the equilibrium length scales of variation of entropy
and pressure changes, given by:
are the equilibrium length scales of variation of entropy
and pressure changes, given by:
| |
|
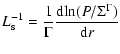 |
(15) |
| |
|
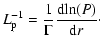 |
(16) |
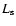 and
and 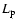 are calculated numerically from the averaged profiles obtained in
the simulations using Eq. (4).
are calculated numerically from the averaged profiles obtained in
the simulations using Eq. (4).
The growth of the unstable modes can form vortices or Rossby waves
in the nonlinear regime (Li et al. 2001).
The Rayleigh criterion states that the disk will be
stable to axisymmetric perturbations when the specific angular
momentum increases with radial distance.
For a Keplerian disk the epicyclic frequency is
always positive,
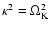 ,
where the Keplerian angular frequency is given by
,
where the Keplerian angular frequency is given by
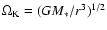 ,
and therefore axisymmetric waves will be stable.
However, when the pressure effects are taken into account it
is possible to have axisymmetric instabilities for a sufficiently
large pressure gradient according to the Solberg-Høiland criterion,
,
and therefore axisymmetric waves will be stable.
However, when the pressure effects are taken into account it
is possible to have axisymmetric instabilities for a sufficiently
large pressure gradient according to the Solberg-Høiland criterion,
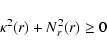 |
(17) |
where
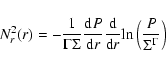 |
(18) |
is the square of the Brunt-Väisälä frequency in the radial direction.
The eigenproblem for the perturbed enthalpy is solved using two semi-analytical methods. One
way of finding the complex eigenfrequency
is the shooting method, where the integration
proceeds from the disk boundaries to an intermediate fitting point, where
continuity of the eigenfunction and its first derivative
is required.
Our implementation uses a leapfrog method to integrate the equation from the
boundaries to the fitting point. The values of the entalphy and its
derivative at the starting points are specified
based on several prescriptions using outgoing spiral waves
(Li et al. 2000)
and vanishing eigenfuntion at the boundaries.
We find that the obtained growth rates do not depend
sensitively on
the choice of boundary conditions.
Several root finding algorithms in the complex plane
can be used to find the unstable modes.
The winding number theorem uses closed-path integrals
(e.g. Kargl & Marston 1989)
to find the number of roots inside a closed contour.
The winding number theorem states that for a complex analytic function 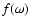 defined inside a contour C
defined inside a contour C
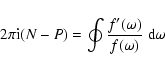 |
(19) |
where N is the number of roots and P is the number of poles inside
the contour C, and the integral is defined in counterclockwise sense.
We look for contours that comprise a single root and are not located
close to solutions or singularities on the real axis.
There are singularities in Eq. (7) at the
corotation resonance
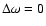 and when a modified
form of the Lindblad resonance for non-barotropic flow is satisfied,
and when a modified
form of the Lindblad resonance for non-barotropic flow is satisfied,
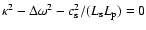 .
It is important to avoid branch points close to the contours
since the winding number method would not give the right
number of roots. In the case of analytical density profiles given by hyperbolic
trigonometric functions the branch points do not affect the contours
used to find solutions with positive growth rate.
.
It is important to avoid branch points close to the contours
since the winding number method would not give the right
number of roots. In the case of analytical density profiles given by hyperbolic
trigonometric functions the branch points do not affect the contours
used to find solutions with positive growth rate.
The solutions are then calculated by
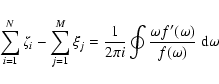 |
(20) |
where 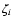 are the zeros and
are the zeros and 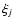 the poles of the complex function
the poles of the complex function 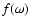 .
The mode frequency can be determined in a contour with a single root.
A multidimensional Newton-Raphson method (Press et al. 1992)
is then employed to locate the roots with arbitrary accuracy.
.
The mode frequency can be determined in a contour with a single root.
A multidimensional Newton-Raphson method (Press et al. 1992)
is then employed to locate the roots with arbitrary accuracy.
Another approach to solve Eq. (7) involves discretizing the equation
on a finite grid and use appropriate boundary conditions to reduce the problem to finding
numerically the roots of the determinant of a complex tridiagonal matrix
(e.g., Laughlin et al. 1998; Li et al. 2000).
We solved the determinant using the previous root finding algorithm
and obtain the radial profile for the eigenfunction 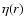 and the perturbed variables.
and the perturbed variables.
We checked these two methods on the
axisymmetric analytical step jump profiles in surface density studied by
Li et al. (2000).
We considered azimuthal mode numbers from m=1 to 10 and calculated the growth
rates of the unstable modes and the corresponding eigenfunctions. For
analytical density profiles with various shapes
both our methods agree with the results of
Li et al. (2000). We tested the dependence of the solution on the shape
of the pressure profile and aspect ratio of the disk.
The eigenfunction for density profiles with a locally isothermal equation of state is
obtained by solving the discretized Eq. (7).
In Fig. 1, we show the real part of the mode frequency
as a function of the azimuthal number for the
averaged density profiles of a NIRVANA simulation (see Sect. 3)
at
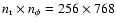 resolution
after 10 orbits. Figure 2 shows the growth rate as a function
of the mode number for the same averaged density profile,
after 10 orbital periods when the threshold for the excitation
of the instability is reached. The density slope in the simulations is described
using two parameters. The depth of the gap is calculated
with respect to the unperturbed density in the inner and
outer disk. The length scale over which the density varies
is estimated to be the difference between the
local maximum and minimum at both inner and
outer disks. An analytical jump function is fitted to the averaged profiles.
resolution
after 10 orbits. Figure 2 shows the growth rate as a function
of the mode number for the same averaged density profile,
after 10 orbital periods when the threshold for the excitation
of the instability is reached. The density slope in the simulations is described
using two parameters. The depth of the gap is calculated
with respect to the unperturbed density in the inner and
outer disk. The length scale over which the density varies
is estimated to be the difference between the
local maximum and minimum at both inner and
outer disks. An analytical jump function is fitted to the averaged profiles.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{7169f1.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg67.gif) |
Figure 1:
Real frequency of the most unstable modes for
a gap opened by a Jupiter-mass planet after 10 periods
as a function of the azimuthal mode number.
The solid line shows the mode frequency at the outer edge of the gap
and the dashed line is the mode frequency at the inner edge
divided by
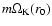 where
where
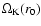 is the
Keplerian angular frequency at the planet position.
is the
Keplerian angular frequency at the planet position. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{7169f2.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg68.gif) |
Figure 2:
Growth rate for a gap opened by a Jupiter-mass planet
after 10 orbits against the azimuthal mode number.
The solid line shows the growth rate at the outer edge of the gap
and the dashed line is the growth rate at the inner edge.
The growth rate of the instability peaks at mode numbers 5-6. |
| Open with DEXTER |
The local maximum at the planet position in the averaged profiles is not expected
to change the growth rates significantly. In addition, most of the gap is clean,
apart from the material close to the planet position and at
Lagrangian points L4, and L5. In the simulations with an initial gap
the averaged profiles do not have local maxima inside
the gap after 100 orbits.
The larger growth rates in Fig. 2 correspond to the more
unstable modes of Eq. (7) that will dominate the solution.
The inner edge of the gap opened by a planet,
shown by the dashed line, has higher growth rate than that of the
outer edge, represented by the solid line, at a given time.
This difference can be due to the fact that the inner
boundary is closer to the location of the instability
in the inner disk than it is the outer boundary to the corresponding
instability outside the planet's radius.
The real frequency of the modes correspond to a radial location
just outside the corotating region where
vortices are formed in the simulations after about 10 orbits.
The number of vortices in the numerical results is consistent
with the growth rates peaking at m = 4-6.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{7169f3.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg69.gif) |
Figure 3:
Radial profile of the eigenfunctions for the outer
edge of the gap at t = 10 periods and mode number m = 5.
From top to bottom the pressure perturbation and radial
and azimuthal perturbed velocity components are shown.
The dotted and dashed lines are the real and imaginary part
of the eigenfunctions. The amplitude is shown by the solid line
which peaks at the position of the edge for the eigenfunction
of the perturbed pressure. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{7169f4.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg70.gif) |
Figure 4:
Radial profile of the eigenfunctions for the inner
edge of the gap at t = 10 periods and mode number m = 5.
From top to bottom the pressure perturbation and radial
and azimuthal perturbed velocity components are shown.
The dotted and dashed lines are the real and imaginary part
of the eigenfunctions. |
| Open with DEXTER |
In Fig. 3 the real and imaginary parts of the radial eigenfunction of the perturbed variables at the outer edge of the gap are plotted for azimuthal mode m=5.
The eigenfunction corresponds to a time when the gap becomes deep enough to generate modes with positive growth rate. The middle and bottom panel show the
eigenfunctions of the perturbations of the velocity components.
The radial eigenfunctions at the inner edge of the gap after 10 orbits
for azimuthal mode m=5 are plotted in Fig. 4.
3 Numerical codes
We performed 2-dimensional hydrodynamical simulations using two independent
grid-based codes, implemented in cylindrical and Cartesian coordinates.
The simulations were run on a uniform grid for 100 orbital periods
Different boundary conditions were tested to avoid reflection of
waves at the boundaries.
3.1 Initial setup
The computations were performed in the radial domain
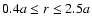 where a is the planet semi-major axis. The disk is assumed to be geometrically thin
and the fluid equations are solved using vertically-integrated variables:
where a is the planet semi-major axis. The disk is assumed to be geometrically thin
and the fluid equations are solved using vertically-integrated variables:
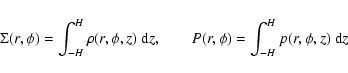 |
(21) |
where H is the vertical scale height.
The planet's gravitational potential was given by the formula
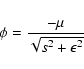 |
(22) |
where 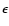 is the gravitational softening and s is the distance from the planet.
The softening is defined as
is the gravitational softening and s is the distance from the planet.
The softening is defined as
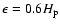 ,
with
,
with 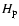 the disc scale height at the planet location. This softening was introduced to reproduce the torque cut-off due to 3-dimensional effects at distance from the planet larger than
the disc scale height at the planet location. This softening was introduced to reproduce the torque cut-off due to 3-dimensional effects at distance from the planet larger than 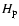 .
The softening length is comparable in size to the characteristic size of the
Roche lobe (along the planet's orbit) and thus it is likely to
affect the flow dynamics in the corotation region but
it is unlikely to strongly affect the dynamics in the regions
where we observe vortex formation. Initially, the gas rotates with Keplerian
angular frequency around the central star.
The mass ratio had the values
.
The softening length is comparable in size to the characteristic size of the
Roche lobe (along the planet's orbit) and thus it is likely to
affect the flow dynamics in the corotation region but
it is unlikely to strongly affect the dynamics in the regions
where we observe vortex formation. Initially, the gas rotates with Keplerian
angular frequency around the central star.
The mass ratio had the values
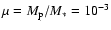 and 10-4,
corresponding to Jupiter and Neptune masses when
the stellar mass is one solar mass. Self-gravity of the
disk was not included in the simulations. The planet was kept in a coplanar, circular orbit
at a=1. We did not consider the accretion
of disk material onto the protoplanet.
and 10-4,
corresponding to Jupiter and Neptune masses when
the stellar mass is one solar mass. Self-gravity of the
disk was not included in the simulations. The planet was kept in a coplanar, circular orbit
at a=1. We did not consider the accretion
of disk material onto the protoplanet.
We assume that the disk radiates efficiently the thermal
energy generated from tidal dissipation and viscous heating.
In the absence of a radiation mechanism the gas would
heat up and the disk could become geometrically thick.
In our models, we use a locally isothermal equations of state,
(Lin & Papaloizou 1985)
with constant aspect ratio
H/r = 0.05.
The vortensity or potential vorticity is calculated in the corotating frame:
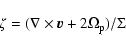 |
(23) |
where
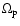 is the orbital frequency of the planet.
is the orbital frequency of the planet.
We perform our simulations in the inviscid limit. In addition, a few cases with
physical viscosity
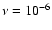 and 10-5
and 10-5
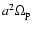 are considered in order to estimate a threshold for the formation of vortices.
Artificial viscosity is not needed to smooth the shocks in our codes, which is
important to study the formation of vortices. The codes are also able to resolve the large density contrast between the corotating region and the rest of the disk.
Diffusion into the gap opened by the planet may result from numerical viscosity or shocks.
The numerical viscosity in our codes is estimated in Appendix A
for inviscid runs without tidal perturbations. These tests confirm that numerical diffusion
is not affecting our results.
are considered in order to estimate a threshold for the formation of vortices.
Artificial viscosity is not needed to smooth the shocks in our codes, which is
important to study the formation of vortices. The codes are also able to resolve the large density contrast between the corotating region and the rest of the disk.
Diffusion into the gap opened by the planet may result from numerical viscosity or shocks.
The numerical viscosity in our codes is estimated in Appendix A
for inviscid runs without tidal perturbations. These tests confirm that numerical diffusion
is not affecting our results.
The initial density was uniform and the gravity of the planet was introduced gradually
with the formula
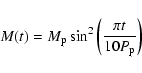 |
(24) |
we have used timescales between 5-10 orbital periods to introduce the gravity from the planet.
Although the time when the instability appears depend on how the gravity is started, there is
agreement between the modal analysis and
numerical simulations for timescales of 5 and 10 orbits.
The results presented in Sect. 4 use a switch-on time of the gravity of 5 orbits.
In some of the calculations we use an initial gap profile
derived under the WKB approximation (e.g., Lubow & D'Angelo 2006)
![\begin{displaymath}%
\Sigma_0(r)= \exp{\left[- \frac{f}{9} \frac{q^2 a^2 \Omega_...
...\nu_{\rm p}}\left(\frac{a}{\Delta_{{\rm p}}}\right)^3\right]},
\end{displaymath}](/articles/aa/full/2007/33/aa7169-07/img81.gif) |
(25) |
where we use
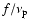 between
between
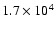 and
and
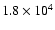 and
and
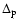 is the maximum of H and |r-a|.
This gap profile allows us to check whether a rapid formation of the gap
is necessary for the presence of instabilities.
is the maximum of H and |r-a|.
This gap profile allows us to check whether a rapid formation of the gap
is necessary for the presence of instabilities.
The Cartesian implementation of FLASH was run on a uniform non-rotating grid at resolution
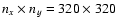 ,
and
,
and
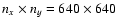 .
The computational domain was
.
The computational domain was
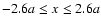 and
and
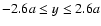 .
.
For computational convenience the unit of time used in the simulations was the orbital period
at the planet location,
![$P_{\rm p} = 2 \pi [a^3/G(M_{\rm *}+M_{\rm p})]^{1/2}=2 \pi$](/articles/aa/full/2007/33/aa7169-07/img90.gif) ,
where
,
where
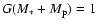 and a=1.
Therefore, the angular frequency of the planet was
and a=1.
Therefore, the angular frequency of the planet was
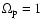 in our units.
in our units.
We used solid boundaries with wave damping zones next to the boundaries to avoid wave reflection
that can create artificial resonances. The damping regions were implemented
in the NIRVANA simulations at
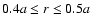 and
and
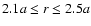 ,
by solving the following equation after each timestep:
,
by solving the following equation after each timestep:
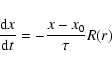 |
(26) |
where x represents the surface density and velocity components,
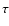 is the orbital period at the corresponding boundary, and
R(r) is a parabolic function which is one at the domain boundary
and zero at the interior boundary of the wave killing regions.
NIRVANA simulations were also run using alternative boundary
conditions to check that the gap profiles and vorticity in the corotating
region do not depend strongly on boundary conditions.
is the orbital period at the corresponding boundary, and
R(r) is a parabolic function which is one at the domain boundary
and zero at the interior boundary of the wave killing regions.
NIRVANA simulations were also run using alternative boundary
conditions to check that the gap profiles and vorticity in the corotating
region do not depend strongly on boundary conditions.
Our NIRVANA implementation is based on the
original version of the code by Ziegler & Yorke (1997).
The Navier-Stokes equations are solved using
a directional operator splitting upwind scheme
which is second-order accurate in space and semi-second-order in
time.
NIRVANA uses a staggered grid where scalar quantities are stored
at the center of grid cells and vectors are stored at the cell boundaries.
The frame is centered on the center of mass of the star-planet system and rotates with the
same angular frequency as the planet orbits the central star.
The code was run with both non-reflective boundary conditions
described above (see also Godon 1996)
and wave-killing zones close to the boundaries (de Val-Borro et al. 2006).
These two types of boundary conditions provide consistent results since in both cases
wave reflection in the boundaries is reduced.
A Courant number of 0.5 was used in the simulations.
Two grid resolutions were considered in which the number of cells
in the radial and azimuthal directions were
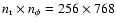 and
and
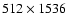 ,
respectively, with uniform spacing
in both dimensions. Therefore, the cells around the planet position
were approximately square.
,
respectively, with uniform spacing
in both dimensions. Therefore, the cells around the planet position
were approximately square.
The FLASH code (Fryxell et al. 2000) is a fully parallel AMR implementation
of the PPM algorithm in its original Eulerian form![[*]](/icons/foot_motif.gif) (Colella & Woodward 1984; Woodward & Colella 1984).
FLASH has been extensively tested in various
compressible flow problems with astrophysical applications
(Calder et al. 2002; Weirs et al. 2005).
(Colella & Woodward 1984; Woodward & Colella 1984).
FLASH has been extensively tested in various
compressible flow problems with astrophysical applications
(Calder et al. 2002; Weirs et al. 2005).
Our implementations of the FLASH code
used both polar coordinates and the original Cartesian formulation of FLASH.
The polar version of FLASH was run in the corotating
coordinate system while the Cartesian implementation
was run in the inertial frame. Our implementations were based on release 2.5 of FLASH
with customized modules for the equation of state and gravity forces,
explicitly ensuring the conservative transport of angular momentum
in the angular sweep. This is particularly important when large density
gradients are present in the disk. The Coriolis forces were treated conservatively as described
by Kley (1998). The isothermal Riemann solver was ported from the AMRA code
(Plewa & Müller 2001).
Courant numbers of 0.7 and 0.8 were used in the simulations.
The Cartesian grid was centered in the center of mass of the system
and the orbits of the planet and the central star were
integrated using a simple Runge-Kutta method.
The grid cells were sized to give the same radial resolution in
both implementations, although since the grid went to r=0in the Cartesian simulations, the grid size had to be larger to achieve the same
resolution. The Cartesian code was run at
resolutions
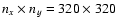 and
and
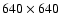 .
To improve the angular resolution close to
the central star, an additional level of refinement was used
in the inner disk in the Cartesian implementation.
Different timesteps were used for each level of refinement
to speed up the simulation.
.
To improve the angular resolution close to
the central star, an additional level of refinement was used
in the inner disk in the Cartesian implementation.
Different timesteps were used for each level of refinement
to speed up the simulation.
The damping condition described in de Val-Borro et al. (2006)
was applied in the ring
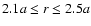 close to the outer boundary but not in the inner disk
for the Cartesian FLASH implementation.
A free outflowing boundary was used at the outer boundaries
close to the outer boundary but not in the inner disk
for the Cartesian FLASH implementation.
A free outflowing boundary was used at the outer boundaries
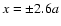 and
and
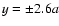 .
and there was free gas flow inside 0.4a.
.
and there was free gas flow inside 0.4a.
The cylindrical implementation used a frame centered on the star with resolutions
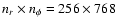 and
and
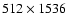 and wave-damping zones close to the inner and outer boundaries.
The Coriolis force, centrifugal force, and indirect terms due to the fact that the center of the frame is displaced from the center of mass
of the system are included in the equation of motion.
and wave-damping zones close to the inner and outer boundaries.
The Coriolis force, centrifugal force, and indirect terms due to the fact that the center of the frame is displaced from the center of mass
of the system are included in the equation of motion.
4 Results
We carried out modal growth analysis on the density profiles of
protoplanetary disks perturbed by an embedded giant planet
ranging from a Neptune to a Jupiter mass.
The time resolved linear analysis was performed on the
azimuthally averaged
density profiles obtained from calculations,
using a locally isothermal equation of state.
In the following description, we will show the results
of inviscid runs at different resolutions with an
embedded Jupiter-mass protoplanet using different
boundary conditions.
Results from runs with physical viscosity will also be presented.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{7169f5a.eps}\vspace*{5mm}
\includegraphics[width=7.5cm,clip]{7169f5b.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg101.gif) |
Figure 5:
Real frequency and growth rates of the unstable modes
with azimuthal number m=5,
as a function of time, for NIRVANA and polar FLASH simulations
with resolution nr 
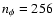  768.
In the top panel, the crosses represent the mode frequencies
at the outer edge of the gap
and the dots are the mode frequencies at the inner edge for NIRVANA.
The circles are the mode frequencies at the outer edge of the gap
and the stars are the mode frequencies at the inner edge for polar FLASH.
The frequencies are
divided by
768.
In the top panel, the crosses represent the mode frequencies
at the outer edge of the gap
and the dots are the mode frequencies at the inner edge for NIRVANA.
The circles are the mode frequencies at the outer edge of the gap
and the stars are the mode frequencies at the inner edge for polar FLASH.
The frequencies are
divided by
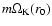 ,
where ,
where
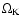 is
the Keplerian angular frequency
and r0 is the radius at the edge of the gap.
The crosses in the bottom panel are the growth rates
at the outer gap edge
and the dots are the growth rates at the inner edge for a NIRVANA calculation.
The circles are the growth rates at the outer edge of the gap
and the stars are the growth rates at the inner edge for a polar FLASH
calculation.
Growth rates are divided by the Keplerian frequency
at the edge of the gap.
is
the Keplerian angular frequency
and r0 is the radius at the edge of the gap.
The crosses in the bottom panel are the growth rates
at the outer gap edge
and the dots are the growth rates at the inner edge for a NIRVANA calculation.
The circles are the growth rates at the outer edge of the gap
and the stars are the growth rates at the inner edge for a polar FLASH
calculation.
Growth rates are divided by the Keplerian frequency
at the edge of the gap. |
| Open with DEXTER |
The real frequency and growth rate of the most unstable modes, as a function of
time, are plotted in Fig. 5 for NIRVANA and FLASH polar simulations
with resolution
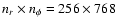 and
wave-damping boundary conditions.
The threshold for the appearance of the instability
occurs after about 5 periods when the gap is sufficiently
deep and the growth rate becomes positive.
The edge of the gap in the simulations
becomes non-axisymmetric at this time and
depressions in vortensity appear along the gap with m=5-6 symmetry
which coincide with the azimuthal number of the
most unstable modes shown in Fig. 2.
Small vortices are observed in the inner and outer disk shortly afterwards
with the same angular distribution.
and
wave-damping boundary conditions.
The threshold for the appearance of the instability
occurs after about 5 periods when the gap is sufficiently
deep and the growth rate becomes positive.
The edge of the gap in the simulations
becomes non-axisymmetric at this time and
depressions in vortensity appear along the gap with m=5-6 symmetry
which coincide with the azimuthal number of the
most unstable modes shown in Fig. 2.
Small vortices are observed in the inner and outer disk shortly afterwards
with the same angular distribution.
In the bottom panel of Fig. 5, the growth rate from the inner disk edge,
represented by crosses and circles for the different models,
is larger than the growth rate at the outer disk, represented by dots and stars.
This difference may be artificial because the inner boundary of the grid is closer to the planet location that the outer boundary is. The mode frequencies and growth rates for NIRVANA
and polar FLASH agree within 10%. This is in agreement with the
vortex sizes obtained from the Fourier analysis of the gravitational torques on
the planet. In the end of the simulation, the growth rate of the instability
is a fraction of the angular velocity at the edge of the gap.
The disk becomes unstable to axisymmetric perturbations at time 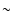 40 orbits
for the Jupiter simulations according to the Rayleigh criterion (Eq. (17)).
The RWI grows exponentially in agreement with the linear analysis
during the first orbits (Li et al. 2001) and produces vortices
that can be sustained by interaction with the spiral arms generated by the planet.
40 orbits
for the Jupiter simulations according to the Rayleigh criterion (Eq. (17)).
The RWI grows exponentially in agreement with the linear analysis
during the first orbits (Li et al. 2001) and produces vortices
that can be sustained by interaction with the spiral arms generated by the planet.
The linear analysis of Cartesian FLASH averaged profiles
shows the presence of unstable modes in the inner and outer disk with growth rates of
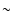
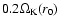 .
In some Cartesian FLASH runs
there are mode solutions with large growth rates that appear at late times,
when the gap is becoming deeper. At the same time there are
indications that some mild instability is happening in the disk. However, these
are not the fast-growing modes found in the polar grid
calculations with azimuthal number m=4-6. We do not find stationary solutions with positive growth rates that remain for a time of order of the growth timescale in the
Cartesian grid models. This is consistent with the fact that no
vortices appear in the edges of the gap in these simulations after tens
of orbital periods, as shown in Fig. 9.
.
In some Cartesian FLASH runs
there are mode solutions with large growth rates that appear at late times,
when the gap is becoming deeper. At the same time there are
indications that some mild instability is happening in the disk. However, these
are not the fast-growing modes found in the polar grid
calculations with azimuthal number m=4-6. We do not find stationary solutions with positive growth rates that remain for a time of order of the growth timescale in the
Cartesian grid models. This is consistent with the fact that no
vortices appear in the edges of the gap in these simulations after tens
of orbital periods, as shown in Fig. 9.
Figure 6 shows the density distribution for Jupiter
inviscid simulations in logarithmic scale using different boundary conditions for
NIRVANA and FLASH models. The left panels show the density contours at t = 50 orbital
periods and the right panels after t = 100 orbits. There are two
vortices moving along the outer edge with different
phase velocities in all the simulations at t = 50 periods.
Those vortices will merge and form a large vortex at
a later time producing strong oscillations on the
torque exerted on the planet.
In Fig. 7 we show the growth rates
with azimuthal number m=5 for the outer edge of the gap
using an initial density with a gap given by Eq. (25).
The gap shape tends to a steady state towards the
end of the simulation. The growth rates agree within
5% (by the end of the simulation) with the results obtained using
an initial uniform density.
Figure 8 shows the profiles averaged over the azimuth
for the NIRVANA simulations using various boundary conditions.
The slope of the gap is steeper at the inner edge
than at the outer edge for the cylindrical schemes.
The density peak in the inner disk is about
50% of the peak at the outer gap edge.
The overall jump in density is larger at the inner edge despite the fact that
the gap is slightly deeper just outside the planet's orbit.
This produces a larger growth rate
inside the corotation region (see Fig. 2).
In the cylindrical FLASH simulation,
the mass loss at the boundaries is greater
but this does not affect the results of the modal calculation.
The Cartesian FLASH results have a deeper gap and smaller
density peaks at the edge of the gap. However, the
growth rate of their most unstable modes is about 50%
compared with that provided by the polar FLASH simulations.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7169f6CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg104.gif) |
Figure 6:
Surface density contours
for cylindrical simulations in logarithmic scale.
From top to bottom, NIRVANA simulation using a damping wave region
as described in Sect. 3 (see also de Val-Borro et al. 2006),
NIRVANA simulation using outgoing-wave boundary conditions
defined by Godon (1996) and polar FLASH.
The left panels show the density after 50 orbital periods
and the right panels show the density after 100 orbits
with the same color scale. The resolution is
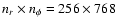 and the planet is located at
and the planet is located at
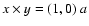 .
There are two elongated vortices forming next to the outer gap edge
at 50 orbits that move with different velocities. The vortices merge
in both simulations and one large vortex is observed in the outer disk
at 100 orbits. .
There are two elongated vortices forming next to the outer gap edge
at 50 orbits that move with different velocities. The vortices merge
in both simulations and one large vortex is observed in the outer disk
at 100 orbits. |
| Open with DEXTER |
The size of the peaks in the power spectrum of the torques on a Jupiter-mass planet,
from different regions in the disks, are shown in Tables 1 and 2. The torques are calculated excluding the material
inside the Roche lobe of the planet, where the resolution may not be good enough to resolve the
circumplanetary disk. NIRVANA calculations have a larger peak, which correspond to
the amplitude of the vortices moving along the edge of the gap.
This is consistent with larger vortices being
observed in the density distributions of NIRVANA calculations
in Fig. 6. FLASH calculations have PDS peaks which
are between one and two orders of magnitude smaller.
The frequencies in the corotating frame are close to the local Keplerian angular frequency
at the edges of the gap. The difference in the peak amplitudes
agrees with the results from the upwind and Godunov schemes studied by de Val-Borro et al. (2006).
This correlation suggests that vortices can be formed by the non-linear evolution of
Rossby waves in protoplanetary disks.
The evolution of the vortensity in the NIRVANA simulation with resolution
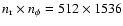 is shown at several times in
Fig. 10. The vortensity and Bernoulli constant are conserved for a barotropic
inviscid fluid in the absence of discontinuities in the flow.
In our case, the vortensity is roughly conserved along the
streamlines in regions outside the Hill radius of the planet.
Shock dissipation close to the protoplanet can lead
to vortensity generation. As the gap is opened and strong trailing shocks are formed,
the vortensity grows at the edge of the gap and along the spiral arms.
The vortensity at 10 orbital periods shows small cavities outside
the peaks at the edge of the gap. These depressions break in 4-5 differentiated vortices
when the growth rate of the RWI becomes positive.
The vortensity peak at the outer gap edge and close to the outer spiral arm
are corrugated while at the inner edge the vortensity
is more stable. As explained before, this is probably an artificial effect
due to the inner edge of the gap being closer to the inner boundary
than the outer gap edge is to the outer boundary.
The minima of vortensity rotating along the edge
correspond to vortices observed in the density maps.
In the bottom right panel of Fig. 10
there is one single vortensity depression which is associated with a
vortex located at azimuth
is shown at several times in
Fig. 10. The vortensity and Bernoulli constant are conserved for a barotropic
inviscid fluid in the absence of discontinuities in the flow.
In our case, the vortensity is roughly conserved along the
streamlines in regions outside the Hill radius of the planet.
Shock dissipation close to the protoplanet can lead
to vortensity generation. As the gap is opened and strong trailing shocks are formed,
the vortensity grows at the edge of the gap and along the spiral arms.
The vortensity at 10 orbital periods shows small cavities outside
the peaks at the edge of the gap. These depressions break in 4-5 differentiated vortices
when the growth rate of the RWI becomes positive.
The vortensity peak at the outer gap edge and close to the outer spiral arm
are corrugated while at the inner edge the vortensity
is more stable. As explained before, this is probably an artificial effect
due to the inner edge of the gap being closer to the inner boundary
than the outer gap edge is to the outer boundary.
The minima of vortensity rotating along the edge
correspond to vortices observed in the density maps.
In the bottom right panel of Fig. 10
there is one single vortensity depression which is associated with a
vortex located at azimuth 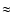
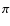 after 100 orbits.
The vortensity inside the corotating region is considerably perturbed
as the vortex moves along the gap.
after 100 orbits.
The vortensity inside the corotating region is considerably perturbed
as the vortex moves along the gap.
In Figs. 11 and 12
the azimuthally averaged vortensity in the inertial frame is shown.
The initial vortensity profile for a disk with uniform density,
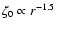 ,
has been subtracted.
The Cartesian FLASH code has a large vortensity excess
in the corotating region where the gap is more depleted
than in the cylindrical codes.
The averaged vortensity in the outer disk is also greater
in our Cartesian FLASH model.
NIRVANA calculation shows vortensity peaks at the gap borders with
a larger spike in the inner disk.
,
has been subtracted.
The Cartesian FLASH code has a large vortensity excess
in the corotating region where the gap is more depleted
than in the cylindrical codes.
The averaged vortensity in the outer disk is also greater
in our Cartesian FLASH model.
NIRVANA calculation shows vortensity peaks at the gap borders with
a larger spike in the inner disk.
The velocity fields plotted over
the density contours in logarithmic scale at t = 100 orbits
is shown in Fig. 13. The velocity vectors are calculated in the corotating
frame of the local maximum of pressure that coincides
with the center of the vortex. The rotation in baroclinic sense is very clearly
visible in the vortex close to the inner edge of the gap.
The vortex in the outer disk interacts with the
spiral wake created by the planet and is perturbed at this particular time.
In Fig. 14, the streamlines are shown in the
frame corotating with the vortex core. They show baroclinic rotation that is perturbed
by interaction with the spiral wakes created by the planet.
In this section we compare the unstable modes
obtained from simulations including Navier-Stokes viscosity
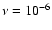 and 10-5 (in code units, see Sect. 3).
and 10-5 (in code units, see Sect. 3).
In Fig. 15 we show the growth rates in the outer disk of the
unstable modes with m=5 as a function of time for
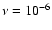 .
The frequencies of unstable modes are
calculated using perturbations on the inviscid
Euler equations for simplicity.
The growth rates at the outer edge of the gap agree within 20% with those obtained from inviscid
simulations (see Fig. 5).
However, notice that the linear analysis gives only an estimate
of the growth rates in the viscous case.
.
The frequencies of unstable modes are
calculated using perturbations on the inviscid
Euler equations for simplicity.
The growth rates at the outer edge of the gap agree within 20% with those obtained from inviscid
simulations (see Fig. 5).
However, notice that the linear analysis gives only an estimate
of the growth rates in the viscous case.
We have studied vortex formation in
protoplanetary disks with an embedded giant planet,
with mass ratios 10-4 and 10-3, using
numerical simulations and linear perturbation analysis.
The modal calculation is done following the
strategy of Lovelace et al. (1999)
for a locally isothermal equation of state
in a vertically-averaged disk.
Vortices are formed in the cylindrical NIRVANA and FLASH
2-dimensional simulations
in agreement with the linear analysis of non-axisymmetric perturbations.
The growth rates calculated for NIRVANA and polar FLASH as a function
of time agree within about 10%.
The results of the linear analysis are consistent with the absence of rapidly
growing vortices near the edge of the gap in our Cartesian-grid PPM
simulations, which is thus not due to artificial numerical damping of
unstable modes. This type of code does not produce the necessary steepness of
the surface density profile and
does not support growing non-axisymmetric
perturbations.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{7169f7.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg108.gif) |
Figure 7:
Growth rates of the unstable modes
with mode number m=5, as a function of time
divided by the local Keplerian frequency.
Dots represent a NIRVANA calculation
with resolution
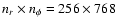 and stars are obtained from a FLASH calculation
with resolution
and stars are obtained from a FLASH calculation
with resolution
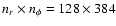 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{7169f8CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg109.gif) |
Figure 8:
Azimuthally averaged surface density profiles for the
Jupiter simulations after 100 orbital periods.
The solid line is the NIRVANA simulation with resolution
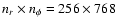 and damping wave boundary conditions
and the short dashed line
is the NIRVANA simulation with resolution
and damping wave boundary conditions
and the short dashed line
is the NIRVANA simulation with resolution
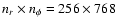 and outgoing-wave boundary conditions.
The profiles are averaged over 5 orbits.
and outgoing-wave boundary conditions.
The profiles are averaged over 5 orbits. |
| Open with DEXTER |
Both our numerical schemes have very low numerical
diffusion, which is estimated in Appendix A.
Runs with an explicit Navier-Stokes viscosity
were also performed.
The unstable modes in the outer disk calculated for
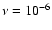 have growth rates
have growth rates 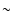
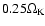 at 100 orbits, which are 20% smaller than in
the inviscid calculations.
at 100 orbits, which are 20% smaller than in
the inviscid calculations.
Table 1:
The frequency in the corotating frame and magnitude of the maxima of the PDS of the
gravitational torques from the inner disk are shown for the Jupiter
simulations. The values are sorted by the magnitude of the PDS at the maximum. The magnitude of the PDS is related with the amplitude of the oscillations at a given frequency. Polar codes
have larger maxima and the frequencies correspond roughly to the Keplerian
frequencies at the gap edges.
Table 2:
The frequency in the corotating frame
and magnitude of the maxima of the PDS of the
gravitational torques from the outer disk are shown for the Jupiter
simulations.
Table 3:
The frequency and magnitude of the maxima of the PDS
of the torques from the inner disk for the Neptune case are
shown sorted by the
magnitude of the PDS at the maximum. NIRVANA calculations have
larger maxima with frequencies close to the Keplerian
frequencies at the outer gap edge.
Table 4:
The frequency and magnitude of the maxima of the PDS
of the torques from the outer disk for the Neptune case are
shown sorted by the magnitude of the PDS at the maximum.
We speculate that the Cartesian-grid implementation may be more diffusive for this problem than
polar geometry (in which the unperturbed Keplerian disk flows along the mesh
structure) hence damping the growth of Rossby waves. The linear theory predicts that unstable modes will be present
in the Cartesian simulations after the gap is sufficiently deep
but these modes have smaller growth rate than those obtained from NIRVANA and FLASH polar
simulations. The growth rate for the inner edge of the gap
is larger than it is at the outer gap edge.
This may be artificial because the inner boundary is closer
to the planet position that the outer boundary is to the outer gap edge.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7169f9CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg123.gif) |
Figure 9:
Surface density distribution after 100 orbital periods for NIRVANA on the left hand side and FLASH on the right hand side
using the same logarithmic color scale.
Both models use the same wave damping condition in the outer disk between 2.1-2.5 a.
while FLASH does not have a damping condition in the inner boundary.
NIRVANA has density enhancements close to the gap opened by the protoplanet.
FLASH has a smooth density distribution and a larger
density peak at the planet position which is saturated in the image. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7169f10CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg124.gif) |
Figure 10:
Vortensity in polar coordinates is shown at times
t = 10, 20, 50 and 100 orbital periods from left to right and top to bottom.
The simulation has resolution
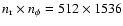 . . |
| Open with DEXTER |
We observe a correlation between the growth rate of the unstable modes in the linear analysis and
the size of the peaks in the power spectrum of the gravitational torque
on the planet exerted by the disk. This correlation suggests that vortices in protoplanetary disks can form
close to the gap, produced by an embedded giant planet,
from the collapse of Rossby waves. Vortices may grow
and be sustained for long timescales by interaction with the planetary wake
(Li et al. 2005; Koller et al. 2003).
The two-dimensional approximation for the disk flow
is anticipated to give qualitatively correct results
although a three-dimensional analysis is needed
to understand heat dissipation in the vertical direction
and refraction effects in radially propagating waves
(Lin et al. 1990). An important restriction of our simulations
is that the planet is kept on a fixed circular
orbit. It would be of interest to study how the vortices
rotating along the edge of the gap
affect the migration rate of a freely
moving protoplanet embedded in a 3-dimensional disk.
In summary, the linear analysis confirms that Rossby waves
are formed in a thin protoplanetary disk with a giant planet with mass ratio
between
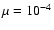 -10-3, within tens of orbital periods.
The unstable modes with larger growth
rates generate a non-axisymmetric perturbation,
with mode number m=4-6, which breaks into
vortices in the nonlinear regime
producing a non-axisymmetric density distribution.
At the time when the growth rate becomes positive, small depressions
in vortensity appear along the gap.
These results do not depend on resolution or
boundary conditions. Simulations with an initial gap also generate vortices
close to the edge of the gap. The growth rates estimated from the linear theory
agree with the growth rates at later times in simulations
with an initially flat density distribution.
A protoplanetary disk with a giant planet becomes
populated with vortices and spiral shocks
that can efficiently transport angular momentum.
This effect can be important in disks that are
not sufficiently ionized to sustain turbulence
via the MRI instability. We conclude that vorticity generation in
protoplanetary disks with an embedded giant planet
is a robust mechanism that
can lead to planet formation and
radial transfer of angular momentum.
-10-3, within tens of orbital periods.
The unstable modes with larger growth
rates generate a non-axisymmetric perturbation,
with mode number m=4-6, which breaks into
vortices in the nonlinear regime
producing a non-axisymmetric density distribution.
At the time when the growth rate becomes positive, small depressions
in vortensity appear along the gap.
These results do not depend on resolution or
boundary conditions. Simulations with an initial gap also generate vortices
close to the edge of the gap. The growth rates estimated from the linear theory
agree with the growth rates at later times in simulations
with an initially flat density distribution.
A protoplanetary disk with a giant planet becomes
populated with vortices and spiral shocks
that can efficiently transport angular momentum.
This effect can be important in disks that are
not sufficiently ionized to sustain turbulence
via the MRI instability. We conclude that vorticity generation in
protoplanetary disks with an embedded giant planet
is a robust mechanism that
can lead to planet formation and
radial transfer of angular momentum.
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{7169f11.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg126.gif) |
Figure 11:
Vortensity profiles averaged over azimuth at different times
t = 10, 20, 50 and 100 orbital periods for the NIRVANA simulation
at resolution
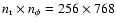 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{7169f12.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg127.gif) |
Figure 12:
Vortensity profiles averaged over azimuth at different times
t = 10, 20, 50 and 100 orbital periods for the FLASH simulation
in Cartesian coordinates. |
| Open with DEXTER |
Acknowledgements
M.d.V.B. was supported by a SAO predoctoral fellowship and a NOT/IAC scholarship.
G.D. acknowledges support from the NASA Postdoctoral Program.
We thank Artur Gawryszczak for providing his numerical code
and enlightening discussions.
The support of the RTN
"Planets'' funded by the European Commission under agreement No. HPRN-CT-2002-0308 is acknowledged during the course of this project.
The FLASH code used in this work is developed in part by the US Department of
Energy under Grant No. B523820 to the Center for Astrophysical Thermonuclear
Flashes at the University of Chicago.
Some of the calculations reported here were performed on Columbia, operated by
NASA Advanced Supercomputing Division, at NASA Ames Research Center.
We thank the anonymous referee for comments that improved the manuscript.
Appendix A: Calibration of numerical viscosity
The calculations presented in this paper are based on inviscid
Euler equations. However, even though neither physical nor
artificial viscosity terms enter these equations, each numerical
scheme has some intrinsic diffusivity that can be interpreted as
a numerical viscosity,
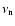 .
.
To calibrate the numerical viscosity in each of the hydrodynamics
codes, we use the numerical setup described in Sect. 3.1
with mass ratio q=0. Tests are performed at two different resolutions
to check for consistency of the results.
Numerical viscosity is bound to depend on the flow properties. The values
reported in this Appendix apply to disks in quiescent conditions
and may therefore represent lower limits for numerical diffusion
in models with uniform initial density and fast gap formation.
In the case of NIRVANA, a time-averaged measure of the numerical
diffusivity is obtained over a 50 orbit period, as a function of the
radial position, by analysing the trajectories of 500 tracer (massless)
particles released in the disk. The equation of motion of each particle
is integrated every hydrodynamics timestep by interpolating the velocity
field at the particle's location and advancing in time its position
by means of a second-order Runge-Kutta method. The spatial interpolation
of the velocity field is also second-order accurate. Hence, trajectories
are formally second-order accurate in both space and time.
We assume that the viscosity is constant in a radial interval
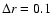 ,
which contains about 25 equally-spaced tracer
particles and is orders of magnitude larger than their diffusion
length scale. We measure the averaged length travelled by the
particles in each radial interval, over about 50 orbits
(at r=1), and estimate the amount of numerical viscosity
under the assumption that the particle drift velocity is
,
which contains about 25 equally-spaced tracer
particles and is orders of magnitude larger than their diffusion
length scale. We measure the averaged length travelled by the
particles in each radial interval, over about 50 orbits
(at r=1), and estimate the amount of numerical viscosity
under the assumption that the particle drift velocity is
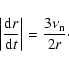 |
(A.1) |
Experiments executed at resolutions
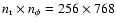 and
and
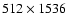 provide very similar results.
provide very similar results.
The largest numerical diffusion is observed close to the inner grid
boundary, where
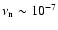 (in code units, see
Sect. 3.1) at
(in code units, see
Sect. 3.1) at
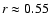 and
and  10-8at
10-8at
 .
In the radial domain between
.
In the radial domain between
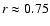 and
and
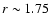 ,
,
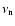 lies between
lies between  10-10 and
10-10 and
 10-9. In the outer part of the simulated disk, the numerical viscosity is
comprised between
10-9. In the outer part of the simulated disk, the numerical viscosity is
comprised between  10-9 and
10-9 and  10-8.
10-8.
The numerical viscosity in FLASH is calibrated using a 2-dimensional
local patch of a Keplerian disk with a massless sink hole
in the center of the domain The sink hole has radius equal to the Roche radius
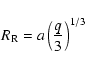 |
(A.2) |
for a protoplanet with mass ratio
q = 10-3.
The dimensions of the
shearing box are
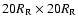 .
We use local Cartesian coordinates in the Hill
approximation corotating with the sink hole. The horizontal axis corresponds to the
radial direction and the vertical axis to the direction
of motion of the flow.
Initially, the unperturbed surface density is uniform
and the velocity of the matter flowing into the
computational domain has only a vertical component given by
the linearized Keplerian velocity
.
We use local Cartesian coordinates in the Hill
approximation corotating with the sink hole. The horizontal axis corresponds to the
radial direction and the vertical axis to the direction
of motion of the flow.
Initially, the unperturbed surface density is uniform
and the velocity of the matter flowing into the
computational domain has only a vertical component given by
the linearized Keplerian velocity
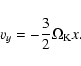 |
(A.3) |
We implement periodic boundaries in the vertical direction.
Our units in the simulation are the Roche radius,
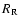 ,
the initial surface density,
,
the initial surface density, 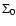 ,
and
the Keplerian angular frequency,
,
and
the Keplerian angular frequency,
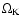 ,
at the center of the shearing box.
A cavity is produced at the orbital radius of the
sink hole while the gas in the vicinity of the hole
is pulled into it on the viscous timescale.
,
at the center of the shearing box.
A cavity is produced at the orbital radius of the
sink hole while the gas in the vicinity of the hole
is pulled into it on the viscous timescale.
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{7169f13CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg141.gif) |
Figure A.1:
Velocity vectors in the corotating frame after 100 periods for the NIRVANA simulation at resolution
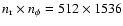 .
The left panel shows the vortex at the inner gap edge
and the right panel shows the vortex at the outer gap edge. .
The left panel shows the vortex at the inner gap edge
and the right panel shows the vortex at the outer gap edge. |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7169f14CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg142.gif) |
Figure A.2:
Streamlines in the corotating frame
of the inner and outer vortices plotted in Fig. 13.
The radial extent of the vortices is about 0.15a.
Spiral arms created by the planet and weaker
shocks associated with the vortices are observed. |
The equation of viscous diffusion for a thin accretion disk can be obtained
in the asymptotic limit assuming constant numerical diffusivity (Bryden et al. 1999; Pringle 1981). Using the boundary conditions 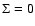 at x=0,
and
at x=0,
and
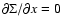 at
at
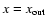 ,
where
,
where
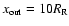 is the distance
from the center of the shearing box to the outer radial boundary, the surface density distribution
for positive x is given by
is the distance
from the center of the shearing box to the outer radial boundary, the surface density distribution
for positive x is given by
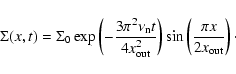 |
(A.4) |
The kinematic viscosity can be evaluated from the ratio of surface densities
at different times
![\begin{displaymath}%
\nu_{{\rm n}} = \frac{4 x_{{\rm out}}^2}{3 \pi^2 (t_2-t_1)} \ln\left[\frac{\Sigma(t_1)}{\Sigma(t_2)}\right]\cdot
\end{displaymath}](/articles/aa/full/2007/33/aa7169-07/img148.gif) |
(A.5) |
We estimate values of
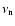 between 10-8 and 10-7using the surface density profiles averaged in the vertical direction
at times close to 50 orbits and grid resolutions of
between 10-8 and 10-7using the surface density profiles averaged in the vertical direction
at times close to 50 orbits and grid resolutions of
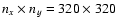 and
and
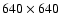 .
.
![\begin{figure}
\par\includegraphics[width=8.65cm,clip]{7169f15.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg149.gif) |
Figure A.3:
Dependence on time of growth rates of modes with m=5 for NIRVANA simulations with resolution
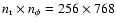 (dots)
and FLASH with resolution
(dots)
and FLASH with resolution
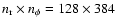 (stars).
The Navier-Stokes viscosity is
(stars).
The Navier-Stokes viscosity is
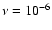 . . |
- Balbus, S. A.
2003, ARA&A, 41, 555 [NASA ADS]
- Balbus, S. A.,
& Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef]
- Balbus, S. A.,
& Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [NASA ADS] [CrossRef]
- Balbus, S. A.,
& Hawley, J. F. 2006, ApJ, 652, 1020 [NASA ADS] [CrossRef]
- Balbus, S. A.,
Hawley, J. F., & Stone, J. M. 1996, ApJ, 467, 76 [NASA ADS] [CrossRef]
- Balmforth, N. J.,
& Korycansky, D. G. 2001, MNRAS, 326, 833 [NASA ADS] (In the text)
- Barge, P., &
Sommeria, J. 1995, A&A, 295, L1 [NASA ADS]
- Barranco, J. A.,
& Marcus, P. S. 2005, ApJ, 623, 1157 [NASA ADS] [CrossRef]
- Barranco, J. A.,
& Marcus, P. S. 2006, J. Comp. Phys., 219, 21 [NASA ADS]
- Bracco, A., Chavanis,
P. H., Provenzale, A., & Spiegel, E. A. 1999, Phys.
Fluids, 11, 2280 [NASA ADS] [CrossRef]
- Bryden, G., Chen, X.,
Lin, D. N. C., Nelson, R. P., & Papaloizou,
J. C. B. 1999, ApJ, 514, 344 [NASA ADS] [CrossRef]
- Calder, A. C.,
Fryxell, B., Plewa, T., et al. 2002, ApJS, 143, 201 [NASA ADS] [CrossRef]
- Ciecielag, P., Plewa,
T., & Rózyczka, M. 2000, Astron. Nachr., 321, 171 [NASA ADS] (In the text)
- Colella, P., &
Woodward, P. 1984, J. Comput. Phys., 54, 174 [NASA ADS] [CrossRef]
- Colgate, S. A.,
Cen, R., Li, H., Currier, N., & Warren, M. S. 2003, ApJ,
598, L7 [NASA ADS] [CrossRef] (In the text)
- de Val Borro, M.,
& Artymowicz, P. 2004, in Extrasolar Planets: Today and
Tomorrow, ed. J. Beaulieu, A. Lecavelier Des Etangs,
& C. Terquem, ASP Conf. Ser., 321, 333
- de Val-Borro, M.,
Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370,
529 [NASA ADS] (In the text)
- Dubrulle, B.,
Marié, L., Normand, C., et al. 2005, A&A, 429, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Fryxell, B., Olson,
K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] (In the text)
- Gammie, C. F.
1996, ApJ, 457, 355 [NASA ADS] [CrossRef] (In the text)
- Godon, P. 1996, MNRAS,
282, 1107 [NASA ADS] (In the text)
- Goldreich, P.,
Goodman, J., & Narayan, R. 1986, MNRAS, 221, 339 [NASA ADS]
- Ji, H., Burin, M.,
Schartman, E., & Goodman, J. 2006, Nature, 444, 343 [NASA ADS] [CrossRef]
- Johnson, B. M.,
& Gammie, C. F. 2006, ApJ, 636, 63 [NASA ADS] [CrossRef]
- Kargl, S. G.,
& Marston, P. L. 1989, Acoust. Soc. Am. J., 85, 1014 [NASA ADS] (In the text)
- Klahr, H. H.,
& Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef]
- Klahr, H., &
Bodenheimer, P. 2006, ApJ, 639, 432 [NASA ADS] [CrossRef]
- Kley, W. 1998,
A&A, 338, L37 [NASA ADS] (In the text)
- Koller, J., Li, H.,
& Lin, D. N. C. 2003, ApJ, 596, L91 [NASA ADS] [CrossRef]
- Laughlin, G.,
Korchagin, V., & Adams, F. C. 1998, ApJ, 504, 945 [NASA ADS] [CrossRef]
- Li, H., Finn,
J. M., Lovelace, R. V. E., & Colgate, S. A.
2000, ApJ, 533, 1023 [NASA ADS] [CrossRef]
- Li, H., Colgate,
S. A., Wendroff, B., & Liska, R. 2001, ApJ, 551, 874 [NASA ADS] [CrossRef] (In the text)
- Li, H., Li, S.,
Koller, J., et al. 2005, ApJ, 624, 1003 [NASA ADS] [CrossRef]
- Lin,
D. N. C., & Papaloizou, J. 1985, in Protostars and
Planets II, ed. D. C. Black, & M. S.
Matthews, 981
(In the text)
- Lin,
D. N. C., Papaloizou, J. C. B., & Savonije,
G. J. 1990, ApJ, 364, 326 [NASA ADS] [CrossRef] (In the text)
- Lovelace,
R. V. E., Li, H., Colgate, S. A., & Nelson,
A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef]
- Lubow, S. H.,
& D'Angelo, G. 2006, ApJ, 641, 526 [NASA ADS] [CrossRef] (In the text)
- Lubow, S. H.,
Seibert, M., & Artymowicz, P. 1999, ApJ, 526, 1001 [NASA ADS] [CrossRef]
- Marcus, P. S.
1988, Nature, 331, 693 [NASA ADS] [CrossRef] (In the text)
- Mukhopadhyay, B.,
Afshordi, N., & Narayan, R. 2005, ApJ, 629, 383 [NASA ADS] [CrossRef]
- Nelson, A. F.,
& Benz, W. 2003, ApJ, 589, 556 [NASA ADS] [CrossRef] (In the text)
- Papaloizou,
J. C. B., & Pringle, J. E. 1984, MNRAS, 208,
721 [NASA ADS]
- Papaloizou,
J. C. B., & Pringle, J. E. 1985, MNRAS, 213,
799 [NASA ADS]
- Papaloizou,
J. C. B., & Pringle, J. E. 1987, MNRAS, 225,
267 [NASA ADS]
- Plewa, T., &
Müller, E. 2001, Comp. Phys. Comm., 138, 101 [NASA ADS] (In the text)
- Press, W. H.,
Teukolsky, S. A., Vetterling, W. T., & Flannery,
B. P. 1992, Numerical recipes in FORTRAN. The art of
scientific computing, 2nd edn. (Cambridge: University
Press)
(In the text)
- Pringle, J. E.
1981, ARA&A, 19, 137 [NASA ADS]
- Richard, D. 2001,
Ph.D. Thesis, AA (Observatoire de Paris GIT/SPEC CEA Saclay)
- Richard, D., &
Zahn, J.-P. 1999, A&A, 347, 734 [NASA ADS]
- Shakura, N. I.,
& Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] (In the text)
- Tagger, M. 2001,
A&A, 380, 750 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tagger, M., &
Melia, F. 2006, ApJ, 636, L33 [NASA ADS] [CrossRef] (In the text)
- Varnière, P.,
& Tagger, M. 2006, A&A, 446, L13 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Weirs, G., Dwarkadas,
V., Plewa, T., Tomkins, C., & Marr-Lyon, M. 2005, Ap&SS,
298, 341 [NASA ADS] [CrossRef]
- Woodward, P., &
Colella, P. 1984, J. Comput. Phys., 54, 115 [NASA ADS] [CrossRef]
- Ziegler, U., & Yorke,
H. W. 1997, Comp. Phys. Comm., 101, 54 [NASA ADS] (In the text)
Copyright ESO 2007
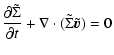
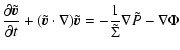
![\begin{displaymath}%
\Omega^2 = \frac{1}{r} \left[
\frac{1}{\Sigma} \frac{{{\rm d}}P}{{{\rm d}}r} +
\frac{{{\rm d}}\Phi}{{{\rm d}}r} \right]
\end{displaymath}](/articles/aa/full/2007/33/aa7169-07/img31.gif)
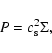
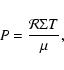
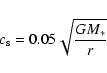
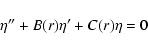
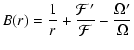
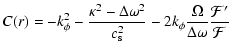
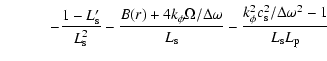
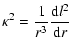
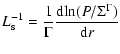
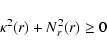
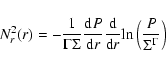
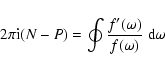
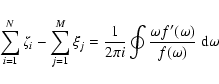
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{7169f1.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg67.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{7169f2.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg68.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{7169f3.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{7169f4.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg70.gif)
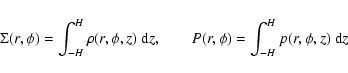
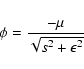
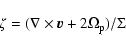
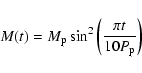
![\begin{displaymath}%
\Sigma_0(r)= \exp{\left[- \frac{f}{9} \frac{q^2 a^2 \Omega_...
...\nu_{\rm p}}\left(\frac{a}{\Delta_{{\rm p}}}\right)^3\right]},
\end{displaymath}](/articles/aa/full/2007/33/aa7169-07/img81.gif)
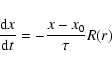
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{7169f5a.eps}\vspace*{5mm}
\includegraphics[width=7.5cm,clip]{7169f5b.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7169f6CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{7169f7.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg108.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{7169f8CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg109.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7169f9CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg123.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7169f10CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg124.gif)
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{7169f11.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg126.gif)
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{7169f12.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg127.gif)
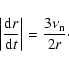
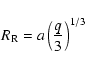
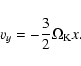
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{7169f13CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg141.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{7169f14CMJN.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg142.gif)
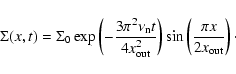
![\begin{displaymath}%
\nu_{{\rm n}} = \frac{4 x_{{\rm out}}^2}{3 \pi^2 (t_2-t_1)} \ln\left[\frac{\Sigma(t_1)}{\Sigma(t_2)}\right]\cdot
\end{displaymath}](/articles/aa/full/2007/33/aa7169-07/img148.gif)
![\begin{figure}
\par\includegraphics[width=8.65cm,clip]{7169f15.eps} \end{figure}](/articles/aa/full/2007/33/aa7169-07/Timg149.gif)