A&A 471, 873-884 (2007)
DOI: 10.1051/0004-6361:20066921

Jet-driven molecular outflows from class 0 sources: younger and stronger than they seem?

T. P. Downes1,2 - S. Cabrit3


1 - School of Mathematical Sciences, Dublin City University, Dublin 9, Ireland
2 - National Centre for Plasma Science and Technology, Dublin City University, Dublin 9, Ireland
3 - LERMA, Observatoire de Paris, UMR 8112 du CNRS, 61 Av. de l'Observatoire, 75014 Paris, France

Received 11 December 2006 / Accepted 4 July 2007

Abstract
Context. The momentum, age and momentum injection rate (thrust) of molecular outflows are key parameters in theories of star formation. Systematic biases in these quantities as inferred from CO line observations are introduced through simplified calculations. These biases were quantified for radially expanding flows. However, recent studies suggest that the youngest outflows may be better described by jet-driven bowshocks, where additional biases are expected.
Aims. We investigate quantitatively the biases in momentum, age, and thrust estimates in the case of young jet-driven molecular outflows, and propose more accurate methods of determining these quantities.
Methods. We use long-duration (1500 yr) high resolution numerical simulations in concert with the standard observational methods of inferring the relevant quantities to quantify the systematic biases in these calculations introduced, in particular, by dissociation, erroneous inclusion of transverse momentum, and hidden material at cloud velocity. Jet/ambient density contrasts of 0.1-1 are considered, leading to bow speeds of 60-135  km s-1.
Results. When mass-weighted velocities are used, lifetimes are overestimated by typically an order of magnitude. The molecular thrust is then underestimated by similar amounts. Using the maximum velocity in CO profiles gives better results, if empirical corrections for inclination are applied. We propose a new method of calculating the lifetime of an outflow which dramatically improves estimates of age and molecular thrust independent of inclination. Our results are applicable to younger flows which have not broken out of their parent cloud.
Conclusions. Published correlations between the molecular flow thrust and the source bolometric luminosity obtained with the maximum CO velocity method should remain valid. However, dissociation at the bow head may cause the observable thrust to underestimate the total flow thrust by a factor of up to 2-4, depending on the bow propagation speed and the magnetic field strength. Detailed evaluation of this effect would greatly help to better constrain the efficiency of the ejection mechanism in protostars.

Key words: hydrodynamics - shock waves - ISM: jets and outflows - ISM: molecules

   
1 Introduction

The cumulative momentum and the momentum injection rate ("thrust'') in swept-up molecular outflows from young stars are both key parameters for theories of star formation: the cumulative outflow momentum is a measure of the feed-back from star formation on cloud turbulence, and its value per unit stellar mass is an essential parameter for theories of self-regulated star formation (e.g. Norman & Silk 1980). The outflow thrust (i.e. the ratio of flow momentum to age) gives a measure of the rate of momentum injection by the protostellar wind, and its ratio to the source luminosity sets a key constraint for theoretical ejection models (cf. Lada 1985; Richer et al. 2000).

To evaluate accurately the above properties, however, it is necessary to have a reasonably good measure of both the total outflow momentum, and of the time over which this momentum was deposited ("flow age''). Systematic biases in these quantities were examined for simple models of radially expanding outflows with a power-law velocity field by Cabrit & Bertout (1990). The method found as the most accurate was then used to derive updated correlations between the outflow thrust and the source luminosity, $L_{\rm bol}$: very high values of wind thrust $\simeq$ $ 1000 /(L_{\rm bol}/c)$ were inferred for low-luminosity outflow sources, strongly favoring magneto-centrifugally driven winds from accretion disks (Cabrit & Bertout 1992). This analysis was extended to higher luminosity sources (e.g. Richer et al. 2000; Beuther et al. 2002).

Since this early work, there has been mounting evidence that the youngest molecular flows, driven by Class 0 protostars, show a kinematic pattern in better agreement with a jet-driven bowshock than with a radially expanding shell (Masson & Chernin 1993; Raga & Cabrit 1993; Smith et al. 1997; Cabrit et al. 1997; Gueth & Guilloteau 1999; Downes & Ray 1999; Lee et al. 2001; Downes & Cabrit 2003; Arce et al. 2006). This situation will introduce new biases in observational derivations of the flow momentum and age, for several reasons:

Therefore we expect outflow ages to be systematically overestimated in a jet-driven outflow, while it is unclear whether the "observed'' momentum (and thrust) will be an over- or under-estimate of the true value.

In this work, we evaluate quantitatively the above biases in momentum, age and thrust estimates in jet-driven molecular outflows using long-duration high resolution numerical simulations reaching timescales of 1500 years. Both a density-matched and a strongly underdense jet (1:10) are considered, to study the effect of the jet/ambient density contrast. We include a treatment of molecular dissociation, to estimate the amount of "unseen'' momentum in atomic gas, as well as a simplified treatment of NLTE CO emission, to gauge additional errors made in the conversion from line intensity to mass assuming LTE. We then apply the methods most widely used by observers to derive the outflow mass, momentum, age, and thrust, and quantify the various errors introduced in these quantities.

Our numerical model is presented in Sect. 2. In Sect. 3 we describe the errors introduced by molecular dissociation, the assumption of constant CO excitation temperature, the erroneous inclusion of transverse momentum, inclination effects, and hidden outflow material at ambient velocities. We then examine the accuracy of inferred timescales and of thrust estimates using the usual methods and introduce a new, more robust method for calculating the age of young jet-driven outflows. We also discuss the limits of applicability of our results. Section 4 outlines our main conclusions.

   
2 Numerical model

In this section we describe the numerical method and initial conditions used to perform the simulations in this work.

2.1 Numerical method

The code is a modified version of that used in Keegan & Downes (2005) to perform long-duration simulations of YSO jets. The main modification is the inclusion of a more accurate H2 cooling function of Le Bourlot, Pineau des Forêts & Flower (1999) valid from T=100 K to 104 K. The hydrodynamic equations are solved using a second order Godunov scheme (e.g. Falle 1991) in which a nonlinear Riemann solver is used for strong rarefactions, while a linear Riemann solver is used for all other flux calculations in order to reduce computational overhead. The simulations presented here were run in cylindrical symmetry.

The code itself is parallelised efficiently and load-balanced in order to ensure that only the active region of the computational domain is being integrated (see Keegan & Downes 2005). This yields a speed-up of a factor of around 4 over traditional domain decomposition which, while not as good as one would expect from adaptive mesh refinement which typically gives a factor of 10, is still significant.

   
2.2 Initial conditions

We considered a typical protostellar jet mean velocity of 215 km s-1 (e.g. Mundt 1987). Superimposed on the jet velocity was a spectrum of sine waves with total amplitude 127 km s-1 and periods of 5, 10, 20 and 50 yrs. The jet temperature was taken to be 1000 K while the ambient temperature in each case was taken to be 100 K. The time-averaged jet Mach number was therefore about 93. Note that, while the ambient temperature is rather high compared with that expected in molecular clouds, reducing the temperature to 10 K does not change the results presented here. This is due to the fact that the jet is hypersonic with respect to the ambient medium in either case.

The molecular fractions in the jet and ambient medium were taken to be the same, with ${n({\rm H_2})}= 9 {n({\rm H})}$ while overall the jet and ambient gases were assumed to be of solar abundances. The total jet number density was set to 100 cm-3. For the jet radius, we adopted a value of $r_j = 5\times 10^{15}$ cm = 333 AU, consistent with an extrapolation of typical atomic jet widths (see e.g. Reipurth et al. 2000) to the propagation distances $\simeq$0.1 pc covered in our simulations. The total injected z-momentum over 1500 yr is then $3.2\times10^{-3}$ $M_{\odot}$ km s-1 and the time-averaged jet thrust is $2.1\times10^{-6}$ $M_{\odot}$ km s-1 yr-1.

Two simulations were run for the purposes of this work, with different values of the mass density contrast $\eta = \rho_j / \rho_a$: a density-matched case ($\eta =1$) where the ambient density was 100 cm-3, and an underdense jet case ($\eta =0.1$) where the ambient density was set to 1000 cm-3. In each case a resolution of $1\times10^{14}$ cm in both the z and r directions was used. Hence the jet diameter was well resolved, being 100 pixels across. Our relatively low densities were chosen to ensure that all shock fronts are also well resolved, an essential condition for an accurate treatment of H2 dissociation and cooling. The full grid size of the $\eta =0.1$ simulation was $3500\times1000$ (0.11 pc $\times$ 0.03 pc) while for the $\eta =1$simulation it was $6500\times500$ (0.21 pc $\times$ 0.016 pc).

The time-averaged advance speed of the bow head is $\simeq$60  km s-1 for $\eta =0.1$ and $\simeq$135  km s-1 for the $\eta =1$ case, hence substantial dissociation occurs in both cases, though in different amounts. These relatively high advance speeds are in line with the proper motions of 150-260  km s-1 observed at the tip of the HH47 redshifted outflow lobe (Eisloeffel & Mundt 1994; Micono et al. 1998), the only measurements of this kind available so far (see Sect. 3.7).

   
3 Results

We examine our simulations (both $\eta =0.1$ and $\eta =1$) at an age of t=1500 yr. As noted in Keegan & Downes (2005) this ensures that the system has overcome initial transients, and characteristics such as the mass-velocity relations have reached a quasi-steady state. As in Downes & Cabrit (2003), we derive the observable properties of the simulated outflows using the NLTE emission formula of McKee et al. (1982) for the CO(2-1) line, assuming optically thin emission. Intensity-velocity distributions for swept-up material integrated over the flow are constructed for various view angles, and used to derive "observed'' outflow mass, momentum, kinetic energy, and age in the same way as usually done by observers. These values are then compared with the actual parameters of our simulated outflow.

For obvious symmetry reasons, we conduct our analysis only on a single lobe of the outflow (that tilted towards the observer). We also exclude any molecular material originating from the jet, as in reality this contribution would depend on the atomic/molecular fraction in Class 0 jets, which is ill-known at present. Finally, we consider that the outflow is young enough that the whole lobe still lies within the confines of the parent molecular cloud, so that its full (projected) length can be measured in CO. This, and the neglect of any wide-angle wind component, mean that our results may not be applicable to evolved flows around Class I sources (see discussion in Sect. 3.7).

The sources of errors that we will examine are the following:

Note that the first two errors do not depend on inclination, while all of the others do.

In observed flows, the assumption of optically thin CO emission introduces an additional error in mass and momentum determinations. We could not quantify this effect in our simulations, as our low adopted densities lead to small swept-up masses (a few $10^{-4} ~M_\odot$, see Tables 1, 2) where the optically thin assumption is in fact well justified. However, Cabrit & Bertout (1990) showed that an empirical correction for CO optical depth using the 13CO to 12CO intensity ratio is usually adequate for typical outflow opacities. Since such an optical-depth correction is now routinely applied in recent observational studies, this source of error is not considered further in our analysis.

   
3.1 Missing material in atomic form

In the jet-driven molecular outflow model, the outflow is accelerated by the bowshock of the driving stellar jet. Downes & Ray (1999) pointed out that there is the possibility of dissociating a substantial fraction of the swept-up gas during this process.

Downes & Cabrit (2003) further showed that molecular dissociation plays a crucial role in producing a break in slope around 20  km s-1 in the m(v) relation of jet-driven flows (contrary to the interpretation of Birks, Fuller & Gibb (2006) who erroneously reported that this work attributed the break to the excitation temperature of the line being observed). The break in m(v)appears as soon as one considers molecular swept-up material only, as illustrated in Fig. 1 for our $\eta =1$ simulation. Line excitation effects only help to further steepen the I(v) relation at higher velocities than the break, yielding CO(2-1) intensity-velocity relations in very good agreement with observations (Bachiller & Tafalla 1999; Downes & Cabrit 2003).

Here we examine the effect of molecular dissociation on the observable swept-up mass, axial momentum along the jet z-axis, and kinetic energy. Tables 1 and 2 contain a summary of the results of our calculations. The "Total'' property refers to the ambient material swept up by the bowshock in both atomic and molecular form, the "H2'' property is only for molecular swept up material. The numbers in parentheses are the proportion of the actual total for that property.

Table 1: Inclination-independent errors for the $\eta =0.1$ underdense jet simulation. The total swept-up mass, the molecular swept-up mass, the mass inferred assuming T=10 K, and the mass inferred assuming T=100 K for the simulation at t=1500 yrs. The numbers in parentheses represent the fraction of the actual mass in the outflow. Also shown are the same quantities for momentum and kinetic energy.

Table 2: Inclination-independent errors for the density-matched $\eta =1$ simulation. Content as in Table 1.

We can see from Tables 1 and 2 that only about 60% of the swept up mass is actually molecular, compared to almost 95% of the unshocked ambient medium (see Sect. 2.2). The result is common between the $\eta =1$ and $\eta =0.1$ simulations.

The effect is more substantial for the axial momentum: Only 45% at $\eta =0.1$, and 26% at $\eta =1$ of the z-momentum in the swept-up outflow is molecular. The results we find here, for our much longer simulations, are in excellent agreement with the results of Downes & Ray (1999). Their model G corresponds most closely to our $\eta =1$ simulation. For this model they found that the proportion of swept-up momentum residing in molecules was about 0.25and we find this figure to be 0.26 from our $\eta =1$simulation. Hence this number does not seem to depend strongly on the flow age.

The fraction residing in molecular material is even smaller for kinetic energy than for momentum, with the molecular kinetic energy being only 31% ($\eta =0.1$) to 14% ($\eta =1$) of the total kinetic energy in the swept-up outflow.


  \begin{figure} \par\includegraphics[width=8cm,clip]{figures/6921fig1.eps} \end{figure} Figure 1: Plots of the mass-velocity relations for all swept-up material (top curve), and for molecular swept-up material only (short-dash) for our $\eta $ =  1 simulation at 1500 yr. Note the break in slope that appears when considering molecular material only (see Downes & Cabrit 2003). Also shown are the mass-velocity relations that would be inferred from the CO(2-1) intensity assuming T=10 K and T=100 K (lowest two curves; see Sect. 3.2). Velocity is projected along the jet z-axis.
Open with DEXTER

We can easily understand why the momentum and kinetic energy estimates are progressively worse than the mass estimates as follows. We know (e.g. Smith et al. 1997; Downes & Ray 1999; Lee et al. 2000; Downes & Cabrit 2003) that the swept-up mass in a jet-driven flow varies with velocity as $m(v) \propto v^{-\gamma}$ with $\gamma = 1.5$-2. This is confirmed for our simulations in Fig. 1. Then the integrated mass, M, for the outflow is given by

 \begin{displaymath}M = \int_{v_{\rm min}}^{v_{\rm max}} m(v)~{\rm d}v \nonumber \propto \left[v^{-\gamma+1}\right]_{v_{\rm min}}^{v_{\rm max}} \end{displaymath}  

while the integrated momentum for the flow, which will just be the axial component Pz(see Sect. 3.3), is given by

 \begin{displaymath}P_z = \int_{v_{\rm min}}^{v_{\rm max}} m(v) v ~ {\rm d}v \non... ...propto \left[v^{-\gamma+2}\right]_{v_{\rm min}}^{v_{\rm max}}, \end{displaymath}  

and the outflow integrated kinetic energy is

 \begin{displaymath}E = {1 \over 2} \int_{v_{\rm min}}^{v_{\rm max}} m(v) v^2 ~ {... ...propto \left[v^{-\gamma+3}\right]_{v_{\rm min}}^{v_{\rm max}}. \end{displaymath}  

Since $\gamma > 1$, the largest contribution to the integrated mass comes from material moving with low velocity. Much of this material will not have passed through very strong shocks, and hence it can be expected that not many of the molecules will have been dissociated (see Fig. 1). This leads to the expectation of a reasonably good estimate of overall mass in an outflow if we only examine the molecular mass (assuming, of course, that the ambient medium is predominantly molecular).

In contrast, since $\gamma < 2$, the largest contribution to P comes from material at the highest velocity. This is precisely the material which will have passed through the strongest shocks, and hence will have the lowest fraction of molecules (again, see Fig. 1). It is clear, then, that we can expect a larger discrepancy between momentum estimates based on molecular material and the true momentum in the outflow than encountered when making mass estimates in the same way. The same argument holds for the energy estimates, leading to the expectation, verified in our simulations, that the kinetic energy in molecular gas is an even more severe underestimate of the total energy than is the case for momentum.

We also find that the effect of dissociation depends on $\eta $. Underestimation of the total momentum and energy due to molecular dissociation is twice as severe in the $\eta =1$ case compared with $\eta =0.1$ (see Tables 1 and 2). This may be attributed to the twice faster propagation speed of the bow head in the density-matched $\eta =1$case, which induces more dissociation at the highest flow velocities than in the under-dense $\eta =0.1$ case, where the bow propagates at only 60  km s-1. Since the molecular momentum and energy are weighted towards high speed material (see above), this differential effect due to the variation in bow speed is clearly noticeable for these quantities. There is little differential effect of $\eta $ for the molecular mass which is dominated by low speed material.

We conclude that molecular dissociation may cause a large fraction of the outflow momentum and kinetic energy to be unobservable in CO. The magnitude of this effect depends on the bow advance speed, controlled by the jet/ambient density contrast. It would be much reduced if $\eta $ is less than 0.01, leading to bow speeds $\le$20  km s-1 (cf. Sect. 3.7). It could also be lowered by the presence of transverse magnetic fields allowing non-dissociative C-shocks at velocities $\geq$25  km s-1 (Le Bourlot et al. 2002). In the following subsections we will thus examine errors introduced in the properties of the observable molecular gas only, and reintroduce the extra effect of molecular dissociation in our final discussion.

   
3.2 Constant temperature assumption

Since information about temperature gradients in outflows would require multi-line analyses at various positions, which is frequently too time consuming to be feasible in practice, observers have usually assumed a constant temperature throughout the molecular outflow when calculating the molecular mass from the emission in CO lines. The assumed temperature is generally of order 10 K (e.g. Tafalla & Myers 1997), as suggested by the typical CO(2-1) to CO(1-0) line ratio, but values as high as 100 K have been used in high-velocity "bullets'' where higher J lines have been detected (Hatchell et al. 1999).

The bottom two rows in Tables 1 and 2 entitled "Inferred'' give the properties which would be inferred by CO(2-1) observations of our simulated outflows, assuming CO is optically thin and in LTE at a constant temperature of 10 K or 100 K across the entire outflow, while the lowest two curves in Fig. 1 plot the mass-velocity relations obtained with these assumed temperatures. These values (and the inferred $m(I_{\rm CO}(v))$ relations in Fig. 1) are calculated using

 \begin{displaymath}{\rm d}m(I({v})) = m_{\rm H_2} \left[\frac{\rm H_2}{\rm CO}\r... ...21} 5 {\rm e}^{-16.6/T}} {4\pi Z(T)}\right)^{-1} I_{\rm CO}(v) \end{displaymath} (1)

where dm(I(v)) is the inferred mass per velocity bin, $I_{\rm CO}(v)$ is the intensity in the CO J=2-1 line, and $Z(T) \simeq kT/hB_0 = T/2.765$ is the CO partition function.

The assumption of T=100 K gives masses 2.2 times larger than assuming T=10 K. This results from the depletion of the J=2 level at temperatures above $\simeq$20 K, as higher energy levels become accessible to the molecule. This "partition function'' effect causes the J=2-1 line emissivity per molecule (expression between parentheses in Eq. (4)) to eventually become inversely proportional to T above 50 K, so that dm(I(v))increases with T.

As can be seen in Tables 1 and 2, an assumption of T=10 K gives a reasonable estimate of the molecular mass and momentum, while kinetic energy tends to be too low (by a factor of 1.5 for $\eta =0.1$, and 3.5 for $\eta =1$). This can be understood from Fig. 1, which shows that m(v) is correctly estimated up to 30  km s-1, but is underestimated for the higher velocity, warmer material that dominates the kinetic energy integral (see previous section). In contrast, the T=100 K assumption gives an overestimate of all molecular parameters (with the exception of molecular kinetic energy for $\eta =1$, which is still significantly too low).

The assumption most commonly used by observers is that $T\simeq10$ K. We have seen that this introduces only a small error in the molecular swept-up momentum for both values of $\eta $. Therefore, the main inclination-independent error on the momentum in outflows will remain that resulting from the neglect of dissociated material (see previous section). On the other hand, molecular kinetic energy is significantly underestimated by this assumption when $\eta =1$ (by a factor of 3.5). Using a specific excitation temperature for high-velocity gas (determined, for example, from high-J CO line ratios; cf. Hatchell Fuller & Ladd 1999) is needed to alleviate this problem. In any case, the error factor is only half of that introduced from the neglect of dissociated material, which contains most of the kinetic energy of swept-up gas in our simulations.

   
3.3 Erroneous inclusion of momentum in transverse motions

Here we investigate the error in the molecular swept-up momentum introduced from taking into account transverse momentum. As noted in Sect. 1, transverse motions in jet-driven outflows result from the "energy-driven'' sideways thermal expansion of hot gas in the immediate post-shock zone behind the working surface (see, e.g., Ostriker et al. 2001). They do not correspond to actual linear z-momentum injected by the jet. Taking transverse momentum into account might, therefore, lead to an overestimate of the momentum necessary to drive the outflow. Such a bias has not been investigated to date. We will examine the influence of the viewing angle on this error, and the effect of applying a global inclination correction.

In a lobe which is driven only by momentum injection in the axial z-direction, the net vector contribution of transverse momentum to the total momentum in the system, $\vec{P}$, is, by symmetry, zero:

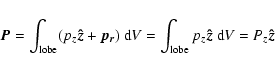\begin{displaymath}\vec{P} = \int_{\rm lobe} (p_z\vec{\hat{z}} + \vec{p_r})~{\rm... ...t_{\rm lobe} p_z \vec{\hat{z}} ~{\rm d}V = P_z \vec{\hat{z}} \end{displaymath} (2)

where $p_z \vec{\hat{z}}$ and $\vec{p_r}$ are the axial (z) and transverse components of momentum density respectively in elementary volume dV.

When the flow is inclined by an angle $\alpha < 90\hbox{$^\circ$ }$ to the plane of the sky, the line of sight velocities include contribution from both the z motions and the transverse motions. The latter may introduce a mix of forward and backward (blueshifted and redshifted) momentum towards a given lobe of the flow. To extract only the z-momentum component (projected onto the line of sight) one must perform a proper vector summation along the line of sight so that transverse momentum from the front and back sides of the bowshock cancel out by symmetry, i.e. one should count positively the momentum towards the observer, and negatively the momentum going away:

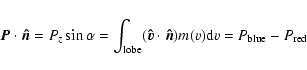\begin{displaymath}\vec{P} \cdot \vec{\hat{n}} = P_z \sin\alpha = \int_{\rm lobe... ...ot \vec{\hat{n}}) m(v) {\rm d}v = P_{\rm blue} - P_{\rm red} \end{displaymath} (3)

where $P_{\rm blue}$ and $P_{\rm red}$ are the absolute values of the line-of-sight momentum approaching and receding within a given lobe and $\vec{\hat{n}}$ is the unit vector along the line of sight. The inclination corrected z-momentum is then given by

 \begin{displaymath}P_z = \frac{P_{\rm blue} - P_{\rm red}}{\sin \alpha}\cdot \end{displaymath} (4)

Instead, observers often sum all momentum in absolute value over a single lobe of an outflow (e.g. Snell et al. 1984; Lada & Fich 1996; Shepherd et al. 2000; Parker et al. 1991), i.e. they take:

 \begin{displaymath}P_{\rm obs} = \int_{\rm lobe} \vert\vec{\hat{v}} \cdot \vec{\hat{n}}\vert m(v) {\rm d}v = P_{\rm blue} + P_{\rm red}, \end{displaymath} (5)

assuming that this will give a lower limit to the actual injected momentum. However, this is not necessarily true if the flow is driven by a jet and transverse motions are important along the line of sight. Furthermore, the inclination-corrected "observed'' momentum, given by

 \begin{displaymath}P^{\rm Corr}_{\rm obs} = \frac{P_{\rm blue} + P_{\rm red}}{\sin \alpha}, \end{displaymath} (6)

will always overestimate the z-momentum in the jet-driven case, as can be seen from comparison with Eq. (7).

A quantitative illustration of both of these effects as a function of inclination to the plane of the sky, $\alpha$, is presented in Fig. 2 for the $\eta =0.1$ simulation, and in Fig. 3 for the $\eta =1$ case. All quantities are normalised to the actual molecular z-momentum in the flow.


  \begin{figure} \par\includegraphics[width=8cm,clip]{figures/6921fig2.eps} \end{figure} Figure 2: Plots of the approaching and receding line-of-sight molecular momentum present in the blueshifted lobe of the $\eta =0.1$simulation, the sum of these components ( $P_{\rm blue} + P_{\rm red}$), and the inclination corrected value $(P_{\rm blue} + P_{\rm red})/\sin \alpha$. Each is normalised to the actual molecular z-momentum in the lobe.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{figures/6921fig3.eps} \end{figure} Figure 3: As Fig. 2 but for the $\eta =1$ simulation.
Open with DEXTER

The behavior of $P_{\rm blue} + P_{\rm red}$ with inclination (star symbols in Figs. 2 and 3) is found to depend upon $\eta $. It increases at smaller $\alpha$ (more edge-on flows) when $\eta =1$, but decreases when $\eta =0.1$. The data here suggest that the $\eta =1$ outflow has more sideways expansion than the $\eta =0.1$ outflow. This is to be expected given that the ambient density in the $\eta =0.1$ outflow is higher and hence the cooling is stronger. It is well known that this leads to narrower bowshocks with post-shock motions oriented more closely to the axis of the driving jet. Despite this difference, for both values of $\eta $, we find that $P_{\rm blue} + P_{\rm red}$remains within a factor of 2 of the actual molecular z-momentum in the outflow, independent of the inclination angle of the flow: by coincidence, the erroneous inclusion of transverse momentum compensates almost exactly for the reduction in line-of-sight z-momentum due to projection effects.

In contrast, the inclination-corrected absolute momentum calculated from Eq. (9) (top curves in Figs. 2 and 3) systematically overestimates the molecular z-momentum in the flow, as expected, even going to infinity as the inclination angle goes to zero. Another source of error, not quantified here, is the error on $\alpha$ itself. The flow inclination is difficult to evaluate accurately without a proper kinematic model, unless there are proper motion measurements for the associated jet, but the latter are rarely available in deeply embedded outflow sources.

As a result, at all values of inclination, $P_{\rm obs} = P_{\rm blue} + P_{\rm red}$ gives a much better estimate of Pz than the inclination-corrected prescription of Eq. (9). Compared with the correct expression of Eq. (7), it also has the advantage of not requiring an accurate inclination value. Therefore, based on our simulations, this would seem like the most robust method to evaluate the injected molecular momentum from observations of jet-driven flows[*].

3.4 Projection effects in kinetic energy

Unlike momentum, the kinetic energy in an outflow is not a conserved quantity - a significant fraction of it is lost through radiative cooling, particularly in post-shock regions. Indeed, the high level of far-infrared line emission from outflows found by the ISO satellite supports the idea that they are driven by highly-radiative, momentum-conserving shocks (e.g. Giannini et al. 2001). Hence, kinetic energy estimates are not as useful in constraining the physical mechanism powering the jet. However, the kinetic energy in molecular swept-up gas will probe the energy mediated through non-dissociative shocks, and will be relevant to compare with the cooling budget of H2, CO, and H2O observed with ISO, Spitzer, and the forthcoming Herschel observatory. We thus include a brief discussion of the projection effects here, as most observers provide estimates of the molecular kinetic energy in an outflow.

Energy estimates do not pose the same problems as momentum estimates since energy is a scalar quantity. In this case it is correct to add all the kinetic energy in the flow lobe together (i.e. both the energy in forward and backward motions within a single lobe). A problem which remains is that there is always some amount of energy which is not in line-of-sight motion, hence using the integral in Eq. (3) (e.g. Lada & Fich 1996; Shepherd et al. 2000) will always give a lower limit. One may consider applying a mean correction factor of $1/\sin^2 \alpha$ to take into account inclination effects on the energy. However, this will be correct only for z-motions, and not for transverse motions.

Figures 4 and 5 illustrate the resulting error on molecular kinetic energy for the $\eta =0.1$ and $\eta =1$ simulation respectively by plotting the line-of-sight kinetic energy (sum of the red-shifted and blue-shifted components) as a function of inclination, as well as the same quantity after global correction by $1/\sin^2 \alpha$.


  \begin{figure} \par\includegraphics[width=8cm,clip]{figures/6921fig4.eps} \end{figure} Figure 4: Plots of the total line-of-sight energy for the $\eta =0.1$simulation, both before and after correction for inclination by a mean factor of $1/\sin^2 \alpha$. The energy is normalised by the total kinetic energy in molecular material.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{figures/6921fig5.eps} \end{figure} Figure 5: As Fig. 4 but for the $\eta =1$simulation.
Open with DEXTER

Table 3: Masses and momenta of the outflows calculated from the $m_{\rm H_2}(v)$ relation using the velocity ranges 2-40  km s-1 and 7-40  km s-1 with a bin width of 1  km s-1. Also shown are $\langle v\rangle_{\rm lobe}$ and $v_{\rm max}$, the latter chosen as the velocity at which $I_{\rm CO}$ is 1/100 that at $v_{\rm min}$ (see text).

In contrast to what we found for the absolute line-of-sight momentum ( $P_{\rm blue} + P_{\rm red}$), the line-of-sight energy in molecular gas always severely underestimates the true molecular kinetic energy. In the $\eta =0.1$ case, the underestimate is a factor of 4 at the median inclination of 30$^\circ$, and up to a factor of 10 in the edge-on case. Even when the flow is viewed pole-on, the energy estimate is slightly too low by 20%. This is due to the presence of kinetic energy in transverse motions perpendicular to the line of sight. The inclination correction $1/\sin^2 \alpha$ works rather well for $\alpha$greater than about $20\hbox{$^\circ$ }$, with errors of less than a factor of 2. However, the corrected values become very much larger than the true value for $\alpha < 20$$^\circ$.

The picture is slightly different for the $\eta =1$ case; the differences arising from the higher transverse motions in this simulation due to the lower ambient density (see the previous section). In this case the variation with inclination angle is lessened, with an underestimate of about a factor of 3 at all angles. As a result, the inclination correction $1/\sin^2 \alpha$works well only at median inclinations $\alpha \simeq 30\hbox{$^\circ$ }$, but over/underestimates the energy significantly at smaller/larger angles.

Overall, it appears difficult to estimate the molecular kinetic energy of swept-up gas to better than a factor of 3 even if inclination corrections are applied.

   
3.5 Hidden outflow material at ambient velocities

In actual observations, CO emission at low velocities is often dominated by ambient molecular cloud material moving turbulently along the line of sight. To avoid contamination of outflow quantities by ambient gas, a low velocity cut-off around 1-2  km s-1 is typically used, while sometimes a cut-off as high as 7  km s-1 is necessary (see, e.g.  Lada & Fich 1996).

The effect of truncating the minimum velocity at which material is considered to be in the flow is illustrated in Table 3 for our jet-driven simulations. The masses and line-of-sight momenta of the outflows are calculated from the $m_{\rm H_2}(v)$ relations at t=1500 yr, with cut-off velocities $v_{\rm min}$ of 2 and 7  km s-1. They are normalised to the true outflow mass and z-momentum in molecular form (from Tables 1 and 2). Momentum is estimated as $P_{\rm blue} + P_{\rm red}$, the prescription found as the most robust against projection effects in Sect. 3.3.

In the typical case of $v_{\rm min} = 2$  km s-1, ignoring low velocity material leads to an underestimate in the molecular mass of typically a factor of 2-3. However, the effect is not as marked for the molecular momentum, which is more heavily weighted towards high velocities (see Sect. 3.1, in particular Eqs. (1) and (2)). The errors on this quantity are very similar to those found previously without a low-velocity cut-off (see Figs. 2 and 3). They remain less than a factor of 2 in most cases, hence it does not appear necessary to correct the absolute line-of-sight momentum for hidden outflow material at cloud velocities when $v_{\rm min}$ is small.

In the extreme case where $v_{\rm min} = 7$ km s-1, molecular mass becomes severely underestimated (less than 10% is recovered), while momentum is always too low by a typical factor of 2-3, even reaching 10-100 in the $\eta =0.1$ outflow at $\alpha \le 30$$^\circ$ (a result of the strongly forward-directed motions in this simulation). Hence we expect that $P_{\rm blue} + P_{\rm red}$ will significantly underestimate the molecular momentum when such large values of $v_{\rm min}$ are used, which is, fortunately, very rare.

It is worth noting that, while one expects inclination effects in these calculations due to the dependence of the m(v) relation on $\alpha$, their effect is small, leading to only roughly a change of a factor of two in the mass and momentum values, except for the $v_{\rm min} = 7$  km s-1, $\eta =0.1$ case. The origin of the dependence on $\alpha$ arises because, depending on the inclination angle used, and the velocity range used, material which at some angles is measured as moving (and therefore contributing to the mass and momentum of the outflow) is, at other angles, counted as being static. The specific details of the bowshock and the velocity ranges determine how significant an effect this is.

3.6 Age and thrust estimates using characteristic velocities

In this section we discuss three methods which have been commonly used to estimate the age and thrust of molecular outflows from observations.

One of the most commonly used ways of doing this is to calculate the intensity-weighted absolute velocity averaged over the entire flow lobe

 \begin{displaymath}\langle v\rangle_{\rm lobe} = \frac{(P_{\rm blue} + P_{\rm red})}{m_{\rm observed}} \end{displaymath} (7)

and then combine it with the overall length of the flow to infer an age (e.g. Snell et al. 1984; Shepherd et al. 2000):

 \begin{displaymath}t_{\rm g} = \frac{L_{\rm lobe}}{\langle v\rangle_{\rm lobe}}, \end{displaymath} (8)

where $L_{\rm lobe}$ is the projected length of the lobe. This method we refer to as the "global'' method. The outflow thrust is estimated by dividing the absolute line-of-sight momentum in the outflow by the dynamical timescale. Hence

 \begin{displaymath}F_{\rm g} = \frac{P_{\rm blue} + P_{\rm red}}{t_{\rm g}}\cdot \end{displaymath} (9)

A second "local'' method introduced by Lada & Fich (1996) instead derives the age of the flow using

 \begin{displaymath}t_{\rm l} = \left<\frac{r_{\rm proj}}{\langle v\rangle_{r_{\rm proj}}}\right>_{\rm lobe}, \end{displaymath} (10)

where $r_{\rm proj}$ is the projected distance of a given line of sight from the central source, $\langle v\rangle_{r_{\rm proj}}$ is the intensity-weighted velocity for the CO spectrum obtained along the same line of sight, and the large angle brackets indicate an average over all lines of sight in the outflow. This "local'' method could be expected to be more accurate since it uses more detail about the kinematic structure of the flow in the calculations. In the same spirit, the local method calculates the outflow thrust as

 \begin{displaymath}F_{\rm l} = \int_{\rm lobe} \frac{v^2 m(v)}{r_{\rm proj}}~{\rm d}v \end{displaymath} (11)

(cf. Eq. (2) of Lada & Fich 1996).

A third " $v_{\rm max}$'' method discussed by Lada (1985), Cabrit & Bertout (1992), and Beuther et al. (2002) uses

 \begin{displaymath}t_{v_{\rm max}} = \frac{L_{\rm lobe}}{v_{\rm max}} \end{displaymath} (12)

where $v_{\rm max}$ is the maximum observed radial velocity in CO profiles. This method would be expected to give a better age than the global method, since the characteristic velocity will be closer to the true advance speed of the bowshock, which determines the flow length. For the outflow thrust, Cabrit & Bertout (1992) used

 \begin{displaymath}F_{v_{\rm max}} = \frac{m_{\rm observed} v_{\rm max}}{t_{v_{\rm max}}} \times 10^{\Delta\log F(\alpha)}, \end{displaymath} (13)

where $\Delta\log F(\alpha)$ is an empirical factor (generally < 0) correcting for projection effects and for outflow material moving at less than $v_{\rm max}$, as estimated from simple radial outflow models (Cabrit & Bertout 1990).

We now compare the results of each of these calculations with the actual age and thrust of the simulated outflows. We will then propose a fourth, "perpendicular'' method to estimate these quantities, which appears more robust for the ages and density contrasts covered by our simulations. Note that we compare the inferred thrusts with the molecular axial thrust only, to see which method best retrieves the properties of the emitting gas. To calculate errors on the total (molecular+atomic) thrust in the simulated outflow, one should multiply the relevant numbers in Tables 4 to 7 by 0.45 (for $\eta =0.1$; see Table 1) or 0.26 (for $\eta =1$; see Table 2).

   
3.6.1 Global method

Table 4: Inferred ages and thrusts of the outflow using the global method and using the velocity ranges 2-40  km s-1 and 7-40  km s-1. The quantities are normalized to the true age and molecular thrust of the outflow. Errors on the total (molecular+atomic) thrust may be obtained by multiplying the relevant numbers by 0.45 ( $\eta =0.1$) or 0.26 ($\eta =1$).

We have taken $L_{\rm lobe}$ to be the projected distance from the the point of injection to the furthest point from this in the simulated bowshock. Values of $L_{\rm lobe}$ and $\langle v\rangle_{\rm lobe}$ for our simulations are listed in the third and fourth column of Table 3. Note that the lengths calculated here are similar to the length of young Class 0 outflows such as HH211 (Gueth & Guilloteau 1999). We then calculate $t_{\rm g}$ and the flow thrust using Eqs. (11) and (12). Table 4 presents the ages and thrusts calculated for $v_{\rm min} = 2$ and 7  km s-1 (see Sect. 3.5).

The values of $\langle v\rangle_{\rm lobe}$ in Table 3 are in good agreement with typical observed values in CO outflows. At the same time, they are clearly much smaller than the mean advance speeds of the bow head in our simulations, which are 60-135  km s-1 for $\eta =0.1$-1. This occurs because the mass-weighted velocity in a bowshock is more representative of the bow wing motions than of the propagation speed of the head of the bowshock (which contains very little mass). It is then clear that estimating the age of a jet-driven outflow using this method will be very misleading: as shown by Table 4, the ages will be always significantly overestimated, unless the flow is very close to the line of sight. The error on age can be as large as a factor of 35, with a median error (at $\alpha = 30$$^\circ$) of a factor of between 10 (for $\eta =0.1$) and 30 (for $\eta =1$). Correcting the age for inclination by multiplying by $\tan \alpha$ would only help significantly for flows close to the plane of the sky. In the extreme case where $v_{\rm min} = 7$  km s-1, the error on age is decreased due to the resulting higher mean velocity.

As a result of the overestimate in the age, the molecular thrust is very significantly underestimated. The typical error is again quite large, with the median estimate being a factor of 20 too low for both values of $\eta $. Similar errors are found for a low-velocity cut-off at $v_{\rm min} = 7$  km s-1, the smaller amount of observable momentum roughly compensating for the shorter ages.

It is interesting to note that the only instance where global age estimates are actually quite accurate is when the flow is closely aligned to the line of sight. This is because the "length'' of the flow lobe on the sky is then the same as its half-width, which expands at a velocity close to $\langle v\rangle_{\rm lobe}$ in our simulations (cf. Sect. 3.6.4). The thrust is then much better estimated as well. However, a pole-on inclination is statistically very unlikely.

   
3.6.2 Local method

Table 5: Inferred ages and thrusts of the outflow using the local method of Lada & Fich (1996) with the velocity ranges 2-40  km s-1 and 7-40  km s-1. The quantities are normalized to the true age and molecular thrust of the outflow. Errors on the total (molecular+atomic) thrust may be obtained by multiplying the relevant numbers by 0.45 ( $\eta =0.1$) or 0.26 ($\eta =1$).

Table 6: Inferred ages and thrusts of the outflow using the $v_{\rm max}$ method of Cabrit & Bertout (1992) and using the velocity ranges 2-40  km s-1 and 7-40  km s-1. The quantities are normalized to the true age and molecular thrust of the outflow. Errors on the total (molecular+atomic) thrust may be obtained by multiplying the relevant numbers by 0.45 ( $\eta =0.1$) or 0.26 ($\eta =1$).

Table 7: Inferred ages and thrusts of the outflow using the perpendicular method and using the velocity ranges 2-40  km s-1 and 7-40  km s-1. The quantities are normalized to the true age and molecular thrust of the outflow. Errors on the total (molecular+atomic) thrust may be obtained by multiplying the relevant numbers by 0.45 ( $\eta =0.1$) or 0.26 ($\eta =1$).


  \begin{figure} \par\includegraphics[width=8cm,clip]{figures/6921fig6.eps} \end{figure} Figure 6: Frequency distribution of the intensity-weighted local dynamical imescales for both the $\eta =0.1$ simulation (top panel) and the $\eta =1$ simulation (bottom panel). Each plot contains the distribution resulting for both $30^\circ $ and $60^\circ $ to the plane of the sky. The number of counts is the number of pixels with projected area on the sky of $1\times 10^{16}$ cm2 ($\approx $10-5 pc2) and the bin-size is 1500 yr.
Open with DEXTER

Figure 6 contains histograms of the frequency distributions of the "local'' timescales calculated from Eq. (13) in both the $\eta =1$ and $\eta =0.1$ simulations for an angle to the plane of the sky of $30^\circ $ and $60^\circ $. These simulated results show a fairly peaked distribution, as observed by Lada & Fich (1996) (their Fig. 5). The peaks move to smaller timescales as the flow is viewed more pole-on, as expected from projection effects.

We have performed these calculations for a number of different spatial resolutions on the sky and find that the results are not strongly dependent on this. The results shown here are for a resolution of 1016 cm ($\approx $ $ 3\times10^{-3}$ pc) on the sky. Table 5 lists the inferred timescales (i.e. the peak of the histogram) and the resulting thrusts.

The local method is found to perform better than the global method. This occurs because most points in the flow have $r_{\rm proj} < L_{\rm lobe}$, yielding shorter timescales (cf. Eq. (13)). However, the ages are still generally overestimated, with a median error of 7.5-13.5 for a typical cut-off velocity $v_{\rm min}$ = 2  km s-1. The errors are again strongly dependent on the inclination angle of the flow, and are reduced only if the flow is close to the line of sight (or if $v_{\rm min}$ is large). Once again we are left with a method which strongly overestimates the age of the outflow, by an order of magnitude typically.

The molecular thrust calculated from Eq. (14) is also better than that obtained with the global method, but is still significantly underestimated (except again in pole-on flows). The median error on molecular thrust is an underestimate by a factor of 5-7 for $v_{\rm min}$ = 2  km s-1, and by a factor of 10-15 for $v_{\rm min}$ = 7  km s-1. Correcting for inclination (assuming $\alpha$ is perfectly known) would reduce the median errors by a factor of around 3.5. For other inclinations, the associated correction would not seem to improve the situation significantly, leading to an overestimate for flows very close to the plane of the sky and an underestimate for flows viewed almost pole-on.

   
3.6.3 The $v_{{\max}}$ method

Values of $v_{\rm max}$ for our simulations were measured at 1/100 of the CO intensity level at $v_{\rm min}$, and are listed in Table 3. The resulting range $\simeq$6-35  km s-1 is typical of observed $v_{\rm max}$ values reported for "standard'' low-velocity CO outflows, excluding localized extremely high-velocity features (e.g. Cabrit & Bertout 1992; Beuther et al. 2002). Table 6 contains the inferred ages and thrusts using Eqs. (15) and (16) and the values of $m_{\rm observed}$ from Table 3. The thrusts were corrected for velocity gradients and projection effects by inter/extrapolating linearly as a function of $i = \pi/2 - \alpha$ the mean correction factors $\Delta\log F_{\rm CO}(i)$ listed in Table 1 of Cabrit & Bertout (1992). The adopted correction factors (in Log10) are thus 0.45, -0.15, -0.35, and -0.65 for $\alpha = 0$$^\circ$, 30$^\circ$, 60$^\circ$, and 90$^\circ$.

Since $v_{\rm max}$ is closer than $\langle v\rangle_{\rm lobe}$ to the true bow advance speed, this method of age estimate is a clear improvement over the local and global methods. The median error is an overestimate by a factor of 2-8 only for $v_{\rm min}$ = 2  km s-1, and even less when $v_{\rm min}$ = 7  km s-1. However there is still a marked inclination dependence, and the age becomes underestimated when the flow is close to the line of sight, due to foreshortening in  $L_{\rm lobe}$.

The molecular thrusts calculated using this method are also better than for the two previous methods. For $v_{\rm min}$ = 2  km s-1, the median error is 0.5-0.7. This is reassuring, given that the adopted inclination corrections were "calibrated'' on highly simplified kinematic outflow models (Cabrit & Bertout 1990). Because of this mismatch, the variation of error with inclination angle is not completely compensated for, but it is reduced (a factor of 2-8, compared to a factor of 20-100 if the correction were not applied). As a result, the error on molecular thrust is less than a factor of 2, except in the $\eta =0.1$ flow viewed edge-on. When $v_{\rm min}$ = 7  km s-1, the thrust underestimate is more significant (median factor of 5-8), though again not as severe as with the previous two methods.

The main limitation of this method remains the need for a reliable inclination estimate. Care must also be exercised, when using Eq. (16), to exclude from $v_{\rm max}$ any faint extremely high-velocity CO "bullets'' at 50-200  km s-1 closely associated with jet working surface(s) (Bachiller & Tafalla 1999): while such high values of  $v_{\rm max}$ would give much better age estimates (being close to the true advance speed of the bow head), they would lead to greatly overestimating the momentum and thrust in the bulk of the swept-up gas (respectively $\propto$ $v_{\rm max}$ and $\propto$ $ v_{\rm max}^2$ in this method).

   
3.6.4 A better method to estimate the flow age and thrust

It is clear from observations of molecular outflows that a very large amount of the material in the outflow is moving rather slowly. If the jet-driven model of molecular outflows is accepted then this slow moving material will be along the wings of the bowshock, and will have predominantly transverse motions. The characteristic length appropriate to measure the age is then the half-width of the lobe - i.e. the perpendicular distance from the jet axis, $R_{\rm lobe}$, rather than the distance from the jet source.

Consider an element of fluid in the ambient medium close to the axis of the jet. As the bowshock, driven by the jet head, sweeps up this element of fluid, a thermal pressure gradient perpendicular to the jet axis is set up. This drives the fluid element away from the jet axis (see Sect. 1). Once the element has propagated a distance significantly greater than the jet radius away from the jet axis, it begins to coast with constant momentum as it no longer feels a significant pressure gradient. Its movement away from the jet axis, as part of the the bow wing, thus becomes progressively slower as it sweeps up more ambient gas along its path. In this case we must account for the fact that the velocity of expansion measured at a given time is lower than the expansion velocity at any previous time. Hence, the bow is younger than one would calculate from its current expansion speed and width. As demonstrated by Masson & Chernin (1993), Wilkin (1996), and Ostriker et al. (2001), the bowshock wings expand asymptotically as $R \propto t^{1/3}$, hence the transverse expansion speed varies with width as $v_\perp(t) \propto t^{-2/3} \propto R(t)^{-2}$. One then finds that the time taken to expand to the current half-width R is

                 t = 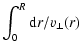$\displaystyle \int_0^R {\rm d}r/v_\perp(r)$  
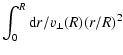  = $\displaystyle \int_0^R {\rm d}r/v_\perp(R) (r/R)^2$  
  = $\displaystyle (1/3) R/v_\perp(R).$ (14)

Taking the intensity-weighted velocity, $\langle v\rangle_{\rm lobe}$, as an estimate of the transverse expansion speed, we may thus compute an alternative "perpendicular'' dynamical timescale:

 \begin{displaymath}t_\perp = \frac{1}{3}\frac{R_{\rm lobe}}{\langle v\rangle_{\rm lobe}}, \end{displaymath} (15)

where $R_{\rm lobe}$ is the maximum outflow radius, measured perpendicular from the jet axis. The molecular thrust obtained with this "perpendicular'' method is estimated as

 \begin{displaymath}F_{\perp} = \frac{P_{\rm blue} + P_{\rm red}}{t_\perp}\cdot \end{displaymath} (16)

Note that $R_{\rm lobe}$ is the same as $L_{\rm lobe}$ when $\alpha = 90\hbox{$^\circ$ }$, so this method will be similar to the global method in pole-on flows, except for the factor of 1/3.

Table 7 shows the inferred age of the outflow, $t_\perp$, and the corresponding molecular thrust, $F_\perp$, normalized to their actual values. We can see that this "perpendicular'' method performs extremely well when compared with any of the previous methods, when $v_{\rm min} = 2$ km s-1. For example, when $\alpha = 0^\circ$, all other methods overestimate the age by a factor of 10 or more, while this method is correct to within 12-17%. The median error is also smaller for this method, with the estimated age being only 9%-36% too low. The largest error, which occurs for an outflow aligned with the line of sight, results in an underestimate of less than a factor of 2.5. The thrusts are also generally more accurate than any other method, especially in highly inclined flows, since timescales are now more accurately determined.

In the extreme case where the molecular cloud shows a lot of broadening, and the cutoff is at $v_{\rm min}$ = 7 km s-1, $t_\perp$underestimates the age by a factor of 3 ($\eta =1$) to 5 ( $\eta =0.1$), independent of inclination. However, the molecular thrust is still better estimated than with any of the other methods, as the shorter flow age partly compensates for the smaller amount of observable momentum at $v \ge$ $v_{\rm min}$.

A further attractive feature of this method is that the inclination dependence of the estimated parameters is relatively minor, as the transverse radius $R_{\rm lobe}$ does not change with inclination, and $\langle v\rangle_{\rm lobe}$ and $P_{\rm blue} + P_{\rm red}$ generally do not vary by more than a factor of 2 (see Table 3). Hence no correction for the flow inclination (which in itself is an uncertain quantity) is required, unlike in the $v_{\rm max}$ method.

The only uncertainty in age in this method is thus introduced by the low-velocity cut-off $v_{\rm min}$, which affects $\langle v\rangle_{\rm lobe}$through the power-law shape of m(v). However, the thrust appears much less affected.

   
3.7 Range of applicability of our results

Our conclusion that dynamical timescales overestimate the age of jet-driven flows appears to contradict the statistics of Class I outflow surveys, which suggest that dynamical ages underestimate the true outflow lifetimes by an order of magnitude (Parker et al. 1991). There is a simple explanation for this discrepancy: We have assumed in our calculations that the flow is young enough that the full length of the bowshock is observable in CO. On the other hand, the discovery of giant, parsec-scale optical outflows from many Class I sources has revealed that their jets have broken well out of their parent molecular cloud (see Reipurth and Bally 2001, for a review). The CO lobes are thus severely truncated compared to the full flow extent, and in this case CO dynamical timescales may indeed be shorter than the source age. This fact resolves the apparent contradiction noted by Parker et al. (1991) without the need to invoke a static CO cavity. It should be noted that the sources of Parker et al. (1991) were selected to be in isolated dark globules, all much less than 1 pc in size, hence one expects the jet to have left the cloud in $1\times10^4$ yr, and all the associated CO flows to be truncated.

One might think that our new "perpendicular'' method for estimating the flow age should remain applicable even in Class I sources as it relies only on the transverse lobe width, which is unaffected by truncation. However, the sideways expansion of bow wings decays as $v_\perp(t) \propto t^{-2/3}$, hence at an age of 105 yr it will fall well below the measurable limit $v_{\rm min}$, while the intensity-weighted $\langle v\rangle_{\rm lobe}$ will remain greater than $v_{\rm min}$ by construction. The assumption of the "perpendicular'' method that $v_\perp \simeq \langle v\rangle_{\rm lobe}$ may thus no longer be valid for Class I jet-driven flows. Another (reverse) problem is that some Class I flows exhibit unexpectedly high expansion speeds, with in a few cases perpendicular timescales $\simeq$104 yr much shorter than the source age, e.g. in L43-RNO91 (Lee & Ho 2005). This phenomenon probably requires an additional uncollimated wind component at late evolutionary stages, not included in the present study.

Therefore, our conclusions about age determinations are not applicable to Class I flows and remain limited to the youngest jet-driven outflows from Class 0 sources.

The situation is slightly different regarding thrust estimates in Class I flows: in a truncated CO flow, the relevant time to compute the thrust injected into the molecular lobe will not be the full lifetime of the jet, but only the time it took for the jet to propagate over the CO lobe length $L_{\rm lobe}$ before leaving the cloud. We would thus expect the thrust of truncated, jet-driven CO outflows to suffer similar underestimates as found here for younger flows. An alternative method to estimate thrust in truncated CO outflows has been proposed by Bontemps et al. (1996), involving the local momentum flux across a section of the lobe. The accuracy of this alternative method will be investigated in a forthcoming paper.

Another limitation of the scope of our results is that they are applicable only to outflows that propagate at relatively high speed of 60-135  km s-1 in the ambient medium. To our knowledge, the only reported measurements of proper motions at the tip of a CO molecular lobe are those obtained in optical and H2 lines in the HH47 counterflow (Eisloeffel & Mundt 1994; Micono et al. 1998). They indicate high proper motions of 150-260  km s-1 at the bow apex, consistent with the values of $\eta $ adopted in the present work. A much lower jet/ambient density contrast of 0.001-0.01 has been invoked by Richer et al. (1992) in the Orion B outflow to alleviate requirements on jet thrust. In such a regime, where the bowshock propagates at only 10-20  km s-1, the effect of dissociation would be negligible. However, such a low propagation speed implies a true age of $4 {-} 6 \times 10^4$ yr for the Orion B flow (Richer et al. 1992), which appears too long given the Class 0 status of the driving source FIR5 (André et al. 2000). Proper motion measurements of CO cavity tips other than HH47 would be highly desirable to verify which range of $\eta $ and propagation speed is relevant over the observable phase of Class 0 jet-driven flows.

   
4 Conclusions

We have investigated the accuracy of observational methods for inferring the physical parameters of young, purely jet-driven molecular outflows, dealing in detail with many of the usual assumptions made when making these calculations. The most important conclusions are the following:

The present results are applicable only to outflows around Class 0 sources, as we have assumed in our calculations that the driving jet has not yet left the parent molecular cloud. Biases in the age and thrust of truncated CO flows from older Class I sources will be the subject of a forthcoming paper. Our conclusions on dissociation and the determination of outflow ages also assume an ambient medium that is at most ten times denser than the jet, as inferred in typical Herbig-Haro objects. Hence the bow head propagates at relatively high speeds of 60-130  km s-1. Proper motion studies of outflow tips in Class 0 sources would be highly desirable to verify this hypothesis, and to improve age and thrust estimates. Large IR arrays and the ALMA interferometer should bring significant progress on this issue.

Acknowledgements
This work was partly funded by the CosmoGrid project, funded under the Programme for Research in Third Level Institutions (PRTLI) administered by the Irish Higher Education Authority under the National Development Plan and with partial support from the European Regional Development Fund. The present work was also supported in part by the European Community's Marie Curie Actions - Human Resource and Mobility within the JETSET (Jet Simulations, Experiments and Theory) network under contract MRTN-CT-2004 005592.

References

 
Copyright ESO 2007