A&A 471, 925-927 (2007)
DOI: 10.1051/0004-6361:20066909
H.-G. Ludwig
GEPI, CIFIST, Observatoire de Paris-Meudon, 5 place Jules Janssen, 92195 Meudon Cedex, France
Received 10 December 2006 / Accepted 6 May 2007
Abstract
Context. Spectral synthesis calculations based on three-dimensional stellar atmosphere models are limited by the affordable angular resolution of the radiation field. This hampers an accurate treatment of rotational line broadening.
Aims. We aim to find a treatment of rotational broadening of a spherical star when the radiation field is only available at a modest number of limb-angles.
Methods. We apply a combination of analytical considerations of the line-broadening process and numerical tests.
Results. We obtain a method which is closely related to classical flux convolution and which performs noticeably better than a previously suggested procedure. It can be applied to rigid as well as differential rotation.
Key words: hydrodynamics - radiative transfer - stars: atmospheres - line: profiles - methods: numerical
Spectral synthesis calculations based on time-series of three-dimensional (3D) background structures from hydrodynamical model atmospheres are computationally demanding and pose limits on the affordable resolution for representing the angular dependence of the radiation field. In such calculations, the number of employed azimuthal directions typically ranges from four to eight, the number of inclined directions representing the center-to-limb variation being between three and five. Obviously, the resolution is not high, and in particular makes an accurate implementation of rotational line broadening somewhat difficult. To our knowledge, the only published method handling rotational broadening in the 3D case is that of Dravins & Nordlund (1990). Here, we describe an alternative procedure which provides higher accuracy at similar computational complexity. It is closely related to standard flux convolution (e.g., Gray 1992). Its development was motivated by the demand for an accurate description of the rotational broadening of spectral lines in the solar spectrum (Caffau et al. 2007).
For the moment, we neglect differential rotation, and treat the star
as spherical and rigidly rotating. Local-box hydrodynamical model
atmospheres provide a statistical realization of a small patch of the surface
flow pattern. Formally, we want to obtain an estimate of the expectation value
of a rotationally broadened, disk-integrated line profile. Rotational symmetry
with respect to the stellar disk center implies that there is no azimuthal
dependence of the radiation field. All we need to know for evaluating the
disk-integrated rotationally broadened line profile are temporal and azimuthal
averages of the emergent radiation intensity of the local model as a function
of asterocentric angle ![]() .
Hence, the problem is equivalent to the
rotational line broadening problem in standard, plane-parallel model
atmospheres.
.
Hence, the problem is equivalent to the
rotational line broadening problem in standard, plane-parallel model
atmospheres.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{f1m6909.eps}
\end{figure}](/articles/aa/full/2007/33/aa6909-06/Timg5.gif) |
Figure 1:
Illustration of the apparent radial velocity distribution on a
stellar disk for solid body rotation: vertical lines of constant radial
velocity are labeled by their velocity in units of
|
| Open with DEXTER | |
We start by describing the procedure of Dravins & Nordlund (1990,
Sect. 2.1) who model rotational broadening as a superposition of line
profiles at various
![]() ,
broadened by the velocity field
along circles
,
broadened by the velocity field
along circles
![]() around the stellar disk center. We refer to
one of these circles as "
around the stellar disk center. We refer to
one of these circles as "![]() -circle'' (see Fig. 1). The
broadening effect of the projected rotational velocity along a
-circle'' (see Fig. 1). The
broadening effect of the projected rotational velocity along a ![]() -circle
located at
-circle
located at
![]() can be expressed as a convolution according to
can be expressed as a convolution according to
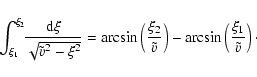 |
(3) |
The original implementation of Dravins & Nordlund did not use a formulation
as convolution but a discrete integration over ![]() -circles using polar
coordinates. While mathematically equivalent to Eq. (1), it
somewhat obscures the critical role of the most extreme velocities on a
-circles using polar
coordinates. While mathematically equivalent to Eq. (1), it
somewhat obscures the critical role of the most extreme velocities on a
![]() -circle for the smoothness of the rotationally broadened spectrum.
-circle for the smoothness of the rotationally broadened spectrum.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f2m6909.eps}
\end{figure}](/articles/aa/full/2007/33/aa6909-06/Timg26.gif) |
Figure 2:
Rotationally broadened line profiles (solid lines) for different total numbers of
asterocentric angles
|
| Open with DEXTER | |
Figure 2 illustrates the result of a test of Dravins & Nordlund's procedure. We broadened an artificial Gaussian line profile with a
rotational speed
![]() of three times the line's Doppler width. The
rotational speed was chosen to be particularly critical. Effects of smaller
rotational velocities become less pronounced due to the smoothing by the
Gaussian line profile, at larger rotational speeds deviations are less
conspicuous since less localized. For the test case we assumed that the
relative line shape is independent of
of three times the line's Doppler width. The
rotational speed was chosen to be particularly critical. Effects of smaller
rotational velocities become less pronounced due to the smoothing by the
Gaussian line profile, at larger rotational speeds deviations are less
conspicuous since less localized. For the test case we assumed that the
relative line shape is independent of ![]() ,
and that the intensity in the
continuum follows a linear limb-darkening law with a limb-darkening
coefficient of 0.6. Hence, standard flux convolution can be applied to obtain
the exact disk-integrated line profile. Figure 2 shows
the convergence of the numerical approximation towards the exact result with
an increasing total number of limb-angles
,
and that the intensity in the
continuum follows a linear limb-darkening law with a limb-darkening
coefficient of 0.6. Hence, standard flux convolution can be applied to obtain
the exact disk-integrated line profile. Figure 2 shows
the convergence of the numerical approximation towards the exact result with
an increasing total number of limb-angles
![]() .
As evident in the figure,
noticeable deviations between the exact and the numerical result are present
up to and including
.
As evident in the figure,
noticeable deviations between the exact and the numerical result are present
up to and including
![]() .
.
The major reason for the "wiggly'' behavior of the broadened line profile
shown in Fig. 2 are the pronounced spikes in the integrand in
Eq. (1). One can reduce their impact by associating a given
![]() not only with an infinitely thin
not only with an infinitely thin ![]() -circle but with a
-circle but with a
![]() -ring (see Fig. 1) of finite extent. The
contribution
-ring (see Fig. 1) of finite extent. The
contribution
![]() to the rotationally broadened flux profile stemming
from the stellar disk area subtended by
to the rotationally broadened flux profile stemming
from the stellar disk area subtended by
![]() is
given by the convolution
is
given by the convolution
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f3m6909.eps}
\end{figure}](/articles/aa/full/2007/33/aa6909-06/Timg39.gif) |
Figure 3: As for Fig. 2 for our broadening procedure. |
| Open with DEXTER | |
Figure 3 illustrates the outcome of this procedure. A comparison with
Fig. 2 shows a more rapid convergence towards the exact result.
The improvement is related to the fact that the new method can at least handle
exactly the simple case of a globally ![]() -independent intensity which is not
the case for the method of Dravins and Nordlund. One could further refine it
by introducing an analytical expression for the
-independent intensity which is not
the case for the method of Dravins and Nordlund. One could further refine it
by introducing an analytical expression for the ![]() -dependence of the
intensity in each
-dependence of the
intensity in each ![]() -ring - perhaps motivated from a fit to the continuum
intensity available at the discrete
-ring - perhaps motivated from a fit to the continuum
intensity available at the discrete
![]() .
However, we did not implement
this since from the test it appeared that the accuracy at an
affordable number of
.
However, we did not implement
this since from the test it appeared that the accuracy at an
affordable number of
![]() is already sufficient. There is a caveat to
this statement: the accuracy of the methods also hinges on the level of the
differential line-shift and -broadening as a function of
is already sufficient. There is a caveat to
this statement: the accuracy of the methods also hinges on the level of the
differential line-shift and -broadening as a function of ![]() which we did
not test here. This should be checked on a case by case basis.
which we did
not test here. This should be checked on a case by case basis.
Up to this point we considered solid body rotation only. However, the previous
discussion made clear that integration over ![]() -rings should also perform
better in the case of differential rotation. The referee made the point that
putting efforts into 3D model and spectral synthesis calculations warrants the
inclusion of effects of differential rotation to maintain highest level of accuracy.
In the following we give a brief demonstration that differential rotation on
the level observed in the Sun can indeed be relevant for resulting line
profiles. We implemented our method for a case of differential rotation.
-rings should also perform
better in the case of differential rotation. The referee made the point that
putting efforts into 3D model and spectral synthesis calculations warrants the
inclusion of effects of differential rotation to maintain highest level of accuracy.
In the following we give a brief demonstration that differential rotation on
the level observed in the Sun can indeed be relevant for resulting line
profiles. We implemented our method for a case of differential rotation.
We chose the possibly simplest parameterization of the solar
differential rotation pattern of the form
Figure 4 depicts an example comparing rotationally broadened
profiles assuming rigid as well as differential rotation. We arbitrarily
selected an Fe I line (at 6082 Å) of a 3D spectral synthesis
calculation for the Sun, and solar-like rotational parameters,
V=1.8 km s-1,
![]() ,
and for the case of differential
rotation
,
and for the case of differential
rotation
![]() .
The plot shows that - as expected - our procedure of
integrating over
.
The plot shows that - as expected - our procedure of
integrating over ![]() -circles (here
-circles (here ![]() )
leaves no obvious imprint of
spikes in the resulting profiles. Moreover, noticeable differences are present
for fixed V and
)
leaves no obvious imprint of
spikes in the resulting profiles. Moreover, noticeable differences are present
for fixed V and ![]() .
One might interpret the smaller degree of
broadening in the differentially rotating case as simply a result of the
the smaller disk-averaged rotation rate for
.
One might interpret the smaller degree of
broadening in the differentially rotating case as simply a result of the
the smaller disk-averaged rotation rate for
![]() .
However,
from Eq. (6) we obtain for the root-mean-square radial
velocity
.
However,
from Eq. (6) we obtain for the root-mean-square radial
velocity
![]() due to the rotation over the stellar disk
due to the rotation over the stellar disk
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f4m6909.eps}
\end{figure}](/articles/aa/full/2007/33/aa6909-06/Timg53.gif) |
Figure 4: Comparison of rotational broadening assuming a rigidly (solid line) and differentially (diamonds) rotating Sun. Thirty times enlarged differences of the resulting profiles (in the sense differential-rigid) are plotted in the lower part of the panel. For further explanations see text. |
| Open with DEXTER | |
The approach suggested in this paper provides an accurate treatment of rotational line broadening of a spherical star employing intensities at a modest number of limb-angles only. This is of practical importance in the context of 3D spectral synthesis calculations where angular resolution is computationally expensive. This also holds for differential rotation but the rotational kernel functions must be evaluated numerically. Our approach is not restricted to the 3D case but could be equally well applied in the standard 1D case. The issue is of course less pertinent in 1D since high angular resolution is affordable making the broadening method uncritical.
Acknowledgements
We thank Ansgar Reiners for helpful discussions about differential rotation. The work was funded by EU grant MEXT-CT-2004-014265 (CIFIST).