A&A 471, 381-384 (2007)
DOI: 10.1051/0004-6361:20077069
The correlations between the spin frequencies and kHz QPOs
of neutron stars in LMXBs
(Research Note)
H. X. Yin1 - C. M. Zhang1 - Y. H. Zhao1 - Y. J. Lei2 -
J. L. Qu2 - L. M. Song2 - F. Zhang2
1 - National Astronomical Observatories,
Chinese Academy of Sciences, Beijing 100012, PR China
2 -
Astronomical Institute, Institute of High Energy Physics,
Chinese Academy of Sciences, Beijing 100039, PR China
Received 9 January 2007 / Accepted 7 May 2007
Abstract
Aims. We studied the correlations between spin frequencies and kilohertz quasi-periodic oscillations (kHz QPOs) in neutron star low-mass X-ray binaries.
Methods. The updated data on kHz QPOs and spin frequencies are statistically analyzed.
Results. We find that when two simultaneous kHz QPOs are present in the power spectrum, the minimum frequency of upper kHz QPO is at least 1.3 times higher than the spin frequency, i.e.
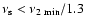 .
We also find that the average kHz QPO peak separation in 6 Atoll sources anti-correlates with the spin frequency in the form
.
We also find that the average kHz QPO peak separation in 6 Atoll sources anti-correlates with the spin frequency in the form
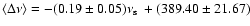 Hz. If we shift this correlation in the direction of the peak separation by a factor of 1.5, this correlation matches the data points of the two accretion-powered millisecond X-ray pulsars, SAX J1808.4-3658 and XTE J1807-294.
Hz. If we shift this correlation in the direction of the peak separation by a factor of 1.5, this correlation matches the data points of the two accretion-powered millisecond X-ray pulsars, SAX J1808.4-3658 and XTE J1807-294.
Key words: X-rays: binaries - accretion, accretion disks - stars:
neutron
Since the launch of the Rossi X-Ray Timing Explorer (RXTE) ten
years ago, kilohertz quasi-periodic oscillations (kHz QPOs) have
been detected in about thirty neutron star low-mass X-ray binaries
(NS/LMXBs; see van der Klis 2006, for a recent review). The kHz QPOs
often occur in pairs, the upper-frequency (
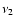 )
and the
lower-frequency (
)
and the
lower-frequency (
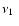 ).
These kHz QPOs appear in four categories of NS/LMXBs, i.e. the
bright Z sources, the less luminous Atoll sources (see Hasinger &
van der Klis 1989, for the definition of Atoll and Z classes),
accretion-powered millisecond X-ray pulsars (AMXPs), and other
unidentified sources (see e.g., van der Klis 2006, and references
therein). The kHz QPOs and other observed characteristic frequencies
in these sources follow tight correlations among each other (e.g.,
Psaltis et al. 1998, 1999a,b; Stella et al. 1999; Belloni et al. 2002, 2005, 2007; Zhang et al. 2006a).
).
These kHz QPOs appear in four categories of NS/LMXBs, i.e. the
bright Z sources, the less luminous Atoll sources (see Hasinger &
van der Klis 1989, for the definition of Atoll and Z classes),
accretion-powered millisecond X-ray pulsars (AMXPs), and other
unidentified sources (see e.g., van der Klis 2006, and references
therein). The kHz QPOs and other observed characteristic frequencies
in these sources follow tight correlations among each other (e.g.,
Psaltis et al. 1998, 1999a,b; Stella et al. 1999; Belloni et al. 2002, 2005, 2007; Zhang et al. 2006a).
A 401 Hz coherent pulsation and a near 401 Hz X-ray burst
oscillation frequency are found in SAX J1808.4-3658 (Chakrabarty et al. 2003; Wijnands et al. 2003), suggesting that the burst frequency is equal to the spin frequency (
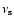 )
in this object
(e.g., Strohmayer & Bildsten 2003; Wijnands et al. 2003;
Muno 2004).
In some sources showing both twin kHz QPOs and spin
frequencies, the peak separation (
)
in this object
(e.g., Strohmayer & Bildsten 2003; Wijnands et al. 2003;
Muno 2004).
In some sources showing both twin kHz QPOs and spin
frequencies, the peak separation (
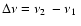 )
is generally
inconsistent with being equal to the spin frequency (e.g. Méndez
& van der Klis 1999; Jonker et al. 2002a).
But the ratio between the peak separation and spin frequency
clusters at around
)
is generally
inconsistent with being equal to the spin frequency (e.g. Méndez
& van der Klis 1999; Jonker et al. 2002a).
But the ratio between the peak separation and spin frequency
clusters at around 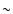 1 or
1 or 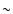 0.5 (e.g., Wijnands et al. 2003;
Wijnands 2005; Linares et al. 2005; Zhang et al. 2006b).
0.5 (e.g., Wijnands et al. 2003;
Wijnands 2005; Linares et al. 2005; Zhang et al. 2006b).
In this research note, we
study the relation between kHz QPOs and spin frequencies.
From 35 NS/LMXBs with the kHz QPOs and/or spin frequencies, 21(6)
sources show twin (single) kHz QPOs, and 22 sources show spin or/and
burst frequencies (7 spin and 17 burst sources; see Table 1).
Table 1:
List of LMXBs with the simultaneously detected twin kHz QPOs or spin frequencies.
In Fig. 1 we plot the distribution of the 22 spin frequencies with an
average value of 440.8 Hz.
For the 8 sources with both twin kHz QPOs and spin frequencies, the
ratio between the minimum upper-frequency and the spin frequency is
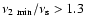 .
If the upper-frequency is interpreted as the Keplerian frequency at
the inner edge of the accretion disk (Miller et al. 1998;
van der Klis 2000, 2006), this lower limit means that the inner edge of
disc penetrates inside the corotation radius where the Keplerian
frequency equals the spin frequency.
If this applies to the other kHz QPO sources, we can use the
relation
.
If the upper-frequency is interpreted as the Keplerian frequency at
the inner edge of the accretion disk (Miller et al. 1998;
van der Klis 2000, 2006), this lower limit means that the inner edge of
disc penetrates inside the corotation radius where the Keplerian
frequency equals the spin frequency.
If this applies to the other kHz QPO sources, we can use the
relation
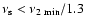 to constrain their spin
frequencies. For example, we could obtain upper limits of spin
frequencies for the 8 Z sources and 5 Atoll sources with
simultaneously detected twin kHz QPOs but with unknown spin
frequencies (see the inferred upper limits of spin frequencies for
these sources in Table 1).
to constrain their spin
frequencies. For example, we could obtain upper limits of spin
frequencies for the 8 Z sources and 5 Atoll sources with
simultaneously detected twin kHz QPOs but with unknown spin
frequencies (see the inferred upper limits of spin frequencies for
these sources in Table 1).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7069fig1.eps}\end{figure}](/articles/aa/full/2007/32/aa7069-07/Timg18.gif) |
Figure 1:
Distribution of the spin frequencies of the 22 neutron
stars in LMXBs. |
| Open with DEXTER |
Table 2:
List of the sources with spin frequencies and peak
separations.
We also notice that, when only a single kHz QPO is detected as in 4U
1608-52 (van Straaten et al. 2003) and 4U 1728-34 (van Straaten et
al. 2002), these QPOs do not satisfy the relation
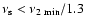 .
We argue that this relation only holds when two simultaneous kHz
QPOs are detected, Our proposal would be ruled out if a pair of kHz
QPOs were found and
.
We argue that this relation only holds when two simultaneous kHz
QPOs are detected, Our proposal would be ruled out if a pair of kHz
QPOs were found and
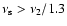 .
.
The sonic-point beat-frequency model (Miller et al. 1998) predicted
a constant 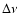 equal to the stellar spin frequency, whereas the
sonic-point and spin-resonance model by Lamb & Miller (2003)
predicts that the kHz QPO peak separation should be approximately
equal to one or half the spin frequency considering that the disk
flow at the spin-resonant radius is smooth or clumped.
To confirm the above conjecture, we average the value of peak
separations and plot
equal to the stellar spin frequency, whereas the
sonic-point and spin-resonance model by Lamb & Miller (2003)
predicts that the kHz QPO peak separation should be approximately
equal to one or half the spin frequency considering that the disk
flow at the spin-resonant radius is smooth or clumped.
To confirm the above conjecture, we average the value of peak
separations and plot
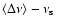 diagram for the six Atoll
sources and two AMXPs in Fig. 2.
We notice that for the sources (XTE J1807-294, 4U 1702-43, 4U
1728-34, and 4U 1915-05) with
diagram for the six Atoll
sources and two AMXPs in Fig. 2.
We notice that for the sources (XTE J1807-294, 4U 1702-43, 4U
1728-34, and 4U 1915-05) with
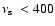 Hz
Hz
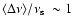 ,
whereas for those (SAX J1808.4-3658, 4U 1608-52, 4U 1636-53, and 4U
1731-28) with
,
whereas for those (SAX J1808.4-3658, 4U 1608-52, 4U 1636-53, and 4U
1731-28) with
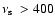 Hz
Hz
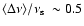 .
Alternatively, the relation between the averaged peak separation and
spin frequency of the six Atoll sources (
.
Alternatively, the relation between the averaged peak separation and
spin frequency of the six Atoll sources (
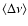 and
and
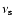 )
can be fitted by a linear relation
)
can be fitted by a linear relation
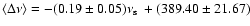 Hz (Fig.
2). The relation that crosses the points of the two AMXPs
is the same relation as for the Atoll sources divided by 1.5 along
the y direction.
Hz (Fig.
2). The relation that crosses the points of the two AMXPs
is the same relation as for the Atoll sources divided by 1.5 along
the y direction.
If the above anti-correlation between
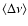 and
and
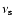 is
real, we can use it to infer the averaged kHz QPO peak separations
of sources, such as EXO 0748-676 (
is
real, we can use it to infer the averaged kHz QPO peak separations
of sources, such as EXO 0748-676 (
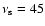 Hz), XB 1254-690
(
Hz), XB 1254-690
(
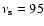 Hz), and XTE J1739-285 (
Hz), and XTE J1739-285 (
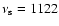 Hz) to be
around 380 Hz, 370 Hz, and 160 Hz, respectively. However, this
anti-correlation is still a conjecture since it is based on data
from only six sources. But if this result were confirmed, it means
that the spin frequency would play a role in the mechanism that
produces the kHz QPOs, but a different one from the one so far
proposed. Further measurements of kHz QPOs in the accretion powered
millisecond X-ray pulsars are required to uncover the role of the
spin of the neutron star in the mechanism that produces the kHz
QPOs.
Hz) to be
around 380 Hz, 370 Hz, and 160 Hz, respectively. However, this
anti-correlation is still a conjecture since it is based on data
from only six sources. But if this result were confirmed, it means
that the spin frequency would play a role in the mechanism that
produces the kHz QPOs, but a different one from the one so far
proposed. Further measurements of kHz QPOs in the accretion powered
millisecond X-ray pulsars are required to uncover the role of the
spin of the neutron star in the mechanism that produces the kHz
QPOs.
![\begin{figure}
\includegraphics[width=8.5cm,clip]{7069fig2.eps}\end{figure}](/articles/aa/full/2007/32/aa7069-07/Timg35.gif) |
Figure 2:
Plot of
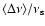 vs.
vs.
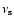 .
The solid curve stands
for .
The solid curve stands
for
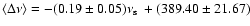 Hz, and the
dashed curve is the result of shifting the solid curve down by a
factor of 1.5 along the direction of the peak separation. Hz, and the
dashed curve is the result of shifting the solid curve down by a
factor of 1.5 along the direction of the peak separation. |
| Open with DEXTER |
Our main conclusions are the following.
- (1)
- We find that for the 8 sources for which twin kHz QPOs and spins
are known, the minimum upper-frequency is at least 1.3 times higher
than the spin frequency, i.e.
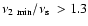 .
This relation
might be used to estimate the spin frequencies of sources with twin
kHz QPOs.
.
This relation
might be used to estimate the spin frequencies of sources with twin
kHz QPOs.
- (2)
- In 6 Atoll sources, the averaged peak separation anti-correlates
with the spin frequency as
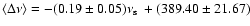 Hz, although their
ratios cluster roughly around either 1 or 0.5 as reported (van der
Klis 2006). This correlation would also apply to the two AMXPs (SAX
J1808.4-3658 and XTE J1807-294) if in this cases the peak separation
is divided by a factor of 1.5 (see Fig. 2). It is noted that this
kind of shifting of about 1.5 is required to reconcile the
frequency-frequency correlation of the AMXPs and the Atoll and Z
sources (see van Straaten et al. 2005; Linares
et al. 2005). This factor 1.5 remains unexplained, but it could
reflect a different stellar magnetic field strength or magnetic
angle between the magnetic polar axis and rotational axis between
these types of sources.
Hz, although their
ratios cluster roughly around either 1 or 0.5 as reported (van der
Klis 2006). This correlation would also apply to the two AMXPs (SAX
J1808.4-3658 and XTE J1807-294) if in this cases the peak separation
is divided by a factor of 1.5 (see Fig. 2). It is noted that this
kind of shifting of about 1.5 is required to reconcile the
frequency-frequency correlation of the AMXPs and the Atoll and Z
sources (see van Straaten et al. 2005; Linares
et al. 2005). This factor 1.5 remains unexplained, but it could
reflect a different stellar magnetic field strength or magnetic
angle between the magnetic polar axis and rotational axis between
these types of sources.
If the above correlations between the spin frequency and kHz QPOs
were confirmed in the future, it implies that the kHz QPOs are
related to the spin frequencies of neutron stars in some manner.
Thus, the spin frequency would play a role in the twin kHz QPO
production (indirectly perhaps), and any successful model of kHz
QPOs should have to take these relations into account.
Usually, we consider the production of kHz QPO to be related to the
magnetosphere radius defined by the instantaneous accretion rate,
then the spin frequency should be involved with the magnetosphere
radius defined by the long-term accretion rate (matched with the
different magnetic B-field when considering Atoll and Z), which is
almost stable in a short observational time. The instantaneous
accretion rate varies around the long-term accretion rate, which
accounts for the variation of kHz QPOs, thus the "averaged'' QPO
variation would be related to the spin frequency. Therefore, in the
sense of the average treatment, the kHz QPO has a relation to the
spin frequency.
Acknowledgements
We thank T. Belloni, M. Méndez, D. Psaltis, S. Boutloukos, and
J. Homan for providing the QPO data. Discussions with J. Petri, P.
Rebusco, J. Horák, V. Karas, S. Boutloukos, T.P. Li, and S.N.
Zhang are highly appreciated. This research has been supported by
the innovative project of CAS of China. We are very grateful for the
comments from M. Méndez.
- Belloni,T.,
Psaltis, D., & van der Klis, M. 2002, ApJ, 572, 392 [NASA ADS] [CrossRef] (In the text)
- Belloni, T.,
Méndez, M., & Homan, J. 2005, A&A, 437, 209 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Belloni, T.,
Méndez, M., & Homan, J. 2007, MNRAS
[arXiv:astro-ph/0702157]
(In the text)
- Bhattacharyya, S. 2006
[astro-ph/0605510]
- Bhattacharyya, S., Strohmayer, T.
E., Markwardt, C. B., et al. 2006, ApJ, 639, L31 [NASA ADS] [CrossRef]
- Boutloukos, S., van der Klis, M.,
Altamirao, D., et al. 2006, ApJ, 653, 1435 [NASA ADS] [CrossRef]
- Chakrabarty, D. 2004
[arXiv:astro-ph/0408004]
- Chakrabarty, D., Morgan, E. H., Muno,
M. P., et al. 2003, Nature, 424, 42 [NASA ADS] [CrossRef] (In the text)
- Di Salvo, T.,
Méndez, M., & van der Klis, M. 2003, A&A, 406,
177 [NASA ADS] [CrossRef] [EDP Sciences]
- Hasinger,
G., & van der Klis, M. 1989, A&A, 225, 79 [NASA ADS]
- Homan, J. 2006,
private communication
- Homan, J., &
van der Klis, M. 2000, ApJ, 539, 847 [NASA ADS] [CrossRef]
- Homan, J., van der
Klis, M., Jonker, P. G., et al. 2002, ApJ, 568, 878 [NASA ADS] [CrossRef]
- Jonker, P. G.,
van der Klis, M., Wijnands, R., et al. 2000, ApJ, 537, 374 [NASA ADS] [CrossRef]
- Jonker, P. G.,
Méndez, M., & van der Klis, M. 2002a, MNRAS, 336, L1 [NASA ADS] (In the text)
- Jonker, P. G.,
van der Klis, M., Homan, J., et al. 2002b, MNRAS, 333, 665 [NASA ADS]
- Kaaret, P.,
Zand, J .J. M. i., Heise, J., et al. 2002, ApJ, 575,1018
- Kaaret, P.,
Zand, J .J. M. i., Heise, J., et al. 2003, ApJ, 598, 481 [NASA ADS] [CrossRef]
- Kaaret, P.,
Morgan, E. H., Vanderspek, R., et al. 2005, ApJ, 638, 963 [NASA ADS] [CrossRef]
- Kaaret, P.,
Prieskorn, Z., in't Zand, J., et al. 2007, ApJ, 657, L97 [NASA ADS] [CrossRef]
- Lamb, F. K., &
Miller, M. C. 2003, [arXiv:astro-ph/0308179]
(In the text)
- Linares, M.,
van der Klis, M., Altamilano, D., et al. 2005, ApJ, 634, 1250 [NASA ADS] [CrossRef] (In the text)
- Markwardt,
C. B., Strohmayer, T. E., & Swank, J. H. 1999, ApJ, 512,
L125 [NASA ADS] [CrossRef]
- Méndez, M.,
& van der Klis, M. 1999, ApJ, 517, L51 [NASA ADS] [CrossRef]
- Méndez, M.,
& van der Klis, M. 2000, MNRAS, 318, 938 [NASA ADS]
- Méndez, M.,
van der Klis, M., Wijnands, R., et al. 1998, ApJ, 505, L23 [NASA ADS] [CrossRef]
- Migliari,
S., van der Klis, M., & Fender, R. 2003, MNRAS, 345, L35 [NASA ADS]
- Miller, M. C.,
Lamb, F. K., & Psaltis, D. 1998, ApJ, 508, 791 [NASA ADS] [CrossRef] (In the text)
- Muno, M. P. 2004,
AIPC, 714, 239 [NASA ADS] (In the text)
- O'Neill, P.
M., Kuulkers, E., Sood, R. K., et al. 2002, MNRAS, 336, 217 [NASA ADS]
- Psaltis, D.,
Mendez, M., Wijnands, R., et al. 1998, ApJ, 501, L95 [NASA ADS] [CrossRef] (In the text)
- Psaltis, D.,
Wijnands, R., Homan, J., et al. 1999a, ApJ, 520, 763 [NASA ADS] [CrossRef] (In the text)
- Psaltis, D.,
Belloni, T., & van der Klis, M. 1999b, ApJ, 520, 262 [NASA ADS] [CrossRef]
- Stella, L.,
Vietri, M., & Morsink, S. 1999, ApJ, 524, L63 [NASA ADS] [CrossRef] (In the text)
- Strohmayer, T., & Bildsten, L. 2003
[arXiv:astro-ph/0301544]
(In the text)
- Strohmayer, T. E., Jahoda, K., Giles, A.
B., et al. 1997, ApJ, 486, 355 [NASA ADS] [CrossRef]
- van der
Klis, M. 2000, ARA&A, 38, 717 [NASA ADS] (In the text)
- van der
Klis, M. 2006, Compact stellar X-ray sources (Cambridge University
Press), 39 [arXiv:astro-ph/0410551]
(In the text)
- van
Straaten, S., Ford, E. C., van der Klis, M., et al. 2000, ApJ, 540,
1049 [NASA ADS] [CrossRef]
- van
Straaten, S., van der Klis, M., Di Salvo, T., et al. 2002, ApJ,
568, 912 [NASA ADS] [CrossRef]
- van
Straaten, S., van der Klis, M., & Méndez, M. 2003, ApJ,
596, 1155 [NASA ADS] [CrossRef]
- van
Straaten, S., van der Klis, M., & Wijnands, R. 2005, ApJ, 619,
455 [NASA ADS] [CrossRef] (In the text)
- Wijnands,
R., 2005, [arXiv:astro-ph/0501264]
(In the text)
- Wijnands,
R., Strohmayer, T. E., & Franco, L. M. 2001, ApJ, 549, 71 [NASA ADS] [CrossRef]
- Wijnands,
R., van der Klis, M., Homan, J., et al. 2003, Nature, 424, 44 [NASA ADS] [CrossRef] (In the text)
- Zhang, C. M.,
Yin, H. X., Zhao, Y. H., et al. 2006a, MNRAS, 366, 1373 [NASA ADS] (In the text)
- Zhang, F., Qu,
J. L., Zhang, C. M., et al. 2006b, ApJ, 646, 1116 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7069fig1.eps}\end{figure}](/articles/aa/full/2007/32/aa7069-07/Timg18.gif)
![\begin{figure}
\includegraphics[width=8.5cm,clip]{7069fig2.eps}\end{figure}](/articles/aa/full/2007/32/aa7069-07/Timg35.gif)