A&A 471, 113-125 (2007)
DOI: 10.1051/0004-6361:20077254
F. Boone1,2 - A. J. Baker3 - E. Schinnerer4 - F. Combes1 - S. García-Burillo5 - R. Neri6 - L. K. Hunt7 - S. Léon8 - M. Krips9 - L. J. Tacconi10 - A. Eckart11
1 - LERMA, Observatoire de Paris,
61 avenue de l'Observatoire, 75014 Paris, France
2 -
Max-Planck-Institut für Radioastronomie, auf dem Hügel 69, 53121 Bonn, Germany
3 -
Department of Physics and Astronomy, Rutgers, the State University of New Jersey, 136 Frelinghuysen Road, Piscataway, NJ 08854, USA
4 -
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117 Heidelberg, Germany
5 -
Observatorio Astronómico Nacional (OAN) - Observatorio de Madrid, C/ Alfonso XII 3, 28014 Madrid, Spain
6 -
Institut de Radio Astronomie Millimétrique,
300 rue de la Piscine, 38406 St. Mt. d'Hères, France
7 -
INAF-Istituto di Radioastronomia/Sezione,
Largo Enrico Fermi 5,
50125 Firenze, Italy
8 -
IRAM Pico Veleta Observatory,
Avenida Divina Pastora 7, Local 20, 18012 Granada, Spain
9 -
Harvard-Smithsonian Center for Astrophysics, SMA project, 645 N A`ohoku Pl., Hilo, HI 96720, USA
10 -
Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312, 85741 Garching, Germany
11 -
Physikalisches Institut, Universität zu Köln,
Zülpicherstrasse 77, 50937 Köln, Germany
Received 7 February 2007 / Accepted 17 May 2007
Abstract
This work is part of the NUGA survey of CO emission in nearby active galaxies. We present observations of NGC 4569, a member of the Virgo Cluster.
We analyse the molecular gas distribution and kinematics in the central region and we investigate a possible link to the strong starburst present at the nucleus. 70![]() of the
of the
![]()
![]()
![]() of molecular gas detected in the inner 20
of molecular gas detected in the inner 20
![]() is found to be concentrated within the inner 800 pc and is distributed along the large scale stellar bar seen in near-infrared observations. A hole in the CO distribution coincides with the nucleus where most of the H
is found to be concentrated within the inner 800 pc and is distributed along the large scale stellar bar seen in near-infrared observations. A hole in the CO distribution coincides with the nucleus where most of the H![]() emission and blue light are emitted.
The kinematics are modelled in three different ways, ranging from the purely geometrical to the most physical. This approach allows us to constrain progressively the physical properties of the galaxy and eventually to emerge with a reasonable fit to an analytical model of orbits in a barred potential. Fitting an axisymmetric model shows that the non-circular motions must be comparable in amplitude to the circular motions (120 km s-1). Fitting a model based on elliptical orbits allows us to identify with confidence the single inner Lindblad resonance (ILR) of the large scale bar. Finally, a model based on analytical solutions for the gas particle orbits in a weakly barred potential constrained by the ILR radius reproduces the observations well.
The mass inflow rate is then estimated and discussed based on the best fit model solution. The gravitational torques implied by this model are able to efficiently funnel the gas inside the ILR down to 300 pc, although another mechanism must take over to fuel the nuclear starburst inside 100 pc.
emission and blue light are emitted.
The kinematics are modelled in three different ways, ranging from the purely geometrical to the most physical. This approach allows us to constrain progressively the physical properties of the galaxy and eventually to emerge with a reasonable fit to an analytical model of orbits in a barred potential. Fitting an axisymmetric model shows that the non-circular motions must be comparable in amplitude to the circular motions (120 km s-1). Fitting a model based on elliptical orbits allows us to identify with confidence the single inner Lindblad resonance (ILR) of the large scale bar. Finally, a model based on analytical solutions for the gas particle orbits in a weakly barred potential constrained by the ILR radius reproduces the observations well.
The mass inflow rate is then estimated and discussed based on the best fit model solution. The gravitational torques implied by this model are able to efficiently funnel the gas inside the ILR down to 300 pc, although another mechanism must take over to fuel the nuclear starburst inside 100 pc.
Key words: galaxies: individual: NGC 4569 - galaxies: active - ISM: kinematics and dynamics
NUGA, for NUclei of GAlaxies (García-Burillo et al. 2003a), is a survey of nearby active galaxies aiming for a deep insight into the mechanisms responsible for feeding the nuclei of active galaxies. High resolution (down to 0.5'') and high sensitivity (rms of ![]() 2 mJy beam s-1 for 10 km s-1 channels) observations of 12 galaxies were obtained with the IRAM Plateau de Bure Interferometer (PdBI) and the IRAM 30 m telescope. The CO J = 1-0 and 2-1 transitions thus mapped allow us to study the dynamics of the molecular gas in the central kiloparsec of the galaxies with a linear resolution as high as
2 mJy beam s-1 for 10 km s-1 channels) observations of 12 galaxies were obtained with the IRAM Plateau de Bure Interferometer (PdBI) and the IRAM 30 m telescope. The CO J = 1-0 and 2-1 transitions thus mapped allow us to study the dynamics of the molecular gas in the central kiloparsec of the galaxies with a linear resolution as high as ![]() 10 pc.
10 pc.
The main results achieved by the NUGA project thus far can be summarized as follows:
NGC 4569 (M90) is a bright SAB(rs)ab galaxy at a distance of 17 Mpc (Bottinelli et al. 1983; Tully 1988) in the Virgo Cluster. A large scale bar is seen in NIR images (Laurikainen & Salo 2002) and is almost aligned with the major axis of the galaxy (PA = 15 ![]() according to Jogee et al. 2005). The galaxy harbours a nucleus of the transition type (type T2 in Ho et al. 1997) which exhibits, by far, the most pronounced nuclear starburst activity among the LINERs and transition nuclei with available UV data (Maoz et al. 1998). As such it became a prime target for studies of the origin of the ionization in transition nuclei. The presence of a supergiant-dominated starburst was established by Keel (1996). Barth & Shields (2000) demonstrated that a starburst with a large population of very hot Wolf-Rayet stars could produce the observed spectrum of the nucleus and AGN activity is ruled out by X-ray (Tschöke et al. 2001; Ho et al. 2001; Terashima et al. 2000) and radio observations (Neff & Hutchings 1992; Hummel et al. 1987). Gabel & Bruhweiler (2002) showed that for the starburst to be the only source of photoionization (no AGN) extreme conditions are required, with
according to Jogee et al. 2005). The galaxy harbours a nucleus of the transition type (type T2 in Ho et al. 1997) which exhibits, by far, the most pronounced nuclear starburst activity among the LINERs and transition nuclei with available UV data (Maoz et al. 1998). As such it became a prime target for studies of the origin of the ionization in transition nuclei. The presence of a supergiant-dominated starburst was established by Keel (1996). Barth & Shields (2000) demonstrated that a starburst with a large population of very hot Wolf-Rayet stars could produce the observed spectrum of the nucleus and AGN activity is ruled out by X-ray (Tschöke et al. 2001; Ho et al. 2001; Terashima et al. 2000) and radio observations (Neff & Hutchings 1992; Hummel et al. 1987). Gabel & Bruhweiler (2002) showed that for the starburst to be the only source of photoionization (no AGN) extreme conditions are required, with ![]() 5
5 ![]() 104 O and B stars squeezed into the inner 30 pc.
104 O and B stars squeezed into the inner 30 pc.
On larger scales Tschöke et al. (2001) detected a large soft X-ray emitting region above the disk of NGC 4569 which implies a large energy input into the halo. Hensler et al. (2003) reported on a bipolar outflow seen in X-rays and a giant outflow (![]() 10 kpc in length) to the western side of the galaxy in H
10 kpc in length) to the western side of the galaxy in H![]() (see also Bomans et al. 2007, submitted). Using the Effelsberg radio telescope at 4.85 GHz and 8.35 GHz, Chyzy et al. (2006) discovered large symmetric lobes of polarized radio emission extending up to 24 kpc from the galactic disk on each side of the nucleus. These lobes may have been powered by the nuclear starburst.
(see also Bomans et al. 2007, submitted). Using the Effelsberg radio telescope at 4.85 GHz and 8.35 GHz, Chyzy et al. (2006) discovered large symmetric lobes of polarized radio emission extending up to 24 kpc from the galactic disk on each side of the nucleus. These lobes may have been powered by the nuclear starburst.
H I line observations reveal that the galaxy is H I deficient compared to galaxies of similar type and it must have lost more than 90% of its atomic gas (Cayatte et al. 1990; Warmels 1988). This was most likely stripped due to rapid motion of the galaxy through the intracluster medium (Boselli et al. 2006; Vollmer et al. 2004).
Interferometric CO observations of NGC 4569 were presented in Helfer et al. (2003), Jogee et al. (2005) and Nakanishi et al. (2005). In this article, higher resolution and higher sensitivity CO(1-0) and, for the first time, CO(2-1) line observations are presented, and the analysis is focused on investigating a possible link between the molecular gas kinematics in the inner kiloparsec and the nuclear starburst. The observations are presented in Sect. 2. The gas kinematics are modeled based on analytical expressions for the gas orbits. Three different models are compared to the observations starting with a pure geometrical model and proceeding to more realistic models in Sect. 3. Comparing the different models to the observations allows us to progressively constrain the kinematic properties of the galaxy and emerge with a reasonable fit. The mass inflow due to gravitational torques based on the best fit version of the most realistic model is estimated in Sect. 4. The goal of this estimate is to quantify the possible contribution of the gravitational torques to the fueling of the nuclear starburst. The results are discussed in Sect. 5 and summarized in Sect. 6.
![\begin{figure}
\par\includegraphics[width=17.1cm,clip]{7254fig1.eps} \end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg20.gif) |
Figure 1:
a) CO(1-0) (grey scale) and CO(2-1) (contours) integrated maps with a clip at zero and no correction for primary beam attenuation. The color scale is given on the right hand-side in Jy beam-1 km s-1. The contours start at 4 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=13.35cm,clip]{7254fig2.ps}\vspace*{5mm}
\includegraphics[width=13.55cm,clip]{7254fig3CMJN.eps}\end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg21.gif) |
Figure 2:
CO(1-0) channel maps. The velocity relative to the systemic velocity of the galaxy (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=13.9cm,clip]{7254fig4.ps} \end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg22.gif) |
Figure 3:
CO(2-1) channel maps. The beam is 1.1'' |
| Open with DEXTER | |
The galaxy was observed with the IRAM Plateau de Bure Interferometer (PdBI) in 2003 (B and C configurations) and 2004 (A configuration) and with the IRAM 30 m telescope in 2004 in the CO(1-0) (115 GHz) and CO(2-1) (230 GHz) emission lines. The PdBI and 30 m telescope receiver characteristics, the observing setup and the observing procedures are the same as in Combes et al. (2004). The quasar 3C 273 was used for PdBI gain calibration. The maps obtained from the 30 m observations are used to compute the short spacings and complete the interferometric measurements using the SHORT-SPACE task in the GILDAS software (Guilloteau & Lucas 2000) as in Combes et al. (2004). The rms in 10 km s-1 wide channels is 3.9 and 5.4 mJy beam-1 for natural weighting and the beamsizes are 2.5'' ![]() 1.6'' and 1.1''
1.6'' and 1.1'' ![]() 0.7'' at 115 GHz and 230 GHz, respectively.
0.7'' at 115 GHz and 230 GHz, respectively.
Both CO(1-0) and CO(2-1) emission are distributed over a region 17'' ![]() 6'' in size (Figs. 1a,b) roughly aligned with the major axis of the galaxy (PA = 24 deg). The CO(1-0) distribution shows three peaks, one peak close to the center and two symmetrical peaks at
6'' in size (Figs. 1a,b) roughly aligned with the major axis of the galaxy (PA = 24 deg). The CO(1-0) distribution shows three peaks, one peak close to the center and two symmetrical peaks at ![]() 5'' from the center and aligned with the overall elongation. The south-western peak is the strongest. The central peak does not coincide with the dynamical center: it appears to be the top of a slightly curved ridge encircling a hole in the CO distribution centered
5'' from the center and aligned with the overall elongation. The south-western peak is the strongest. The central peak does not coincide with the dynamical center: it appears to be the top of a slightly curved ridge encircling a hole in the CO distribution centered ![]() 1'' northwest of the dynamical center. Since our observations have a S/N
1'' northwest of the dynamical center. Since our observations have a S/N ![]() 10 times higher than those presented by Nakanishi et al. (2005), a weaker continuous distribution is detected in addition to the three main peaks, even when going to the highest resolution in the CO(2-1) map.
10 times higher than those presented by Nakanishi et al. (2005), a weaker continuous distribution is detected in addition to the three main peaks, even when going to the highest resolution in the CO(2-1) map.
The integrated CO(1-0) flux within a radius of 20'' is 450 Jy km s-1 with an uncertainty due to calibration errors of 15![]() .
This is compatible with the fluxes measured by Nakanishi et al. (2005) and Jogee et al. (2005). The corresponding H2 mass is
.
This is compatible with the fluxes measured by Nakanishi et al. (2005) and Jogee et al. (2005). The corresponding H2 mass is
![]()
![]()
![]() using a conversion factor of X=2.2
using a conversion factor of X=2.2 ![]() 1020 cm-2 [K km s-1]-1 (Solomon & Barrett 1991). 70
1020 cm-2 [K km s-1]-1 (Solomon & Barrett 1991). 70![]() of this flux is concentrated within a radius of 10'' (
of this flux is concentrated within a radius of 10'' (![]() 800 pc).
800 pc).
The line-of-sight CO velocities span a range of 400 km s-1.
Channel maps are shown in Figs. 2 and 3. The most noticeable features are: (1) the distribution is fairly symmetric with respect to systemic velocity and dynamical center; (2) the emission is elongated in most of the channels (from -150 to +150 km s-1) along a direction close to that of the emission in the integrated map; (3) from one channel to the next as velocity increases, the elongated emission is slightly shifted toward the northwest; (4) the highest velocities (![]() 200 km s-1) are reached at
200 km s-1) are reached at ![]() 5'' from the nucleus, i.e. close to the two outer peaks in the integrated map; and (5) some low-level emission, mostly seen in the CO(1-0) channel maps (Fig. 2) outside the elongated core, seems to follow the "spider'' pattern of rotating disks, i.e. two "arms'' on each side of the major axis shift from the north at low velocities to the south at high velocities. To guide the eyes of the reader the two arms are emphasized with thick red lines drawn by hand and overlaid to the channel maps in the bottom panel of Fig. 2. Due to the low level of the signal these arms appear discontinuous and the spider pattern is not seen in the velocity field of Fig. 4 (the first moment mixes this low signal with the noise).
5'' from the nucleus, i.e. close to the two outer peaks in the integrated map; and (5) some low-level emission, mostly seen in the CO(1-0) channel maps (Fig. 2) outside the elongated core, seems to follow the "spider'' pattern of rotating disks, i.e. two "arms'' on each side of the major axis shift from the north at low velocities to the south at high velocities. To guide the eyes of the reader the two arms are emphasized with thick red lines drawn by hand and overlaid to the channel maps in the bottom panel of Fig. 2. Due to the low level of the signal these arms appear discontinuous and the spider pattern is not seen in the velocity field of Fig. 4 (the first moment mixes this low signal with the noise).
The fact that in individual channels the emission is elongated in a direction close to that of the major axis (PA = 24 deg) implies that significant amounts of gas must lie at "forbidden'' velocities, i.e. velocities of a given sign appear on both sides of the minor axis, as was noted by Jogee et al. (2005). The velocity field is shown in Fig. 4; it is clearly distorted compared to a disk with only circular rotation. In the central region a steep velocity gradient is running in a SE to NW direction, i.e. orthogonal to the major axis. The kinematic line of nodes is therefore orthogonal to the major axis. This steep gradient results from the continuous shift of the emission in the channel maps (feature (3) described above).
The CO(2-1)/(1-0) line ratio was computed after tapering the 230 GHz data and restoring it with the same beam as for the 115 GHz data; the ratio map is shown Fig. 1b. The values are in the range 0.3-1.1 in temperature units. The highest values are reached in the ridge between the central and the southern peaks near the hole in CO. A high line ratio corresponds to high density and/or high temperature gas. A possible interpretation is that the molecular gas in the ridge is being compressed and heated by the nuclear starburst. This interpretation would also be consistent with the presence of a hole in the molecular gas distribution: part of the molecular gas undergoing this pressure might have been dissociated or pushed out of the disk. A fraction of the initial molecular gas in the center must also have been consumed by star formation. The high ratio in the southern peak could be either due to a star forming region or a kinematic shock resulting from the asymmetrically perturbed gravitational potential.
A composite color map from B, V and H broad band images and the V-I color map from HST observations are presented in Fig. 5. Dust lanes are clearly seen along the bar, which in NIR observations extends up to a radius of ![]() 5 kpc (Laurikainen & Salo 2002). The bar appears to be aligned with the major axis of the galaxy, like the CO emission, as noted by Jogee et al. (2005). Also striking is the difference in extinction between the eastern and western sides of the galaxy. This confirms that the near side, i.e. the side that appears as the most extinguished because of a low contribution from foreground bulge stars, is the western side. This geometry is consistent with the spiral arms being trailing as in most spiral galaxies. The two outer CO(1-0) peaks coincide with peaks in dust extinction, the southern one being the more prominent both in extinction and CO(1-0) emission. The central CO(1-0) peak does not coincide with any extinction peak, and the hole in the CO(1-0) distribution close to the location of the nucleus has blue optical colors. This agreement suggests that most of the starburst is concentrated within a region of
5 kpc (Laurikainen & Salo 2002). The bar appears to be aligned with the major axis of the galaxy, like the CO emission, as noted by Jogee et al. (2005). Also striking is the difference in extinction between the eastern and western sides of the galaxy. This confirms that the near side, i.e. the side that appears as the most extinguished because of a low contribution from foreground bulge stars, is the western side. This geometry is consistent with the spiral arms being trailing as in most spiral galaxies. The two outer CO(1-0) peaks coincide with peaks in dust extinction, the southern one being the more prominent both in extinction and CO(1-0) emission. The central CO(1-0) peak does not coincide with any extinction peak, and the hole in the CO(1-0) distribution close to the location of the nucleus has blue optical colors. This agreement suggests that most of the starburst is concentrated within a region of ![]() 100 pc in radius, supporting the hypothesis that the hole in the CO(1-0) emission is a consequence of this concentrated starburst having consumed or expelled the molecular gas from the center. The latter interpretation is further supported by an HST H
100 pc in radius, supporting the hypothesis that the hole in the CO(1-0) emission is a consequence of this concentrated starburst having consumed or expelled the molecular gas from the center. The latter interpretation is further supported by an HST H![]() image (Pogge et al. 2000) which shows strong emission south of the hole and several features elongated toward the east (Fig. 1c). Some H
image (Pogge et al. 2000) which shows strong emission south of the hole and several features elongated toward the east (Fig. 1c). Some H![]() emission is expected due to the ionizing stars of the starburst but part of it might also trace the impact of the starburst on the ISM and the elongated features to the east are suggestive of an outflow perpendicular to the plane. The east side being the far side, the counter-outflow (i.e. emerging from the other side of the plane) might be obscured and therefore not visible in H
emission is expected due to the ionizing stars of the starburst but part of it might also trace the impact of the starburst on the ISM and the elongated features to the east are suggestive of an outflow perpendicular to the plane. The east side being the far side, the counter-outflow (i.e. emerging from the other side of the plane) might be obscured and therefore not visible in H![]() ,
although again visible further to the west as reported by Hensler et al. (2003).
,
although again visible further to the west as reported by Hensler et al. (2003).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7254fig5.eps} \end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg25.gif) |
Figure 4: First moment map of the CO(1-0) emission. Regions with low S/N are masked out. The contour levels are spaced by 10 km s-1. The color scale is given on the right hand-side in km s-1. |
| Open with DEXTER | |
How can the CO emission described in the previous section be interpreted in terms of the radial distribution and kinematics of the molecular gas in the plane of the galaxy? The two outer peaks seen in the integrated map could be due to a ring or to concentrations at the ends of a nuclear bar. The elongated shape seen in the channel maps could result from radial motions (streaming motions inside a density wave or due to shocks at the ends of a bar) or to elongated orbits. To discriminate among these possible interpretations and obtain a quantitative understanding of the deprojected gaseous disk, three different kinematic models are compared to the observations. The approach followed is progressive, starting with a pure geometrical model and proceeding to more "physical'' models, i.e. with more physical underlying hypotheses used to compute the molecular gas motions. This approach allows us to constrain the physical properties of the galaxy step by step and thus to converge more efficiently to a reasonable solution. This is more efficient because the most physical model is very sensitive to variations of the parameters and therefore more difficult to fit without a priori constraints.
Table 1: Circular model parameters.
The first model is based on circular orbits with additional radial motions, while the second model is constructed from elliptical orbits. These are purely geometrical hypotheses, and reality is expected to be more complex. However, the symmetry of the CO emission in the datacube (i.e. with respect to the dynamical center and the systemic velocity) suggests the gas flow is well organized and dominated by m = 2 modes. Thus, if we assume a pure m = 2 symmetry, comparing the observations to the first model can help to quantify the amplitude of non-circular motions and estimate to what extent they can be reproduced by pure radial motions. Comparison to the second model allows us to evaluate the alternative interpretation of non-circular motions, namely the possibility that the clouds populate near-to-closed orbits that are elongated. The third model is based on analytical solutions for gas particle orbits in a barred potential.
![\begin{figure}
\par\includegraphics[width=16.3cm,clip]{7254fig6.ps} \end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg26.gif) |
Figure 5: Left: RGB color image synthesized from B, V and H broad band images obtained from Observatoire de Haute Provence (OHP) and retrieved from the Goldmine database (Gavazzi et al. 2003). North is up and East is left. Right: V-I color index from HST WFPC2-camera observations ( F555W and F814W filters, proposal 05375). The color scale is such that high V-I index appears in yellow and low V-I in blue. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{7254fig7.ps}\includegraphi...
...clip]{7254fig25.ps}\includegraphics[width=4.1cm,clip]{7254fig26.ps} \end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg27.gif) |
Figure 6:
Each row shows a 50'' |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.38cm,clip]{7254fig27.eps}\includegra...
....1mm}
\includegraphics[height=4.05cm,width=4.6cm,clip]{7254fig34.ps}\end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg28.gif) |
Figure 7: Integrated maps ( first row) and first moment maps ( second row) for a) the observed data, b) the axisymmetric model, c) the ellipse orbit model and d) the barred potential model. In the observations, the velocity field can only be computed where the signal-to-noise ratio is high enough, i.e. within a chevron shaped field. For comparison we used the same mask when computing the velocity fields from the models. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.45cm,clip]{7254fig35.eps}\includegra...
...clip]{7254fig36.ps}\includegraphics[width=4.9cm,clip]{7254fig37.ps} \end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg29.gif) |
Figure 8:
Deprojected integrated CO(1-0) emission of a) the axisymmetric model, b) the ellipse orbit model and c) the barred potential model. We recall that, at 17 Mpc, 1'' |
| Open with DEXTER | |
The first two models are entirely specified by a radially varying set of properties similar to that of the widely used "tilted ring model'' (Rogstad et al. 1974). The values of the parameters are specified at some galactocentric radii and linearly interpolated between those radii. The number of radii where the parameter values are specified and their values can be chosen freely, giving us the ability to reproduce any radial distribution to a good approximation. Simulated data cubes are produced by randomly assigning gas particles to the disk according to the distributions specified, projecting them in the datacube and convolving by the synthesized beam. As most of the emission comes from within the PdBI primary beam full width at half maximum (
![]() at 115 GHz), the effect of primary beam attenuation is neglected. For more details about the fitting procedure see Appendix A.1.
at 115 GHz), the effect of primary beam attenuation is neglected. For more details about the fitting procedure see Appendix A.1.
The parameters of the axisymmetric model (see details in Appendix A.2) reproducing the main features of the observations with 7 radii are listed in Table 1. The corresponding channel maps for 5 velocities are shown in the second column of Fig. 6, while the corresponding integrated intensity and velocity maps are shown in Fig. 7b. A face-on view of the model is shown in Fig. 8a.
The three peaks in the integrated map are reproduced by a ring with mean galactocentric radius of ![]() 600 pc and a central concentration. The column density must be higher by a factor of
600 pc and a central concentration. The column density must be higher by a factor of ![]() 10 inside the ring (at 600 pc) with respect to the density at 300 pc and 700 pc. The column density must increase again inside a radius of 300 pc to reach a value higher by a factor of
10 inside the ring (at 600 pc) with respect to the density at 300 pc and 700 pc. The column density must increase again inside a radius of 300 pc to reach a value higher by a factor of ![]() 15 at the center. The distribution of the CO emission in the channel maps requires an inward radial velocity of 120 km s-1 in the ring at 600 pc. Lower radial velocities in the ring fail to reproduce the data.
15 at the center. The distribution of the CO emission in the channel maps requires an inward radial velocity of 120 km s-1 in the ring at 600 pc. Lower radial velocities in the ring fail to reproduce the data.
This model can reproduce the shape of the CO emission in the channel maps at all velocities. The slight shift of the emission toward the northwest from channel to channel and, as a consequence, the twisted isovelocity lines are also well reproduced (compare Fig. 7a with 7b). Moreover, the ring interpretation provides a natural explanation for the fact that the elongated shape is aligned with the major axis of the galaxy: it is merely an inclination effect. The width of the emission along the minor axis, however, is larger than in the observations, and the two symmetrical peaks are not as highly contrasted as observed. Also, the radial velocity in the ring required to reproduce the observations is extremely high and cannot be interpreted as the manifestation of real radial motions.
We conclude from this first modeling that, although a ring of 600 pc radius with a central concentration can explain to some extent the spatial distribution of the CO emission, the amplitude of the non-circular motions is unrealistically high, i.e. comparable to the amplitude of the rotation motions. No physics could explain the collapse of a ring at this speed. This result implies that pure radial motions alone cannot explain the departures from circular rotation, which must be at least partly due to the shapes of the orbits themselves. Paradoxically, while the best fit solution of the circular model reproduces the observations well, it implies that the model is not a good representation of reality and that elongated orbits must be considered.
Although elongated orbits are not expected to be elliptical in general, ellipses provide a first order approximation to any non-circular closed or nearly-closed shape. To estimate a possible contribution from the orbit elongation to the non-circular motions and to get a picture of the orientations of the orbits in the galactic plane (the orbit pattern) we fit a model in which the gas particles populate elliptical orbits and their angular momentum is constant over the orbit. "Nearly-closed'' orbits means orbits that are stable on the time scale of a rotation period, which is possible only if the orbits do not intersect, since otherwise the cloud shocks would re-orient the gas on different orbits. Thus, for this model to be self-consistent, the variations in position angle and ellipticity must satisfy this "no crossing'' condition. The density of clouds on a given orbit is not uniform. If it were assumed independent of the rotation sense it would be inversely proportional to the velocity. However, it is known that molecular clouds are formed in density waves or shocks, from which stars form that then destroy the parent cloud. The density is therefore expected to increase abruptly when entering the density wave or shock and to decrease smoothly after. In this simple model, density waves correspond to overdensities due to orbit crowding, i.e. are kinematic waves: they form at the aphelia of the ellipses when the position angles change with radius. To mimic the formation/destruction of the clouds we apply an exponential taper to the density. The application of this taper significantly improves the model fit. More details about this model are given in Appendix A.3.
The parameters of such a model best reproducing the observations with 10 radii are listed in Table 2. The corresponding channel maps for 5 velocities are shown in the third column of Fig. 6, while the corresponding integrated map and velocity field are shown in Fig. 7c. The face-on view of the model solution is shown in Fig. 8b and the orbital pattern in Fig. 9a.
Strong variations in the column density, the angular momentum, the orbit orientations and the velocity dispersion are required at a radius of ![]() 600 pc to reproduce the peaks in the integrated map and the shape of the distribution in the channel maps. As in the previous model the column density must increase by an order of magnitude at
600 pc to reproduce the peaks in the integrated map and the shape of the distribution in the channel maps. As in the previous model the column density must increase by an order of magnitude at ![]() 600 pc, however inside the
600 pc, however inside the ![]() 600 pc radius the column density only drops by a factor of 4. A central concentration is still required within the innermost 150 pc. The angular momentum must decrease abruptly inside
600 pc radius the column density only drops by a factor of 4. A central concentration is still required within the innermost 150 pc. The angular momentum must decrease abruptly inside ![]() 600 pc. The velocity dispersion must be
600 pc. The velocity dispersion must be ![]() 40 km s-1 at
40 km s-1 at ![]() 600 pc. The most remarkable result is that to reproduce the elongated core in the channel maps, it is necessary to invert the variation of the orbit position angles at the same radius of the column density peak (in the range 500-600 pc). The orbit position angle must be maximum at this radius and equal to
600 pc. The most remarkable result is that to reproduce the elongated core in the channel maps, it is necessary to invert the variation of the orbit position angles at the same radius of the column density peak (in the range 500-600 pc). The orbit position angle must be maximum at this radius and equal to ![]()
![]() .
This feature of the orbit pattern seems to be strongly constrained by the observations.
.
This feature of the orbit pattern seems to be strongly constrained by the observations.
From Fig. 6 it can be seen that the low level emission is well reproduced by this model, giving us confidence that this emission is real and that the rotation velocity of the disk at 5.5 kpc is ![]() 220 km s-1. This value is consistent with the estimates of Guhathakurta et al. (1988) based on H I observations and Rubin et al. (1999) based on optical observations.
220 km s-1. This value is consistent with the estimates of Guhathakurta et al. (1988) based on H I observations and Rubin et al. (1999) based on optical observations.
The main differences between the observed and the modeled channel maps occur at high velocities, with the model being unable to reproduce the emission closest to the center seen up to ![]() 150 km s-1. Moreover the model cannot reproduce the continuous shift of the emission to the northwest and therefore the central velocity gradient present in the velocity field.
150 km s-1. Moreover the model cannot reproduce the continuous shift of the emission to the northwest and therefore the central velocity gradient present in the velocity field.
Table 2: Elliptical orbit model parameters.
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{7254fig38.eps}\hspace*{3mm...
....eps}\hspace*{3mm}\includegraphics[width=5.7cm,clip]{7254fig40.eps} \end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg32.gif) |
Figure 9:
Orbit patterns in the inner 1.5 kpc of the elliptical orbit model ( left) and the barred potential model ( middle). Right-hand side: resonance diagram, with the rotation frequency ( |
| Open with DEXTER | |
Table 3: Barred potential model parameters.
In addition, to obtain emission that is spatially elongated up to high velocities, we must set a velocity dispersion of at least 40 km s-1 in the ring. This is a high velocity dispersion, a fraction of this may come from a shock, but beam averaging of the velocities at the ends of the orbits can also be expected to contribute significantly. This consideration implies that the real orbits must have sharper ends than ellipses.
The orbit pattern and the face-on view of the emission strongly resemble gas kinematics in a barred potential as observed in many galaxies. The large gradient of the orbit position angle at 600 pc mimics a tightly wounded spiral forming a ring. The change in sign of the gradient of the position angle is a remarkable feature that is known to occur at the Inner Lindblad Resonance (ILR) when there is only one, or between ILRs when there are two of them (see e.g. Wada 1994). The fact that this feature coincides with a column density peak, which is expected at resonances, indicates that this is actually a single ILR.
The two symmetric peaks in the face-on integrated map and the large velocity dispersion at the resonance would then correspond to the shocks frequently observed at the locations of dust lanes in bars, which are due to the crowding of orbits that favors cloud collisions (see e.g. Combes 1996).
Identification of the ILR is further supported by the orientation of the bar inferred from the model, which is similar to that of the large scale stellar bar.
Indeed, the shocks are expected to lead the bar (see e.g. Combes 1996), which would therefore have a position angle somewhere between 0 and 30 ![]() (see Fig. 8 and see also the maximum value for the orbit position angle in Table 2: 210
(see Fig. 8 and see also the maximum value for the orbit position angle in Table 2: 210 ![]() =
=
![]() ). This is consistent with the large scale stellar bar position angle of 15
). This is consistent with the large scale stellar bar position angle of 15 ![]() (Jogee et al. 2005). This agreement implies that the resonance observed is unlikely to result from the action of an inner bar, but is rather the ILR of the large scale bar.
(Jogee et al. 2005). This agreement implies that the resonance observed is unlikely to result from the action of an inner bar, but is rather the ILR of the large scale bar.
Is this interpretation supported by a model based on gas orbits in a barred potential? Why is the velocity field with the strong velocity gradient twist in the center not reproduced? Is this due to the elliptical approximation of the orbits or are pure radial motions (as opposed to radial motions intrinsic to non-circular but closed orbits) also contributing? To answer these questions, we compare the observations to a model based on analytical solutions for the gas orbits in a barred potential.
This model was introduced and developed by Sanders & Huntley (1975), Lindblad & Lindblad (1994), Wada (1994), Sakamoto et al. (1999) and Baker (2000). It is based on analytical solutions for the orbits of gas particles obtained by a perturbation calculation of the epicyclic stellar motions.
The potential is described by an axisymmetric component and a weak m = 2 perturbation. The perturbation has the same radial profile as the axisymmetric component and is modulated by a sine in azimuth. The amplitude of the perturbation relative to the axisymmetric component is defined as the strength of the bar. For the radial profile of the potential we use the logarithmic shape. This choice is justified by the ratio of the resonance radii. Indeed, the corotation radius of the large scale bar, assumed to be 1.2 times the bar extension, is ![]() 5 kpc according to Laurikainen & Salo (2002) and according to the elliptical orbit model the ILR radius is 600 pc, implying
5 kpc according to Laurikainen & Salo (2002) and according to the elliptical orbit model the ILR radius is 600 pc, implying
![]()
![]() 8. As shown in Appendix B, for a logarithmic potential this ratio is 6.3. For comparison a Plummer potential gives a ratio of
8. As shown in Appendix B, for a logarithmic potential this ratio is 6.3. For comparison a Plummer potential gives a ratio of ![]() 3 (Wada 1994).
3 (Wada 1994).
As in Baker (2000), two dissipation terms are introduced that characterize the damping of radial and azimuthal oscillations and are assumed to reproduce the dissipative behavior of gas particles. These terms cause the major axis of the orbits to lead the bar, the offset being maximal at the ILR. The limitations of the model are (1) it is singular at corotation; (2) the epicyclic motions used to compute the perturbations are based on the axisymmetric component only so that the model is not fully self-consistent; and (3) computing closed orbits assuming dissipation rates is not self-consistent, because dissipative particles imply open orbits. As a consequence, the radii of the resonances obtained with this model (Appendix B) cannot be taken as accurate results. However, this can be seen as a first order approximation that works only when the real orbits are near to being closed. In this case the resonance radii obtained give a basic picture of the scales involved. The orbit patterns produced by this model exhibit some of the main features expected in barred potentials, e.g., the elongated orbits, the phase shift change at an ILR, and the spiral pattern. Also, they match observations and results of numerical simulations (see Lindblad & Lindblad 1994). This analytical approach should be particularly suitable for NGC 4569 which, as noted in Sect. 2, is rather symmetric and dominated by an m = 2 component in CO and shows a weak stellar bar in the NIR (Laurikainen & Salo 2002). The results of the elliptical orbit fit allow us to fix some of the parameters describing the potential. More details about this model are given in Appendix A.4.
The best fit parameters for 7 radii, including the parameters fixed by the results of the elliptical orbit fit, are listed in Table 3. Some of the channel maps of the simulated data are shown in the last column of Fig. 6; the integrated map and velocity field are shown in Fig. 7d. The face-on view of the model solution is shown in Fig. 8c and the orbital pattern in Fig. 9.
The best fit bar position angle of 20 ![]() is consistent with the large scale stellar position angle of 15
is consistent with the large scale stellar position angle of 15 ![]() derived by Jogee et al. (2005). This result confirms the conclusion drawn from the elliptical orbit model, namely that the kinematics inside the inner kiloparsec are driven by the gravitational potential of the large scale stellar bar
derived by Jogee et al. (2005). This result confirms the conclusion drawn from the elliptical orbit model, namely that the kinematics inside the inner kiloparsec are driven by the gravitational potential of the large scale stellar bar![]() .
.
For this model as for the others, a column density jump of an order of magnitude is required at a radius of 600 pc and a central concentration of similar column density is required. A velocity dispersion of 30 km s-1 is required at the radius of the column density increase. Although this is still a high value, it is less than for the elliptical orbit model because the orbits have much sharper ends (Fig. 9) that contribute significantly to the velocity dispersion through beam averaging. This suggests that the orbit shapes in this model are more realistic than the ellipses.
As can be seen in Fig. 6, this model reproduces the data better than the elliptical orbit model, especially at high velocities. The low level emission is not so well reproduced but this is expected as this model diverges at corotation, making it unreliable at large radii. The velocity field (Fig. 7) is also the closest to the data when compared with the two other models discussed above.
The fact that an analytical model that includes certain physical assumptions (about the potential shape and gas properties) reproduces the data well lends support to its underlying assumptions. In particular, the interpretation of the column density increase at 600 pc as an ILR of the large scale bar is well confirmed by this fit. This also supports the assumption that there is only one ILR or that the ILR region is small with little space for x2 orbits. If there were two ILRs, the gradient of the orbit position angle would change in sign at a similar radius (in the middle of the 2 ILRs as described in Wada 1994), but the maximum position angle of the orbits would be much greater, leading to a much greater position angle for the oval ring unlikely to fit the observations equally well. The good fit also shows that even though this model is not fully self-consistent, the orbit pattern and orbit shapes favored by its best-fitting version may be reasonably close to reality. We note that the configuration of the orbit pattern implies that the velocity field is very sensitive to the orbit shapes. Indeed, the most elongated orbits are almost aligned with the major axis (the bar is almost aligned with the major axis), and the strongest velocity components are therefore orthogonal to the line of sight. As a consequence the velocity field is not only dominated by the elongation of the orbits but it is also sensitive to the orbit shapes, i.e. how the velocity vectors behave at the ends of the orbits. This can explain why the difference between the ellipses and these more realistic orbits implies a significant difference in the velocity field.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{7254fig41.ps}\hspace*{9mm}...
...43.ps}\hspace*{6mm}\includegraphics[width=7.2cm,clip]{7254fig44.ps} \end{figure}](/articles/aa/full/2007/31/aa7254-07/Timg34.gif) |
Figure 10:
a) Net gravity torque, b) radial velocity, c) radial velocity gradient and d) mass accumulation rate versus characteristic radius of the orbits (see Sect. 4 for details). All the quantities computed for the maximum bar strength,
|
| Open with DEXTER | |
Two mechanisms contribute to angular momentum dissipation and mass inflow: gravitational torques, which depend on the potential and on the individual gas orbit shapes and orientations, and viscosity torques, which depend on the cloud-cloud collision rate and on the interstellar turbulence. In the previous section the observed molecular gas kinematics were successfully modeled by analytical solutions for gas particle orbits in a barred potential. We now address the question of the mass inflow based on this model solution.
As the potential of the model solution is known at each point in the galaxy, the gravitational torque can be directly computed for each particle following Eq. (C.2). In addition, as the orbits are known, the torques can be integrated over the orbits to estimate the angular momentum loss over a rotation (Eq. (C.4)) as well as the corresponding radial velocity of the matter inflow (Eq. (C.6)). As already outlined, this approach is not fully self-consistent, since the orbits should not be closed if the angular momentum changes over a rotation, but the angular momentum loss thus computed can be considered as a first order approximation to the case where orbits are nearly closed, i.e., the angular momentum loss due to the gravitational torque is a small fraction of the angular momentum. The good fit of the model to the observations suggests that, on average, the molecular gas in the inner kiloparsec lies in this regime.
The torque is proportional to the bar strength, which is only poorly constrained by the "weak bar'' regime requirement (see discussion Appendix A.4), to ![]() < 0.05. This implies that only upper limits can be derived for the mass inflow. Figure 10 shows the net torque (as defined Eq. (C.3)) for
< 0.05. This implies that only upper limits can be derived for the mass inflow. Figure 10 shows the net torque (as defined Eq. (C.3)) for ![]() = 0.05 on the top left, and the corresponding radial velocity on the top right. Both curves look similar, because the radial change of the angular momentum as determined by the axisymmetric potential is almost constant above 500 pc (see Eq. (C.6)). Due to their circular shape, the orbits with a characteristic radius less than 300 pc undergo no net torque and as a consequence the large scale bar would not be able to fuel the nuclear starburst on these scales via gravitational torques only. The maximum radial velocity is of order 10 km s-1 and occurs for the orbit with a characteristic radius of 650 pc, i.e. at the ILR. The value of this upper limit for the radial velocities is consistent with our working hypothesis, namely, that to first order, radial motions can be neglected compared to rotational motions, consistent with the results of Wong et al. (2004). The variations of the radial velocity, shown on the bottom left of Fig. 10, imply that the radial flow is not steady over the disk and as a consequence that matter must accumulate in some orbits and be depleted in others. The actual mass flow also depends on the gas mass available at each radius (the radial velocity would directly translate into mass flow only if the gas mass did not depend on the radius, i.e., for a column density profile following R-1). Nevertheless, without any assumption about the radial density profile, the variation of the radial velocity shows that the gas will tend to be depleted just outside the ILR (the inward velocity increases with decreasing radius down to 600 pc) and to accumulate inside the ILR (the inward velocity decreases with decreasing radius inside 600 pc). This model is therefore consistent with the formation of rings at ILR as observed in many spiral galaxies (Buta & Combes 1996) and often used as a signature of the ILR.
= 0.05 on the top left, and the corresponding radial velocity on the top right. Both curves look similar, because the radial change of the angular momentum as determined by the axisymmetric potential is almost constant above 500 pc (see Eq. (C.6)). Due to their circular shape, the orbits with a characteristic radius less than 300 pc undergo no net torque and as a consequence the large scale bar would not be able to fuel the nuclear starburst on these scales via gravitational torques only. The maximum radial velocity is of order 10 km s-1 and occurs for the orbit with a characteristic radius of 650 pc, i.e. at the ILR. The value of this upper limit for the radial velocities is consistent with our working hypothesis, namely, that to first order, radial motions can be neglected compared to rotational motions, consistent with the results of Wong et al. (2004). The variations of the radial velocity, shown on the bottom left of Fig. 10, imply that the radial flow is not steady over the disk and as a consequence that matter must accumulate in some orbits and be depleted in others. The actual mass flow also depends on the gas mass available at each radius (the radial velocity would directly translate into mass flow only if the gas mass did not depend on the radius, i.e., for a column density profile following R-1). Nevertheless, without any assumption about the radial density profile, the variation of the radial velocity shows that the gas will tend to be depleted just outside the ILR (the inward velocity increases with decreasing radius down to 600 pc) and to accumulate inside the ILR (the inward velocity decreases with decreasing radius inside 600 pc). This model is therefore consistent with the formation of rings at ILR as observed in many spiral galaxies (Buta & Combes 1996) and often used as a signature of the ILR.
The mass accumulation rate per radial element at a given radius is the gradient of the radial momentum (product of the radial linear density with the radial velocity); it is plotted as a function of the characteristic radius for ![]() = 0.05 in Fig. 10d. To obtain the correct mass units, the column density profile of the model was normalized so that the total mass of gas equals that measured in Sect. 2. We see that the maximum accumulation rate inside the ILR is of order 0.2
= 0.05 in Fig. 10d. To obtain the correct mass units, the column density profile of the model was normalized so that the total mass of gas equals that measured in Sect. 2. We see that the maximum accumulation rate inside the ILR is of order 0.2 ![]() yr-1 pc-1. Outside and close to the ILR the depletion rate is of similar amplitude. The accumulation rate integrated inside the ILR (i.e. over the radius range 300-600 pc) gives an inflow rate of order 20
yr-1 pc-1. Outside and close to the ILR the depletion rate is of similar amplitude. The accumulation rate integrated inside the ILR (i.e. over the radius range 300-600 pc) gives an inflow rate of order 20 ![]() yr-1. This is significantly higher than other inflow rates estimates in the literature which are in the range 1-4
yr-1. This is significantly higher than other inflow rates estimates in the literature which are in the range 1-4 ![]() yr-1 (Laine et al. 1999; Regan et al. 1997; Quillen et al. 1995). But this is an upper limit for this specific model and lower values are not excluded. The accumulation of molecular gas inevitably leads to a density increase and star formation. If the fraction of infalling gas transformed into stars (star formation efficiency) is constant and is of order 10
yr-1 (Laine et al. 1999; Regan et al. 1997; Quillen et al. 1995). But this is an upper limit for this specific model and lower values are not excluded. The accumulation of molecular gas inevitably leads to a density increase and star formation. If the fraction of infalling gas transformed into stars (star formation efficiency) is constant and is of order 10![]() ,
then the star formation rate (SFR) integrated over the accumulation region would be of the order of a few solar masses per year, which is realistic when compared to what is observed at ILRs in other galaxies. In NGC 4569 however, the H
,
then the star formation rate (SFR) integrated over the accumulation region would be of the order of a few solar masses per year, which is realistic when compared to what is observed at ILRs in other galaxies. In NGC 4569 however, the H![]() morphology and the CO(2-1)/(1-0) line ratio suggest that most of the star formation observed in this galaxy is taking place inside the inner 100 pc (see Sect. 2.5). The presence of
morphology and the CO(2-1)/(1-0) line ratio suggest that most of the star formation observed in this galaxy is taking place inside the inner 100 pc (see Sect. 2.5). The presence of ![]() 5
5 ![]() 104 O and B stars in the inner 30 pc (Gabel & Bruhweiler 2002) would imply a constant SFR of order 2
104 O and B stars in the inner 30 pc (Gabel & Bruhweiler 2002) would imply a constant SFR of order 2 ![]() yr-1 (assuming a Salpeter IMF and a life time of 5 Myr for O and B stars).
This implies either that another fueling mechanism is taking over inside the inner 300 pc, or that the nuclear starburst is ending and star formation at the ILR will dominate in the future.
yr-1 (assuming a Salpeter IMF and a life time of 5 Myr for O and B stars).
This implies either that another fueling mechanism is taking over inside the inner 300 pc, or that the nuclear starburst is ending and star formation at the ILR will dominate in the future.
Viscosity torques are intrinsic to the model and are specified through the radial and azimuthal dissipative parameters. However, as outlined in Baker (2000), these parameters lead to closed orbit solutions, so they cannot be directly used to compute the dissipation of angular momentum and the mass inflow rate. Estimating the intensity of the viscosity torques based on the density and velocity dispersion at a given point in the disk would require adopting prescriptions for the visosity that are generally acknowledged as very uncertain. Thus, our model does not allow us to directly constrain the rate of mass inflow due to viscosity torques. It could well be that these torques take over the fueling of the nucleus inside the 300 pc where the gravity torques are not efficient anymore. Alternatively, an inner stellar bar could drive the gas further inward as in NGC 6946 (Schinnerer et al. 2006); however, the current observations do not show any evidence of such a small inner bar.
Models of gas dynamics in galaxies come in two main categories: ballistic models in which the gas is represented by colliding clouds on ballistic orbits (Combes & Gerin 1985; Byrd et al. 1994), and hydrodynamic models in which the gas is assumed to be a continuous dissipative medium (Piner et al. 1995; Wada & Habe 1995; Friedli & Benz 1993; Athanassoula 1992). Comparisons of the two approaches are discussed in Lindblad & Lindblad (1994), Wada (1994), Combes (1996) and Regan et al. (1999). The analytical model of orbits in a barred potential presented in the previous section effectively traces the evolution of gas particles in the gravitational potential as they are subjected to collisions. Although the equations are continuous, they are not based on hydrodynamic assumptions, and the gas is assumed to be an ensemble of independent particles rather than a continuous medium, meaning the model can be classified as ballistic. The good fit of this model to our CO observations presented here seems to validate such a ballistic approach. The results of the two approaches may actually not have so many differences that the observations can distinguish. As already suggested by Lindblad & Lindblad (1994), it may be that the orbits out of this analytical model describe a gas flow similar to the one obtained with a hydrodynamic model. This hypothesis is supported by comparing the orbit pattern as shown in Fig. 9b to the gas flow resulting from a hydrodynamic simulation as shown in Fig. 9 of Regan et al. (1999). The shapes of the orbits resemble the gas streamlines in their model and the dust lane/shock region of their model is well reproduced by the orbit crowding in our model. The main difference is that the largest circular orbit in our model is located well inside the ILR, whereas it defines the ILR in their model. As a consequence, the ring formed at the ILR by gas accumulation is elongated in our model (Fig. 8c) rather than circular. But such a shape has also been seen by Nakanishi et al. (2005) based on Smoothed Particle Hydrodynamics (SPH) simulations of the same galaxy.
The difference between ballistic and hydrodynamic models outlined in Regan et al. (1999) corresponds to the sharp inversion in the radial component of the velocity vector in the shock/dust lane region. This feature is argued to be reproduced by the hydrodynamic models but not by the orbits of ballistic models. However, this argument is based on the assumption that the orbits are elliptical (see their Fig. 10). As emphasized in Sect. 3.5 the analytical orbits of gas clouds in a barred potential used here have much sharper ends than ellipses, blurring the nominal distinction between hydrodynamic and ballistic models.
It is also interesting to note that the conclusions of both approaches in terms of mass inflow are not so different. The inflow stops at the largest circular orbits (the "nuclear ring'') in the model of Regan et al. (1999) and at the largest x2 orbit or at the largest nonlooping x1 orbit in Regan et al. (2004). In all cases, the bars seem to be incapable of driving molecular gas inside a radius of 100 pc. Similarly, in our model, the gravitational torques stop where the orbits become circular at a radius of 300 pc.
The advantage of the method followed here is that we are able to first identify the ILR based on a kinematic argument, namely the inversion of the radial variation of the ellipse orientations in the second model (Sect. 3.4). This allows us to fix the potential parameters of the third model, i.e. the orbit pattern, and to fit the radial profile of the column density and velocity dispersion independently. Although limited in its domain of application (weak bars and inside corotation), this method has the advantage of being insensitive to initial conditions or numerical effects that may affect evolutionary models (ballistic or hydrodynamic). In addition, it is obviously very undemanding in terms of computation resources and well adapted to iterative fitting to observations.
The main results of this article can be summarized as follows:
Acknowledgements
This research has made use of the GOLDMine Database. We thank the scientific and technical staffs at the IRAM 30 m and PdBI for their help in obtaining the observations presented here. We are grateful to the referee, Eric Emsellem, for helpful comments.
The first two models are entirely specified by a radially varying set of properties similar to that of the widely used "tilted ring model'' (Rogstad et al. 1974). The values of the parameters are specified at some galactocentric radii and linearly interpolated between those radii. The third model has additional global parameters.
Thus, the total number of free parameters is adjustable through the number of radii,
![]() ,
and is given by
,
and is given by
![]() ,
where
,
where
![]() is the number of properties specified at each radius including the value of the radius. The number of radii required to reproduce the data satisfactorily was found to be greater than 7. In this case, for all models the number of free parameters is too high compared to the dynamic range of the data (signal-to-noise ratio, spatial dynamic range and spectral dynamic range) to permit a rigorous minimization of an objective function like
is the number of properties specified at each radius including the value of the radius. The number of radii required to reproduce the data satisfactorily was found to be greater than 7. In this case, for all models the number of free parameters is too high compared to the dynamic range of the data (signal-to-noise ratio, spatial dynamic range and spectral dynamic range) to permit a rigorous minimization of an objective function like ![]() over the full parameter space.
Since the goal of this modeling is to test the compatibility of the different hypotheses with the main features of the data, rather than to estimate to a high accuracy the numerous free parameters, the comparison of the simulated data cubes to the real data cubes has been done by eye
over the full parameter space.
Since the goal of this modeling is to test the compatibility of the different hypotheses with the main features of the data, rather than to estimate to a high accuracy the numerous free parameters, the comparison of the simulated data cubes to the real data cubes has been done by eye![]() .
.
In all the models, the inclination of the galaxy is fixed to 70 ![]() (Tully 1988), its position angle to 30
(Tully 1988), its position angle to 30 ![]() (Guhathakurta et al. 1988, except in the third model where the PA is also a free parameter) and its distance to 17 Mpc (Bottinelli et al. 1983; Tully 1988, only used to convert angular scales into physical scales). In addition, in all models we make the effective assumption that mass column density is proportional to the CO intensity with the same constant of proportionality everywhere.
(Guhathakurta et al. 1988, except in the third model where the PA is also a free parameter) and its distance to 17 Mpc (Bottinelli et al. 1983; Tully 1988, only used to convert angular scales into physical scales). In addition, in all models we make the effective assumption that mass column density is proportional to the CO intensity with the same constant of proportionality everywhere.
In the first model, the properties specified are the radii, the rotational velocity, the radial velocity (positive in outward direction), the column density through the disk, the disk scale height (FWHM of the Gaussian profile) and the local velocity dispersion (square root of the Gaussian distribution variance). The number of free parameters is therefore 6 ![]()
![]() .
The vertical distribution of matter and the velocity distribution at a given position are assumed to be Gaussian.
.
The vertical distribution of matter and the velocity distribution at a given position are assumed to be Gaussian.
To mimic the formation/destruction of the clouds we apply an exponential taper to the column density along the orbits.
The taper equals 1 at the aphelion and decreases like
![]() ,
where
,
where ![]() is the azimuth along the ellipse. The sign of
is the azimuth along the ellipse. The sign of ![]() is determined by the sense of rotation of the cloud in the reference frame of the density wave for which a pattern speed needs to be specified. Here we assume that all the gas lies within the corotation radius, and that the density decreases smoothly in the sense of rotation of the whole galaxy, i.e. counter-clockwise.
is determined by the sense of rotation of the cloud in the reference frame of the density wave for which a pattern speed needs to be specified. Here we assume that all the gas lies within the corotation radius, and that the density decreases smoothly in the sense of rotation of the whole galaxy, i.e. counter-clockwise.
The properties of the model are the characteristic radius, the characteristic rotation velocity (the angular momentum), the ellipticity, the position angle of the ellipse, the column density, the velocity dipersion and the scale height. The pattern speed of the entire model was not well constrained by the observations and since the larger the value the worse the fit, it was decided to fix this parameter at zero. The number of free parameters is therefore 7 ![]()
![]() .
As in the previous model, the vertical distribution of matter and the velocity distribution at a given position are assumed to be Gaussian.
.
As in the previous model, the vertical distribution of matter and the velocity distribution at a given position are assumed to be Gaussian.
We use 2 parameters describing the logarithmic potential (the characteristic scale and velocity, see Eq. (B.1)), 3 parameters for the bar perturbation (the position angle relative to the galaxy major axis, the strength, and the pattern speed) and 2 parameters for the gas dissipative properties (the radial and azimuthal dissipation rates). We found it difficult to obtain a good solution with a galaxy position angle of 30 ![]() as in the previous models, so we left this as an additional free parameter here. In addition, the gaseous disk is described by 3 properties (the column density, the velocity dispersion, and the scale height) at different radii as in the previous models (the radius here is the characteristic radius of the orbit, which corresponds to the radius of the circular orbit without bar perturbation). The number of free parameters is therefore 8+4
as in the previous models, so we left this as an additional free parameter here. In addition, the gaseous disk is described by 3 properties (the column density, the velocity dispersion, and the scale height) at different radii as in the previous models (the radius here is the characteristic radius of the orbit, which corresponds to the radius of the circular orbit without bar perturbation). The number of free parameters is therefore 8+4 ![]()
![]() .
.
The results of the elliptical orbit fit allow us to fix some of the parameters describing the potential. First, the characteristic velocity of the axisymmetric component of the potential corresponds to the rotation velocity at infinity. Based on previous results, we take
![]() km s-1, also consistent with the value of Guhathakurta et al. (1988) based on H I observations. Next, the fact that the ILR was identified at 600 pc from the center in the elliptical orbit model allows us to fix the characteristic scale of the potential (using Eq. (B.5)) to
km s-1, also consistent with the value of Guhathakurta et al. (1988) based on H I observations. Next, the fact that the ILR was identified at 600 pc from the center in the elliptical orbit model allows us to fix the characteristic scale of the potential (using Eq. (B.5)) to
![]() pc. Finally, assuming there is only one ILR (as the elliptical orbit model suggests), the pattern speed is set by Eq. (B.6) to
pc. Finally, assuming there is only one ILR (as the elliptical orbit model suggests), the pattern speed is set by Eq. (B.6) to
![]() = 60 km s-1 kpc-1. The remaining global parameters (as opposed to those specified at each radius) are the bar strength, its position angle and the 2 dissipation rates. There is a balance between the bar strength and the dissipation rates, in the sense that the stronger the bar or the smaller the dissipation rates the closer the orbits are to pure stellar orbits. Stellar orbits are organized in families, the so-called x1 and x2 orbits, (Sellwood & Wilkinson 1993; Contopoulos & Grosbol 1989), which are orthogonal to each other, intersect, and can exhibit large loops. As long-lived gas orbits cannot intersect or have loops, a realistic solution for the orbits must keep the bar strength and dissipation rates balanced. The bar strength is required by self-consistency to be in the weak perturbation regime (less than 5
= 60 km s-1 kpc-1. The remaining global parameters (as opposed to those specified at each radius) are the bar strength, its position angle and the 2 dissipation rates. There is a balance between the bar strength and the dissipation rates, in the sense that the stronger the bar or the smaller the dissipation rates the closer the orbits are to pure stellar orbits. Stellar orbits are organized in families, the so-called x1 and x2 orbits, (Sellwood & Wilkinson 1993; Contopoulos & Grosbol 1989), which are orthogonal to each other, intersect, and can exhibit large loops. As long-lived gas orbits cannot intersect or have loops, a realistic solution for the orbits must keep the bar strength and dissipation rates balanced. The bar strength is required by self-consistency to be in the weak perturbation regime (less than 5![]() )
but below this threshold there is a degeneracy with the dissipation rates. The ratio of the two dissipation rates has little effect on the orbits, i.e. there is a degeneracy between them. So these three parameters (bar strength and the two dissipation rates) are not well constrained and only their combination matters.
)
but below this threshold there is a degeneracy with the dissipation rates. The ratio of the two dissipation rates has little effect on the orbits, i.e. there is a degeneracy between them. So these three parameters (bar strength and the two dissipation rates) are not well constrained and only their combination matters.
A logarithmic potential is defined as:
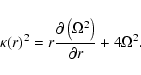 |
(B.3) |
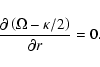 |
(B.4) |
The pattern speed of the bar,
![]() ,
is given by
,
is given by
![]() :
:
| (B.7) |
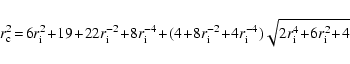 |
(B.8) |
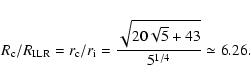 |
(B.10) |
The non-axisymetric component of the potential (the bar component) is given by
| (C.1) |
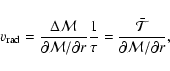 |
(C.5) |