A&A 471, 31-50 (2007)
DOI: 10.1051/0004-6361:20054413
W. Kausch1 - M. Gitti2 - T. Erben3 - S. Schindler1
1 - Institut für Astro- und Teilchenphysik, University of Innsbruck,
Technikerstr. 25, 6020 Innsbruck, Austria
2 -
INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna,
Italy
3 -
Argelander-Institut für Astronomie (AIfA), University of Bonn,
Auf dem Hügel 71, 53121 Bonn, Germany
Received 25 October 2005 / Accepted 6 April 2007
Abstract
We present a detailed analysis of the medium redshift (z=0.2906)
galaxy cluster Z3146 which is part of the ongoing ARCRAIDER project,
a systematic search for gravitational arcs in massive clusters of
galaxies. The analysis of Z3146 is based on deep optical wide field
observations in the B, V and R bands obtained with the
WFI@ESO2.2m, and shallow archival WFPC2@HST taken with the F606Wfilter, which are used for strong as well as weak lensing analyses.
Additionally we have used publicly available XMM/Newton observations
for a detailed X-ray analysis of Z3146. Both methods, lensing and
X-ray, were used to determine the dynamical state and to estimate
the total mass. We also identified four gravitational arc candidates.
We find this cluster to be in a relaxed state, which is confirmed by
a large cooling flow with nominal ![]()
![]() per year,
regular galaxy density and light distributions and a regular shape
of the weak lensing mass reconstruction. The mass content derived
with the different methods agrees well within 25% at
per year,
regular galaxy density and light distributions and a regular shape
of the weak lensing mass reconstruction. The mass content derived
with the different methods agrees well within 25% at
![]() kpc indicating a velocity dispersion of
kpc indicating a velocity dispersion of
![]() km s-1.
km s-1.
Key words: gravitational lensing - galaxies: clusters: individual: Z3146
The combination of lensing and X-ray studies allows us to get important insights into galaxy clusters, as it offers the possibility to obtain physical properties of the cluster members, the Intra Cluster Medium (ICM) and the determination of the cluster gravitational mass and its distribution with independent methods.
However, the mass determination of galaxy clusters is a very difficult task. It is dependent on the method adopted and on the validity of the assumptions used to convert observables to cluster masses. Currently two methods are widely used: (a) From the gas density and temperature profiles measured with X-ray observations it is possible to derive an estimate of the gravitational mass by assuming spherical symmetry and hydrodynamical equilibrium (see e.g. Allen et al. 2002; Voigt & Fabian 2006; Ettori & Lombardi 2003; Pratt & Arnaud 2005; Allen et al. 2001; Pointecouteau et al. 2004). (b) The second method is based on gravitational lensing analyses, using either strongly deformed background sources (arcs) to constrain the cluster mass in the very cluster centre or statistical methods to investigate systematic shape distortions of background objects to map the mass distribution of a cluster (weak lensing method, see e.g. Bartelmann & Schneider 2001 for a review on this topic). The lensing method is affected by the least number of assumptions as it is neither sensitive to the nature of the matter nor its dynamical state. However, this method measures the integrated mass along the line of sight, which can lead to a bias of too high mass estimates (White et al. 2002). Detailed lensing analyses were carried out for several galaxy clusters, e.g. CL0024+1654 (Czoske et al. 2002; Kneib et al. 2003), A2218 (Kneib et al. 1996), A1689 (Broadhurst et al. 2005b,a), A383 (Smith et al. 2001) or RX J1347-1145 (Bradac et al. 2005).
Unfortunately the mass estimates derived from the different methods can be quite inconsistent. In some clusters there are considerable discrepancies up to a factor of 3, e.g. MS0440+0204 (Gioia et al. 1998) or CL0500-24 (Schindler 1999). Allen (1998) found the lensing and X-ray method to be consistent for cooling flow clusters, whereas for non-cooling flow clusters the mass discrepancy between the strong lensing method and the X-ray based mass determinations can differ by a factor of up to 2-4. This mainly comes from the fact that the inner core of clusters, where strong lensing occurs, is not well described by the usual simple models used in X-ray methods, which are based on the assumptions mentioned above. The discrepancies of the weak lensing and the X-ray method seem to be much smaller (Wu et al. 1998).
In this paper we present a combined optical, X-ray and lensing
analysis of Z3146. This cluster of galaxies is located at
![]() ,
,
![]() (J2000)
with a redshift of
(J2000)
with a redshift of
![]() (Schwope et al. 2000) and was the
subject of many previous optical (e.g.
Edge et al. 2002; Sand et al. 2005; Chapman et al. 2002; Edge & Frayer 2003; Crawford et al. 1999) and X-ray
investigations (e.g. Ettori et al. 2001; Edge et al. 1994; Fabian et al. 2002; Hicks & Mushotzky 2005). This prominent cluster is one of the
most X-ray luminous systems in the ROSAT Bright Survey
(Schwope et al. 2000, hereafter RBS) having an X-ray luminosity of about
(Schwope et al. 2000) and was the
subject of many previous optical (e.g.
Edge et al. 2002; Sand et al. 2005; Chapman et al. 2002; Edge & Frayer 2003; Crawford et al. 1999) and X-ray
investigations (e.g. Ettori et al. 2001; Edge et al. 1994; Fabian et al. 2002; Hicks & Mushotzky 2005). This prominent cluster is one of the
most X-ray luminous systems in the ROSAT Bright Survey
(Schwope et al. 2000, hereafter RBS) having an X-ray luminosity of about
![]() erg/s in the 0.5-2 keV ROSAT band. It is
part of a larger sample of X-ray selected galaxy clusters which is
described in Sect. 2 and will be given in more
detail in a forthcoming paper (Kausch et al., in prep.). This paper
contains detailed X-ray and lensing analyses of Z3146 followed by
several optical investigations. The X-ray analysis is presented in
Sect. 3, a description of the optical observations and
the data reduction procedure used for this investigation is given in
Sect. 4. Section 5
contains a lensing analysis based on weak (Sect. 5.1)
and strong lensing (Sect. 5.2).
Section 6 comprises continuative
optical investigations on the cluster. In Sect. 7
we summarize and discuss the results.
erg/s in the 0.5-2 keV ROSAT band. It is
part of a larger sample of X-ray selected galaxy clusters which is
described in Sect. 2 and will be given in more
detail in a forthcoming paper (Kausch et al., in prep.). This paper
contains detailed X-ray and lensing analyses of Z3146 followed by
several optical investigations. The X-ray analysis is presented in
Sect. 3, a description of the optical observations and
the data reduction procedure used for this investigation is given in
Sect. 4. Section 5
contains a lensing analysis based on weak (Sect. 5.1)
and strong lensing (Sect. 5.2).
Section 6 comprises continuative
optical investigations on the cluster. In Sect. 7
we summarize and discuss the results.
Throughout this paper we use
H0=70 h70 km s-1 Mpc-1and
![]() .
Hence
.
Hence
![]() kpc for the cluster
redshift of z=0.2906.
kpc for the cluster
redshift of z=0.2906.
The total sample contains 22 galaxy clusters which were observed
with different telescopes: RBS1316 (RX J1347-1145) is the most X-ray
luminous cluster known (Allen et al. 2002; Gitti & Schindler 2004; Schindler et al. 1997, Gitti et al. 2007,
in prep.) and was observed in the U,
B, V, R and I band with the ESOVLT with the FORS1 instrument
and in the ![]() band with ISAAC (Bradac et al. 2005). All other
clusters were observed at least in the V and R band either with
the SUperb Seeing Imager 2 (SUSI2@ESONTT, ESO-filters V#812 and R#813) or with the Wide Field Imager (BB#V/89_ESO843 and WFI@ESO2.2m, ESO-filters BB#R
band with ISAAC (Bradac et al. 2005). All other
clusters were observed at least in the V and R band either with
the SUperb Seeing Imager 2 (SUSI2@ESONTT, ESO-filters V#812 and R#813) or with the Wide Field Imager (BB#V/89_ESO843 and WFI@ESO2.2m, ESO-filters BB#R![]() /162_ESO844) with usually
half the exposure time in V than in R. We use the deep R band
frame as the primary science band for our lensing analysis, whereas
the shallow V image is used for
colour determinations for a rough division between foreground and background galaxies.
/162_ESO844) with usually
half the exposure time in V than in R. We use the deep R band
frame as the primary science band for our lensing analysis, whereas
the shallow V image is used for
colour determinations for a rough division between foreground and background galaxies.
As our clusters are the most luminous ones of the RBS, we expect
these systems to be very massive due to the
![]() relation
(Schindler 1999; Reiprich & Böhringer 1999). Therefore it is very likely to find
strong gravitational lensing features like arcs or arclets in such
systems. A similar sample of clusters was established by
Luppino et al. (1999), based on the EMSS. In total they found arc(lets)
and candidates in
relation
(Schindler 1999; Reiprich & Böhringer 1999). Therefore it is very likely to find
strong gravitational lensing features like arcs or arclets in such
systems. A similar sample of clusters was established by
Luppino et al. (1999), based on the EMSS. In total they found arc(lets)
and candidates in ![]() 42% of their members. As their X-ray
luminosity limit was chosen to be lower than ours (
42% of their members. As their X-ray
luminosity limit was chosen to be lower than ours (
![]() erg s-1 in the 0.3-3.5 keV regime) we expect
to detect gravitational arcs in 45-60% of the clusters.
erg s-1 in the 0.3-3.5 keV regime) we expect
to detect gravitational arcs in 45-60% of the clusters.
Z3146 was observed by XMM-Newton in December 2000 during rev. 182 (PI: Mushotzky) with the MOS and pn detectors in Full Frame Mode with THIN filter, for an exposure time of 53.1 ks for MOS and 46.1 ks for pn. We used the SASv6.0.0 processing tasks emchain and epchain to generate calibrated event files from raw data. Throughout this analysis single pixel events for the pn data (PATTERN 0) were selected, while for the MOS data sets the PATTERNs 0-12 were used. The removal of bright pixels and hot columns was done in a conservative way applying the expression (FLAG==0). To reject the soft proton flares we accumulated the light curve in the [10-12] keV band for MOS and [12-14] keV band for pn, where the emission is dominated by the particle-induced background, and excluded all the intervals of exposure time having a count rate higher than a certain threshold value (the chosen threshold values are 15 counts/100 s for MOS and 20 counts/100 s for pn). The remaining exposure times after cleaning are 52.3 ks for MOS1, 52.6 ks for MOS2 and 45.7 ks for pn. Starting from the output of the SAS detection source task, we made a visual selection on a wide energy band MOS & pn image of point sources in the FoV. Events from these regions were excluded directly from each event list.
The background estimates were obtained using a blank-sky observation consisting of several high-latitude pointings with sources removed (Lumb et al. 2002). The blank-sky background events were selected using the same selection criteria (such as PATTERN, FLAG, etc.), intensity filter (for flare rejection) and point source removal used for the observation events; this yields final exposure times for the blank fields of 365 ks for MOS1, 350 ks for MOS2 and 294 ks for pn. Since the cosmic ray induced background might slightly change with time, we computed the ratio of the total count rates in the high energy band ([10-12] keV for MOS and [12-14] keV for pn). The obtained normalization factors (0.827, 0.820, 0.836 for MOS1, MOS2 and pn, respectively) were then used to renormalize the blank field data. The blank-sky background files were recast in order to have the same sky coordinates as Z3146. For the pn data, we generated a list of out-of-time events (hereafter OoT) to be treated as an additional background component. The effect of OoT in the current observing mode (Full Frame) is 6.3%. The OoT event list was processed in a similar way as done for the pn observation event file. The background subtraction (for spectra and surface brightness profiles) was performed as described in Arnaud et al. (2002). In case of pn the OoT data were also subtracted.
The source and background events were corrected for vignetting using the weighted method described in Arnaud et al. (2001), the weight coefficients being tabulated in the event list with the SAS task evigweight. This allows us to use the on-axis response matrices and effective areas.
Unless otherwise stated, the reported errors are at 90% confidence level in the entire Sect. 3.
The adaptively smoothed, exposure corrected MOS1 count rate image in the [0.3-10] keV energy band is presented in Fig. 1. The smoothed image was obtained from the raw image corrected for the exposure map (that accounts for spatial quantum efficiency, mirror vignetting and field of view) by running the task asmooth set to a desired signal-to-noise ratio of 20. Regions exposed with less than 10% of the total exposure were not considered.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/4413_f01.eps}\end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg84.gif) |
Figure 1: MOS1 image of ZW3146 in the [0.3-10] keV energy band. The image is corrected for vignetting and exposure and is adaptively smoothed (signal-to-noise ratio = 20). |
| Open with DEXTER | |
We notice a sharp central surface brightness peak at a position
![]() (J2000), in very good agreement (
(J2000), in very good agreement (
![]() ,
,
![]() )
with the optical position of the
central dominant cluster galaxy (Schwope et al. 2000). The morphology of
the cluster is quite regular, thus indicating a relaxed dynamical
state, even though we notice that the central core appears
slightly shifted
to the south-east with respect to the outer envelope, with a
north-west to south-east elongation of the cluster core. The regular
morphology of the cluster is indicative of a relaxed dynamical
state, thus allowing us to derive a good mass estimate based on the
usual assumptions of hydrostatic equilibrium and spherical symmetry
(see Sect. 3.5).
)
with the optical position of the
central dominant cluster galaxy (Schwope et al. 2000). The morphology of
the cluster is quite regular, thus indicating a relaxed dynamical
state, even though we notice that the central core appears
slightly shifted
to the south-east with respect to the outer envelope, with a
north-west to south-east elongation of the cluster core. The regular
morphology of the cluster is indicative of a relaxed dynamical
state, thus allowing us to derive a good mass estimate based on the
usual assumptions of hydrostatic equilibrium and spherical symmetry
(see Sect. 3.5).
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figures/4413_f02.eps}\end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg88.gif) |
Figure 2:
Background
subtracted, azimuthally averaged radial surface brightness profile
in the [0.3-2] keV range. The best fit |
| Open with DEXTER | |
We computed a background-subtracted vignetting-corrected radial
surface brightness profile in the [0.3-2] keV energy band for each
camera separately. The profiles for the three detectors were then
added into a single profile and binned such that at least a
sigma-to-noise ratio of 3 was reached. The cluster emission is
detected up to 1.5 Mpc (![]()
![]() )
and the profile appears
relatively regular and relaxed (see Fig. 2).
The surface brightness profile of the undisturbed cluster was fitted
with the CIAO tool Sherpa with various parametric models,
which were convolved with the XMM-Newton PSF. The overall
PSF was obtained by adding the PSF of each camera
(Ghizzardi 2001), estimated at an energy of 1.5 keV and weighted
by the respective cluster count rate in the 0.3-2 keV energy band. A
single
)
and the profile appears
relatively regular and relaxed (see Fig. 2).
The surface brightness profile of the undisturbed cluster was fitted
with the CIAO tool Sherpa with various parametric models,
which were convolved with the XMM-Newton PSF. The overall
PSF was obtained by adding the PSF of each camera
(Ghizzardi 2001), estimated at an energy of 1.5 keV and weighted
by the respective cluster count rate in the 0.3-2 keV energy band. A
single ![]() -model (Cavaliere & Fusco-Femiano 1976) is not a good description
of the entire profile: a fit to the outer regions
(230
-model (Cavaliere & Fusco-Femiano 1976) is not a good description
of the entire profile: a fit to the outer regions
(230
![]() kpc < r < 1300
kpc < r < 1300
![]() kpc) shows a
strong excess in the centre as compared to the model (see Fig. 2). The peaked emission is a strong indication for a
cooling flow in this cluster. We found that for
230
kpc) shows a
strong excess in the centre as compared to the model (see Fig. 2). The peaked emission is a strong indication for a
cooling flow in this cluster. We found that for
230
![]() kpc < r < 1300
kpc < r < 1300
![]() kpc the data
can be described (
kpc the data
can be described (
![]() for 74 d.o.f.) by a
for 74 d.o.f.) by a
![]() -model with a core radius
-model with a core radius
![]()
![]() kpc and a slope parameter
kpc and a slope parameter
![]() (3
(3![]() confidence level). The single
confidence level). The single ![]() -model functional
form is a convenient representation of the gas density profile in
the outer regions, which is used as a tracer for the potential. The
parameters of this best fit are thus used in the following to
estimate the total mass profile in the region where the single beta
model holds (see Sect. 3.5).
-model functional
form is a convenient representation of the gas density profile in
the outer regions, which is used as a tracer for the potential. The
parameters of this best fit are thus used in the following to
estimate the total mass profile in the region where the single beta
model holds (see Sect. 3.5).
We also considered a double isothermal ![]() -model and found that
it can account for the entire profile, if the very inner and outer
regions are excluded:
for 15 kpc
-model and found that
it can account for the entire profile, if the very inner and outer
regions are excluded:
for 15 kpc
![]() < r < 1300
< r < 1300
![]() kpc the best
fit parameters are
kpc the best
fit parameters are
![]()
![]() kpc,
kpc,
![]()
![]() kpc and
kpc and
![]() (
(
![]() for 95 d.o.f.). A common
for 95 d.o.f.). A common ![]() value
is assumed in this model, but we also tried the fit with two
different
value
is assumed in this model, but we also tried the fit with two
different ![]() values, finding very similar results (
values, finding very similar results (
![]()
![]() kpc,
kpc,
![]()
![]() kpc,
kpc,
![]() and
and
![]() ;
;
![]() for 94 d.o.f.).
for 94 d.o.f.).
The temperature image of the cluster central region shown in Fig. 3 was built from X-ray colours. Specifically, we
extracted mosaiced MOS images in four different energy bands
(0.3-1.0 keV, 1.0-2.0 keV, 2.0-4.5 keV and 4.5-8 keV), subtracted
the background and divided the resulting images by the exposure
maps. A temperature in each pixel of the map was obtained by fitting
values in each pixel of these images with a thermal plasma, fixing
![]() to the Galactic value and the element abundance to 0.3 solar. In particular we note that the very central region is cooler
than the surrounding medium and the north-west quadrant appears
slightly hotter than the south-east one, even though no strong
features are present.
The regularity of the temperature distribution points to a relaxed
dynamical state of the cluster, thus excluding the presence of an
ongoing merger. Since cluster merging can cause strong deviations
from the assumption of an equilibrium configuration, this allows us
to derive a good estimate of the cluster mass (see Sect. 3.5).
to the Galactic value and the element abundance to 0.3 solar. In particular we note that the very central region is cooler
than the surrounding medium and the north-west quadrant appears
slightly hotter than the south-east one, even though no strong
features are present.
The regularity of the temperature distribution points to a relaxed
dynamical state of the cluster, thus excluding the presence of an
ongoing merger. Since cluster merging can cause strong deviations
from the assumption of an equilibrium configuration, this allows us
to derive a good estimate of the cluster mass (see Sect. 3.5).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/4413_f03.ps}\end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg103.gif) |
Figure 3:
Temperature
map obtained by using 4 X-ray colours (0.3-1.0, 1.0-2.0, 2.0-4.5,
4.5-8 keV) and estimating the expected count rate with XSPEC for a
thermal MEKAL model, with fixed Galactic absorption |
| Open with DEXTER | |
Throughout the analysis, a single spectrum was extracted for each
region of interest and was then regrouped to reach a significance
level of at least 3![]() in each bin. The data were modelled
using the XSPEC code, version 11.3.0. Unless otherwise stated, the
relative normalizations of the MOS and pn spectra were left free
when fitted simultaneously. We used the following response matrices:
m1_169_im_pall_v1.2.rmf (MOS1), m2_169_im_pall_v1.2.rmf (MOS2), epn_ff20_sY9.rmf (pn).
in each bin. The data were modelled
using the XSPEC code, version 11.3.0. Unless otherwise stated, the
relative normalizations of the MOS and pn spectra were left free
when fitted simultaneously. We used the following response matrices:
m1_169_im_pall_v1.2.rmf (MOS1), m2_169_im_pall_v1.2.rmf (MOS2), epn_ff20_sY9.rmf (pn).
For each instrument, a global spectrum was extracted from all events
lying within 5
![]() of the cluster emission peak. We tested in
detail the consistency between the three cameras by fitting
separately these spectra with an absorbed MEKAL model with the
redshift fixed at z=0.291 and the absorbing fixed at the galactic
value (
of the cluster emission peak. We tested in
detail the consistency between the three cameras by fitting
separately these spectra with an absorbed MEKAL model with the
redshift fixed at z=0.291 and the absorbing fixed at the galactic
value (
![]() ,
Dickey & Lockman 1990). Fitting the data from all instruments above 0.3 keV
led to inconsistent values for the temperature derived with the MOS
and pn cameras:
kT = 6.18+0.16-0.15 keV (MOS1),
5.72+0.15-0.14 (MOS2),
5.01+0.09-0.08 (pn). We then
performed a systematic study of the effect of imposing various high
and low-energy cutoffs, for each instrument. Good agreement between
the three cameras was found in the [1.0-10.0] keV energy range (
kT
= 6.27+0.21-0.20 keV for MOS1,
5.99+0.20-0.19 for
MOS2,
6.00+0.16-0.15 for pn). On the other hand, we also
found consistent results by fitting the MOS spectra in the [0.4-10] keV energy range and the pn spectrum in the [0.9-10] keV energy
range.The discrepancies observed by fitting the whole energy range
are probably due to some residual calibration uncertainties in the
low-energy response of all instruments. Thus, in order to avoid
inaccurate measurements due to calibration problems, we adopted the
low energy cut-off derived above for the
spectral analysis discussed below.
,
Dickey & Lockman 1990). Fitting the data from all instruments above 0.3 keV
led to inconsistent values for the temperature derived with the MOS
and pn cameras:
kT = 6.18+0.16-0.15 keV (MOS1),
5.72+0.15-0.14 (MOS2),
5.01+0.09-0.08 (pn). We then
performed a systematic study of the effect of imposing various high
and low-energy cutoffs, for each instrument. Good agreement between
the three cameras was found in the [1.0-10.0] keV energy range (
kT
= 6.27+0.21-0.20 keV for MOS1,
5.99+0.20-0.19 for
MOS2,
6.00+0.16-0.15 for pn). On the other hand, we also
found consistent results by fitting the MOS spectra in the [0.4-10] keV energy range and the pn spectrum in the [0.9-10] keV energy
range.The discrepancies observed by fitting the whole energy range
are probably due to some residual calibration uncertainties in the
low-energy response of all instruments. Thus, in order to avoid
inaccurate measurements due to calibration problems, we adopted the
low energy cut-off derived above for the
spectral analysis discussed below.
The combined MOS+pn global temperature and luminosity are
respectively
kT = 5.91+0.09-0.08 keV,
![]() in the
[0.4/0.9-10.0] keV energy range (MOS/pn) and
kT =
6.08+0.11-0.10 keV,
in the
[0.4/0.9-10.0] keV energy range (MOS/pn) and
kT =
6.08+0.11-0.10 keV,
![]() in the [1.0-10.0] keV energy
range. These values are in agreement with ASCA results (Allen et al.
1996; Allen 2000), while Ettori et al. (2001) derived higher
temperature values from BeppoSAX observations. The
simultaneous fit in the [0.4/0.9-10.0] keV energy range (MOS/pn) to
the three spectra is shown in Fig. 4.
in the [1.0-10.0] keV energy
range. These values are in agreement with ASCA results (Allen et al.
1996; Allen 2000), while Ettori et al. (2001) derived higher
temperature values from BeppoSAX observations. The
simultaneous fit in the [0.4/0.9-10.0] keV energy range (MOS/pn) to
the three spectra is shown in Fig. 4.
![\begin{figure*}
\par\includegraphics[width=8.5cm,clip]{figures/4413_f04.eps}\end{figure*}](/articles/aa/full/2007/31/aa4413-05/Timg106.gif) |
Figure 4:
Global MOS ( lower) and pn ( upper) spectra in the
[0.4/0.9-10.0] keV energy range (MOS/pn) integrated in a circular
region of radius 5
|
| Open with DEXTER | |
Table 1:
Results from the spectral fitting in
concentric annular regions in the [0.4/0.9-10.0] keV energy range
(MOS/pn) and in the [1.0-10.0] keV energy range. Temperatures (kT)
are in keV, metallicities (Z) in solar units and [2-10] keV
luminosities (![]() )
in units of
)
in units of
![]() .
The total
.
The total ![]() values and numbers of degrees of freedom (d.o.f.) in
the fits are also listed. Error bars are at the 90% confidence
levels on a single parameter of interest.
values and numbers of degrees of freedom (d.o.f.) in
the fits are also listed. Error bars are at the 90% confidence
levels on a single parameter of interest.
We produced a radial temperature profile by extracting spectra in
annuli centred on the peak of the X-ray emission. The annular
regions are detailed in Table 1. The data from the
three cameras have been modelled simultaneously using a simple,
single-temperature model (MEKAL plasma emission code in XSPEC) with
the absorbing column density fixed at the nominal Galactic value.
The free parameters in this model are the temperature kT,
metallicity Z (measured relative to the solar values, with the
various elements assumed to be present in their solar ratios) and
normalization (emission measure). We separately performed the
spectral fitting in the [0.4/0.9-10.0] keV energy range (MOS/pn) and
in the [1.0-10.0] keV energy range. The best-fitting parameter
values and 90% confidence levels derived from the fits to the
annular spectra are summarized in Table 1. The
projected temperature profile determined with this model is shown in
Fig. 5. We note that, as expected, temperature
values derived in the [1.0-10.0] keV energy range are slightly
higher than those derived in the [0.4/0.9-10.0] keV energy range
(MOS/pn), even though consistent within the 90% confidence level.
In the following discussion we adopt results derived in the
[0.4/0.9-10.0] keV energy range (MOS/pn). The temperature rises from
a mean value of
![]() keV within 90
keV within 90
![]() kpc to
kpc to
![]() keV over the 180-1300 kpc region, where the
cluster can be considered approximately isothermal. The lack of
evidence for a temperature decline in the outer regions is in
agreement with the results by Mushotzky (2003).
keV over the 180-1300 kpc region, where the
cluster can be considered approximately isothermal. The lack of
evidence for a temperature decline in the outer regions is in
agreement with the results by Mushotzky (2003).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/4413_f05.ps}\end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg139.gif) |
Figure 5: Full circles: the projected X-ray gas temperature profile measured from XMM data in the [0.4/0.9-10.0] keV energy range (MOS/pn). Open triangles: same as full circles, but in the [1.0-10.0] keV energy range. |
| Open with DEXTER | |
The metallicity profile is shown in Fig. 6: a
gradient is visible towards the central region, the metallicity
increasing from
![]() over the
260-400
over the
260-400
![]() kpc region to
kpc region to
![]() inside the
central 90
inside the
central 90
![]() kpc.
kpc.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figures/4413_f06.ps}\end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg142.gif) |
Figure 6: Full circles: the projected X-ray gas metallicity profile measured from XMM data in the [0.4/0.9-10.0] keV energy range (MOS/pn). Open triangles: same as full circles, but in the [1.0-10.0] keV energy range. |
| Open with DEXTER | |
The surface brightness profile, the temperature map and the
temperature profile all give hints of the presence of a cooling
core. Here we further investigate the physical properties of the ICM
in the central region. The cooling time is calculated as the time
taken for the gas to radiate its enthalpy per unit volume using the
instantaneous cooling rate at any temperature:
We therefore accumulate the spectrum in the central
![]() .
We compare the MEKAL model already used in Sects. 3.4.1
and 3.4.2 with a model which includes a single
temperature component plus an isobaric multi-phase component (MEKAL + MKCFLOW in XSPEC), where the minimum temperature,
.
We compare the MEKAL model already used in Sects. 3.4.1
and 3.4.2 with a model which includes a single
temperature component plus an isobaric multi-phase component (MEKAL + MKCFLOW in XSPEC), where the minimum temperature,
![]() ,
and the normalization of the multi-phase component, Norm
,
and the normalization of the multi-phase component, Norm
![]() ,
are additional free parameters. The maximum temperature
kT of the MKCFLOW model is linked to the ambient value of the
MEKAL model. This model differs from the standard cooling flow model
as the minimum temperature is not set to zero.
The results, summarized in Table 2, show that the
statistical improvements obtained by introducing an additional
emission component compared to the single-temperature model are
significant at more than the 99% level according to the F-test,
with the temperature of the hot gas being remarkably higher than
that derived in the single-phase model. The fit with the modified
cooling flow model sets tight constraints on the existence of a
minimum temperature (
,
are additional free parameters. The maximum temperature
kT of the MKCFLOW model is linked to the ambient value of the
MEKAL model. This model differs from the standard cooling flow model
as the minimum temperature is not set to zero.
The results, summarized in Table 2, show that the
statistical improvements obtained by introducing an additional
emission component compared to the single-temperature model are
significant at more than the 99% level according to the F-test,
with the temperature of the hot gas being remarkably higher than
that derived in the single-phase model. The fit with the modified
cooling flow model sets tight constraints on the existence of a
minimum temperature (![]() 1.7 keV). We find a very high value of
the nominal mass deposition rate in this empirical model:
1.7 keV). We find a very high value of
the nominal mass deposition rate in this empirical model: ![]()
![]() .
ASCA-ROSAT observations
already found a very strong cooling flow in this cluster (Allen
2000).
.
ASCA-ROSAT observations
already found a very strong cooling flow in this cluster (Allen
2000).
Table 2:
The best-fit parameter values and 90% confidence limits
from the spectral analysis in the central
![]() region.
Temperatures (kT) are in keV, metallicities (Z) as a fraction of
the solar value and normalizations in units of
region.
Temperatures (kT) are in keV, metallicities (Z) as a fraction of
the solar value and normalizations in units of
![]() as done in XSPEC (for the
MKCFLOW model the normalization is parameterized in terms of the
mass deposition rate
as done in XSPEC (for the
MKCFLOW model the normalization is parameterized in terms of the
mass deposition rate ![]() ,
in
,
in
![]() ).
).
In the following we estimate the total mass of the cluster using the
usual assumptions of hydrostatic equilibrium and spherical symmetry.
Under these assumptions, the gravitational mass
![]() of a
galaxy cluster can be written as:
of a
galaxy cluster can be written as:
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figures/4413_f07.eps}\end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg174.gif) |
Figure 7:
Solid line: integrated total mass calculated from
Eq. (4) (with error on the mass calculation coming
from the temperature measurement and |
| Open with DEXTER | |
We also calculate the projected mass along the line-of-sight within
a cylinder of projected radius r. The integration was performed
out to a radius of ![]() 5 Mpc from the cluster centre. The
projected total mass is shown in Fig. 7 as a
dashed-dotted line.
In Fig. 7 we also show (dotted line) the gas mass
profile derived by integrating the gas density given by Eq. (3) in spherical shells and using the
5 Mpc from the cluster centre. The
projected total mass is shown in Fig. 7 as a
dashed-dotted line.
In Fig. 7 we also show (dotted line) the gas mass
profile derived by integrating the gas density given by Eq. (3) in spherical shells and using the ![]() -model
parameters determined in Sect. 3.2.1. The
normalization of Eq. (3) is obtained from the combination of
the best-fit results from the spectral and imaging analyses, which
allows us to determine the conversion count rate - flux used to
derive the bremsstrahlung emissivity that is then integrated along
the line-of-sight and compared with the central surface brightness
value. We note that, since we adopt the parameters of the
-model
parameters determined in Sect. 3.2.1. The
normalization of Eq. (3) is obtained from the combination of
the best-fit results from the spectral and imaging analyses, which
allows us to determine the conversion count rate - flux used to
derive the bremsstrahlung emissivity that is then integrated along
the line-of-sight and compared with the central surface brightness
value. We note that, since we adopt the parameters of the
![]() -model fit in the outer regions, the derived central electron
density (
-model fit in the outer regions, the derived central electron
density (
![]() )
is
that predicted by the extrapolation of the
)
is
that predicted by the extrapolation of the ![]() -model fit to the
centre (see Fig. 2). This procedure is nonetheless
reliable in estimating the gas mass for r >
230
-model fit to the
centre (see Fig. 2). This procedure is nonetheless
reliable in estimating the gas mass for r >
230
![]() kpc, shown in Fig. 7.
kpc, shown in Fig. 7.
In order to allow a direct comparison with our weak lensing studies
in Sect. 5.1 and to derive an estimate of r200 we
perform a fit to the NFW profile (Navarro et al. 1996,1997) given by
Z3146 was observed with WFI@ESO/MPG2.2m in the two observing
programs 68.A-0255 (P.I. S. Schindler) and 073.A-0050 (P.I. P.
Schneider). The first one obtained 8000 s in broad band V(BB#V/89_ESO843) and 16100s in broad band R (ESO filter
BB#Rc/162_ESO844). The second programme observed for another 8900 s
in R and 1500s in B (BB#B/123_ESO878). All data were
processed with our image reduction pipeline developed within the
GaBoDS project. It performs all necessary steps from raw frames to
astrometrically and photometrically calibrated and co-added images.
The individual methods and its performances on WFI data are
described in detail in Schirmer et al. (2003) and Erben et al. (2005). All
data were obtained during clear nights, under good seeing conditions
(![]()
![]() )
and with a large dither box of about
)
and with a large dither box of about
![]() to ensure good flat-fielding and an accurate
astrometric calibration. The images were tied to the astrometric
frame of the USNO-A2 catalogue (Monet et al. 1998), photometrically
calibrated with Stetson standards (Stetson 2000) and finally
co-added with the Swarp tool (Bertin 2002). We produced
several co-added images from our R band exposures mainly to
crosscheck our object shape measurements in the weak lensing
analysis (see Sect. 5.1). The characteristics of all
co-added images used in this work are summarised in
Table 3 and Figs. 8 and 9. Each co-added science image has a pixel scale
of
to ensure good flat-fielding and an accurate
astrometric calibration. The images were tied to the astrometric
frame of the USNO-A2 catalogue (Monet et al. 1998), photometrically
calibrated with Stetson standards (Stetson 2000) and finally
co-added with the Swarp tool (Bertin 2002). We produced
several co-added images from our R band exposures mainly to
crosscheck our object shape measurements in the weak lensing
analysis (see Sect. 5.1). The characteristics of all
co-added images used in this work are summarised in
Table 3 and Figs. 8 and 9. Each co-added science image has a pixel scale
of
![]() and is accompanied by a weight map characterising
its noise properties.
and is accompanied by a weight map characterising
its noise properties.
Table 3:
Characteristics of the co-added WFI images. The limiting
magnitudes quoted in Col. 4 are defined in the Vega system via
![]() ,
where ZP is the magnitude zeropoint,
,
where ZP is the magnitude zeropoint,
![]() is the number
of image pixels in a circle with radius
is the number
of image pixels in a circle with radius
![]() and
and ![]() the sky background noise. The seeing in Col. 5 was measured with
the SExtractor FWHM_IMAGE parameter. The groups in Bonn (B)
and Innsbruck (I) observed Z3146 with an offset of about
the sky background noise. The seeing in Col. 5 was measured with
the SExtractor FWHM_IMAGE parameter. The groups in Bonn (B)
and Innsbruck (I) observed Z3146 with an offset of about
![]() In Ra and
In Ra and
![]() in Dec. The exact layout is given in
Fig. 8. For the R band we created, besides the
individual stacks, a deep mosaic in the common area (A). We note
that the Innsbruck R band has nearly double the exposure time of
the Bonn image but about the same limiting magnitude as it was
observed during less favourable moon phases. The quality of our
photometric calibration is crosschecked in Fig. 9.
in Dec. The exact layout is given in
Fig. 8. For the R band we created, besides the
individual stacks, a deep mosaic in the common area (A). We note
that the Innsbruck R band has nearly double the exposure time of
the Bonn image but about the same limiting magnitude as it was
observed during less favourable moon phases. The quality of our
photometric calibration is crosschecked in Fig. 9.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figures/4413_f08.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg191.gif) |
Figure 8:
Layout of the Z3146 R-band WFI observations
of the Bonn (B; solid lines) and Innsbruck (I; dashed lines)
groups. The orientation with respect to the sky is North-Up and
East-Left. The overlap in the R exposures allows useful tests
in the shape measurement procedures during our weak lensing
analysis (see Sect. 5.1). If not stated otherwise we
use the deep R band stack from both observing campaigns and
work in the common area (A) where we have data in B, V and
R available. It has an extent of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figures/4413_f09.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg192.gif) |
Figure 9: As a control check for our photometric calibration we plot colours of bright, unsaturated stars in our WFI fields compared to isochrones for stars of 10 Gyrs with a metallicity of 0.4% (see Girardi et al. 2002). Magnitudes for the stars were estimated with the SExtracor MAG_AUTO magnitude. Our data are in excellent agreement with the isochrone predictions. |
| Open with DEXTER | |
As a second method for determining the mass and its distribution of Z3146 we performed a weak lensing mass reconstruction. For a broad introduction on weak lensing and its application in cluster mass determinations see for instance Bartelmann & Schneider (2001). In the following we describe the creation of our background galaxy catalogue and the weak lensing analysis. Throughout the analysis we use standard weak lensing notation.
Because of the large offsets between the observations from the Bonn and Innsbruck groups it is not obvious whether we can savely use the deep stack (A) for the lensing analysis or whether we have to work on the individual co-additions (I) and (B). This mainly comes from the assumption of a smooth variation of the PSF over the whole field-of-view when we correct galaxy shapes for PSF effects. With the large offsets we could suffer from discrete jumps in the PSF anisotropy within the (A) mosaic. However, in Fig. 10 we see that the PSFs of all three stacks are well behaved in the (A) area. We performed comparisons of the final shear estimates in the (I), (B) and (A) mosaics and found that they are in excellent agreement (see Figs. 11 and 12). Therefore we decided to use the (A) mosaic, which is the deepest image, for our primary analysis.
The next step is to clean our lensing catalogue from likely cluster
members, foreground galaxies and faint stars. To this end we plot
stars and bright galaxies (R<22.0), which have a high probability
to be at a lower redshift than the cluster, in a colour-colour
diagram (see Fig. 13). We note that all these objects
mostly occupy a limited and well defined area in colour-colour
space. We finally use the following criteria to clean our background
source catalog: we reject all objects with R<22.0 and keep objects
between
22.0<R<23.0 if they do not lie in the following area of
the (B-V) vs. (V-R) diagram:
![]() .
We keep all
objects with R>23.0 as probable background sources. We note that
Clowe & Schneider (2002) and Dietrich et al. (2005) used similar criteria to
identify foreground objects.
.
We keep all
objects with R>23.0 as probable background sources. We note that
Clowe & Schneider (2002) and Dietrich et al. (2005) used similar criteria to
identify foreground objects.
For our final lensing catalogue we additionally exclude all objects
falling in masked image regions (around bright stars, satellite
tracks etc.). This leaves us with about 12 galaxies per sq. arcmin
as direct tracers of the cluster shear. Around the Brightest Cluster
Galaxy (BCG) of Z3146, this average density is reached at a radius
of about
![]() with only very few sources in the cluster
centre.
with only very few sources in the cluster
centre.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/4413_f10.ps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg198.gif) |
Figure 10:
Stellar anisotropies for the fields (I), (B) and (A)
in their common area. The length of the bars gives a measure for the
stellar ellipticity and the direction the orientation of the semi-major
axis. The longest bars correspond to an ellipticity of about |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figures/4413_f11.ps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg199.gif) |
Figure 11:
Galaxy ellipticities after all PSF corrections
from completely independent analyses of the (I), (B) and (A)
images in the overlap area. In the upper panels we compare the
(B) and (I) sets which are independent (in terms of raw images
entering the co-added stacks) from each other. The slopes of the
fitted lines are 0.983 for e1 and 0.95 for e2. For the lower
panels (comparison between (A) and (I)) the slopes are 0.992 for
e1 and 0.974 for e2. The corresponding numbers for (A)-(B) are
1.080 for e1 and 1.091 for e2 (not shown in the figures).
We conclude that the measurements are in
very good agreement with each other. For the fits, the Ordinary
Least Squares bisector method (see Isobe et al. 1990),
which considers errors in e1 and e2, is chosen.
After applying the line fits to the ellipticity components
the mean shear differences are compatible with zero in
all four cases.
We note that the
standard deviation of the residuals
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{figures/4413_f12.ps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg200.gif) |
Figure 12:
Differences of corrected galaxy ellipticity measurements
from the (I) and (A) images as function of image position.
We see no systematic trends of residuals
with object position. Also a closer, visual inspection of the two-dimensional
ellipticity residual distribution reveals no systematics on small
scales. The standard deviation of the ellipticity components around
zero is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figures/4413_f13.ps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg202.gif) |
Figure 13:
To obtain criteria to reject probable low z foreground
objects from our lensing analysis we plot all bright objects with R<22.0 in a colour-colour diagram. Most of them lie in a well defined area which we
use to clean our catalogue. Elliptical cluster galaxies for a z=0.3 cluster are expected around
|
| Open with DEXTER | |
The main interest of the weak lensing analysis
in this work is an estimate of the total cluster mass of Z3146 and
its inter-comparison with the X-ray analysis. We first perform a
standard KS93 cluster mass reconstruction (see Kaiser & Squires 1993)
to investigate the dark matter distribution and to obtain an
estimate for the cluster centre. In addition, we calculate a B-mode map, i.e. we performed another mass reconstruction after
all object ellipticities have been rotated by 45 degrees. This map
should contain noise only if the lensing data are free from
systematics. The results are discussed in Fig. 14.
We see that our lensing centre is in excellent agreement with that
determined from our X-ray analysis (see also Sect. 3.2) and we use the X-ray position for the
following analysis. We estimate significances for peaks in our
reconstructions and errors on the lensing centre with the following
procedure: we randomise the orientation of our galaxies, redo a KS93
mass reconstruction with the new catalogue and repeat this procedure
many times. For the peak significance we count how often the
![]() value in our noise maps exceeds that of the lensing signal.
With 29 700 realisations the probabilities that the cluster peak, the
cluster mass extension and the eastern and western holes in the
B-mode map are pure noise features are 0/29700, 170/29700, 88/29700
and 9/29700. Assuming Gaussian statistics this translates to
significances of >
value in our noise maps exceeds that of the lensing signal.
With 29 700 realisations the probabilities that the cluster peak, the
cluster mass extension and the eastern and western holes in the
B-mode map are pure noise features are 0/29700, 170/29700, 88/29700
and 9/29700. Assuming Gaussian statistics this translates to
significances of >![]() ,
,
![]() ,
,
![]() and
and
![]() respectively. We conclude that the highly significant
cluster peak has no significant extension to the South. Next we
estimate errors on the lensing peak position. The best way to
measure the centroid dispersion would be to use a parametric model
for the mass concentration and to generate noisy mass maps with
randomised ellipticity orientations and galaxy positions. If the
model were true we would obtain accurate error estimates from the
noisy mass realisations. With the data at hand we can follow this
idea by considering the original reconstruction as the input mass
model. We probably overestimate the true error in this way because
our input model already contains measurement noise. We plot the
result of this exercise for 200 maps in the lower left panel of Fig. 15. We find a significant asymmetry in the
distribution of positional differences. The positional accuracy is
about 2.3 times better along RA than in Dec. As the mass
distribution is elongated towards the South we would expect a skewed
distribution of the positional errors towards negative Dec values
but the observed symmetric elongation in the North-South direction
is surprising. We checked that not a few, very elongated galaxies
or shot noise from the galaxy positions (introduced for instance by
object masks) are responsible for this result (see Fig. 15). Given this result we quote the positional
accuracy of our lensing centre as
respectively. We conclude that the highly significant
cluster peak has no significant extension to the South. Next we
estimate errors on the lensing peak position. The best way to
measure the centroid dispersion would be to use a parametric model
for the mass concentration and to generate noisy mass maps with
randomised ellipticity orientations and galaxy positions. If the
model were true we would obtain accurate error estimates from the
noisy mass realisations. With the data at hand we can follow this
idea by considering the original reconstruction as the input mass
model. We probably overestimate the true error in this way because
our input model already contains measurement noise. We plot the
result of this exercise for 200 maps in the lower left panel of Fig. 15. We find a significant asymmetry in the
distribution of positional differences. The positional accuracy is
about 2.3 times better along RA than in Dec. As the mass
distribution is elongated towards the South we would expect a skewed
distribution of the positional errors towards negative Dec values
but the observed symmetric elongation in the North-South direction
is surprising. We checked that not a few, very elongated galaxies
or shot noise from the galaxy positions (introduced for instance by
object masks) are responsible for this result (see Fig. 15). Given this result we quote the positional
accuracy of our lensing centre as
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{figures/4413_f14...
... \includegraphics[angle=-90,width=7.5cm,clip]{figures/4413_f142.ps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg206.gif) |
Figure 14:
KS93 weak lensing cluster mass reconstruction of Z3146
( left panel). The shear field was smoothed with a Gaussian of width
|
| Open with DEXTER | |
While our mass maps give us insight into the dark matter
distribution in Z3146 it is difficult to obtain reliable estimates
for the total lensing mass and the involved errors. The main
problems are that mass reconstructions involve a convolution from
the measurable shear field and, in addition, they become very noisy
at a distance several arcminutes from the cluster centre (see Fig. 14). Moreover, they intrinsically suffer from the
mass-sheet degeneracy. Hence, we will estimate a lensing mass by
directly fitting parametrised lensing models to the shear data. The
error analysis is simplified significantly in this case. Moreover,
model fits break the mass-sheet degeneracy by the explicit
assumption that ![]() at large distances from the lensing centre
is zero. The main drawback is that shear data alone do not allow a
clear discrimination between different, plausible mass models (see
Fig. 16).
at large distances from the lensing centre
is zero. The main drawback is that shear data alone do not allow a
clear discrimination between different, plausible mass models (see
Fig. 16).
For our model fits to the shear data we primarily consider the
universal density profile (NFW) proposed by Navarro et al. (1996). The details
for the calculation of the lensing quantities ![]() and
and ![]() for this profile are given in several publications and the details
are not repeated here (see e.g. Kruse & Schneider 1999; Bartelmann 1996). To
determine our model parameters we use the log-likelihood method
proposed in Schneider et al. (2000). We maximise the likelihood
function:
for this profile are given in several publications and the details
are not repeated here (see e.g. Kruse & Schneider 1999; Bartelmann 1996). To
determine our model parameters we use the log-likelihood method
proposed in Schneider et al. (2000). We maximise the likelihood
function:
Before we apply this method we still have to specify the redshifts
of the source galaxies and the galaxy sample we include in our fits.
In Fig. 16 we show the tangential component of the
shear around the cluster centre. We can trace the cluster shear
signal over the whole field-of-view of
![]()
![]() . Hence, we include all preselected
background galaxies in our estimations. For the dispersion of the
unlensed ellipticities
. Hence, we include all preselected
background galaxies in our estimations. For the dispersion of the
unlensed ellipticities
![]() we use the measured
value of our galaxies
we use the measured
value of our galaxies
![]() averaged over the whole
field-of-view. Here we assume that weak lensing does not change this
value significantly and we estimate
averaged over the whole
field-of-view. Here we assume that weak lensing does not change this
value significantly and we estimate
![]() .
For
the redshift distribution of our background galaxies we use
estimates from Hetterscheidt et al. (2006). The authors obtained photometric
redshifts for 62 000 galaxies with
21.5<R<24.5. Their WFI data
consist of 1.75 sq. degree of deep
.
For
the redshift distribution of our background galaxies we use
estimates from Hetterscheidt et al. (2006). The authors obtained photometric
redshifts for 62 000 galaxies with
21.5<R<24.5. Their WFI data
consist of 1.75 sq. degree of deep ![]() photometry in three
different patches (see Hildebrandt et al. 2006; Hetterscheidt et al. 2006, for details on the data).
The photometric redshift distribution is parametrised by the
following function introduced by Brodwin et al. (2006):
photometry in three
different patches (see Hildebrandt et al. 2006; Hetterscheidt et al. 2006, for details on the data).
The photometric redshift distribution is parametrised by the
following function introduced by Brodwin et al. (2006):
![\begin{displaymath}p_1(z) = \left(\frac{z}{z_0}\right)^\alpha
\exp\left[-\left(\frac{z}{z_0}\right)^\beta\right] \end{displaymath}](/articles/aa/full/2007/31/aa4413-05/img217.gif) |
(8) |
![\begin{displaymath}p_2(z) = \exp{\left[\left(\frac{z_t}{z_1}\right)^\gamma -
\left(\frac{z}{z_1}\right)^\gamma \right]}~p_1(z_{\rm t}); \end{displaymath}](/articles/aa/full/2007/31/aa4413-05/img218.gif) |
(9) |
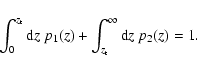 |
(10) |
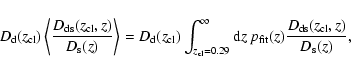 |
(11) |
For our fits to the NFW profile, we consider the concentration cand the radius r200 (see Navarro et al. 1996) as free model
parameters. With our setup, the application of our prescription to
the shear data leads to best fit values of
![]() kpc and
c=3.6+2.8-2.4. The model has a significance of 4.35 over one
with zero mass and the errors on r200 and c are at the
kpc and
c=3.6+2.8-2.4. The model has a significance of 4.35 over one
with zero mass and the errors on r200 and c are at the ![]() confidence level. They were estimated with our likelihood analysis
by keeping c or r200 at its best fit value and leaving
r200 or c as the only free parameter. In Fig. 27b we show confidence contours of our analysis
and note that both parameters are reasonably well constrained except
for low values of c see Sect. 7 for a comparison
to an NFW model based on X-ray data). In addition to the NFW profile
we also modeled our shear data by a Singular Isothermal Sphere (SIS)
characterised by its velocity dispersion
confidence level. They were estimated with our likelihood analysis
by keeping c or r200 at its best fit value and leaving
r200 or c as the only free parameter. In Fig. 27b we show confidence contours of our analysis
and note that both parameters are reasonably well constrained except
for low values of c see Sect. 7 for a comparison
to an NFW model based on X-ray data). In addition to the NFW profile
we also modeled our shear data by a Singular Isothermal Sphere (SIS)
characterised by its velocity dispersion ![]() .
Our best fit
model has
.
Our best fit
model has
![]() km s-1. The errors represent the
90% confidence level and the model has a significance of
km s-1. The errors represent the
90% confidence level and the model has a significance of
![]() compared to the zero mass model. In contrast to the NFW
fit, the significance and the estimated velocity dispersion of the
SIS model show some dependence on the galaxies included close to the
cluster centre. We notice an increase of significance by excluding
the galaxies in a circle
compared to the zero mass model. In contrast to the NFW
fit, the significance and the estimated velocity dispersion of the
SIS model show some dependence on the galaxies included close to the
cluster centre. We notice an increase of significance by excluding
the galaxies in a circle
![]() around the cluster (five
objects) and a smooth decrease of S/N if we reject more galaxies
beyond that point. Hence, we used all galaxies with a distance
greater than
around the cluster (five
objects) and a smooth decrease of S/N if we reject more galaxies
beyond that point. Hence, we used all galaxies with a distance
greater than
![]() from the cluster centre for our SIS
fit.
from the cluster centre for our SIS
fit.
We finally discuss a possible bias of our result due to a systematic
underestimate of the shear. As we showed in Erben et al. (2001) and
within the Shear Testing Program (see Heymans et al. 2005) our
pipeline may underestimate weak shear by 10-15%. We recalculated
the best fit NFW values after boosting all ellipticities by a factor
of 1.15. We then obtain
![]() kpc
and
c=3.66+2.52-2.18 which is well within the error bars of
the original signal. Hence, a possible systematic underestimate of
the shear by about 15% would not change our results significantly.
At the end of this section we show in Fig. 18 the
total mass properties given by our model fits. We also present a
mass-to-light ratio analysis in Sect. 6.3
and will compare our results with masses from X-ray analyses in
Sect. 7.
kpc
and
c=3.66+2.52-2.18 which is well within the error bars of
the original signal. Hence, a possible systematic underestimate of
the shear by about 15% would not change our results significantly.
At the end of this section we show in Fig. 18 the
total mass properties given by our model fits. We also present a
mass-to-light ratio analysis in Sect. 6.3
and will compare our results with masses from X-ray analyses in
Sect. 7.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{figures/4413_f15.ps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg238.gif) |
Figure 15:
The lower left plot shows the lensing centres of our
cluster reconstructions after adding noise realisations to our
signal (see text for details). The quoted distances are with
respect to the original cluster centre. Formal |
| Open with DEXTER | |
| |
Figure 16:
Left: tangential shear signal as function
of radius from the centre of Z3146. The signal is robust and we can trace
the cluster shear up to the border of our data field. The solid line
shows the reduced shear of our best fit NFW model
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{figures/4413_f17.ps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg241.gif) |
Figure 17: The figure shows comparisons of the tangential shear signal around Z3146 from common background objects for the (A) and (B) ( upper panel) and the (A) and (I) sets ( lower panel). The left measurements are from (A) and the shifted ones from (B) and (I) respectively. The catalogues of common sources were created by merging our lensing objects from (A) with the ellipticity catalogues from (I) and (B); see Fig. 11. As in the ellipticity comparisons, the tangential shear signals around the cluster agree reasonably well. A very different behaviour is observed for the first bin to which only about a dozen galaxies contribute. Note that the initial catalogues were created independently and hence the object samples in the two comparisons are not exactly the same. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{figures/4413_f18.eps}
\end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg244.gif) |
Figure 18:
Total weak lensing mass calculated from our best fit mass models
in spheres of radius r around the cluster centre. Solid lines encompass
our best fit NFW model
|
| Open with DEXTER | |
In addition to the weak lensing analysis we have searched the
central cluster region for strongly lensed objects. In ground based
observations usually only arcs tangentially aligned with respect to
the mass centre are visible, as radial arcs are very thin and faint
structures in the vicinity of bright central galaxies of clusters.
In addition, arcs and their counter images have the same spectra and
redshifts ![]()
![]() .
However we do not have
spectra, hence apart from the position and the morphology, the
redshift is the main identification criterion. Therefore we
investigated whether it is possible using our observations to
roughly estimate the photometric redshift or at least to find out
whether an object belongs to a fore- or background population. For
that purpose we have performed simulations using the software
package hyperz
.
However we do not have
spectra, hence apart from the position and the morphology, the
redshift is the main identification criterion. Therefore we
investigated whether it is possible using our observations to
roughly estimate the photometric redshift or at least to find out
whether an object belongs to a fore- or background population. For
that purpose we have performed simulations using the software
package hyperz![]() (Bolzonella et al. 2000). We created a
set of 3000 artificial galaxies with the following parameters:
(Bolzonella et al. 2000). We created a
set of 3000 artificial galaxies with the following parameters:
![]() ,
R magnitude
,
R magnitude
![]() (which
corresponds to the range of the arc candidates), using the simulated
filter WFI R band (ESO844) as the reference filter. The type of
the galaxies was also randomly chosen to be either E, S0, Sa, Sb, Sc
or Sd. The simulations have shown that it is not possible to obtain
any reliable redshift estimate from BVR images only. 38% of all
simulated galaxies with
(which
corresponds to the range of the arc candidates), using the simulated
filter WFI R band (ESO844) as the reference filter. The type of
the galaxies was also randomly chosen to be either E, S0, Sa, Sb, Sc
or Sd. The simulations have shown that it is not possible to obtain
any reliable redshift estimate from BVR images only. 38% of all
simulated galaxies with
![]() were found to be
background objects. On the other hand, 27% of the background
galaxies (defined as
were found to be
background objects. On the other hand, 27% of the background
galaxies (defined as
![]() )
were measured to be located
in front of Z3146. Hence it is even not possible to decide whether
an object of unknown redshift is a foreground or a background object
and we have to restrict our search
for strongly lensed objects to morphological criteria only.
)
were measured to be located
in front of Z3146. Hence it is even not possible to decide whether
an object of unknown redshift is a foreground or a background object
and we have to restrict our search
for strongly lensed objects to morphological criteria only.
Unfortunately there is no common definition of an arc candidate. The
definition we adopt of a gravitational arc candidate is that of an
elongated object, aligned tangentially with respect to the cluster
center, a minimum length of 1
![]() 0 and a length-to-width ratio
0 and a length-to-width ratio
![]() .
However it is not yet clear whether Z3146 can produce
strong lensing or not: the low concentration parameters c obtained
during the modelling of both, the X-ray (
.
However it is not yet clear whether Z3146 can produce
strong lensing or not: the low concentration parameters c obtained
during the modelling of both, the X-ray (
![]() ,
,
![]() kpc, see Sect. 3.5) and
the weak lensing data (
c=3.6+2.8-2.4,
kpc, see Sect. 3.5) and
the weak lensing data (
c=3.6+2.8-2.4,
![]() kpc, see
Sect. 5.1.2) to an NFW profile, leads to an Einstein
ring of only
kpc, see
Sect. 5.1.2) to an NFW profile, leads to an Einstein
ring of only ![]()
![]() .
However, due to the large errors in
both the c and r200 determination and the unknown source
redshift, we cannot exclude the strong lensing ability: a source
redshift of z=2 and adopting the upper limits of c and r200(leading to c=6.4 and
.
However, due to the large errors in
both the c and r200 determination and the unknown source
redshift, we cannot exclude the strong lensing ability: a source
redshift of z=2 and adopting the upper limits of c and r200(leading to c=6.4 and
![]() kpc, based on
weak lensing values) shifts the Einstein ring to
kpc, based on
weak lensing values) shifts the Einstein ring to ![]()
![]() .
Additionally, our adopted SIS model derived in
Sect. 5.1.2 leads to an Einstein radius of the same
size, assuming the source located at the derived mean redshift
.
Additionally, our adopted SIS model derived in
Sect. 5.1.2 leads to an Einstein radius of the same
size, assuming the source located at the derived mean redshift
![]() .
Adopting
.
Adopting
![]() km s-1, the upper limit, leads to a critical curve at
km s-1, the upper limit, leads to a critical curve at ![]()
![]() .
Hence we restrict our search to regions within a
radius of about
.
Hence we restrict our search to regions within a
radius of about
![]() ,
centred on the position of the
Bright Central Galaxy.
,
centred on the position of the
Bright Central Galaxy.
In a deep arc search using the WFPC2 archive, Sand et al. (2005) quote one arc in this archival HST data set (A1 in our data set). Our identification of strong lensing features was done by visual inspection of the WFPC2 frames in direct comparison with the deep WFI exposures. As some of the candidates are very similar to not fully removed cosmics we carefully searched for all identified objects whether there is a corresponding object on all WFI frames. In this way we identified 4 objects in total (denoted as A1,...,A4) in the chosen field as good candidates for being strong lensing features (see Figs. 19 and 20).
A comparison even with shallow space based observations is a good
method to identify possible gravitational arcs due to the missing
atmospheric blurring effects. Several of the arc candidates were
smoothed on the WFI images so as to even lose their tangential
alignment. In particular, objects A3 and A4 are so
strongly influenced by observational effects that they are not
identifyable as arcs in ground based observations. A detailed
comparison between the WFI and WFPC2 images of the arcs is shown in
Fig. 20. Note that the exposure time of the WFI
R-image is 6.9 h, whereas for the WFPC2 it was only
![]() 0.28 h. Nevertheless, the arc candidates visible in the HST
image are clearly recognizable as possible gravitational arcs,
whereas in the WFI frame seeing effects dominate the shape of the
objects.
0.28 h. Nevertheless, the arc candidates visible in the HST
image are clearly recognizable as possible gravitational arcs,
whereas in the WFI frame seeing effects dominate the shape of the
objects.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{figures/4413_f19.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg261.gif) |
Figure 19: HST image of Z3146 obtained by the WFPC2. The exposure time was 1000 s using the filter F606W. The objects A3 and A4 were found on the HST frame by visual inspection (see Sect. 5.2.1 for more details). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{figures/4413_f20.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg262.gif) |
Figure 20:
Detailed comparison of the arc candidates in Z3146 ( top: WFI,
bottom: WFPC2). In all images North is up, East to the left, the FoV is
|
| Open with DEXTER | |
To measure the length-to-width ratio l/w we used SExtractor
to detect the arc candidates on the WFPC2 image as it is not
affected by atmospheric blurring. Due to its shallowness we used a
value of 0.75 for DETECT_THRESH and ANALYSIS_THRESH. The l/wratio itself was determined using the same ansatz as in
Lenzen et al. (2004) and Bertin (2005): we treat the arcs as a set of
pixels with a certain light intensity value at each pixel. The light
distribution of a certain object is then defined by all
corresponding pixels detected by SExtractor shown in the
SEGMENTATION images. Hence we can compute the second moments
![]() and
and ![]() of this light distribution in the usual
way (see e.g. Lenzen et al. 2004; Bertin 2005). Although the length
l is not equal to
of this light distribution in the usual
way (see e.g. Lenzen et al. 2004; Bertin 2005). Although the length
l is not equal to ![]() and the width w is not equal to
and the width w is not equal to
![]() the ratio l/w is equal to
the ratio l/w is equal to
![]() (Jähne 2002). Hence we obtain the
length-to-width ratio by determining
(Jähne 2002). Hence we obtain the
length-to-width ratio by determining ![]() and
and ![]() .
.
The photometry was also performed with the software package SExtractor 2.3.2. In contrast to the determination of l/w we used the WFI frames for this purpose, as those images are much deeper (see Table 3). The photometric measurement on the WFPC2 image was skipped as the F606W filter is fully covered by the V and R band of the WFI observations.
As we concentrate on the cluster itself we restricted the extraction
of object catalogues to a FoV of
![]()
![]() (4.26
(4.26
![]() Mpc
Mpc ![]() 4.26
4.26
![]() Mpc in our
cosmology). The V and R images were convolved with a slight
Gaussian filter of width 0.61 and 0.91 pixels, respectively, to
bring all observations to the same seeing of
Mpc in our
cosmology). The V and R images were convolved with a slight
Gaussian filter of width 0.61 and 0.91 pixels, respectively, to
bring all observations to the same seeing of ![]()
![]() (
(
![]()
![]() )
and hence ensure that all
objects are measured with the same photometric apertures.
)
and hence ensure that all
objects are measured with the same photometric apertures.
We used SExtractor in double image mode with the deep Rband image as detection frame and the following parameters:
DETECT_THRESH=7, ANALYSIS_THRESH=7, and DETECT_MINAREA=3 (the
higher detection threshold compared to the weak lensing analysis is
a result of the seeing correction). All magnitudes are obtained
using MAG_AUTO with PHOT_AUTOPARAMS=1,3.5, as elliptical apertures
and a Kron radius of this size is best suited to our observations.
In order to obtain clean catalogues with a minor fraction of
defective detections like obvious stars/foreground galaxies, traces
of asteroids and spurious detections in bright haloes of stars we
masked such objects to remove them from the final catalogues. The
image of Fig. 21 shows as example the original
R-band image including all masked objects within a FoV of
![]()
![]() (4.26
(4.26
![]() Mpc
Mpc ![]() 4.26
4.26
![]() Mpc in our
cosmology). All masks were identical for the final B and Vimage, except for the individual satellite tracks.
Mpc in our
cosmology). All masks were identical for the final B and Vimage, except for the individual satellite tracks.
The total galaxy catalogue contains 2138 objects having a
CLASS_STAR parameter < 0.95, MAG_AUTO < 99 in all bands
(considering an
E(B-V)=0.126 mag, taken from the
NED![]() , based on
Schlegel et al. 1998) and a FLUX_RADIUS >3.2 pixels in B, Vand R, respectively. In addition we used WEIGHT maps created by
the data reduction pipeline (see Erben & Schirmer 2003; Erben et al. 2005, for more
details).
, based on
Schlegel et al. 1998) and a FLUX_RADIUS >3.2 pixels in B, Vand R, respectively. In addition we used WEIGHT maps created by
the data reduction pipeline (see Erben & Schirmer 2003; Erben et al. 2005, for more
details).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{figures/4413_f21.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg268.gif) |
Figure 21:
R-band image of Z3146. The image has a FoV of |
| Open with DEXTER | |
The results of the photometric and morphological investigations of all 4 arc candidates are summarised in Tables 4 and 5, respectively. In this section we analyse the arc candidates using these informations.
We can roughly estimate the strong lensing mass inside an Einstein
ring at the position of the outer most arc A1 (![]()
![]()
![]() 120 kpc). This mass can be estimated to be
120 kpc). This mass can be estimated to be
![]() ,
where the
main value is derived for
,
where the
main value is derived for
![]() ,
the
mean redshift value obtained in Sect. 5.1.2. The
errors are calculated for
,
the
mean redshift value obtained in Sect. 5.1.2. The
errors are calculated for
![]() .
However, as we do not know either the redshift or the
geometric alignment of the source with respect to the lens, this
procedure gives only a rough upper limit of the mass in the core.
.
However, as we do not know either the redshift or the
geometric alignment of the source with respect to the lens, this
procedure gives only a rough upper limit of the mass in the core.
Table 4:
Table of the arc candidates shown in
Fig.19. "cc'' denotes the cluster centre, the
length-to-width ratio l/w is calculated with the help of
![]() ,
and
,
and ![]() (the second order moments of the light
distribution) and is measured on the WFPC2 images as it is not
affected by atmospheric blurring. A value of =0.75 was chosen for
both, the DETECT_THRESH and ANALYSIS_THRESH due to the shallowness
of the image. The magnitudes are instrumental WFI magnitudes in the
Vega system. All objects are photometrised using SExtractor's
MAG_AUTO.
(the second order moments of the light
distribution) and is measured on the WFPC2 images as it is not
affected by atmospheric blurring. A value of =0.75 was chosen for
both, the DETECT_THRESH and ANALYSIS_THRESH due to the shallowness
of the image. The magnitudes are instrumental WFI magnitudes in the
Vega system. All objects are photometrised using SExtractor's
MAG_AUTO.
Table 5: Photometric properties of the arc candidates and their possible counter images. See Sect. 5.2.4 for more details and discussions.
One of the most interesting questions is the possibility of finding multiple images of one single background source. Unfortunately we do not have spectra of the objects (see Sect. 5.2.1) which allow a secure identification of counter images. Hence we search for counter images in the following way:
Counter images of arcs may not appear as elongated objects in the case of a folded arc system. In addition, they can differ in magnitudes due to the gravitational magnifying effect and can appear in unexpected locations (Broadhurst et al. 2005a), which are not predictable without a precise model. Hence we have to restrict the identification of multiple lensed objects to investigations of the colour information (B-V), (B-R), and (V-R) only, as they are conserved by lensing.
The search for multiple images was performed for all 4 arc
candidates independently in 2 steps: first, we searched the galaxy
catalogue for objects with (a) coinciding colours (V-R), (B-R)and (B-V), and (b) lying in a radius of 30
![]() 0 with respect
to the cluster center position in the RBS. In a second step we
discarded all objects being obvious cluster or
foreground galaxies by visual inspection.
0 with respect
to the cluster center position in the RBS. In a second step we
discarded all objects being obvious cluster or
foreground galaxies by visual inspection.
arc candidate A1: in total we found two objects which
might be counter images of candidate A1, denoted by C1, and C2, respectively (see
Fig. 23). It is hard to judge whether those
objects are counter images as they are hardly visible in the shallow
WFPC2 image. However, C2 is located at a distance of ![]()
![]() with respect to the cluster center and hence we
expect it to be much more sheared at this position if it had
originated from the same object as A1. Additionally, the
colours agree only within their large error bars (see
Table 5 for the numbers). Hence we conclude
that it is quite unlikely that
this object is a counter image of A1.
with respect to the cluster center and hence we
expect it to be much more sheared at this position if it had
originated from the same object as A1. Additionally, the
colours agree only within their large error bars (see
Table 5 for the numbers). Hence we conclude
that it is quite unlikely that
this object is a counter image of A1.
arc candidates A2 and A3: both candidates show colour coincidences with each other and C1 - C3. However, again the colour differences only agree within their error bars (see Table 5 for the numbers). The colour of A2 might be reddened to a certain amount by elliptical galaxies in its vicinity, nevertheless it is very unlikely that these objects have the same source.
arc candidate A4: we did not find any counter image candidates for this object.
Counter images also often occur nearby the central galaxy in the case of a not perfect alignment between the observer, the lens and the source. Hence they lie in the halo of a bright central object affecting their colour and/or are dramatically sheared up to a radial arc (see Sand et al. 2005, for some examples). Therefore we investigated the BCG using the HST image in more detail.
A closer look at the WFPC2 exposure of the BCG reveals some knots in its very central part. To investigate these structures and to look for a possible radial arc we subtracted as a first step an elliptical model derived by fitting ellipses to isophotes of the BCG (done with the help of the IRAF tasks isophote and bmodel in the STSDAS package) as well as an artificial de Vaucouleur profile (task mkobjects in noao.artdata).
Figure 22 shows the central part of Z3146 with and without the subtracted elliptical isophote model of the BCG. The removal of the BCG reveals, apart from several clumps, an elongated substructure in the centre of the BCG along its major axis in the opposite direction to A1. However, we need deeper observations for identification of this object. At the current stage we can neither exclude the possibility of this object of being a radial arc or a filamentary structure common in cooling flow clusters.
However, the fact that we did not find definitive counter images in
our observations does not mean that there are none. Lensed sources
can appear as very faint and thin arclets which are only visible in
deep HST observations. Such arclets are therefore hard to find in
ground based observations. Some prominent examples of lensing
clusters such a large number of faint arc(lets) are e.g. A2218
(see Soucail et al. 2004, and references therein), A1689
(Broadhurst et al. 2005a), A370 (Bézecourt et al. 1999) or CL0024+16
(Kneib et al. 2003; Broadhurst et al. 2000).
![\begin{figure}
\par\includegraphics[width=14cm,clip]{figures/4413_f22.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg289.gif) |
Figure 22: HST image of the innermost part of Z3146. In the right image we subtracted an elliptical model (based on fitting an ellipse to each isophote obtained by the IRAF tasks isophote and bmodel in the STSDAS package). Several distinct substructures are visible, but require deeper observations for their identification. |
| Open with DEXTER | |
In this section we present additional optical investigations on Z314 6 which are based on the WFI frames.
Independent of the previous analyses we have created different
catalogues as we have different selection criteria for the further
investigations. The lensing analysis focuses on background objects,
whereas the following investigations deal with the cluster members.
We extracted a catalogue of cluster members in the
following way:
From the galaxy catalogue created in
Sect. 5.2.3 we made the colour-magnitude
diagram (V-R) vs. R (see Fig. 24). In
this plot we identify a Red Sequence (henceforth RS, marked by the
two solid lines) which is used as the basis for the cluster member
detection. The extraction of the Red Sequence was done by eye. As
the RS galaxies belong to the ellipticals, which are the reddest
ones in a galaxy cluster, we use the upper limit of the RS distribution as the natural colour border and assume all objects
below the upper RS limit as cluster members. Additionally we skipped
all objects with ![]() mag as likely belonging to a
background population, and objects with
mag as likely belonging to a
background population, and objects with ![]() mag as likely
foreground systems. With these criteria we found in total 756 RS galaxies and 1478 cluster members.
mag as likely
foreground systems. With these criteria we found in total 756 RS galaxies and 1478 cluster members.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{figures/4413_f23.eps}
\end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg292.gif) |
Figure 23: R-band image taken with WFI. Possible counter images of the arc candidates are denoted with Cx. See Sect. 5.2.4 for the relations of the Cx to the arc candidates. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{figures/4413_f24.ps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg293.gif) |
Figure 24: (V-R) vs. R colour-magnitude diagram. A distinct Red Sequence is visible, framed by two solid lines. The dashed lines show the limits used for identification of cluster members (see text for more details). |
| Open with DEXTER | |
To investigate the distribution of the RS members we created galaxy
density maps in the following way: a blank image of about
![]() pixels (corresponding to a FoV of
pixels (corresponding to a FoV of
![]()
![]() ,
4.26
,
4.26
![]() Mpc
Mpc ![]() 4.26
4.26
![]() Mpc) was
created with pixel value "0'' everywhere. At each position of the
extracted Red Sequence galaxies (see Sect. 5)
the pixel value was changed to "1'' and a subsequent Gaussian
smoothing with
Mpc) was
created with pixel value "0'' everywhere. At each position of the
extracted Red Sequence galaxies (see Sect. 5)
the pixel value was changed to "1'' and a subsequent Gaussian
smoothing with
![]() pixels (corresponds to
250
pixels (corresponds to
250
![]() kpc) leads to the image in
Fig. 25.
kpc) leads to the image in
Fig. 25.
The galaxy density plot of the main Red Sequence
(Fig. 25) shows one large peak centred on
the main cluster with no distinct subclumps, except one small peak
south of the cluster core. This is an indication that Z3146 is a
relaxed cluster without any ongoing major merger event, which is
confirmed by the massive cooling flow found in previous
investigations (Edge et al. 1994; Fabian et al. 2002) and our own results of
![]()
![]() per year. In particular, the small distance
of about
per year. In particular, the small distance
of about
![]() between the optical and the
X-ray centre (Schwope et al. 2000) also confirms the calm character of this cluster.
between the optical and the
X-ray centre (Schwope et al. 2000) also confirms the calm character of this cluster.
Table 6:
Details of the catalogues, K-corrections values and the
Schechter function parameters ![]() ,
,
![]() and M* for the
three WFI filters. F is the fraction of light which is missing due
to the limiting magnitudes
and M* for the
three WFI filters. F is the fraction of light which is missing due
to the limiting magnitudes
![]() of the catalogue given
in Table 3. For the R band we used the limiting
magnitude for region A (see Table 3). See text for
more details. The Luminosity distance is 1.5 Gpc (distance modulus
m-M=40.88 at z=0.2906).
of the catalogue given
in Table 3. For the R band we used the limiting
magnitude for region A (see Table 3). See text for
more details. The Luminosity distance is 1.5 Gpc (distance modulus
m-M=40.88 at z=0.2906).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{figures/4413_f25.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg312.gif) |
Figure 25:
Galaxy density plot of Z3146. The FOV ( |
| Open with DEXTER | |
To calculate the total luminosity in the V band in solar units we
assume the solar absolute magnitude to be
![]() mag
(Cox 2000). We also assume the cluster members to follow the
standard Schechter luminosity function (Schechter 1976):
mag
(Cox 2000). We also assume the cluster members to follow the
standard Schechter luminosity function (Schechter 1976):
The total luminosity
![]() (see Table 6)
can now be obtained by integrating Eq. (12):
(see Table 6)
can now be obtained by integrating Eq. (12):
| (15) |
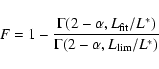 |
(16) |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{figures/4413_f26.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg325.gif) |
Figure 26:
V band light distribution map. The FoV is
|
| Open with DEXTER | |
Figure 26 shows the corresponding light distribution of the Red Sequence galaxies in V. Again, only one single, very distinct peak centred on the BCG is visible. In addition the distribution is very smooth and shows no substructures, confirming the relaxed state of Z3146.
In Sect. 5.1.2 we fitted the mass obtained by the weak
lensing method to an NFW profile with the following best-fit
parameters obtaining
![]() kpc
and
c=3.6+2.8-2.4 as best fit values. This leads to
kpc
and
c=3.6+2.8-2.4 as best fit values. This leads to
![]() .
Using these
values we find a mass-to-light ratio within r200 in the Vband of
.
Using these
values we find a mass-to-light ratio within r200 in the Vband of
![]() .
This value is in
agreement with e.g. Hradecky et al. (2000), who give a median value of
.
This value is in
agreement with e.g. Hradecky et al. (2000), who give a median value of
![]() for eight clusters within a radius of
for eight clusters within a radius of
![]() 1.38 h70-1 Mpc.
1.38 h70-1 Mpc.
We presented a combined investigation of optical and X-ray observations of the prominent galaxy cluster Z3146. This cluster seems to be in a relaxed state, which is confirmed by
We also determined the mass of this cluster with two independent
methods, weak lensing and X-ray measurements. Both data sets, X-ray
and lensing, were used to establish best fits to the commonly used
NFW model. Figure 27
shows the comparison of the confidence levels for these data:
Figure 27(a) - Xray-data: Confidence level
from a NFW fit to the mass profile derived from X-ray data according
to Eq. (4). The contour levels are 2.31, 6.25, 11.90
corresponding to confidence levels of 68.3% (![]() ), 95.4%
(
), 95.4%
(![]() ), 99.73% (
), 99.73% (![]() ).
).
Figure 27(b) - Lensing data: The contours
are at
![]() 2.30, 6.17, 9.21 corresponding to
confidence levels of 63.8%, 90%, 95.4% and 99% if we assume
Gaussian statistics. We varied the galaxy sample of the lensing fit
to investigate the dependence of the result on this parameter. On
the one hand, lowering the maximum radius to which galaxies enter
the calculations to
2.30, 6.17, 9.21 corresponding to
confidence levels of 63.8%, 90%, 95.4% and 99% if we assume
Gaussian statistics. We varied the galaxy sample of the lensing fit
to investigate the dependence of the result on this parameter. On
the one hand, lowering the maximum radius to which galaxies enter
the calculations to
![]() from the galaxy centre (we have
full data coverage around the cluster up to this radius; see Fig. 8) leads to
from the galaxy centre (we have
full data coverage around the cluster up to this radius; see Fig. 8) leads to
![]() kpc; c=4.01.
On the other hand, not considering the inner parts of the cluster
and using only galaxies with a distance larger than
kpc; c=4.01.
On the other hand, not considering the inner parts of the cluster
and using only galaxies with a distance larger than
![]() we obtain
we obtain
![]() kpc; c=1.0. We note that
r200 is reasonably well constrained and that the concentration
c mainly depends on the details near the cluster core. This
behaviour corresponds to the shape of our contours and is typical
for NFW profile fits in weak lensing studies; see e.g.
Clowe & Schneider (2002) and Dietrich et al. (2005). The parameter ranges in cand r200 imply an uncertainty of the total cluster mass of
kpc; c=1.0. We note that
r200 is reasonably well constrained and that the concentration
c mainly depends on the details near the cluster core. This
behaviour corresponds to the shape of our contours and is typical
for NFW profile fits in weak lensing studies; see e.g.
Clowe & Schneider (2002) and Dietrich et al. (2005). The parameter ranges in cand r200 imply an uncertainty of the total cluster mass of
![]() (considering radii of
(considering radii of
![]() Mpc; see also
Fig. 18).
Mpc; see also
Fig. 18).
Figure 27(c) - Direct Comparison: the "x'' marks our best fit lensing value of
![]() kpc
(
kpc
(
![]() kpc) and c=3.61, which lies in the
vicinity of the
kpc) and c=3.61, which lies in the
vicinity of the ![]() X-ray model. The triangle corresponds the
best NFW fit to the X-ray data:
X-ray model. The triangle corresponds the
best NFW fit to the X-ray data:
![]() kpc,
c=3.58 (
kpc,
c=3.58 (
![]() kpc, see Sect. 3.5
for more details). This best fit value is located within the
kpc, see Sect. 3.5
for more details). This best fit value is located within the
![]() contour of the lensing model. Hence both models are in
excellent agreement.
contour of the lensing model. Hence both models are in
excellent agreement.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{figures/4413_f27.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg341.gif) |
Figure 27: Comparison of confidence levels from NFW fits: Panel a) shows the fit to the X-ray data, Panel b) the fit to the shear data. A direct comparison with the corresponding best fit values is presented in Panel c), where the lensing model is represented by the solid lines (best fit marked by "x''), and the X-ray model by the dash-dotted lines (best fit values correspond to the triangle). See Sect. 7 for more details. |
| Open with DEXTER | |
A direct comparison of the mass profiles and the ratio between
![]() is given in Fig. 28,
which shows that the best fit models agree within
is given in Fig. 28,
which shows that the best fit models agree within ![]()
![]() .
.
Comparing the strong and weak lensing masses it seems that they
disagree. At the radius of the outermost arc at
![]() (
(![]() 120 kpc) we obtain a mass within an Einstein ring of about
120 kpc) we obtain a mass within an Einstein ring of about
![]()
![]() for
the strong lensing measurement. The NFW profile of the weak lensing
fit gives
for
the strong lensing measurement. The NFW profile of the weak lensing
fit gives
![]()
![]() at
the same position, which is, the best case assuming, roughly half of
at
the same position, which is, the best case assuming, roughly half of
![]() only. However, due to the large uncertainties in the
strong lensing mass determination (unknown redshifts, unknown
lensing geometry...) we assume this mass only to be a rough upper
value. Hence this discrepancy is likely an artifact of the large
numbers of uncertainties in the determination of the strong lensing
mass.
only. However, due to the large uncertainties in the
strong lensing mass determination (unknown redshifts, unknown
lensing geometry...) we assume this mass only to be a rough upper
value. Hence this discrepancy is likely an artifact of the large
numbers of uncertainties in the determination of the strong lensing
mass.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{figures/4413_f28.eps} \end{figure}](/articles/aa/full/2007/31/aa4413-05/Timg350.gif) |
Figure 28:
Comparison of the best fit NFW models obtained from X-ray data
(black lines) and weak lensing signal (gray lines). Both show good
coincidences within 1 |
| Open with DEXTER | |
Especially in relaxed clusters, the mass estimates obtained from
weak lensing and X-ray mass methods usually seem to agree very well
(Wu et al. 1998; Allen 1998). Recent observations of cooling flow clusters
derived from Chandra and/or XMM-Newton confirm these
results (see e.g. Allen et al. 2002; Cypriano et al. 2005). We find a
temperature of ![]() keV in Z3146, in agreement with the
assumption of Cypriano et al. (2004) that clusters having an ICM
temperature
keV in Z3146, in agreement with the
assumption of Cypriano et al. (2004) that clusters having an ICM
temperature ![]() 8.0 keV are in a relaxed state. In particular
relaxed clusters are interesting for cosmological studies as their
mass content tends to take a spherically symmetric shape, which is
the usual assumption in theoretical approaches. Hence a large sample
of such systems is a useful probe to verify whether the mass density
of galaxy clusters follows an NFW profile (Navarro et al. 1996,1997), or
whether a different profile like the Burkert (Burkert 2000), the
Moore (Moore et al. 1999) or the non-extensive profile
(Kronberger et al. 2006; Leubner 2005)
is a suitable description.
8.0 keV are in a relaxed state. In particular
relaxed clusters are interesting for cosmological studies as their
mass content tends to take a spherically symmetric shape, which is
the usual assumption in theoretical approaches. Hence a large sample
of such systems is a useful probe to verify whether the mass density
of galaxy clusters follows an NFW profile (Navarro et al. 1996,1997), or
whether a different profile like the Burkert (Burkert 2000), the
Moore (Moore et al. 1999) or the non-extensive profile
(Kronberger et al. 2006; Leubner 2005)
is a suitable description.
Acknowledgements
We are very grateful to Ludovic van Waerbeke for his help with the weak lensing cluster mass reconstruction and thank Joachim Wambsganss and Peter Schneider for fruitful comments. The authors also want to thank Rocco Piffaretti for his kind help during the NFW fit of the X-ray data, Eran Ofek for providing very useful MatLab©scripts and Leo Girardi for kindly generating isochrones for the WFI filters. We also thank the anonymous referee for invaluable comments, and S. Ettori for providing the software required to produce the X-ray colour map in Fig. 3. This work is supported by the Austrian Science Foundation (FWF) project number 15868, by the Deutsche Forschungsgemeinschaft (DFG) under the project ER 327/2-1, by NASA grant NNG056K87G and by NASA Long Term Space Astrophysics Grant NAG4-11025.