A&A 470, L17-L20 (2007)
DOI: 10.1051/0004-6361:20077681
LETTER TO THE EDITOR
Was the unusual solar cycle at the end of the XVIII century a result of phase asynchronization?
N. V. Zolotova -
D. I. Ponyavin
Institute of Physics, Saint-Petersburg State University, Russia
Received 19 April 2007 / Accepted 22 May 2007
Abstract
Aims. The problem of the unusual sunspot cycle in 1784-1799 is considered. Why was the length of the 4th solar cycle exceptionally large? Was it really composed of two shorter cycles? Resolving this puzzle seems to be very important for modern dynamo theories trying to explain the solar cyclicity.
Methods. We propose a possible scenario for the solar activity behavior during the 4th solar cycle. Analogies with the phase asynchronization observed at the time of the 20th solar cycle are presented.
Results. We suggest that the length of the 4th solar cycle can be explained by outstanding phase asynchrony between Northern and Southern hemispheric activities reaching a delay up to 4.5 years. The main effect of such asynchronization results in strong North-South asymmetry during the course of the ascending phase of the solar cycle 4.
Key words: Sun: activity - Sun: sunspots - Sun: magnetic
fields
The uncertainty and scarcity of historical records define the main
difficulties in reconstructing any solar activity in the past.
Even a small inaccuracy in sunspot observations can dramatically
change estimations, phase dynamics, and other solar cycle
properties because of the lack of statistics. Therefore careful
routine data mining is an essential part of solar reconstruction.
Not long ago, a sensational suggestion was made by Usoskin et al.
(2001) concerning the loss of one solar cycle at the
beginning of the Dalton minimum. It was supposed that the
generally accepted 4th solar cycle, according to Zürich
numeration, is actually a superposition of two cycles. The
traditional, exceptionally long 4th solar cycle breaks the famous
Gnevyshev-Ohl rule and leads to the phase catastrophe (Vitinsky et al. 1986; Kremliovsky 1994; Usoskin
& Mursula 2003). Two short cycles (9 and 7 years in
lengths) were suggested instead of this kind of abnormally long
cycle.
Krivova et al. (2002) have checked this hypothesis by
performing some statistical tests of available sunspot records and
also considered 10Be, 14C, and auroral proxy data.
According to their results, the presumably lost cycle appears even
more peculiar than the standard 4th cycle. In reply Usoskin et al.
(2003) re analyzed of sunspot statistics. They show
that the average level of sunspot activity in 1792-1793 was
similar to what it was around sunspot cycle minima during the more
recent, well-observed years 1850-1996, but it is significantly
different from the activity either in the mid-declining phase or
around sunspot maxima.
The other implication of the new suggested cycle was the Waldmeier
rule relating the amplitude of a solar cycle to the length of its
phases. Usoskin et al. (2002) show that the new cycle
does not change the cycle-length distribution and only slightly
modifies the formal anti-correlation in the Waldmeier effect.
At the same time, Veselovsky & Tarsina (2002) have
presented the approximate empirical formula that relates the
duration of the ascending phase and the maximal sunspot numbers
for a given solar cycle. Yakovchouk & Veselovsky
(2006) extend this analysis for the group sunspot
numbers and sunspot area datasets. Concerning the lost-cycle
hypothesis they show that including a new short cycle violates
Waldmeier relationships. They go on demonstrate that since 1500
there has been no cycle with duration of ascending phase shorter
than two years. But introducing a new cycle reduces the duration
of the ascending phase to 1.9 years. Analyzing the auroral data
prepared by Silverman (1983) for the period from
1720 to 1850, Yakovchouk & Veselovsky (2006) trace
auroral peaks attributed to descending solar cycle phases. These
peaks seemingly reveal a complex geomagnetic response to solar
activity output, but do not mark the new sunspot cycle.
According to the modern view, geomagnetic activity consists of two
parts: one associated with transient geoeffective phenomena, which
follows the solar activity cycle, and a second associated with
quasistationary, recurrent solar wind streams, which occurred
after the solar activity maximum (e.g. Simon & Legrand
1986; Ruzmaikin & Feynman 2001; Hathaway
& Wilson 2006).
The problem of 4th cycle still remains unsolved. Arguments for and
against the lost-cycle hypothesis hitherto give rise to doubtful
statistics and contradictory results for the Waldmeier effect. Our
paper is an attempt to explain the nature of the exceptionally
long 4th solar cycle as a result of the outstanding phase
asynchrony of the north-south solar activity in 1784-1799.
In the original paper, Usoskin et al. (2001) analyzed
the group sunspot numbers (GSN) provided by Hoyt & Schatten
(1998), due to their higher homogeneity and accuracy
against sunspot numbers. In this work we also used the GSN data
tabulated by the National Geophysical Data Center.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{7681fig1.eps} %
\end{figure}](/articles/aa/full/2007/30/aa7681-07/Timg1.gif) |
Figure 1:
Sunspot activity circa the solar cycle 4. Thin black curve corresponds to the monthly group sunspot numbers.
Suggested smoothed sunspot activities for hemispheres are shown by
gray thick curves, and their sum - by the black thick curve. |
| Open with DEXTER |
We suppose that, at the time of 1785-1788, the sunspot cycle was
first started in one hemisphere. Active regions in the other
hemisphere began to emerge only few years later.
Figure 1 presents the model of sunspot asynchrony during the
course of the 4th cycle. It indicates both the monthly group
sunspot numbers and the suggested smoothed sunspot activities for
hemispheres, along with their sum.
Shapes of the hemispheric cycles can be described in terms of a
simple function with four parameters (Hathaway et al.
1994):
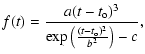 |
|
|
(1) |
where parameter a represents the amplitude, bis related to the time in years from the minimum to the maximum of
a cycle, c gives the asymmetry of the cycle, and 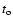 denotes
the starting time.
denotes
the starting time.
For the leading hemisphere we take a = 7, b = 3, c = 0.99,
and
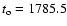 .
For the driven hemisphere - a = 4, b =
3, c = 0.99, and
.
For the driven hemisphere - a = 4, b =
3, c = 0.99, and
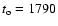 .
Here the time delay between the
onsets of hemispheric cycles is 4.5 years. The lengths of the
cycles are about 9 years. To better fit available data, we suppose
that sunspot hemispheric activities were different in amplitude.
This suggestion comes from analyzing the monthly GSN that were
overestimated and uncertain in 1792-1793.5 (Usoskin et al.
2001).
.
Here the time delay between the
onsets of hemispheric cycles is 4.5 years. The lengths of the
cycles are about 9 years. To better fit available data, we suppose
that sunspot hemispheric activities were different in amplitude.
This suggestion comes from analyzing the monthly GSN that were
overestimated and uncertain in 1792-1793.5 (Usoskin et al.
2001).
Thus we suggest that the solar cycle 4 is composed of two
relatively short hemispheric cycles time-shifted each other by a
few years. Its length depends on phase synchronization between
opposite hemispheres. Due to phase asynchrony, an exceptionally
long 4th cycle disrupted phase dynamics and caused phase
catastrophe.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7681fig2.eps} %
\end{figure}](/articles/aa/full/2007/30/aa7681-07/Timg6.gif) |
Figure 2:
Sunspot activity circa the solar cycle 20.
a) Black thin curve is smoothed monthly means
of a sunspot area for the northern and gray thin curve - for the
southern hemisphere. The total sunspot area is shown by a thick
black curve. b) The same, but with a time-shift of the southern
hemispheric activity. |
| Open with DEXTER |
Another case of strong phase asynchrony was observed during the
20th cycle (Fig. 2a). Curious similarities between sunspot
patterns appear to be repeated every 16 solar cycles (Fairbridge
& Hameed 1983). Here we have used smoothed (by
moving one-year averages), monthly means of sunspot area for the
northern and southern hemispheres. The length of the 20th cycle
over the total smoothed sunspot area is 12.5 years. It is the
longest cycle since 1874. Also the cycle has a long descending
phase of about 6.5 years. Southern hemispheric activity produced
peaks in 1972 and 1974.5 that are similar to the descending phase
of the 4th cycle, where we suspect significant phase
asynchronization.
Lag in the onsets of sunspot activities between the northern and
southern hemispheres was more than a year in the beginning of the
20th cycle. Zolotova & Ponyavin (2006) have shown
that sunspot phase asynchronization between the cycles 19-20 was
the highest since 1874 (up to 3 years).
Figure 2b represents results of fitting hemispheric solar cycle
shapes according to activity onsets. The South was shifted
backward to 13 months and the time axis for the South is marked in
the top panel. It is seen that some small delay significantly
changed the common shape of the solar cycle 20 forming the more
pronounced double-peak structure and shorter descending phase. It
seems that the duration of the cycle due to their phase shift
between opposite hemispheres is reduced to 10 years.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{7681fig3.eps} %
\end{figure}](/articles/aa/full/2007/30/aa7681-07/Timg7.gif) |
Figure 3:
a) Durations of solar cycles versus time. The gray
thin curve corresponds to the lengths of group sunspot cycles. The
black thick curve shows lengths of smoothed sunspot area cycles.
b) The lengths of smoothed monthly sunspot area cycles. The gray
solid curve corresponds to the northern hemisphere and gray dashed
curve - to the southern hemisphere. Thick black curve represents
the total Sun (see Table 1). |
| Open with DEXTER |
Table 1:
Lengths of sunspot area cycles defined using minima for the hemispheres and the total solar surface.
Here we discuss how the significant effect of sunspot hemispheric
asynchronization is. How strong the duration of solar cycle
depends on the phase relationships between hemispheric activities?
Figure 3a demonstrates the variability of cycle durations with
time. It shows the lengths of group sunspot cycles defined as the
time difference between two successive sunspot minima (Usoskin &
Mursula 2003) and the lengths of smoothed monthly
sunspot area cycles defined using sunspot minima. It is
interesting to note that the two biggest deviations in the sunspot
synchronization between hemispheres occur during the solar cycles
14-15 and 19-20 (Zolotova & Ponyavin 2006).
Figure 3b illustrates the lengths of smoothed sunspot area cycles
defined from minimum to minimum for both hemispheres and for the
total Sun (see Table 1). Uncertainties in determining the cycle
length from minimum to minimum extend up to more than a year
(Mursula & Ulich 1998).
It is seen that the duration of the total cycle 14 was defined by
the length of the southern hemispheric cycle. During the solar
cycle 20, the opposite was formed by the northern hemisphere.
Thus, in spite of large phase asynchrony observed at the beginning
of the 20th cycle, its length strongly depends on the duration of
the northern cycle.
According to Fig. 3b the length of the total sunspot cycle (N+S)
can be less than the lengths for the northern and southern
hemispheres as happened in cycles 15 and 19 (see Table 1). This
illusory contradiction comes from fluctuations of solar activity
and phase relationships between time series around the sunspot
minimum.
As an example, Fig. 4a presents the time profile of the solar
cycle 19, and the color labelling is the same as in Fig. 2.
Figures 4b and 4c show two zoomed successive minima. Arrows mark
those time moments when hemispheric and total sunspot activities
have the lowest values. The difference between these dates
corresponds to the cycle length. It is seen that the activity
minimum of the northern hemisphere (Fig. 4b) leads activity minima
of the southern hemisphere and total Sun to 0.08 year. At the end
of the 19th cycle, in contrast the south minimum delays north and
total activity minima to 0.5 year (Fig. 4c). As a result the
length of the total 19th cycle is 10.09; for the northern
hemisphere it is 10.17 and for the southern hemisphere 10.59.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{7681fig4.eps} \end{figure}](/articles/aa/full/2007/30/aa7681-07/Timg8.gif) |
Figure 4:
Sunspot activity circa the solar cycle 19.
a) The smoothed monthly means of sunspot area for the northern
(black thin) and southern hemispheres (gray thin). The total
sunspot area is shown by a thick black curve. b) Segment of the
sunspot activity minimum at the beginning of the solar cycle 19.
Arrows mark time moments in which hemispheric and total activities
have the lowest values. c) The same but for the end of the 19th
cycle. |
| Open with DEXTER |
The idea that strong asynchrony between northern and southern
activities existed during the course of solar cycle 4 can be
checked by analyzing the historic data. The asynchrony should
result in a strong North-South asymmetry during the first years of
solar cycle 4. We hope that later findings (e.g. Vaquero et al.
2007) will prove (or disprove) our hypothesis.
Noteworthy is the outstanding discovery by Ribes & Nesme-Ribes
(1993) of strong North-South asymmetry during the
Maunder Minimum (1645-1715) that stimulated dynamo theories trying
to explain solar secular variations (e.g. Sokoloff & Nesme-Ribes
1994; Serre & Nesme-Ribes 2000; Wang &
Sheeley 2003; Charbonneau 2005).
In this paper we have proposed a scenario to explain the origin of
the exceptionally long 4th solar cycle. We suggest that in
1784-1799 no cycle was lost. The duration of the 4th cycle can be
the result of the outstanding phase asynchrony of the north-south
solar activity. We suppose that the main contribution of
asynchrony was significant the difference in the onset times of
solar cycles in the northern and southern hemispheres. The
difference between time onsets reached at least 3 years. The
sunspot maximum of the leading hemisphere was between 1788 and
1790, and for driven hemisphere between 1793 and 1795. The
descending phase of the solar cycle after 1795 can be mainly
formed either by activity presented only in one hemisphere or by
activities in both hemispheres as happened in the 20th cycle.
Phase asynchronization and delay disappeared during the descending
phase.
We suggest that suppressed and delayed activity in the driven
hemisphere at the end of XVIII century can be one reason for the
solar cycle length increasing and subsequent grand minima of the
solar activity. Some evidence of the length increasing just before
the prolonged minimum, like Dalton and Maunder, was demonstrated
early by Chernosky (1955) and Frick et al.
(1997).
A similar situation for the big phase delay was observed during
the ascending phase of solar cycle 20. However, the length of this
cycle is defined mainly by the length of the cycle in the northern
hemisphere. Another cycle whose length was defined by predominant
hemispheric activity is the 14th cycle.
Finally we would like to note that coupling between lengths of the
cycles and phase hemispheric asynchrony are significant but most
likely have a nonlinear nature. To determine the solar cycle
length not only the cycle overlapping but phase hemispheric
relationships also have to be taken into account.
Acknowledgements
We thank the anonymous referee for his/her useful comments that
helped to improve the paper. This research was supported by an
INTAS Fellowship Grant for Young Scientists Ref. No. 06-1000014-6022.
-
Charbonneau, P. 2005, Sol. Phys., 229, 345 [NASA ADS] [CrossRef] (In the text)
- Chernosky, E.
J. 1955, PASP, 67, 117 [NASA ADS] [CrossRef] (In the text)
- Fairbridge,
R. W., & Hameed, S. 1983, AJ, 88, 867 [NASA ADS] [CrossRef] (In the text)
- Frick, P., Galyagin,
D., Hoyt, D. V., et al. 1997, A&A, 328, 670 [NASA ADS] (In the text)
- Hathaway, D.
H., & Wilson, R. M. 2006, Geophys. Res. Lett., 33, 18101 [NASA ADS] [CrossRef] (In the text)
- Hathaway, D.
H., Wilson, R. M., & Reichmann, E. J. 1994, Sol. Phys., 151,
177 [NASA ADS] [CrossRef] (In the text)
- Hoyt, D. V., &
Schatten, K. 1998, Sol. Phys., 179, 189 [NASA ADS] [CrossRef] (In the text)
-
Kremliovsky, M. N. 1994, Sol. Phys., 151, 351 [NASA ADS] [CrossRef] (In the text)
- Krivova, N. A.,
Solanki, S. K., & Beer, J. 2002, A&A, 396, 235 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mursula, K.,
& Ulich, Th. 1998, Geophys. Res. Lett., 25, 1837 [NASA ADS] [CrossRef] (In the text)
- Ribes, J. C., &
Nesme-Ribes, E. 1993, A&A, 276, 549 [NASA ADS] (In the text)
- Ruzmaikin,
A., & Feynman, J. 2001, J. Geophys. Res., 106, 15783 [NASA ADS] [CrossRef] (In the text)
- Serre, T., &
Nesme-Ribes, E. 2000, A&A, 360, 319 [NASA ADS] (In the text)
- Silverman, S.
M. 1983, J. Geophys. Res., 88, 8123 [NASA ADS] (In the text)
- Simon, P. A., &
Legrand, J.-P. 1986, A&A, 155, 227 [NASA ADS] (In the text)
- Sokoloff, D.,
& Nesme-Ribes, E. 1994, A&A, 288, 293 [NASA ADS] (In the text)
- Usoskin, I. G.,
& Mursula, K. 2003, Sol. Phys., 218, 319 [NASA ADS] [CrossRef] (In the text)
- Usoskin, I. G.,
Mursula, K., & Kovaltsov, G. A. 2001, A&A, 370, L31 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Usoskin, I. G.,
Mursula, K., & Kovaltsov, G. A. 2002, Geophys. Res. Lett., 29,
36 [CrossRef] (In the text)
- Usoskin, I. G.,
Mursula, K., & Kovaltsov, G. A. 2003, A&A, 403, 743 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vaquero, J. M.,
Trigo, R. M., Gallego, M. C., & Moreno-Corral, M. A. 2007, Sol.
Phys., 240, 165 [NASA ADS] [CrossRef] (In the text)
- Veselovsky,
I. S., & Tarsina, M. V. 2002, Adv. Space Res., 29, 417 [NASA ADS] (In the text)
- Vitinsky, Yu.
I., Kopecky, M., & Kuklin, G. V. 1986, Statistics of Sunspot
Activity (Moscow: Nauka)
(In the text)
- Wang, Y.-M., &
Sheeley, N. R., Jr. 2003, ApJ, 591, 1248 [NASA ADS] [CrossRef] (In the text)
- Yakovchouk,
O. S., & Veselovsky, I. S. 2006, in Quasiperiodical processes
on the Sun and their geoeffective manifestations, ed. A. V.
Stepanov, A. A. Soloviev, & Yu. A. Nagovitsyn (St. Petersburg),
Proc. X Pulkovo Int. Conf. Solar Phys., 155
(In the text)
- Zolotova, N.
V., & Ponyavin, D. I. 2006, A&A, 449, L1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{7681fig1.eps} %
\end{figure}](/articles/aa/full/2007/30/aa7681-07/Timg1.gif)
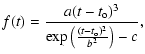
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{7681fig2.eps} %
\end{figure}](/articles/aa/full/2007/30/aa7681-07/Timg6.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{7681fig3.eps} %
\end{figure}](/articles/aa/full/2007/30/aa7681-07/Timg7.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{7681fig4.eps} \end{figure}](/articles/aa/full/2007/30/aa7681-07/Timg8.gif)