A&A 470, 661-673 (2007)
DOI: 10.1051/0004-6361:20077457

Origin of the early-type R stars: a binary-merger solution to a century-old problem?

R. G. Izzard1,3 - C. S. Jeffery2 - J. Lattanzio3


1 - Astronomical Institute Utrecht, Postbus 80000, 3508 TA Utrecht, The Netherlands
2 - Armagh Observatory, College Hill, Armagh BT61 9DG, Northern Ireland
3 - School of Mathematical Sciences, PO Box 28M, Monash University, Victoria 3800, Australia

Received 12 March 2007 / Accepted 2 May 2007

Abstract
The early-R stars are carbon-rich K-type giants. They are enhanced in $^{12}{\rm C}$, $^{13}{\rm C}$ and $^{14}{\rm N}$, have approximately solar oxygen, magnesium isotopes, s-process and iron abundances, have the luminosity of core-helium burning stars, are not rapid rotators, are members of the Galactic thick disk and, most peculiarly of all, are all single stars. Conventional single-star evolutionary models cannot explain such stars, but mergers in binary systems have been proposed to explain their origin. We have synthesized binary star populations to calculate the number of merged stars with helium cores which could be early-R stars. We find many possible evolutionary channels. The most common of which is the merger of a helium white dwarf with a hydrogen-burning red giant branch star during a common envelope phase followed by a helium flash in a rotating core which mixes carbon to the surface. All the channels together give ten times more early-R stars than we require to match recent Hipparcos observations - we discuss which channels are likely to be the true early-R stars and which are not. For the first time we have constructed a viable model of the early-R stars with which we can test some of our ideas regarding common envelope evolution in giants, stellar mergers, rotation, the helium flash and the origin of the early-R stars.

Key words: stars: AGB and post-AGB - stars: binaries: general - stars: carbon - stars: rotation - stars: chemically peculiar

1 Introduction and history

 The early-R stars are one of several classes of carbon star, all distinguished spectroscopically by the presence of strong absorption due to an excess of molecular carbon. While many of these carbon stars are now relatively well understood, the early-R stars have defied satisfactory explanation for nearly one hundred years. In a nutshell, the problem is to explain how a single star which is a giant, and hence has finished core-hydrogen burning, but is not sufficiently luminous to have completed core-helium burning, can have a surface which is contaminated by excess carbon. It may be argued that such a straightforward statement of the problem is too simplistic; it probably is. Therefore it is necessary to review here the main characteristics of the early-R stars, to define the problem in more detail, and thence introduce one approach to its solution.

1.1 Spectral class definition

 Stars with peculiar banding in their spectra were identified by Secchi (1868) and were later identified as carbon stars by Rufus (1916). They are easily identified by strong absorption features due to ${\rm C}_{2}$, CN or CH molecules. A subset of these, the R-type stars, was first classified by Fleming & Pickering (1908) based on the observations of Fleming & Pickering (1896). The R stars "contain rays of much shorter wave length than ordinary fourth type stars'' which, in modern parlance, means they are bluer and hotter ( $T_{{\rm eff}}\gtrsim4000~{\rm K}$, similar to the K-type stars, e.g. Dominy 1984) than the normal N-type carbon stars (with $T_{{\rm eff}}\la 3500~{\rm K}$) which are probably asymptotic giant branch (AGB) stars (Iben & Renzini 1983). The R stars are very common, apparently accounting for 1% of all K and G giants (Dominy 1984), and are 10 times more numerous than N stars according to Blanco (1965).

Later, as part of the Henry Draper catalogue (Cannon & Pickering 1918) and subject to revision by Shane (1928), the R class was split into R0 to R8, where R0-4 (the hot/early/warm-R stars) are warm, equivalent to normal K-type stars, while the cool/late-R stars of type R5-8 are the carbon-rich equivalent of M stars. All R and N stars were merged into a single type C by Keenan & Morgan (1941), but this was a "retrogressive step'' according to Eggen (1972), who reclassified late-R stars as N stars and left the early-R stars as a distinct class. Other types of carbon stars complicate the issue, especially in binaries where mass transfer can pollute the secondary star with enough carbon to turn it into a dwarf carbon star or CH star (see e.g. Wallerstein & Knapp 1998, Sects. 3 and 5). The J stars, which are similar to N stars with enhanced $^{13}{\rm C}$, are also of uncertain origin but are clearly redder and more luminous than the early-R stars (Abia & Isern 2000). Example spectra of all the carbon star types can be found in the atlas of Barnbaum et al. (1996). There is an alternative classification scheme developed by Bergeat et al. (2002a) who identify R0-3 stars as members of their HC1-HC3 class (where HC stands for hot carbon).

Standard single-star evolutionary models of AGB stars undergoing third dredge-up (e.g. Karakas et al. 2002) correctly, if sometimes only qualitatively, predict most of the properties of the late-R and N type carbon stars. The early-R stars remain a distinct group of stars with an unknown origin, just as they were in 1908. More information about the carbon star family is given by Abia et al. (2003), although also useful are the reviews of Lloyd Evans (1986), Lodders & Fegley (1998) and Wallerstein & Knapp (1998).

1.2 Spectroscopic studies

 Spectroscopic studies of the early-R stars have shed some light on their origin. The most comprehensive analysis is that of Dominy (1984). He found that early-R stars, despite having ${\rm C}/{\rm O}>1$, have a low $^{12}{\rm C}/^{13}{\rm C}$ratio (similar to the J stars), a solar or slightly sub-solar iron abundance, enhanced nitrogen relative to solar, a solar oxygen abundance, solar $^{17,18}{\rm O}/^{16}{\rm O}$ ratios and no s-process enhancement. This is in contrast to N-type carbon stars, and late-R stars, which show evidence of s-process elements, supporting the idea that late-R stars are really just misclassified N stars. Zamora et al. (2006) confirm the findings of Dominy and support the idea that late-R and N type stars are probably equivalent. Zamora (private communication) also finds that early-R stars have $0.4\la \log\epsilon({\rm Li})\la 3.5$- perhaps indicative of some enhancement? - while late-R stars have $-0.5\la \log\epsilon({\rm Li})\la 0.5$, similar to G and K giants (Lambert et al. 1980). Late-R stars pulsate, like N stars, but early-R stars do not, like K-type stars (Barnbaum et al. 1996; Bergeat et al. 2002b, Fig. 8).

The luminosity of early-R stars is around $100~{L_{\odot}}$, typical of core helium burning (CHeB) stars (the red clump in a colour-magnitude diagram, Cannon 1970; Faulkner & Cannon 1973; Scalo 1976; Cannon & Lloyd 1969), while the luminosity of N and late-R stars is more than $1000~{L_{\odot}}$, typical of AGB stars (Vandervort 1958; Baumert 1974; Scalo 1976; Bergeat et al. 2002a).

1.3 CH Stars

 There remains the possibility that the early-R stars are the CHeB counterparts of the CH stars in which, for some reason, s-process elements are undetectable or not present. CH stars, both dwarfs and giants, are formed by mass transfer to a main sequence companion from an AGB star which has undergone third dredge-up. They are rich in s-process elements and carbon which were formed in the primary AGB star and are all binaries. The polluted secondary evolves to the CHeB phase, perhaps remaining carbon-rich (although see Stancliffe et al. 2007). Metallicity affects the CH-formation process in two ways. First, third dredge-up is more efficient at sub-solar metallicities compared to solar (Karakas et al. 2002) so more primary carbon is made and transferred to the main sequence star. Second, the initial abundance of oxygen is lower than at solar metallicity so less carbon is required to be mixed into the stellar envelope to form a carbon star (for which $\rm C/O\geq1$ by number). There is a threshold metallicity, around $Z\sim0.4~Z_{\odot}$, above which CH stars cannot form (Abia et al. 2002). Both these facts are at odds with the properties of the early-R stars, which have solar or slightly sub-solar iron and oxygen abundances (Dominy 1984).

1.4 Binary fraction

 The nail in the AGB mass-transfer coffin came with the work of McClure (1997) who found that 22 early-R stars - all those in his sample - are single stars, even though $20\%$ of late-type giants are binaries. The implication is that the early-R stars originate in binary mergers, as it is hard to envisage a physical process which makes carbon stars only in single stars and not in wide binaries. That they are single and not s-process enhanced has been used to distinguish early-R stars from CH stars (Abia et al. 2003). McClure also found that the early-R stars are not rapidly rotating, a feature which must be explained by any potential early-R star model.

1.5 Space density and distribution

 Knapp et al. (2001) determined the absolute magnitudes and space density of the early-R stars using Hipparcos data. They found that the early-R stars have magnitudes similar to the red clump (i.e. CHeB) stars, the space density of the early-R stars is $4.5{-}15\times10^{-8}~{\rm pc}^{-3}$ and the R to red clump number ratio is $0.04{-}0.14\%$. Bergeat et al. (2002b) calculated the space density in the Galactic plane to be $1.66\times10^{-8}~{\rm pc}^{-3}$for early-R stars[*], $13.4\times10^{-8}~{\rm pc}^{-3}$ for N stars, a ratio of $\sim$16. The two papers give different number densities, but actually their projected number densities are about the same.

That the R stars are Galactic disk objects was recognised by Eggen (1972). Dominy (1984) finds that N stars are younger disk objects than, and distinct from, the R stars, while Ishida (1960), Stephenson (1973) and Barbaro & Dallaporta (1974) found that the N and R stars are distributed differently across the sky, with N stars more condensed in the Galactic plane. These results were confirmed by Bergeat et al. (2002b) who found that R stars are, on average, three times further from the Galactic plane. The solar or slightly sub-solar iron abundance and velocity dispersion of the R stars suggests they are members of the Galactic thick disk (Sanford 1944; Dahn 1964; Eggen 1972; Vandervort 1958; Keenan & Heck 1994; Bergeat et al. 2002b).

Third dredge up only occurs in solar-metallicity AGB stars above about $1.3{-}1.5~{M_{\odot}}$ (Karakas et al. 2002; Bessell et al. 1983), corresponding to a stellar lifetime of  $5~{\rm Gyr}$. Hence the early-R stars cannot be intrinsic AGB stars if they are older than about $5~{\rm Gyr}$.

1.6 Stellar models

 The early-R stars pose a problem for stellar evolution theory. Standard models of single stars are not carbon rich except for thermally pulsing AGB stars and some massive Wolf-Rayet stars. R-stars are too dim to be either of these, indeed their luminosities are those of the CHeB (red clump) evolutionary phase. The problem we face is twofold: when is carbon made in these stars and how do we get it to the surface?

The binary star merger model satisfies most of the observational constraints. We know there are no early-R stars dimmer than the red clump, so the merger must lead to a carbon-rich, CHeB star. This naturally implies that something odd happens immediately prior to the CHeB phase during helium ignition at the tip of the giant branch. Canonical models of the helium flash do not predict mixing of carbon-rich material from the core to the stellar surface (Härm & Schwarzschild 1966). However, these models are one-dimensional and non-rotating, while a binary merger leads to a three-dimensional, rotating system, so it is quite possible that the merger and/or ignition leads to non-standard mixing. One-dimensional models with parameterised rotational mixing and/or low metallicity (with off-centre helium ignition) have led to some mixing of carbon-rich core material with the stellar envelope (Mengel & Gross 1976; Hollowell et al. 1990; Paczynski & Tremaine 1977). The models of Iben (1990) simulate accretion of helium onto a helium white dwarf (HeWD) and show that off-centre helium ignition is a natural consequence of this process.

A number of two-dimensional simulations have been carried out by Deupree and collaborators (Cole & Deupree 1981; Deupree 1996; Cole & Deupree 1980; Deupree & Wallace 1987) some of which suggest the possibility of mixing material from a core helium flash into the stellar envelope. It is hard to draw a conclusion from these models as the results vary with both resolution and model sophistication, and it is not clear how to apply the results to a rapidly rotating binary merger.

Recently, full three dimensional models of the helium flash have been constructed (Dearborn et al. 2006; Lattanzio et al. 2006) although these are of single stars, not binary mergers (in the latter paper slow rotation was introduced). Simulations of HeWD mergers have been constructed with a smooth particle hydrodynamics (SPH) approach (Guerrero et al. 2004). While these do not evolve to the helium flash, they do show that the cores lose very little mass, or angular momentum, during their merger.

1.7 Summary

In this paper we will make, for the first time, a quantitative estimate of the number of and properties of early-R stars using our binary population nucleosynthesis model. We investigate possible channels for early-R star formation by a binary merger process and subsequent helium flash in a rapidly rotating core and also extrinsic (CH-star) channels by accretion from a companion. We determine the effect of varying model parameters on the early-R to red clump and early-R to N star ratios, and compare these to observations. Section 2 describes our model, Sect. 3 our results, Sect. 4 discusses the ramifications and we conclude with some ideas for future research.

2 Modelling the mystery

 We model populations of single and binary stellar stars with the synthetic model of Hurley et al. (2002), updated to include nucleosynthesis (Izzard et al. 2004; Izzard et al. 2006, and changes outlined below). Our model follows the evolution of stars using analytic fits to luminosity, radius, core mass etc. Interactions with a companion due to tides, wind accretion and Roche-lobe overflow (RLOF) are taken into account. Common envelope evolution is treated with an $\alpha$-prescription (Livio & Soker 1988; Tout et al. 1997), where $\alpha$ is the fraction of the orbital energy which is transferred to the envelope during the spiral-in phase. In most of our models we use $\alpha =1$ and an envelope binding energy factor $\lambda =0.5$(Regös & Tout 1995). Our synthetic AGB model is based on the full evolutionary models of Karakas et al. (2002) and includes surface abundance changes due to third dredge-up and hot-bottom burning. We also follow the surface abundances of massive stars based on the models of Dray & Tout (2003), as well as yields due to supernovae and novae, but these are not important with regard to the early-R stars.

2.1 Stellar evolution

 Our synthetic stars have solar-scaled initial abundances according to Anders & Grevesse (1989), with metallicities $10^{-4}\leq Z\leq0.03$. There are many other parameters in our model which are discussed in detail in Izzard et al. (2006). Where a parameter choice affects our results, we vary the parameter within a reasonable range (see Sect. 3.9). The main parameters which influence R-star formation are the metallicity Z and the common envelope parameters $\alpha$ and $\lambda$. These are Z=0.02 (which we refer to as solar metallicity), $\alpha =1$and $\lambda =0.5$ unless stated otherwise.

We have updated the Izzard et al. (2006) treatment of case-B RLOF in binaries with primary masses between 0.75 and  $2.0~M_{\odot}$, which turn out to be our prototype early-R stars. We follow the surface abundances of $^{1}{\rm H}$, $^{4}{\rm He}$, $^{12}{\rm C}$, $^{14}{\rm N}$ and $^{16}{\rm O}$ as a function of mass co-ordinate based on detailed terminal main-sequence models constructed with the TWIN stellar evolution code (Eggleton & Kiseleva-Eggleton 2002). As mass is stripped during RLOF, transferred material is enhanced in helium and nitrogen but deficient in carbon and oxygen because of CNO cycling during the main sequence evolution of the primary. This is transferred to the secondary star, enhancing its abundance of helium and nitrogen while reducing hydrogen and carbon.

We modify the common envelope prescription of Hurley et al. (2002) by removing their algorithm which instantaneously ignites merging degenerate helium cores[*]. Instead, in our model the less massive core is disrupted into a disc around the more massive core and accretes until a single, rapidly rotating core is formed (Guerrero et al. 2004). The merged core then grows by hydrogen-shell burning until helium ignites in a nuclear runaway (the helium flash). For all our merged stars we assume that the ignition process, in a rapidly rotating core, mixes some carbon into the stellar envelope as found by Paczynski & Tremaine (1977). The star then settles into its CHeB phase as an early-R star.

According to the Hurley et al. (2000) formalism, helium ignites when the stellar luminosity reaches a critical value which is a function of the stellar mass and metallicity. This may not apply to our merged stars which have abnormally large cores for their total mass and stage of evolution, but given that we are ignoring the lifting of degeneracy due to the merger we can probably do no better without detailed models of early-R star progenitors. In our main merger channels (see below) application of the Hurley et al. (2000) prescription leads to minimum helium-ignition core masses of between 0.35 and  $0.45~{M_{\odot}}$, compatible with the off-centre HeWD ignition models of Iben (1990) which have a core mass of  $0.38~{M_{\odot}}$. In contrast, an SPH simulation of the merger of two $0.4~{M_{\odot}}$HeWDs does not lead to a helium flash even though the maximum temperature reached is $2\times10^{8}~{\rm K}$ (Guerrero et al. 2004) - any excess energy goes into lifting the degeneracy and expansion of the white dwarfs. These simulations do not model the evolution of the star beyond a few minutes after the collision, so it is possible that the core contracts and/or increases in mass on a longer timescale, but ignites while still rapidly rotating.

2.2 Stellar population model

 Our single star and binary primary masses are distributed according to the initial mass function (IMF) of Kroupa et al. (1993) in the range[*] $0.1\leq M/{M_{\odot}}\leq80$, secondary star masses are chosen from a distribution which is flat in q=M1/M2 such that $0.1~{M_{\odot}}/M_{1}\leq q\leq1$ and initial separations a are chosen from a distribution flat in $\log a$ for $3\leq a/{R}_{\odot}\leq10^{4}$. We usually assume all binary orbits are circular (e=0) and stars evolve to a maximum age of $13.7~{\rm Gyr}$. Given these distributions, the probability assigned to each binary system is $\Psi(M_{1},M_{2},a)$and the contribution to the number of stars of a given type is $\int_{{\rm time}}\int_{M_{1},M_{2},a}S\times\delta({\rm type})\times\Psi~ {\rm d}t$, where $\delta({\rm type})=1$ when the star is of the required type, 0 otherwise. A similar calculation is performed for single stars and the results combined with a $50\%$ binary fraction. We set S, the star formation rate, to 1 because we compare only number ratios and relative number counts.

2.3 Age selection criterion

 The early-R stars are associated with the Galactic disk, particularly the thick disk (Bergeat et al. 2002b). We select model stars older than the lower limit of the age-metallicity relation for thick disk stars of Bensby et al. (2004), which we fit to $5.61{-}6.68f~{\rm Gyr}$ where $f=\max\left(-0.65,\left[{\rm Fe}/{\rm H}\right]\right)$. At solar metallicity ( $[{\rm Fe}/{\rm H}]=0$) this gives a minimum age of $5.61\ {\rm Gyr}$, which is too old for intrinsic carbon star formation according to our models (Karakas et al. 2002).

The imposition of the age limit is equivalent to ending star formation $4.5~{\rm Gyr}$ ago, which is not applicable to the whole Galactic disk, even if it is correct for the thick disk. It implies, for example, that there are no intrinsic N type stars, which is incorrect in the thin disk so we must be careful when comparing R to N star number count ratios with the results of our model.

2.4 N and red clump stars

 We define N-type carbon stars as giant branch (GB) or AGB stars with $N_{{\rm C}}/N_{{\rm O}}\geq1$. All our N stars are extrinsic: there are no intrinsic carbon stars in our simulated populations because such stars are younger than our $\sim$ $4~{\rm Gyr}$ age limit.

The red clump is synonymous with the CHeB phase of stellar evolution (as defined by Hurley et al. 2002) in low-mass stars, equivalent to the horizontal branch at higher mass.

   
2.5 Early-R star formation channels

The Hurley et al. (2002) model defines many common-envelope merger channels which lead to a CHeB star, any of which could be the early-R stars. We define our R-star formation channels as follows:

R1.
Merger of a naked main-sequence helium star (HeMS) with a GB star.

R2.
Merger of a core-helium burning star (CHeB) with a GB star.

R3.
Merger of a helium white dwarf (HeWD) with the core of a GB star.

R4.
Accretion from an AGB companion, which is now a white dwarf (at low metallicity, these are CH stars).

R5.
Merger of a HeWD with a Hertzsprung gap (HG) star which has a partially degenerate helium core.

R6.
Merger of a GB star with a HG star.

R7.
Merger of two HG stars.

R8.
Merger of an AGB star with a helium-cored star. The helium and CO cores mix completely to give a new, CO-rich helium core which behaves as an evolved CHeB star.

R9.
Merger of two naked helium stars.

R10.
Merger of a CO or ONe white dwarf (i.e. the core of an AGB star) with an AGB star. This is similar to channel 8 but one star has its envelope stripped.

R11.
Merger of two GB stars, similar to channel 3 but both stars have a hydrogen envelope.

Our early-R stars are defined as those which have gone through one of the above channels, are of the appropriate age (see Sect. 2.3) and are in the CHeB (red clump) phase. We assume that all the above mergers make early-R stars by the rotating core helium flash mechanism.

   
3 Results

Table 1: The fraction of each merger channel which contributes to our synthetic, standard Z=0.02 early-R star population as defined in Sect. 2.5. The left column labels the channel (R1...11), the middle column the relative formation rate for each channel and the right column the relative number of early-R stars (assuming a constant star formation rate and the Kroupa et al. 1993 IMF). The missing channels do not contribute to our R star population and channel R4 is not a merger (we identify these with the CH stars and treat them separately, see Sect. 3.3).

Table 1 gives the relative formation rate and numbers of stars which form in each of our model early-R star channels in our standard Z=0.02 population. The R3 (HeWD-GB) and R6 (HG-GB) channels together represent more than $90\%$ of our early-R star progenitors - we discuss these stars below in some detail. We identify channel R4 with the CH stars. These form in appreciable numbers at low metallicity, but not at all at solar metallicity, as predicted by Abia et al. (2002) - we discuss these separately in Sect. 3.4. R5 (HeWD-HG) and R11 (GB-GB merger) possibly are early-R stars, forming most of the remaining $10\%$. There are small contributions from the R7 and R8 channels and none in the R1, R2, R9 and R10 channels.

The parameter space of initial masses and periods which goes on to form our early-R star candidates is shown in Fig. 1.

  \begin{figure} \par\includegraphics[clip]{7457fig1a.eps}\hspace*{8mm} \includegraphics[clip]{7457fig1b.eps} \end{figure} Figure 1: a) Initial secondary mass vs. initial primary mass and b) initial period vs. initial primary mass for all our early-R star merger progenitors (i.e. not including channel R4, the CH stars). (Z=0.02, $\alpha =1$, $\lambda =0.5$.) The symbols are as follows: R3 (HeWD-GB) small grey circles, R5 (HeWD-HG) squares, R6 (GB-HG) upward-pointing triangles ( $\bigtriangleup $), R7 (HG-HG) downward-pointing triangles ( $\bigtriangledown $), R8 (AGB) large diamonds ($\diamond $), R11 (GB-GB) open circles. The contribution from omitted channels is negligible. In panel  b) it is clear that there are two distinct populations of R3, R6 and R11, the short period binaries which have one common envelope phase, and the long period binaries which have two.
Open with DEXTER


  \begin{figure} \par\begin{tabular}{@{}c@{\hskip6mm}c@{}} \textbf{(a)}\includegra... ...udegraphics[scale=0.35]{7457fig2b.eps}\tabularnewline \end{tabular} \end{figure} Figure 2: Pre-common envelope HeWD mass vs. giant mass a) and giant core mass b) for our R3 channel. (Z=0.02, $\alpha =1$, $\lambda =0.5$.) In both plots the group of points on the left side comes from our R3a (initially short-period binary) models, while the points on the right are from the (initially long-period) R3b channel. The R3b stars have such large cores that they are probably too bright to be the observed R stars.
Open with DEXTER

  
3.1 Subtype R3: HeWD + GB merger (Z = 0.02)

The R3 channel consists of HeWD-GB mergers and dominates our early-R star progenitor population at solar metallicity (Z=0.02). We have split the R3 type into subtypes R3a and R3b representing initially short and long period binaries as follows:

Both the R3 subtypes originate from two phases of mass transfer, the second of which is the common envelope phase which leads to merger of two helium cores.

3.1.1 R3a Sub-type

 In our R3a stars the first phase of mass transfer is conservative RLOF when the more massive primary exhausts its core hydrogen, crosses the Hertzsprung Gap (HG) and begins ascent of the giant branch (GB). Initially, while q<1, the orbit shrinks, but when enough mass is transferred that q>1 the orbit widens. The primary completely loses its envelope and is left as a $\sim$ $0.2~{M_{\odot}}$HeWD (similar to the detailed models of Kippenhahn et al. 1967). The secondary accretes a significant amount of mass and becomes a blue straggler because it is more massive, hence bluer, than it should be for its age. It is also nitrogen and $^{13}{\rm C}$ rich because it accretes material which is stripped from CN-processed layers deep inside the primary. The separation of these binaries, prior to the evolution of the secondary up the giant branch, is about $20~{R_{\odot}}$.

The R3a channel contains the majority, $77\%$, of the R3 channel stars because they have a higher formation rate and they have smaller cores than R3b so spend longer in the CHeB phase.

3.1.2 R3b Sub-type

 The R3b stars begin their evolution in a relatively wide binary. When the primary evolves onto the GB it overflows its Roche lobe and a common envelope results. During the spiral-in of the helium core and main sequence star, the envelope of the giant is lost, leaving a $0.38{-}0.48~{M_{\odot}}$ HeWD with a $1{-}1.2~{M_{\odot}}$main sequence (MS) star in a reasonably close ( $a\sim20~{R_{\odot}}$) binary. The HeWD is about twice as massive in this scenario as compared to R3a because the giant evolves further up the giant branch before the first mass transfer. Note that in this scenario, the secondary accretes only a small amount of mass (typically $\sim$ $0.01~{M_{\odot}}$) so while technically it is a blue straggler, it might not be detected as such. Also, the secondary does not accrete much $^{13}{\rm C}$or $^{14}{\rm N}$ from the stripped primary.

3.1.3 Formation of R3 stars

 In both the R3a and R3b channels, after the first mass transfer the secondary evolves on its nuclear timescale and eventually exhausts its core hydrogen. As it crosses the HG and ascends the GB, RLOF begins and common envelope evolution results.

Figure 2 shows the distribution of masses and core masses just prior to the final common-envelope phase and core merger. In both panels of the figure the R3a stars are on the left and the R3b on the right. The giant core and the HeWD merge during the ensuing common envelope phase to form a new singleGB star with a core of $0.3{-}0.45~{M_{\odot}}$ for the R3a and $0.5{-}0.7~{M_{\odot}}$ for the R3b channel. The post-merger object is not immediately an early-R star, but is a GB star with an abnormally large core. In the case of R3b and more massive R3a stars, the core is massive enough that the star very quickly ignites helium. In the lowest-mass R3a stars some hydrogen shell burning drives the core mass up to a minimum of $0.36~{M_{\odot}}$when helium ignites. Once helium ignition has started, the luminosity of the star drops and it settles into the red clump as a candidate early-R star.

Because the R3b stars have massive cores they have a mean luminosity of about $650~{L_{\odot}}$. This is rather large, both compared to the observed early-R stars and to our R3a channel, which has a mean luminosity of about $170~{L_{\odot}}$. Once the core-helium burning R-star phase is complete, these stars ascend the AGB, possibly as J-type stars (see Sect. 4.6).

3.2 The other merger channels (Z = 0.02)

 The other merger channels arise in much the same way as R3, with initially close binaries undergoing conservative mass transfer onto a companion and initially wide binaries passing through two common-envelope phases. These other phases are considerably rarer because the initial binary parameters must be just right such that the second mass-transfer phase occurs e.g. during the HG rather than GB phase. Consequently, channels R5 (HeWD-HG), R7 (HG-HG), R8 (AGB) and R11 (GB-GB) are rare compared to R3. The R8 (AGB-merger) channel is almost certainly not related to the early-R stars because the resulting merged stars have luminosities around $10^{3}~{L_{\odot}}$, typical of stars with evolved CO cores (late-R stars or N stars). We make no R9 or R10 stars at solar metallicity and although some R10 (CO WD-GB or ONe WD-GB mergers) systems do exist at lower metallicity their numbers are very few. We never make any R1 or R2 systems because we select only old stars and potential R2 stars merge as GB-GB systems (i.e. prior to the GB-CHeB phase).

Channel R6, the merger of a GB star with a HG star, is relatively common. Most of these systems ($85\%$) are similar to the R3a systems but with an initially more massive secondary, such that it is a HG star (rather than a MS star) when the primary overflows its Roche lobe. As a result, a common envelope forms during the first mass transfer phase and the cores merge.

The remainder of the R6 systems, and most of the R11 systems, are initially wide binaries containing a HeWD and a HG (or GB, in the case of R11) star. The wind from the HG star is accreted onto the HeWD at a rate sufficient to form a new envelope and rejuvenate the HeWD as a GB star. A common envelope phase soon follows and the HeWD merges with the HG star. These systems suffer the same problem as the R3b channel, their cores are massive ( $0.6{-}0.8~{M_{\odot}}$) and they are are too luminous ($\ga$ $600~{L_{\odot}}$) to be early-R stars.

3.3 Channel R3 vs R4 (CH) as a function of metallicity

 

  \begin{figure} \par\includegraphics[width=8cm,clip]{7457fig3.eps} \end{figure} Figure 3: Our model predictions for the relative fractions of the R3 and R4 channels as a function of metallicity. While R4 dominates at low metallicity (these are halo CH stars), channel R3 (HeWD-GB mergers) dominates at around solar metallicity - these are our prime candidates for the early-R stars.
Open with DEXTER

Figure 3 shows the relative number of the R3 and R4 channels as a function of metallicity. The CH-star channel R4 dominates our early-R star population for $Z\la 0.004$ while above this metallicity the binary merger channel R3 is predominant. The reason for this is a combination of increasing oxygen abundance (proportional to Z) and decreasing third dredge-up efficiency, as discussed in Sect. 1.3. Our conclusion is that for $Z\la 0.004$, e.g. in the Galactic halo, most carbon-rich red clump stars are probably CH stars, with enhanced s-process abundances and a binary companion, while at higher metallicity (in the Galactic disk) the merger model dominates and all carbon-rich red clump stars should be single early-R stars. This is just as is observed (see Sect. 4.2).

3.4 The effect of metallicity on merger channels

 

  \begin{figure} \par\includegraphics[width=8cm,clip]{7457fig4.eps} \end{figure} Figure 4: The relative number of our early-R star merger candidates as a function of metallicity, arbitrarily normalized to 1 for the R3 channel at Z=0.03. The frequency of most merger types decreases as the metallicity drops. The symbols are the same as in Fig. 1.
Open with DEXTER

Figure 4 shows the effect of metallicity on the relative number of each merger channel. Lowering the metallicity reduces the number of mergers of all types mainly because of our age-selection criterion (see Sect. 2.3). The R5 channel (HeWD-HG) increases because as the metallicity drops the stellar lifetime for a given mass decreases, so lower mass stars evolve off the main sequence faster than they would at solar metallicity. The IMF favours low-mass stars, hence the increase in R5.

3.5 Early-R to red clump ratio

 The ratio of the number of R to red clump stars was determined to be $0.04{-}0.14\%$ by Knapp et al. (2001). Figure 5 compares the results of our models to this ratio and it is obvious that our model overestimates the number of early-R stars (or underestimates the number of CHeB stars). In our R-star selection criteria we have tried to be as inclusive as possible, so (for example) if only $10\%$ of our R3 stars go on to mix carbon into their envelopes when they ignite helium, then our models would agree with the observations - we discuss this further in Sect. 4. It is unlikely that we have underestimated the number of CHeB stars by a factor of ten.

  \begin{figure} \par\includegraphics[width=8cm,clip]{7457fig5.eps} \end{figure} Figure 5: Our calculated R to CHeB (red clump) number ratio as a function of metallicity for channels R3 to R7. The other channels are negligible. The symbols are the same as in Fig. 4. The thick error bar shows the observational bounds from Knapp et al. (2001) for the Galactic disk. The R3, 5, 6 and 7 subtypes could all be the real early-R stars, although in the case of R3 and R6 only a subset of our model stars can be true early-R stars because we make too many.
Open with DEXTER

3.6 The early-R to N ratio

 The ratio of the number of R to the number of N stars is about 10 (Dominy 1984). Our models give $N_{{\rm R}}/N_{{\rm N}}\sim10{-}100$, but this is spurious because we do not include young, intrinsic N stars and some of the R stars used to calculate the observed ratio are probably cool/late-R (i.e. N type). Also, the observed ratio depends very strongly on Galactic latitude (e.g. Sanford 1944, compare Figs. 1 and 2) and/or height above the Galactic plane (Bergeat et al. 2002b). To test this one would build a Galactic population model, with separate thick and thin disk populations, but this is beyond the scope of this paper.


  \begin{figure} \par\includegraphics[width=8cm,clip]{7457fig6.eps} \end{figure} Figure 6: Distribution of the mass of carbon which must be dredged up in order to convert our merger stars into a carbon star (Z=0.02 standard model). The thick black line is the sum of all our R-merger channels, the lines with points are the individual channels.
Open with DEXTER

On the other hand, our model results are not inconsistent with the observations. We can estimate the ratio $N_{{\rm R}}/N_{{\rm CHeB}}$from the observed $N_{{\rm R}}/N_{{\rm N}}$ by calculating $N_{{\rm R}}/N_{{\rm N}}\times N_{{\rm N}}/N_{{\rm CHeB}}$. Bergeat et al. (2002b) give $N_{{\rm R}}/N_{{\rm N}}\sim0.32$in the Galactic plane[*], while we can approximate $N_{{\rm N}}/N_{{\rm CHeB}}$ from $\Delta t_{{\rm N}}/\Delta t_{{\rm CHeB}}\sim2/150=0.013$ where the $\Delta t$s are the lifetimes (in ${\rm Myr}$) of the AGB and CHeB evolutionary phases for a Z=0.02, $1.3~{M_{\odot}}$star. This results in $N_{{\rm R}}/N_{{\rm CHeB}}\sim0.4\%$, similar to the $0.1\%$ Knapp et al. (2001) find and within the range of our results.

3.7 Early-R/GK giant ratio

 The R to GK giant ratio is 1% according to Dominy (1984), although the source of this number is not given (it is presumably calculated from the carbon star catalogue of Stephenson 1973 and probably includes late-R stars). If we define GK giants as GB and AGB stars with $3800\leq T_{{\rm eff}}/{\rm K}\leq5850$which satisfy our age criterion, which is quite conservative as we should probably include CHeB stars as well, then at solar metallicity (Z=0.02) our early-R to GK giant ratio is about $0.5\%$. Given that our early-R star count is as high as we can possibly make it (it should be a factor of ten less to match the R to red clump ratio) and we do not include younger GK giants, our R to GK giant ratio is clearly different to that quoted by Dominy.

3.8 Dredge-up during the core helium flash

 We postulate that, during the core helium flash of our merged objects, there must be some dredge up of carbon from the core into the envelope. We cannot model this in detail, but we can estimate the minimum amount of carbon, $\Delta_{{\rm C}}$, required to make  ${\rm C}/{\rm O}=1$. We find

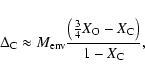\begin{displaymath}\Delta_{{\rm C}} \approx M_{{\rm env}}\frac{\left(\frac{3}{4}X_{{\rm O}}-X_{{\rm C}}\right)}{1-X_{{\rm C}}} , \end{displaymath} (1)

where $M_{{\rm env}}$ is the common envelope mass and $X_{{\rm C}}$and $X_{{\rm O}}$ are the abundances of carbon and oxygen initially present in the stellar envelope (the derivation of this formula is in Appendix A.1). In our Z=0.02 simulations $\Delta_{{\rm C}}$ is usually in the range 0.003 to  $0.01~{M_{\odot}}$, as shown in Fig. 6.

Deupree (1986) finds a much smaller amount of carbon, around $10^{-6}~{M_{\odot}}$, is mixed to the stellar envelope in two-dimensional calculations of the helium flash. These simulations were necessarily of low resolution, and did not include rotation, which should be important in mixing material out of the core and through the hydrogen-burning shell (Mengel & Gross 1976 see also our Sect. 4.4).

3.9 Variation of model parameters

 The initial metallicity is the parameter which most affects the formation of early-R stars by the binary merger channel. Here we consider some other parameters of our model which may affect the formation of early-R stars.

We have not considered changing the initial distributions such as the IMF, separation distribution etc. Such an effort is beyond the scope of this paper. Strictly, we should apply a Galactic metallicity and star-formation rate distribution (perhaps as a function of height above the Galactic plane) rather than compare single-population, constant star-formation rate populations. Again, this is beyond the scope of this paper but we hope to examine this problem in the future.

4 Discussion and hope

 Our common-envelope merger followed by rotating core helium flash model makes a sufficient number of early-R stars to match observations. This raises hope of understanding these stars at last, but many questions remain. Here we discuss the merits of the different channels and consider the mixing and angular momentum transport which may occur during the core merger.

4.1 The R-channels (Z = 0.02)

 All our R channels together cannot be the equivalent of the observed early-R stars because we make too many by a factor of about ten. There are advantages and disadvantages to each channel which, in our opinion, make some more likely candidates than others.

R3
The HeWD-GB mergers. The major disadvantage of the initially short-period R3a channel is the delay time, about $2.5~{\rm Myr}$, between the core merger and helium ignition. The equivalent in the R3b channel is less than $1~{\rm Myr}$. A lengthy delay may allow transfer of material and/or angular momentum from the (pre-flash) core to the envelope, which would slow the core rotation and reduce the likelihood of mixing of carbon into the envelope during the helium flash.

The advantage of the R3a channel is that the cores are of low enough mass, mostly $\la$ $0.45~{M_{\odot}}$, to be degenerate when helium ignites, provided they can lose any energy they gained from the merger process (which would otherwise lift the degeneracy, as in Guerrero et al. 2004) and still remain rapidly rotating. If $M_{{\rm c}}$ (the merged-core mass) is the parameter which determines whether the helium flash mixes material into the envelope then only a small range ($\sim$ $0.02~{M_{\odot}}$ e.g. $0.38{-}0.40~{M_{\odot}}$) in $M_{{\rm c}}$ selects the required $10\%$ of R3 stars. The relatively high core mass of the R3b channel means its stars are many times brighter than the observed R stars, with $\log L/{L_{\odot}}\sim2.5{-}3.0$. They also span a wider effective temperature range, from $\log T_{{\rm eff}}/{\rm K}=3.55$to 3.9, than the R3a stars which cluster at $\log T_{{\rm eff}}/{\rm K}\sim3.68$. Possibly these would be observed as J stars or as A and/or F giants.

R3a stars, and our other R channels which involve significant accretion from a giant companion, are enhanced in $^{13}{\rm C}$ and $^{14}{\rm N}$, as seen in the early-R stars (Dominy 1984). These enhancements may also be due to mixing across a hydrogen shell (see Sect. 4.4).

R4
The binary R4 channel, equivalent to CH stars, cannot work at solar metallicity (see Sect. 4.2 below) and does not lead to single stars, so this is definitely not the channel which makes the early-R stars.
R5
Channel R5, the HeWD-HG mergers, is similar to R3 but contributes a factor of 17 fewer stars in our standard Z=0.02 model. Its main advantages are that the number of early-R stars formed is similar to that which is observed and that HG stars are less compact than GB stars so more likely to keep their envelopes and merge in a common envelope phase (Taam & Ricker 2006). The disadvantage is that the core of a HG star may not be sufficiently degenerate for helium to ignite soon after the merger so the core has time to lose its angular momentum. On the other hand, the merged core mass is always low (about  $0.3~{M_{\odot}}$) because the HG star is relatively unevolved compared to an equivalent mass GB star. Assuming the merged core can maintain its rotation rate as the R5 star ascends the giant branch these may be the early-R stars.
R6
The GB-HG mergers occur at a rate around 1/4 that of the R3 channel - still too many compared to the observations, but a better match than R3. As in R5, the advantage of a HG star is that it is likely to survive the common envelope phase, but they may not be degenerate or massive enough to be still rotating when helium ignites. A fraction of R6 forms from double common-envelope systems and, as in channel R3b, these are more luminous than observed R stars.
R7
These are the HG-HG mergers, which are very rare (150 times fewer than the R3 channel) so are probably not the early-R stars.
R8
These AGB-helium core mergers are also rare, with numbers similar to R7. It is also not likely that the assumption of our model - that the helium core completely mixes with the CO core of the AGB star - is true. In any case, these are too bright to be the early-R stars (but may be J/N/late-R stars).
R11
GB-GB mergers are rare, a factor of 15 less than the R3 channel, but cannot be ruled out as potential early-R star progenitors. However, they are the binaries most likely to lose their envelopes when they merge. Both cores are degenerate and usually of low mass and often one member of the binary is a rejuvenated WD with a very thin envelope, so these are very similar to R3 mergers. Stars in this channel span a wide range in luminosities (from $60~{L_{\odot}}$ to  $900~{L_{\odot}}$) and effective temperatures ( $\log T_{{\rm eff}}/{\rm K}=3.53{-}3.9$). In a few cases the post-merger object has a very thin envelope, so is very blue ( $T_{{\rm eff}}\sim40~000~{\rm K}$).
R1, 2, 9 and 10
None or very few of these are made in our populations.
Most likely only some fraction of our model early-R stars will ignite and mix carbon into the envelope, but we do not know which stars these are. Our population synthesis model predicts too many early-R stars. This is a positive result, because we have tried to select every possible merger channel. It is also an interesting challenge because we do not know the true R-star formation channel.

4.2 R/CH stars, metallicity and population

 Above a threshold metallicity $[{\rm Fe}/{\rm H}]\sim-0.3$ and in an exclusively old stellar population, our models suggest that the early-R stars should be the only carbon stars. The Galactic bulge, which is old and of (super-)solar metallicity (Zoccali et al. 2003), is an obvious target for R star surveys. In fact, large numbers of low-luminosity carbon stars have already been found in the bulge and have been identified as early-R stars in the surveys of Azzopardi et al. (1985, 1991) and Westerlund et al. (1991). This is in contrast to the very few or even total lack of N-type stars in the bulge (Rich 1998), in agreement with our results.

At metallicities typical of the Galactic halo, the number of CH stars vastly exceeds the number of early-R stars. That is not to say there are no early-R stars in the halo, because according to our models there should be. With regard to the detection of early-R stars in the halo, there are several reasons it may be difficult:

1.
There should be many more CH stars than early-R stars in the halo. At $[{\rm Fe}/{\rm H}]=-2.3$ we predict ${\rm R}3/{\rm R}4\sim7\%$which means the early-R/CH ratio will be much smaller (R4 only includes core helium burning CH stars, the true CH population will contain both these and giants and possibly dwarfs) especially if we reduce our figure by a factor of ten to agree with the Hipparcos observations.
2.
Halo stars are rare compared to disk stars, so there are simply not as many population-II early-R stars.
3.
CH stars are likely to be selected by colour, which may omit early-R stars.
4.
Giant branch CH stars are somewhat brighter than CHeB stars, so any survey aimed at CH stars (rather than C dwarfs) must be quite sensitive to relatively dim stars in order to detect an early-R star.
5.
Is it possible to distinguish easily between early-R and (core-helium burning) CH stars? According to Abia et al. (2003) the only differences are the presence of s-process isotopes and binarity, data which are often difficult to obtain. As such, early-R stars already found in the halo could have been misclassified as CH stars. A recent survey has detected a few halo early-R stars and gives a method for differentiating between early-R and CH stars (Goswami 2005).
The Westerlund et al. (1995) survey of the Large Magellanic Cloud (see also Rebeirot et al. 1993), which has a sub-solar metallicity $[{\rm Fe}/{\rm H}]\sim-0.3$ (Cioni et al. 2006a), finds a menagerie of N, R and J type stars, over a wide range of luminosities, in qualitative agreement with our model population. We should caution, however, that the LMC probably contains a significantly younger population of intrinsic N type stars (Cioni et al. 2006b) which makes a statistical comparison difficult because our population model does not include young stars.

We also have not considered the impact of the latest determinations of the solar oxygen abundance (Asplund et al. 2005; Allende Prieto et al. 2001) which decreases the amount of oxygen by a factor of two relative to Anders & Grevesse (1989). This reduces our estimate of the mass of carbon which must be mixed into the envelope during helium ignition, $\Delta_{{\rm C}}$, and shifts the metallicity at which CH stars form, but does not significantly change our conclusions.

Finally, we are not sure why Galactic early-R stars are located only in the thick disk (Bergeat et al. 2002b). Some of their HC1-3 (R-type) stars are of low radial velocity, so could be members of the thin disk. Alternatively, the initial binary fraction, and hence number of mergers, may be higher in the thick disk compared to the thin disk (Grether & Lineweaver 2006).

4.3 Progenitors observed

 The progenitors of our early-R stars are binaries in which one star is a WD, the other a blue straggler - one such star has been observed (Landsman et al. 1997). Recently, models of MS+WD blue straggler systems were constructed by Tian et al. (2006) but they cannot take their calculations through the final common envelope phase. Regarding the MS+WD phase, however, they find quite similar results to ours despite their use of a full stellar evolution rather than synthetic code.

Blue stragglers (BSs) are most easily identified in globular clusters (GCs) because the stars in a particular cluster are of the same age so BSs are easily seen to be brighter and bluer than the tip of the main sequence. However, binary mergers may be rare because of the low binary fraction in the core of clusters (Ivanova et al. 2005) - or perhaps the binary fraction is low because of mergers. To search for progenitors of our R-star mergers it would be best to search for HeWD-BS binaries in high metallicity, old GCs, such as those in the Galactic bulge e.g. NGC 6553 or 6528, (Zoccali et al. 2004; Barbuy et al. 2004), with metallicities $[{\rm Fe}/{\rm H}]\sim-0.2$, or the LMC clusters (Lloyd Evans 1986).

The FK Com stars (Bopp & Rucinski 1981; Bopp & Stencel 1981) may be post-common envelope mergers: they are single, rapidly rotating (close to or even beyond break-up e.g. Ayres et al. 2006; Huenemoerder et al. 1993), G/K-type giants which are thought to have evolved through a binary merger (Welty & Ramsey 1994). They are rare, about $2\times10^{-8}~{\rm pc}^{-3}$(Collier Cameron 1982; Hagen & Stencel 1985), which is quite similar to the R-star space density.

4.4 Merger mixing and modelling

 In our merger scenario at Z=0.02 the amount of carbon which is required to be mixed from the core into the envelope during the helium flash is $0.003{-}0.01~{M_{\odot}}$, assuming ${\rm C/O}=1$ in the R-star envelope. The analysis of Dominy (1984) shows carbon and nitrogen are similarly enhanced in early-R stars, with the $^{12}{\rm C}/^{13}{\rm C}$ratio just above the CN-cycle equilibrium value of 4. These observations strongly suggest there is some hydrogen burning of the carbon-rich material from the helium flash en route to the surface of the early-R star. This would mean we have underestimated the amount of carbon dredge up by a factor of about two because half the carbon is converted to nitrogen. However, because some $^{13}{\rm C}$ and $^{14}{\rm N}$may come from the deposition of material stripped from the primary star during the first period of mass transfer, for some channels (e.g. R3a) we require less CN burning.

Lithium poses a problem because the latest data of Zamora (private communication, see also Sect. 1.2) suggest that early-R stars may be enhanced with lithium relative to normal G/K giants. The fate of lithium during a stellar merger is not clear: there will be some dilution and destruction, but perhaps also creation by outward transport of $^{7}{\rm Be}$ in a way similar to that of Denissenkov & Weiss (2000).

Hydrogen burning implies production of helium, which would be mixed to the surface. However, hydrogen would have to be very deficient to alter the spectrum and indeed this is not seen in the early-R stars. In all our channels except R9 (the merger of two helium stars, which has a negligible formation rate) a hydrogen envelope sits on top of the merged core so the star would be observed as hydrogen rich.

As discussed above, there may be a delay between the merger and helium ignition. If the core can settle to hydrostatic equilibrium it should be possible to model it with a one-dimensional stellar evolution code which includes rotation and angular momentum transport (e.g. Heger et al. 2000; Langer 1998 and the series of papers by Meynet & Maeder 1997, onward). The SPH models of Guerrero et al. (2004) suggest that merged cores settle down rapidly (minutes) compared to their nuclear burning timescale (Myr) so the problem is tractable. Certainly, some one-dimensional exploration of the problem would be useful.

This leads us to the realm of two and three dimensional modelling of the core merger and associated mixing. Two dimensional simulations without rotation (Cole & Deupree 1981; Deupree 1996; Cole & Deupree 1980; Deupree & Wallace 1987) do not show significant mixing of material from the core to the surface - yet we have good grounds, based on our population model and a lack of alternatives, to suggest that it does happen. The only way forward may be a full three-dimensional simulation of a merger of two HeWDs inside a hydrogen-rich giant envelope including nuclear burning. This is some way off, and might not even be possible with current methods such as SPH, but is perhaps not impossible in the near future using codes such as Djehuty (Dearborn et al. 2006).

4.5 Angular momentum

 In Appendix A.2 we show that when two HeWD cores merge the velocity of the resultant object exceeds its breakup velocity by a factor of about two, in agreement with Gourgouliatos & Jeffery (2006). There must be some form of angular momentum transport out of the merged core, perhaps by magnetic fields coupling the core to the envelope or shear mixing across the core-envelope boundary (it has recently been suggested by Soker & Harpaz 2007 that shear mixing may mix helium-rich, but not carbon-rich, material out of the core of a red giant).

We show in Appendix A.3 that if we conserve angular momentum and mass for the whole star, after the merger it is rotating at about its breakup velocity. However, it is not the case if some mass is lost during the common envelope phase as this may remove enough angular momentum to stabilise the star (Davies et al. 1991; Lovekin & Sills 2003). It is still rotating at a significant fraction of its breakup velocity, often many tens of ${\rm km}~{\rm s}^{-1}$. This contradicts the observations of McClure (1997) which show that early-R stars are not rapidly rotating. There must be some angular momentum loss, such as magnetic braking, which slows the early-R star, especially because it contracts after helium ignites at the tip of the giant branch.

4.6 After the R-star...

 The early-R stars are CHeB stars but eventually they will exhaust their supply of helium and ascend the giant branch again as $^{12}{\rm C}$-, $^{13}{\rm C}$- and $^{14}{\rm N}$-rich AGB stars. They may be observed as J-type stars and indeed, perhaps early-R stars are the progenitors of some of the J stars, as suggested by Lloyd Evans (1986). If this is the case then J stars should also be single stars, but it is not clear if this is true. J stars are apparently 15% of carbon-rich giants stars (Abia & Isern 2000) and further work regarding their formation rate will determine if early-R stars are the progenitors of some of them.

5 Conclusions

 We have shown by means of a binary population synthesis technique that binary mergers are a viable channel for the formation of the early-R stars. Our models naturally reproduce most of the properties of the early-R stars, namely that they are single, K-type stars which show enhanced $^{12}{\rm C}$, $^{13}{\rm C}$ and $^{14}{\rm N}$ without s-process or iron enhancement relative to the sun.

We estimated the number of early-R stars from different binary merger channels involving objects with helium cores. The most common merger is that of a helium white dwarf with a red giant star and this makes about ten times as many stars as we require if we are to match the early-R to red clump number ratio to the observed value. We did, however, assume that the helium core of every merger is rotating and mixes carbon into the envelope upon helium ignition. It is more likely that a small fraction of our stars ignite helium while rotating rapidly enough to mix carbon into their envelope.

Other possible channels include mergers of a red giant with a Hertzsprung gap star, a helium white dwarf with a Hertzsprung gap star or the merger of two red giants. There must be other parameters which control whether a merged star becomes an early-R star, such as the core mass or core-rotation rate. Our model early-R stars are rapidly rotating core-helium burning giants so must undergo some kind of rapid magnetic braking to slow them down, because observed early-R stars are not rotating quickly.

As pointed out by Dominy (1984) and McClure (1997) it is difficult to envisage an alternative evolutionary pathway which leads to the early-R stars. Ten years on, we finally have a potential explanation for their existence and their number. It is our hope that this will stimulate further research in the area of helium-core mergers inside common envelopes because for once we think we understand the outcome of the merger process.

Acknowledgements
Our work on the early-R stars commenced at the "Nucleosynthesis in Binary Stars'' workshop at the Lorentz centre, Leiden, 2005. R.G.I. is supported by the Nederlands Organisatie voor Wetenschappelijk Onderzoek (NWO). He thanks Armagh Observatory and Monash University for funding extended visits. He is grateful to the numerous people who have shared their ideas with him over the past year on the subject of the paper, especially Evert Glebbeek, Onno Pols and Pilar Gil-Pons for reading the manuscript. CSJ acknowledges financial support from the Northern Ireland Dept. of Culture Arts and Leisure (DCALNI), the UK Particle Physics and Astronomy Research Council (PPARC) and the Netherlands Research School for Astronomy (NOVA). Other aspects of this research were supported by the DEST and the Australian Research Council. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.

   
Appendix A: Appendix

   
A.1 Carbon dredge up

We define abundances by mass fraction to be X prior to the merger, Y post-merger. We then require

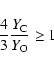\begin{displaymath}\frac{4}{3}\frac{Y_{{\rm C}}}{Y_{{\rm O}}} \geq 1 \end{displaymath} (A.1)

to be a carbon star. The common envelope is of mass M and the amount of carbon required from the core is $\Delta_{{\rm C}}$(a similar mass of material is mixed back down into the core). We neglect the minor isotopes $^{13}{\rm C}$, $^{17}{\rm O}$and $^{18}{\rm O}$ because their abundances are small (at most 1/4 of ${\rm C}$ is $^{13}{\rm C}$). The final mass of carbon in the envelope is

\begin{displaymath}Y_{{\rm C}}M_{{\rm env}} = X_{{\rm C}}(M-\Delta_{{\rm C}})+\Delta_{{\rm C}} , \end{displaymath} (A.2)

which gives

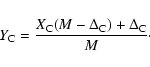\begin{displaymath}Y_{{\rm C}} = \frac{X_{{\rm C}}(M-\Delta_{{\rm C}})+\Delta_{{\rm C}}}{M}\cdot \end{displaymath} (A.3)

If we assume the oxygen abundance is unchanged, i.e. $Y_{{\rm O}}=X_{{\rm O}}$, and there is no CN cycling of dredged up carbon, we have

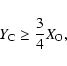\begin{displaymath}Y_{{\rm C}} \geq \frac{3}{4}X_{{\rm O}} , \end{displaymath} (A.4)

which with the previous expression and some algebraic manipulation gives us

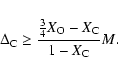\begin{displaymath}\Delta_{{\rm C}} \geq \frac{\frac{3}{4}X_{{\rm O}}-X_{{\rm C}}}{1-X_{{\rm C}}}M_{{\rm }} . \end{displaymath} (A.5)

If a fraction f of the dredged-up carbon is converted to nitrogen as it passes through the hydrogen shell, the amount of dredged-up carbon and nitrogen is

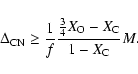\begin{displaymath}\Delta_{{\rm CN}} \geq \frac{1}{f}\frac{\frac{3}{4}X_{{\rm O}}-X_{{\rm C}}}{1-X_{{\rm C}}}M_{{\rm }} .\end{displaymath} (A.6)

A.2 Merged core angular momentum

 Here we consider the angular momentum in the early-R star core as a result of the merger. When the least massive helium core, of mass $m_{{\rm c}2}$, enters RLOF, the orbital period is given by Kepler's law


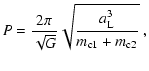$\displaystyle P = \frac{2\pi}{\sqrt{G}}\sqrt{\frac{a_{{\rm L}}^{3}}{m_{{\rm c1}}+m_{{\rm c}2}}}~,$     (A.7)

where $a_{{\rm L}}$ is the separation and $m_{{\rm c}1}$ is the mass of the more massive core. The equivalent orbital angular velocity is then $\Omega=2\pi/P$. We can estimate the angular momentum in the twin-core system J by neglecting the spins of the stars such that
                J = $\displaystyle J_{{\rm c}1}+J_{{\rm c}2}+J_{{\rm orb},{\rm c}}$  
  $\textstyle \simeq$ $\displaystyle J_{{\rm orb},{\rm c}}=\mu\Omega a_{{\rm L}}^{2}$ (A.8)

where $J_{{\rm c}1,2}$ are the spin angular momenta of the stars and $\mu$ is the reduced mass. Then we have, by substitutions of the expression for $\Omega$,
 
               $\displaystyle J_{{\rm orb,c}}$ = $\displaystyle \frac{m_{{\rm c}1}m_{{\rm c}2}}{m_{{\rm c}1}+m_{{\rm c}2}}\Omega a_{{\rm L}}^{2}$  
  = $\displaystyle m_{{\rm c}1}m_{{\rm c}2}\sqrt{\frac{Ga_{{\rm L}}}{m_{{\rm c}1}+m_{{\rm c}2}}}\cdot$ (A.9)

Now, if we conservatively assume that no angular momentum is lost from the cores during the merger then we can calculate the orbital angular velocity $\omega$ of the merger product,
               $\displaystyle \omega$ = $\displaystyle \frac{J_{{\rm orb,c}}}{km_{{\rm c}}r_{{\rm c}}^{2}}$  
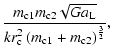  = $\displaystyle \frac{m_{{\rm c}1}m_{{\rm c}2}\sqrt{Ga{\rm _{{\rm L}}}}}{kr_{{\rm c}}^{2}\left(m_{{\rm c}1}+m_{{\rm c}2}\right)^{\frac{3}{2}}} ,$ (A.10)

where $m_{{\rm c}}=m_{{\rm c}1}+m_{{\rm c}2}$ and $r_{{\rm c}}$are the mass and radius of the merged core respectively and k is its radius of gyration. The velocity at the surface of the merged core is
                $\displaystyle v_{{\rm F}}$ = $\displaystyle \omega r_{{\rm c}}$  
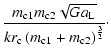  = $\displaystyle \frac{m_{{\rm c}1}m_{{\rm c}2}\sqrt{Ga{\rm _{{\rm L}}}}}{kr_{{\rm c}}\left(m_{{\rm c}1}+m_{{\rm c}2}\right)^{\frac{3}{2}}}\cdot$ (A.11)

We can easily compare this to the break-up velocity

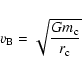\begin{displaymath}v_{{\rm B}} = \sqrt{\frac{Gm_{{\rm c}}}{r_{{\rm c}}}}\end{displaymath} (A.12)

to see

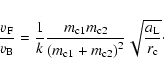\begin{displaymath}\frac{v_{{\rm F}}}{v_{{\rm B}}} = \frac{1}{k}\frac{m_{{\rm c}... ...rm c}2}\right)^{2}}\sqrt{\frac{a_{{\rm L}}}{r_{{\rm c}}}}\cdot \end{displaymath} (A.13)

The separation at RLOF is $a_{{\rm L}}=\max\left[r_{{\rm c1}}/f(q),~ r_{{\rm c}2}/f(1/q)\right]$where f is given by the function of Eggleton (1983), and given  $m_{{\rm c}1}$ and $m_{{\rm c}2}$ we obtain the core radii from the formulae of Tout et al. (1997). We set k=0.21 as for an n=3/2 polytrope. For $0.1\leq m_{{\rm c}1}=m_{{\rm c}2}\leq0.5$the ratio $1.9\la v_{{\rm F}}/v_{{\rm B}}\la 2.7$so there must be some form of outward angular momentum transport in order for the cores to merge.

A.3 Rotational velocity of the post-CE star

 We can derive the maximum velocity of the star which results from common envelope evolution by conserving angular momentum during the merger. At the beginning of the CE phase the binary system has a total angular momentum $J=J_{{\rm orb}}+J_{1}+J_{2}$where J1 and J2 are the spin angular momenta of the stars and $J_{{\rm orb}}$ is the orbital angular momentum. The final angular velocity $\omega$ is calculated from a solid-body approximation, assuming angular momentum is conserved during the merger,

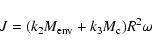\begin{displaymath}J = (k_{2}M_{{\rm env}}+k_{3}M_{{\rm c}})R^{2}\omega \end{displaymath} (14)

where $M_{{\rm env}}$ , $M_{{\rm c}}$, R are the envelope and core mass and the radius of the merged star respectively. The constant k3=0.21 as previously, but k2 depends on the structure of the giant star (it is about 0.15-0.2). We then solve for the velocity $v=\omega R$ and compare to the breakup velocity $v_{{\rm B}}$ (cf. Sect. A.2). For a typical R3a system, with initial parameters $M_{1}=1.25~{M_{\odot}}$, $M_{2}=0.5~{M_{\odot}}$, $P=1.6~{\rm days}$, Z=0.02, $\alpha_{{\rm CE}}=1$, $\lambda_{{\rm CE}}=0.5$, e=0, no extra CRAP, we find the merged stellar mass is $1.34~{M_{\odot}}$( $0.05~{M_{\odot}}$ is lost during the common envelope phase, we have not taken into account the loss of angular momentum due to this mass) with a core of mass $0.41~{M_{\odot}}$and k2=0.143, hence $v=125~{\rm km}~{\rm s}^{-1}$, about $95\%$ of the break up velocity ( $132~{\rm km}~{\rm s}^{-1}$). The ratio reduces to $60\%$ if we assume the angular momentum in the cores does not contribute to the rotation of the envelope, which is required for the core to be rapidly spinning when it ignites helium. If we attempt to take into account the angular momentum that is lost in the $0.05~{M_{\odot}}$ of material ejected during the common envelope phase, presumably at approximately the breakup velocity so $\Delta J=v_{{\rm B}}R\times0.05~{M_{\odot}}$, the ratio $v/v_{{\rm B}}$ drops further to $28\%$ ( $v=37~{\rm km}~{\rm s}^{-1}$). It would seem these systems are, in general, quite rapidly rotating (at least tens of ${\rm km}~{\rm s}^{-1}$), but are not all at the breakup velocity.

References

 
Copyright ESO 2007