A&A 470, 405-409 (2007)
DOI: 10.1051/0004-6361:20077260
A. Shalchi - I. Kourakis
Institut für Theoretische Physik, Lehrstuhl IV: Weltraum- und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
Received 8 February 2007 / Accepted 21 April 2007
Abstract
We present an improved nonlinear theory for the perpendicular transport of charged particles. This approach is based on an improved nonlinear treatment of field-line random walk in combination with a generalized compound
diffusion model. The generalized compound diffusion model employed is more systematic and reliable, in comparison with previous theories. Furthermore, the theory shows remarkably good agreement with
test-particle simulations and solar wind observations.
Key words: diffusion - scattering - turbulence - gamma rays: theory
The long-standing problem of particle transport perpendicular to a magnetic background field in turbulent magnetized plasmas is revisited in this article. Although this problem has been discussed in several papers (e.g. Jokipii 1966; Bieber & Matthaeus 1997; Kóta & Jokipii 2000; Matthaeus et al. 2003; Shalchi et al. 2004; Webb et al. 2006; Shalchi 2006), a final solution has not been provided so far. The perpendicular transport of charged particles is a central problem in astrophysics, since the knowledge of the diffusion tensor for particle transport parallel and perpendicular to the prescribed external magnetic field is essential for describing solar energetic particles (Dröge 2000), the modulation of Galactic cosmic rays (Burger & Hattingh 1998), diffusive shock acceleration, and the lifetime of cosmic rays in the Galaxy (Jokipii & Parker 1969). Furthermore, there are measurements of perpendicular mean free paths in the heliosphere (Chenette et al. 1977; Palmer 1982; Burger et al. 2000) that still await a theoretical explanation.
An early treatment of particle transport has relied on a quasilinear description of cosmic ray propagation (Jokipii 1966). In the
quasilinear theory (QLT) it is assumed that particles follow the magnetic field-lines while they move unperturbed in the direction
parallel to the background field. Thus, the corresponding result is often referred to as the field-line random walk limit (FLRW-limit).
According to this result, which has originally been derived for the slab turbulence model, the perpendicular mean-square deviation
(MSD) of the particle increases linearly with time, viz.
![]() .
This linear time dependence is
usually referred to as a classical Markovian diffusion process.
Thirty-four years later, Kóta & Jokipii (2000) formulated a compound diffusion model that assumes that the particle moves
along the magnetic field-lines while it is scattered diffusively in the parallel direction. Relying on the Taylor-Green-Kubo-formulation (e.g. Kubo 1957), in combination with the assumption of
diffusive field-line wandering, Kóta & Jokipii (2000) have found a subdiffusive behavior of particle transport of the
form
.
This linear time dependence is
usually referred to as a classical Markovian diffusion process.
Thirty-four years later, Kóta & Jokipii (2000) formulated a compound diffusion model that assumes that the particle moves
along the magnetic field-lines while it is scattered diffusively in the parallel direction. Relying on the Taylor-Green-Kubo-formulation (e.g. Kubo 1957), in combination with the assumption of
diffusive field-line wandering, Kóta & Jokipii (2000) have found a subdiffusive behavior of particle transport of the
form
![]() .
In the same years, particle propagation in magnetized plasmas was explored
by making use of test-particle simulations (e.g. Giacalone & Jokipii 1999; Mace et al. 2000; Qin et al. 2002a,b), where it was clearly confirmed that
.
In the same years, particle propagation in magnetized plasmas was explored
by making use of test-particle simulations (e.g. Giacalone & Jokipii 1999; Mace et al. 2000; Qin et al. 2002a,b), where it was clearly confirmed that
![]() ,
so long as a slab model is considered
for the turbulence geometry (see Qin et al. 2002a). By using improved test-particle codes (see Qin et al. 2002b for instance), it
has been demonstrated that for a non-slab model, diffusion is recovered (though only partially, as demonstrated in Sect. 3 of this paper).
This recovery of diffusion cannot been explained by the method of Kóta & Jokipii (2000).
,
so long as a slab model is considered
for the turbulence geometry (see Qin et al. 2002a). By using improved test-particle codes (see Qin et al. 2002b for instance), it
has been demonstrated that for a non-slab model, diffusion is recovered (though only partially, as demonstrated in Sect. 3 of this paper).
This recovery of diffusion cannot been explained by the method of Kóta & Jokipii (2000).
Various other theories have been proposed for perpendicular transport, mainly based on nonlinear extensions of QLT, such as the nonlinear closure approximation of Owens (1974) or model-based approaches such as the one proposed by Bieber & Matthaeus (BAM 1997). However, these theories provide a diffusive behavior of perpendicular transport for the slab model, in disagreement with simulations. One more promising theory, namely the nonlinear guiding-center theory (NLGC-theory), has been derived by Matthaeus et al. (2003). Although this theory shows agreement with some test-particle simulations in slab/2D geometries, the theory cannot reproduce subdiffusion for the slab model. An extended nonlinear guiding-center (ENLGC) theory was therefore formulated by Shalchi (2006), which agrees with simulations for slab and non-slab models. However, this theory is very close to the original NLGC-theory and uses nearly the same crude approximation: exponential form of the velocity correlation function, magnetic fields and particle velocities are uncorrelated.
In this paper we propose a more reliable theoretical approach that uses less ad-hoc assumptions and ansätze than the NLGC-theory. The layout of this article goes as follows. In Sect. 2, we argue that field-line wandering behaves superdiffusively for non-slab models. In Sect. 3, we employ a generalized compound diffusion model to deduce an analytic form for the perpendicular MSD of particles. By comparing with test-particle simulations (Sect. 4) and solar wind observations (Sect. 5) we show that our theory provides the correct result.
The key input into our new formulation is the MSD of the magnetic field-lines
![]() .
In several previous papers
(e.g. Jokipii 1966; Matthaeus et al. 1995; Ragot 2006; Ruffolo et al. 2006), field-line wandering (or random walk) has been described by applying linear and nonlinear formulations. In a recent paper (Shalchi & Kourakis 2007), an improved formulation
for nonlinear field-line random walk in magnetostatic turbulence has been developed, thus criticizing the validity of those previous
approaches. The approach of Shalchi & Kourakis (2007) is a direct generalization of the theory proposed by Matthaeus et al. (1995)
and further applied by Ruffolo et al. (2006). For a diffusive behavior of field-lines this theory can be obtained by the
theory of Shalchi & Kourakis (2007) as a special limit. However, our theory can also be applied in non-diffusive transport cases.
A further advantage of this theory is its analytical tractability, which enriches and complements the existing numerical toolbox on
field-line wandering (see e.g. Ragot 2006).
.
In several previous papers
(e.g. Jokipii 1966; Matthaeus et al. 1995; Ragot 2006; Ruffolo et al. 2006), field-line wandering (or random walk) has been described by applying linear and nonlinear formulations. In a recent paper (Shalchi & Kourakis 2007), an improved formulation
for nonlinear field-line random walk in magnetostatic turbulence has been developed, thus criticizing the validity of those previous
approaches. The approach of Shalchi & Kourakis (2007) is a direct generalization of the theory proposed by Matthaeus et al. (1995)
and further applied by Ruffolo et al. (2006). For a diffusive behavior of field-lines this theory can be obtained by the
theory of Shalchi & Kourakis (2007) as a special limit. However, our theory can also be applied in non-diffusive transport cases.
A further advantage of this theory is its analytical tractability, which enriches and complements the existing numerical toolbox on
field-line wandering (see e.g. Ragot 2006).
In view of modeling field-line random walk, the turbulence model has to be specified in terms of the magnetic correlation
tensor
![]()
![]() .
According to Bieber et al. (1994)
the so-called slab/2D composite model is a realistic model for solar wind turbulence. This two-component model
ignores the usually smaller parallel field turbulent variance (
.
According to Bieber et al. (1994)
the so-called slab/2D composite model is a realistic model for solar wind turbulence. This two-component model
ignores the usually smaller parallel field turbulent variance (
![]() )
and only includes excitations with
wavevectors either purely parallel or purely perpendicular to the mean magnetic field
)
and only includes excitations with
wavevectors either purely parallel or purely perpendicular to the mean magnetic field ![]() ,
leading to the following form of the correlation tensors:
,
leading to the following form of the correlation tensors:
![]() with
with
![]() and
and
![]() .
For the two wave spectra
.
For the two wave spectra
![]() and
and
![]() ,
we employ a standard form that has also been proposed by Bieber et al. (1994)
,
we employ a standard form that has also been proposed by Bieber et al. (1994)
It can easily be demonstrated (see e.g. Jokipii 1966; Matthaeus et al. 1995) that, for pure slab geometry, the field-lines behaves diffusively
In the previous section, we discussed results regarding the field-line wandering in the slab/2D composite model as a function of z. However, charged particles experience parallel scattering while moving through the turbulence. Thus,
the parameter z becomes a statistical variable in particle transport studies. If we assume that the particles (or, more precisely,
their guiding-centers) follow the magnetic field-lines (guiding center approximation), we have
Equation (4) can also be obtained from the Chapman-Kolmogorov equation (see, e.g., Webb et al. 2006), which has the form
A further standard assumption in the cosmic ray transport theory is the assumption of a Gaussian particle distribution, see e.g. Matthaeus et al. (2003):
By using Eq. (3) for the field-line MSD in combination with Eq. (6) for the particle distribution, we can evaluate Eq. (4) to find
For pure slab geometry, however, we deduce by combining Eqs. (2) and (6) with Eq. (4):
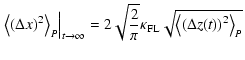 |
(10) |
In this section numerical tests are employed to assess the accuracy of the GCD-model. By choosing the same turbulence model as used for the application of the GCD-model (magnetostatic turbulence, slab/2D composite geometry, the wave spectra of Eq. (1)) test-particle simulations can be performed easily. The diffusion coefficient is computed numerically using procedures described previously (Giacalone & Jokipii 1999; Qin et al. 2002a,b).
We have considered test-particle dynamics for the following set of parameters:
![]() ,
,
![]() ,
and 20%/80% slab/2D composite geometry. In Fig. 1, we depict the ratio of perpendicular and parallel
diffusion coefficients
,
and 20%/80% slab/2D composite geometry. In Fig. 1, we depict the ratio of perpendicular and parallel
diffusion coefficients
![]() as a function of the dimensionless time
as a function of the dimensionless time
![]() for the
dimensionless cosmic ray rigidity value
for the
dimensionless cosmic ray rigidity value
![]() .
We have chosen a low value of R to ensure that the guiding-center approximation is valid. The new results are compared to
those obtained from the NLGC- and ENLGC-theories and also to test-particle simulations. For the NLGC-results we have
assumed a parameter value of a2 = 1, which corresponds to the assumption that guiding-centers
follow magnetic field-lines. Obviously the GCD-model provides a result much closer to the simulations than the NLGC-theory and the
ENLGC-theory. However, it should be emphasized that the main advantage of the GCD-model is its more systematic nature.
.
We have chosen a low value of R to ensure that the guiding-center approximation is valid. The new results are compared to
those obtained from the NLGC- and ENLGC-theories and also to test-particle simulations. For the NLGC-results we have
assumed a parameter value of a2 = 1, which corresponds to the assumption that guiding-centers
follow magnetic field-lines. Obviously the GCD-model provides a result much closer to the simulations than the NLGC-theory and the
ENLGC-theory. However, it should be emphasized that the main advantage of the GCD-model is its more systematic nature.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7260fig1.eps}\end{figure}](/articles/aa/full/2007/29/aa7260-07/Timg61.gif) |
Figure 1:
The ratio of perpendicular and parallel diffusion coefficients (
|
| Open with DEXTER | |
By assuming the simple form
![]() ,
we can deduce the time dependence from numerical data by
using
,
we can deduce the time dependence from numerical data by
using
![]() in the high time limit (
in the high time limit (
![]() denotes the dimensionless diffusion coefficients obtained by the simulations).
The exponents for the parallel
denotes the dimensionless diffusion coefficients obtained by the simulations).
The exponents for the parallel
![]() and perpendicular
and perpendicular ![]() diffusion coefficients are depicted in Fig. 2 for different values of the parameter R.
As shown, the test particle code provides a weakly superdiffusive behavior of parallel transport, in addition to a weakly subdiffusive behavior of perpendicular transport. In all cases considered, the GCD-model agrees well with the simulations.
diffusion coefficients are depicted in Fig. 2 for different values of the parameter R.
As shown, the test particle code provides a weakly superdiffusive behavior of parallel transport, in addition to a weakly subdiffusive behavior of perpendicular transport. In all cases considered, the GCD-model agrees well with the simulations.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7260fig2.eps}\end{figure}](/articles/aa/full/2007/29/aa7260-07/Timg65.gif) |
Figure 2:
The parameters
|
| Open with DEXTER | |
It is difficult to directly compare our new (non-diffusive) result with solar wind observations.
In this section, we attempt a rough comparison by averaging our non-diffusive result over the characteristic scattering time
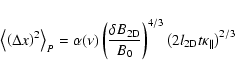 |
(13) |
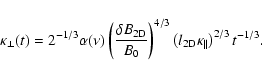 |
(14) |
| |
= | 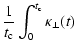 |
|
| = | 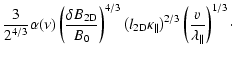 |
(15) |
The values for the perpendicular mean free paths obtained from Jovian electrons (Chenette et al. 1977) and Ulysses measurements of Galactic protons (Burger et al. 2000) are similar. Thus we conclude that the generalized compound diffusion model can reproduce solar wind observations for the perpendicular mean free paths.
To reproduce these observations we applied Eq. (16), which can be obtained from the more general result of Eq. (7) by averaging over the scattering time. According to our new theory and test-particle simulations, parallel as well as perpendicular transport behaves non-diffusively. However, the non-diffusivity is very weak, thus Eqs. (16) and (17) should be good approximations.
By combining a compound diffusion model - cf. Eq. (4) - with a nonlinear treatment of field-line wandering (namely Eq. (3)), a new theoretical treatment for the perpendicular transport of cosmic rays is presented in this article.
In Table 1, the assumptions of this new theory are compared to the NLGC-theory, as representative of existing transport
theories. Obviously the new approach relies on less approximations and model assumptions. Therefore the GCD-model is less restricted and thus more reliable.
In Table 2, we compare different theories and their results for the parameter ![]() ,
which denotes the time dependence of
the diffusion coefficient via
,
which denotes the time dependence of
the diffusion coefficient via
![]() .
Furthermore, the theory is easily applicable due to its simple analytical
form (see Eqs. (7) and (8)).
.
Furthermore, the theory is easily applicable due to its simple analytical
form (see Eqs. (7) and (8)).
Table 1: Comparison between the assumptions used in our GCD-model and the assumptions used in the NLGC-theory.
Table 2:
Comparison between results for the parameter ![]() from various theories: QLT, BAM-model, NLGC-theory, WNLT, ENLGC-theory,
and the GCD-model. Negative values of
from various theories: QLT, BAM-model, NLGC-theory, WNLT, ENLGC-theory,
and the GCD-model. Negative values of ![]() correspond to subdiffusion, positive values to superdiffusion, and
correspond to subdiffusion, positive values to superdiffusion, and
![]() corresponds to diffusion.
corresponds to diffusion.
Through comparison with direct numerical simulations of test particles, we have demonstrated that the GCD-model behaves very well and provides a noticeably improved description of perpendicular transport compared to several other theories considered in the tables for reference. Furthermore, by averaging over the scattering time, we have derived a simple formula (Eq. (16)) for the perpendicular mean free path. This formula can easily be applied for solar wind parameters and can be compared with observations. As demonstrated, there is very good agreement between the GCD-model and the observations discussed by Chenette et al. (1977), Palmer (1982), and Burger et al. (2000), similar to the results of the NLGC-theory and its extended version. However, the NLGC-theory, as well as the ENLGC-theory, predict very large perpendicular mean free paths for certain limits (see Bieber et al. 2004; Shalchi 2006). These limits do not exist as shown in the current article, hence Eqs. (7) and (8) represent perpendicular tranport for all parameter regimes within the two-component model. Thus, besides the weak superdiffusivity discovery in the article, the GCD-model clearly disagrees with the NLGC-theory that has been applied in several transport theory studies. It is the subject of our current work to study the application of the present theory in space physics and astrophysics in the hope that an improved formulation of perpendicular transport might be useful in solving a number of observational puzzles. Mainly the non-diffusivity of particle transport for turbulence models that have been considered in the past as realistic models for solar wind turbulence could be important for reproducing heliospheric observations.
Acknowledgements
This research was supported by the Deutsche Forschungsgemeinschaft (DFG) under the Emmy-Noether Programm (grant SH 93/3-1). As a member of the Junges Kolleg, A. Shalchi also aknowledges support by the Nordrhein-Westfälische Akademie der Wissenschaften. The authors are grateful to Prof. W. H. Matthaeus, Dr. G. Qin, and especially Dr. J. Minnie of the Bartol Research Institute and Department of Physics and Astronomy, University of Delaware for providing the test-particle code used in this paper. Futher information of the code can be found at http://www.bartol.udel.edu/%7Ewhmgroup/Streamline/streamline.html