C. Noël¹ - Y. Busegnies¹ - M. V. Papalexandris² - V. Deledicque² - A. El Messoudi¹

1 - Institut d'Astronomie et d'Astrophysique, Université Libre de Bruxelles, Campus plaine CP 226, Boulevard du Triomphe, 1050 Bruxelles, Belgium
2 - Département de Mécanique, Université catholique de Louvain, 1348 Louvain-la-Neuve, Belgium

Abstract
Aims. This work presents a new hydrodynamical algorithm to study astrophysical detonations. A prime motivation of this development is the description of a carbon detonation in conditions relevant to superbursts, which are thought to result from the propagation of a detonation front around the surface of a neutron star in the carbon layer underlying the atmosphere.
Methods. The algorithm we have developed is a finite-volume method inspired by the original MUSCL scheme of van Leer (1979). The algorithm is of second-order in the smooth part of the flow and avoids dimensional splitting. It is applied to some test cases, and the time-dependent results are compared to the corresponding steady state solution.
Results. Our algorithm proves to be robust to test cases, and is considered to be reliably applicable to astrophysical detonations. The preliminary one-dimensional calculations we have performed demonstrate that the carbon detonation at the surface of a neutron star is a multiscale phenomenon. The length scale of liberation of energy is 10⁶ times smaller than the total reaction length. We show that a multi-resolution approach can be used to solve all the reaction lengths. This result will be very useful in future multi-dimensional simulations. We present also thermodynamical and composition profiles after the passage of a detonation in a pure carbon or mixed carbon-iron layer, in thermodynamical conditions relevant to superbursts in pure helium accretor systems.

Key words: hydrodynamics - methods: numerical - shock waves - stars: neutron - X-rays: bursts - nuclear reactions, nucleosynthesis, abundances

1 Introduction

Superbursts have been discovered by long term monitoring of the X-ray sky with instruments such as RXTE and BeppoSAX. Compared to normal type I X-ray bursts, they are 1000 times more energetic (integrated burst energies of about 10⁴² erg), 1000 times longer (they last from hours to half a day), and have recurrence times of the order of years. They are very rare, only 13 such events having been found from 8 sources (for reviews see Kuulkers 2004; Cumming 2005, and references therein).

They also exhibit similarities with normal type I X-ray bursts, like a rapid rise in the light curve, a quasi-exponential decay, and a hardening of the spectrum during the rise followed by a softening during the decay, which are well represented by a blackbody model with an effective temperature growing during the rise and decreasing during the decay phase (Kuulkers 2004). This leads to the suggestion that superbursts, like normal type I bursts, are thermonuclear in origin (Cornelisse et al. 2000). The current view is that superbursts are due to the thermally unstable ignition of ¹²C at densities of about 10⁸-10⁹ g cm^-3 (Cumming 2001; Strohmayer & Brown 2002; Cumming 2005).

Most superbursts have been observed in systems accreting a mix of H and He (Kuulkers 2004). In these H/He accretors a very small amount of ¹²C remains after the combustion of H and He via the rp-process (Wallace & Woosley 1981; Shatz et al. 2001). For these systems, Cumming & Bildsten (2001) have shown that a small residual amount of ¹²C $(X_{ ^{12}{\rm C}} \approx 0.1)$ in a heavy element bath might be enough to ignite a superburst. Indeed, the low thermal conductivity of the rp-process ashes gives a large temperature gradient in the ocean which favours an unstable ignition of ¹²C (Cumming & Bildsten 2001), By ocean, we mean the region far below the zone where the accreted matter is decelerated from its free-fall velocity, and directly underneath the hydrogen/helium burning layer (Brown & Bildsten 1998). Moreover Shatz et al. (2003) have shown that, at the high temperature reached in superbursts (T>10⁹ K), the photodesintegration of the heavy rp-process ashes releases a quantity of nuclear energy which can be larger than the energy release from the fusion of carbon. If this is true, superbursts are the only known cosmic phenomena where photodisintegration of heavy elements is the main energy source. This interesting nucleosynthesis aspect will be considered in a future work.

This paper deals only with the case of pure He accretion. Pure He accretors are rare systems. There is only one superburst which has been observed in a system where the accreted material likely has a very high He abundance. This system is 4U 1820-30 (Strohmayer & Brown 2002, hereafter SB02). It is an ultra compact binary where the companion star is probably a low-mass helium dwarf (SB2002, Cumming 2003). This superburst detected by RXTE was $\approx$ 3 h long, had a peak luminosity of ${\approx} 3.4 \times 10^{38}$ erg s^-1, an observed energy release of $1.5 \times 10^{42}$ erg, and was preceded by a normal type I burst (20 s duration, SB02). SB02 showed that this superburst is thermonuclear in origin, fueled by the burning of carbon produced by the stable burning of the accreted helium between bursts. As neutrinos carry away most of the energy, the total energy of the superburst must be much greater than the observed one ( ${\approx} 10^{44}$ erg). The ashes of He burning depend on the stability of the combustion. If stable, C is the main product (Brown & Bildsten 1998), while an unstable combustion during normal type I bursts produces iron group elements (SB02). SB02 have shown that the iron made during bursts may mix with the carbon made during stable burning between bursts, so that the deep ocean is a mixture of the two. For this reason, we will study here the characteristics of a detonation wave in pure ¹²C and in a mixture $X_{ ^{12}{\rm C}} = 0.3$ and $X_{ ^{52}{\rm Fe}} = 0.7$ , which are the limiting cases considered by SB02. Due to the lack of protons, no rp-process can develop, which implies the absence of photodisintegration of heavy rp nuclides. In such conditions, a restricted nuclear reaction network is sufficient to describe the nucleosynthesis. This greatly eases the hydrodynamical simulations. We use a 13 species $\alpha$ chain network commonly used in other astrophysical hydrodynamics code (Fryxell et al. 1989).

Previous works concerning superbursts focused on the thermodynamical state of the surface layers just before ignition, and on the cooling following the bursts (Weinberg et al. 2006), but detailed hydrodynamic calculations are still missing. The observation of oscillations during the 2001 February 22 (UT) superburst from 4U 1636 53 suggests some departure from spherical symmetry in the superburst phenomenon (Strohmayer & Brown 2002b). Indeed, as it was suggested for normal type I X-ray bursts (Shara 1982), it is unlikely that ignition conditions will be achieved over the entire surface simultaneously. It appears more likely that burning is initiated locally, and then spreads laterally around the neutron star. Since the neutron star is rotating, the oscillations might be understood with a model including rotation and a non-uniform surface brightness, as well as the spreading of the combustion around the surface (Spitkovsky et al. 2002).

A combustion front may propagate in different ways (Williams 1965). According to Weinberg et al. (2006) the superburst rise evolves through three nuclear burning stages: an hour-long convective stage, a runaway stage, and a hydrodynamic stage. A combustion wave forms and may propagate from the site of the runaway as a detonation.

The only previous numerical studies of the propagation of a detonation front at the surface of a neutron star were made by Fryxell & Woosley (1982) and by Zingale et al. (2001). They considered only a detonation propagating in the He layer and not in the underlying C layer of relevance to superbursts. This paper presents the first hydrodynamical simulation of the C-detonation type. This simulation helps illustrate the performance of a new code we have developed. We limit ourselves here to the one-dimensional case. Two-dimensional results will be presented in a forthcoming paper.

Our code is based on a new MUSCL-type parallelized algorithm introduced by Papalexandis et al. (2002) and extended to cope with astrophysical conditions. It is described in Sect. 2. Our time-dependent simulations of detonation in pure ¹²C or in a mixture of ¹²C and ⁵²Fe at constant pressure and density typical of superbursts are compared in Sect. 3 with steady state predictions. The importance of the resolution is discussed for different initial conditions. Section 4 contains our conclusions and perspectives.

2 Numerical method

Our simulations are performed with a modified version of the unsplit, shock-capturing algorithm for multi-dimentional systems of hyperbolic conservations laws with source terms proposed by Papalexandis et al. (2002). It is a finite-volume method in the spirit of the original MUSCL scheme of van Leer (1979). The algorithm is of second-order in the smooth part of the flow. It avoids dimensional splitting. For the purpose of our astrophysical study, the original algorithm is extended to treat a stellar equation of state and a thermonuclear reaction network. We have implemented a Riemann solver based on the one of Colella & Glaz (1985), which is able to treat a general equation of state like an astrophysical one (Fryxell et al. 1989). The parallelization, deemed necessary in order to handle the computational requirements for the problem in hand, is based on the "mpi'' library, as described in Deledicque & Papalexandris (2006).

2.1 Hydrodynamics

The algorithm solves the adiabatic Euler's equations for compressible, non viscous gas dynamics with source terms in two dimensions. The equations can be written in conservative form as

$\begin{displaymath} \frac{\partial {\vec U}}{\partial t}+{\bf {\nabla}}\cdot {\vec F}({\vec U})={\vec G}({\vec U}) , \end{displaymath}$

(1)

$\begin{displaymath} {{\vec U}} = \left( \begin{array}{c} \rho\\ \rho {\vec... ...^{\rm nuc} \\ \rho R^{\rm nuc}_i \end{array} \right) . \end{displaymath}$

(2)

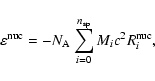$\begin{displaymath}\varepsilon^{\rm nuc} = -N_{\rm A} \sum_{i=0}^{n_{\rm sp}}M_ic^2 R^{\rm nuc}_i , \end{displaymath}$

(5)

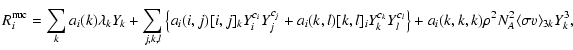$\displaystyle R^{\rm nuc}_i = \sum_k a_i(k)\lambda_k Y_k + \sum_{j,k,l}\big\{a_... ...c_k} Y_l^{c_l}\big\} + a_i(k,k,k)\rho^2 N_A^2\langle\sigma v\rangle_{3k}Y_k^3 ,$

(6)

where $[i,j]_k = \rho N_{\rm A} \langle\sigma v\rangle_{i+j\rightarrow k} ,$ $N_{\rm A}$ is the Avogadro number, $n_{\rm sp}$ is the number of species in the system and M_ic² is the rest mass energy of species i. The notation $\langle\sigma v\rangle_{i+j\rightarrow k}$ represents the thermonuclear reaction rate of the process $i+j \rightarrow k+l$ per pair of particles (i,j). The quantities a_i are statistical factors determined by the c_i,j,k,l (Arnett 1996).

2.2 The algorithm

$\begin{displaymath} \frac{\rm d}{{\rm d} t}\int_V\rho {\rm d}V + \int_S \rho {\vec u} \cdot {\rm d}{\vec S} =0 , \end{displaymath}$

(7)

$\begin{displaymath} \frac{\rm d}{{\rm d} t}\int_V \rho {\vec u} {\rm d}V + \int... ...}{\vec u} \cdot {\rm d}{\vec S} +\int_S p {\rm d}{\vec S}=0 , \end{displaymath}$

(8)

$\begin{displaymath} \frac{\rm d}{{\rm d} t}\int_V \rho e_t {\rm d}V + \int_S \r... ...m d}{\vec S} - \int_V \rho \varepsilon^{\rm nuc} {\rm d}V=0 , \end{displaymath}$

(9)

$\begin{displaymath} \frac{\rm d}{{\rm d} t}\int_V \rho Y_i {\rm d}V + \int_S \r... ...cdot {\rm d}{\vec S} - \int_V \rho R^{\rm nuc}_i {\rm d}V=0 . \end{displaymath}$

(10)

$\begin{displaymath} {{\vec U}}^{n+1}=\mathcal{L}_s^{\Delta t/2}\mathcal{L}_f^{\Delta t}\mathcal{L}_s^{\Delta t/2}({{\vec U}}^n) , \end{displaymath}$

(11)

$\begin{displaymath} \frac{\partial}{\partial t}{\vec U}+{\bf {\nabla}}\cdot{\vec F}({\vec U})=0 , \end{displaymath}$

(12)

and $\mathcal{L}_s$ is the numerical solution operator for the system of ordinary differential equations

It is obtained from the semi-implicit extrapolation method of Bader & Deuflhard (1983) which is used to solve the nuclear part of the system of Eqs. (7)-(10).

The procedure of discretization and numerical evaluation of the hydrodynamical part of the integrals (7-10) at each computational cell is the same as in Papalexandris et al. (2002). However the gamma-law Riemann solver of the initial algorithm is replaced by one based on the method of Colella & Glaz (1985) able to treat a general equation of state of the form given by Eqs. (3)-(4).

The numerical scheme, which evaluates the solution at time $(n+1)\Delta t$ from the solution at the previous time $n\Delta t$ for the hydrodynamical part of the system (Eq. (12)) can be written as

(m_i,j)ⁿ⁺¹	=	$\displaystyle (m_{i,j})^{n} - \Delta t\left[(l{\vec n}_S \cdot {\vec F}_m)_{i+1/2,j}^{n+1/2}- (l{\vec n}_S \cdot {\vec F}_m)_{i-1/2,j}^{n+1/2}\right]$
		$\displaystyle - \Delta t \left[(l{\vec n}_S \cdot {\vec F}_m)_{i,j+1/2}^{n+1/2}-(l{\vec n}_S \cdot {\vec F}_m)_{i,j-1/2}^{n+1/2}\right] ,$	(14)

(m_i,j u_i,j)ⁿ⁺¹	=	(m_i,ju_i,j)ⁿ
		$\displaystyle - \Delta t\left[(l{\vec n}_S \cdot {\vec F}_u)_{i+1/2,j}^{n+1/2}- (l{\vec n}_S \cdot {\vec F}_u)_{i-1/2,j}^{n+1/2}\right]$
		$\displaystyle -\Delta t \left[(l{\vec n}_S \cdot {\vec F}_u)_{i,j+1/2}^{n+1/2}-(l{\vec n}_S \cdot {\vec F}_u)_{i,j-1/2}^{n+1/2}\right] ,$	(15)

(m_i,j v_i,j)ⁿ⁺¹	=	(m_i,jv_i,j)ⁿ
		$\displaystyle -\Delta t\left[(l{\vec n}_S \cdot {\vec F}_v)_{i+1/2,j}^{n+1/2}- (l{\vec n}_S \cdot {\vec F}_v)_{i-1/2,j}^{n+1/2}\right]$
		$\displaystyle - \Delta t \left[(l{\vec n}_S \cdot {\vec F}_v)_{i,j+1/2}^{n+1/2}-(l{\vec n}_S \cdot {\vec F}_v)_{i,j-1/2}^{n+1/2}\right] ,$	(16)

(m_i,j e_{t i,j})ⁿ⁺¹	=	(m_i,je_{t i,j})ⁿ
		$\displaystyle - \Delta t\left[(l{\vec n}_S \cdot {\vec F}_e)_{i+1/2,j}^{n+1/2}- (l{\vec n}_S \cdot {\vec F}_e)_{i-1/2,j}^{n+1/2}\right]$
		$\displaystyle - \Delta t \left[(l{\vec n}_S \cdot {\vec F}_e)_{i,j+1/2}^{n+1/2}-(l{\vec n}_S \cdot {\vec F}_e)_{i,j-1/2}^{n+1/2}\right] ,$	(17)

(m_i,j Y_i,j,k)ⁿ⁺¹	=	(m_i,jY_i,j,k)ⁿ
		$\displaystyle - \Delta t\left[(l{\vec n}_S \cdot {\vec F}_{Y_k})_{i+1/2,j}^{n+1/2}- (l{\vec n}_S \cdot {\vec F}_{Y_k})_{i-1/2,j}^{n+1/2}\right]$
		$\displaystyle - \Delta t \left[(l{\vec n}_S \cdot {\vec F}_{Y_k})_{i,j+1/2}^{n+1/2}-(l{\vec n}_S \cdot {\vec F}_{Y_k})_{i,j-1/2}^{n+1/2}\right] ,$	(18)

where l and ${\vec n}_S$ are the length of a cell interface and the unit vector normal to a cell interface, respectively. The flux vectors are given by

2.3 Equation of state and nuclear reaction network

In the thermodynamical conditions relevant to the surface of a neutron star, the plasma can be considered as fully ionized. Our equation of state accounts for partially degenerate and partially relativistic electrons and positrons. The ions are treated as a Maxwell-Boltzmann gas, and the radiation, considered to be at local thermodynamic equilibrium with the matter, follows the Planck law. We use a tabulated equation of state in the spirit of Timmes's one (Timmes & Arnett 1999). Coulomb interactions of the bare nuclei with the surrounding electron-positron gas are not taken into account here, and will be included in a future work.

The selected nuclear reaction network is the one usually adopted in astrophysical hydrodynamics simulations in order to provide an energy source representative of explosive helium and carbon burning in absence of hydrogen. It involves 13 nuclides (⁴He, ¹²C, ¹⁶O, ²⁰Ne, ²⁴Mg, ²⁸Si, ³²S, ³⁶Ar, ⁴⁰Ca, ⁴⁴Ti, ⁴⁸Cr, ⁵²Fe and ⁵⁶Ni) linked by 27 reactions comprising the 11 $(\alpha,\gamma)$ reactions from ¹²C $(\alpha,\gamma)$ ¹⁶O to ⁵²Fe $(\alpha,\gamma)$ ⁵⁶Ni, the corresponding 11 endothermic photodesintegrations, the three heavy-ion reactions ¹²C(¹²C, $\alpha$ )²⁰Ne, ¹²C(¹⁶O, $\alpha$ )²⁴Mg and ¹⁶O(¹⁶O, $\alpha$ )²⁸Si, and the triple-alpha reaction and its inverse. As in Fryxell et al. (1989), the reaction rates are taken from Thielemann et al. (1986), where each reaction rate is given in the temperature interval $10^8 \leq T \leq 10^{10}$ K by

$\displaystyle N_A \langle\sigma v\rangle = \exp\left(c_1+c_2 T_9^{-1}+c_3T_9^{-1/3}+c_4T_9^{1/3} + c_5T_9+c_6T_9^{5/3}+c_7\ln(T_9)\right) ,$

(24)

where T₉=10⁹ K and the values of the numerical coeficients c_k are given by the authors. The network equations are constructed as described by Eq. (13), and are solved with the use of the variable order Bader-Deuflhard semi-implicit time integrator (Bader & Deuflhard 1983) suggested by Timmes (1999). The way this method is introduced in the algorithm is the same as in Press et al. (1992).

2.4 Validation tests

The comparaison of our time-dependent results with a steady state calculation, as presented in Sect. 3, also validate the accuracy of our algorithm.

3 Detonation profiles

One-dimensional steady-state calculations (i.e. calculations where the detonation speed remains constant) provide the main parameters characterizing a detonation, such as the characteristic time and length-scales and the reaction-zone structure. These basic detonation properties are necessary to set the initial parameters and boundary conditions in the time-dependent calculations. The treatment of the steady-state case is called the ZND model (Fickett & Davis 1979). According to this model, the detonation consists of an infinitely thin shock followed by a burning zone. All the reactions take place inside this zone and the released energy sustains the shock. In the laboratoy frame, these steady-state equations are

$\begin{displaymath} \frac{{\rm d} e}{{\rm d}t}=\frac{P}{\rho^2}\frac{{\rm d} \rho}{{\rm d}t}+\varepsilon^{\rm nuc} , \end{displaymath}$

(26)

where D, Z and $\rho_0$ are the detonation speed, the distance behind the shock and the density of the unburnt matter. The quantity $\Phi = \varepsilon^{\rm nuc}(\partial p/\partial e)_{\rho,Y_i}$ is the thermicity, $a_f=(\partial p/ \partial \rho)_{S,Y_i}^{1/2}$ is the frozen sound speed and S is the entropy (Khoklov 1989). The system of Eqs. (25)-(28) is closed by the equation of state (Eqs. (3)-(4)). For a given detonation speed, we compute a post-shock state using the Hugoniot relations (Khoklov 1988) and we integrate from the shock to the end of the burning zone (when the $R^{\rm nuc}_i$ vanish) using Eqs. (25)-(28).

Since superbursts in pure He accreting systems may be due to pure C detonation at high density and temperature we calculate the ZND profiles for a detonation in pure ¹²C at a temperature T=10⁸ K and a density $\rho = 10^8$ g cm^-3. The nuclear mass fraction profiles of some of the most abundant species are presented in Fig. 1 (thin solid lines). As can be seen a large variety of length scales are at work. The total reaction length given by the ZND model is of the order of 10⁴ cm. Significant changes in the nuclear mass fractions occur already at 10^-4 cm. This suggests that the full resolution of the detonation requires a time-dependent simulation over a domain as large as 10⁴ cm with a resolution of 10^-4 cm. Owe to computational time limitations we are unable to reach this resolution. However, following Gamezo et al. (1999), we have been able to perform two sets of calculations, one with a resolution of 10 cm over a domain of 10⁴ cm, and one with a resolution of 10^-4 cm over a domain of 1 cm.

$\begin{figure} \par\includegraphics[width=7.7cm,clip]{7123fig1.eps} \end{figure}$

Figure 1: Nuclear mass fraction profiles of ⁴He, ¹²C, ¹⁶O, ²⁸Si, ³²S, ⁵²Fe and ⁵⁶Ni for a detonation front in pure ¹²C at T=10⁸ K and $\rho = 10^8$ g cm^-3. Z is the distance to the shock in cm. The thin solid lines give the steady state solution of the ZND model. The heavy dots (the density of the dots is so high that they form thick curves) are obtained with the time-dependent calculations with two different resolutions (mesh size 10^-4 cm and 10 cm).

Open with DEXTER

The system of length l = 10⁴ cm is considered with an inflow boundary condition at x = 0 cm and an outflow boundary condition at x= 10⁴ cm. As initial conditions, we select pure ¹²C at T=10⁸ K, $\rho = 10^8$ g cm^-3 and a material velocity of 0 cm s^-1. To trigger the detonation we set the initial conditions in an ignition zone between x = 0 cm and x = 10³ cm to a temperature of $4.46 \times 10^{9}$ K, a density of $3.01 \times 10^8$ g cm^-3, a material velocity of $8.07 \times 10^8$ cm s^-1 and pure ⁵⁶Ni. We take 1000 numerical cells in the domain, leading to a resolution of 1 cm.

The simulation of a detonation of pure ¹²C in the same thermodynamic conditions as above has also been performed on a much smaller domain of lenght l = 1 cm with 10⁴ numerical cells, so that a resolution of 10^-4 cm is achieved. The initial discontinuity is positioned at 0.1 cm.

We have superimposed the profiles of the nuclear mass fractions of some of the most abundant species as a function of the distance to the shock obtained with the ZND algorithm and with the hydrodynamic algorithm. The ZND profiles are obtained for a velocity of propagation of the detonation wave $D=1.3 \times 10^9$ cm s^-1, which is the velocity of the detonation front in the time-dependent hydrodynamic simulation. As can be seen in Fig. 1, the time-dependent profiles are very close to the steady state ones. So, as in Gamezo et al. (1999), the partial resolution approach can be applied for the simulation of detonations in this system. This will be very useful in future 2D calculations where the computational time is crucial.

The preceding comparison between the steady-state and the time-dependent results was made without taking nuclear reaction rate screening effects into account. However, at high densities, screening may be important (Cox & Giuli 1968). and all the following results are obtained with the adoption of the screening corrections of Wallace et al. (1982). With this correction we have performed the simulation of a detonation of pure ¹²C in the same thermodynamic conditions as above at four different resolutions: one with a domain of length l = 1 cm, one with l = 100 cm, one with l = 1000 cm, and one with l = 10⁴ cm, always using 1000 numerical cells. The four corresponding nuclear mass fraction profiles are presented in Fig. 2. One sees the impact of the screening effects by comparing Figs. 1 and 2. Screening decreases the reaction length, increases the detonation velocity, and modifies the final composition. However these effects are small (less than 1% of the detonation velocity).

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{7123fig2.eps} \end{figure}$	Figure 2: Same as Fig. 1, but with screening effects taken into account. Results only obtained with the time-dependent calculations for four resolutions (from left to right: mesh size 10^-3 cm, 0.1 cm, 1 cm and 10 cm).
Open with DEXTER

The profiles of temperature, velocity, density and pressure at time $t = 5 \times 10^{-6}$ s for a resolution of 10 cm are presented in Fig. 3. The same profiles, and the nuclear energy generation profiles at time $t = 6 \times 10^{-10}$ s for a resolution of 0.1 cm are presented in Figs. 4 and 5. Ninety percent of the nuclear energy is already liberated over a distance of 10^-2 cm.

$\begin{figure} \par\includegraphics[width=8cm,clip]{7123fig3.eps} \end{figure}$	Figure 3: Temperature (in K), velocity (in cm s^-1), density (in g cm^-3) and pressure (in erg cm^-3) profiles of a detonation front in pure ¹²C at T=10⁸ K and $\rho = 10^8$ g cm^-3 at time = $5 \times 10^{-6}$ s. X is in cm.
Open with DEXTER

If we want to study the propagation of the detonation around a neutron star surface, we will be mainly interested in the structure of the end of the reaction zone. Indeed the detonation travels approximately $6 \times 10^6$ cm ( $R_{\rm NS} \approx 10$ km). What happens on 10^-2 cm is thus quite irrelevant, even if 90% of the nuclear energy is alredy liberated there. With a resolution of only 10 cm, we can already infer the global properties of the detonation in spite of the fact that we miss the destruction of C, the production and destruction of O, the production of Si and of S. All these reactions occur within one computational cell just behind the shock, but this has no global impact on the mean thermodynamic value at the end of the reaction length. This can be seen by comparing the thermodynamic profiles obtained with both resolutions (Figs. 3 and 4). However, fully resolving the detonation would be very important for the study of the extinction of the detonation (Maier & Niemeyer 2006). This question is not tackled here. The profiles of Fig. 3 give approximate values only, as the detonation is not perfectly resolved.

A simulation with a composition $X_{ ^{12}{\rm C}} = 0.3$ and $X_{ ^{52}{\rm Fe}} = 0.7$ (SB02) has also been conducted, the ignition conditions being the same as for pure $^{12}{\rm C}$ . The temperature, velocity, density and pressure profiles at time $t = 7 \times 10^{-6}$ s are presented in Fig. 6. In Fig. 7 the nuclear mass fraction of some species is shown as a function of the distance to the shock. We have only performed a simulation with a 10 cm resolution for the reasons explained above.

From these two sets of results (detonation in pure ¹²C and in a mixture of ¹²C and ⁵²Fe), we see that the composition of the material before the passage of the detonation wave affects the velocity of propagation of the detonation wave and the composition in the burned material. For pure ¹²C the velocity of propagation of the detonation is $D \approx 1.3 \times 10^9$ cm s^-1, and for the mixture of ¹²C and ⁵²Fe, $D \approx 1.22 \times 10^9$ cm s^-1. The pure ¹²C detonation mainly produces ⁴He, and the mixed detonation leads essentially to ⁵⁶Ni.

$\begin{figure} \par\includegraphics[width=7.9cm,clip]{7123fig5.eps} \end{figure}$	Figure 5: Nuclear energy generation (erg g^-1 s^-1) profile of a detonation front in pure ¹²C at T=10⁸ K and $\rho = 10^8$ g cm^-3 at time = $6 \times 10^{-10}$ s with a resolution of 10^-3 cm. X is in cm.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{7123fig6.eps} \end{figure}$	Figure 6: Same as Fig. 3, but at time = $7 \times 10^{-6}$ s and for a mixture $X_{ ^{12}{\rm C}} = 0.3$ and $X_{ ^{52}{\rm Fe}} = 0.7$ .
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.7cm,clip]{7123fig7.eps} \end{figure}$	Figure 7: Nuclear mass fraction profiles of a detonation front in a mixture $X_{ ^{12}{\rm C}} = 0.3$ and $X_{ ^{52}{\rm Fe}} = 0.7$ at T=10⁸ K and $\rho = 10^8$ g cm^-3 at time = $7 \times 10^{-6}$ s. Z is the distance to the shock in cm.
Open with DEXTER

4 Conclusions

Our hydrodynamical algorithm for modeling astrophysical detonations has been shown to be robust to test cases. In particular it reproduces quite well the steady state solution obtained with a totally different code. This give us confidence for future multi-dimensional simulations. Some improvements still need to be made, like the inclusion of gravity, of non-ideal terms in the equation of state, and more up-to-date data for the nuclear reaction network.

We have underlined the large difference between the total reaction length and the length on which some species (e.g. carbon) burn in conditions relevant to superbursts. This difference leads to enormous numerical difficulties because all the length scales cannot be resolved at the same time during a single simulation (except possibly with some sub-grid models). We have shown that the carbon detonation in superburst conditions might be studied by a partial resolution approach. This is important, especially in multidimensional simulations where the computation time is a crucial limitation.

Our simulations give the global thermodynamic state of the material after the passage of the detonation in the carbon layer at the surface of a neutron star. These conditions are not very sensitive to the exact initial composition of the matter, in contrast to the final composition. In both cases, however, all the carbon is burned. It has to be replenished to allow the occurence of a subsequent superburst.

It is unlikely that the entire carbon layer ignites at the same time. More probably, ignition spots develop. Since the detonation velocity depends on the composition of the carbon layer before ignition, the time for the detonation to propagate laterally around the neutron star also depends on the composition.

In a subsequent paper we will investigate a larger parameter space of thermodynamic condition. In particular, we will study the impact of the initial temperature or density. It would also be more realistic to introduce an initial temperature and density profile. Two-dimentional superburst simulations are under study and will complement the work of Zingale et al. (2001) for normal type I X-ray bursts. We will also investigate the vertical propagation of the detonation and its interaction with an overlying helium layer. One of the aims of this simulation is to examine if the penetration of a detonation wave into the helium layer could given rise to the precursor observed prior to the superburst from 4U 1820-30.

Hydrodynamical simulation of detonations in superbursts

I. The hydrodynamical algorithm and some preliminary one-dimensional results