A&A 470, 191-210 (2007)
DOI: 10.1051/0004-6361:20077168
M. Wittkowski1 - D. A. Boboltz2 - K. Ohnaka3 - T. Driebe3 - M. Scholz4,5
1 -
European Southern Observatory, Karl-Schwarzschild-Str. 2,
85748 Garching bei München, Germany
2 -
United States Naval Observatory, 3450 Massachusetts Avenue,
NW, Washington, DC 20392-5420, USA
3 -
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121 Bonn, Germany
4 -
Institut für Theoretische Astrophysik der Univ. Heidelberg,
Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
5 -
Institute of Astronomy, School of Physics,
University of Sydney, Sydney NSW 2006, Australia
Received 25 January 2007 / Accepted 18 April 2007
Abstract
Aims. We present the first multi-epoch study that includes concurrent mid-infrared and radio interferometry of an oxygen-rich Mira star.
Methods. We obtained mid-infrared interferometry of S Ori with VLTI/MIDI at four epochs in December 2004, February/March 2005, November 2005, and December 2005. We concurrently observed v=1, J=1-0 (43.1 GHz), and
v=2, J=1-0 (42.8 GHz) SiO maser emission toward S Ori with the VLBA in January, February, and November 2005. The MIDI data are analyzed using self-excited dynamic model atmospheres including molecular layers, complemented by a radiative transfer model of the circumstellar dust shell. The VLBA data are reduced to the spatial structure and kinematics of the maser spots.
Results. The modeling of our MIDI data results in phase-dependent continuum photospheric angular diameters of 9.0 ![]() 0.3 mas (phase 0.42), 7.9
0.3 mas (phase 0.42), 7.9 ![]() 0.1 mas (0.55), 9.7
0.1 mas (0.55), 9.7 ![]() 0.1 mas (1.16), and 9.5
0.1 mas (1.16), and 9.5 ![]() 0.4 mas (1.27). The dust shell can best be modeled with Al2O3 grains using phase-dependent inner boundary radii between 1.8 and 2.4 photospheric radii. The dust shell appears to be more compact with greater optical depth near visual minimum (
0.4 mas (1.27). The dust shell can best be modeled with Al2O3 grains using phase-dependent inner boundary radii between 1.8 and 2.4 photospheric radii. The dust shell appears to be more compact with greater optical depth near visual minimum (
![]() ), and more extended with lower optical depth after visual maximum (
), and more extended with lower optical depth after visual maximum (
![]() ). The ratios of the 43.1 GHz/42.8 GHz SiO maser ring radii to the photospheric radii are 2.2
). The ratios of the 43.1 GHz/42.8 GHz SiO maser ring radii to the photospheric radii are 2.2 ![]() 0.3/2.1
0.3/2.1 ![]() 0.2 (phase 0.44), 2.4
0.2 (phase 0.44), 2.4 ![]() 0.3/2.3
0.3/2.3 ![]() 0.4 (0.55), and 2.1
0.4 (0.55), and 2.1 ![]() 0.3/1.9
0.3/1.9 ![]() 0.2 (1.15). The maser spots mark the region of the molecular atmospheric layers just beyond the steepest decrease in the mid-infrared model intensity profile. Their velocity structure indicates a radial gas expansion.
0.2 (1.15). The maser spots mark the region of the molecular atmospheric layers just beyond the steepest decrease in the mid-infrared model intensity profile. Their velocity structure indicates a radial gas expansion.
Conclusions. S Ori shows significant phase-dependences of photospheric radii and dust shell parameters. Al2O3 dust grains and SiO maser spots form at relatively small radii of ![]() 1.8-2.4 photospheric radii. Our results suggest increased mass loss and dust formation close to the surface near the minimum visual phase, when Al2O3 dust grains are co-located with the molecular gas and the SiO maser shells, and a more expanded dust shell after visual maximum. Silicon does not appear to be bound in dust, as our data show no sign of silicate grains.
1.8-2.4 photospheric radii. Our results suggest increased mass loss and dust formation close to the surface near the minimum visual phase, when Al2O3 dust grains are co-located with the molecular gas and the SiO maser shells, and a more expanded dust shell after visual maximum. Silicon does not appear to be bound in dust, as our data show no sign of silicate grains.
Key words: techniques: interferometric - masers - stars: AGB and post-AGB - stars: atmospheres - stars: mass-loss - stars: individual: S Orionis
The conditions close to the stellar surface can be studied well by means of optical long-baseline interferometry. This technique has provided information regarding the stellar photospheric diameter, effective temperature, center-to-limb intensity variation (CLV), and atmospheric molecular layers for a number of Mira variables (see, e.g., Quirrenbach et al. 1992; Haniff et al. 1995; van Belle et al. 1996; Thompson et al. 2002; Mennesson et al. 2002; Hofmann et al. 2002; van Belle et al. 2002; Perrin et al. 2004; Millan-Gabet et al. 2005).
Woodruff et al. (2004) and Fedele et al. (2005) have recently shown that observed near-infrared K-band visibilities of the oxygen-rich prototype Mira variables o Cet and R Leo are very different from uniform disc (UD) models already in the first lobe of the visibility function, and that they correspond closely to predictions by self-excited dynamic Mira model atmospheres that include effects from molecular layers (models by Hofmann et al. 1998; Tej et al. 2003b; Ireland et al. 2004a,b). Ohnaka et al. (2006b) studied the comparison of the same dynamic Mira model atmospheres with mid-infrared interferometric and spectroscopic observations. Recently, Ireland & Scholz (2006) added the formation of dust in a self-consistent way to the same dynamic Mira model atmospheres. They find that dust would form at 2-3 times the average photospheric radius for certain plausible parameter values.
The structure of the atmospheric molecular shells located above
the photosphere, as well as the dust shell, can be probed by
mid-infrared interferometry.
This has been successfully demonstrated by Ohnaka et al.
(2005) using the spectro-interferometric
capabilities of the VLTI/MIDI facility for observations of
the oxygen-rich Mira star RR Sco.
The model used in this work includes a warm molecular
layer consisting of SiO and H2O, as well as an
optically-thin dust shell of Al2O3 and silicate.
Recent VLTI/MIDI observations of the carbon-rich
Mira star V Oph by Ohnaka et al. (2007)
indicate that carbon-rich Miras
also have extended atmospheric layers of polyatomic
molecules (C2H2) and dust shells (amorphous carbon and SiC).
Information on dust shells around Mira variables has
also been derived using mid-infrared interferometry with the
Berkeley Infrared Spatial Interferometer ISI
(see e.g., Danchi et al. 1994;
Weiner et al. 2006; Tatebe et al. 2006).
Ireland et al. (2005) recently used 0.9 ![]() m
interferometric polarimetry measurements of the Mira
variables R Car and RR Sco to place
constraints on the distribution of the dust shell.
m
interferometric polarimetry measurements of the Mira
variables R Car and RR Sco to place
constraints on the distribution of the dust shell.
Complementary information regarding the molecular shells around oxygen-rich AGB stars can be obtained by observing the maser radiation that some of these molecules emit. Maser emission from the three most common maser molecules, SiO, H2O, and OH, traces regions of the CSE on scales from a few to several hundred AU. Masers provide a unique probe of structure, kinematics, and polarization properties of the environment of these stars. The SiO maser radiation in the CSE of oxygen-rich Mira variables has been mapped using the Very Long Baseline Array (VLBA) by, e.g., Diamond et al. (1994), Kemball & Diamond (1997), Boboltz et al. (1997), Diamond & Kemball (2003), Cotton et al. (2004), Boboltz & Wittkowski (2005, hereafter BW05), Boboltz & Diamond (2005), and Cotton et al. (2006). The SiO maser emission is typically found to arise from a clumpy ring within a few stellar radii of the photosphere, indicating a tangential amplification process. Humphreys et al. (1996,2002) have predicted the location at which SiO molecules form in the CSE of Mira variables by combining maser models with hydrodynamic pulsation models. Their model predictions are roughly consistent with the measurements mentioned above.
Observational results regarding the detailed relationships between the stellar photosphere, the molecular layer, the dust shell, and the SiO maser ring often suffer from uncertainties inherent in comparing observations of variable stars widely separated in time and stellar phase, as discussed in BW05. To overcome this limitation, we have established a program of concurrent infrared interferometry using the VLTI and radio interferometry at the VLBA. The former aims at constraining the photospheric radius, the characteristics of atmospheric molecular layers, and parameters of the dust shell. The latter aims at concurrently mapping the SiO maser emission. Our final goal is a better understanding of the mass-loss process and its connection to stellar pulsation. Our pilot study in BW05 on the Mira variable S Ori included coordinated near-infrared K-band interferometry to constrain the stellar photospheric diameter and VLBA mapping of the SiO maser radiation toward this source.
A further uncertainty in comparing photospheric radii to the extensions of the dust and maser shells arises from the complication that near- and mid-infrared CLVs of finite bandwidth include a blend of intensities from continuum-forming layers and overlying molecular layers. This effect has often resulted in over-estimated continuum photospheric diameter values (see, e.g. the discussions in Jacob & Scholz 2002; Mennesson et al. 2002; van Belle et al. 2002; Woodruff et al. 2004; Ireland et al. 2004a,b; Perrin et al. 2004; Fedele et al. 2005). An overestimated photospheric diameter would result in biased relative distances of the dust shell and the maser ring from the stellar surface, even if obtained at the same stellar phase and cycle. A detailed comparison of observations to dynamic model atmospheres, as mentioned above, can be used to relate the observable quantities to the continuum photospheric radius and thus to overcome this limitation.
Here, we present VLTI/MIDI mid-infrared interferometry of S Ori at 4 epochs/stellar phases and coordinated VLBA mapping of the SiO 42.8 GHz and 43.1 GHz maser transitions at 3 epochs/stellar phases that are contemporaneous to the first 3 of our 4 MIDI epochs. The first two epochs are located near the stellar minimum, and the later epochs shortly after the following stellar maximum.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7168fig1.ps}\par\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{7168fig2.ps}\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg30.gif) |
Figure 1:
Visual lightcurve of S Ori as a function of Julian Date
and stellar cycle/phase. Data are from the AAVSO (Henden et al. 2006) and AFOEV (CDS) databases. We adopt a
period of
|
| Open with DEXTER | |
The distance to S Ori, as for many Mira stars, is not well
known. Van Belle et al. (2002) have estimated the
distance to S Ori to
![]() based on a
calibration of the period-luminosity relationship by
Feast et al. (1989), and we adopt this value.
based on a
calibration of the period-luminosity relationship by
Feast et al. (1989), and we adopt this value.
The near-infrared K-band UD
angular diameter
![]() of S Ori has been
measured by van Belle et al. (1996),
Millan-Gabet et al. (2005), and by BW05
to values between 9.6 mas and 10.5 mas at different
phases.
Diameter measurements of S Ori at other wavelengths have so
far not been reported.
of S Ori has been
measured by van Belle et al. (1996),
Millan-Gabet et al. (2005), and by BW05
to values between 9.6 mas and 10.5 mas at different
phases.
Diameter measurements of S Ori at other wavelengths have so
far not been reported.
S Ori exhibits SiO and OH maser emission
(Benson et al. 1990), while a detection
of H2O maser
toward S Ori has not been reported. The maps of the
SiO maser emission in BW05 are the first toward S Ori.
They derived average distances and standard deviations
of the SiO maser spots from the center
of their distribution at phase 0.73 of
![]() and
and
![]() for the
for the
![]() and
and
![]() transitions, respectively.
transitions, respectively.
Table 1: VLTI/MIDI observations of S Ori.
Sloan & Price (1998) report on a relatively low
dust-emission coefficient (Dec, the total emission of the dust
to the total emission of the star in the wavelength range
7.7-14.0
![]() )
for S Ori of 0.24, i.e. similar
to RR Sco (
)
for S Ori of 0.24, i.e. similar
to RR Sco (
![]() )
or R Leo (
)
or R Leo (
![]() ), indicating
an optically thin dust shell.
), indicating
an optically thin dust shell.
We obtained mid-infrared (8-13 ![]() m) interferometry
of S Ori with the instrument MIDI (Leinert et al.
2003) at the ESO VLT Interferometer (VLTI;
Glindemann et al. 2003) in service mode between
31 December 2004 and 30 December 2005. Light was combined from
two 8 m Unit Telescopes (UTs). We chose to use the prism with
spectral resolution
m) interferometry
of S Ori with the instrument MIDI (Leinert et al.
2003) at the ESO VLT Interferometer (VLTI;
Glindemann et al. 2003) in service mode between
31 December 2004 and 30 December 2005. Light was combined from
two 8 m Unit Telescopes (UTs). We chose to use the prism with
spectral resolution
![]() to disperse
the interferograms. Two various techniques of beam
combinations were used, namely HIGH_SENS (HS, 2004-12-31
to 2005-03-03) and SCI_PHOT (SP, 2005-11-12 to 2005-12-30)
combinations. Using the HS combination, all arriving light is
first combined interferometrically, and the photometric spectrum
for each incoming beam is recorded sequentially. Using the
SP combination, beam splitters are used to record the
interferograms and the photometric spectra simultaneously.
An estimate of the photometric count rates at the time of
recording the interferometric data is needed to compute the
raw visibility values, and the SP technique is thus expected to
result in a higher precision of the visibility measurement for bright targets.
Our observations followed the standard procedures for
MIDI service mode observations as described in detail in the
MIDI user manual
to disperse
the interferograms. Two various techniques of beam
combinations were used, namely HIGH_SENS (HS, 2004-12-31
to 2005-03-03) and SCI_PHOT (SP, 2005-11-12 to 2005-12-30)
combinations. Using the HS combination, all arriving light is
first combined interferometrically, and the photometric spectrum
for each incoming beam is recorded sequentially. Using the
SP combination, beam splitters are used to record the
interferograms and the photometric spectra simultaneously.
An estimate of the photometric count rates at the time of
recording the interferometric data is needed to compute the
raw visibility values, and the SP technique is thus expected to
result in a higher precision of the visibility measurement for bright targets.
Our observations followed the standard procedures for
MIDI service mode observations as described in detail in the
MIDI user manual![]() .
For principles of observations with MIDI see
also Leinert et al. (2004).
.
For principles of observations with MIDI see
also Leinert et al. (2004).
The details of our observations are listed in
Table 1. Listed are the
epoch, date, time, and Julian Date (JD) of the observation;
the visual phase
![]() ;
the baseline configuration used with its ground length B;
the dispersive element and beam combiner BC
(HS for High_Sens and SP for Sci_Phot);
and the projected
baseline length
;
the baseline configuration used with its ground length B;
the dispersive element and beam combiner BC
(HS for High_Sens and SP for Sci_Phot);
and the projected
baseline length ![]() and its position angle PA on sky (deg.
east of north). The last two columns describe the ambient
conditions DIMM seeing, and coherence time
and its position angle PA on sky (deg.
east of north). The last two columns describe the ambient
conditions DIMM seeing, and coherence time ![]() ,
both
at 500 nm.
Dates of observation were combined into 4 epochs A, B, C, D.
Each epoch has a width of less than 17 days, i.e. less than 5% of S Ori's variability period. The dates of observation and
the epochs compared to the visual
lightcurve are indicated in Fig. 1.
We estimate the uncertainty in assigning a visual phase value
to each of our observing epochs to
,
both
at 500 nm.
Dates of observation were combined into 4 epochs A, B, C, D.
Each epoch has a width of less than 17 days, i.e. less than 5% of S Ori's variability period. The dates of observation and
the epochs compared to the visual
lightcurve are indicated in Fig. 1.
We estimate the uncertainty in assigning a visual phase value
to each of our observing epochs to ![]() 0.1, taking into
account both the time widths of our epochs and the uncertainty in
the choice of S Ori's current variability period and
date of last maximum (see Sect. 2).
Epochs A and B are located around stellar minimum with a
separation of about 2 months (phase difference
0.1, taking into
account both the time widths of our epochs and the uncertainty in
the choice of S Ori's current variability period and
date of last maximum (see Sect. 2).
Epochs A and B are located around stellar minimum with a
separation of about 2 months (phase difference ![]() 0.1),
while epochs C and D occurred about a year later
shortly after the following stellar maximum with a separation
of 6 weeks.
Additional MIDI/UT data on S Ori from 2004-12-29, 2005-01-02,
2005-02-28, 2006-03-12, 2006-03-12, as well as MIDI/AT data
taken between October 2005 and March 2006 were not used because
of various technical problems with these data sets.
The interferometric field of view of MIDI used with the UTs
is
0.1),
while epochs C and D occurred about a year later
shortly after the following stellar maximum with a separation
of 6 weeks.
Additional MIDI/UT data on S Ori from 2004-12-29, 2005-01-02,
2005-02-28, 2006-03-12, 2006-03-12, as well as MIDI/AT data
taken between October 2005 and March 2006 were not used because
of various technical problems with these data sets.
The interferometric field of view of MIDI used with the UTs
is ![]() 250 mas, which corresponds to about 25 times
the expected photospheric angular diameter of S Ori.
250 mas, which corresponds to about 25 times
the expected photospheric angular diameter of S Ori.
We used ![]() CMa (HD 50778) as the interferometric
calibrator, a K4 giant at a distance on sky of 27
CMa (HD 50778) as the interferometric
calibrator, a K4 giant at a distance on sky of 27![]() ,
which
was observed within about 30 min of each S Ori observation.
A number of observations of other MIDI calibration stars using
the same instrument settings were obtained during some of our
observation nights for other programs, and we make use of these
data as well. Table 2 lists the calibration stars
and their properties. These parameters are taken
from the instrument consortium's
catalog
,
which
was observed within about 30 min of each S Ori observation.
A number of observations of other MIDI calibration stars using
the same instrument settings were obtained during some of our
observation nights for other programs, and we make use of these
data as well. Table 2 lists the calibration stars
and their properties. These parameters are taken
from the instrument consortium's
catalog![]() .
Listed are the HD number, the name, the
spectral type, the limb-darkened diameter
.
Listed are the HD number, the name, the
spectral type, the limb-darkened diameter
![]() ,
the effective temperature
,
the effective temperature
![]() ,
the
flux at 12
,
the
flux at 12 ![]() m, and the distance on sky from S Ori
m, and the distance on sky from S Ori ![]() .
The UD diameter for K giants in the mid-infrared
based on spherical model atmospheres is smaller by
.
The UD diameter for K giants in the mid-infrared
based on spherical model atmospheres is smaller by ![]() 5%
than
5%
than
![]() (estimated with procedures as used in
Wittkowski et al. 2006).
HD 50778 is our main calibrator. The other calibrators
were observed during some of our observation nights for other
programs. Among the interferometric calibration stars listed
in Table 2,
absolutely calibrated spectra are available for HD 31421 and
HD 61935 (Cohen et al. 1999).
(estimated with procedures as used in
Wittkowski et al. 2006).
HD 50778 is our main calibrator. The other calibrators
were observed during some of our observation nights for other
programs. Among the interferometric calibration stars listed
in Table 2,
absolutely calibrated spectra are available for HD 31421 and
HD 61935 (Cohen et al. 1999).
Table 2: Properties of the MIDI calibration stars used.
Mean coherence factors and photometric count rates were obtained for each data set of S Ori and the calibration stars using the MIA+EWS software package, version 1.4 (Jaffe, Koehler, Cotton, Chesneau, et al.Calibrated visibility spectra for S Ori were derived using the transfer function obtained for our calibrator HD 50778. The scatter of all obtained transfer functions during the night was used to estimate its uncertainty. The latter depends on the sample of calibrations stars available per night, and we assumed a minimum uncertainty of the transfer function of 0.1 based on nights when many values were obtained. The total error of our calibrated S Ori visibility spectrum includes the errors of the raw coherence factors computed by EWS, the uncertainty of the calibrator diameters, and the scatter of the transfer function during the night. The total error is dominated by systematic uncertainties for the height of the interferometric transfer function, so that the relative accuracy of the visibility values among the spectral channels is better than indicated by our total error bars.
We absolutely calibrated the photometric spectrum of S Ori for
each data set using the interferometric calibrator HD 50778 also
as the photometric calibration star.
The absolutely calibrated photometric spectrum of HD 50778 was
not available directly. We used instead the average of the
available spectra of HD 20644 and HD 87837
(Cohen et al. 1999), scaled with the
IRAS 12 ![]() m flux (Beichmann et al. 1988)
to the level of HD 50778. These stars
have the same spectral type (K4 III) and very similar effective
temperatures as HD 50778 (4058 K and 4094 K versus 4049 K).
In addition, we calibrated the
photometric spectrum of HD 50778 using the spectro-photometric
calibrator HD 31421, which was observed close in time during
the night 2005-03-03, and verified that our
synthetic HD 50778 spectrum is valid.
We obtained integrated 8.0-13.0
m flux (Beichmann et al. 1988)
to the level of HD 50778. These stars
have the same spectral type (K4 III) and very similar effective
temperatures as HD 50778 (4058 K and 4094 K versus 4049 K).
In addition, we calibrated the
photometric spectrum of HD 50778 using the spectro-photometric
calibrator HD 31421, which was observed close in time during
the night 2005-03-03, and verified that our
synthetic HD 50778 spectrum is valid.
We obtained integrated 8.0-13.0 ![]() m S Ori flux densities for our
MIDI epochs A to D of
m S Ori flux densities for our
MIDI epochs A to D of
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() .
For comparison, the integrated
IRAS LRS flux density for the same bandpass (8.0-13.0
.
For comparison, the integrated
IRAS LRS flux density for the same bandpass (8.0-13.0 ![]() m)
is 169 Jy.
m)
is 169 Jy.
The MIDI calibrated visibility, as well as calibrated flux values, are detailed in Table A.1.
As an alternative and probably more intuitive quantity compared to the visibility values, we calculated the equivalent UD diameters. The equivalent UD diameter was computed for each projected baseline length and spectral channel separately and defined as the diameter of that uniform disc that results in the same visibility value at each separate data point. Note that the true intensity profile is not expected to be a uniform disc. As a result, the equivalent UD diameters for different projected baseline lengths are not expected to coincide (not even for a circularly symmetric intensity profile). However, these values are fully equivalent to the calibrated visibility values and can provide a first rough estimate of the characteristic size of the target.
Figures 2-5 show, for MIDI epochs A-D, respectively, the obtained MIDI flux spectra, the MIDI visibility values as a function of wavelength, the MIDI visibility values as a function of spatial frequency for the example of three spectral channels and the equivalent UD diameter values. Also shown are the synthetic visibility and flux values of the atmosphere and dust models described below in Sect. 3.3 in each panel, as well as the intensity profiles of these models for the example of three bandpasses in the bottom panels.
The general shape of our S Ori visibility functions, or
equivalent UD diameter values, in
Figs. 2-5 is qualitatively similar
to the MIDI data of the Mira variable RR Sco described
in Ohnaka et al. (2005). Objects such as these are
characterized by a partially resolved stellar disc, including
atmospheric molecular layers that are optically thick at mid-infrared
wavelengths, surrounded by a spatially resolved, optically
thin dust shell. The visibility increases between about
8-9 ![]() m, corresponding to a quasi-constant equivalent
UD diameter that is roughly twice the continuum
photospheric size. Here, the observed intensity is
dominated by radiation from optically thick molecular layers at
distances up to roughly two continuum photospheric radii.
Beyond about 9-10
m, corresponding to a quasi-constant equivalent
UD diameter that is roughly twice the continuum
photospheric size. Here, the observed intensity is
dominated by radiation from optically thick molecular layers at
distances up to roughly two continuum photospheric radii.
Beyond about 9-10 ![]() m, the visibility function flattens,
corresponding to an increasing equivalent UD diameter.
In this wavelength region, spatially resolved, optically thin
radiation from the dust shell starts to represent a
considerable part of the total intensity. In addition,
extinction of the stellar light by the dust shell becomes
important. At the longest wavelengths of MIDI, spatially
resolved radiation from the dust shell dominates the measured
intensity.
A detailed model of S Ori's atmosphere and dust shell is
described in Sects. 3.3
and 3.4.
m, the visibility function flattens,
corresponding to an increasing equivalent UD diameter.
In this wavelength region, spatially resolved, optically thin
radiation from the dust shell starts to represent a
considerable part of the total intensity. In addition,
extinction of the stellar light by the dust shell becomes
important. At the longest wavelengths of MIDI, spatially
resolved radiation from the dust shell dominates the measured
intensity.
A detailed model of S Ori's atmosphere and dust shell is
described in Sects. 3.3
and 3.4.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{7168fig3.eps}
\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg59.gif) |
Figure 2:
Results of our VLTI/MIDI 8-13 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7168fig4.eps}\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg60.gif) |
Figure 3:
Results of our VLTI/MIDI 8-13 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7168fig5.eps}\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg61.gif) |
Figure 4:
Results of our VLTI/MIDI 8-13 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7168fig6.eps}\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg62.gif) |
Figure 5:
Results of our VLTI/MIDI 8-13 |
| Open with DEXTER | |
Mid-infrared photometric and interferometric data of Mira stars are in general sensitive to details of the structure of the stellar atmosphere in which molecular layers of various geometrical and optical characteristics (e.g., Tej et al. 2003a) lie above the continuum-forming photosphere, as well as to the surrounding dust shell (cf. e.g., Ohnaka et al. 2005,2006b; Ireland & Scholz 2006; Weiner et al. 2006). We used the P and M model atmosphere series (Ireland et al. 2004a,b) to describe the stellar atmosphere including the continuum photosphere and overlying molecular layers, and added an ad-hoc radiative transfer model of the dust shell. The details of our modeling are described in the following.
Few dynamic atmosphere models for oxygen-rich Mira stars
are available that include the effects of molecular
layers (see, e.g., Scholz 2001,2003). The
P and M model series (Ireland et al.
2004a,b)
are complete self-excited dynamic model atmosphere of Mira
stars, and they have successfully explained a lot of observational
data (e.g.; Hofmann et al. 2000,2001,2002;
Woodruff et al. 2004;
Fedele et al. 2005).
These model series have been constructed to match the prototype
oxygen-rich Mira stars o Cet and R Leo.
The P and M series differ with respect to the mass of the
so-called "parent star'', which is the hypothetical
non-pulsating equivalent of the pulsating Mira variable.
The geometric pulsation of the Mira occurs around the parent
star's Rosseland radius
![]() (Ireland et al. 2004a,b).
The parent star has solar metallicity, luminosity
(Ireland et al. 2004a,b).
The parent star has solar metallicity, luminosity
![]() ,
period 332 days,
mass
,
period 332 days,
mass
![]() (P series) and 1.2 (M),
radius
(P series) and 1.2 (M),
radius
![]() (P) and 260 (M)
(Hofmann et al. 1998). The moderately
larger radius of the M-series parent star leads to a slightly
lower effective temperature for the parent star and
systematically lower phase-dependent effective temperatures
for the pulsating Mira compared to the P series.
The M models tend to exhibit less pronounced cycle-to-cycle
variations than the P models and to have more compact
atmospheres (Ireland et al. 2004b).
Effects on interferometric diameter measurements resulting from
the differences between the P and M model series are subtle.
When comparing P and M models of similar phases to near-infrared
interferometric data of R Leo, the resulting
Rosseland angular diameter values were found to agree
within
(P) and 260 (M)
(Hofmann et al. 1998). The moderately
larger radius of the M-series parent star leads to a slightly
lower effective temperature for the parent star and
systematically lower phase-dependent effective temperatures
for the pulsating Mira compared to the P series.
The M models tend to exhibit less pronounced cycle-to-cycle
variations than the P models and to have more compact
atmospheres (Ireland et al. 2004b).
Effects on interferometric diameter measurements resulting from
the differences between the P and M model series are subtle.
When comparing P and M models of similar phases to near-infrared
interferometric data of R Leo, the resulting
Rosseland angular diameter values were found to agree
within ![]() 1.5% (Fedele et al. 2005).
1.5% (Fedele et al. 2005).
Compared to o Cet and R Leo, for which the P and M model series are designed, S Ori is a slightly
cooler Mira variable (M6.5-M9.5 versus M5-M9/M6-M9.5,
Samus et al. 2004) with a longer
period (420 d versus 332 d/310 d,
Samus et al. 2004), a larger main sequence precursor
mass (1.3 ![]() versus 1.0
versus 1.0 ![]() /1.2
/1.2 ![]() ,
Wyatt & Cahn 1983), and a larger radius
(mean continuum photospheric radii roughly
,
Wyatt & Cahn 1983), and a larger radius
(mean continuum photospheric radii roughly ![]()
![]() versus
versus ![]() 350
350 ![]() ;
based on
BW05, Woodruff et al. 2004; Fedele et al. 2005).
However, when scaled to variability phases between 0 and 1 and
to the corresponding angular size on sky, the general model
results are not expected to be dramatically different for
S Ori compared to Mira stars, such as o Cet and R Leo.
Hereby, the M series is expected to be better-suited
to describing S Ori than the P series because of its
higher parent-star mass.
We concluded that the use of the M series is currently
the best available option for describing S Ori's atmosphere
including the continuum photosphere and overlying atmospheric
molecular layers.
;
based on
BW05, Woodruff et al. 2004; Fedele et al. 2005).
However, when scaled to variability phases between 0 and 1 and
to the corresponding angular size on sky, the general model
results are not expected to be dramatically different for
S Ori compared to Mira stars, such as o Cet and R Leo.
Hereby, the M series is expected to be better-suited
to describing S Ori than the P series because of its
higher parent-star mass.
We concluded that the use of the M series is currently
the best available option for describing S Ori's atmosphere
including the continuum photosphere and overlying atmospheric
molecular layers.
Except for the dust-enshrouded very-long-period Mira IW Hya (Jeong et al. 2003), models that self-consistently combine detailed dynamic atmosphere models and the formation of dust shells are currently not readily available for oxygen-rich AGB stars. However, the first attempts in this direction have just been made (Ireland & Scholz 2006, Woitke 2006).
Dust shells around AGB stars have often been modeled using
ad-hoc radiative transfer calculations (see; for instance;
Danchi et al. 1994; Lorenz-Martins & Pompeia
2000; Ohnaka et al.
2005,2006a), and we followed
this approach as the only currently available option
for describing S Ori's dust shell.
We employed the Monte Carlo radiative transfer
code mcsim_mpi (Ohnaka et al. 2006a) to
calculate the dust shell model of S Ori. For the central
radiation source of the radiative transfer model, we used
the spectral energy distribution (SED) of the respective
M model atmosphere for the wavelength range
from 0.32 ![]() m to 23
m to 23 ![]() m and extended it by a
blackbody approximation for longer wavelengths.
Dust temperatures were calculated in radiative equilibrium.
m and extended it by a
blackbody approximation for longer wavelengths.
Dust temperatures were calculated in radiative equilibrium.
Our MIDI spectra of S Ori do not exhibit any prominent silicate
feature, indicating that silicate grains are not a major
constituent of the dust shell. Lorenz-Martins &
Pompeia (2000) have investigated the envelopes
of 31 oxygen-rich AGB stars using the IRAS LRS spectra. They
classify the objects into three groups, whose IRAS LRS spectra
can be modeled using either silicate grains, Al2O3
grains, or a mix thereof. S Ori is part of their study
and belongs to the group of objects that can be modeled well
with Al2O3 grains alone. They show that a blend of
alumina Al2O3 grains (Koike et al. 1995)
for
![]() m and porous amorphous Al2O3 grains
(Begemann et al. 1997) for
m and porous amorphous Al2O3 grains
(Begemann et al. 1997) for
![]() m gives
the best agreement with the IRAS spectra, so we followed this
approach (as in Ohnaka et al. 2005 for the case of
RR Sco). Likewise, we considered small amounts of warm silicates
(Ossenkopf et al. 1992) following the same works.
The grain size was set to 0.1
m gives
the best agreement with the IRAS spectra, so we followed this
approach (as in Ohnaka et al. 2005 for the case of
RR Sco). Likewise, we considered small amounts of warm silicates
(Ossenkopf et al. 1992) following the same works.
The grain size was set to 0.1 ![]() m for both Al2O3 and silicates.
We used the same inner boundary radius and density distribution
for both dust species. The amount of dust of each species was
characterized by the optical depths at a wavelength of
0.55
m for both Al2O3 and silicates.
We used the same inner boundary radius and density distribution
for both dust species. The amount of dust of each species was
characterized by the optical depths at a wavelength of
0.55 ![]() m, denoted
m, denoted ![]() (Al2O3) and
(Al2O3) and ![]() (silicate).
The density distribution
(silicate).
The density distribution ![]() was described by a single
power law with index p (
was described by a single
power law with index p (
![]() ).
We used the inner boundary radii in units of the
stellar photospheric radius
).
We used the inner boundary radii in units of the
stellar photospheric radius
![]() .
All radiative transfer models of the dust shell
were calculated with an outer radius, so that the shell
thickness is
.
All radiative transfer models of the dust shell
were calculated with an outer radius, so that the shell
thickness is
![]() .
.
The stellar atmospheric structure including the effects from
atmospheric molecular layers is fully described by the choice of
the specific model of the M series.
The M series consists of 20 models for different phase and cycle
combinations as detailed in Ireland et al. (2004b).
Here, we used a grid of the six M models of cycle 2 of the series,
which are M20 (model visual phase 0.05), M21n (0.10),
M22 (0.25), M23n (0.30), M24n (0.40), and M25 (0.50). These
models cover the range of our observations at phases 0.16
(epoch C), 0.27 (epoch D), 0.42 (epoch A), and 0.55 (epoch D).
The absolute model phases with respect to observations
are uncertain by at least 0.1, with relative uncertainties
of 0.01 to 0.02 between different models of the series
(Ireland et al. 2004b). Likewise, the
absolute assignment of visual phases to our epochs of
observation is uncertain by about 0.1
(see Sect. 3).
For each of these 6 atmosphere models, whose SEDs are used as
central source, we calculated a grid of radiative transfer models
of the dust shell. These grids included all combinations of optical depths
![]() (Al2O3)=1.0, 1.5, 2.0, 2.5, 3.0;
(Al2O3)=1.0, 1.5, 2.0, 2.5, 3.0;
![]() (silicate
(silicate![]() ,
10% of
,
10% of ![]() (Al2O3); inner boundary radii
(Al2O3); inner boundary radii
![]() ,
2.0, 2.2, 2.4, 2.6;
and gradients p=2.0, 2.5, 3.0, 3.5, 4.0.
,
2.0, 2.2, 2.4, 2.6;
and gradients p=2.0, 2.5, 3.0, 3.5, 4.0.
Any overall model was thus defined with this set of
five independent parameters: (1) choice of the dust-free M
model, (2) ![]() (Al2O3), (3)
(Al2O3), (3) ![]() (silicate),
(4)
(silicate),
(4)
![]() ,
(5) p. We used the well-defined
continuum photospheric radius at
,
(5) p. We used the well-defined
continuum photospheric radius at
![]()
![]() m R1.04
of the respective dust-free M model to characterize the
photospheric radius
m R1.04
of the respective dust-free M model to characterize the
photospheric radius
![]() ;
i.e. we set
;
i.e. we set
![]() .
Any overall model is rigid; i.e. the distance of any model layer
from
.
Any overall model is rigid; i.e. the distance of any model layer
from
![]() is fixed with the parameters given above.
The corresponding angular diameter
is fixed with the parameters given above.
The corresponding angular diameter
![]() was
treated as the only fit parameter when comparing any such
overall model to our MIDI data.
was
treated as the only fit parameter when comparing any such
overall model to our MIDI data.
The visibility values based on the stellar contribution were calculated for each spectral channel c of MIDI as
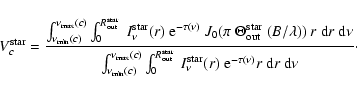 |
(1) |
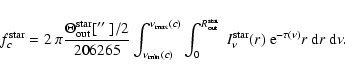 |
(2) |
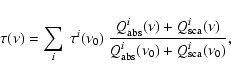 |
(3) |
 |
(4) |
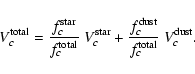 |
(5) |
For any given overall model separately, we optimized the angular
diameter
![]() using a standard least-square fit that
minimizes the
using a standard least-square fit that
minimizes the ![]() value between synthetic and observed
visibility and flux values. Hereby,
value between synthetic and observed
visibility and flux values. Hereby,
![]() was treated as the only free parameter. The resulting reduced
was treated as the only free parameter. The resulting reduced
![]() values among our full grid of different overall
models were compared in order to find the best-fitting set of
model parameters. This analysis was separately performed for
each of our epochs A-D.
values among our full grid of different overall
models were compared in order to find the best-fitting set of
model parameters. This analysis was separately performed for
each of our epochs A-D.
Table 3: Fit results of our MIDI measurements of S Ori.
Table 4:
Reduced
![]() values obtained for our grid of
overall models.
values obtained for our grid of
overall models.
Table 3 lists for each of our MIDI epochs
the parameter set of the best-fitting overall model of our grid.
Listed are for each of our 4 epochs the best-fitting
atmosphere model of the M series; its model phase;
the difference between observed and model phase;
the best-fitting parameters of the dust shell
(![]() (Al2O3),
(Al2O3), ![]() (Silicate),
(Silicate),
![]() (Silicate), p); the best-fitting angular diameter
(Silicate), p); the best-fitting angular diameter
![]() ;
the reduced
;
the reduced
![]() value;
the number of data points used (n); and the formal and model errors.
The model errors are
derived as the standard deviations of
value;
the number of data points used (n); and the formal and model errors.
The model errors are
derived as the standard deviations of
![]() values
based on different overall models of our grid that are
consistent at the 1
values
based on different overall models of our grid that are
consistent at the 1![]() level based on application of
the F-test. The model errors of epochs A and D are larger than
those of epochs B and C, which can be explained by the use of
only one baseline configuration at these epochs.
Table 4 lists for each epoch and for each grid parameter the
best
level based on application of
the F-test. The model errors of epochs A and D are larger than
those of epochs B and C, which can be explained by the use of
only one baseline configuration at these epochs.
Table 4 lists for each epoch and for each grid parameter the
best
![]() value that could be obtained by any combination
of all other parameters. The best
value that could be obtained by any combination
of all other parameters. The best
![]() value for each epoch is marked by boxes.
value for each epoch is marked by boxes.
The synthetic visibility
and flux values corresponding to the best-fitting overall
models are shown in Figs. 2-5
in comparison to the measured values. Panels (d), which show
the equivalent UD diameter values, also
indicate the photospheric angular diameter
![]() and the inner dust shell
boundary
and the inner dust shell
boundary
![]() derived from the model fit. Panels (e) show
the intensity profiles of the overall models that fit
our MIDI data best for three bandpasses at 8-9
derived from the model fit. Panels (e) show
the intensity profiles of the overall models that fit
our MIDI data best for three bandpasses at 8-9 ![]() m,
10-11
m,
10-11 ![]() m, and 12-13
m, and 12-13 ![]() m. These panels have a
bottom and a top abscissa indicating (bottom) the radius as
a function of the model photospheric radius
m. These panels have a
bottom and a top abscissa indicating (bottom) the radius as
a function of the model photospheric radius
![]() and (top) the corresponding angular scale using the best-fitting
angular diameter
and (top) the corresponding angular scale using the best-fitting
angular diameter
![]() .
Panels (e) also indicate the inner dust shell
radius
.
Panels (e) also indicate the inner dust shell
radius
![]() ,
as well as the mean SiO maser
ring radii R42.8 and R43.1, which are derived
in Sect. 4. A two-dimensional pseudo-color
image of the mid-infrared model intensity showing the molecular
layers and the dust shell is displayed
in Fig. 7.
The photospheric disk is represented by a light blue color.
Overlaid are the images of the SiO maser radiation described in Sect. 4.
,
as well as the mean SiO maser
ring radii R42.8 and R43.1, which are derived
in Sect. 4. A two-dimensional pseudo-color
image of the mid-infrared model intensity showing the molecular
layers and the dust shell is displayed
in Fig. 7.
The photospheric disk is represented by a light blue color.
Overlaid are the images of the SiO maser radiation described in Sect. 4.
In BW05, we estimated S Ori's photospheric
angular diameter at phase 0.73 to ![]() 9.2 mas, based
on our K-band UD diameter measurements and
using correction factors from UD to photospheric
diameters from Ireland et al. (2004a,b).
This value is consistent with the photospheric diameters
derived here, as the estimate of 9.2 mas at phase 0.73
from BW05 lies as expected in between the values
of 7.9 mas at phase 0.54 and 9.6 mas at phase 1.16 derived
in the present paper.
9.2 mas, based
on our K-band UD diameter measurements and
using correction factors from UD to photospheric
diameters from Ireland et al. (2004a,b).
This value is consistent with the photospheric diameters
derived here, as the estimate of 9.2 mas at phase 0.73
from BW05 lies as expected in between the values
of 7.9 mas at phase 0.54 and 9.6 mas at phase 1.16 derived
in the present paper.
The K-band UD diameter of 10.54 mas ![]() 0.68 mas
by van Belle et al. (1996) was obtained at
phase 0.56. At phases close to this value, the M series
results in a ratio between the K-band UD diameter
and the photospheric diameter of
0.68 mas
by van Belle et al. (1996) was obtained at
phase 0.56. At phases close to this value, the M series
results in a ratio between the K-band UD diameter
and the photospheric diameter of ![]() 1.35 (Fig. 7
of Ireland et al. 2004b). With this correction,
the photospheric diameter corresponding to this measurement
at phase 0.56 would be 7.8 mas
1.35 (Fig. 7
of Ireland et al. 2004b). With this correction,
the photospheric diameter corresponding to this measurement
at phase 0.56 would be 7.8 mas ![]() 0.5 mas,
and would thus be fully consistent with our value
of 7.9 mas
0.5 mas,
and would thus be fully consistent with our value
of 7.9 mas ![]() 0.1 mas at the same phase (Epoch B at
phase 0.54).
0.1 mas at the same phase (Epoch B at
phase 0.54).
Millan-Gabet et al. (2005) obtained a K-band
UD diameter of 9.6 mas ![]() 0.2 mas at phase 0.1.
At this phase, the ratio between K-band UD diameter
and photospheric diameter is predicted to be close to
unity (Ireland et al. 2004b).
This measurement thus also agrees well with our
photospheric diameter of 9.6 mas
0.2 mas at phase 0.1.
At this phase, the ratio between K-band UD diameter
and photospheric diameter is predicted to be close to
unity (Ireland et al. 2004b).
This measurement thus also agrees well with our
photospheric diameter of 9.6 mas ![]() 0.4 mas at
phase 1.16 (epoch C).
0.4 mas at
phase 1.16 (epoch C).
The good agreement of the photospheric angular diameters derived from our MIDI measurements in the present paper with previous near-infrared diameter measurements increases confidence in the validity of our modeling using the M model series complemented by a radiative transfer model of the dust shell.
The differences in visual stellar phase of the best-fitting M model compared to the visual phase at the epochs of observation are -0.17, -0.15, +0.14, and -0.17, respectively. These differences may be due to the uncertainties of the absolute assignments of visual phases to the model series as well as to the dates of observation, which are both on the order of 0.1. The relative phase values are expected to agree better, which is true for epochs A, B, and D. Differences between these phases might also occur owing to the different radius and pulsation period of the model series' parent star compared to S Ori. These parameters might have an effect on the extension of the atmosphere, so that the best-fitting extension of the atmosphere might belong to a model at a different visual phase. An effect such as this might explain the clearly different phase difference between observation and model at epoch C compared to the three other epochs.
The good agreement of the shape of the synthetic visibility
function with our observations at the wavelength range
from 8 ![]() m to 9
m to 9 ![]() m and the simultaneous agreement
with the measured flux level again confirms that the
M model series is usable for S Ori.
m and the simultaneous agreement
with the measured flux level again confirms that the
M model series is usable for S Ori.
As an indication of the extension of the molecular layers of the
best-fitting M models, the 50%/10% intensity radii of the
N-band (8-13 ![]() m) model CLVs are 1.5/1.6, 1.8/1.9, 1.6/1,7,
and 1.4/1.9 photospheric radii
m) model CLVs are 1.5/1.6, 1.8/1.9, 1.6/1,7,
and 1.4/1.9 photospheric radii
![]() for epochs A-D, i.e. for
models M22, M24n, M23n, and M21n, respectively.
for epochs A-D, i.e. for
models M22, M24n, M23n, and M21n, respectively.
The total optical depth of the dust shell is mainly constrained by the height and shape of the MIDI total flux spectrum. The radial density profile described by the inner boundary radius and the density gradient is mostly constrained by the shape of the visibility function versus wavelength. Here, the values at shorter wavelengths, probing warmer dust, constrain the inner boundary radius best. The density gradient is mostly constrained by the visibility values at longer wavelengths and shorter baseline lengths, with which the dust shell is less resolved.
We obtain best-fitting inner boundary radii of 1.8, 2.0, 2.2, and 2.4 photospheric radii
![]() at our phases 0.42, 0.55, 1.16, and 1.27, respectively.
These radii are well-constrained and do not significantly
change for variations in other model parameters.
We estimate the uncertainty of this parameter to about
at our phases 0.42, 0.55, 1.16, and 1.27, respectively.
These radii are well-constrained and do not significantly
change for variations in other model parameters.
We estimate the uncertainty of this parameter to about
![]() .
The formation of dust consisting
of Al2O3 grains at these short distances from the
stellar surface is consistent with the empirical
results by Lorenz-Martins & Pompeia (2000),
as well as with the recent theoretical calculations
by Ireland & Scholz (2006)
and Woitke (2006).
.
The formation of dust consisting
of Al2O3 grains at these short distances from the
stellar surface is consistent with the empirical
results by Lorenz-Martins & Pompeia (2000),
as well as with the recent theoretical calculations
by Ireland & Scholz (2006)
and Woitke (2006).
Best-fitting density gradients p at the same phases
are 3.5, 3.5, 3.0, and 2.5, respectively, and
best-fitting optical depths ![]() are 2.5, 2.5,
1.5, and 1.5.
Taking the inner boundary radii, the density gradients,
and the optical depth values together, our fits indicate
more compact dust shells with larger optical depth near
the stellar minimum and more extended dust shells with lower
optical depth after stellar maximum.
are 2.5, 2.5,
1.5, and 1.5.
Taking the inner boundary radii, the density gradients,
and the optical depth values together, our fits indicate
more compact dust shells with larger optical depth near
the stellar minimum and more extended dust shells with lower
optical depth after stellar maximum.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{7168fig7.eps}\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg112.gif) |
Figure 6:
Density profiles of radiatively driven wind models calculated
with the DUSTY code (Ivezic & Elitzur 1997;
Ivezic et al. 1999) for input parameters from
Table 3, together with
|
| Open with DEXTER | |
Table 5: VLBA observations of S Ori.
The data were correlated at the VLBA correlator operated by NRAO in
Socorro, New Mexico. Auto and cross-correlation spectra consisting
of 256 channels with channel spacings
of 31.25 kHz (![]() 0.2 km s-1)
were produced by the correlator. Calibration was performed using the
Astronomical Image Processing System (AIPS) maintained by NRAO. The
data were calibrated in a manner similar to what was performed in BW05.
For each epoch, residual delays due to the instrumentation were corrected
by performing a fringe fit on the continuum calibrator scans. Residual group
delays for each antenna were determined and applied to the spectral line
data. Variations in the residual delays ranged from 2-4 ns resulting in
phase errors of no more than 1.5-3
0.2 km s-1)
were produced by the correlator. Calibration was performed using the
Astronomical Image Processing System (AIPS) maintained by NRAO. The
data were calibrated in a manner similar to what was performed in BW05.
For each epoch, residual delays due to the instrumentation were corrected
by performing a fringe fit on the continuum calibrator scans. Residual group
delays for each antenna were determined and applied to the spectral line
data. Variations in the residual delays ranged from 2-4 ns resulting in
phase errors of no more than 1.5-3![]() across the 8-MHz band.
across the 8-MHz band.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{7168fig8.eps}\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg119.gif) |
Figure 7:
The (red) v=2, J=1-0 (42.8 GHz) and
(green) v=1, J=1-0 (43.1 GHz) maser images overlaid onto
pseudo-color representations of the infrared intensity.
The continuum photosphere (in fact mostly hidden behind the molecular
atmosphere in the N-band) is enhanced to a light blue color. The
darker blue shades represent our model intensity profile as in panels
(e) of Figs. 2-5, and the green shades
represent the location of the Al2O3 dust shell on top of the
low-intensity extended wings of the molecular atmosphere. The true location
of the star relative to the maser images is unknown. Here, we assume that the
center of the star coincides with the
center of the maser spot distribution.
Synthesized beam sizes
for epoch A are
|
| Open with DEXTER | |
The bandpass response was determined from scans on the continuum calibrators and used to correct the target-source data. The time-dependent gains of all antennas relative to a reference antenna were determined by fitting a total-power spectrum (from the reference antenna with the target source at a high elevation) to the total power spectrum of each antenna. The absolute flux density scale was established by scaling these gains by the system temperature and gain of the reference antenna. Errors in the gain and pointing of the reference antenna and atmospheric opacity variations contribute to the error in the absolute amplitude calibration, which is accurate to about 15-20%.
Residual fringe rates were obtained by fringe-fitting a strong reference
feature in the spectrum of each maser transition. For epoch A we used the
channel at velocity
![]() km s-1 for the v=1
transition and the channel at velocity
km s-1 for the v=1
transition and the channel at velocity
![]() km s-1
for the v=2 transition. For epoch B we used channels
at
km s-1
for the v=2 transition. For epoch B we used channels
at
![]() km s-1 and
km s-1 and
![]() km s-1
for the v=1 and v=2 transitions, respectively. Finally, for epoch C
we used the same velocity channel for both transitions
km s-1
for the v=1 and v=2 transitions, respectively. Finally, for epoch C
we used the same velocity channel for both transitions
![]() km s-1. The resulting fringe-rate solutions
were applied to all channels in each spectrum. An iterative
self-calibration and imaging procedure was then performed to map this
reference channel for each transition. The resulting residual phase and
amplitude corrections from the reference channels at 42.8 GHz
and 43.1 GHz were applied to all channels in the respective
bands. This procedure was repeated for each transition at
each epoch.
km s-1. The resulting fringe-rate solutions
were applied to all channels in each spectrum. An iterative
self-calibration and imaging procedure was then performed to map this
reference channel for each transition. The resulting residual phase and
amplitude corrections from the reference channels at 42.8 GHz
and 43.1 GHz were applied to all channels in the respective
bands. This procedure was repeated for each transition at
each epoch.
In order to accurately compare the distributions of the two maser transitions, it is desirable to determine a common spatial reference point. However, after the fringe-fitting step to determine residual fringe-rates, all absolute position information is lost for the VLBA data. To accomplish this registration, we used the same technique employed in BW05 with the residual fringe-rates, phases, and amplitudes from one transition (e.g., v=2, 42.8 GHz) used to calibrate the other transition (e.g., v=1, 43.1 GHz) in order to determine an offset between the two phase centers.
The final image cubes of the SiO maser emission consisting
of
![]() pixels (
pixels (![]()
![]() mas) were generated
for each transition at each of the three epochs.
Images were produced for all spectral channels containing SiO maser
emission in each transition at each epoch. Synthesized beam sizes
used for epoch A were
mas) were generated
for each transition at each of the three epochs.
Images were produced for all spectral channels containing SiO maser
emission in each transition at each epoch. Synthesized beam sizes
used for epoch A were
![]() mas and
mas and
![]() mas for
the v=1 and v=2 transitions, respectively. For epoch B these
sizes were
mas for
the v=1 and v=2 transitions, respectively. For epoch B these
sizes were
![]() mas and
mas and
![]() mas.
For epoch C the beam sizes used in the imaging were
mas.
For epoch C the beam sizes used in the imaging were
![]() mas and
mas and
![]() mas.
Note that the resolution was greatly reduced in epoch A due to the
loss of the Mauna Kea, HI VLBA antenna mentioned previously. The
resolution of epoch B is slightly worse than that of epoch C due to
the loss of half the data, thus reducing the uv coverage of the
array. Using the procedure described above, the image cubes from the two
transitions were spatially aligned for each epoch.
Off-source rms noise estimates in the images ranged
from 5 mJy to 9 mJy for epoch A, 3 mJy to 7 mJy for epoch B,
and 7 mJy to 18 mJy for epoch C. Figure 7
shows the total intensity images of the v=1, 43.1-GHz
and v=2, 42.8-GHz SiO maser emission toward S Ori
overlaid onto a pseudo-color representation of the mid-infrared
intensity profile obtained in Sect. 3.
mas.
Note that the resolution was greatly reduced in epoch A due to the
loss of the Mauna Kea, HI VLBA antenna mentioned previously. The
resolution of epoch B is slightly worse than that of epoch C due to
the loss of half the data, thus reducing the uv coverage of the
array. Using the procedure described above, the image cubes from the two
transitions were spatially aligned for each epoch.
Off-source rms noise estimates in the images ranged
from 5 mJy to 9 mJy for epoch A, 3 mJy to 7 mJy for epoch B,
and 7 mJy to 18 mJy for epoch C. Figure 7
shows the total intensity images of the v=1, 43.1-GHz
and v=2, 42.8-GHz SiO maser emission toward S Ori
overlaid onto a pseudo-color representation of the mid-infrared
intensity profile obtained in Sect. 3.
The six resulting image cubes (2 transitions at 3 epochs) were
then analyzed to extract relevant maser parameters.
Two-dimensional Gaussian functions were fit to maser
emission above a cut-off flux density of 100 mJy in each
spectral (velocity) channel using the AIPS task SAD. This
fitting yielded velocities, flux densities, and positions in right
ascension and declination for all emission components identified
in the images. Errors in right ascension and declination of
identified components were computed using the fitted source size
divided by twice the signal-to-noise ratio (s/n) in the image
and ranged from 1 ![]() as for features with high s/n, to 28
as for features with high s/n, to 28 ![]() as
for features with lower s/n.
as
for features with lower s/n.
The remaining analysis of the maser component identifications was
performed outside of the AIPS package. For comparison with the
total flux densities derived from the MIDI data, we summed the flux
densities and their errors for all fitted components in all channels
for each transition/epoch. These integrated flux densities are
discussed further in Sect. 5.
Since the ![]() 0.2 km s-1 channel spacing is sufficient to
resolve the masers spectrally, features typically appear in multiple
adjacent spectral channels. Positions in right ascension and declination
and center velocities for the masers were determined using a
flux-density-squared weighted average for features identified in two or
more adjacent channels with a spatial coincidence of 0.5 mas. The flux
assigned to the maser averages was the maximum single-channel flux density.
The results from the image analysis and component averaging are described
in the next section.
0.2 km s-1 channel spacing is sufficient to
resolve the masers spectrally, features typically appear in multiple
adjacent spectral channels. Positions in right ascension and declination
and center velocities for the masers were determined using a
flux-density-squared weighted average for features identified in two or
more adjacent channels with a spatial coincidence of 0.5 mas. The flux
assigned to the maser averages was the maximum single-channel flux density.
The results from the image analysis and component averaging are described
in the next section.
The maser features characterized using the procedures described
above are listed in Tables A.2-A.4 and are shown in Fig. 8, where
there are six panels ordered by epoch left to right and by transition
top to bottom. Within each panel there are two
sub-panels. Each upper sub-panel shows the spectrum of the maser emission
with flux density plotted as a function of local standard of rest (LSR)
velocity. Point sizes are proportional to the logarithm of the flux
density and are color-coded according to velocity bin in increments
of 1.7 km s-1. The bottom sub-panels of Fig. 8
show the spatial distribution of the SiO masers as observed in the images.
Point sizes are again proportional to the logarithm of the flux density
with the same velocity color-coding as in the top sub-panels.
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{7168figa.eps}\hspace*{2mm}...
...eps}\hspace*{2mm}
\includegraphics[width=5.6cm,clip]{7168figf.eps} \end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg127.gif) |
Figure 8:
LOS velocity structure of the ( top)
v=1, J=1-0 (43.1 GHz)
and ( bottom)
v=2, J=1-0 (42.8 GHz) SiO maser emission
toward S Ori. The epochs of observations are from left to
right Epoch A (
|
| Open with DEXTER | |
Examining the upper sub-panels and the component tables, we find that the masers have shifted slightly toward the blue end of the spectrum from our previous BW05 observations. There the maser velocities ranged from 11.1 to 24.7 km s-1, while for these latest three epochs the masers span a velocity range from 8.6 to 19.0 km s-1. The velocity range for our latest three epochs is consistent with earlier spectral measurements by Jewell et al. (1991), who measured a velocity range of 7.1 to 19.6 km s-1 for the v=1 masers. Spectral ranges measured by Cho et al. (1996) were much narrower at 11.0-16.0 km s-1 for the v=1 and 12.0-14.7 km s-1for the v=2 masers, respectively. For the three epochs discussed here, flux densities of the peak component in the spectrum ranged from 3.0 to 5.4 Jy beam-1 for the v=1 masers and 1.3 to 6.4 Jy beam-1 for the v=2 masers. These are close to our BW05 results for which we measured peaks of 4.3 Jy beam-1 and 5.3 Jy beam-1 for the v=1 and v=2 masers, respectively.
When compared to the spectrally-averaged total-intensity images (Fig. 7), the maser component maps in lower sub-panels of Fig. 8 provide an accurate representation of the spatial structure of the maser emission summed over all velocity channels in the image cube. The component maps all show that the SiO masers in both transitions form partial to full rings of emission with the typical clumpy distribution. The top three panels show the v=1, J=1-0 to form a partial ring for epoch A with a gap to the north, nearly a full ring for epoch B, and again a partial ring dominated by emission in the northern and western regions for epoch C. For the v=2, J=1-0 SiO masers shown in the bottom three panels, we observe nearly a full ring of emission for epoch A, a partial ring with a gap to the south for epoch B, and a partial ring dominated by northern and western features for epoch C. In all three epochs the v=1 masers appear to be distributed over a larger area on the sky than the v=2 masers. In addition, the v=1 rings appear thicker than the corresponding v=2 rings at each epoch. It should be noted that, while epochs A and B were spaced only 42 days apart, there are significant differences in the number and distribution of the masers in both transitions. This is not unexpected since previous multi-epoch VLBI studies (e.g. Diamond & Kemball 2003) have shown the fine structure of the SiO masers to vary significantly over periods as short as two weeks. This variation, combined with the relative complexity of the maser structures, precluded us from tracking individual maser components in order to determine maser proper motions.
To better characterize the apparent size and thickness of the SiO maser
distributions, we computed the average angular distance of the masers
from the center of their distribution (![]() ). To accomplish this,
we first determined the center of the distribution by performing a
least-square fit of a circle to the combined v=1 and v=2 maser
positions. We were able to combine the two sets of masers only because we had
previously aligned the images of the two transitions following the procedure
described in Sect. 4.1. This fit produced a common center
from which we computed the mean maser angular
distance
). To accomplish this,
we first determined the center of the distribution by performing a
least-square fit of a circle to the combined v=1 and v=2 maser
positions. We were able to combine the two sets of masers only because we had
previously aligned the images of the two transitions following the procedure
described in Sect. 4.1. This fit produced a common center
from which we computed the mean maser angular
distance
![]() and the standard deviation
for each transition independently for each epoch.
and the standard deviation
for each transition independently for each epoch.
The mean angular distances from the center for the observed SiO masers at
v=1, 43.1 GHz and v=2, 42.8 GHz are listed in
Table 6. These distances are also indicated by
a dashed circle in each of the six panels in Fig. 8.
The standard deviations in the mean distances are also listed in
Table 6 and represented in Fig. 8
as the error on the mean. Two times the
standard deviation also provides an indication of the thickness of the shell.
The listed parameters in Table 6 are for each epoch
of observation/visual phase and each of the two transitions,
the apparent mean angular distances from the center of the masers
spots
![]() ,
the ratio of the
mean distances of the two transitions
,
the ratio of the
mean distances of the two transitions
![]() /
/
![]() ,
as well as the mean LOS velocities
,
as well as the mean LOS velocities
![]() and their ratio
and their ratio
![]() /
/
![]() .
.
From Table 6 we see that ![]() ranges from 8.6 to 10.2 mas. At every epoch we find that the v=1 masers have a
greater mean distance from center than the v=2 masers. This finding
is consistent with BW05 in which we found
ranges from 8.6 to 10.2 mas. At every epoch we find that the v=1 masers have a
greater mean distance from center than the v=2 masers. This finding
is consistent with BW05 in which we found
![]() mas
and
mas
and
![]() mas. In BW05, however, we were unable to make a
definitive statement about the relative sizes of the two maser distributions
because we had only the one epoch of observations, and at this epoch,
the v=2 masers were primarily confined to a small region on the northwest
side of the shell. In our more recent epochs, the rings of emission are much
more complete making the comparison between transitions easier. Although the
differences in
mas. In BW05, however, we were unable to make a
definitive statement about the relative sizes of the two maser distributions
because we had only the one epoch of observations, and at this epoch,
the v=2 masers were primarily confined to a small region on the northwest
side of the shell. In our more recent epochs, the rings of emission are much
more complete making the comparison between transitions easier. Although the
differences in ![]() for epochs A, B, and C are less than the standard
deviation (thickness of the ring), they are still greater than the resolution
of the images given earlier by the synthesized beam sizes
of
for epochs A, B, and C are less than the standard
deviation (thickness of the ring), they are still greater than the resolution
of the images given earlier by the synthesized beam sizes
of
![]() mas for epoch A and
mas for epoch A and
![]() mas for
epochs B and C.
The fact that the v=1 ring is consistently larger than the v=2 ring
suggests that for S Ori the two sets of masers are not co-spatial.
mas for
epochs B and C.
The fact that the v=1 ring is consistently larger than the v=2 ring
suggests that for S Ori the two sets of masers are not co-spatial.
Table 6: Results from our VLBA observations of the v=1, 43.1 GHz and v=2, 42.8 GHz SiO maser transition toward S Ori.
The relative separation of the v=1 and v=2 masers for S Ori is also
consistent with recent results obtained for the SiO masers around other stars
including: IRC +10011 (Desmurs et al. 2000);
TX Cam (Desmurs et al. 2000;
Yi et al. 2005); o Cet, U Ori, and R Aqr
(Cotton et al. 2006).
In addition, numerical simulations of SiO masers
(Humphreys et al. 1996; Gray & Humphreys 2000)
show the
v=1, J=1-0 masers to occur farther from the star than the
v=2, J=1-0 masers throughout the entire pulsation. The simulations
of Gray & Humphreys (2000) also show that the mean thickness
of the v=1 shell is roughly twice that of the v=2 shell throughout the
stellar cycle. In our measurements, we find the v=2 shell to be thicker
in the BW05 observations, the v=1 shell to be thicker in epochs A and C, and the two transitions to be roughly equivalent in epoch B. In the two
cases for which the v=1 shell was thicker, the ratio of the two thicknesses
is 1.3-1.4, much less than the 2 determined by Gray & Humphreys.
The angular sizes of the maser shells are reported in
Table 7. At the assumed distance
for S Ori of
![]() (van Belle et al. 2002), 1 mas is roughly equivalent to 0.48 AU.
Thus the linear-scale sizes for maser distributions range from 8.3 to 9.8 AU
and the maser shell thickness (twice the standard deviation) ranges from
roughly 0.9 to 1.3 AU.
(van Belle et al. 2002), 1 mas is roughly equivalent to 0.48 AU.
Thus the linear-scale sizes for maser distributions range from 8.3 to 9.8 AU
and the maser shell thickness (twice the standard deviation) ranges from
roughly 0.9 to 1.3 AU.
The LSR stellar velocity of S Ori has not been measured particularly well.
In the
General Catalog of Stellar Radial Velocities (Wilson 1953),
the value listed for S Ori is 22 km s-1. Young (1995)
observed the sub-millimeter CO (3-2) and CO (4-3) lines
toward S Ori and determined values of
![]() and
and
![]() km s-1 from fits to the spectra, respectively.
Winters et al. (2003) derived
km s-1 from fits to the spectra, respectively.
Winters et al. (2003) derived
![]() km s-1based on fits of the CO (1-0) and CO (2-1) lines.
Since the SiO masers are not distributed evenly about any of the above
velocities, we computed an average LOS velocity from the masers
themselves for each transition at epoch.
The values of
km s-1based on fits of the CO (1-0) and CO (2-1) lines.
Since the SiO masers are not distributed evenly about any of the above
velocities, we computed an average LOS velocity from the masers
themselves for each transition at epoch.
The values of
![]() for each of the epochs are reported
in Table 6 with errors of 15% estimated from the
uncertainty of the absolute amplitude calibration.
Although the differences are well within the error bars, it appears that
the v=2 masers are shifted slightly toward the blue end of the spectrum
relative to the v=1 masers at all three epochs. In addition
to computing values for individual transitions and epochs, we also
combined the three epochs and computed a mean LOS velocity for each
transition.
We obtained mean values of
for each of the epochs are reported
in Table 6 with errors of 15% estimated from the
uncertainty of the absolute amplitude calibration.
Although the differences are well within the error bars, it appears that
the v=2 masers are shifted slightly toward the blue end of the spectrum
relative to the v=1 masers at all three epochs. In addition
to computing values for individual transitions and epochs, we also
combined the three epochs and computed a mean LOS velocity for each
transition.
We obtained mean values of
![]() km s-1 and
km s-1 and
![]() km s-1 for the
42.8 GHz and 43.1 GHZ masers, respectively.
These values are shown in
Fig. 9. Again we see that
km s-1 for the
42.8 GHz and 43.1 GHZ masers, respectively.
These values are shown in
Fig. 9. Again we see that
![]() is slightly
redder than
is slightly
redder than
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7168figg.eps}\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg146.gif) |
Figure 9:
Histogram of the LOS velocities of our SiO maser spots combining
VLBA epochs A-C. Panel a) shows the histogram for the v=2 42.8 GHz
masers and panel b) for the v=1 43.1 GHz masers. Also indicated
are the mean values
|
| Open with DEXTER | |
To verify the notion that the higher-velocity masers are found closer
to the star, we plotted component distance from the center of the
distribution (radius) versus its velocity relative to the average
LOS velocity for that transition (
![]() ).
The results are shown in Figs. 10
and 11 for the
v=1, J=1-0 43.1 GHz and
the
v=2, J=1-0 42.8 GHz transitions, respectively. In the figures we
plotted each epoch with a different symbol. The masers in both transitions
appear to have the same distribution with a central peak near
).
The results are shown in Figs. 10
and 11 for the
v=1, J=1-0 43.1 GHz and
the
v=2, J=1-0 42.8 GHz transitions, respectively. In the figures we
plotted each epoch with a different symbol. The masers in both transitions
appear to have the same distribution with a central peak near
![]() and decreasing maser radius as
a function of increasing values of
and decreasing maser radius as
a function of increasing values of
![]() .
.
A simple model that is often used in the case of OH (e.g. Reid et al. 1977) and H2O (e.g. Yates & Cohen 1994) maser
kinematics is that of a uniformly expanding thin shell. In this
model the projected distance from center (a) of a maser on the shell is
related to its LOS velocity
![]() by the expression:
by the expression:
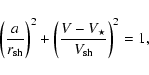 |
(6) |
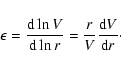 |
(7) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7168figh.eps}\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg162.gif) |
Figure 10:
Distances of the 43.1 GHz maser components from the common
center of the distribution (radius) versus their velocity relative to the
average LOS velocity for the 43.1 GHz
transition (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7168figi.eps}\end{figure}](/articles/aa/full/2007/28/aa7168-07/Timg163.gif) |
Figure 11: As Fig. 10, but for the 42.8 GHz transition. The axes' scales are identical for the two figures. Compared to Fig. 10, it is evident that the 42.8 GHz maser spots lie at systematically closer distances to the center of the common maser distribution than the 43.1 GHz maser spots. |
| Open with DEXTER | |
Plotted along with the data in Figs. 10 and 11 are four curves computed using the above
equations. They represent shells at the inner and outer
boundaries of the SiO masers.
For the masers in each transition, we used an inner
shell radius equivalent to the smallest average distance minus its
standard deviation from Table 6.
Similarly, for the outer shell radius we used the largest average distance
plus its standard deviation from Table 6.
For the scenario of a logarithmic velocity gradient,
the velocity at the inner v=2 boundary was set at 7 km s-1 and
the velocities of the other shells computed assuming
![]() .
The velocity of the outermost shell of the v=1 transition
is
.
The velocity of the outermost shell of the v=1 transition
is
![]() km s-1.
km s-1.
For the scenarion of a constant velocity expansion (
![]() ),
the best by-eye fit results in
),
the best by-eye fit results in
![]() km s-1.
In this case, the higher expansion velocity at the inner boundary of
the v=2 transition is
required in order to provide a reasonable fit to the outer boundaries of
both transitions. For the
km s-1.
In this case, the higher expansion velocity at the inner boundary of
the v=2 transition is
required in order to provide a reasonable fit to the outer boundaries of
both transitions. For the
![]() case, the inner v=2 velocity
can be lower with the radial acceleration allowing for a better
fit to the outer boundaries. For comparison, the escape velocities
computed for the innermost v=2 and outermost v=1 shells, assuming
a mass for S Ori of 1.0
case, the inner v=2 velocity
can be lower with the radial acceleration allowing for a better
fit to the outer boundaries. For comparison, the escape velocities
computed for the innermost v=2 and outermost v=1 shells, assuming
a mass for S Ori of 1.0 ![]() ,
are 22.1 and 18.0 km s-1,
respectively. Therefore, even at the velocities bracketed by the curves,
the maser gas is still gravitationally bound.
,
are 22.1 and 18.0 km s-1,
respectively. Therefore, even at the velocities bracketed by the curves,
the maser gas is still gravitationally bound.
From the SiO maser data on S Ori, we cannot definitively rule out constant velocity expansion; however, the SiO maser region is very dynamic, influenced by the pulsation of the star and the passage of shocks. Theoretical studies all seem to include some form of velocity gradient across the SiO maser region. In addition, constant velocity expansion would be more conducive to masers along the line of sight to the star because of the increased velocity coherence. SiO masers are rarely observed in front of the stellar disc, and for S Ori in particular, such masers have not be seen. We therefore consider some form of acceleration in the region the more likely scenario.
The canonical interpretation of the rings formed by the SiO masers is
that the masers are tangentially amplified and primarily confined to a region
close to the plane of the sky. Under this interpretation, the
ring size and thickness are direct indicators of the equivalent 3-D shell size
and thickness. The radially expanding spherical shell described above
will naturally result in a projection effect where masers out of the plane
of the sky have smaller angular distances from center due to the projection.
In the case of S Ori, this projection is rather small. The equation for the
angle ![]() measured between the LOS and a point on the shell locating
the maser can be written in terms of the velocities as
measured between the LOS and a point on the shell locating
the maser can be written in terms of the velocities as
![\begin{displaymath}\sin \theta = \biggl[1 - \biggl( \frac{V}{V_{\rm sh}} \biggr)^2
\biggr]^{1/2}.
\end{displaymath}](/articles/aa/full/2007/28/aa7168-07/img166.gif) |
(8) |
Table 7: Overview of the photometric and spatial parameters of S Ori as a function of stellar phase, derived from both our VLTI and VLBA observations.
Table 7 provides an overview on the
photometric and spatial parameters of S Ori as a function
of observational epoch/stellar phase, as derived from both
our VLTI/MIDI and VLBA observations in Sects. 3
and 4.
The listed photometric parameters include the V magnitude
based on the lightcurve in Fig. 1,
the N-band flux based on our photometric MIDI data
(Sect. 3.1), and the total flux values of
the two maser transitions (Sect. 4.1).
The listed spatial information includes the photospheric
angular diameter
![]() (Sect. 3.4), the inner dust shell
diameter
(Sect. 3.4), the inner dust shell
diameter
![]() (Sect. 3.4),
and the maser ring angular diameters
(Sect. 3.4),
and the maser ring angular diameters
![]() and
and
![]() (Sect. 4.2.1).
To compare the continuum photospheric diameter, the inner
dust shell diameter, and the maser shell diameters, the ratios
(Sect. 4.2.1).
To compare the continuum photospheric diameter, the inner
dust shell diameter, and the maser shell diameters, the ratios
![]() ,
,
![]() ,
and
,
and
![]() are listed as well.
As an absolute scale, the stellar photospheric
radius
are listed as well.
As an absolute scale, the stellar photospheric
radius
![]() at each phase is derived
from
at each phase is derived
from
![]() and the adopted distance
to S Ori (Sect. 2).
Here, the variability
phases are the mean values of the respective phases of
the MIDI and VLBA observations.
and the adopted distance
to S Ori (Sect. 2).
Here, the variability
phases are the mean values of the respective phases of
the MIDI and VLBA observations.
The continuum photospheric radii
![]() ,
the inner dust shell radii
,
the inner dust shell radii
![]() (corresponding to
(corresponding to
![]() and the maser shell radii R43.1 and R42.8(corresponding to
and the maser shell radii R43.1 and R42.8(corresponding to
![]() )
are indicated
in panels (d) of Figs. 2-5,
which show the synthetic mid-infrared CLVs. This
allows a comparison of these radii to each other and to the
profile of the extended molecular atmosphere.
Figure 7 provides as well a
graphical comparison of the photospheric disc, the molecular layers,
the dust shell, and the maser spots for each epoch.
)
are indicated
in panels (d) of Figs. 2-5,
which show the synthetic mid-infrared CLVs. This
allows a comparison of these radii to each other and to the
profile of the extended molecular atmosphere.
Figure 7 provides as well a
graphical comparison of the photospheric disc, the molecular layers,
the dust shell, and the maser spots for each epoch.
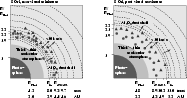 |
Figure 12: Sketch of the radial structure of S Ori's CSE at ( left) near-minimum and ( right) post-maximum visual phase as derived in this work. Shown are the locations of the continuum photosphere (dark gray), the at N-band optically thick molecular atmosphere (medium dark gray), the at N-band optically thin molecular atmosphere (light gray), the Al2O3 dust shell (dashed arcs), and the 42.8 GHz and 43.1 GHz maser spots (circles/triangles). The numbers below and beside the panels are the mean values of ( left) epochs A & B and ( right) epochs C & D from Table 7. |
| Open with DEXTER | |
The mid-infrared MIDI data are sensitive to the structure of the atmosphere consisting of the continuum photosphere and overlying molecular layers, as well as to the properties of the dust shell. The MIDI visibilities and flux densities are modeled using the recent M model atmosphere series by Ireland et al. (2004b), which is a dust-free self-excited dynamic model atmosphere series, to which we add an ad-hoc radiative transfer calculation of the dust shell. The constrained model parameters include the continuum photospheric angular diameter, as well as characteristics of the dust shell. The MIDI visibility and total flux data at all epochs can be described well by the chosen approach of combining the dust-free M model atmosphere series with an ad-hoc radiative transfer model of the dust shell. Different model parameters can be constrained by different subsets of our MIDI data.
The resulting continuum photospheric angular diameters at visual variability
phases 0.42, 0.55, 1.16, and 1.27 are 9.0 ![]() 0.3 mas,
7.9
0.3 mas,
7.9 ![]() 0.1 mas, 9.7
0.1 mas, 9.7 ![]() 0.1 mas, and
9.5
0.1 mas, and
9.5 ![]() 0.4 mas, respectively. The photospheric radius thus shows
a significantly phase-dependent size with amplitude of
0.4 mas, respectively. The photospheric radius thus shows
a significantly phase-dependent size with amplitude of ![]() 20%
that is well correlated in phase with the visual lightcurve.
20%
that is well correlated in phase with the visual lightcurve.
The dust shell can be modeled well with Al2O3 grains alone, and our
data show no indication of silicates, consistent with the modeling of the
IRAS LRS spectra by Lorenz-Martins & Pompeia (2000).
The inner dust shell angular diameters are 16.2 ![]() 1.9 mas,
15.9
1.9 mas,
15.9 ![]() 1.6 mas, 21.2
1.6 mas, 21.2 ![]() 1.9 mas, and
22.8
1.9 mas, and
22.8 ![]() 2.1 mas, respectively, for the visual phases given above,
corresponding to 1.8, 2.0, 2.2, and 2.4 times the continuum photospheric
diameters. Thus, dust starts to form very close to the stellar surface,
corresponding to the region of the low-intensity wings of the
atmospheric molecular layers of our dust-free atmosphere model.
In particular, the inner dust shell radius is smallest at the
near-minimum phases, located directly outside of the steep decrease in the
dust-free, mid-infrared model intensity. The inner dust-shell boundary
expands to larger distances from the stellar surface at our post-maximum
phases.
The overall Al2O3 optical depth, as well as the density gradient,
is largest at our near-minimum phases and significantly lower at the
post-maximum stellar phases. These dust shell characteristics can be
explained by a radiatively driven wind with increased mass-loss near
visual stellar minimum occurring close to the stellar surface,
and an expanded dust shell at the post-maximum phases.
2.1 mas, respectively, for the visual phases given above,
corresponding to 1.8, 2.0, 2.2, and 2.4 times the continuum photospheric
diameters. Thus, dust starts to form very close to the stellar surface,
corresponding to the region of the low-intensity wings of the
atmospheric molecular layers of our dust-free atmosphere model.
In particular, the inner dust shell radius is smallest at the
near-minimum phases, located directly outside of the steep decrease in the
dust-free, mid-infrared model intensity. The inner dust-shell boundary
expands to larger distances from the stellar surface at our post-maximum
phases.
The overall Al2O3 optical depth, as well as the density gradient,
is largest at our near-minimum phases and significantly lower at the
post-maximum stellar phases. These dust shell characteristics can be
explained by a radiatively driven wind with increased mass-loss near
visual stellar minimum occurring close to the stellar surface,
and an expanded dust shell at the post-maximum phases.
The 43.1 GHz and 42.8 GHz maser spots show the typical structure of
partial to full rings with a clumpy distribution. There is no sign of a
globally asymmetric gas distribution.
The 43.1 GHz mean maser ring angular diameters at visual phases 0.46, 0.56,
and 1.14 are 19.6 ![]() 2.8 mas, 19.0
2.8 mas, 19.0 ![]() 2.6 mas, and
20.4
2.6 mas, and
20.4 ![]() 2.4 mas, respectively. The values for the 42.8 GHz maser
are systematically smaller by 3-19% and amount to 19.0
2.4 mas, respectively. The values for the 42.8 GHz maser
are systematically smaller by 3-19% and amount to 19.0 ![]() 2.0 mas,
17.8
2.0 mas,
17.8 ![]() 3.4 mas, and 17.8
3.4 mas, and 17.8 ![]() 1.8 mas. The indication of
systematically smaller mean maser ring diameters of the 42.8 GHz transition
compared to the 43.1 GHz transition is consistent with earlier results
in the literature on other Mira stars.
The velocity structure of both maser transitions indicate an expansion of
the maser shell. This expansion is most likely an accelerated expansion, but
we cannot completely rule out a uniform expansion. The expansion velocity
for both transitions ranges between about 7 km s-1 and
about 10 km s-1 between the inner and outer shell radii based
on a scenario of an accelerated expansion or amounts
to about 10 km s-1
based on a scenario with uniform expansion.
1.8 mas. The indication of
systematically smaller mean maser ring diameters of the 42.8 GHz transition
compared to the 43.1 GHz transition is consistent with earlier results
in the literature on other Mira stars.
The velocity structure of both maser transitions indicate an expansion of
the maser shell. This expansion is most likely an accelerated expansion, but
we cannot completely rule out a uniform expansion. The expansion velocity
for both transitions ranges between about 7 km s-1 and
about 10 km s-1 between the inner and outer shell radii based
on a scenario of an accelerated expansion or amounts
to about 10 km s-1
based on a scenario with uniform expansion.
Compared to the continuum photospheric radius
![]() ,
the 43.1 GHz/42.8 GHz SiO maser ring radii are located at
2.2
,
the 43.1 GHz/42.8 GHz SiO maser ring radii are located at
2.2 ![]() 0.3/2.1
0.3/2.1 ![]() 0.2 (phase 0.44),
2.4
0.2 (phase 0.44),
2.4 ![]() 0.3/2.3
0.3/2.3 ![]() 0.4 (0.55),
and 2.1
0.4 (0.55),
and 2.1 ![]() 0.3/1.9
0.3/1.9 ![]() 0.2 (1.15) times
0.2 (1.15) times
![]() .
These values are consistent with theoretical estimates
and earlier observations available in the literature.
Compared to the molecular atmosphere, the maser shells mark the region of
the molecular atmosphere just beyond the steepest decrease in the
mid-infrared model intensity.
Compared to the dust shell, the maser spots are co-located with the inner
dust shell near stellar minimum. At our post-maximum phases, the maser spots
remain at about the same location, while the dust shell has expanded outward.
.
These values are consistent with theoretical estimates
and earlier observations available in the literature.
Compared to the molecular atmosphere, the maser shells mark the region of
the molecular atmosphere just beyond the steepest decrease in the
mid-infrared model intensity.
Compared to the dust shell, the maser spots are co-located with the inner
dust shell near stellar minimum. At our post-maximum phases, the maser spots
remain at about the same location, while the dust shell has expanded outward.
Altogether, our observations indicate a pulsation of the stellar photosphere
approximately in phase with the visual lightcurve. Our measurements suggest
an increased mass-loss rate near stellar minimum and formation of
Al2O3 dust grains occurring close to the stellar surface at about 1.8-2.0 photospheric radii directly outward of the dense molecular atmosphere,
co-located with the extended low-intensity wings of the molecular
atmosphere and with the SiO maser spots. At the post-maximum phases,
the dust shell has expanded to about 2.2-2.4 photospheric radii, while
the mean radius of the maser spots remains at ![]() 2.0 photospheric radii.
2.0 photospheric radii.
Figure 12 shows a sketch of S Ori and its CSE near
visual minimum and post-maximum illustrating the findings of the present
work.
Our results on S Ori are largely consistent
with the canonical scheme of the CSE of AGB stars
discussed for instance in Reid & Menten (1997). However, our
results indicate an inner dust shell boundary that is located closer to the
optical photosphere compared to the Reid & Menten scheme
at about two photospheric radii, and SiO maser shells that
are co-located with the low-intensity molecular atmosphere and
with Al2O3 dust grains near visual minimum. In the case of S Ori,
the dust shell consists only of Al2O3 grains.
For Mira stars that also show a dust shell of silicates, the inner boundary
of silicate grains is still expected at
greater distances of ![]() 4 photospheric radii
(Lorenz-Martins & Pompeia 2000). In addition to a static
picture of a Mira star's CSE, our observations suggest the formation
of a dust shell close to the surface near minimum phase and an expansion
by
4 photospheric radii
(Lorenz-Martins & Pompeia 2000). In addition to a static
picture of a Mira star's CSE, our observations suggest the formation
of a dust shell close to the surface near minimum phase and an expansion
by ![]()
![]() of the inner dust-shell boundary toward post-maximum phase.
of the inner dust-shell boundary toward post-maximum phase.
Our modeling approach of adding the CLVs of a dust-free M model to that of a radiative transfer model of the pure dust shell includes two uncertainties. Firstly, the M model series is designed for the prototype Miras o Cet and R Leo and used here for the longer-period Mira S Ori. Secondly, we omit a possible interaction of gas and dust outward of the inner dust shell boundary. Both effects might add some additional uncertainty to the absolute values of the obtained photospheric diameter values and dust shell characteristics. However, our data can be described well by our modeling approach and these additional uncertainties are not expected to be significantly larger than the diameter errors given in Table 7 and the step sizes of the dust shell parameters in Table 4. Furthermore, the relative accuracy of the obtained parameters among the four epochs of observations are clearly less affected by possible systematic uncertainties. Currently, the chosen approach appears to be the best available one. Similar studies of S Ori and other long-period Mira stars in the future would benefit from new dynamic model atmosphere series tailored to Mira stars with a longer period and a higher mass compared to o Cet and R Leo, as well as from self-consistent calculations of dynamic atmospheres and dust formation.
Our mid-infrared interferometric data, in particular at the lower edge of MIDI's wavelength range, together with the use of the M model series provide constraints on the continuum photospheric angular diameter of S Ori. The resulting values are in good agreement with several earlier diameter measurements obtained in the near-infrared K-band by different instruments and at different stellar phases, which increases the confidence in our modeling approach. Additional confidence in the continuum photospheric diameters and the validity of the dynamic model atmospheres can in future be reached by time series of high spectral resolution ( R=1000-10 000) near-infrared interferometry with the VLTI/AMBER (Petrov et al. 2003) instrument concurrent to VLTI/MIDI observations.
Our results obtained at 4 epochs within one pulsation cycle suggest the formation of a dust layer consisting of Al2O3grains close to the stellar surface near stellar minimum and an expanded dust shell after stellar maximum. Our understanding of the connection between the dust formation frequency and the stellar pulsation will be further improved by using more epochs within one pulsation cycle. Dust-forming episodes may also have their own timescale that may not be directly related to the visual variability (e.g., Höfner & Dorfi 1997; Nowotny et al. 2005), a study of which requires observations extended over more than one pulsation cycle. Since the data of S Ori do not show any sign of silicate grains, similar observations of targets that belong to the intermediate class group of Lorenz-Martins & Pompeia (exhibiting Al2O3 and silicate grains) would be required to study the detailed relationship among the Al2O3 shell, the silicate shell, and the photospheric pulsation.
Both our MIDI data and the images of the SiO maser shell do not show any signature of a globally asymmetric distribution of dust or gas in the case of S Ori within our uncertainties. In general, asymmetric distributions of gas and dust are to be expected for some Mira stars (e.g., Weigelt et al. 1996; Boboltz & Diamond 2005; Tatebe et al. 2006). A detection of asymmetric structures can be performed at the VLTI by sequentially using baselines of similar length but different orientation close in time/stellar phase to MIDI and by using the closure-phase instrument AMBER with baseline triangles comprised of baselines with different orientation.
The relative positions of star and SiO maser shells in our current study is unknown. Our comparison of the extension of the SiO maser shells to the continuum photospheric diameter is based on the assumption that the center of the maser spot distribution coincides with the center of the star. This assumption is the most likely scenario for stars that do not show any sign of asymmetric dust and gas distributions, such as S Ori. In principle, the relative position of the maser shells could be related relative to the radio photosphere, which was detected by Reid & Menten (1997) for a sample of 6 Mira and semi-regular variables. Additional measurements of H2O and OH masers relative to the SiO masers could give additional information on the structure and kinematics of the more extended CSE.
Acknowledgements
We thank Walter Jaffe, Rainer Köhler, Christian Hummel, and others involved for making publicly available the MIDI data reduction software packages and tools EWS, MIA, and MyMidiGui, as well as for helpful discussions on MIDI data reduction. We are grateful for support by the ESO DGDF. The work of MS was supported by a grant of the Deutsche Forschungsgemeinschaft on "Time Dependence of Mira Atmospheres''. We acknowledge with thanks the variable-star observations from the AAVSO International Database contributed by observers worldwide and used in this research. This research has made use of the AFOEV and SIMBAD databases, operated at the CDS, France. This research has made use of NASA's Astrophysics Data System.