A&A 469, 1109-1115 (2007)
DOI: 10.1051/0004-6361:20077196
S. Parenti1 - J.-C. Vial2
1 - Royal Observatory of Belgium, 3 Av. Circulaire, 1180 Bruxelles, Belgium
2 - Institut d'Astrophysique Spatiale, Bât. 121, Université Paris Sud-CNRS, 91405 Orsay, France
Received 30 January 2007 / Accepted 21 March 2007
Abstract
Context. A solar prominence and the quiet-Sun (QS) were observed with SOHO/SUMER in October 1999. With this dataset we built the first comprehensive UV spectral atlas in the range 800-1250 Å for a prominence, thus complementing the existing reference atlases for the QS.
Aims. This is a detailed study based on the information in this atlas, with the aim of deriving the plasma parameters in two distinct regions. The large amount of information available allows us to establish these parameters with lower uncertainty than in previous studies, leading to reference values for theoretical investigations.
Methods. The measured lines' FWHM were used to derive the distribution of the non-thermal velocities at various temperatures. The lines intensities were used to derive the electron densities at temperatures of
![]() and the differential emission measure.
and the differential emission measure.
Results. The comparison with the QS shows lower velocities in the prominence for temperature T with
![]() .
The velocities derived in the highest part of the prominence show a lower gradient with the temperature. The value obtained for the electron density indicates a low pressure prominence. We conclude with a discussion of the energy budget in the prominence.
.
The velocities derived in the highest part of the prominence show a lower gradient with the temperature. The value obtained for the electron density indicates a low pressure prominence. We conclude with a discussion of the energy budget in the prominence.
Key words: Sun: UV radiation - Sun: prominences - atlases - Sun: atmospheres
Solar prominences consist of a dense and cold cloud of partially-ionized plasma embedded in the hot corona and supported by the magnetic field (Patsourakos & Vial 2000; Tandberg-Hanssen 1995).
The particular environment of prominences involves complex physical processes that complicate their understanding. Several thermodynamic properties are still only partially known (Patsourakos & Vial 2000), especially the interface region with the corona (the prominence corona transition region, PCTR), which is an important source of information on the processes at work.
With the use of the high-resolution SUMER spectrometer onboard SOHO, Parenti et al. (2005b) (hereafter Paper I) have built a prominence spectral atlas in the wavelength range 800-1250 Å. This work also includes a quiet Sun (QS) atlas in the same wavelength range that complements the previous QS atlases (Curdt et al. 2001,2004; Feldman et al. 1997). A particular goal of our work is to describe of the full line profiles in terms of position, full width half maximum (FWHM) and radiance. These spectroscopic properties are essential for the understanding of the environment of the object observed. They provide information on fundamental plasma conditions such as density, temperature, and the dynamic. This extends earlier work (Parenti et al. 2005a) where we studied the H I Ly-continuum.
In the present paper we analyze the profiles of the lines listed in Paper I and provide quantitative results for plasma parameters. Here we focus on the plasma non-thermal velocities (NTV, Sect. 3), the differential emission measure (DEM, Sect. 4) and the electron density (Sect. 5). Energetic considerations follow in Sect. 6 and conclusions in Sect. 7.
The data used to build the atlas were obtained on 8 October 1999 with SUMER, observing a quiescent prominence and a reference QS area the day after. The observations were made with the
![]() slit and detector A. This provided data with resolution elements of
slit and detector A. This provided data with resolution elements of
![]() (spatial) and 45 mÅ/pixel (spectral, at 800 Å). The wavelength range was covered by a sequence of exposures, each covering about 42 Å. The wavelength range used here was covered in about three hours. This introduces possible temporal changes in the spectra, as we showed in Paper I. The prominence appeared filamented in the emission of
(spatial) and 45 mÅ/pixel (spectral, at 800 Å). The wavelength range was covered by a sequence of exposures, each covering about 42 Å. The wavelength range used here was covered in about three hours. This introduces possible temporal changes in the spectra, as we showed in Paper I. The prominence appeared filamented in the emission of
![]() and showed important intensity differences from region to region (see Fig. 1 in Parenti et al. 2004).
For this reason we constructed the atlas of prominence for two sections of the structure,
named A
and showed important intensity differences from region to region (see Fig. 1 in Parenti et al. 2004).
For this reason we constructed the atlas of prominence for two sections of the structure,
named A![]() and A
and A![]() .
In the case of the QS, we constructed the atlas from the spectra averaged over the entire slit.
Details on the observations are given in Parenti et al. (2004). The atlas provides radiance, position, and FWHM for about 440 lines in the prominence and about 550 lines in the QS, covering the temperature range of
.
In the case of the QS, we constructed the atlas from the spectra averaged over the entire slit.
Details on the observations are given in Parenti et al. (2004). The atlas provides radiance, position, and FWHM for about 440 lines in the prominence and about 550 lines in the QS, covering the temperature range of
![]() .
.
We derived the non-thermal velocities using the FWHM measured in the three datasets (A![]() ,
A
,
A![]() ,
and QS) of the spectral atlas.
The lines chosen for this analysis were carefully selected in the following way. Given the large amount of data, most ions emitting at low temperature are represented in the atlas by several lines. This allowed us to make a selection of only those lines that were most isolated and intense to reduce the line-width uncertainty. After the line selection,
several ions are represented by more than one line and we decided not to consider the averaged parameters. In such a way we can show the range of variability found for the given ion's velocity due, for example, to the possible temporal variation in the data.
,
and QS) of the spectral atlas.
The lines chosen for this analysis were carefully selected in the following way. Given the large amount of data, most ions emitting at low temperature are represented in the atlas by several lines. This allowed us to make a selection of only those lines that were most isolated and intense to reduce the line-width uncertainty. After the line selection,
several ions are represented by more than one line and we decided not to consider the averaged parameters. In such a way we can show the range of variability found for the given ion's velocity due, for example, to the possible temporal variation in the data.
The line profile parameters were measured assuming a Gaussian shape and using a multi-fitting procedure. This assumption is correct for optically thin lines, and it is valid for most of the lines used for this analysis. For those lines that may be affected by absorption, the width measured with this method will be overestimated. As a result, the associated NTV value will be higher than the real one. However, for prominences, one can anticipate lower or very low opacities in most spectra lines recorded with SUMER. This is mainly due to the faint emission of the prominence (the QS-to-prominence emission ratio can be about 10, leading to a similar ratio for the absorption coefficients). This means that optically thick lines in the QS become thin in prominences. We discuss this point in more detail in the next section.
The measured FWHM were corrected for the instrumental width using the standard SUMER software available on the SSW (
![]() ).
From these corrected widths (
).
From these corrected widths (
![]() )
we obtained the NTV (
)
we obtained the NTV (![]() )
using
)
using
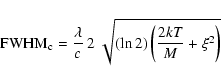 |
(1) |
Table 1 lists the lines chosen for the analysis. The first eight columns give the logarithm of the formation temperature of the line (![]() ), the derived NTV for the QS (
), the derived NTV for the QS (
![]() ), and the prominence sections (
), and the prominence sections (
![]() and
and
![]() ), together with their uncertainties (
), together with their uncertainties (
![]() ), which were evaluated through the error propagation of Eq. (1) and using the uncertainties obtained by the fitting procedure of our spectra.
), which were evaluated through the error propagation of Eq. (1) and using the uncertainties obtained by the fitting procedure of our spectra.
The values for the formation temperature listed in the table were taken from Chae et al. (1998, hereafter CSL) for the neutrals and CHIANTI v. 4.2 for the others (Young et al. 2003). This was to avoid complications when comparing our results with previous ones. However, in the case of neutrals, the coronal approximation is not an accurate hypothesis (e.g. Baudin et al. 2007) for a non-LTE analysis in the case of the QS). For this reason the assumed temperatures for neutrals are only indicative.
There are some differences in the choice of the sets of lines for the three regions, because of the change in intensity and width of the same line when moving from the QS to prominence. Some lines become faint or disappear in the prominence (which increases the uncertainty in the line profile measurement). On the contrary, some blended lines that could be not used for the QS are entirely free of blends in the prominence.
Figure 1 shows the non-thermal velocity derived for the QS (top) and the prominence (middle and bottom) as a function of the maximum formation temperature of the ion. In the left plots, we distinguished the neutrals from ionized species.
In the right column of Fig. 1 we show the same plots but with each element identified by a different symbol.
In the QS the variation of the velocity with temperature is similar to
what was previously found for this region (see for example CSL): the motions increase with temperature, reaching a maximum in the transition region (at about
![]() ). Then it decreases again at coronal temperatures. Some differences between QS and prominences are noticeable. We discuss them in more detail in the next sections.
). Then it decreases again at coronal temperatures. Some differences between QS and prominences are noticeable. We discuss them in more detail in the next sections.
![\begin{figure}
\par\includegraphics[scale=.5]{7196f1a.eps}\includegraphics[scale...
...hics[scale=.5]{7196f1e.eps}\includegraphics[scale=.5]{7196f1f.eps}
\end{figure}](/articles/aa/full/2007/27/aa7196-07/Timg21.gif) |
Figure 1:
Non-thermal velocities as function of the ion formation temperature for the QS ( top row) and prominence sections A |
| Open with DEXTER | |
To determine the turbulent velocity of chromospheric lines, such as singly-ionized or low-ionized species, is quite a difficult task, particularly in the QS. Several of these lines were found to be optically thick on the Sun. However we expect to find most of them optically thin in the prominence plasma, as the low intensity (as compared to the QS) indicates.
For all temperatures lower than
![]() ,
the prominence NTV is lower than those derived for the QS (Fig. 1). In prominence A
,
the prominence NTV is lower than those derived for the QS (Fig. 1). In prominence A![]() the velocity steadily increases with temperature.
In contrast, the velocity stays almost unchanged in the range
the velocity steadily increases with temperature.
In contrast, the velocity stays almost unchanged in the range
![]() in
prominence A
in
prominence A![]() .
.
The NTV-measurements of S I, Si II, and Fe II in the QS were previously made by CSL using the SUMER spectra. They found these lines broader than other optically thin lines emitted at similar temperatures, deducing that they are optically thick. However, with SUMER prominence data, Stellmacher et al. (2003) find those lines larger than in previous measurements (Mariska et al. 1979) made with the NRL spectrograph on Skylab. They attribute this effect to the underestimated instrumental profile of SUMER. Our measurements are somewhat intermediate between these previous results. The widths we measure in our prominence are larger than those found by Mariska et al. (1979) but narrower than that found by Stellmacher et al. (2003).
CSL have shown the doublet O I 1040.9, 1041.7 Å to be optically thick in the QS. Their line ratio was 1.12 as opposed to the value 2 that would be expected for optically thin lines. In our case the ratio is 1.12, so very similar to the CSL value. We can expect that here also we are in optically thick conditions (opacities of 4 and 2, respectively). Because the other O I lines used for the analysis show similar widths, we deduce that they are also affected by absorption. Our velocity values are consistent with the measurements of de Boer et al. (1998), who also noticed some absorption. In the prominence, the ratio O I 1040.9, 1041.7 Å is about 1.9, so we exclude opacity effects.
All velocities derived from the most intense N I lines are consistent. In the QS they are slightly lower than those from the O I. However, we may expect the lines to be optically thick. Only the faint line at 953.6 Å, which is visible in the QS, is extremely narrow. In the prominence all of the N I lines are narrower than in the QS.
We tried to use the doublet S II 1250.5, 1253.8 Å to check for opacity effects at this
temperature. The measured ratio is 2.35 in the QS. However, the faintest line (1250.5 Å) is blended and no definitive conclusion can be derived here.
Our S II 1253.8 Å line in the QS gives a non-thermal velocity of about
![]() (which also corresponds to the average value for all the S II lines used here). This value agree very well with that reported by CSL. Kjeldseth Moe & Nicolas (1977) found a higher value observing near the limb with Skylab/ATM. The largest width is found in the faint 996 Å line, where we also expect a large uncertainty.
(which also corresponds to the average value for all the S II lines used here). This value agree very well with that reported by CSL. Kjeldseth Moe & Nicolas (1977) found a higher value observing near the limb with Skylab/ATM. The largest width is found in the faint 996 Å line, where we also expect a large uncertainty.
The C II doublet 1037, 1036.3 Å was found to be thick in the QS (CSL). In our case the line ratio is 1.21, which confirms the results of these authors. We found the same line ratio in the prominence, indicating that here such lines are also optically thick.
Several isolated lines from allowed transitions are also visible lying on top of the H I Ly-continuum. Such lines have widths comparable to those of the C II doublet 1037,
1036.3 Å. We believe they also are optically thick. The narrowest line from this ion in the QS was measured at 1092.726 Å. Its width gives a non-thermal velocity of 17
![]() that is almost 10
that is almost 10
![]() less than for the doublet. The former value is consistent with the velocity found by CSL at this temperature, after their correction for opacity. This can be an indication that this faint line is thin.
In the prominence we could only use the lines from the C II 1037, 1036.3 Å doublet. They show a reduced velocity of about 10
less than for the doublet. The former value is consistent with the velocity found by CSL at this temperature, after their correction for opacity. This can be an indication that this faint line is thin.
In the prominence we could only use the lines from the C II 1037, 1036.3 Å doublet. They show a reduced velocity of about 10
![]() at
at
![]() .
The brightest line (1085.7 Å) of the N II multiplet at 1085 Å is blended and cannot be used. The doublet at 1084 Å again gives a difference of about 8
.
The brightest line (1085.7 Å) of the N II multiplet at 1085 Å is blended and cannot be used. The doublet at 1084 Å again gives a difference of about 8
![]() between QS and prominence.
between QS and prominence.
Our O II lines all fall on top of the H I Ly-continuum. The widths we found are the same as those measured by Doschek (2002) in the QS with SUMER, where opacity effects were observed. An important reduction of the width (equivalent to more than
![]() )
is observed in the prominence spectrum.
In the present analysis we excluded the He lines because they are heavily affected by absorption.
)
is observed in the prominence spectrum.
In the present analysis we excluded the He lines because they are heavily affected by absorption.
At about
![]() the velocities from Si III and S III are in excellent agreement in the QS and in prominence A
the velocities from Si III and S III are in excellent agreement in the QS and in prominence A![]() .
In both prominence datasets, the S III lines vary only a little, while the
Si III line narrows significantly in region A
.
In both prominence datasets, the S III lines vary only a little, while the
Si III line narrows significantly in region A![]() .
Our results for S III in A
.
Our results for S III in A![]() confirm the value derived by Mariska et al. (1979) for the same line.
A possible explanation for the different behaviors of these two ions
is the temporal variation. In fact, the exposures including these lines were taken about 50 minutes apart. Unfortunately we could not further investigate such a behavior because the other lines from these ions are too faint or blended.
confirm the value derived by Mariska et al. (1979) for the same line.
A possible explanation for the different behaviors of these two ions
is the temporal variation. In fact, the exposures including these lines were taken about 50 minutes apart. Unfortunately we could not further investigate such a behavior because the other lines from these ions are too faint or blended.
In the QS the C III multiplet at around 1175 Å cannot be used here because the lines are all blended. This is not the case for the prominence data where the results are all in excellent agreement. The velocity found in the QS can be an upper limit. In fact Peter (2002) found a broader second velocity component in lines from the same ion. This effect was also found in other measurements of bright Si IV lines, which are formed at a similar transition region temperature (Dere & Mason 1993; Kjeldseth Moe & Nicolas 1977; Chae et al. 1998).
Much more variability is shown by the Si IV lines. In the QS the line at 1066.6 Å is narrower and more intense than the line at 818.1 Å, which may be affected by the H I Ly-continuum absorption. However the velocity for the latter looks consistent with the results of the other lines that are formed at a similar temperature. For this ion, CSL found velocities in the QS that are in between our values. In the prominence data we could also select the line at 1128.4 Å, which is blended in the QS. Its width is still consistent with other lines formed at a similar temperature. However, the line at 1066.6 Å is systematically narrowed.
The O III lines at short wavelengths all give a NTV value of about 30
![]() in the QS. They are on top of the H I Ly-continuum and absorption effects may be present. In Fig. 1 we only plotted the 833.742 Å line (also the 835.292 Å in A
in the QS. They are on top of the H I Ly-continuum and absorption effects may be present. In Fig. 1 we only plotted the 833.742 Å line (also the 835.292 Å in A![]() ), because it is the most isolated and also the one with the smallest uncertainty.
In the prominence, lower NTV values were obtained, even if they are still among the highest ones at this TR temperature. Some absorption may be still present.
), because it is the most isolated and also the one with the smallest uncertainty.
In the prominence, lower NTV values were obtained, even if they are still among the highest ones at this TR temperature. Some absorption may be still present.
Fe III lines are scarcely studied lines, and we do not have much information on their behavior. Here from the comparison with the velocities from other ions at a similar temperature, we deduce that these lines are thick in the QS.
The S IV lines form at about
![]() .
At such a temperature CSL showed a lower velocity in the QS compared to our data, while Dere & Mason (1993) found rather comparable values.
The S IV lines measured in the prominence also show differences in their NTV.
The line at 1062.7 Å is quite close to a faint Fe III line at 1062.27 Å. This is very visible, but not completely resolved in the QS.
Recently, Curdt et al. (2004) identified the coronal emission at 1062.4 Å as arising from an Fe VIII line. This line is not resolved in our QS spectra, but it is visible as a very faint line in the wing of the S IV in the farthest part of the prominence, probably as coronal contribution. This fact can explain the difference in the widths between the two S IV lines observed in the prominence spectra. We did not have other available lines for this ion. Stellmacher et al. (2003), for example could observe the 944.5 Å line that, in our case, is blended with the bright Si VIII at 944.64 Å.
.
At such a temperature CSL showed a lower velocity in the QS compared to our data, while Dere & Mason (1993) found rather comparable values.
The S IV lines measured in the prominence also show differences in their NTV.
The line at 1062.7 Å is quite close to a faint Fe III line at 1062.27 Å. This is very visible, but not completely resolved in the QS.
Recently, Curdt et al. (2004) identified the coronal emission at 1062.4 Å as arising from an Fe VIII line. This line is not resolved in our QS spectra, but it is visible as a very faint line in the wing of the S IV in the farthest part of the prominence, probably as coronal contribution. This fact can explain the difference in the widths between the two S IV lines observed in the prominence spectra. We did not have other available lines for this ion. Stellmacher et al. (2003), for example could observe the 944.5 Å line that, in our case, is blended with the bright Si VIII at 944.64 Å.
In the temperature range
![]() ,
NTV values remain almost constant or decrease with temperature in all datasets. We do not observe large variations in the three datasets.
The S VI emission shows slightly higher NTV values with respect to N V, even if they have a similar formation temperature. This behavior has already been noticed by Stellmacher et al. (2003), even if these authors did not separate the thermal from the turbulent component.
The velocities we derive from N V and S VI lines in the QS confirm the values found by CSL. The velocity derived for the O VI line in the prominence is consistent with the results reported by Vial et al. (1980).
,
NTV values remain almost constant or decrease with temperature in all datasets. We do not observe large variations in the three datasets.
The S VI emission shows slightly higher NTV values with respect to N V, even if they have a similar formation temperature. This behavior has already been noticed by Stellmacher et al. (2003), even if these authors did not separate the thermal from the turbulent component.
The velocities we derive from N V and S VI lines in the QS confirm the values found by CSL. The velocity derived for the O VI line in the prominence is consistent with the results reported by Vial et al. (1980).
The intense H I Ly![]() wing in the QS and A
wing in the QS and A![]() spectra aggravates the uncertainty of the O V FWHM.
At coronal temperatures there are few lines available for the analysis. Their general behavior shows little change in the three datasets. This shows that the corona along the line of sight is not much affected by the prominence much.
spectra aggravates the uncertainty of the O V FWHM.
At coronal temperatures there are few lines available for the analysis. Their general behavior shows little change in the three datasets. This shows that the corona along the line of sight is not much affected by the prominence much.
Figure 1 compares the NTV of different ions. At a given temperature the observed differences may, besides the opacity effect already discussed, be caused by the uncertainty of the assumed ion temperature and even possible abundance variations. In the prominence at the low TR temperature we find quite a good agreement of the C , N , Si , and S ions, while O and Fe ions show greater deviations.
The DEM gives information on the plasma temperature distribution. Along the line of sight (h), the DEM is defined by:
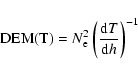 |
(2) |
where G(T) is the contribution function that only depends on the temperature for the lines from allowed transitions, and A(X) is the abundance of the element with respect to hydrogen.
The DEM(T) can be derived applying an inversion technique (available in the CHIANTI software, Young et al. 2003) to Eq. (3) for a set of observed line intensities. With the large number of lines available in our atlas we may constrain the solution over a wide range of temperatures (last three columns of Table 1).
For this calculation we applied the ionization balance of Mazzotta et al. (1998) and assumed photospheric abundances and a constant pressure (in terms of
![]() )
of
)
of
![]() and
and
![]() for the prominence and QS respectively. Figure 2 shows the results for the QS (top) and the prominence (A
for the prominence and QS respectively. Figure 2 shows the results for the QS (top) and the prominence (A![]() in the middle and A
in the middle and A![]() in the bottom panels). The error bar on the data points plotted in Fig. 2 is the uncertainty of the radiance that results from the line-fitting procedure.
in the bottom panels). The error bar on the data points plotted in Fig. 2 is the uncertainty of the radiance that results from the line-fitting procedure.
We only chose intense lines with small uncertainty and intentionally left out neutrals, because they are probably affected by opacity absorption. For the same reason we also excluded those lines that lie in the H I Ly-continuum. As a result of these criteria, the line list for this analysis is slightly different from what is used for the derivation of non-thermal motions.
![\begin{figure}
\par\hspace*{-.3cm}
\includegraphics[scale=.38,angle=90]{7196f2a....
...
\hspace*{.1cm}
\includegraphics[scale=.38,angle=90]{7196f2c.eps}
\end{figure}](/articles/aa/full/2007/27/aa7196-07/Timg37.gif) |
Figure 2:
Differential emission measure for the QS ( top) and prominence sections (A |
| Open with DEXTER | |
The QS DEM derived from our data is consistent with the values found in the CHIANTI database (top plot of Fig. 2). There may be an underestimation of this parameter at chromospheric temperatures due to absorption effects that we found on our data (see Sect. 3.1). Beside this, we decided to use all the lines available from ionized species to give an estimate of the DEM, even at the lowest temperatures.
As expected, the DEM of the QS is higher at all temperatures up to
![]() .
In particular, between
.
In particular, between
![]() and
and
![]() the prominence emission measure is less than the QS emission by a factor 2.5-10. At 1 MK, the coronal emission of the prominence plasma becomes more important than in the QS. This is mostly due to the background and foreground emission of the hot plasma that surrounds the cooler prominence. We did not have background coronal data available in the region surrounding the prominence to remove such a contribution from our data.
The minimum in the DEM is found at a lower temperature for the prominence (
the prominence emission measure is less than the QS emission by a factor 2.5-10. At 1 MK, the coronal emission of the prominence plasma becomes more important than in the QS. This is mostly due to the background and foreground emission of the hot plasma that surrounds the cooler prominence. We did not have background coronal data available in the region surrounding the prominence to remove such a contribution from our data.
The minimum in the DEM is found at a lower temperature for the prominence (![]()
![]() )
than for the QS, confirming previous measurements (Engvold 1989; Cirigliano et al. 2004; Wiik et al. 1993) and a theoretical calculation (Chiuderi & Chiuderi Drago 1991).
)
than for the QS, confirming previous measurements (Engvold 1989; Cirigliano et al. 2004; Wiik et al. 1993) and a theoretical calculation (Chiuderi & Chiuderi Drago 1991).
The DEM for A![]() does not differ much from that of A
does not differ much from that of A![]() .
We find that some lines behave differently than others at a similar temperature. This was observed in all datasets.
These problematic lines belong to the Li and Na isoelectronic groups. Previous studies report similar anomalies (Del Zanna et al. 2002). The inconsistencies may be attributed either to atomic data problems or incomplete physics used to describe the plasma environment.
We tested the calculation of the DEM using both photospheric and coronal abundances. We found that these discrepancies could not be resolved by varying the abundances. We conclude that they can be attributed either to the temporal variation of the observed plasma (we already discussed this point), or to problems in the atomic physics used.
.
We find that some lines behave differently than others at a similar temperature. This was observed in all datasets.
These problematic lines belong to the Li and Na isoelectronic groups. Previous studies report similar anomalies (Del Zanna et al. 2002). The inconsistencies may be attributed either to atomic data problems or incomplete physics used to describe the plasma environment.
We tested the calculation of the DEM using both photospheric and coronal abundances. We found that these discrepancies could not be resolved by varying the abundances. We conclude that they can be attributed either to the temporal variation of the observed plasma (we already discussed this point), or to problems in the atomic physics used.
The DEMs derived in this work are used to estimate the radiative loss rate in our regions
through
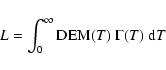 |
(4) |
To determine
![]() we used the CHIANTI database, assuming the ionization ratios of Mazzotta et al. (1998) and photospheric abundances. There is an large difference in the radiative loss function depending on the parameter used for the calculation (Landi et al. 1999), in particular the abundance adopted.
we used the CHIANTI database, assuming the ionization ratios of Mazzotta et al. (1998) and photospheric abundances. There is an large difference in the radiative loss function depending on the parameter used for the calculation (Landi et al. 1999), in particular the abundance adopted.
The integrated flux of energy (L) due to radiative losses deduced for the QS and the prominence are derived using Eq. (6) and plotted in Fig. 3.
For temperatures higher than
![]() ,
the QS flux is
,
the QS flux is ![]()
![]() ,
which is close to the value found by Athay & White (1978) and Withbroe & Noyes (1977). These values are slightly lower than the ones found by Dere & Mason (1993). At such temperatures the integrated loss rate of the QS and prominence are comparable. This is due to the strong contribution of the off-limb coronal emission with respect to the on-disk emission at similar temperatures.
In prominence sections A
,
which is close to the value found by Athay & White (1978) and Withbroe & Noyes (1977). These values are slightly lower than the ones found by Dere & Mason (1993). At such temperatures the integrated loss rate of the QS and prominence are comparable. This is due to the strong contribution of the off-limb coronal emission with respect to the on-disk emission at similar temperatures.
In prominence sections A![]() and A
and A![]() we derived similar integrated losses.
we derived similar integrated losses.
![\begin{figure}
\par\includegraphics[scale=.5]{7196f3.eps}
\end{figure}](/articles/aa/full/2007/27/aa7196-07/Timg49.gif) |
Figure 3:
Integrated radiative loss rates for the QS (dash-dotted) and the prominence (A |
| Open with DEXTER | |
The electron density was derived using the line-ratio technique applied to C III 977 Å and 1174.9 Å lines (Cirigliano et al. 2004; Mason & Monsignori Fossi 1994). In prominence A![]() we obtained
we obtained
![]() (
(
![]() at
at
![]() )
and in section A
)
and in section A![]()
![]() (
(
![]() ), respectively.
The corresponding pressures agrees with the low-pressure models of Heasley & Milkey (1978) and Heinzel & Anzer (2001).
), respectively.
The corresponding pressures agrees with the low-pressure models of Heasley & Milkey (1978) and Heinzel & Anzer (2001).
There is a large difference in the density of the two prominence sections. This reflects the change in observed spectra, as has already been noticed in Paper I. In this particular case we see that while in A![]() the 1174.9 Å line is more intense than in A
the 1174.9 Å line is more intense than in A![]() ,
this is not the case for the 997 Å line. This could be either a temporal effect due to the time delay between the exposures (we recall that each exposure covers 40 Å in the spectrum) or a real inhomogeneity of the prominence.
,
this is not the case for the 997 Å line. This could be either a temporal effect due to the time delay between the exposures (we recall that each exposure covers 40 Å in the spectrum) or a real inhomogeneity of the prominence.
The quantities derived in the previous sections can be interpreted in terms of energy budgets for the prominence. Let us assume that the NTV are the signature of wave propagation. In
Fig. 4 we compare the radiative losses in the prominence to the energy fluxes carried by Alfvén and sound waves.
In the case of Alfvén waves, the energy flux density along the magnetic field is given by
Alfvén speeds of
![]() in A
in A![]() and
and
![]() in A
in A![]() were obtained assuming a field of 10
were obtained assuming a field of 10 ![]() .
For the sound-wave energy flux, we
replaced
.
For the sound-wave energy flux, we
replaced ![]() by
by ![]() .
Figure 4 shows that in A
.
Figure 4 shows that in A![]() such waves are not efficient enough for transporting the energy needed to compensate for the radiative losses. In contrast, for the A
such waves are not efficient enough for transporting the energy needed to compensate for the radiative losses. In contrast, for the A![]() area, the Alfvén wave flux is sufficient for temperatures higher than
area, the Alfvén wave flux is sufficient for temperatures higher than
![]() and the sound wave flux becomes important for temperatures higher than
and the sound wave flux becomes important for temperatures higher than
![]() .
.
![\begin{figure}
\includegraphics[scale=.5]{7196f4a.eps}\\
\includegraphics[scale=.5]{7196f4b.eps}
\end{figure}](/articles/aa/full/2007/27/aa7196-07/Timg64.gif) |
Figure 4:
Integrated energy losses for the prominence (solid) as function of temperature compared to the energy flux carried by Alfvén waves (dashed) and sound waves (dot-dashed). The top plot refers to A |
| Open with DEXTER | |
Using our UV spectral atlas we have derived reference values for the non-thermal velocities in a prominence and QS as function of the temperature. A few studies in these regions have shown that a correlation may exist between the line intensity and its width (e.g. Dere & Mason 1993; de Boer et al. 1998; Wiik et al. 1999; Jordan 1994).
The prominence shows smaller NTV motions with respect to the quiet Sun, particularly for temperatures of the lower transition region. Mariska et al. (1979) and Cirigliano et al. (2004) have already found a difference in the temperature gradients in the prominence-corona interface and the chromosphere-corona interface. Our results confirm this trend.
However, Wiik et al. (1993) also noticed how such a gradient may change with the activity level of the prominence. In particular, several observations showed an increase of the NTV towards the peripheral regions (de Boer et al. 1998; Mouradian & Leroy 1977). This does not seem to being the case in our prominence, in agreement with the results of Mariska et al. (1979) and Vial et al. (1979).
In our case, the two analyzed regions show a similar trend up to
![]() ,
where the A
,
where the A![]() velocity profile seems to flatten, up to
velocity profile seems to flatten, up to
![]() .
This different trend in temperature, observed by Wiik et al. (1993)
and Stellmacher et al. (2003), was also observed in the line intensity. Wiik et al. (1993) attributes such behavior to a different distribution of the cooler and hotter transition region plasmas. However, the impossibility of resolving the prominence threads imposes ambiguities in the interpretation on their fine structure.
.
This different trend in temperature, observed by Wiik et al. (1993)
and Stellmacher et al. (2003), was also observed in the line intensity. Wiik et al. (1993) attributes such behavior to a different distribution of the cooler and hotter transition region plasmas. However, the impossibility of resolving the prominence threads imposes ambiguities in the interpretation on their fine structure.
We derived the DEM in the QS and a prominence. Compared to previous calculations, this work can rely on a large number of observed lines whose formation temperature spans the range
![]() .
This imposes stronger constraints on the inversion problem.
.
This imposes stronger constraints on the inversion problem.
The DEM profile derived for the prominence shows a temperature minimum at about
![]() .
This is lower than previous measurements (Kucera & Landi 2006; Cirigliano et al. 2004) and lower than what is observed in the QS. We also estimated that the emission of the PCTR is
2.5 - 10 times less than the chromosphere corona transition region. Chiuderi & Chiuderi Drago (1991) showed how the PCTR thickness differs with the angle between the magnetic field direction and the temperature gradient. In particular, they claim a thinner PCTR when the angle approaches
.
This is lower than previous measurements (Kucera & Landi 2006; Cirigliano et al. 2004) and lower than what is observed in the QS. We also estimated that the emission of the PCTR is
2.5 - 10 times less than the chromosphere corona transition region. Chiuderi & Chiuderi Drago (1991) showed how the PCTR thickness differs with the angle between the magnetic field direction and the temperature gradient. In particular, they claim a thinner PCTR when the angle approaches ![]() .
Actually, the PCTR thickness may well vary continuously according to its orientation with respect to the field lines, as shown by Heinzel et al. (2005). To establish the DEM profile with small uncertainties, it is essential to verifying these theoretical results.
.
Actually, the PCTR thickness may well vary continuously according to its orientation with respect to the field lines, as shown by Heinzel et al. (2005). To establish the DEM profile with small uncertainties, it is essential to verifying these theoretical results.
However, a residual uncertainty in our DEM estimate arises from the assumption that we are dealing with an optically thin plasma. For temperatures lower than ![]()
![]() ,
we have shown that it is not often the case. The opacity effect results in decreasing radiative losses at such temperatures, with respect to the thin case as shown by Kuin & Poland (1991). This means that our DEM may be overestimated at chromospheric temperatures (Kuin & Poland 1991).
,
we have shown that it is not often the case. The opacity effect results in decreasing radiative losses at such temperatures, with respect to the thin case as shown by Kuin & Poland (1991). This means that our DEM may be overestimated at chromospheric temperatures (Kuin & Poland 1991).
In this work we also neglect the possible contribution of radiative excitation processes in the formation of prominence lines (Zirin 1956). We checked this on the O VI doublet and found that the collisional contribution to the line intensities is at least six times that of the radiative one with
the density and dilution factor values found for our prominence (Parenti et al. 2005a). These electron density values lead to relatively low pressures, in agreement with values derived from radiative transfer modeling
(e.g.
![]() in Heinzel et al. 2005).
in Heinzel et al. 2005).
The results presented here were used to calculate the integrated radiative losses and wave energy flux for
the energy budget in the prominences. Anzer & Heinzel (1999), using different models, investigated the energy balance in prominence plasmas by studying the detailed requirements of their inner and outer parts. However, they did not give details on the heating mechanisms. In a later work, Anzer & Heinzel (2000) investigated the possible role of steady mass inflow. They found that this mechanism can be sufficient for thin (<
![]() )
and relatively cold prominences (
)
and relatively cold prominences (
![]() )
to balance the radiative losses. Our prominence may belong to this category (Parenti et al. 2005a). We also investigated the role of wave energy flux in the energy budget.
We tested the energy flux transported by Alfvén and sound waves and found that they may partially contribute to the prominence energy budget. In the QS, Dere & Mason (1993)and
CSL found the Alfvén waves to be abundant enough to compensate for the radiative losses for
)
to balance the radiative losses. Our prominence may belong to this category (Parenti et al. 2005a). We also investigated the role of wave energy flux in the energy budget.
We tested the energy flux transported by Alfvén and sound waves and found that they may partially contribute to the prominence energy budget. In the QS, Dere & Mason (1993)and
CSL found the Alfvén waves to be abundant enough to compensate for the radiative losses for
![]() .
Our results
seem to indicate that this happens at higher temperatures in the prominence. However, if we overestimated the DEM, such waves can already be efficient enough at lower temperatures.
.
Our results
seem to indicate that this happens at higher temperatures in the prominence. However, if we overestimated the DEM, such waves can already be efficient enough at lower temperatures.
Acknowledgements
S.P. wishes to thank the MEDOC team at Orsay for providing the data and Giulio Del Zanna for providing the software used for the DEM calculation. S.P. is also grateful to Philippe Lemaire for helpful discussions. The authors thank John Leibacher for the help during the revision of the manuscript and the anonymous referee for helpful comments and corrections. S.P. acknowledges the support from the Belgian Federal Science Policy Office through the ESA-PRODEX program. SUMER is supported by DLR, CNES, NASA, and the ESA PRODEX program (Swiss contribution). SOHO is a mission of international cooperation between ESA and NASA. CHIANTI is a collaborative project involving NRL (USA), RAL (UK), and the following Universities: Univeristy College London (UK), Cambridge (UK), George Mason (USA), and Florence (Italy).
Table 1:
Non-thermal velocities (![]() )
in
)
in
![]() and their uncertainties
and their uncertainties ![]() for the QS and prominence data. The last three columns list the lines used for the DEM analysis.
for the QS and prominence data. The last three columns list the lines used for the DEM analysis.