A&A 469, 1013-1025 (2007)
DOI: 10.1051/0004-6361:20066861

The s-process in stellar population synthesis: a new approach to understanding AGB stars[*]

A. Bonacic Marinovic - R. G. Izzard - M. Lugaro - O. R. Pols

Sterrekundig Instituut Utrecht (SIU), Universiteit Utrecht, PO Box 80000, 3508 TA Utrecht, The Netherlands

Received 2 December 2006 / Accepted 5 March 2007

Abstract
Context. Thermally pulsating asymptotic giant branch (AGB) stars are the main producers of slow neutron capture (s-) process elements, but there are still large uncertainties associated with the formation of the main neutron source, 13C, and with the physics of these stars in general. Observations of s-process element enhancements in stars can be used as constraints on theoretical models.
Aims. For the first time we have applied stellar population synthesis to the problem of s-process nucleosynthesis in AGB stars, in order to derive constraints on free parameters describing the physics behind the third dredge-up and the properties of the neutron source.
Methods. We utilize a rapid evolution and nucleosynthesis code to synthesize different populations of s-enhanced stars, and compare them to their observational counterparts to find out which values of the free parameters in the code produce synthetic populations that fit the observed populations best. These free parameters are the amount of third dredge-up, the minimum core mass for third dredge-up, the effectiveness of 13C as a source of neutrons, and the size in mass of the 13C pocket.
Results. We find that galactic disk objects are reproduced by a spread of a factor of two in the effectiveness of the 13C neutron source. Lower metallicity objects can be reproduced only by lowering the average value of the effectiveness of the 13C neutron source needed for the galactic disk objects by at least a factor of 3. Using observations of s-process elements in post-AGB stars as constraints we find that dredge-up has to start at a lower core mass than predicted by current theoretical models, that it has to be substantial ( $\lambda\ga 0.2$) in stars with mass $M\la 1.5~M_{\odot}$, and that the mass of the 13C pocket must be about 1/40 that of the intershell region.

Key words: stars: AGB and post-AGB - stars: abundances - nuclear reactions, nucleosynthesis, abundances

1 Introduction

About half of elements that are heavier than iron are produced by slow neutron captures (s-process) in the deep layers of thermally pulsating (TP-) asymptotic giant branch (AGB) stars, which represent the late evolutionary phase of objects with an initial mass of $M\la 8~M_{\odot}$. These stars have degenerate carbon-oxygen cores surrounded by two burning shells, and they undergo a cyclic instability of the helium-burning shell known as thermal pulses. The s-process elements are believed to be synthesized in the thin helium-rich layer between the helium-burning and hydrogen-burning shells known as the inter-shell region, or intershell. After each thermal pulse the hydrogen-rich convective envelope may penetrate into the intershell and bring the synthesized heavy elements, together with the products of helium burning (mainly carbon), to the stellar surface in a phenomenon called third dredge-up (TDU). Strong stellar winds gradually ablate the envelope and enrich the interstellar medium with the nucleosynthesis products. Many of the physical processes taking place in TP-AGB stars are still highly uncertain, such as how the main source of free neutrons required for the s-process is produced (see below), under which conditions TDU occurs and how efficient it is, and the what strength and driving mechanism of mass loss is. Many of these uncertainties are related to our poor understanding of mixing processes in stars. For a recent review of AGB stars see Herwig (2005), and for a discussion of uncertainties in AGB stellar models see, e.g., Lugaro et al. (2003).

The synthesis of s-process elements requires a source of free neutrons that can be captured by iron seeds to build up heavier nuclei along the isotopic stability valley. During the period of quiescent hydrogen-shell burning in between thermal pulses, the inter-pulse period, the conditions in the intershell (temperature, density and helium abundance) favour the ${\rm ^{13}C}(\alpha,n)^{16}{\rm O}$ reaction. For this reaction to be an effective source of free neutrons, a 13C-rich region or pocket in the intershell is needed. The production of 13C takes place by means of the ${\rm ^{12}C}(p,\gamma){\rm ^{13}N}(\beta^+\nu){\rm ^{13}C}$ reaction. It is assumed that the protons needed for this reaction penetrate the top of the intershell after TDU has occurred, as a result of a mixing process of an as yet uncertain nature: semi-convection (Hollowell & Iben 1988), hydrodynamical overshooting (Herwig et al. 1997), rotation (Herwig et al. 2003; Langer et al. 1999), and gravity waves (Denissenkov & Tout 2003) have all been proposed. As a consequence large uncertainties exist in the mass size of the 13C pocket and the 13C abundance profile inside it. In addition, due to the existence of several neutron poisons, especially 14N, not all free neutrons released by the ${\rm ^{13}C}(\alpha,n)^{16}{\rm O}$ reaction participate in the s-process, so the effectiveness of 13C as a neutron source for the s-process is also very uncertain. Another neutron burst is also released in the convective intershell during the thermal pulses due to the ${\rm ^{22}Ne}(\alpha,n)^{25}{\rm Mg}$ reaction, but the activation of this reaction is only marginal, which makes its contribution to the neutron exposure smaller than that of the ${\rm ^{13}C}(\alpha,n)^{16}{\rm O}$ reaction (see Busso et al. 1999, for a review of s-process nucleosynthesis in AGB stars).

Among stars that are enhanced in s-process elements (s-enhanced stars), one distinguishes intrinsic and extrinsic objects. Intrinsic s-enhanced stars are typically late-type giants of spectral classes S and C that show over-abundances of s-process elements (see, e.g., Smith & Lambert 1990; Abia et al. 2002), including the radioactive element Tc (Merrill 1952). With a half-life of a few million years, the presence of Tc lines indicates that the synthesis of s-process elements happened recently and in situ. Therefore intrinsic s-enhanced stars must be objects in the TP-AGB phase or post-AGB phase, which have recently experienced thermal pulses and TDU. The study of elemental abundances in these stars gives clues to the uncertain physical phenomena that take place in their interiors. Extrinsic s-enhanced stars also show over-abundances of s-process elements, but no Tc lines are present (Jorissen et al. 1993). This indicates that Tc has decayed since the s-process elements were synthesized. In addition, extrinsic stars are often observed to be in an evolution phase earlier than the TP-AGB; i.e., they are (sub)giants or main sequence stars. This implies that the s-process elements were not produced in situ, but that they have been accreted from a more massive TP-AGB companion star. These stars can therefore act as probes for studying mass transfer processes in binaries and for tracing the nucleosynthesis that occurred in their companion stars.

Busso et al. (2001) carried out a detailed comparison between observations of s-process enhanced stars and model predictions for the s-process in single AGB stars of different metallicities. They found that a large spread (a factor of $\sim $20) in the effectiveness (see Sect. 2.3 for a definition of this parameter) of the main neutron source 13C was needed to match spectroscopic observations at a given metallicity. Their analysis is based on a small set of initial stellar masses, and they have taken only the final abundances of their stars into consideration. In this paper we improve on their analysis by comparing observations of different types of stars belonging to the AGB family to stellar population synthesis models computed with the inclusion of the s-process. Our use of a rapid synthetic evolution code allows us to study a large set of finely spaced initial masses and metallicities and to trace the complete AGB evolution of each star. Using this method we are able to put much tighter constraints on the effectiveness of 13C as a neutron source. In addition, by comparing our models to post-AGB observations, we also put constraints on the minimum core mass for TDU, the TDU efficiency, and the size of the 13C pocket.

The AGB stellar models and the associated free parameters are described in Sect. 2. Our stellar population synthesis method is described in Sect. 3 and the results are presented in Sect. 4. In Sect. 5 we discuss our results and draw our conclusions.

   
2 The AGB models

Our TP-AGB star models are calculated with a modified version of the rapid evolutionary code by Hurley et al. (2000) and Izzard et al. (2004). We limit ourselves to a brief overview of the ingredients of this code and a discussion of the most important free parameters. A detailed description of our modifications and improvements can be found in Appendix A. Stellar evolution and nucleosynthesis are modelled synthetically, i.e., by means of analytical fits to the detailed evolutionary models of Karakas et al. (2002) and Stancliffe et al. (2004), and in some cases by tabular interpolation of these detailed models. Fits and interpolations depend on global stellar parameters, such as metallicity, mass, and core mass. This synthetic approach makes the calculation of the evolution very fast. The s-process element nucleosynthesis is calculated by interpolating results based on detailed models by Gallino et al. (1998), as described below. With these models we are able to follow the chemical abundances of stars as a function of time, from their initial abundances at the beginning of the main sequence, for which we use those of Anders & Grevesse (1989), to their chemically enhanced abundances of the latest evolutionary TP-AGB and post-AGB phases.

Many uncertainties exist in the detailed evolutionary models, which we treat as free parameters. In the following subsections we discuss the free parameters that are most relevant for stellar chemical evolution.

2.1 Minimum core mass for third dredge-up

Detailed models of TP-AGB stellar evolution which find TDU show that it only occurs when the stellar core mass is greater than about 0.6 $M_{\odot }$ (e.g., Boothroyd & Sackmann 1988; Straniero et al. 1997; Lattanzio 1989), but there is disagreement of about $10\%$ on the exact value of this minimum core mass (see, e.g., Lugaro et al. 2003). The luminosity and surface abundances of carbon and s-process elements in TP-AGB stars of mass $M\la2~M_{\odot}$depend strongly on this minimum core mass. We have modelled the TDU by using the fit to the models of Karakas et al. (2002) from Izzard et al. (2004), which includes the free parameter $\Delta M_{\rm c}^{\rm min}$. This parameter offsets the minimum core mass by a fixed amount compared to the results of Karakas et al. (2002), allowing stars of low mass to undergo TDU, even if they do not do so in the detailed models.

2.2 Third dredge-up efficiency

Detailed evolution models disagree on the amount of third dredge-up that occurs in a star of a particular mass and metallicity, i.e., how deep the convective envelope penetrates the intershell (see, e.g., Frost & Lattanzio 1996; Mowlavi 1999, for discussion). The amount of dredge-up can be measured by the third dredge-up efficiency

\begin{displaymath}\lambda=\frac{\Delta M_{\rm TDU}}{\Delta M_{\rm H}}, \end{displaymath} (1)

where $\Delta M_{\rm TDU}$ is the reduction in mass of the hydrogen exhausted core as a result of dredge-up and $\Delta M_{\rm H}$ is the amount of mass by which the hydrogen-exhausted core increased due to hydrogen burning during the previous inter-pulse period. Thus, if $\lambda=0$there is no dredge-up at all, while if $\lambda=1$ there is no net growth of the hydrogen-exhausted core. We apply the parametrization from Izzard et al. (2004) in which $\lambda$ grows asymptotically with pulse number to a maximum value of

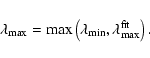\begin{displaymath}\lambda_{\rm max}=\max\left(\lambda_{\rm min}, \lambda_{\rm max}^{\rm fit}\right). \end{displaymath} (2)

Here $\lambda_{\rm max}^{\rm fit}$ is a function of mass and metallicity, which fits the $\lambda_{\rm max}$ value of the detailed models (Karakas et al. 2002), and the free parameter $\lambda _{\rm min}$ is used to set a lower limit. In this way stars that show negligible TDU efficiency in the detailed models are allowed to have a substantial TDU efficiency when $\lambda _{\rm min}$ is set to be greater than zero.

   
2.3 Effectiveness of 13C as a neutron source

At the end of a TDU episode protons from the bottom of the H-rich envelope may penetrate beyond the chemical boundary into the helium- and carbon-rich intershell. They react with 12C to produce 13N, which decays into 13C forming the 13C pocket. If there are enough protons, 13C will also capture protons and produce 14N. The 13C in the pocket is a source of neutrons by means of the ${\rm ^{13}C}(\alpha,n)^{16}{\rm O}$ reaction, but it has to compete with 14N as a sink of free neutrons due to the $^{14}{\rm N}(n,p)^{14}{\rm C}$ reaction, which has a relatively high neutron capture cross section. As a result of this competition an effective local ${\rm ^{13}C}$ abundance can be defined, which parametrizes the number of free neutrons per heavy seed nucleus in the intershell available for the s-process to take place. The abundance ratios of s-process elements in the ${\rm ^{13}C}$ pocket are determined by this local 13C abundance, which is scaled relative to a standard case. This standard case was defined by Gallino et al. (1998) and Busso et al. (2001), based on the 13C pocket found by Hollowell & Iben (1988) in their detailed evolutionary calculations. Gallino et al. (1998) show that, with this pocket, low-mass AGB stars of half solar metallicity produce the main s-process component for the Sun. We denote this scaled effective 13C abundance as ${\rm ^{13}C}_{\rm eff}$, so that the standard case corresponds to ${\rm ^{13}C}_{\rm eff}=1$.

Comparing the absolute elemental abundances produced by s-process models directly to observations is difficult because they depend on the dilution of material from the intershell into the envelope, which in turn depends on several uncertain factors such as the size in mass of the ${\rm ^{13}C}$ pocket, the amount of TDU, mass loss, and mass accretion. However, the s-process element abundance ratios mostly remain unaffected by these processes, so they provide direct constraints on ${\rm ^{13}C}_{\rm eff}$ (see Sect. 4).

2.4 Size of the 13C pocket

In order to calculate the abundances in the stellar envelope we must know the element mass fraction in the intershell at the moment when the star undergoes TDU. For s-process elements, we calculate these intershell abundances by using the results of detailed models from Gallino et al. (1998), which consist of a grid of intershell elemental abundances at the time of TDU for stellar masses of 1.5, 3, and 5 $M_{\odot }$, metallicities $10^{-4}\leq Z\leq 0.02$, effective local ${\rm ^{13}C}$abundance ( $1/24\leq{\rm ^{13}C}_{\rm eff}\leq 2$) and number of thermal pulse followed by TDU ( $2\leq N_{\rm TDU}\leq 29$). We know the mass of the 13C pocket and of the intershell in these detailed models, which we use to trace back the local element mass fractions in the 13C pocket just before the thermal pulse occurs. We map a grid of s-process element mass fractions in the 13C pocket for different stellar masses, metallicities, ${\rm ^{13}C}_{\rm eff}$, and pulse number, which is independent of the choice of the size of the 13C pocket and that of the intershell. We interpolate linearly on this grid and if the stellar mass and/or pulse number needed for the calculation is out of the grid bounds we use the result of the closest point on the grid.

Note that with this procedure we do not properly account for the 22Ne neutron source. However, this neutron source does not contribute to defining the overall s-process distribution, at least for stellar models of mass $M\la4~M_{\odot}$, which are believed to be the counterparts of the observed s-process enhanced stars that we will discuss in Sect. 4 (e.g., Abia et al. 2001).

We assume that the 13C pocket mass is a fixed fraction, $f_{{\rm ^{13}C,IS}}$, of the mass of the intershell at the moment just before TDU occurs, $M_{\rm IS}$, which in turn is approximated well by the maximum mass of the convective intershell pocket during the thermal pulse. We employ the relation proposed by Iben (1977) for the maximum convective intershell mass,

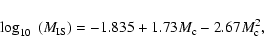\begin{displaymath}\log_{10}~(M_{\rm IS})=-1.835+1.73M_{\rm c}-2.67M_{\rm c}^2, \end{displaymath} (3)

where $M_{\rm c}$ is the mass of the H-exhausted core. This relation is derived for core masses higher than 0.95 $M_{\odot }$, but when extrapolated to lower core masses, it yields intershell mass values similar to those considered by Gallino et al. (1998) in their detailed models. The value of $f_{{\rm ^{13}C,IS}}$ can be constrained by observations of surface abundances of s-process elements, although these abundances also depend on the amount of dredge-up that the star has experienced. This degeneracy is broken by studying the abundances of other elements that are not synthesized via the s-process, as discussed in Sect. 4.1.4.

2.5 Mass loss

Mass loss is an uncertain factor in AGB evolution which affects the enhancement of s-process elements on the surface of a TP-AGB star (Straniero et al. 2003). The mass loss rate determines the stellar lifetime as a TP-AGB star by truncating it when the envelope is lost. In the models of Gallino et al. (1998) the intershell s-process abundance ratios vary from one pulse to another, until after roughly 20 pulses they reach an asymptotic value. The asymptotic values are usually considered to be the s-element ratios of a typical pulse and are often compared to the observed ratios (e.g., Reyniers et al. 2004; Busso et al. 2001; Straniero et al. 2003). Depending on the mass loss rate applied in the models, a star with mass $M\la 1.5~M_{\odot}$ can undergo from very few thermal pulses (or none) to several tens, which affects its surface composition and yield during the TP-AGB phase. In this work we use the mass-loss prescription by Vassiliadis & Wood (1993):
$\displaystyle {\rm log}_{10}\frac{\dot{M}_{\rm AGB}}{{M_{\odot}~\rm yr^{-1}}}= ... ...ac{P}{\rm day} -100 \max\left(\frac{M-2.5~M_{\odot}}{M_{\odot}},0\right)\Bigg],$     (4)

where log P/day = -2.07+1.94 log $R/R_{\odot}-0.9 \log M/M_{\odot}$ is the logarithm of the Mira pulsation period. We do not attempt to vary the AGB mass-loss rate, but we discuss the consequences of this assumption on our results in Sect. 5.

The mass-loss rate during the giant branch phase affects the envelope mass at the moment when a star begins its TP-AGB phase. We have modelled mass-loss from giant branch stars with the widely used prescription by Reimers (1975),


 \begin{displaymath} \dot{M}_{\rm GB}=4\times10^{-13}\eta_{\rm GB} \left({L}/{L_{... ...ght) \left({M}/{M_{\odot}}\right)^{-1}{M_{\odot}~\rm yr^{-1}}, \end{displaymath} (5)

with $\eta_{\rm GB}=0.3$, which is within the limits set by the morphology of horizontal branch stars in the galactic globular clusters (Iben & Renzini 1983; Carraro et al. 1996).


  \begin{figure} \par\includegraphics[width=8cm,clip]{6861fig1.eps} \end{figure} Figure 1: Range of initial masses, $M_{\rm i}$, of our population synthesis grid as a function of metallicity, depicted by the shaded area. For a given metallicity this shows the initial-mass range of stars which can be observed in the TP-AGB phase, with a maximum mass of 8 $M_{\odot }$.
Open with DEXTER

   
3 Population synthesis

We make use of our synthetic evolutionary models to carry out population synthesis of single stars, on a grid of 50 logarithmically spaced metallicities ranging between $10^{-4}\leq Z\leq 0.025$and 500 logarithmically spaced initial masses, whose range depends on the metallicity and on whether we are modelling a population of intrinsic or extrinsic s-enhanced stars.

In the case of intrinsic stars, for each metallicity we apply the initial mass ranges shown in Fig. 1, with 8 $M_{\odot }$ as a maximum. We derive these ranges from combining our stellar evolution models with the age-metallicity relation (AMR) for the galactic disk of Pont & Eyer (2004)

 \begin{displaymath} \left[\frac{\rm Fe}{\rm H}\right]= {\rm log_{10}}\left(\frac{t-17.82}{-23.24}\right)\pm 0.25{\rm ~dex}, \end{displaymath} (6)

where the notation for the element number density ratio ${\Big[\frac{X}{Y}\Big]= \log_{10}\left(\frac{n_X}{n_Y}/\frac{n_{X_{\odot}}}{n_{Y_{\odot}}}\right)}$is used and t is the age in Gyr, with the age of the Universe (13.7 Gyr) as its upper limit. Then, from our single-star models we consider the range of initial masses for which a star spends at least some of its TP-AGB life within the age range allowed by the AMR. The probability for an intrinsic star to have a given abundance is weighted by the time it spends showing this abundance and by its contribution according to the initial mass function (IMF). We use the IMF, $\xi$, of Kroupa et al. (1993), given by

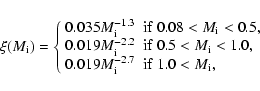\begin{displaymath}\xi(M_{\rm i})=\left\{ \begin{array}{cl} 0.035M_{\rm i}^{-1.... ...{\rm i}^{-2.7}& {\rm if}~1.0 <M_{\rm i},\\ \end{array}\right. \end{displaymath} (7)

where $M_{\rm i}$ is the initial stellar mass in solar units.

Given that we employ single stellar models, we treat the case of extrinsic stars indirectly. These stars have acquired their s-process enhancements by accreting part of the mass ejected by an initially more massive binary companion. Therefore we assume a simple model in which the initial mass of the companion is assumed to be distributed according to the single-star IMF. Hence the probability of an extrinsic star to show a given elemental abundance is weighted by the amount of mass which is lost by its companion in the form of that element and by the IMF weight of this companion. Because mass transfer could have occurred at any time since the formation of the system, we consider all stars whose evolution is beyond the TP-AGB phase, which in each metallicity bin corresponds to initial masses greater than the lower limit in Fig. 1 and smaller than 8 $M_{\odot }$. For the models with [Fe/H] <-1 we consider 0.8 $M_{\odot }$ to be the lower initial mass limit.

   
4 Results

In this section we present the results of our population synthesis models and compare them to different sets of observational data. The observations provide measurements of the surface abundances of s-process elements relative to that of iron. Following the convention, we calculate for each star in our grid its heavy s-process (hs) element abundance ratio,

\begin{displaymath}\rm { \left[\frac{hs}{Fe}\right]=\frac{1}{5}\left(\left[\frac... ...\left[\frac{Nd}{Fe}\right]+\left[\frac{Sm}{Fe}\right]\right)}, \end{displaymath} (8)

and light s-process (ls) element abundance ratio,

\begin{displaymath}\rm { \left[\frac{ls}{Fe}\right]=\frac{1}{2}\left(\left[\frac{Y}{Fe}\right]+ \left[\frac{Zr}{Fe}\right]\right)}. \end{displaymath} (9)

These ratios are altered by dilution in the stellar envelope, which is affected by several uncertain factors such as the size in mass of the ${\rm ^{13}C}$ pocket, the amount of TDU, mass loss and, in the case of binaries, mass accretion. We also study the ratio of hs-elements to ls-elements,

\begin{displaymath}\rm {\left[\frac{hs}{ls}\right]=\left[\frac{hs}{Fe}\right]- \left[\frac{ls}{Fe}\right]}\cdot \end{displaymath} (10)

This ratio reaches the [hs/ls] values of the intershell after a number of pulses asymptotically, making it mostly unaffected by dilution.

The asymptotic envelope ratio is therefore only determined by ${\rm ^{13}C}_{\rm eff}$ (see Sect. 2.3), but not by other free parameters in our model, such as the size of the ${\rm ^{13}C}$ pocket ( $f_{{\rm ^{13}C,IS}}$). Figure 2 shows the envelope [hs/ls] ratios obtained from the models of Busso et al. (2001), which in each model reach their corresponding intershell asymptotic value, but take a number of pulses to do so. Hence, considering stars that have experienced only a few TDU episodes, either because they are in an early stage of the TP-AGB phase or because they have masses of $M\la 1.5~M_{\odot}$, results in a natural spread of [hs/ls] values. Only in AGB stars with $M\ga5~M_{\odot}$ is the amount of dredged-up material is so small that the surface [hs/ls] ratios differ from those of the intershell.


  \begin{figure} \par\includegraphics[width=8cm,clip]{6861fig2.eps} \end{figure} Figure 2: Envelope [hs/ls] during the evolution of 1.5 $M_{\odot }$ and 3 $M_{\odot }$ star models of different metallicity, as indicated in the panel, and with 13C $_{\rm eff}=1$.
Open with DEXTER

To compare these abundance ratios with the observed data we have binned the resulting number distribution with a resolution of 0.1 dex. Whenever a star has a certain abundance ratio, its probability is added to the corresponding bin. This is done separately for the different metallicity bins and in each we normalize the resulting probability distribution by dividing it by its highest value.


  \begin{figure} \par\includegraphics[width=17cm,clip]{6861fig3.eps} \end{figure} Figure 3: Intrinsic MS/S stellar population synthesis results compared to the observations. The panels show our results calculated with four increasing $^{13}{\rm C}_{\rm eff}$ values as indicated above the panels. The grey scale is a logarithmic measure of the normalized number distribution of stars over [hs/ls]. The crosses are the observational data gathered by Busso et al. (2001), which have an average error given by the size of the cross in the upper right of each plot.
Open with DEXTER

We select those stars to be s-enhanced that have [ls/Fe] and/or [hs/Fe] larger than 0.1 dex. First we analyse the [hs/ls] ratios of intrinsic s-enhanced stars, which only have a strong dependence on the $^{13}{\rm C}_{\rm eff}$ value. In all the runs we use $\Delta M_{\rm c}^{\rm min}= -0.065~M_{\odot}$, $\lambda _{\rm min}=0.2$, and $f_{\rm ^{13}C,IS}=1/40$, based on our attempts to fit the post-AGB star observations of [Zr/Fe] ratios and carbon abundances, as explained in detail in Sect. 4.1.4. In Sect. 4.2 we study the [hs/ls] ratios, but this time of extrinsic s-enhanced stars, which give clues on $^{13}{\rm C}_{\rm eff}$ at metallicities lower than that of the galactic disk.


  \begin{figure} \par\includegraphics[width=16.5cm,clip]{6861fig4.eps} \end{figure} Figure 4: As Fig. 3, but for intrinsic SC and C stars. The horizontal crosses are observational data of intrinsic SC/C star gathered by Busso et al. (2001), complemented with data of Abia et al. (2002). The squares are SC/C stars in which the presence of Tc is doubtful (Abia et al. 2002) and the diagonal crosses are halo C stars from Busso et al. (2001). The observations have an average error given by the size of the cross in the upper right of each plot.
Open with DEXTER

   
4.1 Intrinsic s-enhanced stars

   
4.1.1 [hs/ls] ratios of MS/S stars
The MS/S stars are late-type giants that show lines of ZrO and TiO, indicating that they are enhanced in s-element abundance, have low surface temperature, and their C/O ratio is lower than unity. To account for these stars we selected s-enhanced stars in the TP-AGB phase of evolution from our population synthesis with a surface effective temperature lower than 3500 K and C/O < 1 in their envelope. We compared our results for the [hs/ls] ratio to observational data of intrinsic MS/S stars gathered by Busso et al. (2001). In Fig. 3 our results only appear at [Fe/H$] \ga-0.6$ because low-metallicity stars that undergo TDU episodes are too hot to be classified as MS/S objects. This is consistent with the observations. Increasing $^{13}{\rm C}_{\rm eff}$ in our models increases the [hs/ls] ratios on the low-metallicity side of the plot, but at high metallicities the [hs/ls] ratios are decreased. This is explained as follows. If the number of heavy iron seeds is decreased for a given number of available free neutrons, then the [ls/Fe] ratio increases due to s-process reactions and [hs/ls] decreases, as is observed at high metallicities in our results. But if [Fe/H] is decreased even more, the synthesis of ls-elements saturates and the hs-element abundance increases with respect to iron, raising both ratios [hs/Fe] and [hs/ls], as can be seen in our models at low metallicities (Busso et al. 2001; Travaglio et al. 1999). Thus $^{13}{\rm C}_{\rm eff}$ basically determines at which metallicity our models will show [hs/ls] ratios below solar and where they will rise to solar and beyond. This effect cannot be seen clearly in our MS/S star synthesis due to the lack of s-enhanced MS/S stars below [Fe/H $] \sim-0.6$, but is common to all the stellar populations that we have synthesized and is more evident in SC and C stars and post-AGB stars (Sect. 4.1.2 and Sect. 4.1.3, respectively). In contrast with other studies where only the asymptotic values of [hs/ls] are considered (e.g., Busso et al. 2001; Goriely & Mowlavi 2000), a natural spread in this ratio is observed in our results. This is explained by our tracing of the whole TP-AGB evolution, where the initial dozen pulses have different s-process ratios. Stars of mass $M\la 1.5~M_{\odot}$, which are the most numerous due to the IMF and which do not undergo more than 10-20 pulses, contribute most to this effect. Figure 3 shows that the best fit to the observed distribution of MS/S stars is obtained with $^{13}{\rm C}_{\rm eff}\approx4/3$ and a spread in $^{13}{\rm C}_{\rm eff}$ values is not needed to match all the observations. Given that the error bars on the individual observations are large (as indicated in Fig. 3), and that the observed [hs/ls] values are close to 0, the value of $^{13}{\rm C}_{\rm eff}$ is not strongly constrained by these observations. The (on average) negative values of [hs/ls] are matched, within observational errors, by the models if $^{13}{\rm C}_{\rm eff}$ is between 2/3 and 2. As the [hs/ls] ratio is not sensitive to dilution, changes in the other free parameters do not affect these results.


  \begin{figure} \par\includegraphics[width=16.5cm,clip]{6861fig5.eps} \end{figure} Figure 5: As Fig. 3, but for post-AGB stars The horizontal crosses are the observational data (see references in the text), which have an average error given by the size of the cross in the upper right of each plot.
Open with DEXTER

   
4.1.2 [hs/ls] ratios of SC and C stars
SC and C stars are late-type giants that show lines of carbide molecules in their spectrum, which indicates that there is more C than O by number. In the case of the SC stars, the C/O ratio is close to unity, given that they also show ZrO lines. To reproduce these stars we select from our population synthesis results those s-enhanced TP-AGB stars which have C/O >1. We compare our synthetic [hs/ls] ratios with the observational data gathered by Busso et al. (2001) and from Abia et al. (2002) as shown in Fig. 4. The spread in the [hs/ls] ratio is explained in the same way as for MS/S stars. The spread is smaller at low metallicities due to the small range of initial stellar masses considered at these metallicities resulting from the AMR (see Fig. 1). The effect of changing $^{13}{\rm C}_{\rm eff}$ on our synthetic [hs/ls] ratios is clearer in this population of stars than in the MS/S stars, particularly for ${\rm [Fe/H]}\la-0.4$. As in the case of the MS/S stars, the other free parameters do not affect the [hs/ls] ratios. Most of the observed SC and C stars cluster around ${\rm [Fe/H]}\approx0$ and slightly negative values of [hs/ls]. These stars can be fitted with any value of  $^{13}{\rm C}_{\rm eff}$. The diagonal crosses in Fig. 4 are halo C stars suspected to be intrinsic. They are not expected to follow the same AMR as those in the galactic disk, but the fact that they are old and of low mass is approximately modelled by our AMR. Three of these stars are matched by our models for values of $^{13}{\rm C}_{\rm eff}\ga2/3$, but a lower $^{13}{\rm C}_{\rm eff}$ cannot reproduce their [hs/ls]. The lack of stars below [Fe/H$] \sim-1$ in our models is due to the fact that, with our adopted AMR, lower metallicity stars do not become TP-AGB stars within the age of the Universe. This effect is observed in all our results involving intrinsic stars and is consistent with the observations.

   
4.1.3 [hs/ls] ratios of post-AGB stars
Post-AGB stars are in the fast evolutionary phase between the AGB and white dwarf track. They suffer from strong mass loss and are hot, but not hot enough to ionize their circumstellar medium. We select them from our models by choosing those s-enhanced TP-AGB stars that have less than 0.03 $M_{\odot }$ left in their envelopes. We compare our synthetic population to the observational data gathered by Busso et al. (2001), van Winckel (2003), Reyniers et al. (2004), and Giridhar & Arellano Ferro (2005). Figure 5 shows a spread, mostly at high metallicities, which is due to the different initial stellar masses taken into account in our population synthesis, the range of which becomes narrower towards low metallicities as we follow the AMR. Stars with $M\la 1.5~M_{\odot}$ experience a small number of TDU episodes. After their last thermal pulse (when they are observed as post-AGB stars) they have not yet reached the asymptotic [hs/ls] ratio, which contributes to the spread observed. Most of the data can be fitted with $2/3\la {^{13}{\rm C}}_{\rm eff}\la4/3$, within the observational errors. There is only one exception at [Fe/H$] \sim-1$, which apparently needs a somewhat smaller $^{13}{\rm C}_{\rm eff}$. This object, IRAS07134+1005, has a very high heliocentric velocity (Van Winckel & Reyniers 2000) suggesting that it belongs to the galactic halo rather than the galactic disk.

   
4.1.4 Zr and C abundances of post-AGB stars

Post-AGB stars can also be used to provide constraints on the minimum core mass for TDU, the TDU efficiency, and the size of the 13C pocket. The observed values of [Zr/Fe] show a bimodal distribution: ${\rm [Zr/Fe]}\approx0$ and $1\la{\rm [Zr/Fe]}\la2$, which suggests that some post-AGB stars did not experience TDU, while others did and suffered a strong enhancement of Zr (van Winckel 2003). This can be explained when we consider low mass stars ( $M\la 1.5~M_{\odot}$) at sub-solar metallicities. They have low-mass envelopes which easily become strongly s-enhanced. As shown in Fig. 6, only one TDU episode after the intershell material has become s-enriched is enough to raise their envelope abundance ratios by almost 1 dex. We compare the observational [Zr/Fe] ratios of van Winckel (2003), Reyniers et al. (2004) and Giridhar & Arellano Ferro (2005) to our models, from which we consider all post-AGB stars, both s-enhanced and not s-enhanced.


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{6861fig6.eps} \end{figure} Figure 6: Enhancement of Zr in TP-AGB stars as function of time. The models shown are for [Fe/H] =-0.5, with initial masses as indicated in the figure. When the stars reach the post-AGB phase, i.e., by the end of their evolution, there is a strong Zr enhancement ($\sim $1 dex) as long as at least one s-enriched dredge-up episode has taken place. If no dredge-up occurs there is no enhancement at all, as seen in the case of the 1 $M_{\odot }$ star.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{6861fig7.eps} \end{figure} Figure 7: Ratio of the number of s-enhanced post-AGB stars which have ${\rm C/O}<1$ ( $N_{s,{\rm noC}}$) to the number of s-enhanced post-AGB stars (Ns) from our synthetic models. The curves show the ratios calculated with different values of $\lambda _{\rm min}$, as indicated in the figure. The straight dash-dotted and double-dotted lines show the upper limit to the $N_{s,{\rm noC}}/N_{s}$ ratio at [Fe/H $]~{\protect\la}~-0.3$, with a confidence of 68% and 95%, respectively, given the distribution of the observed data.
Open with DEXTER

Intrinsically s-enhanced post-AGB stars are observed at metallicities as low as ${\rm [Fe/H]}\sim-1.0$(van Winckel 2003). When taking into account the AMR, this implies that at metallicities [Fe/H$] \la-0.7$stars with initial masses above 0.9 $M_{\odot }$ must experience TDU. At [Fe/H$] \la-0.3$, the observed number of s-enhanced stars (which experienced TDU) is comparable to that of stars with ${\rm [Zr/Fe]}\approx0$ (which did not undergo TDU). Thus, taking into account the IMF and the initial mass range given by the AMR at low metallicities, we estimate the minimum initial mass at which TDU must take place so that the number of s-enhanced stars is similar to that of non-enhanced stars. Applying this in our models, we find the corresponding minimum core mass for TDU as a function of metallicity. The resulting relation between minimum core mass and metallicity is best modelled by the fitting formula of Karakas et al. (2002), with an offset $\Delta M_{\rm c}^{\rm min}= -0.065~M_{\odot}$. This outcome depends somewhat on the adopted age-metallicity relation that sets the initial mass range of TP-AGB stars at each metallicity (Fig. 1), but the sensitivity of the mass of a low-mass star to its lifetime is only slight. Our result depends more strongly on the choice of mass loss. To test this we applied different mass-loss rates on the TP-AGB with the prescription of Reimers (1975), Eq. (5), by varying the coefficient $\eta_{\rm GB}$from 0.5 to 3.0, and find that $0.055\la\Delta M_{\rm c}^{\rm min}\la0.075$. This result is consistent with the findings of, e.g., Groenewegen & de Jong (1993), Marigo et al. (1999), Izzard et al. (2004), and Stancliffe et al. (2005) when studying the carbon star luminosity functions of the Small and Large Magellanic Clouds.

We now address the question of how much intershell material is dredged up to the surface. The surface s-process enhancement in our models is controlled by the dredge-up efficiency ($\lambda$) and by the fractional mass of the 13C pocket relative to the intershell ( $f_{{\rm ^{13}C,IS}}$). The carbon enrichment in the envelope depends only on the amount of dredge-up, independent of the size of the 13C pocket. The observations show that below [Fe/H $] \sim-0.3$ all s-enhanced post-AGB stars have C/O >1 and that the non-enhanced ones have C/O <1 (van Winckel 2003). We use this information to break the degeneracy between $\lambda$ and $f_{{\rm ^{13}C,IS}}$. Let $N_{s{\rm ,noC}}$ be the observed number of s-enriched post-AGB stars that have C/O <1 and Ns be total number of s-enriched post-AGB objects. Figure 7 illustrates the ratio $N_{s{\rm ,noC}}/N_{s}$as a function of metallicity calculated with our models for different values of $\lambda _{\rm min}$. With a simple application of Bayesian statistics we calculate that, given the observed data distribution, $N_{s{\rm ,noC}}/N_{s}=0$ and Ns=11, there is a 32% probability that $N_{s{\rm ,noC}}/N_{s}>0.09$ and only a 5% probability that $N_{s{\rm ,noC}}/N_{s}>0.23$. The latter sets the 95% confidence limit $\lambda_{\rm min}\ga0.2$, as shown in Fig. 7. With this lower limit we calibrate $f_{{\rm ^{13}C,IS}}$to fit the Zr enhancement of post-AGB stars. Figure 8 shows our population synthesis results for the [Zr/Fe] ratio calculated with different values of $\lambda _{\rm min}$ and $f_{{\rm ^{13}C,IS}}$, compared to the observations. The upper left panel shows our results for $\lambda_{\rm min}=0$. With this choice there are no s-enhanced post-AGB stars at low metallicities ( ${\rm [Fe/H]}\la-0.4$) since these would all be low-mass stars due to the AMR and they experience negligible dredge-up. This is in contradiction to the observations. Moreover, as shown above (Fig. 7), a choice of $\lambda_{\rm min}<0.2$ is not compatible with the number of carbon enhanced stars. If we choose $\lambda _{\rm min}=0.2$ (upper right panel) then low-metallicity s-enhanced post-AGB stars are indeed produced. The large spread in the s-enhancement at higher metallicities is due to stars with mass $M\ga3~M_{\odot}$. However, the choice $f_{\rm ^{13}C,IS}=0.05$, which roughly corresponds to that used by Gallino et al. (1998) for their detailed nucleosynthesis calculations, gives too much Zr for many of the s-enhanced post-AGB stars with ${\rm [Fe/H]}\la-0.5$. The lower right panel shows that most of the observations can be reproduced with $\lambda _{\rm min}=0.2$ and $f_{\rm ^{13}C,IS}\approx 1/40$, with two exceptions which are extremely s-enhanced. From the constraint that all s-enhanced post-AGB stars are carbon stars, there is a 68% confidence lower limit on $\lambda _{\rm min}$of 0.4. This implies that $f_{\rm ^{13}C,IS}\approx 1/100$ is needed to fit the post-AGB observations (lower right panel of Fig. 8). However, this choice of $f_{{\rm ^{13}C,IS}}$gives synthesized [ls/Fe] and [hs/Fe] ratios which are too small to reproduce those observed in MS/S, SC, and C stars. Figure 9 shows a comparison of the observed [ls/Fe] and [hs/Fe] of MS/S, SC, and C stars to our models, calculated with $\Delta M_{\rm c}^{\rm min}= -0.065~M_{\odot}$, $\lambda _{\rm min}=0.2$, $f_{\rm ^{13}C,IS}=1/40$and $^{13}{\rm C}_{\rm eff}=4/3$. Most of the MS/S star abundances are fitted within the errors, with two high-metallicity exceptions that are only matched with a larger choice of $^{13}{\rm C}_{\rm eff}$ or $f_{{\rm ^{13}C,IS}}$. The s-process abundances of most of the SC and C stars in the galactic disk are also matched well using the same choice of free parameters, except for three low metallicity objects that need a smaller $^{13}{\rm C}_{\rm eff}$.

From the combined evidence of MS/S, SC, C, and post-AGB stars, we find that with a few exceptions, all observations of intrinsic s-enhanced stars can be matched by models with the following set of parameters:

However, the constraints we have set here depend somewhat on our choice of other rather uncertain parameters, namely the mass-loss rate and age-metallicity relation (see Sect. 5).


  \begin{figure} \par\includegraphics[width=16.5cm,clip]{6861fig8.eps} \end{figure} Figure 8: Post-AGB stellar population synthesis results compared to the observations. The grey scale is a logarithmic measure of the normalized number distribution of stars in the [Zr/Fe]-[Fe/H] plane for $^{13}{\rm C}_{\rm eff}=2/3$. As indicated above the panels, plots are presented for different values of  $\lambda _{\rm min}$ and $f_{{\rm ^{13}C,IS}}$. The crosses are the observational data (see references in the text), which have an average error given by the size of the cross in the upper right of each plot.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=16.5cm,clip]{6861fig9.eps} \end{figure} Figure 9: Stellar population synthesis results of MS/S stars ( top panels) and SC/C stars ( bottom panels) compared to the observations. The grey scale is a logarithmic measure of the normalized number distribution of stars in the [ls/Fe]-[Fe/H] plane ( left panels) and the [hs/Fe]-[Fe/H] plane ( right panels), using $^{13}{\rm C}_{\rm eff}=4/3$ (as derived in Sects. 4.1.1 and 4.1.2), $\lambda _{\rm min}=0.2$ and $f_{{\rm ^{13}C,IS}}=0.025$. The observational data are from the same references and with the same coding as those of Figs. 3 and 4, which have an average error given by the size of the cross in the upper right of each plot.
Open with DEXTER

   
4.2 Extrinsic s-enhanced stars


  \begin{figure} \par\includegraphics[width=16.5cm,clip]{6861fg10.eps} \end{figure} Figure 10: Population synthesis results for single-star yields compared to observations of extrinsic s-enhanced stars for different values of 13C $_{\rm eff}$. The grey scale is a normalized logarithmic distribution of [hs/ls] for a population of stars as a function of metallicity. The symbols indicate observed data from different stellar types and references as follows: + MS/S stars; $\times $ Ba II giants; $\Diamond $ CH sub-giants; $\square $ CH giants; $\blacksquare $ C giant; $\blacktriangledown $ halo CH giant; $\medbullet $ halo yellow symbiotic; $\triangle $ halo C-rich giant; $\blacktriangle $ halo C-rich sub-giant; $\triangledown $ halo N-rich dwarf, all previous gathered by Busso et al. (2001); $\medcirc $ C stars from Abia et al. (2002); $\Diamondblack $ lead stars gathered by Bisterzo et al. (2006). The observed data have an average error given by the size of the upper right cross in each plot.
Open with DEXTER

Extrinsic s-enhanced stars can be in any evolutionary stage prior to the TP-AGB phase, but they are mainly giants and main sequence stars. Their absolute s-process abundances cannot be studied without complete binary evolution models, but the abundance ratios of s-process elements are not substantially affected by binary processes. The [hs/ls] ratio represents that of the former TP-AGB companion which produced the s-process elements and it can be reasonably approximated by taking into account the yields of single stellar evolution models. Figure 10 shows a comparison of our synthetic [hs/ls] ratios to the extrinsic star data from Busso et al. (2001), Aoki et al. (2002), Abia et al. (2002) and van Eck et al. (2003). Similar to our results for intrinsic stars, the spread observed in these results is due to the range of initial masses that we use, although, in this case the mass range is wider and includes AGB stars up to 7-8 $M_{\odot }$. An AGB star of $M\ga5~M_{\odot}$ has a very thin intershell and a massive envelope, so its surface [hs/ls] ratio varies smoothly between its value in the intershell and the solar ratio.

We focus first on the galactic disk ( ${\rm [Fe/H]}\ga -1$) stars. Figure 10 shows that no single choice of $^{13}{\rm C}_{\rm eff}$ value can make our results fit all the observational data, but almost all observations can be fitted with a range of values $2/3\la {^{13}{\rm C}}_{\rm eff}\la4/3$. This is consistent with what we found for the intrinsic s-enhanced stars (see Sect. 4.1).

For ${\rm [Fe/H]}\la -1$, our synthetic [hs/ls] ratios are relatively insensitive to changes in $^{13}{\rm C}_{\rm eff}$ because the hs-element synthesis saturates, opening the way to the synthesis of lead. There is some indication that a smaller value of $^{13}{\rm C}_{\rm eff}$ is needed to reproduce objects with [Fe/H$] \la-2$ which have a high [hs/ls], but even when using small $^{13}{\rm C}_{\rm eff}$values [hs/ls] does not exceed about 1 dex. Thus we are unable to explain the extreme low-metallicity objects with ${\rm [hs/ls]}\ga1.2$. Our synthetic calculations do not extend below [Fe/H] <-2.3 because of the lack of detailed models with metallicity below this value.

4.2.1 Lead stars
Lead stars have an enhanced lead abundance and are found at low metallicities. As discussed above, the [hs/ls] ratio remains roughly constant at low metallicities due to the saturation of the ls- and hs-element synthesis, which indicates that lead is being synthesized (Gallino et al. 1998). Consequently, the ratio of Pb to hs-elements is sensitive to the choice of $^{13}{\rm C}_{\rm eff}$. We use [Pb/hs] data gathered by Bisterzo et al. (2006) to compare with our synthesis results. In the [Pb/hs] vs. [Fe/H] plane (Fig. 12) we see that our results show a pattern that shifts in metallicity if $^{13}{\rm C}_{\rm eff}$ is varied, similar to the shift in [hs/ls] pattern at higher metallicities. The reason for this behaviour is the change in ratio of the number of free neutrons to the number of seed nuclei, as explained in Sect. 4.1.1. We find that also for [Pb/hs] a spread naturally arises in our population synthesis results. This spread is mostly due to the fact that, as discussed by Gallino et al. (1998) (see their Fig. 6), the neutron exposure in the 13C pocket decreases with pulse number. This effect is even more pronounced at lower metallicities, causing the [Pb/hs] ratio to shift to much lower values as the evolution proceeds. This is illustrated by the models computed by Busso et al. (2001), shown in Fig. 11. As a consequence, there are two ridges of high probability in the model results shown in Fig. 12. One follows the higher [Pb/hs] values and corresponds to the contribution of low-mass stars (about 1 $M_{\odot }$), which is high due to their large IMF weight. The other ridge, which follows intermediate values, is the contribution of stars with masses around 2.5 $M_{\odot }$. Despite their smaller IMF weight, the ejecta of these stars are massive enough to make their contribution comparable to that of the low-mass stars. This effect is also visible in our synthetic [hs/ls] results, e.g., in the top panels of Fig. 10. Most observations are fitted by the contribution of $\sim $ $2.5~M_{\odot}$ stars when choosing $^{13}{\rm C}_{\rm eff}\approx1/3$ (lower left panel in Fig. 12), except for two outliers which have ${\rm [Pb/hs]<0}$. These outliers, however, have large error bars which extend to ${\rm [Pb/hs]\approx0}$(van Eck et al. 2003). The upper left panel in Fig. 12 shows that a value of $^{13}{\rm C}_{\rm eff}$ as small as 1/12 still marginally fits the low-metallicity stars ( ${\rm [Fe/H]}\la -2$). On the other hand, a choice of $^{13}{\rm C}_{\rm eff}\approx2/3$ results in too large [Pb/hs] values (lower right panel in Fig. 12). This result reaffirms our results for the extrinsic-star [hs/ls] values which suggest that a somewhat smaller value of $^{13}{\rm C}_{\rm eff}$ is needed to fit low-metallicity halo stars compared to those in the galactic disk. This is also consistent with what we found in Sect. 4.1.3, regarding the object IRAS07134+1005.

As stated above our calculations do not extend below ${\rm [Fe/H]}<-2.3$, but we notice that lead stars with lower metallicity could also be explained if the trend shown by our models continues at lower metallicities. This seems likely because [Pb/hs] does depend mostly on $^{13}{\rm C}_{\rm eff}$ and not on other uncertain parameters in our models, however, explaining those stars at ${\rm [Fe/H]}<-2$ which show ${\rm [hs/ls]}\ga1.2$ is still a problem.

Finally, we note that Cui & Zhang (2006) also presented a possible solution to explain the spread of [Pb/hs] observed in low-metallicity stars. These authors obtained a spread of neutron exposures (and hence [Pb/hs]) in low-metallicity AGB stars due to variations of the inter-pulse period in stars of different masses. Their results are based on the assumption that the neutron irradiation time is proportional to the inter-pulse period. However, this assumption is incorrect since the neutron irradiation time depends instead on the timescale at which the ${\rm ^{13}C}(\alpha,n)^{16}{\rm O}$ reactions occur. At the temperature of 108 K that Cui & Zhang (2006) use in their models, the timescale for $\alpha$ captures is of the order of 300 yr (see Fig. 2 of Gallino et al. 1998), and this is independent of the inter-pulse period. In our models, instead, the spread in [Pb/hs] derives naturally from the fact that the neutron exposure changes with time, especially at low metallicities.

   
5 Conclusions and discussion

Based on the results of our population synthesis study, we find that it is not possible to reproduce the observed heavy-element abundances of s-enhanced stars with the standard set of values for the free parameters in our AGB models. The minimum core mass for TDU has to be reduced by at least 10 per cent with respect to what theoretical models predict; low-mass stars must have a significant TDU efficiency and the 13C pocket mass must be somewhat lower than what is usually considered standard. We also find that the observations can be matched with a narrow range of $^{13}{\rm C}_{\rm eff}$ values and that the mean $^{13}{\rm C}_{\rm eff}$ value in this range apparently decreases with metallicity.

The observations in the metallicity range ${\rm [Fe/H]}\ga -1$ are fitted well by $2/3\la {^{13}{\rm C}}_{\rm eff}\la4/3$, i.e., a spread of a factor of 2, while Busso et al. (2001) needed a factor of $\sim $20. This is a consequence of the natural spread that we find in the s-process element ratios caused mainly by the truncation of AGB evolution due to the total loss of the stellar envelope. Stars with initial mass $M\la 1.5~M_{\odot}$ start the TP-AGB phase with a relatively similar core mass, but different envelope mass. Consequently, a star with a certain low mass will experience fewer thermal pulses than one with a slightly higher mass, which affects its yields and composition during its life as a TP-AGB star. A different choice of mass loss in our models, either during the red giant branch or the AGB phase, would move the mass range in which this effect takes place, but not eliminate it.

At ${\rm [Fe/H]}\la -1$ a spread in [Pb/hs] arises because of the shift in the neutron exposure. Observations at these lower metallicities need a somewhat lower value $^{13}{\rm C}_{\rm eff}\approx1/3$, perhaps down to $\approx$1/12. This result may be due to the increasingly important effect of $\alpha$-enhanced light neutron poisons at low metallicities (Busso et al. 1999), which needs to be investigated in more detail.

  \begin{figure} \par\includegraphics[width=8cm,clip]{6861fg11.eps} \end{figure} Figure 11: [Pb/hs] during the evolution of 1.5 $M_{\odot }$ and 3 $M_{\odot }$ models of [Fe/H]=-2.3 with 13C $_{\rm eff}=1/3$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=16.5cm,clip]{6861fg12.eps} \end{figure} Figure 12: [Pb/hs] results from our population synthesis of lead stars, shown in the same way as in Fig. 10 and compared to the data gathered by Bisterzo et al. (2006). The upper right cross shows the average error of the data points.
Open with DEXTER

It is reassuring that our conclusion of a small spread in $^{13}{\rm C}_{\rm eff}$ is reached independently by the study of isotopic s-process signatures in pre-solar silicon carbide (SiC) grains from carbon stars. While Lugaro et al. (2003) needed a spread of $\sim $24 in the values of $^{13}{\rm C}_{\rm eff}$ to cover the SiC data, by eliminating the effect of contamination of solar material, more recent laboratory studies (Marhas et al. 2007; Barzyk et al. 2007) have also reduced the spread of the $^{13}{\rm C}_{\rm eff}$ values needed to cover the grain data to exactly the same range we found here. Although pre-solar grains can only give us information on the s-process taking place in stars with ${\rm [Fe/H]}\ga -1$, such an independent check also gives us confidence in our results at lower metallicities.

Now the question arises as to whether the small spread that we find is compatible with the possible mechanisms currently proposed for the proton diffusion leading to the formation of the 13C pocket. We note that semi-convection (Hollowell & Iben 1988), hydrodynamical overshooting (Herwig et al. 1997), and gravity waves (Denissenkov & Tout 2003), which are three out of the four proposed mechanisms, produce a proton profile with the number of protons varying continuously from the envelope value to zero. The possible shapes of the proton profile were discussed by Goriely & Mowlavi (2000,  see their Fig. 10), who concluded that "the s-process predictions are only weakly dependent on the shape of the H-profile''. Hence we would not expect a wide range of neutron exposures to occur in the current scenario. Future work should quantitatively link the shape of the proton profile to the range of $^{13}{\rm C}_{\rm eff}$ we found in this study. The fourth process proposed for the formation of the $^{13}{\rm C}$ neutron source is rotation (Herwig et al. 2003; Langer et al. 1999). Also in this case the formation of the $^{13}{\rm C}$ pocket starts from a continuous proton profile; however, current models find that further mixing during the inter-pulse period completely inhibits the s-process (Herwig et al. 2003; Siess et al. 2004). Future work is needed to ascertain this point.

To explain the existence of Galactic post-AGB stars that are s-process enhanced at [Fe/H$] \sim-1$, we find that the minimum core mass for TDU must be 0.055-0.075 $M_{\odot }$ smaller than that found in the models of Karakas et al. (2002) and Stancliffe et al. (2004). This is consistent with the findings of several authors who studied the carbon-star luminosity functions of the SMC and LMC (e.g., Groenewegen & de Jong 1993; Marigo et al. 1999; Izzard et al. 2004; Stancliffe et al. 2005) and sets a strong constraint on future detailed evolutionary model results.

We find that to account for the fact that all 11 Zr-enhanced post-AGB stars observed so far are also C enhanced, $\lambda_{\rm min}\ga0.2$ in stars of mass $M\la 1.5~M_{\odot}$. The precise value of this lower limit may depend somewhat on our adopted choices for mass loss, the AMR, and the minimum core mass for TDU. We leave a detailed analysis of this dependence for future study. However, it is clear from our results that a value of $\lambda=0$ cannot reproduce the observations, and we are therefore confident in concluding that stars of mass $M\la 1.5~M_{\odot}$must experience a significant amount of TDU.

The amount of Zr enhancement in post-AGB stars is determined by the amount of third dredge-up and the size of the 13C pocket. Assuming $\lambda _{\rm min}=0.2$ indicates that in our models the 13C pocket must have a mass of 1/40 of that of the intershell to fit the observed data from Zr-enhanced post-AGB stars. This is somewhat smaller than the size of the 13C pocket assumed in the models of Gallino et al. (1998), which is about 1/20 of the mass of the intershell.

Future detailed modelling of AGB stars will need to address the constraints we have set here. We are currently extending our analysis of extrinsic s-enhanced stars by means of binary population synthesis, i.e., by explicitly following the evolution and interaction processes of populations of binary stars.

Acknowledgements
The authors are deeply indebted to Roberto Gallino for providing the data from his detailed nucleosynthesis models and for insightful discussions and comments on this work. A.B.M. thanks Maarten Reyniers and Hans van Winckel for useful discussions and for providing data on post-AGB stars. A.B.M. also thanks Selma de Mink for refreshing his knowledge of statistical analysis. R.G.I. is supported by NWO. M.L. is supported by NWO (VENI fellow).

References

 

  
Online Material

   
Appendix A: Details of the synthetic TP-AGB model

Hurley et al. (2000, hereafter H00) have developed a comprehensive synthetic evolution code for single stellar evolution, based on detailed models of Pols et al. (1998, hereafter P98). The P98 models include convective core overshooting, but do not undergo thermal pulses during the AGB phase. To model TP-AGB stars, H00 apply the same luminosity-core mass relation as in the early (E-) AGB phase. The TP-AGB section of the H00 code was improved by Izzard et al. (2004, hereafter I04) with a synthetic code based on the detailed model calculations by Karakas et al. (2002, hereafter K02) that undergo thermal pulses. The latest version (Izzard et al. 2006) also follows the nucleosynthesis of many s-process isotopes based on the models of Gallino et al. (1998).

However, unlike the P98 detailed models, the K02 detailed models do not include convective overshooting. This means that the transition from the E-AGB to the TP-AGB phase is not self-consistent in the I04 code, leading to discontinuities in the evolution of the stellar core mass, of the luminosity, and of the radius of the AGB star. To overcome these problems, we have made modifications to the I04 code, which are explained in detail below.

A.1 TP-AGB initial H-depleted core mass

For an AGB star to enter the TP-AGB phase, its helium intershell mass must be small enough to undergo a flash. This occurs at the end of the E-AGB phase when the helium-burning shell almost reaches the hydrogen-burning shell. In our code the H-depleted core mass at the beginning of the TP-AGB phase, $M_{\rm c,1TP}$, is given by the mass of the H-depleted core at the base of the AGB, $M_{\rm c,BAGB}$. However, stars with $M_{\rm c,BAGB} \sim0.8~M_{\odot}$ and larger undergo second dredge-up by the end of the E-AGB phase, which makes $M_{\rm c,1TP}<M_{\rm c,BAGB}$.

When convective overshooting is taken into account, the value of $M_{\rm c,1TP}$ for a star with a given initial mass is higher than that of a star with the same initial mass without overshooting. The effects of overshooting become important in AGB stars of $M\ga 2.5~M_{\odot}$[*], having a direct impact on the subsequent evolution.

We have improved the linear relation between $M_{\rm c,BAGB}$ and $M_{\rm c,1TP}$ from H00 (denoted as $M_{\rm c,DU}$ in that paper) with a quadratic one, based on data from the P98 models (hereafter OV):

$\displaystyle M_{\rm c,1TP,OV}=9.292\times10^{-2}M_{\rm c,BAGB} \times (M_{\rm c,BAGB}+1.983) +5.865\times10^{-1},$     (A.1)

in solar units. This fit is not very good for stars with $M\la 1.5~M_{\odot}$, but in these the effects of overshooting become negligible and the fit to the K02 models ( $M_{\rm c,1TP,K02}$) is appropriate, so we instead use
$\displaystyle M_{\rm c,1TP}={\rm max}\Big[{\rm min}\big(M_{\rm c,1TP,OV},M_{\rm c,BAGB}\big), ~~ M_{\rm c,1TP,K02}\Big].$     (A.2)

Figure A.1 shows a luminosity-core mass plot where the core-mass prescriptions of the different synthetic models can be compared.

A.2 CO core mass and luminosity on E-AGB phase


  \begin{figure} \par\includegraphics[width=8cm,clip]{6861fgA1.eps} \end{figure} Figure A.1: Luminosity-core mass relation of a 3 $M_{\odot }$ star with metallicity Z=0.01. The arrows show the way in which the core evolves in time. During the E-AGB phase, the hydrogen-exhausted core mass remains constant at 0.716 $M_{\odot }$. In our model the core mass at the start of the TP-AGB is the same as in the H02 model, which is greater than in the I04 model.


  \begin{figure} \par\includegraphics[width=8cm,clip]{6861fgA2.eps} \end{figure} Figure A.2: Evolution of luminosity in time of the same star as in Fig. A.1. The E-AGB evolution is slightly modified in our model and the discontinuity in luminosity is fixed.

As in H00, we model the luminosity during the E-AGB phase with a power-law relation of the form $L_{\rm E-AGB}=l_1M_{\rm CO}^{l_2}$, where $M_{\rm CO}$ is the mass of the CO core during the E-AGB phase. The coefficients l1 and l2 are found from the values of $L_{\rm E-AGB}$ and $M_{\rm CO}$ at the beginning and at the end of the E-AGB phase.

For the beginning we use Eq. (56) from H00 for the luminosity at the base of the AGB and the following relation for $M_{\rm CO}$ at the base of the AGB

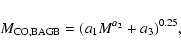\begin{displaymath}M_{\rm CO,BAGB}=(a_1M^{a_2}+a_3)^{0.25}, \end{displaymath} (A.3)

which fits the data from the P98 detailed models, expressed in solar units. The coefficients depend on metallicity and are calculated with the formula

 \begin{displaymath}a_i=a_{i,1}+{\rm [Fe/H]}{\big(}a_{i,2}+{\rm [Fe/H]}(a_{i,3}+{\rm [Fe/H]}a_{i,4}){\big)}, \end{displaymath} (A.4)

where ai,j are the dimensionless coefficients listed in Table A.1.

For a smooth transition to the TP-AGB phase, we require

\begin{displaymath}M_{\rm CO,end}=M_{\rm c,1TP}~~~{\rm and}~~~L_{\rm E-AGB,end}=L_{\rm 1TP}, \end{displaymath} (A.5)

where $M_{\rm CO,end}$ and $L_{\rm E-AGB,end}$ are the CO core mass and the luminosity at the end of the E-AGB phase, respectively. The luminosity at the beginning of the TP-AGB phase, $L_{\rm 1TP}$, is discussed in Sect. A.3. A comparison between the time evolution of the luminosity described by the different synthetic models is shown in Fig. A.2.

Table A.1: Coefficients ai,j for Eq. (A.4).


  \begin{figure} \par\includegraphics[width=15cm,clip]{6861fgA3.eps} \end{figure} Figure A.3: Examples of our analytic fit (solid lines) compared to the data from the detailed models (dashed lines) from Stancliffe et al. (2004) for different stellar masses and metallicities, as indicated in the panels.

   
A.3 Luminosity during the TP-AGB phase

Following Paczynski (1970), it has become the usual practice to apply a linear luminosity-core mass relation in synthetic AGB models. However, this relation fails in the presence of dredge-up and hot bottom burning. This becomes a problem when comparing models that include overshooting to models that do not: two TP-AGB stars with the same core mass, but different envelope mass, do not behave in the same way. To overcome this we designed a luminosity relation that depends on both the core mass and the envelope mass of the star. It successfully reproduces both the P98 models that include overshooting and models calculated with the same code used by P98, which do not include overshooting. Stancliffe et al. (2004, hereafter S04) employed a modified version of the code used by P98 and computed detailed models that do not include overshooting, but do undergo thermal pulses. In an attempt to make our rapid TP-AGB models more self-consistent, we have modified our luminosity relation to fit the S04 models, assuming that with the inclusion of overshooting the S04 models are modified in the same way as those of P98. In addition to this, we find that in the presence of third dredge-up the results of the detailed stellar evolution models are better represented by relating the luminosity to  $M_{\rm c,NODUP}$, the core mass as it would be in the absence of dredge-up:

 
        $\displaystyle \log_{10}(L_{\rm c,NODUP})$ = $\displaystyle \Bigg(\log_{10}(15300+9440Z)$  
    $\displaystyle +\frac{3.45~\log_{10} (M_{\rm c,NODUP}+0.1)} {3M_{\rm c,NODUP}-M_{\rm c,1TP}}\Bigg)$  
    $\displaystyle \times\left(\frac{M_{\rm c,1TP}}{M_{\rm c,NODUP}}\right)^{0.045}+0.08,$ (A.6)

in solar units and where Z is the metallicity. In stars with a massive convective envelope ( $M_{\rm env}\ga2.5~M_{\odot}$), the temperature at the bottom of the envelope is high enough for hot bottom burning (HBB), which enhances the luminosity of the star by a factor  $f_{\rm HBB}$ due to the enhanced hydrogen abundance in the H-burning shell. The expression
 
$\displaystyle \log_{10}(f_{\rm HBB})= \max\Bigg\{1.3~\log_{10}\left[ \frac{M_{\rm env,1TP} (1-0.53~{\rm [Fe/H]})}{M_{\rm env,HBB}}\right] -0.08~,~0\Bigg\}$     (A.7)

fits $f_{\rm HBB}\times L_{\rm c,NODUP}$ to the luminosity of the S04 models, where $M_{\rm env,1TP}$ is the mass of the envelope at the beginning of the TP-AGB, and we set the threshold mass for the onset of HBB $M_{\rm env,HBB}=2.4~M_{\odot}$.

The S04 models have no mass loss, so we have to use a different set of models to fit the behaviour of the luminosity in terms of the loss of the envelope mass. Based on the K02 models, the contribution of the envelope to the luminosity can be modelled as

 
$\displaystyle \log_{10}(f_{\rm env})= \max\Bigg\{\log_{10}(f_{\rm HBB}) +\left.... ...10}~\left(\frac{M_{\rm env}} {M_{\rm env,1TP}}\right),0\right]~,~0\right\}\cdot$     (A.8)

The expression $f_{\rm env}\times L_{\rm c,NODUP}$matches the asymptotic behaviour of the luminosity observed in the S04 detailed models, which is reached after several pulses. To model the first few pulses, we write the luminosity as

 \begin{displaymath} L=\left[\frac{L_{\rm c,NODUP}\times f_{\rm env}} {L_{\rm TP1}}\right]^{f}L_{\rm TP1}, \end{displaymath} (A.9)

where $L_{\rm TP1}$ is fitted to the S04 models with the expression

 \begin{displaymath} \log_{10}(L_{\rm TP1})=-1.8427M_{\rm c,TP1}^2+5.3861M_{\rm c,TP1}+0.97823, \end{displaymath} (A.10)

and

 \begin{displaymath} f=1- \left[1-\frac{M_{\rm c,NODUP}-M_{\rm c,1TP}}{0.075}\right]^{25/3} \end{displaymath} (A.11)

accounts for the luminosity growth during the early pulses to its asymptotic value $L_{\rm c,NODUP}\times f_{\rm env}$. In Eqs. (A.10) and (A.11), all quantities are expressed in solar units. Figure A.3 shows a comparison between our fit and the S04 detailed models. In the worst cases, our fits have an error smaller than 10% in luminosity, which is less than the difference between the S04 and K02 detailed models.

A.4 Radius during TP-AGB phase

We use the H00 radius-luminosity relation, given that it accurately fits the S04 models, but we have modified the interpolation procedure slightly. The H00 radius-luminosity relation (Eq. (74) in that paper) was designed to fit the P98 models at seven different metallicities in the following way:

 \begin{displaymath}R_{\rm AGB}=A(L^{b_1}+b_2L^{b_3}), \end{displaymath} (A.12)

where L is the luminosity, A depends on the mass and bi, on the metallicity. For intermediate metallicities the radius was calculated after interpolating linearly in Z between the coefficients that fit these seven metallicities. Some of these coefficients are exponents, and we found the results for interpolated metallicities to behave erratically. We therefore interpolate linearly in Zbetween the radius values calculated with Eq. (A.12) for the adjacent known metallicities, which is in much better agreement with detailed models at intermediate metallicities calculated with the same code as used by P98.


Copyright ESO 2007