A&A 469, 839-842 (2007)
DOI: 10.1051/0004-6361:20066743
Theoretical explanation of the large observed cosmic ray parallel mean free paths in the solar system
A. Shalchi
Institut für Theoretische Physik, Lehrstuhl IV:
Weltraum- und Astrophysik, Ruhr-Universität Bochum,
44780 Bochum, Germany
Received 14 November 2006 / Accepted 12 April 2007
Abstract
In recent observations large parallel mean free paths of charged cosmic rays which interact with the solar wind plasma
have been discovered. The traditional approach to reproduce these measurements theoretically is the assumption that
a large part of the magnetic fluctuations is in so-called 2D modes which are expected to be ineffective in scattering. By considering
very recent results of particle scattering studies is is argued in this article that the assumption that 2D modes are ineffective in scattering is ruther questionable. By replacing
the standard form of the wavespectrum of the magnetic fluctuations by a more realistic model an alternative explanation of
observed cosmic ray parallel mean free paths in the solar system is provided by this article.
Key words: Sun: solid wind - turbulence - diffusion - scattering - elementary particles
It is one of the fundamental problems of modern cosmic ray physics to understand the mechanism by which
energetic charged particles scatter in turbulent magnetic fields. Fitting cosmic ray observations to transport
models, expecially in solar energetic particle events, has allowed us to determine representative values
of the mean free path parallel to the magnetic field of the sun and has given some indications of how the parallel
mean free path varies with particle energy (Palmer 1982; Bieber et al. 1994; Dröge 2000).
The first theoretical description of particle transport in the solar wind has been achieved by applying the so-called
standard quasilinear theory (SQLT, Jokipii 1966).
Within SQLT a quasilinear transport theory is combined with a magnetostatic slab model, in which the turbulence
is assumed to be time-independent and in which the wavevectors of the turbulent fluctuations are aligned with
the mean magnetic field (magnetic field of the sun). Nearly 20 years later, Palmer (1982) compared
SQLT predictions with observations mainly obtained within the HELIOS 2 mission. Palmer concluded that the
theoretical results of the parallel mean free path are much smaller than the observations. The years after this
discrepancy has been discovered several modifications have been formulated to solve this problem.
One of the most prominent suggestions has been proposed by Bieber et al. (1994) who argued that the simple
magnetostatic slab model used in SQLT has to be replaced by a dynamical turbulence model in combination
with a slab/2D composite model which can be confirmed by solar wind observations (Bieber et al. 1996).
By additionally using a wave spectrum with dissipation-range Bieber et al. (1994) were indeed
able to reproduce the so-called Palmer consensus range which is the band or box shown in Fig. 3
representing the heliospheric observations. In the following years most space scientists concentrated on the
formulation of a transport theory for perpendicular diffusion of cosmic rays. Due to the compound diffusion character
(parallel diffusion has a strong influence onto perpendicular transport) the most of these theories had a nonlinear
structure. E.g. within the nonlinear guiding center theory of Matthaeus et al. (2003) a nonlinear
integral equation has been derived. Bieber et al. (2004) and Shalchi et al. (2006) demonstrated that this
nonlinear approach can explain the values for the perpendicular mean free path suggested by Palmer (1982).
In the same time, it has been discovered by using advanced theoretical tools that nonlinear effects have also a
strong influence onto parallel diffusion. Quantitatively this mutual influence of parallel and
perpendicular transport can be described by using the weakly nonlinear theory (WNLT) of Shalchi et al. (2004). Within the
WNLT we find a much steeper rigidity dependence of the parallel mean free path due to the influence of perpendicular
diffusion. Because of this effect which has been confirmed by test-particle simulations (Qin et al. 2006) and by recent
observations (Mason et al. 2006) the idea of generating much larger parallel mean free paths simply by turning from the
slab model to the slab/2D model seems to be questionable.
In Fig. 1 results of test-particle simulations and WNLT are compared with QLT. As demonstrated the assumption
that 2D modes are ineffective in scattering is ruther questionable. It can easily be seen in Fig. 1 that the turbulence
geometry (represented by the so-called slab fraction
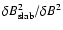 )
has a very weak influence onto the parallel
mean free path.
)
has a very weak influence onto the parallel
mean free path.
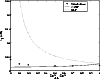 |
Figure 1:
The parallel mean free path as a function of the ratio
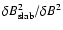 for moderate amplitude turbulence
(
for moderate amplitude turbulence
(
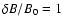 )
with )
with
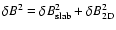 .
Shown are results of the weakly nonlinear theory (solid line), simulations (dots) and QLT (dotted line) for .
Shown are results of the weakly nonlinear theory (solid line), simulations (dots) and QLT (dotted line) for
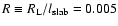 .
Here the Larmor-radius .
Here the Larmor-radius 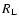 and the slab-bendover-scale
and the slab-bendover-scale
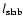 have been used.
As shown, particle scattering due to the 2D fluctuations cannot be neglected. The parallel mean free path is nearly independent of
the turbulence geometry represented by the slab fraction
have been used.
As shown, particle scattering due to the 2D fluctuations cannot be neglected. The parallel mean free path is nearly independent of
the turbulence geometry represented by the slab fraction
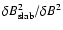 .
The figure is taken from Shalchi et al. (2004). .
The figure is taken from Shalchi et al. (2004). |
| Open with DEXTER |
Independent of these advances in cosmic ray transport theory, further observations have been performed. For instance,
Gloeckler et al. (1995) concluded from Ulysses observations that the parallel mean free path of pickup protons
is 2 AU at 2.4 MV rigidity (they stated conservatively that
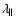 is of order 1 AU but actually they obtained
the best fit for 2 AU). Möbius et al. (1998) concluded from AMPTE (Active Magnetospheric Particle Tracer Explorers)
spacecraft measurements that the parallel mean free paths of pickup helium ranges from 0.16 to 0.76 AU at 5.6 MV rigidity
in the data they have analyzed. Both values are even larger than the Palmer consensus range.
Therefore the Palmer consensus has to be revisited in light of these new theoretical and observational results. It is the
intention of this article to provide an alternative explanation of the parallel mean free paths obtained from spacecraft
measurements by using an improved form of the turbulence wave spectrum.
is of order 1 AU but actually they obtained
the best fit for 2 AU). Möbius et al. (1998) concluded from AMPTE (Active Magnetospheric Particle Tracer Explorers)
spacecraft measurements that the parallel mean free paths of pickup helium ranges from 0.16 to 0.76 AU at 5.6 MV rigidity
in the data they have analyzed. Both values are even larger than the Palmer consensus range.
Therefore the Palmer consensus has to be revisited in light of these new theoretical and observational results. It is the
intention of this article to provide an alternative explanation of the parallel mean free paths obtained from spacecraft
measurements by using an improved form of the turbulence wave spectrum.
In several previous articles (e.g. Bieber et al. 1994; Shalchi et al. 2006) a spectrum of the form
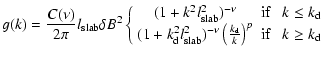 |
|
|
(1) |
has been used which we refer to as standard spectrum. The spectrum is shown and explained in Fig. 2.
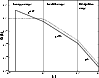 |
Figure 2:
Shown are the different forms of the wave spectrum considered in this article: the standard form (dotted line) is constant
in the energy-range wheras the improved form (solid line) descreases. Shown is the function
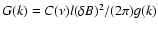 as a function of k l. For pure slab geometry the parameter l has to be identified with the slab-bendover-scale
as a function of k l. For pure slab geometry the parameter l has to be identified with the slab-bendover-scale
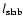 . . |
| Open with DEXTER |
In Eq. (1) the normalization constant
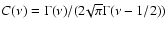 ,
the bendover-scale
,
the bendover-scale
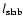 ,
the strength of the turbulent fields
,
the strength of the turbulent fields
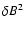 and the inertial-range spectral index
and the inertial-range spectral index 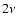 are used. The parameter
are used. The parameter 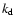 indicates the dissipation wavenumber and p is the dissipation-range spectral index. Appropriate values for the solar wind
plasma are shown in Table 1.
indicates the dissipation wavenumber and p is the dissipation-range spectral index. Appropriate values for the solar wind
plasma are shown in Table 1.
Table 1:
Parameters used for the calculations performed in this article. The values should be appropriate for the solar wind at 1 AU
heliocentric distance.
A detailed discussion of interplanetary wavespectra has been presented in Bruno & Carbone (2005). In a recent article (Döring & Shalchi 2007)
it is argued that a wavespectrum of the following form is more appropriate for solar wind turbulence:
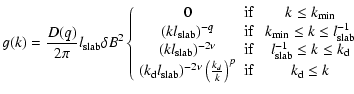 |
|
|
(2) |
with
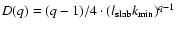 .
In Fig. 2 this improved spectrum in shown and compared with
the standard form of Eq. (1). In Eq. (2) two additional parameters have been introduced: q denots the
energy-range spectral index and
.
In Fig. 2 this improved spectrum in shown and compared with
the standard form of Eq. (1). In Eq. (2) two additional parameters have been introduced: q denots the
energy-range spectral index and  is the smallest wavenumber. The only difference between these two spectra is the behaviour
in the energy-range: the standard spectrum assumes
is the smallest wavenumber. The only difference between these two spectra is the behaviour
in the energy-range: the standard spectrum assumes
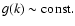 whereas in the improved spectrum we have
whereas in the improved spectrum we have
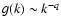 .
The spectrum is correctly normalized if 1<q<2 and if
.
The spectrum is correctly normalized if 1<q<2 and if
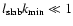 .
To calculate the parallel mean free path we assume pure slab geometry and we apply the damping model of
dynamical turbulence of Bieber et al. (1994).
At first glance the use of the slab model seems to be inappropriate for solar wind turbulence, since
there is evidence for a strong perpendicular component from heliospheric measurements (see e.g. Bieber et al. 1996).
More precisely the assumption of 20% slab / 80% 2D as used in Bieber et al. (1994, see discussion in the introduction)
seems to be much more realistic. In previous articles this two-component model was combined with quasilinear theory
which provides a much larger parallel mean free path if the slab/2D composite model is used instead of the
slab model. As demonstrated in several previous articles (e.g. Bieber et al. 1994; Shalchi et al. 2006) these
large parallel mean free paths are close to measurements. However, in Shalchi et al. (2004) and Qin et al. (2006)
it was demonstrated that quasilinear theory is not the correct approach to describe parallel propagation of charged
particles in slab/2D composite geometry, since nonlinear effects are important. More precisely, the true parallel mean free
obtained nonlinearly for composite geometry is similar to the well known slab result (see Fig. 1). Thus the application
of quasilinear theory is questionable. The most reliable approach to describe heliospheric particle
transport would be a combination of a nonlinear transport theory with the realistic wavespectrum, the
two-component turbulence model, and dynamical turbulence. However, such calculation are difficult to
perform due to mathematical problems. In the current article we thus simply apply the slab model by assuming
that the turbulence geometry has only a weak influence onto the size of parallel mean free paths. This assumption
is in agreement with recent test-particle simulations (see Fig. 1).
.
To calculate the parallel mean free path we assume pure slab geometry and we apply the damping model of
dynamical turbulence of Bieber et al. (1994).
At first glance the use of the slab model seems to be inappropriate for solar wind turbulence, since
there is evidence for a strong perpendicular component from heliospheric measurements (see e.g. Bieber et al. 1996).
More precisely the assumption of 20% slab / 80% 2D as used in Bieber et al. (1994, see discussion in the introduction)
seems to be much more realistic. In previous articles this two-component model was combined with quasilinear theory
which provides a much larger parallel mean free path if the slab/2D composite model is used instead of the
slab model. As demonstrated in several previous articles (e.g. Bieber et al. 1994; Shalchi et al. 2006) these
large parallel mean free paths are close to measurements. However, in Shalchi et al. (2004) and Qin et al. (2006)
it was demonstrated that quasilinear theory is not the correct approach to describe parallel propagation of charged
particles in slab/2D composite geometry, since nonlinear effects are important. More precisely, the true parallel mean free
obtained nonlinearly for composite geometry is similar to the well known slab result (see Fig. 1). Thus the application
of quasilinear theory is questionable. The most reliable approach to describe heliospheric particle
transport would be a combination of a nonlinear transport theory with the realistic wavespectrum, the
two-component turbulence model, and dynamical turbulence. However, such calculation are difficult to
perform due to mathematical problems. In the current article we thus simply apply the slab model by assuming
that the turbulence geometry has only a weak influence onto the size of parallel mean free paths. This assumption
is in agreement with recent test-particle simulations (see Fig. 1).
In Fig. 3 the quasilinear parallel mean free path are calculated numerically and the results are compared
with observations and with the results of the standard spectrum (also for pure slab geometry). The technical details of
such calculations and the
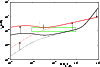 |
Figure 3:
The parallel mean free path as a function of the particle Larmor-radius 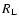 devided by the slab-bendover-scale
devided by the slab-bendover-scale
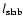 .
Shown are QLT results for electrons (solid lines) and protons (dotted lines) for the standard spectrum (black) and
the improved spectrum (red) in comparison with different observations: Palmer consensus range (Palmer 1982, green box),
Ulysses observations (Gloeckler et al. 1995, yellow), AMPTE spacecraft observations (Möbius et al. 1998,
blue). All theoretical results are for slab turbulence and the damping model of dynamical turbulence. .
Shown are QLT results for electrons (solid lines) and protons (dotted lines) for the standard spectrum (black) and
the improved spectrum (red) in comparison with different observations: Palmer consensus range (Palmer 1982, green box),
Ulysses observations (Gloeckler et al. 1995, yellow), AMPTE spacecraft observations (Möbius et al. 1998,
blue). All theoretical results are for slab turbulence and the damping model of dynamical turbulence. |
| Open with DEXTER |
corresponding formulas can be found in Bieber et al. (1994) and Shalchi et al. (2006). To perform these calculations the turbulence
parameters shown in Table 1 are applied. For the energy-range spectral index q=1.07
is used as suggested by Bruno & Carbone (2005) and for the cut-off wavenumber
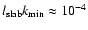 is
assumed. All other parameter values which have been used for the performed calculations are listed in Table 1.
is
assumed. All other parameter values which have been used for the performed calculations are listed in Table 1.
As shown in Fig. 3 we find a strong increase of the parallel mean free path by changing from the
standard spectrum to the improved spectrum.
The reason for this increase can easily be understood by using simple physical arguments: by holding the total turbulence
energy constant (e.g.
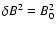 ), and by increasing the spectrum in the energy-range, we practically transfer
magnetic energy from small to large turbulence scales. Thus if the particles interact resonantly with small scales the parallel
mean free path increases and for interaction with large scales the interaction becomes stronger and we find reduced
parallel mean free paths. These statements formulated on the basis of physical arguments are in agreement with the
quantitative results visualized in Fig. 3. By assuming interaction with smaller scales the difference
between the standard spectrum (q=0) and the improved spectrum (q>1) comes due to the different normalization
factors. Thus we can estimate
), and by increasing the spectrum in the energy-range, we practically transfer
magnetic energy from small to large turbulence scales. Thus if the particles interact resonantly with small scales the parallel
mean free path increases and for interaction with large scales the interaction becomes stronger and we find reduced
parallel mean free paths. These statements formulated on the basis of physical arguments are in agreement with the
quantitative results visualized in Fig. 3. By assuming interaction with smaller scales the difference
between the standard spectrum (q=0) and the improved spectrum (q>1) comes due to the different normalization
factors. Thus we can estimate
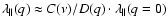 .
If we
set q=1.07 which should be the appropriate value in the solar wind we find
.
If we
set q=1.07 which should be the appropriate value in the solar wind we find
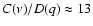 .
By simply
replacing the standard form of the wave spectrum by a realistic spectrum we can increase the parallel mean free path
of small and medium energetic particles in order of one magnitude.
.
By simply
replacing the standard form of the wave spectrum by a realistic spectrum we can increase the parallel mean free path
of small and medium energetic particles in order of one magnitude.
In this article the Palmer consensus is revisited. The motivation for this report is based on two statements:
- 1)
- The traditional explanation of observed parallel mean free paths is that a large part of the magnetic fluctuations is in 2D modes
which are expected to be ineffective in scattering. However, as demonstrated in recent articles (e.g. Shalchi et al. 2004; Qin et al. 2006),
the assumption of ineffective scattering in 2D fluctuations is questionable (see Fig. 1). Thus, the replacement of the slab
model by the slab/2D composite model cannot reproduce the observations because only within quasilinear theory the parallel mean
free path can be increased.
- 2)
- The constant behaviour of the wave spectrum in the energy-range disagrees with observations of interplanetary turbulence
(see Bruno & Carbone 2005). Hence, the spectrum has to be replaced by a descreasing spectrum in the energy-range as
suggested by Döring & Shalchi (2007).
Furthermore, it is assumed in this article that slab parallel mean free paths are similar to the (nonlinear) slab/2D composite parallel
mean free paths (see Fig. 1). Requiring validity of this assumption, the slab model which is applied in the current work
should be a good approximation. By using the improved spectrum, the damping model of dynamical turbulence, and by applying
quasilinear theory, the parallel mean free path is calculated for solar wind turbulence parameters. As demonstrated in Fig. 3
the new results are in agreement with the discussed observations. By changing the additional parameters q and  the parallel mean free path can further be increased or descreased. For large heliocentric distance for instance we
expect higher values of q and thus an increasing parallel mean free path. This effect is necessary to reproduce the
observations of Gloeckler et al. (1995).
the parallel mean free path can further be increased or descreased. For large heliocentric distance for instance we
expect higher values of q and thus an increasing parallel mean free path. This effect is necessary to reproduce the
observations of Gloeckler et al. (1995).
As demonstrated, considering a larger value of the energy-range spectral index is another method to increase the parallel
mean free path which is essential to reproduce heliospheric observations.
Another effect caused by larger values of the energy-range spectral index is the recovery of perpendicular
diffusion in the slab model (see Döring & Shalchi 2007). Thus one expects that the improved form
of the wave spectrum is in general important for particle transport in the solar wind. It must be
subject of future work to achieve reliable measurements of the additional parameters q and  to
achieve an accurate comparison between theoretical mean free paths and the corresponding observed
parameters. Furthermore, it must be subject of future work to combine reliable nonlinear transport
theories with the spectrum used in this article. Then we are also able to apply the two-component turbulence
model which is a more accurate model for solar wind turbulence.
to
achieve an accurate comparison between theoretical mean free paths and the corresponding observed
parameters. Furthermore, it must be subject of future work to combine reliable nonlinear transport
theories with the spectrum used in this article. Then we are also able to apply the two-component turbulence
model which is a more accurate model for solar wind turbulence.
Acknowledgements
This research was supported by Deutsche Forschungsgemeinschaft (DFG) under the Emmy-Noether program
(grant SH 93/3-1). As a member of the Junges Kolleg A. Shalchi also aknowledges
support by the Nordrhein-Westfälische Akademie der Wissenschaften (academy of science).
- Bieber, J. W.,
Matthaeus, W. H., Smith, C. W., et al. 1994, ApJ, 420, 294 [NASA ADS] [CrossRef] (In the text)
- Bieber, J. W.,
Wanner, W., & Matthaeus, W. H. 1996, J. Geophys. Res., 101,
2511 [NASA ADS] [CrossRef] (In the text)
- Bieber, J. W.,
Matthaeus, W. H., Shalchi, A., & Qin, G. 2004, Geophys. Res.
Lett., 31, L10805 [NASA ADS] [CrossRef] (In the text)
- Bruno, R., &
Carbone, V. 2005, Liv. Rev. Sol. Phys., 2, 4 (In the text)
- Döring, H.,
& Shalchi, A., Ap&SS, submitted
(In the text)
- Dröge, W. 2000,
ApJ, 537, 1073 [NASA ADS] [CrossRef] (In the text)
- Gloeckler,
G., Schwadron, N. A., Fisk, L. A., & Geiss, J. 1995, Geophys.
Res. Lett., 22, 2665 [NASA ADS] [CrossRef] (In the text)
- Jokipii, J. R.
1966, ApJ, 146, 480 [NASA ADS] [CrossRef] (In the text)
- Mason, G. M., Desai,
M. I., Cohen, C. M. S., et al. 2006, ApJ, 647, L65 [NASA ADS] [CrossRef] (In the text)
- Matthaeus, W.
H., Qin, G., Bieber, J. W., & Zank, G. P. 2003, ApJ, 590,
L53 [NASA ADS] [CrossRef] (In the text)
- Möbius, E.,
Rucinski, D., Lee, M. A., & Isenberg, P. A. 1998, J. Geophys.
Res., 10, 257 [NASA ADS] [CrossRef] (In the text)
- Palmer, I. D. 1982,
Rev. Geophys. Space Phys., 20, 2, 335
(In the text)
- Qin, G., Matthaeus, W.
H., & Bieber, J. W. 2006, ApJ, 640, L103 [NASA ADS] [CrossRef] (In the text)
- Shalchi, A.,
Bieber, J. W., Matthaeus, W. H., & Qin, G. 2004, ApJ, 616,
617 [NASA ADS] [CrossRef] (In the text)
- Shalchi, A.,
Bieber, J. W., Matthaeus, W. H., & Schlickeiser, R. 2006, ApJ,
642, 230 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007


![]() is of order 1 AU but actually they obtained
the best fit for 2 AU). Möbius et al. (1998) concluded from AMPTE (Active Magnetospheric Particle Tracer Explorers)
spacecraft measurements that the parallel mean free paths of pickup helium ranges from 0.16 to 0.76 AU at 5.6 MV rigidity
in the data they have analyzed. Both values are even larger than the Palmer consensus range.
Therefore the Palmer consensus has to be revisited in light of these new theoretical and observational results. It is the
intention of this article to provide an alternative explanation of the parallel mean free paths obtained from spacecraft
measurements by using an improved form of the turbulence wave spectrum.
is of order 1 AU but actually they obtained
the best fit for 2 AU). Möbius et al. (1998) concluded from AMPTE (Active Magnetospheric Particle Tracer Explorers)
spacecraft measurements that the parallel mean free paths of pickup helium ranges from 0.16 to 0.76 AU at 5.6 MV rigidity
in the data they have analyzed. Both values are even larger than the Palmer consensus range.
Therefore the Palmer consensus has to be revisited in light of these new theoretical and observational results. It is the
intention of this article to provide an alternative explanation of the parallel mean free paths obtained from spacecraft
measurements by using an improved form of the turbulence wave spectrum.


![]() ), and by increasing the spectrum in the energy-range, we practically transfer
magnetic energy from small to large turbulence scales. Thus if the particles interact resonantly with small scales the parallel
mean free path increases and for interaction with large scales the interaction becomes stronger and we find reduced
parallel mean free paths. These statements formulated on the basis of physical arguments are in agreement with the
quantitative results visualized in Fig. 3. By assuming interaction with smaller scales the difference
between the standard spectrum (q=0) and the improved spectrum (q>1) comes due to the different normalization
factors. Thus we can estimate
), and by increasing the spectrum in the energy-range, we practically transfer
magnetic energy from small to large turbulence scales. Thus if the particles interact resonantly with small scales the parallel
mean free path increases and for interaction with large scales the interaction becomes stronger and we find reduced
parallel mean free paths. These statements formulated on the basis of physical arguments are in agreement with the
quantitative results visualized in Fig. 3. By assuming interaction with smaller scales the difference
between the standard spectrum (q=0) and the improved spectrum (q>1) comes due to the different normalization
factors. Thus we can estimate
![]() .
If we
set q=1.07 which should be the appropriate value in the solar wind we find
.
If we
set q=1.07 which should be the appropriate value in the solar wind we find
![]() .
By simply
replacing the standard form of the wave spectrum by a realistic spectrum we can increase the parallel mean free path
of small and medium energetic particles in order of one magnitude.
.
By simply
replacing the standard form of the wave spectrum by a realistic spectrum we can increase the parallel mean free path
of small and medium energetic particles in order of one magnitude.
![]() the parallel mean free path can further be increased or descreased. For large heliocentric distance for instance we
expect higher values of q and thus an increasing parallel mean free path. This effect is necessary to reproduce the
observations of Gloeckler et al. (1995).
the parallel mean free path can further be increased or descreased. For large heliocentric distance for instance we
expect higher values of q and thus an increasing parallel mean free path. This effect is necessary to reproduce the
observations of Gloeckler et al. (1995).