![\begin{figure}
\par\includegraphics[width=9cm,clip]{7351fig1.eps} %
\end{figure}](/articles/aa/full/2007/26/aa7351-07/Timg1.gif) |
Figure 1: One dimensional data points taken from a normal distribution are moved so that the density of the resultant points can be represented accurately by an ideal Gaussian curve. |
| Open with DEXTER | |
A&A 469, 793-797 (2007)
DOI: 10.1051/0004-6361:20077351
M. de Villiers
South African Square Kilometer Array / Karoo Array Telescope (SKA/KAT), Lonsdale Building, Lonsdale Way, Pinelands 7405, Republic of South Africa
Received 26 February 2007 / Accepted 11 April 2007
Abstract
Context. This study pertains to the optimization of the layout of a single configuration interferometric array to achieve a desired natural tapering for the density distribution of its UV plane coverage. Existing techniques that seek this goal determine a two dimensional density gradient that acts on the UV samples and in turn on the antenna positions. This gradient is commonly computed by gridding the UV plane, and is sometimes averaged over a number of different scales due to the sparseness of the UV samples.
Aims. The goal of this study is to demonstrate a new method that can move antenna positions to achieve an ideal density distribution for the UV samples without the need for gridding.
Methods. An approach is described where the UV samples are projected into a one dimensional vector. If an equivalent projection is done for an ideal model distribution, the difference between these vectors yields correction terms which can be mapped to new antenna positions. Such modifications are made in all directions until a close match is achieved to the desired UV plane coverage and equivalently, by the Fourier transform, the ideal point spread function.
Results. Results are provided that relate achievable resolution (for Gaussian UV coverage) to the number of antennas available to the algorithm, for a few different observation modes. Preliminary layouts are shown for the Square Kilometer Array pathfinder project, the Karoo Array Telescope.
Conclusions. The proposed method is applicable to very few as well as a large number of antennas. Multiple objective optimization is not considered.
Key words: instrumentation: interferometers - methods: numerical
The Karoo Array Telescope (KAT), which is currently being developed, is a South African pathfinder project for the Square Kilometer Array (SKA). The instrument was originally envisaged to consist of 20 unmovable antennas with 15 m diameter dishes, but this may be reduced to 7 initially and later be expanded to 100 or 230 antennas. Since it is unclear at this stage for which science cases the instrument should be optimized, a general purpose tool has been developed to facilitate the configuration design given possible experiment conditions. This paper discusses the optimization technique used for antenna placement and reports on some early results.
Conceptually, the proposed algorithm is only concerned with the optimization of the layout of an interferometer array for imaging where the number of antennas and the diameter of the dishes are predetermined. It is only the positions of the antennas that need to be optimized for a given mode of observation (specified by the parameters: site latitude, declination, frequency, fractional bandwidth, number of channels, duration, correlator dump rate, on-source and off-source time), subject to terrain constraints at the site. A few authors have addressed this problem previously.
An algorithm by Keto (1997) optimizes the zenith snapshot UV coverage of a layout. It is advocated that a uniform UV density distribution has superior imaging properties. The algorithm draws a random two dimensional coordinate from a uniform probability distribution and moves the closest and neighbouring UV samples towards that position by adjusting the antenna positions. The neighbourhood size and the distance moved are decreased over time, and after numerous iterations, the resultant layout very interestingly resembles the Reuleaux triangle.
A paper by Boone (2001) explores the effects of different observation conditions on the layout design while imposing terrain constraints. In this method, two dimensional pressure forces are calculated for UV samples falling into cylindrical coordinate segments in the UV plane. The current UV density distribution is compared to that of an ideal model to produce the pressure forces that act on the UV samples. This method moves antenna positions according to their geometric relationship with UV samples due to earth rotation synthesis. Since the number of UV samples are finite, larger segments are necessary to achieve good estimates of the density values. However, smaller segments are necessary to retain good position accuracy. Consequently, a range of segment sizes are used in this method.
In the current paper, the goal remains as above to realize an ideal model UV distribution, yet an entirely different implementation is suggested that avoids gridding the relatively sparse number of UV samples. This is done by tomographic projection to reduce the problem to one dimension. The need to consider different neighbourhood sizes becomes moot.
First a fundamental conceptual one dimensional problem is defined and solved in Sect. 2. This solution is then extended to two dimensions in Sect. 3 and integrated into the problem of correcting a two dimensional distribution of UV samples in Sect. 4. The paper continues by presenting simulated results in Sect. 5, suggesting possible layouts for KAT, and ends with conclusions about the design method.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{7351fig1.eps} %
\end{figure}](/articles/aa/full/2007/26/aa7351-07/Timg1.gif) |
Figure 1: One dimensional data points taken from a normal distribution are moved so that the density of the resultant points can be represented accurately by an ideal Gaussian curve. |
| Open with DEXTER | |
Consider the problem where a vector of independent data points is given, and it is necessary to determine quantitatively how closely the density distribution of the values in this vector follow an ideal model. It is also required to calculate how these data points should be moved so that its density distribution matches the ideal model precisely. In the text below, a classical approach is outlined briefly for context before the recommended method is discussed.
One approach of determining the closeness numerically could be to bin the data points into a histogram, and then to compute the root mean square error between its counts and the ideal model that has been rescaled and sampled appropriately. The points could be moved in the direction of the local gradient of the difference between the histogram and the ideal, similar to the discussion in Boone for the two dimensional case. This would be acceptable if there is a large number of data points, but remains problematic in the choice of bin size and bin edge position. The spacing must be increased to ensure enough data points fall into a bin, yet be small enough so that the histogram shape remains representative of the density distribution, since some position information is lost in the binning process. Boone considers multiple bin sizes in an attempt to alleviate this problem.
Figure 1 illustrates quantities that are used to describe a method for solving the problem addressed in this section. A vector of N points ![]() taken from a normal distribution is displayed above its histogram which gives a crude visualization of the density distribution of the points. An ideal density profile
taken from a normal distribution is displayed above its histogram which gives a crude visualization of the density distribution of the points. An ideal density profile ![]() ,
where
,
where ![]() is the position variable, is superimposed over the histogram to show that there is a poor match between the ideal and the data points for such a small number of random points.
is the position variable, is superimposed over the histogram to show that there is a poor match between the ideal and the data points for such a small number of random points.
It is useful, as will be apparent shortly, to determine cumulative distribution functions (Leon-Garcia 1994) of the data points and that of the ideal distribution. For the data points ![]() ,
a discrete cumulative distribution is obtained simply by sorting the values in the vector in ascending order to
,
a discrete cumulative distribution is obtained simply by sorting the values in the vector in ascending order to ![]() defining
defining
![]() with
with
![]() where i is the index. For the ideal density distribution
where i is the index. For the ideal density distribution ![]() ,
the cumulative distribution
,
the cumulative distribution ![]() is scaled
is scaled
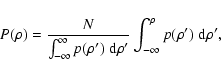 |
(1) |
For a particular index which corresponds to a data point in Fig. 1, the difference in position, between the ideal cumulative distribution and the cumulative data points distribution yields the amount by which the particular data point must be displaced in order to achieve the ideal density distribution. This can be expressed as
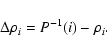 |
(2) |
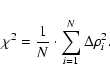 |
(3) |
A two dimensional distribution is uniquely specified by a set of its one dimensional projections taken over a range of 180 degrees, according to work by Radon (Kak & Slaney 1988). This principle is widely exploited in the field of computed axial tomography to reconstruct gridded images from line integral data. The method described below relies on this principle to ensure that the ideal distribution is attained, provided that the projections are made equal to that of the ideal distribution.
The top left diagram in Fig. 2 shows how N two dimensional data points
(xi',yi') are projected into one dimensional data points ![]() at an angle
at an angle ![]() ,
by the equation
,
by the equation
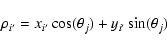 |
(4) |
For the general case of an arbitrary (asymmetric) ideal distribution, the Radon transform must be employed at a particular angle ![]() using
using
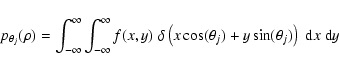 |
(5) |
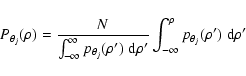 |
(6) |
The data points
(xi',yi') are updated in the direction orthogonal to that of the projection as depicted in the middle column of Fig. 2 using
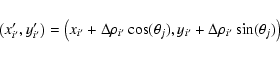 |
(7) |
This procedure is repeated for 1000 different projection angles ![]() ,
,
![]() ,
resulting in the distributions in the right hand column of the figure. Good results are, however, already achieved for iterations less than N, the number of data points. The angle
,
resulting in the distributions in the right hand column of the figure. Good results are, however, already achieved for iterations less than N, the number of data points. The angle ![]() is picked at random from a uniform distribution over the indicated range.
is picked at random from a uniform distribution over the indicated range.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{7351fig2.eps} %
\end{figure}](/articles/aa/full/2007/26/aa7351-07/Timg26.gif) |
Figure 2: Data points taken from a bivariate normal distribution ( left column) are displaced in one direction ( middle column) so that the density of the resultant points closely follows a precomputed ideal profile (not shown explicitly) in that direction. This process is repeated in a number of different directions until the points appear to be uniformly spaced within a disc ( top and middle rows) or donut ( bottom row). |
| Open with DEXTER | |
In the previous section, independent data points were considered. However, the UV samples, which need to be manipulated towards an ideal density distribution in order to achieve the desired point spread function, cannot be moved independently. These UV samples are all the permutations of relative antenna displacements that are transformed by linear mappings due to earth rotation and multi frequency synthesis (Taylor et al. 2003). Moving a single UV sample can be done accurately by moving two antennas equally, relative to each other. This, however, causes all the other UV samples associated with these two antennas to be moved as well (by half of the distance travelled by that single UV sample) and effects the resultant UV density distribution adversely.
In practice, this problem is addressed by determining values for ![]() in Eq. (8), as described in the next paragraph, which changes depending on the observation settings and the number of antennas. If the technique described in Sect. 3 was iterated for a fixed value of
in Eq. (8), as described in the next paragraph, which changes depending on the observation settings and the number of antennas. If the technique described in Sect. 3 was iterated for a fixed value of ![]() ,
where
,
where ![]() is too large, then results become unstable, while convergence is slow if
is too large, then results become unstable, while convergence is slow if ![]() is too small.
is too small.
It is, however, easy to perform a line search (the line search algorithm) to determine which ![]() minimizes
minimizes
When M=2, the algorithm converges quickly to a subset of solutions, but not a single solution, and the line search interestingly reveals that ![]() approximately equals a constant for any number of iterations. In fact, once
approximately equals a constant for any number of iterations. In fact, once ![]() and its variability is known, it may no longer be necessary to perform a line search at each iteration.
and its variability is known, it may no longer be necessary to perform a line search at each iteration.
For larger M, the algorithm converges to a smaller subset of solutions, or even a single solution. In this case ![]() eventually decreases with iteration but more computation is needed for each line search and more iterations are needed to reach good results because
eventually decreases with iteration but more computation is needed for each line search and more iterations are needed to reach good results because ![]() is generally smaller. For these reasons, M=2 is recommended and used throughout.
is generally smaller. For these reasons, M=2 is recommended and used throughout.
It remains useful simply to iterate using a fixed small value for ![]() (neglecting the line search, hence called the fixed
(neglecting the line search, hence called the fixed ![]() algorithm) to achieve a result that closely resembles a preferred layout used as a starting point. A suitable value for
algorithm) to achieve a result that closely resembles a preferred layout used as a starting point. A suitable value for ![]() can be determined experimentally or using a line search.
can be determined experimentally or using a line search.
![\begin{figure}
\par\subfigure[Data (for 2 extreme observation conditions only)]{...
...Fitted results]{\includegraphics[width=7.4cm,clip]{7351fg3b.eps} }
\end{figure}](/articles/aa/full/2007/26/aa7351-07/Timg30.gif) |
Figure 3: Typical half power beamwidth resolutions at 1.4 GHz are shown as a function of the number of antennas available to the algorithm to generate layouts having Gaussian UV coverage. Results are provided for 4 different optimization criterion as indicated by the labels (continuum imaging assumes a fractional bandwidth of 0.2). All layouts have a minimum antenna spacing of 30 m. |
| Open with DEXTER | |
The algorithm defined above (3000 iterations) was used to generate different layouts with Gaussian UV coverage. From 3 up to 250 antenna layouts were optimized for the cases of snapshot and 8 h track (a snapshot every 5 min) observations about the zenith for spectral and continuum imaging (multi frequency synthesis with a fractional bandwidth of 0.2) at a site latitude of -30 degrees. For each instance the target resolution was 40 arcsec at 1.4 GHz and the maximum and minimum baselines were recorded.
It was found that layouts with fewer antennas have larger minimum baselines than those with a large number of antennas to achieve the same resolution. Also, increasing the observation time or fractional bandwidth increases the ratio between maximum and minimum baselines in the resultant layouts. Both these types of synthesis increase the density of short baseline UV samples making a larger beam for a given layout, implying that the fixed optimization target resolution occurs at an increased layout size.
To get good UV coverage at low spatial frequencies, the minimum baseline should be as small as possible. The minimum antenna spacing is limited by the dish diameter physically, and also by the impact of shadowing on sensitivity. In order to make a meaningful comparison of the results above which were optimized for a fixed target resolution, the layouts are rescaled so that the minimum separation between antennas equals double the dish diameter (i.e. 30 m) which ensures that no shadowing occurs for 8 h observations or for the range of declinations from -90 to +30 degrees. From this it follows that the natural solutions for Gaussian UV coverage produced by this algorithm suggest resolutions for layouts as a function of the number of antennas as indicated in Fig. 3. Higher resolutions in this figure indicate smaller minimum antenna spacings for the fixed target resolution optimization results mentioned above.
If higher resolutions are seeked with fewer antennas than these graphs indicate, then either the lowest spatial frequencies are not sampled or the point spread function is no longer Gaussian-like (which can be corrected at a loss in sensitivity by weighting the UV samples). If more antennas are used to create a layout at a given resolution, then the minimum antenna spacing is reduced to retain a Gaussian-like point spread function, and then shadowing may worsen the sensitivity.
The variability in data points in Fig. 3a is attributed to the fact that a perfect fit of the UV samples to a Gaussian model is unattainable, and some layouts are better optimized than others. In Eq. (9), M=2 only and the orientation is chosen at random. This causes the line search cost function to change significantly at each iteration. Increasing the number of projections, M, will evaluate the shape of the UV coverage distribution more thoroughly and prevent one projection from being overfitted at the expense of projections at other angles. The value of M=2 is chosen to tradeoff the computational speed to this variability.
The layout of an interferometer such as KAT should ideally be optimized over a multitude of experiment conditions for which the instrument will be used. Since the science cases for KAT remain vague, and the algorithm as implemented thusfar optimizes a layout for a single imaging experiment at a time only, the preliminary layouts presented here are simply optimized for 8 h (spectral/continuum) imaging observations about the zenith. Optimization is performed subject to topographical constraints of one of the candidate sites at a latitude of 30.715 degrees South.
The three cases being considered are 20, 100 and 230 antenna layouts which are illustrated in Fig. 4. Notice how the layouts appear to have filled rounded triangular shapes. The 20 and 100 antenna layouts are optimized for continuum imaging while the 230 antenna layout is optimized for spectral imaging to restrict the maximum baseline to be around 5 km. Observation parameter details are given in Table 1. The table also presents peak sidelobe levels of artefacts remaining in the natural point spread functions of Fig. 4, and maximum baseline results for the three layouts.
Table 1: Observation parameters and layout results.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{7351fig4.eps} \end{figure}](/articles/aa/full/2007/26/aa7351-07/Timg32.gif) |
Figure 4: Results for layouts of 20, 100 and 230 antennas with Gaussian UV coverage are shown in the top, middle and bottom rows respectively. From left to right are the layouts (flash flood watercourses and dams in white), UV coverages, UV coverage histograms and natural point spread functions for the observation conditions that the layouts are optimized. Both the 20 and 100 antenna layouts are optimized for continuum imaging observations, while the 230 antenna layout is optimized for spectral imaging observation as defined in Table 1. The point spread function images are contrast-stretched to display only the range from -2% to +2% of their peak values. |
| Open with DEXTER | |
This paper presented a method for optimizing an interferometer layout to achieve a desired natural point spread function for one targeted observation mode. The method avoids the need for gridding the UV data points and avoids estimating a two dimensional density function, since it acts in one direction at a time only. Layouts with very few and many antennas can be optimized.
Of particular interest are layouts that have Gaussian UV coverage. It is shown that the algorithm imposes resolution as a function of the number of antennas given constraints on the minimum baseline and also the observation parameters. These results can be used to estimate scale sizes of layouts in designing KAT. A few layouts have been suggested which appear to have rounded triangular boundaries but the connection with the Reuleaux triangle has not been explored.
The advantage of performing optimization over a range of observations has not been quantified and is sometimes regarded to be negligible over simply optimizing for zenith snapshot conditions (Taylor et al. 2003, p. 554). In this paper the approach was to achieve an optimal point spread function for the observation which requires the highest sensitivity. Although the same point spread function will not be retained for different observation settings, its shape can be manipulated by weighting the UV samples at some loss in sensitivity.
In the end a layout is seeked that performs well for all observation modes of importance. Towards this final goal, there remains scope for follow-up work to optimize for multiple objectives using a population based approach that utilizes the algorithm described here as a tool to produce new layouts.
Acknowledgements
The author is employed on the development team of the South African SKA/KAT project of the Department of Science and Technology. This work forms part of the CONRAD computing collaboration between SKA/KAT and the Australian ATNF. Special thanks to Tim Cornwell, Rudolph van der Merwe, Richard Lord and Adriaan Hough.