A&A 469, 595-605 (2007)
DOI: 10.1051/0004-6361:20066962
Statistical properties of dust far-infrared emission
M.-A. Miville-Deschênes1,2 - G. Lagache1 -
F. Boulanger1 - J.-L. Puget1
1 - Institut d'Astrophysique Spatiale, Université Paris-Sud,
Bât. 121, 91405 Orsay, France
2 -
Canadian Institute for Theoretical Astrophysics,
University of Toronto, 60 St. George Street, Toronto, ON, M5S 3H8, Canada
Received 18 December 2006 / Accepted 4 April 2007
Abstract
Context. Far-infrared dust emission has a self-similar structure which reveals the complex dynamical processes that shape the interstellar medium. The description of the statistical properties of this emission gives important constraints on the physics of the interstellar medium but it is also a useful way to estimate the contamination of diffuse interstellar emission in the cases where it is considered a nuisance.
Aims. The main goals of this analysis of the power spectrum and non-Gaussian properties of far-infrared dust emission are 1) to estimate the power spectrum of interstellar matter density in three dimensions; 2) to review and extend previous estimates of the cirrus noise due to dust emission; and 3) to produce simulated dust emission maps that reproduce the observed statistical properties.
Methods. To estimate the statistical properties of dust emission we analyzed the power spectrum and wavelet decomposition of 100 IRIS data (an improved version of the IRAS data) over 55% of the sky. The simulation of realistic infrared emission maps is based on modified Gaussian random fields.
Results. The main results are the following. 1) The cirrus noise level as a function of brightness has been previously overestimated. It is found to be proportional to
 instead of
instead of
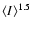 ,
where
,
where
 is the local average brightness at 100 . This scaling is in accordance with the fact that the brightness fluctuation level observed at a given angular scale on the sky is the sum of fluctuations of increasing amplitude with distance on the line of sight. 2) The spectral index of dust emission at scales between 5 arcmin and 12.5
is the local average brightness at 100 . This scaling is in accordance with the fact that the brightness fluctuation level observed at a given angular scale on the sky is the sum of fluctuations of increasing amplitude with distance on the line of sight. 2) The spectral index of dust emission at scales between 5 arcmin and 12.5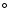 is
is
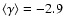 on average but shows significant variations over the sky. Bright regions have systematically steeper power spectra than diffuse regions. 3) The skewness and kurtosis of brightness fluctuations are high, indicative of strong non-Gaussianity. Unlike the standard deviation of the fluctuations, the skewness and kurtosis do not depend significantly on brightness, except in bright regions (>10 MJy sr-1) where they are systematically higher, probably due to contrasted structures related to star formation activity. 4) Based on our characterization of the 100 power spectrum we provide a prescription of the cirrus confusion noise as a function of wavelength and scale. 5) Finally we present a method based on a modification of Gaussian random fields to produce simulations of dust maps which reproduce the power spectrum and non-Gaussian properties of interstellar dust emission.
on average but shows significant variations over the sky. Bright regions have systematically steeper power spectra than diffuse regions. 3) The skewness and kurtosis of brightness fluctuations are high, indicative of strong non-Gaussianity. Unlike the standard deviation of the fluctuations, the skewness and kurtosis do not depend significantly on brightness, except in bright regions (>10 MJy sr-1) where they are systematically higher, probably due to contrasted structures related to star formation activity. 4) Based on our characterization of the 100 power spectrum we provide a prescription of the cirrus confusion noise as a function of wavelength and scale. 5) Finally we present a method based on a modification of Gaussian random fields to produce simulations of dust maps which reproduce the power spectrum and non-Gaussian properties of interstellar dust emission.
Key words: methods: statistical - ISM: structure - infrared: ISM - ISM: dust, extinction
The interstellar medium emission shows fluctuations at all observable scales,
revealing the self-similar nature of its density structure.
The physical processes responsible for this self-similarity of the interstellar medium (ISM) structure
is yet to be fully identified. It could be related to turbulent motions
but also to chemical and thermal instabilities which trigger phase transitions
and play an important role in shaping the medium.
Faced with the challenge to understand and characterize the
great structural complexity of interstellar emission,
astronomers have used several statistical tools
(power spectrum, correlation and structure functions,
wavelets, area-perimeter relation, principal component analysis,...)
on several interstellar tracers : molecules
(Brunt 2003; Bensch et al. 2001; Hobson 1992; Padoan et al. 2003; Stutzki et al. 1998; Falgarone et al. 1991),
atomic hydrogen
(Dickey et al. 2001; Miville-Deschênes et al. 2003a; Stanimirovic et al. 1999; Elmegreen et al. 2001; Crovisier & Dickey 1983; Green 1993; Stanimirovic & Lazarian 2001),
extinction (Padoan et al. 2002, 2006)
or
dust emission (Jewell 2001; Gautier et al. 1992; Ingalls et al. 2004; Abergel et al. 1996).
The analysis of the results of these tools is made difficult by projection,
and instrumental effects but also by the fact that no observation is a
perfect tracer of the total gas column density.
Several works have been dedicated to the understanding of these effects
(Padoan et al. 2001; Miville-Deschênes et al. 2003b; Elmegreen et al. 2001; Goldman 2000)
and specifically on how one can retrieve
the three-dimensional statistical properties of interstellar matter
from astronomical observations.
The recent theoretical progresses made in that area open interesting perspectives on
the use of statistical tools to determine the three-dimensional structure
of the gas and to identify privileged scales at which physical processes
are important.
The characterization of the statistical properties of
the interstellar emission is relevant for the understanding of
the physics of the ISM but is also of importance for studies where
interstellar emission is a nuisance. This is the case of the study of pre-stellar
cores in molecular clouds but also of the analysis of the
Cosmic Microwave Background (CMB) and Cosmic Infrared Background (CIB)
radiations. In these cases the interstellar emission is considered
as a noise (the so-called "cirrus noise'') for which one needs a
detailed statistical description in order to remove it and account
for it in the error budget.
In that respect the interstellar medium is a rather complex noise source
due to its highly non-white and non-Gaussian brightness fluctuations.
The present paper is a study of the power spectrum of interstellar dust emission
at 100 . The main goals are to use such analysis to put some constrains on the density structure of the interstellar medium
but also to propose a caveat for estimation and simulation of cirrus noise.
Gautier et al. (1992) showed that the power spectrum of
the IRAS 100 emission is characterized by a power law
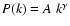 where the exponent
where the exponent
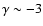 is independant of the brightness.
Moreover Gautier et al. (1992) showed that the normalisation
factor of the power spectrum depends on the mean brightness
is independant of the brightness.
Moreover Gautier et al. (1992) showed that the normalisation
factor of the power spectrum depends on the mean brightness
 of the
region considered, with
of the
region considered, with
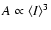 .
This study has been conducted on a relatively small number of regions
and at a time where the instrumental response of IRAS was not
well known. In this paper we would like to revisit the work of
Gautier et al. (1992) by extending it to 55% of the
sky
and by taking advantage of the recent reprocessing of the ISSA plates
by Miville-Deschênes & Lagache (2005).
.
This study has been conducted on a relatively small number of regions
and at a time where the instrumental response of IRAS was not
well known. In this paper we would like to revisit the work of
Gautier et al. (1992) by extending it to 55% of the
sky
and by taking advantage of the recent reprocessing of the ISSA plates
by Miville-Deschênes & Lagache (2005).
In Sect. 2 we present the data used in this analysis.
The results of the power spectrum analysis and the implication on the ISM density structure
are presented in Sect. 3.
An estimate of the cirrus noise level in the FIR-submm is provided in Sect. 4
and a method to produce realistic dust emission maps is given in Sect. 5.
Table 1:
Average, median and most probable value of the 100 brightness
over 98% of the sky at an angular resolution of 4.3 arcmin. The bottom portion of the table
gives the fraction of the sky with brightness lower than the value given in the left column.
2 The IRAS survey and IRIS
In 1983 the Infrared Astronomical Satellite (IRAS) has made a survey
of 98% of the sky in four bands : 12, 25, 60 and 100 .
Since then this dataset has been used extensively in almost
all area of astrophysics. In the early 90s the IRAS team
released the IRAS Sky Survey Atlas, a set of 430 fields with better calibration.
Each field is a
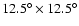 image with a pixel size of
image with a pixel size of
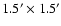 .
Recently Miville-Deschênes & Lagache (2005) reprocessed the ISSA maps
to correct for residual calibration defects and stripping. This new set
of ISSA plates, named IRIS, improves significantly the quality of the IRAS data
by lowering the noise level and improving the photometry of the four bands.
Our analysis is based on the 100 IRIS maps, available in native
.
Recently Miville-Deschênes & Lagache (2005) reprocessed the ISSA maps
to correct for residual calibration defects and stripping. This new set
of ISSA plates, named IRIS, improves significantly the quality of the IRAS data
by lowering the noise level and improving the photometry of the four bands.
Our analysis is based on the 100 IRIS maps, available in native
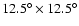 cartesian maps or in Healpix vector at http://www.cita.utoronto.ca/~mamd/IRIS/.
cartesian maps or in Healpix vector at http://www.cita.utoronto.ca/~mamd/IRIS/.
One important parameter of our analysis is the estimate of the instrumental
noise contribution to the power spectrum. We used only the IRIS maps for which we could
compute the contribution of the noise. To do so we used the fact that
the original ISSA plates are
the combination of up to three HCON images. The power spectrum
of the noise can be estimated by taking the power spectrum of
the difference between two HCON images, as described
in more details by Miville-Deschênes et al. (2002).
We selected only maps
for which each pixel has been observed at least two times so that a noise map can be computed,
which represent 236 maps (out of 430).
Most maps of our sample have an average brightness
 lower than 20 MJy sr-1.
This is representative of the whole sky statistics, as seen in Fig. 1
(see also Table 1)
where the probability density function (PDF) and cumulative histogram of the 100 brightness (CIB and zodiacal light subtracted)
over the whole sky is presented. This figure, together with Table 1, show that 90% of the sky has a brightness lower or equal to 20 MJy sr-1 (or
lower than 20 MJy sr-1.
This is representative of the whole sky statistics, as seen in Fig. 1
(see also Table 1)
where the probability density function (PDF) and cumulative histogram of the 100 brightness (CIB and zodiacal light subtracted)
over the whole sky is presented. This figure, together with Table 1, show that 90% of the sky has a brightness lower or equal to 20 MJy sr-1 (or
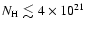 according to Lagache et al. 2000). This simple statistics of 100 brightness reveals that there is less than 2% of the sky with
according to Lagache et al. 2000). This simple statistics of 100 brightness reveals that there is less than 2% of the sky with
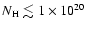 .
.
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f1a.ps}\par\includegraphics[width=7.5cm, draft=false]{6962f1b.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg26.gif) |
Figure 1:
Top: cumulative histogram of 100 surface brightness
over 98% of the sky (solid line): fraction of the sky with a brightness lower or equal to I100.
The dashed line represent what would be expected from a cylindrical disk (cosecant law).
Bottom: histogram of I100 brightness over the whole sky with bin scaled logarithmically.
For both curves we used the IRIS data projected on the Healpix grid (equal area pixels - http://healpix.jpl.nasa.gov)
with a pixel size of 1.7 arcmin (nside = 2048). A background of 0.78 MJy sr-1 was removed
from the data to take into account the cosmic infrared background and any zodiacal light residual
(Lagache et al. 2000; Hauser et al. 1998). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.3cm, draft=false]{6962f2.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg27.gif) |
Figure 2:
Power spectrum of
a typical IRIS map (point sources removed) with its associated noise power spectrum and the estimated CIB level (convolved
by the IRAS beam). The power law at large scale (small k) is due to the Galactic
dust emission. The cutoff at 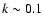 arcmin-1 is due to the IRAS beam. arcmin-1 is due to the IRAS beam. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f3.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg28.gif) |
Figure 3:
Spectral index 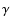 of the power spectrum for
our sample. Top. Histogram of the spectral index values. Median is -2.93,
average is -2.96 and standard deviation is 0.3.
Bottom. Spectral index as a function of average 100 brightness (CIB and zodiacal light subtracted).
of the power spectrum for
our sample. Top. Histogram of the spectral index values. Median is -2.93,
average is -2.96 and standard deviation is 0.3.
Bottom. Spectral index as a function of average 100 brightness (CIB and zodiacal light subtracted).
|
| Open with DEXTER |
3 Power spectrum analysis
The power spectrum has been extensively used in the analysis of image structure.
Working in Fourier (or spherical harmonics) space offers considerable advantages;
this formalism allows for the quadratic separation of uncorrelated sources
in the image (e.g., noise and signal)
and deconvolution of the instrumental function.
In addition working in Fourier space facilitates the comparison with
numerical simulations of turbulent flows.
The power spectrum of an image f(x,y) of Fourier Transform
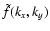 is computed from the
amplitude
A(kx, ky) defined as
A(k_x,k_y) = f(k_x,k_y)f^(k_x,k_y) =
| f(k_x,k_y) |^2.
The power spectrum
is computed from the
amplitude
A(kx, ky) defined as
A(k_x,k_y) = f(k_x,k_y)f^(k_x,k_y) =
| f(k_x,k_y) |^2.
The power spectrum
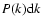 is an angular average
of
A(kx,ky) between k and
is an angular average
of
A(kx,ky) between k and
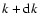 where
where
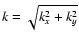 .
The method we use to compute the power spectrum is the one
described by Miville-Deschênes et al. (2002).
To minimize edges effects in Fourier space we apodize the image, from which
the mean was removed, using a cosine tapper of 15 pixels wide.
.
The method we use to compute the power spectrum is the one
described by Miville-Deschênes et al. (2002).
To minimize edges effects in Fourier space we apodize the image, from which
the mean was removed, using a cosine tapper of 15 pixels wide.
The main goal of our analysis is to characterize the power
spectrum of the interstellar diffuse emission, but several astrophysical
signals and artifacts may contribe to the power spectrum of the IRIS maps.
The power spectrum P(k) of the IRIS maps may be formalized by the following equation:
P(k) = B(k) (P_ism (k) + P_sources (k) + P_cib) + N(k)
where B(k) is the effective beam of the IRIS maps (which includes
the instrumental beam and the map making),
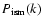 ,
,
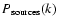 ,
,
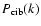 and N(k) are respectively the
contributions of the interstellar medium, detected point sources, the
unresolved CIB and the noise. All these contributions have to be estimated
to characterize the interstellar component.
and N(k) are respectively the
contributions of the interstellar medium, detected point sources, the
unresolved CIB and the noise. All these contributions have to be estimated
to characterize the interstellar component.
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f4.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg36.gif) |
Figure 4:
Normalisation P(0.01) of the power spectrum at 0.01 arcmin-1 of each map
as a function of its mean 100 brightness.
The solid line is our fit to the data (see Eqs. (5)
and (6)). The dashed line is the relation given by Gautier et al. (1992). |
| Open with DEXTER |
A typical power spectrum of a faint region of the sky is shown in
Fig. 2.
At large scales (low k), the power spectrum follows a power law
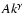 ;
this is the signature of the cirrus cloud emission (Gautier et al. 1992).
At smaller scales, the power spectrum flattens due to the combination
of the noise, point sources and the CIB. These three components
have a power spectrum signature that is flatter than the cirrus emission.
;
this is the signature of the cirrus cloud emission (Gautier et al. 1992).
At smaller scales, the power spectrum flattens due to the combination
of the noise, point sources and the CIB. These three components
have a power spectrum signature that is flatter than the cirrus emission.
As stated in Sect. 2,
the power spectrum of the noise is estimated by taking the power spectrum of
the difference between two HCON images. An example of a noise map
and its power spectrum is shown in Fig. 1 of Miville-Deschênes et al. (2002).
The power spectrum of the noise is well described by a k-1
power spectrum over most of the k range.
To subtract the contribution of bright point sources
we prefered to removed them directly in the IRIS maps
prior to compute the power spectrum. To do so
we used the point source extraction method
described by Miville-Deschênes & Lagache (2005).
For the CIB we assumed a flat power spectrum at the level determined
by Miville-Deschênes et al. (2002) (
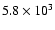 Jy2 sr-1 at 100 ).
Like Miville-Deschênes et al. (2002) we made the assumption that the effective
beam of the IRIS maps is Gaussian with a FWHM of 4.3 arcmin.
Jy2 sr-1 at 100 ).
Like Miville-Deschênes et al. (2002) we made the assumption that the effective
beam of the IRIS maps is Gaussian with a FWHM of 4.3 arcmin.
To obtain the spectral index of the dust emission in each IRIS map,
we computed the power spectrum of the point source subtracted map
and the power spectrum of the corresponding noise map.
We then subtracted the noise power spectrum,
divide the result by the Gaussian PSF and remove the CIB contribution.
Following what was done by Gautier et al. (1992) we have fitted the power spectrum
of the Galactic emission in the
range between k=0.004 and k=0.08 arcmin-1 using a power law:
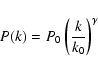 |
(1) |
where P0 is the power spectrum value at k0=0.01 arcmin-1.
The power spectrum of the interstellar emission is in general very
well fitted by such a power law.
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f5.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg40.gif) |
Figure 5:
Standard deviation as a function of the average interstellar brightness
at 100
for each map of our sample. The noise level of each map and the CIB fluctuation level
(0.09 MJy sr-1 - see Miville-Deschênes et al. 2002)
were removed quadratically from 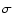 .
The solid line represents the two regimes given by Eqs. (7)
and (8). .
The solid line represents the two regimes given by Eqs. (7)
and (8). |
| Open with DEXTER |
The compilation of the power spectrum spectral index measured on our sample of 236 maps is shown
in Fig. 3.
The most probable spectral index is
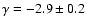 ,
in accordance with what was measured
by Gautier et al. (1992). On the other hand, contrary to Gautier et al. (1992) who
did their statistical analysis on only four regions, our larger sample allowed us to
highlight a significant variation of the spectral index with the average brightness of the maps.
Brighter regions on the sky tend to have a steeper power spectrum (see the lower panel of Fig. 3).
The decrease of the spectral index with brightness can be approximated by:
,
in accordance with what was measured
by Gautier et al. (1992). On the other hand, contrary to Gautier et al. (1992) who
did their statistical analysis on only four regions, our larger sample allowed us to
highlight a significant variation of the spectral index with the average brightness of the maps.
Brighter regions on the sky tend to have a steeper power spectrum (see the lower panel of Fig. 3).
The decrease of the spectral index with brightness can be approximated by:
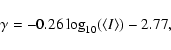 |
(2) |
where
 is the mean 100 brightness of the
is the mean 100 brightness of the
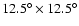 map.
map.
![\begin{figure}
\par\includegraphics[width=16.5cm, draft=false]{6962f6_col.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg44.gif) |
Figure 6:
Left: a typical IRIS map at 100 . Center: a classical fBm map with same power spectrum as the IRIS map shown on the left.
This fBm has Gaussian brightness fluctuations at all scale and everywhere.
Right: a modified version of the classical fBm with only positive values and the same average,
standard deviation and skewness values as the IRIS map. The fBm has been modified in order to reproduce
the
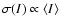 relation which results in stronger brightness fluctuations in brighter
regions.
relation which results in stronger brightness fluctuations in brighter
regions. |
| Open with DEXTER |
Regarding the normalization of the power spectrum Gautier et al. (1992) estimated that
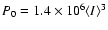 ,
where
,
where
 is the mean 100 brightness at the 12.5
is the mean 100 brightness at the 12.5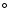 scale,
given in MJy sr-1, and P0 is in Jy2 sr-1.
In Fig. 4 we present the variation of P0 with
scale,
given in MJy sr-1, and P0 is in Jy2 sr-1.
In Fig. 4 we present the variation of P0 with
 for our sample,
together with the relation of Gautier et al. (1992) (dashed line).
The result of our analysis showed that the relation of Gautier et al. (1992)
generally overestimates the fluctuation level at a given mean brightness.
This discrepancy could be partly attributed to the fact that we used better calibrated IRAS data
compare to the early IRAS product used by Gautier et al. (1992).
On the other hand it is important to point out that
the normalization relation given by Gautier et al. (1992) is compatible
with the fact that they used only two faint (
for our sample,
together with the relation of Gautier et al. (1992) (dashed line).
The result of our analysis showed that the relation of Gautier et al. (1992)
generally overestimates the fluctuation level at a given mean brightness.
This discrepancy could be partly attributed to the fact that we used better calibrated IRAS data
compare to the early IRAS product used by Gautier et al. (1992).
On the other hand it is important to point out that
the normalization relation given by Gautier et al. (1992) is compatible
with the fact that they used only two faint (
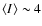 MJy sr-1)
and two bright regions (
MJy sr-1)
and two bright regions (
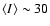 MJy sr-1).
MJy sr-1).
Using a much larger sample than Gautier et al. (1992) we found that the normalization of the power spectrum
is better described by two regimes (solid line in Fig. 4):
on 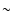 80% of the sky P(0.01) is proportional to
80% of the sky P(0.01) is proportional to
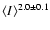 instead of
instead of
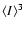 .
For
.
For
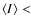 10 MJy sr-1 we find
10 MJy sr-1 we find
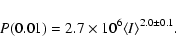 |
(3) |
and for
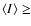 10 MJy sr-1 we find
10 MJy sr-1 we find
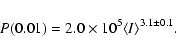 |
(4) |
A similar trend was also observed by Jeong et al. (2005) using ISOPHOT observations (see their Fig. 12).
Another way of looking at the
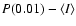 relation is to plot the
standard deviation
relation is to plot the
standard deviation
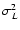 of each map as a function of
of each map as a function of
 (see Fig. 5).
Here we made sure to remove quadratically the contribution of the instrumental noise
and the CIB to each values of
(see Fig. 5).
Here we made sure to remove quadratically the contribution of the instrumental noise
and the CIB to each values of
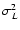 .
Like for the power spectrum normalisation, two regimes are apparent in the
.
Like for the power spectrum normalisation, two regimes are apparent in the
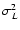 vs.
vs.
 relation with a transition around
relation with a transition around
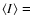 10 MJy sr-1.
Separating the data sample in two gives the following fits.
for
10 MJy sr-1.
Separating the data sample in two gives the following fits.
for
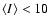 MJy sr-1:
MJy sr-1:
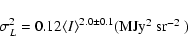 |
(5) |
and for
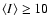 MJy sr-1
MJy sr-1
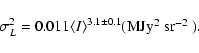 |
(6) |
Most spectral indexes measured here fall in the range between
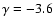 to
to
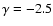 .
This is compatible with what was found by Wright (1998)
(
.
This is compatible with what was found by Wright (1998)
(
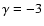 )
in a power spectrum analysis of the DIRBE data at 60, 100, 140 and 240 on
scales greater than 40 arcminutes.
Other studies also estimated the equivalent of the power spectrum spectral index
of the 100 emission using the area-perimeter relation.
Following Stutzki et al. (1998) there is a direct relation between the fractal dimension
D deduced from the area-perimeter relation (
)
in a power spectrum analysis of the DIRBE data at 60, 100, 140 and 240 on
scales greater than 40 arcminutes.
Other studies also estimated the equivalent of the power spectrum spectral index
of the 100 emission using the area-perimeter relation.
Following Stutzki et al. (1998) there is a direct relation between the fractal dimension
D deduced from the area-perimeter relation (
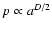 )
and the spectral
index
)
and the spectral
index 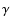 of the power spectrum (
of the power spectrum (
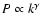 ):
):
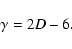 |
(7) |
Bazell & Desert (1988) and Dickman et al. (1990) measured
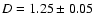 (corresponding to
(corresponding to
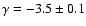 )
for relatively bright regions at 100 (
)
for relatively bright regions at 100 (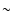 10 MJy sr-1).
These values of
10 MJy sr-1).
These values of 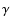 are rather high (steep power spectrum)
but not incompatible with our analysis. In a similar analysis on fainter regions Vogelaar & Wakker (1994)
measured
are rather high (steep power spectrum)
but not incompatible with our analysis. In a similar analysis on fainter regions Vogelaar & Wakker (1994)
measured
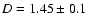 ,
corresponding to
,
corresponding to
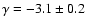 which is very similar
to our results.
which is very similar
to our results.
The interpretation of these results in terms of the density structure of the ISM
and the comparison with what is deduced from gas tracers
can only be done by considering a model for the 100 emission.
At this wavelength the interstellar emission is dominated by the grey body emission
from big dust grains at thermal equilibrium with the radiation field (Desert et al. 1990).
For a given model of the composition of dust grain (Li & Draine 2001; Desert et al. 1990)
the conversion of 100 brightness to gas column density depends on the
gas/dust mass ratio (known to be rather constant in the ISM) and on the big grain equilibrium
temperature. The big grain equilibrium temperature is related to the local radiation field strength
and spectrum which depends on the presence or not of nearby heating sources and on the extinction.
Variation of the dust equilibrium temperature can also occur locally due to variation of
the grain structure which can affect their emissivity![[*]](/icons/foot_motif.gif) .
.
In diffuse regions of the sky at high Galactic latitudes, far from star-forming regions,
clouds are optically thin to stellar radiation,
and the radiation field is uniform which result in very limited variations
of dust equilibrium temperature.
Localised variations of the dust grain temperature were observed in cirrus clouds (Bernard et al. 1999),
but overall several studies (Boulanger et al. 1996; Boulanger & Pérault 1988) showed a strong correlation between
the 100 micron and the hydrogen column density which is in favor of
a rather uniform gas/dust ratio and limited variations of the dust temperature.
Based on these results we believe that the 100 micron can not be used as a
perfect surrogate for gas column density but overall it does not introduce
a systematic bias in the determination of the column density power spectrum.
In this context, and considering that the power spectrum of the column density gives
directly the power spectrum of the density structure (Miville-Deschênes et al. 2003b),
we consider that the 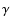 values measured here in the diffuse regions (for
values measured here in the diffuse regions (for
 < 10 MJy sr-1)
are typical of the spectral index of the density field in three dimensions in the solar neighborhood.
< 10 MJy sr-1)
are typical of the spectral index of the density field in three dimensions in the solar neighborhood.
In bright regions (
 >10 MJy sr-1) the power spectrum is observed to be significantly steeper
(Fig. 3).
A steepening of the power spectrum with brightness was also found by Kiss et al. (2003)
on 90-200 ISOPHOT observations.
We observed that this steepening coincides with a departure from the
>10 MJy sr-1) the power spectrum is observed to be significantly steeper
(Fig. 3).
A steepening of the power spectrum with brightness was also found by Kiss et al. (2003)
on 90-200 ISOPHOT observations.
We observed that this steepening coincides with a departure from the
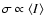 relation (see Fig. 4) and a systematic increase of the skewness and kurtosis of the brightness
fluctuations (see Fig. 11).
This variation of
relation (see Fig. 4) and a systematic increase of the skewness and kurtosis of the brightness
fluctuations (see Fig. 11).
This variation of 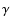 with
with
 might reflect, at least in part, local variations of the density power spectrum.
It could also be attributed to the effect of gravity or anisotropic radiation fields
which would both increase the large scale coherence (like in star forming regions or at Galactic scale in the plane)
and therefore steepen the power spectrum of the 100 emission. The effect of extinction
in these parts of the sky will also induce important dust temperature variations which will affect
the power spectrum. These effects will certainly have an impact on the observed brightness fluctuations
and make the interpretration of the power spectrum difficult.
might reflect, at least in part, local variations of the density power spectrum.
It could also be attributed to the effect of gravity or anisotropic radiation fields
which would both increase the large scale coherence (like in star forming regions or at Galactic scale in the plane)
and therefore steepen the power spectrum of the 100 emission. The effect of extinction
in these parts of the sky will also induce important dust temperature variations which will affect
the power spectrum. These effects will certainly have an impact on the observed brightness fluctuations
and make the interpretration of the power spectrum difficult.
To compare the results obtained here with statistical analysis of gas emission,
it is important to point out that the 100 emission traces all the interstellar components:
atomic, molecular and ionized gas. Gas observations (21 cm and CO) showed that
diffuse and dense gas have different density structure.
In general regions of cold and dense gas have stronger small scale fluctuations
(and therefore a flatter density power spectrum
- see for instance Stutzki et al. (1998) who measured
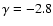 on CO observations of the Polaris flare,
a dense cirrus cloud with a significant fraction of molecular gas)
than regions of diffuse gas (Miville-Deschênes et al. (2003a) measured
on CO observations of the Polaris flare,
a dense cirrus cloud with a significant fraction of molecular gas)
than regions of diffuse gas (Miville-Deschênes et al. (2003a) measured
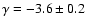 on 21 cm observations of a diffuse cirrus cloud).
This behavior seems also in accordance with numerical simulations (see Audit & Hennebelle 2005, for instance).
on 21 cm observations of a diffuse cirrus cloud).
This behavior seems also in accordance with numerical simulations (see Audit & Hennebelle 2005, for instance).
This could reflect the fact that molecular tracers like CO reveal only the density structure of
dense regions and miss the more diffuse and large scale structure of molecular clouds.
In that respect dust emission would be a more reliable tracer of the global density structure of
the ISM as the observed spectral index at 100 is a weighted mean of the various contributions
from dense and diffuse media on the line of sight.
One striking example of that comes from the direct comparison of infrared and 21 cm emission in high-latitude clouds
where dust emission usually shows stronger brightness
fluctuations at small scale than , this being attributed to the presence of localized molecular regions
(see for instance Joncas et al. 1992).
Here we would like to propose one interpretation for the scaling of
the power spectrum normalization P(0.01) (or equivalently the brightness
standard deviation 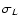 )
with average brightness
)
with average brightness
 (Eqs. (5) and (7)).
(Eqs. (5) and (7)).
Lets consider a three-dimensional scalar field 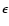 ,
which could be a
dust emissivity field, of size
,
which could be a
dust emissivity field, of size 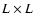 on the plane of the sky and of depth H.
In the case of constant dust temperature and neglecting opacity
effects, the projection of this 3D field on 2D would correspond to a dust emission map:
on the plane of the sky and of depth H.
In the case of constant dust temperature and neglecting opacity
effects, the projection of this 3D field on 2D would correspond to a dust emission map:
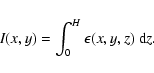 |
(8) |
What would be the relation between the average and standard deviation of the projected brightness
for such a field?
The average brightness of the dust map is simply
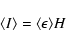 |
(9) |
where
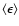 is the volume averaged of
is the volume averaged of 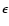 .
.
On the other hand to compute the standard deviation of the dust map (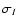 )
one should consider that brightness fluctuations are added quadratically
along the line of sight. Each slice dz of the cube contributes
)
one should consider that brightness fluctuations are added quadratically
along the line of sight. Each slice dz of the cube contributes
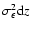 to
to
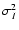 :
:
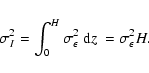 |
(10) |
Combined with Eq. (11) this leads to
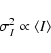 |
(11) |
which is not what is observed.
Cartesian coordinates used in the previous demonstration is
in fact not a realistic representation when it comes to estimate 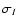 .
In fact, with the increase of the depth of the line of sight z,
a given angular scale
.
In fact, with the increase of the depth of the line of sight z,
a given angular scale 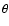 on the sky corresponds to increasing physical size l :
on the sky corresponds to increasing physical size l :
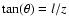 .
.
In the integral of Eq. (12) we made the assumption that
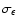 is the standard deviation at scale L. In fact we should have taken into account
that
is the standard deviation at scale L. In fact we should have taken into account
that
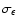 varies with z.
For a power spectrum following a power law (
varies with z.
For a power spectrum following a power law (
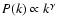 )
the
variance of brightness fluctuations as a function
of scale l is (Brunt & Heyer 2002):
)
the
variance of brightness fluctuations as a function
of scale l is (Brunt & Heyer 2002):
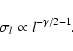 |
(12) |
Therefore we can rewrite Eq. (12)
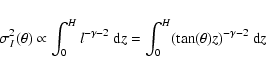 |
(13) |
which leads to
There are two important results to extract from the previous equation. First
the fact that we observe structure of increasing physical size with zat a given angular scale 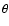 does not modify the slope of the power law for
does not modify the slope of the power law for
 :
both
:
both
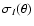 and
and
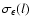 have the same spectral index
have the same spectral index
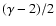 .
Secondly the dependence of
.
Secondly the dependence of 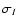 on
on
 is now related to the spectral index
is now related to the spectral index 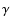 .
For a typical value of
.
For a typical value of 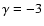 we obtain
we obtain
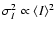 which is exactly
the observed relation for
which is exactly
the observed relation for
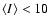 MJy sr-1.
MJy sr-1.
For larger
 the departure from a simple
the departure from a simple
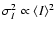 can be explained
partly because the spectral index
can be explained
partly because the spectral index 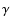 decreases but most of all it is important to notice
that brightness fluctuations become highly non-Gaussian (high skewness and kurtosis -
see Fig. 11). In this regime the standard deviation becomes
significantly affected by non-Gaussian fluctuations which could be related to localized
star forming regions in the image.
decreases but most of all it is important to notice
that brightness fluctuations become highly non-Gaussian (high skewness and kurtosis -
see Fig. 11). In this regime the standard deviation becomes
significantly affected by non-Gaussian fluctuations which could be related to localized
star forming regions in the image.
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f7.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg99.gif) |
Figure 7:
Cirrus noise at 100 for a 1 m diffraction limited telescope
( FHWM = 33 arcsec) as a function of I100 brightness.
Solid line is our estimate and dotted line is the estimate of Helou & Beichman (1990). |
| Open with DEXTER |
4 Cirrus noise
In this section we use the properties of the power spectrum of 100 emission
to estimate the level of cirrus confusion noise of dust emission.
To estimate the level of fluctuations as a function of scale and brightness
it is convenient to use the real-space representation given by Eq. (14), as opposed
to a Fourier one.
Using the value of 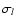 measured at
measured at
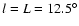 (see Eqs. (7) and (8))
we can normalize Eq. (14) and estimate
the level of brightness fluctuation of interstellar dust (in MJy sr-1) at scale l (in degree)
and wavelength
(see Eqs. (7) and (8))
we can normalize Eq. (14) and estimate
the level of brightness fluctuation of interstellar dust (in MJy sr-1) at scale l (in degree)
and wavelength 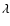 .
For the two regimes identified in this study
(lower and higher than
.
For the two regimes identified in this study
(lower and higher than
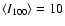 MJy sr-1) we have the following relations:
MJy sr-1) we have the following relations:
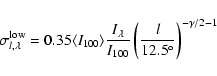 |
(15) |
and
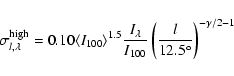 |
(16) |
where
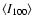 is in MJy sr-1,
is in MJy sr-1, 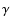 is given by Eq. (4)
and
is given by Eq. (4)
and
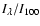 is an estimate of the dust brightness ratio at wavelength
is an estimate of the dust brightness ratio at wavelength 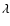 and 100 . Such ratio can be estimated using a grey body model like the one of Desert et al. (1990)
and 100 . Such ratio can be estimated using a grey body model like the one of Desert et al. (1990)
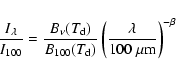 |
(17) |
where
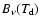 is the Planck function at grain temperature
is the Planck function at grain temperature 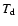 and
and 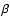 is the dust emissivity index.
Typical values in the diffuse ISM for the dust temperature
is the dust emissivity index.
Typical values in the diffuse ISM for the dust temperature 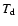 and emissivity index
and emissivity index 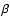 are
are
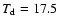 K and
K and 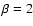 .
In the sub-millimeter and millimeter ranges the dust emission departs from this simple model and
one might want to use a combination of two dust components (see Finkbeiner et al. 1999, for an example of such model).
.
In the sub-millimeter and millimeter ranges the dust emission departs from this simple model and
one might want to use a combination of two dust components (see Finkbeiner et al. 1999, for an example of such model).
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f8.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg113.gif) |
Figure 8:
Contrast of interstellar emission: the standard deviation
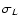 is the standard deviation of interstellar fluctuations at the
is the standard deviation of interstellar fluctuations at the 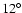 scale.
Left: contrast values as a function of average brightness.
Right: histogram of contrast values. According to Eq. (7), the contrast is close to
constant for
scale.
Left: contrast values as a function of average brightness.
Right: histogram of contrast values. According to Eq. (7), the contrast is close to
constant for
 lower than 10 MJy sr-1. Outliers at low brightness corresponds to regions
where there are bright structures on a very low level background, like the Magellanic Clouds.
lower than 10 MJy sr-1. Outliers at low brightness corresponds to regions
where there are bright structures on a very low level background, like the Magellanic Clouds. |
| Open with DEXTER |
Equations (17) and (18) give the surface brightness fluctuation level of dust
at any scale, brightness and wavelength. One useful specific case to consider is the contribution
of cirrus noise at the scale of an instrument beam, to estimate the effective point source detection level for instance.
Following Helou & Beichman (1990) and Gautier et al. (1992) we consider the cirrus noise level at a scale two times the
beam size b (i.e., l=2b, where b is the beam FWHM).
This noise level (in mJy/beam) at wavelength 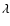 is simply
is simply
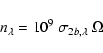 |
(18) |
where 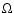 is the beam in steradian
is the beam in steradian
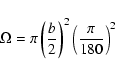 |
(19) |
and b is in degrees.
The cirrus noise in mJy/beam is then given by
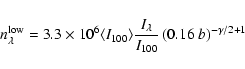 |
(20) |
and
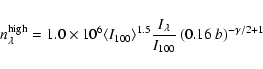 |
(21) |
where 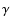 is still given by Eq. (4).
is still given by Eq. (4).
These relations can be compared with the prescription of Helou & Beichman (1990) often used
to estimate cirrus confusion noise. These authors considered the situation where the beam of the instrument
is given by the diffraction limit of a telescope of diameter D. In this case
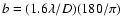 .
.
![\begin{figure}
\par\includegraphics[width=16.5cm, draft=false]{6962f9_col2.eps} %\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg120.gif) |
Figure 9:
Wavelet decomposition of the IRIS map shown in
Fig. 6-left.
Top: wavelet coefficients map at scales 4, 8, 16 and 32 pixels (1 pixel = 1.5').
Bottom: Histogram of the wavelet coefficients in linear-log.
A Gaussian fit to the histogram is superposed highlighting the non-Gaussian behavior. |
| Open with DEXTER |
The comparison between our estimate of the cirrus noise and the one given by Helou & Beichman (1990) for a 1m telescope
at 100 is shown in Fig. 7.
The difference is important in several aspects. First at low brightness the slopes of
n(I100) are very different,
due to the
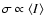 regime revealed in our study. The change of slope has the implication
that our estimate of the cirrus noise in low brightness regions is much higher. This is also due to
the flattening of the power spectrum index
regime revealed in our study. The change of slope has the implication
that our estimate of the cirrus noise in low brightness regions is much higher. This is also due to
the flattening of the power spectrum index 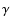 at low brightness.
On the other hand our cirrus noise estimate is much lower than the estimate of Helou & Beichman (1990)
at large brightness. This effect is caused by the fact that we observe steeper power spectra
in bright regions. Therefore the brightness fluctuations are much smaller when extrapolated to small scale.
at low brightness.
On the other hand our cirrus noise estimate is much lower than the estimate of Helou & Beichman (1990)
at large brightness. This effect is caused by the fact that we observe steeper power spectra
in bright regions. Therefore the brightness fluctuations are much smaller when extrapolated to small scale.
The prescriptions given here to estimate the level of cirrus noise is only indicative.
It would be strictly correct for a Gaussian field which is not the case of interstellar emission.
As it will be described in more details in the next section, dust emission
has non-Gaussian brightness fluctuations at all scales.
For the sake of data interpretation, confusion estimate
or tests of component separation algorithms (including point source extraction)
it is useful to produce realistic simulations of dust emission maps
with proper non-Gaussian properties. It is the topic of the next section.
![\begin{figure}
\par\includegraphics[width=16.5cm, draft=false]{6962f10_col2.eps} %\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg121.gif) |
Figure 10:
Wavelet decomposition of the classical fBm map shown
in Fig. 6-center. See Fig. 9 for details. |
| Open with DEXTER |
5 Construction of artificial dust emission maps
Fractional Brownian motions (fBm, also known as Gaussian random fields) are often
used to simulate interstellar emission (e.g., Miville-Deschênes et al. 2003b; Stutzki et al. 1998).
By construction such objects can reproduce the power spectrum of any image,
with the limitation that its phase is random. A comparison of a typical IRIS map and a
fBm with the same power spectrum is given in Fig. 6.
The fBm reproduces well the self-similar structure of the interstellar emission.
On the other hand the fBm seems smoother and less contrasted than the observation.
Because of the Gaussian nature of their fluctuations, fBms with positive values only
can't have a large contrast.
If we define the contrast of a map I as
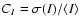 ,
positive fBms are restricted
to
,
positive fBms are restricted
to
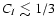 as the average
as the average
 needs to be greater than
needs to be greater than 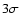 to have
only positive values
to have
only positive values![[*]](/icons/foot_motif.gif) .
This can be compared with the contrast of real IRIS map given in Fig. 8,
where we used
.
This can be compared with the contrast of real IRIS map given in Fig. 8,
where we used
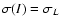 (i.e., the standard deviation at a scale of 12.5
(i.e., the standard deviation at a scale of 12.5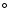 ).
The median contrast is 0.3 which indicate the limitation of the use of fBms used to simulate realistic
infrared dust maps. In addition one would notice that the contrast increases significantly
with brightness and especially for
).
The median contrast is 0.3 which indicate the limitation of the use of fBms used to simulate realistic
infrared dust maps. In addition one would notice that the contrast increases significantly
with brightness and especially for
 greater than 10 MJy sr-1, in accordance with Eqs. (7)
and (8).
In addition, CI will increase with scale as
greater than 10 MJy sr-1, in accordance with Eqs. (7)
and (8).
In addition, CI will increase with scale as 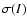 depends on scale
(according to Eq. (14))
but not
depends on scale
(according to Eq. (14))
but not
 (at high Galactic latitude).
Based only on the contrast, the use of fBm becomes limited to small (a few degrees) and faint regions of the sky.
(at high Galactic latitude).
Based only on the contrast, the use of fBm becomes limited to small (a few degrees) and faint regions of the sky.
Apart from the global contrast limitation, there is a fundamental difference between
fBms and observations which is related to the non-Gaussian properties of the interstellar
emission.
The brightness fluctuations seen in infrared dust maps show contrasted structures, often filaments,
that reflect their non-Gaussian nature. Using a wavelet decomposition
of 100 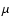 m maps, Jewell (2001) showed clearly that, contrary to random-phase realisations,
the histograms of brightness fluctuations at a given scale are highly non-Gaussian.
Abergel et al. (1996) and Aghanim et al. (2003) gave also striking examples of that.
Wavelet transforms are powerful
tools to study the statistical moments higher than two and estimate the non-Gaussian
properties of images (Aghanim et al. 2003).
They complement the power spectrum analysis which gives only the
variation of the second moment - the standard deviation - with scale.
m maps, Jewell (2001) showed clearly that, contrary to random-phase realisations,
the histograms of brightness fluctuations at a given scale are highly non-Gaussian.
Abergel et al. (1996) and Aghanim et al. (2003) gave also striking examples of that.
Wavelet transforms are powerful
tools to study the statistical moments higher than two and estimate the non-Gaussian
properties of images (Aghanim et al. 2003).
They complement the power spectrum analysis which gives only the
variation of the second moment - the standard deviation - with scale.
To illustrate that we present in Figs. 9 and 10 the
wavelet decomposition obtained using the "à trou'' algorithm (Starck & Murtagh 1998)
for the IRIS and fBm maps of Fig. 6.
As expected the distribution of brightness fluctuations at a given scale are Gaussian
for fBms (see Fig. 10). On the other hand
the distribution of wavelet coefficients of an IRIS map (see Fig. 9) follows an
asymmetrical distribution with exponential wings, which results in significant
skewness and kurtosis.
In Fig. 11 are compiled
the skewness and kurtosis of the wavelet coefficients found for all 236 maps of our sample,
for scales from l=4 pixels (12 arcmin) to 32 pixels (48 arcmin).
There is a not a strong correlation of the skewness and kurtosis with brightness, unlike
for the standard deviation (Fig. 5).
There is a slight increase of skewness and kurtosis at small scale and low brightness
that should be attributed to noise and CIB![[*]](/icons/foot_motif.gif) .
On the other hand one would note a sharp increase of the skewness and kurtosis
for
.
On the other hand one would note a sharp increase of the skewness and kurtosis
for
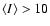 MJy sr-1.
MJy sr-1.
Finally, apart from the global difference of the wavelet coefficient distribution between fBms and
observations, one would notice that brightness fluctuations at a given scale in the IRIS map
are generally greater in bright regions of the map, contrary to the fBm where the amplitude of
fluctuations at a given scale is independent of position.
This just reflects the fact that brightness fluctuations are generally stronger in bright region,
in accordance with Eqs. (7) and (8).
By construction fBms do not behave like that; the amplitude of fluctuations is uniform and independant
of local variations of the average brightness.
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f11.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg130.gif) |
Figure 11:
Skewness ( top) and Kurtosis ( bottom)
of the wavelet coefficients from l=4 to 32 pixels for each IRIS map of our sample. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.5cm, draft=false]{6962f12_col2.eps} %\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg131.gif) |
Figure 12:
Wavelet decomposition of the modified fBm map shown
in Fig. 6-right. See Fig. 9 for details. The histogram
of the wavelet coefficients of the IRIS map are over plotted (dots) showing how well the
modified fBm reproduces the observed statistics. |
| Open with DEXTER |
In this section we propose a method to modify fBms such that they better reproduce
the statistical properties of the infrared emission. We want
to produce simulations of dust emission maps that would satisfy a given number of assumptions:
- 1.
- positive values only;
- 2.
- power spectrum following a power law :
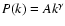 ;
;
- 3.
- greater brightness fluctuations in bright regions (following
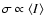 ).
).
Several attempts have been made to generate non-Gaussian maps, especially to produce
non-Gaussian realizations of the Cosmic Microwave Background (CMB) (Rocha et al. 2005; Vio et al. 2002,2001).
In general these methods involve a modification of a Gaussian realization but they don't
comply with all our requirements. Especially in the context of the CMB there is no need
to produce maps with only positive values and to
have stronger brightness fluctuations in bright regions.
Here is how we proceeded to construct a non-Gaussian fBm map
with the same statistical properties as an
IRIS map I and with only positive values.
The method presented here is similar to the one
used by Elmegreen (2002); Brunt & Heyer (2002).
First we generate a classical fBm F with same standard deviation as map I.
We add an offset to force all values to be positives
and to be as close as possible to the average of I.
We then create a modified fBm F' such that:
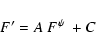 |
(22) |
and such that F' has the same average, standard deviation and skewness than Iand only positive values. The parameters A, 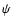 and C are thus constrained iteratively
so to match the first three statistical moments of the map I.
Such a modified fBm is shown in Fig. 6 and its wavelet decomposition
in Fig. 12. The effect of the exponent
and C are thus constrained iteratively
so to match the first three statistical moments of the map I.
Such a modified fBm is shown in Fig. 6 and its wavelet decomposition
in Fig. 12. The effect of the exponent 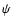 is to produce
greater fluctuations in bright regions, in accordance with the observations. The
wavelet decomposition is quite illustrative in that respect. In particular the
histograms of wavelet coefficients are almost impossible to discriminate from the
ones of the IRIS map.
is to produce
greater fluctuations in bright regions, in accordance with the observations. The
wavelet decomposition is quite illustrative in that respect. In particular the
histograms of wavelet coefficients are almost impossible to discriminate from the
ones of the IRIS map.
The key parameter in this transformation is 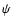 which
control the amount of non-Gaussianity introduced in the map.
We did such a simulation for each of the 236 maps of our sample and the results are summarized
in Fig. 13. One would note
the scaling of
which
control the amount of non-Gaussianity introduced in the map.
We did such a simulation for each of the 236 maps of our sample and the results are summarized
in Fig. 13. One would note
the scaling of 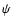 with skewness
with skewness 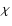 ,
which clearly indicate the impact
of that parameter on the non-Gaussianity of the map. The median value of
,
which clearly indicate the impact
of that parameter on the non-Gaussianity of the map. The median value of 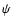 is
is 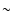 2 (see Fig. 13).
2 (see Fig. 13).
Even though it reproduces very well several statistical properties of the observed emission,
it is important to note that one important limitation of this method
is that it produces only isotropic fluctuations and failed to reproduce to filamentary structure
of the ISM.
To estimate the capabilities and performances of some instruments at observing
diffuse interstellar emission it is often needed to extrapolate low resolution
observations to smaller angular scales. One example of that would be the estimate
of the diffuse emission structure that will be observed at a scale of 8 arcsec by Herschel-PACS
given the IRAS data at 5 arcmin resolution.
In this context it is useful to produce constrained realisations of the interstellar diffuse
emission based on low resolution observations. The statistical analysis presented here
provides a theoretical basis (
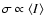 )
on which to add small scales using
larger scale informations.
)
on which to add small scales using
larger scale informations.
Given a low resolution map I0 characterized by a beam B0, a higher resolution I1of beam B1 can be computed using the following method:
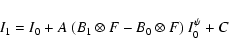 |
(23) |
where F is a classical positive fBm map,
and A, 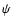 and C are determined as described in the previous section.
In the previous equation the difference
and C are determined as described in the previous section.
In the previous equation the difference
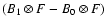 extends the
structure up to the higher resolution beam B1.
The modulation of the small scale fluctuations by
extends the
structure up to the higher resolution beam B1.
The modulation of the small scale fluctuations by
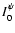 assures
that they follow the
assures
that they follow the
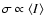 relation.
relation.
In this paper we presented an analysis of the power spectrum and wavelet decomposition
of the IRIS/IRAS 100 emission over 55% of the sky.
The main goals of this work were 1) to review and extend the study of Gautier et al. (1992)
using better calibrated IRAS maps, estimates of the noise and CIB contributions
and a larger sample; 2) provide a more precise prescription for cirrus noise; and 3)
suggest a technique to simulate dust emission map with proper statistical properties.
We found an average spectral index (
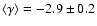 )
compatible with Gautier et al. (1992) (
)
compatible with Gautier et al. (1992) (
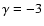 )
but with a significant variation from
)
but with a significant variation from
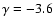 to
to
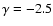 .
Considering that 100 emission is a relatively reliable tracer of column density in faint regions,
these values of
.
Considering that 100 emission is a relatively reliable tracer of column density in faint regions,
these values of 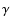 should be representative of the spectral index of density in three dimensions
in the local interstellar medium. The comparison with other tracers leads to the conclusion
that there is most probably a significant contribution from cold gas
to the brightness fluctuations observed.
We also found a slight variation of
should be representative of the spectral index of density in three dimensions
in the local interstellar medium. The comparison with other tracers leads to the conclusion
that there is most probably a significant contribution from cold gas
to the brightness fluctuations observed.
We also found a slight variation of 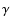 with
with
 which could be explained by the
impact of gravity or spatial variations of dust temperature in star forming regions.
which could be explained by the
impact of gravity or spatial variations of dust temperature in star forming regions.
We also found that the amplitude of the brightness fluctuations were
generally overestimated by Gautier et al. (1992). In regions with a 100 average brightness
 lower than 10 MJy sr-1 the brightness fluctuation level is proportional to
lower than 10 MJy sr-1 the brightness fluctuation level is proportional to
 and
not
and
not
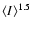 as stated by Gautier et al. (1992).
We showed that this behavior can be explained by the fact that
the brightness fluctuation level observed at a given angular size on the sky
is the sum of fluctuations of increasing amplitude with distance.
as stated by Gautier et al. (1992).
We showed that this behavior can be explained by the fact that
the brightness fluctuation level observed at a given angular size on the sky
is the sum of fluctuations of increasing amplitude with distance.
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f13.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg139.gif) |
Figure 13:
Top: Histogram of all the exponent 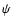 used to simulate realistic fBm for each IRIS map of our sample. Bottom:
Exponent
used to simulate realistic fBm for each IRIS map of our sample. Bottom:
Exponent 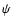 as a function of the skewness
as a function of the skewness 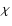 of each IRIS map.
The straight line is
of each IRIS map.
The straight line is
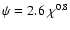 . . |
| Open with DEXTER |
This detailed description of the power spectrum properties of the 100 emission
allowed us to determine a new prescription of the cirrus confusion noise in the
far-infrared and sub-millimeter as a function of column density and scale.
On the other hand we stressed that this cirrus noise estimate relies on the hypothesis of Gaussian
fluctuations, which is clearly not the case for interstellar emission.
In that context we proposed a method to
modify Gaussian random fields such that it reproduces the power spectrum but also
the level of non-Gaussianity observed which is related to
the fact that bright regions have stronger brightness fluctuations than faint ones.
Such images could be used to tests component separation algorithms (including point source extraction)
that have to deal with non-Gaussian components.
The main limitation of the technique we propose is that it does not reproduce the obvious filamentarity
seen in observations.
Acknowledgements
Some of the results in this paper have been obtained using the HEALPix package
(Gorski et al. 2005). This work was supported by the Canadian Space Agency.
It is a pleasure to thank J. Richard Bond for enlightening discussions.
- Abergel,
A., Boulanger, F., Delouis, J. M., Dudziak, G., &
Steindling, S. 1996, , 309, 245
- Aghanim, N.,
Kunz, M., Castro, P. G., & Forni, O. 2003, , 406, 797
(In the text)
- Audit, E., &
Hennebelle, P. 2005, , 433, 1
(In the text)
- Bazell, D.,
& Desert, F. X. 1988, , 333, 353
(In the text)
- Bensch, F.,
Stutzki, J., & Ossenkopf, V. 2001, , 366, 636
- Bernard,
J. P., Abergel, A., Ristorcelli, I., et al. 1999, , 347,
640
(In the text)
-
Boulanger, F., & Pérault, M. 1988, , 330, 964
-
Boulanger, F., Abergel, A., Bernard, J. P., et al. 1996,
, 312, 256
- Brunt,
C. M., & Heyer, M. H. 2002, , 566, 276
(In the text)
- Brunt, C. M.
2003, , 583, 280
-
Crovisier, J., & Dickey, J. M. 1983, , 122, 282
- Desert,
F. X., Boulanger, F., & Puget, J. L. 1990, , 237,
215
(In the text)
- Dickey,
J. M., McClure-Griffiths, N. M., Stanimirovic, S.,
Gaensler, B. M., & Green, A. J. 2001, , 561, 264
- Dickman,
R. L., Margulis, M., & Horvath, M. A. 1990, , 365,
586
(In the text)
-
Elmegreen, B. G. 2002, , 564, 773
-
Elmegreen, B. G., Kim, S., & Staveley-Smith, L. 2001, ,
548, 749
-
Falgarone, E., Phillips, T. G., & Walker, C. K. 1991,
, 378, 186
-
Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999,
, 524, 867
(In the text)
- Gautier, T.
N. I., Boulanger, F., Perault, M., & Puget, J. L.
1992, , 103, 1313
- Goldman, I.
2000, , 541, 701
- Gorski,
K. M., Hivon, E., Banday, A. J., et al. 2005, , 622,
759
(In the text)
- Green, D. A.
1993, , 262, 327
- Hauser,
M. G., Arendt, R. G., Kelsall, T., et al. 1998, ,
508, 25
- Helou, G., &
Beichman, C. A. 1990, The confusion limits to the sensitivity
of submillimeter telescopes, in From Ground-Based to Space-Borne
Sub-mm Astronomy, ESA, 117
(In the text)
- Hobson,
M. P. 1992, , 256, 457
- Ingalls,
J. G., Miville-Deschênes, M. A., Reach,
W. T., et al. 2004, ApJS, 154, 281 [NASA ADS] [CrossRef]
- Jeong,
W. S., Mok Lee, H., Pak, S., et al. 2005, , 357, 535
(In the text)
- Jewell, J.
2001, , 557, 700
- Joncas, G.,
Boulanger, F., & Dewdney, P. E. 1992, , 397, 165
(In the text)
- Kiss, C., Abraham,
P., Klaas, U., et al. 2003, , 399, 177
(In the text)
- Lagache,
G., Haffner, L. M., Reynolds, R. J., & Tufte,
S. L. 2000, , 354, 247
(In the text)
- Li, A., & Draine,
B. T. 2001, , 554, 778
- Miville-Deschênes,
M. A., & Lagache, G. 2005, , 157, 302
(In the text)
- Miville-Deschênes,
M. A., Lagache, G., & Puget, J. L. 2002, , 393,
749
(In the text)
- Miville-Deschênes,
M. A., Joncas, G., Falgarone, E., & Boulanger, F. 2003a, ,
411, 109
- Miville-Deschênes,
M. A., Levrier, F., & Falgarone, E. 2003b, , 593, 831
- Padoan, P.,
Rosolowsky, E. W., & Goodman, A. A. 2001, , 547,
862
- Padoan, P.,
Cambrésy, L., & Langer, W. 2002, , 580, L57
- Padoan, P.,
Goodman, A. A., & Juvela, M. 2003, , 588, 881
- Padoan, P.,
Cambrésy, L., Juvela, M., et al. 2006, , 649, 807
- Rocha, G.,
Hobson, M. P., Smith, S., Ferreira, P., & Challinor, A.
2005, , 357, 1
-
Stanimirovic, S., & Lazarian, A. 2001, , 551, L53
-
Stanimirovic, S., Staveley-Smith, L., Dickey, J. M., Sault,
R. J., & Snowden, S. L. 1999, , 302, 417
- Starck,
J. L., & Murtagh, F. 1998, PASP, 110, 193 [NASA ADS] [CrossRef] (In the text)
- Stepnik, B.,
Abergel, A., Bernard, J. P., et al. 2003, , 398, 551
- Stutzki, J.,
Bensch, F., Heithausen, A., Ossenkopf, V., & Zielinsky, M.
1998, , 336, 697
- Vio, R., Andreani,
P., & Wamsteker, W. 2001, PASP, 113, 1009 [NASA ADS] [CrossRef]
- Vio, R., Andreani,
P., Tenorio, L., & Wamsteker, W. 2002, PASP, 114, 1281 [NASA ADS] [CrossRef]
- Vogelaar,
M. G. R., & Wakker, B. P. 1994, , 291, 557
(In the text)
- Wright,
E. L. 1998, , 496, 1
(In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f1a.ps}\par\includegraphics[width=7.5cm, draft=false]{6962f1b.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg26.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm, draft=false]{6962f2.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f3.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f4.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg36.gif)
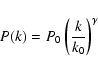
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f5.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg40.gif)
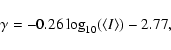
![\begin{figure}
\par\includegraphics[width=16.5cm, draft=false]{6962f6_col.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg44.gif)
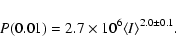
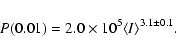
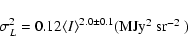
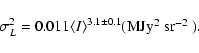
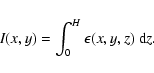
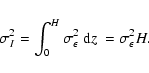
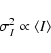
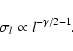
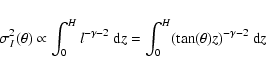
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f7.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg99.gif)
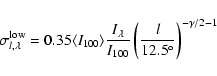
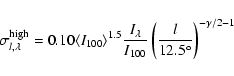
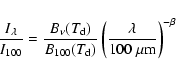
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f8.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg113.gif)
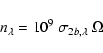
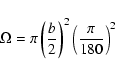
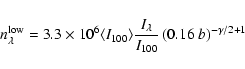
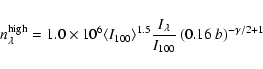
![\begin{figure}
\par\includegraphics[width=16.5cm, draft=false]{6962f9_col2.eps} %\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg120.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm, draft=false]{6962f10_col2.eps} %\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg121.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f11.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg130.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm, draft=false]{6962f12_col2.eps} %\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg131.gif)
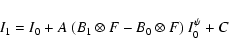
![\begin{figure}
\par\includegraphics[width=7.5cm, draft=false]{6962f13.ps}
\end{figure}](/articles/aa/full/2007/26/aa6962-06/Timg139.gif)