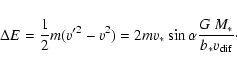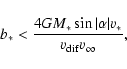A&A 469, 471-481 (2007)
DOI: 10.1051/0004-6361:20066718
Bar-driven injection of intergalactic matter into galactic
halos
M. López-Corredoira
Instituto de Astrofísica de Canarias, C/.Vía Láctea, s/n,
38200 La Laguna (S/C de Tenerife), Spain
Received 8 November 2006 / Accepted 15 March 2007
Abstract
Aims. The non-conservative gravitational potential of barred galaxies, or of any other non-axisymmetric structure, produces a loss of energy in infalling particles of the intergalactic medium into the galaxy, which are trapped in its potential. This dynamical friction can contribute towards increasing the total mass of barred galaxies.
Methods. Analytical calculations of the energy loss are carried out using the orbits of the particles derived numerically. Theoretical predictions are compared with observations through the statistical analysis of the rotation curves of barred and non-barred galaxies, either in cluster or field galaxies.
Results. There is a net effect of accretion, but it is normally very low in relative terms. It is only significant (>10% of the total mass of the dark matter halo in the life of the galaxy) if the density of the intergalactic medium is higher than 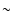
 /Mpc3 (or considerably lower in cases of motions of the galaxies close to the IGM average motion, or perpendicular to the plane of the galaxy, or when the halo mass is low).
/Mpc3 (or considerably lower in cases of motions of the galaxies close to the IGM average motion, or perpendicular to the plane of the galaxy, or when the halo mass is low).
Data on rotation curves do not show clear trends towards higher halo mass for barred galaxies, only slight trends for early-type spiral galaxies. In any case, the statistical uncertainties are limited to the detection of differences in masses >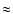 20%, so the effect of bar-driven injection of intergalactic matter into galactic halos might be present with relative contributions to the average mass of these barred galaxies lower than 20%.
20%, so the effect of bar-driven injection of intergalactic matter into galactic halos might be present with relative contributions to the average mass of these barred galaxies lower than 20%.
Key words: galaxies: kinematics and dynamics - intergalactic medium -
galaxies: evolution - galaxies: halos - galaxies: statistics
Intergalactic matter (IGM) is still a field of astrophysics with many open
questions and few answers. There are either theoretical arguments
or interpretations of observations that suggest the existence of
an IGM, although the definitive details of important
parameters such as the mean density, whether continuous or in
the form of clouds, etc. are not clear yet.
Cold dark matter models predict substructure within
galactic- and cluster-mass halos
that form in a hierarchical accretion Universe (Klypin et al. 1999;
Moore et al. 1999) that could constitute some of the clumpy structures in
the IGM. Indeed,
stellar and cold gas in galaxies contribute
8 (+4-5)%
of the total amount of the Big Bang-produced baryonic matter predictions
(Bell et al. 2003); this implies a low overall efficiency of galaxy formation,
and that the rest of the baryonic material must be some way away from the
visible galaxies, possibly in the IGM.
Some interstellar gas is ejected into the IGM by
tidal interactions between galaxies (Morris & van den Bergh 1994),
SN explosions, etc. Of course, the existence
of intracluster gas in rich and irregular clusters,
which have diffuse emission and X-ray emission associated with
hot gas, is well established. Possibly, some high-velocity clouds (HVCs)
observed in the radio are located outside our Galaxy, i.e.
belonging to the IGM (Blitz et al. 1999; Braun & Burton 1999).
There is also a large number of lines visible in optical at high redshifts
or UV in low redshifts - the Lyman-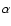 forest - which are presumably
caused by clouds along the line of sight of QSOs (Rauch 1998).
forest - which are presumably
caused by clouds along the line of sight of QSOs (Rauch 1998).
There is a need for a substantial accretion of low
angular momentum material from the IGM into the galaxies (Fraternali et al.
2007). Chemical evolution in the local Galactic disc (the G-dwarf problem,
9Be abundance and others; Rocha-Pinto & Maciel 1996; Casuso & Beckman
1997) needs a continual but episodic infall of
metal-poor gas that mixes slowly with the rest of
the interstellar medium. López-Corredoira et al. (1999) deduce that
the IGM mass must currently
represent at least around one half of the total mass of the Local Group,
given that the accretion rate, as inferred from chemical evolution, has not
decreased significantly during the disc lifetime.
The existence of matter in the IGM should have some effects
on the formation and evolution of the galaxies. For instance,
it is a possible explanation for the formation of warps in spiral
galaxies (López-Corredoira et al. 2002a). It is also, as said,
a likely explanation for the chemical evolution of galaxies
(Casuso & Beckman 1997). Here, we study another effect:
the accretion of this IGM matter due to dynamical friction.
It is clear that the disc mass might be fed by the
collisional friction of baryonic matter with disc gas.
The enrichment of the halo by means of a gravitational interaction
is instead the topic to be treated here. In particular, the
component of the galaxy responsible of this gravitational interaction
will be the bar.
Bar-halo interactions have been studied for several reasons.
For instance, as a mechanism of angular momentum transfer.
It is well established that strong bars rotating in dense halos generally
slow down as they lose angular momentum to the halo through dynamical
friction (Debattista & Sellwood 1998, 2000; Athanassoula 2003, 2005).
This friction can be avoided or found to be anomalously weak in some
circumstances and bar slowdown
can be delayed for a period in a metastable state
(Sellwood & Debattista 2006), although Sellwood & Debattista
(2006) demonstrate that mild external, or internal, perturbations quickly
restore the usual frictional drag; it is therefore unlikely that a
strong bar in a galaxy having a dense halo could rotate for a long period
without friction. A more
long-lasting effect to be considered is that the velocity dispersion of the
halo particles is high enough to stop the resonances from absorbing
considerable amounts of angular momentum (Athanassoula 2003), hence
prohibiting bar slowdown. Owing to this angular momentum transfer and
self-consistent re-equilibration, strong realistic bars will modify the
cusp profile, lowering the central densities within about 30%
of the bar radius in a few bar orbits (Weinberg & Katz 2007).
In this paper, another effect of the bar will be explored,
also using the dynamical friction of this kind of gravitational interaction:
the influence of the bar to produce the accretion of IGM matter (initially non-gravitationally linked to the galaxy)
into the halo.
That is, the interaction with the bar will produce
the loss of energy of some particles that cross the galaxy
and that will be trapped in it, since they do not have escape velocity, to form part of the galactic halo.
This mechanism applies to both baryonic and non-baryonic
matter because the friction is purely gravitational.
In Sect. 2 this loss
of energy and the amount of accreted matter depending
on IGM parameters for a Milky-Way-like galaxy is calculated semianalytically.
In Sect. 3, it is explained that other factors of the non-conservative
potential, for example approaches to individual stars, produce
a much lower effect that is totally negligible.
In Sect. 4, statistics with observational data
are performed in order to see whether barred galaxies have
larger masses.
2 Variations of energy in a barred potential
We analyse the variations of the energy in particles
that follow orbits in certain kinds of non-conservative potentials:
those in which the gravitational force varies with time.
This happens, for instance, in a barred galaxy, because the
rotation of a non-axisymmetric structure produces variations
in the potential due to the bar with respect to an inertial
frame. However, the rotating disc has
a stationary potential since the axial distribution of mass
does not change. If the bar rotates with angular velocity 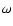 ,
the variation in the energy of a particle along
its path (orbit) is:
,
the variation in the energy of a particle along
its path (orbit) is:
in cylindrical coordinates, where 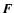 is the gravitational
force produced by the bar.
If we change to the variable
is the gravitational
force produced by the bar.
If we change to the variable
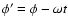 (that is,
we adopt the frame that is moving with the bar):
(that is,
we adopt the frame that is moving with the bar):
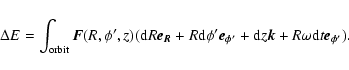 |
(2) |
If the orbits of particles begin at infinite distance and finish at
infinite distance:
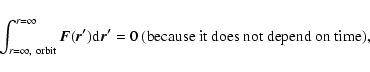 |
(3) |
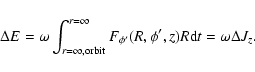 |
(4) |
The Jacobi integral
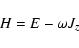 |
(5) |
is conserved.
Let us consider a monodimensional bar. This is an approximate description
of real 3D-bars because the major axis is considerably larger than the other
axis - otherwise, they would not be bars - as can be observed, for instance,
in the galaxies NGC 1300, NGC 7479, NGC 4123, NGC 1433, NGC 4999, etc.
(Sandage & Bedke 1994) or in our own Galaxy (López-Corredoira
et al. 2001, 2007). The mass density distribution will be
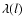 as a function of the
distance l to its centre. The azimuthal component of the gravitational
force produced by this bar of radius R0 on a particle of mass m will be:
as a function of the
distance l to its centre. The azimuthal component of the gravitational
force produced by this bar of radius R0 on a particle of mass m will be:
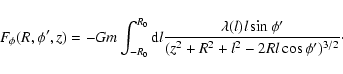 |
(6) |
If we assume
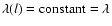 ,
the integral can be solved:
,
the integral can be solved:
![\begin{displaymath}F_\phi [\vec{r}'(R,\phi ',z)]=\frac{-Gm\lambda \sin \phi '}{z^2+R^2(1-\cos ^2\phi ')}
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img22.gif) |
(7) |
Therefore, if we want to calculate the gain/loss of energy of the particle,
we must just know its orbit
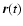 and use expressions (4)
and (6) to calculate
and use expressions (4)
and (6) to calculate 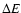 .
.
For our problem, we use
semianalytical calculations. The solution of Eqs. (4), (6) is calculated numerically, and the orbit of each
particle itself is not solved numerically as an outcome of
a numerical simulation in which all particles interact with each other
but as the numerical integration of its motion equation.
Indeed, we can consider the gravitational potential
of the infalling particles as due only to the components of the galaxies
and neglect the interaction due to other IGM particles.
Analytically, we cannot calculate the orbit of a particle in a
galactic potential; the integrals are too complex to find the solution.
But we can calculate
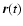 simply by numerical calculation
of the differential equation
simply by numerical calculation
of the differential equation
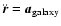 ,
the
total acceleration produced by the total potential of the galaxy.
It is then straightforward to obtain
,
the
total acceleration produced by the total potential of the galaxy.
It is then straightforward to obtain
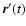 (the position in
the frame that is moving with the bar) from
(the position in
the frame that is moving with the bar) from
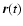 by using
by using
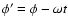 .
In this case, of course, for the calculation of the orbit, all the potentials
are to be taken into account not only the potential of
the bar. We can approximate this potential as the sum of several
components:
.
In this case, of course, for the calculation of the orbit, all the potentials
are to be taken into account not only the potential of
the bar. We can approximate this potential as the sum of several
components:
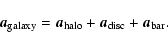 |
(8) |
We give analytical expressions for these acceleration
terms as integrals. All these integrals will be performed
numerically with the Simpson algorithm, and the solution to
the differential equation
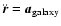 will be carried out with a variable step depending
on the acceleration:
will be carried out with a variable step depending
on the acceleration:
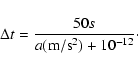 |
(9) |
The Jacobi integral H is conserved for each orbit
within variations of 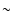 0.1%.
The accuracy in the orbit calculation was also checked by testing
that the orbit is approximately the same when decreasing this step
0.1%.
The accuracy in the orbit calculation was also checked by testing
that the orbit is approximately the same when decreasing this step 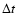 by a factor of 50 (
by a factor of 50 (
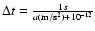 ):
the difference in the position of both calculations after a travelled
path of more than 1000 kpc (once the particle fell from a distance r0towards the centre and, after that, it
crosses the shell at r=r0; with
r0=400-500 kpc) is
):
the difference in the position of both calculations after a travelled
path of more than 1000 kpc (once the particle fell from a distance r0towards the centre and, after that, it
crosses the shell at r=r0; with
r0=400-500 kpc) is 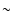 0.4 kpc on average.
These errors are not important for the present
calculations because we do not require too much accuracy in the orbit;
it is only used for the path integral of Eq. (4).
Moreover, a small random error added to the orbit is equivalent to a
small random variation of the initial conditions, which in comparison
with the range of impact parameters (0-200 kpc) is negligible.
0.4 kpc on average.
These errors are not important for the present
calculations because we do not require too much accuracy in the orbit;
it is only used for the path integral of Eq. (4).
Moreover, a small random error added to the orbit is equivalent to a
small random variation of the initial conditions, which in comparison
with the range of impact parameters (0-200 kpc) is negligible.
We approximate the halo as spherical, i.e. we neglect the ellipticity:
![\begin{displaymath}\vec{a}_{\rm halo}(\vec{r})=-\frac{[4\pi G\int _0^r{\rm d}t\ t^2
\rho _{\rm halo}(t) ]\vec{r}}{r^3}\cdot
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img33.gif) |
(10) |
We then use a truncated flat model by Battaglia et al. (2005):
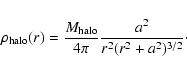 |
(11) |
For the disc, we use a typical exponential function considering
its thickness to be negligible. In order to reduce the
calculation to only one integral, which reduces the calculation time very considerably,
we express it in elliptic integrals (Binney & Tremaine 1987, Eq. (2-142b)):
![\begin{displaymath}\vec{a}_{\rm disc}[\vec{r}(R,\phi ,z)]=-\frac{\partial \phi _...
...vec{e_R}- \frac{\partial \phi _{\rm disc}}{\partial z}\vec{k}
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img35.gif) |
(12) |
where
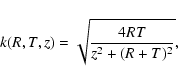 |
(14) |
and K(k) are the complete elliptic integrals of the first kind,
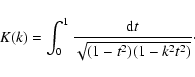 |
(15) |
The two derivatives of 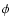 are:
are:
| |
|
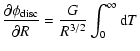 |
|
| |
|
![$\displaystyle \times \left[K(k)-\frac{1}{4}\left(\frac{k^2}
{1-k^2}\right)\left(\frac{T}{R}-\frac{R}{T}+\frac{z^2}{RT}\right)
E(k)\right]k\sigma (T)\sqrt{T}$](/articles/aa/full/2007/26/aa6718-06/img43.gif) |
(16) |
(Binney & Tremaine 1987, Eq. (2-146)), and
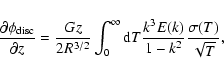 |
(17) |
where E(k) are the complete elliptic integrals of the second kind,
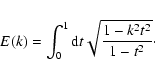 |
(18) |
We assume an exponential disc such that:
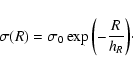 |
(19) |
For the bar, as said, we adopt a monodimensional structure
rotating with angular velocity 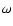 :
:
![\begin{displaymath}\vec{a}_{\rm bar}=-G\int _{-R_0}^{R_0}{\rm d}l\frac{\lambda (...
...vec{j}]]}
{(z^2+R^2+l^2-2Rl\cos (\phi -\omega t))^{3/2}}
\cdot\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img47.gif) |
(20) |
Other bar potentials could be used (e.g., Athanassoula 1992) but
this one is used for its simplicity. The IGM particles will
never cross this 1D structure, because there is zero probability
that the path by chance crosses the line of the bar, so this
potential will not give problems of divergence.
The potential also behaves well at large distance, as shown
in Fig. 1, the
acceleration falling as 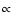 r-2.
r-2.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6718fig1.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg49.gif) |
Figure 1:
Modulus of the acceleration in a monodimensional bar potential
with the parameters of Sect. 2.1.4.
Logarithmic scale. Range of x and y between -20 kpc and 20 kpc. |
| Open with DEXTER |
2.1.4 Parameters for our numerical calculations
The parameters that we used are those more
or less typical for Milky Way-like galaxies.
A total mass for the halo
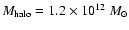 ,
and a=105 kpc
(Battaglia et al. 2005).
The mass within a radius r would be
,
and a=105 kpc
(Battaglia et al. 2005).
The mass within a radius r would be
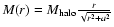 .
96.7% of the halo mass is within r<400 kpc, so it can be
approximated for r>400 kpc as a Keplerian potential of mass equal to
.
96.7% of the halo mass is within r<400 kpc, so it can be
approximated for r>400 kpc as a Keplerian potential of mass equal to
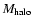 (plus the mass of the disc and the bar).
(plus the mass of the disc and the bar).
For the disc, we adopt
 kg/m2 (in agreement with the
solar neighbourhood measurements by Kuijken & Gilmore 1989) and
hR=3.4 kpc (a typical value in a Milky Way-like galaxy;
López-Corredoira et al. 2002b). The corresponding total mass of
the disc is
kg/m2 (in agreement with the
solar neighbourhood measurements by Kuijken & Gilmore 1989) and
hR=3.4 kpc (a typical value in a Milky Way-like galaxy;
López-Corredoira et al. 2002b). The corresponding total mass of
the disc is
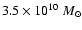 .
.
For the bar, we assume a total mass of
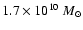 (Sevenster et al. 1999), more
or less in agreement with Kuijken & Dubinski's (1995) self-consistent
models of the Galaxy. This gives a constant distribution
(Sevenster et al. 1999), more
or less in agreement with Kuijken & Dubinski's (1995) self-consistent
models of the Galaxy. This gives a constant distribution
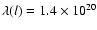 kg/m for a radius R0=4 kpc
(estimated value of the long-bar radius in our Galaxy,
López-Corredoira et al. 2001, 2007).
This mass of the long bar is indeed not well known (López-Corredoira
et al. 2007) and the bar of Sevenster et al. (1999) is 35% shorter
(the axial ratio difference is not so important, as we will see below)
than López-Corredoira et al. (2007) bar, so we are not setting
the parameters of the bar accurately, but as a more or less correct order of magnitude
(see further discussion in Sect. 2.6 of
what would happen with more or less massive bars).
kg/m for a radius R0=4 kpc
(estimated value of the long-bar radius in our Galaxy,
López-Corredoira et al. 2001, 2007).
This mass of the long bar is indeed not well known (López-Corredoira
et al. 2007) and the bar of Sevenster et al. (1999) is 35% shorter
(the axial ratio difference is not so important, as we will see below)
than López-Corredoira et al. (2007) bar, so we are not setting
the parameters of the bar accurately, but as a more or less correct order of magnitude
(see further discussion in Sect. 2.6 of
what would happen with more or less massive bars).
The angular rotation velocity, 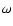 ,
is taken
as
,
is taken
as
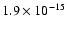 s-1 (as measured
in the Milky Way; Debattista et al. 2002). Most strong bars in real
galaxies appear to rotate rapidly (Aguerri et al. 2003), so it is
not expected that this velocity will slow down too much.
Although the dynamical halo-bar friction predicts a quick
slowdown in this velocity (Debattista & Sellwood 1998, 2000; Athanassoula
2003, 2005), there
might be a metastable state in which the bar-halo also remains a long time
without friction (Sellwood & Debattista 2006), or a state in
which the velocity dispersion of the
halo particles is high, so as to stop the resonances from absorbing
considerable amounts of angular momentum (Athanassoula 2003), thus
prohibiting bar slow down. Whatever
the explanation, the fact of fast bars in most
barred galaxies remains, and we therefore
do not consider any friction or change in
s-1 (as measured
in the Milky Way; Debattista et al. 2002). Most strong bars in real
galaxies appear to rotate rapidly (Aguerri et al. 2003), so it is
not expected that this velocity will slow down too much.
Although the dynamical halo-bar friction predicts a quick
slowdown in this velocity (Debattista & Sellwood 1998, 2000; Athanassoula
2003, 2005), there
might be a metastable state in which the bar-halo also remains a long time
without friction (Sellwood & Debattista 2006), or a state in
which the velocity dispersion of the
halo particles is high, so as to stop the resonances from absorbing
considerable amounts of angular momentum (Athanassoula 2003), thus
prohibiting bar slow down. Whatever
the explanation, the fact of fast bars in most
barred galaxies remains, and we therefore
do not consider any friction or change in 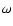 with time.
with time.
With these parameters, the stationary (Lagrangian)
points of the Galactic potential are at:
L1, L2:
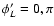 ,
z=0,
RL=5.25 kpc; L4, L5:
,
z=0,
RL=5.25 kpc; L4, L5:
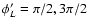 ,
z=0, RL=4.59 kpc
(for more information about the Lagrangian points in a
barred potential see Pfenninger 1990 or Athanassoula 1992),
whose Jacobi integrals are:
,
z=0, RL=4.59 kpc
(for more information about the Lagrangian points in a
barred potential see Pfenninger 1990 or Athanassoula 1992),
whose Jacobi integrals are:
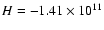 J and
J and
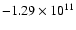 J respectively.
The fact that the Lagrangian points L4, L5 are 13% closer to the
centre than the Lagrangian points L1, L2 is expected for average strong
bars; the difference is typically 6% for average bar models according
to Athanassoula (1992) but it may be as large as 20% for the strongest bars.
The strength of the bar can be compared with another parameter defined
by Athanassoula (1992): half of the quadrupole moment along its
major axis
J respectively.
The fact that the Lagrangian points L4, L5 are 13% closer to the
centre than the Lagrangian points L1, L2 is expected for average strong
bars; the difference is typically 6% for average bar models according
to Athanassoula (1992) but it may be as large as 20% for the strongest bars.
The strength of the bar can be compared with another parameter defined
by Athanassoula (1992): half of the quadrupole moment along its
major axis
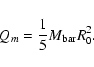 |
(21) |
This expression is derived from Eq. (5) of Athanassoula with a=R0,
b=0 (infinite axial ratio a/b), n=0 (constant density along the bar).
With our parameters we get
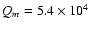 (in units
(in units
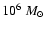 kpc2, as in Athanassoula 1992). This is again an indication that
the strength of our bar is a typical one within strong bars
(weak bars have
kpc2, as in Athanassoula 1992). This is again an indication that
the strength of our bar is a typical one within strong bars
(weak bars have
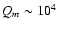 ,
very strong bars have
,
very strong bars have
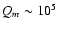 ;
Athanassoula 1992). It is also remarkable that the infinite axial ratio
a/b in a monodimensional bar does not significantly alter the effects
of a bar with finite but high axial ratios since
;
Athanassoula 1992). It is also remarkable that the infinite axial ratio
a/b in a monodimensional bar does not significantly alter the effects
of a bar with finite but high axial ratios since
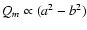 (Athanassoula 1992, Eq. (5)) and
(Athanassoula 1992, Eq. (5)) and
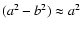 for high a/b,
either finite or infinite.
for high a/b,
either finite or infinite.
2.1.5 Initial conditions of the IGM particles
We assume now that our galaxy is moving with respect to the IGM
(or the IGM is moving with respect to the galaxy).
This hypothesis was already used in López-Corredoira et al. (2002a)
as an explanation to produce warps in disc galaxies and now will be
explored just to calculate the fraction of the particles that are
gravitationally trapped in the galactic potential due to a negative
energy variation. Basically, the model consists of a constant
density (
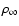 )
medium which has at infinite distance from the
galaxy an average velocity
)
medium which has at infinite distance from the
galaxy an average velocity
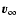 with respect to the centre of galaxy, and
an angle of
with respect to the centre of galaxy, and
an angle of
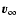 with respect to the plane of the galaxy
equal to
with respect to the plane of the galaxy
equal to
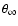 .
We neglect the effect of the
dispersion of velocities with respect to this average velocity.
.
We neglect the effect of the
dispersion of velocities with respect to this average velocity.
We randomly distribute the values of b (impact parameter with respect to the centre
of the galaxy), 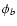 (azimuthal angle in cylindrical coordinates
with the vector
(azimuthal angle in cylindrical coordinates
with the vector
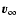 as vertical axis) following the
conditions for a homogeneous distribution, equivalent to do integrals
in the way
as vertical axis) following the
conditions for a homogeneous distribution, equivalent to do integrals
in the way
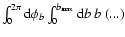 .
We set
.
We set
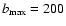 kpc. That
is, we neglect the contribution of particles whose impact parameter is
larger than 200 kpc; this is justified because, as we shall see in following
subsections, the particles which lose more energy have lower value of b,
except in cases with low
kpc. That
is, we neglect the contribution of particles whose impact parameter is
larger than 200 kpc; this is justified because, as we shall see in following
subsections, the particles which lose more energy have lower value of b,
except in cases with low 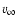 .
.
Since an infinite distance cannot be introduced in the computer
(integration of the orbit would take an infinite time), we must
begin the integration from a finite distance,
which we choose to be at
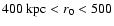 kpc. We
distribute our particles randomly at a shell with this range of radii.
The distribution with different r0 is useful to integrate over
different positions of the bar
when the particle reaches the galactic disc; that is, it is equivalent
to doing an integration with different initial bar angles
kpc. We
distribute our particles randomly at a shell with this range of radii.
The distribution with different r0 is useful to integrate over
different positions of the bar
when the particle reaches the galactic disc; that is, it is equivalent
to doing an integration with different initial bar angles
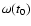 .
The time to cross 100 kpc at
around 70 km s-1 (the velocity of the particle at radius r0 assuming
.
The time to cross 100 kpc at
around 70 km s-1 (the velocity of the particle at radius r0 assuming
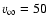 km s-1) is 1.4 Gyr, so doing the integration
between
km s-1) is 1.4 Gyr, so doing the integration
between
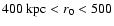 kpc
is equivalent to doing an integration over a time of 1.4 Gyr, equivalent
to 14 cycles of the bar (one cycle/100 Myr); moreover, there is an
added dispersion in the position of the bar when the particle reaches
the centre of the galaxy because the different values of
kpc
is equivalent to doing an integration over a time of 1.4 Gyr, equivalent
to 14 cycles of the bar (one cycle/100 Myr); moreover, there is an
added dispersion in the position of the bar when the particle reaches
the centre of the galaxy because the different values of 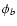 and bget different infall times to reach the centre, so in practice
we are integrating over a range larger than 1.4 Gyr.
This ensures that all angles of the bar are covered more or less
uniformly (departures from uniformity are negligible and less
important than Poissonian or other fluctuations).
In this way, we are doing a Monte Carlo simulation over the
variables b,
and bget different infall times to reach the centre, so in practice
we are integrating over a range larger than 1.4 Gyr.
This ensures that all angles of the bar are covered more or less
uniformly (departures from uniformity are negligible and less
important than Poissonian or other fluctuations).
In this way, we are doing a Monte Carlo simulation over the
variables b, 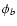 and r0.
and r0.
At the distance of 400-500 kpc the non-monopolar terms of the gravitational
potential are negligible and almost the entire mass of the galaxy is within
this radius, so the potential can be approximated as one produced by
a point-like source in the centre of the galaxy with its total mass.
Nonetheless, this potential is not totally negligible at these
distances, so we must correct the initial conditions with respect
to the conditions at infinite distance:
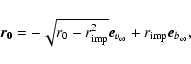 |
(22) |
where
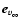 is the unit vector parallel to the
initial velocity at infinity,
and
is the unit vector parallel to the
initial velocity at infinity,
and
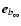 is the vector perpendicular to
is the vector perpendicular to
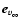 in the plane perpendicular to the one defined
by
in the plane perpendicular to the one defined
by 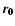 and
and
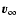 ,
i.e.
the direction of the impact parameter, pointing towards an
increase in b.
,
i.e.
the direction of the impact parameter, pointing towards an
increase in b.
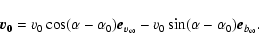 |
(23) |
The parameters v0,
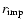 and
and 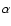 ,
,
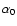 are derived
from the analytical expressions of a hyperbolic orbit (see
López-Corredoira et al. 2002a; Sect. 3.3) and taking into account
that the angular momentum is constant along the orbit:
are derived
from the analytical expressions of a hyperbolic orbit (see
López-Corredoira et al. 2002a; Sect. 3.3) and taking into account
that the angular momentum is constant along the orbit:
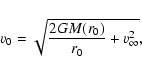 |
(24) |
![\begin{displaymath}r_{\rm imp}=r_0\vert\sin [\beta -\cos ^{-1}(-1/\epsilon )]\vert
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img86.gif) |
(25) |
![\begin{displaymath}\beta =\cos ^{-1}\left[\frac{\left(\frac{\epsilon}{A\ r_0}-1\right)}
{\epsilon }\right]
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img87.gif) |
(26) |
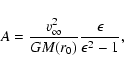 |
(27) |
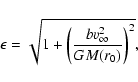 |
(28) |
 |
(29) |
 |
(30) |
The results of the orbit with these analytical expressions were compared
with the results of numerical calculations, and they agree. By applying these
formulae, we do not need to do numerical calculations beyond 400-500 kpc.
2.2 Histogram of energy variations
The only free parameters for the calculation of the energy variation
of each particle once the galactic parameters
are established are
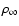 ,
,
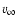 and
and
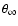 .
We could also consider
.
We could also consider
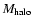 as a third free parameter instead of a fixed
value of
as a third free parameter instead of a fixed
value of
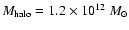 ,
since the total mass
of the halo might be variable with the time, precisely because of
the accreting mechanism proposed in this paper: the loss of energy
of some particles which are trapped when this loss of energy is higher
than
,
since the total mass
of the halo might be variable with the time, precisely because of
the accreting mechanism proposed in this paper: the loss of energy
of some particles which are trapped when this loss of energy is higher
than
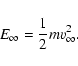 |
(31) |
As an example, let us set
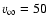 km s-1 (a typical value for the peculiar
motion of a galaxy) and
km s-1 (a typical value for the peculiar
motion of a galaxy) and
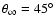 ,
with
,
with
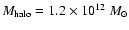 .
The results for 10 000 particles are in Figs. 2-4,
which show that the loss of energy is high enough to be trapped
only for b<100 kpc or
.
The results for 10 000 particles are in Figs. 2-4,
which show that the loss of energy is high enough to be trapped
only for b<100 kpc or
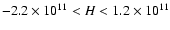 J
(for comparison, the Jacobi integrals
of the Lagrangian points are
J
(for comparison, the Jacobi integrals
of the Lagrangian points are
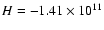 J and
J and
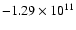 J), and
only 426 of the 10 000 particles lose an energy higher than
J), and
only 426 of the 10 000 particles lose an energy higher than 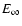 .
Equations (4) and (6) were
applied to calculated
.
Equations (4) and (6) were
applied to calculated 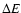 for each particle once it moves away
from the galaxy. There are, as observed in Fig. 2,
practically the same number of particles which gain
for each particle once it moves away
from the galaxy. There are, as observed in Fig. 2,
practically the same number of particles which gain
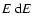 as those
which lose
as those
which lose
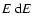 .
.
Let R200 be the ratio of particles within b<200 kpc which are
trapped by the halo. According to the above, this is
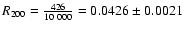 .
Hence, the accretion ratio will be:
.
Hence, the accretion ratio will be:
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6718fig2.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg102.gif) |
Figure 2:
Histogram of distribution of energy gain/loss per unit mass (kg). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6718fig3.eps}
\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg103.gif) |
Figure 3:
Energy gain/loss in the simulation of particles with
different impact parameter (b). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6718fig4.eps}
\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg104.gif) |
Figure 4:
Energy gain/loss in the simulation of particles as
a function of its Jacobi integral. For comparison, the Jacobi integrals
for the Lagrangian points are
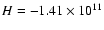 J and J and
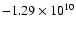 J. J. |
| Open with DEXTER |
The dependence on the angle
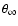 is illustrated
in Fig. 5. The R200 ratios are:
is illustrated
in Fig. 5. The R200 ratios are:
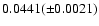 for
for
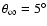 ,
,
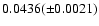 for
for
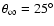 ,
,
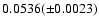 for
for
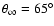 ,
and
,
and
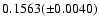 for
for
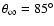 .
R200 does not change appreciably
except for
.
R200 does not change appreciably
except for
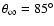 ,
which is 3-4 times higher.
The polar accretion seems to favour the mechanism.
The dependence is roughly described by a law:
,
which is 3-4 times higher.
The polar accretion seems to favour the mechanism.
The dependence is roughly described by a law:
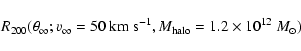 |
(33) |
Since we are interested in calculating the order of
magnitude, we can disregard this dependence and leave for our
remaining calculations a value of
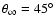 .
.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{6718fig5.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg115.gif) |
Figure 5:
Histogram of distribution of energy loss as a function of
the initial infall angle. |
| Open with DEXTER |
2.2.2 Dependence on the initial velocity
However, the dependence on initial velocity is high.
The histograms in Fig. 6 show it.
The ratios R200 are (note that 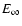 varies with
varies with
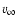 ):
>0.4966 for
):
>0.4966 for
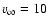 km s-1,
km s-1,
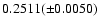 for
for
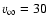 km s-1,
km s-1,
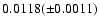 for
for
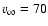 km s-1,
km s-1,
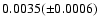 for
for
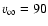 km s-1,
and
km s-1,
and
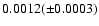 for
for
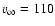 km s-1.
The ratio of higher energy loss
is maximum for lower initial velocities, both in terms of absolute energy and
relative energy with respect to
km s-1.
The ratio of higher energy loss
is maximum for lower initial velocities, both in terms of absolute energy and
relative energy with respect to 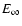 .
The explanation for
this is multiple. First, for higher velocities the particles go very fast
when they reach the bar, and since
.
The explanation for
this is multiple. First, for higher velocities the particles go very fast
when they reach the bar, and since 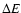 in Eq. (4)
is proportional to the time the particle spends near the bar, the
loss of energy is lower. Second, the capacity to attract towards the
centre particles with high b is larger for lower values of the initial
velocity. Moreover,
in Eq. (4)
is proportional to the time the particle spends near the bar, the
loss of energy is lower. Second, the capacity to attract towards the
centre particles with high b is larger for lower values of the initial
velocity. Moreover, 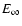 is higher for higher
initial velocities, so the rate of energy loss is lower too.
For the cases
is higher for higher
initial velocities, so the rate of energy loss is lower too.
For the cases
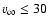 km s-1, it is observed that some particles
with b>200 kpc also lose
km s-1, it is observed that some particles
with b>200 kpc also lose
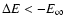 ;
therefore, the
trapped mass is even higher than the ratio given in Eq. (32).
The dependence is roughly described by the law:
;
therefore, the
trapped mass is even higher than the ratio given in Eq. (32).
The dependence is roughly described by the law:
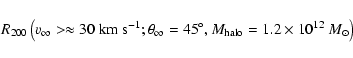 |
(34) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6718fig6.eps}
\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg129.gif) |
Figure 6:
Histogram of distribution of energy loss as a function of
the initial velocity. |
| Open with DEXTER |
The effect of the variation of halo mass is similar to the effect
of the variation in the initial velocity because the amount of mass
is proportional to the acceleration, and consequently is related to
the velocity of the particle. Figure 7 illustrates this.
A maximum accretion is obtained for the largest mass.
Lower masses have lower capacities to trap particles with high b.
The values of R200 obtained are:
0.0049(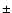 0.0007) for
0.0007) for
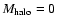 ,
0.0092(
,
0.0092( 0.0010) for
0.0010) for
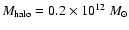 ,
0.0220(
,
0.0220(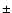 0.0015) for
0.0015) for
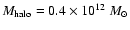 ,
0.0299(
,
0.0299(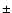 0.0017) for
0.0017) for
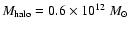 ,
0.0362(
,
0.0362(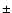 0.0019) for
0.0019) for
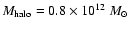 ,
and 0.0396(
,
and 0.0396(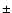 0.0020) for
0.0020) for
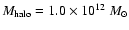 .
It is clear that it is proportional to the halo mass, roughly according
to:
.
It is clear that it is proportional to the halo mass, roughly according
to:
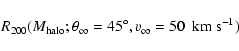 |
(35) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6718fig7.eps}
\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg139.gif) |
Figure 7:
Histogram of distribution of energy loss as a function of
halo mass. |
| Open with DEXTER |
The gain or loss of mass in the
halo due to other mechanisms will not be considered in this paper, but only the mechanism related to
the dynamical friction with the bar. There are other mechanisms
of accretion, such as friction with the disc of particles or
clouds that cross it. There are also ways for the halo to lose mass,
such as galaxy stripping in interactions with other galaxies or the
IGM, or the escape of particles when they reach
a velocity larger than escape velocity due to multiple interactions.
We neglect these other mechanisms because we want to consider
only the effect of the bar in increasing the halo mass independently
of other effects. The reality is more complex, of course, but
here we just consider a toy model for rough estimates of the net
effect of an increase in the accretion of mass in barred galaxies with
respect to non-barred galaxies.
The non-conservative potential of the bar could also produce an
increment of the energy of the halo particles and these could reach
the escape velocity producing some kind of "evaporation'' of the
halo. The mechanism is the same as the one explained in previous subsections
but the initial conditions will be different from those explained
in Sect. 2.1.5. Indeed, the fact that we get some net accretion
of some IGM particles arises because some of them go through the centre of the
galaxy, but the virialized halo has totally different initial conditions.
Assuming that the halo particles have an initial velocity corresponding
to a circular velocity plus isotropic dispersion velocities with
a component in the radial direction (given the isotropy, the dispersion
in other directions will be the same; the isotropic representation,
while more or less correct in the inner
halo, is not correct in the outer halo (Dehnen
& McLaughlin 2005), but we consider it here as a rough approximation)
![\begin{displaymath}\sigma _r(r)\propto [\rho (r) r^\alpha]^{1/3}
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img140.gif) |
(36) |
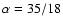 (Dehnen & McLaughlin 2005), in agreement with
simulations and analytical solutions of self-gravitating dynamical
equilibriums; with the halo density of Eq. (11), and
(Dehnen & McLaughlin 2005), in agreement with
simulations and analytical solutions of self-gravitating dynamical
equilibriums; with the halo density of Eq. (11), and
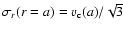 (Dehnen & McLaughlin 2005), where
(Dehnen & McLaughlin 2005), where
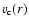 is the circular velocity, we can perform
again the numerical calculation of the orbits and the increment of
energy according to Eqs. (4) and (6).
The result with 10 000 halo particles whose initial conditions are
distributed randomly according to the probability densities
of positions and velocities including the dispersions, during 14 Gyr orbit calculation,
gives the result that none of these particles gets
an increase in energy
is the circular velocity, we can perform
again the numerical calculation of the orbits and the increment of
energy according to Eqs. (4) and (6).
The result with 10 000 halo particles whose initial conditions are
distributed randomly according to the probability densities
of positions and velocities including the dispersions, during 14 Gyr orbit calculation,
gives the result that none of these particles gets
an increase in energy
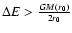 ,
where r0 is
the initial distance from the centre of the galaxy. This means
that the increase in the halo evaporation due to the bar-halo
interaction is negligible:
,
where r0 is
the initial distance from the centre of the galaxy. This means
that the increase in the halo evaporation due to the bar-halo
interaction is negligible:
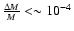 during
the whole life of the galaxy.
during
the whole life of the galaxy.
Let us suppose that the dependence on the initial angle, initial velocity
and the halo mass are separable. This is not strictly correct, but may be appropriate as
a rough estimation. In this case, a generalization
of the expression (32) will be:
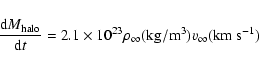 |
(37) |
Here we are assuming that the disc and the bar do not change with time.
The solution of this differential equation will be:
![\begin{displaymath}M_{\rm halo}(t)=-1.8\times 10^{11}~{M}_\odot +
[1.8\times 10^{11}~{M}_\odot +M_{\rm halo}(t=0)]\times {\rm e}^E\!,\
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img149.gif) |
(38) |
and the total accretion in the lifetime of the Galaxy
(we take
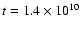 yr) due
to this mechanism is
yr) due
to this mechanism is
![\begin{displaymath}
\Delta M_{\rm halo}=[1.8\times 10^{11}~{M}_\odot +M_{\rm halo}(t=0)]
\times [{\rm e}^E-1]
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img153.gif) |
(39) |
The necessary conditions for a fraction F of the halo mass to be accreted
by this mechanism (
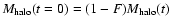 ,
,
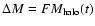 ;
assuming there are no other mechanisms
of accretion) are:
;
assuming there are no other mechanisms
of accretion) are:
![\begin{displaymath}F=\left[1+\frac{1.8\times 10^{11}~{M}_\odot}{M_{\rm halo}(t)}\right]
\times \left(1+\frac{1}{{\rm e}^E-1}\right)^{-1}\cdot
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img158.gif) |
(40) |
Particularly, for
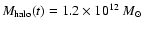 ,
,
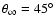 and
and
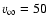 km s-1,
km s-1,
![\begin{displaymath}F=1.15\left(1+\frac{1}
{\exp{[4.3\times 10^{22}\rho _\infty ({\rm kg/m^3})]}-1}
\right)^{-1}\cdot
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img160.gif) |
(41) |
This expression has sense only for
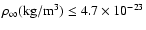 kg/m3 (
kg/m3 (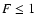 ), for
higher densities the mass of the halo should be larger.
In Fig. 8, the values of F for different densities
are plotted. Densities of the IGM
around 10-24 kg/m3 (including baryonic and
non-baryonic matter)
are able to produce a significant amount of
accretion by means of this mechanism.
), for
higher densities the mass of the halo should be larger.
In Fig. 8, the values of F for different densities
are plotted. Densities of the IGM
around 10-24 kg/m3 (including baryonic and
non-baryonic matter)
are able to produce a significant amount of
accretion by means of this mechanism.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6718fig8.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg163.gif) |
Figure 8:
Fraction of halo mass accreted by means of the mechanism
proposed in this paper. |
| Open with DEXTER |
In order to have at least 10% of the total halo matter accreted
by this mechanism (F=0.1) it is necessary that (we keep
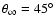 ,
,
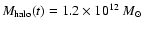 )
)
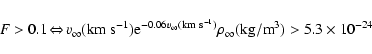 |
(42) |
The expression (42) for F>0.1 indicates
that for
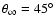 ,
,
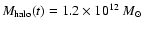 ,
,
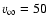 km s-1we need a density of
km s-1we need a density of
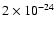 kg/m
kg/m
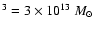 /Mpc
/Mpc
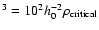 .
This is a high density and may be reached
by the intracluster gas in some groups or clusters of galaxies,
especially in the richest ones, which can have a density much higher
than this (including dark matter). The typical IGM densities in clusters are between 10-25 and 10-23 kg/m3 (Roussel
et al. 2000). However, the relative velocities
in such environments are also higher, thus decreasing the desired effect
(see the next subsection).
For cases such as the Local Group this density is too high.
The average IGM density of the Local Group is <
.
This is a high density and may be reached
by the intracluster gas in some groups or clusters of galaxies,
especially in the richest ones, which can have a density much higher
than this (including dark matter). The typical IGM densities in clusters are between 10-25 and 10-23 kg/m3 (Roussel
et al. 2000). However, the relative velocities
in such environments are also higher, thus decreasing the desired effect
(see the next subsection).
For cases such as the Local Group this density is too high.
The average IGM density of the Local Group is <
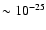 kg/m3
(assuming a total IGM mass of <
kg/m3
(assuming a total IGM mass of <
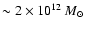 (López-Corredoira et al. 1999) in a volume of
(López-Corredoira et al. 1999) in a volume of 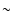 1 Mpc3).
1 Mpc3).
The product
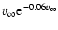 is maximum for
is maximum for
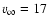 km s-1, at which a density
km s-1, at which a density
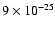 kg/m3 produces according
to Eq. (42) a F=0.1. The density might be even lower because,
as discussed in Sect. 2.2.2, the accretion of particles with
an impact parameter higher than 200 kpc will be considerable (and we
are considering in our calculation only particles within b<200 kpc).
Lower densities are more in the range
of possible values of intracluster density in small groups.
However, the velocity of 10-20 km s-1 is somewhat low.
For comparison, the velocity of the centre of the Galaxy with respect
to the barycentre of the Local Group is 81 km s-1
(Braun & Burton 1999; Eq. (3)). Maybe in the first stages of the
halo formation, when the galactic masses were much lower than
kg/m3 produces according
to Eq. (42) a F=0.1. The density might be even lower because,
as discussed in Sect. 2.2.2, the accretion of particles with
an impact parameter higher than 200 kpc will be considerable (and we
are considering in our calculation only particles within b<200 kpc).
Lower densities are more in the range
of possible values of intracluster density in small groups.
However, the velocity of 10-20 km s-1 is somewhat low.
For comparison, the velocity of the centre of the Galaxy with respect
to the barycentre of the Local Group is 81 km s-1
(Braun & Burton 1999; Eq. (3)). Maybe in the first stages of the
halo formation, when the galactic masses were much lower than
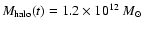 ,
the velocities
of the galaxies with respect to the average IGM
were also lower, since the gravitational potential responsible for
such dynamics produced lower accelerations.
A more developed study is necessary to clarify the question.
,
the velocities
of the galaxies with respect to the average IGM
were also lower, since the gravitational potential responsible for
such dynamics produced lower accelerations.
A more developed study is necessary to clarify the question.
In any case, statistically, it is possible to find a significant
fraction of galaxies with low velocities with respect to the average
IGM. The present
mechanism would apply to these few galaxies.
Up to now, we have considered the standard model of galaxies
with massive dark matter halos. However, some authors have
questioned the very existence of such halos since its evidence
is weak on galactic scales (Battaner & Florido 2000;
Sellwood & Kosowsky 2001; Evans 2001; etc.) and the rotation
curves or satellite motions can be explained by alternative
hypotheses such as magnetic fields (Battaner & Florido 2000)
or MOND (Sanders & McGaugh 2002).
If we consider a
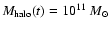 ,
necessary to explain the rotation curve of the Galaxy up to 15 kpc
(Honma & Sofue 1996)
together with a disc + bar mass of
,
necessary to explain the rotation curve of the Galaxy up to 15 kpc
(Honma & Sofue 1996)
together with a disc + bar mass of
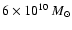 ,
we would find from Eq. (40) that (we keep
,
we would find from Eq. (40) that (we keep
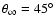 )
)
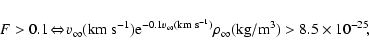 |
(43) |
in which the necessary density is 6 times lower than in expression (42).
If the halo mass were still lower than 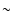
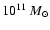 ,
we could reach the conclusion that most of the halo mass was
accreted by this mechanism (F close to unity). Here, however,
we have not included any alternative effects such as magnetic fields or
MOND, which would be necessary to make compatible the rotation curves
with this low value of the halo.
,
we could reach the conclusion that most of the halo mass was
accreted by this mechanism (F close to unity). Here, however,
we have not included any alternative effects such as magnetic fields or
MOND, which would be necessary to make compatible the rotation curves
with this low value of the halo.
If the mass of the halo were much higher (Conroy et al. 2005, give
typical masses for the halo of the galaxies of 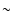
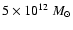 ), the relative fraction F would be around 15% lower than
in expression (42), although,
of course, the amount of accreted matter is nearly
proportional to the halo mass, so in absolute terms the number
of accreted solar masses would be higher.
), the relative fraction F would be around 15% lower than
in expression (42), although,
of course, the amount of accreted matter is nearly
proportional to the halo mass, so in absolute terms the number
of accreted solar masses would be higher.
2.6 Strength of the bar
In the present paper, we have fixed the parameters of the bar as
given in Sect. 2.1.4 which are typical for a normal strong
bar:
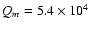 (in units
(in units
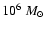 kpc2, as in Athanassoula 1992). A weak bar would have
kpc2, as in Athanassoula 1992). A weak bar would have
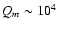 (Athanassoula 1992). Since the energy loss is
proportional to
(Athanassoula 1992). Since the energy loss is
proportional to 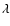 and,
and, 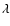 is proportional
to the mass of the bar (Eqs. (4), (6)),
it is straightforward
to deduce that within the linear regime of accretion (
is proportional
to the mass of the bar (Eqs. (4), (6)),
it is straightforward
to deduce that within the linear regime of accretion (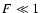 )
F will be proportional to mass of the bar. Hence, a weak bar,
typically with a mass five times lower than that used here,
would reduce F by a factor of five.
)
F will be proportional to mass of the bar. Hence, a weak bar,
typically with a mass five times lower than that used here,
would reduce F by a factor of five.
3 Other kinds of dynamical friction
As said in Sect. 2, when the gravitational force varies with time,
we get a non-conservative potential; that is, a potential in which
the energy of the particle in this potential is not constant.
Apart from the bar/triaxial bulge, there are other non-axisymmetric
structures in the galaxy, which, due to galactic rotation, produce
this variation in the potential; for instance, the spiral arms or
the warps in the disc. However, these structures normally have a mass much
lower than that of the bar (the spiral arm of the Milky Way
would have a 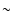 10% of the disc mass
according to the model of Bissantz & Gerhard 2002; and the mass
of the external disc, where the warp is present (López-Corredoira
et al. 2002b) is also lower than 10% of the disc mass);
therefore, their effect should be considerably lower, except
perhaps in some cases with prominent spiral arms. These cases
will not be explored in the present paper.
10% of the disc mass
according to the model of Bissantz & Gerhard 2002; and the mass
of the external disc, where the warp is present (López-Corredoira
et al. 2002b) is also lower than 10% of the disc mass);
therefore, their effect should be considerably lower, except
perhaps in some cases with prominent spiral arms. These cases
will not be explored in the present paper.
A way to produce changes in energy is in the interaction of the
accreted particles with individual stars. Since individual stars move,
the potential of the interaction is not
steady, although it is only predominant with respect to the global
potential of the whole galaxy when the particle approaches too close
to the star. The effect is similar to the exchange of energy of
a comet/spacecraft in an approach to a planet the Solar System.
The velocity of a particle when it approaches a star of mass M* with respect to this star is
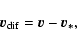 |
(44) |
where 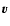 is the velocity of the particle with respect to the
centre of the galaxy, and
is the velocity of the particle with respect to the
centre of the galaxy, and 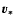 is the rotation(+peculiar) velocity
of the star around the centre of the galaxy.
The final velocity of the particle when it
recedes from the star after the interaction is
is the rotation(+peculiar) velocity
of the star around the centre of the galaxy.
The final velocity of the particle when it
recedes from the star after the interaction is
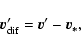 |
(45) |
where 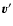 is the final velocity with respect to the centre of the
galaxy. The star may be considered point-like and the path
of the particle in the interaction with the star as a hyperbola
with impact parameter b*,
which follows (see Sect. 3.3 of López-Corredoira et al. 2002a)
is the final velocity with respect to the centre of the
galaxy. The star may be considered point-like and the path
of the particle in the interaction with the star as a hyperbola
with impact parameter b*,
which follows (see Sect. 3.3 of López-Corredoira et al. 2002a)
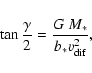 |
(46) |
where 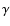 is the angle of deviation of the trajectory due
to the interaction as represented in Fig. 9.
is the angle of deviation of the trajectory due
to the interaction as represented in Fig. 9.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6718fig9.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg187.gif) |
Figure 9:
Graphical representation of the hyperbolic trajectory
of a particles which a approach a star (at the centre O). |
| Open with DEXTER |
Table 1:
Comparison of
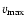 [km s-1] (maximum velocity of
rotation curves) and
[km s-1] (maximum velocity of
rotation curves) and
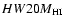 [km s-1]
(Half of the HI profile between points where
the intensity falls to 20% of the highest
channels in each half of the profile and corrected for relativistic effects;
Note: average only with the galaxies which have this datum available)
for spiral galaxies in Mathewson et al. (1992) catalogue in barred and
non-barred cases as a function of the galaxy type.
[km s-1]
(Half of the HI profile between points where
the intensity falls to 20% of the highest
channels in each half of the profile and corrected for relativistic effects;
Note: average only with the galaxies which have this datum available)
for spiral galaxies in Mathewson et al. (1992) catalogue in barred and
non-barred cases as a function of the galaxy type.
The final velocity with respect to the star will be:
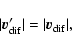 |
(47) |
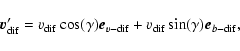 |
(48) |
with the unit vector as specified in Fig. 9,
and with respect to the centre of the galaxy:
Hence,
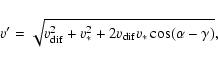 |
(50) |
while the initial velocity with respect to the centre of the galaxy is
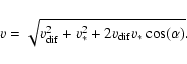 |
(51) |
This implies an increment of the energy of the particle
![\begin{displaymath}\Delta E=\frac{1}{2}m(v'^2-v^2)=mv_{\rm dif}v_*
[\cos (\alpha - \gamma)-\cos (\alpha)]
.\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img224.gif) |
(52) |
An approximation for small interactions (
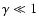 ),
using (46),
),
using (46),
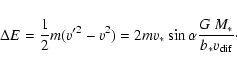 |
(53) |
The particles trapped by the galaxy due to this interaction will
be those with
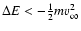 (
(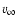 as the velocity of the particle at infinite distance always
is); that is, those
particles with impact parameter
as the velocity of the particle at infinite distance always
is); that is, those
particles with impact parameter
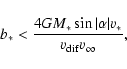 |
(54) |
For
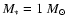 ,
v*=200 km s-1 (the rotation as the main component),
,
v*=200 km s-1 (the rotation as the main component),
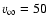 km s-1,
for an average case of
km s-1,
for an average case of
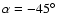 and
and
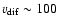 km s-1,
the constraint is
km s-1,
the constraint is
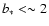 AU. With the typical surface density
in the galactic disc of 10-100 star/pc2 (López-Corredoira et al. 2002b),
the probability of a particle having an impact parameter less than 2 AU
is
AU. With the typical surface density
in the galactic disc of 10-100 star/pc2 (López-Corredoira et al. 2002b),
the probability of a particle having an impact parameter less than 2 AU
is 
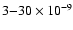 .
This is just a rough estimate but
the order of magnitude should be more or less correct. Therefore,
the accretion ratio is much lower than the values of R200 obtained
in Sect. 2.2, and a much lower accretion (totally negligible)
is expected to be produced in terms of the star/particle interaction.
.
This is just a rough estimate but
the order of magnitude should be more or less correct. Therefore,
the accretion ratio is much lower than the values of R200 obtained
in Sect. 2.2, and a much lower accretion (totally negligible)
is expected to be produced in terms of the star/particle interaction.
4 Comparison with observations: the effect of the bar on the
halo mass
Table 2:
Comparison of OW3 [km s-1] (measured velocity width in optical
profiles with corrections for the shape of the rotation curve,
cosmological stretch and converted to edge-on viewing measured
at twice the scale length), RW2 [km s-1] (measured 21 cm line profile velocity
corrected and converted to edge on viewing;
Note: average only with the galaxies which have this datum available),
M/L [solar units] (corrected mass to light [I-band] ratio;
Note: average only with the galaxies which have this datum available)
for spiral galaxies in Vogt et al. (2004) catalogue in barred and
non-barred cases as a function of the galaxy type. There are no
barred galaxies with available data in this catalogue of types +6 or
later.
Table 3:
Same as Table 2 but only with galaxies
considered bona fide members of a cluster of galaxies. There is
only one barred galaxy of type +4 "in a cluster'' of Vogt et al. (2004)
catalogue, which is not included.
It is not straightforward to check this effect on real galaxies.
We would need to know the complete history of each galaxy, the epoch
of formation of its bar and other characteristics which are not
directly available. Nonetheless, we can analyse whether spiral
galaxies with a prominent bar have different rotation-curve amplitudes from the same type of galaxies without bar.
Indeed, this analysis cannot be a
definitive proof of the present mechanism because there
are other possible alternative explanations in terms of
the interaction between halo and bar. For instance,
halos might allow bars to become stronger
(Athanassoula & Misiriotis 2002;
Athanassoula 2002, 2003). In any case, the present section might be
a first step in the search of this effect.
In order to do this, we use first the data from the Mathewson et al. (1992) catalogue on rotation curves, which contains data
for 1355 spiral galaxies. We subdivide the sample into 12 groups:
morphological type from +3 to +8 (equivalently from Sb to Sd) and each of
them with or without bar (either SB/SAB or S/SA; according to the
classification in this survey similar to the RC3 catalogue). This is a rough
classification, because indeed most of the spiral galaxies should
have a bar to some degree (e.g., Knapen et al. 2000; Fathi 2004).
From Mathewson et al. (1992),
we take the maximum rotation velocity.
This catalogue includes data from optical H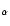 rotation curves
and HI profiles. The results
are given in Table 1.
The table, although not conclusive, seems to show larger
rotation velocities for earlier types (for +4, the average
rotation velocity of barred galaxies is 2.9
rotation curves
and HI profiles. The results
are given in Table 1.
The table, although not conclusive, seems to show larger
rotation velocities for earlier types (for +4, the average
rotation velocity of barred galaxies is 2.9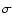 higher than
the non-barred galaxies) and vice verse for later types
(for +7, the average
rotation velocity of barred galaxies is 3.1
higher than
the non-barred galaxies) and vice verse for later types
(for +7, the average
rotation velocity of barred galaxies is 3.1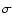 lower than
the non-barred galaxies). The first thing might be explained
in terms of the mechanisms proposed in this paper: throughout their lifetimes, bars
help to accrete matter and this is more
remarkable in earlier types because the bars are more prominent
in these types. The hypothesis that halos allow bars to become
stronger is also a good possible explanation; indeed, the simulations in
Athanassoula & Misiriotis (2002) and Athanassoula (2002, 2003)
refer only to early-type disc galaxies, with no or
hardly any gas, and this would explain why this effect is not
necessarily seen in later types.
The second fact is intriguing: it might
have to do with the history of the galaxy, in which these late-type
galaxies without bars had one in the past, or with a major role of the
spiral arms in non-barred galaxy. Also, errors in the classification
of the galaxy type could be the cause of this different velocity
in barred and non-barred galaxies (the bar could contribute to wrong
visual classification).
lower than
the non-barred galaxies). The first thing might be explained
in terms of the mechanisms proposed in this paper: throughout their lifetimes, bars
help to accrete matter and this is more
remarkable in earlier types because the bars are more prominent
in these types. The hypothesis that halos allow bars to become
stronger is also a good possible explanation; indeed, the simulations in
Athanassoula & Misiriotis (2002) and Athanassoula (2002, 2003)
refer only to early-type disc galaxies, with no or
hardly any gas, and this would explain why this effect is not
necessarily seen in later types.
The second fact is intriguing: it might
have to do with the history of the galaxy, in which these late-type
galaxies without bars had one in the past, or with a major role of the
spiral arms in non-barred galaxy. Also, errors in the classification
of the galaxy type could be the cause of this different velocity
in barred and non-barred galaxies (the bar could contribute to wrong
visual classification).
HI profiles with extension of the wings up to a 20%
of the maximum trace the halo mass within larger radius, so
the width of this HI profile (
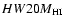 in Table 1) is also considered.
The results are similar to the results
with the rotation curves for late-type spiral galaxies, and
no trend is found for early-type ones.
in Table 1) is also considered.
The results are similar to the results
with the rotation curves for late-type spiral galaxies, and
no trend is found for early-type ones.
The same comparison between barred and non-barred galaxies could
be useful if made in galaxies in clusters. There are very
few galaxies of Mathewson et al. (1992) classified as SB
and "in cluster'': according to the
SIMBAD database (http://simbad.u-strasbg.fr/), only 5 of the 95 barred galaxies are known to be in clusters ("GiC''), so this
catalogue is not useful for this purpose.
We can use another catalogue with fewer galaxies in total (329 galaxies)
but with a higher ratio of cluster members: Vogt et al. (2004).
Results are shown in Table 2 for all the galaxies,
and in Table 2 only for galaxies in clusters.
Nothing new is observed with respect to the Mathewson et al. (1992)
analysis, which shows more or less the same trends. Analysis of
barred galaxies in clusters (there are in total 23 for our analysis;
not many, but more than the 5 galaxies in Mathewson et al. 1992)
does not show a clearer trend of distinction with the non-barred galaxies:
Table 3.
It would be better to obtain information on the total mass of
halos rather than the mass within a few tens of kpc, as is the
case for rotation curves, but this information is not available
for a large sample of galaxies, and the errors in the estimates
(through satellites orbit measures; e.g. Conroy et al. 2005) are
inaccurate and not available for a large sample of individual galaxies to
do statistics.
A new mechanism has been proposed in the interaction of bars with
the surrounding medium, which
produces a variation of energy of the particles crossing
the galaxy. On average, the energy gained is equal to the loss
energy by these particles, so this does not produce variations
of energy in the average halo. However, for the external IGM
particles which cross the galaxy, this mechanism causes some
of them to be trapped to form part of the halo because their
velocities are reduced to less than the escape velocity.
By means of this, an extra amount of IGM matter can
be accreted onto barred galaxies.
The increase in the evaporation of the halo due to bar
dynamical friction, however, is negligible.
Rough calculations of the amount of accreted matter show that this
must be negligible in most cases with normal expected conditions
of density and galaxy-IGM velocity, and only in galaxies of
galaxy-IGM velocities < 70 km s-1with IGM density similar to that of the cluster of galaxies does it
produce significant (>10%) amounts of halo mass accreted by
this mechanism. The IGM density might be lower
with motions of the galaxies close to the IGM average motion,
or with motion perpendicular to the plane of the galaxy.
Clusters of galaxies also have other mechanisms
of galaxy stripping that can counteract the accretion; indeed,
the IGM and halos are mixed and we could even talk about a
common halo for all the galaxies in a cluster. This means that we might find
that there is no important increase in mass in the barred galaxies of
clusters.
70 km s-1with IGM density similar to that of the cluster of galaxies does it
produce significant (>10%) amounts of halo mass accreted by
this mechanism. The IGM density might be lower
with motions of the galaxies close to the IGM average motion,
or with motion perpendicular to the plane of the galaxy.
Clusters of galaxies also have other mechanisms
of galaxy stripping that can counteract the accretion; indeed,
the IGM and halos are mixed and we could even talk about a
common halo for all the galaxies in a cluster. This means that we might find
that there is no important increase in mass in the barred galaxies of
clusters.
The analysis of observational data of rotation curves
shows no clear trends.
There is a slight increase in the average mass of early-type barred
spiral galaxies with respect to non-barred galaxies of the same type,
and viceverse for late-type spiral galaxies, but some sort of selection
factor might explain it. No effect could be observed for galaxies
embedded in clusters, although we cannot exclude the possibility that the effect
proposed in this paper is present to some non-negligible degree
because it might be lower
than the error bars. In Tables 1-3 the relative error bars of
the velocities are higher than 10%, which implies a mass error
higher than 20%, so possible slight average variations of
less than  20% in mass would not be detectable.
20% in mass would not be detectable.
The fashion in galactic models nowadays is to include very massive halos whose
matter comes from the evolution of the initial fluctuations of
the large scale structure (e.g., Betancort-Rijo & López-Corredoira
2002) and the accretion of dwarf galaxies, the hierarchical scenario
(e.g., White & Frenk 1991). The mechanism presented in this paper is part of
the possible mechanisms of accretion and it can also be applied
to the satellite dwarf galaxies. Nevertheless, if the very massive
dark matter halos did not exist and the rotation curves were explained
by mechanisms different from dark matter (e.g., MOND, Sanders & McGaugh
2002; magnetic fields, Battaner & Florido 2000), the present
mechanism could be much more important as a relative contributor to
the accretion of matter onto the galaxy, and it would not be detected
by analysing rotation curves because these
would not be related to the halo mass.
What is noteworthy in this paper is that the present mechanism does
not suppose any speculative scenario about the galaxies themselves.
The mechanism should be present "always''. The only question is
whether the amount of accreted matter in barred galaxies
is significant enough to be detected or not, because this depends on the
conditions of the IGM.
Acknowledgements
Discussions with J. E. Beckman (IAC, Tenerife, Spain) have produced
some ideas which were used as a basis for the development of the present
paper. Thanks are given to E. Athanassoula (Obs. Marseille, France)
and the anonymous referee
for helpful comments on the draft of this paper and suggestions to
improve it; and T. J. Mahoney (IAC, Tenerife, Spain) for proof-reading
of this paper. This research has made use of the SIMBAD database,
operated at CDS, Strasbourg, France.
- Aguerri, J.
A. L., Debattista, V. P., & Corsini, E. M. 2003, MNRAS, 338,
465 [NASA ADS] (In the text)
-
Athanassoula, E. 1992, MNRAS, 259, 328 [NASA ADS] (In the text)
-
Athanassoula, E. 2002, ApJ, 569, L83 [NASA ADS] [CrossRef] (In the text)
-
Athanassoula, E. 2003, MNRAS, 341, 1179 [NASA ADS] (In the text)
-
Athanassoula, E. 2005, Celest. Mech. Dynam. Astron. 91, 9
(In the text)
-
Athanassoula, E., & Misiriotis, A. 2002, MNRAS, 330, 35 [NASA ADS] (In the text)
-
Battaglia, G., Helmi, A., Morrison, H., et al. 2005, MNRAS, 364,
433 [NASA ADS] (In the text)
- Battaner,
E., & Florido, E. 2000, Fund. Cosmic Phys., 21, 1 [NASA ADS] (In the text)
- Bell, F. B.,
McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJ, 585,
L117 [NASA ADS] [CrossRef] (In the text)
-
Betancort-Rijo, J., & López-Corredoira, M. 2002, ApJ, 566,
623 [NASA ADS] [CrossRef] (In the text)
- Binney, J.,
& Tremaine, S. 1987, Galactic dynamics (Princeton: Princeton
University Press)
(In the text)
- Bissantz,
N., & Gerhard, O. E. 2002, MNRAS, 330, 591 [NASA ADS] (In the text)
- Blitz, L.,
Spergel, D., Teuben, P., Hartmann, D., & Burton, W. B. 1999,
ApJ, 514, 818 [NASA ADS] [CrossRef] (In the text)
- Braun, R., &
Burton, W. B. 1999, A&A, 341, 437 [NASA ADS] (In the text)
- Casuso, E.,
& Beckman, J. E. 1997, ApJ, 475, 155 [NASA ADS] [CrossRef] (In the text)
- Conroy, C.,
Newman, J. A., Davis, M., et al. 2005, ApJ, 635, 982 [NASA ADS] [CrossRef] (In the text)
-
Debattista, V. P., & Sellwood, J. A. 1998, ApJ, 493, L5 [NASA ADS] [CrossRef] (In the text)
-
Debattista, V. P., & Sellwood, J. A. 2000, ApJ, 543, 704 [NASA ADS] [CrossRef] (In the text)
-
Debattista, V. P., Gerhard, O. E., & Sevenster, M. N. 2002,
MNRAS, 334, 355 [NASA ADS] (In the text)
- Dehnen, W.,
& McLaughlin, D. E. 2005, MNRAS, 363, 1057 [NASA ADS] (In the text)
- Evans, N. W.
2001, in proceedings of the 3rd International Workshop on the
Identification of Dark Matter, ed. N. J. C. Spooner, & V.
Kudryavtsev (Singapore: World Scientific), 85
(In the text)
- Fathi, K. 2004,
Ph.D. Thesis, Univ. Groningen
(In the text)
-
Fraternali, F., Binney, J., Oosterloo, T., & Sancisi, R. 2007,
New Astron. Rev., 51, 95 [NASA ADS] (In the text)
- Honma, M., &
Sofue, Y. 1996, PASJ, 48, L103 [NASA ADS] (In the text)
- Klypin, A.,
Kravtsov, A. V., Valenzuela, O., & Prada, F. 1999, ApJ, 522,
82 [NASA ADS] [CrossRef] (In the text)
- Knapen, J. H.,
Shlosman, I., & Peletier, R. F. 2000, ApJ, 529, 93 [NASA ADS] [CrossRef] (In the text)
- Kuijken, K.,
& Gilmore, G. 1989, MNRAS, 239, 605 [NASA ADS] (In the text)
- Kuijken, K.,
& Dubinski, J. 1995, MNRAS, 277, 1341 [NASA ADS] (In the text)
-
López-Corredoira, M., Beckman, J. E., & Casuso, E. 1999,
A&A, 351, 920 [NASA ADS] (In the text)
-
López-Corredoira, M., Hammersley, P. L., Garzón, F., et
al. 2001, A&A, 373, 139 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
López-Corredoira, M., Betancort-Rijo, J., & Beckman, J. E.
2002a, A&A, 386, 169 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
López-Corredoira, M., Cabrera-Lavers, A., Garzón, F.,
& Hammersley, P. L. 2002b, A&A, 394, 883 [CrossRef] [EDP Sciences] (In the text)
-
López-Corredoira, M., Cabrera-Lavers, A., Mahoney, T. J., et
al. 2007, AJ, 133, 154 [NASA ADS] [CrossRef] (In the text)
-
Mathewson, D. S., Ford, V. L., & Buchhorn, M. 1992, ApJS, 81,
413 [NASA ADS] [CrossRef] (In the text)
- Moore, B.,
Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [NASA ADS] [CrossRef] (In the text)
- Morris, S. L.,
& van den Bergh, S. 1994, ApJ, 427, 696 [NASA ADS] [CrossRef] (In the text)
-
Pfenninger, D. 1990, A&A, 230, 55 [NASA ADS] (In the text)
- Rauch, M. 1998,
ARA&A, 36, 267 [NASA ADS] (In the text)
- Rocha-Pinto, H.
J., & Maciel, W. J. 1996, MNRAS, 279, 447 [NASA ADS] (In the text)
- Roussel, H.,
Sadat, R., & Blanchard, A. 2000, A&A, 361, 429 [NASA ADS] (In the text)
- Sandage, A.,
& Bedke, J. 1994, The Carnegie Atlas of Galaxies, Carnegie
Institution of Washington with The Flintridge Foundation,
Washington D.C.
(In the text)
- Sanders, R.
H., & McGaugh, S. S. 2002, ARA&A, 40, 263 [NASA ADS] (In the text)
- Sellwood,
J. A., & Debattista, V. P. 2006, ApJ 639, 868
(In the text)
- Sellwood,
J. A., & Kosowsky, A. 2001, in Gas & Galaxy Evolution, ed.
J. E. Hibbard, M. P. Rupen, & J. van Gorkom, ASP, S. Francisco,
311
(In the text)
-
Sevenster, M. N., Prasenjit, S., Valls-Gabaud, D., & Fux, R.
1999, MNRAS, 307, 584 [NASA ADS] (In the text)
- Vogt, N. P.,
Haynes, M. P., Herter, T., & Giovanelli, R. 2004, AJ, 127,
3273 [NASA ADS] [CrossRef] (In the text)
- Weinberg,
M. D., & Katz, N. 2007, MNRAS, 375, 460 [NASA ADS] (In the text)
- White, S., &
Frenk, C. 1991, ApJ, 379, 52 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
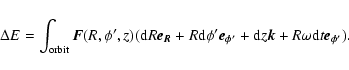
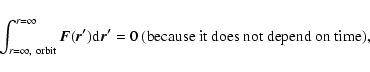
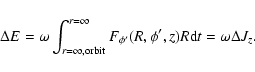
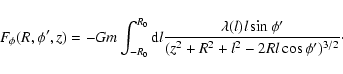
![\begin{displaymath}F_\phi [\vec{r}'(R,\phi ',z)]=\frac{-Gm\lambda \sin \phi '}{z^2+R^2(1-\cos ^2\phi ')}
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img22.gif)
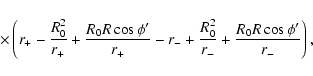
![\begin{displaymath}\vec{a}_{\rm halo}(\vec{r})=-\frac{[4\pi G\int _0^r{\rm d}t\ t^2
\rho _{\rm halo}(t) ]\vec{r}}{r^3}\cdot
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img33.gif)
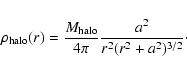
![\begin{displaymath}\vec{a}_{\rm disc}[\vec{r}(R,\phi ,z)]=-\frac{\partial \phi _...
...vec{e_R}- \frac{\partial \phi _{\rm disc}}{\partial z}\vec{k}
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img35.gif)
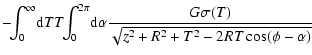
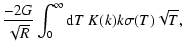
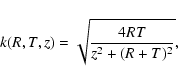
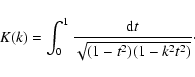
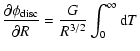
![$\displaystyle \times \left[K(k)-\frac{1}{4}\left(\frac{k^2}
{1-k^2}\right)\left(\frac{T}{R}-\frac{R}{T}+\frac{z^2}{RT}\right)
E(k)\right]k\sigma (T)\sqrt{T}$](/articles/aa/full/2007/26/aa6718-06/img43.gif)
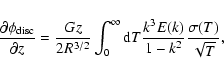
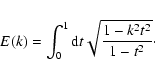
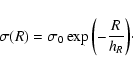
![\begin{displaymath}\vec{a}_{\rm bar}=-G\int _{-R_0}^{R_0}{\rm d}l\frac{\lambda (...
...vec{j}]]}
{(z^2+R^2+l^2-2Rl\cos (\phi -\omega t))^{3/2}}
\cdot\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img47.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6718fig1.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg49.gif)
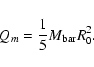
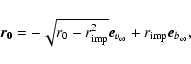
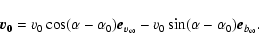
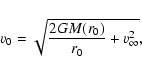
![\begin{displaymath}r_{\rm imp}=r_0\vert\sin [\beta -\cos ^{-1}(-1/\epsilon )]\vert
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img86.gif)
![\begin{displaymath}\beta =\cos ^{-1}\left[\frac{\left(\frac{\epsilon}{A\ r_0}-1\right)}
{\epsilon }\right]
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img87.gif)
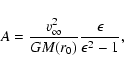
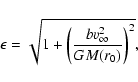


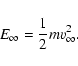
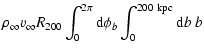
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6718fig2.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg102.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6718fig3.eps}
\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg103.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6718fig4.eps}
\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg104.gif)
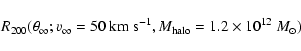
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{6718fig5.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg115.gif)
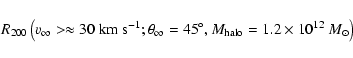
![\begin{displaymath}\ \ \ \ \ \ \ \ \ \approx 0.82\exp{[-0.06v_\infty ({\rm km~s^{-1}})]}
.\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img128.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6718fig6.eps}
\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg129.gif)
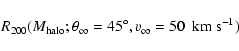
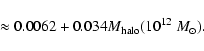
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6718fig7.eps}
\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg139.gif)
![\begin{displaymath}\sigma _r(r)\propto [\rho (r) r^\alpha]^{1/3}
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img140.gif)
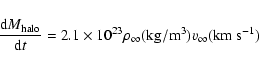
![\begin{displaymath}\times\exp{[-0.06v_\infty ({\rm km~s^{-1}})]}
[1+4.7\exp{[-0.12[90- \theta _\infty ({\rm deg})]]}]
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img147.gif)
![\begin{displaymath}\times
[1+5.5\times 10^{-12}M_{\rm halo}({M}_\odot )]
{\ M_\odot /\rm yr}
.\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img148.gif)
![\begin{displaymath}M_{\rm halo}(t)=-1.8\times 10^{11}~{M}_\odot +
[1.8\times 10^{11}~{M}_\odot +M_{\rm halo}(t=0)]\times {\rm e}^E\!,\
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img149.gif)
![\begin{displaymath}E=1.2\times 10^{12}\rho _\infty ({\rm kg/m^3})
v_\infty ({\rm km~s^{-1}})\times \exp{[-0.06v_\infty ({\rm km~s^{-1}})]}
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img150.gif)
![\begin{displaymath}
\Delta M_{\rm halo}=[1.8\times 10^{11}~{M}_\odot +M_{\rm halo}(t=0)]
\times [{\rm e}^E-1]
,\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img153.gif)
![\begin{displaymath}E=1.7\times 10^{22}\rho _\infty ({\rm kg/m^3})
v_\infty ({\rm km~s^{-1}})\times \exp{[-0.06v_\infty ({\rm km~s^{-1}})]}
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img154.gif)
![\begin{displaymath}F=\left[1+\frac{1.8\times 10^{11}~{M}_\odot}{M_{\rm halo}(t)}\right]
\times \left(1+\frac{1}{{\rm e}^E-1}\right)^{-1}\cdot
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img158.gif)
![\begin{displaymath}F=1.15\left(1+\frac{1}
{\exp{[4.3\times 10^{22}\rho _\infty ({\rm kg/m^3})]}-1}
\right)^{-1}\cdot
\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img160.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6718fig8.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg163.gif)
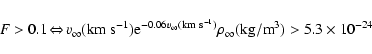
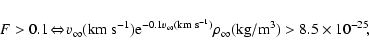
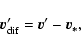
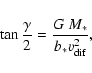
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6718fig9.eps}\end{figure}](/articles/aa/full/2007/26/aa6718-06/Timg187.gif)
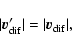
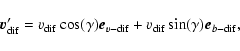
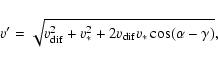
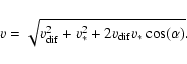
![\begin{displaymath}\Delta E=\frac{1}{2}m(v'^2-v^2)=mv_{\rm dif}v_*
[\cos (\alpha - \gamma)-\cos (\alpha)]
.\end{displaymath}](/articles/aa/full/2007/26/aa6718-06/img224.gif)