A&A 469, 671-680 (2007)
DOI: 10.1051/0004-6361:20066353
E. Josselin - B. Plez
GRAAL, Université Montpellier II - ISTEEM, CNRS, Place Eugène Bataillon, 34095 Montpellier Cedex, France
Received 6 September 2006 / Accepted 1 February 2007
Abstract
Context. Red supergiant stars represent a key phase in the evolution of massive stars. Recent radiative hydrodynamic simulations suggest that their atmospheres may be the location of large-scale convective motions.
Aims. As supergiant convection is expected to generate supersonic motions and shocks, we seek constraints on these atmospheric motions and their possible relation with mass-loss rates.
Methods. We present high-resolution, visible spectroscopy of a sample of red supergiants (spectral type M I) and analyse them with a tomographic technique.
Results. We observe steep velocity gradients, characterising both upward and downward supersonic motions, which are time variable on time scales of a few hundred days.
Conclusions. These convective motions will generate turbulent pressure, which will strongly decrease the effective gravity. We suggest that this decrease, combined with radiative pressure on molecular lines, initiate the mass loss in red supergiant stars.
Key words: supergiants - stars: atmospheres - stars: mass-loss
Red supergiants (RSG) are evolved massive
(10 ![]()
![]()
![]() 40
40 ![]() )
stars, in the core helium-burning
phase, preceding Wolf-Rayet stars and/or type II supernovae.
Thanks to their high-peak infrared luminosity, red supergiants are potential
powerful tracers of galactic structure, efficiently probing regions of high
interstellar extinction. They may also become extragalactic distance indicators,
if their fundamental parameters are properly calibrated.
)
stars, in the core helium-burning
phase, preceding Wolf-Rayet stars and/or type II supernovae.
Thanks to their high-peak infrared luminosity, red supergiants are potential
powerful tracers of galactic structure, efficiently probing regions of high
interstellar extinction. They may also become extragalactic distance indicators,
if their fundamental parameters are properly calibrated.
This task is hampered by the difficulty of carrying out a proper analysis of RSG optical spectra. Because of their low effective temperature, these spectra are dominated by strong molecular bands (esp. TiO), which lead to an ill-defined continuum. Furthermore, spectral lines exhibit a strong broadening, which can be parameterized by an ad-hoc high macroturbulent velocity of the order of 15 km s-1, indicating probable supersonic motions (Josselin & Plez 2004). In addition, non-LTE line formation is suspected for electronic molecular transitions (Hinkle & Lambert 1975) and may also affect atomic lines, regarding the low surface gravity of RSG. RSG lower atmospheres are convectively unstable. Already 30 years ago Schwarzschild (1975) claimed that large-scale convective motions were to be expected, with only a few granules covering the surface.
Josselin et al. (2000, hereafter Paper I) analysed infrared photometric and millimeter spectroscopic observations of a sample of RSG. They showed in particular that the dust mass-loss rate is not correlated with luminosity. Furthermore, the molecular gas-to-dust ratio shows a very large scatter and is generally higher than what is observed towards asymptotic giant branch (hereafter AGB) stars. Finally, Josselin et al. found strong indications of circumstellar inhomogeneities for at least one object, VY CMa. Most RSG are irregular variables with small amplitudes (type SRc or Lc), contrary to AGB stars (mostly of Mira or SRa type). Thus, models of mass loss for AGB stars, based on pulsations and radiation pressure on dust grains, are very unlikely to be applicable to RSG. Indeed, theoretical models have failed up to now to reproduce the observed mass-loss rates (Salasnish et al. 1999). Processes linked to chromospheric activity, convection or rotation may play an important role (Mallick 1993; Langer & Heger 1998).
In this paper we investigate the properties of the stars themselves, through high-resolution optical spectroscopy. The sample and observations are described in Sect. 2. We then present the results (Sect. 3) and analyse them in terms of the determination of the atmospheric dynamics (Sect. 4). Conclusions are given in Sect. 5.
The sample studied here consists of 21 late-type stars, mostly M type supergiants. Most of them (16 objects) are part of the sample studied in Paper I, which itself consisted mainly of M supergiants found in Humphreys (1978) catalogue of the brightest Galactic stars. Fourteen of them have known distance and interstellar extinction, thanks to their OB association memberships (Levesque et al. 2005). The sample is presented in Table 1. V magnitudes, extinction and distance moduli are taken from Lesveque et al. (2005). The latter two were determined on the basis of memberships to OB associations. The lack of data means that either the star was not identified as a member of such a cluster, or is not in Humphreys catalog.
Table 1: Supergiants of our program.
Distance and extinction estimates rely on the assumption that the
stars indeed belong to OB associations, which is not definitely
established. In most cases, the properties deduced from
this hypothesis are fully consistent (Levesque et al. 2005).
However, some cases may be more questionable. For
example, BC Cyg has a parallax measured by HIPPARCOS of 2.84 ![]() 0.87 mas,
corresponding to a distance of at most 500 pc (1
0.87 mas,
corresponding to a distance of at most 500 pc (1![]() error), while
the distance modulus gives a distance of 1.5 kpc. Other peculiar cases
are discussed hereafter.
error), while
the distance modulus gives a distance of 1.5 kpc. Other peculiar cases
are discussed hereafter.
High-resolution optical spectroscopy was obtained at the Haute-Provence Observatory with the echelle spectrograph ELODIE (Baranne et al. 1996). The spectra cover the range from 391 nm to 681 nm, with a spectral resolving power of 42 000 corresponding to 7.0 km s-1.
Automatic reduction, including bias subtraction, localisation of the orders, flat-field correction, and wavelength calibration, was achieved with the INTER-TACOS program, developed at the Geneva Observatory by D. Queloz and L. Weber (Queloz 1995). This instrument and the associated reduction package are primarily aimed at the search of extrasolar planets. This means that special care is given to wavelength calibration. Indeed radial velocities can be measured with an accuracy better than 0.1 km s-1 (in the observing mode we used, i.e. without simultaneous observation of a calibration lamp, in contrast to exo-planet searches) and a great stability.
A first set of data was obtained in August 1999 for the whole sample.
Series of spectra were subsequently obtained for 13 of these objects
from April 2003 to July 2004. We considered those
as the most relevant to studying atmospheric dynamics. In particular,
we did not follow (suspected) spectroscopic binaries,
or the faintest ones, to ensure a sufficient signal-to-noise ratio (S/N).
Eleven observational runs were devoted to this
follow-up, for a total of 29 nights, resulting in an average of 7 spectra per object, and up to 11 spectra for some objects. (Pointing limitations
due to the equatorial mounting of the telescope, and bad weather conditions
during the winter months, limited the time sampling in some cases.) The spectra
have typical S/N in the range 50-100 at 500 nm.
Because of the lower sensitivity of the CCD in the blue, where most of the
spectral lines used in the masks are located, and the fact that RSG spectra are
very red, the (S/N) of most of the observed spectral lines is an order of magnitude
lower. However, even with an
![]() ,
the maximum error on e.g. the
velocity broadening measurement through the cross-correlation technique
is
,
the maximum error on e.g. the
velocity broadening measurement through the cross-correlation technique
is ![]() 1 km s-1, i.e. below the typical
microturbulence of RSG, for a spectral resolving power of 40 000
(Queloz 1995)
1 km s-1, i.e. below the typical
microturbulence of RSG, for a spectral resolving power of 40 000
(Queloz 1995)![]() .
.
RW Cep - This object was included in our sample as it is
classified as an M0 I star in Humphreys (1978). However its spectrum
does not exhibit strong the TiO bands typical of M stars, so a spectral
type of G8 or K Ia (Morgan & Roman 1950) is clearly favoured. We nevertheless
keep this star in our sample as it shows qualitatively the same
behaviour as RSG, but with stronger asymmetries. As it is not
associated with any OB cluster, we adopt a distance of 840 pc (HIPPARCOS
parallax 1.19 ![]() 0.54 mas) in the following analysis,
keeping in mind that this value suffers strong uncertainty.
0.54 mas) in the following analysis,
keeping in mind that this value suffers strong uncertainty.
Spectroscopic binaries - Four spectroscopic binaries, namely
XX Per, HD 203338, VV Cep, and U Lac, were included in our initial sample.
VV Cep and HD 203338 are in fact triple systems of the same kind
and the binarity of XX Per and U Lac has been confirmed
(Burki & Mayor 1983). In the unique spectrum obtained for each
of them, we note that they all display asymmetries and velocity
gradients similar to those found for single RSGs. The effects of binarity (and
perhaps accretion disks) is nevertheless probably important, as attested
by e.g. the peculiar H![]() line profiles of VV Cep and U lac,
which have strong emission components. We thus did not follow these objects.
line profiles of VV Cep and U lac,
which have strong emission components. We thus did not follow these objects.
HD 37536 - Humphreys (1978) gives a spectral type of M2 Iab
and an association to Aur OB1 cluster, leading to a distance of 1.4 kpc.
But its HIPPARCOS parallax is 2.38 ![]() 0.97 mas (i.e.
0.97 mas (i.e. ![]() 420 pc).
Our spectrum shows a strong Li 6707 Å line and Van Eck et al. (1998)
indicate it is a Tc star. No significant velocity gradient was found
for this object. It is thus more probably a misclassified AGB star and
is excluded from the following analysis.
420 pc).
Our spectrum shows a strong Li 6707 Å line and Van Eck et al. (1998)
indicate it is a Tc star. No significant velocity gradient was found
for this object. It is thus more probably a misclassified AGB star and
is excluded from the following analysis.
Velocity fields in stellar atmospheres, and convective motions in particular,
can in principle be deduced from the study of line profiles. An illustration is convective blueshifts and "C'' shaped bisectors of solar lines (e.g. Asplund et al. 2000). However, studies of individual line profiles require observations of unblended lines at a resolving power of at least 105 and a high S/N (![]() 100) (see e.g. Dravins 1982, for a review of the method and some results). The important veiling of spectra of late-type stars by molecular lines hampers these studies in the optical.
100) (see e.g. Dravins 1982, for a review of the method and some results). The important veiling of spectra of late-type stars by molecular lines hampers these studies in the optical.
An alternative is to use lower-resolution spectra such
as those we obtained, together with the tomographic technique developed by
Alvarez et al. (2001). The spectra are cross-correlated with numerical masks
(series of holes placed at the selected line positions) that
probe layers at different optical depths. The resulting
cross-correlation functions (CCF) may be seen as average line profiles typical
of a given depth of formation, with higher S/N and resolution than
the original data. Eight masks were used, designated C1 to C8, respectively, probing
the innermost (faint lines, with excitation potentials of
![]() eV) to
the outermost layers (strong lines,
eV) to
the outermost layers (strong lines,
![]() eV).
eV).
In the case of a hydrostatic, spherically-symmetric star, a given radial optical depth can be associated with a unique atmospheric height. The CCF will then appear symmetric. In the absence of peculiar velocity fields, such as the expansion of the atmosphere or the propagation of a shock wave, the CCF obtained from each mask will be shifted at the same velocity, corresponding to the radial velocity of the star. Any deviation from one of these two cases will thus probe atmospheric dynamics.
The underlying assumption in this method is that all the lines that compose
a given mask (up to ![]() 800 lines for the masks probing the innermost
atmospheric layers) are indeed formed at the same optical depth in the
atmosphere and thus probe similar physical conditions. A careful examination of the
composition of the masks shows that
the lines share a wide variety of properties, in terms of elements (and thus
abundance and ionisation potentials), excitation potentials,
and oscillator strengths.
800 lines for the masks probing the innermost
atmospheric layers) are indeed formed at the same optical depth in the
atmosphere and thus probe similar physical conditions. A careful examination of the
composition of the masks shows that
the lines share a wide variety of properties, in terms of elements (and thus
abundance and ionisation potentials), excitation potentials,
and oscillator strengths.
In order to check the reliability of the method, we thus examined the excitation
conditions of the lines that make up each mask.
The optical depth at the central wavelength of a given line is
approximately given by
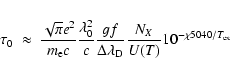
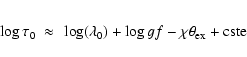
This factor, corrected for abundance effects, is displayed in Fig. 1, with special emphasis on neutral iron lines. Despite the noticeable presence of resonance lines in every mask, there is a clear tendency toward decreasing excitation temperature as one proceeds from mask C1 to mask C8. A strong dispersion exists however, which can be considerably reduced if one considers only one element in a given ionisation state (Fe I here).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{6353fig1.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg27.gif) |
Figure 1:
Properties of the lines within each mask defined by
Alvarez et al. (2001) for the tomography of stellar atmospheres.
the abundance |
| Open with DEXTER | |
Thus, to confirm that asymmetries found in a given CCF result from complex velocity fields at a given optical depth (which we are looking for) and are not influenced by velocity fields from different optical depths (i.e. probed by lines with different contribution functions but grouped in the same mask), we computed CCF with smaller masks made uniquely of Fe I lines.
Displayed in Fig. 2 are examples of CCF obtained for one RSG at two epochs. We chose to show the case of RW Cep as it is the object that has the most asymmetric CCF, so is a good test to see if the original masks do not produce asymmetries of undesirable origin. One can see that CCFs obtained either with full masks or with Fe I line masks are consistent within the increase in the noise level induced by the smaller number of lines in the Fe I masks. In particular the central velocity of the different CCF does not change by more than 1-2 km s-1, which is approximately the same as the uncertainty in the profile fitting (see hereafter). The subsequent analysis is thus based on CCFs obtained with the full masks, as the noise in the CCFs decreases with the increasing number of lines in the masks.
We want to emphasise here that the C8 Fe I line mask is primarily made
of lines with excitation potentials of
![]() eV. Excluding the few resonance
lines does not affect the observed asymmetries. The CCF can thus be considered
free of any circumstellar component, either in emission or absorption.
eV. Excluding the few resonance
lines does not affect the observed asymmetries. The CCF can thus be considered
free of any circumstellar component, either in emission or absorption.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{6353fig2.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg29.gif) |
Figure 2: Comparison of the cross-correlation functions (CCF) obtained for RW Cep at two epochs (corresponding to the largest observed variations in velocities). The full lines are the CCF obtained with the original masks, the dashed lines are those obtained with Fe I lines (see text for details). |
| Open with DEXTER | |
In agreement with the expectation of complex atmospheric dynamics for RSG, we observe strongly asymmetric CCF. In order to quantify such line asymmetries, the traditional technique consists in determining their bisectors. We consider that this is not applicable here. As mentioned above, the strong molecular veiling observed in cool-star spectra and the spectral resolution of our observations renders this technique inaccurate. Furthermore, as many CCF exhibit two distinct minima (especially those corresponding to strong lines), the usual definition of the bisector becomes inapplicable.
Thus, in order to characterise the atmospheric dynamics, we instead chose to determine characteristic velocities by fitting one or two Gaussians or Lorentzians to the CCFs. We measured four characteristic velocities for each spectrum. First, we determined an average atmospheric velocity by cross-correlating the spectra with a global mask, built from a synthetic spectrum of Arcturus (Baranne et al. 1996), which does not probe a particular atmospheric layer. Note that we refer here to atmospheric velocities, as the intrinsic stellar velocity is poorly defined, due to the lack of reliable indicator for these objects. We then adjust a single gaussian to the CCF obtained with mask C1, which gives access to the mean velocity of the innermost atmospheric layers of each star. This velocity is very similar to the global velocity, as almost all lines contained in masks C1 to C8 are included in the Arcturus mask, and lines contained in mask C1 are much more numerous than in any other mask and thus dominate the velocity measurement. We had to adjust two components to reproduce the more complex profiles obtained with the mask C8, and we thus measure two velocities for the outermost layers. Lorentzians give more satisfactory fits than gaussians (or a combination of both). The limitation to two components is questionable, as is the choice of lorentzians. But given the resolution, more complex adjustments would be meaningless. Given the number of free parameters in these adjustements (position, depth, and width of each component), we estimate that the uncertainty in the determination of these velocities is at most 2 km s-1 (i.e. the maximum difference in the velocities found with CCF obtained with complete masks and with Fe I line masks; see above).
Naturally, even if the fits with two components are apparently satisfactory, this does not mean that some layers are indeed characterised by two distinct velocities. Some combinations of the contribution functions and velocity laws as a function of optical depth (even monotonic) can lead to similar line profiles (e.g. Kulander & Jefferies 1966). The two velocities deduced from the CCF obtained with mask C8 may thus be considered as indicators of the amplitude of the velocity dispersion in the corresponding line-forming regions.
From these velocities we define three atmospheric velocity "gradients''
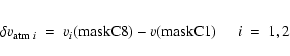
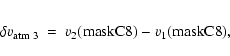
Figure 3 displays the observed variations of the average atmospheric velocity.
Half of the stars have "low'' variations (![]()
![]() 5 km s-1), while the average
atmospheric velocity varies strongly for the others.
Furthermore, some objects experience both local minima and maxima in
their velocity variations during our observations, while an apparently
continuous increase appears for two of them (BI Cyg and BC Cyg;
but because of the scarcity of the data a minimum may have been missed).
The amplitude of velocity variations may thus be seen as a lower limit, as
variation timescales may exceed the duration of our monitoring.
The best-sampled object,
5 km s-1), while the average
atmospheric velocity varies strongly for the others.
Furthermore, some objects experience both local minima and maxima in
their velocity variations during our observations, while an apparently
continuous increase appears for two of them (BI Cyg and BC Cyg;
but because of the scarcity of the data a minimum may have been missed).
The amplitude of velocity variations may thus be seen as a lower limit, as
variation timescales may exceed the duration of our monitoring.
The best-sampled object, ![]() Cep, experiences variations that may be periodic,
with a timescale of about 300 days, to be compared with the longer period of
photometric variations (
Cep, experiences variations that may be periodic,
with a timescale of about 300 days, to be compared with the longer period of
photometric variations (![]() 860 days, Kiss et al. 2006).
860 days, Kiss et al. 2006).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{6353fig3.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg33.gif) |
Figure 3: Velocity curves as a function of time. The velocities are those measured with the CCF obtained with the Arcturus mask. For each panel, the velocity range is fixed to 20 km s-1, in order to emphasise the relative amplitude of variations between each star. |
| Open with DEXTER | |
The CCFs present a wide variety of shapes (i) for each star from one
mask to another and (ii) from one star to another. Some general
properties can nevertheless be derived. First, the CCFs probing the
innermost layers (mask C1) are systematically blueshifted compared
to CCFs probing outer layers (masks C5 to C8). The asymmetry of the
CCFs increases as one progresses from the inner to the outer layers.
While mask C1 produces a rather symmetric profile (within the limit
of the resolution of the observations), mask C8 produces a much
more complex profile, with line doubling most of the time.
In the outermost layers, when two components are found,
one is systematically blueshifted and one redshifted relative
to the innermost layers. Both
![]() span the same range
of values, up to
span the same range
of values, up to ![]() 25 km s-1.
25 km s-1.
The depth, the "central'' velocity, and the asymmetries of the CCFs are also time variable. Changes in the velocity of a given component or CCF can reach up to 13 km s-1 on a time scale of about one year. These variations are far from regular. Variations of 2-3 km s-1 within one month are sometimes observed, followed by an apparent stability during a few months.
Two characteristic examples of sequences of CCFs are displayed in
Figs. 4 and 5, obtained for SW Cep and ![]() Cep,
respectively. In the first case, the line doubling appears rather deep in the
atmosphere, giving rise to very broad and doubled line
profiles in the outer atmosphere. In the second case,
variations still exist, but seem much smoother, apparently because
of a larger broadening of the lines, or their components.
Even in the outer atmosphere, profiles appear more asymmetric rather than split into two components, these components being separated by less than
Cep,
respectively. In the first case, the line doubling appears rather deep in the
atmosphere, giving rise to very broad and doubled line
profiles in the outer atmosphere. In the second case,
variations still exist, but seem much smoother, apparently because
of a larger broadening of the lines, or their components.
Even in the outer atmosphere, profiles appear more asymmetric rather than split into two components, these components being separated by less than
![]() 20 km s-1, the typical FWHM of these lines.
20 km s-1, the typical FWHM of these lines.
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{6353fig4.ps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg35.gif) |
Figure 4: CCF profiles for SW Cep. The dashed vertical lines indicate the central velocity measured in mask C1 at first epoch (upper left profile). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{6353fig5.ps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg36.gif) |
Figure 5:
Correlation profiles for |
| Open with DEXTER | |
The relations between the different velocity gradients are displayed
in Fig. 6. A correlation between
![]() (C8r-C1; which may be considered as indicative of downward motions)
and
(C8r-C1; which may be considered as indicative of downward motions)
and
![]() (C8r-C8b; convective velocity amplitude)
appears, while there seems to be no clear relation
between
(C8r-C8b; convective velocity amplitude)
appears, while there seems to be no clear relation
between
![]() (upward motions) and
(upward motions) and
![]() .
Upward and downward motions in the upper atmosphere are not symmetric
relative to the velocity of the deeper layers. Indeed, the upward velocity is
v(C8b)
.
Upward and downward motions in the upper atmosphere are not symmetric
relative to the velocity of the deeper layers. Indeed, the upward velocity is
v(C8b) ![]() v(C1) + 8 km s-1, while the downward velocity v(C8r) varies between 5 and 25 km s-1 w.r.t. v(C1).
v(C1) + 8 km s-1, while the downward velocity v(C8r) varies between 5 and 25 km s-1 w.r.t. v(C1).
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{6353fig6.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg41.gif) |
Figure 6: Relations between the three velocity gradients. Filled symbols correspond to time-averaged velocities, and empty ones to the maximum absolute gradients reached during our observations. C8b and C8r refer to the blue and red components in the CCF found with the mask C8. |
| Open with DEXTER | |
Regarding the correlation between
![]() and
and
![]() ,
the apparent lack of correlation between
,
the apparent lack of correlation between
![]() and
and
![]() may seem surprising. In fact, as illustrated in Fig. 7 for two objects, neither the average nor the extrema correspond to a situation met at any time in the star. For example,
when
may seem surprising. In fact, as illustrated in Fig. 7 for two objects, neither the average nor the extrema correspond to a situation met at any time in the star. For example,
when
![]() is maximum,
is maximum,
![]() is minimum, and
reciprocally. It is remarkable that qualitative agreement is found with simulations
of convection in the Sun (Stein & Nordlund 1998): downflows have higher velocities
than upflows.
is minimum, and
reciprocally. It is remarkable that qualitative agreement is found with simulations
of convection in the Sun (Stein & Nordlund 1998): downflows have higher velocities
than upflows.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{6353fig7.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg43.gif) |
Figure 7:
Relations between the three velocity gradients for |
| Open with DEXTER | |
The CCF profiles reveal irregular atmospheric dynamics, with velocities reaching supersonic values
(the sound speed is typically ![]()
![]() 5 km s-1 in RSG).
Because these velocities are supersonic, one expects the propagation of shock
waves in the atmosphere. We thus examined the possible occurrence of phase
shift between the variations of each velocity, such as those observed in pulsating
cool stars (e.g. Mathias et al. 1997). The velocity-velocity diagrams are shown in
Fig. 8 for our objects with a good time coverage.
No cyclic behaviour is observed, probably meaning that the atmosphere of RSG
is not vertically stratified in a simple fashion, and shock waves are not
spherically symmetric.
5 km s-1 in RSG).
Because these velocities are supersonic, one expects the propagation of shock
waves in the atmosphere. We thus examined the possible occurrence of phase
shift between the variations of each velocity, such as those observed in pulsating
cool stars (e.g. Mathias et al. 1997). The velocity-velocity diagrams are shown in
Fig. 8 for our objects with a good time coverage.
No cyclic behaviour is observed, probably meaning that the atmosphere of RSG
is not vertically stratified in a simple fashion, and shock waves are not
spherically symmetric.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{6353fig8.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg45.gif) |
Figure 8: Velocity-velocity diagrams for 4 RSG. In each panel, the black, solid curve corresponds to v(C8r) vs. v(C8b) (ordinate vs. abscissa), the red, dashed curve to v(C8r) vs. v(C1) and the blue, dotted curve to V(C8b) vs. v(C1). |
| Open with DEXTER | |
Examples of time variations in both depth and velocity for each component is shown in Fig. 9. Here again, no cyclic or regular behaviour is found, confirming the irregular nature of the variations, probably associated with (or due to) the asymmetric atmospheric structure.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{6353fig9.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg46.gif) |
Figure 9: Depth as a function of velocity for the CCF obtained with mask C1 (central black, solid curve in each panel) and the two components of the CCF obtained with mask C8 (left, blue, dotted and right, red, dashed curves). |
| Open with DEXTER | |
To establish the origin of the atmospheric dynamics,
we first have to derive the fundamental parameters of our stars.
With this aim, we used the photometry and the bolometric fluxes given in Paper I
and the distances and extinction (AV) from Levesque et al. (2005)![]() . Following Schlegel et al. (1998),
we adopt AK = 0.112 AV. For
. Following Schlegel et al. (1998),
we adopt AK = 0.112 AV. For ![]() Ori, we adopt a distance
of 140 pc from its Hipparcos parallax.
Ori, we adopt a distance
of 140 pc from its Hipparcos parallax.
The temperatures are based on the (V-K) colour and Bessell et al. (1998)
polynomial fit to
![]() for giants (their Table 7).
We chose the (V-K) colour as it is more sensitive to temperature than
any visible colour (e.g. B-V) and weakly sensitive to gravity.
Almost identical results (within 20 K) were obtained using the fit provided by
Levesque et al. (2005), based on more recent MARCS supergiant model
atmospheres. The temperature based on (V-K) for RW Cep
is incompatible with its early spectral type. This ambiguity is probably
at least partially due to erroneous extinction correction. (Humphreys 1978
derived the adopted value assuming an M0 spectral type.) We thus adopt a value
of 4200 K based on its spectral type (G8 Ia).
for giants (their Table 7).
We chose the (V-K) colour as it is more sensitive to temperature than
any visible colour (e.g. B-V) and weakly sensitive to gravity.
Almost identical results (within 20 K) were obtained using the fit provided by
Levesque et al. (2005), based on more recent MARCS supergiant model
atmospheres. The temperature based on (V-K) for RW Cep
is incompatible with its early spectral type. This ambiguity is probably
at least partially due to erroneous extinction correction. (Humphreys 1978
derived the adopted value assuming an M0 spectral type.) We thus adopt a value
of 4200 K based on its spectral type (G8 Ia).
These temperatures allow the stars to be placed in an HR diagram. In Fig. 10,
stars are plotted together with evolutionary tracks from Meynet & Maeder
(2003). As already noted by Levesque et al. (2005), the general agreement
with the new evolutionary models is very good with this warmer effective
temperature scale. We determined the initial stellar masses
of the objects from these evolutionary tracks. They range between ![]() 10
and 25
10
and 25 ![]() .
We keep in mind that given the inversed-square
dependence of luminosity on distance,
these estimates may be uncertain by at least 25% (or 0.1 dex), which roughly
corresponds to an uncertainty of 0.4 dex on the luminosity (or 0.2 dex on the distance,
which is conservative, as long as the membership in OB associations is reliable).
.
We keep in mind that given the inversed-square
dependence of luminosity on distance,
these estimates may be uncertain by at least 25% (or 0.1 dex), which roughly
corresponds to an uncertainty of 0.4 dex on the luminosity (or 0.2 dex on the distance,
which is conservative, as long as the membership in OB associations is reliable).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{6353fig10.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg48.gif) |
Figure 10: HR diagram for the sample of RSG, together with evolutionary tracks from Meynet & Maeder (2003). Full-line tracks are non-rotating models and dashed-line tracks correspond to models with an initial rotational velocity of 300 km s-1. |
| Open with DEXTER | |
Following Bessell et al. (1998), we adopt
![]() = 4.74
and
= 4.74
and
![]() = 5780 K. Stellar radii are thus calculated according to
= 5780 K. Stellar radii are thus calculated according to
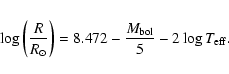
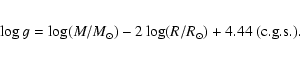
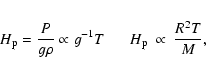
Finally, as it will appear hereafter, it is useful to evaluate the density in
the atmospheres of RSG. As no simple relation based on fundamental
parameters exists, we examined the behaviour of the density in the photosphere
(
![]() = 1) of MARCS models (Gustafsson et al. 1975; Plez et al. 1992; Gustafsson et al. 2003). In the range 3500
= 1) of MARCS models (Gustafsson et al. 1975; Plez et al. 1992; Gustafsson et al. 2003). In the range 3500 ![]()
![]()
![]() 4000
and
4000
and
![]() ,
we found the following relation:
,
we found the following relation:
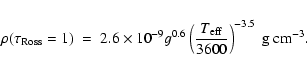
Table 2: Stellar parameters and velocity gradients of our stars.
Velocity gradients measured on the CCF suggest both ascending and descending gas in the outermost layers of RSG atmospheres. These kinds of movements may have a convective origin. If this is the case, the comparison with the well-studied case of the Sun is instructive. As mentioned above, the pattern is in qualitative agreement, but the convective velocities are much higher than in the Sun. Furthermore, in the case of a small-scale granulation, the line profiles resulting from the sum of many components would produce undetectable line asymmetries at the resolution of our observations. In addition to higher velocities, we thus naturally suspect much larger convective cells.
Developing an idea of Stothers & Leung (1971), Schwarzschild (1975)
suggested the occurrence of giant convective cells in the atmosphere
of red (super)giants. He considered that the pressure scale height
determines the characteristic scale of convection (in agreement
with the mixing length theory of convection, hereafter MLT) and adopted a constant ratio (diameter of a granule)/(depth of a granule) ![]() 3.
Then, extrapolating solar values, he found that the entire surface
of a red supergiant should be occupied by at most a dozen cells. Irregular
light variations could then be attributed to changes of
these few convective elements with time. The typical timescale would be
3.
Then, extrapolating solar values, he found that the entire surface
of a red supergiant should be occupied by at most a dozen cells. Irregular
light variations could then be attributed to changes of
these few convective elements with time. The typical timescale would be
![]()
![]()
![]() (h = typical dimension of a convective
element, and
(h = typical dimension of a convective
element, and ![]() = average convective velocity). With
= average convective velocity). With ![]()
![]() sound velocity (
sound velocity (![]() 5 km s-1), Schwarzschild found
5 km s-1), Schwarzschild found
![]()
![]() 150 days for a typical RSG (M = 15
150 days for a typical RSG (M = 15 ![]() ,
,
![]() = 3700 K).
This timescale is compatible with our observed velocity
variations (Fig. 3).
= 3700 K).
This timescale is compatible with our observed velocity
variations (Fig. 3).
It is nevertheless clear that the MLT is inapproriate
in such a scenario. A validation of this hypothesis thus requires
detailed radiative hydrodynamics simulations. This is currently
performed by Freytag et al. (2002). Their models confirm the occurrence
of large convective cells, with a convective turn-over time ![]() 1 yr,
about the same as Schwarzschild's timescale.
1 yr,
about the same as Schwarzschild's timescale.
Such supersonic convective motions could produce hot spots and
"chromospheric'' heating (the word chromosphere being probably inappropriate,
as this region must be very inhomogeneous and thus not spherical),
which may be seen as blue and/or near-ultraviolet excess in the
spectral energy distribution. This could be linked with such an excess
observed toward ![]() Ori (Carpenter et al. 1994; Harper et al. 2001)
and maybe with that detected by Massey et al. (2005) in a number of RSGs.
Ori (Carpenter et al. 1994; Harper et al. 2001)
and maybe with that detected by Massey et al. (2005) in a number of RSGs.
We now examine the relation between the atmospheric velocities and the stellar
parameters. As shown in Fig. 11, the velocity gradients themselves do
not exhibit any convincing correlation with the stellar parameters considered here.
This may not be surprising, as the velocity gradients do not vary by more than
a factor ![]() 2 within our sample, making any search for a correlation difficult.
Rather than the atmospheric velocities themselves, it may be more meaningful
to consider the ratio between these velocities and characteristic ones, such
as the sound speed or the escape velocity. For example, based on simulations
of dwarfs and giants (
2 within our sample, making any search for a correlation difficult.
Rather than the atmospheric velocities themselves, it may be more meaningful
to consider the ratio between these velocities and characteristic ones, such
as the sound speed or the escape velocity. For example, based on simulations
of dwarfs and giants (
![]() ), Freytag (2001) found an empirical
relation between the ratio of convective-to-escape velocities and gravity:
), Freytag (2001) found an empirical
relation between the ratio of convective-to-escape velocities and gravity:
![]()
![]() g-1/4.
But this relation actually reflects the relation between escape velocity and
gravity (
g-1/4.
But this relation actually reflects the relation between escape velocity and
gravity (
![]() ). Thus again, any search
for a meaningful correlation is hampered by the narrow range
spanned by velocity gradients.
). Thus again, any search
for a meaningful correlation is hampered by the narrow range
spanned by velocity gradients.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{6353fig11.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg72.gif) |
Figure 11:
The time-averaged velocity gradient
|
| Open with DEXTER | |
Since the first "images'' of Betelgeuse surface (Gilliland & Dupree 1996)
and the results of global simulations of RSG radiative hydrodynamics
(Freytag et al. 2002), which both favour the occurrence of giant cells
and/or hot spots on RSG surfaces, the reality of these features
has been debated. In particular, Gray (2001) performed high-resolution
(R ![]() 105) spectroscopic observations of Betelgeuse (91 spectra over 17 months). He found that both line broadening and shapes are remarkably
stable, so argues against giant convective cells.
The changes in the strength of the lines (deeper lines, brighter star)
could be explained by variations in the continuous opacity.
105) spectroscopic observations of Betelgeuse (91 spectra over 17 months). He found that both line broadening and shapes are remarkably
stable, so argues against giant convective cells.
The changes in the strength of the lines (deeper lines, brighter star)
could be explained by variations in the continuous opacity.
In order to see if our observations are compatible or not with these
findings, we examined the profile variations of two of the three lines studied by
Gray (2001) in ![]() Ori spectra that we obtained (the third line, the
Ori spectra that we obtained (the third line, the
![]() 6251 Å line of V I, falls between two orders of the ELODIE spectrograph and was thus not observed). They are shown in Fig. 12. We also show the CCF obtained with the mask C5. which includes the Ti I line. The Fe I line is not present in any mask but is similar to other lines present in masks C4/C5.
6251 Å line of V I, falls between two orders of the ELODIE spectrograph and was thus not observed). They are shown in Fig. 12. We also show the CCF obtained with the mask C5. which includes the Ti I line. The Fe I line is not present in any mask but is similar to other lines present in masks C4/C5.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{6353fig12.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg74.gif) |
Figure 12: Spectroscopic observations of Betelgeuse made in 2003-2004. Upper panels: two of the lines used by Gray (2001) to study the variability of line profiles. Lower left panel: CCF profiles calculated with the mask C5, which includes the Ti I line, and Fe I lines sharing similar properties with the 6219 Å line (which is not included in any mask). Lower right panel: zoom on the central part of the CCF. |
| Open with DEXTER | |
In contrast to Gray's assessment, we do find time-variable Doppler shifts and line depressions (it is not clear how radial velocity information could be extracted from Gray's observations). Asymmetries are very weak for these lines, but, as shown above, the most asymmetric lines have lower excitation potentials (see Figs. 4 and 5). It is true however that Betelgeuse is among the least variable stars in our sample. Furthermore one cannot exclude that, during Gray's observations, Betelgeuse was in a rather quiet state, if thinking of quite irregular variations found in other RSGs. Finally we recall here that Freytag et al. (2002) models are not aimed at reproducing the case of Betelgeuse itself, but rather a typical RSG, in terms of temperature and gravity. The existing simulations have effective temperatures at the very lower end of the effective temperature scale of RSG and are probably more typical of very cool RSG, or AGB stars. We are now conducting simulations that are more appropriate for warmer RSG with B. Freytag.
To conclude, Gray (2001) claims that "time-variable structure in line profiles is a natural and necessary consequence of giant convective cells''. This is exactly what we observe among RSGs in general and, to a lesser degree of amplitude, in Betelgeuse.
As mentioned in the introduction, the mass-loss process
operating in RSG remains unknown.
The extrapolation of the theory of the mass loss of AGB stars
seems irrelevant, as (1) RSG have irregular, small-amplitude variations
(and are thus not pulsating in a similar manner); (2) significant amounts of dust
are only found at larger radii (typically ![]() 20 stellar radii, Danchi et al. 1994)
so radiation pressure on dust cannot occur in the wind acceleration zone.
20 stellar radii, Danchi et al. 1994)
so radiation pressure on dust cannot occur in the wind acceleration zone.
Besides theory suggesting that acoustic waves (and thus
convective motions) could initiate mass loss in RSG (Pijpers & Hearn 1989),
there are some observational indications that convection could play a key role in the mass-loss process. In particular, VY CMa, one of the RSG with
the highest observed mass-loss rate, exhibits an asymmetric nebula,
with arcs probably resulting from multiple ejections. Smith et al. (2001) argue
that these arcs were most likely produced by ejection events localised on the
stellar surface, suggesting a link with giant convective cells.
Strong circumstellar inhomogeneities such as plumes or clumps have also been
observed in ![]() Ori shell (Plez & Lambert 2001).
Ori shell (Plez & Lambert 2001).
We thus examined whether the observed velocity fields present any relation with mass-loss rates. Unfortunately, because of the weak emission of circumstellar molecular gas (Paper I) and the difficulty of observing atomic gas, only dust mass-loss rates are available for our sample. The circumstellar dust-to-gas ratio is not known and may vary within RSG.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{6353fig13.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg76.gif) |
Figure 13:
Upper panel: dust mass-loss rate as a function of
|
| Open with DEXTER | |
We show in Fig. 13 the relation between the dust mass-loss rate and
![]() ,
as well as between the ratio
,
as well as between the ratio
![]() ,
i.e. the rate of flow, and
,
i.e. the rate of flow, and
![]() .
A clear tendency toward higher
rates with higher values of
.
A clear tendency toward higher
rates with higher values of
![]() appears, again suggesting
that convection may play a key role in the mass-loss process operating in RSG.
The typical photospheric escape velocity for a RSG (with a mass of 15
appears, again suggesting
that convection may play a key role in the mass-loss process operating in RSG.
The typical photospheric escape velocity for a RSG (with a mass of 15 ![]() and
a radius of 500
and
a radius of 500 ![]() )
is
)
is ![]() 100 km s-1. Because of the short
mean free path of atoms in the atmosphere of RSG compared to the atmospheric extent,
a simple evaporation, such as the Darwin's mechanism operating in planetary
atmospheres, cannot explain the observed mass-loss rates alone.
We recall here that, as only dust mass-loss rates are available for most of the RSG
in our sample, no definite conclusion can be drawn as long as total mass-loss
rates are not evaluated. Indeed, the dust condensation efficiency, and thus dust-to-gas ratio,
may also be influenced by convective velocities and by related shock waves (through
local density enhancements).
100 km s-1. Because of the short
mean free path of atoms in the atmosphere of RSG compared to the atmospheric extent,
a simple evaporation, such as the Darwin's mechanism operating in planetary
atmospheres, cannot explain the observed mass-loss rates alone.
We recall here that, as only dust mass-loss rates are available for most of the RSG
in our sample, no definite conclusion can be drawn as long as total mass-loss
rates are not evaluated. Indeed, the dust condensation efficiency, and thus dust-to-gas ratio,
may also be influenced by convective velocities and by related shock waves (through
local density enhancements).
In order to understand the impact convection has on the atmospheric
structure, we may try to follow a very simple argument, based
on the property of hydrostatic atmospheres. Additional details can be found
in Gustafsson & Plez (1992), who discuss the impact of
turbulent pressure on density inversions and mass loss in hypergiant stars.
We have shown above that the velocities we measured most probably reflect
the convective velocity amplitude.
If we suppose these convective motions
are turbulent, they give rise to a turbulent pressure of the order of
![]() .
We assumed further that
.
We assumed further that
![]() (in km s-1) is a constant throughout the
atmosphere (This may not be true, but still the gradient of turbulent
pressure will be dominated by the density gradient) and that the atmosphere is
isothermal. Including this pressure term in the hydrostatic
equilibrium equation leads then to
(in km s-1) is a constant throughout the
atmosphere (This may not be true, but still the gradient of turbulent
pressure will be dominated by the density gradient) and that the atmosphere is
isothermal. Including this pressure term in the hydrostatic
equilibrium equation leads then to
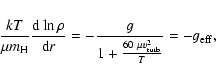
It is possible to estimate the maximum rate of kinetic energy flux injected by turbulent
motions as
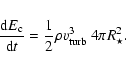
![\begin{figure}
\par\includegraphics[angle=-90,width=8.45cm,clip]{6353fig14.eps}\end{figure}](/articles/aa/full/2007/26/aa6353-06/Timg91.gif) |
Figure 14: Maximum rate of kinetic energy flux injected by turbulent motions as a function of stellar luminosity. |
| Open with DEXTER | |
We therefore suggest that mass loss is initiated in RSG by the combined effect of a vigorous convection and radiative pressure on molecular lines. Detailed calculations for radiative-hydrodynamical models of RSG will be presented in a forthcoming paper.
Other and/or additional origins of mass loss, in particular magnetic fields, are not excluded.
In AGB stars, large-scale fields may be strong enough to form
magnetic cool spots, which could regulate dust formation, hence
mass loss. Coupling Freytag's model for ![]() Ori with a MHD code,
Dorch (2004) found that surface magnetic fields up to
Ori with a MHD code,
Dorch (2004) found that surface magnetic fields up to ![]() 500 Gauss can be produced, in agreement with recent measurements by Vlemmings et al. (2005). These strong magnetic
fields could be generated by convective motions, through
500 Gauss can be produced, in agreement with recent measurements by Vlemmings et al. (2005). These strong magnetic
fields could be generated by convective motions, through
![]() -dynamo (Blackman et al. 2001).
-dynamo (Blackman et al. 2001).
High-resolution spectroscopic time-series observations of a sample of RSG, analysed with a tomography technique, reveal variable velocity fields in the atmosphere of RSG, probably of convective origin. These velocities are supersonic and vary with time scales of a few 100 days. The strong line asymmetries generated by these velocity fields indicate that convection must consist of giant cells, as also suggested by recent radiative hydrodynamics modelling (Freytag et al. 2002). We find a behaviour of upward, downward, and horizontal velocities similar to that characterising solar convection. Such constraints will be used to test new RHD simulations.
These convective motions could play an important role in the mass-loss process operating in RSGs, because of the strong decrease in effective gravity due to turbulent pressure.
Further improvements in our understanding of these puzzling objects will be presented in a future paper (Chiavassa et al., in preparation), which will compare radiative hydrodynamic simulations with these observations.
Acknowledgements
We are grateful to Rodrigo Alvarez for providing his correlation procedures and his numerical masks, and to Bernd Freytag and Nicolas Mauron for fruitful discussions. We also thank the referee for useful comments. We acknowledge the staff of the Haute-Provence Observatory for help during the observations.