A&A 468, 1075-1081 (2007)
DOI: 10.1051/0004-6361:20066977
Generation of a secondary shock wave during the oblique collision between a current sheet
and a fast magnetosonic shock wave
J. I. Sakai - Y. Tanaka
Laboratory for Plasma Astrophysics, Faculty of Engineering, University of Toyama,
3190 Gofuku, Toyama, 930-8555, Japan
Received 20 December 2006 / Accepted 1 March 2007
Abstract
Aims. We investigate what happens when a fast magnetosonic shock wave associated with a coronal mass ejection (CME) collides obliquely with a coronal streamer with a stable current sheet.
Methods. A two-dimensional relativistic and fully electromagnetic Particle-In-Cell (PIC) code is used.
Results. It is shown that the fast magnetosonic shock with initial Alfvén Mach
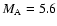 compresses the current sheet, resulting in strong deformation of the current sheet. In the later stage a secondary fast magnetosonic shock wave can be generated almost perpendicular to the current sheet, and it propagates away to the opposite side of the original shock. This newly generated shock wave may emit a type II radio burst. The simulation results may be applied to a split of electromagnetic wave emissions when a shock wave associated with CMEs collides obliquely with a coronal streamer. For weak initial Alfvén Mach
compresses the current sheet, resulting in strong deformation of the current sheet. In the later stage a secondary fast magnetosonic shock wave can be generated almost perpendicular to the current sheet, and it propagates away to the opposite side of the original shock. This newly generated shock wave may emit a type II radio burst. The simulation results may be applied to a split of electromagnetic wave emissions when a shock wave associated with CMEs collides obliquely with a coronal streamer. For weak initial Alfvén Mach
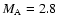 ,
a secondary shock wave does not appear, while the current sheet can be deformed and become unstable for tearing-like modes associated with magnetic reconnection.
,
a secondary shock wave does not appear, while the current sheet can be deformed and become unstable for tearing-like modes associated with magnetic reconnection.
Key words: plasmas - shock waves - radiation mechanisms: non-thermal - methods: numerical - Sun: radio radiation
The shock waves generated by coronal mass ejections (CMEs) are observed in the interplanetary (IP)
medium since they accelerate electrons, which can emit type II radio waves. Recent observations of IP type II bursts imply
that changes in the shock and CMEs dynamics can be caused by interaction with some structures in the IP medium, such as collision with another CME or shock-shock collision (Gopalswamy et al. 2001). Recently Sakai et al. (2005) showed that the electron Bernstein waves or
Z-modes generated near the shock front can be converted into extraordinary electromagnetic waves (type II radio
bursts) through direct linear mode conversion. Sakai et al. (2006) also simulated the shock-shock collision
observed by Gapalswamy et al. (2001) and found that the type II radio bursts can be enhanced after the
shock-shock collision.
Sheeley et al. (2000)
show examples of the fast CMEs associated with the deflection of coronal streamers, and van der Holst et al. (2002)
observe that when the fast CME collides with a helmet streamer, a split occurs in the type II emission. They
modeled this CME-streamer interaction by using a 2D MHD simulation. Mancuso & Abbo (2004) investigate the observed bifurcation of the radio emission lanes by modeling the interaction of a piston-driven spherical shock
with a vertical current sheet located above the active region.
Previous theoretical and simulation models of the interaction between a current sheet and a fast
magnetosonic shock wave are based on MHD models. To understand the physical processes of the emissions of type II
radio bursts during the shock-streamer collision, we must take plasma kinetic processes into account by using
particle-in-cell (PIC) simulation.
Recently, Haruki et al. (2006) investigated how the emission of electromagnetic waves can be enhanced when a
fast magnetosonic shock wave associated with CMEs collides perpendicular to a coronal streamer with a stable
current sheet, by using a two-dimensional relativistic and fully electromagnetic PIC code. It
was shown that the ions in front of the shock can be accelerated by the shock-surfing acceleration mechanism (Sagdeev & Shapiro 1973; Lee et al. 1996; Lipatov & Zank 1999; Hoshino & Shimada 2002; Lee et al. 2005; Dieckmann et al. 2006). This shock compresses the current sheet, resulting in the local electron temperature anisotropy. Electron Bernstein
waves are generated by the local electron temperature anisotropy and are converted into electromagnetic waves
(X-mode) through the linear mode conversion due to density inhomogeneity (Murtaza & Shukla 1984; Yin et al. 1999). The nonlinear excitation process of the
electron Bernstein waves in a pinching current sheet was investigated by Haruki & Sakai (2001). There, the
electromagnetic waves are observed in both forward and backward regions of the shock. These simulation results were
applied to the enhancement of electromagnetic wave emission when a shock wave associated with a CME collides
with a coronal streamer.
In the present paper we extend the above work by Haruki et al. (2006) to investigate what happens when a fast magnetosonic
shock wave associated with a CME collides obliquely with a coronal streamer with a
stable current sheet. It is shown that the fast magnetosonic shock for strong initial Alfvén Mach
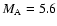 compresses the current sheet, resulting in
strong deformation of the current sheet.
In the later stage a secondary fast magnetosonic shock wave can be generated almost perpendicular to the current sheet, and it propagates to the
opposite side of the original shock. This newly generated shock may emit the type II radio burst, as shown by Sakai et al. (2005). For weak initial Alfvén Mach
compresses the current sheet, resulting in
strong deformation of the current sheet.
In the later stage a secondary fast magnetosonic shock wave can be generated almost perpendicular to the current sheet, and it propagates to the
opposite side of the original shock. This newly generated shock may emit the type II radio burst, as shown by Sakai et al. (2005). For weak initial Alfvén Mach
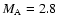 a secondary shock wave does not appear, while the current sheet can be deformed and become unstable for tearing-like modes associated with magnetic reconnection.
a secondary shock wave does not appear, while the current sheet can be deformed and become unstable for tearing-like modes associated with magnetic reconnection.
This paper is organized as follows. In Sect. 2 we present our simulation model and in Sect. 3 we show our
simulation results. In the final section we summarize our results.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6977f1.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg14.gif) |
Figure 1:
Schematic picture of the coronal mass ejection (CME) associated with a shock wave that collides obliquely with Harris type current sheet and the coordinate system used in the simulation. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6977f2.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg15.gif) |
Figure 2:
The initial magnetic field structure of a Harris type current sheet and proton density. The square high-density region moves
with Alfvén Mach speed
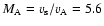 ,
resulting in formation of a shock wave. ,
resulting in formation of a shock wave. |
| Open with DEXTER |
Figure 1 shows a schematic picture of our simulation model. It is assumed that a CME originating in the
lower corona produces a shock and that this shock undergoes a oblique collision with a coronal streamer that
contains a current sheet as shown. The initial magnetic field and plasma number
density for a Harris type current sheet are the same as in Haruki et al. (2006). Figure 2 shows the initial magnetic field
and the proton density distribution. As shown in Fig. 2 we impose a dense plasma cloud (square region) far from the center of the
current sheet to excite a fast magnetosonic shock wave by imposing the plasma velocity with Alfvén Mach speed
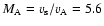 on the cloud. The initial velocity of the cloud is
on the cloud. The initial velocity of the cloud is
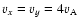 .
.
The code used here is a 2D relativistic and fully electromagnetic PIC code, modified from the 3D TRISTAN
code (Buneman 1993). The system size in 2D is
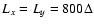 ,
where
,
where
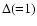 is the simulation grid size. It is assumed that the physical
quantities are constant in z, i.e.,
is the simulation grid size. It is assumed that the physical
quantities are constant in z, i.e.,
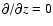 .
The average number density of background
electrons and ions is 100 per cell. The given particles fill the whole domain. Charge neutrality is initially kept because of having the
same position for the electron and proton. Periodic boundary conditions in the x-direction and free boundary conditions
in the y-direction are imposed on particles and fields.
.
The average number density of background
electrons and ions is 100 per cell. The given particles fill the whole domain. Charge neutrality is initially kept because of having the
same position for the electron and proton. Periodic boundary conditions in the x-direction and free boundary conditions
in the y-direction are imposed on particles and fields.
First, we impose the following Harris type current sheet (Harris 1962; Pritchett 2001) that is characterized by the magnetic field, current,
and plasma particle number density, namely,
where
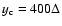 and half thickness
and half thickness
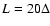 .
We assume a low beta plasma
.
We assume a low beta plasma
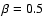 and
electron thermal velocity
and
electron thermal velocity
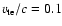 (c is light speed) in the background plasma, and then
(c is light speed) in the background plasma, and then
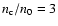 and
and
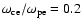 are obtained theoretically, where
are obtained theoretically, where
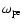 and
and
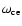 are
electron plasma and cyclotron frequencies, respectively. Moreover, the Alfv
are
electron plasma and cyclotron frequencies, respectively. Moreover, the Alfv
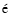 n velocity far from
the center of the current sheet is automatically solved with about
n velocity far from
the center of the current sheet is automatically solved with about
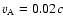 .
Next, to excite a shock wave far
from the center of the current sheet, we impose a dense plasma cloud whose number density is 400 per cell from
.
Next, to excite a shock wave far
from the center of the current sheet, we impose a dense plasma cloud whose number density is 400 per cell from
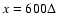 to
to
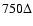 and
and
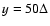 to
to
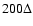 .
The cloud velocity is set up with
.
The cloud velocity is set up with
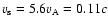 .
.
The other parameters used for this simulation are as follows. The simulation time step is
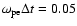 ,
where
,
where
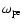 is used as a normalization of time. The Debye length is
is used as a normalization of time. The Debye length is
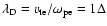 .
The electron skin depth is
.
The electron skin depth is
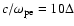 ,
which is also used as a normalization of space. The mass
ratio of electron and proton is
,
which is also used as a normalization of space. The mass
ratio of electron and proton is
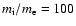 ,
whose value is artificial due to computer memory. The temperatures of the
electrons and protons are the same,
,
whose value is artificial due to computer memory. The temperatures of the
electrons and protons are the same,
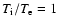 .
The Larmor radii of electrons and protons are
.
The Larmor radii of electrons and protons are 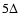 and
and 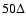 ,
respectively.
,
respectively.
We performed another simulation case without the dense plasma cloud. We confirmed that the
current sheet is very stable until
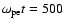 .
For this case, we did not observe any wave generation.
.
For this case, we did not observe any wave generation.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{6977f3.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg45.gif) |
Figure 3:
Time development of proton number density 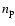 and magnetic field Bx in the x-y plane at
and magnetic field Bx in the x-y plane at
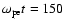 ( a-1, b-1), 200( a-2, b-2), and 250( a-3, b-3). ( a-1, b-1), 200( a-2, b-2), and 250( a-3, b-3). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=13.3cm,clip]{6977f4.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg46.gif) |
Figure 4:
Time development of proton phase space,
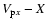 ( a-1- a-3) and ( a-1- a-3) and
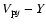 ( b-1- b-3) at ( b-1- b-3) at
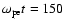 ( a-1, b-1), 200( a-2, b-2), and250( a-3, b-3). ( a-1, b-1), 200( a-2, b-2), and250( a-3, b-3). |
| Open with DEXTER |
The square high-density region with Alfvén Mach speed
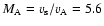 in Fig. 2 approaches the current sheet at an angle of
in Fig. 2 approaches the current sheet at an angle of
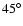 ,
resulting in the formation of shock wave. To see the shock formation stage, we show the time development of proton number density
,
resulting in the formation of shock wave. To see the shock formation stage, we show the time development of proton number density 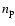 and magnetic field Bx in the x-y plane at
and magnetic field Bx in the x-y plane at
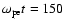 (a-1, b-1), 200(a-2, b-2), and 250(a-3, b-3) in Fig. 3.
We find that the shock front speed at near
(a-1, b-1), 200(a-2, b-2), and 250(a-3, b-3) in Fig. 3.
We find that the shock front speed at near
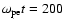 is about
is about
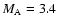 .
The proton density near
the shock front at
.
The proton density near
the shock front at
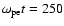 is increased about 6.5 times of background density due to the density inhomogeneity. The shock enhancement due to density inhomogeneity near the current sheet was studied by Sakai (1973). In Fig. 4 we show the time development of proton phase space,
is increased about 6.5 times of background density due to the density inhomogeneity. The shock enhancement due to density inhomogeneity near the current sheet was studied by Sakai (1973). In Fig. 4 we show the time development of proton phase space,
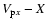 and
and
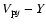 at
at
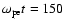 (a-1, b-1), 200(a-2, b-2), and 250(a-3, b-3).
The average bulk velocity of the cloud is about 0.08c in both x- and y-directions which gives us about
(a-1, b-1), 200(a-2, b-2), and 250(a-3, b-3).
The average bulk velocity of the cloud is about 0.08c in both x- and y-directions which gives us about
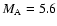 close to the initial cloud velocity. It is seen from the shock front that a small fraction of protons are
accelerated ahead of the shock front.
close to the initial cloud velocity. It is seen from the shock front that a small fraction of protons are
accelerated ahead of the shock front.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{6977f5.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg51.gif) |
Figure 5:
Time development of proton density distribution at a)
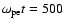 ,
b) ,
b)
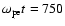 ,
c) ,
c)
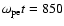 ,
and d) ,
and d)
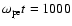 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{6977f6.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg52.gif) |
Figure 6:
a) Proton density distribution at
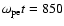 for
for
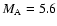 .
b) Proton phase space plot ( .
b) Proton phase space plot (
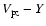 )
at )
at
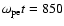 .
c) Magnetic field Bx and d) electric field Ey at .
c) Magnetic field Bx and d) electric field Ey at
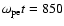 . . |
| Open with DEXTER |
The generated fast magnetosonic shock wave collides with the current sheet and moves along the
current sheet with strong deformation. In Fig. 5 we show the time development of the proton number density in the x-y plane at a
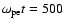 ,
b 750, c 850, and d 1000. As seen in the region of
,
b 750, c 850, and d 1000. As seen in the region of
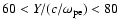 ,
a fast magnetosonic wave with a bow-like structure
propagates to the upper direction. While near the upper part of the current sheet where strong density deformation is seen, the strong proton density detachment can be observed in Fig. 5b. This enhanced density cloud propagates to the positive y direction almost perpendicular to the current sheet,
as seen in Figs. 5b-d. This plasma cloud detached from the current sheet can develop to a secondary fast magnetosonic shock wave. The shock front speed is about 0.06c, which gives us about
,
a fast magnetosonic wave with a bow-like structure
propagates to the upper direction. While near the upper part of the current sheet where strong density deformation is seen, the strong proton density detachment can be observed in Fig. 5b. This enhanced density cloud propagates to the positive y direction almost perpendicular to the current sheet,
as seen in Figs. 5b-d. This plasma cloud detached from the current sheet can develop to a secondary fast magnetosonic shock wave. The shock front speed is about 0.06c, which gives us about
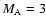 by using
by using
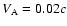 .
.
In Fig. 6 we present the spacial structure associated with the secondary generated shock wave at
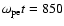 .
Figures 6a, c, and d show proton density distribution, magnetic field Bx, and electric field Ey near the the shock front, respectively. Figure 6b shows the proton phase space plot (
.
Figures 6a, c, and d show proton density distribution, magnetic field Bx, and electric field Ey near the the shock front, respectively. Figure 6b shows the proton phase space plot (
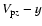 )
at
)
at
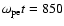 .
Some protons near Y=70 can be accelerated to the positive z-direction.
These protons are accelerated by the shock surfing acceleration mechanism (Sagdeev & Shapiro 1973) near the secondary generated shock wave. We can estimate the maximum proton velocity obtained near the shock front as
.
Some protons near Y=70 can be accelerated to the positive z-direction.
These protons are accelerated by the shock surfing acceleration mechanism (Sagdeev & Shapiro 1973) near the secondary generated shock wave. We can estimate the maximum proton velocity obtained near the shock front as
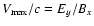 .
We obtain
.
We obtain
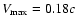 by using the field data of Ey=0.14 and Bx=0.76 at X=36.6 and Y=72.9. This value is almost consistent with the simulation result seen in Fig. 6b. Therefore we may expect that the secondary generated fast magnetosonic shock wave can emit the type II radio bursts shown in Sakai et al. (2005). To see the wave emission in this simulation, we need larger simulation box.
by using the field data of Ey=0.14 and Bx=0.76 at X=36.6 and Y=72.9. This value is almost consistent with the simulation result seen in Fig. 6b. Therefore we may expect that the secondary generated fast magnetosonic shock wave can emit the type II radio bursts shown in Sakai et al. (2005). To see the wave emission in this simulation, we need larger simulation box.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{6977f7.eps} \end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg59.gif) |
Figure 7:
Time development of proton density distribution for
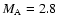 at a)
at a)
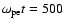 ,
b) ,
b)
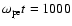 and c)
and c)
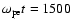 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6977f9.eps} \end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg61.gif) |
Figure 9:
Time development of vector plots of magnetic fields for
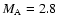 at a)
at a)
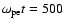 ,
b) ,
b)
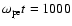 and c)
and c)
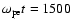 . .
|
| Open with DEXTER |
Finally we present simulation results with a different Mach number that is smaller than the above case.
We show the case where the initial driving flow velocity is
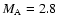 .
Figure 7 shows the time development of proton number density at a)
.
Figure 7 shows the time development of proton number density at a)
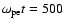 ,
b)
,
b)
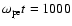 ,
and c)
,
and c)
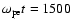 .
As seen in Fig. 7b, the plasma cloud associated with the shock moves along the current sheet, resulting in the bending of the current sheet. In this case there appears no secondary shock wave as observed in the previous case. During the later stage (see Fig. 7c), the current sheet breaks into two current filaments. Figure 8 shows the spacial distribution of current Jz at
.
As seen in Fig. 7b, the plasma cloud associated with the shock moves along the current sheet, resulting in the bending of the current sheet. In this case there appears no secondary shock wave as observed in the previous case. During the later stage (see Fig. 7c), the current sheet breaks into two current filaments. Figure 8 shows the spacial distribution of current Jz at
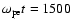 ,
corresponding to Fig. 7c. In Fig. 9 we show the time development of vector plots of magnetic fields corresponding to Fig. 7. From Fig. 9c we see the formation of magnetic islands corresponding to the current filaments seen in Fig. 7c. From all this, we conclude that for a weak Mach number like
,
corresponding to Fig. 7c. In Fig. 9 we show the time development of vector plots of magnetic fields corresponding to Fig. 7. From Fig. 9c we see the formation of magnetic islands corresponding to the current filaments seen in Fig. 7c. From all this, we conclude that for a weak Mach number like
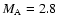 the current sheet can be deformed and become unstable for tearing-like modes associated with magnetic reconnection.
the current sheet can be deformed and become unstable for tearing-like modes associated with magnetic reconnection.
By using a 2D relativistic and fully electromagnetic PIC code, we investigated the oblique collision between a fast magnetosonic shock and a Harris type current sheet.
It was shown that the fast magnetosonic shock with Mach number
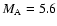 compresses the current sheet, resulting in
strong deformation of it.
In the later stage a secondary fast magnetosonic shock wave can be generated almost perpendicular to the current
sheet and it propagates away to the
opposite side of the original shock. This newly generated shock wave may emit the type II radio burst. The simulation results may
be applied to a split of electromagnetic wave emissions when a shock wave associated with CMEs collides
obliquely with a coronal streamer.
compresses the current sheet, resulting in
strong deformation of it.
In the later stage a secondary fast magnetosonic shock wave can be generated almost perpendicular to the current
sheet and it propagates away to the
opposite side of the original shock. This newly generated shock wave may emit the type II radio burst. The simulation results may
be applied to a split of electromagnetic wave emissions when a shock wave associated with CMEs collides
obliquely with a coronal streamer.
While for a weak shock with
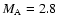 ,
the secondary shock wave does not appear. But the current sheet can be deformed and become unstable for tearing-like modes associated with magnetic reconnection.
,
the secondary shock wave does not appear. But the current sheet can be deformed and become unstable for tearing-like modes associated with magnetic reconnection.
Acknowledgements
The authors thank the anonymous referee for useful comments that improved our original paper.
- Buneman, O. 1993,
in Computer Space Plasma Physics, Simulation Techniques and
Software, ed. H. Matsumoto, & Y. Omura (Tokyo: Terra
Scientific), 67
(In the text)
- Dieckmann, M.
E., Eliasson, B., Shukla, P. K., Sircombe, N. J., & Dendy, R.
O. 2006, Plasma Phys. Controll. Fusion, 48, B303 (In the text)
- Gapalswamy,
N. S., Yashiro, S., Kaiser, M. L., Howard, R. A., & Bougeret,
J.-L. 2001, ApJ, 548, L91 [NASA ADS] [CrossRef] (In the text)
- Harris, E. G. 1962,
Nuovo Cimento, 23, 115 (In the text)
- Haruki, T., &
Sakai, J. I. 2001, ApJ, 552, L175 [NASA ADS] [CrossRef] (In the text)
- Haruki, T., Sakai,
J. I., & Saito, S. 2006, A&A, 455, 1099 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hoshino, M.,
& Shimada, N. 2002, ApJ, 572, 880 [NASA ADS] [CrossRef] (In the text)
- Lee, M. A., Shapiro, V.
D., & Sagdeev, R. Z. 1996, JGR, 101, 4777 [NASA ADS] [CrossRef] (In the text)
- Lee, R. E., Chapman, S.
C., & Dendy, R. O. 2005, Phys. Plasmas, 12, 012901 [NASA ADS] [CrossRef] (In the text)
- Lipatov, A. S.,
& Zank, G. P. 1999, PRL, 82, 3609 [NASA ADS] [CrossRef] (In the text)
- Mancuso, S.,
& Abbo, L. 2004, A&A, 415, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Murtaza, G.,
& Shukla, P. K. 1984, J. Plasma Phys., 31, 423 [NASA ADS] (In the text)
- Pritchett, P.
L. 2001, JGR, 106, 3783 [NASA ADS] [CrossRef] (In the text)
- Sagdeev, R. Z.,
& Shapiro, V. D. 1973, JETP Lett., 17, 279 [NASA ADS] (In the text)
- Sakai, J. I. 1973,
Ap&SS, 23, 285 [NASA ADS] (In the text)
- Sakai, J. I., Mori,
T., & Saito, S. 2005, A&A, 442, 687 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sakai, J. I., Mori,
T., Saito, S., Tanaka, Y., & Aurass, H. 2006, A&A, 454,
983 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sheeley, N. R.,
Hakala, W. N., & Wang, Y. M. 2000, J. Geophys. Res., 105,
5081 [NASA ADS] [CrossRef] (In the text)
- van der Holst, B.,
van Drel-Gesztelvi, L., & Poedts, S. 2002, in Solar
variability: from core to outer frontiers, ESA SP-506, 1, 71
(In the text)
- Yin, L., &
Ashour-Abdalla, M. 1999, Phys. Plasmas, 6, 449 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6977f1.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg14.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6977f2.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg15.gif)
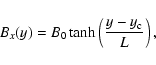
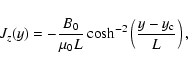
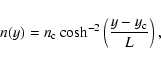
![\begin{figure}
\par\includegraphics[width=14cm,clip]{6977f3.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg45.gif)
![\begin{figure}
\par\includegraphics[width=13.3cm,clip]{6977f4.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg46.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{6977f5.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg51.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{6977f6.eps}
\end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg52.gif)
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{6977f7.eps} \end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{6977f8.eps} \end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg60.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6977f9.eps} \end{figure}](/articles/aa/full/2007/24/aa6977-06/Timg61.gif)