A&A 468, 937-950 (2007)
DOI: 10.1051/0004-6361:20066673
M. Huertas-Company1,4 - D. Rouan1 - G. Soucail2 - O. Le Fèvre3 - L. Tasca3 - T. Contini2
1 - LESIA-Paris Observatory,
5 place Jules Janssen, 92195 Meudon, France
2 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, CNRS-UMR 5572 and Université Paul Sabatier Toulouse III, 14 avenue Belin, 31400 Toulouse, France
3 -
LAM-Marseille Observatory, Traverse du Siphon, Les trois Lucs, BP 8, 13376 Marseille Cedex 12, France
4 -
IAA-C/ Camino Bajo de Huétor, 50-18008 Granada, Spain
Received 31 October 2006 / Accepted 13 March 2007
Abstract
Context. We present the results of an imaging program of distant galaxies (![]() )
at high spatial resolution (
)
at high spatial resolution (![]() 0.1'') aiming at studying their morphological evolution. We observed 7 fields of
0.1'') aiming at studying their morphological evolution. We observed 7 fields of
![]() with the NACO Adaptive Optics system (VLT) in
with the NACO Adaptive Optics system (VLT) in ![]() (
(![]() m) band with typical
m) band with typical ![]() guide stars and 3 h integration time per field. Observed fields are selected within the COSMOS survey area, in which multi-wavelength photometric and spectroscopic observations are ongoing. High angular-resolution K-band data have the advantage of probing old stellar ulations in the rest-frame, enabling a determination of galaxy morphological es unaffected by recent star formation, which are more closely linked to the erlying mass than classical optical morphology studies (HST). Adaptive optics on ground based telescopes is the only method today for obtaining such a high resolution in the K-band, but it suffers from limitations since only small fields are observable and long integration times are necessary.
guide stars and 3 h integration time per field. Observed fields are selected within the COSMOS survey area, in which multi-wavelength photometric and spectroscopic observations are ongoing. High angular-resolution K-band data have the advantage of probing old stellar ulations in the rest-frame, enabling a determination of galaxy morphological es unaffected by recent star formation, which are more closely linked to the erlying mass than classical optical morphology studies (HST). Adaptive optics on ground based telescopes is the only method today for obtaining such a high resolution in the K-band, but it suffers from limitations since only small fields are observable and long integration times are necessary.
Aims. In this paper we show that reliable results can be obtained and establish a first basis for larger observing programs.
Methods. We analyze the morphologies by means of B/D (bulge/disk) decomposition with GIM2D and C-A (concentration-asymmetry) estimators for 79 galaxies with magnitudes between
![]() and classify them into three main morphological types (late type, early type and irregulars). Automated and objective classification allows precise error estimation. Simulations and comparisons with seeing-limited (CFHT/Megacam) and space (HST/ACS) data are carried out to evaluate the accuracy of adaptive optics-based observations for morphological purposes.
and classify them into three main morphological types (late type, early type and irregulars). Automated and objective classification allows precise error estimation. Simulations and comparisons with seeing-limited (CFHT/Megacam) and space (HST/ACS) data are carried out to evaluate the accuracy of adaptive optics-based observations for morphological purposes.
Results. We obtain the first estimate of the distribution of galaxy types at redshift ![]() as measured from the near infrared at high spatial resolution. We show that galaxy parameters (disk scale length, bulge effective radius, and bulge fraction) can be estimated with a random error lower than
as measured from the near infrared at high spatial resolution. We show that galaxy parameters (disk scale length, bulge effective radius, and bulge fraction) can be estimated with a random error lower than ![]() for the bulge fraction up to
for the bulge fraction up to
![]() (AB=21) and that classification into the three main morphological types can be done up to
(AB=21) and that classification into the three main morphological types can be done up to
![]() (AB=22) with at least 70% of the identifications correct. We used the known photometric redshifts to obtain a redshift distribution over 2 redshift bins (z<0.8, 0.8<z<1.5) for each morphological type.
(AB=22) with at least 70% of the identifications correct. We used the known photometric redshifts to obtain a redshift distribution over 2 redshift bins (z<0.8, 0.8<z<1.5) for each morphological type.
Key words: galaxies: fundamental parameters - galaxies: high-redshift - galaxies: evolution - instrumentation: adaptive optics
The process of galaxy formation and the way galaxies evolve is still one
of the key unresolved problems in modern astrophysics. In the
currently accepted hierarchical picture of structure formation, galaxies
are thought to be embedded in massive dark halos that grow from density
fluctuations in the early universe (Fall & Efstathiou 1980) and initially contain
baryons in a hot gaseous phase. This gas subsequently cools, and some
fraction eventually condenses into stars (Lilly et al. 1996; Madau et al. 1998). However,
many of the physical details remain uncertain, in particular the process
and history of mass assembly. One classical observational way to test
those models is to classify galaxies according to morphological criteria
defined in the nearby Universe (de Vaucouleurs 1948; Sandage 1961; Hubble 1936), which can be
related to physical properties, and to follow this classification across
time. (Simard et al. 2002; Abraham et al. 1996,2003). Indeed, since galaxies were recognized as
distinct physical systems, one of the main goals in extragalactic astronomy
has been to characterize their shapes. Comparison of distant populations with
the ones found in the nearby Universe might help to clarify the role
of merging as one of the main drivers in galaxy evolution.
(Baugh et al. 1996; Cole et al. 2000). Progress in this field has
come from observing deeper and larger samples, but also from obtaining
higher spatial resolution at a given flux and at a given redshift. In the
visible, progress has been simultaneous on those two fronts, thanks in particular to the
ultra-deep HDF fields observed with the Hubble Space Telescope. HST imaging has brought observational evidence that galaxy evolution
is differentiated with respect to morphological type and that a large
fraction of distant galaxies have peculiar morphologies that do not fit
into the elliptical-spiral Hubble sequence. (Ilbert et al. 2006b; Wolf et al. 2003; Brinchmann et al. 1998). These results can however be biased by the fact that most of the sampled
galaxies are at large redshift and are analyzed through their UV
rest-frame emission, which is more sensitive to star formation processes
and to extinction. Moreover,
it now seems clear that evolution strongly depends on the galaxy mass
in the sense that massive systems appear to have star formation histories that peak at higher redshifts, whereas less massive systems have star formation histories that peak at progressively lower redshifts and are extended over a longer time interval (downsizing scenario; Bundy et al. 2005; Brinchmann & Ellis 2000; Cowie et al. 1996). This could explain the fact that the population of massive E/S0 seems to be in place at ![]() and evolve passively towards lower redshifts (Zucca et al. 2006; De Lucia et al. 2006). However, most of these studies are based on spectral type classifications, and their interpretation in the framework of galaxy formation is not straightforward since galaxies move from one spectral class to another by passive evolution of the stellar populations.
and evolve passively towards lower redshifts (Zucca et al. 2006; De Lucia et al. 2006). However, most of these studies are based on spectral type classifications, and their interpretation in the framework of galaxy formation is not straightforward since galaxies move from one spectral class to another by passive evolution of the stellar populations.
In this context, high-resolution near-infrared observations are particularly important because the K-band flux is less dependent on the recent history of star formation, which peaks in the UV in rest frame, and thus gives a galaxy type from the distribution of old stars that is more closely related to the underlying total mass than optical observations. This is why a large number of K-band surveys have been carried out using ground-based telescopes with different spatial coverages and limiting magnitudes in order to perform cosmological tests by means of galaxy counts essentially (Glazebrook et al. 1995; Bershady et al. 1998; Gardner et al. 1993; McLeod et al. 1995; McCracken et al. 2000; Maihara et al. 2001). However, no morphological information can be found in particular due to the seeing limited resolution, even with superb image quality as in the ongoing CFHT/WIRCAM survey. Conselice et al. (2000) prove that only when the ratio of the angular diameter substending 0.5 h-175 kpc at a given distance to the angular resolution of the image is around 1 can reliable morphological estimators such as the asymmetry be obtained.
Consequently, adaptive optics (AO) installed on ground-based telescopes will be a powerful method for obtaining near-infrared high-resolution data in the future and an excellent complement to space observations, such as those that will be performed with the HST (WFC3, 2008) and with the JWST (2014).
The use of classical AO for deep surveys suffers, however, from inherent limitations such as the non-stationary PSF on long integration times and the finite isoplanetic field. This is why preliminary studies to probe the accuracy of adaptive optics are required, before launching very wide surveys. In particular, it is important to determine whether automated morphological classifications can be performed. Indeed, given the large number of galaxies, such automated methods for morphological classifications are desirable.
Minowa et al. (2005) published first results based on adaptive optics
observations. They achieved the impressive limiting magnitude of
![]() with the Subaru Adaptive Optics system with a total integration time of
26.8 h over one single field of
with the Subaru Adaptive Optics system with a total integration time of
26.8 h over one single field of
![]() .
They proved that the use
of adaptive optics significantly improves detection of faint sources but did not obtain morphological information. In a recently submitted paper, Cresci et al. (2006) perform a morphological analysis based on AO data for the first time. They observed a 15 arcmin2 in the
.
They proved that the use
of adaptive optics significantly improves detection of faint sources but did not obtain morphological information. In a recently submitted paper, Cresci et al. (2006) perform a morphological analysis based on AO data for the first time. They observed a 15 arcmin2 in the ![]() band with NACO (SWAN survey) and classified distant galaxies into two morphological bins (late type, early type) by performing a model fitting with a Sersic law. They compared number counts and size-magnitude relation, for early and late-types separately, with hierarchical and pure luminosity evolution (PLE) models, respectively. They conclude that hierarchical models are not consistent with the observed number counts of elliptical galaxies and that PLE models are preferred. However, as discussed in several studies (Gardner 1998), despite galaxy counts still being one of the classical cosmological tests, their
interpretation remains difficult. It is thus not realistic to expect galaxy counts alone to strongly constrain the cosmological geometry or even to constrain galaxy evolution. A more complete study needs redshift estimates, which is lacking in the SWAN survey. That is the main reason for having select the COSMOS (Scoville & COSMOS Team 2005) field to conduct our pilot program since multi-wavelength photometric and spectroscopic observations are performed. This ensures a reliable redshift estimate for all our objects.
band with NACO (SWAN survey) and classified distant galaxies into two morphological bins (late type, early type) by performing a model fitting with a Sersic law. They compared number counts and size-magnitude relation, for early and late-types separately, with hierarchical and pure luminosity evolution (PLE) models, respectively. They conclude that hierarchical models are not consistent with the observed number counts of elliptical galaxies and that PLE models are preferred. However, as discussed in several studies (Gardner 1998), despite galaxy counts still being one of the classical cosmological tests, their
interpretation remains difficult. It is thus not realistic to expect galaxy counts alone to strongly constrain the cosmological geometry or even to constrain galaxy evolution. A more complete study needs redshift estimates, which is lacking in the SWAN survey. That is the main reason for having select the COSMOS (Scoville & COSMOS Team 2005) field to conduct our pilot program since multi-wavelength photometric and spectroscopic observations are performed. This ensures a reliable redshift estimate for all our objects.
In this paper, we continue this AO validation task by morphologically classifying a sample of 79 galaxies
observed
using parametric
(GIM2D, Simard et al. 2002) and non-parametric (C-A, Abraham et al. 1994) methods and comparing them. Fields, observed with NAOS/CONICA adaptive optics system, are distributed over a 7 arcmin2 area. We obtain for the first time an estimate of the
distribution of galaxies in three morphological types (E/S0, S, Irr) at redshift ![]() as measured from the
near infrared at high spatial resolution. We then use the photometric
redshifts to look for evolution clues as a function of morphology.
as measured from the
near infrared at high spatial resolution. We then use the photometric
redshifts to look for evolution clues as a function of morphology.
The paper proceeds as follows: the data set and the reduction procedures
are presented in the next section. In Sect. 3, we focus on the detection
procedures and the sample completeness. In Sect. 4 we discuss the estimate
of redshifts using the multi-wavelength photometric data from COSMOS. The morphological analysis is
discussed in Sect. 5 using bulge/disk decompositions and concentration
and asymmetry estimators. Simulations
for error characterization are carried out for both classification
methods, and comparisons between classifications are shown. In Sect. 6
we compare the data with ground and space observations and use
those comparisons to discus the morphological evolution in the last section. Throughout this
paper magnitudes are given in the Vega system. We use the following
cosmological parameters:
![]() and
and
![]() .
.
Seven fields of
![]() were observed in
were observed in ![]() band (
band (![]() m) with the
NAOS/CONICA-assisted infrared camera installed on the VLT
m) with the
NAOS/CONICA-assisted infrared camera installed on the VLT![]() . The fields were selected within the COSMOS survey
area
. The fields were selected within the COSMOS survey
area![]() . In order
to ensure a reliable AO correction, relatively bright stars (
. In order
to ensure a reliable AO correction, relatively bright stars (![]() )
were selected. We added a color criterium (B-R < 1.0) in order
to benefit from a large attenuation of the flux in the near-IR and thus a smaller occultation of the central region of the images. The pixel
scale (
)
were selected. We added a color criterium (B-R < 1.0) in order
to benefit from a large attenuation of the flux in the near-IR and thus a smaller occultation of the central region of the images. The pixel
scale (
![]() )
was chosen to be twice the Nyquist-Shannon requirements with respect to the telescope diffraction limit in order to have larger fields. With such a pixel sampling, the
PSF FWHM would only be one pixel width in the limit of perfect AO correction. However, we will show in Sect. 5 that our PSF reconstruction procedure can handle such undersampled data.
We also note that only partial AO correction was actually achieved during our observations,
and our PSF reconstruction is thus more than adequate here. Figure 1 compares the radial profiles of 5 detected stellar objects. Indeed, this program is pushed to its limits in terms of field size, exposure time, and brightness of the guide star.
)
was chosen to be twice the Nyquist-Shannon requirements with respect to the telescope diffraction limit in order to have larger fields. With such a pixel sampling, the
PSF FWHM would only be one pixel width in the limit of perfect AO correction. However, we will show in Sect. 5 that our PSF reconstruction procedure can handle such undersampled data.
We also note that only partial AO correction was actually achieved during our observations,
and our PSF reconstruction is thus more than adequate here. Figure 1 compares the radial profiles of 5 detected stellar objects. Indeed, this program is pushed to its limits in terms of field size, exposure time, and brightness of the guide star.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6673fig1.eps}
\end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg32.gif) |
Figure 1:
Radial
profile of all detected stellar objects with
|
| Open with DEXTER | |
Table 1: Summary of observations for the seven analyzed fields. The mean seeing is estimated when faint stars were detected.
Data are reduced in a standard way: exposures are taken in the
auto-jitter mode, which means that the pointing is randomly shifted within
a 7
![]() box, in order to improve flat fielding, bad pixel correction, and sky background withdrawal. The sky value in each pixel is estimated by performing a clipped median of all the exposure frames: the
box, in order to improve flat fielding, bad pixel correction, and sky background withdrawal. The sky value in each pixel is estimated by performing a clipped median of all the exposure frames: the ![]() faintest and brightest values are removed from the computation.
Cosmic ray and flat corrections were applied,
and recentering was done using a standard cross-correlation method. Recentering is done at a sub-pixel level. For that purpose a cubic interpolation of resampling was performed. After stacking, a global estimate of the sky background was performed by computing the stacked image spatial median. The final image was obtained after substraction of this value.
faintest and brightest values are removed from the computation.
Cosmic ray and flat corrections were applied,
and recentering was done using a standard cross-correlation method. Recentering is done at a sub-pixel level. For that purpose a cubic interpolation of resampling was performed. After stacking, a global estimate of the sky background was performed by computing the stacked image spatial median. The final image was obtained after substraction of this value.
Photometric zeropoints were determined using 2MASS stars
(Kleinmann 1992). We performed aperture photometry on the guide stars and compared it to 2MASS data to deduce the zeropoints. Note that the change of detector between periods
P73 and P75 resulted in different zeropoint values for each run. The average zeropoint
for the first period is:
![]() and for the second period
and for the second period
![]() .
We also used the ESO calibration data set standard stars (Persson et al. 1998) to validate our measurements (ESO pipeline computations and our own measurements on the standard stars images). There is good agreement between all these values.
.
We also used the ESO calibration data set standard stars (Persson et al. 1998) to validate our measurements (ESO pipeline computations and our own measurements on the standard stars images). There is good agreement between all these values.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{6673fig2.eps} \end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg39.gif) |
Figure 2: Objects classification using the MAG_AUTO-MU_MAX plane. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{6673fig3.eps}
\end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg40.gif) |
Figure 3:
NAOS/CONICA |
| Open with DEXTER | |
The sample completeness for point sources was estimated by creating
artificial point sources from fields stars (see Sect. 5 for detailed
explanations) with apparent magnitudes ranging from
![]() to
to
![]() and placing them at random positions. We ran SE XTRACTOR with the same
configuration as for real sources and looked for the fraction of detected
objects. We find that the sample is
and placing them at random positions. We ran SE XTRACTOR with the same
configuration as for real sources and looked for the fraction of detected
objects. We find that the sample is ![]() complete
at
complete
at
![]() (or AB=24.5) for point sources. Completeness for extended
sources is estimated in a similar way: we generate 1000 galaxies
with exponential and de Vaucouleurs profiles of different morphological
types (bulge fraction ranging from 0 to 1) and with galaxy parameters
uniformly distributed. In particular, the sizes of disks and bulges are distributed uniformly between
(or AB=24.5) for point sources. Completeness for extended
sources is estimated in a similar way: we generate 1000 galaxies
with exponential and de Vaucouleurs profiles of different morphological
types (bulge fraction ranging from 0 to 1) and with galaxy parameters
uniformly distributed. In particular, the sizes of disks and bulges are distributed uniformly between
![]() and
and
![]() as detailed in Sect. 5. This leads to half-luminosity radii ranging from
as detailed in Sect. 5. This leads to half-luminosity radii ranging from
![]() .
We find that the sample is 50% complete at
.
We find that the sample is 50% complete at
![]() (or AB=23.5) for this population of extended sources (Fig. 4). We used this completeness to compute number counts and to compare it to other near-infrared surveys in Appendix A.
(or AB=23.5) for this population of extended sources (Fig. 4). We used this completeness to compute number counts and to compare it to other near-infrared surveys in Appendix A.
| |
Figure 4:
Completeness for extended sources. Galaxies with parameters ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{6673fig5.eps} \end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg51.gif) |
Figure 5:
Le Phare photometric redshift distribution for the 60 matched
objects. The distribution is peaked around |
| Open with DEXTER | |
All these data are used for a direct estimate of the
photometric redshifts of the galaxies detected in the NACO fields,
computed with the code Le
Phare![]() .
A standard
.
A standard ![]() method
is implemented, including an iterative zero-point
refinement combined with a template optimization procedure and the
application of a Bayesian approach (Ilbert et al. 2006a). We used 1095 spectroscopic redshifts taken from the zCOSMOS Survey (Lilly & The Zcosmos Team. 2006) to measure the photometric redshifts.
This method allows to
reach an accuracy of
method
is implemented, including an iterative zero-point
refinement combined with a template optimization procedure and the
application of a Bayesian approach (Ilbert et al. 2006a). We used 1095 spectroscopic redshifts taken from the zCOSMOS Survey (Lilly & The Zcosmos Team. 2006) to measure the photometric redshifts.
This method allows to
reach an accuracy of
![]() with
with ![]() catastrophic errors, defined as
catastrophic errors, defined as
![]() .
.
The multi-color catalog of the COSMOS survey (Capack et al. 2006) consists
of photometry measurements over 3 arcsec diameter apertures for deep
Bj, Vj, g+, r+, i+, z+ Subaru data taken with SuprimeCam, u*, i*bands with MegaCam (CFHT),
u',g',r',i',z' information from the Sloan
Digital Sky Survey (SDSS), ![]() magnitude from KPNO/CTIO, and F816WHST/ACS magnitude. Objects were matched between the COSMOS and the NACO
catalogs within a radius of 2
magnitude from KPNO/CTIO, and F816WHST/ACS magnitude. Objects were matched between the COSMOS and the NACO
catalogs within a radius of 2
![]() which takes possible
astrometry differences between the calalogues into account. We matched 60 objects out
of the 79 detected in the NACO fields. Figure 5 shows
the photometric redshift distribution for these 60 matched objects.
As expected for a galaxy sample limited to
which takes possible
astrometry differences between the calalogues into account. We matched 60 objects out
of the 79 detected in the NACO fields. Figure 5 shows
the photometric redshift distribution for these 60 matched objects.
As expected for a galaxy sample limited to
![]() ,
the redshift
distribution peaks around
,
the redshift
distribution peaks around
![]() (Mignoli et al. 2005).
(Mignoli et al. 2005).
Throughout this section, we use extensive simulations for error
estimates and calibration of the automated classifications as explained below. For all the simulations, we assumed that bulges
are pure de Vaucouleurs profiles (n = 4) and that disks are
exponential profiles. We then generate galaxies with parameters uniformly distributed in the following parameter space: 0<B/T<1,
![]() ,
,
![]() ,
,
![]() ,
and 0<e<0.7. Both bulge and disk position angles were fixed to
,
and 0<e<0.7. Both bulge and disk position angles were fixed to
![]() .
The goal of these simulations is to characterize biases and
errors; the uniformity of the parameter distributions adopted
here is therefore perfectly suitable, even though real galaxy parameters
may not be so distributed. For the same reason, we
do not take any redshift effect into account. Each simulation
was convolved with the reconstructed PSF as explained in 5.2.2.
The same PSF was used in both creating and analyzing the simulations,
so the results will not include any error due to PSF
mismatch. In order to simulate background noise, objects are
embedded at random positions in the fields and detected with
the same SE XTRACTOR parameters as for the real sources.
.
The goal of these simulations is to characterize biases and
errors; the uniformity of the parameter distributions adopted
here is therefore perfectly suitable, even though real galaxy parameters
may not be so distributed. For the same reason, we
do not take any redshift effect into account. Each simulation
was convolved with the reconstructed PSF as explained in 5.2.2.
The same PSF was used in both creating and analyzing the simulations,
so the results will not include any error due to PSF
mismatch. In order to simulate background noise, objects are
embedded at random positions in the fields and detected with
the same SE XTRACTOR parameters as for the real sources.
![\begin{figure}
\par\includegraphics[width=8cm,height=6.5cm,clip]{6673fig6.eps}\h...
...e*{4mm}
\includegraphics[width=8cm,height=6.5cm,clip]{6673fig7.eps}\end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg66.gif) |
Figure 6: Separation between regular and irregular objects. Left: simulated objects (empty squares), right: real objects (crosses). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6673fig8.eps} \end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg67.gif) |
Figure 7: Asymmetry versus magnitude: asymmetry begins to grow only at magnitudes greater then 22.2 which is greater than the limiting magnitude. |
| Open with DEXTER | |
As said previously, rotational asymmetry is affected by noise even
after correction. This means that fainter objects might appear more
asymmetric and can thus induce a bias in the number of irregular objects
at the faint end of the sample. To estimate this error, we plotted
the asymmetry parameter for a sample of 1000 simulated galaxies with
magnitudes ranging between
![]() (Fig. 7). The plot
shows that asymmetry begins to be affected by noise only at magnitudes
greater than 22.2, which is the magnitude limit of our working sample.
In summary, we found the location of the irregular/peculiar objects by simulating a set of regular galaxies and defining the peculiar area as the area outiside. Then, we plotted the observed data on this plane and count the galaxies in this peculiar area. We counted 10 observed objects in this zone, i.e.
(Fig. 7). The plot
shows that asymmetry begins to be affected by noise only at magnitudes
greater than 22.2, which is the magnitude limit of our working sample.
In summary, we found the location of the irregular/peculiar objects by simulating a set of regular galaxies and defining the peculiar area as the area outiside. Then, we plotted the observed data on this plane and count the galaxies in this peculiar area. We counted 10 observed objects in this zone, i.e. ![]() of the sample. We can attempt to quantify the error in this classification by considering the regular simulated objects that fall in the irregular zone. This gives the fraction of regular objects that are misclassified. We counted 27 objects out of 1000. we conclude that
of the sample. We can attempt to quantify the error in this classification by considering the regular simulated objects that fall in the irregular zone. This gives the fraction of regular objects that are misclassified. We counted 27 objects out of 1000. we conclude that
![]() of our sample corresponds to peculiar
objects, in the magnitude range
of our sample corresponds to peculiar
objects, in the magnitude range
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.3cm,height=7cm,clip]{6673fig9.eps}\h...
...e*{4mm}
\includegraphics[width=8.3cm,height=7cm,clip]{6673fig10.eps}\end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg70.gif) |
Figure 8: C-A calibration and classification. Boundaries are drawn using an automated classification method (SVM) that avoids the use of a nearby sample and subjective visual classifications. Left: simulated objects, open squares: objects with B/T<0.2, filled squares: objects with B/T>0.8. Right: real objects. |
| Open with DEXTER | |
Table 2: Error estimates of the C-A classification. Fraction of misclassified objects for several magnitude ranges.
We developed a simple algorithm that uses field stars to generate
Nyquist-Shannon-sampled PSFs by means of a fitting procedure in Fourier
space. The process is as follows: we generate an artificial PSF with
a diffraction-limited core and a Gaussian halo, with the distribution
Working in Fourier space avoids including the background estimate and PSF position as a fit parameter, which is particularly delicate in our case, since the FWHM is less than 2 pixels large. In the few cases where the fitting procedure does not converge a second Gaussian halo is added. Figure 9 shows the result of the fitting for one star in the spatial frequency domain. In this paper, we do not consider variations in the PSF caused by adaptive optics, such as anisoplanetism, but we are working on building a complete model for PSF estimate for future observations.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6673fig11.eps} \end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg82.gif) |
Figure 9: Example of PSF fitting in Fourier space. Squares: observations, dashed line: seeing-limited MTF, dotted line: diffraction-limited MTF. The AO MTF contains higher frequencies than the seeing-limited one. The telescope diffraction limit is not reached however in this example due to the undersampling of the instrumental setup. |
| Open with DEXTER | |
Table 3:
GIM2D output for some objects. Left: original images, middle: GIM2D models, right: residuals. The small thumbnails show
the real and the model galaxy. The image size is
![]()
We ran GIM2D on the 79 objects with magnitudes ranging between
![]() ,
using a two components model and the artificial
PSF built as described above. We used the GIM2D mode that allows use of oversampled PSFs to deal with undersampled data, since the PSF recovered with the method explained above is Nyquist sampled.The fitting converged for the whole
sample, and the results are quite convincing in terms of residual
images (Table 3).
,
using a two components model and the artificial
PSF built as described above. We used the GIM2D mode that allows use of oversampled PSFs to deal with undersampled data, since the PSF recovered with the method explained above is Nyquist sampled.The fitting converged for the whole
sample, and the results are quite convincing in terms of residual
images (Table 3).
Visual inspection of the models compared to the real images
(Table 3) also reveals good agreement, in particular for
bright sources. For the faintest objects, however, it is more difficult
to estimate the fitting accuracy. Indeed, inspection of image residuals is not a robust accuracy test, since there may still be strong degeneracies even when the image residuals do not show any features.This is why objective and systematic
error characterization is needed. To do so we generated a sample of 1000 synthetic galaxies with known galaxy parameters uniformly distributed:
0<B/T<1,
![]() ,
,
![]() ,
0<e<0.7,
,
0<e<0.7,
![]() .
The Sersic bulge index was fixed at n=4, and both bulge and disk
position angles were fixed to
.
The Sersic bulge index was fixed at n=4, and both bulge and disk
position angles were fixed to
![]() .
As explained in Simard et al. (2002),
the goal of these simulations is to characterize biases and error.
The uniformity of the parameter distributions adopted here is therefore
perfectly suitable even though real galaxy parameters may not be so
distributed. Each simulation is convolved with the reconstructed PSF. The
same PSF is used in both creating and analyzing the simulations, so
the results will not include any error due to PSF mismatch. In order to
simulate background noise, objects are embedded at random positions in the
fields and detected with the same Sextractor parameters as for the real
sources. Finally, the GIM2D output files are processed through the same
scripts to produce a catalog of final recovered structural parameters.
.
As explained in Simard et al. (2002),
the goal of these simulations is to characterize biases and error.
The uniformity of the parameter distributions adopted here is therefore
perfectly suitable even though real galaxy parameters may not be so
distributed. Each simulation is convolved with the reconstructed PSF. The
same PSF is used in both creating and analyzing the simulations, so
the results will not include any error due to PSF mismatch. In order to
simulate background noise, objects are embedded at random positions in the
fields and detected with the same Sextractor parameters as for the real
sources. Finally, the GIM2D output files are processed through the same
scripts to produce a catalog of final recovered structural parameters.
Table 4:
Error analysis of the bulge fraction B/T for different recovered
magnitude ranges and different bins in recovered galaxy size. The galaxy size
is represented by the half-light radius and is distributed into 4 bins
in
![]() .
In the top left corner bright and
small objects are found whereas faint and large objects are placed in the
bottom right corner.
.
In the top left corner bright and
small objects are found whereas faint and large objects are placed in the
bottom right corner.
![]() is the average difference between introduced and
recovered values of B/T, while
is the average difference between introduced and
recovered values of B/T, while
![]() is the dispersion (see text for details).
N is the number of simulations used for each bin.
is the dispersion (see text for details).
N is the number of simulations used for each bin.
Following the Simard et al. (2002) procedure, we decided to represent errors
in a set of two-dimensional maps giving systematic and random errors at
each position. The GIM2D parameter space is a complex space with 11
dimensions, so these maps can only offer a limited representation of the
complex multidimensional error functions but makes interpretation much
simpler. The error analysis presented in this paper focuses
on the error made on the main morphological estimator, the bulge fraction,
as a function of two main parameters: apparent magnitude and half light
radius. Systematic errors are computed as the mean difference between the introduced and the recovered value:
![]() and random errors as the square root of the variance of the difference:
and random errors as the square root of the variance of the difference:
![]() .
Table 4 precisely shows in details the sources of
errors on B/T as a function of galaxy magnitude and half-light radius.
.
Table 4 precisely shows in details the sources of
errors on B/T as a function of galaxy magnitude and half-light radius.
The main result after looking at the results of simulations is that, for objects brighter than
![]() (
(![]() ), the bulge fraction is recovered with a bias close to zero and a random error around
), the bulge fraction is recovered with a bias close to zero and a random error around ![]() .
This is true even for small objects (
.
This is true even for small objects (
![]() ), and it is comparable to what is obtained for the brightest objects in the I-band with HST (Simard et al. 2002). For fainter
magnitudes, we can see two main effects:
), and it is comparable to what is obtained for the brightest objects in the I-band with HST (Simard et al. 2002). For fainter
magnitudes, we can see two main effects:
We classified the galaxies into three main morphological types according
to the fitting results. One of the main results is that about
![]() of our sample corresponds to peculiar or irregular
objects (10 objects out of 79).
For the rest of the sample, the GIM2D analysis finds 21 (
of our sample corresponds to peculiar or irregular
objects (10 objects out of 79).
For the rest of the sample, the GIM2D analysis finds 21 (![]()
![]() )
bulge-dominated galaxies (B/T > 0.5) and 48 (
)
bulge-dominated galaxies (B/T > 0.5) and 48 (![]()
![]() )
disk-dominated (B/T < 0.5) while for the C-A classification, we find 54 (
)
disk-dominated (B/T < 0.5) while for the C-A classification, we find 54 (![]()
![]() )
disk-dominated galaxies and 15 (
)
disk-dominated galaxies and 15 (![]()
![]() )
bulge-dominated ones.
)
bulge-dominated ones.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6673fig30.eps}
\end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg124.gif) |
Figure 10: Comparison of classification methods, show the probability that a galaxy classified with GIM2D is classified in the same morphological type by C-A. (see text for details). |
| Open with DEXTER | |
Looking in more detail into the relaibility of the two
classification schemes, we did a one-to-one comparison of the
morphological types assigned by the GIM2D analysis or the C-A one
(Fig. 10): we computed
the probability that a galaxy classified using the GIM2D classification
is classified with the same morphological type by C-A. The probability was computed by dividing the number of galaxies in each morphological C-A
bin by the total number of galaxies of the same type selected with GIM2D.
Overall, there is good agreement between both classifications in
the whole sample. The probability that a disk dominated galaxy identified by
GIM2D has the same morphological type in C-A classification is p=0.81,
but only p=0.30 for bulge-dominated galaxies including the faintest objects
(
![]() ). For irregulars, it is obviously p=1 since the detection
procedure is the same in both methods.
). For irregulars, it is obviously p=1 since the detection
procedure is the same in both methods.
There might be two reasons why the classifications are not exactly
the same. First, the S/N might cause discrepancies. Indeed, as we
show in Sect. 5.2.2, at low S/N, GIM2D tends to under estimate
the bulge fraction. This implies that some galaxies detected by GIM2D as disk-dominated are in fact detected as bulge-dominated by C-A. Figure 10
shows the effect of reducing the limiting magnitude to
![]() :
the
fraction of objects classified as bulge dominated by GIM2D and C-A rises
up to 0.67. Second, it might be a problem of definition. Indeed, the
morphological bins are not exactly the same in both classifications. In
particular, objects with intermediate morphological type (i.e.
:
the
fraction of objects classified as bulge dominated by GIM2D and C-A rises
up to 0.67. Second, it might be a problem of definition. Indeed, the
morphological bins are not exactly the same in both classifications. In
particular, objects with intermediate morphological type (i.e.
![]() )
might cause discrepancies. If we remove those objects from the sample,
)
might cause discrepancies. If we remove those objects from the sample, ![]() of the bulge-dominated objects and
of the bulge-dominated objects and ![]() of the disk-dominated objects detected
by GIM2D are also detected by C-A with the same classification.
of the disk-dominated objects detected
by GIM2D are also detected by C-A with the same classification.
Either way, the comparison of both classifications allows a quantification of the error in classification of regular galaxies in the sense that it seems reasonable to think that the true value should be somewhere between the two results. The GIM2D estimate thus gives a lower limit for the early-type fraction and C-A the upper-limit and vice versa for the late-type fraction. This way, we conclude that the mixing of population in our sample is:
![]() of early-type galaxies,
of early-type galaxies,
![]() of late-type galaxies, and
of late-type galaxies, and
![]() of irregular/peculiar galaxies.
of irregular/peculiar galaxies.
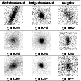 |
Figure 11:
Example of classification in the three main morphological types at different redshifts. The image size is
|
| Open with DEXTER | |
Our results offer the first direct measurement of the distribution of galaxy in three morphological types at ![]() from high spatial-resolution imaging in the K-band. We observe that the fraction of
from high spatial-resolution imaging in the K-band. We observe that the fraction of ![]() of irregular objects at z=1 is significantly higher than the fraction of these objects in the local Universe, confirming from rest-frame data at
of irregular objects at z=1 is significantly higher than the fraction of these objects in the local Universe, confirming from rest-frame data at ![]() 1 microns the well documented trend of this population increasing with redshift (e.g. Brinchmann et al. 1998). However, this result must be taken with
caution. Indeed GIM2D accuracy decreases for objects fainter than
1 microns the well documented trend of this population increasing with redshift (e.g. Brinchmann et al. 1998). However, this result must be taken with
caution. Indeed GIM2D accuracy decreases for objects fainter than
![]() ,
which represents
,
which represents ![]() of the
sample. Moreover at the faint end, the fraction of irregular objects can
be overestimated because of the low S/N.
But there are good reasons to
consider this result significant. Even though there is an over estimation
of disks in the faint end, the morphological classification bins are large
enough to reduce the number of false classifications. Indeed, even in
the zones where the random error in the bulge fraction estimate is
of the
sample. Moreover at the faint end, the fraction of irregular objects can
be overestimated because of the low S/N.
But there are good reasons to
consider this result significant. Even though there is an over estimation
of disks in the faint end, the morphological classification bins are large
enough to reduce the number of false classifications. Indeed, even in
the zones where the random error in the bulge fraction estimate is ![]() 0.3 or larger, we do not classify a pure bulge (
0.3 or larger, we do not classify a pure bulge (![]() )
as a disk.
)
as a disk.
In this section we compare our AO observations with ground-based and space observations.
Effective radii of local galaxies, except for compact dwarf
galaxies, range from ![]() 1.0 to
1.0 to ![]() 10 kpc depending on their
luminosity (Bender et al. 1992; Impey et al. 1996). Our spatial resolution of
10 kpc depending on their
luminosity (Bender et al. 1992; Impey et al. 1996). Our spatial resolution of ![]()
![]() corresponds to about 1 kpc at
corresponds to about 1 kpc at ![]() and we should be able to
determine morphological types even at z>1.
Thus, in order to estimate the performance of AO deep imaging and to
justify the automated morphology classification, we compared our images
with deep I-band seeing-limited images taken from the
Canada-France-Hawaii Telescope Legacy Survey
(CFTHLS)
and we should be able to
determine morphological types even at z>1.
Thus, in order to estimate the performance of AO deep imaging and to
justify the automated morphology classification, we compared our images
with deep I-band seeing-limited images taken from the
Canada-France-Hawaii Telescope Legacy Survey
(CFTHLS)![]() .
One of the so-called deep fields is
centered on the COSMOS field, although it is smaller than the total
COSMOS area (1 square degree out of 2). Here we used the release T0003 images (March 2006)
.
One of the so-called deep fields is
centered on the COSMOS field, although it is smaller than the total
COSMOS area (1 square degree out of 2). Here we used the release T0003 images (March 2006)![]() ,
especially the deep i' one,
corresponding to a total integration time of 20 h, with an
average FWHM of
,
especially the deep i' one,
corresponding to a total integration time of 20 h, with an
average FWHM of ![]()
![]() .
.
We compared real data by selecting a galaxy classified as a disk
by GIM2D and C-A in the NACO data and by comparing it to the results
obtained with CFHTLS data.
We computed the surface brightness profile within the isophotal area enclosed by pixels ![]() above the sky level. The corresponding limiting surface brightness is
above the sky level. The corresponding limiting surface brightness is ![]() mag arcsec-2 for the NACO image and
mag arcsec-2 for the NACO image and ![]() mag arcsec-2 for the MegaCam image. Sky levels and the corresponding isophotal areas were both determined using SE XTRACTOR.
mag arcsec-2 for the MegaCam image. Sky levels and the corresponding isophotal areas were both determined using SE XTRACTOR.
The surface brightness profile was fitted with both a
PSF-convolved de Vaucouleurs profile
and a PSF-convolved exponential profile. Figure 12 shows that, with
seeing-limited observations, it is more difficult to establish a
clear separation between both profiles at small distances from the galaxy center (i.e. ![]()
![]() ), even if the determination
of the brightness profile is
possible at much larger distance (i.e.
), even if the determination
of the brightness profile is
possible at much larger distance (i.e. ![]()
![]() )
thanks to the depth of the images
and the low noise level of the sky background. This supports the results obtained with GIM2D, which show that a correct estimate of the bulge fraction is possible for small objects. Although ultra-deep
sub-arcsecond imaging is powerful in terms of high number statistics,
thanks to the wide field coverage, we consider that it is more rewarding to look at a smaller sample of
galaxies, but with more reliable morphology determinations thanks to the spatial
gain of the AO.
)
thanks to the depth of the images
and the low noise level of the sky background. This supports the results obtained with GIM2D, which show that a correct estimate of the bulge fraction is possible for small objects. Although ultra-deep
sub-arcsecond imaging is powerful in terms of high number statistics,
thanks to the wide field coverage, we consider that it is more rewarding to look at a smaller sample of
galaxies, but with more reliable morphology determinations thanks to the spatial
gain of the AO.
![\begin{figure}
\par\includegraphics[width=8.5cm,height=7cm,clip]{6673fig40.eps}\...
...e*{4mm}
\includegraphics[width=8.5cm,height=7cm,clip]{6673fig41.eps}\end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg136.gif) |
Figure 12:
Comparison with ground-based observations. We performed a profile
fitting on the same real
galaxy observed with NACO ( left) and MegaCam (CFHTLS-i' band, right). The galaxy magnitude is
KAB=20.5 and i'=21.3. Surface brightness profiles were computed within the isophotal areas enclosed by pixels |
| Open with DEXTER | |
We compare our images with space data taken from the COSMOS survey. Since our observed fields were selected within the COSMOS area, the same objects were observed with the HST-ACS in the I-band at high spatial resolution. We thus morphologically classified the 60 objects for which the photometric
redshift are known (Sect. 4). We used those results to both estimate the effect of the observation band on morphology and to validate our method to divide the C/A plane. The C-A
estimators were calibrated with simulations using the same method as for the K band data. Standard boundaries, from other existing works, were used to divide the C-A plane. Figure 16 shows the C-A plane cut. The figure also shows the border between bulge-dominated and disk-dominated galaxies obtained with the automatic method described in Sect. 5.2.1 for this population. We again find a
negative slope for the border between disk and bulge dominated objects. We
find for the whole sample
![]() irregulars,
irregulars,
![]() disk-dominated, and
disk-dominated, and
![]() bulge dominated.
bulge dominated.
As said, the computed boundaries of the C-A plane are different from what can be found in the literature. Previous works have been done in the I-band using HST imaging (Abraham et al. 1996; Brinchmann et al. 1998). As we have a sample observed in the I-band, we are able to establish whether the change in the boundaries has significant consequences in the morphological classifications. To do so, we classified the I-band sample using the Brinchmann et al. (1998) boundaries and compared the results to the ones obtained with our method (Fig. 14). We find that there are no significant discrepancies between both classifications. We conclude that our method is valid and moreover has the key advantage being free of subjective judgments.
We observe some discrepancies in the global morphological distributions between the I and K bands, in particular more perturbed morphologies are seen in the I band. When we look at each object individually (Fig. 13) we confirm this trend: there are uncertainties between K irregulars and I disks and between I disks and K bulges. Indeed an important fraction of bulge-dominated objects and disk-dominated objects detected by NACO are seen as disk-dominated and irregulars respectively, by ACS, as if there was a systematic trend that moves objects to later types when we move to shorter wavelengths. Certainly, the number of objects is small and a few mismatches cause high discrepancies in Fig. 13. However, this is an expected effect since ACS probes younger stellar populations. A visual inspection of some of the objects that present different morphologies reveals that some of the ACS irregulars are in fact well-resolved spiral galaxies with inhomogeneities that probably increase the asymmetry indices.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{6673fig42.eps} \end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg140.gif) |
Figure 13: Galaxy distribution: comparison between K-band and I band C-A classifications. The figure shows the probability that a galaxy in the K-band is classified in the same morphological type in the I-band. |
| Open with DEXTER | |
In order to correctly compare both classifications we need to correct the measurements to estimate how galaxies would look if they were observed locally in the same photometric band. As a matter of fact, Brinchmann et al. (1998) showed that high-z galaxies imaged by HST differ in appearance from their local counterparts because of their reduced apparent size and sampling characteristics, a lower S/N and reduced surface brightness with respect to the sky background and a shift in the rest wavelength of the observations. These effects combine to give some uncertainty in the morphological classifications of galaxies.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{6673fig43.eps}
\end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg141.gif) |
Figure 14: Comparison of classifications with different boundaries. We repeat the morphological classification with the boundaries used by Brinchmann et al. (1998). We conclude that the results do not change significantly which supports the validity of the employed method. |
| Open with DEXTER | |
The shift in the rest-frame wavelength of observations is however
more difficult to estimate. Indeed the question that arises here is whether the morphological type estimated at high redshift
would be the same if observed at low redshift. When observing a galaxy in
the K-band at redshift ![]() ,
the equivalent rest-frame wavelength
will be around the z band, however, when observed in the I-band, the
rest-frame will be around the B band. That implies that a
mismatch can exist in the morphological classification since we are not probing
the same morphological blocks. To correct for this effects we need to
"move the objects'' into a common rest-frame wavelength. This is the called
morphological k correction. The method employed by Brinchmann et al. (1998)
consists in determining the morphology from a local sample, redshifting
the objects using SED models, and looking at the fraction of galaxies
that move in to an other morphological class. A drift coefficient that
characterizes the drift from category X to category Y is thus defined as
,
the equivalent rest-frame wavelength
will be around the z band, however, when observed in the I-band, the
rest-frame will be around the B band. That implies that a
mismatch can exist in the morphological classification since we are not probing
the same morphological blocks. To correct for this effects we need to
"move the objects'' into a common rest-frame wavelength. This is the called
morphological k correction. The method employed by Brinchmann et al. (1998)
consists in determining the morphology from a local sample, redshifting
the objects using SED models, and looking at the fraction of galaxies
that move in to an other morphological class. A drift coefficient that
characterizes the drift from category X to category Y is thus defined as
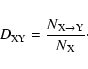 |
(2) |
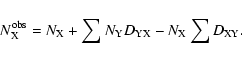 |
(3) |
We use the coefficients computed by Brinchmann et al. (1998) to correct the ACS morphology and divide the sample into two redshift bins (z<0.8 and z>0.8). Results are shown in Fig. 15.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6673fig44.eps}\end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg144.gif) |
Figure 15: Redshift distribution for the three morphological types. We plotted the Brinchmann et al. (1998) sample (circles) and our sample observed with ACS (squares) and with NACO (triangles). Brinchmann et al. (1998) and ACS data are corrected to the R rest-frame band. The NACO sample is observed from the K-band and no correction has been applied. The ACS and NACO samples have been separated into two redshift bins (z<0.8and z>0.8). The represented redshifts are the median redshifts of each bin. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,height=7cm,clip]{6673fig45.eps}\...
...{4mm}
\includegraphics[width=8.5cm,height=7cm,clip]{6673fig46.eps} \end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg145.gif) |
Figure 16: C-A cut for the ACS images. The same classification procedure has been repeated for the same sample observed with ACS in the I-band. Left: simulated objects. Right: real objects. Circles: B/T<0.2, Filled squares: B/T>0.8, crosses: real objects. Dotted line is the border used in Brinchmann et al. (1998) to separate bulge dominated from disk dominated, dashed line is the one computed in the paper. |
| Open with DEXTER | |
Table 5:
Morphological k correction: morphological differences when
observing in the K and I-bands. The same objects observed in the K and I bands present different morphologies. The images size is
![]() .
.
From this work it seems clear that adaptive optics can be used for observational cosmology with reliable accuracy, and consequently data of this type should contribute to a better understanding of galaxy evolution in the future. However, it is still a new technique and technical difficulties exist, such as variable PSF, small fields, subsampling and the need of guide stars that make the use of classical reduction methods more difficult. This is now easier with laser guide stars becoming available and new sets of utilities like the ones we are developing to enable easy data processing and analysis of adaptive optics data for the community. This opens the way to observing the large samples required to reach a robust statistical accuracy. We are planning to enlarge our sample by observing a large number of areas around bright stars in the COSMOS field, which will strongly reduce uncertainties in the study of morphological evolution.
Acknowledgements
The authors want to thank the anonymous referee for many useful comments that greatly improved this paper.
Table 6: Summary of the morphological classifications for the 79 detected objects. For each object we show the I and K band magnitudes and the estimated morphological type from AO imaging in the K-band (with GIM2D and C-A) and from HST-ACS in the I-band. BD stands for bulge-dominated, DD for disk-dominated and I for irregular.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{6673fig61.eps}
\end{figure}](/articles/aa/full/2007/24/aa6673-06/Timg166.gif) |
Figure A.1:
Ks corrected number counts compared with other K-band
surveys. The solid line is the best fitting power-law in the range
|
We perform galaxy number counts up to
![]() .
Above this magnitude
limit, counts are no longer reliable as they must be corrected by a
factor as large as the uncertainties; they are consequently not represented.
We compute a power-law fitting in the range
.
Above this magnitude
limit, counts are no longer reliable as they must be corrected by a
factor as large as the uncertainties; they are consequently not represented.
We compute a power-law fitting in the range
![]() since the K-band
number counts tend to show a slope change at
since the K-band
number counts tend to show a slope change at ![]() (Gardner et al. 1993). We find
a mean slope of
(Gardner et al. 1993). We find
a mean slope of
![]() ,
which is in good agreement with
previous works (Bershady et al. 1998; McCracken et al. 2000). This slope is however much larger than
the one derived from the SWAN observations (Cresci et al. 2006), also performed
with an adaptive optics system. Indeed they claim to find a mean slope
of
,
which is in good agreement with
previous works (Bershady et al. 1998; McCracken et al. 2000). This slope is however much larger than
the one derived from the SWAN observations (Cresci et al. 2006), also performed
with an adaptive optics system. Indeed they claim to find a mean slope
of
![]() in the range
in the range
![]() .
As stated
in Baker et al. (2003), the SWAN fields present, however, a selection bias at the bright
end, since the fields were chosen to have an excess of bright galaxies. This could explain this difference despite that the excess becomes
significant at
.
As stated
in Baker et al. (2003), the SWAN fields present, however, a selection bias at the bright
end, since the fields were chosen to have an excess of bright galaxies. This could explain this difference despite that the excess becomes
significant at
![]() ,
which is out of the computation range.
,
which is out of the computation range.