A&A 468, 613-616 (2007)
DOI: 10.1051/0004-6361:20066624
A 3-mode variable ejection velocity, precessing jet model for HH 30
A. Esquivel1 - A. C. Raga1 - F. De Colle2
1 - Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Ap. 70-543, 04510 D. F., México
2 -
Dublin Institute of Advanced Studies, 5 Merrion Sq., Dublin, Ireland
Received 23 October 2006 / Accepted 16 March 2007
Abstract
Context. HH 30 is a Herbig-Haro (HH) jet showing a chain of aligned knots (with knots covering a range of sizes and knot separations), pointing towards what appears to be a highly fragmented "head''. The chain of knots is detected out to 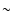 140'', and the head is an elongated group of knots centred at a distance of
140'', and the head is an elongated group of knots centred at a distance of 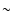 290'' from the source.
290'' from the source.
Aims. In the paper of Anglada et al. (2006, A&A, submitted), it is suggested that this jet is the result of a multi-period variable velocity ejection, and also having a precession of the outflow axis. The question that we address in our paper is whether or not this ejection variability results in a leading working surface with the high fragmentation of the "head'' of the HH 30 jet.
Methods. In order to do this, we take at face value the parameters calculated by Anglada et al. (2006) for the ejection variability and the precession and use them to compute a 3D, radiative jet simulation. Our simulation includes a treatment of the non-equilibrium ionization state of the gas, and allows us to compute synthetic emission line maps, which can be compared directly with previously published images of HH 30.
Results. We find that our simulation does produce a leading working surface with a striking resemblance to the head of HH 30. We obtain a fragmented emission structure with an extent both along and across the outflow axis that agrees well with the observed jet head.
Conclusions. It then appears to be clear that the variable ejection implied by the chain of knots close to the HH 30 source has a direct effect on the head of the jet, producing a highly fragmented structure that is comparable with observations. This is the first time that such a connection has been proven for an HH outflow.
Key words: ISM: Herbig-Haro objects - ISM: individual objects: HH30 - ISM: jets and outflows - stars: formation
Hergig-Haro (HH) jets sometimes show chains of aligned knots close to the outflow source (i.e., at distances from a few to up to 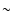 30'') and/or brighter, spatially more extended "heads'' at larger distances from the source (see, e.g., the old review of Reipurth 1989). These "heads'' can be more or less organized, showing morphologies ranging from relatively well organized bow shock-like structures, to rather chaotic collections of emitting knots.
30'') and/or brighter, spatially more extended "heads'' at larger distances from the source (see, e.g., the old review of Reipurth 1989). These "heads'' can be more or less organized, showing morphologies ranging from relatively well organized bow shock-like structures, to rather chaotic collections of emitting knots.
This range of possible morphologies is nicely illustrated by the HH 1/2 outflow, which has a jet with a chain of aligned knots pointing towards the relatively well organized, compact structure of HH 1 (see, e.g., the paper on HST proper motions of Bally et al. 2002). This object has been modeled as the head of an HH jet in repeated opportunities (see, e.g., Henney 1996).
On the other hand the (invisible) counterjet powers HH 2, which is a spatially more extended, chaotic structure of emitting knots (see, e.g., Böhm & Solf 1992). It has been proposed that the qualitative, morphological difference between HH 1 and 2 could be due to the fact that HH 2 might be interacting with a clumpy, molecular medium (see, e.g., Girart et al. 2002).
Another possibility for the production of a clumpy "head'' would be as a result of a jet with both a time-dependent ejection velocity variability and a precession of the outflow axis. Raga & Biro (1993) showed that such a jet breaks into a number of clumps (travelling in different directions within the precession cone).
Raga et al. (2004) computed a model of a variable, precessing jet for HH 32. This object has a fragmented head that can indeed be reproduced with such a model (see, e.g., Curiel et al. 1997; and Beck et al. 2004). However, due to the unusual, close to the line-of-sight orientation and to the lack of a chain of knots close to the source, for HH 32 it is not possible to determine direct constraints on the ejection time-variability and the precession. Therefore, there is a large amount of freedom for choosing the model parameters that will indeed result in a fragmentation of the head of the jet.
A much more favourable case is presented by the HH 30 jet. This is one of the objects of the catalogue of Herbig (1974), and also one of the first HH objects to be identified as jets
(Mundt & Fried 1983; Cohen & Jones 1987; Mundt et al. 1988). A detailed spectroscopic study of this jet was presented by Bacciotti, et al. (1999), and a very high angular and spectral resolution observation was carried out by Appenzeller et al. (2005).
The HST proper motion measurements of the knots within a few second of arc of the HH 30 source carried out by Burrows et al. (1996) are one of the most spectacular observations ever of HH jets.
López et al. (1995) found a collection of knots centred along the northern prolongation of the HH 30 jet, at 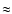 290'' from the source. Their speculation that these knots corresponded
to a fragmented "head'' of the jet was later supported by radial velocity (Raga et al. 1997) and proper motion determinations (López et al. 1996), which show that they have kinematical
properties consistent with the ones of the knots along the HH 30 jet.
290'' from the source. Their speculation that these knots corresponded
to a fragmented "head'' of the jet was later supported by radial velocity (Raga et al. 1997) and proper motion determinations (López et al. 1996), which show that they have kinematical
properties consistent with the ones of the knots along the HH 30 jet.
As the HH 30 jet shows a wiggly structure, indicating the possible existence of a precession of the outflow axis, as well as evidence (provided by the existence of the chain of aligned knots) of
an ejection velocity time variability, this flow appears to be ideal for testing whether or not these two effects can be responsible for the existence of a fragmented jet head. In the present paper, we study this possibility by carrying out a 3D radiative jet simulation with the precession and ejection variability that can be deduced from the chain of knots close to the HH 30 source.
In Sect. 2, we describe the choice of parameters, based on the published observations of HH 30, as well as the numerical setup of our numerical simulation. In Sect. 3, we describe the results obtained from the simulation, and carry out a qualitative comparison between these results and the observations of HH 30. Finally, the results are summarized in Sect. 4.
We used the "yguazú-a'' code (described by Raga et al. 2000), in a 6-level binary adaptive grid with a maximum resolution of
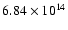 cm (along the three Cartesian axes). The computational domain had an extent of
cm (along the three Cartesian axes). The computational domain had an extent of
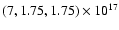 cm. At the highest resolution
it would correspond to
cm. At the highest resolution
it would correspond to
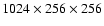 points on a uniform grid.
points on a uniform grid.
The 3D gas-dynamic equations are integrated together with a 17-species atomic/ionic reaction network. This network, as well as the cooling functions and the atomic abundances are identical to the ones described by Raga et al. (2004).
Due to computational constraints, previous models of HH flows with the "yguazú-a'' code by Masciadri et al. (2002) relied in decreasing the resolution allowed in the code with increasing distance from the source. With newer machines, in the present work, we have not imposed such additional restrictions on the resolution.
Anglada et al. (2006) propose that in order to explain the knot structure of the HH 30 jet in terms of a variable ejection velocity flow it is necessary to have three variability periods:
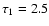 ,
,
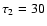 and
and
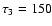 yr. They also propose a fourth period (of 1500 yr) that might be necessary if the observed "head'' of the HH 30 jet were also an internal working surface. We choose to model this head as the "leading'' working surface of the jet flow, and therefore avoid this fourth ejection variability mode.
yr. They also propose a fourth period (of 1500 yr) that might be necessary if the observed "head'' of the HH 30 jet were also an internal working surface. We choose to model this head as the "leading'' working surface of the jet flow, and therefore avoid this fourth ejection variability mode.
We then propose a sinusoidal ejection velocity variability of the form:
![\begin{displaymath}v_{\rm j}(t)=v_0+\Delta v~\left[\sin\left({2\pi t\over \tau_1...
...tau_2}\right)
+\sin\left({2\pi t\over \tau_3}\right)\right]\!,
\end{displaymath}](/articles/aa/full/2007/23/aa6624-06/img13.gif) |
(1) |
with a mean velocity v0=300 km s-1 and a single,
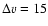 km s-1 amplitude for the three modes. This choice of amplitude reflects the fact that there is no direct observational
constraint for this parameter, other than the fact that HH 30 has a low excitation spectrum.
km s-1 amplitude for the three modes. This choice of amplitude reflects the fact that there is no direct observational
constraint for this parameter, other than the fact that HH 30 has a low excitation spectrum.
Also, from the observed structure of HH 30 Anglada et al. (2006) deduce that the direction of the HH 30 outflow precesses with a period
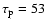 yr on a cone of half-opening angle
yr on a cone of half-opening angle
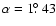 .
We then impose a precession with these parameters in our numerical simulation.
.
We then impose a precession with these parameters in our numerical simulation.
We give the initially top hat jet a constant ejection density
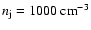 ,
temperature
,
temperature
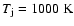 and radius
and radius
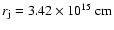 (5 cells at the highest resolution
grid, which is always present at the place of injection). We also consider that the environment is initially homogeneous, with density
(5 cells at the highest resolution
grid, which is always present at the place of injection). We also consider that the environment is initially homogeneous, with density
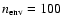 cm-3 and temperature
cm-3 and temperature
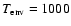 K. Both the jet and the environment are initially neutral, except for C and S which are singly ionized.
K. Both the jet and the environment are initially neutral, except for C and S which are singly ionized.
We place the origin of the coordinate system on one end of the longer (i.e., x) axis of the computational domain, and on the centre of the x=0 plane. We then apply a reflection
boundary on the x=0 plane, and outflow conditions on all of the other boundaries.
We now place the jet source at
(x,y,z)=(0,0,0) with the precession axis parallel to the x-axis. At the initial t=0 time, the outflow lies on the yz-plane, pointing in the +x-direction, and rotating towards the +y-axis. With this setup, we integrate in time until the jet reaches the end of the x-extent of the computational grid. The results of this integration are described in the following section.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{6624f1.eps}\end{figure}](/articles/aa/full/2007/23/aa6624-06/Timg24.gif) |
Figure 1:
Structure of the flow after an integration time of t=500 yr. The grey-scale depicts the column density (integrated along the z-axis), in logarithmic scale. The entire computational domain is shown on by the rectangle in the left plot) is shown on the right panel.
On the left we show proper motions of a few selected dense structures in the head, the length of the arrows is proportional to the magnitude of the proper motions, which are of
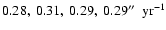 (from bottom to top, assuming a 150 pc distance to the object). On the right panel we overlay the velocity field of the perturbed flow (averaged in the z-direction), the largest arrow corresponding to a velocity of
(from bottom to top, assuming a 150 pc distance to the object). On the right panel we overlay the velocity field of the perturbed flow (averaged in the z-direction), the largest arrow corresponding to a velocity of 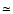
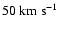 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6624f2.eps}\end{figure}](/articles/aa/full/2007/23/aa6624-06/Timg26.gif) |
Figure 2:
Same as Fig. 1, but for t=900 yr. The magnitude of the proper motions ( left panel, from bottom to top) in this case is 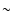
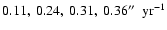 .
The largest arrow on the right panel corresponds to an average velocity of .
The largest arrow on the right panel corresponds to an average velocity of 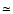 70 km s-1 70 km s-1 |
| Open with DEXTER |
With the setup described in Sect. 2, we have carried out a numerical integration up to a time t=900 yr, by which the jet has traveled through most of the computational domain. In Fig. 1, we show the column density (integrated along the z-axis), for a t=500 yr time-frame. In the plot showing all of the computational domain we also show the proper motions (computed by measuring the
positions of the column density peaks on two successive frames with a
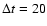 yr separation) of the knots in the head of the jet.
yr separation) of the knots in the head of the jet.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6624f3.eps}\end{figure}](/articles/aa/full/2007/23/aa6624-06/Timg28.gif) |
Figure 3:
[S II] 6716+30 emission integrated over the z-direction for t=500 yr. The intensity is given in a logarithmic grey-scale. The left panel shows the entire computational domain, the right
panel the innermost region indicated by the rectangle on the left. |
| Open with DEXTER |
Figure 1 also shows a blow up of the region close to the outflow source. In this plot, we also show the flow velocity averaged (along the z-axis) over all of the perturbed flow region (i.e., not including the region of the computational domain which is still filled up with the undisturbed environment). There is a high velocity region extending out to several jet radii on each side of the outflow axis. Figure 2 shows the same things as Fig. 1, but for the configuration of the flow at t=900 yr.
Figures 3 and 4 show [S II] 6716+30 emission maps for the t=500 and t=900 yr time frames, respectively. These maps were computed by calculating the appropriate emission line coefficient (solving a 5-level atom problem) and integrating it along the z-axis (i.e., assuming that the xy-plane coincides with the plane of the sky).
From Fig. 4, we see that in the t=900 yr flow configuration there is a wiggling chain of
emitting knots extending out to 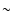 0.05 pc (
0.05 pc (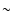 75'' at the 140 pc distance of HH 30), and an axially extended, diffuse emission that fills the "cocoon'' excavated by the jet, up to distances
of
75'' at the 140 pc distance of HH 30), and an axially extended, diffuse emission that fills the "cocoon'' excavated by the jet, up to distances
of 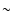 0.10 pc (
0.10 pc (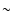 150'' at the distance of HH 30). We then see an isolated group of knots offset to one side of the outflow axis at
150'' at the distance of HH 30). We then see an isolated group of knots offset to one side of the outflow axis at 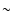 0.11 pc (160'') from the source, and from there up to the leading head of the jet (0.22 pc, 325''), we see smaller condensations.
This fragmented head emission region has a width (across the jet axis) of
0.11 pc (160'') from the source, and from there up to the leading head of the jet (0.22 pc, 325''), we see smaller condensations.
This fragmented head emission region has a width (across the jet axis) of 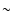 0.02 pc (
0.02 pc (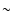 30'').
30'').
If we look at the [S II] 6716+30 morphology of the HH 30 jet (e.g., in the images of López et al. 1995 and Anglada et al. 2006), we see that it has a chain of knots extending out to 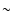 50'' from the source, and an axially extended emission feature from
50'' from the source, and an axially extended emission feature from 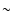
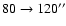 .
This feature is
confused with the bright reflection nebula surrounding the HL Tauri star. Finally, the fragmented "head'' of the HH 30 jet is a collection of knots extending from
.
This feature is
confused with the bright reflection nebula surrounding the HL Tauri star. Finally, the fragmented "head'' of the HH 30 jet is a collection of knots extending from 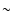
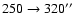 from the source, with a distribution extending for
from the source, with a distribution extending for 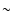 20'' across the outflow axis.
20'' across the outflow axis.
From the description of the synthetic and observed [S II] 6716+30 emission maps given in the two previous paragraphs, we see that the modeled and observed emission structures are very similar. In particular, the variable, precessing ejection (assumed in the model, required by the wiggling chain of aligned knots close ti the jet source) produces a fragmented working surface with the correct axial extent, and a somewhat broader knot distribution (of 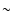 30'' across the outflow axis) than
the observed width (of
30'' across the outflow axis) than
the observed width (of  20'', see above and López et al. 1995).
20'', see above and López et al. 1995).
We have computed a 3D simulation of a variable, precessing jet with the parameters deduced from the observed structure of knots along the HH 30 jet. With this model, we produce a fragmented "head'' structure which has a strong, qualitative resemblance to the collection of knots which has been identified (because of their position along the outflow axis and their kinematical properties) as the head of HH 30. From this, we conclude that the highly fragmented structure of the head of this HH jet could very well be a direct result of the combination of the variability and the precession of the ejection.
This result is interesting because of the following. The well observed chain of knots close to the outflow source gives direct constraints on the parameters of the ejection variability and precession that would be necessary to produce the observed knot structure. Through our 3D numerical simulation, we then show that this observationally determined variability+precession does indeed give rise to a jet head with the appropriate spatial structure. This result is a quite convincing proof (at least as far as these things go) that the fragmentation of the head of HH 30 is a direct result of the properties of the ejection.
An alternative option for producing a fragmented head in a HH flow would be the presence of a clumpy surrounding medium. Such clumps could of course be present in the region into which the HH 30 is travelling. However, we have proven that such a clumpy medium is not necessary for producing the fragmentation of the head of HH 30, because the ejection variability and precession of this jet (necessary for explaining the curved chain of knots at the base of HH 30) results in a fragmentation of the jet head which is similar to the observed one (even for the case of a jet travelling into a uniform medium).
We should note that while the extent along the outflow axis of the predicted "head'' knot structure is very similar to the observed one, the predicted knot structure is somewhat wider (across the
outflow axis) than the observed one. This difference could be reduced by considering a somewhat smaller opening angle for the precession cone, and also possibly by considering an environment
with different properties (e.g., with a somewhat higher density, or with a density stratification). Also, the possible presence in this object of a relative motion between the outflow source and the surrounding medium (see, e.g., Cantó & Raga 1995; Lim & Raga 1998) might have the desired effect of reducing the width of the head knot structure in a moderate way.
Acknowledgements
The work of A.E., and A.R. was supported by the CONACyT grants 43103-F and 46828-F, the DGAPA (UNAM) grant IN 108207-2 and the "Macroproyecto de Tecnologías para la Universidad de la Información y la Computación'' (Secretaría de Desarrollo Institucional de la UNAM, Programa Transdisciplinario en Investigación y Desarrollo para Facultades y Escuelas, Unidad de Apoyo a la Investigación en Facultades y Escuelas). F.D.C. acknowledges support of the European Community's Marie Curie Actions - Human Resource and Mobility within the JETSET (Jet Simulations, Experiments and Theory) network under contract MRTN-CT-2004 005592. We thank Enrique Palacios and Martín Cruz for supporting the servers in which the calculations of this paper were carried out.
- Anglada, G.,
López, R., Estalella, R., et al. 2006, A&A, submitted
(In the text)
-
Appenzeller, I., Bertout, C., Stahl, & O. 2005, A&A, 434,
1005 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Bacciotti, F., Eislöffel, J., & Ray, T. P. 1999, A&A,
350, 917 [NASA ADS] (In the text)
- Bally, J.,
Heathcote, S., Reipurth, B., et al. 2002, AJ, 123, 2627 [NASA ADS] [CrossRef] (In the text)
- Beck, T. L., Riera,
A., Raga, A. C., & Aspin, C. 2004, AJ, 127, 408 [NASA ADS] [CrossRef] (In the text)
- Böhm, K. H.,
& Solf, J. 1992, AJ, 104, 1193 [NASA ADS] [CrossRef] (In the text)
- Burrows, C.,
Stapelfeldt, K., Watson, A., et al. 1996, ApJ, 473, 437 [NASA ADS] [CrossRef] (In the text)
- Cantó, J.,
& Raga, A. C. 1995, MNRAS, 277, 1120 [NASA ADS] (In the text)
- Cohen, M., &
Jones, B. F. 1987, ApJ, 321, 846 [NASA ADS] [CrossRef] (In the text)
- Curiel, S.,
Raga, A. C., Raymond, J. C., Noriega-Crespo, A., & Cantó,
J. 1997, AJ, 114, 2736 [NASA ADS] [CrossRef] (In the text)
- Girart, J. M.,
Viti, S., Williams, D. A., Estalella, R., & Ho, P. T. P. 2002,
A&A, 388, 1004 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Henney, W. J.
1996, RMxAA, 32, 3 [NASA ADS] (In the text)
- Herbig, G. H.
1974, Lick Obs. Bull., 658, 1 [NASA ADS] (In the text)
- Lim, A. J., &
Raga, A. C. 1998, MNRAS, 298, 871 [NASA ADS] (In the text)
- López, R.,
Raga, A. C., Riera, A., Anglada, G., & Estalella, R. 1995,
MNRAS, 274, L19 [NASA ADS] (In the text)
- López, R.,
Riera, A., Raga, A. C., Anglada, G., & Estalella, R. 1996,
MNRAS, 282, 470 [NASA ADS] (In the text)
-
Masciadri, E., de Gouveia Dal Pino, E. M., Raga, A. C., &
Noriega-Crespo, A. 2002, ApJ, 580, 950 [NASA ADS] [CrossRef] (In the text)
- Mundt, R., &
Fried, J. W. 1983, ApJ, 274, L83 [NASA ADS] [CrossRef] (In the text)
- Mundt, R., Ray,
T. P., & Bührke, T. 1988, ApJ, 333, L69 [NASA ADS] [CrossRef] (In the text)
- Raga, A. C., &
Biro, S. 1993, MNRAS, 264, 758 [NASA ADS] (In the text)
- Raga, A. C.,
López, R., Riera, A., Estalella, R., & Anglada, G. 1997,
RMxAA, 33, 127 [NASA ADS] (In the text)
- Raga, A. C.,
Navarro-González, R., & Villagrán-Muniz, M., 2000,
RMxAA, 36, 67 [NASA ADS] (In the text)
- Raga, A. C., Riera,
A., Masciadri, E., et al. 2004, AJ, 127, 1081 [NASA ADS] [CrossRef] (In the text)
- Reipurth,
B. 1989, in Low mass star formation and pre-main sequence objects,
ed. B. Reipurth (ESO: Garching bei München), 247
(In the text)
Copyright ESO 2007
![\begin{displaymath}v_{\rm j}(t)=v_0+\Delta v~\left[\sin\left({2\pi t\over \tau_1...
...tau_2}\right)
+\sin\left({2\pi t\over \tau_3}\right)\right]\!,
\end{displaymath}](/articles/aa/full/2007/23/aa6624-06/img13.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{6624f1.eps}\end{figure}](/articles/aa/full/2007/23/aa6624-06/Timg24.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6624f2.eps}\end{figure}](/articles/aa/full/2007/23/aa6624-06/Timg26.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6624f3.eps}\end{figure}](/articles/aa/full/2007/23/aa6624-06/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6624f4.eps}\end{figure}](/articles/aa/full/2007/23/aa6624-06/Timg29.gif)