A&A 468, 353-377 (2007)
DOI: 10.1051/0004-6361:20065724
The XMM-Newton extended survey of the Taurus molecular cloud
M. Güdel1 -
K. R. Briggs1 -
K. Arzner1 -
M. Audard2,![]() -
J. Bouvier3 -
E. D. Feigelson4 -
E. Franciosini5 -
A. Glauser1 -
N. Grosso3 -
G. Micela5 -
J.-L. Monin3 -
T. Montmerle3 -
D. L. Padgett6 -
F. Palla7 -
I. Pillitteri8 -
L. Rebull6 -
L. Scelsi8 -
B. Silva9,10 -
S. L. Skinner11 -
B. Stelzer5 -
A. Telleschi1
-
J. Bouvier3 -
E. D. Feigelson4 -
E. Franciosini5 -
A. Glauser1 -
N. Grosso3 -
G. Micela5 -
J.-L. Monin3 -
T. Montmerle3 -
D. L. Padgett6 -
F. Palla7 -
I. Pillitteri8 -
L. Rebull6 -
L. Scelsi8 -
B. Silva9,10 -
S. L. Skinner11 -
B. Stelzer5 -
A. Telleschi1
1 - Paul Scherrer Institut, Würenlingen and Villigen,
5232 Villigen PSI, Switzerland
2 -
Columbia Astrophysics Laboratory,
Mail Code 5247, 550 West 120th Street,
New York, NY 10027,
USA
3 -
Laboratoire d'Astrophysique de Grenoble,
Université Joseph Fourier - CNRS,
BP 53,
38041 Grenoble Cedex,
France
4 -
Department of Astronomy & Astrophysics,
Penn State University,
525 Davey Lab,
University Park, PA 16802,
USA
5 -
INAF - Osservatorio Astronomico di Palermo,
Piazza del Parlamento 1,
90134 Palermo,
Italy
6 -
Spitzer Science Center,
California Institute of Technology,
Mail Code 220-6, Pasadena, CA 91125,
USA
7 -
INAF - Osservatorio Astrofisico di Arcetri,
Largo Enrico Fermi, 5,
50125 Firenze,
Italy
8 -
Dipartimento di Scienze Fisiche ed Astronomiche,
Università di Palermo, Piazza del Parlamento 1,
90134 Palermo,
Italy
9 -
Centro de Astrofísica da Universidade do Porto, Rua das Estrelas, 4150
Porto, Portugal
10 -
Departamento de Matemática Aplicada, Faculdade de Ciêcias da
Universidade do Porto, 4169 Porto, Portugal
11 -
CASA, 389,
University of Colorado,
Boulder, CO 80309-0389,
USA
Received 31 May 2006 / Accepted 5 August 2006
Abstract
Context. The Taurus Molecular Cloud (TMC) is the nearest large star-forming region, prototypical for the distributed mode of low-mass star formation. Pre-main sequence stars are luminous X-ray sources, probably mostly owing to magnetic energy release.
Aims. The XMM-Newton Extended Survey of the Taurus Molecular Cloud (XEST) presented in this paper surveys the most populated ![]() 5 square degrees of the TMC, using the XMM-Newton X-ray observatory to study the thermal structure, variability, and long-term evolution of hot plasma, to investigate the magnetic dynamo, and to search for new potential members of the association. Many targets are also studied in the optical, and high-resolution X-ray grating spectroscopy has been obtained for selected bright sources.
5 square degrees of the TMC, using the XMM-Newton X-ray observatory to study the thermal structure, variability, and long-term evolution of hot plasma, to investigate the magnetic dynamo, and to search for new potential members of the association. Many targets are also studied in the optical, and high-resolution X-ray grating spectroscopy has been obtained for selected bright sources.
Methods. The X-ray spectra have been coherently analyzed with two different thermal models (2-component thermal model, and a continuous emission measure distribution model). We present overall correlations with fundamental stellar parameters that were derived from the previous literature. A few detections from Chandra observations have been added.
Results. The present overview paper introduces the project and provides the basic results from the X-ray analysis of all sources detected in the XEST survey. Comprehensive tables summarize the stellar properties of all targets surveyed. The survey goes deeper than previous X-ray surveys of Taurus by about an order of magnitude and for the first time systematically accesses very faint and strongly absorbed TMC objects. We find a detection rate of 85% and 98% for classical and weak-line T Tau stars (CTTS resp. WTTS), and identify about half of the surveyed protostars and brown dwarfs. Overall, 136 out of 169 surveyed stellar systems are detected. We describe an X-ray luminosity vs. mass correlation, discuss the distribution of X-ray-to-bolometric luminosity ratios, and show evidence for lower X-ray luminosities in CTTS compared to WTTS. Detailed analysis (e.g., variability, rotation-activity relations, influence of accretion on X-rays) will be discussed in a series of accompanying papers.
Key words: stars: formation - stars: pre-main sequence - X-rays: stars - gravitational waves
Studies of star-forming regions have drawn a picture in which cool, molecular gas, contracting to protostars with surrounding accretion disks, co-exists with high-energy radiation. The latter is emitted by plasma in the stellar environment that is continuously heated to temperatures beyond one million degrees. This radiation is most prominently seen in the soft (0.1-10 keV) X-ray range and is conventionally attributed to the presence of magnetically trapped plasma in the outer stellar atmosphere. This plasma is reminiscent of, in the broadest sense, the solar coronal plasma. There is little doubt that both lower-energy (extreme ultraviolet) and higher-energy (hard X-ray and gamma - ray) radiation is amply present, but strong photoelectric absorption or, respectively, extremely low flux precludes direct detection. Further, non-thermal radio emission from relativistic electrons trapped in the magnetic fields gives unambiguous evidence for the presence of an accelerated population of electrons similar to populations seen in the solar and in stellar coronae during flares (Güdel 2002). Again, by implication from the solar analogy, we expect that high-energy, non-thermal particles (electrons and ions) play a crucial role also outside the confines of the magnetic stellar atmosphere.
But in contrast to the solar case, high-energy radiation from forming stars has a profound influence on its environment as dense accretion disks and the larger-scale molecular envelope are irradiated, heated, and ionized by high-energy photons and particles. There are numerous consequences of these processes. Ultraviolet and X-ray irradiation of molecular disks heats their upper layers (Alexander et al. 2004; Glassgold et al. 2004), making them accessible to magnetic fields, thus inducing, for example, the magnetorotational instability (Balbus & Hawley 1991). The latter is thought to be a prime source for increased disk viscosity, which in turn is the main driver of the accretion process and thus the stellar formation process in the first place. Complex chemical networks are also put in operation by heating and ionizing the molecular environment (Glassgold et al. 2004), thus fundamentally altering composition, opacity, and cooling behavior of the material. Magnetic fields are thought to attach to the inner border of the lightly ionized accretion disk, thus transporting material to the stellar surface while at the same time applying torques to the star that may regulate its rotation period (Montmerle et al. 2000). If the stellar magnetic fields are generated in a solar-like dynamo in which rotation is a key parameter, then the long-term evolution of the magnetic field production and thus of the high-energy radiation is indeed directly controlled by the accretion process in the feedback loop sketched above. Further, magnetic fields and ionization of the disk may be relevant for the launch of bipolar jets and molecular outflows (Pudritz & Norman 1986), a widely observed but poorly understood mechanism that seems to regulate the mass buildup of the forming star. Alternatively, these jets may originate from the magnetic fields spanning between the star and the disk (Shu et al. 1994), or from plasma clouds ejected in the process of magnetic reconnection of these same fields (Hayashi et al. 1996).
The origin of the X-ray emission is still not entirely clear. While the bulk of the X-rays from T Tau stars is thought to originate in a magnetically trapped corona consisting of complex magnetic loops anchored in photospheric magnetic regions like in the Sun, features unknown to the Sun may exist. Speculation has arisen that some very soft X-rays may be formed in accretion shocks near the stellar surface (e.g., Kastner et al. 2002). Herbig-Haro objects far from the forming stars have been detected to be very soft X-ray emitters due to shock interactions with the interstellar medium (e.g., Bally et al. 2003; Pravdo et al. 2001; Güdel et al. 2005), but new spectral phenomenology suggests that appreciable X-ray emission may also be formed close to the stars, at the (spatially unresolved) base of the jets otherwise seen in radio and in the optical (Güdel et al. 2005). Whatever the analogy to the Sun, we also note that the level of the X-ray luminosity (between a few times 1028 erg s-1 and 1031 erg s-1 for low-mass pre-main sequence stars) and the measured plasma temperatures of up to 100 MK are extreme and may imply heating mechanisms related to continuous flaring (Wolk et al. 2005; Güdel et al. 2003).
Studies of X-ray radiation in pre-main sequence stars are thus crucial
for our further understanding of star formation, accretion processes, angular momentum
transport, and mass outflow mechanisms in the earliest stages of a star's life. For recent
reviews of X-rays from pre-main sequence stars, we refer the reader to Feigelson & Montmerle (1999),
Güdel (2004), and Feigelson et al. (2007). XMM-Newton and Chandra penetrate dense molecular envelopes
providing unequaled information on high-energy processes. A recent, large survey of the Orion
Nebula Cluster (ONC) with Chandra (the COUP project, Getman et al. 2005) has
monitored approximately 1400 young stars in a
![]() field around the
Trapezium. This study has provided unprecedented information on the ONC stellar population and
the evolution of X-ray production. For example, Preibisch et al. (2005) concluded that a significant
correlation between rotation and X-ray luminosity consistently found in main-sequence stars is
absent in the ONC sample, arguing for a different magnetic dynamo process or a very different
internal structure of these youngest stars. X-ray radiation was found to be largely variable,
with numerous flares contributing significantly to the overall X-ray production (Wolk et al. 2005).
We refer the interested reader to a special volume of papers from this study (Getman et al. 2005 and
associated papers), or to a summary provided by Feigelson et al. (2007).
field around the
Trapezium. This study has provided unprecedented information on the ONC stellar population and
the evolution of X-ray production. For example, Preibisch et al. (2005) concluded that a significant
correlation between rotation and X-ray luminosity consistently found in main-sequence stars is
absent in the ONC sample, arguing for a different magnetic dynamo process or a very different
internal structure of these youngest stars. X-ray radiation was found to be largely variable,
with numerous flares contributing significantly to the overall X-ray production (Wolk et al. 2005).
We refer the interested reader to a special volume of papers from this study (Getman et al. 2005 and
associated papers), or to a summary provided by Feigelson et al. (2007).
The ONC represents the so-called "clustered mode'' of star formation in which hundreds to thousands of low-mass stars form around massive O-type stars such as those in the Trapezium. Such environments produce extreme stellar densities, and the presence of hot stars has a decisive impact on star formation. UV radiation and the winds of the central O stars have a deteriorating effect on the molecular environment, the pre-stellar cores and the circumstellar disks by ionizing and dispersing the molecular material, prematurely altering the accretion environment (O'Dell 1998) and eventually halting the star formation process altogether (Dolan & Mathieu 2001). The ionized H II Orion Nebula is the most vivid expression of this environment.
Star formation occurs, however, also in relatively unspectacular low-mass star forming regions devoid of the influence of radiation and outflow-related effects from luminous O stars. These so-called "dark clouds'' typically form a smaller number of stars and often do so in a "dispersed'' or "isolated mode'' in which stars or very small groups of stars form in relative isolation. Stars form in a similar manner also in high-mass star formation regions, outside the clusters and at larger distances from the central OB stars (Carpenter 2000).
The closest and best-studied large, low-mass star formation region
is the Taurus Molecular Cloud (TMC) complex that extends to
the adjacent Auriga Clouds. TMC has served as a testbed for low-mass star-formation theory
and has provided some of the best examples of phenomenology relevant to star formation.
There are only a few Herbig Ae/Be stars in this vast region (V892 Tau and AB Aur in our survey). The
rest are predominantly sub-solar in mass although there have been claims that a substantial
population of non-accreting B stars may be members of the Taurus population (Walter & Boyd 1991), in
agreement with expectations from the initial mass function.
Owing to the near-absence of massive stars and their mechanical/radiative effects, the molecular gas is
still present in large amounts (
![]() ,
Ungerechts & Thaddeus 1987)
much in excess of the total mass in stars already formed
(
,
Ungerechts & Thaddeus 1987)
much in excess of the total mass in stars already formed
(
![]() of order
of order
![]() ).
).
The Taurus region is quite large (some 10-15 degrees in diameter,
corresponding to about 25-35 pc at a distance of 140 pc), making comprehensive studies
of the entire population difficult. We have initiated a large X-ray study of
the TMC with the XMM-Newton X-ray observatory, concentrating on the denser cloud areas that contain
the majority of the TMC stellar population. The emphasis of this XMM-Newton Extended Survey of the Taurus
Molecular Cloud (XEST henceforth) is on a wide-field sampling
rather than on long exposures. It goes systematically deeper by about an order of magnitude than
previous Taurus X-ray surveys. While it is less sensitive than the COUP survey, it surveys an area about
60 times larger (![]() 5 square degrees), which is required because of the low surface density of Taurus members.
The survey is accompanied by a deep, large-field optical
survey with the Canada-France-Hawaii Telescope (CFHT)
and a mid-infrared survey of the entire cloud complex with the Spitzer Space Telescope
(Padgett et al. 2007). These latter surveys will be presented separately (see summary of all three surveys in
Güdel et al. 2007a). All studies combined provide an unsurpassed database for the nearest
major star-forming cloud complex.
5 square degrees), which is required because of the low surface density of Taurus members.
The survey is accompanied by a deep, large-field optical
survey with the Canada-France-Hawaii Telescope (CFHT)
and a mid-infrared survey of the entire cloud complex with the Spitzer Space Telescope
(Padgett et al. 2007). These latter surveys will be presented separately (see summary of all three surveys in
Güdel et al. 2007a). All studies combined provide an unsurpassed database for the nearest
major star-forming cloud complex.
The purpose of the present paper is to give an introduction to the XEST project, to present an overview of the surveyed stellar sample, and to discuss the strategies followed during the data reduction and analysis. The detailed results are described in a series of associated papers.
The outline of this paper is as follows. We discuss some pivotal properties of the TMC in Sect. 2, including results from previous studies that support the key role of this region for further star-formation studies. Section 3 introduces the TMC X-ray survey, and Sect. 4 presents the data reduction and analysis strategies. Section 5 contains an overview of the basic results, presenting detected and undetected stellar populations, accompanied by comprehensive tabulations of fundamental properties of all surveyed objects and spectral X-ray results from the detections. We summarize overall statistical properties of XEST in Sect. 6.
The subsequent series of papers related to this survey discusses X-ray properties in the context of stellar class and accretion (Telleschi et al. 2007a), rotation-activity relations (Briggs et al. 2007), a dedicated study of the L1495E subsample (Silva et al., in preparation), correlated behavior of X-rays and optical/ultraviolet emission (Audard et al. 2007), X-rays from jet-driving stars in TMC (Güdel et al. 2007b), high-resolution X-ray spectroscopy of classical and weak-line T Tau stars (Telleschi et al. 2007b), X-rays from brown dwarfs (Grosso et al. 2007a), a U-band survey of brown dwarfs with the XMM-Newton Optical Monitor (Grosso et al. 2007b), light-curve variability studies (Stelzer et al. 2007), interpretation of X-ray flares (Franciosini et al. 2007), an investigation of statistical fluctuations in X-ray light curves (Arzner et al. 2007a), an investigation of spectral parameters in extremely faint sources (Arzner et al. 2007b), an analysis of the gas-to-dust ratio in IRAS 04158+2805 (Glauser et al. 2007), a study of the gas-to-dust ratios in the TMC in general (Glauser et al., in preparation), a case study of the accreting, prototypical CTTS T Tau (Güdel et al. 2007c), a study of the supposedly single Herbig star in TMC, AB Aurigae (Telleschi et al. 2007c), and a search for new TMC members based on near-infrared and X-ray properties of field sources detected in XEST (Scelsi et al. 2007).
TMC has figured prominently in star-formation studies at all wavelengths. It has provided
the best-characterized sample of classical and weak-line T Tau stars (CTTS and WTTS, respectively,
or "Class II'' and "Class III'' objects in the infrared classification - Kenyon & Hartmann 1995);
most of our current picture of low-density star formation is indeed based on IRAS studies of
Taurus (Weaver & Jones 1992; Strom et al. 1989). Among the key results from TMC studies as listed in Kenyon & Hartmann (1995)
figure the following: i) more than 50% of the TMC objects have IR excess beyond the photospheric
contribution, correlating with other activity indicators (H![]() ,
UV excess etc.) and indicating
the presence of warm circumstellar material predominantly in the form of envelopes for Class I
protostars and circumstellar disks for Class II stars. ii) Class III sources (mostly to be identified
with WTTS) are distinctly different from Class I-II objects by not revealing optically thick disks or
signatures of accretion. iii) Star formation has been ongoing at a similar level during the past
1-2 Myr, with the Class-I protostars having ages of typically 0.1-0.2 Myr. iv) There is clear support
for an evolutionary sequence Class I
,
UV excess etc.) and indicating
the presence of warm circumstellar material predominantly in the form of envelopes for Class I
protostars and circumstellar disks for Class II stars. ii) Class III sources (mostly to be identified
with WTTS) are distinctly different from Class I-II objects by not revealing optically thick disks or
signatures of accretion. iii) Star formation has been ongoing at a similar level during the past
1-2 Myr, with the Class-I protostars having ages of typically 0.1-0.2 Myr. iv) There is clear support
for an evolutionary sequence Class I
![]() II
II
![]() III, although there is little
luminosity evolution along this sequence, indicating different evolutionary
speeds for different objects (see also Hartmann 2002). The infall time scale is a few times
105 yrs, while the disk phase amounts to a few times 106 yrs. An evolutionary scenario is
also suggested from the different spatial distribution of Class
0/I stars vs. CTTS/WTTS with respect to the gas distribution: the
former classes are still within the boundaries of the high density gas, while
the latter are found in regions of lower density (Palla & Stahler 2001).
III, although there is little
luminosity evolution along this sequence, indicating different evolutionary
speeds for different objects (see also Hartmann 2002). The infall time scale is a few times
105 yrs, while the disk phase amounts to a few times 106 yrs. An evolutionary scenario is
also suggested from the different spatial distribution of Class
0/I stars vs. CTTS/WTTS with respect to the gas distribution: the
former classes are still within the boundaries of the high density gas, while
the latter are found in regions of lower density (Palla & Stahler 2001).
TMC has also been well-studied at millimeter wavelengths. This region has better high-resolution molecular line maps than any other star-forming region (Onishi et al. 2002). Most of the higher-mass CTTS and Class I protostars have been surveyed by millimeter interferometers for molecular line emission from disks (Ohashi et al. 1996; Dutrey et al. 1996, etc.) and many detailed studies of individual sources have been published (e.g., Duchêne et al. 2003; Qi et al. 2003). A variety of millimeter continuum observations of these sources have enabled studies of cold disk frequency into substellar mass ranges and raised the possibility of grain growth within circumstellar disks (Rodman et al. 2006; Kitamura et al. 2002; Scholz et al. 2006; Wolf et al. 2003, etc.). Due to its proximity and easy accessibility to northern hemisphere radio telescopes, the TMC has served as a template for millimeter studies of young stellar objects.
Although TMC has been regarded, together with the ![]() Oph dark cloud, as the prototypical
low-mass star-forming region, a few apparent peculiarities deserve to be mentioned. TMC contains
an anomalous number of binaries (Duchêne 1999; Ghez et al. 1993), compared with other SFRs
(e.g., Orion) or with field stars.
In TMC, about two thirds of all members are bound in multiple systems, with an average
separation of about
Oph dark cloud, as the prototypical
low-mass star-forming region, a few apparent peculiarities deserve to be mentioned. TMC contains
an anomalous number of binaries (Duchêne 1999; Ghez et al. 1993), compared with other SFRs
(e.g., Orion) or with field stars.
In TMC, about two thirds of all members are bound in multiple systems, with an average
separation of about
![]() (e.g., Simon et al. 1995; Mathieu 1994; White & Ghez 2001; Leinert et al. 1993; Duchêne et al. 1999; Hartigan & Kenyon 2003). Petr et al. (1998) reported, at the 96% confidence
level, a three times higher binary occurrence in TMC compared to Orion for component separations
in the range of 63-225 AU.
Also, TMC cloud cores are comparatively small and of low
mass, at least when compared with cores in Orion or Perseus (Kun 1998).
(e.g., Simon et al. 1995; Mathieu 1994; White & Ghez 2001; Leinert et al. 1993; Duchêne et al. 1999; Hartigan & Kenyon 2003). Petr et al. (1998) reported, at the 96% confidence
level, a three times higher binary occurrence in TMC compared to Orion for component separations
in the range of 63-225 AU.
Also, TMC cloud cores are comparatively small and of low
mass, at least when compared with cores in Orion or Perseus (Kun 1998).
Initially, TMC was also found to be deficient of lowest-mass stars and brown dwarfs, with a mass
distribution significantly enriched in 0.5-1 M![]() stars, compared to Orion samples
(Briceño et al. 2002; Luhman 2000). It was speculated that the formation of brown dwarfs could be different
in the low-density environment of TMC compared to the dense packing of stars in Orion. However, a new wide-field
search for low-mass TMC members now indicates that there is no BD deficit in Taurus (Guieu et al. 2006).
stars, compared to Orion samples
(Briceño et al. 2002; Luhman 2000). It was speculated that the formation of brown dwarfs could be different
in the low-density environment of TMC compared to the dense packing of stars in Orion. However, a new wide-field
search for low-mass TMC members now indicates that there is no BD deficit in Taurus (Guieu et al. 2006).
In X-rays, Taurus has again played a key role in our understanding of high-energy processes and circumstellar magnetic fields around pre-main sequence stars. Taurus X-ray studies provided the first detailed view of the X-ray behavior of T Tauri stars (Walter & Kuhi 1981; Feigelson & Kriss 1981; Feigelson & DeCampli 1981). Among the key surveys of the entire region are those by Feigelson et al. (1987), Walter et al. (1988), Bouvier (1990), Strom et al. (1990), Damiani & Micela (1995), Damiani et al. (1995), based on Einstein Observatory observations, and the work by Strom & Strom (1994), Neuhäuser et al. (1995), and Stelzer & Neuhäuser (2001) based on ROSAT. These surveys have characterized the overall luminosity behavior of TTS and studied the dependence of X-ray activity on rotation. Bally et al. (2003) and Favata et al. (2003) reported, respectively, Chandra and XMM-Newton studies of the L1551 cloud region (the longer exposure from XMM-Newton will be included in our survey; the Chandra exposure contains no additional sources).
But again, for reasons very poorly understood, TMC differs from other SFRs significantly also with regard to X-ray properties. Whereas no X-ray activity-rotation correlation (analogous to that in main-sequence stars) is found for samples in the Orion star-forming regions, perhaps suggesting that all stars are in a saturated state (Preibisch et al. 2005; Flaccomio et al. 2003a), the X-ray activity in TMC stars has been reported to decrease for increasing rotation period (e.g., Neuhäuser et al. 1995; Stelzer & Neuhäuser 2001; Damiani & Micela 1995). Also, claims have been made that the X-ray behavior of TMC CTTS and WTTS is significantly different, CTTS being less luminous than WTTS (Damiani et al. 1995; Neuhäuser et al. 1995; Strom & Strom 1994; Stelzer & Neuhäuser 2001). This contrasts with other star-forming regions (Preibisch & Zinnecker 2001; Flaccomio et al. 2000), but recent reports reveal a similar segregation also for Orion and some other SFRs (Preibisch et al. 2005; Flaccomio et al. 2003b). Some of these discrepancies may be due to selection and detection bias (e.g., WTTS are predominantly identified in X-ray studies, in contrast to CTTS), but also to incomplete samples due to high detection limits. Issues related to rotation and selection biases will be discussed in detail in one of the companion papers, see Briggs et al. (2007).
The scientific goals of XEST are:
XEST is a wide-field X-ray survey obtained with the XMM-Newton X-ray observatory, principally based on combined CCD camera exposures, but complemented by exposures of a few bright targets with the reflection grating spectrometers and fields observed with the optical monitor. A few complementary observations obtained with the Chandra X-Ray Observatory have also been included.
XMM-Newton (Jansen et al. 2001) orbits the Earth in a 48 hr orbit, permitting long,
uninterrupted exposures. It carries three high-throughput telescopes feeding two
suites of X-ray instruments, and also features an optical telescope. A short description
of the instruments and the chosen setups follows.![]()
i) The European Photon Imaging Cameras (EPICs) are three CCD-based X-ray cameras,
one per telescope, that operate entirely independently. Two cameras are of the MOS type
(Turner et al. 2001), and one is of the PN type (Strüder et al. 2001). The circular field of view of
each camera has a diameter of 30![]() ,
and the three telescopes are nearly co-aligned. The PN camera
provides
most counts because the beams to the MOS cameras are intersected by the reflection gratings
that consume approximately half of the X-ray flux. The MOS PSF has a full-width-at-half-maximum
(FWHM) of about 4-5
,
and the three telescopes are nearly co-aligned. The PN camera
provides
most counts because the beams to the MOS cameras are intersected by the reflection gratings
that consume approximately half of the X-ray flux. The MOS PSF has a full-width-at-half-maximum
(FWHM) of about 4-5
![]() ,
while the half-energy width (HEW) is larger, amounting to
some 13-15
,
while the half-energy width (HEW) is larger, amounting to
some 13-15
![]() .
The cameras provide pixel sizes of 1.1
.
The cameras provide pixel sizes of 1.1
![]() (MOS)
or 4
(MOS)
or 4
![]() (PN). The energy resolution is approximately
(PN). The energy resolution is approximately
![]() at 6.7 keV,
scaling as E-1/2. To prevent the spectra from
being altered by optical load, various filters can be inserted.
at 6.7 keV,
scaling as E-1/2. To prevent the spectra from
being altered by optical load, various filters can be inserted.
We usually
applied the medium filter to all EPIC cameras, providing a combined on-axis effective area for
all three cameras of ![]() 1800 cm2 at 1.5 keV. Exceptions were exposure XEST-26 for
which the thick filter was used for the two MOS cameras to suppress optical load
from the Herbig star AB Aur (the PN camera was not recording), and
exposures XEST-27 and XEST-28 for which the thick filter was used for each EPIC camera.
All cameras were operated in full window mode, i.e., the entire field of view was exposed,
confining the time resolution to 2.6 s for the MOS and to 73 ms for the PN camera, entirely
appropriate for the moderate brightness of our sources. The only exceptions here were the fields
around V773 Tau (XEST-20) where MOS2 was operated in the small-window mode, and the field
of T Tau (XEST-01) for which MOS1 was operated in small-window mode, and MOS2 was operated in large-window
mode. These modes confine the central CCD to
1800 cm2 at 1.5 keV. Exceptions were exposure XEST-26 for
which the thick filter was used for the two MOS cameras to suppress optical load
from the Herbig star AB Aur (the PN camera was not recording), and
exposures XEST-27 and XEST-28 for which the thick filter was used for each EPIC camera.
All cameras were operated in full window mode, i.e., the entire field of view was exposed,
confining the time resolution to 2.6 s for the MOS and to 73 ms for the PN camera, entirely
appropriate for the moderate brightness of our sources. The only exceptions here were the fields
around V773 Tau (XEST-20) where MOS2 was operated in the small-window mode, and the field
of T Tau (XEST-01) for which MOS1 was operated in small-window mode, and MOS2 was operated in large-window
mode. These modes confine the central CCD to
![]() and
and
![]() pixels,
respectively, compared to
pixels,
respectively, compared to
![]() pixels for the full window mode, but avoiding
pile-up during potential large flares.
pixels for the full window mode, but avoiding
pile-up during potential large flares.
ii) Two Reflection Grating Spectrometers (RGS, den Herder et al. 2001) are each fed by about
50% of the light of one of the telescopes. The dispersed spectra comprise the wavelength
range from 5 to 35Å, although in each spectrometer, one of the nine chips has failed
earlier in the mission, leaving a gap in the 10.6-13.8 Å range for RGS1 and in the
20.0-24.1 Å range for RGS2. The first-order spectral resolution is approximately
60-70 mÅ (FWHM) at any wavelength, corresponding to
![]() at
at
![]() Å. The combined first-order effective area is
Å. The combined first-order effective area is
![]() cm2
at 15 Å.
cm2
at 15 Å.
iii) The Optical Monitor (OM, Mason et al. 2001) is a microchannel-plate enhanced CCD camera
fed by a 30 cm mirror co-aligned with the EPIC cameras. Its square field of view is, however,
somewhat smaller than the latters', amounting to 17![]() side-length, i.e., a radius
of 12
side-length, i.e., a radius
of 12![]() along the diagonal. The OM can be used in combination with various filters.
Filter use may be dictated by the brightness of the stars in the field of view. We obtained
most of the exposures with the U band filter inserted, given the diagnostic importance of this band for
both chromospheric flare processes and accretion mechanisms. In a few cases, another
near-UV filter was used (UVW1: 2500-3500 Å; UVW2: 1700-2500 Å) to suppress excessive optical load. The window
mode we applied essentially observed the entire field of view. The detector area is split up into
a series of windows, some of which are sequentially exposed and read out. The exposure time for one
of these frames determines the time resolution for any source within the window. This time
resolution is of order 1000-2000 s but varies within any given XEST OM field, and is also not identical
between different XEST fields. A detailed presentation is given by Audard et al. (2007). Additionally, if
a bright source was present on-axis, the central
along the diagonal. The OM can be used in combination with various filters.
Filter use may be dictated by the brightness of the stars in the field of view. We obtained
most of the exposures with the U band filter inserted, given the diagnostic importance of this band for
both chromospheric flare processes and accretion mechanisms. In a few cases, another
near-UV filter was used (UVW1: 2500-3500 Å; UVW2: 1700-2500 Å) to suppress excessive optical load. The window
mode we applied essentially observed the entire field of view. The detector area is split up into
a series of windows, some of which are sequentially exposed and read out. The exposure time for one
of these frames determines the time resolution for any source within the window. This time
resolution is of order 1000-2000 s but varies within any given XEST OM field, and is also not identical
between different XEST fields. A detailed presentation is given by Audard et al. (2007). Additionally, if
a bright source was present on-axis, the central
![]() of the OM field were
exposed within a high-time resolution window that collects photons with a time resolution of 0.5 s.
of the OM field were
exposed within a high-time resolution window that collects photons with a time resolution of 0.5 s.
Our initial project collected 19 fields in the TMC coherently with exposure times of about 30 ks each. The effective exposure time varied between 31.2 ks and 41.9 ks. Relevant information is given in Table 1. The start and end times of the observations as listed in Table 1 are the times of the earliest and latest recording of any of the three EPIC cameras, and the quoted exposure time is the difference between end and start times. The pointing coordinates are the nominal boresight coordinates, which are not identical with the coordinates of the center of the EPIC fields of view, the latter being slightly misaligned (e.g., to avoid the PN CCD edges crossing the exact field center). The last column gives the filter used for the OM (U band, or one of the ultraviolet filters, UVW1 or UVW2). A letter F indicates that the central star was recorded in fast mode (see Audard et al. 2007).
Table 1: Observing log of XEST program.
Table 2: Complementary Chandra observations.
The fields of view were selected such that they cover the densest
concentrations of CO gas, which also show the strongest accumulations of TMC stellar and substellar
members. We complemented this sample with exposures that were obtained as part of separate
projects, partly retrieved from the XMM-Newton archive (marked in Table 1);
in all of these observations very similar instrument setups were used,
although in most cases the exposure times were longer and the strategies for the use of the OM were
different. The eight additional fields are:
1) L1495 centered at V410 Tau (XEST exposures 23 and 24, see Table 1; two exposures totaling 117.9 ks; PI F. Walter);
2) L1551, centered near L1551 IRS-5 (XEST exposure 22, 56.9 ks, PI F. Favata);
3) a field centered at AA Tau (eight exposures of 16-19.5 ks each of which we use only one [XEST exposure 25]
that reveals the strongly variable AA Tau X-ray source in an average state - details in
Grosso et al., in preparation; PI J. Bouvier);
4) a field centered at HD 283572 (XEST exposure 21, 46.2 ks, PI R. Pallavicini);
5) a field around BP Tau (XEST exposure 28, 131.3 ks, PI J. Schmitt);
6) a field around SU Aur (XEST exposure 26, 129.6 ks, PI R. Pallavicini);
7) a field around ![]() Per (XEST exposure 27, 43.4 ks, PI W. Waldron);
8) a field around T Tau (XEST exposure 1, 83.0 ks - a special discussion of this observation
is given by Güdel et al. (2007c);
PI M. Güdel).
The entire survey includes approximately 5 sq. degrees in total, with a total exposure time
of about 1.3 Ms. The spatial coverage is illustrated in Fig. 1.
Per (XEST exposure 27, 43.4 ks, PI W. Waldron);
8) a field around T Tau (XEST exposure 1, 83.0 ks - a special discussion of this observation
is given by Güdel et al. (2007c);
PI M. Güdel).
The entire survey includes approximately 5 sq. degrees in total, with a total exposure time
of about 1.3 Ms. The spatial coverage is illustrated in Fig. 1.
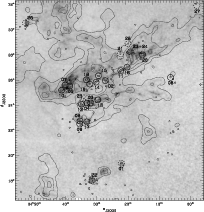 |
Figure 1:
Map of the TMC region (oriented in RA - dec, north is up, east to the left). The grayscale background
map is an extinction ( |
| Open with DEXTER | |
We have included a few exposures obtained by Chandra that contain important objects outside the XMM-Newton coverage, or faint objects not detected by XMM-Newton but detected by Chandra. Objects that were covered by the XEST program (regardless of their detection status) and were not detected in these Chandra exposures will not be reported in our survey tables. The additional fields are defined in Table 2. Note that different detectors were used for these observations. The entire fields of view were scanned for TMC objects that add to the project, but no systematic survey of all X-ray sources in the fields was performed. The exposure around GV Tau does not contain new sources beyond those detected in the XMM-Newton field but provides better angular resolution for the study of the origin of the X-rays in this binary system (Güdel et al. 2007b). We also add the strong X-ray detection coincident with HD 28867 = HR 1442 that has been suspected to be a late-B (non-Herbig) binary member of the TMC (e.g., Walter & Boyd 1991). This object has been extensively studied by Walter et al. (2003) who found evidence for a G-type companion to one of the B-type components.
The XEST work presented here and in the accompanying papers addresses X-ray properties of the commonly known stellar and substellar population. A considerable number of hitherto unrecognized Taurus members may be present in the survey, e.g., deeply embedded sources or extincted stars on the far side of the clouds. An attempt to identify some objects of this population has been undertaken by Scelsi et al. (2007).
Our XMM-Newton data analysis procedure predominantly uses tasks provided in the XMM-Newton Science Analysis Software (SAS) v6.1.0, augmented by procedures in FTOOLS, and is tied together in Perl scripts developed at the Paul Scherrer Institut. Source identification was based on procedures involving maximum-likelihood algorithms and wavelet analysis. In order to optimize detection of faint sources, periods of high background radiation levels due to local particles were cut out. All programs named below can be assumed to be SAS tasks unless otherwise noted.
An event list was produced for each active EPIC instrument from the original data files using the standard SAS procedures EPCHAIN and EMCHAIN. MOS event lists were filtered to include only events flagged as `good' and with patterns 0-12 (Kirsch 2006). PN event lists were filtered using the selection expression (FLAG & 0xfb0825) =0, which rejects events with patterns >12, close to CCD windows or on-board bad pixels, in spoiled frames, or outside the field of view, but retains events on or next to offset columns, close to bright pixels or dead pixels. Remaining bright pixels, columns and partial columns observed in images at energies >300 eV were further added to the bad pixel list and rejected.
Source detection was performed in three energy bands: soft
(500-2000 eV), hard (2001-7300 eV) and full (500-7300 eV). These
were chosen with consideration of the energy-dependent sensitivity of
the EPIC instruments, the expected spectra of our sources of interest,
the energies of strong fluorescent spectral features from the detectors
(particularly Ni, Cu and Zn K![]() at energies 7.3-9 keV), and
compatibility of count-rates and fluxes derived therefrom with those
quoted using previous and current instruments for X-ray astronomy.
We give an outline of the source detection procedure here and describe
each stage in more detail below.
at energies 7.3-9 keV), and
compatibility of count-rates and fluxes derived therefrom with those
quoted using previous and current instruments for X-ray astronomy.
We give an outline of the source detection procedure here and describe
each stage in more detail below.
For each EPIC instrument and energy band:
In almost every observation the background count-rate was highly variable,
by factors up to several hundred![]() . To optimize sensitivity to
the detection of faint sources, it was necessary to exclude intervals
of highest background count-rate. Good time intervals (GTIs) were defined
independently for each instrument and energy band as follows.
. To optimize sensitivity to
the detection of faint sources, it was necessary to exclude intervals
of highest background count-rate. Good time intervals (GTIs) were defined
independently for each instrument and energy band as follows.
A light curve was extracted of the whole active detector area (excluding bright
sources, as described in the creation of background maps, below) with
a binning of 52 s, scaled to a 1 sq. arcsec area, and ordered by increasing
count-rate. Its cumulative distribution was made and the source
count-rate required to give a ![]() detection in a circular region
of 15 arcsec
detection in a circular region
of 15 arcsec![]() was
calculated for each bin, and the minimum was found. This defined the
maximum background count-rate accepted, and hence the good time
intervals (see Fig. 2). In some observations, the source
count-rate required for a
was
calculated for each bin, and the minimum was found. This defined the
maximum background count-rate accepted, and hence the good time
intervals (see Fig. 2). In some observations, the source
count-rate required for a ![]() detection is a factor three higher
than would be expected for a 30-ks observation performed with
background at the quiescent level. The total accepted good exposure
times for the full energy band for each instrument in each observation
are listed in Table 3.
detection is a factor three higher
than would be expected for a 30-ks observation performed with
background at the quiescent level. The total accepted good exposure
times for the full energy band for each instrument in each observation
are listed in Table 3.
![\begin{figure}
\par\includegraphics[width=8.5cm]{5724fig2.ps}\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg41.gif) |
Figure 2:
The selection of good time intervals to reject times affected by
high background and so optimize sensitivity to the detection of faint sources.
The background count rate per unit area in the 0.5-7.3 keV energy band is
shown in the top panel. The expected quiescent background level in this band is
marked by the green dot-dashed lines. The bottom panel shows the background
count-rate sorted in ascending order. The middle panel shows as a function of
accumulated good exposure time the minimum source count-rate that will give a
4 |
| Open with DEXTER | |
An image was created for each instrument and each
energy band, in sky coordinates with pixel size
![]() ,
using data in good time intervals only. The intrinsic pixel sizes
of the PN and MOS detectors are 4
,
using data in good time intervals only. The intrinsic pixel sizes
of the PN and MOS detectors are 4
![]() and 1.1
and 1.1
![]() ,
respectively. In
processing, a randomization of the event position within a pixel is
performed to avoid fixed pattern noise. 2
,
respectively. In
processing, a randomization of the event position within a pixel is
performed to avoid fixed pattern noise. 2
![]() was simply found to
provide much better separation of close sources than 4
was simply found to
provide much better separation of close sources than 4
![]() .
.
For each energy band, the images from the three detectors were
mosaicked to use the full sensitivity of the combined EPIC cameras.
The relative astrometry of the EPIC detectors is less than
1.5
![]() ,
so we applied no offset between the images.
,
so we applied no offset between the images.
An exposure map was generated for each image using EEXPMAP. A summed exposure map was also produced for each energy band, but first MOS exposure maps were scaled to account for the lower sensitivity compared with the PN. The scaling factors used were 0.370, 0.345 and 0.385 in the full, soft and hard bands, respectively: these factors are strictly dependent on the individual source spectrum; the values used are median values found for all sources detected in the first 12 analyzed observations. The count rates resulting from our source detection are therefore approximate PN-equivalent count rates.
A background map was created for each image: each instrument and energy
band. The basic method was to mask out regions of the image affected
by source counts and apply a 2D Gaussian smoothing filter of
![]() .
The background map was produced in three iterations which successively
improved the source parameterization and hence the mask. We first used
the SAS wavelet transform algorithm EWAVELET to locate and approximately
parameterize sources. The resultant source list and background map were
input into the maximum-likelihood fitting algorithm EMLDETECT to produce
an improved background which was input into a second
run of EMLDETECT to produce the final background map.
The mask, produced using REGION, masked out each source with
an elliptical area, whose eccentricity reflected the shape of the
point-spread function at the source position and whose size reflected
the number of source counts.
Smoothing was performed using ASMOOTH.
EMLDETECT outputs an image of the parameterized sources, which was
masked and smoothed in the same way as the image and subtracted from
the background to remove the effect of remaining source counts in the
background map.
Out-of-time events (OOTEs) in PN images were modeled into the background
map. An image of OOTEs was created
.
The background map was produced in three iterations which successively
improved the source parameterization and hence the mask. We first used
the SAS wavelet transform algorithm EWAVELET to locate and approximately
parameterize sources. The resultant source list and background map were
input into the maximum-likelihood fitting algorithm EMLDETECT to produce
an improved background which was input into a second
run of EMLDETECT to produce the final background map.
The mask, produced using REGION, masked out each source with
an elliptical area, whose eccentricity reflected the shape of the
point-spread function at the source position and whose size reflected
the number of source counts.
Smoothing was performed using ASMOOTH.
EMLDETECT outputs an image of the parameterized sources, which was
masked and smoothed in the same way as the image and subtracted from
the background to remove the effect of remaining source counts in the
background map.
Out-of-time events (OOTEs) in PN images were modeled into the background
map. An image of OOTEs was created![]() and smoothed only along
the CCD readout direction, subtracted from the true image before
source detection and smoothing, and added to the resulting background map.
Where a central MOS CCD observed a bright source in a window mode such that no reliable background
level could be assessed from this CCD, the
background in that CCD was estimated as 1.15 times the mean background
in the other CCDs, as measured from MOS observations in full frame mode
lacking a bright central source.
For each energy band, we mosaicked the background maps from all EPIC detectors.
and smoothed only along
the CCD readout direction, subtracted from the true image before
source detection and smoothing, and added to the resulting background map.
Where a central MOS CCD observed a bright source in a window mode such that no reliable background
level could be assessed from this CCD, the
background in that CCD was estimated as 1.15 times the mean background
in the other CCDs, as measured from MOS observations in full frame mode
lacking a bright central source.
For each energy band, we mosaicked the background maps from all EPIC detectors.
Source candidates in the mosaicked EPIC image in each energy band were
located using two wavelet transform algorithms: the SAS task EWAVELET, and
PWXDETECT developed at the Osservatorio Astronomico di Palermo (Damiani et al. 1997).
In PWXDETECT the wavelet transform (WT) is obtained from the rate image (image/exposure map) r(x,y) as:
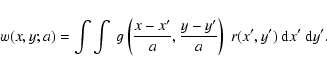 |
(1) |
Since sources are defined as local maxima in the WT space, thresholds for
detection at a given confidence level must be assessed for each field and each
band. This is obtained by means of extensive simulations on summed PN and MOS
images containing only background photons. The number of background photons in
each simulated PN or MOS image is evaluated from the observed image relevant to
that band, instrument and field. To avoid rejecting possible source
candidates, unconservative thresholds were adopted so as to give about 150 spurious
detections due to
background fluctuations, per band and per field. These simulations were also used to
assess the number of false detections expected after maximum likelihood fitting of the
candidate sources (see below). EWAVELET uses a similar methodology and we used a
similarly low detection significance threshold of ![]() .
For each algorithm the source lists in the three bands were merged to
create a single list input to EMLDETECT.
.
For each algorithm the source lists in the three bands were merged to
create a single list input to EMLDETECT.
Source candidates were parameterized in the three energy bands simultaneously via maximum likelihood fitting of the spatially-varying point spread function (PSF) using EMLDETECT. The free fit parameters were the source location, fixed to be the same in all energy bands, and the count rate in each energy band.
We retained detections with maximum likelihood ML > 8 in at least one band. Extensive tests of simulated blank-field EPIC images have demonstrated that we expect approximately 1.5 false detections per full-band image due to background fluctuations alone.
Detections were overplotted on the image and examined by eye. Obvious false detections, e.g. in the wings of the point spread function of bright sources, were removed and the maximum likelihood fitting repeated.
This procedure was run using the EWAVELET candidate list and the PWXDETECT candidate list. The two source lists were merged, adding 0-5 extra sources per observation, and the maximum likelihood fitting repeated.
For each source, the parameters fitted by EMLDETECT were retained in each band where the source was detected with ML > 5, else upper limits were calculated at the 95 per cent confidence level using the prescription of Kraft et al. (1991).
2MASS counterpart positions were used to correct X-ray source
positions for systematic shifts; this boresight correction was made
iteratively. First, we cross-correlated the XEST catalog and the
2MASS All-Sky Catalogue of Point Sources (Cutri et al. 2003),
using a 5
![]() correlation radius and keeping only the
minimum-distance match to compute the XEST-2MASS position
offsets. The XEST positions were corrected by subtracting the median
position offset. Then, we repeated this correction process, using a
3.5
correlation radius and keeping only the
minimum-distance match to compute the XEST-2MASS position
offsets. The XEST positions were corrected by subtracting the median
position offset. Then, we repeated this correction process, using a
3.5
![]() correlation radius, until the median position offset became
zero, which was obtained in a few steps. The boresight corrections are small
(0.4
correlation radius, until the median position offset became
zero, which was obtained in a few steps. The boresight corrections are small
(0.4
![]() -3.8
-3.8
![]() ), and the final residual registration error between
2MASS and XEST sources is 0.9
), and the final residual registration error between
2MASS and XEST sources is 0.9
![]() -2.2
-2.2
![]() .
.
The resultant boresight correction was
applied to the X-ray source positions. The RMS error on the boresight
shift of each field was calculated and added in quadrature to the
statistical positional error calculated for each source in that field
by EMLDETECT to give a ![]() positional error circle.
positional error circle.
We applied the same
method to OM sources using 10
![]() and 3
and 3
![]() radii. We found larger
boresight corrections (1
radii. We found larger
boresight corrections (1
![]() -8
-8
![]() )
but with residual registration
errors lower than 1.6
)
but with residual registration
errors lower than 1.6
![]() .
.
To assess membership in TMC of the detected X-ray sources, we compiled a comprehensive membership catalog mostly based on the following references: Cohen & Kuhi (1979), Kenyon & Hartmann (1995), Briceño et al. (1998), White & Ghez (2001), Briceño et al. (2002), Hartmann (2002), Hartigan & Kenyon (2003), Luhman et al. (2003), Luhman (2004), Luhman (2006), White & Hillenbrand (2004), Andrews & Williams (2005), and Guieu et al. (2006). The catalog was subsequently used to decide which X-ray sources to use for the physical interpretation, and to assess which TMC members remained undetected. The adopted coordinates (mostly from 2MASS) are described in more detail below (Sect. 5.2.1).
Source events were extracted from circular regions centered on the
EMLDETECT source positions. Although the off-axis PSF is
obviously elongated, there is currently no available parameterization
of an elliptical form of the PSF and the enclosed energy correction
calculated by the SAS task ARFGEN in creating the ancillary response
file is not energy dependent unless a circular source extraction
region is used. We calculated the source extraction radius that
maximized the source signal-to-noise ratio in the full energy band
using: the total number of source counts derived by EMLDETECT for the full-band
mosaicked EPIC image, the expected number of background counts per unit area
in the source region, calculated from the full-band EPIC background
map, and the circularly-symmetric EPIC PSF formulation of
Ghizzardi et al. (2002). The SAS task REGION was used to
calculate smaller extraction radii in cases where nearby contaminating
sources existed. The source extraction radius was constrained to be
between 8
![]() and 60
and 60
![]() .
.
Annular background extraction regions were calculated by the REGION task, with inner radii calculated such that the source count density (counts per sq. arcsec) had fallen to 30 per cent of the local background count density. The task excluded neighboring sources using the same criterion. The outer radius was simply 3 times the inner radius. For each case where a source of interest was clearly contaminated by counts from a neighboring source, the background region was individually defined to account for these, as an annulus around the contaminating source with inner and outer radii exactly enclosing the extraction region of the source of interest (with the source itself excluded with a larger circle), or as a number of circles within this annulus of identical size to the extraction region of the source of interest, chosen to avoid other nearby sources.
The same source and background regions were used for the extraction of PN and MOS products. Background products were scaled by the ratio of active detector area in the source region to that in the background region.
Light curves and spectra were extracted for all sources identified as members of Taurus-Auriga, for all other sources with more than 150 EPIC counts (see e.g. Scelsi et al. 2007), and all other sources detected by the Optical Monitor (Audard et al. 2007).
Light curves were extracted for each instrument in the full-band only and used all available exposure time. Time intervals affected by high background were not excluded as intrinsic source variability can still be detected in these times. Also, the background flares provide a sensitive test of the reliability of the background subtraction.
The active exposure time in each bin was calculated, accounting for intervals when the instrument (or CCD) was not live, which are frequent when the instrument experiences high event rates during background flares. The background light curve was corrected for differences in active exposure
The time bin size was calculated such that the average number of EPIC source counts in each bin was 20. However, the minimum bin size was fixed to 100 s to produce easily-viewed plots and the maximum bin size was fixed to 1000 s, the timescale on which flares are typically observed, to avoid short bright flares on faint sources being smoothed out. The same bin size was used for PN and MOS light curves to enable simple summation to form an EPIC light curve.
The light curves often have few counts per bin, in which case the
traditional approach - calculating the source counts as T - B, where
T is the total number of counts in the source extraction region and B
is the number of expected background counts, with a symmetric ![]() uncertainty calculated by propagating
uncertainty calculated by propagating ![]() errors - breaks down.
We used the Bayesian approach of Kraft et al. (1991) to
calculate the most-likely source count-rate and the 68 percent confidence
interval in each bin with fewer than 20 net source counts or where the
traditional
errors - breaks down.
We used the Bayesian approach of Kraft et al. (1991) to
calculate the most-likely source count-rate and the 68 percent confidence
interval in each bin with fewer than 20 net source counts or where the
traditional ![]() uncertainty extended below zero.
uncertainty extended below zero.
We also calculated a summed EPIC light curve. The counts in the PN, MOS1 and MOS2 source light curves were summed, as were those in the background light curves, and the net source light curve was calculated as described above. A PN-effective count rate was calculated for each bin by scaling the MOS active exposure time by the factor 0.370 (see above) and dividing the summed net counts by the sum of active exposure times in each bin. Two example light curves are shown in Fig. 3, one containing a strong flare (IQ Tau = XEST-14-006), and one containing some low-level activity (V807 Tau = XEST-04-012) seen in most stellar light curves in XEST.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm]{5724fig3a.ps}\vskip 0.3truecm
\includegraphics[angle=-90,width=8.8cm]{5724fig3b.ps}\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg51.gif) |
Figure 3: Two X-ray light curves, summed from all three EPIC detectors in the energy range 0.5-7.3 keV. The total count rate has been re-normalized to the effective area of the PN. The upper panel shows IQ Tau = XEST-14-006 that flared strongly in the second half of the observation. The low-level episode used for spectral fitting was defined to cover the first 18 ks (bin size: 250 s). The lower panel shows V807 Tau = XEST-04-012, exhibiting low-level flaring variability seen in most XEST objects (bin size: 150 s). Here, all data were used for the spectral fits. |
| Open with DEXTER | |
Source and background spectra were produced for each instrument using data in the GTIs used for source detection. This may be too conservative for some bright sources, but in trying to extract products automatically for sources with a wide range of count-rates, this is most straightforward. For sources whose light curves showed clear flares we also excluded times of flaring emission where possible, as we aimed to avoid measuring properties of a source in a temporary peculiar state.
PN spectra were extracted using events with patterns 0-4, as the spectral response is not calibrated for higher patterns. Ancillary responses files (ARFs) were produced for each source spectrum using the SAS task ARFGEN. We used the canned response matrix files (RMFs) appropriate for SAS v6.1.0. For each source spectrum we used the PN RMF appropriate for patterns 0-4, the observing mode and the source position on the CCD, and MOS RMFs appropriate for Imaging mode, patterns 0-12, and the orbit (date) of observation.
Three examples of EPIC PN spectra are shown in Fig. 4 together with the best DEM fits (see below).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm]{5724fig4a.ps}\vskip 0...
...skip 0.3truecm
\includegraphics[angle=-90,width=8.6cm]{5724fig4c.ps}\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg52.gif) |
Figure 4:
Three example CCD spectra from the EPIC PN camera. All spectra extracted from the source position were binned to a minimum
of 15 cts per bin. The histograms show the best fits derived from DEM fits.
Top: Hubble 4 = XEST-23-056, an X-ray strong WTTS with modest absorption (total of 27648 cts in EPIC,
|
| Open with DEXTER | |
An example of a rich EPIC field in L1495, centered at V410 Tau, is displayed in Figure 5,
showing a particularly deep observation within our survey.
A typical exposure of ![]() 30 ks duration with an average background contamination level reached a detection
threshold of
30 ks duration with an average background contamination level reached a detection
threshold of ![]()
![]() erg s-1 on-axis and
erg s-1 on-axis and ![]()
![]() erg s-1 at 10
erg s-1 at 10![]() off-axis for an X-ray
source with a thermal spectrum characteristic of T Tau stars (see below) subject to
a hydrogen absorption column density of
off-axis for an X-ray
source with a thermal spectrum characteristic of T Tau stars (see below) subject to
a hydrogen absorption column density of
![]() cm-2. This
threshold turns out to be appropriate to detect essentially every
T Tau star in the surveyed fields. The precise detection limits depend on the level of
particle background contamination (hence the exposure time obtained during low background
radiation), and the off-axis angle. The effective area drops to about 50% at 10
cm-2. This
threshold turns out to be appropriate to detect essentially every
T Tau star in the surveyed fields. The precise detection limits depend on the level of
particle background contamination (hence the exposure time obtained during low background
radiation), and the off-axis angle. The effective area drops to about 50% at 10![]() distance from the center and to 35% at the border of the detectors (15
distance from the center and to 35% at the border of the detectors (15![]() distance).
distance).
 |
Figure 5:
Example of an XMM EPIC image (the field around V410 Tau = L1495).
The field diameter is 30 |
| Open with DEXTER | |
A typical XEST exposure contained between 50 and 100 X-ray point sources (Table 3) of which, however, a minority (of order 10) are known TMC stellar members. The remainder are probably mostly extragalactic sources, but a non-negligible contribution may be defined by as yet unidentified new TMC members that may be embedded or be located behind the molecular cloud complex (see Scelsi et al. 2007 for a detailed study).
The few exposures obtained with Chandra were reduced using standard strategies for ACIS,
while we used the standard, reduced events file for the HRC-I observation around HR 1442.
The ACIS-S observations of the fields around DG Tau and FS Tau used the "Very Faint Mode'' of ACIS, while those around
the fields of GV Tau, V410 Tau, L1527 used the "Faint Mode''.
The data were reduced in CIAO vers. 3.3.0.1 following the standard analysis
threads![]() . These procedures
included, for ACIS, corrections for charge transfer inefficiency and afterglow, and selection
of good time intervals. Spectra were extracted from level 2 event
files with DMEXTRACXT, and response and ancillary response files were generated with the
MKRMF and MKARF tasks, respectively. We re-emphasize that these data are
added here as they provide information on some objects undetected by XMM-Newton,
but the observations have been obtained with rather different exposure times, and the
detectors in use vary (ACIS-S, ACIS-I, HRC-I). Some of the objects were at large off-axis
angles and were thus subject to severe distortion (PSF FWHM up to several arcseconds). The data
quality, e.g., positional accuracy or spectral information, is therefore very inhomogeneous for
this sample.
. These procedures
included, for ACIS, corrections for charge transfer inefficiency and afterglow, and selection
of good time intervals. Spectra were extracted from level 2 event
files with DMEXTRACXT, and response and ancillary response files were generated with the
MKRMF and MKARF tasks, respectively. We re-emphasize that these data are
added here as they provide information on some objects undetected by XMM-Newton,
but the observations have been obtained with rather different exposure times, and the
detectors in use vary (ACIS-S, ACIS-I, HRC-I). Some of the objects were at large off-axis
angles and were thus subject to severe distortion (PSF FWHM up to several arcseconds). The data
quality, e.g., positional accuracy or spectral information, is therefore very inhomogeneous for
this sample.
For the spectral analysis, the MOS spectra provide little or no additional constraints for the
many fainter sources, with a total count rate smaller than the count rate of the PN. To
keep our analysis as uniform as possible, we therefore used only the PN spectrum for
our spectral fits. Exceptions are those sources for which the PN data were not
available, e.g., for sources whose image falls into a PN CCD gap, or for all sources
in XEST exposure 26 for which the PN was not operational.
To derive basic X-ray properties from the spectra, we followed two strategies.
First, conventional one- or two-component spectral fits (1-T or 2-T henceforth) were performed.
The two components define two plasmas with different temperatures T1,2 and emission measures EM1,2.
The latter parameters were fitted in XSPEC (Arnaud 1996) using the vapec thermal collisional
ionization equilibrium model that includes emission lines and continua. The abundances were fixed
at values typical for pre-main sequence or extremely active zero-age main-sequence stars (based on
results from Telleschi et al. 2005; Argiroffi et al. 2004; Garcia-Alvarez et al. 2005; and Scelsi et al. 2005)![]() . The spectral components were
subject to photoelectric absorption based on the Morrison & McCammon (1983) cross sections.
The equivalent hydrogen column density,
. The spectral components were
subject to photoelectric absorption based on the Morrison & McCammon (1983) cross sections.
The equivalent hydrogen column density, ![]() ,
was treated as a further fit parameter. For the
faintest sources, a 2-T fit provided too many free parameters for the information
contained in the spectrum. A 1-T fit was performed in these cases.
,
was treated as a further fit parameter. For the
faintest sources, a 2-T fit provided too many free parameters for the information
contained in the spectrum. A 1-T fit was performed in these cases.
For highly absorbed spectra, the multi-thermal fit method can become problematic because the softer component
is strongly suppressed or may not be detected at all, biasing the fits toward high
temperatures. This may further bias the total X-ray luminosity and ![]() .
We therefore, in an alternative approach,
combined several thermal components in such a way
that they describe the shape of the differential emission measure distribution (DEM) in a similar way as previously
found for nearby pre-main sequence stars or extremely active zero-age main sequence
stars (Garcia-Alvarez et al. 2005; Argiroffi et al. 2004; Telleschi et al. 2005; Scelsi et al. 2005). In short, we have adopted a model in which the DEM
shows one peak located at the temperature T0,
and two power-law distributions toward lower and higher temperatures, characterized by
their power-law indices
.
We therefore, in an alternative approach,
combined several thermal components in such a way
that they describe the shape of the differential emission measure distribution (DEM) in a similar way as previously
found for nearby pre-main sequence stars or extremely active zero-age main sequence
stars (Garcia-Alvarez et al. 2005; Argiroffi et al. 2004; Telleschi et al. 2005; Scelsi et al. 2005). In short, we have adopted a model in which the DEM
shows one peak located at the temperature T0,
and two power-law distributions toward lower and higher temperatures, characterized by
their power-law indices ![]() and
and ![]() ,
respectively. Given the poor temperature discrimination
of CCD spectra in the softer X-ray range (in particular in the presence of significant photoelectric absorption),
the power-law index on the low-temperature side was kept
fixed at a value often found for magnetically active main-sequence and pre-main sequence stars, namely
,
respectively. Given the poor temperature discrimination
of CCD spectra in the softer X-ray range (in particular in the presence of significant photoelectric absorption),
the power-law index on the low-temperature side was kept
fixed at a value often found for magnetically active main-sequence and pre-main sequence stars, namely
![]() ,
while
,
while ![]() was treated as a free parameter. The DEM was cut off at
was treated as a free parameter. The DEM was cut off at
![]() below which
EPIC is not sensitive to photons, and at
below which
EPIC is not sensitive to photons, and at
![]() above which EPIC is insensitive to temperature.
Within this range, the DEM was binned to
above which EPIC is insensitive to temperature.
Within this range, the DEM was binned to
![]() ,
i.e., 20 bins (centered at
,
i.e., 20 bins (centered at ![]() 6.0, 6.1, ...7.9)
were used. The element abundances were fixed
at the same values as those adopted for the 1- or 2-T fits. Again, the absorbing hydrogen column density
6.0, 6.1, ...7.9)
were used. The element abundances were fixed
at the same values as those adopted for the 1- or 2-T fits. Again, the absorbing hydrogen column density
![]() was also fitted to the spectrum. The final fit parameter was the normalization, defined as the EM
in the temperature bin at T0. This method thus assumes that the DEM can be described by four fit parameters, namely T0,
was also fitted to the spectrum. The final fit parameter was the normalization, defined as the EM
in the temperature bin at T0. This method thus assumes that the DEM can be described by four fit parameters, namely T0, ![]() ,
EM0, and
,
EM0, and ![]() .
We summed the EM over all EM bins used for the calculation to obtain the total EMt.
.
We summed the EM over all EM bins used for the calculation to obtain the total EMt.
We set the following
hard limits to the parameters:
![]() ,
,
![]() MK. In exceptional cases (very hard, absorbed
spectra), we extended the range for T0 to slightly higher values, although we emphasize that at such temperatures,
the dominant contribution to the spectrum is a featureless bremsstrahlung continuum, apart from the Fe K complex
at 6.7 keV.
MK. In exceptional cases (very hard, absorbed
spectra), we extended the range for T0 to slightly higher values, although we emphasize that at such temperatures,
the dominant contribution to the spectrum is a featureless bremsstrahlung continuum, apart from the Fe K complex
at 6.7 keV.
For very faint sources, such fits provide too many degrees of freedom. We thus fixed one or more
of the following parameters: ![]() ,
usually fixed at a value of -1 which is often found
for brighter sources, or
,
usually fixed at a value of -1 which is often found
for brighter sources, or ![]() ,
fixed at a value corresponding to the tabulated
,
fixed at a value corresponding to the tabulated ![]() assuming a standard
gas-to-dust ratio (after Vuong et al. 2003), or both. In a few cases, it was necessary to fix
T0 as well, usually at
assuming a standard
gas-to-dust ratio (after Vuong et al. 2003), or both. In a few cases, it was necessary to fix
T0 as well, usually at
![]() .
Finally, for non-detections with reasonably well-known
.
Finally, for non-detections with reasonably well-known ![]() ,
we derived
upper limits to
,
we derived
upper limits to ![]() as follows: We used the 95% confidence upper limits to the count rates derived at the optical or
infrared position of the star, and then adopted an
as follows: We used the 95% confidence upper limits to the count rates derived at the optical or
infrared position of the star, and then adopted an ![]() derived from
derived from ![]() .
We thus estimated the upper limit using an
average thermal model.
For brown dwarfs and very-low mass stars, we adopted
.
We thus estimated the upper limit using an
average thermal model.
For brown dwarfs and very-low mass stars, we adopted
![]() and
and
![]() ,
characteristic values found
for the detected low-mass objects. For more massive T Tau stars, we adopted
,
characteristic values found
for the detected low-mass objects. For more massive T Tau stars, we adopted
![]() and
and
![]() ,
again characteristic
values found for the detected stars. These upper limits should only be used as rough estimates. For embedded
sources, uncertain visual or infrared extinctions and the strong influence of
,
again characteristic
values found for the detected stars. These upper limits should only be used as rough estimates. For embedded
sources, uncertain visual or infrared extinctions and the strong influence of ![]() on the measured count rate
make such estimates unreliable, which will therefore not be given. As we will predominantly use the DEM-fit results,
we have not derived upper limits based on 1-T plasmas.
on the measured count rate
make such estimates unreliable, which will therefore not be given. As we will predominantly use the DEM-fit results,
we have not derived upper limits based on 1-T plasmas.
For both models, the total X-ray luminosity was computed for the energy range 0.3-10 keV based on the integration of the best-fit model. We adopted a distance of 140 pc for all objects.
The same spectral-fit procedures were applied to the Chandra ACIS data if feasible
(most of the faint sources were interpreted only with a 1-T model). For the HRC data, we assumed
a standard electron temperature of 10 MK and estimated ![]() from
from ![]() using standard interstellar
conversion ratios (Vuong et al. 2003 and references therein). The unabsorbed source flux and the
corresponding luminosity were then estimated based on the PIMMS
software
using standard interstellar
conversion ratios (Vuong et al. 2003 and references therein). The unabsorbed source flux and the
corresponding luminosity were then estimated based on the PIMMS
software![]() .
.
Tables 4 - 11 summarize basic X-ray parameters and fundamental properties of all observed TMC members. We reproduce the first ten entries per table for illustration. The entire tables with comments and references are available in the electronic version of this paper.
All tables are of identical length, each line number referring to the same observation of the same target across all tables. The tables are sorted in increasing right ascension. The first column of each table gives the XEST catalog entry. This number is composed of the two-digit code corresponding to the exposure number listed in Table 1, followed by the X-ray source number for this exposure (including every X-ray source regardless of TMC membership). This source number is `000' for X-ray non-detections of known TMC members. The second column gives a conventional name frequently used in the literature. Preference was mostly given to variable-star names if available. Note that several objects were observed twice within the principal XEST project (in particular in exposures 23 and 24). They are listed as separate entries. XEST-25 is one of a series of exposures containing the TMC member AA Tau. This star is highly X-ray variable probably due to variable absorption by its disk. We use only one observation to report the typical X-ray properties of this star. A more detailed analysis of the temporal behavior of AA Tau is given by Grosso et al. (in preparation). There are no other known TMC stellar members in this field.
The final portion of each table refers to results from the complementary Chandra
observations. Here, we list TMC objects that were either not covered by XMM-Newton, regardless of
their detection status with Chandra, or objects that were detected by Chandra but not by
XMM-Newton. We also add FS Tau because XMM-Newton observed this star during a slow flux decrease, presumably
from a flare, and Haro 6-5 B which is slightly contaminated by the wings of FS Tau A in the
XMM-Newton observation. GV Tau is added because of the higher resolution of Chandra that
attributes the flux to GV Tau A (Güdel et al. 2007b), while the embedded object Haro 6-10 B at
![]() remains undetected.
remains undetected.
Table 4: X-ray parameters of targets in XEST (1): Positions and count rates [first ten entries].
Table 5: X-ray parameters of targets in XEST (2): Plasma parameters from the DEM fits [first ten entries].
Table 6: X-ray parameters of targets in XEST (3): Plasma parameters from the 1-T and 2-T fits [first ten entries].
Table 7: Fundamental parameters of targets in XEST (1): Names and coordinates [first ten entries].
Table 8: Fundamental parameters of targets in XEST (2): Multiplicity [first ten entries].
Table 9: Fundamental parameters of targets in XEST (3): Photometry and spectroscopy [first ten entries].
Table 10: Fundamental parameters of targets in XEST (4): Age, mass, radius, rotation [first ten entries].
Table 11: Fundamental parameters of targets in XEST (5): Accretion and evolution [first ten entries].
Table 4 provides a summary of detection results for each XEST TMC member. The table lists
the detection coordinates with statistical errors and the offsets from the expected position as given
later in Table 7. For non-detections, the expected coordinates of the source is given (see below), which
were used to calculate upper limits to the count rates.
Then, the maximum likelihood (ML) is given for each detection, referring to the full (0.5-7.3 keV) band. Non-detections
show ML = 0. For the Chandra observations in Table 4, we list the "significance'' of the detection as
provided by the CIAO WAVDETECT algorithm instead of ML
![]() .
Then, we list the total number of detected EPIC counts, the effective PN-equivalent
on-axis exposure time that corrects for vignetting and also takes the (lower-sensitivity) MOS data into account,
as described above. For Chandra, these numbers refer to the respective detector used for the observations.
For XMM-Newton non-detections, the 95% upper limits are reported.
Next, the table gives the average count rate (on-axis equivalent rate for PN). Finally,
we report a variability flag from inspection of the light curves; the codes have the following meaning:
0 = no or only low-level variability, no flares visible that may dominate the X-ray spectrum;
1 = clear flaring observed and flare intervals removed in spectral fit;
2 = clear flaring observed but flare intervals not removed;
3 = slow decay of flare throughout the observation, all data used. Examples for light curves with
flag 1 (IQ Tau) and flag 0 (V807 Tau)
are shown in Fig. 3. In the former case, spectral fits were obtained using only
data during the low-level episode, defined by the first 18 ks of the light curve. A more quantitative
analysis of light curve variability and an interpretation of the role of flares in coronal heating
will be given by Stelzer et al. (2007).
.
Then, we list the total number of detected EPIC counts, the effective PN-equivalent
on-axis exposure time that corrects for vignetting and also takes the (lower-sensitivity) MOS data into account,
as described above. For Chandra, these numbers refer to the respective detector used for the observations.
For XMM-Newton non-detections, the 95% upper limits are reported.
Next, the table gives the average count rate (on-axis equivalent rate for PN). Finally,
we report a variability flag from inspection of the light curves; the codes have the following meaning:
0 = no or only low-level variability, no flares visible that may dominate the X-ray spectrum;
1 = clear flaring observed and flare intervals removed in spectral fit;
2 = clear flaring observed but flare intervals not removed;
3 = slow decay of flare throughout the observation, all data used. Examples for light curves with
flag 1 (IQ Tau) and flag 0 (V807 Tau)
are shown in Fig. 3. In the former case, spectral fits were obtained using only
data during the low-level episode, defined by the first 18 ks of the light curve. A more quantitative
analysis of light curve variability and an interpretation of the role of flares in coronal heating
will be given by Stelzer et al. (2007).
Table 5 summarizes the basic spectral-fit results from our DEM method.
The abundances were kept fixed at characteristic values as described in Sect. 4.12.
The columns provide ![]() ,
the temperature of the DEM peak, T0, the power-law index
,
the temperature of the DEM peak, T0, the power-law index ![]() of
the high-temperature DEM slope, the total EM integrated over all bins centered at values of
logT = 6.0 to logT = 7.9 in steps of
of
the high-temperature DEM slope, the total EM integrated over all bins centered at values of
logT = 6.0 to logT = 7.9 in steps of
![]() ,
and the inferred
,
and the inferred ![]() in the 0.3-10 keV range.
We list 68% (1
in the 0.3-10 keV range.
We list 68% (1![]() )
confidence ranges for
)
confidence ranges for ![]() ,
,
![]() ,
and T0 in parentheses.
For fixed parameters, no error range is given. For non-detections,
the spectral parameters used to estimate upper limits to
,
and T0 in parentheses.
For fixed parameters, no error range is given. For non-detections,
the spectral parameters used to estimate upper limits to ![]() are also given as fixed parameters.
The next columns list the logarithms of the normalized luminosities
are also given as fixed parameters.
The next columns list the logarithms of the normalized luminosities
![]() where the stellar bolometric
luminosity L* is adopted from
Table 9, and the average electron temperature that is obtained as a mean of
where the stellar bolometric
luminosity L* is adopted from
Table 9, and the average electron temperature that is obtained as a mean of ![]() over the entire DEM,
where DEM(T) is used as a weight function, calculated analytically as follows:
over the entire DEM,
where DEM(T) is used as a weight function, calculated analytically as follows:
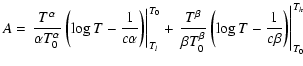 |
(2) | ||
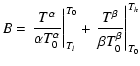 |
(3) | ||
| (4) |
Table 6 equivalently reports the results from 2-T or, for faint sources,
1-T fits. The columns give ![]() (with errors if fitted), T1, T2, and the corresponding EM1, EM2. If only one component was fitted,
its temperature and EM values are listed in the columns for T2 and EM2 if the temperature exceeds
10 MK, and in the columns for T1 and EM1 otherwise. If a temperature was held fixed, its value is preceded by a "='' sign.
Further, the table gives
(with errors if fitted), T1, T2, and the corresponding EM1, EM2. If only one component was fitted,
its temperature and EM values are listed in the columns for T2 and EM2 if the temperature exceeds
10 MK, and in the columns for T1 and EM1 otherwise. If a temperature was held fixed, its value is preceded by a "='' sign.
Further, the table gives ![]() ,
,
![]() ,
and
,
and
![]() ,
the latter defined as the EM-weighted logarithmic average
of the temperature in the case of two non-vanishing components:
,
the latter defined as the EM-weighted logarithmic average
of the temperature in the case of two non-vanishing components:
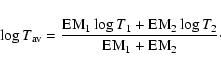 |
(5) |
Errors of EM and ![]() are difficult to compute, and their meaning is not unequivocal.
Our EM models are rather crude approximations to true emission measure distributions.
Formal error ranges for the EM values may therefore bear little relevance. Further,
are difficult to compute, and their meaning is not unequivocal.
Our EM models are rather crude approximations to true emission measure distributions.
Formal error ranges for the EM values may therefore bear little relevance. Further, ![]() is a complicated
function of the thermal emission model. Although resolved spectral features can usually be fitted sufficiently well
in a
is a complicated
function of the thermal emission model. Although resolved spectral features can usually be fitted sufficiently well
in a ![]() sense using a number of thermal components that describe the absorbed, observed spectral flux density,
the major uncertainty in
sense using a number of thermal components that describe the absorbed, observed spectral flux density,
the major uncertainty in ![]() is introduced by fitting (and correcting for)
is introduced by fitting (and correcting for) ![]() .
An instability
discussed below makes determinations of
.
An instability
discussed below makes determinations of ![]() rather uncertain once cool plasma components are subject
to large absorption while the spectrum is of modest quality. To quantify this latter effect that dominates
the uncertainty of
rather uncertain once cool plasma components are subject
to large absorption while the spectrum is of modest quality. To quantify this latter effect that dominates
the uncertainty of ![]() in many cases, we proceeded as follows. We adopted the upper and lower 1
in many cases, we proceeded as follows. We adopted the upper and lower 1![]() bounds
of
bounds
of ![]() (if
(if ![]() was a fit parameter), kept these values fixed and refitted the spectrum. The
was a fit parameter), kept these values fixed and refitted the spectrum. The ![]() values
thus determined,
values
thus determined,
![]() and
and
![]() for the lower and the upper bound, are taken to bracket the error range
of the tabulated
for the lower and the upper bound, are taken to bracket the error range
of the tabulated ![]() .
We performed this error analysis for the DEM fit method. We graphically show the magnitude
of the ratio
.
We performed this error analysis for the DEM fit method. We graphically show the magnitude
of the ratio
![]() in Fig. 6 as a function of the best-fit
in Fig. 6 as a function of the best-fit ![]() (set to
(set to
![]() cm-2for sources with
cm-2for sources with ![]() smaller than this value) and the number of
counts used in the spectral fit. Expectedly, the error range is largest for faint and strongly absorbed
sources, and smallest for bright and weakly absorbed sources. For 83 sources,
smaller than this value) and the number of
counts used in the spectral fit. Expectedly, the error range is largest for faint and strongly absorbed
sources, and smallest for bright and weakly absorbed sources. For 83 sources,
![]() and for
48 sources,
and for
48 sources,
![]() .
For 99 sources,
.
For 99 sources,
![]() and for
32 sources,
and for
32 sources,
![]() .
Gagné et al. (2004) described a similar analysis performed for errors in
.
Gagné et al. (2004) described a similar analysis performed for errors in ![]() for Chandra observations of the
for Chandra observations of the ![]() Ophiuchus Cloud, with similar conclusions.
Ophiuchus Cloud, with similar conclusions.
![\begin{figure}
{\resizebox{8.5cm}{!}{\includegraphics[clip]{5724fig6.ps}} }
\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg106.gif) |
Figure 6:
Magnitude of the error ranges for |
| Open with DEXTER | |
We note, however, that T Tau stars are manifestly variable on timescales of hours, typically within a factor of at
least two, while most of the EM errors are formally much smaller. A detailed variability analysis of all XEST sources
will be presented by Stelzer et al. (2007). Therefore, for the majority of our sources, the formal uncertainties
from the spectral fits underestimate the true uncertainty. Realistically, thus,
standard error bars of (at least) 0.3 dex should be adopted for all values of ![]() (and EM). Larger statistical
errors from spectral fits are typically found for
(and EM). Larger statistical
errors from spectral fits are typically found for
![]() cm-2 and
cm-2 and ![]() cts in the spectrum,
or in regions where cts
cts in the spectrum,
or in regions where cts
![]() .
.
Tables 7-11 identify the X-ray sources and provide a summary of the fundamental properties of the stellar systems. The parameters were extracted from the existing literature, in particular from Cohen & Kuhi (1979), Kenyon & Hartmann (1995), Briceño et al. (1998), White & Ghez (2001), Briceño et al. (2002), Hartmann (2002), Hartigan & Kenyon (2003), Luhman et al. (2003), Luhman (2004), White & Hillenbrand (2004), Andrews & Williams (2005), and Guieu et al. (2006). Several further references are listed in the bibliography summary in the table section. For the suspected late-B member of TMC, HD 28867, all basic information except for the 2MASS identification comes from Walter et al. (2003) and references therein. A short description of the table entries follows.
Table 7 lists the 2MASS catalog entry likely to be identified with the X-ray source.
For this identification, we first adopted object coordinates mostly from
Briceño et al. (2002), Luhman et al. (2003), Luhman (2004), and Guieu et al. (2006) if available, or
from SIMBAD in other cases, and then identified the closest object in the most recent 2MASS catalog version (Cutri et al. 2003)
within a circle of radius 5
![]() around this position. In three cases, no 2MASS object was found within 5
around this position. In three cases, no 2MASS object was found within 5
![]() .
The next columns of Table 7 give the nearest IRAS catalog entry, confined to a search radius of 10
.
The next columns of Table 7 give the nearest IRAS catalog entry, confined to a search radius of 10
![]() or directly identified from SIMBAD, and a selection of commonly used alternative names.
Finally, the J2000.0 coordinates refer to the adopted 2MASS identifications. If no
2MASS identification is given, the coordinates were taken from SIMBAD,
marked with '(S)' after the coordinates.
or directly identified from SIMBAD, and a selection of commonly used alternative names.
Finally, the J2000.0 coordinates refer to the adopted 2MASS identifications. If no
2MASS identification is given, the coordinates were taken from SIMBAD,
marked with '(S)' after the coordinates.
Table 8 provides binary information, i.e.,
the number of components, the approximate component
separations, and references. Note that binary components with a separation of
![]() are unresolved in XMM-Newton observations, and pairs at 5-10
are unresolved in XMM-Newton observations, and pairs at 5-10
![]() are difficult
to separate. Typically, binaries with separations up to about
are difficult
to separate. Typically, binaries with separations up to about
![]() have been recorded
as a single X-ray source (e.g., V819 Tau, but note the case of HP Tau/G2 and G3, two stars with a separation of
10
have been recorded
as a single X-ray source (e.g., V819 Tau, but note the case of HP Tau/G2 and G3, two stars with a separation of
10
![]() for which a joint spectral model was derived, while the count rates and thus the luminosities
were estimated separately based on PSF fitting).
for which a joint spectral model was derived, while the count rates and thus the luminosities
were estimated separately based on PSF fitting).
Table 9 lists spectral types, visual and J-band extinctions (![]() and AJ, respectively, the latter only
for the primary in multiple systems),
effective temperatures (
and AJ, respectively, the latter only
for the primary in multiple systems),
effective temperatures (
![]() ;
for binaries, separately given for primary and secondary if available),
and bolometric luminosities (L*) of the stars. The latter are bolometric luminosities of the
stellar photospheres derived from the optical or near-IR except in cases where only the IR bolometric
luminosity, possibly including contributions from the disk and/or the envelope, was available (these cases
are marked with "Lb'' in the reference column). In the case of binaries, L*is given for the primary and the secondary if available, and the entire system. The component and the system
values may originate from different references, which accounts for some discrepancies with regard
to the sum of the component L*. Because spectral types,
;
for binaries, separately given for primary and secondary if available),
and bolometric luminosities (L*) of the stars. The latter are bolometric luminosities of the
stellar photospheres derived from the optical or near-IR except in cases where only the IR bolometric
luminosity, possibly including contributions from the disk and/or the envelope, was available (these cases
are marked with "Lb'' in the reference column). In the case of binaries, L*is given for the primary and the secondary if available, and the entire system. The component and the system
values may originate from different references, which accounts for some discrepancies with regard
to the sum of the component L*. Because spectral types, ![]() ,
AJ, and
L* sensitively depend on the interpretation of the measured
,
AJ, and
L* sensitively depend on the interpretation of the measured
![]() and the optical
and near-infrared photometry, we attempted to use the same references for these parameters for a given star,
and opted predominantly for Briceño et al. (2002), Luhman et al. (2003) and Luhman (2004), and
Kenyon & Hartmann (1995) (in this sequence) for single stars or integrated multiple systems, and for White & Ghez (2001)
and Hartigan & Kenyon (2003) for binary components. Significant information for deeply embedded sources was
adopted from White & Hillenbrand (2004), and for
brown dwarfs from Guieu et al. (2006), Luhman et al. (2003), and Luhman (2004). Grosso et al. (2007a) rederived
and the optical
and near-infrared photometry, we attempted to use the same references for these parameters for a given star,
and opted predominantly for Briceño et al. (2002), Luhman et al. (2003) and Luhman (2004), and
Kenyon & Hartmann (1995) (in this sequence) for single stars or integrated multiple systems, and for White & Ghez (2001)
and Hartigan & Kenyon (2003) for binary components. Significant information for deeply embedded sources was
adopted from White & Hillenbrand (2004), and for
brown dwarfs from Guieu et al. (2006), Luhman et al. (2003), and Luhman (2004). Grosso et al. (2007a) rederived
![]() of some BDs from the spectral types, while we report here values as originally
published. Strict consistency
was not possible, in particular for
of some BDs from the spectral types, while we report here values as originally
published. Strict consistency
was not possible, in particular for ![]() and AJ that had to be adopted from different authors
and that are inconsistent in several cases (the second references in the last column mostly refer to
and AJ that had to be adopted from different authors
and that are inconsistent in several cases (the second references in the last column mostly refer to
![]() ).
).
Table 10 lists ages and masses, M, that we derived from
![]() and L* as listed
in Table 9 using the Siess et al. (2000) isochrones. For binaries, component ages and masses
are given if the fundamental parameters were available separately. In a few cases, we did not
find a solution from the Siess et al. (2000) tracks; if available, some masses (and ages) were therefore
taken directly from the literature (see footnotes to Table 10). The references specifically
used for
and L* as listed
in Table 9 using the Siess et al. (2000) isochrones. For binaries, component ages and masses
are given if the fundamental parameters were available separately. In a few cases, we did not
find a solution from the Siess et al. (2000) tracks; if available, some masses (and ages) were therefore
taken directly from the literature (see footnotes to Table 10). The references specifically
used for
![]() and L* are listed. Assessing the uncertainties of these parameters is
difficult because the uncertainties in
and L* are listed. Assessing the uncertainties of these parameters is
difficult because the uncertainties in
![]() and L* are usually not reported in
the literature. If multiple measurements have been reported for an object, then the agreement
was (for the TMC) within 100 K for
and L* are usually not reported in
the literature. If multiple measurements have been reported for an object, then the agreement
was (for the TMC) within 100 K for
![]() for about half of the objects, and within 150 K for two thirds.
We conservatively adopt an error of
for about half of the objects, and within 150 K for two thirds.
We conservatively adopt an error of ![]() K for
K for
![]() .
Using the Siess et al. calculations for the regions of densest population in the HRD
(
.
Using the Siess et al. calculations for the regions of densest population in the HRD
(
![]() and 3500 K with
L* = 2, 1, and 0.1
and 3500 K with
L* = 2, 1, and 0.1 ![]() ,
respectively),
we find mass uncertainties of
,
respectively),
we find mass uncertainties of ![]() (0.07-0.16)
(0.07-0.16)![]() or a fractional mass uncertainty of about
or a fractional mass uncertainty of about ![]() (10-20)%
(higher for cooler stars). An uncertainty in
(10-20)%
(higher for cooler stars). An uncertainty in
![]() also affects the age estimate, resulting in
typical deviations of
also affects the age estimate, resulting in
typical deviations of
![]() dex (factors of 1.3-1.5) from the best-fit value. The age
estimate is further affected by uncertainties in L* (while L* has little influence on the mass
estimate in the region where the evolutionary tracks are nearly vertical). We found that in the
region of
dex (factors of 1.3-1.5) from the best-fit value. The age
estimate is further affected by uncertainties in L* (while L* has little influence on the mass
estimate in the region where the evolutionary tracks are nearly vertical). We found that in the
region of
![]() K, a shift of
K, a shift of
![]() in
in ![]() results in a shift
of approximately
results in a shift
of approximately
![]() in age. For
in age. For ![]() 80% of the TMC objects with multiple
reports of L* in the literature, deviations are up to a factor of 2 (0.3 dex), but often much smaller.
We thus adopt a conservative, characteristic uncertainty of factors of 2.6-3.0 for the ages, noting that this
is a gross overestimate for many objects, while for a minority of objects, in particular for embedded
protostars with poor L* determinations, ages may become entirely unreliable.
80% of the TMC objects with multiple
reports of L* in the literature, deviations are up to a factor of 2 (0.3 dex), but often much smaller.
We thus adopt a conservative, characteristic uncertainty of factors of 2.6-3.0 for the ages, noting that this
is a gross overestimate for many objects, while for a minority of objects, in particular for embedded
protostars with poor L* determinations, ages may become entirely unreliable.
The radius, R, was calculated from
![]() ,
where
,
where
![]() erg cm-2 s-1 K-4 is the Stefan-Boltzmann
constant. Rotation periods P are given as measured by various authors. The values were taken
from Rebull et al. (2004) who give a comprehensive list of references (not reproduced here). That work includes periods
of the lower-mass sample. We have added further rotation periods (Rebull, private communication)
extracted from the same bibliography. If not available from the literature, rotation periods
were estimated as upper
limits if spectroscopic
erg cm-2 s-1 K-4 is the Stefan-Boltzmann
constant. Rotation periods P are given as measured by various authors. The values were taken
from Rebull et al. (2004) who give a comprehensive list of references (not reproduced here). That work includes periods
of the lower-mass sample. We have added further rotation periods (Rebull, private communication)
extracted from the same bibliography. If not available from the literature, rotation periods
were estimated as upper
limits if spectroscopic ![]() measurements were available (listed in Col. 9, with references in
column 10, many again referring to the tabulations and the bibliography given by Rebull et al. 2004).
In those cases,
measurements were available (listed in Col. 9, with references in
column 10, many again referring to the tabulations and the bibliography given by Rebull et al. 2004).
In those cases,
![]() ,
and the reference column for these calculated
periods contains a "C''.
,
and the reference column for these calculated
periods contains a "C''.
Table 11 provides parameters relevant for the interpretation of the evolutionary status. Column 3 lists mass accretion rates
![]() .
Accretion rates may be variable, and different indirect methods have been used by previous studies
to estimate
.
Accretion rates may be variable, and different indirect methods have been used by previous studies
to estimate ![]() ,
hence significantly discrepant values may be found in
the published literature. In those cases, we provide ranges, giving a reference for each the
minimum and maximum values reported. The same applies to the equivalent width of the H
,
hence significantly discrepant values may be found in
the published literature. In those cases, we provide ranges, giving a reference for each the
minimum and maximum values reported. The same applies to the equivalent width of the H![]() line
[EW(H
line
[EW(H![]() )], reported in Col. 5. In multiple systems, both of the above values refer to the primary star
even if, in a few cases, a separate measurement was available for a companion. We adopted this strategy
because the primary star is most likely also to be the dominant X-ray source.
)], reported in Col. 5. In multiple systems, both of the above values refer to the primary star
even if, in a few cases, a separate measurement was available for a companion. We adopted this strategy
because the primary star is most likely also to be the dominant X-ray source.
We assessed the "T Tauri'' type (classical or weak-line) based on EW as follows. For spectral types
G and K, stars with EW(H
![]() Å are defined as classical T Tauri stars (C), all other stars are weak-line T Tauri
stars (W). For early-M stars, the separation
was adopted at EW(H
Å are defined as classical T Tauri stars (C), all other stars are weak-line T Tauri
stars (W). For early-M stars, the separation
was adopted at EW(H![]() ) = 10 Å, and for mid-M type stars, we adopted EW(H
) = 10 Å, and for mid-M type stars, we adopted EW(H![]() ) = 20 Å for discrimination. For late-M stars, i.e., typically BDs, the low continuum makes a sensible definition
difficult. We will therefore not include BDs when studying differences between CTTS and WTTS, although we have
adopted the criterion described by Barrado y Navascués & Martín (2003) that defines accreting stars and BDs as those that show
) = 20 Å for discrimination. For late-M stars, i.e., typically BDs, the low continuum makes a sensible definition
difficult. We will therefore not include BDs when studying differences between CTTS and WTTS, although we have
adopted the criterion described by Barrado y Navascués & Martín (2003) that defines accreting stars and BDs as those that show
![]() greater than the chromospheric saturation limit. This criterion also supports our
classifications at earlier spectral types. Borderline cases are marked with a question mark. In such cases,
we also included other supporting evidence. For example, KPNO-Tau 14 (XEST-18-004) was classified as "W?'' (and subsequently
as "type 3'', see below)
despite one published measurement of EW(H
greater than the chromospheric saturation limit. This criterion also supports our
classifications at earlier spectral types. Borderline cases are marked with a question mark. In such cases,
we also included other supporting evidence. For example, KPNO-Tau 14 (XEST-18-004) was classified as "W?'' (and subsequently
as "type 3'', see below)
despite one published measurement of EW(H![]() )
somewhat higher than the saturation limit, because there is one report
with much lower EW(H
)
somewhat higher than the saturation limit, because there is one report
with much lower EW(H![]() ), a very low upper limit to
), a very low upper limit to ![]() ,
and no K band excess (Muzerolle et al. 2005; Luhman et al. 2003).
"C*'' denotes sources for which accretion signatures are evident, but that are embedded and share characteristics
with protostars. We have added some "C' and "W'' designations from Luhman (2004) even if the explicit EW values
were not given.
,
and no K band excess (Muzerolle et al. 2005; Luhman et al. 2003).
"C*'' denotes sources for which accretion signatures are evident, but that are embedded and share characteristics
with protostars. We have added some "C' and "W'' designations from Luhman (2004) even if the explicit EW values
were not given.
Column 8 lists the "Young Stellar Object'' (YSO) infrared class as derived from the infrared spectral energy distribution, which is thought to provide information on the presence of disks and molecular envelopes. Class 0 and I objects are protostars, Class II objects are disk-surrounded T Tau stars, whereas disk signatures are weak or absent in Class III stars. "FS'' designates "flat spectrum'' sources, intermediate between Class I and II. Most entries refer to IRAS measurements (and were mostly adopted from Kenyon & Hartmann 1995), but some recent information from Spitzer is also available (Hartmann et al. 2005). If discrepant entries are given, they are separated by a semi-colon, and so are the corresponding references in the subsequent column. References referring to the same classification are separated by a comma. Transition objects are designated by two types separated by a "/'', while for multiple systems with different component classifications, we give the two classes separated by "+''.
There is a rather good correlation between TTS type indicating presence or absence of accretion (CTTS and WTTS) and YSO infrared class (Classes II and III, respectively) indicating the presence or absence of circumstellar disks. There are, however, exceptions that may be borderline cases or in which IR companions may bias the YSO classification. We therefore adopted a final classification scheme that is predominantly based on the accretion signatures (WTTS vs. CTTS) and takes the IR classification as supporting evidence in borderline cases, except for protostars for which the IR classification is the only relevant parameter. Hence, in col. 10, "0'' and "1'' stand, respectively, for a protostar of Class 0 or Class I, "2'' for an accreting (classical) T Tau star that usually shows a Class-II IR spectrum; "3'' corresponds to a weak-line or Class-III object; "4'' designates a brown dwarf (spectral class equal to or later than M6.25) irrespective of its accretion signatures; and "5'' marks the Herbig Ae/Be stars in TMC. For uncertain classifications or other object types, we use the code "9''.
![\begin{figure}
{\resizebox{8cm}{!}{\includegraphics[clip]{5724fig7a.ps}} }
\par\...
...e*{3mm}
{\resizebox{8cm}{!}{\includegraphics[clip]{5724fig7b.ps}} }
\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg126.gif) |
Figure 7:
Comparison of |
| Open with DEXTER | |
To assess the quality of our spectral interpretations, we now compare results derived
from the two fit methods (DEM vs 1- or 2-T plasma).
Figure 7 compares ![]() values derived from the DEM fits (shown along the abscissa)
and from the 1- or 2-T fits (along the ordinate). We show results for bright spectra
(>600 cts for the source counts parameter in Table 4 of which typically about half
are found in the PN camera) and for faint spectra (<600 cts) separately. The agreement is
excellent. The brighter sources show a trend toward
values derived from the DEM fits (shown along the abscissa)
and from the 1- or 2-T fits (along the ordinate). We show results for bright spectra
(>600 cts for the source counts parameter in Table 4 of which typically about half
are found in the PN camera) and for faint spectra (<600 cts) separately. The agreement is
excellent. The brighter sources show a trend toward ![]() being slightly lower for the
1-T or 2-T fit than for the DEM fit. This can be understood as follows. The DEM model assumes
the presence of cool material down to
being slightly lower for the
1-T or 2-T fit than for the DEM fit. This can be understood as follows. The DEM model assumes
the presence of cool material down to
![]() .
This plasma accounts for some of the soft emission
where the 1- or 2-T model may be subject to an EM deficit. To account for the same spectral flux,
the trend is to lower
.
This plasma accounts for some of the soft emission
where the 1- or 2-T model may be subject to an EM deficit. To account for the same spectral flux,
the trend is to lower ![]() for the spectrum with deficient cool EM. The scatter obviously becomes
larger for fainter sources, but the error bars grow accordingly so that the agreement is of similar
quality (lower plot).
for the spectrum with deficient cool EM. The scatter obviously becomes
larger for fainter sources, but the error bars grow accordingly so that the agreement is of similar
quality (lower plot).
![\begin{figure}
{\resizebox{8cm}{!}{\includegraphics[clip]{5724fig8a.ps}} }
\par\...
...e*{3mm}
{\resizebox{8cm}{!}{\includegraphics[clip]{5724fig8b.ps}} }
\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg128.gif) |
Figure 8:
Comparison of |
| Open with DEXTER | |
![\begin{figure}
{\resizebox{8cm}{!}{\includegraphics[clip]{5724fig9a.ps}} }
\par\...
...e*{3mm}
{\resizebox{8cm}{!}{\includegraphics[clip]{5724fig9b.ps}} }
\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg129.gif) |
Figure 9:
Comparison of |
| Open with DEXTER | |
Figure 8 analogously compares ![]() .
For most of the brighter stars, the agreement is
excellent although there are a few cases for which the 1- or 2-T fit produces significantly higher
.
For most of the brighter stars, the agreement is
excellent although there are a few cases for which the 1- or 2-T fit produces significantly higher ![]() .
The reason for this deviation is the following. Soft components can be added with relatively little constraints
if they are sufficiently absorbed. The temperature then becomes uncertain. A cooler plasma subject to photoelectric absorption
will, however, require a much larger EM to produce the same observed flux. If the cool EM is a free fit parameter,
an instability may occur with T converging to low values while
.
The reason for this deviation is the following. Soft components can be added with relatively little constraints
if they are sufficiently absorbed. The temperature then becomes uncertain. A cooler plasma subject to photoelectric absorption
will, however, require a much larger EM to produce the same observed flux. If the cool EM is a free fit parameter,
an instability may occur with T converging to low values while ![]() and EM grow excessively.
This becomes more evident for fainter sources (lower plot). In several cases, we
therefore fixed
and EM grow excessively.
This becomes more evident for fainter sources (lower plot). In several cases, we
therefore fixed ![]() at the value expected from
at the value expected from ![]() for the DEM fit, whereas the 1-T fits, requiring one parameter less,
were performed without this constraint. The sources that likely suffer from this numerical instability in the 1-T fit are
CIDA 7 (XEST-10-034), HO Tau (XEST-09-010), V410 X6 (XEST-23-061), CFHT-Tau 7 (XEST-03-017), MHO 9 (XEST-22-013), and
V410 A25 (XEST-23-029) that all show
for the DEM fit, whereas the 1-T fits, requiring one parameter less,
were performed without this constraint. The sources that likely suffer from this numerical instability in the 1-T fit are
CIDA 7 (XEST-10-034), HO Tau (XEST-09-010), V410 X6 (XEST-23-061), CFHT-Tau 7 (XEST-03-017), MHO 9 (XEST-22-013), and
V410 A25 (XEST-23-029) that all show ![]() from the 1-T or 2-T fits at least 3 times higher compared to the DEM fit.
In the former, they show
from the 1-T or 2-T fits at least 3 times higher compared to the DEM fit.
In the former, they show ![]() considerably higher than in the latter, or much higher than expected from
considerably higher than in the latter, or much higher than expected from ![]() ,
while the dominant
electron temperature was very low, between 1 MK and 3.3 MK. The first four of those six stars are faint, while MHO 9
is at the limit between bright and faint as defined for the plots in Fig. 8.
,
while the dominant
electron temperature was very low, between 1 MK and 3.3 MK. The first four of those six stars are faint, while MHO 9
is at the limit between bright and faint as defined for the plots in Fig. 8.
Given that the DEM model is more rigid and avoids biases toward strongly absorbed soft emission
from large amounts of cool EM, we will base most of our statistical investigations in the accompanying papers
on the DEM results. This model is also more physically meaningful because work on bright spectra of
nearby stars has clearly shown continuous emission measure distributions of this kind (e.g., Telleschi et al. 2005).
As shown here and below, however, the results for ![]() ,
,
![]() ,
and
,
and
![]() from the two methods
agree well for the brighter spectra. Caution is in order essentially only for spectra defined as "faint'' here.
from the two methods
agree well for the brighter spectra. Caution is in order essentially only for spectra defined as "faint'' here.
![\begin{figure}
{\resizebox{7.6cm}{!}{\includegraphics[clip]{5724fig10a.ps}} }
\p...
...
{\resizebox{7.6cm}{!}{\includegraphics[clip]{5724fig10b.ps}} }
\par\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg130.gif) |
Figure 10:
Comparison of
|
| Open with DEXTER | |
Figure 9 shows the same comparison for weakly absorbed sources
(upper plot, for
![]() cm-2) and for more strongly absorbed sources
(lower plot, for
cm-2) and for more strongly absorbed sources
(lower plot, for
![]() cm-2). It is evident that higher absorption introduces
more uncertainty to the precise determination of
cm-2). It is evident that higher absorption introduces
more uncertainty to the precise determination of ![]() .
Also, these sources obviously
tend to be fainter (in terms of count rates).
.
Also, these sources obviously
tend to be fainter (in terms of count rates).
Figure 10 compares the average electron temperature,
![]() ,
derived from
the DEM and the 2-T or 1-T fits. Given the rather different methodology, the
agreement is satisfactory for the brighter sources, while the
scatter increases for faint sources, making accurate statements on electron temperatures difficult.
The few outliers among the bright sources show very low average temperatures in 1-T or 2-T fits
probably due to the same numerical instability described above. The worst agreement is found for the very faint spectrum
of LR 1 (XEST-23-048) for which T0 of the DEM fit is unconstrained despite fixed
,
derived from
the DEM and the 2-T or 1-T fits. Given the rather different methodology, the
agreement is satisfactory for the brighter sources, while the
scatter increases for faint sources, making accurate statements on electron temperatures difficult.
The few outliers among the bright sources show very low average temperatures in 1-T or 2-T fits
probably due to the same numerical instability described above. The worst agreement is found for the very faint spectrum
of LR 1 (XEST-23-048) for which T0 of the DEM fit is unconstrained despite fixed
![]() .
In the presence
of severe absorption, the DEM fit finds a low best-fit T0, while the 1-T fit converges to a very high temperature. Both
.
In the presence
of severe absorption, the DEM fit finds a low best-fit T0, while the 1-T fit converges to a very high temperature. Both
![]() are reasonable, while the DEM fit converges to a higher
are reasonable, while the DEM fit converges to a higher ![]() which is preferred in the light of the very high AJ of
this star.
which is preferred in the light of the very high AJ of
this star.
Concluding from this comparison, we are confident that ![]() values are meaningful within factors of about 1.5
for the brighter sample and mostly within factors of 2 for the fainter sample. X-ray luminosities appear
to be reasonably constrained within a factor of two (although with exceptions), which is a typical
range of variability for most sources in any case.
values are meaningful within factors of about 1.5
for the brighter sample and mostly within factors of 2 for the fainter sample. X-ray luminosities appear
to be reasonably constrained within a factor of two (although with exceptions), which is a typical
range of variability for most sources in any case.
Figure 11 shows an Hertzsprung-Russell Diagram (HRD) of all sources observed in the framework of this survey with isochrones and evolutionary tracks (after Siess et al. 2000) overplotted. The source symbols indicate the source type, and the symbol size corresponds to the X-ray luminosity.
The following
characteristics are noteworthy: i) The surveyed sources cover a broad range of masses, from the
substellar range up to 2.5-3 ![]() ,
the three most massive stars being HD 28867 and the
Herbig stars AB Aur and V928 Tau (the latter being a multiple system). Most objects are concentrated
at ages between
,
the three most massive stars being HD 28867 and the
Herbig stars AB Aur and V928 Tau (the latter being a multiple system). Most objects are concentrated
at ages between
![]() yr, and very few at ages around 107 yr.
ii) As pointed out by Kenyon & Hartmann (1995), CTTS and WTTS (Class II and III, shown in gray and white,
respectively) occupy the same region in the HRD. In fact, this is also true for the detected Class-I protostars.
The low-mass and substellar HRD will be more specifically discussed by Grosso et al. (2007a).
iii) Most undetected sources are in the
very low-mass/substellar regimes and/or have the largest isochronal ages, although for some of the
latter objects, the fundamental parameters are poorly determined, as detailed below.
yr, and very few at ages around 107 yr.
ii) As pointed out by Kenyon & Hartmann (1995), CTTS and WTTS (Class II and III, shown in gray and white,
respectively) occupy the same region in the HRD. In fact, this is also true for the detected Class-I protostars.
The low-mass and substellar HRD will be more specifically discussed by Grosso et al. (2007a).
iii) Most undetected sources are in the
very low-mass/substellar regimes and/or have the largest isochronal ages, although for some of the
latter objects, the fundamental parameters are poorly determined, as detailed below.
A few objects are apparently located below the zero-age main sequence (ZAMS) which is likely to be a consequence of
poor photometry. This is particularly true for embedded sources
where scattered light distorts photometric measurements. The stars below the ZAMS are, in order of
increasing
![]() :
HH 30 (XEST-22-000, an edge-on star-disk system, Burrows et al. 1996),
IRAS S04301+261 (XEST-18-000, a highly reddened object probably primarily detected in scattered light,
Briceño et al. 2002),
Haro 6-5 B = FS Tau B (XEST-11-054 = C2-1, a near-edge-on star-disk system, Padgett et al. 1999, with
:
HH 30 (XEST-22-000, an edge-on star-disk system, Burrows et al. 1996),
IRAS S04301+261 (XEST-18-000, a highly reddened object probably primarily detected in scattered light,
Briceño et al. 2002),
Haro 6-5 B = FS Tau B (XEST-11-054 = C2-1, a near-edge-on star-disk system, Padgett et al. 1999, with
![]() mag), HBC 353 (XEST-27-000), and HBC 352 (XEST-27-115). These
stars will not be considered in statistical studies whenever L* is required (e.g., in
mag), HBC 353 (XEST-27-000), and HBC 352 (XEST-27-115). These
stars will not be considered in statistical studies whenever L* is required (e.g., in
![]() ). A few
stars are located between the 10 Myr isochrone and the ZAMS, making them much older than the bulk
population in Taurus. Several of these objects are relatively poorly studied and may suffer from
inaccurate photometry. For most of them, no
). A few
stars are located between the 10 Myr isochrone and the ZAMS, making them much older than the bulk
population in Taurus. Several of these objects are relatively poorly studied and may suffer from
inaccurate photometry. For most of them, no ![]() has been given, or the extinction is large, and indeed several
of them have not been detected (crosses in Fig. 11). These objects
are, in order of increasing
has been given, or the extinction is large, and indeed several
of them have not been detected (crosses in Fig. 11). These objects
are, in order of increasing
![]() above the 0.1
above the 0.1 ![]() track: ITG 33A (XEST-07-000, suggested to
be an edge-on star-disk system, Martín 2000:
track: ITG 33A (XEST-07-000, suggested to
be an edge-on star-disk system, Martín 2000:
![]() mag), FS Tau (XEST-11-057, a strongly extincted
close binary of CTTS,
mag), FS Tau (XEST-11-057, a strongly extincted
close binary of CTTS,
![]() mag),
CoKu Tau 1 (XEST-23-000, an edge-on star-disk system, Padgett et al. 1999,
mag),
CoKu Tau 1 (XEST-23-000, an edge-on star-disk system, Padgett et al. 1999,
![]() mag),
HN Tau (C5-2), LR 1 (XEST-23-048, with a large
AJ = 6.4 mag), V955 Tau (XEST-10-020,
mag),
HN Tau (C5-2), LR 1 (XEST-23-048, with a large
AJ = 6.4 mag), V955 Tau (XEST-10-020,
![]() mag),
V410 A20 (XEST-23-000, with a large
AJ = 6.57 mag),
and V410 A24 (XEST-23-000, with a large
AJ = 6.73 mag - see Table 9 for
mag),
V410 A20 (XEST-23-000, with a large
AJ = 6.57 mag),
and V410 A24 (XEST-23-000, with a large
AJ = 6.73 mag - see Table 9 for ![]() and AJ values).
and AJ values).
![\begin{figure}
{\resizebox{14.3cm}{!}{\includegraphics[clip]{5724fig11.ps}} }
\par\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg138.gif) |
Figure 11:
HRD of all observed TMC objects for which L* and
|
| Open with DEXTER | |
The detection statistics of our X-ray survey is summarized in Table 12
(considering only the XMM-Newton observations),
based on our final classification scheme in Table 11. Here, the protostar L1551 IRS5 has been treated as a non-detection as the source closely associated with this binary has been interpreted as X-ray emission from the jets (Favata et al. 2002; Bally et al. 2003). We also list the statistics (in parentheses) if Chandra detections and non-detections are counted (note that DG Tau B and FV Tau/c have been counted as non-detections in the XMM-Newton sample, while they are detections with Chandra).
An important point for further statistical studies is that the X-ray sample
of detected CTTS and WTTS is nearly complete for the surveyed fields (as
far as the population is known). Most of the few remaining, undetected objects are
considerably extincted and by implication X-ray absorbed:
IRAS S04301+261 = XEST-18-000 with
![]() ,
and CoKu Tau 1 = XEST-23-000, CFHT-Tau 19 = XEST-11-000,
FV Tau/c = XEST-02-000, CFHT-Tau 20 = XEST-13-000, ITG33 A = XEST-07-000, CFHT-Tau 8 = XEST-07-000,
and HH 30 = XEST-22-000 with
,
and CoKu Tau 1 = XEST-23-000, CFHT-Tau 19 = XEST-11-000,
FV Tau/c = XEST-02-000, CFHT-Tau 20 = XEST-13-000, ITG33 A = XEST-07-000, CFHT-Tau 8 = XEST-07-000,
and HH 30 = XEST-22-000 with
![]() ,
7.3, 3.25, 3.6, 3.5, 1.8, and
,
7.3, 3.25, 3.6, 3.5, 1.8, and ![]() 3 mag and
CFHT-Tau 12 = XEST-17-000 with
AJ = 3.44 mag,
where the
3 mag and
CFHT-Tau 12 = XEST-17-000 with
AJ = 3.44 mag,
where the ![]() of IRAS S04301+261, CoKu Tau 1, HH 30, ITG 33A may have been severely underestimated owing
to scattered light and strong extinction by near-edge-on disks (see above). FV Tau/c was, however, detected
in a Chandra observation (C3-1) reported here, with an unexpectedly high photoelectric absorption
corresponding to
of IRAS S04301+261, CoKu Tau 1, HH 30, ITG 33A may have been severely underestimated owing
to scattered light and strong extinction by near-edge-on disks (see above). FV Tau/c was, however, detected
in a Chandra observation (C3-1) reported here, with an unexpectedly high photoelectric absorption
corresponding to
![]() cm-2. Some of the non-detections are very-low mass
stars with late spectral types (CFHT-Tau 19 = XEST-11-000, CFHT-Tau 20 = XEST-13-000, CFHT-Tau 12 = XEST-17-000,
and CFHT-Tau 8 = XEST-07-000 with spectral types of M5.25, M5.5, M6, and M5.5, respectively). Very little is known
about IRAS 04108+2803 A. Its companion, a Class I object, was detected, its light curve showing
a strong flare and its spectrum revealing very strong absorption. Perhaps, both objects are
subject to similar absorption. The only formally undetected WTTS in the XMM-Newton sample is HBC 353, but
it is located on the wings of HBC 352 = XEST-27-115, falls into a CCD gap of the
PN detector, and is located far off-axis, elevating the corresponding detection limit to
cm-2. Some of the non-detections are very-low mass
stars with late spectral types (CFHT-Tau 19 = XEST-11-000, CFHT-Tau 20 = XEST-13-000, CFHT-Tau 12 = XEST-17-000,
and CFHT-Tau 8 = XEST-07-000 with spectral types of M5.25, M5.5, M6, and M5.5, respectively). Very little is known
about IRAS 04108+2803 A. Its companion, a Class I object, was detected, its light curve showing
a strong flare and its spectrum revealing very strong absorption. Perhaps, both objects are
subject to similar absorption. The only formally undetected WTTS in the XMM-Newton sample is HBC 353, but
it is located on the wings of HBC 352 = XEST-27-115, falls into a CCD gap of the
PN detector, and is located far off-axis, elevating the corresponding detection limit to
![]() 180 cts. From Table 8, we derive that only 3 out of 45 multiple systems remain
undetected (2/47 including Chandra results),
while 29 out of 114 single stars are undetected (31/122 including Chandra results).
In total, 45 of the 159 systems surveyed by XMM-Newton are multiple
(47/169 including Chandra results).
180 cts. From Table 8, we derive that only 3 out of 45 multiple systems remain
undetected (2/47 including Chandra results),
while 29 out of 114 single stars are undetected (31/122 including Chandra results).
In total, 45 of the 159 systems surveyed by XMM-Newton are multiple
(47/169 including Chandra results).
Table 12: XEST X-ray detection statistics.
Previous X-ray surveys of TMC did not detect the intrinsically fainter TTS population. Those previous
surveys covered a wider field in Taurus (e.g., the ROSAT surveys by Neuhäuser et al. 1995; Stelzer & Neuhäuser 2001)
but were about ten times less sensitive and were confined
to soft sources. Stellar classes that were thus inaccessible by these earlier surveys but are
systematically (albeit not completely) detected in XEST are: i) strongly absorbed, embedded protostars
or T Tau stars absorbed by their own disks seen nearly edge-on; their non-detection in previous surveys
is little surprising given the strong photoelectric absorption. Most of the detected protostars
show no X-ray counts below
2 keV. ii) Low-![]() brown dwarfs; in XEST, the detection rate of BDs
(50% for the XMM-Newton sample, 53% if one detection from Chandra is added)
is high; the remaining objects of this class are
likely to be intrinsically fainter than our detection limit rather than being
excessively absorbed by gas (
brown dwarfs; in XEST, the detection rate of BDs
(50% for the XMM-Newton sample, 53% if one detection from Chandra is added)
is high; the remaining objects of this class are
likely to be intrinsically fainter than our detection limit rather than being
excessively absorbed by gas (![]() of those objects typically being no more than
a few magnitudes; see Grosso et al. 2007a for further discussion).
iii) Several T Tau stars with double-peaked X-ray spectra in which a strongly absorbed hard component
is accompanied by a soft excess (Güdel et al. 2007b).
of those objects typically being no more than
a few magnitudes; see Grosso et al. 2007a for further discussion).
iii) Several T Tau stars with double-peaked X-ray spectra in which a strongly absorbed hard component
is accompanied by a soft excess (Güdel et al. 2007b).
The incomplete statistics in previous surveys potentially introduces bias into statistical correlations and population studies. On the other hand, we emphasize that the so far cataloged population of Taurus members may not be complete either. In particular, WTTS are predominantly detected by their X-rays (e.g., Neuhäuser et al. 1995). The WTTS statistics in Taurus may thus be incomplete in particular with regard to faint X-ray sources or WTTS located behind the TMC. Several dozen new TMC member candidates are indeed reported from XEST (Scelsi et al. 2007) but will require spectroscopic follow-up observations to confirm membership.
Table 13 summarizes statistical properties of the surveyed sources, providing
median, mean, and standard deviation of the sample for various parameters. The sample sizes vary (given in the last
column, N) because not all parameters are available for all sources (see details in the
footnotes of the table). The salient features of
this compilation are the following: i) The agreement between the sample X-ray parameters derived from the
DEM model ("DEM'' in column 2) and the 1-T or 2-T model ("2-T'' in column 2) is excellent.
ii) Characteristic electron temperatures are around 6-8 MK as characterized by T0 in the DEM
model and by T1 in the 1-T or 2-T model. The hotter component shows a mean and median around 23 MK.
iii) The large majority of the sample shows
![]() .
iv) Protostars are,
as expected, significantly more extincted in the visual band (
.
iv) Protostars are,
as expected, significantly more extincted in the visual band (![]() )
in our sample than T Tau stars;
among the latter, objects of type 2 (CTTS, Class-II objects) are more strongly extincted than objects
of type 3 (WTTS, Class III). The median extinction of the detected sources is
)
in our sample than T Tau stars;
among the latter, objects of type 2 (CTTS, Class-II objects) are more strongly extincted than objects
of type 3 (WTTS, Class III). The median extinction of the detected sources is
![]() mag,
corresponding to a hydrogen column density of
mag,
corresponding to a hydrogen column density of
![]() ,
close to the measured median of
,
close to the measured median of
![]() .
iv) As pointed out on the HRD, the L*
distributions of objects of type 1, 2, and 3 strongly overlap, although a marginal trend
is seen toward a decreasing sample mean of L* with increasing type, perhaps reflecting some overall
evolutionary trend. v) A wide range of accretion rates is covered (for protostars and CTTS), with a mean and
median around
.
iv) As pointed out on the HRD, the L*
distributions of objects of type 1, 2, and 3 strongly overlap, although a marginal trend
is seen toward a decreasing sample mean of L* with increasing type, perhaps reflecting some overall
evolutionary trend. v) A wide range of accretion rates is covered (for protostars and CTTS), with a mean and
median around
![]() yr-1.
yr-1.
Table 13: XEST parameter statistics.
In Fig. 12 we characterize the detected stellar population by plotting ![]() (from the DEM
models) as a function of mass
M for all observed stars and substellar objects with known masses, although we exclude
the following objects: DG Tau A (XEST-02-022), GV Tau (XEST-13-004), DP Tau (XEST-10-045), and CW Tau (XEST-20-046)
have composite X-ray spectra that may originate from two unrelated sources (Güdel et al. 2007b). L1551 IRS5 is a deeply
embedded protostar, while the X-ray source seen close to it is only lightly absorbed and may be related to the jet
(Favata et al. 2002; Bally et al. 2003). Finally, the light curves of DH Tau (XEST-15-040), FS Tau (XEST-11-057), and V830 Tau (XEST-04-016)
showed a decay presumably from large flares. For objects that were observed and detected
twice, the logarithmic average of
(from the DEM
models) as a function of mass
M for all observed stars and substellar objects with known masses, although we exclude
the following objects: DG Tau A (XEST-02-022), GV Tau (XEST-13-004), DP Tau (XEST-10-045), and CW Tau (XEST-20-046)
have composite X-ray spectra that may originate from two unrelated sources (Güdel et al. 2007b). L1551 IRS5 is a deeply
embedded protostar, while the X-ray source seen close to it is only lightly absorbed and may be related to the jet
(Favata et al. 2002; Bally et al. 2003). Finally, the light curves of DH Tau (XEST-15-040), FS Tau (XEST-11-057), and V830 Tau (XEST-04-016)
showed a decay presumably from large flares. For objects that were observed and detected
twice, the logarithmic average of ![]() has been adopted. Although for pre-main sequence
stars there is no strict correlation between L* and M, it is interesting
that we find a rather well-developed correlation between
has been adopted. Although for pre-main sequence
stars there is no strict correlation between L* and M, it is interesting
that we find a rather well-developed correlation between ![]() and M. The correlation coefficient for the
and M. The correlation coefficient for the
![]() vs.
vs. ![]() sample is C = 0.79 for 99 data points. For the subsample of type 2 ("CTTS'') and type 3 objects ("WTTS''), we find
C = 0.75 and C = 0.85 for 45 and 43 data points, respectively. All values point to a very significant correlation.
We find a linear regression,
sample is C = 0.79 for 99 data points. For the subsample of type 2 ("CTTS'') and type 3 objects ("WTTS''), we find
C = 0.75 and C = 0.85 for 45 and 43 data points, respectively. All values point to a very significant correlation.
We find a linear regression,
![]() .
The slopes for
type 2 and type 3 objects are, respectively,
.
The slopes for
type 2 and type 3 objects are, respectively,
![]() and
and
![]() .
While these regressions are not significantly
different, we note the larger errors for type 2 objects, and also their lower correlation coefficient, which is due
to a larger scatter of
.
While these regressions are not significantly
different, we note the larger errors for type 2 objects, and also their lower correlation coefficient, which is due
to a larger scatter of ![]() at a given mass. Similar trends have been
noted in Orion (Preibisch et al. 2005), with
at a given mass. Similar trends have been
noted in Orion (Preibisch et al. 2005), with
![]() for the entire sample.
This coincidence between XEST and COUP reveals that in TMC and ONC,
the basic X-ray production mechanism scales precisely the same way
with the most basic property of the stellar objects, namely their mass, regardless of any differences
in age distribution, star-formation mode, or the presence or (near-) absence of high-mass stars.
Part of this correlation might be explained by higher-mass stars being larger, i.e.,
providing more surface area for coronal active regions. Assuming similar average internal stellar density, the
correlation between surface area and
for the entire sample.
This coincidence between XEST and COUP reveals that in TMC and ONC,
the basic X-ray production mechanism scales precisely the same way
with the most basic property of the stellar objects, namely their mass, regardless of any differences
in age distribution, star-formation mode, or the presence or (near-) absence of high-mass stars.
Part of this correlation might be explained by higher-mass stars being larger, i.e.,
providing more surface area for coronal active regions. Assuming similar average internal stellar density, the
correlation between surface area and ![]() is, however, considerably weaker than the trend shown
in Fig. 12, so that additional effects may play a role (convection zone depth, convective mass, etc).
is, however, considerably weaker than the trend shown
in Fig. 12, so that additional effects may play a role (convection zone depth, convective mass, etc).
![\begin{figure}
{\resizebox{8.5cm}{!}{\includegraphics[clip]{5724fig12.ps}} }
\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg165.gif) |
Figure 12:
X-ray luminosity |
| Open with DEXTER | |
The figure shows another important feature of our survey. Almost all sources plotted are at ![]() considerably
higher than our approximate detection limit of
considerably
higher than our approximate detection limit of ![]() 1028 erg s-1. There are hardly any objects
in the range of
1028 erg s-1. There are hardly any objects
in the range of
![]() erg s-1 although they would have been detected. Exceptions are
the brown dwarfs. This again testifies to the near-completeness of our survey within the observed fields.
erg s-1 although they would have been detected. Exceptions are
the brown dwarfs. This again testifies to the near-completeness of our survey within the observed fields.
Figure 13 shows the distribution of the ![]() (derived from the DEM models)
as a function of the (stellar, photospheric)
bolometric luminosity L* for all spectrally
modeled TTS and protostars, and also including BDs. We again exclude the peculiar
spectral sources with two absorbers, the protostar L1551 IRS5,
the three stars with gradually decaying light curves (DH Tau = XEST-15-040, FS Tau = XEST-11-057, V830 Tau = XEST-04-016),
and also all sources located below the ZAMS in the HRD.
For stars observed and detected twice, we again plot the logarithmic average of
(derived from the DEM models)
as a function of the (stellar, photospheric)
bolometric luminosity L* for all spectrally
modeled TTS and protostars, and also including BDs. We again exclude the peculiar
spectral sources with two absorbers, the protostar L1551 IRS5,
the three stars with gradually decaying light curves (DH Tau = XEST-15-040, FS Tau = XEST-11-057, V830 Tau = XEST-04-016),
and also all sources located below the ZAMS in the HRD.
For stars observed and detected twice, we again plot the logarithmic average of ![]() .
Most stars cluster between
.
Most stars cluster between
![]() as is often found in star-forming regions
(see Preibisch et al. 2005 for a similar analysis for the Orion sample). The value
as is often found in star-forming regions
(see Preibisch et al. 2005 for a similar analysis for the Orion sample). The value
![]() corresponds to the saturation value for rapidly rotating main-sequence stars. One key parameter that drives
the X-ray output is obviously L*.
corresponds to the saturation value for rapidly rotating main-sequence stars. One key parameter that drives
the X-ray output is obviously L*.
![\begin{figure}
{\resizebox{9cm}{!}{\includegraphics[clip]{5724fig13.ps}} }
\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg169.gif) |
Figure 13:
X-ray luminosity |
| Open with DEXTER | |
We finally present the X-ray luminosity function (XLF) of our Taurus sample in Fig. 14. The XLF has been calculated using
the Kaplan-Meier estimator in the ASURV software package (Lavalley et al. 1992) that considers upper limits to ![]() also. Non-detections for which no
reasonable upper limit can be given were not included. We also dropped the same non-standard X-ray sources excluded above
(double-absorber spectra, L1551 IRS 5, and sources with gradual flare decays), but include BDs and Herbig stars, thus using 136 X-ray
luminosity values, including 17 upper limits. We also plot
separately the XLF for type 2 (CTTS, 56 values, including 6 upper limits) and type 3 (WTTS, 49 values, 1 upper limit). We note
the shift of the CTTS distribution toward lower luminosities compared to WTTS, by a factor of about two. This is also evident for
also. Non-detections for which no
reasonable upper limit can be given were not included. We also dropped the same non-standard X-ray sources excluded above
(double-absorber spectra, L1551 IRS 5, and sources with gradual flare decays), but include BDs and Herbig stars, thus using 136 X-ray
luminosity values, including 17 upper limits. We also plot
separately the XLF for type 2 (CTTS, 56 values, including 6 upper limits) and type 3 (WTTS, 49 values, 1 upper limit). We note
the shift of the CTTS distribution toward lower luminosities compared to WTTS, by a factor of about two. This is also evident for
![]() (Telleschi et al. 2007a). A two-sample test based on the Wilcoxon test and the logrank test performed in ASURV
indicates a probability of only 6-9% that the two distributions are drawn from the same parent population. A more detailed discussion
on distinctions between CTTS and WTTS is given by Telleschi et al. (2007a).
(Telleschi et al. 2007a). A two-sample test based on the Wilcoxon test and the logrank test performed in ASURV
indicates a probability of only 6-9% that the two distributions are drawn from the same parent population. A more detailed discussion
on distinctions between CTTS and WTTS is given by Telleschi et al. (2007a).
![\begin{figure}
{\resizebox{8.5cm}{!}{\includegraphics[clip]{5724fig14.ps}} }
\end{figure}](/articles/aa/full/2007/23/aa5724-06/Timg171.gif) |
Figure 14: X-ray luminosity function for the entire sample (black), type 2 objects (red), and type 3 objects (blue). |
| Open with DEXTER | |
The XEST project gives near-complete access to the entire pre-main sequence population
of the Taurus Molecular Clouds within the ![]() 5 sq. degrees covered by this survey.
Essentially all WTTS and nearly all CTTS have been detected, exceptions being a few low-mass,
strongly absorbed sources. About half of the embedded protostellar sample is detected,
and a similar fraction of the BDs. This survey thus goes deeper than previous X-ray
surveys of Taurus (e.g., Neuhäuser et al. 1995; Stelzer & Neuhäuser 2001)
by about an order of magnitude for low-extinction objects and provides systematic
access to the protostellar and the brown-dwarf samples for the first time. The survey forms
the basis for more specialized studies as discussed in the accompanying series of papers.
5 sq. degrees covered by this survey.
Essentially all WTTS and nearly all CTTS have been detected, exceptions being a few low-mass,
strongly absorbed sources. About half of the embedded protostellar sample is detected,
and a similar fraction of the BDs. This survey thus goes deeper than previous X-ray
surveys of Taurus (e.g., Neuhäuser et al. 1995; Stelzer & Neuhäuser 2001)
by about an order of magnitude for low-extinction objects and provides systematic
access to the protostellar and the brown-dwarf samples for the first time. The survey forms
the basis for more specialized studies as discussed in the accompanying series of papers.
Furthermore, the survey will provide a useful database for correlation studies at other wavelengths. In particular, gas-to-dust ratio studies and investigations of the effects of accretion disks on magnetic fields in pre-main sequence systems will be undertaken in conjunction with a wide-field survey available from the Spitzer Space Telescope (Padgett et al. 2007).
Acknowledgements
The XEST project was made possible by the co-operation of many individuals. In particular, we thank the XMM-Newton SOC team in Vilspa for its excellent support before, during, and after the observations. We warmly thank the International Space Science Institute (ISSI) in Bern for their financial support of the project and their hospitality during several XEST team meetings at ISSI. Thanks go in particular to Vittorio Manno, Brigitte Fasler, and Saliba F. Saliba for their efforts to make these events enjoyable. In the course of the scientific analysis, we obtained advice from numerous colleagues, of which we mention in particular Claude Catala, Laurence DeWarf, Ed Fitzpatrick, Sylvain Guieu, Antonio Maggio, and Karl Stapelfeldt. Francesco Damiani is thanked for giving us access to his private version of PWXDETECT for XMM-Newton data. We are grateful to the referee, Marc Gagné, for his competent review of this paper and his constructive comments that helped improve the paper. This research is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA member states and the USA (NASA). This publication makes use of data products from the Two Micron All Sky Survey (2MASS), which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. Further, our research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. We have made use of the ASURV statistical software package maintained by Penn State. X-ray astronomy research at PSI has been supported by the Swiss National Science Foundation (grants 20-66875.01 and 20-109255/1). MA acknowledges support by NASA grants NNG05GF92G. The Palermo group acknowledges financial contributions from contract ASI-INAF I/023/05/0.
Table 3:
Accepted good exposure time and fraction of total exposure time remaining after filtering out
intervals of high background in the full energy band (0.5-7.3 keV). Calculated for each EPIC instrument
in each XMM-Newton observation used in XEST. The penultimate column lists the approximate lowest
detectable count-rate for a 4![]() detection in the PN; for a 30 ks exposure in purely quiescent background,
this would be 1.1 c ks-1. For XEST-26 only the MOS cameras were used and the MOS1 value has been multiplied
by a factor 2.7 to calculate a PN-equivalent source count-rate. The final column lists the total number of
detections made in the summed EPIC images.
detection in the PN; for a 30 ks exposure in purely quiescent background,
this would be 1.1 c ks-1. For XEST-26 only the MOS cameras were used and the MOS1 value has been multiplied
by a factor 2.7 to calculate a PN-equivalent source count-rate. The final column lists the total number of
detections made in the summed EPIC images.
References cited in the tables:
2 = Bouvier (2006)
9 = DeWarf & Fitzpatrick (2006)
15 = Finkenzeller & Mundt (1984)
16 = Ghez et al. (1993)
17 = Ghez et al. (1997)
18 = Guieu et al. (2006)
19 = Guieu (2006)
22 = Hartmann (2002)
24 = Herbig et al. (1986)
25 = Itoh et al. (2005)
28 = Kenyon et al. (1993)
29 = Kenyon et al. (1998)
33 = Luhman (2004)
34 = Luhman et al. (2003)
35 = Martín (2000)
37 = Martín et al. (1994)
38 = Martín et al. (1999)
39 = Martín et al. (2001)
40 = McCabe et al. (2006)
42 = Moneti & Zinnecker (1991)
43 = Monin et al. (1998)
47 = Prato & Simon (1997)
48 = Rebull et al. (2004) and references therein
49 = Reipurth & Zinnecker (1993)
52 = Simon et al. (1992) and references therein
53 = Simon et al. (1995)
54 = Smith et al. (2005)
55 = Strom & Strom (1994)
56 = Walter et al. (1988)
57 = White & Basri (2003)
58 = White & Ghez (2001)
59 = White & Hillenbrand (2004)
60 = Mundt et al. (1983)
61 = Welty (1995)
62 = Woitas (2003)
63 = Calvet et al. (2004)
65 = Walter et al. (2003) and references therein
66 = Luhman (2006)
67 = Simon et al. (1996)
Table 4: X-ray parameters of targets in XEST (1): Positions and count rates.
Table 5: X-ray parameters of targets in XEST (2): Plasma parameters from the DEM fits.
Table 6: X-ray parameters of targets in XEST (3): Plasma parameters from the 1-T and 2-T fits.
Table 7: Fundamental parameters of targets in XEST (1): Names and coordinates.
Table 8: Fundamental parameters of targets in XEST (2): Multiplicity.
Table 9: Fundamental parameters of targets in XEST (3): Photometry and spectroscopy.
Table 10: Fundamental parameters of targets in XEST (4): Age, mass, radius, rotation.
Table 11: Fundamental parameters of targets in XEST (5); Accretion and evolution.
The complete catalog of all X-ray sources detected in the XEST fields (not including the complementary fields from Chandra) is available in electronic form. The data reduction and source identification procedures are described in Sect. 4. The catalog also provides errors of the source counts and the count rates (not given in Table 4 for the "Scts'' and "Rate'' columns). The numbering scheme is as defined in Sect. 5, all TMC members being included. The catalog is sorted in right ascension and contains a total of 2347 identified X-ray sources. If two XEST fields overlap, the same sources may have been identified twice, with different XEST IDs assigned. The first ten entries of the catalog are given in the Table A.1 below for illustration. Note that if ML < 5 in any band the number of counts and the count rate are 95% upper limits in that band. The HR is the upper (or lower) limit as appropriate in these situations with the low and high values set to -1 and to the HR upper limit, respectively (or to the HR lower limit and to +1, respectively).
Table A.1: XEST Catalog (first ten entries).
A description of the columns follows:
Figures B.1-B.10 show all 28 XEST EPIC exposures. Each field of view is presented in two versions. The left panel shows a co-added EPIC image, logarithmically compressed in intensity and slightly smoothed. The colors code for hardness, where hardness increases from red to yellow to green to blue. Saturated (bright) stellar images are black. The right panel shows an unsmoothed, co-added EPIC image with an RA(J2000.0) - Dec(J2000.0) coordinate grid. Also plotted are the locations of known TMC members (red circles), labeled with their XEST source IDs (srcnr). The latter are located directly above the source circles except in crowded areas where labels may have been shifted.
 |
Figure B.10: Co-added EPIC images of field XEST-28. Left: Smoothed image, color coded for hardness; right: coordinate grid and TMC identifications included. |