A&A 468, 151-161 (2007)
DOI: 10.1051/0004-6361:20077073

Towards absolute scales for the radii and masses of open clusters

A. E. Piskunov^1,2,3 - E. Schilbach¹ - N. V. Kharchenko^1,3,4 - S. Röser¹ - R.-D. Scholz³

1 - Astronomisches Rechen-Institut, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
2 - Institute of Astronomy of the Russian Acad. Sci., 48 Pyatnitskaya Str., 109017 Moscow, Russia
3 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
4 - Main Astronomical Observatory, 27 Academica Zabolotnogo Str., 03680 Kiev, Ukraine

Received 10 January 2007 / Accepted 19 February 2007

Abstract
Aims. In this paper we derive tidal radii and masses of open clusters in the nearest kiloparsecs around the Sun.
Methods. For each cluster, the mass is estimated from tidal radii determined from a fitting of three-parameter King profiles to the observed integrated density distribution. Different samples of members are investigated.
Results. For 236 open clusters, all contained in the catalogue ASCC-2.5, we obtain core and tidal radii, as well as tidal masses. The distributions of the core and tidal radii peak at about 1.5 pc and 7-10 pc, respectively. A typical relative error of the core radius lies between 15% and 50%, whereas, for the majority of clusters, the tidal radius was determined with a relative accuracy better than 20%. Most of the clusters have tidal masses between 50 and 1000 $m_\odot$, and for about half of the clusters, the masses were obtained with a relative error better than 50%.

Key words: Galaxy: open clusters and associations: general - solar neighbourhood - Galaxy: stellar content

1 Introduction

At a minimum for describing a stellar cluster, one needs to specify the position of a cluster centre and its apparent (angular) size. Both parameters serve to identify a cluster on the sky. Also, these parameters are very common, since present in numerous catalogues of clusters and presently available for about 1700 galactic open clusters (see e.g. Dias et al. 2002). In the majority of cases, however, they are derived from visual inspection of a cluster area on the sky, so the parameters may be strongly biased due to the size of the detector field and/or by contamination of field stars, thereby presenting a lower limit on the real size of a cluster. As shown by Kharchenko et al. (2005a), these data from the literature are normally smaller by a factor of two with respect to cluster radii drawn from analysis of a uniform membership based on photometric and spatio-kinematic constraints. These data are in turn subject to various biases (see Schilbach et al. 2006) and need to be reduced to a uniform system to give physical insight into the structural properties of the population of galactic open clusters.

Besides the morphological description of a cluster itself, the structural parameters hold important information on its basic physical properties like mass and on the surrounding galactic tidal field (von Hoerner 1957). King (1962) proposed an empirical set of cluster parameters as a quantifier of the structure of spherical systems and later showed (King 1966) that they correspond to theoretical density profiles of quasi-equilibrium configurations and suit stellar clusters with masses spanning those of open clusters to globular ones. King (1962) introduced three spatial parameters $r_{\rm c},~r_{\rm t}$, and k, hereafter referred to as King's parameters ($r_{\rm c}$ is the so-called core radius, $r_{\rm t}$ the tidal radius, and k a profile normalization factor), fully describing the distribution of the projected density in a cluster. Since that time, this parameter set is widely used to quantitatively describe the density laws of globular clusters. Here we mention a number of studies where King's parameters were determined both for galactic globular clusters (e.g. Peterson and King 1975; Trager et al. 1995; Lehmann & Scholz 1997), and for extragalactic ones (Kontizas 1984, Hill & Zaritski 2006) in the SMC, or LMC (Elson et al. 1987).

The application of King's parameters might be useful for open clusters as well, especially from the point of view of establishing a uniform scale of structural parameters and providing independent estimates of cluster masses. However, the literature on the determination of King's parameters of open clusters is much scarcer than that of globulars. We mention here the following studies based on three-parameter fits of selected clusters: King (1962), Leonard (1988), Raboud & Mermilliod (1998a,b). Among other complicating reasons making the study of King's parameters in open clusters difficult, such as an insufficient stellar population and heavy and irregular fore/background, we emphasise the difficulty of acquiring data in wide-field areas around a cluster. The latter is due to the much larger size of a typical open cluster compared to the fields of view of detectors currently used in studies of individual clusters. Recently, when a number of all-sky catalogues have become available, studies exploring the unlimited neighbourhood of clusters were published (Adams et al. 2001, 2002; Bica et al. 2005a, 2005b, 2006). Froebrich et al. (2007) have been searching the 2MASS survey for new clusters and provided spatial parameters for all newly identified cluster candidates derived from fitting the surface density patterns with King profiles.

Mass is one of the fundamental parameters of star clusters. There are several independent methods for estimating cluster masses. Each of them has its advantages and disadvantages with respect to the other ones. But so far there is no method that can be regarded as absolutely satisfactory. The simplest and most straightforward way is to count cluster members and to sum up their masses. Since there is no cluster with a complete census of members, one always observes only a subset of cluster stars, truncated by the limiting magnitude and by the limited area covered by a study, therefore, masses from star counts should be regarded as lower estimates of the real mass of a cluster. The extrapolation of the mass spectrum to an unseen lower limit of stellar masses, along with some template of the IMF frequently applied in such studies, leads to unjustified and unpredictable modifications of the observed mass and should be avoided. The farther away the cluster is, the larger the uncounted fraction of faint members, often residing in the cluster periphery. In fact, this method could be applied with a reasonable degree of safety to the nearest clusters observed with deep, wide-area surveys, thereby providing secure and complete membership. Due to its simplicity, the method is currently widely accepted, and it is possibly the only technique that is applied to relatively large samples of open clusters (see Danilov & Seleznev 1994; Tadross et al. 2002; Lamers et al. 2005).

The second method is the classical one, namely applying the virial theorem. It gives the mass of a cluster from an estimate of the stellar velocity dispersion and average interstellar distances. It does not require the observation and membership determination of all cluster stars. The application of the method is, however, limited to sufficiently massive stellar systems (globulars and dwarf spheroidals) with dispersions of internal motions large enough to be measurable. For open clusters with typcal dispersions of the order of or less than 1 km s^-1, present-day accuracies of both proper motions and radial velocities are fairly rough and are marginally available for a few selected clusters only. In spite of this, several attempts have been undertaken for clusters with the most accurate proper motions (Jones 1970, 1971; McNamara & Sanders 1977, 1983; McNamara & Sekiguchi 1986; Girard et al. 1989; Leonard & Merritt 1989) or for clusters with mass determination from radial velocities (Eigenbrod et al. 2004).

The third method uses the interpretation of the tidal interaction of a cluster with the parent galaxy, and requires knowledge of the tidal radius of a cluster. Considering globular clusters which, in general, have elliptical orbits, King (1962) differentiates between the tidal and the limiting radius of a cluster. For open clusters revolving at approximately circular orbits, one can expect the observed tidal radius to be approximately equal to the limiting one, although a probable deviation of the cluster shape from sphericity may have some impact on the computed cluster mass. Nevertheless, this method gives a mass estimate of a cluster (Raboud & Mermilliod 1998a,b) that is independent of the results of the two methods mentioned above. Due to the cubic dependence on $r_{\rm t}$, masses drawn from tidal radii are strongly influenced by the uncertainties on $r_{\rm t}$, however. Taking these circumstances into account, one usually reverses the relation and calculates tidal radii from counted masses.

For our studies of open clusters, we use the All-Sky Compiled Catalogue of 2.5 million stars (ASCC-2.5, Kharchenko 2001), including absolute proper motions in the Hipparcos system, B, V magnitudes in the Johnson photometric system, supplemented with spectral types and radial velocities, if available. The ASCC-2.5 is complete down to about V=11.5 mag. Based on the ASCC-2.5, we were able to construct reliable combined kinematic-photometric membership probabilities of bright stars ( $V\lesssim 12$) for 520 open clusters (Kharchenko et al. 2004, Paper I), to compute a uniform set of astrophysical parameters for clusters, (Kharchenko et al. 2005a, Paper II), as well as to identify 130 new clusters (Kharchenko et al. 2005b, Paper III) in ASCC-2.5. Currently, we have a sample of 650 open clusters, which is complete within a distance of about 1 kpc from the Sun. This sample was used to study the population of open clusters in the local Galactic disk by jointly analysing the spatial and kinematic distributions of clusters (Piskunov et al. 2006, Paper IV), for an analysis of different biases affecting the apparent size of open clusters and the segregation of stars of different mass in open clusters (Schilbach et al. 2006, Paper V).

In this paper we determine King's parameters and tidal masses for a large fraction of open clusters from our sample to get an independent basis for constructing a uniform and objective scale of spatial parameters and masses. In Sect. 2 we briefly discuss our input data, Sect. 3 contains the description of the pipeline we apply to the determination of King's parameters, in Sect. 4 we construct and discuss our sample, in Sect. 5 we compare our results with published data on King's parameters and with independent estimates of cluster masses. In Sect. 6 we summarise the results.

  
2 Data

In this study, we made use of our results on the cluster membership (Paper I) and on the parameter determination (Paper II and Paper III, respectively) for 650 open clusters. Together with other basic parameters, like the position of the cluster centre, age, distance, and angular size (the apparent radii of the core r₁ and the corona r₂), stellar density profiles in the wider neighbourhood of each cluster are available from our data. According to the membership probability $P_{\rm ap}$, density profiles were constructed for four groups of stars in each cluster: (a) the most probable members ( $P_{\rm ap}>61$%), so called $1\sigma$-members, (b) possible members ( $P_{\rm ap}>14$%), or $2\sigma$-members, (c) stars with $P_{\rm ap}>1$%, or $3\sigma$-members, and finally, (d) all stars in the cluster area which, for convenience, we call "$4\sigma$-members''.

Figure 1: Apparent density profiles of two open clusters used for determining tidal radii. The Pleiades are shown in the top panel, NGC 129 in the bottom panel. The different colours indicate different samples of stars considered: black for $1\sigma$-members (group (a), see text), magenta for $2\sigma$-members (group (b)), blue for $3\sigma$-members (group (c)), and green for "$4\sigma$-members'' (group (d)). Vertical lines show the radii r1 (solid) and r2 (dashed).

Open with DEXTER

To construct the density profiles, we counted stars in concentric rings around the cluster centre up to 5 r₂, where r₂ is the apparent radius of the corona. Due to the relatively bright magnitude limit of the ASCC-2.5, the number of cluster members available for the profile construction is rather low (on average, about 45 $2\sigma$-members per cluster). In general, the number of identified cluster members decreases with increasing distance modulus of a cluster. In order to have a statistically relevant number of stars per concentric ring, one has to chose steps of larger linear size for remote clusters. Therefore, we counted stars in concentric rings of equal angular width (0 $\hbox{$.\!\!^\circ$ }$05). This homogeneous approach makes the linear profile spacing automatically larger for more distant clusters. Since in the following analysis we intend to derive 3 unknown King's parameters from the profile fitting, we need at least four bins in the observed profile, and so we select only clusters with $r_2\geqslant 0\hbox{$.\!\!^\circ$ }2$ and with more than 10 stars above the background level within r₂. Under these constraints, the sample contains 290 clusters but not for all of them, an acceptable solution was obtained (see Sect. 3).

In order to give the reader an idea of the quality of the input data for determining tidal radii, we show two examples of apparent density profiles in Fig. 1: the Pleiades, one of the "best-quality'' clusters in our sample (top panel), and NGC 129, a remote cluster and one of the "low-quality'' clusters (bottom panel). The corresponding data on the density profiles for all 650 clusters can be found in the Open Cluster Diagrams Atlas (OCDA) available from the CDS.

  
3 Determination of tidal radii and cluster masses

3.1 Fitting cluster profiles

The method we applied is based on the well-known empirical model of King (1962), describing the observed projected density profiles f(r) in globular clusters with three parameters $r_{\rm c}$, $r_{\rm t}$, and k:

$$f(r)=k\left\{ \left[1+(r/r_{\rm c})^{2}\right]^{-1/2}-\left[1+(r_{\rm t}/r_{\rm c})^{2}\right]^{-1/2} \right\}^{2}.$$ (1)

According to King's definition, $r_{\rm c}$ is the core radius, $r_{\rm t}$ the tidal radius (approximately equal to the limiting radius in the case of an open cluster), and k is a normalization factor that is related to the central density of the cluster. This approach has also been successfully applied for determining the King parameters in several nicely populated open clusters (see e.g., Raboud & Mermilliod 1998a,b). Nevertheless, the direct way of fitting the observed density distribution by the model (Eq. (1)) does not work for the majority of the clusters in our sample. The main reason is the relatively bright magnitude limit of the ASCC-2.5 and, consequently, the low number of cluster members, which causes uncertainties in the observed density profiles. In order to weaken the influence of poor statistics, we used the integrated form of King's formula:

 

$$n(r) = \pi~ r_{\rm c}^{2}k~\Big\{ \ln[1+(r/r_{\rm c})^{2}]-4\frac... ...{2}\right]^{1/2}} +\frac{(r/r_{\rm c})^{2}}{1+(r_{\rm t}/r_{\rm c})^{2}}\Big\},$$ (2)

where n(r) is the number of stars within a circle of radius r. Since the spatial boundaries of observed open clusters are not clearly defined, and the proportion of field stars projected on the cluster area is relatively high, we must take special care to choose the integration limits and the background level if using Eq. (2).

In contrast to globular clusters, where the statistical errors of empirical density profiles are negligibly low and the data fix a model safely in internal regions of the cluster area, in open clusters a fit based on the inner area is less reliable and can lead to a significant bias in the resulting tidal radius. Therefore, we must consider the behaviour of the density profile in the exterior regions of a cluster and even outside the cluster limits, which, a priori, we do not know. On the other hand, as one can see from Eq. (1), the value of f(r) increases at $r>r_{\rm t}$ and tends to a finite limit $f(r\rightarrow\infty)$, whereas n(r)goes to infinity for $r\rightarrow\infty$ in Eq. (2). This contradicts the physical meaning of n(r) since the number of cluster members should be finite, independent of how far one expands the counts. Therefore, for a physically correct application of Eq. (2), one should complement it by a boundary condition $n(r\geqslant r_{\rm t}) = N$ where N is the number of cluster stars. Again, $r_{\rm t}$ and N are unknown.

In order to overcome the problem, we tried to find a range $\Delta r$ where n(r) is practically flat (see for illustration Fig. 2, left panel). This range includes $r_{\rm t}$, and its length depends on the concentration $c=\log r_{\rm t}/r_{\rm c}$. The range $\Delta r$ degenerates to a point $r=r_{\rm t}$ at c=0 and increases with increasing c.

Figure 2: The general scheme of fitting cluster density profiles. Left panel: a theoretical, integrated King's profile for $r_{\rm c}=1$ pc, $r_{\rm t}=20$ pc with the fitting range $r_{\rm fit}$and tolerance $\theta$ as indicated. Right panel: the density profiles of the open cluster Trumpler 3 from the $2\sigma$-sample. The measured profile is shown by the short-dashed line. The empirical profile corrected for the background (see text) is indicated by crosses, the bars are Poisson errors. The vertical (blue) solid and dashed lines mark the empirical parameters r1and r2, respectively.

Open with DEXTER

For each cluster, a given membership sample may include a number of field stars having, by chance, the proper motions and photometry that are compatible with those of real cluster members. Therefore, before we can try to localize $\Delta r$ in the empirical, integrated density profiles, the residual background contamination has to be removed. If not, the profiles would increase steadily with increasing r. This is especially important for $3\sigma$- and "$4\sigma$''-samples that are strongly contaminated by field stars, although it can be essential for $1\sigma$ and $2\sigma$-samples, too.

The background correction was done in a uniform way for all clusters and membership samples. Assuming that the majority of stars at r>r₂ are not cluster members, we took the average density of a given membership group in a ring r₂ < r <2 r₂to be the initial background level in the internal cluster area (r<r₂). Outside r₂ (r₂ < r<5   r₂), the initial background was first set to the observed stellar density in each radial bin. The final, smooth background profile over the complete area 0<r<5  r₂ was then recomputed as a running average of the initial values with a filter size of 0 $\hbox{$.\!\!^\circ$ }$55 and a step of 0 $\hbox{$.\!\!^\circ$ }$05. Finally, the background profile was subtracted from the original density distribution. An example of an observed profile before and after background correction is shown in the right panel of Fig. 2. Except for a few cases of poor and extended clusters projected on a heavy and variable background, we obtained reasonable results.

The general scheme of the profile fitting is shown in Fig. 2(left) and is explained in the following:

Step 1: we start with the determination of an initial value $\tilde{r_2}$ of the fit radius $r_{\rm fit}$. Assuming the empirical cluster sizes r₁ and r₂ to be $r_{\rm c}$ and $r_{\rm t}$, respectively, we compute $\tilde{r_2}$ from King's profile of the concentration class $\tilde{c}=\log r_2/r_1$as the distance from the cluster centre where the profile does not differ from n(r₂) by more than an assumed tolerance $\theta$. The tolerance is chosen depending on the observation quality of a given cluster and is defined as the average of the Poisson errors of the profile outside r₂: $\theta=\langle\sigma_r(r > r_2 )\rangle,~~\sigma_r=\sqrt{n(r)}$.

Step 2: now we are able to apply a nonlinear fitting routine based on the Levenberg-Marquardt optimization method (Press et al. 1993) to Eq. (2) for $r = 0...\tilde{r_2}$. As initial-guess parameters we chose $r^0_{\rm c}=r_1$ and $r^0_{\rm t}=r_2$, whereas k⁰ is obtained from the solution of Eq. (2) at r=r₂. Empty bins in the differential density distribution were omitted from the integrated profile fitting. As a result of successive iterations, we get King's parameters, together with their rms errors and a $\chi^2$-value. The iterations are stopped when two successive $\chi^2$-values do not differ by more than 10^-3, and the solution is accepted when the number of iterations are less than 100. Then we compute the $\chi^2$-probability function $Q(\chi^2,\nu)$, which can be used as a measure of the goodness of fit. For a given degree of freedom $\nu$, $Q(\chi^2,\nu)$ is the probability that the difference between the observations and the fitted function can be considered random, and their sum of the squares is allowed to be greater than $\chi^2$. According to Press et al. (1993), the fit can be accepted when $Q(\chi^2,\nu)>0.1$.

Although a choice of $r_{\rm fit} = \tilde{r_2}$ fits a reasonable portion of King's profile to the observations, we consider this fit range as the lower limit of $r_{\rm fit}$.

Step 3: in order to check whether a better convergence can be achieved, we ran the fitting routine (i.e. Step 2) for different $r_{\rm fit}$ ranging from $\tilde{r_2}$ to 3 r₂. If several acceptable solutions (i.e. $Q(\chi^2,\nu)>0.1$) were obtained, we selected the one that yielded the smallest rms errors in $r_{\rm c}$ and $r_{\rm t}$.

The complete pipeline, including the background elimination and the profile fitting, was applied to all four membership groups. Although the initial guess $\tilde{r_2}$ of the fit radius is usually $\approx$1.5 r₂, the final fit radius $r_{\rm fit}$ turns out to be about 2 r₂, and the best $r_{\rm t}$ ranges from 1 r₂ to 2 r₂.

However, we must keep in mind that Eqs. (1) and (2) assume spherical symmetry in the spatial distribution of cluster stars, whereas a real open cluster is expected to have an elongated form with the major axis directed towards the Galactic centre (Wielen 1985). Thus, depending on the orientation of the line of sight, an observer measures a projection rather than the real size of a cluster, and the values of $r_{\rm t}$ derived via Eqs. (1) and (2) give generally lower limits of the tidal radii.

Table 1: Normalized values of King's parameters computed with four different membership groups.

  
3.2 Cluster masses

According to King (1962), the mass $M_{\rm c}$ of a cluster at the galactocentric distance R_G follows the relation

$$M_{\rm c}=\frac{4~ A~(A-B)~ r_{\rm t}^{3}}{G},$$ (3)

where A and B are Oort's constants valid for $R_{\rm G}$, and G is the gravitational constant (see Standish 1995). Since the bulk of our clusters is located within 2 kpc from the Sun, the linear approximation to the velocity field of the disk seems to be reasonable. Thus, Oort's constants could be easily expressed by their local values $A_0=14.5\pm0.8$ km s^-1kpc^-1, $B_0=-13.0\pm1.1$ km s^-1 kpc^-1 derived in Paper IV for the open cluster subsystem

$$\begin{eqnarray*}A&=&A_0 -A_0~\delta R_{\rm G} \\ A-B&=&A_0-B_0-2~A_0~\delta R_{\rm G} \end{eqnarray*}$$

where $\delta R_{\rm G}=(R_{\rm G}-R_{\rm G,0})/R_{\rm G,0}$, and $R_{\rm G,0}=8.5$ kpc.

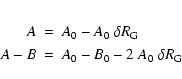
Table 2: Sample table of King parameters and tidal masses for 236 open clusters. The full table is available in machine readable form only at the CDS. See text for further explanations.

A relative random error of the cluster mass $\delta_{M_{\rm c}}=\varepsilon_{M_{\rm c}}/M_{\rm c}$ can be derived from Eq. (3) as

$$\delta_{M_{\rm c}}^{2}=9~\delta_{r_{\rm t}}^{2}+\left(\frac{2... ...2} \delta_{A}^{2}+\left(\frac{B}{A-B}\right)^{2}\delta_{B}^{2}$$ (4)

where $\delta_{r_{\rm t}}=\varepsilon_{r_{\rm t}}/r_{\rm t}$, $\delta_{A}=\varepsilon_{A}/A$, and $\delta_{B}=\varepsilon_{B}/B$ stand for relative random errors of the tidal radius and of Oort's constants, respectively. The cluster masses and their relative errors are computed with Eqs. (3) and (4) and are discussed in Sect. 4.3.

Equation (4) can be also used to get a "rule of thumb'' for the prediction of the expected accuracy of cluster masses derived from tidal radii. Assuming at first $A\approx A_0$ and $B\approx B_0$, one obtains $\delta{}_{A}\approx 0.06$, $\delta_{B}\approx 0.08$. Taking further into account that typically $\delta_{r_{\rm t}}>0.1$ (see Sect. 4), one finds that the relative error of mass determination is dominated strongly by the uncertainties of the tidal radius i.e.,

$$9~\delta_{r_{\rm t}}^{2}\gg\left(\frac{2A-B}{A-B}\right)^{2}\delta_{A}^{2}+\left( \frac{B}{A-B}\right)^{2}\delta_{B}^{2},$$

and therefore

$$\delta_{M_{\rm c}}\approx3~\delta_{r_{\rm t}}.$$ (5)

  
4 King's parameters: results

  
4.1 Construction of the output sample

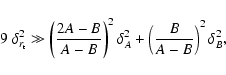
For 236 out of 290 clusters in the input list, we obtained at least one set of King's parameters by applying the method described in Sect. 3.1. Depending on the membership group, each of these clusters got from one to four different solutions, and the total number of solutions was 708. Per cluster, we have at least one set of parameters that are larger than their rms errors, i.e. with relative errors of $\delta_{r_{\rm c}}=\varepsilon_{r_{\rm c}}/r_{\rm c}<1$, $\delta_{r_{\rm t}}=\varepsilon_{r_{\rm t}}/r_{\rm t}<1$, and $\delta_{\rm k}=\varepsilon_{k}/k<1$. Since, for the majority of clusters, more than one set of King's parameters was obtained, we need a decision strategy for using the results in further analysis. From the point of view of membership, the parameters from 1$\sigma$-members should be the most reliable, but they are more uncertain from the point of view of statistics due to the relatively low number of stars. The opposite is true of "4$\sigma$-members''.

In order to compare the solutions derived from different membership groups, to check possible systematics between them and to define more or less objective criteria for parameter selection, we considered a subset of 114 clusters. This subset includes all clusters having four different solutions. For each of these clusters, we computed the mean from the four solutions for a given parameter and used this mean as a normalizing factor. If a normalized parameter is significantly smaller than one, we concluded that a given membership group delivers a significantly smaller parameter than the other groups, and vice versa. Table 1 gives the corresponding normalized parameters averaged over 114 clusters.

The most impressive feature of Table 1 is that the core radii $\bar{r}_{\rm c}$do not depend on the membership group used for computation, and tidal radii $\bar{r}_{\rm t}$ show only a slight systematic dependence on the membership groups. On average, the tidal radii obtained with the "$4\sigma$''-membership samples are smaller only by a factor of 1.1 than those with $1\sigma$-members. In contrast, the parameter k increases towards the "$4\sigma$''-membership sample and correlates strongly with the normalized number of cluster members n₂ located within an area of a radius r=r₂. This is a logical behaviour that follows from the meaning of k and n₂ in Eq. (2). A relation between the normalized parameter k and the number of the sample i ( i = 1,...,4) used for the solution can be approximated by

$$\bar{k} = (0.18\pm 0.04)\times i + (0.54\pm 0.11).$$ (6)

As expected, the relative errors in determining the parameters $\bar{\delta}_{r_{\rm c}}$, $\bar{\delta}_{r_{\rm t}}$, and $\bar{\delta}_{k}$are largest for the $1\sigma$-solution. The $1\sigma$-sample contains the most probable cluster members, but their number is relatively low compared to the other membership samples. This is the reason for relatively large Poisson errors and, consequently, for higher rms errors in the fitted parameters.

The goodness of a fit is given by the $Q(\chi^2,\nu)$-probability, an output parameter of the fitting pipeline (see Sect. 3.1). The normalized $\overline{Q}(\chi^2,\nu)$-parameters averaged over 114 clusters are also given in Table 1. The systematic trend in $\overline{Q}(\chi^2,\nu)$indicates a more suitable fitting with $1\sigma$- and $2\sigma$-samples than with "$4\sigma$''-groups.

Based on the statistics in Table 1, we chose the following ranking of the solutions. We give the highest weight to the solutions with the highest $Q(\chi^2,\nu)$-probability. If, for a given cluster, there are more than one solution of the same quality (i.e., the $Q(\chi^2,\nu)$-probabilities differ by less than 0.1%), we used an additional criterion based on $\chi^2$-values supplied by the fitting pipeline. Since $\chi^2$ does depend on the sample size n and on the degree of freedom $\nu$ , a readjustment of the $\chi^2$-estimate was needed when we compared fitting results derived with different membership samples. Therefore, we selected a solution with a lower value $\chi^2_{\nu,n} = \chi^2/(\nu \times n)$, which is, in fact, an average mean square deviation of the observed from the fitted profiles in units of Poisson errors computed per star. In a few cases when even the $\chi^2_{\nu,n}$-parameters differ insignificantly (by less than 0.001) for two solutions, we gave priority to the solution with smaller error $\varepsilon_{r_{\rm t}}$.

According to the selection procedure, the solution from the $1\sigma$-samples gets the best ranking in 94 cases out of 236, from $2\sigma$-samples - in 72 cases, from $3\sigma$-samples - in 39 cases, and "$4\sigma$''-samples - in 31 cases.

The data on the structural parameters are compiled in a table that is available in machine-readable form only. Table 2 lists a few entries of the complete data as an example. Column 1 gives the cluster number in the COCD catalogue, columns 2 through 9 are taken from the COCD, while columns 10 through 20 include the information obtained in this work. For each of the 236 clusters we give: name (2), galactic coordinates (3, 4), the distance from the Sun in pc (5), the reddening (6), the logarithm of the cluster age in years (7), empirical angular radii (in degrees) of the core r₁ (8) and of the corona r₂ (9). Column (10) is the number of the acceptable solutions of King's parameters from the four membership groups. Column (11) gives the number of the membership sample ($1\sigma$, $2\sigma$, $3\sigma$, or "$4\sigma$'') chosen by the selection procedure as providing the best solution, whereas column (12) is the number of cluster members of this sample within r₂after background correction. Columns 13 through 18 give the corresponding King parameters $r_{\rm c},~r_{\rm t},~k$ with their rms errors. The parameters are taken as obtained from the selected solution. Depending on the applications desired, the reader is advised to take into account the empirical relations between the selected solution for $r_{\rm t}$ and k and the membership sample used to obtain these parameters (cf. Table 1 and Eq. (6)). Finally, columns (19, 20) provide the logarithm of the cluster mass and its rms error computed from $r_{\rm t}$ by use of Eq. (3) and discussed in Sect. 4.3.

4.2 Properties of the sample of King's parameters for open clusters

	Figure 3: Distributions of King's radii and their relative errors for 236 open clusters. Panels a) and b) are for the core radius $r_{\rm c}$ and the tidal radius $r_{\rm t}$ measured in pc. Distributions of relative errors in core radius $\delta _{r_{\rm c}}$ and in tidal radius $\delta _{r_{\rm t}}$ are shown in panels c) and d), respectively.
Open with DEXTER

Figure 4: Examples of radial profiles from our final sample ordered by the priority of the solution. The uppermost row represents the $1\sigma$-sample. The second row is for $2\sigma$-solutions, the third and fourth rows illustrate $3\sigma$ and $4\sigma$samples. The crosses show empirical data corrected for the background, the vertical bars are Poisson errors. The vertical lines indicate the derived radii. The solid lines show r1 and $r_{\rm c}$, the broken lines r2 and $r_{\rm t}$. The empirical parameters are shown with blue colour, while the fitted data are shown in red. Horizontal bars indicate the value of the rms error of the parameter. The solid curve is the fitted King profile, the broken curve (yellow) is the total profile not corrected for background.

Open with DEXTER

In Figs. 3a,b we show the distribution of 236 clusters over the derived parameters $r_{\rm c}$ and $r_{\rm t}$. The distributions are rather compact with peaks at about 1.5 pc for the core radii and at about 7-10 pc for the tidal radii. According to Figs. 3c,d, the relative error $\delta _{r_{\rm c}}$ of the core radius is typically between 15% and 50%, whereas the tidal radius is more accurate: the majority of the clusters have the tidal radius determined with a relative error $\delta _{r_{\rm t}}$ better than 20%. Therefore, for these clusters, we expect to obtain reasonable estimates of masses from the present data (cf. Eqs. (4), (5)). As a rule, clusters that are more distant and/or less populated got relatively large errors in $r_{\rm t}$. In these cases the method reaches its limitations. Probably, if applied to deeper photometric data, the method may provide acceptable results for a large portion of these clusters. Nevertheless, there is a number of clusters with "irregular'' density profiles, and fitting them by a model proposed for spherical systems in equilibrium does not offer much prospect of success.

In order to give the reader an idea of typical profiles, we show a set of different cases selected from the final sample in Fig. 4. Compared to the empirical cluster radius r₂, the tidal radius $r_{\rm t}$ ranges between 1 r₂ and 2 r₂. For clusters with relatively accurate radii ( $\delta_{r_{\rm c}}< 0.33$and $\delta_{r_{\rm t}} <0.33$), the averaged relation is

$$r_{\rm t} = (1.54\pm0.02)\times r_2.$$

Therefore, we conclude that the empirical parameter r₂ scales the tidal radius reasonably well.

  
4.3 Cluster masses

Using Eq. (3) and the tidal radius $r_{\rm t}$, we estimated masses for each of the 236 open clusters. The results are shown in Fig. 5 where the distribution of clusters over mass is given in panel a), while panel b) shows the distribution of relative errors in mass. Most of the clusters in our sample have masses in a range $\log M_{\rm c}/m_\odot= 1.6$-2.8, though a few clusters have masses as low as $10~m_\odot$. Three objects have masses of about $10^5~m_\odot$. They are the associations Nor OB5, Sco OB4, and Sco OB5. For 139 clusters, the masses were obtained with a relative accuracy better than 60%. Their distribution shows the same features as the complete sample.

We note that the masses based on $r_{\rm t}$ from Eq. (2) do not take a possible flattening of clusters into account, which arises due to the tidal coupling with the Milky Way. Because of this, a stellar cluster has a shape of a three-axial ellipsoid with the major axis oriented in the direction of the Galactic centre. In general, we obtain a projection of the tidal radius on the celestial sphere from Eq. (2), and the relation between the tidal radius and this projection depends on the mutual position of the Sun and a given cluster. Comparing masses of two clusters with different locations in the Galactic disk, the corresponding effect must, therefore, be taken into account.

  
5 Comparison with other determinations

5.1 King's radii from a three parameter fit

In contrast to massive spherical systems, there are only a few results reported on the determination of structural parameters of open clusters via direct parameter fits of King's profiles to the observed density distributions. Some of them consider remote clusters (e.g., King 1962; Leonard 1988) or newly detected cluster candidates (Froebrich et al. 2007), which are absent in our cluster sample. Others are based on a two-parameter fit (Keenan 1973; Bica 2006; Bonatto et al. 2005b),so that these results cannot be compared directly with ours. We found only seven papers where a three-parameter fit was applied to open clusters. In these papers only four clusters are in common with our sample. These are two nearby clusters, the Pleiades and Praesepe, NGC 2168 (M 35) at 830 pc from the Sun, and the relatively distant cluster NGC 2477, at 1.2 kpc.

Table 3: Comparison of our results with the literature data on King's parameters for the clusters in common.

In Table 3 we compare the results obtained in this paper with those found in the literature for the four clusters. Column 1 is the cluster identification. In columns 2 through 6 we provide our results: the number of members within the empirical cluster radius r₂ (Col. 2), $r_{\rm fit}$ i.e. a radius found as best-suited for the profile fitting (Col. 3) (cf. Sect. 3.1). The results of the fitting, King's radii $r_{\rm c}$, and $r_{\rm t}$ are listed in Cols. 4 and 5, together with their rms errors, whereas the corresponding tidal mass is given in Col. 6. Columns 7 through 10 show the data from the literature: Cols. 7 and 8 give the number of stars used to construct the density profiles and the radius of the area considered, respectively. The King radii are listed in Cols. 9 and 10. Note that we are not able to keep a uniform format for these data due to the different presentations of the results in different papers.

	Figure 5: Distributions of cluster masses (panel a)) and their relative rms errors(panel b)). Clusters with accurate masses( $\delta _M< 60\%$) are shown as the dark histogram in panel  a).
Open with DEXTER

We found three different estimates of the tidal radius published for the Pleiades. A direct comparison with our results can be made only with radii obtained by Raboud and Mermilliod (1998a), who consistently applied the 3-parameter fitting technique both to various sub-samples of the Pleiades stellar population and to the total membership sample. From Table 3 we conclude that their findings of $r_{\rm c}$ and $r_{\rm t}$ coincide with our results. A slightly different method was applied by Pinfield et al. (1998) to derive a tidal radius for the Pleiades. They used differential density profiles, which were constructed for cluster members falling in different mass ranges and tidal radii computed for each of these sub-samples. The results were used to derive the partial and total masses of the cluster. The tidal radius for the cluster as a whole was then computed from the cluster mass via Eq. (3). A similar approach was used by Adams et al. (2001) who applied a 3-parameter fit to a sample of low-mass ( $m<1~m_\odot$) members of the Pleiades. Again, the tidal radius $r_{\rm t}$ was derived from stellar mass counts in the cluster by Eq. (3). The approach by Pinfield et al. (1998) and Adams et al. (2001) provides a lower value for $r_{\rm t}$ and higher value for $r_{\rm c}$ (for Pleiades members less massive than $1.2~m_\odot$) than a direct 3-parameter fitting of the density distribution applied to the full sample of cluster members. Nevertheless, taking into account that the three studies and ours are based both on observations of different spatial and magnitude coverage and on an independent membership evaluation, the agreement between the results is quite acceptable.

We arrived at similar conclusions in the case of Praesepe. Our estimate for $r_{\rm t}$ is compatible with the result by Raboud & Mermilliod (1998b) within the rms errors, and it coincides with the finding of Adams et al. (2002) who, as in the case of the Pleiades, fitted the King profile to low-mass (m=0.1-1 $m_\odot$) cluster members. With respect to $r_{\rm c}$, we achieved good agreement with the estimate by Raboud & Mermilliod (1998b), whereas $r_{\rm c}$ from Adams et al. (2002) is significantly higher. Such a systematic difference can possibly be explained by the considerably deeper survey used by Adams et al. (2002) in studies of the Pleiades and the Praesepe. Since their empirical profiles are based on USNO POSS I E and POSS II F plate scans and on the 2MASS catalogue, the input data are dominated by lower-mass stars that, due to the energy equipartition process, show a wider distribution than the more massive stars.

For the last two clusters in Table 3, there are only two papers reporting the determinations of King's parameters. Leonard & Merritt (1989) studied the central area of the NGC 2168 cluster, so were only able to set probable limits for the cluster radii. Our estimates of $r_{\rm c}$ and $r_{\rm t}$ fit these limits well. For the relatively distant and rich cluster NGC 2477, the King radii were published by Eigenbrod et al. (2004). The authors defined the membership sample on the basis of radial velocities for numerous red giants and constructed density profiles for groups of stars of various masses. The core and tidal radii of the cluster were determined from the comparison of the structure parameters of single groups. Also in this case, their results are in good agreement with our estimates of $r_{\rm c}$ and $r_{\rm t}$, though NGC 2477 belongs to the poorer clusters in our sample due to its large distance from the Sun. With 10 members within r₂, NGC 2477 marginally satisfies our constraints. Nevertheless, the fitted parameters coincide well with the corresponding estimates obtained with the much deeper survey (V<17) by Eigenbrod et al. (2004).

5.2 Various scales of cluster masses

Although the adopted values of Oort's constants and of a distance to a cluster can slightly influence its mass estimate, the tidal radius is the major source of uncertainty in the mass determination via Eq. (3), simply due to the cubic power relation between tidal radius and cluster mass. Analysing different groups of the Pleiades members, Raboud & Mermilliod (1998a) concluded that the tidal mass of the Pleiades is about $1400~m_\odot$ with a $1\sigma$ confidence interval of $[530,~2900]~m_\odot$. With Oort's constants A = 15 km s^-1kpc^-1, B = -12 km s^-1kpc^-1and a cluster distance of 125 pc adopted by the authors, a strict application of Eq. (3) would provide a tidal mass of $1620~m_\odot$ $([330,~4600]~m_\odot)$for the Pleiades. From a similar analysis for Praesepe, Raboud & Mermilliod (1998b) derived a tidal mass of $440~ m_\odot$ $([157,~987]~m_\odot)$ (a consequent use of Eq. (3) would give $520~m_\odot$ $([90,~1570]~m_\odot)$). We conclude that the disagreement between our estimates and those of Raboud & Mermilliod (1998a,b) for the Pleiades and Praesepe are mainly caused by statistical uncertainties in the determination of the tidal radii (cf. Table 3).

In the case of NGC 2477, the situation is less clear. For this cluster, Eigenbrod et al. (2004) estimated the tidal and virial masses to be $M_{\rm tid}=5400~m_\odot$ and $M_{\rm vir}=5300~m_\odot$, respectively. This result differs considerably from our estimate. Moreover, it contradicts the value of their tidal radius of $r_{\rm t}=8.1$ pc, which should give a tidal mass of $M_{\rm tid} \approx 170~m_\odot$ according to Eq. (3). Therefore, the coincidence achieved by Eigenbrod et al. (2004) between the tidal and virial masses should be considered with caution. We note that NGC 2477 has not been studied very much, and its membership is poorly established. Therefore, a contamination of the stellar sample from Eigenbrod et al. (2004) is very probable. This could be one reason for overestimating the velocity dispersion and, consequently, the virial mass of the cluster. The presently high uncertainties in kinematical data for determing virial masses can also cause these discrepancies. (see Appendix A for more detail). On the other hand, this large disagreement can be partly explained by an underestimation of the tidal radius. If this relatively distant cluster is subject to strong mass segregation, low-mass stars on the cluster edges can be beyond the magnitude limit even in a deep survey.

Since literature data on tidal masses of open clusters are rather scarce, we looked for recent publications on cluster masses estimated with other methods. We omit here a discussion of the determination of virial masses of open clusters and refer the reader to Appendix A where this method is discussed in more detail. To compare our results on cluster masses, we considered only those publications where cluster masses are obtained for a relevant number of open clusters rather than for a single cluster. Under these constraints, we found three publications on mass determination for galactic open clusters, Danilov & Seleznev (1994), Tadross et al. (2002), and Lamers et al. (2005). In Fig.6 we compare the different results for mass estimates.

Danilov & Seleznev (1994) derived masses for 103 compact, distant (>1 kpc) clusters from star counts down to B=16 from homogeneous wide-field observations with the 50-cm Schmidt camera of the Ural university. For each cluster, the authors estimated the average mass of a star observed in a cluster and then computed the total visible cluster mass. The average mass is found either from star counts or from an extrapolation of the Salpeter IMF down to the magnitude limit B=16. On one hand, their cluster masses should be underestimated due to their magnitude-limited survey, and the bias should increase with increasing distance modulus of a cluster. On the other hand, without membership information, the masses could be overestimated for clusters located at relatively low distances from the Sun. In a certain respect, these biases may partly compensate for each other.

Based on UBV-CCD observations compiled from the literature, Tadross et al. (2002) redetermined ages and distances for 160 open clusters and derived cluster masses from counts of photometrically selected cluster members. Since they used observations taken with different telescopes, i.e., for different clusters one expects different limiting magnitudes, it is rather difficult to estimate possible biases. In any case, a large portion of clusters should get underestimated masses due to the relatively small area of the sky usually covered by CCD observations in the past.

Lamers et al. (2005) used data from the COCD to determine cluster masses. For each cluster, the authors normalized the Salpeter IMF in the mass range of stars present in COCD (V < 11.5), and the normalized Salpeter IMF was extrapolated from large masses down to $m=0.15~m_\odot$. For distant clusters with V-M_V>8, the extrapolation was done over a very wide range, from masses larger than $\approx$ $1.5~m_\odot$ (or M_V<3.5) to masses of $0.15~m_\odot$ (or $M_V \approx 13$), where the IMF is still not very well known. If the IMF at low masses were flatter than the Salpeter IMF (see e.g. Kroupa et al. 1993), the approach by Lamers et al. (2005) would overestimate cluster masses. Moreover, in a segregated cluster one should expect different forms of the mass function in the central area and at the edges. Integration of the Salpeter IMF over the complete cluster area would also result in overestimating the cluster mass. A comparison of our cluster masses with those of Lamers et al. (2005) is especially interesting: since both papers use the same observational basis, we can estimate the uncertainties caused by the different approaches.

According to our determination of cluster masses based on tidal radii, we expect possible biases for relatively distant clusters where we observe only the tip of bright stars. Especially in segregated clusters, the brightest stars are more concentrated in the cluster centre due to energy equipartition and do not reproduce the correct tidal radius. Nevertheless, for distant clusters we can see a distance-dependent effect only in the upper panel of Fig. 6, where we compare our masses with those of Danilov & Seleznev (1994). Since the $M_{\rm D}/M_{\rm C}$-relations decrease with distance modulus, we suppose that our method manages biases better than the approach by Danilov and Seleznev (1994). Moreover, the dependence of the $M_{\rm D}/M_{\rm C}$-relations on distance modulus may be explained alone by the biases in the mass determination by Danilov and Seleznev (1994) described above, i.e. overestimated masses for clusters at low distances and underestimated masses for distant clusters. This interpretation seems to be plausible, but we cannot completely exclude distance-dependent biases in our determinations.

Furthermore, due to a possibly elongated form of open clusters (cf. Sect. 3), our estimates provide a lower limit for cluster masses. This can be one of the reasons for systematic differences in cluster masses from Lamers et al. (2005). Except for nearby clusters with V-M_V<8, their masses are, on average, larger by a factor of 10. On the other hand, masses from Lamers et al. (2005) are systematically higher than masses from Danilov and Seleznev (1994) and Tadross et al. (2002), too. Therefore, we cannot exclude that the approach by Lamers et al. (2005) is, at least partly, responsible for these differences.

Figure 6: Comparison of tidal masses $M_{\rm c}$ of open clusters derived in the present study with literature values on counted- and MF-scaled masses as a function of the distance modulus. From top to bottom we show ratios of: counted masses of Danilov & Seleznev (1994) ($M_{\rm D}$ to tidal masses); counted masses of Tadross et al. (2002) ($M_{\rm T}$ to tidal masses); and the IMF-scaled masses of Lamers et al. (2005) ($M_{\rm L}$ to tidal masses). The last panels show intercomparisons of literature data.

Open with DEXTER

  
6 Conclusions

In an ideal case - i.e. if, for a given cluster, the membership is determined with certainty and completeness - the cluster mass could simply be derived from counting masses of individual members. In the future, with deeper surveys and an increasing accuracy of kinematic and photometric data, this primary method will provide sufficiently accurate and uniform mass estimates for a significant number of open clusters in the Galaxy. At present, however, there is no way to measure the masses of open clusters directly. The methods currently applied require a number of assumptions, and depending on the method and assumptions used, the results can differ by a factor of 100 for individual clusters (cf. Fig. 6). Therefore, the determination of cluster masses is still a very challenging task.

Our aim was to estimate masses for a larger number of clusters by applying a uniform and possibly objective method and to obtain an independent basis for statistical studies of the distribution of cluster masses in the Galaxy. In our work we could benefit from the homogeneous set of cluster parameters derived for 650 open clusters with good membership based on the astrometric and photometric data of the ASCC-2.5. The estimation of cluster masses was done via tidal radii determined from a three-parameter fit of King's profiles to the observed density distribution (King 1962). This method is weakly dependent on assumptions and can be applied to all spherical systems in equilibrium with well-defined density profiles. Since these requirements are not always met in the case of open clusters, we could only obtain solutions for 236 clusters, i.e. for less than half of the clusters in our sample. However, this number is considerably larger than the small number of clusters with tidal masses determined before.

The main difficulties in the practical application of King's model to open clusters arise from the relatively poor stellar population (compared to globular clusters) and from the higher degree of contamination by field stars in the Galactic disk. Using an all-sky survey, we could rely on the completeness of data in the selected sampling areas, down to the limiting magnitude of the ASCC-2.5. Further, since we were free to select the size of the sampling areas, we were able to optimize the boundary condition for each cluster as much as possible. As a result, we could partly decrease the influence of the above-mentioned problems in applying King's method and could improve the solutions by taking the outermost regions of the clusters into account and by excluding residual field stars from the solution.

Together with a realistic membership based on both kinematic and photometric constraints, a good profile fitting could be achieved even for clusters with a relatively low number of members. The highest quality of the fitting (goodness-of-fit) was achieved with the best-determined membership sample (so-called "$1\sigma$''-members) and, hence, a low contamination by field stars. However, it turned out that the membership criterium alone did not have very strong impact on the values of the fitted parameters $r_{\rm c}$ and $r_{\rm t}$ themselves. In fact, for compact and relatively distant clusters, we sometimes found the best results without a preliminary membership selection (so-called "$4\sigma$''-members). In conclusion, this paper could be seen as justification for a simple application of King's method to observed brightness profiles of compact open clusters whether membership is determined or not, provided that the observed density profiles are properly corrected for the background.

Acknowledgements

We are grateful to Henny Lamers for providing us with unpublished data on cluster masses. This study was supported by DFG grant 436 RUS 113 /757/0-2, and RFBR grant 06-02-16379.

  
Appendix A: Virial masses of open clusters: current status

Figure A.1: Masses and internal velocity dispersions for the open clusters: Pleiades, Praesepe, NGC 6494, NGC 2168, NGC 2682, and NGC 6705 (the clusters are ordered with distance). Upper panel: internal velocity dispersion versus distance. Dots are for proper motion dispersions, triangles for tangential velocity dispersions. Bars are rms-errors of the dispersions: bars with hats are for proper motions and bars without hats for tangential velocities (for the Pleiades and Praesepe, the symbols for the proper motion dispersions are shifted to the left for a better visibility). The line shows a linear fit to the tangential velocity dispersion data. Lower panel: cluster mass versus distance (based on literature data, see text for more detail). Crosses mark virial masses obtained from proper motion dispersions, and squares show counted masses.

All our attempts have failed to compute reasonable cluster masses from the dispersion of proper motions and/or radial velocities taken from the ASCC-2.5 catalogue for cluster members. The main reason is the accuracy of kinematical data, which is still too low in current all-sky surveys.

Up to now, the best published data on velocity dispersions were obtained for a few open clusters from proper motions obtained from long-term observations with the Yerkes 40-inch refractor (F = 19.3 m, a scale of 10.7 arcsec/mm, a typical epoch difference of more than 55 years, and a typical rms-error of the proper motions of a few 0.1 mas/y). The clusters are the Pleiades (Jones 1970), Praesepe (Jones 1971), NGC 6705 (McNamara & Sanders 1977), NGC 6494 (McNamara & Sanders 1983), NGC 2168 (McNamara & Sekiguchi 1986), NGC 2682 (Girard et al. 1989). In these papers, the internal proper motion dispersions are corrected for different biases, and virial as well as counted masses, are determined for four clusters i.e., the Pleiades, Praesepe, NGC 6494, NGC 6705. The results are shown in Fig. A.1.

Independent of the methods of mass determination, the masses in Fig. A.1 show a correlation with cluster distance. Since the number of clusters is very low, the correlation does not need to be real, but can appear by chance, due to the small sample. In order to understand the effect, we transformed the proper motion dispersions $\sigma_{\mu}$ published for 6 clusters to one-dimensional tangential velocity dispersions $\sigma_{v}$ via $\sigma_{v} = 4.74~ d~ \sigma_{\mu}$, where d is the distance of a cluster adopted in the original papers. In the upper panel of Fig. A.1 we show $\sigma_{\mu}$ and $\sigma_{v}$ as functions of distance d. Whereas $\sigma_{\mu}$ is independent of the cluster distance, the tangential velocity dispersion $\sigma_{v}$ indicates a strong correlation that is well-described by a first-order polynomial. Therefore, we suppose a non negligible random component in $\sigma_{v}$ resulting instead from residual rms errors in proper motions but not from the internal velocity dispersion. This is not surprising, because, for all clusters at distances larger than the Pleiades and Praesepe, the dispersions are of the order of the rms errors of the proper motion measurements. Assuming that the internal velocity dispersion $\bar{\sigma}_{v}$ was similar for all these clusters, we obtained $\bar{\sigma}_{v} = 0.31$ km s^-1 by extrapolating the linear regression polynomial to d=0. In other words, we need tangential velocities determined with an accuracy better than 0.3 km s^-1(or proper motions with an accuracy better than 0.06-0.07 mas/y for a cluster at d= 1 kpc) for a more or less reliable estimate of its virial mass. Even the Hipparcos proper motions with typical rms errors of 1 mas/yr do not meet this requirement.

With respect to radial velocities, one may suppose that these give a better basis for the determination of the internal velocity dispersion since their accuracy does not depend on distance. Recently, radial velocities have been measured in several open clusters for a sufficient number of cluster members (see e.g., Eigenbrod et al. 2004 for NGC 2477, or Fürész et al. 2006 for NGC 2264). The derived velocity dispersions are, however, somewhat too large, 0.93 km s^-1 in NGC 2477, and 3.5 km s^-1 in NGC 2264. This may be a consequence of biases that still affect the data and that are very difficult to take into account. Among them may be the contamination by field stars and by unresolved binaries, or motions within stellar atmospheres.

References

• Adams, J. D., Stauffer, J. R., Monet, D. G., Skrutskie, M. F., & Beichman, C. A. 2001, AJ, 121, 2053 [NASA ADS] [CrossRef] (In the text)
• Adams, J. D., Stauffer, J. R., Skrutskie, M. F., et al. 2002, AJ, 124, 1570 [NASA ADS] [CrossRef] (In the text)
• Bica, E., Bonatto, C., & Blumberg, R. 2006, A&A, 460, 83 [NASA ADS] [CrossRef] [EDP Sciences]
• Bonatto, C., & Bica, E. 2005, A&A, 437, 483 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Bonatto, C., Bica, E., & Santos, J. F. C. 2005, A&A, 433, 917 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Danilov, V. M., & Seleznev, A. F. 1994, Astron. Astrophys. Trans., 6, 85 (In the text)
• Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Eigenbrod, A., Mermilliod, J.-C., Clariá, J. J., Andersen, J., & Mayor, M. 2004, A&A, 423, 189 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Elson, R. A. W., Fall, M., & Freeman, K. C. 1987, ApJ, 323, 54 [NASA ADS] [CrossRef] (In the text)
• Froebrich, D., Scholz, A., & Raftery, C. L. 2007, MNRAS, 374, 399 [NASA ADS] (In the text)
• Fürész, G., Hartmann, L. W., Szentgyorgyi, A. H., et al. 2006, ApJ, 648, 1090 [NASA ADS] [CrossRef] (In the text)
• Girard, T. M., Grundy, W. M., Lopez, C. E., & van Altena, W. F. 1989, AJ, 98, 227 [NASA ADS] [CrossRef] (In the text)
• Hill, A., & Zaritsky, D. 2006, AJ, 131, 414 [NASA ADS] [CrossRef] (In the text)
• von Hoerner, S. 1957, ApJ, 125, 451 [NASA ADS] [CrossRef] (In the text)
• Jones, B. F. 1970, AJ, 75, 563 [NASA ADS] [CrossRef] (In the text)
• Jones, B. F. 1971, AJ, 76, 470 [NASA ADS] [CrossRef] (In the text)
• Keenan, D. W., Innanen, K. A., & House, F. C. 1973, AJ, 78, 173 [NASA ADS] [CrossRef] (In the text)
• King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] (In the text)
• King, I. 1966, AJ, 71, 64 [NASA ADS] [CrossRef] (In the text)
• Kharchenko, N. V. 2001, Kinematics and Physics of Celestial Bodies, 17, 409 (In the text)
• Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2004, Astron. Nachr., 325, 743 [NASA ADS] (Paper I) (In the text)
• Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005a, A&A, 438, 1163 [NASA ADS] [CrossRef] [EDP Sciences] (Paper II) (In the text)
• Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005b, A&A, 440, 403 [NASA ADS] [CrossRef] [EDP Sciences] (Paper III) (In the text)
• Kontizas, M. 1984, A&A, 131, 58 [NASA ADS] (In the text)
• Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] (In the text)
• Lamers, H. J. G. L. M., Giles, M., Bastian, N., et al. 2005, A&A, 441, 117 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Lehmann, I., & Scholz, R.-D. 1997, A&A, 320, 776 [NASA ADS] (In the text)
• Leonard, J. T. 1988, AJ, 95, 108 [NASA ADS] [CrossRef] (In the text)
• Leonard, J. T., & Merrit, D. 1989, ApJ, 339, 195 [NASA ADS] [CrossRef] (In the text)
• McNamara, B. J., & Sanders, W. L. 1977, A&A, 54, 569 [NASA ADS] (In the text)
• McNamara, B. J., & Sanders, W. L. 1983, A&A, 118, 361 [NASA ADS] (In the text)
• McNamara, B. J., & Sekiguchi, K. 1986, ApJ, 310, 613 [NASA ADS] [CrossRef] (In the text)
• Petersen, C. J., & King, I. R. 1975, AJ, 80, 427 [NASA ADS] [CrossRef] (In the text)
• Pinfield, D. J., Jameson, R. F., & Hodgkin, S. T. 1998, MNRAS, 299, 955 [NASA ADS] (In the text)
• Piskunov, A. E., Kharchenko, N. V., Röser, S., Schilbach, E., & Scholz, R.-D. 2006, A&A, 445, 545 [NASA ADS] [CrossRef] [EDP Sciences] (Paper IV) (In the text)
• Press, W. H., Flannery, B. P., Teukolsky, S. S., & Vettrling, W.T. 1993, Numerical Recipes (Cambridge: Cambridge Univ. Press) (In the text)
• Raboud, D., & Mermilliod, J.-C. 1998a, A&A, 329, 101 [NASA ADS] (In the text)
• Raboud, D., & Mermilliod, J.-C. 1998b, A&A, 333, 897 [NASA ADS] (In the text)
• Schilbach, E., Kharchenko, N. V., Piskunov, A. E., Röser, S., & Scholz, R.-D. 2006, A&A, 456, 523 [NASA ADS] [CrossRef] [EDP Sciences] (Paper V) (In the text)
• Standish, E. M. 1995, Report of the IAU WGAS Sub-Group on Numerical Standards, Table 1, in Highlights of Astronomy, ed. I. Appenzeller (Dordrecht: Kluwer Academic Publishers) (In the text)
• Tadross, A. L., Werner, P., Osman, A., & Marie, M. 2002, NewA, 7, 553 [NASA ADS] [CrossRef] (In the text)
• Trager, S. C., King, I. R., & Djorgovski, S. 1995, AJ, 109, 218 [NASA ADS] [CrossRef] (In the text)
• Wielen, R. 1985, in Dynamics of star clusters, eds. J. Goodman, & P. Hut (Dordrecht: D. Reidel Publishing Co.) 449 (In the text)