A&A 468, 233-254 (2007)
DOI: 10.1051/0004-6361:20066688
Stellar and wind properties of massive stars in the central parsec of the Galaxy
F. Martins1 -
R. Genzel1,2 -
D. J. Hillier3 -
F. Eisenhauer1 -
T. Paumard1,4 -
S. Gillessen1 -
T. Ott1 -
S. Trippe1
1 - Max-Planck Institüt für extraterrestrische Physik, Postfach-1312, 85741, Garching, Germany
2 -
Department of Physics, University of California, Berkeley, CA 94720, USA
3 -
Department of Physics and Astronomy, University of Pittsburgh, 3941 O'Hara St., Pittsburgh, PA 15260, USA
4 -
LESIA, Observatoire de Paris, 5 Place Jules Janssen, 92195, Meudon, France
Received 3 November 2006 / Accepted 1 March 2007
Abstract
Context. How star formation proceeds in the Galactic Center is a debated question. Addressing this question will help us understand the origin of the cluster of massive stars near the supermassive black hole, and more generally, starburst phenomena in galactic nuclei. In that context, it is crucial to know the properties of young massive stars in the central parsec of the Galaxy.
Aims. The main goal of this study is to derive the stellar and wind properties of the massive stars orbiting the supermassive black hole SgrA in two counter-rotating disks.
in two counter-rotating disks.
Methods. We use non-LTE atmosphere models including winds and line-blanketing to reproduce H and K band spectra of these stars obtained with SINFONI on the ESO/VLT.
Results. The GC massive stars appear to be relatively similar to other Galactic stars. The currently known population of massive stars emit a total 6.0  1050 s-1 (resp. 2.3
1050 s-1 (resp. 2.3  1049 s-1) H (resp. He I) ionising photons. This is sufficient to produce the observed nebular emission and implies that, in contrast to previous claims, no peculiar stellar evolution is required in the Galactic Center. We find that most of the Ofpe/WN9 stars are less chemically evolved than initially thought. The properties of several WN8 stars are given, as well as two WN/C stars confirmed quantitatively to be stars in transition between the WN and WC phase. We propose the sequence (Ofpe/WN9
1049 s-1) H (resp. He I) ionising photons. This is sufficient to produce the observed nebular emission and implies that, in contrast to previous claims, no peculiar stellar evolution is required in the Galactic Center. We find that most of the Ofpe/WN9 stars are less chemically evolved than initially thought. The properties of several WN8 stars are given, as well as two WN/C stars confirmed quantitatively to be stars in transition between the WN and WC phase. We propose the sequence (Ofpe/WN9
 LBV)
LBV)
 WN8
WN8
 WN/C for most of the observed GC stars. Quantitative comparison with stellar evolutionary tracks including rotation favour high mass loss rates in the Wolf-Rayet phase in these models. In the OB phase, these tracks nicely reproduce the average properties of bright supergiants in the Galactic Center.
WN/C for most of the observed GC stars. Quantitative comparison with stellar evolutionary tracks including rotation favour high mass loss rates in the Wolf-Rayet phase in these models. In the OB phase, these tracks nicely reproduce the average properties of bright supergiants in the Galactic Center.
Key words: stars: early-type - stars: Wolf-Rayet - stars: atmospheres -
stars: fundamental parameters - stars: winds, outflows - Galaxy: center
1 Introduction
The center of our Galaxy is a unique environment to study massive
stars. It harbors three of the most massive clusters of the Galaxy -
the Arches, Quintuplet and central clusters. Heavily extinguished and
only accessible at infrared (and longer) wavelengths or in X-rays,
each of these clusters has a population of more than a hundred massive
stars. Even more interesting is the difference in their ages: 2.5, 4
and 6 Myr for the Arches, the Quintuplet and the central cluster
respectively (Figer et al. 1999,2002; Paumard et al. 2006). Such a spread implies the
presence of different types of massive objects, naturally sampling
stellar evolution in the upper HR diagram. The youth of these
clusters, together with their total mass in excess of 104 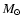 ,
partly explains the large number of massive stars in the Galactic
Center. But another reason may be the top-heavy mass function:
Stolte et al. (2002) for the Arches and Paumard et al. (2006) for the central
cluster have shown that the slope
,
partly explains the large number of massive stars in the Galactic
Center. But another reason may be the top-heavy mass function:
Stolte et al. (2002) for the Arches and Paumard et al. (2006) for the central
cluster have shown that the slope 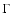 of the present-day mass
function was shallower than the standard Salpeter value (-0.8instead of -2.35). This may be due to mass segregation or to a true
feature of the initial mass function. In that case the
Galactic Center could be a peculiar environment for the formation of
massive stars.
of the present-day mass
function was shallower than the standard Salpeter value (-0.8instead of -2.35). This may be due to mass segregation or to a true
feature of the initial mass function. In that case the
Galactic Center could be a peculiar environment for the formation of
massive stars.
As a peculiar environment, the central cluster is especially interesting since it harbors the supermassive black hole SgrA .
The first stars ever observed in this region were the
so-called "AF'' and "IRS16'' stars (Allen et al. 1990; Forrest et al. 1987). Their
K-band spectrum showed strong emission lines - in particular the
He I 2.058
.
The first stars ever observed in this region were the
so-called "AF'' and "IRS16'' stars (Allen et al. 1990; Forrest et al. 1987). Their
K-band spectrum showed strong emission lines - in particular the
He I 2.058  m feature - and they were immediately classified as Ofpe/WN9, a class of evolved massive stars. Further observations by Krabbe et al. (1991) revealed a few additional He I emission line
stars. They argued that this population most probably resulted from a burst of star formation a few Myr ago (Krabbe et al. 1995). Detailed spectroscopic analysis with atmosphere models by Najarro et al. (1994,1997) established that these objects were post-main sequence massive
stars. Their UV flux was able to ionise the ISM and produce the
nebular Br
m feature - and they were immediately classified as Ofpe/WN9, a class of evolved massive stars. Further observations by Krabbe et al. (1991) revealed a few additional He I emission line
stars. They argued that this population most probably resulted from a burst of star formation a few Myr ago (Krabbe et al. 1995). Detailed spectroscopic analysis with atmosphere models by Najarro et al. (1994,1997) established that these objects were post-main sequence massive
stars. Their UV flux was able to ionise the ISM and produce the
nebular Br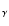 emission, but was far too soft to explain the nebular
He I emission. The presence of a population of hotter objects not
accessible to observations was thus inferred.
emission, but was far too soft to explain the nebular
He I emission. The presence of a population of hotter objects not
accessible to observations was thus inferred.
This population was unraveled in recent years. Paumard et al. (2001)
found additional stars with broader lines than the initial "He
I'' stars and typical of Wolf-Rayet stars. Genzel et al. (2003) deduced
the presence of even more massive stars from the absence of CO absorption bands. The advent of adaptive-optics assisted integral
field spectroscopy lead to a new breakthrough: Paumard et al. (2006)
spectroscopically identified nearly a hundred massive stars, including
various types of Wolf-Rayet stars, O and B supergiants, and even
dwarfs (see also Horrobin et al. 2004; Paumard et al. 2004). Previously,
Ghez et al. (2003) and Eisenhauer et al. (2005) had shown that the group of stars
located in the central arcsecond of the Galaxy and orbiting very close
to the black hole (the so-called "S-stars'') was composed of early to
late B dwarfs.
This latter group of stars is at the heart of an issue usually
referred to as the "paradox of youth'' of the Galactic center: how
could star formation (traced by the presence of young massive stars)
have happened so close to the black hole, where the tidal forces
should prevent any molecular cloud from collapsing (Morris 1993)?
Two scenarios are invoked to solve this problem. In the "in-situ
formation'' scenario, a disk forms around the supermassive black hole
with a density large enough to be self-gravitating so that tidal
forces do not perturb the collapse of molecular material
(e.g. Levin & Beloborodov 2003; Nayakshin & Cuadra 2005). In the alternate "in-spiraling cluster''
scenario, young massive stars are born in a dense cluster several tens
of parsec away from SgrA and its hostile environment, and
are subsequently brought to the central region by spiral-in of the
parent cluster due to dynamical friction
(e.g. Gerhard 2001; Kim & Morris 2003). The former picture (star formation in
a self-gravitating disk) appears more attractive since it accounts for
a larger number of observational facts (Paumard et al. 2006), but the question
is not completely settled.
and its hostile environment, and
are subsequently brought to the central region by spiral-in of the
parent cluster due to dynamical friction
(e.g. Gerhard 2001; Kim & Morris 2003). The former picture (star formation in
a self-gravitating disk) appears more attractive since it accounts for
a larger number of observational facts (Paumard et al. 2006), but the question
is not completely settled.
In that context, it is especially important to get a better knowledge
of the physical properties of the massive stars in the central parsec
of the Galaxy. In parallel to the development of powerful infrared
observational techniques, reliable atmosphere models have become
available in recent years. This is due to a huge effort from different
groups to include thousands of metallic lines in such models
("line-blanketing''). The use of such models has quantitatively
changed our knowledge of the stellar and wind properties of massive
stars. To name a few, their effective temperatures are lower
(Repolust et al. 2004; Martins et al. 2002; Crowther et al. 2002) and their winds are highly clumped
(Fullerton et al. 2006; Hillier et al. 2003; Bouret et al. 2005). In addition to these significant
developments, special attention was given to the infrared
range. Several studies have been undertaken to compare the parameters
derived from IR diagnostics with those obtained from classical optical
features (Repolust et al. 2005; Bohannan & Crowther 1999). It appears that the differences are
usually small, and certainly within the uncertainties on the derived
parameters. Then, both new observational data and better atmosphere
models are now available. A quantitative investigation of the stellar
and wind properties of massive stars in the central parsec of the
Galaxy, in the context of the "paradox of youth'', is thus possible.
We present such a study in this paper. Section 2 describes
the observational data. In Sect. 3, we present our
atmosphere models and explain our method to derive stellar and wind
properties. This is followed by a detailed analysis of individual
stars (Sect. 4). We then discuss the results with special
emphasis on ionising fluxes (Sect. 5), stellar evolution
(Sect. 6), metallicity (Sect. 7), stellar
winds (Sect. 8) and chemical composition of OB stars
(Sect. 9). We finally summarize our findings in Sect. 10.
2 Observations
The observations analysed here were conducted with the integral field
spectrograph SPIFFI/SINFONI on the ESO/VLT Yepun 8 m telescope
(Eisenhauer et al. 2003b,a; Bonnet et al. 2004) as part of the MPE-Garching GTO program "Galactic Center''. A first mosaic of data cubes was obtained
on Apr. 8 2003 using the 250 mas scale in the K band mode,
allowing a resolution of
2003 using the 250 mas scale in the K band mode,
allowing a resolution of  4000. A second mosaic was observed in
H+K band on the same scale on Apr. 9
4000. A second mosaic was observed in
H+K band on the same scale on Apr. 9 2003. These
observations were conducted in seeing limited mode since at that time
the AO system MACAO was not yet coupled to SPIFFI. A new SINFONI
mosaic was obtained on Aug. 18-19
2003. These
observations were conducted in seeing limited mode since at that time
the AO system MACAO was not yet coupled to SPIFFI. A new SINFONI
mosaic was obtained on Aug. 18-19 2004 in K band with the
100 mas scale in adaptive optics mode. Finally, several fields of the
region
2004 in K band with the
100 mas scale in adaptive optics mode. Finally, several fields of the
region  15'' north of SgrA
15'' north of SgrA were observed on
Mar. 16-17
were observed on
Mar. 16-17 2005. Additional information on all these data
cubes can be found in Paumard et al. (2006). Two new fields were obtained in
the configuration H+K/0.1 mas scale on Apr. 20
2005. Additional information on all these data
cubes can be found in Paumard et al. (2006). Two new fields were obtained in
the configuration H+K/0.1 mas scale on Apr. 20 2006 and
Aug. 16
2006 and
Aug. 16 2006.
2006.
To extract the spectra out of these cubes, we defined "source''
pixels showing spectral signatures of the massive stars identified by
Paumard et al. (2006) from which we removed neighboring "continuum'' sources
to correct for the local background. In the definition of the
"continuum'' pixels in crowded regions, we paid special attention not
to include pixels contaminated by neighboring stellar sources. We used
several combinations of source-continuum pixels to check the
reliability of the extracted spectrum. We found that as long as
contaminating sources are not included, the spectra can safely be
extracted. Figure 1 shows typical spectra of various types
of stars analysed here together with line identification.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig1.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg26.gif) |
Figure 1:
SINFONI K-band spectra of four post main sequence massive
stars observed in the GC. The main lines are marked. Note that all
lines are not present simultaneously in one spectrum: depending on the
stellar and wind parameters (in particular
 and abundances),
only a subset of the marked lines is observed in a given star.
and abundances),
only a subset of the marked lines is observed in a given star. |
| Open with DEXTER |
3 Modeling
3.1 Atmosphere models
In order to derive the stellar and wind properties of the massive
stars in the central parsec of the Galaxy, we have used state of the
art atmosphere models computed with the code CMFGEN (Hillier & Miller 1998). Such
models include the main ingredients necessary to produce realistic
atmospheric structures and emergent spectra, namely a non-LTE treatment, winds and line-blanketing. The latter has been included
only recently since in combination with the two former ingredients it
leads to complicated and numerically demanding simulations. But the
effects of line-blanketing are qualitatively and quantitatively very
important. Most stellar parameters have to be revised when determined
with line-blanketed models due to the strong modification of the
radiative transfer caused by additional opacities from metals.
CMFGEN computations proceed in two steps: first the atmospheric
structure and radiative field are computed in an iterative process;
second, a formal solution of the radiative transfer equation with
opacities given by the first step is determined, leading to the
detailed emergent spectrum. Details about the code CMFGEN are
discussed by Hillier & Miller (1998) and here we only recall the main
characteristics:
Table 1:
Observational properties of the stars analyzed in this paper. Spectral types are from Paumard et al. (2006). Values of extinction are taken from Schoedel et al. (2007). A distance of 7.62 kpc is adopted (Eisenhauer et al. 2005).
3.2 Method
The main diagnostics we used for the analysis were: 1) K band
photometry and 2) normalized spectra. The number of diagnostics is
relatively limited, which sometimes results in degeneracies in the
derived parameters, especially when
 cannot be accurately
constrained. The procedure to derive the stellar and wind parameters
is as follows:
cannot be accurately
constrained. The procedure to derive the stellar and wind parameters
is as follows:
The uncertainties in the derived parameters are the following: 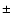 3000 K for
3000 K for
 (
(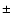 6000 K for the Ofpe/WN9 stars),
6000 K for the Ofpe/WN9 stars), 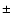 0.2 in
0.2 in
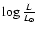 ,
0.2 dex for
,
0.2 dex for  ,
30% for the abundances. They are
not statistical errors (the estimate of such errors would
imply the computation of a huge number of models to sample the
parameter space around the best fit solution). Instead, they reflect
the range of values leading to acceptable fits of the observed
spectra. Our errors also do not include any systematic
contribution due to uncertainties in atomic data such as collisional
and dielectronic recombination cross-sections. This has to be kept in
mind when considering the values we quote.
,
30% for the abundances. They are
not statistical errors (the estimate of such errors would
imply the computation of a huge number of models to sample the
parameter space around the best fit solution). Instead, they reflect
the range of values leading to acceptable fits of the observed
spectra. Our errors also do not include any systematic
contribution due to uncertainties in atomic data such as collisional
and dielectronic recombination cross-sections. This has to be kept in
mind when considering the values we quote.
4 Analysis of individual stars
In this section, we give the results of the detailed analysis of
individual stars. We mainly focus on Wolf-Rayet and the so-called
"He I'' stars since their spectra have large enough S/N ratios to
allow quantitative spectroscopy. OB supergiants are studied by means
of the average spectrum of 10 of them (Paumard et al. 2006). The results are summarized in Table 2. The global
methodology presented in Sect. 3.2 is not repeated for each
star: we only give specific comments when necessary.
However, as a preamble, we would like to say a few words about the
behavior of He I 2.058  m. It is well known that this line is extremely
sensitive to any detail of the modeling, and in particular to the
amount of UV radiation. Indeed, the upper level of He I 2.058
m. It is well known that this line is extremely
sensitive to any detail of the modeling, and in particular to the
amount of UV radiation. Indeed, the upper level of He I 2.058  m is directly
coupled to the ground state by a transition at 584 Å. Dramatic
improvement has been achieved in recent years in the prediction of
this UV radiation, mainly due to the inclusion of line-blanketing in
the models. However, as we will see in the following analysis, He I 2.058
m is directly
coupled to the ground state by a transition at 584 Å. Dramatic
improvement has been achieved in recent years in the prediction of
this UV radiation, mainly due to the inclusion of line-blanketing in
the models. However, as we will see in the following analysis, He I 2.058  m is still poorly reproduced in several stars. Recently, Najarro et al. (2006)
have shown that the radiation at 584 Å was partly controlled by the
strength of two Fe IV lines: artificially changing the strength
of these lines improved the fit of optical singlet He I lines. We
have tried the same kind of tests in the present study, but it turned
out that the resulting He I 2.058
m is still poorly reproduced in several stars. Recently, Najarro et al. (2006)
have shown that the radiation at 584 Å was partly controlled by the
strength of two Fe IV lines: artificially changing the strength
of these lines improved the fit of optical singlet He I lines. We
have tried the same kind of tests in the present study, but it turned
out that the resulting He I 2.058  m line profiles were little changed. The
reason is partly that in the Wolf-Rayet stars studied here, He I 2.058
m line profiles were little changed. The
reason is partly that in the Wolf-Rayet stars studied here, He I 2.058  m is
an emission line and is controlled by recombination processes, while
in the O stars analysed by Najarro et al. (2006), He I 2.058
m is
an emission line and is controlled by recombination processes, while
in the O stars analysed by Najarro et al. (2006), He I 2.058  m is in absorption and
depends much more on pure radiative transfer effects. Besides, the
optical depth of the He I 584 Å line is large in Wolf-Rayet
stars, partly controlling the population of the He I 2.058
m is in absorption and
depends much more on pure radiative transfer effects. Besides, the
optical depth of the He I 584 Å line is large in Wolf-Rayet
stars, partly controlling the population of the He I 2.058  m upper
level. This does not mean that He I 2.058
m upper
level. This does not mean that He I 2.058  m is not sensitive to the UV continuum: as we will discuss in Sect. 7, subtle blanketing effects can significantly change the appearance of He I 2.058
m is not sensitive to the UV continuum: as we will discuss in Sect. 7, subtle blanketing effects can significantly change the appearance of He I 2.058  m. Having said that, we now turn to the detailed study of individual GC stars.
m. Having said that, we now turn to the detailed study of individual GC stars.
4.1 Ofpe/WN9 stars
In this section we present the analysis of five Ofpe/WN9 stars. We
deliberately exclude the stars IRS16SW and IRS16NE since they are
binaries (or candidates, see Martins et al. 2006).
4.1.1 IRS34W
IRS34W is an Ofpe/WN9 star and the faintest of the LBV candidates
identified in the Galactic Center (Paumard et al. 2004). Trippe et al. (2006)
also showed that it had recently experienced photometric variability
attributed to the formation of dust in material possibly ejected in a LBV-like outburst.
Due to the absence of a strong
 indicator, we could find several
solutions to the fit of the K band spectrum by varying the He content,
the luminosity, and the mass loss rate for
indicator, we could find several
solutions to the fit of the K band spectrum by varying the He content,
the luminosity, and the mass loss rate for
 in the range
in the range  20 000-
20 000- 33 000 K. Figure 2 shows one of the
possible best fit models. For the acceptable effective temperatures,
the He/H ratio is larger than solar, in the range 0.25-0.6, while
the mass loss rate goes from 6
33 000 K. Figure 2 shows one of the
possible best fit models. For the acceptable effective temperatures,
the He/H ratio is larger than solar, in the range 0.25-0.6, while
the mass loss rate goes from 6 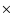 10-6-2
10-6-2 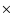 10-5
10-5 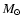 yr-1 and the luminosity is found in between 3 and 6
yr-1 and the luminosity is found in between 3 and 6 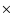
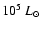 .
It is important to note that these parameters are not independent and only certain combinations within these ranges are
acceptable. For example, low
.
It is important to note that these parameters are not independent and only certain combinations within these ranges are
acceptable. For example, low
 imply low luminosities, large
imply low luminosities, large
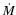 and large He/H ratio.
and large He/H ratio.
The morphology of Br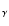 is well sampled in our observed spectrum. In
particular, the blue side of the Br
is well sampled in our observed spectrum. In
particular, the blue side of the Br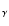 emission line shows a "shoulder'' and, at even shorter wavelengths, a small absorption dip. This results from the combination of two effects: first, Br
emission line shows a "shoulder'' and, at even shorter wavelengths, a small absorption dip. This results from the combination of two effects: first, Br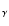 is a P-Cygni profile for which the blue absorption dip is partially
filled by emission; second, several He lines with both emission and
absorption profiles add to this Br
is a P-Cygni profile for which the blue absorption dip is partially
filled by emission; second, several He lines with both emission and
absorption profiles add to this Br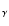 shape. The contribution of each
element is shown in the insert in Fig. 2. The exact
shape of this complex profile depends on the wind density in the line
formation region, and consequently depends on both
shape. The contribution of each
element is shown in the insert in Fig. 2. The exact
shape of this complex profile depends on the wind density in the line
formation region, and consequently depends on both 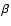 and the
filling factor f (in addition to the mass loss rate and the He/H ratio). In order to fit this profile, we had to choose
and the
filling factor f (in addition to the mass loss rate and the He/H ratio). In order to fit this profile, we had to choose 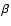 in the
range 2.0-4.0, i.e. larger than 1, the value commonly found in O supergiants. This is due to the fact that larger
in the
range 2.0-4.0, i.e. larger than 1, the value commonly found in O supergiants. This is due to the fact that larger 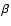 leads to
narrower profiles with stronger absorption dips and emission peaks
(see Martins et al. 2004). Similarly, the best fits were obtained with
unclumped models. This is at odds with the current knowledge
that winds of massive stars are strongly inhomogeneous. However, since
this complex line profile depends on several parameters, we refrain
from concluding that the wind of IRS34W (and the other similar
Ofpe/WN9 stars) are homogeneous. More detailed investigations with
high resolution spectroscopy should help to better resolve this line
and improve our determination.
leads to
narrower profiles with stronger absorption dips and emission peaks
(see Martins et al. 2004). Similarly, the best fits were obtained with
unclumped models. This is at odds with the current knowledge
that winds of massive stars are strongly inhomogeneous. However, since
this complex line profile depends on several parameters, we refrain
from concluding that the wind of IRS34W (and the other similar
Ofpe/WN9 stars) are homogeneous. More detailed investigations with
high resolution spectroscopy should help to better resolve this line
and improve our determination.
The only feature not well reproduced by our models is the emission at
2.112-2.115
 :
it is wider in the observed spectrum than in our
models. The main reason is that this emission is a blend of several
lines, the identification of which is still under debate. The
concensus is that both He I 2.112
:
it is wider in the observed spectrum than in our
models. The main reason is that this emission is a blend of several
lines, the identification of which is still under debate. The
concensus is that both He I 2.112  m (blue part, through P-Cygni profiles)
and N III 2.115
m (blue part, through P-Cygni profiles)
and N III 2.115  m (red part) contribute to the emission. Clearly, the
He I emission is present in our models but we are not able to
reproduce the N III emission. Actually, we are not convinced
that this emission is really due to N III since we do not
detect the lines N III 2.247
m (red part) contribute to the emission. Clearly, the
He I emission is present in our models but we are not able to
reproduce the N III emission. Actually, we are not convinced
that this emission is really due to N III since we do not
detect the lines N III 2.247
 and N III 2.251
and N III 2.251
 .
Geballe et al. (2006) recently claimed that O III could be
responsible for that emission. Since the oscillator strength for this
transition is very uncertain, we decided not to fit the red part of
the emission complex at 2.112-2.115
.
Geballe et al. (2006) recently claimed that O III could be
responsible for that emission. Since the oscillator strength for this
transition is very uncertain, we decided not to fit the red part of
the emission complex at 2.112-2.115
 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig2.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg47.gif) |
Figure 2:
Best fit (red dot-dashed line) of the observed K band spectrum of IRS34W (Ofpe/WN9, black solid line). The insert is a zoom on the Br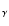 line, showing the contribution of H (blue dashed line) and He I (green dotted line) to the total synthetic profile (red dot-dashed line).
line, showing the contribution of H (blue dashed line) and He I (green dotted line) to the total synthetic profile (red dot-dashed line). |
| Open with DEXTER |
4.1.2 IRS16NW
The spectrum of IRS16NW is similar to IRS34W with the exception that
the emission part of the 2.112
 complex is weaker and the He lines on the blue wing of Br
complex is weaker and the He lines on the blue wing of Br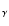 are mainly in absorption. However,
IRS16NW is 2.5 mag brighter, leading to a higher luminosity. The best
fit model of its K band spectrum is shown in Fig. 3. For
this star too, the only problem is the emission at 2.112
are mainly in absorption. However,
IRS16NW is 2.5 mag brighter, leading to a higher luminosity. The best
fit model of its K band spectrum is shown in Fig. 3. For
this star too, the only problem is the emission at 2.112
 which
is absent in our model. As for IRS34W, large
which
is absent in our model. As for IRS34W, large 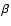 and unclumped
models gave the best fits.
and unclumped
models gave the best fits.
Compared to the analysis of Najarro et al. (1997), we find a larger
 ,
although the range of values for which a fit can be achieved
encompasses their value. The luminosity is lower by a factor 2.4,
while
,
although the range of values for which a fit can be achieved
encompasses their value. The luminosity is lower by a factor 2.4,
while 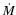 is lower by a factor of 4.7. We also find a terminal
velocity smaller by 150 km s-1. The main difference with Najarro et al. (1997)
is the He content that we find larger than solar but smaller than the
H content. In our case, this indicates that IRS16NW has probably only
recently left the main sequence and is in an early evolved status.
is lower by a factor of 4.7. We also find a terminal
velocity smaller by 150 km s-1. The main difference with Najarro et al. (1997)
is the He content that we find larger than solar but smaller than the
H content. In our case, this indicates that IRS16NW has probably only
recently left the main sequence and is in an early evolved status.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig3.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg48.gif) |
Figure 3:
Best fit (red dot-dashed line) of the observed K band spectrum of IRS16NW (Ofpe/WN9, black solid line). |
| Open with DEXTER |
4.1.3 IRS16C
IRS16C is the brightest star of our sample. It is one of the Ofpe/WN9 stars first discovered in the GC. As for the other stars of the same spectral type, its
 is poorly constrained. Figure 4 shows one of the best fit models. A large value of
is poorly constrained. Figure 4 shows one of the best fit models. A large value of 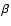 as well as
an unclumped wind are favoured as for IRS34W. The feature at 2.115
as well as
an unclumped wind are favoured as for IRS34W. The feature at 2.115
 is not reproduced in our model, as well as the one at 2.100
is not reproduced in our model, as well as the one at 2.100
 .
These lines could be from N III, but the absence of
N III 2.247
.
These lines could be from N III, but the absence of
N III 2.247
 and N III 2.251
and N III 2.251
 emission weakens
this possibility. We detect a Mg II emission at 2.138
emission weakens
this possibility. We detect a Mg II emission at 2.138
 .
This emission is reproduced by our model for a twice solar Mg content. However, this value should be interpreted with care given the uncertainty in
.
This emission is reproduced by our model for a twice solar Mg content. However, this value should be interpreted with care given the uncertainty in
 and the weakness of the line.
and the weakness of the line.
As for IRS16NW, we find a lower He content and a lower mass loss rate
compared to the results of Najarro et al. (1997).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig4.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg49.gif) |
Figure 4:
Best fit (red dot-dashed line) of the observed K band spectrum of IRS16C (Ofpe/WN9, black solid line). |
| Open with DEXTER |
4.1.4 IRS33E
The spectrum of IRS33E is similar to IRS34W, IRS16NW and IRS16C, and
so are the derived properties. The best fit model is shown in Fig. 5. As for IRS16C, the weak emission lines at 2.100
 and 2.115
and 2.115
 are not reproduced. Note that the structure of the Br
are not reproduced. Note that the structure of the Br emission is real and is observed at different epochs.
emission is real and is observed at different epochs.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig5.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg50.gif) |
Figure 5:
Best fit (red dot-dashed line) of the observed K band spectrum of IRS33E (Ofpe/WN9, black solid line). |
| Open with DEXTER |
4.1.5 AF star
The AF star is one of the first GC stars discovered and
analysed. Based on its SINFONI K band spectrum, Forrest et al. (1987),
Allen et al. (1990) and Najarro et al. (1994) classified it as a Ofpe/WN9 star.
However, compared to the other stars of the same type presented above,
AF has much broader lines. This indicates a stronger wind and possibly
a more advanced evolutionary state (see also Sect. 6.2).
The best fit to the H+K band spectrum is shown in Fig. 6. The effective temperature is poorly constrained due
to the absence of He II lines, as for the other Ofpe/WN9 stars. This implies a degeneracy between
 and He/H: models with
and He/H: models with
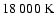
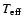
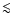
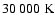 and 0.5
and 0.5 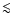
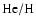
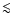 5.0 gave reasonable fits (lower He/H being required at
larger
5.0 gave reasonable fits (lower He/H being required at
larger
 ). Such behavior was already noted by
Najarro et al. (1994). We also found that
). Such behavior was already noted by
Najarro et al. (1994). We also found that 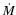
 10-4
10-4 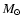 yr-1 were
necessary to fit emission at low
yr-1 were
necessary to fit emission at low
 ,
while values of the order 1.5
,
while values of the order 1.5 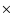 10-4
10-4 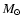 yr-1 were sufficient at high
yr-1 were sufficient at high
 .
The luminosity is in
the range 1-2
.
The luminosity is in
the range 1-2 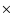
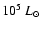 .
The values derived by
Najarro et al. (1994) are consistent with our cool/He-rich/large
.
The values derived by
Najarro et al. (1994) are consistent with our cool/He-rich/large 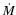 models. The analysis of this star illustrates perfectly the degeneracy
one has to face when
models. The analysis of this star illustrates perfectly the degeneracy
one has to face when
 is poorly constrained. In contrast to the
other Ofpe/WN9 stars analysed before, the shape of the Br
is poorly constrained. In contrast to the
other Ofpe/WN9 stars analysed before, the shape of the Br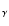 complex
is dominated by the wind, so that the contribution of the He lines
blueward of Br
complex
is dominated by the wind, so that the contribution of the He lines
blueward of Br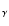 is not resolved. Hence, the He content is poorly
constrained. In the comparison to the Najarro et al. (1994) results, it is
also important to note that a different extinction was used. We
adopted
AK = 2.2 while Najarro et al. had
AK =
3.0. This influences the results, in particular the luminosity and
the mass loss rates (through their influence on MK, see
Sect. 3.2).
is not resolved. Hence, the He content is poorly
constrained. In the comparison to the Najarro et al. (1994) results, it is
also important to note that a different extinction was used. We
adopted
AK = 2.2 while Najarro et al. had
AK =
3.0. This influences the results, in particular the luminosity and
the mass loss rates (through their influence on MK, see
Sect. 3.2).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig6.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg56.gif) |
Figure 6:
Possible fit (red dot-dashed line) of the observed H+K band spectrum of the AF star (Ofpe/WN9, black solid line). Other combinations of
 ,
He/H and ,
He/H and 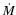 lead to similar fits. The observed spectrum around 1.85
lead to similar fits. The observed spectrum around 1.85
 is noisy and should be disregarded. See text for discussion.
is noisy and should be disregarded. See text for discussion. |
| Open with DEXTER |
4.2 WN stars
In the following, we present the results of the detailed study of 5 WN8, 3 WN7, 1 WN5/6 and 2 WN8/WC9 stars. For all the WN8 stars, the H content is relatively low, but we cannot discriminate between H free stars and stars with X(H) of a few percent. We thus quote a H mass
fraction 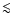 0.1.
0.1.
4.2.1 IRS15NE
Figure 7 shows our best fit spectrum of the WN8 star
IRS15NE. The He II lines at 2.037, 2.189 and 2.346
 are
well reproduced and allow a good estimate of the effective
temperature. The fit of the N III 2.247, 2.251
are
well reproduced and allow a good estimate of the effective
temperature. The fit of the N III 2.247, 2.251  m features is good, providing an accurate N abundance determination. The main discrepancy concerns
the He I 2.058
m features is good, providing an accurate N abundance determination. The main discrepancy concerns
the He I 2.058  m line which is too weak. Reducing
m line which is too weak. Reducing
 improves the
fit but weakens the He II lines. The Si IV feature at
2.427
improves the
fit but weakens the He II lines. The Si IV feature at
2.427
 is also slightly too weak if a solar abundance is used for Si. Figure 7 shows the effect of increasing the Si content
by a factor of 2.5 and 7. Interestingly, the fit of the SiIV line
improves, as well as the fit of He I 2.058
is also slightly too weak if a solar abundance is used for Si. Figure 7 shows the effect of increasing the Si content
by a factor of 2.5 and 7. Interestingly, the fit of the SiIV line
improves, as well as the fit of He I 2.058  m! However, several weak Si lines
appear around 1.98 and 2.08
m! However, several weak Si lines
appear around 1.98 and 2.08
 .
We do not detect these lines. Hence,
we cannot safely conclude that a super-solar Si abundance is required
for IRS15NE. The problem of Si IV 2.427
.
We do not detect these lines. Hence,
we cannot safely conclude that a super-solar Si abundance is required
for IRS15NE. The problem of Si IV 2.427
 in the initial
model may be due to incorrect atomic data for this line. In terms of
atmospheric structure, changing the Si content translates into a slight variation of the temperature structure (T is reduced in the outer atmosphere) which is then responsible for the strengthening of He I 2.058
in the initial
model may be due to incorrect atomic data for this line. In terms of
atmospheric structure, changing the Si content translates into a slight variation of the temperature structure (T is reduced in the outer atmosphere) which is then responsible for the strengthening of He I 2.058  m (see also Sect. 7.2). This highlights once more
the extreme sensitivity of He I 2.058
m (see also Sect. 7.2). This highlights once more
the extreme sensitivity of He I 2.058  m to the very details of the modeling.
m to the very details of the modeling.
IRS15NE was previously studied by Najarro et al. (1997) who found a lower
 ,
a larger luminosity and a larger mass loss rate. The terminal
velocity and He content were similar to the present value.
,
a larger luminosity and a larger mass loss rate. The terminal
velocity and He content were similar to the present value.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig7.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg57.gif) |
Figure 7:
Best fit (red dot-dashed line) of the observed K band spectrum of IRS15NE (WN8, black solid line). The different broken lines indicates models with similar parameters except the Si content. When it increases, the fits of Si IV 2.427
 and He I 2.058
and He I 2.058  m are improved. See text for discussion. m are improved. See text for discussion. |
| Open with DEXTER |
4.2.2 AFNW
AFNW is located North West of the AF star and was assigned a spectral
type WN8 by Paumard et al. (2006). The presence of both He I and
He II lines allows a rather robust
 determination (see
Fig. 8). Only He I 2.058
determination (see
Fig. 8). Only He I 2.058  m is too weak and He I 1.700
m is too weak and He I 1.700
 too strong in our model.
too strong in our model.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig8.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg58.gif) |
Figure 8:
Best fit (red dot-dashed line) of the observed H band ( left) and K band ( right) spectrum of AFNW (WN8). |
| Open with DEXTER |
4.2.3 IRS9W
IRS9W is the WN8 star of our sample with the cleanest spectrum and the
strongest He II lines. Figure 9 shows that our best
model is able to perfectly reproduce most of the features, with the
notable exception of He I 2.058  m. Given the quality of the observed spectrum
and the presence of several He I and He II lines very well
reproduced by our model, we think the effective temperature is well
constrained (see in particular the ratio of He II 2.189
m. Given the quality of the observed spectrum
and the presence of several He I and He II lines very well
reproduced by our model, we think the effective temperature is well
constrained (see in particular the ratio of He II 2.189  m to
He I 2.184
m to
He I 2.184  m). Decreasing
m). Decreasing
 to strengthen He I 2.058
to strengthen He I 2.058  m leads to weaker
He II 2.037, 2.189 and 2.346
m leads to weaker
He II 2.037, 2.189 and 2.346
 lines. Modifying the
luminosity and mass loss rate so that they still lead to a good match
of the observed K band magnitude and of the strength of emission lines
does not lead to any improvement as far as He I 2.058
lines. Modifying the
luminosity and mass loss rate so that they still lead to a good match
of the observed K band magnitude and of the strength of emission lines
does not lead to any improvement as far as He I 2.058  m is
concerned. Interestingly, the situation got better when we tried to
increase the global metallicity to a value of 2 times
m is
concerned. Interestingly, the situation got better when we tried to
increase the global metallicity to a value of 2 times 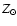 .
In
that case, we could get a strong He I 2.058
.
In
that case, we could get a strong He I 2.058  m line without degrading the fit
of the other diagnostics. This points once again to the extreme
sensitivity of He I 2.058
m line without degrading the fit
of the other diagnostics. This points once again to the extreme
sensitivity of He I 2.058  m to UV opacities, a larger metallicity
corresponding to a softer UV radiation. A more detailed discussion of
the behavior of He I 2.058
m to UV opacities, a larger metallicity
corresponding to a softer UV radiation. A more detailed discussion of
the behavior of He I 2.058  m as regards metallicity changes is given in
Sect. 7.2.
m as regards metallicity changes is given in
Sect. 7.2.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig9.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg59.gif) |
Figure 9:
Best fit of the observed K band spectrum of IRS9W (WN8, black solid line). The blue dotted line is a model with
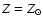 while the red dot-dashed line is for Z = 2
while the red dot-dashed line is for Z = 2 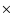
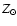 .
Note the change of He I 2.058 .
Note the change of He I 2.058  m with metallicity, tracing its extreme sensitivity to UV radiation. m with metallicity, tracing its extreme sensitivity to UV radiation. |
| Open with DEXTER |
4.2.4 IRS7E2
The best fit model to the K band spectrum of IRS7E2 is shown in Fig. 10. All lines are well reproduced, except He I 2.058  m. The
excellent fit of the N III 2.247, 2.251
m. The
excellent fit of the N III 2.247, 2.251  m line allows a good N abundance
determination.
m line allows a good N abundance
determination.
 is also well constrained since He II 2.189
is also well constrained since He II 2.189  m, He II 2.037
m, He II 2.037  m and He II 2.346
m and He II 2.346  m are clearly detected. As for IRS9W, we have tried to
increase the metallicity to improve the fit of He I 2.058
m are clearly detected. As for IRS9W, we have tried to
increase the metallicity to improve the fit of He I 2.058  m, but this time,
the line barely reacted and remained too weak.
m, but this time,
the line barely reacted and remained too weak.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig10.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg60.gif) |
Figure 10:
Best fit (red dot-dashed line) of the observed K band spectrum of IRS7E2 (WN8, black solid line). |
| Open with DEXTER |
4.2.5 IRS13E2
IRS13E2 is the brightest member of the IRS13E cluster and is
classified as WN8. Our best fit model is shown in Fig. 11. An effective temperature of 29 000 K was required to fit the He spectrum. It is the most luminous WN8 star of our sample
However, the presence of dust in the IRS13E cluster may hamper our
determination. We will argue in Sects. 4.3 and 6.5 that we probably derive only an upper limit on the luminosity.
Najarro et al. (1997) already mentioned the stars of IRS13E in their study,
but at that time they could not resolve the components and analysed
the global spectrum. Hence, a direct comparison with their results is
meaningless.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig11.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg61.gif) |
Figure 11:
Best fit (red dot-dashed line) to the observed K band spectrum of IRS13E2 (WN8, black solid line). |
| Open with DEXTER |
4.2.6 IRS7SW
Paumard et al. (2006) classified IRS7SW as WN8, but in view of the present
results (see below), we refine its identification to WN8/WC9. Our best
fit model is presented in Fig. 12. The preferred
 allows a reasonable fit of the Carbon lines and of He II 2.189
allows a reasonable fit of the Carbon lines and of He II 2.189  m, but seems a little too low to account for He II 2.037
m, but seems a little too low to account for He II 2.037  m and He II 2.346
m and He II 2.346  m. However, increasing
m. However, increasing
 leads to a too strong He II 2.189
leads to a too strong He II 2.189  m line. The presence of C IV
and C III as well as N III lines indicates that IRS7SW
is likely a WN/WC star. This is confirmed by the abundance
determination (see also Sect. 6.3 for a quantitative
discussion). We also note two unidentified lines: one feature at 2.140
m line. The presence of C IV
and C III as well as N III lines indicates that IRS7SW
is likely a WN/WC star. This is confirmed by the abundance
determination (see also Sect. 6.3 for a quantitative
discussion). We also note two unidentified lines: one feature at 2.140
 ,
and another one at 2.224
,
and another one at 2.224
 .
The former cannot be attributed
to Mg II 2.138
.
The former cannot be attributed
to Mg II 2.138  m since
m since
 is too high. Besides, Mg II 2.138
is too high. Besides, Mg II 2.138  m is a doublet while
we clearly see only one component. The line at 2.224
m is a doublet while
we clearly see only one component. The line at 2.224
 cannot be
due to Na I since again
cannot be
due to Na I since again
 is too large. Interestingly,
these lines are also found in most of the WC9 stars of our sample, as
well as in the WN8/WC9 star IRS15SW (see next section). We conclude
that they are typical of C-rich stars. Note that these lines are also
present and not identified in the WC9 stars of the Figer et al. (1997)
sample (see their Fig. 9).
is too large. Interestingly,
these lines are also found in most of the WC9 stars of our sample, as
well as in the WN8/WC9 star IRS15SW (see next section). We conclude
that they are typical of C-rich stars. Note that these lines are also
present and not identified in the WC9 stars of the Figer et al. (1997)
sample (see their Fig. 9).
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig12.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg62.gif) |
Figure 12:
Best fit to the observed H+K band spectrum of IRS7SW (WN8/WC9). |
| Open with DEXTER |
4.2.7 IRS15SW
IRS15SW is a late WN star showing C lines in its K band spectrum so
that it was classified as WN8/WC9 by Paumard et al. (2006). Most of the lines
are reproduced by our best model (Fig. 13). A notable
exception is the He I/He II complex around 2.185
 .
The emission is stronger than our model. Changing
.
The emission is stronger than our model. Changing
 does
not help since we fit either the blue or red side of the emission but
never the whole complex. Besides,
does
not help since we fit either the blue or red side of the emission but
never the whole complex. Besides,
 is relatively well
constrained by the other He II lines. We also do not perfectly
fit the blue absorption dip of He I 2.058
is relatively well
constrained by the other He II lines. We also do not perfectly
fit the blue absorption dip of He I 2.058  m. This may require a larger
m. This may require a larger
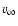 ,
but in that case the other emission lines are too broad. The C lines
are perfectly matched, allowing a reliable abundance (and
,
but in that case the other emission lines are too broad. The C lines
are perfectly matched, allowing a reliable abundance (and
 )
determination. IRS15SW will be further discussed in Sect. 6.3.
)
determination. IRS15SW will be further discussed in Sect. 6.3.
IRS15SW was studied by Najarro et al. (1997). We find a much larger
 ,
essentially because we can rely on several He II lines and on
the C IV/C III ratio (note the good fit of C lines in
Fig. 13). We also find a much lower luminosity and a lower clumping corrected mass loss rate. The terminal velocity and H content are however similar (see Fig. 13 for a complete view of the He and H spectrum).
,
essentially because we can rely on several He II lines and on
the C IV/C III ratio (note the good fit of C lines in
Fig. 13). We also find a much lower luminosity and a lower clumping corrected mass loss rate. The terminal velocity and H content are however similar (see Fig. 13 for a complete view of the He and H spectrum).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig13.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg63.gif) |
Figure 13:
Best fit (red dot-dashed line) to the observed K band spectrum of IRS15SW (WN8/WC9, black solid line). |
| Open with DEXTER |
4.2.8 AFNWNW
AFNWNW is a WN7 star. Most of its lines are reasonably well reproduced
by our best fit model (see Fig. 14). The main problems
are the too weak He I 2.058  m line and the too narrow He I/He II complex at
2.18-2.19
m line and the too narrow He I/He II complex at
2.18-2.19
 .
Note however that the S/N ratio is rather low,
preventing an accurate determination of the physical parameters. The
absence of C IV emission indicates an upper limit of 10-4 for C/He. Note that our best fit model is unclumped. We cannot derive the
clumping factor from the observed spectrum due to the poor S/N ratio.
.
Note however that the S/N ratio is rather low,
preventing an accurate determination of the physical parameters. The
absence of C IV emission indicates an upper limit of 10-4 for C/He. Note that our best fit model is unclumped. We cannot derive the
clumping factor from the observed spectrum due to the poor S/N ratio.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig14.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg64.gif) |
Figure 14:
Best fit (red dot-dashed line) to the observed H+K band
spectrum of AFNWNW (WN7, black solid line). The region around P was cut since it is not reliable. The observed spectrum was also
smoothed for clarity. was cut since it is not reliable. The observed spectrum was also
smoothed for clarity. |
| Open with DEXTER |
4.2.9 IRS34NW
IRS34NW is a WN7 star. It has narrower and weaker lines than AFNWNW,
reflecting its weaker wind. The C IV lines indicate a slightly sub-solar C abundance (see best fit in Fig. 15). Together with the N content derived from N III lines, this reveals an early stage of CNO processing (compared to
AFNWNW which has no detectable C IV lines). IRS34NW still has a significant amount of Hydrogen. We conclude that IRS34NW is less
evolved than AFNWNW in spite of a similar spectral type. This likely
reflects different initial masses.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig15.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg65.gif) |
Figure 15:
Best fit (red dot-dashed line) to the observed K band
spectrum of IRS34NW (WN7, black solid line). |
| Open with DEXTER |
4.2.10 IRS16SE2
IRS16SE2 is the earliest WN star of our sample (WN5/6,
see Paumard et al. 2006). Consequently, it also has the highest effective
temperature (41 000 K) which is quite well constrained by the presence
of both He I and He II lines in the K band
spectrum. Helium is indeed doubly ionised in most of the atmosphere,
except in the very outer part where it recombines, leading to the
He I absorption trough near 2.044
 .
This feature being due
to a blueshifted He I 2.058
.
This feature being due
to a blueshifted He I 2.058  m absorption, we have a good estimate of the wind
terminal velocity (2500 km s-1). The absence of C IV emission
around 2.08
m absorption, we have a good estimate of the wind
terminal velocity (2500 km s-1). The absence of C IV emission
around 2.08
 - expected for such a large
- expected for such a large
 - sets an upper
limit on the carbon abundance (
- sets an upper
limit on the carbon abundance (
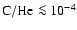 by number),
indicating CNO processing.
by number),
indicating CNO processing.
Crowther & Smith (1996) studied two WN6 stars with K band spectra very similar
to IRS16SE2. Their results are in excellent agreement with the present
ones:
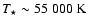 ,
,
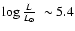 and
and
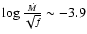 .
Since Crowther & Smith (1996) found no
difference between their IR analysis and optical results, we are
confident that the parameters we derive for IRS16SE2 for pure IR diagnostics are reliable.
.
Since Crowther & Smith (1996) found no
difference between their IR analysis and optical results, we are
confident that the parameters we derive for IRS16SE2 for pure IR diagnostics are reliable.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig16.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg70.gif) |
Figure 16:
Best fit (red dot-dashed line) of the observed K band spectrum of IRS16SE2 (WN5/6, black line). |
| Open with DEXTER |
4.3 WC9 stars
Here, the stellar and wind parameters of three WC9 stars are
derived. One important word of caution is necessary though. WC9 stars
are often associated with dust (Williams et al. 1987). The origin of this
dust is not completely understood, but wind-wind interaction in binary
systems is the favoured mechanism. Observation of dust spirals (also
named "pinwheels'') around several WC9 stars strongly support this
scenario (Tuthill et al. 1999). Recent observations of the "Cocoon stars''
after which the Quintuplet cluster was named showed such pinwheels
(Tuthill et al. 2006).
The presence of dust in WC9 stars complicates the analysis of their IR spectra since it produces an additional emission which adds to the
stellar+wind continuum. In practice, if WC9 stars are analysed under
the assumption that they are dust-free, their continuum is
over-estimated. Consequently, when normalizing their spectra, lines
appear weaker. This implies under-estimates of the mass loss rates and
abundances. In addition, the derived luminosity is over-estimated
since the total continuum is composed of both the stellar+wind
continuum and the dust emission. Note however that
 estimates
are less affected, since the ratio of lines is only weakly affected by
the presence of dust.
estimates
are less affected, since the ratio of lines is only weakly affected by
the presence of dust.
In the following, we discuss for each star the observational evidence
for dust and the reliability of the derived parameters.
4.3.1 IRS7W
L-band observations of IRS7W were recently performed by
Moultaka et al. (2005) ![[*]](/icons/foot_motif.gif) . Inspection of their Table 1
shows that the colors of IRS7W are consistent with the extinction law
of the GC, at least in the HKL bands. A possible excess emission is
only seen in the M band due to a red L-M color. Consequently, we think
that our modelling, restricted to the H+K band spectrum, is not
hampered by any dust emission. The derived parameters can be trusted
within their error bars.
. Inspection of their Table 1
shows that the colors of IRS7W are consistent with the extinction law
of the GC, at least in the HKL bands. A possible excess emission is
only seen in the M band due to a red L-M color. Consequently, we think
that our modelling, restricted to the H+K band spectrum, is not
hampered by any dust emission. The derived parameters can be trusted
within their error bars.
Our best fit is shown in Fig. 17. The effective
temperature is relatively well constrained by the presence of several
He II lines as well as C IV and C III features. The main discrepancy is once again the too weak He I 2.058  m in
our model. In addition, we note the two unidentified lines at 2.140
and 2.224
m in
our model. In addition, we note the two unidentified lines at 2.140
and 2.224
 as in WN/C stars.
as in WN/C stars.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig17.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg71.gif) |
Figure 17:
Best fit (red dot-dashed line) of the observed H and K band spectra of IRS7W (WC9, black solid line). |
| Open with DEXTER |
4.3.2 IRS7SE
IRS7SE is a WC9 star very similar to IRS7W. Unfortunately, we do not
have any information on its photometry (except for the K-band). We are
thus not able to check the possible contamination by dust. Adopting a conservative approach, we consider that our results are only limits
(lower for 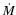 and the C abundance, upper for
and the C abundance, upper for
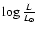 ). Figure 18 shows a fit of similar quality compared to IRS7W,
with the same caveats (He I 2.058
). Figure 18 shows a fit of similar quality compared to IRS7W,
with the same caveats (He I 2.058  m, unidentified lines).
m, unidentified lines).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig18.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg72.gif) |
Figure 18:
Best fit (red dot-dashed line) of the observed H+K band spectrum of IRS7SE (WC9, black solid line). |
| Open with DEXTER |
4.3.3 IRS13E4
Maillard et al. (2004) presented a detailed investigation of the stellar
content of IRS13E. Using HKL photometry, they report the discovery of
several very red sources in addition to the bright components IRS13E2
and IRS13E4. They interpret these sources as dusty Wolf-Rayet
stars. Unfortunately, IRS3E4 is not detected in their L band images,
so that the presence of a dust component in the spectrum of the WC9 star cannot be tested. It is however interesting to note that
IRS13E2, the WN8 star analysed in Sect. 4.2.5, has a quite large
K-L color. The entire cluster IRS13E is also known to be at the top
of a very prominent gas stream in L band (Clénet et al. 2004). Taken
together, these arguments indicate that the stars of IRS13E may well
all bathe in a continuum emission due to hot dust. We thus conclude
that their derived parameters must be regarded as only indicative (see
also Sect. 6.5).
With this restriction in mind, we show a tentative fit of the spectrum
of the WC9 star IRS13E4 in Fig. 19. The main C lines are
reasonably well reproduced by our model. However, the He I 2.184  m and
He II 2.189
m and
He II 2.189  m lines, while having the right line ratio, are too
strong. Reducing them would require a reduction of the mass loss
rate. This is at the cost of a reduction of the C lines (which could
be compensated by an increase in the C abundance), and of a modification of the shape of the lines. With lower
m lines, while having the right line ratio, are too
strong. Reducing them would require a reduction of the mass loss
rate. This is at the cost of a reduction of the C lines (which could
be compensated by an increase in the C abundance), and of a modification of the shape of the lines. With lower 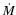 ,
lines get
narrower and more centrally peaked because the density decreases. In
conclusion, and given the above discussion, we argue that the near-IR
spectrum of IRS13E4 is certainly contaminated by dust emission. Such a component could explain that the He I and He II lines
are too weak (being diluted). Carbon lines are also certainly diluted,
so that our C abundance estimate is likely a lower limit. We also
probably over-estimate the total luminosity.
,
lines get
narrower and more centrally peaked because the density decreases. In
conclusion, and given the above discussion, we argue that the near-IR
spectrum of IRS13E4 is certainly contaminated by dust emission. Such a component could explain that the He I and He II lines
are too weak (being diluted). Carbon lines are also certainly diluted,
so that our C abundance estimate is likely a lower limit. We also
probably over-estimate the total luminosity.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig19.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg73.gif) |
Figure 19:
Tentative fit (red dot-dashed line)of the K band spectra of the IRS13E4 (WC9, black solid line). See text for discussion of the discrepancies. |
| Open with DEXTER |
4.4 OB supergiants
Due to the rather limited signal to noise ratio of most of the spectra
of the OB stars known in the central cluster (S/N of the order of a few tens on average), we have restricted ourselves to a general study of the properties of these stars. For that, we have used the average spectra of 10 supergiants presented in
Paumard et al. (2006). Hence, we have derived average stellar and wind
parameters for this population of OB stars.
Figure 20 shows the best fit model. The main parameters
used for this model are:
 = 27 500 K,
= 27 500 K, 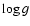 = 3.25,
= 3.25,
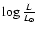 = 5.33,
= 5.33,
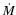 = 3
= 3 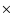 10-7
10-7 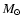 yr-1,
yr-1,
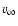 = 1850 km s-1, X(He) = 0.3 and
= 1850 km s-1, X(He) = 0.3 and
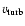 = 15 km s-1. Additionally, a rotational velocity of
= 15 km s-1. Additionally, a rotational velocity of  100 km s-1 could be estimated from the overall shape of all absorption lines
100 km s-1 could be estimated from the overall shape of all absorption lines![[*]](/icons/foot_motif.gif) . The effective
temperature is very difficult to constrain, just as in the Ofpe/WN9 stars studied previously. We can only put a constraint on the upper limit of
. The effective
temperature is very difficult to constrain, just as in the Ofpe/WN9 stars studied previously. We can only put a constraint on the upper limit of
 from the absence of He II lines, especially He II 2.189
from the absence of He II lines, especially He II 2.189  m. This upper limit is of around 32 000 K. Giving a lower limit is
more challenging. We tried several values between 25 000 and 32 500 K. This range is thought to be appropriate since all stars contributing to our average spectrum are late O / early B supergiants. For these types of stars,
m. This upper limit is of around 32 000 K. Giving a lower limit is
more challenging. We tried several values between 25 000 and 32 500 K. This range is thought to be appropriate since all stars contributing to our average spectrum are late O / early B supergiants. For these types of stars,
 is expected to be around
25 000-30 000 K (Martins et al. 2005). Reasonable fits could be obtained for
these different
is expected to be around
25 000-30 000 K (Martins et al. 2005). Reasonable fits could be obtained for
these different
 .
As we have no diagnostic to better constrain
.
As we have no diagnostic to better constrain
 ,
we finally adopted 27 500 K as a typical value. For the
luminosity, we also adopted
,
we finally adopted 27 500 K as a typical value. For the
luminosity, we also adopted
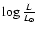 = 5.3 since this is typical of late O supergiants (e.g. Martins et al. 2005).
= 5.3 since this is typical of late O supergiants (e.g. Martins et al. 2005).
The mass loss rate is not strongly constrained either since most lines
are seen in absorption and do not appear to be filled by wind
emission. Here too, an upper limit on 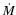 of a few 10-6
of a few 10-6 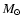 yr-1 can be given, above which Br
yr-1 can be given, above which Br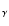 cannot be reproduced any more.
cannot be reproduced any more.
Finally, the He abundance is tentatively constrained from the
strength of He I 2.112  m, He I 2.150
m, He I 2.150  m, He I 2.161
m, He I 2.161  m and He I 2.184
m and He I 2.184  m. The strength of these
lines not only depends on the He content, but also on the
microturbulent velocity. The slope of the velocity law (the
m. The strength of these
lines not only depends on the He content, but also on the
microturbulent velocity. The slope of the velocity law (the 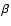 parameter) plays a role too. As we have no independent way of
determining all these parameters, we tried different combinations with
reasonable values (10 <
parameter) plays a role too. As we have no independent way of
determining all these parameters, we tried different combinations with
reasonable values (10 <
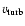 < 20 km s-1, 1.0 <
< 20 km s-1, 1.0 < 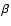 < 2.0). In the end, we found that good fits could be achieved for He/H ratios in the range 0.2-0.35. This value will be discussed in Sect. 9. Finally, we stress that we do not reproduce the 2.115
< 2.0). In the end, we found that good fits could be achieved for He/H ratios in the range 0.2-0.35. This value will be discussed in Sect. 9. Finally, we stress that we do not reproduce the 2.115
 emission. As discussed in Sect. 4.1.1, this line is not clearly identified and we did not try to fit it.
emission. As discussed in Sect. 4.1.1, this line is not clearly identified and we did not try to fit it.
5 Ionising radiation in the Galactic Center
One of the crucial issues revealed by early studies of the Galactic
Center was the apparent incompatibility between the ionisation of the
gas and the ionising flux provided by the population of massive
stars. This was highlighted by Najarro et al. (1997) and more recently by
Lutz (1999) in a detailed analysis of ISO observations (see
also Thornley et al. 2000). In view of our new quantitative analysis, we
argue that this issue is solved. Since this is an important result, we
give a detailed explanation of the different aspects of the problem
together with the proposed solutions.
Table 2:
Derived stellar and wind parameters. The typical errors are: 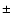 3000 K on temperatures (
3000 K on temperatures (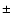 6000 K for Ofpe/WN9 stars),
6000 K for Ofpe/WN9 stars), 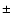 0.2 dex on
0.2 dex on
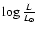 and
and
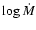 ,
100 km s-1 on terminal velocities and
,
100 km s-1 on terminal velocities and 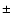 30% on abundances (except special cases; see comments on individual stars).
30% on abundances (except special cases; see comments on individual stars).
5.1 H and He I ionising photons
The first part of the "ionisation problem'' concerns the total number
of H and He I ionising photons produced by the GC massive stars
(i.e. ionising photons short-ward of 912 Å - 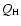 - and 504 Å -
- and 504 Å -
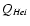 -). Nebular emission from the central H II region
was used to constrain the various ionising fluxes. Radio measurements
of the free-free continuum by Ekers et al. (1983) showed that
-). Nebular emission from the central H II region
was used to constrain the various ionising fluxes. Radio measurements
of the free-free continuum by Ekers et al. (1983) showed that
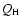 =
=
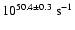 (see also Genzel et al. 1994). Later,
Krabbe et al. (1991) derived
(see also Genzel et al. 1994). Later,
Krabbe et al. (1991) derived
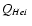

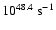 from a study
of the nebular He I 2.058
from a study
of the nebular He I 2.058  m emission. These measurements could then be
compared to the results of the quantitative modeling of the stellar
properties of the "He I'' stars by Najarro et al. (1997). Their conclusion
was that the "He I'' stars provided enough H ionising photons, but
failed by several orders of magnitude to produce the extreme UV flux
required to account for the nebular He ionisation. An underlying
population of stars hotter than the "He I'' stars but not detected was
suspected to be responsible for this harder flux.
m emission. These measurements could then be
compared to the results of the quantitative modeling of the stellar
properties of the "He I'' stars by Najarro et al. (1997). Their conclusion
was that the "He I'' stars provided enough H ionising photons, but
failed by several orders of magnitude to produce the extreme UV flux
required to account for the nebular He ionisation. An underlying
population of stars hotter than the "He I'' stars but not detected was
suspected to be responsible for this harder flux.
Such a population has recently reported by Paumard et al. (2006). Hence, a re-estimate of the ionising power of the central cluster is
required. Table 2 gives 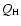 and
and
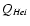 for the stars
analysed in the present paper. In addition to these, Paumard et al. (2006)
identified 15 other evolved massive stars and 59 OB stars. To estimate
the total ionisation flux delivered by this population we used the
following approach: for the WC9 stars not analysed here, we adopted
the ionising fluxes of Smith et al. (2002) using their model WC number 3;
for the 2 Ofpe/WN9 stars IRS16NE and IRS16SW, we adopted the
parameters of IRS16C; for the WN7 stars not studied, we adopted the
values of AFNWNW, another WN7 star included in our sample; finally,
for the O stars, we adopted the calibration of Martins et al. (2005) (see
their Table 4). Since all supergiants have a spectral type between
O8.5 and B2 but some of them suffer from a classification uncertainty
of up to 2 spectral sub-types, we adopted the ionising flux of a O9.5I star as typical of the GC supergiants. As for O dwarfs, the values of
for the stars
analysed in the present paper. In addition to these, Paumard et al. (2006)
identified 15 other evolved massive stars and 59 OB stars. To estimate
the total ionisation flux delivered by this population we used the
following approach: for the WC9 stars not analysed here, we adopted
the ionising fluxes of Smith et al. (2002) using their model WC number 3;
for the 2 Ofpe/WN9 stars IRS16NE and IRS16SW, we adopted the
parameters of IRS16C; for the WN7 stars not studied, we adopted the
values of AFNWNW, another WN7 star included in our sample; finally,
for the O stars, we adopted the calibration of Martins et al. (2005) (see
their Table 4). Since all supergiants have a spectral type between
O8.5 and B2 but some of them suffer from a classification uncertainty
of up to 2 spectral sub-types, we adopted the ionising flux of a O9.5I star as typical of the GC supergiants. As for O dwarfs, the values of
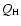 and
and
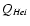 of Martins et al. (2005) for a O9.5V star were chosen. For the
B dwarfs, we simply adopted a value ten times smaller than for OV stars. This is a rough approximation which however has very little impact
on the final result, B stars providing a negligible ionising
flux. This leaves us with the following numbers:
of Martins et al. (2005) for a O9.5V star were chosen. For the
B dwarfs, we simply adopted a value ten times smaller than for OV stars. This is a rough approximation which however has very little impact
on the final result, B stars providing a negligible ionising
flux. This leaves us with the following numbers:
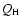 = 6.0
= 6.0 
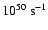 and
and
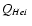 = 2.3
= 2.3 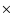
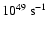 (or
(or
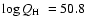 and
and
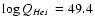 ). The contribution of the different
classes of stars are gathered in Table 3. We thus conclude
that not only the H ionising flux but also the He I ionising
flux required to reproduce the nebular emission can be provided by the
population of massive stars. In fact, they may even produce slightly
more ionising photons, indicating that the H II region might be
density bounded. A final comment on the total He I ionising
flux is needed. Krabbe et al. (1991) state that
). The contribution of the different
classes of stars are gathered in Table 3. We thus conclude
that not only the H ionising flux but also the He I ionising
flux required to reproduce the nebular emission can be provided by the
population of massive stars. In fact, they may even produce slightly
more ionising photons, indicating that the H II region might be
density bounded. A final comment on the total He I ionising
flux is needed. Krabbe et al. (1991) state that
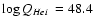 s-1, but also that
s-1, but also that
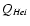 /
/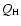 = 0.06. We find
= 0.06. We find
 /
/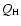 = 0.04, in very good agreement. The difference in the absolute
= 0.04, in very good agreement. The difference in the absolute
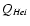 values
between our study and Krabbe et al. (1991) is their lower reference
values
between our study and Krabbe et al. (1991) is their lower reference 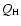 (
(
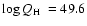 ).
).
At this point, a comment on the contribution of the "He I'' stars is necessary. Najarro et al. (1997) showed that the 8 stars they
analysed could account for most of the ionising radiation of the
region. We see that with the current estimate, this conclusion would
not be valid. Why is that? The answer is rooted in 1) our lower
bolometric luminosities and 2) the inclusion of line-blanketing in the
atmosphere models. This ingredient was not available at the time of
the Najarro et al. (1997) study. Test models reveal that in such stars,
line-blanketing effects lead to a large redistribution of the blocked
UV flux to longer wavelengths, mainly above 912 Å. Consequently,
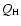 is reduced significantly.
is reduced significantly.
Table 3:
Contribution of the different types of stars to the ionising fluxes.
5.2 Ionising radiation and stellar population
The second important issue concerning the ionising radiation in the
Galactic Center was highlighted by Lutz (1999). In his study of
nebular fine structure mid-IR lines of metals observed with ISO, Lutz
pointed out that stellar evolution appears to fail to explain the GC massive stellar population. This claim was based on computations of
population synthesis models for a single burst of star formation and a standard Salpeter IMF. After 7 Myr, the age of the population thought to be appropriate at that time, the fraction of the total ionising luminosity provided by the part of the HR diagram where the
"He I'' stars are lying (
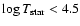 and
and 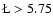 )
was of the order of 1%. This was at odds with the results of
Najarro et al. (1997) who argued that these stars could account for more than
half the total ionising luminosity. This discrepancy lead
Lutz (1999) to the conclusion that stellar evolution - indirectly
tested here through synthesis population models - was not producing
enough cool stars or equivalently that the time spent by a massive
star in the cool part of its track was much too short.
)
was of the order of 1%. This was at odds with the results of
Najarro et al. (1997) who argued that these stars could account for more than
half the total ionising luminosity. This discrepancy lead
Lutz (1999) to the conclusion that stellar evolution - indirectly
tested here through synthesis population models - was not producing
enough cool stars or equivalently that the time spent by a massive
star in the cool part of its track was much too short.
This statement is no longer valid. Only six stars analysed here
have
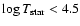 and
and
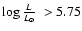 .
And this is in the
case we include IRS13E2 for which we only have an upper limit on
.
And this is in the
case we include IRS13E2 for which we only have an upper limit on
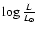 .
To these four stars, we need to add the binary IRS16SW and the binary candidate IRS16NE. Both stars likely have properties similar to IRS16C. In total, the H ionising flux of these stars represents about 9% of the total
.
To these four stars, we need to add the binary IRS16SW and the binary candidate IRS16NE. Both stars likely have properties similar to IRS16C. In total, the H ionising flux of these stars represents about 9% of the total  .
This is an upper limit due to the possible
overestimate of IRS13E2's luminosity. If we exclude IRS13E2, the
remaining 7 stars contribute only 4% of
.
This is an upper limit due to the possible
overestimate of IRS13E2's luminosity. If we exclude IRS13E2, the
remaining 7 stars contribute only 4% of
 .
This is in excellent agreement with what is expected from a burst of star formation after 7 Myr (which is within the age range now stated for the population, see Paumard et al. 2006). Once again, this is mainly due to the recent discovery of a hot population of OB and
Wolf-Rayet stars responsible for the majority of the ionising
luminosity. Table 3 shows that the OB supergiants and
Wolf-Rayet stars contribute more than 90% of the ionising flux. The
main conclusion is that standard stellar evolution - used in
population synthesis models - is able to account for the GC massive stars.
.
This is in excellent agreement with what is expected from a burst of star formation after 7 Myr (which is within the age range now stated for the population, see Paumard et al. 2006). Once again, this is mainly due to the recent discovery of a hot population of OB and
Wolf-Rayet stars responsible for the majority of the ionising
luminosity. Table 3 shows that the OB supergiants and
Wolf-Rayet stars contribute more than 90% of the ionising flux. The
main conclusion is that standard stellar evolution - used in
population synthesis models - is able to account for the GC massive stars.
5.3 Mid-IR nebular Ne lines
The third problem with the ionisation of the Galactic Center region
was also pointed out by Lutz (1999) (see
also Thornley et al. 2000). It concerned the low ionisation of the local gas
as derived from the ratio of fine structure mid-IR lines of different
ionisation states of Ne, namely Ne III 15.5
 and
Ne II 12.8
and
Ne II 12.8
 .
ISO observations revealed that
[Ne III]/[Ne II] was 0.05. Using the SED predicted by
the synthesis population model described in the previous section as an input of a photoionisation model performed with the code CLOUDY (Ferland et al. 1998), Lutz revealed that after 7 Myr,
[Ne III]/[Ne II] was still as large as 1 to 2, or a factor 50 to 100 more than the observed value.
.
ISO observations revealed that
[Ne III]/[Ne II] was 0.05. Using the SED predicted by
the synthesis population model described in the previous section as an input of a photoionisation model performed with the code CLOUDY (Ferland et al. 1998), Lutz revealed that after 7 Myr,
[Ne III]/[Ne II] was still as large as 1 to 2, or a factor 50 to 100 more than the observed value.
To investigate this issue, we have performed photoionisation models
with CLOUDY (version C06.02). As an input SED, we have simply added
all individual SEDs computed for the stars presently studied. For
those stars which were not explicitly treated here, we have adopted
the SEDs of Martins et al. (2005) or those of similar stars present in the
current sample. Adopting the same density as Lutz (1999) (3000 cm-3) and our total ionising flux implies an ionisation parameter
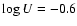
![[*]](/icons/foot_motif.gif) . With these values, we obtain a ratio [Ne III]/[Ne II] of 0.9-1.7 depending on the
geometry. This is still larger than the observed value (0.05). Note
however that if we use the ionisation parameter as Lutz (1999)
(
. With these values, we obtain a ratio [Ne III]/[Ne II] of 0.9-1.7 depending on the
geometry. This is still larger than the observed value (0.05). Note
however that if we use the ionisation parameter as Lutz (1999)
(
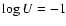 ), we get [Ne III]/[Ne II]
), we get [Ne III]/[Ne II]  0.5-0.7. This is a factor 2-3 lower than the values of Lutz.
0.5-0.7. This is a factor 2-3 lower than the values of Lutz.
How can we explain the still large values of
[Ne III]/[Ne II]? One possibility is that we
underestimate the density. There is evidence that values as large as
104-5 cm-3 are required to produce [O I],
[O III] and [Fe II] lines
(Genzel et al. 1984,1985). Using such large values (and the
corresponding ionisation parameter,
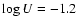 and -1.6),
CLOUDY models with our total stellar SED give [Ne III]/[Ne II]
and -1.6),
CLOUDY models with our total stellar SED give [Ne III]/[Ne II]  0.5 (for 104 cm-3) and
0.5 (for 104 cm-3) and  0.1 (for 105 cm-3). This is in better agreement with
the observed ratio, although still a factor 2-10 too
large. Shields & Ferland (1994) argued that the nebular spectrum of the Galactic
Center could be reproduced only if several gas components with
different densities were involved. In view of the present result, it
may well be that the Ne ionisation requires a large density material
(we can reproduce the observed [Ne III]/[Ne II] ratio
for a density of 3
0.1 (for 105 cm-3). This is in better agreement with
the observed ratio, although still a factor 2-10 too
large. Shields & Ferland (1994) argued that the nebular spectrum of the Galactic
Center could be reproduced only if several gas components with
different densities were involved. In view of the present result, it
may well be that the Ne ionisation requires a large density material
(we can reproduce the observed [Ne III]/[Ne II] ratio
for a density of 3  105 cm-3).
105 cm-3).
Another explanation of the large theoretical
[Ne III]/ [Ne II] ratio could be that we still overestimate
the flux at 41 eV, i.e. the Ne II ionisation energy probed by
the [Ne III]/[Ne II] ratio. This part of the spectrum is
quite sensitive to blanketing effects. A slight increase in
metallicity could lead to a reduced flux and consequently a lower
[Ne III]/[Ne II] ratio (e.g. Morisset et al. 2004).
One may also wonder what type of star contributes significant flux at
41 eV. It turns out that the total SED is completely
dominated by a single star at this energy: the hot WN5/6 star
IRS16SE2. To test the influence of this star on the ionisation of the
GC gas, we removed its contribution to the total SED and ran test
CLOUDY models. Amazingly, for a density of 3000 cm-3 (and
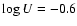 ), the [Ne III]/[Ne II] ratio drops to 0.008,
less than the observed value. This shows that this ratio is extremely
sensitive to the local radiation field. One can imagine that most of
the ionised gas is not illuminated by the IRS16SE2 radiation due to
shielding by local structures in molecular clouds. In that case, the
remaining radiation field is soft enough to maintain a low
[Ne III]/[Ne II] ratio.
), the [Ne III]/[Ne II] ratio drops to 0.008,
less than the observed value. This shows that this ratio is extremely
sensitive to the local radiation field. One can imagine that most of
the ionised gas is not illuminated by the IRS16SE2 radiation due to
shielding by local structures in molecular clouds. In that case, the
remaining radiation field is soft enough to maintain a low
[Ne III]/[Ne II] ratio.
In conclusion, one could say that a revised nebular modelling taking
into account both the spatial distribution of the gas and of the
ionising sources is required to solve the Ne ionisation problem. This
is well beyond the scope of the present paper.
6 Stellar evolution in the Galactic Center
In this section we discuss, in view of the results of our quantitative
analysis, the evolution of massive stars beyond the main sequence. It
is generally accepted that stars in the mass range 25-60 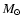 evolve
from O stars to WN H-poor stars through a LBV and/or red supergiant
phase before becoming WC stars (for M > 40
evolve
from O stars to WN H-poor stars through a LBV and/or red supergiant
phase before becoming WC stars (for M > 40 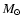 ). In the following,
we refine this scenario in the particular case of the GC, establishing
a plausible evolutionary sequence between Ofpe/WN9, WN8 and WN/C stars
(Sects. 6.1, 6.2, 6.3). We also
quantitatively compare the position of the GC Wolf-Rayet stars in the
HR diagram to evolutionary tracks including rotation (Sect. 6.4). Finally we discuss the properties of the IRS13E cluster stars (6.5).
). In the following,
we refine this scenario in the particular case of the GC, establishing
a plausible evolutionary sequence between Ofpe/WN9, WN8 and WN/C stars
(Sects. 6.1, 6.2, 6.3). We also
quantitatively compare the position of the GC Wolf-Rayet stars in the
HR diagram to evolutionary tracks including rotation (Sect. 6.4). Finally we discuss the properties of the IRS13E cluster stars (6.5).
6.1 Ofpe/WN9 stars
In the present study, we have analysed five stars classified Ofpe/WN9
by Paumard et al. (2006). Among these five stars, three have been studied by
Najarro et al. (1997): IRS16C, IRS16NW and AF. Compared to the Najarro et al. analysis, we find a similar range of luminosities (although for
IRS16C our luminosity is lower) and the same terminal velocities
(within the uncertainty). The effective temperatures are higher in our
study, partly due to the inclusion of line-blanketing in our models as
already discussed. Nevertheless,
 remains poorly constrained so
that the range of acceptable values overlap with the temperatures of
Najarro et al. (1997). As a consequence of the hotter
remains poorly constrained so
that the range of acceptable values overlap with the temperatures of
Najarro et al. (1997). As a consequence of the hotter
 ,
our radii are
smaller. But the main differences concern 1) the mass loss rates and
2) the He content. Both parameters are linked to some extent: when
fitting He I 2.058
,
our radii are
smaller. But the main differences concern 1) the mass loss rates and
2) the He content. Both parameters are linked to some extent: when
fitting He I 2.058  m, He I 2.112
m, He I 2.112  m and Br
m and Br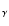 ,
adopting a larger He/H content will
require a larger
,
adopting a larger He/H content will
require a larger 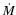 in order to reproduce the level of
Br
in order to reproduce the level of
Br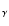 emission. Of course, in that case He I 2.058
emission. Of course, in that case He I 2.058  m and He I 2.112
m and He I 2.112  m get stronger
too. But their absolute strength is also controlled by the He ionisation which in turn depends on the effective temperature and the
line-blanketing effect. Since we used more realistic atmosphere models
as well as better spectra (higher S/N ratio and spectral resolution,
good correction from nebular emission), we argue that our derived
parameters represent an improvement over the result of
Najarro et al. (1997). In practice, we find values of
m get stronger
too. But their absolute strength is also controlled by the He ionisation which in turn depends on the effective temperature and the
line-blanketing effect. Since we used more realistic atmosphere models
as well as better spectra (higher S/N ratio and spectral resolution,
good correction from nebular emission), we argue that our derived
parameters represent an improvement over the result of
Najarro et al. (1997). In practice, we find values of 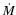 3 to 10 times
lower than Najarro et al., and much lower He contents (He/H
3 to 10 times
lower than Najarro et al., and much lower He contents (He/H  0.2-0.5 compared to 1.3-3.0).
0.2-0.5 compared to 1.3-3.0).
These revised parameters are important for assessing the evolutionary
status of the Ofpe/WN9 stars (see next section). They are also very
interesting since they bring the GC Ofpe/WN9 stars closer to other
Galactic and LMC stars of this type. Crowther & Smith (1997) analysed a sample
of LMC Ofpe/WN9 stars and found that their He content was much smaller
than in the GC stars, which was tentatively attributed to
possible metallicity effects. Our new values are in better agreement
with the Crowther et al. measurement, showing that the LMC and GC Ofpe/WN9 stars are chemically similar. In contrast, Pasquali et al. (1997)
found He/H  0.5 (by number) for a sample of LMC Ofpe/WN9 stars
partly overlapping with the Crowther et al. sample. These He contents
are only marginally larger than ours, and are certainly lower than the
values of Najarro et al. (1997). Concerning the mass loss rates, we find that
on average
0.5 (by number) for a sample of LMC Ofpe/WN9 stars
partly overlapping with the Crowther et al. sample. These He contents
are only marginally larger than ours, and are certainly lower than the
values of Najarro et al. (1997). Concerning the mass loss rates, we find that
on average 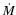 is systematically smaller than in the Crowther & Smith (1997)
and Pasquali et al. (1997) studies. This difference is surprising since
the lower metallicity of the LMC should lead to lower mass
loss rates. Combined with the slightly larger He content, this may be an indication of a more advanced evolution. Another indicator points to
the same conclusion: the terminal velocities of the GC Ofpe/WN9 stars
are usually larger than for stars of the same spectral type
(see Pasquali et al. 1997; Bresolin et al. 2002). Interestingly enough, the only
Galactic star of this type studied by Crowther & Smith (1997) had a much larger
is systematically smaller than in the Crowther & Smith (1997)
and Pasquali et al. (1997) studies. This difference is surprising since
the lower metallicity of the LMC should lead to lower mass
loss rates. Combined with the slightly larger He content, this may be an indication of a more advanced evolution. Another indicator points to
the same conclusion: the terminal velocities of the GC Ofpe/WN9 stars
are usually larger than for stars of the same spectral type
(see Pasquali et al. 1997; Bresolin et al. 2002). Interestingly enough, the only
Galactic star of this type studied by Crowther & Smith (1997) had a much larger
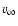 than the LMC stars. Schaerer (1996) explained such a trend
by a more advanced evolution in the Ofpe/WN9 phase for stars in the LMC, with the consequence of greater proximity to the Eddington limit and implying a lower terminal velocity.
than the LMC stars. Schaerer (1996) explained such a trend
by a more advanced evolution in the Ofpe/WN9 phase for stars in the LMC, with the consequence of greater proximity to the Eddington limit and implying a lower terminal velocity.
In conclusion, in view of our study, the class of Ofpe/WN9 seems to be
more homogeneous than previously believed. The difference between GC
and LMC Ofpe/WN9 stars is likely due to a different state of chemical
evolution: massive stars become Ofpe/WN9 stars later in a low Z environment such as the LMC, mainly due to lower mass loss rates.
6.2 An evolutionary link between Ofpe/WN9 and WN8 stars
On the basis of their K band morphology, all of the initial
"He I'' stars have been classified as either Ofpe/WN9 or WN8 stars by Paumard et al. (2006). These two spectral types are indeed characteristic of relatively cool evolved massive stars. In the K band, they are defined by strong He I and Br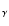 emission
lines. The relative intensity of these different lines is similar in
both spectral types: He I 2.058
emission
lines. The relative intensity of these different lines is similar in
both spectral types: He I 2.058  m is usually stronger than Br
m is usually stronger than Br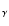 ,
while He I 2.112
,
while He I 2.112  m is weaker or of equal strength. The main differences are 1) the shape
of the lines (Ofpe/WN9 stars show P-Cygni profiles in the He I lines, while WN8 stars have strong pure emission lines); 2) their width (WN8 stars have broader lines); 3) their absolute strength (stronger lines in WN8 stars); and 4) the presence of weak He II lines in WN8 stars. Inspection of Table 2 reveals that
quantitatively, these morphological differences are due to larger mass
loss rates (and to a lesser extent wind terminal velocities) as well
as higher effective temperatures for WN8 stars. Indeed,
m is weaker or of equal strength. The main differences are 1) the shape
of the lines (Ofpe/WN9 stars show P-Cygni profiles in the He I lines, while WN8 stars have strong pure emission lines); 2) their width (WN8 stars have broader lines); 3) their absolute strength (stronger lines in WN8 stars); and 4) the presence of weak He II lines in WN8 stars. Inspection of Table 2 reveals that
quantitatively, these morphological differences are due to larger mass
loss rates (and to a lesser extent wind terminal velocities) as well
as higher effective temperatures for WN8 stars. Indeed,
 ranges
from 30 000 to 41 000 K for WN8 stars, while they are lower than 30 000 K
for Ofpe/WN9 stars. Mass loss rates are
ranges
from 30 000 to 41 000 K for WN8 stars, while they are lower than 30 000 K
for Ofpe/WN9 stars. Mass loss rates are  2-4 times smaller in
Ofpe/WN9 stars. Luminosities are also slightly lower in WN8 stars. This comparison indicates that Ofpe/WN9 stars and WN8 stars may be physically related and may well represent consecutive phases of a single evolutionary sequence.
2-4 times smaller in
Ofpe/WN9 stars. Luminosities are also slightly lower in WN8 stars. This comparison indicates that Ofpe/WN9 stars and WN8 stars may be physically related and may well represent consecutive phases of a single evolutionary sequence.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig21.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg114.gif) |
Figure 21:
Hydrogen mass fraction as a function of luminosity. Solid lines are the Geneva evolutionary tracks with rotation and
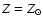 (Meynet & Maeder 2005). The ZAMS masses for each track are indicated. Stars show the position of the Ofpe/WN9 stars (IRS16C, IRS16NW, IRS33SE, IRS34W, AF) analysed here, while the triangles are the WN8 stars of our sample. The AF star lies at
(Meynet & Maeder 2005). The ZAMS masses for each track are indicated. Stars show the position of the Ofpe/WN9 stars (IRS16C, IRS16NW, IRS33SE, IRS34W, AF) analysed here, while the triangles are the WN8 stars of our sample. The AF star lies at
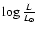 = 5.3 and X(H) = 0.3. See Sect. 6.4 for discussion. = 5.3 and X(H) = 0.3. See Sect. 6.4 for discussion. |
| Open with DEXTER |
Figure 21 displays the H content as a function of luminosity in
evolutionary models (solid lines) and shows the position of the
Ofpe/WN9 and WN8 stars. It is clear that both types of stars gather in
different parts of the diagram: Ofpe/WN9 stars still show a significant amount of hydrogen in their atmospheres whereas WN8 stars are mainly H free. This can be interpreted as an evolutionary sequence
where Ofpe/WN9 stars evolve into WN8 stars. Such a scenario would be
consistent with the properties reported above. Ofpe/WN9 stars could
well be on the cool part of an evolutionary track. This track will
then loop back to the hot part of the HR diagram. As a star follows
this track, it evolves chemically, gets hotter and strengthens its wind
on its way to the WR phase. The hotter
 and larger
and larger 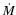 explains the appearance of He II lines and the stronger emission
lines, and the lower H content reveals the chemical evolution of the
star. In this scenario, the AF star could be in an intermediate
state. Its spectral morphology is similar to WN8 stars except that it
does not show He II lines, indicating a relatively cool
explains the appearance of He II lines and the stronger emission
lines, and the lower H content reveals the chemical evolution of the
star. In this scenario, the AF star could be in an intermediate
state. Its spectral morphology is similar to WN8 stars except that it
does not show He II lines, indicating a relatively cool
 (confirmed by the quantitative analysis, see Table 2). Its
mass loss rate is also more typical of WN8 stars. In Fig. 21,
the AF star lies in between the groups of Ofpe/WN9 and WN8 stars, with
a H mass fraction
(confirmed by the quantitative analysis, see Table 2). Its
mass loss rate is also more typical of WN8 stars. In Fig. 21,
the AF star lies in between the groups of Ofpe/WN9 and WN8 stars, with
a H mass fraction 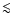 0.3. Hence, it is also more evolved than
Ofpe/WN9 stars, but less than WN8 stars, and nicely fits in the
evolutionary scenario we suggest.
0.3. Hence, it is also more evolved than
Ofpe/WN9 stars, but less than WN8 stars, and nicely fits in the
evolutionary scenario we suggest.
Another argument in favour of this scenario is the variability of both
types of objects. On the one hand, the Ofpe/WN9 stars in the Galactic
Center have been claimed to be LBV candidates, or even LBVs in a quiescent phase (Trippe et al. 2006; Paumard et al. 2004). This is based on spectral
similarities between these stars and objects elsewhere in the Galaxy
and LMC known to be related to LBV stars. Besides, one of them -
IRS34W - was shown to be photometrically variable on timescales of
months-years. Trippe et al. (2006) interpreted that as a sign of
obscuration by dust produced in material ejected in an LBV-type
outburst of the star. On the other hand, WN8 stars are known to be the
class of Wolf-Rayet stars experiencing the strongest variability
(Marchenko et al. 1998; Antokhin et al. 1995). This high degree of variability may be related
to the LBV phenomenon. A link between WN8 stars and LBVs is also
favoured by the presence of LBV-like nebulosities around most of them
(Crowther et al. 1995b).
We thus argue that the GC Ofpe/WN9 stars are precursors of WN8 stars,
and are in a state closely related to the LBV phase. This picture is
fully consistent with the scenario of Crowther et al. (1995b), further
extended by Crowther & Smith (1997): a 25-60 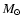 star evolves into a WN9-11 star (similar to Ofpe/WN9, see Crowther et al. 1995a) before
experiencing a LBV phase and becoming a WN8 Wolf-Rayet star. The
properties of the WN8 stars analysed by Crowther et al. (1995b) and
Herald et al. (2001) are very similar to those of our sample WN8 stars. The only difference is a larger spread in H content: while we find all WN8 to be almost H free, Crowther et al. (1995b) have both H free
stars and stars still showing a significant amount of
hydrogen. Herald et al. (2001) also found X(H)
star evolves into a WN9-11 star (similar to Ofpe/WN9, see Crowther et al. 1995a) before
experiencing a LBV phase and becoming a WN8 Wolf-Rayet star. The
properties of the WN8 stars analysed by Crowther et al. (1995b) and
Herald et al. (2001) are very similar to those of our sample WN8 stars. The only difference is a larger spread in H content: while we find all WN8 to be almost H free, Crowther et al. (1995b) have both H free
stars and stars still showing a significant amount of
hydrogen. Herald et al. (2001) also found X(H)  20% by
mass. However, this H content remains much lower than in the GC Ofpe/WN9 stars. Hence, the suggested evolutionary scenario remains valid.
20% by
mass. However, this H content remains much lower than in the GC Ofpe/WN9 stars. Hence, the suggested evolutionary scenario remains valid.
6.3 WN/C stars
WN/C stars are Wolf-Rayet stars showing both strong C and N lines
(Willis & Stickland 1990; Massey & Grove 1989). Carbon is produced by the triple 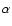 reaction, while Nitrogen results mainly from CNO processing. It is widely accepted that WN/C stars are core He burning stars with a CNO-enriched envelope in which mixing processes have created a layer
with both H and He burning products. When mass loss reveals this
layer, the star turns into a WN/C star (Meynet & Maeder 2003,2005; Langer 1991). Quantitatively, such WN/C stars have C/N ratios of the order 1.
reaction, while Nitrogen results mainly from CNO processing. It is widely accepted that WN/C stars are core He burning stars with a CNO-enriched envelope in which mixing processes have created a layer
with both H and He burning products. When mass loss reveals this
layer, the star turns into a WN/C star (Meynet & Maeder 2003,2005; Langer 1991). Quantitatively, such WN/C stars have C/N ratios of the order 1.
For a long time, the fraction of WR stars in the WN/C state observed
in the Galaxy has been difficult to explain with evolutionary
models. Abundance profiles in such models were usually very steep in
the transition region between H and He burning products, so that the
region where both type of products were present was extremely
thin. Consequently, it was quickly removed by the stellar wind,
resulting in a very short lifetime of the WN/C phase. Consequently, the
number of WN/C stars predicted by such models was much lower than the
observed value. Significant improvements have been made in the last
years mainly due to the inclusion of mixing processes triggered by
rotation. Meynet & Maeder (2003) have shown that rotation created shallower
abundance gradients in stellar interiors, increasing the size of the
mixed H and He burning products. As a consequence, the lifetime of the
WN/C phase is lengthened, resulting in a total number of WN/C stars in
better agreement with observations.
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{6688fig22.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg119.gif) |
Figure 22:
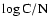 as a function of
as a function of
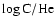 (by number) from evolutionary tracks with rotation (dot-dashed line) from Meynet & Maeder (2005). Filled symbols are the WR stars analysed in the present paper (triangles: WN stars; diamonds: WN/C stars; circles: WC9 stars). Open diamonds are the WN/C stars WR8 and WR145 from Crowther et al. (1995d). IRS7SW and IRS15SW, the two WN/C stars of our sample, have C/N and C/He ratios very similar to WR8 and WR145. The GC WN stars all lie at
(by number) from evolutionary tracks with rotation (dot-dashed line) from Meynet & Maeder (2005). Filled symbols are the WR stars analysed in the present paper (triangles: WN stars; diamonds: WN/C stars; circles: WC9 stars). Open diamonds are the WN/C stars WR8 and WR145 from Crowther et al. (1995d). IRS7SW and IRS15SW, the two WN/C stars of our sample, have C/N and C/He ratios very similar to WR8 and WR145. The GC WN stars all lie at
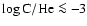 .
For these stars, we have only upper limits on the C abundance, and consequently on .
For these stars, we have only upper limits on the C abundance, and consequently on
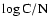 and
and
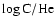 .
The WC9 stars analysed here have large C/He ratios and only lower limits on C/N since no N lines are present in the spectra and only an upper limit on the N abundances can be estimated. .
The WC9 stars analysed here have large C/He ratios and only lower limits on C/N since no N lines are present in the spectra and only an upper limit on the N abundances can be estimated. |
| Open with DEXTER |
What about the GC Wolf-Rayet population? Our analysis of IRS15SW and
IRS7SW has revealed that they were significantly enriched in Carbon
compared to other WN stars, leading to a classification as WN8/WC9 stars. Figure 22 shows
the position of our sample stars in a
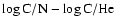 diagram. It turns out that IRS15SW and IRS7SW lie in between WN stars
(stars with low C content) and the C-rich WC9 stars. Their position is
also in excellent agreement with WR8 and WR145, two WN/C stars studied
by Crowther et al. (1995d), and with the prediction of evolutionary
models. Hence we have a quantitative confirmation that IRS15SW and
IRS7SW are core He burning objects on their way to a WC phase. Meynet & Maeder (2003) argue that only stars with initial masses in the
range 30-60
diagram. It turns out that IRS15SW and IRS7SW lie in between WN stars
(stars with low C content) and the C-rich WC9 stars. Their position is
also in excellent agreement with WR8 and WR145, two WN/C stars studied
by Crowther et al. (1995d), and with the prediction of evolutionary
models. Hence we have a quantitative confirmation that IRS15SW and
IRS7SW are core He burning objects on their way to a WC phase. Meynet & Maeder (2003) argue that only stars with initial masses in the
range 30-60 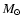 go through the WN/C phase: more massive stars have very
strong winds that quickly remove the CNO enriched envelope;
lower mass stars have a too H-rich envelope and He burning products
are too diluted. Estimates of the present-day masses of IRS15SW and
IRS7SW from the mass luminosity relation of Heger & Langer (1996) for H free WR stars gives 10.3 and 20.0
go through the WN/C phase: more massive stars have very
strong winds that quickly remove the CNO enriched envelope;
lower mass stars have a too H-rich envelope and He burning products
are too diluted. Estimates of the present-day masses of IRS15SW and
IRS7SW from the mass luminosity relation of Heger & Langer (1996) for H free WR stars gives 10.3 and 20.0  respectively, implying that these
stars have lost 30 to 80
respectively, implying that these
stars have lost 30 to 80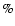 of their mass through stellar winds.
of their mass through stellar winds.
![\begin{figure}
\par\subfigure[]{\includegraphics[width=8.15cm,clip]{6688fig23a.e...
...
\subfigure[]{\includegraphics[width=8.15cm,clip]{6688fig23b.eps} }
\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg122.gif) |
Figure 23:
HR diagram of WR stars in the GC. Left: solar metallicity tracks with rotation (V sini = 300 km s-1 on the main sequence). Right: twice solar metallicity tracks including rotation. Star symbols are Ofpe/WN9 stars, triangles WN8 stars, pentagons WN5-7 stars and circles WC9 stars. Different line thickness indicates different evolutionary tracks (the thicker the line, the higher the mass). ZAMS masses are marked for each track. The Humphreys-Davidson limit is also shown in the right upper part of each diagram. |
| Open with DEXTER |
If we compare the properties of IRS15SW and IRS7SW to WR8 and WR145
(see Crowther et al. 1995d), the luminosities are all similar, in the
range
105.1-5.5 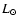 ,
which in turn implies that the present-day
mass of these four objects are also very close (10-20
,
which in turn implies that the present-day
mass of these four objects are also very close (10-20 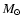 ). The
clumping corrected mass loss rates are also similar, with
). The
clumping corrected mass loss rates are also similar, with
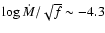 .
However, the terminal velocities of the
GC stars are smaller than for WR8 and WR145 (700-800 km s-1 as opposed
to 1390-1590 km s-1) as well as the stellar temperatures (32-37 kK vs.
41-48 kK). These differences reflect the different spectral types of
the two samples: while the GC WN/C stars are late type WR stars
(WN8/WC9), WR8 and WR145 are earlier (WN6/WC4,
see Crowther et al. 1995d). Earlier WN and WC type stars have higher effective
temperatures and larger terminal velocities (see Fig. 25). This can explain the observed trend: both types of
stars (early and late WN/C stars) have the same luminosity but early
WN/C stars are hotter, which implies that their radius is
smaller. Consequently, their escape velocity, scaling as
(M/R)0.5, is larger (the present mass being approximately the same). Since the terminal velocity is directly proportional to the
escape velocity, one naturally finds larger
.
However, the terminal velocities of the
GC stars are smaller than for WR8 and WR145 (700-800 km s-1 as opposed
to 1390-1590 km s-1) as well as the stellar temperatures (32-37 kK vs.
41-48 kK). These differences reflect the different spectral types of
the two samples: while the GC WN/C stars are late type WR stars
(WN8/WC9), WR8 and WR145 are earlier (WN6/WC4,
see Crowther et al. 1995d). Earlier WN and WC type stars have higher effective
temperatures and larger terminal velocities (see Fig. 25). This can explain the observed trend: both types of
stars (early and late WN/C stars) have the same luminosity but early
WN/C stars are hotter, which implies that their radius is
smaller. Consequently, their escape velocity, scaling as
(M/R)0.5, is larger (the present mass being approximately the same). Since the terminal velocity is directly proportional to the
escape velocity, one naturally finds larger
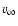 in early WN/C stars.
in early WN/C stars.
We argue that the GC WN/C stars are most likely the descendents of WN8 stars. Their spectral morphology is extremely similar, except for the
presence of C IV and C III lines in the WN/C stars. The
quantitative analysis confirms their "twin'' character: the ranges of
values for
 luminosities, mass loss rates, terminal velocities,
He and N content are the same for both WN8 and WN/C stars (see Table 2). The only possible exceptions are IRS13E2 (but see
discussion in Sect. 6.5) and IRS9W. Figure 22
shows that the WN/C stars are more chemically evolved than WN stars. Hence, we conclude that most of the GC WN8 stars will go through a WN/C phase as two of them are currently doing.
luminosities, mass loss rates, terminal velocities,
He and N content are the same for both WN8 and WN/C stars (see Table 2). The only possible exceptions are IRS13E2 (but see
discussion in Sect. 6.5) and IRS9W. Figure 22
shows that the WN/C stars are more chemically evolved than WN stars. Hence, we conclude that most of the GC WN8 stars will go through a WN/C phase as two of them are currently doing.
Summarizing the last three sections, we argue that in the Galactic
Center, stars with initial masses in the range 30-60 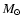 follow
the evolutionary sequence
follow
the evolutionary sequence
on their way to the supernova explosion. On the main
sequence, they probably appear as mid/early O stars. After the WN/C phase, they most likely become late WC stars. Indeed the effective temperatures of WN/C stars are slightly lower than the WC9 stars of our sample. Hence, we can expect them to enter the WC sequence from
the low ionisation (or equivalently the low
 )
side and appear as
WC9 stars. The (Ofpe/WN9
)
side and appear as
WC9 stars. The (Ofpe/WN9
 LBV) sequence in the
suggested scenario indicates that Ofpe/WN9 and LBV stars are closely
inter-related and most likely represent different states of a single
evolutionary phase (see discussion in Trippe et al. 2006).
LBV) sequence in the
suggested scenario indicates that Ofpe/WN9 and LBV stars are closely
inter-related and most likely represent different states of a single
evolutionary phase (see discussion in Trippe et al. 2006).
6.4 Are stellar evolutionary tracks too luminous?
The direct comparison between derived parameters and evolutionary
tracks by means of a classical HR diagram (
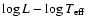 )
is
not straightforward for Wolf-Rayet stars. In evolutionary models, the
"effective'' temperature (noted
)
is
not straightforward for Wolf-Rayet stars. In evolutionary models, the
"effective'' temperature (noted
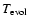 in the present
discussion) is defined at the outer boundary by Eq. (3). However, there is no atmosphere in such models and
strictly speaking, the radius in this case (noted
in the present
discussion) is defined at the outer boundary by Eq. (3). However, there is no atmosphere in such models and
strictly speaking, the radius in this case (noted
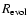 )
is
not the one for which the optical depth is equal to 2/3 (exact
definition of
)
is
not the one for which the optical depth is equal to 2/3 (exact
definition of
 ). It corresponds more to a hydrostatic radius. In
Wolf-Rayet stars, such a radius - for which the atmosphere is
quasi-static - is at an optical depth much larger than 2/3. Said
differently, R2/3 for which
). It corresponds more to a hydrostatic radius. In
Wolf-Rayet stars, such a radius - for which the atmosphere is
quasi-static - is at an optical depth much larger than 2/3. Said
differently, R2/3 for which
 can be defined is much larger
than
can be defined is much larger
than
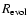 .
Consequently,
.
Consequently,
 is lower than
is lower than
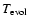 .
To overcome this problem, one usually defines a radius
.
To overcome this problem, one usually defines a radius
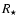 (and the corresponding temperature
(and the corresponding temperature 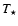 ,
see Eq. (3)) at an optical depth equal to 20. Such a radius is more comparable to
,
see Eq. (3)) at an optical depth equal to 20. Such a radius is more comparable to
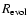 so that
so that 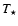 and
and
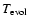 can be directly compared.
can be directly compared.
In Fig. 23, we show the HR diagram built using 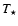 for our program stars (see Table 2). They are shown by the
filled symbols (see next section for a discussion of the two stars
represented by open symbols). The evolutionary tracks including
rotation of Meynet & Maeder (2005) for solar metallicity (left) and twice solar
metallicity (right) are overplotted. In the diagram at
for our program stars (see Table 2). They are shown by the
filled symbols (see next section for a discussion of the two stars
represented by open symbols). The evolutionary tracks including
rotation of Meynet & Maeder (2005) for solar metallicity (left) and twice solar
metallicity (right) are overplotted. In the diagram at
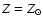 ,
we clearly see that the Ofpe/WN9 stars populate the
coolest region, while the more evolved Wolf-Rayet stars are hotter and,
on average, less luminous. Qualitatively, this trend is similar to the
40
,
we clearly see that the Ofpe/WN9 stars populate the
coolest region, while the more evolved Wolf-Rayet stars are hotter and,
on average, less luminous. Qualitatively, this trend is similar to the
40 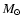 track: coming back from its redward extension, this track
goes to lower temperatures. However, this track, as well as the ones
for other masses, always remains at
track: coming back from its redward extension, this track
goes to lower temperatures. However, this track, as well as the ones
for other masses, always remains at
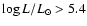 ,
in
contrast to most of the Wolf-Rayet stars of our sample which have
,
in
contrast to most of the Wolf-Rayet stars of our sample which have
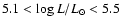 .
Hence, we see that quantitatively the
solar metallicity evolutionary tracks do not seem to explain the
evolution of the GC Wolf-Rayet stars. Note that this is independent of
any definition of the temperature, since the problem is due to
luminosities.
.
Hence, we see that quantitatively the
solar metallicity evolutionary tracks do not seem to explain the
evolution of the GC Wolf-Rayet stars. Note that this is independent of
any definition of the temperature, since the problem is due to
luminosities.
If we now focus on the HR diagram where the Z = 2 
 metallicity tracks are plotted, we see that lower luminosities are
reached. This is due to the stronger mass loss rates in these tracks
which "peel off'' the star more quickly, reducing its radius and
consequently its luminosity. Does that mean that the GC stars have a supersolar metallicity? We will see in Sect. 7 that the
question is still largely debated. The position of the GC Wolf-Rayet
stars in the HR diagram may be an indication of a super-solar
environment. But this can also be due to inadequate mass loss rates in
evolutionary calculation at solar metallicity. If the amount of mass
lost during the Wolf-Rayet phase is underestimated in such
calculations, the tracks will be too luminous. Large
metallicity tracks are plotted, we see that lower luminosities are
reached. This is due to the stronger mass loss rates in these tracks
which "peel off'' the star more quickly, reducing its radius and
consequently its luminosity. Does that mean that the GC stars have a supersolar metallicity? We will see in Sect. 7 that the
question is still largely debated. The position of the GC Wolf-Rayet
stars in the HR diagram may be an indication of a super-solar
environment. But this can also be due to inadequate mass loss rates in
evolutionary calculation at solar metallicity. If the amount of mass
lost during the Wolf-Rayet phase is underestimated in such
calculations, the tracks will be too luminous. Large 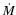 can be
produced by a fast rotation (see Maeder & Meynet 2000), but the analysis of
OB stars average spectrum do not point to any particularly high
V sini (see Sect. 9). As long as the GC metallicity
remains poorly constrained, a quantitative test of evolutionary tracks
and their input parameters, such as mass loss rates, is thus not
feasible. We will see in Sect. 7 that more work is needed
to narrow the range of acceptable values for Z in the Galactic Center.
can be
produced by a fast rotation (see Maeder & Meynet 2000), but the analysis of
OB stars average spectrum do not point to any particularly high
V sini (see Sect. 9). As long as the GC metallicity
remains poorly constrained, a quantitative test of evolutionary tracks
and their input parameters, such as mass loss rates, is thus not
feasible. We will see in Sect. 7 that more work is needed
to narrow the range of acceptable values for Z in the Galactic Center.
6.5 The stars of IRS13E
In the previous section, we have deliberately excluded two stars from the
discussion: the ones represented by open symbols in Fig. 23. These stars are the two Wolf-Rayet components of the cluster IRS13E, namely IRS13E2 and IRS13E4. The
reason is that they show peculiar properties compared to the bulk of
the GC Wolf-Rayet stars. Take first IRS13E2. It is a WN8 star (see its
spectrum in Fig. 11) with parameters in marginal
agreement with the other WN8 stars of our sample, with the notable
exception of its luminosity (
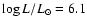 )
which is
much larger than the range of values for WN8 stars (5.1-5.5, see
Table 2 and Crowther et al. 1995b). The same statement is true
for IRS13E4. It is a WC9 star but exceptionally bright: while most
stars of this type have
)
which is
much larger than the range of values for WN8 stars (5.1-5.5, see
Table 2 and Crowther et al. 1995b). The same statement is true
for IRS13E4. It is a WC9 star but exceptionally bright: while most
stars of this type have
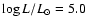 (see an example
in Crowther et al. 2006), IRS13E4 is nearly 10 times more luminous. In addition,
it shows a large, although not unprecedented, terminal velocity (see
Fig. 25).
(see an example
in Crowther et al. 2006), IRS13E4 is nearly 10 times more luminous. In addition,
it shows a large, although not unprecedented, terminal velocity (see
Fig. 25).
How can we interpret these results? First, the most obvious
explanation is binarity. IRS13E was initially thought to be a single
star (Krabbe et al. 1991) before being resolved into several components
(Maillard et al. 2004). The cluster is extremely compact and it is quite
possible that the bright components might actually be multiple
stars. But even with better spatially reduced images, it may not be
sufficient to distinguish between the components of a massive
binary. Spectrophotometric monitoring should then be used to test the
binary hypothesis. So far, IRS13E2 and IRS13E4 (Figs. 11
and 19) do not show any sign of double line spectrum. In
addition, photometric observations over the recent years (but with a very coarse sampling) show a flat light-curve for both stars (Trippe
et al., in prep.). Better monitoring is required, but so far no clear
evidence for binarity exists for IRS13E2 and IRS13En.
But the most important factor was mentioned in Sect. 4.3:
dust contamination. There is evidence of a large dust content in
IRS13E which may affect the infrared spectra of its stellar
components. As a consequence, the luminosities are most likely upper
limits. However, the luminosity difference between IRS13E4 and IRS7W
is 0.7 dex, or a factor of 5. Assuming that both stars have the same
luminosity and same spectral energy distribution, this means that the
total K band flux is 5 times larger than the stellar+wind flux. This
is exactly what is found by Crowther et al. (2006) in their analysis of the
WC9 star HD164270: dust contributes 80% of the continuum. Note that
their estimate is at 3
 and not in the K-band, where dust
contamination is smaller. But Crowther et al. (2006) also claim that HD164270
has a weak dust shell compared to other dusty WC stars. Hence, for a typical WC star a 80% dust contribution to the K band continuum is not unrealistic.
and not in the K-band, where dust
contamination is smaller. But Crowther et al. (2006) also claim that HD164270
has a weak dust shell compared to other dusty WC stars. Hence, for a typical WC star a 80% dust contribution to the K band continuum is not unrealistic.
Although further high spatial resolution photometric data in the
near/mid IR range are needed to establish the true SED of each
component, it is likely that dust explains most of the peculiar
properties of the IRS13E Wolf-Rayet stars.
7 Metallicity in the central parsec
We first present a determination of the global metallicity in the GC
by means of WN stars, and we then discuss its effect on He I 2.058  m.
m.
7.1 Metallicity from N content of WN stars
Najarro et al. (2004) presented a new method for deriving metallicity in
evolved massive stars. Their idea relies on the fact that the surface
nitrogen content of massive stars reaches a maximum during evolution
due to production of N through the CNO cycle. Observationally, this
maximum is obtained in WN stars. Its exact value is independent
of the initial mass and of the wind properties. It changes with the
initial metal content since the amount of Nitrogen synthesized is
directly linked to the initial CNO content. Hence, the comparison of
derived N abundances in WN stars to evolutionary tracks is an indirect
tracer of the initial metallicity.
In Table 2 we list our derived nitrogen mass
fraction. Only for WN stars such an estimate could be performed due to
the presence of N III lines in the K band spectrum, especially
N III 2.247, 2.251  m. For most stars, we have
m. For most stars, we have
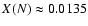 ,
with the
exception of IRS15SW and AFNW which show a larger N content (up to
0.0326). However, for the latter star the uncertainty on the N abundance determination is quite large due to the low resolution and
low S/N ratio of our spectrum. A direct comparison of this range of
values to predictions of surface enrichment in evolutionary models
(see e.g. Fig. 4 of Najarro et al. 2004) indicates an initial metallicity
between solar and twice solar. If IRS15SW and AFNW are not taken into
account, then a solar metallicity is favoured. Strictly speaking, we
derive a lower limit since one cannot be sure that all WN stars have
reached the phase in which their surface N abundance is
maximum. Indeed, although this phase is long for initially very
massive stars, it is quite short for stars with M
,
with the
exception of IRS15SW and AFNW which show a larger N content (up to
0.0326). However, for the latter star the uncertainty on the N abundance determination is quite large due to the low resolution and
low S/N ratio of our spectrum. A direct comparison of this range of
values to predictions of surface enrichment in evolutionary models
(see e.g. Fig. 4 of Najarro et al. 2004) indicates an initial metallicity
between solar and twice solar. If IRS15SW and AFNW are not taken into
account, then a solar metallicity is favoured. Strictly speaking, we
derive a lower limit since one cannot be sure that all WN stars have
reached the phase in which their surface N abundance is
maximum. Indeed, although this phase is long for initially very
massive stars, it is quite short for stars with M  20-50
20-50 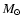 which is more appropriate for our WN8 stars. In conclusion, we
estimate the stellar GC metallicity to be at least
solar. Stronger constraints cannot be derived from the present set of
data/models.
which is more appropriate for our WN8 stars. In conclusion, we
estimate the stellar GC metallicity to be at least
solar. Stronger constraints cannot be derived from the present set of
data/models.
Stellar studies usually indicate a solar metallicity for the GC. Najarro et al. (2004) found
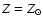 for WN stars in the Arches cluster. This is also comparable to the determinations of
Carr et al. (2000) and Ramírez et al. (2000) who also derived a solar [Fe/H]
from the study of iron lines in red supergiants in the central 2.5 pc.
for WN stars in the Arches cluster. This is also comparable to the determinations of
Carr et al. (2000) and Ramírez et al. (2000) who also derived a solar [Fe/H]
from the study of iron lines in red supergiants in the central 2.5 pc.
Abundances have also been derived from interstellar gas
studies. Shields & Ferland (1994) derived solar Ne content and twice solar Ar and N based on photoionisation models aimed at reproducing nebular fine
structure lines in the mid infrared. However, improvements in the
knowledge of the Ar collisional strengths led to a revision of the Ar abundance down to a nearly solar value (see discussion
in Carr et al. 2000). This is to be contrasted by the recent analysis of ISO data by Giveon et al. (2002) who found Ne  1.4 Ne
1.4 Ne and Ar
and Ar  2.5 Ar
2.5 Ar .
Similarly, Martín-Hernández et al. (2003) revised the Galactic metallicity gradients. Extrapolating their results to the
Galactic Center, one should expect
.
Similarly, Martín-Hernández et al. (2003) revised the Galactic metallicity gradients. Extrapolating their results to the
Galactic Center, one should expect
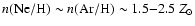 and
and
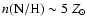 .
.
Finally, observations of K shell Fe lines by Chandra have been used by
Maeda et al. (2002) to derive an iron content as large as 4 times solar
for the H II region SgrA East. Such a large metallicity was
recently confirmed on a larger scale by X-ray observations with Suzaku
(Koyama 2006).
Clearly, the measurement of the metallicity in the Galactic Center
needs more investigation. We have seen in Sects. 4.1.3 and 4.2.1 that individual elemental abundances could be super-solar
(Mg, Si). But the uncertainties associated to these estimates did not
allow a reliable statement. The use of high signal to noise, high
spectral resolution data is mandatory in order to resolve weak
metallic lines of Ofpe/WN9 stars, red supergiants as well as AGB stars. The distinction between  element and Iron abundances is also crucial.
element and Iron abundances is also crucial.  elements are essentially produced in massive stars while Iron is mainly synthesized in low mass stars during the
type Ia supernova phase. The ratio of
elements are essentially produced in massive stars while Iron is mainly synthesized in low mass stars during the
type Ia supernova phase. The ratio of 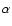 elements to Iron
abundances is thus an indirect tracer of the slope of the IMF.
elements to Iron
abundances is thus an indirect tracer of the slope of the IMF.
7.2 Metallicity effect on He I 2.058  m
m
We have seen in Sect. 4.2.3 that He I 2.058  m is extremely sensitive to
the metal content. Indeed, the higher the metallicity, the stronger
the line emission so that Z = 2
m is extremely sensitive to
the metal content. Indeed, the higher the metallicity, the stronger
the line emission so that Z = 2 
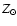 was actually
preferred for IRS9W. Such a behavior was previously noted by
Crowther et al. (1998) and Bohannan & Crowther (1999) and was attributed to the sensitivity
of He I 2.058
was actually
preferred for IRS9W. Such a behavior was previously noted by
Crowther et al. (1998) and Bohannan & Crowther (1999) and was attributed to the sensitivity
of He I 2.058  m to the EUV radiation field, which in turn depends critically
on the heavy-metal content. Figure 24 shows the He ionisation and temperature structure of the models for IRS9W with
m to the EUV radiation field, which in turn depends critically
on the heavy-metal content. Figure 24 shows the He ionisation and temperature structure of the models for IRS9W with
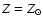 and Z = 2
and Z = 2 
 .
This figure helps us
understand in detail what happens when the metal content is
increased. Due to the larger blocking of radiation by metal
opacities, the EUV flux is reduced which reduces the ionisation in the
outer part of the atmosphere (see lower panel of Fig. 24). In addition, the escape of radiation through metallic lines is favored so that the efficiency of line cooling is
enhanced, leading to a reduction of the temperature for
.
This figure helps us
understand in detail what happens when the metal content is
increased. Due to the larger blocking of radiation by metal
opacities, the EUV flux is reduced which reduces the ionisation in the
outer part of the atmosphere (see lower panel of Fig. 24). In addition, the escape of radiation through metallic lines is favored so that the efficiency of line cooling is
enhanced, leading to a reduction of the temperature for
 (upper panel of Fig. 24). Both effects (line cooling and line blocking)
increase the He I content in the outer atmosphere. In Fig. 24, we also indicate the line formation region of
He I 2.058
(upper panel of Fig. 24). Both effects (line cooling and line blocking)
increase the He I content in the outer atmosphere. In Fig. 24, we also indicate the line formation region of
He I 2.058  m and He II 2.189
m and He II 2.189  m. We see that He II 2.189
m. We see that He II 2.189  m emerges from a zone where the
atmospheric structure is barely modified, so that its strength is
similar in both models (see Fig. 9). On the other hand,
He I 2.058
m emerges from a zone where the
atmospheric structure is barely modified, so that its strength is
similar in both models (see Fig. 9). On the other hand,
He I 2.058  m is produced in the outer atmosphere where the amount of He
I is larger in the Z = 2
m is produced in the outer atmosphere where the amount of He
I is larger in the Z = 2 
 model. Consequently,
He I 2.058
model. Consequently,
He I 2.058  m is stronger in the high metallicity model. Note that this
explanation is fully consistent with the approach of Najarro et al. (1994):
when metallicity is increased, the He I content increases which
leads to a decrease of the escape probability of the He I 584 Å line controlling the upper level of He I 2.058
m is stronger in the high metallicity model. Note that this
explanation is fully consistent with the approach of Najarro et al. (1994):
when metallicity is increased, the He I content increases which
leads to a decrease of the escape probability of the He I 584 Å line controlling the upper level of He I 2.058  m - He II being the dominant ionisation state. This implies a stronger
emission at 2.058
m - He II being the dominant ionisation state. This implies a stronger
emission at 2.058
 (see Eq. (2) of Najarro et al. 1994).
(see Eq. (2) of Najarro et al. 1994).
Does that mean that a twice solar metallicity should be adopted for
IRS9W? This would be an over-interpretation of the results. Indeed,
what the previous exercise reveals is that He I 2.058  m is extremely
sensitive to the EUV radiation. We cannot be absolutely sure that we
correctly predict this part of the spectrum. Indeed, our models are
limited in the sense that we cannot include all lines from
all elements. He I 2.058
m is extremely
sensitive to the EUV radiation. We cannot be absolutely sure that we
correctly predict this part of the spectrum. Indeed, our models are
limited in the sense that we cannot include all lines from
all elements. He I 2.058  m may also suffer from inaccuracies in
metal atomic data. Hence, it may well be that increasing the metal
content artificially compensates for the lack of metallic lines /
elements. Besides, we have discussed only one example for which a larger metal content improves the fit of He I 2.058
m may also suffer from inaccuracies in
metal atomic data. Hence, it may well be that increasing the metal
content artificially compensates for the lack of metallic lines /
elements. Besides, we have discussed only one example for which a larger metal content improves the fit of He I 2.058  m. But there are other
stars (e.g. IRS7E2) for which having a higher Z does not help, He I 2.058
m. But there are other
stars (e.g. IRS7E2) for which having a higher Z does not help, He I 2.058  m remaining too weak. Hence, we conclude that the metallicity cannot be
accurately derived from its effect on He I 2.058
m remaining too weak. Hence, we conclude that the metallicity cannot be
accurately derived from its effect on He I 2.058  m.
m.
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{6688fig24.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg138.gif) |
Figure 24:
Temperature ( upper panel) and He ionisation ( lower panel) structure of the best fit model for IRS9W. The solid line is the model with solar metallicity, while the dashed line is for Z = 2 
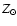 .
In the upper panel, the line formation regions of He I 2.058 .
In the upper panel, the line formation regions of He I 2.058  m and He II 2.189 m and He II 2.189  m are indicated by horizontal lines. m are indicated by horizontal lines. |
| Open with DEXTER |
8 Wind properties of Wolf-Rayet stars
We have derived the wind properties of a homogeneous and reasonably
large sample of Wolf-Rayet stars, mainly composed of WN and Ofpe/WN9 stars. In order to see if the GC stellar winds are similar to other Galactic WR stars, we inspect the behavior of the terminal velocities and mass loss rates (corrected for clumping).
Terminal velocities for other Galactic stars are taken from the
catalog of van der Hucht (2001) and are compared to our sample in Fig. 25. We see that there is a remarkable agreement. We have
seen in Sect. 6.1 that
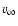 is usually larger in the GC
than in the LMC for Ofpe/WN9 stars, but this was at least
qualitatively explained by a different metallicity/evolutionary
state. We then conclude that the terminal velocities of the GC Wolf-Rayet stars are identical to other Galactic stars.
is usually larger in the GC
than in the LMC for Ofpe/WN9 stars, but this was at least
qualitatively explained by a different metallicity/evolutionary
state. We then conclude that the terminal velocities of the GC Wolf-Rayet stars are identical to other Galactic stars.
The mass loss rates of WN and Ofpe/WN9 stars are shown in Fig. 26 as a function of luminosity![[*]](/icons/foot_motif.gif) . We also plot the results of Crowther et al. (1995c),
Crowther et al. (1995b), Morris et al. (2000), (all in blue open symbols) and
Hamann et al. (2006) (black filled symbols). The GC mass loss
rates are in good agreement with the Crowther et al./Morris et al. results for late WN stars (triangles). For early WN stars, the samples
are too small to draw any conclusion. On the contrary,
there is a large discrepancy between our results and those of
Hamann et al. (2006), at least for late WN stars. This difference is not so
much due to the mass loss rates themselves as it is to
luminosities. Indeed, both samples have similar values of
. We also plot the results of Crowther et al. (1995c),
Crowther et al. (1995b), Morris et al. (2000), (all in blue open symbols) and
Hamann et al. (2006) (black filled symbols). The GC mass loss
rates are in good agreement with the Crowther et al./Morris et al. results for late WN stars (triangles). For early WN stars, the samples
are too small to draw any conclusion. On the contrary,
there is a large discrepancy between our results and those of
Hamann et al. (2006), at least for late WN stars. This difference is not so
much due to the mass loss rates themselves as it is to
luminosities. Indeed, both samples have similar values of
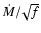 ,
but the luminosities in the GC are lower. Since
most of the stars of the Hamann et al. sample have poorly constrained
distances (only a few are in clusters), while the distance to the GC
is accurately known, we argue that the main reason for the observed
difference is an overestimate of the luminosities in the Hamann et al. sample. An additional explanation to the GC/Hamann et al. WNL luminosity difference could be that their sample contains several H-rich WN stars. These stars are thought to be very massive stars with
a Wolf-Rayet appearance but possibly still core H burning objects
on/close to the main sequence (e.g. Moffat et al. 2006). Such stars are
expected to be very luminous. However, they usually have spectral
subtypes earlier than WN7 (e.g. Crowther & Dessart 1998). A significant
fraction of the very luminous stars in the Hamann et al. sample
(represented by filled triangles around
,
but the luminosities in the GC are lower. Since
most of the stars of the Hamann et al. sample have poorly constrained
distances (only a few are in clusters), while the distance to the GC
is accurately known, we argue that the main reason for the observed
difference is an overestimate of the luminosities in the Hamann et al. sample. An additional explanation to the GC/Hamann et al. WNL luminosity difference could be that their sample contains several H-rich WN stars. These stars are thought to be very massive stars with
a Wolf-Rayet appearance but possibly still core H burning objects
on/close to the main sequence (e.g. Moffat et al. 2006). Such stars are
expected to be very luminous. However, they usually have spectral
subtypes earlier than WN7 (e.g. Crowther & Dessart 1998). A significant
fraction of the very luminous stars in the Hamann et al. sample
(represented by filled triangles around
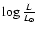
 6.0-6.2 in Fig. 26) do not fall into this category (they are later WN stars). Their luminosity is thus most likely overestimated due to
poorly known distance.
6.0-6.2 in Fig. 26) do not fall into this category (they are later WN stars). Their luminosity is thus most likely overestimated due to
poorly known distance.
In Fig. 26, we also plot the mass loss rates of the GC Ofpe/WN9 stars together with Galactic O supergiants. We see that in
terms of 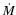 ,
the Ofpe/WN9 stars are closer to O stars than to WN stars. This is another indication that Ofpe/WN9 stars are precursors
of WN8 stars as we have argued in Sect. 6.2.
,
the Ofpe/WN9 stars are closer to O stars than to WN stars. This is another indication that Ofpe/WN9 stars are precursors
of WN8 stars as we have argued in Sect. 6.2.
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{6688fig25.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg140.gif) |
Figure 25:
Terminal velocity of GC WR stars (filled symbols) and other Galactic stars (open symbols) as a function of spectral type. The data for galactic stars are taken from the compilation of van der Hucht (2001). Upper panel: WN stars; Lower panel: WC stars. |
| Open with DEXTER |
9 He abundance in OB stars
We have seen in Sect. 4.4 that the stellar and wind parameters
of the average OB stars in the central parsec were not strongly
constrained. Most of them have only upper limits (
 ,
,
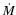 ). For
the helium content, we could estimate
). For
the helium content, we could estimate
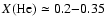 .
This
value is larger than the standard solar abundance (0.1).
.
This
value is larger than the standard solar abundance (0.1).
Since OB supergiants are massive stars evolving away from the main
sequence, chemical enrichment is the most likely explanation. The
question is whether or not the amount of He observed is consistent
with such a mechanism. In that respect, the inclusion of rotation in
evolutionary models is a key ingredient since it triggers additional
mixing which modifies the He surface abundance X(He). In the recent
models of Meynet & Maeder (2005), X(He) evolves slowly from the initial value
during all the "O'' phase, and then dramatically increases when the
star enters the Wolf-Rayet phase. At the end of the O phase, a He content as large as 0.3-0.4 can be obtained. This is compatible with
our derived value. We have also seen in Sect. 4.4 that the
average projected rotational velocity of the brightest OB supergiants
was of the order 100 km s-1. Inspection of Fig. 1 of Meynet & Maeder (2003)
reveals that after 4-8 Myr (age of the GC population of early type
stars), stars with initial masses in the range 25-60  (appropriate for the OB supergiants) have indeed V sini between 40
and 200 km s-1 (depending on the exact age / mass). This is another
indication that 1) the evolutionary tracks with rotation are adequate
for the present discussion, and 2) that the GC massive stars do not
have exceptionally large rotational velocities, as could be suspected
for such a dense environment where interactions should be frequent.
(appropriate for the OB supergiants) have indeed V sini between 40
and 200 km s-1 (depending on the exact age / mass). This is another
indication that 1) the evolutionary tracks with rotation are adequate
for the present discussion, and 2) that the GC massive stars do not
have exceptionally large rotational velocities, as could be suspected
for such a dense environment where interactions should be frequent.
How does our He determination compare to other analyses of massive
stars? The answer is given in Fig. 27. Blue circles show
the He content of Galactic O supergiants. It is important to note that
the uncertainty usually quoted in such determinations is
 0.05-0.1. The circle with the error bars in Fig. 27
represents the average OB supergiants in the GC. We see that although
large, the He content of these stars is still compatible with the
range of values found for O supergiants. In conclusion, the GC OB supergiants are on average similar to other Galactic stars in
terms of He enrichment. This abundance is in addition compatible with
present evolutionary tracks.
0.05-0.1. The circle with the error bars in Fig. 27
represents the average OB supergiants in the GC. We see that although
large, the He content of these stars is still compatible with the
range of values found for O supergiants. In conclusion, the GC OB supergiants are on average similar to other Galactic stars in
terms of He enrichment. This abundance is in addition compatible with
present evolutionary tracks.
Paumard et al. (2006) noted that a few OB supergiants had a strong He absorption on the blue side of Br and suggested that these stars
are significantly He-rich. Unfortunately, given the low S/N ratio
spectra of these stars, we could not derive quantitative constraints
on the He abundance.
and suggested that these stars
are significantly He-rich. Unfortunately, given the low S/N ratio
spectra of these stars, we could not derive quantitative constraints
on the He abundance.
10 Conclusion
We have carried out a detailed analysis of 18 evolved massive stars
(Ofpe/WN9 and Wolf-Rayet) located in the central parsec of the Galaxy
from H and K band spectroscopy obtained with SINFONI on the
ESO/VLT. The average spectrum of 10 bright OB supergiants was also
examined. For quantitative analysis, we have used state of the art
non-LTE atmosphere models including winds and line-blanketing computed
with the code CMFGEN. The main results are:
- The population of massive stars in the central parsec
is able to supply the amount of H and He I ionising
photons required to reproduce the nebular emission. The contribution
of the bright, cool post-main sequence massive stars, first discovered
by Forrest et al. (1987) and Allen et al. (1990) and analysed by
Najarro et al. (1997), accounts for only
 4% of the total H ionising flux
reconciling stellar evolution with observations in the Galactic
Center. State of the art evolutionary and atmosphere models also
reconcile the observed stellar content with a population synthesis
model of a starburst of age
4% of the total H ionising flux
reconciling stellar evolution with observations in the Galactic
Center. State of the art evolutionary and atmosphere models also
reconcile the observed stellar content with a population synthesis
model of a starburst of age  6 Myr.
6 Myr.
- Ofpe/WN9 stars are evolved massive stars close to a LBV phase. Compared to
Najarro et al. (1997), we find they are less He rich, slightly hotter
(although the temperature is poorly constrained) and have lower mass
loss rates. WN8 stars are found to have properties similar to other
Galactic Wolf-Rayet stars of the same spectral type. From
morphological as well as quantitative arguments, they are likely the
descendents of Ofpe/WN9 stars. Two stars are classified as WN8/WC9 stars. Their quantitative analysis reveals that, as suggested by their
spectral type, they show both H and He burning products at their
surface. A direct evolutionary link between the GC Ofpe/WN9, WN8 and
WN/C stars of the form
(Ofpe/WN9
 LBV)
LBV)
 WN8
WN8
 WN/C
WN/C
is proposed, similar to Crowther et al. (1995b).
- Quantitatively, stellar evolutionary tracks with
rotation and
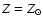 overpredict the luminosity of the GC Wolf-Rayet stars. Tracks with Z = 2
overpredict the luminosity of the GC Wolf-Rayet stars. Tracks with Z = 2 
 are more
appropriate. This may indicate that the mass loss rates adopted in the
current evolutionary tracks during the Wolf-Rayet phase are too
low. However, accurate metallicity determinations are needed to solve
this issue.
are more
appropriate. This may indicate that the mass loss rates adopted in the
current evolutionary tracks during the Wolf-Rayet phase are too
low. However, accurate metallicity determinations are needed to solve
this issue.
- On average, GC OB supergiants are He rich, but not
significantly richer than other galactic supergiants. Their present
projected rotational velocities is
 100 km s-1. These properties
are quantitatively compatible with stellar evolution with rotation on
and close to the main sequence.
100 km s-1. These properties
are quantitatively compatible with stellar evolution with rotation on
and close to the main sequence.
- The wind properties of WN stars in the Galactic
center are very similar to other Galactic stars of the same spectral
type. The luminosities of late WN stars are lower in the GC than in
the sample of Hamann et al. (2006) but in good agreement with the results
of Crowther et al. (1995b). We argue that the difference with the results
of Hamann et al. is due to uncertain distances for their sample stars,
while in our case the distance to the GC is well constrained.
Our study has shown that the GC massive stars are, on average, similar
to other Galactic stars. This strongly suggests that they follow a common evolution, regardless of their possible different formation
process. A key question which remains to be addressed in future
studies is the metallicity in the GC. A better knowledge of this
parameter is crucial to quantitatively test evolutionary models. It is
also crucial in the context of the chemical evolution of the
Galaxy. Also important is the study of nebular emission in the GC by
means of recently developed 3D photo-ionization models. Our total
stellar SED will be a crucial input for such models which will likely
constrain the geometry and density of the ionised gas.
Acknowledgements
We thank F. Najarro for interesting discussions. F.M. acknowledges
support from the Alexander von Humboldt foundation.
- Allen, D. A.,
Hyland, A. R., & Hillier, D. J. 1990, MNRAS, 244,
706 [NASA ADS]
- Anderson, L. 1991, in
Stellar Atmospheres - Beyond Classical Models, NATO ASIC Proc.,
341, 29
(In the text)
- Antokhin, I., Bertrand,
J.-F., Lamontagne, R., Moffat, A. F. J., & Matthews,
J. 1995, AJ, 109, 817 [NASA ADS] [CrossRef]
- Bohannan, B., &
Crowther, P. A. 1999, ApJ, 511, 374 [NASA ADS] [CrossRef]
- Bonnet, H., Abuter,
R., Baker, A., et al. 2004, The Messenger, 117, 17 [NASA ADS]
- Bouret, J.-C., Lanz, T.,
Hillier, D. J., et al. 2003, ApJ, 595, 1182 [NASA ADS] [CrossRef]
- Bouret, J.-C., Lanz, T.,
& Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences]
- Bresolin, F.,
Kudritzki, R.-P., Najarro, F., Gieren, W., & Pietrzynski, G.
2002, ApJ, 577, L107 [NASA ADS] [CrossRef]
- Carr, J. S.,
Sellgren, K., & Balachandran, S. C. 2000, ApJ, 530,
307 [NASA ADS] [CrossRef] (In the text)
- Clénet, Y.,
Rouan, D., Gendron, E., et al. 2004, A&A, 417, L15 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Crowther, P. A.,
Bohannan, B., & Pasquali, A. 1998, in Properties of Hot
Luminous Stars, ed. I. Howarth, ASP Conf. Ser., 131, 38
(In the text)
- Crowther, P. A., &
Dessart, L. 1998, MNRAS, 296, 622 [NASA ADS] (In the text)
- Crowther, P. A.,
& Smith, L. J. 1996, A&A, 305, 541 [NASA ADS] (In the text)
- Crowther, P. A.,
& Smith, L. J. 1997, A&A, 320, 500 [NASA ADS] (In the text)
- Crowther,
P. A., Hillier, D. J., & Smith, L. J. 1995a,
A&A, 293, 172 [NASA ADS] (In the text)
- Crowther,
P. A., Hillier, D. J., & Smith, L. J. 1995b,
A&A, 293, 403 [NASA ADS] (In the text)
- Crowther,
P. A., Smith, L. J., & Hillier, D. J. 1995c,
A&A, 302, 457 [NASA ADS] (In the text)
- Crowther,
P. A., Smith, L. J., & Willis, A. J. 1995d,
A&A, 304, 269 [NASA ADS] (In the text)
- Crowther, P. A.,
Hillier, D. J., Evans, C. J., et al. 2002, ApJ, 579,
774 [NASA ADS] [CrossRef]
- Crowther, P. A.,
Morris, P., & Smith, J. D. 2006, ApJ, in press
- Eisenhauer, F.,
Abuter, R., Bickert, K., et al. 2003a, in Instrument Design
and Performance for Optical/Infrared Ground-based Telescopes,
ed. I. Masanori, A. F. M. Moorwood, Proc. SPIE,
4841, 1548
- Eisenhauer, F., Tecza,
M., Thatte, N., et al. 2003b, The Messenger, 113, 17 [NASA ADS]
- Eisenhauer, F.,
Genzel, R., Alexander, T., et al. 2005, ApJ, 628, 246 [NASA ADS] [CrossRef] (In the text)
- Ekers, R. D.,
van Gorkom, J. H., Schwarz, U. J., & Goss, W. M.
1983, A&A, 122, 143 [NASA ADS] (In the text)
- Evans, C. J.,
Crowther, P. A., Fullerton, A. W., & Hillier,
D. J. 2004, ApJ, 610, 1021 [NASA ADS] [CrossRef]
- Ferland, G. J.,
Korista, K. T., Verner, D. A., et al. 1998, PASP,
110, 761 [NASA ADS] [CrossRef] (In the text)
- Figer, D. F.,
McLean, I. S., & Najarro, F. 1997, ApJ, 486, 420 [NASA ADS] [CrossRef] (In the text)
- Figer, D. F.,
McLean, I. S., & Morris, M. 1999, ApJ, 514, 202 [NASA ADS] [CrossRef]
- Figer, D. F.,
Najarro, F., Gilmore, D., et al. 2002, ApJ, 581, 258 [NASA ADS] [CrossRef]
- Forrest,
W. J., Shure, M. A., Pipher, J. L., & Woodward,
C. E. 1987, in The Galactic Center, ed. D. C.
Backer, AIP Conf. Proc., 155, 153
- Fullerton,
A. W., Massa, D. L., & Prinja, R. K. 2006, ApJ,
637, 1025 [NASA ADS] [CrossRef]
- Geballe,
T. R., Najarro, F., Rigaut, F., & Roy, J.-R. 2006,
ApJ
(In the text)
- Genzel, R., Watson,
D. M., Townes, C. H., et al. 1984, ApJ, 276,
551 [NASA ADS] [CrossRef]
- Genzel, R.,
Crawford, M. K., Townes, C. H., & Watson, D. M.
1985, ApJ, 297, 766 [NASA ADS] [CrossRef]
- Genzel, R.,
Hollenbach, D., & Townes, C. H. 1994, Rep. Progr. Phys.,
57, 417 [NASA ADS] (In the text)
- Genzel, R.,
Schödel, R., Ott, T., et al. 2003, ApJ, 594, 812 [NASA ADS] [CrossRef] (In the text)
- Gerhard, O. 2001,
ApJ, 546, L39 [NASA ADS] [CrossRef]
- Ghez, A. M.,
Duchêne, G., Matthews, K., et al. 2003, ApJ, 586,
L127 [NASA ADS] [CrossRef] (In the text)
- Giveon, U.,
Morisset, C., & Sternberg, A. 2002, A&A, 392, 501 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Grevesse, N., & Sauval,
A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
- Hamann, W., Gr
 fener, G., & Liermann, A. 2006, A&A, 457,
1015 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
fener, G., & Liermann, A. 2006, A&A, 457,
1015 [NASA ADS] [CrossRef] [EDP Sciences] (In the text) - Heger, A., & Langer, N.
1996, A&A, 315, 421 [NASA ADS] (In the text)
- Herald, J. E.,
Hillier, D. J., & Schulte-Ladbeck, R. E. 2001, ApJ,
548, 932 [NASA ADS] [CrossRef] (In the text)
- Herrero, A., Puls, J.,
Corral, L. J., Kudritzki, R. P., & Villamariz,
M. R. 2001, A&A, 366, 623 [NASA ADS] [CrossRef] [EDP Sciences]
- Hillier, D. J., &
Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] (In the text)
- Hillier, D. J.,
Lanz, T., Heap, S. R., et al. 2003, ApJ, 588, 1039 [NASA ADS] [CrossRef]
- Horrobin, M.,
Eisenhauer, F., Tecza, M., et al. 2004, Astron. Nachr., 325,
88 [NASA ADS]
- Hubeny, I., & Lanz, T.
1995, ApJ, 439, 875 [NASA ADS] [CrossRef] (In the text)
- Kim, S. S., &
Morris, M. 2003, ApJ, 597, 312 [NASA ADS] [CrossRef]
- Koyama, K.
E. A. 2006, PASJ, in press
(In the text)
- Krabbe, A., Genzel,
R., Drapatz, S., & Rotaciuc, V. 1991, ApJ, 382, L19 [NASA ADS] [CrossRef] (In the text)
- Krabbe, A., Genzel,
R., Eckart, A., et al. 1995, ApJ, 447, L95 [NASA ADS] [CrossRef] (In the text)
- Lamers,
H. J. G. L. M., & Cassinelli, J. P.
1999, Introduction to Stellar Winds (Introduction to Stellar Winds,
ed. Henny J. G. L. M. Lamers, &
Joseph P. Cassinelli (Cambridge, UK: Cambridge University
Press), 452
(In the text)
- Langer, N. 1991,
A&A, 248, 531 [NASA ADS]
- Lenorzer, A.,
Mokiem, M. R., de Koter, A., & Puls, J. 2004, A&A,
422, 275 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Levin, Y., &
Beloborodov, A. M. 2003, ApJ, 590, L33 [NASA ADS] [CrossRef]
- Lutz, D. 1999, in The
Universe as Seen by ISO, ed. P. Cox, & M. Kessler,
ESA SP-427, 623
(In the text)
- Maeda, Y., Baganoff,
F. K., Feigelson, E. D., et al. 2002, ApJ, 570,
671 [NASA ADS] [CrossRef] (In the text)
- Maeder, A., & Meynet,
G. 2000, ARA&A, 38, 143 [NASA ADS] (In the text)
- Maillard,
J. P., Paumard, T., Stolovy, S. R., & Rigaut, F.
2004, A&A, 423, 155 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Marchenko,
S. V., Moffat, A. F. J., Eversberg, T., et al.
1998, MNRAS, 294, 642 [NASA ADS]
- Markova, N.,
Puls, J., Repolust, T., & Markov, H. 2004, A&A, 413,
693 [NASA ADS] [CrossRef] [EDP Sciences]
-
Martín-Hernández, N. L., van der Hulst, J. M.,
& Tielens, A. G. G. M. 2003, A&A, 407,
957 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Martins, F., Schaerer,
D., & Hillier, D. J. 2002, A&A, 382, 999 [NASA ADS] [CrossRef] [EDP Sciences]
- Martins, F., Schaerer,
D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Martins, F., Schaerer, D.,
Hillier, D. J., & Heydari-Malayeri, M. 2004, A&A, 420,
1087 [NASA ADS] [CrossRef] [EDP Sciences]
- Martins, F.,
Trippe, S., Paumard, T., et al. 2006, ApJ, 649, L103 [NASA ADS] [CrossRef] (In the text)
- Massey, P., & Grove, K.
1989, ApJ, 344, 870 [NASA ADS] [CrossRef]
- Meynet, G., & Maeder,
A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences]
- Meynet, G., & Maeder,
A. 2005, A&A, 429, 581 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Moffat,
A. F. J., Schnurr, O., Chené, A.-N., St-Louis, N.,
& Casoli, J. 2006, Calibrating the Top of the Stellar M-L
Relation, 26th meeting of the IAU, Joint Discussion 5,
16 August 2006, Prague, Czech Republic, JD05, #1, 5
(In the text)
- Morisset, C.,
Schaerer, D., Bouret, J.-C., & Martins, F. 2004, A&A, 415,
577 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Morris, M. 1993,
ApJ, 408, 496 [NASA ADS] [CrossRef] (In the text)
- Morris, P. W.,
van der Hucht, K. A., Crowther, P. A., et al. 2000,
A&A, 353, 624 [NASA ADS] (In the text)
- Moultaka, J.,
Eckart, A., Schödel, R., Viehmann, T., & Najarro, F. 2005,
A&A, 443, 163 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Najarro, F., Hillier,
D. J., Kudritzki, R. P., et al. 1994, A&A, 285,
573 [NASA ADS]
- Najarro, F., Figer,
D. F., Hillier, D. J., & Kudritzki, R. P. 2004,
ApJ, 611, L105 [NASA ADS] [CrossRef] (In the text)
- Najarro, F., Hillier,
D. J., Puls, J., Lanz, T., & Martins, F. 2006, A&A,
456, 659 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Najarro, F., Krabbe,
A., Genzel, R., et al. 1997, A&A, 325, 700 [NASA ADS]
- Nayakshin, S., &
Cuadra, J. 2005, A&A, 437, 437 [NASA ADS] [CrossRef] [EDP Sciences]
- Pasquali, A.,
Langer, N., Schmutz, W., et al. 1997, ApJ, 478, 340 [NASA ADS] [CrossRef] (In the text)
- Paumard, T.,
Maillard, J. P., Morris, M., & Rigaut, F. 2001, A&A,
366, 466 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Paumard, T.,
Genzel, R., Maillard, J. P., et al. 2004, in Young Local
Universe, Proceedings of XXXIXth Rencontres de Moriond, La Thuile,
Aosta Valley, Italie, March 21-28, 2004, ed. A.
Chalabaev, T. Fukui, T. Montmerle, & J. Tran-Thanh-Van (Paris:
Éditions Frontieres), 377
- Paumard, T., Genzel, R.,
Martins, F., et al. 2006, ApJ, 643, 1011 [NASA ADS] [CrossRef]
- Puls, J., Kudritzki,
R.-P., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS]
- Ramírez,
S. V., Sellgren, K., Carr, J. S., et al. 2000, ApJ,
537, 205 [NASA ADS] [CrossRef] (In the text)
- Repolust, T.,
Puls, J., & Herrero, A. 2004, A&A, 415, 349 [NASA ADS] [CrossRef] [EDP Sciences]
- Repolust, T.,
Puls, J., Hanson, M. M., Kudritzki, R.-P., & Mokiem,
M. R. 2005, A&A, 440, 261 [NASA ADS] [CrossRef] [EDP Sciences]
- Schaerer, D.
1996, in ASP Conf. Ser.: AGN, Dense Stellar Systems, and Galactic
Environments, ed. S. Lamb, & J. Perry
(In the text)
- Schoedel, R.,
et al. 2007, A&A
(In the text)
- Shields, J. C., &
Ferland, G. J. 1994, ApJ, 430, 236 [NASA ADS] [CrossRef] (In the text)
- Smith, L. J.,
Norris, R. P. F., & Crowther, P. A. 2002, MNRAS,
337, 1309 [NASA ADS] (In the text)
- Stolte, A., Grebel,
E. K., Brandner, W., & Figer, D. F. 2002, A&A,
394, 459 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Thornley,
M. D., Schreiber, N. M. F., Lutz, D., et al.
2000, ApJ, 539, 641 [NASA ADS] [CrossRef] (In the text)
- Trippe, S.,
Martins, F., Ott, T., et al. 2006, A&A, 448, 305 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tuthill,
P. G., Monnier, J. D., & Danchi, W. C. 1999,
Nature, 398, 487 [NASA ADS] [CrossRef] (In the text)
- Tuthill, P.,
Monnier, J., Tanner, A., et al. 2006, Science,
in press
(In the text)
- van der Hucht, K. A.
2001, VizieR Online Data Catalog, 3215, 0 (In the text)
- Williams,
P. M., van der Hucht, K. A., & The, P. S. 1987,
A&A, 182, 91 [NASA ADS] (In the text)
- Willis, A. J.,
& Stickland, D. J. 1990, A&A, 232, 89 [NASA ADS]
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig1.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg26.gif)
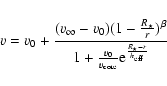
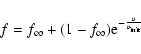
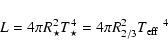
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig2.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg47.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig3.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig4.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg49.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig5.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg50.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig6.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig7.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg57.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig8.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg58.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig9.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig10.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg60.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig11.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg61.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig12.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg62.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig13.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig14.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig15.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig16.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig17.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig18.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg72.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig19.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg73.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6688fig20.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6688fig21.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg114.gif)
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{6688fig22.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg119.gif)
![\begin{figure}
\par\subfigure[]{\includegraphics[width=8.15cm,clip]{6688fig23a.e...
...
\subfigure[]{\includegraphics[width=8.15cm,clip]{6688fig23b.eps} }
\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg122.gif)
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{6688fig24.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg138.gif)
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{6688fig25.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg140.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6688fig26.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg142.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6688fig27.eps}\end{figure}](/articles/aa/full/2007/22/aa6688-06/Timg144.gif)