A&A 467, 1025-1036 (2007)
DOI: 10.1051/0004-6361:20066788
M. Gullieuszik1,2 - E. V. Held1 - L. Rizzi3 - I. Saviane4 - Y. Momany1 - S. Ortolani2
1 - Osservatorio Astronomico di
Padova, INAF, vicolo dell'Osservatorio 5, 35122 Padova, Italy
2 -
Dipartimento di Astronomia, Università di Padova, vicolo dell'Osservatorio 2, 35122 Padova, Italy
3 -
Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
4 -
European Southern Observatory, Casilla 19001, Santiago 19, Chile
Received 22 November 2006 / Accepted 6 March 2007
Abstract
Aims. We present a study of the evolved stellar populations in the dwarf spheroidal galaxy Fornax based on wide-area near-infrared observations, aimed at obtaining new independent estimates of its distance and metallicity distribution. Assessing the reliability of near-infrared methods is most important in view of future space- and ground-based deep near-infrared imaging of resolved stellar systems.
Methods. We have obtained JHK imaging photometry of the stellar populations in Fornax. The observations cover an
![]() 18.5 arcmin2 central area with a mosaic of SOFI images at the ESO NTT. Our data sample all the red giant branch (RGB) for the whole area. Deeeper observations reaching the red clump of helium-burning stars have also been obtained for a
18.5 arcmin2 central area with a mosaic of SOFI images at the ESO NTT. Our data sample all the red giant branch (RGB) for the whole area. Deeeper observations reaching the red clump of helium-burning stars have also been obtained for a
![]() arcmin2 region.
arcmin2 region.
Results. Near-infrared photometry led to measurements of the distance to Fornax based on the K-band location of the RGB tip and the red clump. Once corrected for the mean age of the stellar populations in the galaxy, the derived distance modulus is (m-M)0 =
![]() ,
corresponding to a distance of 141 Kpc, in good agreement with estimates from optical data. We have obtained a photometric estimate of the mean metallicity of red giant stars in Fornax from their (J-K) and (V-K) colors, using several methods. The effect of the age-metallicity degeneracy on the combined optical-infrared colors is shown to be less important than for optical or infrared colors alone. By taking age effects into account, we have derived a distribution function of global metallicity [M/H] from optical-infrared colors of individual stars. Our photometric Metallicity Distribution Function covers the range
,
corresponding to a distance of 141 Kpc, in good agreement with estimates from optical data. We have obtained a photometric estimate of the mean metallicity of red giant stars in Fornax from their (J-K) and (V-K) colors, using several methods. The effect of the age-metallicity degeneracy on the combined optical-infrared colors is shown to be less important than for optical or infrared colors alone. By taking age effects into account, we have derived a distribution function of global metallicity [M/H] from optical-infrared colors of individual stars. Our photometric Metallicity Distribution Function covers the range
![]() ,
with a main peak at
,
with a main peak at
![]() and a long tail of metal-poor stars, and less metal-rich stars than derived by recent spectroscopy. If metallicities from Ca II triplet lines are correct, this result confirms a scenario of enhanced metal enrichment in the last 1-4 Gyr.
and a long tail of metal-poor stars, and less metal-rich stars than derived by recent spectroscopy. If metallicities from Ca II triplet lines are correct, this result confirms a scenario of enhanced metal enrichment in the last 1-4 Gyr.
Key words: galaxies: dwarf - galaxies: individual: Fornax - Local Group - galaxies: stellar content
Stellar populations in dwarf spheroidal galaxies (dSph) are important for our understanding of galaxy formation and evolution. Dwarf spheroidals in the Local Group can be studied in detail, giving strong constraints on the star formation history (SFH) and chemical evolution of these systems. Galaxies of the dSph type all started forming stars at an old epoch (>10 Gyr), but in most cases this early stellar generation was later followed by major star-formation episodes giving rise to significant or even dominant intermediate age populations. While old and intermediate age stellar populations of dSph galaxies have been the subject of many studies in optical bands (see, e.g., Grebel 2005; Held 2005, and references therein), they have been little studied in the near-infrared (NIR).
However, NIR bands have several advantages when studying evolved stars in these stellar systems. Infrared photometry of evolved low-mass and intermediate-mass stars on the red giant branch (RGB) and the helium-burning phases (e.g., red clump, RC) can be used to derive the basic properties of galaxies (distance, metallicity). Techniques to measure such properties from near-infrared observations are becoming increasingly important since the NIR wavelength domain will be central to future instrumentation (ELT adaptive optics, JWST, etc.). There are advantages in using near-infrared photometry for RGB stars, and even more so in combining optical and NIR data. As we will show in this paper, the age-metallicity degeneracy affecting the color of RGB stars (and therefore metallicity determinations) is much less severe using optical-infrared colors.
In order to explore the information contained in the near-infrared spectral window, we have undertaken an imaging study of the evolved stellar populations in Local Group dwarf galaxies. The first galaxy we consider is Fornax, one of the most interesting cases to study, being one of the most massive and luminous dSph satellites of the Milky Way (Mateo 1998). This galaxy was one of the first to provide evidence of an intermediate age stellar population, probed by the presence of luminous carbon star on the asymptotic giant branch (AGB) (Aaronson & Mould 1985; Azzopardi et al. 1999; Aaronson & Mould 1980). Another indicator of a conspicuous intermediate-age stellar population is the well populated red clump of helium-burning stars (Stetson et al. 1998; Saviane et al. 2000a).
A wide plume of main-sequence turnoff stars indicates that the star
formation history of Fornax has been continuous from galaxy's formation
up to recent times (Buonanno et al. 1999; Stetson et al. 1998; Saviane et al. 2000a; Pont et al. 2004).
The luminosity of the brightest blue stars shows evidence that Fornax
has been forming stars at least up to 200 Myr ago, while it does not
contain any stars younger than 100 Myr (Stetson et al. 1998; Saviane et al. 2000a).
An old population is also present, as shown by the
presence of an horizontal branch (HB) and RR-Lyrae
(Greco et al. 2006; Bersier & Wood 2002),
although the blue part of the HB is poorly
populated, so that the old and metal-poor population must be small
(Buonanno et al. 1999; Stetson et al. 1998; Saviane et al. 2000a).
The picture emerging from the above
mentioned studies indicates that Fornax began forming stars
at the epoch of formation of the Galactic
globular clusters (GGCs) ![]() 13 Gyr ago. The star formation
rate was quite low in the first Gyr, and then increased rapidly; Fornax
formed most of its stars 4-10 Gyr ago.
Given the presence of recent star formation, one would expect to
find some gas associated with the galaxy.
Young (1999) searched for neutral hydrogen out to the tidal radius,
and found none.
More recent observations by Bouchard et al. (2006) revealed an extended H I cloud in the direction of Fornax that may (or may not) be within the
galaxy.
13 Gyr ago. The star formation
rate was quite low in the first Gyr, and then increased rapidly; Fornax
formed most of its stars 4-10 Gyr ago.
Given the presence of recent star formation, one would expect to
find some gas associated with the galaxy.
Young (1999) searched for neutral hydrogen out to the tidal radius,
and found none.
More recent observations by Bouchard et al. (2006) revealed an extended H I cloud in the direction of Fornax that may (or may not) be within the
galaxy.
Two studies of the chemical enrichment history of Fornax from the
spectra of red giant stars, using the Ca II infrared lines equivalent
widths, have recently been presented (Battaglia et al. 2006; Pont et al. 2004).
Pont et al. (2004) found a metallicity distribution of Fornax centered at
![]() (on the scale of Carretta & Gratton 1997, hereafter
CG97), with a metal poor tail extending to
(on the scale of Carretta & Gratton 1997, hereafter
CG97), with a metal poor tail extending to
![]() and a metal-rich population reaching
and a metal-rich population reaching
![]() .
The derived age-metallicity relation is well described by a chemical
evolution model with a low effective yield, in which an initial rapid
enrichment is followed by a period of slower enrichment, reaching
.
The derived age-metallicity relation is well described by a chemical
evolution model with a low effective yield, in which an initial rapid
enrichment is followed by a period of slower enrichment, reaching
![]() -1 about 3 Gyr ago. Then a high star formation rate produced an
acceleration, increasing the
-1 about 3 Gyr ago. Then a high star formation rate produced an
acceleration, increasing the
![]() to a recent value of
to a recent value of ![]() -0.4 dex.
These results agree with those previously obtained for a few stars
by Tolstoy et al. (2003) using high resolution spectroscopy.
In a large spectroscopic study of RGB stars in Fornax, Battaglia et al. (2006)
noted the lack of stars more metal poor than [Fe/H] = -2.7 and confirmed
the presence of a metal-rich tail up to
-0.4 dex.
These results agree with those previously obtained for a few stars
by Tolstoy et al. (2003) using high resolution spectroscopy.
In a large spectroscopic study of RGB stars in Fornax, Battaglia et al. (2006)
noted the lack of stars more metal poor than [Fe/H] = -2.7 and confirmed
the presence of a metal-rich tail up to
![]() .
They also
found that the metal-rich stellar populations are more centrally
concentrated, having also a lower velocity dispersion than metal-poor
stars.
.
They also
found that the metal-rich stellar populations are more centrally
concentrated, having also a lower velocity dispersion than metal-poor
stars.
This paper presents the results of a near-infrared study of RGB and RC stars in Fornax, aimed at obtaining new independent estimates of its distance as well as information on its metallicity distribution function from a combination of optical and NIR photometry. This study may represent a local example of NIR studies of more distant resolved stellar systems with future ground-based and space instrumentation. Section 2 presents the observations and the reduction, with special care for the mosaicing techniques, and provides photometric catalogs.
Color-magnitude diagrams are presented in Sect. 3. In Sect. 4, the luminosity functions of red giant stars and helium-burning red clump stars are obtained and used to provide new estimates of the distance to Fornax. The mean metallicity and metallicity distribution of red giant stars is derived in Sect. 5 from their (V-K) color distribution and compared with recent spectroscopic work. Finally, our results are summarized and briefly discussed in Sect. 6.
Near-infrared observations of Fornax were carried out in November 10-11, 2000, using the SOFI camera at the ESO NTT telescope. The camera employed a
![]() pixel Hawaii HgCdTe detector which was read in Double Correlated mode. We used SOFI in Large Field mode, yielding a
pixel scale of 0
pixel Hawaii HgCdTe detector which was read in Double Correlated mode. We used SOFI in Large Field mode, yielding a
pixel scale of 0
![]() 29 pixel-1 and a total field-of-view of about
29 pixel-1 and a total field-of-view of about
![]() .
.
Table 1: Observation log.
Two complementary sets of images were taken in the
![]() filters. The first was a wide-area series of 16 SHALLOW contiguous
fields, in a square array of
filters. The first was a wide-area series of 16 SHALLOW contiguous
fields, in a square array of
![]() covering about
covering about
![]() arcmin2. Secondly, we obtained a dithered sequence of images of
a central field of the galaxy providing DEEP photometry for a
arcmin2. Secondly, we obtained a dithered sequence of images of
a central field of the galaxy providing DEEP photometry for a
![]() arcmin2 area. We used an 8-points dithering pattern with
shifts of up to 10
arcmin2 area. We used an 8-points dithering pattern with
shifts of up to 10
![]() from the central position.
The observing parameters are given in Table 1, which lists the
number of images N of each sequence along with the Detector
Integration Time (DIT) and the number of co-added integrations per image (NDIT). The on-target exposure times are 960 s in J,H,K for the
DEEP image, and 60 s for the SHALLOW mosaic. The observation
strategy is further illustrated in Fig. 1.
from the central position.
The observing parameters are given in Table 1, which lists the
number of images N of each sequence along with the Detector
Integration Time (DIT) and the number of co-added integrations per image (NDIT). The on-target exposure times are 960 s in J,H,K for the
DEEP image, and 60 s for the SHALLOW mosaic. The observation
strategy is further illustrated in Fig. 1.
![\begin{figure}
\includegraphics[width=8.5cm,bb=20 100 850 850,clip=yes]{6788fig1.ps}\end{figure}](/articles/aa/full/2007/21/aa6788-06/Timg36.gif) |
Figure 1: Map of the mosaic of 16 SHALLOW fields observed in Fornax dSph, plotted on a DSS2-red image. The location of the DEEP field is shown as a grey box. |
| Open with DEXTER | |
Given the non-negligible crowding of our Fornax field, we adopted an observing strategy based on offset sky images alternated to on-target images. For the DEEP image, the "chopping'' time interval varied between 120 s for J,H and 60 s for the K band, while it was 60 s for all bands for the SHALLOW observations. The offset pattern was a dithered cross pattern for the DEEP image and a simple offset in declination for the SHALLOW scans. Although expensive in terms of observing time, this strategy proved to give extremely good sky subtraction on scales comparable with the Point Spread Function (PSF) size, improving the quality of the photometry.
Standard stars (including very red stars) from Persson et al. (1998) were observed on a regular basis during the nights at airmasses comparable with those of target objects, to provide photometric calibration. For each standard star, five images were taken, with the star located at the center of the detector and in the middle of the four quadrants of the frame.
The reduction steps were implemented in
IRAF![]() as described in Momany et al. (2003).
For the SHALLOW imaging, the basic observation and reduction unit was
one "strip'' consisting of 4 science and 4 sky
frames. The sky images were scaled to a common median, after
rejecting the highest and lowest pixels, and averaged to produce a
master sky frame to be subtracted from all science images of
the strip. The reduction steps were similar for the DEEP imaging,
using the four offset sky frames closest in time to each science image.
The sky-subtracted images were then corrected for bad pixels and
flat-fielded. Illumination correction frames (as well as bad pixels
maps) available from the ESO Web pages were found suitable to this
purpose.
For the DEEP imaging, all individual images, after sky subtraction,
correction of bad pixels, and flat-fielding, were registered and
averaged using the task IMCOMBINE with rejection of the brightest
and faintest pixel for cleaning of cosmic ray hits.
as described in Momany et al. (2003).
For the SHALLOW imaging, the basic observation and reduction unit was
one "strip'' consisting of 4 science and 4 sky
frames. The sky images were scaled to a common median, after
rejecting the highest and lowest pixels, and averaged to produce a
master sky frame to be subtracted from all science images of
the strip. The reduction steps were similar for the DEEP imaging,
using the four offset sky frames closest in time to each science image.
The sky-subtracted images were then corrected for bad pixels and
flat-fielded. Illumination correction frames (as well as bad pixels
maps) available from the ESO Web pages were found suitable to this
purpose.
For the DEEP imaging, all individual images, after sky subtraction,
correction of bad pixels, and flat-fielding, were registered and
averaged using the task IMCOMBINE with rejection of the brightest
and faintest pixel for cleaning of cosmic ray hits.
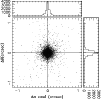 |
Figure 2:
Residuals in the (
|
| Open with DEXTER | |
For the SHALLOW scans, mosaicing is a complex task because of the modest overlap of the individual images. We resorted to absolute astrometry to effectively and accurately register the scans, match the photometry catalogs, and produce a single mosaic image. To this purpose, we used the IRAF package MSCRED (Valdes 1998) along with the WFPRED script package designed at the Padua Observatory by two of us (LR, EVH) for reduction of CCD mosaics. The first step in the mosaicing was the characterization of the astrometric properties of SOFI. This was done using a catalog of secondary astrometric standards in the central region of Fornax established from ESO-WFI observations (Rizzi et al. 2007). This secondary catalog, in turn tied to the USNO-A2.0 reference system (Monet et al. 1998), is required to provide a sufficiently high surface density of stars needed to map distortions in the small field of SOFI.
The field distortion of SOFI was actually found to be negligible. Once a distortion map was constructed, all the individual exposures were registered and resampled to a distortion-corrected coordinate grid with a common reference World Coordinate System (WCS). As a result, a large-area mosaic image was reconstructed in each of the JHK filters.
As a check of our astrometric calibration, we measured the right
ascension and declination of the secondary standard stars on the
WCS-calibrated JHK frames. Figure 2 shows the difference
between stellar coordinates on the SOFI wide-field catalog,
and the
![]() of the same stars in the reference optical
catalog.
This consistency test shows the internal precision of the
astrometric calibration, which is the really important figure for image
and catalog registration. The absolute (systematic) accuracy of
the coordinates is that of the reference catalog, estimated to be of the
order 0.2 arcsec.
The standard deviation of the residuals is not larger than 0
of the same stars in the reference optical
catalog.
This consistency test shows the internal precision of the
astrometric calibration, which is the really important figure for image
and catalog registration. The absolute (systematic) accuracy of
the coordinates is that of the reference catalog, estimated to be of the
order 0.2 arcsec.
The standard deviation of the residuals is not larger than 0
![]() 12 on
both coordinates.
12 on
both coordinates.
Stellar photometry was obtained for the DEEP and SHALLOW images using DAOPHOT II/ ALLSTAR (Stetson 1987). For the DEEP photometry, the PSFs were generated from a list of isolated stars on the coadded images. A P ENNY function with a quadratic dependence on position in the frame was adopted, to account for the elongation of the stellar profiles especially affecting the left side of the chip (this was traced to a misalignment of the Large Field objective). The photometry was finally performed on the stacked images using ALLSTAR. For the SHALLOW images, simple aperture photometry with an aperture with radius equal to the FWHM of the stellar profile was found to yield the best photometric precision. For both catalogs, the pixel coordinates provided by DAOPHOT II were converted to the equatorial system using the calculated WCS astrometric calibration.
The photometric calibration techniques are similar to those adopted by
Momany et al. (2003) and will be only briefly outlined here.
Photometry of the standard stars through increasing apertures was
obtained with the IRAF APPHOT task. For the "total'' magnitude,
we adopted a reference aperture of 18 pixel radius,
close to the 10
![]() aperture used by Persson et al. (1998). The 5
measurements of each standard star were averaged after checking their
uniformity.
The instrumental magnitudes were finally normalized to 1 s exposure time
and zero airmass; for a magnitude
aperture used by Persson et al. (1998). The 5
measurements of each standard star were averaged after checking their
uniformity.
The instrumental magnitudes were finally normalized to 1 s exposure time
and zero airmass; for a magnitude
![]() ,
calculated for an
observation with exposure time
,
calculated for an
observation with exposure time
![]() and airmass X,
we defined the normalized magnitude m as
and airmass X,
we defined the normalized magnitude m as
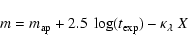 |
(1) |
Given the small number of red stars observed each night, we used for
calibration all data available for five observing nights (including
data previously
obtained in Feb. 2000 with the same SOFI setup). All the
measurements were scaled to a common zero point
and a first least square fit was done to compute the color terms of the
calibration relations.
Then, assuming fixed color terms, we measured the zero point variations
through the run (in particular between the two nights of Nov. 10, 11)
and found them to be very small, comparable with the measurements
errors; a single zero point was therefore adopted for the run, with
uncertainties 0.02 mag in J, H, and K. The
resulting calibration relations are:
The photometric catalogs of Fornax stars were calibrated using the Eqs. (2) after magnitude-scale and aperture correction. This was based on APPHOT large-aperture photometry and growth-curve analysis of a few relatively bright, isolated stars in the DEEP and SHALLOW fields. The uncertainties on aperture correction are of the order 0.03 mag, yielding total calibration uncertainties 0.04 mag.
In order to test the photometric calibration and rule out
the presence of photometric bias in the SHALLOW photometry, we compare
the zero points of the DEEP and SHALLOW photometry in
Fig. 3. For the stars in common the photometry shows an
excellent internal consistency down to
![]() ,
with zero point
differences of the order 0.01 mag.
Figure 4 shows a comparison of our SHALLOW catalog with
2MASS photometry (Cutri et al. 2003) on the same area. We have selected
only 2MASS measurements with S/N>10. The systematic differences are
negligible considering the errors in the 2MASS catalog and the aperture
correction uncertainties.
,
with zero point
differences of the order 0.01 mag.
Figure 4 shows a comparison of our SHALLOW catalog with
2MASS photometry (Cutri et al. 2003) on the same area. We have selected
only 2MASS measurements with S/N>10. The systematic differences are
negligible considering the errors in the 2MASS catalog and the aperture
correction uncertainties.
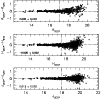 |
Figure 3: Comparison of the DEEP and SHALLOW photometry of Fornax. |
| Open with DEXTER | |
 |
Figure 4:
Comparison of SHALLOW
catalog with 2MASS photometry. Filled circles are data that
passed a |
| Open with DEXTER | |
The photometry lists obtained for the individual pointings were merged
into a single SHALLOW catalog. The stars were matched on the basis of
right ascension and declination, using an error box of 1
![]() 5.
Finally, the coordinates of stars in the two catalogs were matched to
those of BVI photometry (selecting objects with V<23) from ESO WFI
observations (Rizzi et al. 2007), thus producing a final list with BVIJHKmagnitudes.
The SHALLOW and DEEP catalogs of near-infrared photometry of Fornax
stars are presented in Tables 2 and 3 (the entire
catalogs are made available electronically at the CDS).
5.
Finally, the coordinates of stars in the two catalogs were matched to
those of BVI photometry (selecting objects with V<23) from ESO WFI
observations (Rizzi et al. 2007), thus producing a final list with BVIJHKmagnitudes.
The SHALLOW and DEEP catalogs of near-infrared photometry of Fornax
stars are presented in Tables 2 and 3 (the entire
catalogs are made available electronically at the CDS).
The completeness of our photometric catalogues was evaluated from
artificial star experiments. We performed
20 test runs by adding 400 stars to
the scientific frames in each run.
Since the crowding is uniformly low over the 16 SHALLOW pointings, with
only about 1000 stars per pointing on average, the experiments were
limited to one of the SHALLOW pointings.
The input magnitudes and colors of the artificial stars were chosen
along a sequence corresponding to the Fornax RGB.
The stars were placed on a grid of equilateral triangles with a side of 40 pixels
(![]()
![]() ), much larger than the stellar PSF. In each
experiment the grid was then randomly shifted in order to uniformly
cover all the frame. The results from artificial star experiments on the SHALLOW and
DEEP photometry are shown in Figs. 5 and 6, respectively. We note that the DEEP data are comparatively rather noisy in the H band with respect to the J and
K bands.
), much larger than the stellar PSF. In each
experiment the grid was then randomly shifted in order to uniformly
cover all the frame. The results from artificial star experiments on the SHALLOW and
DEEP photometry are shown in Figs. 5 and 6, respectively. We note that the DEEP data are comparatively rather noisy in the H band with respect to the J and
K bands.
Table 2:
The SHALLOW near-infrared catalog of Fornax stars over a
![]() area. A few lines are shown here for
guidance regarding its form and content, while the full catalog is
available from the CDS.
area. A few lines are shown here for
guidance regarding its form and content, while the full catalog is
available from the CDS.
Table 3:
The first rows of the DEEP near-infrared catalog of stars in
a
![]() central region of Fornax. The entire
catalog is available only electronically at the CDS.
central region of Fornax. The entire
catalog is available only electronically at the CDS.
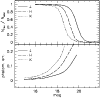 |
Figure 5: Completeness and photometric errors from artificial star experiments for the SHALLOW photometry. Upper panel: completeness calculated as the number of artificial stars recovered as a function of observed magnitude. Lower panel: photometric errors, i.e. the standard deviation of the differences between input and output magnitudes. |
| Open with DEXTER | |
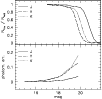 |
Figure 6: The results of artificial star experiments for the DEEP photometry. |
| Open with DEXTER | |
Another well-known observational effect is the fact that the mean difference between input and output magnitudes is generally biased towards brighter output magnitudes (e.g., Gallart et al. 1996). In our experiments for the SHALLOW data, the mean difference of input and output magnitudes resulted to be less than 0.05 mag for K < 18.2. This is also an upper limit for the (J-K) color shift down to this limiting magnitude. However, the color bias is negligible (<0.01 mag) in the first 2 mag below the RGB tip used for the metallicity measurements.
![\begin{figure}
\par\includegraphics[width=8.cm]{6788fig7a.ps}\includegraphics[wi...
...[width=8.cm]{6788fig7c.ps}\includegraphics[width=8.cm]{6788fig7d.ps}\end{figure}](/articles/aa/full/2007/21/aa6788-06/Timg61.gif) |
Figure 7: The color-magnitude diagrams of Fornax from the SHALLOW catalog, obtained by combining optical and near-infrared photometry. Stars on the extended AGB, chosen redder than (J-K) = 1 and brighter than K = 14.5, are shown as filled circles. Superimposed on the K, (J-K) diagram are theoretical isochrones from Girardi et al. (2002, G02, dashed lines) and Pietrinferni et al. (2004, P04, solid lines). The isochrone age is 7 Gyr and the metal abundances are the closest to the metallicity of Fornax for each model set: Z=0.001 and 0.004 for G02, Z=0.001 and 0.002 for P04. Typical photometric errors as derived from artificial star experiments are also shown as crosses in the upper-left panel. |
| Open with DEXTER | |
The near-infrared and optical-infrared color-magnitude diagrams (CMDs) of Fornax dSph in the SHALLOW sample are presented in Fig. 7. Given the better image quality and spatial resolution of our optical photometry, we used the ALLSTAR shape parameter sharp for the V measurements to remove bad and non-stellar objects from our photometric catalogues. Only objects with -0.3 < sharp < 0.3were selected.
The most noteworthy feature in the CMD in Fig. 7 is the well defined sequence of intermediate-age AGB stars. A fraction of AGB stars have red colors typical of carbon (C) stars, and a few stars show extremely red colors possibly indicating dust-enshrouded AGB stars. The properties of near-infrared selected AGB stars in Fornax will be discussed in more detail in a separate paper. We only remark here the dramatic change in their distribution when optical and near-infrared bands are used. Note, for example, that the redder AGB stars become progressively fainter in the bluer optical bands, so that even the brightest (in terms of bolometric luminosity) are missed in optical CMDs. For the reddest AGB stars the (B-V) colors saturate. Thus, selection in the near-infrared appears to be extremely important to investigate the evolution of luminous AGB stars. Also, an advantage of optical-near-infrared colors is the improved discrimination against field contamination by foreground stars and background galaxies, as is evident, for example, when comparing the V, (B-V) and K, (J-K) diagrams in Fig. 7.
The shallow, large-area catalog provides the statistics for studying the
AGB stars, the RGB tip, and the stellar populations of Fornax. The
fainter limiting magnitude and better precision of our DEEP photometry
of a smaller central region allows us to characterize the RGB down to
the so-called "AGB bump'' and the red clump.
Our DEEP color-magnitude diagram is presented in
Fig. 8, together with the RGB fiducial lines of Milky Way
globular clusters (Valenti et al. 2004a). This diagram is similar to that
obtained by Pietrzynski et al. (2003) with ISAAC at the VLT.
Note that the RGB of Fornax is relatively thin in this small central
field. It lies between the fiducial RGB lines of M 4
![]() on the Carretta & Gratton 1997 abundance scale) and
M 107 (
on the Carretta & Gratton 1997 abundance scale) and
M 107 (
![]() ). This suggests a metallicity
). This suggests a metallicity
![]() on the same scale.
on the same scale.
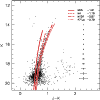 |
Figure 8: The near-infrared CMD of Fornax derived from our DEEP photometry, showing the RGB and the prominent "red clump'' of intermediate-age He-burning stars. Superposed on the RGB are the fiducial lines of Galactic globular clusters from Valenti et al. (2004a), with metallicities on the scale of Carretta & Gratton (1997). Typical photometric errors as derived from artificial star experiments are shown as crosses. |
| Open with DEXTER | |
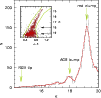 |
Figure 9: The K-band luminosity function of evolved stars in Fornax, corrected for completeness effects. This LF, derived from the DEEP catalog, shows the location of the red clump and the AGB bump. The inset illustrates our sample selection. A histogram with a 0.1 mag bin is shown as a dotted line, while the solid line represents a multibin histogram. |
| Open with DEXTER | |
Using the DEEP data shown in Fig. 8, we constructed a luminosity function (LF) extended down to the red clump of Fornax (Fig. 9). The LF was corrected by taking into account the incompleteness factor derived in Sect. 2.4. Our sample of RGB and He-burning stars was selected as shown in the inset. Using this LF, new estimates of the distance to Fornax have been obtained based on the mean K-band luminosity of the red clump and the K magnitude of the RGB tip.
Several authors have pointed out that distance measurements based on the
magnitude of the RC are most reliable in the near-infrared, because of
the smaller dependence of the RC mean luminosity on metallicity and age
in the K-band, along with the reduced reddening relative to the
optical wavelengths (e.g., Alves 2000; Grocholski & Sarajedini 2002; Pietrzynski et al. 2003).
Pietrzynski et al. (2003) employed VLT-ISAAC photometry of RC stars to measure
the Fornax distance. An independent distance estimate based on our own
measurement of
![]() is presented here, and the two
determinations compared.
is presented here, and the two
determinations compared.
In order to reduce the dependence from the bin choice, the LF was
constructed as a multibin histogram by averaging 10 LFs with a fixed 0.1 mag bin and starting points shifted in steps of 0.01 mag.
A mean level
![]() was measured following the
standard procedure, i.e. by fitting the sum of a Gaussian and a
polynomial to the magnitude distribution of stars in the color range
0.30 < J-K < 0.85 (see, e.g., Pietrzynski et al. 2003).
The mean
was measured following the
standard procedure, i.e. by fitting the sum of a Gaussian and a
polynomial to the magnitude distribution of stars in the color range
0.30 < J-K < 0.85 (see, e.g., Pietrzynski et al. 2003).
The mean
![]() value and its standard deviation are the results of 5000 experiments with bootstrap resampling of the luminosity function.
Based on our artificial star experiments, any magnitude shift
due to a photometric bias is negligible (
value and its standard deviation are the results of 5000 experiments with bootstrap resampling of the luminosity function.
Based on our artificial star experiments, any magnitude shift
due to a photometric bias is negligible (![]() 0.01 mag) for the DEEP data at the RC level.
Other sources of error are considered in the following, in
addition to the 0.02 mag fitting error, to evaluate the total
uncertainty in the distance to Fornax dSph.
0.01 mag) for the DEEP data at the RC level.
Other sources of error are considered in the following, in
addition to the 0.02 mag fitting error, to evaluate the total
uncertainty in the distance to Fornax dSph.
In order to compute the distance, our magnitudes (tied to the LCO
system of Persson et al. 1998) need to be transformed onto the photometric
system used in the RC luminosity calibration of Alves (2000).
Since our K-band photometry agrees very well with the 2MASS system
(Sect. 2.3; see also Carpenter 2001), we simply
adopted the transformation from 2MASS to the Bessell & Brett (1988)
system,
![]() .
The latter is very close to
the Koornneef (1983) system used by Alves (2000)
(see Carpenter 2001; Grocholski & Sarajedini 2002).
.
The latter is very close to
the Koornneef (1983) system used by Alves (2000)
(see Carpenter 2001; Grocholski & Sarajedini 2002).
We therefore applied the relation
| (3) |
In the LF presented in Fig. 9 another bump is clearly seen.
Its K band magnitude was measured by fitting also in this case the
sum of a polynomial and a Gaussian function and found to be
![]() with a bootstrap technique similar to that used for the red clump. This
feature is identified with the AGB bump, which is the signature in the
CMD of the beginning of the AGB phase. At the beginning of this
evolutionary phase the increase of luminosity of a star is slower than
in subsequent AGB phase, and thus a bump in the
LF is produced (Alves & Sarajedini 1999; Gallart 1998; Castellani et al. 1991).
with a bootstrap technique similar to that used for the red clump. This
feature is identified with the AGB bump, which is the signature in the
CMD of the beginning of the AGB phase. At the beginning of this
evolutionary phase the increase of luminosity of a star is slower than
in subsequent AGB phase, and thus a bump in the
LF is produced (Alves & Sarajedini 1999; Gallart 1998; Castellani et al. 1991).
We also explored the possible identification of this feature with the
RGB bump. using the Valenti et al. (2004b) calibration of the RGB bump.
Assuming a metallicity
![]() for the old population of Fornax
(Greco et al. 2006; Bersier & Wood 2002), we derived that the expected RGB bump
magnitude is K=18.52. As discussed by Saviane et al. (2000a), the RGB bump
is fainter that the bump in Fig. 9 and not visible because
it is too close to the overwhelming red clump. We note that the
metallicity assumed here,
for the old population of Fornax
(Greco et al. 2006; Bersier & Wood 2002), we derived that the expected RGB bump
magnitude is K=18.52. As discussed by Saviane et al. (2000a), the RGB bump
is fainter that the bump in Fig. 9 and not visible because
it is too close to the overwhelming red clump. We note that the
metallicity assumed here,
![]() ,
is appropriate for the old
population of Fornax and a lower limit to the actual mean metallicity of
intermediate age stellar populations (see following sections).
The RGB bump magnitude derived by Valenti et al. (2004b) becomes fainter at
increasing metallicity, and therefore our estimate of the RGB bump
magnitude is to be considered a lower limit. We therefore identify the
feature observed at K= 17.99 with the AGB bump.
,
is appropriate for the old
population of Fornax and a lower limit to the actual mean metallicity of
intermediate age stellar populations (see following sections).
The RGB bump magnitude derived by Valenti et al. (2004b) becomes fainter at
increasing metallicity, and therefore our estimate of the RGB bump
magnitude is to be considered a lower limit. We therefore identify the
feature observed at K= 17.99 with the AGB bump.
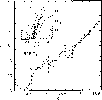 |
Figure 10: The luminosity function of the upper RGB, from the SHALLOW catalog. The inset shows how RGB stars have been selected. The RGB cutoff was measured by fitting an error-convolved step function ( green long-dashed line) to a multibin histogram ( continuous line). The dotted line shows an example of a simple LF with 0.1 mag bins. |
| Open with DEXTER | |
Figure 10 shows a close-up view of the brighter part
of the RGB luminosity function in Fornax, obtained by selecting
red giant stars from the wide field SHALLOW catalog.
This catalog was chosen
because of the better statistics, and, indeed, the RGB cutoff appears
very well defined. We obtained an objective estimate of the magnitude
of the RGB tip by fitting the LF with the
convolution of a step function with a Gaussian kernel representative of
the measurement errors, as in Momany et al. (2002).
The function is composed of a constant value
brighter than the RGB cutoff, and a power law (on a ![]() scale)
below the RGB cutoff.
Since the tip is located at
scale)
below the RGB cutoff.
Since the tip is located at
![]() where our photometry is
complete (see Fig. 5), no completeness
correction was applied to the LF.
As before, a multibin LF was used, obtained by averaging 10 LFs
with a fixed 0.1 mag bin and intervals shifted by 0.01 mag.
Using this procedure the RGB tip was detected at
where our photometry is
complete (see Fig. 5), no completeness
correction was applied to the LF.
As before, a multibin LF was used, obtained by averaging 10 LFs
with a fixed 0.1 mag bin and intervals shifted by 0.01 mag.
Using this procedure the RGB tip was detected at
![]() .
The uncertainty includes the fitting error and the error associated
with the binning of the LF. The internal measurement error at the level
of the RGB tip gives a minor contribution (
.
The uncertainty includes the fitting error and the error associated
with the binning of the LF. The internal measurement error at the level
of the RGB tip gives a minor contribution (![]() 0.01 mag).
0.01 mag).
An independent measurement of the RGB tip was also
obtained using the Maximum
Likelihood Algorithm described by Makarov et al. (2006). The TRGB was found
at
![]() .
Since the two independent measurements agree
within the errors, we adopt the mean value
.
Since the two independent measurements agree
within the errors, we adopt the mean value
![]() (random)
(random) ![]() (systematic)
as our final measure of the tip, where the systematic uncertainty
reflects the photometric zero point error (Sect. 2).
(systematic)
as our final measure of the tip, where the systematic uncertainty
reflects the photometric zero point error (Sect. 2).
The age and metallicity dependence of the RGB tip is larger in Kthan in the I-band, so that the application of the RGB tip method is
more uncertain in this case (e.g., Salaris & Girardi 2005).
Intermediate-age stars show a fainter RGB tip than old stars, with a
difference that can be as large as ![]() 0.1 mag in K in the age
interval 4-13 Gyr. On the other hand, if younger populations become
more metal-rich as a result of galactic chemical evolution, their RGB
tip becomes brighter, because the TRGB K luminosity rises with
increasing metallicity.
0.1 mag in K in the age
interval 4-13 Gyr. On the other hand, if younger populations become
more metal-rich as a result of galactic chemical evolution, their RGB
tip becomes brighter, because the TRGB K luminosity rises with
increasing metallicity.
Since the bulk of stellar populations in Fornax is of intermediate age,
a population correction is required to compute the distance.
To this aim, we modeled the combined effects of age and metallicity on the
RGB tip by constructing a synthetic CMD containing 100 000 stars in the
upper RGB. Our simulations are based on the ZVAR code
(Bertelli et al. 1992), the Padova isochrones
(Girardi et al. 2002), and adopt the chemical evolution history by
Pont et al. (2004) and the SFH from Tolstoy et al. (2003).
We obtained the population correction for the luminosity of the RGB tip
by measuring the cutoff in the simulated CMD for (i) the full stellar
population mix (representative of the Fornax RGB), and (ii) only stars
older that 10 Gyr. As a consequence of the adopted metal enrichment
history, the TRGB in the overall synthetic CMD turns out to be
brighter than that for old stars alone.
The difference in the TRGB K magnitude is
![]() mag.
mag.
By taking this population correction into account, the distance modulus
of Fornax was calculated using Valenti et al. (2004b) empirical calibration
of the
![]() as a function of metallicity, based on
Galactic globular clusters:
as a function of metallicity, based on
Galactic globular clusters:
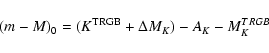 |
(5) |
It is interesting that, once the stellar content is properly taken into account, the K-band RGB tip provides an estimate of the distance to Fornax in good agreement with our determination from the RC and other estimates in the literature. However, the uncertainty remains high, given the strong dependence of the TRGB on age and metallicity and the error on the calibration relation.
In summary, the distance modulus derived here from near-infrared data and methods appears to confirm those measured by Saviane et al. (2000a) from the I magnitude of the RGB tip, (m-M)0 = 20.70, and from the mean magnitude of old HB stars, (m-M)0 = 20.76. New distance measurements based on wide-field optical observations are presented by Rizzi et al. (2007), where the different results in the literature are compared and discussed in some detail.
Table 4: The mean metallicity of Fornax from photometric indices of Valenti et al. (2004a) and Kuchinski & Frogel (1995).
The mean metallicity of the stellar populations that make up the Fornax RGB were estimated by comparing the near-infrared and optical-infrared colors of red giants to the RGB fiducial lines of Galactic globular clusters of known metal abundance. Valenti et al. (2004a) calibrated the RGB colors at fixed K-band luminosities in the near-infrared CMDs of Milky Way globular clusters as a function of metallicity. They give color-metallicity relations for (V-K)0 and (J-K)0 at MK=-5.5, -5.0, -4.0, -3.0 against the [Fe/H] of GGCs on the scale of Carretta & Gratton (1997).
They also provide calibrations against [M/H], a mean metallicity
measuring the abundance of all heavy elements. This parameter is
particularly important to estimate the metallicities of dwarf spheroidal
galaxies by comparison with the photometric properties of Milky Way
globular clusters. These objects are known to show non-solar abundance
patterns, with an overabundance of ![]() -elements relative to iron
that is a function of the cluster metallicity
(Pritzl et al. 2005, and references therein).
In contrast, dwarf spheroidal galaxies tend to have
[
-elements relative to iron
that is a function of the cluster metallicity
(Pritzl et al. 2005, and references therein).
In contrast, dwarf spheroidal galaxies tend to have
[![]() /Fe] ratios closer to solar (e.g., Shetrone et al. 2003).
Salaris et al. (1993) have shown that the color of red giant stars is driven
by the overall metal abundance rather than the Fe abundance. Thus, the
iron [Fe/H] scale of Galactic globular clusters is not immediately
applicable to dwarf galaxies. Instead, the [M/H] provides a suitable
parameter for comparing stellar systems with different abundance
patterns and rank them againsts Milky Way globular clusters. For the
sake of comparison with previous works, we provide here both the [Fe/H]
and [M/H] rankings, but recommend the [M/H] as the most appropriate
values.
/Fe] ratios closer to solar (e.g., Shetrone et al. 2003).
Salaris et al. (1993) have shown that the color of red giant stars is driven
by the overall metal abundance rather than the Fe abundance. Thus, the
iron [Fe/H] scale of Galactic globular clusters is not immediately
applicable to dwarf galaxies. Instead, the [M/H] provides a suitable
parameter for comparing stellar systems with different abundance
patterns and rank them againsts Milky Way globular clusters. For the
sake of comparison with previous works, we provide here both the [Fe/H]
and [M/H] rankings, but recommend the [M/H] as the most appropriate
values.
The mean [Fe/H] and
![]() values of Fornax RGB stars computed using the
Valenti et al. (2004a) calibrations are presented in Table 4,
together with errors calculated from color uncertainties by error
propagation. The average values are
values of Fornax RGB stars computed using the
Valenti et al. (2004a) calibrations are presented in Table 4,
together with errors calculated from color uncertainties by error
propagation. The average values are
![]() and
and
![]() (on the scale of Carretta & Gratton 1997). Using the
calibrations against [M/H], we obtain a mean metallicity
(on the scale of Carretta & Gratton 1997). Using the
calibrations against [M/H], we obtain a mean metallicity
![]() and
and
![]() .
Alternatively, a robust metallicity indicator is represented by the RGB
slope. The Kuchinski & Frogel (1995) calibration yields
.
Alternatively, a robust metallicity indicator is represented by the RGB
slope. The Kuchinski & Frogel (1995) calibration yields
![]() on the Zinn & West (1984, <)1918#>ZW84# scale, corresponding
to
on the Zinn & West (1984, <)1918#>ZW84# scale, corresponding
to
![]() on the CG97 scale (using the conversion of Carretta et al. 2001). This value is confirmed by the recent re-calibration
of the slope by Valenti et al. (2004a), yielding
on the CG97 scale (using the conversion of Carretta et al. 2001). This value is confirmed by the recent re-calibration
of the slope by Valenti et al. (2004a), yielding
![]() or [M/H] =-1.03, in good agreement with other methods.
or [M/H] =-1.03, in good agreement with other methods.
Table 5:
Galactic globular clusters used as RGB metallicity
templates. We list metallicities on the Zinn & West (1984) and
Carretta et al. (2001) [Fe/H] scales, as well as "global'' metallicities
![]() (see text).
(see text).
The metallicity of RGB stars can also be estimated by interpolating the colors of individual stars across a grid of empirical RGB templates. In this way, we also obtain an observable related to the metallicity distribution function (MDF) of the red giant stars. The method used here (see Saviane et al. 2000b) consists in building up a family of hyperbolae that best fit the RGB fiducial lines of GGCs of known metallicity, and then use interpolation over that family of curves to derive the metallicity of RGB stars. A previous application of the method to the (V-K), MK plane can be found in Zoccali et al. (2003), where it is discussed in some detail for stars in the Galactic bulge.
Table 5 lists the reference globular clusters with their
adopted metallicities. In the present implementation of the method we
have employed
![]() values from Valenti et al. (2004a), with the updated
values from Valenti et al. (2004a), with the updated
![]() scale of Carretta et al. (2001).
scale of Carretta et al. (2001).
The resulting "photometric MDF'' is shown in Fig. 11 along
with an illustration of the interpolation method.
We also estimated the statistical uncertainty of our photometric
metallicity determinations using a Monte Carlo approach. A synthetic CMD
was generated by randomly choosing 10 000 stars along the best fit line
in Fig. 11. Errors were added to the synthetic magnitudes
according to a Gaussian distribution with standard deviations
0.01 in V and
according to the results of artificial star experiments in K (see Sect. 2.4).
We then used the same algorithm applied to the Fornax CMD to retrieve individual metallicities.
The recovered metallicities have a nearly Gaussian distribution with a dispersion
![]() dex. This scatter was taken as the statistical uncertainty associated to our individual metallicities.
We note that the photometric completeness in the region of the CMD used to compute the MDF is 100%, so that no completeness correction is needed.
dex. This scatter was taken as the statistical uncertainty associated to our individual metallicities.
We note that the photometric completeness in the region of the CMD used to compute the MDF is 100%, so that no completeness correction is needed.
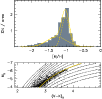 |
Figure 11: Derivation of a photometric Metallicity Distribution Function of RGB stars in Fornax using (V-K) colors. Upper panel: the photometric metallicity distribution function of red giants in Fornax. The solid line is a fit of the sum of two Gaussian functions ( dashed lines) to the data. The method is illustrated in the lower panel: the stars on the upper RGB of Fornax are interpolated across analytical fits ( dotted lines) to the RGB fiducial lines of template Galactic globular clusters. The yellow line marks the best-fit mean metallicity. |
| Open with DEXTER | |
The optical-near-IR
data confirm the extended metallicity distribution of Fornax stars
suggested by Saviane et al. (2000a). The distribution is formally modeled by
the sum of two Gaussians, with a main peak at
![]() and a
secondary peak at
and a
secondary peak at
![]() .
The mode corresponds to
about
.
The mode corresponds to
about
![]() and -1.3 on the CG97 and ZW84 scales,
respectively.
The standard deviation of the Gaussian corresponding to the
main peak is 0.11 dex, which is much larger than the scatter of 0.06 dex due to photometric error.
We remind that our "metallicity distribution'' is representative of the MDF only for old stellar populations with age comparable to the old globular clusters in the Milky Way. This is certainly not true for Fornax stars, whose mean age is about 5-6 Gyr (Saviane et al. 2000a).
and -1.3 on the CG97 and ZW84 scales,
respectively.
The standard deviation of the Gaussian corresponding to the
main peak is 0.11 dex, which is much larger than the scatter of 0.06 dex due to photometric error.
We remind that our "metallicity distribution'' is representative of the MDF only for old stellar populations with age comparable to the old globular clusters in the Milky Way. This is certainly not true for Fornax stars, whose mean age is about 5-6 Gyr (Saviane et al. 2000a).
In all cases, however, this distribution represents an important observable that models of galactic evolution should be able to reproduce.
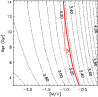 |
Figure 12: Contours of constant (V-K) color at MK=-5.0 as a function of age and [M/H] ( dotted lines), using the model isochrones of Pietrinferni et al. (2004). This plot allows a quantification of the age-metallicity degeneracy in the metallicity estimates based on optical-infrared colors. The red solid line corresponds to the color of the RGB of Fornax. An arrow shows the change in metallicity at this fixed color between 12.5 Gyr old globular clusters and a 7.5 Gyr old galaxy (representative of Fornax dSph). |
| Open with DEXTER | |
Since the bulk of the stellar populations in Fornax is younger than stars in GGCs, the red giants stars in Fornax are on average slightly bluer than globular cluster stars of the same metallicity. As a consequence, the metallicity obtained from the mean RGB color is systematically underestimated. Using optical-near-infrared colors, however, this "age-metallicity degeneracy'' is much reduced with respect to optical colors. This is illustrated in Fig. 12, where we show the effects of age and metallicity variations on RGB colors at MK=-5.0 using the Pietrinferni et al. (2004) isochrones. In this figure, contour lines of equal color are nearly vertical. This means that the effects of a change in age (or those of an age spread) on the color shift and the color dispersion are much smaller than those produced by metallicity variations.
We have used this plot to estimate a mean correction to metallicity, by
assuming that the age of GGCs and Fornax dSph are 12.5 and 7.5 Gyr, respectively. The correction is the difference in metallicity needed to keep the color constant while moving from 12.5 Gyr to 7.5 Gyr.
We found a correction
![]() ,
yielding for Fornax an age-corrected metallicity
,
yielding for Fornax an age-corrected metallicity
![]() in terms of global metallicity (we consider the mode of the photometric MDF).
in terms of global metallicity (we consider the mode of the photometric MDF).
This result is in good agreement with previous results in the
literature. Saviane et al. (2000a) derived a mean age-corrected metallicity
![]() from the (V-I) color of the RGB, on the ZW84 scale
(corresponding to [Fe/H]
from the (V-I) color of the RGB, on the ZW84 scale
(corresponding to [Fe/H]
![]() ).
).
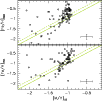 |
Figure 13:
Comparison of metallicities of
individual stars inferred from near-infrared colors and metal abundances
derived from the strengths of Ca II triplet lines. Lower panel:
spectroscopic data from Pont et al. (2004); upper panel: data from
Battaglia et al. (2006). The solid line indicates one-to-one
correlation, while a dashed line shows the shift expected by
taking into account the mean age of stellar populations in Fornax.
Error crosses represent the mean uncertainties of spectroscopic measures,
and the |
| Open with DEXTER | |
Our mean metallicity agrees well with the results of low-resolution
spectroscopic analyses of RGB stars, yielding a mean metallicity
![]() and
and
![]() (Pont et al. 2004; Tolstoy et al. 2001) on the CG97
scale. This value has been confirmed by high-resolution
spectroscopy of (two) stars by Tolstoy et al. (2003).
Since the extended star formation of Fornax leads
to an abundance ratio
(Pont et al. 2004; Tolstoy et al. 2001) on the CG97
scale. This value has been confirmed by high-resolution
spectroscopy of (two) stars by Tolstoy et al. (2003).
Since the extended star formation of Fornax leads
to an abundance ratio
![]() (Shetrone et al. 2003), we can assume that our [M/H] values are
directly comparable with the spectroscopic measurements.
(Shetrone et al. 2003), we can assume that our [M/H] values are
directly comparable with the spectroscopic measurements.
The relatively large overlap between our optical-near-IR photometry and the spectroscopic samples of Fornax RGB stars with metallicities derived by Ca II triplet spectroscopy (Battaglia et al. 2006; Pont et al. 2004) allows us a direct comparison of metal abundances on a star-by-star basis. This comparison is especially interesting to assess the reliability of photometric MDF determinations for all systems that are too distant for (even low-resolution) spectroscopy.
Figure 13 plots the metallicities of individual stars derived from (V-K) colors against those estimated from the equivalent widths of the Ca II triplet lines by Pont et al. (2004) (lower panel) and Battaglia et al. (2006) (upper panel). For the comparison with Pont et al. (2004) results we used only spectra with noise below a given threshold (F. Pont, priv. comm.). The spectroscopic values for metal-rich stars are those corrected by the authors by comparison with high-metallicity stars in the LMC (see Pont et al. 2004, their Sect. 3). While a few stars appear too red or too blue for their spectroscopic metallicity, the general trend is that of an overall correlation. A discrepancy is apparent at the metal-rich end, where the metallicity estimates from photometry appear to saturate. A similar trend, with a worse correlation, is noticed in the comparison with Battaglia et al. (2006) data, where there is a large excess of metal-rich stars with respect to the photometric estimates.
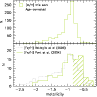 |
Figure 14: Comparison of the metallicity distribution inferred from the optical-infrared colors of RGB stars (this paper, upper panel) and the MDF obtained from Ca II triplet spectroscopy (Battaglia et al. 2006; Pont et al. 2004, lower panel). The shaded part of the histogram from Pont et al. (2004) ([Fe/H] > -0.8) contains extrapolated metallicities. A mean age correction, resulting in a shift of 0.15 dex, has been applied to our histogram. |
| Open with DEXTER | |
The metallicity distribution of Fornax RGB stars is shown in Fig. 14, together with the MDFs obtained from Ca II spectroscopy. In this case, the distribution of photometric [M/H] values in Fig. 14 was corrected by 0.15 dex toward higher metallicities to take into account the fact that intermediate age stars (the bulk of Fornax stars) are bluer than the GGC template stars of the same metallicity. Although this correction clearly represents a first order approximation, it is interesting to note the agreement in the mode of the metallicity distribution with the results of spectroscopy.
Clearly, the first explanation for the discrepancy at the metal-rich end is the age-metallicity degeneracy in RGB star colors that even optical-infrared color indices cannot completely overcome. Assuming that the Ca II triplet methods provides the correct metallicities, the behavior noticed in Figs. 13 and 14 appears to be consistent with a late metal enrichment scenario suggested by the cited spectroscopic studies. Indeed, the redder optical-infrared colors of a young population of metal-rich red giants are compensated for by the younger age. However, spectroscopic abundances from Ca II triplet line strengths are also somewhat uncertain, especially in the high-metallicity regime (where an extrapolation may be needed) and when the Ca II triplet calibration, which is based on globular cluster stars, is applied to the spectra of young (1-4 Gyr old) stars. Accurate abundance measurements from high-resolution spectroscopy may be useful to definitively clarify the issue.
We have presented a near-infrared photometry of the stars in the Fornax
dwarf spheroidal galaxy. Our study provides color-magnitude diagrams and
photometric catalogs of red giant and AGB stars in Fornax over a
![]() area, and deep photometry over a
area, and deep photometry over a
![]() central field.
The main results are the following:
central field.
The main results are the following:
Acknowledgements
We are indebted with F. Pont, G. Battaglia and collaborators for kindly providing unpublished information about their spectroscopic results. We thank M. Salaris for helpful discussions of the properties red clump stars. We also thank an anonymous referee for comments and suggestions that improved the presentation of the paper. M.G. and E.V.H. acknowledge support by MIUR, under the scientific projects PRIN 2002028935 and PRIN 2003029437. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.