A&A 467, 427-436 (2007)
DOI: 10.1051/0004-6361:20066994

Weak lensing mass reconstruction of the galaxy cluster Abell 209[*],[*]

S. Paulin-Henriksson1 - V. Antonuccio-Delogu1 - C. P. Haines2 - M. Radovich2 - A. Mercurio2 - U. Becciani1


1 - INAF / Osservatorio Astrofisico di Catania via S. Sofia, 78, 95123 Catania, Italy
2 - INAF, Osservatorio Astronomico di Capodimonte, Salita Moiariello 16, 80131 Napoli, Italy

Received 21 December 2006 / Accepted 5 February 2007

Abstract
Context. Weak lensing applied to deep optical images of clusters of galaxies provides a powerful tool to reconstruct the distribution of the gravitating mass associated to these structures.
Aims. We use the shear signal extracted by an analysis of deep exposures of a region centered around the galaxy cluster ABCG 209, at redshift $z\sim 0.2$, to derive both a map of the projected mass distribution and an estimate of the total mass within a characteristic radius.
Methods. We use a series of deep archival R-band images from CFHT-12k, covering an area of $\sim$0.3 deg2. We determine the shear of background galaxy images using a new implementation of the modified Kaiser-Squires-Broadhurst KSB+ pipeline for shear determination, which we has been tested against the "Shear TEsting Program 1 and 2'' simulations. We use mass aperture statistics to produce maps of the 2 dimensional density distribution, and parametric fits using both Navarro-Frenk-White and singular-isothermal-sphere profiles to constrain the total mass.
Results. The projected mass distribution shows a pronounced asymmetry, with an elongated structure extending from the SE to the NW. This is in general agreement with the optical distribution previously found by other authors. A similar elongation was previously detected in the X-ray emission map, and in the distribution of galaxy colours. The circular NFW mass profile fit gives a total mass of $M_{200} = 7.7^{+4.3}_{-2.7}\times 10^{14}~{M}_\odot$ inside the virial radius $r_{200} = 1.8\pm 0.3~$Mpc.
Conclusions. The weak lensing profile reinforces the evidence for an elongated structure of ABCG 209, as previously suggested by studies of the galaxy distribution and velocities.

Key words: gravitational lensing - galaxies: clusters: individual: Abell 209

   
1 Introduction

The study of the origin and structure of clusters of galaxies occupies a central place in the current efforts to understand the origin and evolution of the Universe. In particular, the determination of the mass distribution of clusters can prove crucial for verifying the existence of dark matter in the Universe and eventually to determine its abundance and dynamical evolution.

Cluster masses have traditionally been derived through the virial analysis of the velocity dispersion of cluster galaxies, with the assumption of dynamical equilibrium (e.g. Girardi et al. 1998; Girardi & Mezzetti 2001), and/or from the X-ray temperature of the hot intracluster gas, assuming hydrostatic equilibrium (Rosati et al. 2002, and references therein). Since using these methods one has to assume the dynamical and hydrostatic equilibrium, these mass estimates are affected by the ignorance about the dynamical state of the cluster. Weak lensing analysis offers a unique opportunity to determine the cluster mass distribution without such assumptions on its equilibrium, as the effect is due to the gravitational deflection of the light that is dependent solely on the distribution of matter. In particular, one application of weak lensing analysis is the detection of the weak shear around galaxy clusters, yielding an estimate of the total cluster mass and allowing a full mass reconstruction of mainly low ( $0.2 \la z \la 0.5$) redshift clusters (Bardeau et al. 2005; Clowe et al. 2006,2004). As a possible target for a weak lensing analysis the galaxy cluster ABCG 209 is particularly interesting, because the photometric and evolutionary properties of its galaxy populations have been already thoroughly studied (Mercurio et al. 2003a,2004; Haines et al. 2004).

In this paper we present the weak lensing mass reconstruction of the galaxy cluster ABCG 209 at z=0.21 (Mercurio et al. 2003b, and references therein) using archival wide-field R-band imaging. ABCG 209 is a rich (richness class R=3, Abell et al. 1989), X-ray luminous ( $L_{{\rm X}} (0.1{-}2.4$ keV $) \sim 14\;h_{50}^{-2}\times 10^{44}~$erg s-1, Ebeling et al. 1996), moderately hot ( $T_{{\rm X}}\sim10$ keV, Rizza et al. 1998) and massive cluster (Mercurio et al. 2003b; Dahle et al. 2002). It is characterized by the presence of substructures, which is shown by an elongation and asymmetry in the X-ray emission maps, with two main clumps (Rizza et al. 1998). Moreover, the young dynamical state is indicated by the presence of a radio halo (Venturi et al. 2006; Giovannini et al. 1999), which has been suggested to be the result of a recent cluster merger, through the acceleration of relativistic particles by the merger shocks (Feretti 2002).

The plan of the paper is as follows. In Sect. 2 we will shortly review the data reduction procedures. In Sect. 3 we will present the software pipeline which we have developed to perform this analysis, based on the KSB+ algorithm (Luppino & Kaiser 1997; Kaiser et al. 1995). There exist many variants of this algorithm (see Massey et al. 2006; Heymans et al. 2006, for a presentation and comparison of some implementations), so we will describe in some detail our particular implementation (the OACt pipeline). In Sect. 4 we will describe the preparation of the galaxy catalogue, and the technique adopted to extract the shear information. Section 5 will be devoted to present the mass estimated and a mass aperture reconstruction obtained from the shear maps. In Sect. 6 we will compare the mass maps with the galaxy distributions and the X-ray maps. Section 7 will present the conclusions.

   
2 Data description

A detailed description of the data and reduction techniques has been given elsewhere (Haines et al. 2004), so here we will only summarize the main steps. The data were obtained from the Canada-France-Hawaii telescope (CFHT) science archive (PI J.-P. Kneib), and comprise a wide-field R-band image centered on the cluster. The observations were made on 14-16 November 1999, using the CFHT12K mosaic camera, an instrument made up of 12  $4096\times2048$ CCDs, set at the prime focus of the 3.6-m CFHT. The CCDs have a pixel scale of $0.206^{\prime\prime}$, resulting in a total field of view of $42\times28~{\rm arcmin}^{2}$, corresponding to $8.6\times5.7~h^{-2}_{70}~{\rm Mpc}^{2}$ at the cluster redshift. The total exposure time is 7200 s, made up of twelve 600 s exposures, jittered to cover the gaps between the CCDs.

Standard IRAF tools were used to bias-subtract the images, using bias exposures and the overscan regions of each CCD, before flat-fielding using a superflat made up of all science images from the same observing run, registering and Co-adding the images. The resultant images have a median seeing of $0.73^{\prime\prime}$.

The photometric calibration was performed in the the Johnson-Kron-Cousins photometric system, using observations of $\sim$300 secondary standard stars (14<R<17) in fields 6 and 7 of Galadi-Enriquez et al. (2000), resulting in a zero-point uncertainty of 0.005 mag.

For the weak lensing analysis we have masked: (i) saturated stars and hot pixels; (ii) a $1^{\prime}$ (i.e. 300 pixels) border all around the field, where the point-spread function (hereafter PSF) is too complex to be properly modelled (e.g. concave and/or varying too rapidly on small scales); (iii) CCD gaps (i.e. area covered by several CCD on stacked images), where the PSF is also too complex.

The data set does also contain B-band imaging of the field with seeing and depth significantly lower than on the R-band image. On this B-band image, the bright star density is too low to interpolate the PSF, so it is not used to compute the shape parameters, but to help distinguish between cluster, foreground and background galaxies. Using an algorithm which takes into account the R-band magnitude, B-R colour and the local density, Haines et al. (2004) attribute to each galaxy a probability of belonging to the cluster. Given the lack of spectroscopic information, this probability is the most accurate information we have to discriminate among cluster and field galaxies.

   
3 Weak gravitational shear estimate

We extract the shear signal from observed polarisation of background galaxies, corrected for the effects of the PSF, via the standard KSB+ method (Luppino & Kaiser 1997; Kaiser et al. 1995), improved as described in the following sections. We have blind tested our pipeline on the Shear-TEsting-Program (STEP) simulated data (Massey et al. 2006; Heymans et al. 2006), where altogether 16 different weak lensing pipelines have been tested and compared. For reasonable PSFs, as the one sampled by the images presented in this paper turned out to be, the shear we measure $\vec{\gamma}^{\rm meas.}$ is a linear function of the true (i.e. simulated) one  $\vec{\gamma}^{\rm true}$:

 \begin{displaymath} \vec{\gamma}^{\rm meas.} = (m+1) \vec{\gamma}^{\rm true} + \vec{C} \end{displaymath} (1)

where m is the calibration bias and $\vec{C}$ is a systematic effect, mainly describing the anisotropy of PSF residuals. Both m and $\vec{C}$ depend on the PSF, but contain a constant factor intrinsic to the pipeline, which can be subtracted. After subtraction, one has:
 
    -0.05 < m < 0  
    $\displaystyle -0.02 < \vert\vec{C}\vert < 0.02.$ (2)

For the current data set these systematics are well below statistical errors. These statistical errors are mostly due to the intrinsic distribution of galaxy polarisations and to the background galaxy density.

We present in Sects. 3.1 and 3.2 the basic KSB+ formalism, and in Sect. 3.3 the details specific to the OACt pipeline.

   
3.1 Polarisation as a shear estimator

The observed polarisation of a galaxy offers an estimate of the local gravitational shear, and can be defined using the weighted quadrupole moments of the brightness distribution (Kaiser et al. 1995):

 \begin{displaymath} Q_{ij} = \frac{\int ~ {\rm d}^2\theta ~ W(\theta) ~ I(\thet... ...a_i \theta_j} {\int {\rm d}^2\theta ~ W(\theta) ~I(\theta) }, \end{displaymath} (3)

where I is the surface brightness of the object, $\theta$ is the angular distance from the object center and W is a window function, whose introduction is necessary to reduce the shot noise to a reasonable level at large distances from the centroid. Note that the indexes i and j are symmetric, so we have Q12=Q21. Using the weighted quadrupoles, we define the complex polarisation $\vec{e}=e_1+{\rm i}~e_2$ as:

 \begin{displaymath} \left( \begin{array}{c} e_1\\ e_2 \end{array}\right) = \fra... ...begin{array}{c} Q_{11} - Q_{22}\\ 2Q_{12} \end{array}\right). \end{displaymath} (4)

For an elliptical object and a constant window function $W(\theta )=1$, $\vec{e}$ is simply related to the axis ratio $\beta$. Defining a position angle $\theta$ of the major axis, measured counter-clockwise from the x axis, one obtains:

 \begin{displaymath} \left( \begin{array}{c} e_1\\ e_2 \end{array}\right) = \fra... ...gin{array}{c} \cos 2\theta\\ \sin 2\theta \end{array}\right). \end{displaymath} (5)

In the weak lensing limit (defined by: $\vert\vec{\gamma}\vert \ll 1$, where $\vec{\gamma} = \gamma_1 + {\rm i}\gamma_2$ is the complex shear field), and assuming that the real (i.e. unobserved) polarisation distribution has a null average, $\vec{\gamma}$ is directly related to the average observed polarisation, $\vec{\gamma}\approx\vec{e}/2$.

   
3.2 The KSB method

The current KSB+ method is the result of a series of successive improvements (Luppino & Kaiser 1997; Hoekstra et al. 1998) of the original method proposed by Kaiser et al. (1995). It provides a gravitational shear estimate by first-order subtraction of the PSF smearing and shearing from the galaxy polarisation. The 2D vector KSB+ shear estimator of a single galaxy $\widehat{\vec{\gamma}}$ is given by:

 \begin{displaymath} \widehat{\gamma}_\alpha = \left(P^\gamma \right)^{-1}_{\alpha \beta} \left[e_{\beta} - P^{\rm sm}_{\beta\mu}q_{\mu}\right] \end{displaymath} (6)

where we have adopted the standard convention on the summation rule of indices, and $\vec{q}$ is the anisotropic component of the PSF, $\vec{P}^{\rm sm}$ is the smear polarisability tensor, and $\vec{P}^{\gamma}$ is the pre-seeing shear polarisability tensor, the latter being defined as:

 \begin{displaymath} \vec{P}^{\gamma} = \vec{P}^{\rm sh}-\left(\vec{P}^{\rm sm}_{... ...ht)^{-1}\cdot\vec{P}^{\rm sh}_{\rm PSF}\cdot\vec{P}^{\rm sm} . \end{displaymath} (7)

Here $\vec{P}^{\rm sh}$ is the shear polarisability tensor, and the subscript "PSF'' signals that the quantity is computed for the PSF. In Eq. (6), $\vec{q}$ and  $\vec{P}^{\gamma}$ depend on the PSF and are estimated from the images of the surrounding stars.

The actual prescription to estimate $\vec{q}$, $\vec{P}^{\gamma}$ and the PSF-subscripted tensors, the choice of the window function W in Eq. (3), the algorithm of pixelised summations, and finally the approximations, vary from one implementation of the method to another. Our algorithm is described in the following section.

   
3.3 The OACt pipeline

3.3.1 Smoothing radius, significance, Window function, centroid and Summation algorithm

We determine the significance $\nu$ and the optimal smoothing radius $r_{\rm g}$ of each object. $\nu$ and $r_{\rm g}$ are defined as usual in weak lensing: when convolving the image with a Mexican-hat filter, the radius $r_{\rm g}$ is the smoothing radius for which the object has the best signal-to-noise ratio, and the significance $\nu$ is this best signal-to-noise ratio.

The window function W of Eq. (3) is taken to be a circular Gaussian centered on the weighted centroid, having a standard deviation equal to $r_{\rm g}$. The weighted centroid, computed iteratively, is the point for which weighted dipoles are equal to zero:

 \begin{displaymath} \int ~ {\rm d}^2\theta ~ W(\theta) ~ I(\theta) ~ \theta_i = 0. \end{displaymath} (8)

Due to the finite size of pixels, all the integrals are replaced by discrete sums with steps of 0.25 pixel in x and y directions, truncated at a distance of $4r_{\rm g}$. The flux at a given position is the linear interpolation of the flux in the four nearest pixels, and the background flux in a pixel is estimated by SExtractor (more details on the actual parameters adopted are given in Sect. 4.1).

   
3.3.2 Shape computation
We compute the ellipticities, smear polarisability tensors and shear polarisability tensors of background galaxies as described above (Sect. 3.2). We do the same for stars, except that we do not use the smoothing radii $r_{\rm g}$ of stars themselves, but we perform the calculation for every single 0.1 pixel-bin of $r_{\rm g}$ in the range $0.95<r_{\rm g}<9.05$. This bin width of 0.1 pixel is chosen to be much smaller than the accuracy of the measured $r_{\rm g}$ (this accuracy is of few tenths of pixel), and the range is given by extremum values of $r_{\rm g}$ in usual data. This gives a total of 81 $r_{\rm g}$ bins.

After computation of the shape parameters and shear estimator, we discard the objects for which: (i) the standard deviation on the centroid is larger than 0.2 pixel; (ii) the polarisation $\vert\vec{e}\vert$ is greater than 1; (iii) the shear estimator $\vert\vec{\gamma}\vert$ is greater than 2; (iv) the trace of the $\vec{P}^{\gamma}$ tensor is lower than 0.2. For the current data set, this corresponds to 5% of the background galaxies. Even on noisier data sets this usually corresponds to less than 10%.

3.3.3 Subtracting the smearing and shearing effects of the PSF

The corrective factors of a given galaxy are all computed in the $r_{\rm g}$bin corresponding to the $r_{\rm g}$ of the galaxy itself. In other words, we interpolate PSF properties from stars in every single $r_{\rm g}$ bin independently for each galaxy. In all the $\vec{P}^{\rm sm*}$ and $\vec{P}^{\rm sh*}$tensors of stars, the off-diagonal terms are completely dominated by shot-noise, and typically they are more than one order of magnitude smaller than the diagonal terms. For this reason, following similar implementations (Hoekstra et al. 2000), we systematically neglect these off-diagonal terms. Also the non-diagonal terms of the tensor $\vec{P}^{\gamma}$ are extremely noisy, and we then approximate this tensor as a scalar equal to half its trace. These approximations imply that the vector $\vec{q}$ of Eq. (6) (i.e. the anisotropic component of the PSF) is the interpolation of:

 \begin{displaymath} q_\alpha = \frac{e_\alpha^*}{P^{\rm sm*}_{\alpha\alpha}} \end{displaymath} (9)

and

 \begin{displaymath} P^\gamma = \frac{1}{2}\sum_\alpha\left(P^{\rm sh}_{\alpha\al... ...}{P^{\rm sm*}_{\alpha\alpha}}P^{\rm sm}_{\alpha\alpha}\right). \end{displaymath} (10)

Finally, we compute the shear estimator following this simplified version of Eq. (6):

 \begin{displaymath} \widehat{\gamma}_\alpha = \frac{1}{P^\gamma}\left[e_{\alpha} - \sum_i P^{\rm sm}_{\alpha i} q_i\right]. \end{displaymath} (11)

   
3.3.4 Mapping PSF properties
From the star catalogues, we interpolate the 4 ratios: $(e_\alpha^*~/~P^{\rm sm*}_{\alpha\alpha})$ and $(P^{\rm sh*}_{\alpha \alpha}~/~P^{\rm sm*}_{\alpha \alpha})$ (with $\alpha=1$ or 2) over the entire region (where the asterisks refer to parameters measured on stars). The former two terms give $\vec{q}$ (Eq. (9)) and the latter two give $\vec{P}^{\gamma}$through Eq. (10). For each term, we fit a 2-dimensional, 2-degree polynomial independently on each CCD (and also independently in each $r_{\rm g}$ bin).

As we will see in the following, in order to keep a relatively high star density, we use a rather permissive star selection criterion. As a consequence, our star catalogue is contaminated by small galaxies. In order to reject these small galaxies when fitting PSF properties, the fits are iterative: after the first fit is performed, we reject all objects with at least one residual at more than $3\sigma$, and we continue to iteratively perform new fits until convergence. Typically, this procedure converges after 2 or 3 iterations.

   
4 Detection of the weak lensing signal

To extract the weak shear information from the reduced and calibrated CHFT12k images presented in Sect. 2, we first build the star-field and the background-galaxy-field catalogues. Background galaxies contain the weak lensing signal, smeared and sheared by the PSF, while stars are measures of the local PSF. We first detect all the objects within the field and then select those relevant for weak lensing. Stars are selected according to their sizes and their magnitudes, while the background galaxies are selected by cross-checking our relevant object catalogue with the galaxy catalogue of Haines et al. (2004). The latter contains all galaxies within the field and assigns to each a probability of belonging to the field rather than to the cluster itself. All these steps are described in Sect. 4.1. We then compute shape parameters of stars and background galaxies (Sect. 3.3.2), using the stars to map the PSF (as described in Sect. 3.3.4), and finally compute a shear estimator for each background galaxy.

   
4.1 Star and background galaxy catalogues

We detect all the objects on the image using SExtractor, with very low thresholds. We also get a large proportion ($\sim$$50\%$) of spurious detections but these are rejected later. We demand detected objects to have at least 5 pixels above $1.5\sigma$, where $\sigma$ is the standard deviation of the local background (i.e. DETECT_THRESH and ANALYSIS_THRESH set to 1.5, DETECT_MINAREA set to 5), where the local background is estimated with keywords BACK_SIZE set to 70 and BACK_FILTERIZE set to 5. SExtractor is also used to measure the flux and the half-light-radius $r_{\rm h}$ of each object. We then compute $r_{\rm g}$ and $\nu$, as described in Sect. 3.3. We then successively remove from the catalogues : (i) the objects with $\nu <3$; (ii) the objects with at least one neighbor nearer than $3(r_{\rm g}+r_{\rm g}({{\rm neighbor}}))$; (iii) the objects with at least one pixel belonging to the masked area within an aperture of $3~r_{\rm g}$ (the masked area is described in Sect. 2); (iv) the objects with $r_{\rm g}$ lower than the local smoothing radius of stars. Finally, we compute the shapes of the remaining objects and apply shape cuts, as described in Sect. 3.3.2. After having performed these steps, we have a catalogue of $\sim$30 000 detections, containing all the weak-lensing-relevant background galaxies but also stars, cluster galaxies and a large proportion of spurious events due to the low thresholds used with SExtractor.

We build a star catalogue with a loose selection based on 5 parameters: the significance $\nu$; the magnitude R; the surface brightness in the central pixel $R_{\rm max}$; the half-light-radius $r_{\rm h}$, and the smoothing radius $r_{\rm g}$. We demand: $\nu>10$; $R\le 24.0$; $R+2.6\le R_{\rm max}\le R+3.3$; $1.9<\frac{r_{\rm h}(R)}{1~{\rm pixel}}<2.5$; $1.3<\frac{r_{\rm g}(R)}{1~{\rm pixel}}<1.7$. This returns 1588 objects ( $\sim$1.5 objects arcmin-2) uniformly distributed in the field. We define this catalogue loose because $\nu$, $r_{\rm g}$ and $r_{\rm h}$ of stars show variations of $\sim$$30\%$ through the field with the PSF (while we apply these constant cuts). Thus, these cuts result in a star catalogue which contains $20{-}45\%$ of non-stellar detections, most of them being small galaxies. These fake stars are iteratively rejected during the PSF property fits, as described in Sect. 3.3.4. At the end of iterations, we are left with $\sim$0.9 stars arcmin-2, as shown in Fig. 2.


  \begin{figure} \par\includegraphics[width=8cm,clip]{6994fig1.eps}\par\hspace*{2mm}\includegraphics[width=7.8cm,clip]{6994fig2.eps} \end{figure} Figure 1: Top ( bottom respectively) panel: magnitude - central magnitude (optimal smoothing radius $r_{\rm g}$ - magnitude resp.) diagram for all objects detected in the image. Objects selected as possible stars are in red, those selected as possible background galaxies are in blue. Other objects are in black.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{6994fig3.eps}\par\vspace*{2mm} \includegraphics[width=7.8cm,clip]{6994fig4.eps} \end{figure} Figure 2: Star polarisations in the field. Top panel: before any correction (i.e. measured polarisations). Bottom panel: after the anisotropic correction. In both panels, the vectors are oriented along the major axis of the ellipsoid, their length being proportional to the polarisation: $\vert\vec{e}\vert=\sqrt{(Q_{11}-Q_{22})^2+4~Q_{12}^2}~/~(Q_{11}+Q_{22})$. The scale shown in the upper right corners is $\vert\vec{e}\vert=0.03$. The straight lines show the (masked) regions covered by several unstacked images.
Open with DEXTER

We select background galaxies from the remaining objects in two steps. First, we reject fake detections and cluster galaxies by cross-checking the remaining objects with the catalogue of Haines et al. (2004), which includes all the galaxies within the field, together with their accurate photometry and the probability for each galaxy of belonging to the field rather than to the cluster itself (see Sect. 2). We include in our final catalogue those galaxies identified in the catalogue of Haines et al. (2004) marked as having a probability larger than 80% to belong to the field. Second, we reject most of the foreground galaxies with the cut R>21 (since the R-band magnitude is the only information we have at this stage). In order to reject too faint background galaxies for which the shape parameters are not reliable, we cut the $\sim$$3\%$ faintest galaxies for which R>25.5.

These cuts are optimised to give a background galaxy catalogue with low foreground contamination, while keeping almost all the relevant background galaxies. They are illustrated in Fig. 1, where the star sequence is clearly visible in red, while background galaxies are in blue. The final background galaxy catalogue contains 16 708 galaxies (16.7 galaxies arcmin-2). When combining individual galaxy shears to produce shear maps, mass reconstructions or density profile fits (see Sects. 4.3 and 5), we weight galaxies according to their significance, as proposed by Clowe et al. (2006): we do not consider objects with $\nu<5$, while for $\nu>5$ the weight is set equal to ${\rm min}(\nu~;~40)$. In other words, for a given galaxy i, the weight wi is defined as:

 
               wi = $\displaystyle 0 \quad ;~{\rm if~~ } \nu_i<5$  
wi = $\displaystyle \nu_i \quad ;~{\rm if~~ } 5\le\nu_i\le 40$ (12)
wi = $\displaystyle 40 \quad ;~{\rm if~~ } \nu_i>40.$  

The weighted galaxy number is $\Sigma_{i}w_{i}/{\rm max}(w_{i}) = \Sigma_{i} w_{i}/40 = 8816$ (8.8 weighted galaxies arcmin-2).

   
4.2 Testing the PSF subtraction

Figure 2 shows the star polarisations over the field before and after the anisotropic correction (i.e. the subtraction of $\sum_i P^{\rm sm}_{\alpha i} q_i$ in Eq. (11)). One can notice the lack of large scale correlations due to the PSF anisotropies, after the subtraction. The correction also reduces the average amplitude and anisotropy of the PSF, as it is clear from Fig. 3. The corrected distribution of ellipticities is more isotropic, and has also a smaller scatter dispersion.

   
4.3 Combining the individual shears, building shear maps

To get a shear map, we divide the field into $17\times 11$ square cells with an overlap of 50% (i.e. 50% of the galaxies in one cell belong only to this cell, while the remaining 50% belong also to at least one of the 8 neighbouring cells). In each cell we average $\vec{\gamma}$ according to the weighting scheme described in Sect. 4.1. The resulting shear map is shown in Fig. 4. One can see a characteristic pattern of increased tangential shear, which coincides with the central region of the cluster, as defined by the optical distribution of galaxies. This visual impression is confirmed by the mass aperture map, as we will see in the following sections.


  \begin{figure} \par\includegraphics[width=8cm,clip]{6994fig5.eps}\par\vspace*{2mm} \hspace*{4mm}\includegraphics[width=7.6cm,clip]{6994fig6.eps}\end{figure} Figure 3: Distribution of stellar polarisations. Upper panel: e1 against e2 of stars before (black) and after (red) the anisotropic correction. Bottom panel: $\vert\vec{e}\vert$ distribution (same colours).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{6994fig7.eps} \end{figure} Figure 4: Shear map of the whole field obtained with an overlap of 50% (i.e. 50% of the field area is accounted into more than one cell). The scale is given by the thick line in the upper right corners: $\gamma = 0.05$.
Open with DEXTER

   
5 Mass distribution

There are quite a few different methods to deduce the mass distribution from the individual shears of background galaxies (see e.g. Bartelmann & Schneider 2001, for a review). A class of these methods makes use of the 2D smoothed shear maps to get the projected surface density distribution: examples of this class are the mass reconstruction method (Seitz & Schneider 2001,1995; Schneider & Seitz 1995), or the mass aperture technique (Schneider 1996). These methods suffer from the sheet mass degeneracy: they provide a reliable reconstruction of the surface density, but this is known except for a constant value. The alternative is to assume a priori a given mass profile, so that the degeneracy is removed, then attempt a parametric fitting. These latter methods are useful to get an estimate of the total mass of the cluster. Both methods suffer from possible systematic effects, for instance the contamination from background sources.


  \begin{figure} \par\includegraphics[width=14cm,clip]{6994fig8.eps}\end{figure} Figure 5: Total mass inside the radius R for the two models SIS (in blue) and NFW (in red). Dashed lines are the 66% confidence level regions. The black vertical lines show the virial radius $R_{200}=1.81^{+0.30}_{-0.26}~{\rm Mpc}$ given by the NFW fit: straight line for the best fit and dashed lines for the 66% confidence level region. The black cross (in the upper right corner) shows the measure of $M({<}R_{\rm vir})$ and $R_{\rm vir}$ by Mercurio et al. (2003a) from internal dynamics, discussed in Sect. 6.1.
Open with DEXTER

In Sect. 5.1, we fit two different parametric spherical density profiles: a Singular Isothermal Sphere (SIS) and a Navarro-Frenk-White (NFW) (Navarro et al. 1996). In Sect. 5.2, we map the mass distribution using mass aperture statistics.

In order to derive actual values of the mass from the shear parametric, we have to know the critical surface density:

 \begin{displaymath} \Sigma_{\rm crit} = \frac{c^2}{4\pi G} \frac{\left\langle D_{\rm {ls}} / D_s \right\rangle^{- 1}}{D_{\rm {l}}} \end{displaymath} (13)

where $D_{\rm ls}$, $D_{\rm l}$ and $D_{\rm s}$ are the lens-source, observer-lens and observer-source distances respectively. We do not have however any redshifts of the background galaxies, so we approximate their redshift distribution by a single median value (i.e. we adopt a source plane approximation). As described in Sect. 4.1, we restrict the background galaxies to the range 21 < R < 25.5: in this magnitude range, we can assume the median redshift to be $z \sim 1$ (Gavazzi et al. 2004). Then the critical density at the redshift of ABCG 209 (z=0.21) becomes:
 
                    $\displaystyle \Sigma_{\rm crit}$ $\textstyle \simeq$ $\displaystyle 1.62\times 10^{14}~{M}_\odot~{\rm arcmin}^{-2}$  
  $\textstyle \simeq$ $\displaystyle 3.91\times 10^{15}~{M}_\odot~{\rm Mpc}^{-2}$ (14)

for the basic $\Lambda$CDM cosmological model derived from the 3-year WMAP data (Spergel et al. 2006): $\Omega_{\rm M} = 0.27$, $\Omega_{\Lambda} = 0.73$, H0 = 70 km s-1 Mpc-1 and w=-1.

   
5.1 Parametric model fitting

For both profiles we have performed a $\chi^{2}$ minimization of the tangential shear:

 \begin{displaymath} \chi^{2} = \sum_{i=1}^{N} w_{i}\left(\gamma^{\rm T}_{i} - \gamma^{\rm T}_{\rm model}(r_{i})\right)^{2} \end{displaymath} (15)

where $\gamma^{\rm T}$ is the tangential shear (i.e. the shear projected along the direction orthogonal to the line connecting the galaxy position to the cluster center), wi is the weight (as defined in Eq. (12)) and ri is the distance to the cluster center of mass. The latter is defined as the point for which the signal-to-noise of the $\gamma^{\rm T}$ profile attains its maximum value:

 \begin{displaymath} \frac{S}{N}(\alpha ,\delta )= \sum_{i=1}^N w_i~\gamma^{\rm T}_i(\alpha ,\delta ). \end{displaymath} (16)

By maximising Eq. (16), we find the center at $\alpha=1$h31m51.6s ; $\delta=-13^\circ 36^\prime$, offset by about $36^{\prime\prime}$ from the cD galaxy, as shown in Fig. 6.

For the NFW fit we have either assumed that each galaxy provides an estimate of the underlying shear field, (so the summation in Eq. (15) extends to the full sample) or we have binned the data and minimised over the averages in the bins. We have verified that both procedures give compatible results.

We exclude from the fits galaxies lying within an inner central region of the cluster, where the weak lensing approximation ( $\kappa < 1$) is not everywhere valid, and outside an outer region, where the statistics are very weak.

The actual fitted region lies within the following bounds: $1\hbox{$^\prime$ }< \theta < 10\hbox{$^\prime$ }$ ( $0.2~{\rm Mpc} < R < 2~{\rm Mpc}$) around the cluster center of mass.

   
5.1.1 Fitting a NFW profile

The NFW profile has often been used as a good fit of numerically simulated halos (Navarro et al. 1997,1995). Although this fit was originally made only for simulated halos in standard CDM models, it turned out to be a good fit for halos which formed in $\Lambda$CDM models. The mass density of the NFW profile is described by:

                     $\displaystyle \rho(r)$ = $\displaystyle \frac{\delta_{\rm c} \rho_{\rm c}}{(r/r_{\rm s})(1+r/r_{\rm s})^2}$ (17)
$\displaystyle \mbox{where:} ~~~ \delta_{\rm c}$ = $\displaystyle \frac{200}{3} \frac{c^3}{\ln(1+c)-c/(1+c)}$ (18)
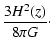$\displaystyle \mbox{and:} ~~~\rho_{\rm c}$ = $\displaystyle \frac{3 H^2(z)}{8 \pi G}\cdot$ (19)

In the equations above r is the distance to the cluster center, $r_{\rm s}$ is the scale radius, H(z) the Hubble parameter at the redshift of the cluster and $c = r_{200}/r_{\rm s}$ is the concentration parameter, where r200 is the virial radius. The NFW density profile is shallower than the SIS profile near the center but steeper in the outer parts. The total mass inside the radius R, shown in Fig. 5, is:

 \begin{displaymath} M({<}R) = 4\pi~\delta_{\rm c}~\rho_{\rm c}~r_{\rm s}^3~\left(\ln (1+R/r_{\rm s}) -1 + \frac{1}{1+R/r_{\rm s}} \right)\cdot \end{displaymath} (20)

Exact expressions for the tangential shear due to this mass distribution are given by Wright & Brainerd (2000). It has two highly correlated degrees of freedom: $r_{\rm s}$ and c. From a non-linear least-squares fit (Levenberg-Marquardt) we obtain:
 
c = 3.4+3.1-1.6      
$\displaystyle r_{\rm s} = 0.50^{+0.60}_{-0.25}~{\rm Mpc}.$     (21)

This corresponds to virial radius r200 and mass M200:
$\displaystyle r_{200} = 1.81^{+0.30}_{-0.26}~{\rm Mpc}$      
$\displaystyle M_{200} = 7.7^{+4.3}_{-2.7}~10^{14}~{M}_\odot.$     (22)

   
5.1.2 Fitting a SIS profile

For a SIS model, the density and shear profiles are respectively given by:

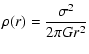$\displaystyle \rho(r) = \frac{\sigma^2}{2\pi G r^2}$     (23)
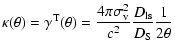$\displaystyle \kappa(\theta) = \gamma^{\rm T}(\theta) = \frac{4\pi\sigma_{\rm v}^2}{c^2}\frac{D_{\rm ls}}{D_{\rm S}}\frac{1}{2 \theta}$     (24)

where $\sigma_{\rm v}$ is the velocity dispersion, the only free parameter in this model. The total mass inside the radius R (shown in Fig. 5) is:

 \begin{displaymath} M({<}R) = \frac{2}{G}~\sigma_{\rm v}^2~R. \end{displaymath} (25)

A linear least-squares fit provides:

 \begin{displaymath} \sigma_{\rm v} = 924\pm 84~{\rm km~s}^{-1}. \end{displaymath} (26)

The previous analysis from Dahle et al. (2002) gives a significantly lower value ( $\sigma_{\rm v} = 680_{-130} ^{+120}~$km s-1), but the authors adopt a less restrictive criterion to eliminate cluster galaxies before the weak lensing analysis, so their weak lensing signal, and consequently $\sigma_{\rm v}$, could be underestimated. Although the total mass of a SIS model diverges, we can however show the integrated mass inside a given radius R (Fig. 5). At the virial radius $R=r_{200}\sim 1.8~$Mpc, as provided by the NFW profile fit (previous section), the mass inside the radius is almost the same both for SIS and NFW profiles: $M({<}R)= M_{200}\sim 7.7\times 10^{14}~M_\odot$.

In Fig. 5 we show the total mass inside the radius R, according to the two different fits we find. Note that the $\pm$$1\sigma$ region of NFW is much larger than in the SIS case. This is a direct consequence of Eqs. (20) and (25): in the SIS model M(<R) is proportional to $\sigma_{\rm v}^2$ and so the confidence region has a width of $\sim$$\pm$$20\%$, while in the NFW model M(<R) depends on $\delta_{\rm c}r_{\rm s}^3f(r_{\rm s},R)$. This makes the $\pm$$1\sigma$ region to have a minimum $\sim$$\pm$$50\%$ width for $R\sim 1.3~$Mpc.

   
5.2 Mass aperture statistics


  \begin{figure} \par\includegraphics[width=8cm,clip]{6994fig9.eps}\end{figure} Figure 6: Comparison of the weak lensing mass reconstruction with the galaxy distribution for ABCG 209. The black contours represent the isodensity contours from the $M_{\rm ap}$ statistics, corresponding to mass densities $5\times10^{13}~{M}_{\odot}$ arcmin-2 (thin dot-dashed curve) to $1\times10^{14}~{M}_{\odot}$ arcmin-2 (tick solid curve), with each contour separated by $1\times10^{13}~{M}_{\odot}$ arcmin-2. The cluster center of mass as defined by Eq. (14) is indicated by the red diamond. The grayscale filled black contours represent the surface density of R<23.0 galaxies (background-corrected), corresponding respectively to 0 (dashed curve) 2 (solid), 3.3, 5, 7.5, 10.0 and 12.5 cluster galaxies arcmin-2.
Open with DEXTER

The mass within an aperture radius r can be obtained directly from the shear using the aperture densitometry statistics $\zeta$, defined as in Fahlman et al. (1994):

 
                   $\displaystyle \zeta (R_1, R_2)$ = $\displaystyle \bar{\kappa} (R_1) - \bar{\kappa} (R_1, R_2)$ (27)
  = $\displaystyle \frac{2}{1 - R^2_{^{} 1^{}} / R^2_{^{} 2^{}}} \int^{R_2}_{R_1}\left\langle \gamma_{\rm T} \right\rangle_{r}~{\rm d}~ \ln r.$ (28)

The mass inside the annulus defined by (R1, R2) is connected to the above quantity by: $M_{\rm ap} = \pi r^2 \zeta \Sigma_{\rm crit}$. This is in fact a lower limit on the true mass, but only dependent on the tangential shear. Thus, it is not affected by residual B-modes and gives a non-parametric representation of the matter density at a given point.


  \begin{figure} \par\includegraphics[width=13cm,clip]{6994fi10.eps}\end{figure} Figure 7: Comparison of the weak lensing mass reconstruction with the X-ray emission for ABCG 209. The red contours represent the isodensity contours from the $M_{\rm ap}$ statistics, as in Fig. 6. The black grayscale-filled contours represent the X-ray emission based on the XMM imaging. The contours are logarithmically spaced, adjacent contours indicating a factor two change in flux density.
Open with DEXTER

Following the approach of Schneider (1996), we build the (2D) mass aperture statistics by computing the aperture densitometry at each point of a grid on the field. The mass density $M_{\rm ap}$ at a given point is given by:

 \begin{displaymath} M_{\rm ap} = \frac{\Sigma_i~\gamma_{Ti}~w_i~Q_i}{\Sigma_i~w_i~Q_i} \end{displaymath} (29)

where the sum extends over all the background galaxies and Q is a smoothing-weighting function. We use the window function Q that maximises the total signal-to-noise ratio (S/N) for a SIS (Schneider 1996):

 \begin{displaymath} \begin{array}{lclr} Q(x) & = & 6\pi~x^2\times(1 - x^2) & {; x<0}\\ & = & 0 & {; x\ge 0} \end{array}\end{displaymath} (30)

where: $x=r/r_{\rm an}$, r being the distance to the center of the annulus, and $r_{\rm an}=5~$arcmin (equivalent to = 1500 pixels = 1 Mpc) is the external radius of the annulus. The only free parameter, i.e. the filter scale $r_{\rm an}$, is chosen as a compromise between different needs. On one side, $r_{\rm an}$ needs to be as small as possible to avoid to wash out small scale structures. On the other hand the annulus needs to be large enough to encompass a significant number of background galaxies (typically 1000) everywhere on the field, in order to get a good and spatially stable S/N. Figure 6 shows the mass aperture density map of the $\sim$100 arcmin2 patch centered on ABCG 209, together with the cluster center of mass defined by Eq. (16). The mass aperture statistics show the elongated structure of the mass distribution. The mass distribution is far from the circular symmetry as assumed by SIS and NFW profile fits. This explains why these fits give only a rough estimate of the total mass, as discussed in Sect. 7.

6 Comparisons with other observations

   
6.1 Comparison with the galaxy distribution

Figure 6 shows the galaxy distribution (shown as the grayscale-filled black contours) as represented by the surface density of R<23.0 cluster galaxies (i.e. after correcting for background/foreground galaxies, see Haines et al. 2004). The galaxy distribution is strongly elongated in the same SE-NW axis as observed for the weak-lensing reconstructed projected mass distribution. The center of the galaxy distribution appears somewhat offset to the NW by about $1^{\prime}$ with respect to the center of mass obtained from the weak lensing reconstruction. There is also a substructure about $5^\prime$ to the North of the cluster center, which could be connected with the observed substructure in the reconstructed mass distribution that extends northwards from the central mass concentration.

The internal dynamics of the cluster was studied by Mercurio et al. (2003a) through a spectroscopic survey of 112 cluster members. A high value of the line-of-sight velocity dispersion was found, with $\sigma_{\nu}=1250_{+84}^{-98}$ km s-1 after removing seven interlopers. Assuming dynamical equilibrium, this value of $\sigma_\nu$ leads to a virial radius of $R_{\rm vir}\sim 3.28\pm0.55~h_{70}^{-1}~$Mpc and a virial mass of $M({<}R_{\rm vir})=3.02^{+0.86}_{-0.89},\times~10^{15}~h_{70}^{-1}~{M}_\odot$ in a $\Lambda$CDM model, with $\Omega_{\rm m}=0.27$ and $\Omega_{\Lambda} = 0.73$. We report this value in Fig. 5, for a direct comparison with the results of the NFW and SIS analyses showed in this paper. The difference in the estimates of the virial mass and the virial radius obtained by the kinematics and weak lensing could be due to the presence of substructures which results in an over estimate of the velocity dispersion. Another source of uncertainties in the kinematics could be the anisotropy parameter of the cluster velocity distribution. On the other hand, the lensing values could be biased because of the elongation of the cluster mass distribution (see Sect. 7).

Evidence in favour of the cluster undergoing a dynamical evolution is found in the form of a velocity gradient acting along a SE-NW axis, which is the same preferential direction found from the elongation in the spatial distribution of galaxies, as well as that of the cD galaxy. There is also significant deviation of the velocity distribution from a Gaussian, with evidence for two secondary clumps at z=0.199 and z=0.215, which appear spatially segregated from the main cluster. These all indicate that ABCG 209 is undergoing strong dynamic evolution with the merging of two or more sub-clumps along the SE-NW direction.


  \begin{figure} \par\includegraphics[width=14cm,clip]{6994fi11.eps}\end{figure} Figure 8: Comparison of the weak lensing mass reconstruction with the mean colours of galaxies across ABCG 209. The black contours represent the isodensity contours from the $M_{\rm ap}$ statistics, as in Fig. 6. The coloured contours indicate the mean B-R colour of the R<21 cluster galaxy population (after statistically correcting for field contamination) as a function of spatial position.
Open with DEXTER

   
6.2 Comparison to X-ray emission

The X-ray data are taken from the XMM science archive (Prop #8423, PI. J.-P. Kneib, see Marty et al. (2003) for an analysis). The observations were made in Jan 2001, with an exposure time of 20 ks. The EPIC MOS1, MOS2 and pn images were combined over the temperature range 0.5-12 keV and the resulting spatial distribution of the X-ray emission is shown in Fig. 7 by the grayscale-filled contours. The X-ray emission is centered on the cD galaxy ($\alpha=1$h31m52.5s, $\delta=-13^\circ 36^\prime 40^{\prime\prime}$, z=0.2097), making it slightly offset ( $36^{\prime\prime}$) from the center of mass determined from the weak lensing by Eq. (16). The X-ray emission is elongated along the same SE-NW direction as seen for the weak lensing reconstructed mass distribution, the emission being most extended towards the NW. There is no evidence of excess X-ray emission from the substructure seen in the weak-lensing reconstruction $\sim$$3^\prime$ to the North of the cluster center.

From an analysis of a 10 ks Chandra ACIS-I (0.3-10 keV) X-ray observation of the cluster, Mercurio et al. (2003a) obtained a best-fitting temperature of $T_{\rm X}=10.2_{-1.2}^{+1.4}$ keV which, assuming $\beta_{\rm spec}=1$, would correspond to $\sigma_{\rm v}\sim1300~$km s-1, and is consistent with the high value of $L_{\rm X}(0.1{-}2.4~$keV $) \sim 14\;h_{50}^{-2}\;10^{44}~$erg s-1 (Ebeling et al. 1996). This value of the velocity dispersion produces a virial mass estimate of $3.3\times 10^{15}~{M}_\odot$.

The mass estimates obtained through our weak lensing analysis are lower than those based on the X-ray temperature and galaxy velocity dispersions. In a weak lensing analysis of 35 X-ray luminous clusters at 0.15<z<0.30, Dahle (2006) finds a large scatter in the relation between the weak lensing mass estimates and the X-ray luminosity, producing a mass uncertainty of $\sigma_{\rm M}=0.44$ dex. In a weak lensing study of 24 X-ray luminous clusters at 0.05<z<0.31, Cypriano et al. (2004) found that on average the mass estimates based on X-ray temperatures and velocity dispersions were 13-27% higher than those from the weak lensing analysis. In particular they found the discrepancy to be much greater for the most massive clusters ( $T_{\rm X}>8$ keV or $\sigma_{\nu}>1122$ km s-1), where the mass excess from the X-ray temperatues or velocity dispersions were 40-75%. They found that the discrepancy was largest for the two clusters with the largest X-ray temperatures ( $T_{\rm X}\sim13$ keV) and velocity dispersions, which were known to be undergoing a merging event, and are far from equilibrium. The high X-ray temperatures would then be probably due to recent shocks, and the high velocity dispersions due to substructures and the complex dynamical situation.

   
6.3 Comparison with Galaxy colours

The star-formation history of galaxies is known to correlate strongly with their local environment. In Fig. 8 we compare the mass distribution with the mean B-R colour of the R<21 cluster galaxy population as a function of spatial position. Each galaxy is weighted according to the probability that it belongs to the cluster, and then the mean colour of cluster galaxies calculated as a function of spatial position using an adaptive kernel method. This analysis is described in details in Haines et al. (2004): the mean galaxy colours (and hence their star-formation histories) are strongly correlated with the dynamical state of the cluster, with an alignment of the colours with the main SE-NW axis. The region with the reddest mean galaxy colours, and hence the oldest stellar populations, is found at the cluster center of mass. There are also two regions of red galaxies outside the cluster core that are aligned with the dark matter distribution, confirming that galaxy evolution is strongly dependent on the hierarchical build up of clusters through mergers. Given the uncertain effects cluster dynamics have on the X-ray emission and galaxy velocity distributions, maps of the mass distribution based on weak lensing analyses provide an important tool for understanding the relation between galaxy evolution and the underlying dark matter distribution (Gray et al. 2004).

   
7 Conclusions

We have performed a weak lensing analysis of the galaxy cluster ABCG 209 through a new implementation of the KSB+ algorithm (the OACt pipeline), and we have also performed a mass reconstruction using Mass Aperture and parametric statistics. We clearly find a measurable weak lensing signal, and the comparison with optical and X-ray data for this cluster brings some interesting conlusions.

First, the centers of the X-ray emission, dark matter, and galaxy distribution all appear offset from one another, with the center of mass found from the weak lensing analysis lying between that of the X-ray and galaxy distributions, and all the three centers of mass aligned on the main SE-NW axis of the cluster. Such an effect is seen for the more extreme Bullet cluster (Clowe et al. 2004), and appears to reflect the different responses of the gas and dark matter components to the merger, briging a further hint at a cluster merging scenario for ABCG 209.

Second, we confirm that ABCG 209 is a massive cluster, although the mass estimated by weak lensing is lower than the estimates obtained by Mercurio et al. (2003a) from the analysis of the dynamical properties of the galactic population (assuming the dynamical equilibrium). On the weak lensing side, there are two sources of error not taken into account in this analysis, that could explain this discrepancy. First, the 2D-mass distribution of the cluster is not circular and this fit of a circular profile is possibly not accurate. Second, we have not taken into account the uncertainty on the critical surface density (Eqs. (13) and (14)), which has been computed according to the single-source plane approximation at z=1. Considering these uncertainties, the agreement we find among the different mass estimates should be regarded as satisfactory.

Acknowledgements
The work of S. Paulin-Henriksson, V. Antonuccio-Delogu and U. Becciani has been partially supported through the EC Transfer of Knowledge Marie Curie grant MTKD-CT-002995, project: COSMOCT, EC-VI Framework Programme for R&D. C. P. Haines acknowledges the financial supports provided through the European Community's Human Potential Program, under contract HPRN-CT-2002-0031 SISCO. This work is partially supported by the Italian Ministry of Education, University and Research (MIUR) grant COFIN200420323 and by the INAF grant "PRIN 2005''. S. Paulin and V. Antonuccio-Delogu would like to thank N. Kaiser for the online version of IMCAT, A. Réfrégier and D. Clowe for useful suggestions.

References

 
Copyright ESO 2007