A&A 467, 385-394 (2007)
DOI: 10.1051/0004-6361:20066006
S. Buitink1 - W. D. Apel2 - T. Asch9 - F. Badea2 - L. Bähren3 - K. Bekk2 - A. Bercuci4 - M. Bertaina5 - P. L. Biermann6 - J. Blümer2,7 - H. Bozdog2 - I. M. Brancus4 - M. Brüggemann8 - P. Buchholz8 - H. Butcher3 - A. Chiavassa5 - F. Cossavella2 - K. Daumiller2 - F. Di Pierro5 - P. Doll2 - R. Engel2 - H. Falcke1,2,6 - H. Gemmeke9 - P. L. Ghia10 - R. Glasstetter11 - C. Grupen8 - A. Haungs2 - D. Heck2 - J. R. Hörandel7 - A. Horneffer1 - T. Huege2 - K.-H. Kampert11 - Y. Kolotaev8 - O. Krömer9 - J. Kuijpers1 - S. Lafebre1 - H. J. Mathes2 - H. J. Mayer2 - C. Meurer2 - J. Milke2 - B. Mitrica4 - C. Morello10 - G. Navarra5 - S. Nehls2 - A. Nigl1 - R. Obenland2 - J. Oehlschläger2 - S. Ostapchenko2 - S. Over8 - M. Petcu4 - J. Petrovic1 - T. Pierog2 - S. Plewnia2 - H. Rebel2 - A. Risse13 - M. Roth7 - H. Schieler2 - O. Sima4 - K. Singh1 - M. Stümpert7 - G. Toma4 - G. C. Trinchero10 - H. Ulrich2 - J. van Buren2 - W. Walkowiak8 - A. Weindl2 - J. Wochele2 - J. Zabierowski13 - J. A. Zensus6 - D. Zimmermann8
1 - Radboud University Nijmegen, Department of Astrophysics, IMAPP,
PO Box 9010, 6500 GL Nijmegen, The Netherlands
2 -
Institut für Kernphysik, Forschungszentrum Karlsruhe,
76021 Karlsruhe, Germany
3 -
ASTRON, 7990 AA Dwingeloo, The Netherlands
4 -
Horia Hulubei National Institute of Physics and Nuclear Engineering (IFIN-HH), 077125 Magurele-Bucharest, Romania
5 -
Dipartimento di Fisica Generale dell'Università, 10125 Torino, Italy
6 -
Max-Planck-Institut für Radioastronomie, 53010 Bonn, Germany
7 -
Institut für Experimentelle Kernphysik, Universität Karlsruhe, 76021 Karlsruhe, Germany
8 -
Fachbereich Physik, Universität Siegen, 57068 Siegen, Germany
9 -
Inst. Prozessdatenverarbeitung und Elektronik, Forschungszentrum Karlsruhe, 76021 Karlsruhe, Germany
10 -
Istituto di Fisica dello Spazio Interplanetario, INAF, 10133 Torino, Italy
11 -
Fachbereich Physik, Universität Wuppertal, 42097 Wuppertal, Germany
12 -
Radioastronomisches Institut der Universität Bonn, 53121 Bonn, Germany
13 -
Soltan Institute for Nuclear Studies, 90950 Lodz, Poland
Received 10 July 2006 / Accepted 14 February 2007
Abstract
Context. The detection of radio pulses from cosmic ray air showers is a potentially powerful new detection mechanism for studying spectrum and composition of ultra high energy cosmic rays that needs to be understood in greater detail. The radiation consists in large part of geosynchrotron radiation. The intensity of this radiation depends, among other factors, on the energy of the primary particle and the angle of the shower axis with respect to the geomagnetic field.
Aims. Since the radiation mechanism is based on particle acceleration, the atmospheric electric field can play an important role. Especially inside thunderclouds large electric fields can be present. In this paper we examine the contribution of an electric field to the emission mechanism theoretically and experimentally.
Methods. Two mechanisms of amplification of radio emission are considered: the acceleration radiation of the shower particles and the radiation from the current that is produced by ionization electrons moving in the electric field. For both mechanisms analytical estimates are made of their effects on the radio pulse height. We selected LOPES data recorded during thunderstorms, periods of heavy cloudiness and periods of cloudless weather. We tested whether the correlations with geomagnetic angle and primary energy vary with atmospheric conditions.
Results. We find that during thunderstorms the radio emission can be strongly enhanced. The present data suggests that the observed amplification is caused by acceleration of the shower electrons and positrons. In the near future, extensions of LOPES and the construction of LOFAR will help to identify the mechanism in more detail. No amplified pulses were found during periods of cloudless sky or heavy cloudiness, suggesting that the electric field effect for radio air shower measurements can be safely ignored during non-thunderstorm conditions.
Key words: acceleration of particles - elementary particles - radiation mechanisms: non-thermal - methods: data analysis - telescopes
The first detection of radio pulses from extensive air showers (EAS) was in 1964 (Jelley et al. 1965) and several emission mechanisms have been proposed to explain them. Askaryan (1962) calculated the Cherenkov radiation resulting from the negative charge excess in extensive air showers. Kahn & Lerche (1966) considered two more mechanisms, both driven by the geomagnetic field. Firstly, the geomagnetic field separates the negative and positive charges. The electric dipole created in this way will emit Cherenkov-like radiation in the atmosphere. Secondly, the transverse current that is generated by the charge separation produces a radiation field which is strongly beamed forwards in the direction of the EAS. They predicted the latter mechanism to be dominant.
The atmospheric electric field also contributes to the total radio emission. Charman (1967) calculated the effect of charge separation due to electric fields and concluded that this effect can contribute significantly when a large electric field is present in the atmosphere. Furthermore, Wilson (1957) and Charman (1968) suggested that ionization electrons, left behind by the EAS, emit radiation when accelerated in a background electric field. Inside thunderclouds the electric field can be large enough to accelerate the ionization electrons up to energies high enough to produce ongoing ionization (typically 100 kV m-1). This effect is called runaway breakdown and a calculation of the associated radio pulse is done by Gurevich et al. (2002).
In the 1970's several groups did experiments with shower arrays and radio antennas. One of their aims was to infer the correct emission mechanism from polarization measurements. Although most experiments were in favour of the transverse current mechanism, a large contribution of other mechanisms could not be excluded. Large spreads in radio intensity, inability to filter out radio interference, and the significant but unknown effects of atmospheric conditions led to the abandonment of these experiment (see Baggio et al. 1977). Excessively large radio pulses of EAS during thunderstorms were found experimentally by Mandolesi et al. (1974).
Recently, Gurevich et al. (2004) reported the discovery of radio pulses of duration ![]()
![]() s associated with EAS during thunderstorms at the Tien Shan Scientific Station in Kazakhstan.
These were detected with antennas sensitive to frequencies between 0.1 and 30 MHz. The FORTE satellite has detected strong intracloud radio pulses in the 26-48 MHz
band, which are correlated with discharge processes inside the thundercloud (Jacobson 2003).
s associated with EAS during thunderstorms at the Tien Shan Scientific Station in Kazakhstan.
These were detected with antennas sensitive to frequencies between 0.1 and 30 MHz. The FORTE satellite has detected strong intracloud radio pulses in the 26-48 MHz
band, which are correlated with discharge processes inside the thundercloud (Jacobson 2003).
The development of LOFAR revived the interest in radio detection of EAS. Falcke & Gorham (2003) describe the emission in terms of coherent geosynchrotron emission. Although no explicit comparisons are made, they expect this mechanism to be largely equivalent to the transverse current mechanism, since it also results from charge separation and is beamed forward. Detailed simulations of the geosynchrotron emission from EAS are presented in Huege & Falcke (2003) and Huege & Falcke (2005).
The LOPES experiment was set up at the KASCADE array site in Karlsruhe, consisting of 10 and later 30 radio antennas sensitive to radiation in the band 40-80 MHz. The presence of the KASCADE particle detectors on the site, new techniques and modern hardware allow higher resolution and a higher detection rate than the old experiments. In Falcke et al. (2005) it was shown that the measured antenna electric field is strongly correlated with the muon number and the angle of the shower axis with the geomagnetic field. The first correlation is a strong indication that the radio emission from EAS is coherent, while the latter correlation proves that the dominant emission mechanism is of geomagnetic nature.
In this paper we investigate theoretically and experimentally the effect of atmospheric conditions on the radio emission. We compare sets of events that were recorded by LOPES under various weather conditions: fair weather, large nimbostratus clouds, and thunderstorms. Under violent weather conditions, the effect of geoelectric mechanisms increases. When this increase is large enough it may dominate over the geomagnetic emission mechanism. Understanding the effect of atmospheric conditions on the emitted radiation is crucial for a correct determination of the primary energy from observed radio pulses.
We present some general characteristics of thunderstorms based on the information provided by MacGorman & Rust (1998).
In fair weather, i.e. atmospheric conditions in which electrified clouds are absent, there is a downward electric field present with a field strength of ![]() 100 V m-1 at ground
level. The field strength decreases rapidly with altitude and has values below 10 V m-1 at altitudes of a few hunderd meter and higher. The associated fair weather current charges up cloud boundaries, because clouds have lower conductivity than the free
atmosphere. Other effects, such as ion capture and collisions between polarized cloud particles, also contribute to the charging up of clouds. Clouds can typically gain field
strengths of a few hundred V m-1. Nimbostratus clouds, which have a typical
thickness of more than 2000 m can have fields of the order of 10 kV m-1. The largest electric fields are found inside thunderstorms, where locally field strengths can reach
values up to 100 kV m-1.
In most clouds this field is directed vertically (either upwards or downwards, depending on the type of cloud), but thunderclouds contain complex charge distributions and
can have local fields in any direction. Thunderclouds can have a vertical extent of
100 V m-1 at ground
level. The field strength decreases rapidly with altitude and has values below 10 V m-1 at altitudes of a few hunderd meter and higher. The associated fair weather current charges up cloud boundaries, because clouds have lower conductivity than the free
atmosphere. Other effects, such as ion capture and collisions between polarized cloud particles, also contribute to the charging up of clouds. Clouds can typically gain field
strengths of a few hundred V m-1. Nimbostratus clouds, which have a typical
thickness of more than 2000 m can have fields of the order of 10 kV m-1. The largest electric fields are found inside thunderstorms, where locally field strengths can reach
values up to 100 kV m-1.
In most clouds this field is directed vertically (either upwards or downwards, depending on the type of cloud), but thunderclouds contain complex charge distributions and
can have local fields in any direction. Thunderclouds can have a vertical extent of ![]() 10 km.
The electric field at ground level is strongly affected by the electric processes inside thunderclouds. Although it can not be used to estimate the field strength inside the cloud, a change in the (polarity of) the ground field is a strong indication that large electric fields are present overhead. In the context of EAS radio emission, ground level
electric field mills can be used as a warning system for violent electric phenomena in the atmosphere.
10 km.
The electric field at ground level is strongly affected by the electric processes inside thunderclouds. Although it can not be used to estimate the field strength inside the cloud, a change in the (polarity of) the ground field is a strong indication that large electric fields are present overhead. In the context of EAS radio emission, ground level
electric field mills can be used as a warning system for violent electric phenomena in the atmosphere.
The atmospheric electric field acts on the radio emission from EAS in various ways. We distinguish two generations of electrons: the relativistic electrons from pair creation in the EAS (called shower electrons from here) and the non-relativistic electrons resulting from the ionization of air molecules by the EAS particles (called ionization electrons from here). The shower electrons are created together with an equal amount of positrons. In this section, we will use Gaussian units.
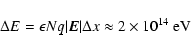 |
(1) |
The radiation part of the electric field of a moving electric charge can be expressed as (Jackson 1975):
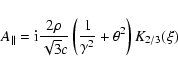 |
(5) |
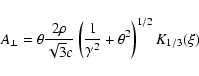 |
(6) |
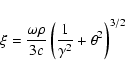 |
(7) |
| |
Figure 1: The electrons and positrons travel along curved trajectories in the magnetic field, emitting synchrotron radiation. |
| Open with DEXTER | |
The radiated power of an accelerated charge can be expressed in the following form, known as the Liénard result (Jackson 1975):
![\begin{displaymath}%
P=\frac{2}{3}\frac{e^2}{c}\gamma^{6}\left[ (\dot{\vec{\beta}})^{2} - (\vec{\beta}\times\dot{\vec{\beta}})^2\right]
\end{displaymath}](/articles/aa/full/2007/20/aa6006-06/img27.gif) |
(9) |
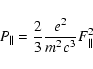 |
(10) |
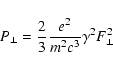 |
(11) |
For a more detailed view we turn our attention to the vector potential. We will treat a general case in which a linear force and a perpendicular force act on a charge and evaluate the vector potentials caused by these two forces. We define the unit vector ![]() as
perpendicular to the particle's velocity
as
perpendicular to the particle's velocity
![]() and lying in the orbital plane of the particle. From Eq. (4) we know that the emission
from an electron/positron pair is strongly polarized in this direction. We therefore evaluate the vector potentials of linear and
perpendicular acceleration along this unit vector for an observer in the orbital plane.
Since both the charge and
and lying in the orbital plane of the particle. From Eq. (4) we know that the emission
from an electron/positron pair is strongly polarized in this direction. We therefore evaluate the vector potentials of linear and
perpendicular acceleration along this unit vector for an observer in the orbital plane.
Since both the charge and
![]() in Eq. (2) have
different signs for electrons and positrons, the resulting field is the same for both types of particles. For linear acceleration Eqs. (2) and (3) reduce to:
in Eq. (2) have
different signs for electrons and positrons, the resulting field is the same for both types of particles. For linear acceleration Eqs. (2) and (3) reduce to:
![\begin{displaymath}%
\vec{A}_{\parallel}(\theta,t)=\frac{e}{\sqrt{4\pi c}}\left[...
...})^{3}}
\dot{\beta}_{\parallel}\right]_{{\rm ret}} \hat{e}_{1}
\end{displaymath}](/articles/aa/full/2007/20/aa6006-06/img42.gif) |
(14) |
![\begin{displaymath}%
\vec{A}_{\perp}(\theta,t)=\frac{e}{\sqrt{4\pi c}}\left[ \fr...
...a^{2})^{3}}
\dot{\beta}_{\perp}\right]_{{\rm ret}} \hat{e}_{1}
\end{displaymath}](/articles/aa/full/2007/20/aa6006-06/img43.gif) |
(15) |
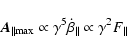 |
(16) |
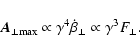 |
(17) |
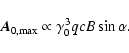 |
(18) |
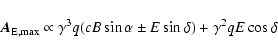 |
(19) |
| |
Figure 2: The electrons and positrons make curved trajectories in the magnetic field. Under influence of a downward directed electric field, the positrons (electrons) are accelerated (decelerated). The asymmetry in the trajectories will be reflected in the radio emission. |
| Open with DEXTER | |
Three effects can be distinguished that cause amplification:
| |
Figure 3: Electron/positron pairs are created in a horizontal shower. The downward electric force works in the same direction as the Lorentz force for both species. The radio emission is amplified. |
| Open with DEXTER | |
So far, only the emission of a single particle pair was discussed. Equation (20) does not apply to complete showers, consisting of many electron-positron pairs with
varying pitch angles, energies and track lengths. An observer at ground level can see the emission of a particle only for a fraction of its
lifetime, since the particle follows a curved trajectory. When the emission from a particle is amplified due to an electric force, this does
not necessarily mean that an observer will see an increase in emission.
The observed pulses of single particles have a duration of
![]() s while the total pulse of a shower is of the order
s while the total pulse of a shower is of the order
![]() s, where L is the
length of the total shower. The pulses of individual particles are distributed over the period
s, where L is the
length of the total shower. The pulses of individual particles are distributed over the period ![]() ,
so the emission is not totally
coherent. Since the number of particles is much higher than
,
so the emission is not totally
coherent. Since the number of particles is much higher than
![]() the emission is also not completely incoherent.
the emission is also not completely incoherent.
The radius of curvature of a relativistic particle is given by Eq. (8). The time width of a single pulse, as measured by a ground observer, depends on the Lorentz factor and the applied force as
![]() .
Some of the amplification effects mentioned in the section above will therefore not contribute to a total increase of emission.
.
Some of the amplification effects mentioned in the section above will therefore not contribute to a total increase of emission.
The total amplification of a radio pulse from a complete shower depends on the distribution of particles and the position of the ground observer and cannot be easily predicted. A detailed Monte Carlo simulation with realistic particle distribution will give more reliable results and is subject of further research. For now, we can regard the amplification factor as given in Eq. (20) as an upper limit for the observed amplification.
The shower particles ionize air molecules and leave behind free electrons and positive ions. The electrons can recombine with the ions in a time scale of seconds, but on a much
shorter time scale of a few tens of nanoseconds the electrons attach to oxygen molecules forming negative ions (Wilson 1957). When an electric field is present
the free electrons are accelerated producing a current pulse. Because of frequent collisions they gain a drift velocity of ![]() 100 m/s (Charman 1968).
The duration of the pulse depends on the attachment time
100 m/s (Charman 1968).
The duration of the pulse depends on the attachment time
![]() of electrons to oxygen molecules (which is a function
of the electron energy) and the angle under which the shower is viewed. In contrast to the radio emission from the shower electrons/positrons the radiation is not beamed forward
since the free electrons do not become relativistic.
The associated frequency up to which the emission is coherent is
of electrons to oxygen molecules (which is a function
of the electron energy) and the angle under which the shower is viewed. In contrast to the radio emission from the shower electrons/positrons the radiation is not beamed forward
since the free electrons do not become relativistic.
The associated frequency up to which the emission is coherent is ![]() 10 MHz for an observer in the direction of the shower (inverse of
10 MHz for an observer in the direction of the shower (inverse of
![]() ns).
ns).
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{6006fig4.eps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg77.gif) |
Figure 4: An EAS passes through a thunderstorm cloud emitting the usual geosynchrotron emission. The ionization electrons are accelerated inside the cloud. In this picture the radiation pattern is displayed as dipole radiation. The real pattern of a current pulse suffers from diffraction. |
| Open with DEXTER | |
When ionized electrons gain an energy of
![]() MeV they can ionize new molecules. If the electric field is strong enough to accelerate ionization
electrons to such energies a process called runaway breakdown (Gurevich et al. 1992) can occur. The critical field strength of
MeV they can ionize new molecules. If the electric field is strong enough to accelerate ionization
electrons to such energies a process called runaway breakdown (Gurevich et al. 1992) can occur. The critical field strength of
![]() kV/m, needed for this effect, is present only inside
thunderclouds. In the runaway breakdown process two generations of electrons are created: relativistic runaway electrons and slow thermal electrons, which can both contribute to the
radio signal. In Fig. 4 the contribution of the ionization electrons is schematically displayed. A simple current would produce a dipolar radiation field. The real radiation
pattern will be more complex because of the finite length of the current, the transverse width of the current and the existence of relativistic electrons.
The radiation pattern of the runaway breakdown is calculated in Gurevich et al. (2002) for a vertical shower and resembles that of a current pulse. The pulse amplitude is calculated to be several orders of magnitude higher than the geosynchrotron emission from the EAS.
kV/m, needed for this effect, is present only inside
thunderclouds. In the runaway breakdown process two generations of electrons are created: relativistic runaway electrons and slow thermal electrons, which can both contribute to the
radio signal. In Fig. 4 the contribution of the ionization electrons is schematically displayed. A simple current would produce a dipolar radiation field. The real radiation
pattern will be more complex because of the finite length of the current, the transverse width of the current and the existence of relativistic electrons.
The radiation pattern of the runaway breakdown is calculated in Gurevich et al. (2002) for a vertical shower and resembles that of a current pulse. The pulse amplitude is calculated to be several orders of magnitude higher than the geosynchrotron emission from the EAS.
Both mechanisms can be responsible for an amplification of the radio pulse from EAS. There are several ways to distinguish between them:
![\begin{figure}
\par\includegraphics[angle=270,width=6.8cm,clip]{6006fig5.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg83.gif) |
Figure 5: Layout of the LOPES experiment. Boxes indicate positions of KASCADE detector stations, filling up an area of 200 m by 200 m, and circles indicate antenna positions. |
| Open with DEXTER | |
In 2004, the LOPES array consisted of 10 dipole antennas, placed on the same location as the KASCADE experiment (Antoni et al. 2003) which provides triggers for
LOPES and records the muon and electron components of the EAS, used to reconstruct the energy of the primary and its direction.
Presently, LOPES measures only the polarization in the east-west plane. A layout of the experiment is shown in Fig. 5. Details about the experimental setup and the reduction of
the data can be found in Horneffer et al. (2004).
Additional information about the weather was obtained from a weather station at Karlsruhe (49![]() 02'N 8
02'N 8![]() 22'E) in the
archive of a free weather server
22'E) in the
archive of a free weather server![]() .
.
Four sets of data were selected from the 2004 database of LOPES:
To determine whether the radio peak is significant or not a cross-correlation beam was created. A combined signal of all LOPES antennas is reconstructed by temporal shifting of the pulses in accordance with the arrival direction in the KASCADE EAS data. The CC-beam is then calculated by adding correlations of all possible antenna pairs. The radio signal as a function of time is fitted with a Gaussian and is considered a detection when the fitted peak is larger than the background noise by 3 sigma. Since the amplitude calibration of the antennas is not yet completed, the pulse heights are given in arbitrary units. In the scope of this paper this is not a problem, since we investigate relative differences between sets of events.
Table 1: Applied cuts on selections.
![\begin{figure}
\par\includegraphics[angle=270,width=7.7cm,clip]{6006fig6.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg89.gif) |
Figure 6: Normalized pulse height of the events from selection 1 of Sect. 4, plotted against the geomagnetic angle. Excess pulse heights are defined as the normalized pulse height minus this fit. |
| Open with DEXTER | |
In Falcke et al. (2005) it was shown that the strength of the radio signal depends on the geomagnetic angle as
![]() when it is normalized with the (truncated) muon number. We show this correlation here, using the selection of
events that is the first set listed in Sect. 4 and applying the cuts listed in
Table 1 under "largest''. In Fig. 6 the normalized pulse heights are plotted against geomagnetic angle and a fit is made. The normalization is done by dividing
by the truncated muon number and multiplying by 106. In order to compare data points to this fit we will calculate the difference between the
points and the fit, not the ratio. The reason for this is that the ratio is a value that is normalized for geomagnetic value. For an amplified pulse caused by an electric field this normalization is not suitable. The total radiation can be seen as consisting of a geomagnetic
part (which scales with geomagnetic angle) and an electric field part (which does not scale with geomagnetic angle). We therefore define the pulse
height excess as the normalized pulse height minus the fit value (the difference between a data point and the fit in Fig. 6). The
error-weighed mean pulse height excess is calculated as:
when it is normalized with the (truncated) muon number. We show this correlation here, using the selection of
events that is the first set listed in Sect. 4 and applying the cuts listed in
Table 1 under "largest''. In Fig. 6 the normalized pulse heights are plotted against geomagnetic angle and a fit is made. The normalization is done by dividing
by the truncated muon number and multiplying by 106. In order to compare data points to this fit we will calculate the difference between the
points and the fit, not the ratio. The reason for this is that the ratio is a value that is normalized for geomagnetic value. For an amplified pulse caused by an electric field this normalization is not suitable. The total radiation can be seen as consisting of a geomagnetic
part (which scales with geomagnetic angle) and an electric field part (which does not scale with geomagnetic angle). We therefore define the pulse
height excess as the normalized pulse height minus the fit value (the difference between a data point and the fit in Fig. 6). The
error-weighed mean pulse height excess is calculated as:
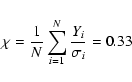 |
(21) |
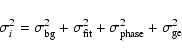 |
(22) |
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{6006fig7.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg100.gif) |
Figure 7: Pulse height excess is plotted against zenith angle for conservative cut. |
| Open with DEXTER | |
In Fig. 8 the excess pulse height for events of different weather selections are plotted against geomagnetic angle, where the distant cut is applied.
Figures 9-12 contain the same data points, now plotted against
respectively EAS energy as estimated by KASCADE, zenith angle, azimuth angle and mean distance of the antennas to the shower axis. There is a bias towards events with a positive pulse height excess, because these have a higher chance to be detected on a 3![]() level.
The mean pulse height excesses are listed in Table 2.
level.
The mean pulse height excesses are listed in Table 2.
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{6006fig8.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg101.gif) |
Figure 8: Pulse height excess is plotted against geomagnetic angle for distant cut. |
| Open with DEXTER | |
Table 2: Mean pulse height excess.
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{6006fig9.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg103.gif) |
Figure 9: Pulse height excess is plotted against shower energy for distant cut. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{6006fg10.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg104.gif) |
Figure 10: Pulse height excess is plotted against zenith angle for distant cut. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{6006fg11.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg105.gif) |
Figure 11: Pulse height excess is plotted against azimuth angle to the shower axis for distant cut. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{6006fg12.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg106.gif) |
Figure 12: Pulse height excess is plotted against mean distance to the shower axis for distant cut. KASCADE reconstruction of muon number becomes unreliable above 91 m. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.75cm,clip]{6006fg13.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg107.gif) |
Figure 13: Signals of ten LOPES antennas for a very radio bright event (event K in Fig. 15). (Field strength values are not calibrated.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.75cm,clip]{6006fg14.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg108.gif) |
Figure 14: Cross correlation beam of the ten signals of Fig. 13. The blue line is the cross correlated signal and the purple line is a Gaussian fit. (Field strength values are not calibrated.) |
| Open with DEXTER | |
Some events have extremely nice radio pulses like in Fig. 13. The signal-to-noise ratio in the cross-correlation beam (see Fig. 14) is much larger than for other events and the coherence is very high. A selection of these events was made by eye ("radio'' cut in Table 1) and the pulse height excesses are plotted in Fig. 15. All of these events have signal-to-noise ratios of >10. In the fair weather selection, 5 out of 9455 events had such strong radio emission (0.05%), in the nimbostratus selection 1 out of 2659 (0.04%) and in the thunderstorm selection 11 out of 3510 events (0.3%). The events that show a bright pulse because of the shower size appear near the bottom of the plot, because of the normalization with muon number. Bright pulses from showers with a relatively small muon number appear in the upper part of the plot. Only thunderstorm events are present in this region.
To further check the uniqueness of the high excess thunderstorm events, new selections of twin events were made from the LOPES database. For each thunderstorm event (A
through K in Fig. 15) a selection was made of events with approximately the same muon and electron number (both within 5%). The zenith angle and mean distance to the shower axis of these twin events is
not necessarily the same. The pulse height excesses, corrected for geomagnetic angle by dividing by the fit in Fig. 6, of all events are plotted in Fig. 17 by
group. For groups A through F the pulse height excess of the thunderstorm event is significantly larger than those of their twins, while in groups G through K the thunderstorm events have
excesses similar to those of their twins. The pulse heights are not normalized for mean distance to the shower core, since this dependence is not yet clearly established. Any reasonable
normalization (e.g. ![]()
![]() m)) will not change the appearance of Fig. 17 significantly, i.e. the thunderstorm events of groups A through F still have much
larger pulse height excesses than their twins.
m)) will not change the appearance of Fig. 17 significantly, i.e. the thunderstorm events of groups A through F still have much
larger pulse height excesses than their twins.
All the events that show a large excess in Fig. 15 have significantly larger pulse heights than their twins, while the low excess events have pulse heights similar to their twins. In group E two of the twin events have a large pulse height excess. Lightning maps and data from the weather station show that these events have also occured under thunderstorm conditions. (They were not in the original selection because no lightning strikes were visible in the dynamic spectrum during these thunderstorms.)
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{6006fg15.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg111.gif) |
Figure 15: Pulse height excess is plotted against the zenith angle for radio cut. The thunderstorm events are labelled A through K. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{6006fg16.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg112.gif) |
Figure 16: Pulse height excess is plotted against the geomagnetic angle for radio cut. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.55cm,clip]{6006fg17.ps}\end{figure}](/articles/aa/full/2007/20/aa6006-06/Timg113.gif) |
Figure 17: Pulse height excess, corrected for geomagnetic angle, for thunderstorm events A through K and their twins. In group E, two of the twin events are probably also thunderstorm events (see text for details). |
| Open with DEXTER | |
It is found that during thunderstorms the radio signal from EAS can be strongly amplified. Due to the low number of events for which the weather conditions could be reliably reconstructed, it was necessary to include events that were more than 91 m away from the array core. The KASCADE reconstruction of the muon number is not fully reliable for showers with large zenith angle or a distant core. When the estimation of the muon number is too low the calculated excess values will be too high. The conservative cut is the most reliable but leaves the fewest data points. The distant cut leaves more data points simply because there are many events with a distant core, not because they are detected more efficiently. Although the number of data points in the conservative cut is too low for statistics, it reflects the structure of the plots where the distant cut is applied. Large excesses for thunderstorm events were found, while the spread for fair weather and nimbostratus events is small.
Although some thunderstorm events show a large excess, others fall inside the same spread as fair weather and nimbostratus events. This can be because the selected time windows for the thunderstorm selection probably contains some time before and after the thunderstorms. Also, even when the thunderstorm is at its strongest, the amplification of the radio emission will depend on the local field distribution inside the cloud and the angle of the shower axis with the electric field.
During nimbostratus conditions no amplified radio emission was found. This could be because the electric field is too weak, or because these clouds have a smaller vertical extent than thunderstorm clouds and most showers reach their maximum above the nimbostratus cloud, where no large electric field is present.
Figures 9 through 12 show no correlations between the pulse height excess and other EAS parameters (primary energy, zenith angle, azimuth angle and distance to the shower axis), which indicates that the observed amplification is caused by the weather condition. Figure 16 and perhaps Fig. 8 seem to indicate that the amplified pulses cluster at low geomagnetic angles. The statistics are not good enough to make a statement on whether this feature is coincidental or not. More data is needed to study this possible correlation.
The twin events in Fig. 17 have the same muon and electron number, but other EAS parameters vary. The values in this plot are normalized with muon number and corrected for geomagnetic angle. The spread in pulse height excess within a group of twin events can be due to differences in zenith angle, azimuth angle or distance. The spread is, in groups A through F, small compared to the pulse height excess value of the thunderstorm event(s). When, in the future, a larger database of events is available a similar analysis can be done for twin events that also share the same zenith angle, azimuth angle and distance.
Radio pulses observed with LOPES typically have a width of 50-60 ns. Due to the 40-80 MHz band filtering any radio pulse shorter than that will appear broadened.
Broader radio pulses, however, do maintain more or less their original width.
The observed pulses of the amplified thunderstorm events have widths of ![]() 50 ns (see e.g. Fig. 14) like all other LOPES events, and are
probably not ionization current pulses, which would have widths of at least 100 ns (see Sect. 3.3)
We suspect therefore that it is the direct influence of the electric field on the shower electrons and positrons that is responsible for the amplification of the radio emission
during thunderstorm conditions.
50 ns (see e.g. Fig. 14) like all other LOPES events, and are
probably not ionization current pulses, which would have widths of at least 100 ns (see Sect. 3.3)
We suspect therefore that it is the direct influence of the electric field on the shower electrons and positrons that is responsible for the amplification of the radio emission
during thunderstorm conditions.
The small distances between the antennas does not allow an evaluation of the lateral distribution of the radio emission and LOPES only measures one polarization, so no additional tests can be done to identify the mechanism at the moment.
It is shown that during thunderstorm conditions the radio emission of EAS is largely amplified. There are two mechanisms which can explain this amplification:
acceleration radiation from the shower electrons and radiation from a current pulse of (runaway) ionization electrons.
The measured pulse widths (![]() 50 ns) suggest that the latter cannot be the observed mechanism.
To identify the mechanism with more certainty, more information about the
real pulse width, lateral distribution and polarization is needed. At the moment, the LOPES experiment is unable to provide this information, but with future
additions to the experiment, such as dual polarization, it will be possible to resolve this problem. Also, in the short future,
LOFAR stations will be able to help find the answer, since they occupy a larger ground area, operate in a wider frequency range and measure polarization.
50 ns) suggest that the latter cannot be the observed mechanism.
To identify the mechanism with more certainty, more information about the
real pulse width, lateral distribution and polarization is needed. At the moment, the LOPES experiment is unable to provide this information, but with future
additions to the experiment, such as dual polarization, it will be possible to resolve this problem. Also, in the short future,
LOFAR stations will be able to help find the answer, since they occupy a larger ground area, operate in a wider frequency range and measure polarization.
For both the LOPES and the LOFAR experiment it is advisable to keep detailed weather information, like cloud coverage, ground level electric field and the occurence of lightning strikes.
With LOFAR it will be possible to trace lightning activity by three dimensional imaging. This technique allows localization and mapping of lightning strikes, and possibly also thunderstorm processes emitting weaker radiation such as stepped leaders and high altitude lightning. This offers unique opportunities and promises significant further advances in this area.
Acknowledgements
LOPES was supported by the German Federal Ministry of Education and Research. The KASCADE-Grande experiment is supported by the German Federal Ministry of Education and Research, The MIUR of Italy, te Polish Ministry of Science and Higher Education and the Romanian Ministry of Education and Research (grant CEEX 05-D11-79/2005).